名思教育个性化辅导教案反比例 期中
《反比例》数学教案(经典15篇)

《反比例》数学教案(经典15篇)《反比例》数学教案1教学内容:《反比例的意义》是六年制小学数学(北师版)第十二册第二单元中的内容。
是在学过“正比例的意义”的基础上,让学生理解反比例的意义,并会判断两个量是否成反比例关系,加深对比例的理解。
学生分析:在此之前,他们学习了正比例的意义,对“相关联的量”、“成正比例的两个量的变化规律”、“如何判断两个量是否成正比例”已经有了认识,这为学习《反比例的意义》奠定了基础。
教学目标:1、知识与技能目标:使学生认识成反比例的量,理解反比例的意义,并学会判断两种相关联的量是否成反比例。
进一步培养学生观察、学析、综合和概括等能力。
初步渗透函数思想。
2、过程与方法:为学生营造一个经历知识产生过程的情境。
3、情感与态度目标:使学生在自主探索与合作交流中体验成功的乐趣,进一步增强学好数学的信心。
教学重点:理解反比例的意义。
教学难点:两种相关联的量的变化规律。
教学准备:学生准备:复习正比例关系,预习本节内容。
教师准备:投影片3张,每张有例题一个。
教学过程设计:一、谈话引入,激发兴趣。
1、谈话:通过最近一段时间的观察,我发现同学们越来越聪明了,会学数学了,这是因为同学们掌握了一定的数学学习的基本方法。
下面请回想一下,我们是怎样学习成正比例的量的?这节课我们用同样的学习方法来研究比例的另外一个规律。
2、导入:在实际生活中,存在着许多相关联的量,这些相关联的量之间有的是成正比例关系,有的成其他形式的关系,让我们一起来探究下面的问题。
二、创设情景引新:(出示:十二个小方块)师:同学们,这十二个小方块有几种排法?(生答后,老师板书下表的排列过程)每行个数行数师:请你观察上表中每行个数与行数成正比例关系吗?为什么?生:……师:这两种量这间有关系吗?有什么关系?这就是我们今天要研究的内容。
(出示课题:反比例的意义)三、合作自学探知1、学习例4。
(1)出示例4。
师:请同学们在小组内互相交流,并围绕这三个问题进行讨论,再选出一位组员作代表进行汇报。
反比例数学教案

反比例数学教案标题:反比例数学教案设计一、教学目标:1. 让学生理解并掌握反比例的概念,能通过实例进行判断。
2. 使学生能够应用反比例知识解决实际问题,提高其分析和解决问题的能力。
3. 培养学生的观察力、思考力和逻辑思维能力。
二、教学内容:1. 反比例的定义2. 反比例关系的表示方法3. 反比例在生活中的应用三、教学过程:(一) 导入新课教师可以以生活中的实例引入反比例的概念,如“你跑步的速度越快,完成一千米所需的时间就越短”,让学生初步感知反比例的关系。
(二) 新授课程1. 反比例的定义教师解释:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,那么我们就说这两种量成反比例关系。
例如:路程=速度×时间,当速度增大时,时间就会相应减少,反之亦然,但速度与时间的乘积(即路程)始终保持不变,因此,速度和时间成反比例关系。
2. 反比例关系的表示方法教师介绍:可以用y=k/x来表示反比例关系,其中k是常数,x和y分别是变量。
比如在上述例子中,我们可以设y为时间,x为速度,k为路程,那么就得到了y=k/x的表达式。
(三) 实践活动教师设计一些实践活动,让学生通过实践操作进一步理解和掌握反比例的概念。
例如,可以让学生分组做实验,测量不同高度的物体自由落体所需的时间,并记录数据,然后用图表的形式展示出来,最后引导学生发现,物体下落的高度和所需时间成反比例关系。
(四) 小结教师对本节课的主要内容进行总结,强调反比例的定义和表示方法,以及反比例在生活中的应用。
(五) 作业布置教师可以根据学生的学习情况,适当布置一些习题,以巩固和深化学生对反比例的理解和应用。
四、教学评价:通过对学生课堂表现和作业完成情况进行评价,了解学生对反比例的理解程度,及时调整教学策略。
五、教学反思:在教学过程中,教师要关注学生的学习状态,及时调整教学方法,确保每个学生都能理解和掌握反比例的概念。
《反比例》数学教案(精选19篇)

《反比例》数学教案《反比例》数学教案(精选19篇)作为一名老师,就有可能用到教案,教案是教学活动的依据,有着重要的地位。
教案应该怎么写才好呢?下面是小编精心整理的《反比例》数学教案,欢迎阅读,希望大家能够喜欢。
《反比例》数学教案篇1教学内容:教科书第22—24页反比例的意义,练习六的第4—6题。
教学目的:1.使学生理解反比例的意义.能够正确判断两种量是不是成反比例。
2.使学生进一步认识事物之间的相互联系和发展变化规律。
3.初步渗透函数思想。
教具准备:投影仪、投影片、小黑板。
教学过程:一、复习1.让学生说说什么是成正比例的量:2.用投影片出示下面的题:(1)下面各题中哪两种量成正比例?为什么?①笔记本单价一定,数量和总价:⑨汽车行驶速度一定.行驶的路程和时间。
②工作效率一定.’工作时间和工作总量。
①一袋大米的重量一定.吃了的和剩下的。
(2)说出每小时加工零件数、加工时间和加工零件总数三者间的数量关系。
在什么条件下,其中两种量成正比例?二、导入新课教师:如果加工零件总数一定。
每小时加工数和加工时间会成什么样的变化.关系怎样?就是我们这节课要学习的内容。
三、新课1.教学例4。
出示例4;丰机械厂加工一批机器零件。
每小时加工的数量和所需的加工时间如下表。
让学生观察这个表,然后每四人一组讨论下面的问题:(1)表中有哪两种量?(2)所需的加工时间怎样随着每小时加工的个数变化?(3)每两个相对应的数的乘积各是多少?学生分组讨论后集中发言。
然后每个小组选代表回答上面的问题。
随着学生的回答,教师板书如下:每小时加工数加工时间10 × 60 =600。
30 × 20 =600。
40 × 15 =600,“这个积600。
实际上是什么?”在“加工时间”后面板书:零件总数“积一定,就说明零件总数怎样?”在零件总数后面板书:(一定)“每小时加工数、加工时间和零件总数这三种量有什么关系呢?”学生回答后,教师小结:通过刚才的观察分析.我门可以看出。
六年级数学小升初一对一个性化辅导教案(1)

六年级数学小升初一对一个性化辅导教案(1)个性化教育辅导教案学科:数学任课老师:授课时间:姓名:XXX年级:六年级性别:男课题:比例的判定及应用题第一课知识点:比例列式、应用题列式。
教学考点:生产、浓度等比例问题的求解;简单应用题的求解。
目标能力:比例列式和应用题列式。
教学方法:讲解法,题法。
重点:生产、浓度等比例问题的求解;简单应用题的求解。
难点:课前作业完成情况:优□ 良□ 中□ 差□建议:教学过程:一、组比例与解比例:1.组比例:把比值相等的两个比用等号连接起来。
判断两个比能否组成比例的方法:1)一种方法是求出两个比的比值,若比值相等,就可以组成比例;2)另一种方法先假设两个比已组成比例,分别求出内,外项的积,若积相等,则能组成比例。
2.解比例:求比例中的未知项,叫做解比例。
练:1)3118X:2=X:52)X:5=0.46:4.6二、正反比例1.正比例和反比例的区别与联系不同点:成比例关系相同点:两种量相对应的两个数的比例一定特征:正比例关系:两种量相对应的两个数的积一定反比例关系:两种相关联的量,一种发生变化,另一种也随着变化关系式:3:5;9:10;10:11这三个比中能不能组成比例,把能组成的比例写出来。
3:5=9:159:1010:112.判断两种量是成正比例、反比例或不成比例的方法:方法一:1.找出两种相关联的量;2.根据两种相关联的量与第三个量的关系列出数量关系式。
方法二:根据数量关系式进行判断:看这第三个量是比值(商)还是积,若是比值(商)一定,就是成正比例的量;若是积一定,就是成反比例的量。
(↑↓箭头法)三、正反比例解应用题:例1:给一座房屋的地面铺方砖,用边长5分米的方砖需要2000块,若改成边长4分米的方砖需用多少块?分析:给房屋的地面铺方砖,如果方砖的面积越大,需要方砖的块数就越少,相对应的两个量是成反比例关系的,满足积一定。
解:设需用x块5×5×2000=4×4×xx=3125(块)答:需用3125块例2:水泵厂原计划每月生产120台水泵,半年完成任务,实际提前两个月完成,平均每月生产多少台水泵?分析:工作总量是不变的,如果工作效率越高,时间就越少,它们是成反比例,满足积一定。
反比例函数的图像与性质一个性化辅导讲义

课 题 反比函数的图像与性质(一)教学目标 1、会画反比例函数xk y =(k ≠0)的图像; 2、掌握反比例函数的图像和性质;3、根据反比例函数的图像求反比例函数的解析式。
教学内容考点一:反比函数的图像的性质及画法(重点)★一般地,反比函数x k y =(k 是常数,k ≠0)的图像有下面的性质: (1)反比函数xk y =(k 是常数,k ≠0)的图像是有两个分支组成的双曲线,当0k 时,图像在一、三象限;当0k 时,图像在二、四象限;(2)由于反比例函数中自变量x ≠0,函数y ≠0,所以,它的图像与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴;(3)反比函数xk y =(k 是常数,k ≠0)的图像关于直角坐标系的原点成中心对称。
★反比例函数图像的画法(描点法)第一步:列表第二步:描点第三步:连线例题1:画出反比函数x6-y x 6y ==与 的图像。
x... -6 -3 -2 -1 1 2 3 6 ... x 6y =... -1 -2 -3 -6 6 3 2 1 ...x 6-y =... 1 2 3 6 -6 -3 -2 -1 ...针对练习:画出反比例函数y=的图象,并根据图象回答下列问题:(1)根据图象指出x=﹣2时y 的值.(2)根据图象指出当﹣2<x <1时,y 的取值范围.(3)根据图象指出当﹣3<y <2时,x 的取值范围.解答:解:根据题意,作出y=的图象,(1)根据图象,过(﹣2,0)作与x轴垂直的直线,与抛物线相交,过交点向y轴引垂线y=﹣3,故当x=﹣2时y的值为﹣3,(2)根据图象,当﹣2<x<1时,可得y<﹣3或y>6.(3)同理,当﹣3<y<2时,x的取值范围是x<﹣2或x>3.例题2:一次函数y=﹣2x+1和反比例函数y=的大致图象是()A.B.C.D.分析:根据一次函数的性质,判断出直线经过的象限;再根据反比例函数的性质,判断出反比例所在的象限即可.解答:解:根据题意:一次函数y=﹣2x+1的图象过一、二、四象限;反比例函数y=过一、三象限.故选D.点评:此题主要考查了一次函数的图象及反比例函数的图象,重点是注意y=k1x+b中k1、b及yk2的取值.针对练习1、反比例函数y=的图象如图所示,则一次函数y=kx+k的图象大致是(D)A.B.C.D.2、反比例函数y=(k≠0)与一次函数y=kx+k(k≠0)在同一平面直角坐标系内的图象可能是(D)A.B.C.D.例题3:在平面直角坐标系中,反比例函数y=图象的两个分支分别在()A.第一、三象限B.第二、四象限C.第一、二象限D.第三、四象限分析:把a2﹣a+2配方并根据非负数的性质判断出是恒大于0的代数式,再根据反比例函数的性解答:解:a2﹣a+2,=a2﹣a+﹣+2,=(a﹣)2+,∵(a﹣)2≥0,∴(a﹣)2+>0,∴反比例函数图象的两个分支分别位于第一、三象限.故选A.点评:本题考查了反比例函数图象的性质,先判断出a2﹣a+2的正负情况是解题的关键,对于反数(k≠0),(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象四象限内.针对练习:1、如图是反比例函数的图象,那么实数m 的取值范围是 m >2 .例题4:如图,反比例函数y=的图象与经过原点的直线相交于点A 、B ,已知A 的坐标为(﹣2,1),则点B 的坐标为 (2,﹣1) .分析:反比例函数的图象是中心对称图形,则与经过原点的直线的两个交点一定关于原点对称解答:解:点A 与B 关于原点对称,则B 点的坐标为(2,﹣1). 点评:本题考查反比例函数图象的中心对称性,较为简单,容易掌握.针对练习 :如图,双曲线y=与直线y=mx 相交于A ,B 两点,B 点的坐标为(﹣2,﹣3),则A 点的坐标为 (2,3) .考点二:反比函数xk y =(k ≠0)中比例系数k 的几何意义(重点) 例题5:如图,点P 是反比例函数6y x=图象上的一点,则矩形PEOF 的面积是 .专题:计算题。
初中数学八年级期中复习教学案(3):反比例函数

期中复习教学案(3):反比例函数知识点: 函数xk y =(k ≠0)是双曲线.当k >0时,图象在第一、第三象限;在每个象限中,y 随x 的增大而减小;当k <0时,图象在第二、第四象限.在每个象限中,y 随x 的增大而增大. 典型例题例1 (2006年常德市)已知P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3)是反比例函数y=2x 的图象上的三点,且x 1<x 2<0<x 3,则y 1,y 2,y 3的大小关系是( )A .y 3<y 2<y 1B .y 1<y 2<y 3C .y 2<y 1<y 3D .y 2<y 3<y 1例2(2006·盐城市) 一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;(2)如果该司机匀速返回时,用了48小时,求返回时的速度.例3(2006·资阳市)已知一次函数y =x +m 与反比例函数2y x =的图象在第一象限的交点为P (x 0,2).(1) 求x 0及m 的值;(2) 求一次函数的图象与两坐标轴的交点坐标.例4(2006年烟台市)如图,一次函数y=kx+b 的图象与反比例函数y=m x图象交于A (-2,1),B (1,n )两点.(1)求反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围.例5(2006年十堰市)某校科技小组进行野外考察,途中遇到一片十几米宽的料泥地.为了完全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,•构筑成一条临时通道,木板对地面的压强P (Pa )是木板面积S (m 2)的反比例函数,•其图象如下图所示.(1)请直接写出一函数表达式和自变量取值范围;(2)当木板面积为0.2m 2时,压强是多少?(3)如果要求压强不超过6000Pa,木板的面积至少要多大?例6(2006年崇文区)在平面直角坐标系XOY中,直线y=-x绕点O顺时针旋转90°得到直线L,直线L与反比例函数y=kx的图象的一个交点为A(a,3),试确定反比例函数的解析式.例7某厂从2002年起开始投入技术改进资金,经技术改进后,•某产品的生产成本不断降(1能表示其变化规律,说明确定是这种函数而不是其他函数的理由,并求出它的解析式;(2)按照这种变化规律,若2006年已投入技改资金5万元.①预计生产成本每件比2005年降低多少万元?②如果打算在2006年把每件产品成本降低到3.2万元,则还需投入技改资金多少万元?(结果精确到0.01万元)。
八年级期中复习教案反比例函数
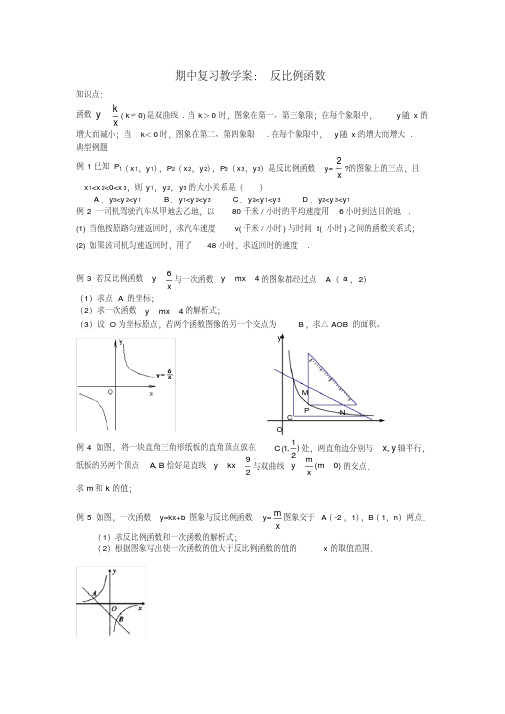
16. 如图,在直角坐标系 xOy 中,一次函数 y= k1x+ b 的图象与反比
例函数 y k 2 的图象交于 A(1, 4)、B(3, m)两点。 x
(1) 求一次函数的解析式; (2) 求△AOB 的面积。
17.在平面直角坐标系
xOy 中,反比例函数 y
k
的图象与
y
x
又与直线 y=ax+ 2 交于点 A(m, 3),试确定 a 的值。
(2) 若等腰梯形 ABCD的顶点 A、B在这个一次函数的图象上 , 顶点 C、D在这个反比例函数的图象
上, 且 BC∥ AD∥ y轴 ,A 、 B两点的横坐标分别是 a和a+2(a>0), 求 a的值 .
思路点拨:( 2)中,利用 A、 B在这个一次函数的图象上 , 设 A( a, 3 a— 7), B( a+2, 2
2
y= ?的图象上的三点,且
x
x 1<x 2<0<x 3,则 y 1, y 2, y3 的大小关系是( )
A . y3<y 2<y 1
B. y1<y 2<y 3
C. y 2<y 1<y 3
D . y2<y 3<y1
例 2 一司机驾驶汽车从甲地去乙地,以 80 千米 / 小时的平均速度用 6 小时到达目的地 .
例 5 如图,一次函数 y=kx+b 图象与反比例函数 y= m 图象交于 A( -2 ,1),B( 1,n)两点. x
( 1)求反比例函数和一次函数的解析式;
( 2)根据图象写出使一次函数的值大于反比例函数的值的
x 的取值范围.
例 6 在平面直角坐标系 XOY中,直线 y=-x 绕点 O顺时针旋转 90°得到直线
正比例和反比例的意义教案

正比例和反比例的意义教案一、教学目标1. 让学生理解正比例和反比例的概念。
2. 培养学生识别正比例和反比例关系的能力。
3. 引导学生运用正比例和反比例的知识解决实际问题。
二、教学内容1. 正比例的概念及特点2. 反比例的概念及特点3. 正比例和反比例的判断方法4. 正比例和反比例在实际中的应用三、教学重点与难点1. 教学重点:正比例和反比例的概念、特点及判断方法。
2. 教学难点:正比例和反比例在实际中的应用。
四、教学方法1. 采用直观演示法,让学生通过观察实例理解正比例和反比例的概念。
2. 运用对比法,分析正比例和反比例的特点及区别。
3. 采用实践操作法,让学生通过实际操作,掌握正比例和反比例的判断方法。
4. 运用案例教学法,引导学生运用正比例和反比例的知识解决实际问题。
五、教学过程1. 导入:通过生活中的实例,如身高与年龄的关系,引入正比例和反比例的概念。
2. 讲解:讲解正比例和反比例的定义、特点及判断方法。
3. 实践操作:让学生进行实际操作,巩固正比例和反比例的判断方法。
4. 应用拓展:引导学生运用正比例和反比例的知识解决实际问题,如购物时如何选择优惠方案等。
5. 总结:对本节课的内容进行总结,强调正比例和反比例的概念及应用。
教案示例:一、教学目标1. 让学生理解正比例和反比例的概念。
2. 培养学生识别正比例和反比例关系的能力。
3. 引导学生运用正比例和反比例的知识解决实际问题。
二、教学内容1. 正比例的概念及特点2. 反比例的概念及特点3. 正比例和反比例的判断方法4. 正比例和反比例在实际中的应用三、教学重点与难点1. 教学重点:正比例和反比例的概念、特点及判断方法。
2. 教学难点:正比例和反比例在实际中的应用。
四、教学方法1. 采用直观演示法,让学生通过观察实例理解正比例和反比例的概念。
2. 运用对比法,分析正比例和反比例的特点及区别。
3. 采用实践操作法,让学生通过实际操作,掌握正比例和反比例的判断方法。
《反比例》(教案)

《反比例》(教案)反比例是小学数学中的一个较为重要的概念。
它是指两个量的乘积的值为一个定值,其中一个量变大,另一个量就会变小。
本教案将为一些小学生介绍反比例的概念及其基本求解方法。
一、教学目标1.认识反比例的概念和特点。
2.学会运用公式求解反比例相关问题。
3.培养学生分析和解决问题的能力。
二、教学内容1.反比例的概念和特点。
2.反比例的求解方法。
三、教学重难点1.理解反比例的概念,区分反比例与比例的概念。
2.掌握反比例的求解方法。
四、教学过程1.导入给学生出示两个数列:6, 3和8, 2,请问它们有什么相同点和不同点?引导学生思考,说出这两个数列是反比例数列。
2.概念讲解通过口头叙述和图表的方式向学生讲解什么叫反比例,以及反比例的特点。
可以演示一下,若两个量之间成反比例,则它们的乘积恒定。
比如,若A与B成反比例,则A×B=常数。
3.方程求解对于解反比例方程,需要比较多的数学运算。
可以通过简单的例子来讲解,比如图书馆中的人数与书架数。
当书架数增加时,每个书架上分配的图书个数也会减少,反之亦然。
4.练习请学生完成反比例的练习,以帮助他们巩固所学的概念和方法。
五、教学效果的展示采用小组合作的方式,请每个小组分享自己的反比例解题过程。
其中,展示的过程中,学生要说出自己掌握的学科知识和解决问题的技巧。
六、作业1.阅读相应的课外书籍,巩固所学知识。
2.自主完成反比例练习,巩固所学的基本知识和方法。
3.在进行数学学习、解决问题的过程中,学会发现和运用反比例这一数学概念。
七、教学总结本次教学通过让学生了解反比例的概念和特点,以及如何使用反比例运算方法来解决问题,能够加深对反比例的认识,提高解决数学问题的能力,增强学生对数学知识的掌握力。
八、教学扩展在进一步了解反比例的概念和公式的运用过程中,可以让学生分析实际问题中的各种情况,并使用反比例的概念来解决问题。
例如,如果问题中涉及到速度和时间的关系,那么就可以尝试使用反比例来解决。
反比例教学设计

反比例教学设计教学内容:反比例。
教学目标:1.使学生理解反比例的意义,能正确地判断两种相关联的量是不是成反比例的量。
2.让学生经历反比例意义的探究过程,体验观察比较、推理、归纳的学习方法。
重点难点:引导学生总结出成反比例的量的特点,进而抽象概括出反比例的关系式。
利用反比例的意义,正确判断两个量是否成反比例。
教学准备:多媒体课件。
复习导入:1.让学生说说什么是正比例,然后用投影出示下面的题。
下面各题中哪两种量成正比例?为什么?(1)每公顷产量一定,总产量和公顷数。
(2)一袋大米的重量一定,吃了的和剩下的。
(3)修房屋时,粉刷的面积和所需涂料的数量。
2.说出每小时加工零件数、加工零件总数和加工时间三者之间的关系。
在什么条件下,其中两种量成正比例?教师:如果加工零件总数一定,每小时加工数和加工时间会成什么变化?关系怎样?这就是我们这节课要学习的内容。
新课讲授1.教学例2。
创设情境。
教师:把相同体积的水倒入底面积不同的杯子,高度会怎样变化?出示教材第47页例2的情境图和表格。
请学生认真观察表中数据的变化情况,组织学生分小组讨论:(1)水的高度和底面积变化有关系吗?(2)水的高度是怎样随着底面积变化的?(3)水的高度和底面积的变化有什么规律?学生不难发现:底面积越大,水的高度越低;底面积越小,水的高度越高,而且高度和底面积的乘积(水的体积)一定。
教师板书配合说明这一规律:30×10=20×15=15×20=……=300教师根据学生的汇报说明:高度和底面积有这样的变化关系,我们就说高度和底面积成反比例的关系,高度和底面积叫做成反比例的量。
2.归纳反比例的意义。
组织学生小组内讨论:反比例的意义是什么?教师总结:像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
3.用字母表示。
如果用字母x和y表示两种相关联的量,用k表示它们的乘积(一定),反比例关系的式子怎么表示?x×y=k(一定)4.师:生活中还有哪些成反比例的量?在教师的引导下,学生举例说明。
小学六年级个性化辅导方案:正比例和反比例、比例尺

个性化教学辅导教案1.解决问题。
哥哥买来84个红气球,红气球和黄气球的个数的比是7:5,黄气球有多少个?(用比例解)2.列比例计算我能行。
(1)与的比等于x比,求x。
(2)一个比例的两个内项分别是8和x,两个外项分别是4和16,求x。
3.解方程:= 6×3﹣1.8x=7.2 x﹣x=9.45.1.下面各题中哪两种量成正比例?为什么?(1)每公顷产量一定,总产量和公顷数。
(2)一袋大米的重量一定,吃了的和剩下的。
(3)修房屋时,粉刷的面积和所需涂料的数量。
2.说出每小时加工零件数、加工零件总数和加工时间三者之间的关系。
在什么条件下,其中两种量成正比例?3.小明家要搬新家了,他特别高兴。
可是,他很担心新家离学校太远。
小明的爸爸按比例为他画了一幅图,并且告诉他旧家与学校之间的距离是900m。
小明量得新家到学校的图上距离是7cm,旧家到学校的距离是3cm。
同学们,你们能帮助小明算算新家与学校之间的距离吗?4.填空。
一个长方形长3dm,宽2dm,按3∶1放大,放大后的长是()dm,宽是()dm,放大后的长方形与原长方形的周长比是( ∶ ),面积比是(∶)。
学科原因:1、学生不理解正比例的意义,无法正确判断成正比例的量。
2、学生不理解反比例的意义,不能正确地判断两种相关联的量是不是成反比例的量。
3、不理解比例尺的含义,不会求一幅图的比例尺。
4、无法根据比例尺求图上距离或实际距离。
5、不能按要求将图形放大或缩小。
学生原因:1.成正比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。
用字母表示y/x=k (一定)2.成反比例的量:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。
用字母表示x×y=k (一定)3.比例尺:图上距离:实际距离=比例尺要求会求比例尺;已知图上距离和比例尺求实际距离;已知实际距离和比例尺求图上距离。
《反比例》教学设计

《反比例》教学设计教学目标:1.结合丰硕的生活实例,熟悉反比例。
2.能按照反比例的意义,判断两个相关的量是不是反比例关系。
3.利用反比例解决一些简单的生活问题,感受反比例关系在生活中的普遍应用。
教学重点:反比例的意义教学难点:正确判断两种量是不是成反比例。
教学进程:一、温习旧知1.说说正比例的意义是什么?2.判断两种量是不是成正比例关系的关键是什么?3.判断下列各题中的两种量是不是成正比例。
(1)笔记本的单价必然,数量和总价。
(2)汽车行驶的速度必然,行驶的路程和时间。
(3)一袋大米的质量必然,吃了的和剩下的。
(4)工作效率必然,工作总量和工作时间。
二、创设情境,揭露学习目标。
1.老师这里有100元钱,我想把它换成零钱。
若是换成面额为1元的,能换多少张,若是都换成面额为2元的能换多少张?(学生说,师板书)师:还可以都换成那种面值的?能换多少张?师:从这个进程里,你有什么发现,或你有什么要说的?2.今天,咱们就用适才的思想和方式去学习另一种有趣的现象---反比例(板书)3.下面先让咱们来看看今天的学习目标:(1)归纳出反比例的意义。
(2)正确判断两种量是不是是反比例。
三、新课探讨1.自学探讨(出示例题1)(1)小组合作,把表格填写完整,并观察每一个表格中是那两个转变的量?(2)这两个量是如何转变的?转变的进程中什么没变?2.自学展示3.课件出示例题2(1)表中有哪两种量?时间是如何随着速度的转变和转变的?每两个相对应数的乘积是多少?你发现了什么?你能写出关系式吗?(2)总结并展示:速度和时间两个量,速度转变,所用的时间也随着转变且速度与时间的伺机(也就是路程)必然,咱们就说速度和时间成反比例。
(3)例1中那个表中的数据是正比例关系呢?(4)师总结板书:两种相关联的量,其中一种量在转变,另一种量也随着转变,而且这两种量中相对应的两个数的乘积是必然的。
像这样的两种相关联的量就成反比例。
用字母表示其关系式为:xy=k(必然)要判断两个量是不是成反比例,关键是什么?四、巩固应用1.照顾开头的例子(课件出示)a.把表格补充完整。
正比例和反比例
掌握情况
海到无边天作岸,山高绝顶我为峰
1
联的量,用k表示它们的比值,正比例关系可以用这样的式子来表示:
y = K(一定) 。 x
2、用“描点法”可以得到正比例的图像,正比例的图像是一条直线。对照图像,能根据一种量的值,估计另一种 量相对应的值。
典型例题
例 1、 (正比例的意义)一列火车行驶的时间和路程如下表。这两种量有什么关系?
2
名思教育-----我们的成功不是偶然!
例 2、 (判断是否成正比例) 练习本的单价一定,买练习本的数量和总价是不是成正比例?为什么? 分析与解:根据正比例的意义,看两个变量的比值是否一定,如果两个变量的比值一定,那么这两个变量就成正 比例,反之,则不成正比例。 买练习本的数量和总价是两种相关联的量,它们与练习本的单价有下面的关系:
120 240 360 = 120, = 120, = 120„„这个比值就是火车的行 1 2 3
路程 = 速度(一定) 。 时间
具备了这两个条件,我们就可以得到结论:行驶的路程和时间成正比例关系;行驶的路程和时间成正 比例的量。
点评:判断两种量是不是成正比例,分三步:一看它们是不是相关联的两种量;二是看一种量变化,另一种量是 不是也随着变化;满足了前面两个条件,再看它们的比值是否一定。不要省去任何一步。如果用字母x和 y分别表示两种相关联的量,用k表示它们的比值,正比例关系可以用这样的式子来表示:
名思教育-----我们的成功不是偶然!
同学个性化教学设计
年 级: 教 师: 日 期: 科 目: 时 段: 班 主 任:
课题
正比例和反比例例题讲解分析
1、使学生结合实际情境认识成正比例和反比例的量,能根据正、反比例的意义判断两种相关联 的量是否成正比例或反比例。 2、使学生初步认识正比例的图像是一条直线,能利用给出的具有正比例关系的数据在方格纸上
反比例教案

反比例教案一、教学目标:1. 知识与技能:了解反比例的概念,掌握反比例函数的基本性质和解题方法。
2. 过程与方法:培养学生的观察和归纳能力,培养学生的逻辑思维和分析问题的能力。
3. 情感态度与价值观:培养学生的主动学习、合作学习和创新意识。
二、教学重点与难点:1. 重点:了解反比例的概念,掌握反比例函数的基本性质和解题方法。
2. 难点:学会在实际问题中应用反比例的知识解决问题。
三、教学过程:1. 导入(10分钟)教师出示一对生活中常见的反比例关系,例如:A工人一天能挖20立方米土,B工人一天能挖30立方米土,问两个工人一起工作一天可以挖多少立方米土?引导学生思考两个工人一起工作与分开工作的情况有什么不同。
教师出示反比例的图像,引导学生观察图像的变化。
2. 探究(20分钟)教师引导学生通过观察和实验总结反比例的概念和特点,帮助学生理解反比例的性质。
学生根据实验结果,总结出反比例函数 y=k/x 的定义和性质,并解释为什么是反比例。
3. 讲解(20分钟)教师讲解反比例函数的基本形式 y=k/x,并引导学生掌握反比例函数的性质,例如:当x>0时,y>0;当x>0时,y递减;当x>0时,y趋于无穷大;当x>0时,y通式为y=k/x。
教师通过例题讲解反比例函数的解题方法,例如:给出一组x和y的值,求y与x的关系;给出y和k的值,求x与k的关系;给出x和k的值,求y和k的关系。
4. 拓展运用(20分钟)教师出示一些实际问题,引导学生运用反比例的知识解决问题。
例如:小明每小时能走5公里,他打算今天走50公里,需要走多少个小时?现在有一块土地,两个农民合作耕种可以耕种10天,其中一个农民独立耕种需要耕种25天,问另一个农民独立耕种需要耕种多少天?5. 总结归纳(10分钟)教师引导学生归纳总结反比例的概念和性质,培养学生的思维能力和归纳能力。
四、课堂作业:1. 完成课后习题集上的相关练习。
《反比例》精品教案

教学过程
一、复习导入
同学们,上面我们复习了成正比例的量,我们知道两种相关联的量的数值的比一定的时候,这两种量是成正比例的量。今天我们来共同学习成另外一种关系的两种相关联的量。
(板书课题:反比例)
二、新课讲授
1.探究反比例的意义,理解成反比例的量。
出示教学例2课件
学生思考,尝试回答问题。
生1:表中有杯子的底面积和水的高度这两种量。
生2:从表中可以看出:水的高度随着杯子的底面积的变大而不断变小,这两种量是相关联的两种量。
生3:我来回答(3),相对应的杯子的底面积与水的高度的乘积分别是:10×30=300,15×20=300,20×15=300,30×10=300,60×5=300,…
(板书反比例的意义)
3.用字母表示反比例关系:xy=k(一定)。(板书)
4.生活中成反比例关系的例子。
师:我们购物时经常用到的数量关系是什么?
生:数量×单价=总价。
师:根据这一关系,和刚才学到的反比例意义,说出你经历的成反比例关系的购物事件吧!
生1:一天,我去文具店发现钢笔的价格有0.5元、1.00元、2.00元、5.00元的,我一共拿了10.00元钱。如果只买一种,那么数量应是:20支、10支、5支、2支,这时,单价和数量就成反比例,因为总价10.00元是一定的。
底面积×高=体积
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
用字母表示:xy=k(一定)
教学反思
反比例的知识比较抽象、难懂,历来都是学生怕学的内容。为了用最常见最熟悉的事,理解反比例关系,我从身边的现实生活中发掘素材,让学生从生活中发现数学问题,从而引入学习目标。学生展开热烈的讨论,激发了学习数学的兴趣,也激起了他们参与的积极性和主动性,为自主探究新知创设了背景。学生通过对正、反比例的例题进行比较,归纳出成反比例的量的几个特点,再以此和正比例做比较,猜想出反比例的意义。最后学生经过验证,得出反比例的意义和关系式,既达到了本课的知识目标,又提高了学生的推理能力。总之,在本课的教学活动中,让学生寻找生活中的反比例关系,我想是有一点难度的,所以为了降低学生学习的难度,特意设计了教师引路的方法,使学生少走弯路,快速达到学习目的,并从中获得成功的喜悦。
《反比例》教案

《反比例》教案教学内容:成正比例的量教学目标:1.使学生理解正比例的意义,会正确判断成正比例的量。
2.使学生了解表示成正比例的量的图像特征,并能根据图像解决有关简单问题。
教学重点:正比例的意义。
教学难点:正确判断两个量是否成正比例的关系。
教学过程:一揭示课题1.在现实生活中,我们常常遇到两种相关联的量的变化情况,其中一种量变化,另一种量也随着变化,你以举出一些这样的例子吗?在教师的此导下,学生会举出一些简单的例子,如:(1)班级人数多了,课桌椅的数量也变多了;人数少了,课桌椅也少了。
(2)送来的牛奶包数多了,牛奶的总质量也多了;包数少了,总质量也少了。
(3)上学时,去的速度快了,时间用少了;速度慢了,时间用多了。
(4)排队时,每行人数少了,行数就多了;每行人数多了。
行数就少了。
2.这种变化的量有什么规律?存在什么关系呢?今天,我们首先来学习成正比例的量。
板书:成正比例的量二探索新知1.教学例 1(1)出示例题情境图。
问:你看到了什么?生:杯子是相同的。
杯中水的高度不同,水的体积也不同,高度越高体积越大;高度越低,体积越小。
(2)出示表格。
高度/㎝24681012体积/㎝350100150200250300底面积/㎝2问:你有什么发现?学生不难发现:杯子的底面积不变,是25㎝2。
板书:教师:体积与高度的比值一定。
(2)说明正比例的意义。
①在这一基础上,教师明确说明正比例的意义。
因为杯子的底面积一定,所以水的体积随着高度的变化而变化。
水的高度增加,体积也相应增加,水的高度降低,体积也相应减少,而且水的体积和高度的比值一定。
板书出示:像这样,两种相关联的量,一种量变化,另一种子量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种理就叫做成正比例的量,它们的关系叫做正比例关系。
②学生读一读,说一说你是怎么理解正比例关系的。
要求学生把握三个要素:第一,两种相关联的量;第二,其中一个量增加,另一个量也增加;一个量减少,另一个量也减少。
《反比例》(教案)2023-2024学年数学六年级下册

《反比例》(教案)2023-2024学年数学六年级下册一、教学目标1. 让学生理解反比例的概念,掌握反比例的判定方法,并能运用反比例解决实际问题。
2. 培养学生观察、分析、归纳的能力,提高学生的数学思维水平。
3. 培养学生合作交流、积极参与的态度,增强学生的团队协作意识。
二、教学内容1. 反比例的概念2. 反比例的判定方法3. 反比例的应用三、教学重点与难点1. 教学重点:反比例的概念和判定方法。
2. 教学难点:反比例的应用,特别是在实际问题中的运用。
四、教具与学具准备1. 教具:PPT课件、黑板、粉笔、教学视频等。
2. 学具:练习本、草稿纸、计算器等。
五、教学过程1. 导入:通过生活中的实例,引出反比例的概念,激发学生的学习兴趣。
2. 新课:讲解反比例的定义、判定方法,并通过例题进行演示。
3. 练习:让学生独立完成练习题,巩固所学知识。
4. 应用:讲解反比例在实际问题中的应用,让学生学会如何运用反比例解决问题。
5. 总结:对本节课所学内容进行总结,强调重点和难点。
6. 作业布置:布置课后作业,巩固所学知识。
六、板书设计1. 《反比例》2. 目录:教学目标、教学内容、教学重点与难点、教具与学具准备、教学过程、板书设计、作业设计、课后反思3. 正文:根据教学过程,逐步呈现反比例的概念、判定方法、应用等。
七、作业设计1. 基础题:让学生巩固反比例的基本概念和判定方法。
2. 提高题:让学生运用反比例解决实际问题,提高学生的应用能力。
3. 思考题:引导学生深入思考反比例的本质,培养学生的创新思维。
八、课后反思1. 教师要关注学生对反比例概念的理解程度,及时调整教学策略。
2. 在教学过程中,要注意引导学生积极参与,培养学生的合作意识。
3. 课后要关注学生的作业完成情况,及时解答学生的疑问,提高教学效果。
总之,本节课通过讲解反比例的概念、判定方法以及在实际问题中的应用,使学生掌握了反比例的知识,提高了学生的数学思维水平和解决问题的能力。
《反比例》教案

《反比例》教案《反比例》教案《反比例》教案1教学目标:1、理解反比例的意义。
2、能根据反比例的意义,正确判断两种量是否成反比例。
3、培养学生的抽象概括能力和判断推理能力。
教学重点:引导学生理解反比例的意义。
教学难点:利用反比例的意义,正确判断两种量是否成反比例。
教学过程:一、复习铺垫1、成正比例的量有什么特征?2、下表中的两种量是不是成正比例?为什么?二、自主探究(一)教学例11.出示例1,提出观察思考要求:从表中你发现了什么?这个表同复习的表相比,有什么不同?(1)表中的两种量是每小时加工的数量和所需的加工时间。
教师板书:每小时加工数和加工时间(2)每小时加工的数量扩大,所需的加工时间反而缩小;每小时加工的数量缩小,所需的加工时间反而扩大。
教师追问:这是两种相关联的量吗?为什么?(3)每两个相对应的数的乘积都是600.2.这个600实际上就是什么?每小时加工数、加工时间和零件总数,怎样用式子表示它们之间的关系?教师板书:零件总数每小时加工数×加工时间=零件总数3.小结通过刚才的研究,我们知道,每小时加工数和加工时间是两种相关联的量,每小时加工数变化,加工时间也随着变化,每小时加工数乘以加工时间等于零件总数,这里的零件总数是一定的。
(二)教学例21.出示例2,根据题意,学生口述填表。
2.教师提问:(1)表中有哪两种量?是相关联的量吗?教师板书:每本张数和装订本数(2)装订的.本数是怎样随着每本的张数变化的?(3)表中的两种量有什么变化规律?(三)比较例1和例2,概括反比例的意义。
1.请你比较例1和例2,它们有什么相同点?(1)都有两种相关联的量。
(2)都是一种量变化,另一种量也随着变化。
(3)都是两种量中相对应的两个数的积一定。
2.教师小结像这样的两种量,我们就把它们叫做成反比例的量,它们的关系叫做反比例关系。
3.如果用字母x和y表示两种相关联的量,用k表示它们的积一定,反比例关系可以用一个什么样的式子表示?教师板书:xy=k(一定)三、课堂小结1、这节课我们学习了成反比例的量,知道了什么样的两种量是成反比例的量,也学会了怎样判断两种量是不是成反比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
名思教育个性化辅导教案
学科:授课老师:授课时间:年月日时分——时分
学生姓
名
年级课时
课题及
教学内
容
教学目
标
教学
重、难
点
环节教师授课过程反
思
主要知识考点一已知面积,求反比例函数的解析式(或比例系数k)
【例1】如图,直线OA与反比例函数的图象在第一象限交
于A点,AB⊥x轴于点B,△OAB的面积为2,则k=.
分析:由图象知,k>0,由结论及已知条件得∴k=4
(2)如图,已知双曲线()经过矩形的边的
中点,且四边形的面积为2,则.
分析:连结OB,∵E、F分别为AB、BC的中点
∴
而由四边形OEBF的面积为2得解得k=2
评注:第①小题中由图形所在象限可确定k>0,应用结论可直接求k值。
第②小题首先应用三角形面积的计算方法分析得出四个三角形面积相等,列出含k的方程求k值。
如图,矩形ABOD的顶点A是函数与函数在第二象限的交点,轴于B,轴于D,且矩形ABOD的面积为3.
(1)求两函数的解析式.
(2)求两函数的交点A、C的坐标.
(3)若点P是y轴上一动点,且,求点P的坐标.
解:(1)由图象知k<0,由结论及已知条件得-k=3∴
∴反比例函数的解析式为,一次函数的解
析式为
(2)由,解得,
∴点A、C的坐标分别为(,3),(3,)
(3)设点P的坐标为(0,m)直线与y轴的交点坐标为M(0,2)
∵
∴∣PM∣=,即∣m-2∣=,∴或,∴点P的坐标为(0,)或(0,)
评注:依据图象及结论求k值是本题的关键,只有求出k代值,才能通过解方程组求A、C两点的坐标,然后才能解决第③小问。
考点二已知反比例函数解析式,求图形的面积
【例2】(1)在反比例函数的图象中,阴影部分的面积不等于4的是( B )
分析:因为过原点的直线与双曲线交点关于原点对称,故B、C、D的面积易求。
对于A:S=4,对
于B:阴影中所含的三个小直角三角形面积相等,故S=,对于C:S=4,对于D:S=4 故选(B)
(2)(2009年牡丹江市)如图,点、是双曲线上的点,分别经过
、两点向轴、轴作垂线段,若则.
分析:由结论知,∴S1+1=S2+1=3 ∴S1=S2=2 S1+S2=4
评注:过双曲线上作坐标轴垂线所围成的矩形的面积可直接由结论求解,过程简单。
考点三利用点的坐标及面积公式求面积
【例3】如图,已知,是一次函数的图像和反比例函数
的图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线与轴的交点的坐标及三角形的面积.
解:(1)在上.反比例函数的解析式为:
.
点在上
经过,,
解之得一次函数的解析式为:
(2)是直线与轴的交点
当时,点
如图,直线与反比例函数(<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标
为-4.
(1)试确定反比例函数的关系式;
(2)求△AOC的面积.
.解:(1)∵点A(-2,4)在反比例函数图象上
∴k=-8 ∴反比例函数解析式为y=
(2)∵B点的横坐标为-4,∴纵坐标为y=2 ∴B(-4,2)
∵点A(-2,4)、点B(-4,2)在直线y=kx+b上
∴4=-2k+b 且2=-4k+b解得k=1 b=6
∴直线AB为y=x+6与x轴的交点坐标C(-6,0)∴S==12
评注:对于例4、例5类型的题目,其解题方法基本上都是分
三步:先由条件求函数解析式,再通过解方程组求交点坐标,
最后由面积公式计算面积。
难度属中档题。
考点四、利用对称性求反比例函数有关的面积
问题
【例4】已知, A、B、C、D、E是反比例函数(x>0)图
象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是(用含π的代数式表示)分析:∵x,y为正整数,∴x=1,2,4,8,16
即A、B、C、D、E五个点的坐标为
(1,16),(2,8),(4,4),(8,2),(16,1),因五个橄榄形关于y=x对称,故有
S==13π-26
如图,⊙A 和⊙B 都与x 轴和y 轴相切,圆心A 和圆心B 都在反比例函数
的图象上,则图中阴影部分的面积等于 .
分析:因为圆心A 中的非阴影部分与圆B 中的阴影部分为对称图形,圆A 中的阴影部分与圆B 中的非阴影部分也关于原点对称,故两阴影部分面积的和等于圆的面积。
设圆A 的圆心A 的坐标为(x,y),由图可知,x=y
∵A 点在反比例函数图象上,∴ 解得x=1从而所求面积
为π
评注:对于较复杂的图形面积计算问题,先应观察图形的特征,若具有对称特征,则应用对称关系可以简化解题过程。
一、 巩固练习: (1) 选择题
1、反比例函数x
k
y =
的图象如图所示,点M 是该函数图象上一点,MN 垂直于x 轴,垂足是点N ,如果S △MON =2,则k 的值为( )D (A)2 (B)-2 (C)4 (D)-4
2、(四川绵阳)若A (a 1,b 1),B (a 2,b 2)是反比例函数x
y 2
-
=图象上的两个点,且a 1<a 2,则b 1与b 2的大小关系是( )D
A .b 1<b 2
B .b 1 = b 2
C .b 1>b 2
D .大小不确定 3、(福建龙岩)函数y x m =+与(0)m
y m x
=≠在同一坐标系内的图象可以是( )B
(2) 填空题
4、(湖北潜江)如图,反比例函数x
y 5
=
的图象与直线)0(>=k kx y 相交于B 两点,AC ∥y 轴,BC ∥x 轴,则△ABC 的面积等于 个面积单位. 10
(3)解答题
x
y O A .
x
y
O
B .
x
y
O C .
x
y
O D .
5、如图 所示,反比例函数y k
x
=
的图象经过点()
A b -3,,过点A 作A
B 垂直x 轴于点B ,△AOB 的面积为3。
(1)求k 和b 的值; (2)若一次函数y a x =+1
的图象经过点A ,并且与x 轴相交于点M ,求AB :OM 的值。
分析:以面积为突破口,可求出A 点纵坐标b 和系数k ,结合A 点的双重特性(A 点既在直线上,又在反比例函数图象上)求解相应问题。
解:(1)∵AB ⊥BO ,A 点坐标为()
-3,b ∴·即·∴又∵点在双曲线上
∴△S AB BO b b A y k
x
k AOB ==-====⨯-=-1
2
3
1
2
332
2323
||()
(2)∵点A 在直线y a x =+1上 ∴231=-+a ∴a =-33∴y x =-+3
3
1
当y=0时,x =3所以M 点的坐标为
(
)
30,∴::AB OM =23
点评:纵观近年来的中考试题,关于反比例函数的综合题大多是与一次函数相结合,做题时
常利用交点的双重特性来构造方程(组)解决问题。
6.如图,一次函数y=kx+b 的图象与反比例函数y=
m
x
的图象交于A (-2,1),B (•1,n )两点. (1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围.
7.已知:如图,函数y=-x+2的图象与x 轴、y 轴分别交于点A 、B ,一直线L 经过点C (1,0)将
△AOB 的面积分成相等的两部分. (1)求直线L 的函数解析式;
(2)若直线L 将△AOB 的面积分成1:3两部分,求直线L 的函数解析式.
二、拓展训练
已知:如图,正比例函数的图象与反比例函数的图
象交于点
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当取何值时,反比例函数
的值大于正比例函数的值?
(3)是反比例函数图象上的一动点,其中过
点作直线轴,交轴于点;过点作直线
轴交轴于点,交直线于点.当四边形的面积
为6时,请判断线段与的大小关系,并说明理由.
分析:(1)由点A(3,2)在两函数图象上,可求得
k=6,a=,正比例函数为,反比例函数为
(2)0<x<3
(3)设D点坐标为(3,t),则M点坐标为(
由四边形OADM的面积为6得3+6+3=3t 解得t=4
故点M为(D点为(3,4)从而M点为BD中点,BM=DM
评注:第①小问考查求正比例和反比例函数解析式的基本方法,第②小问考查分析图形的能力,第③小问考查反比例函数中的面积的计算问题。
三个小问题层次分明,有梯度,是一道较好的中考题目
学生签字: 教研组长签字:校长签字:。
