实验二 离散信道及其容量
实验二 离散信道及其容量

实验二 离散信道及其容量一、[实验目的]1、理解离散信道容量的内涵;2、掌握求二元对称信道(BSC )互信息量和容量的设计方法;3、掌握二元扩展信道的设计方法并会求其平均互信息量。
二、[实验环境]windows XP,MATLAB 7三、[实验原理]若某信道输入的是N 维序列x ,其概率分布为q(x ),输出是N 维序列y ,则平均互信息量记为I(X ;Y ),该信道的信道容量C 定义为()max (X;Y)q x C I =。
四、[实验内容]1、给定BSC 信道,信源概率空间为信道矩阵 0.990.010.010.99P ⎡⎤=⎢⎥⎣⎦求该信道的I(X;Y)和容量,画出I(X;Y)和ω、C 和p 的关系曲线。
2 、编写一M 脚本文件t03.m ,实现如下功能:在任意输入一信道矩阵P 后,能够判断是否离散对称信道,若是,求出信道容量C 。
3、已知X=(0,1,2);Y=(0,1,2,3),信源概率空间和信道矩阵分别为求: 平均互信息量;4、 对题(1)求其二次扩展信道的平均互信息I(X;Y)。
五、[实验过程] XP 0 10.6 0.4= XPx 0 1 2 0.3 0.5 0.2= 0.1 0.3 0 0.6 0.3 0.5 0.2 0 0.1 0.7 0.1 0.1P=每个实验项目包括:1)设计思路2)实验中出现的问题及解决方法;1)设计思路1、信道容量( )max (X; Y)q xC = I,因此要求给定信道的信道容量,只要知道该信道的最大互信息量,即求信道容量就是求信道互信息量的过程。
程序代码:clear all,clc;w=0.6;w1=1-w;p=0.01;XP01= 0.6 0.4p1=1-p;save data1 p p1;I_XY=(w*p1+w1*p)*log2(1/(w*p1+w1*p))+(w*p+w1*p1)*log2(1/(w*p+w1*p1))- ...(p*log2(1/p)+p1*log2(1/p1));C=1-(p*log2(1/p)+p1*log2(1/p1));fprintf('互信息量:%6.3f\n信道容量:%6.3f',I_XY,C);p=eps:0.001:1-eps;p1=1-p;C=1-(p.*log2(1./p)+p1.*log2(1./p1));subplot(1,2,1),plot(p,C),xlabel('p'),ylabel('C');load data1;w=eps:0.001:1-eps;w1=1-w;I_XY=(w.*p1+w1.*p).*log2(1./(w.*p1+w1.*p))+(w.*p+w1.*p1).*log2(1./(w.*p+w1.*p1))- . ..(p.*log2(1./p)+p1.*log2(1./p1));subplot(1,2,2),plot(w,I_XY)xlabel('w'),ylabel('I_XY');实验结果:互信息量:0.891信道容量:0.919I(X;Y)和ω、C和p的关系曲线图:0 0.5 10.10.20.30.40.50.60.70.80.91pC0 0.5 10.10.20.30.40.50.60.70.80.91wI X Y2、离散对称信道:当离散准对称信道划分的子集只有一个时,信道关于输入和输出对称。
实验二 计算信道容量

PXi[i] = ((PXi[i] * a[i]) / sum);
}
n ++;
}
}while(cap_max-cap_result>= e);
printf("\n\n迭代次数为:%d\n" ,n);
for(i=0;i<X_num;i++)
{
printf("最佳信源概率:%f\n" ,PXi[i]);
}
/**************************************************************************
函数名:double Calculate_cap_result(double PXi[],double a[])
功能:计算并输出迭代法所需的参数cap_result
double Calculate_cap_max(double a[])
{
int i;
double max_a = a[0];
for(i=0;i<X_num;i++)
{
if(a[i] > max_a)
{
max_a = a[i];
}
}
printf("较大值=%f",log(max_a));
return log(max_a);
for(i=0;i<X_num;i++)
{
for(j=0;j<Y_num;j++)
{
printf("P[%d][%d]=",i,j);
scanf("%lf",&P[i][j]);
离散信道及其信道容量

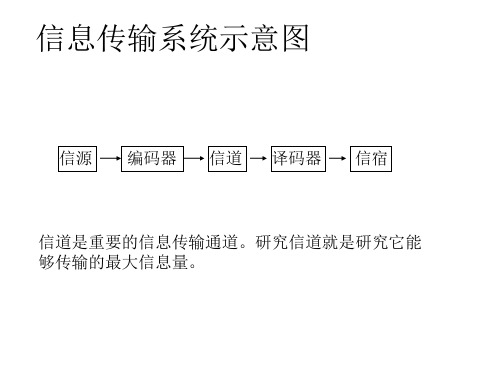
信道的任务是以信号方式传输信息和存储信息。 研究信道中能够传送或存储的最大信息量,即信道容量。
2.1
信道的数学模型和分类
干扰源
信源
编码器
调制器
物理信道 实际信道
解调器
译码器
信宿
编码信道
等效信道
图2.1.1 数字通信系统的一般模型
一、信道的分类
根据载荷消息的媒体不同
邮递信道
C max { I ( X ;Y )}
解:X:{0,1} Y:{0,1,2} 此时,r =2,s =3, 传递矩阵为:
0 0 1 2 1
1- p
q
1
p 1 p 0 0 1 q q
符号“2”表示接收到了“0”、“1”以外的特殊符 号
• 一般离散单符号信道的传递概率可用矩阵形式表示,即 b1 b2 … bs
a1 P(b1|a1) P(b2|a1) … P(bs|a1) a2 P(b1|a2) P(b2|a2) … P(bs|a2) … …. … …
R = I(X;Y) = H(X) – H(X|Y) (比特/符号)
• 信道中每秒平均传输的信息量----信息传输速率Rt (设传递一个符号用时为t).
Rt = R/t = I(X;Y)/t = H(X)/t – H(X|Y)/t (比特/秒)
一、 信道容量的定义
I ( X ; Y ) I (Y ; X ) P( xy ) log
a1 a2 b1 b2
X
.
. ar
P(bj/ai)
.
. bs
Y
[例1] 二元对称信道,[BSC,Binary Symmetrical Channel] 解:此时,X:{0,1} ; Y:{0,1} ; r=s=2,a1=b1=0;a2=b2=1。 传递概率: 1-p
信息论—离散信道及其信道容量
I ( X ; Y | Z ) H ( X | Z ) H ( X | YZ )
I ( X ; YZ ) I ( X ; Y ) I ( X ; Z | Y ) I ( X ; Z ) I ( X ;Y | Z )
例题
四个等概率分布的消息 M1 , M 2 , M 3 , M 4 被送入一个二 元无记忆对称信道进行传送。通过编码使
已知y,z的条件下,总共获得关于x的互信息
P( x | yz) P( x | y ) P( x | yz) I ( x; yz) log log log P( x) P( x) P( x | y ) I ( x; y ) I ( x; z | y)
同样
I ( x; yz) I ( x; z ) I ( x; y | z )
信道的分类
用户数 输入与输出的 关系
与时间的关系 输入、输出信 号的特点
两端(单用户)信道 多端(多用户)信道 无反馈信道 有反馈信道 固定参数信道 时变参数信道
离散信道、连续信道、半离散 或半连续信道、波形信道
离散信道的数学模型
X
X ( X1 ,, X i , X N )
信道
P( y | x )
r s
s
s
r
平均互信息
I ( X ;Y ) H ( X ) H ( X | Y )
1 1 I ( X ; Y ) P( x) log P( xy) log P( x) X ,Y P( x | y ) X P( y | x) P( xy) log P( y ) X ,Y
用矩阵来表示
0 1 0 1 p p 1 p 1 p
信息论基础第3章离散信道及其信道容量

《信息论基础》
3.6 多符号离散信道及其信道容量
【例】求图所示的二元无记忆离散对称信道的二次 扩展信道的信道容量。
【例】 已知两个独立的随机变量 X、Y 的分布律如下。
X P(x)
a1 0.5
a2 0.5
,
Y P( y)
b1 0.25
b2 b3 0.25 0.5
计算 H X , H Y , H XY , H X |Y , H Y | X , I X ;Y 。
《信息论基础》
3.4 信道容量的定义
I (ai ) 减去已知事件 bj 后对 ai 仍然存在的不确定性 I (ai | bj ) ,实际就是事件
bj 出现给出关于事件 ai 的信息量。
【例】 甲在一个16 16 的方格棋盘上随意放一枚棋
子,在乙看来棋子放入哪一个位置是不确定的。如果甲 告知乙棋子放入棋盘的行号,这时乙获得了多少信息 量?
《信息论基础》
第3章 离散信道及其信道容量
通信系统的基本功能是实现信息的传递,信道是信息 传递的通道,是信号传输的媒质。一般而言,信源发出的 消息,必须以适合于信道传输的信号形式经过信道的传输, 才能被信宿接收。
从信源的角度看,信源发出的每个符号承载的平均信 息量由信源熵来定量描述;而从信宿的角度看,信宿收到 的每个符号平均能提供多少信息量由平均互信息来定量描 述。在信息论中,信道问题主要研究在什么条件下,信道 能够可靠传输的信息量最大,即信道容量问题。
《信息论基础》
3.7 信源与信道的匹配
信息论离散信道及其容量

p(x 1, y 0) p(x 1) p( y 0 | x 1) p p(x 1, y 1) p(x 1) p( y 1| x 1) p
p(Y 0) p(0, 0) p(1, 0) p (1 ) p p p
p(Y 1) p(0,1) p(1,1) p (1 ) p p p
pXY (0?) pY (?) pXY (1?) pY (?)
pXY pY
(01) (1)
1
pXY pY
(11) (1)
0
1 3 2 3
0 P( X ,Y )PY
1
由此可得
H ( X ) 1 log 1 3 log 3 0.811 4 44 4
H (Y ) 1 log 1 3 log 3 1 log 1 1.406 8 88 82 2
第4章 离散信道及其 容量
通信系统模型
信息论的研究基础是通信系统模型。
信源
编码器
信道
消息
信号
干扰
干扰器
译码器
信宿
消息
4.1 信道的数学模型及其分类
信道是信息传输的通道。
干扰
X
信道
Y
由于干扰的存在,信道的输出Y与信道的输入X不
完全相同,用条件概率p(y|x)描述。
而输入和输出又有各自的统计特性,分别用 表示。
离散信道中常用的几种概率
先验概率:p(ai),PX=[p(a1) p(a2) … p(ar)]
联合概率:p(aibj)=p(ai)p(bj|ai)=p(bj)p(bj|ai)
p11 p12 L p1s
信道传递概率:p(bj|ai)=pij,P
p21 M
p22 M
L M
p2s
离散信道及其信道容量课件

离散信道的应用场景
01
02
数据通信
数字电视
03 数字电话
CHAPTER
离散信道模型
输入输出符号集
输入符号集
输出符号集
输入输出概率分布
输入概率分布
输出概率分布
转移概率
定义
转移概率表示在给定输入符号下,输出符号出现的条件概率,即$P(Y=y|X=x)$。
计算方法
根据输入输出概率分布和转移概率的定义,可以通过以下公式计算转移概率: $P(Y=y|X=x) = frac{P(X=x, Y=y)}{P(X=x)}$。
CHAPTER
离散信道容量
信道容量的定 义 01 02
单符号离散信道容量
在无记忆信道中,每个符号独立地通 过信道,信道状态与符号无关,因此 单符号离散信道容量可以通过概率计 算得出。
多符号离散信道容量
多符号离散信道容量是指多个符号在 离散有记忆信道中能够传输的最大信 息量。
多符号离散信道容量的计算方法包括 互信息法、迭代法和密度进化法等。
离散信道容量的应用
数据 传
数据压缩
错误控制编码
通信系统设计
通信协议设计
在通信系统设计中,离散信道容量提供 了关于通信系统性能的理论限制。这有 助于设计者根据这些限制优化通信协议, 提高系统的整体性能。
VS
频谱效率
频谱效率是通信系统设计的重要指标之一。 通过理解和利用离散信道容量,可以更有 效地利用频谱资源,提高频谱效率,从而 在有限的带宽内传输更多的信息。
CHAPTER
离散信道容量的计算方法
解析法
解析法是一种基于概率论和组合数学的计算离散信道容量的方法。它通 过将输入和输出符号之间的概率关系表示为数学表达式,然后求解这些 表达式来计算信道容量。
离散信道及容量

平均信息量之和; H XY H X H Y
(b)一个符号不能提供有关另一符号的任何信息。
IX ;Y IY; X 0
HX ,Y 0
当两个信源相关时 (a)联合熵小于两个信源的熵的和:
H XY H X H Y
(b)平均互信息量等于两信源熵重合的部分; (c)信源的条件熵等于其熵减去平均互信息量:
3. 平均互信息的交换性(对称性)
I (X ;Y ) I (Y; X )
4. 平均互信息 I ( X ; Y ) 的凸状性
I ( X ;Y ) P(xy) log P( y | x)
X ,Y
P( y)
P(x)P( y | x) log X ,Y
P( y | x) P(x)P( y | x)
p0 / 0 0.99
0
0
p0 /1 0.01
p1/ 0 0.01
错误的概率为0.01。
1
1
即有
p1/1 0.99
p yi / xi p0/ 0 p1/1 0.99
p yj / xi p1/ 0 p0 /1 0.01 i j
转移矩阵
pY / X p y j / xi
满足其的充要条件是:
N
P(Y X ) p( y1y2...yN x1x2...xN ) p( yi xi ) i1
对任意的N值和x,y值上式都成立。
3.有干扰有记忆信道 信道中某一瞬间的输出符号不但与对应时刻的输入符号 有关,而且还与此前其它时刻信道的输入符号有关,则该信 道称有记忆信道。 此时 P(Y X ) 不满足:
p(xi ) p( y j
N
xi )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二离散信道及其容量
一、[实验目的]
1、理解离散信道容量的内涵;
2、掌握求二元对称信道(BSC)互信息量和容量的设计方法;
3、掌握二元扩展信道的设计方法并会求其平均互信息量。
二、[实验环境]
windows XP,MATLAB 7
三、[实验原理]
若某信道输入的是N 维序列x ,其概率分布为q(x ),输出是N 维序列y ,则平均互信息量记为I(X ;Y ),该信道的信道容量C 定义为()
max (X;Y)q x C I =。
四、[实验内容]
1、给定BSC 信道,信源概率空间为
信道矩阵0.990.010.010.99P ⎡⎤=⎢⎥⎣⎦
求该信道的I(X;Y)和容量,画出I(X;Y)和ω、C 和p 的关系曲线。
2、编写一M 脚本文件t03.m,实现如下功能:
在任意输入一信道矩阵P 后,能够判断是否离散输出对称信道。
3、对题1求其二次扩展信道的平均互信息I(X;Y)。
五、[实验过程]
每个实验项目包括:
1)设计思路
1、信道容量
()max (X;Y)q x C I =,因此要求给定信道的信道容量,只要知道该信道的最大互信息量,即求信道容量就是求信道互信息量的过程。
程序代码:
clear all,clc;
w=0.6;
w1=1-w;
p=0.01;X
P 0
10.60.4
=
p1=1-p;
save data1p p1;
I_XY=(w*p1+w1*p)*log2(1/(w*p1+w1*p))+(w*p+w1*p1)*log2(1/(w*p+w1*p1))-...
(p*log2(1/p)+p1*log2(1/p1));
C=1-(p*log2(1/p)+p1*log2(1/p1));
fprintf('互信息量:%6.3f\n信道容量:%6.3f',I_XY,C);
p=eps:0.001:1-eps;
p1=1-p;
C=1-(p.*log2(1./p)+p1.*log2(1./p1));
subplot(1,2,1),plot(p,C),xlabel('p'),ylabel('C');
load data1;
w=eps:0.001:1-eps;
w1=1-w;
I_XY=(w.*p1+w1.*p).*log2(1./(w.*p1+w1.*p))+(w.*p+w1.*p1).*log2(1./(w.*p+w1.*p1))-.. .(p.*log2(1./p)+p1.*log2(1./p1));
subplot(1,2,2),plot(w,I_XY)
xlabel('w'),ylabel('I_XY');
实验结果:
互信息量:0.891
信道容量:0.919
I(X;Y)和ω、C和p的关系曲线图:
C
X
2、离散对称信道:当离散准对称信道划分的子集只有一个时,信道关于输入和输出对称。
离散准对称信道:若一个离散无记忆信道的信道矩阵中,按照信道的输出集Y 可以将信道划分成n个子集,每个子矩阵中的每一行都是其他行同一组元素的不同排列。
实验代码:
clc;clear;
P=input('输入信道转移概率矩阵:');
[r,c]=size(P);
if sum(P,2)-1~=zeros(1,r)';
error('输入的信道矩阵不合法!');%矩阵行和一定要为1
end
l=1;
Sum=0;
for j=2:c
for i=1:r%i是行变量
for k=1:r
if P(k,j)==P(i,1)
Sum=Sum+1;
break;
end
end
end
end
if Sum==r*(c-1)
fprintf('是离散输出对称信道!\n',j);
else fprintf('不是对称信道!');
end
实验结果:
输入信道转移概率矩阵:[0.010.99;0.990.01]
是离散输出对称信道!
输入信道转移概率矩阵:[0.40.6;0.30.7]
不是对称信道!
3、二次扩展信道的互信息量I(X;Y)=H(Y)-H(Y|X).
实验代码:
clc,clear;
p=0.01;
P_X1=[0.6,0.4];
p1=1-p;
X2=[0,0;0,1;1,0;1,1];%二次扩展输入符号阵
Y2=X2;%二次扩展输出符号
P_X2=[P_X1(1)^2,P_X1(1)*P_X1(2),P_X1(2)*P_X1(1),P_X1(2)^2];
%求二次扩展后信道矩阵N
N=zeros(4);
for i=1:4
for j=1:4
l=length(find(xor(X2(i,:),Y2(j,:))==0));%比较得正确传递元素个数
N(i,j)=p1^l*p^(2-l);
end
end
%下面求I
P_Y2=P_X2*N;
P_XY2=[P_X2(1)*N(1,:);P_X2(2)*N(2,:);P_X2(3)*N(3,:);P_X2(4)*N(4,:)];%联合分布
H_Y2=sum(-P_Y2.*log2(P_Y2));
H_Y_X2=sum(sum(-P_XY2.*log2(N)));
I_XY2=H_Y2-H_Y_X2;
fprintf('2次扩展信道的平均互信息为:%5.3f',I_XY2);
实验结果:
2次扩展信道的平均互信息为:1.783
2)实验中出现的问题及解决方法;
1、信道容量与互信息量有关,而互信息量又与信源熵相关,所以要求得信道容量就必须知道信道传递概率,然后根据公式一步一步计算。
2、对于判断离散对称信道,不需要弄清楚的是它的概念,根据定义来判断。
3、对于扩展信道,分有记忆的和无记忆的,在不确定的情况下计算扩展信源的熵,我们要根据定义来计算。
六、[实验总结]
通过本次实验,我对于信道的分类,各种信道的特点有了一定的认识和了解。
实验中涉及的主要是二元对称信道,而它的最佳分布是输入和输出均对称。
实验中最主要的部分还是关于信道容量的计算,此次实验,让我们验证了课本上的定理,也让我们更好地理解和掌握了课堂上所学的知识。
