等式的性质
合集下载
等式的性质
a b （c≠ 0） 如果 a = b，那么 c c
3、解一元一次方程的实质就是利用等式的 性质求出未知数的值x=a(常数)
学科网
则 4x +
= 7x
要求： 1、观察等式变形前后两边各 有什么变化 2、应怎么变化可使等式依然相等
(2) 若 3a + 4 = 8
关键：同侧对比 注意符号
则 3a = 8 +
.
你又发现了什么？
你又发现了什么？
• 等式的性质2: 等式两边都乘以 同一个数，或都除以同一个不为 0的数，结果仍相等。
(4) 如果-2x=4, ，那么x =________ 。 -2
(5) 如果2x1 2 3题的括号内，填上使等式成立的依据.
（1）2 x 8
得x 4 （ 2） 3x 2 2 x 得 x 2
1 x2 （ 3） 3 （4） x 5 1 （ 5） y 6
于是 所以 -9x=3 x=-3
1 x 3
练习2：下列各式的变形正确的是（ D ）
x A.由 0 ，得到 x = 2 2 x B.由 3 ，得到 x = 1 3
x=0 x=9
2 a= C.由－2 a = －3，得到 a = 3
D.由 x－1 = 4，得到 x = 5
3 2
你会吗？
判断对错，对的说明根据等式的哪一条性质；错的 说出为什么。
(1)如果x=y,那么
（× ）
(2)如果x=y,那么 x 5 a y 5 a （ √ ） x y (3)如果x=y,那么 5 a 5 a （ × ）
5 x 5 y (4)如果x=y,那么
（×）
(5)如果x=y,那么
《等式的性质》
同时加
3，得到
8=10，等式仍然成
立。
即：若 a=b，则 a+c=b+c（或 ac=b-c）。
等式的乘法性质
等式两边同时乘以（或 除以） 同一个非零数，等式仍然成立 。
即：若 a=b 且 c≠0，则 ac=bc（或 a/c=b/c）。
示例：若 6=9，两边同时乘以 2，得到 12=18，等式仍然成 立。
等式与不等式在解决实际问题中的应用
等式常用于求解未知数或验证数学定理；
不等式则更常用于解决实际问题中的大小、范围、最值等问题；
举例：利用不等式求解最优化问题（如线性规划），或者通过等式和不等式联合求 解实际问题（如方程组和不等式组的综合应用）。
高级等式性质与应
04
用
移项与合并同类项
移项
通过移项操作，可以将等式中的某些项移到等式的另一侧， 从而简化等式或解决问题。在移项时，需要保持等式的平衡 ，即等号两边的数学表达式在移项后仍然相等。
实际问题解决
等式的基本性质在几何中也有应用，例如 证明几何定理时，可以通过构建等式并应 用等式性质进行推导。
等式的基本性质可以用于解决实际问题中 的方程问题，如距离、速度、时间之间的 关系等。
等式的运算性质
02
等式的加法性质
等式两边同时加上（ 或 减去）同一个数 ，等式仍然成立。
示例：若 5=7，两边
学习等式性质的意义与价值
培养逻辑思维能力
通过学习等式的性质，我们可以培养逻辑思维能力，学会 从已知条件出发，通过逻辑推理得出未知数的解。
解决实际问题的基础
等式性质在实际问题中有广泛的应用，例如工程问题、经 济问题等。掌握等式的性质，能够帮助我们更好地解决这 些实际问题。
等式的基本性质
等ຫໍສະໝຸດ 的两边同时加上相等的数，等式不变。
设一个花盆的重量为a克，一个花瓶的重量为b克。
a+b=4b
a+b-b=4b-b a=3b
等式的基本性质一：
等式的两边同时加上或减去相等的数，等式不变。
设一瓶墨水的重量为a克，一个文具盒的重量为b克。
a=2b
a×2=2b×2 2a=4b
设一个排球的重量为a克，一个小皮球的重量为b克。
人教版五年级数学上册第四单元
芦溪二小 童驰
设一个茶壶的重量为a克，一个茶杯的重量为b克。
a=2b
a+b=2b+b a+a=2b+a
1把茶壶的重量＝2个茶杯的重量 1把茶壶的重量＋1个茶杯的重量＝2个茶杯的重量＋1个茶杯的重量 1把茶壶的重量＋2个茶杯的重量＝2个茶杯的重量＋2个茶杯的重量 1把茶壶的重量＋1把茶壶的重量＝2个茶杯的重量＋1把茶壶的重量
2a=6b
2a÷2=6b÷2
a=3b
等式的基本性质二：
等式的两边同时乘或除以相等的数（0 除外），等式不变。
X＋4=48
x＋4 ○ □ =48 ○ □
X－4=48
x－4 ○ □ =48 ○ □ x÷4=48 x÷4 ○ □ =48 ○ □
x × 4=48
x × 4 ○ □ =48 ○ □
设一个花盆的重量为a克，一个花瓶的重量为b克。
a+b=4b
a+b-b=4b-b a=3b
等式的基本性质一：
等式的两边同时加上或减去相等的数，等式不变。
设一瓶墨水的重量为a克，一个文具盒的重量为b克。
a=2b
a×2=2b×2 2a=4b
设一个排球的重量为a克，一个小皮球的重量为b克。
人教版五年级数学上册第四单元
芦溪二小 童驰
设一个茶壶的重量为a克，一个茶杯的重量为b克。
a=2b
a+b=2b+b a+a=2b+a
1把茶壶的重量＝2个茶杯的重量 1把茶壶的重量＋1个茶杯的重量＝2个茶杯的重量＋1个茶杯的重量 1把茶壶的重量＋2个茶杯的重量＝2个茶杯的重量＋2个茶杯的重量 1把茶壶的重量＋1把茶壶的重量＝2个茶杯的重量＋1把茶壶的重量
2a=6b
2a÷2=6b÷2
a=3b
等式的基本性质二：
等式的两边同时乘或除以相等的数（0 除外），等式不变。
X＋4=48
x＋4 ○ □ =48 ○ □
X－4=48
x－4 ○ □ =48 ○ □ x÷4=48 x÷4 ○ □ =48 ○ □
x × 4=48
x × 4 ○ □ =48 ○ □
等式的性质ppt课件
科学实验中的应用
化学反应平衡
在化学实验中，等式性质可用于描述化学反应的平衡状态，确保 实验结果准确可靠。
生物学中的能量平衡
在生物学研究中，等式性质可用于描述生物体内的能量平衡，以了 解生物体的生存和生长状况。
物理学中的力矩平衡
在物理学中，等式性质可用于描述力矩的平衡，以解决与物体运动 相关的问题。
函数图像的对称性
函数图像的对称性
等式在研究函数图像的对称性方面具 有重要作用。通过对等式的分析，我 们可以确定函数的对称轴和对称中心 。
奇偶函数的性质
对称性与周期性的关系
函数的对称性和周期性是密切相关的 ，通过对等式的研究，我们可以深入 了解这种关系。
奇函数和偶函数具有不同的对称性质 ，这些性质可以通过等式进行描述和 证明。
可除性证明
假设a=b且c≠0，那么根据等 式的定义，我们可以得出 a/c=b/c。
02 等式的运算规则
等式的加减法规则
总结词
等式的加减法规则是基本的运算规则，它遵循相同的数学原理。
详细描述
等式的加减法规则是指在进行等式运算时，将等式两边的数值进行加减运算，如 果等式两边同时加上或减去同一个数，等式仍然成立。例如，对于等式 (2 + 3 = 5)，如果两边同时加上(2)，得到 (4 + 3 = 7)，等式仍然成立。
几何图形的等分与对称
几何图形的等分
等式在几何图形中等分方面具有 应用，例如通过等式确定点、线 或面的位置，将图形等分为若干
部分。
图形的对称性
图形的对称性可以通过等式进行 描述和证明，例如平行四边形、
矩形和圆的对称性质。
等分与对称的应用
在几何图形中，等分和对称的应 用非常广泛，例如在建筑设计、 艺术和工程等领域中都有应用。
等式的基本性质
叫做方 未知数的值 )叫做方 )。 。 ) )
(2)求方程的解的过程叫做 解方程 求方程的解的过程叫做( 求方程的解的过程叫做
(3)比x多5的数是 。列方程为 X+5=10 比 多 的数是 的数是10。列方程为( (4)8与x的和是 。方程为 8+X=56 与 的和是 的和是56。方程为( (5)比x少1.06的数是 比 少 的数是21.5。列方程为 的数是 。 ( )。 。 X-1.06=21.5
同学们，你知道小学数学教科书的印刷过程吗？ 同学们，你知道小学数学教科书的印刷过程吗？
在一张大纸的 两面分别印上 16页教材。 页教材。 页教材
对折四次后， 对折四次后， 每页的面积是 689.75cm2。
经过装订、 经过装订、裁 边后就成了我 们看到的教科 书。
一、填空。 (1)使方程左右两边相等的 使方程左右两边相等的( 使方程左右两边相等的 程的解。 程的解。
等式两边同时乘或除以一个相同的数（ 除外），等式大小不变 除外），等式大小不变。 等式两边同时乘或除以一个相同的数（0除外），等式大小不变。
解方程 3x = 18
x x x
方程两边同时除以同 一个不等于0的数，左 一个不等于 的数， 的数 右两边仍然相等。 右两边仍然相等。
解：3x÷（3）= 18÷（3 ） ÷ ÷ x =（6） （
100g
100+x＝250
100+x=100+150 100+150=250, 所以x=150。
100+x＝250 x＝150
使方程左右两边相等的未知数的值，叫做 方程的解。 像上面，x=150就是方程100+x=250的解。 求方程的解的过程叫做解方程。
等式的性质
（3）（5-a）x=(5-a)y
（4） x = y
5a
5a
方法总结：运用等式的性质，可以将等
式进行变形，变形时等式两边必须同时
进行相同的四则运算，否则就会破坏原 来的相等关系
学以致用
例1 利用等式的性质解下列方程
x+7=26
3x=2x-4
解：两边减7，得 x+7-7=26-7, X=19
解：两边减2x,得 3x-2x=2x-2x-4, X=-4
么发现？
把一个等式看做一个天平，把 等号两边的式子看做天平两边 的砝码，则等式成立就可看做 是天平保持两边平衡
等式的性质1：等式两边加（或减）同 一个数（或式子），结果仍相等。
如果a=b,那么ac=bc
等式的性质2：等式两边乘同一个数， 或除以同一个不为0的数，结果仍相等
如果a=b,那么ac=bc
如果a=b,那么 a = b
c
c
探究一：应用等式的性质对等式进行变形
例1 用适当的数或整式填空，使所得结果仍为整式 （1）如果2x+7=10,那么2x=10-_____ （2）如果-3x=8,那么x=______
思考：若x=y,则下列等式是否成立，说明理由
（1）x+5=y+5
（2）x-a=y-a
例2 解方程：-4x+8=-5x-1
解：两边减8，得 -4x+8-8=-5x-1-8 -4x=-5x-9 两边加5x,得 -4x+5x=-5x+5x-9 X=-9
当堂训练：
1，解方程并检验：-6x+3=2-7x
两边减3，得 -6x=-7x-1 两边加7x，得 X=-1
检验：把x=-1代入方程： 左边=-6x(-1)+3=9 右边=2—7x(-1)=9 左边=右边 所以x=-1时原方程的解
等式的性质
答：根据等式的性质2,两 边同时除以2。
（4）如果 0.2x=5 那么x=_.
随堂练习：
1.填空并说出是根条性质及怎 样变形（改变式子的形式）
（4）如果 0.2x=5, 那么x=_25_. 答：根据等式性质2，两
边都乘以5。
练习2： 以下等式变形，正确的是（ B）
① 由x = y，得到 x＋5 ＝ y＋5
等式的性质1:
等式两边加（或减）同一个数（或式子）， 结果仍相等。
数学语言：如果 a = b，那么 a ± c = b ± c
等式的性质2：
等式两边乘同一个数（或式子），或除以同 一个非0的数（或式子）结果仍相等。
数学语言：如果 a = b，那么 a c = b c
如果
a
=
b，那么
a c
bc（c≠ 0）
习惯上，我们写为x=8.
归纳总结
1、等式的两条性质； ① 如果 a = b，那么 a ± c = b ± c ② 如果 a = b，那么 a c = b c 如果 a = b，那么 a b（c≠ 0）
cc
2、解一元一次方程的实质就是利用等式的 性质求出未知数的值
② 若 －x = y，根据_等__式_的__性__质__2_，得到 x =_－__y_ 。
随堂练习： 1.填空并说出是根据等式的哪 条性质及怎样变形（改变式子 的形式） （1）如果3x+7=8，那么
3x=8－______.
随堂练习： 1.填空并说出是根据性质及怎 样变形（改变式子的形式） （1）如果3x+7=8那么 3x=8－_7_;
② 由 2 a +1 = b+1，得到 2 a = b
③ 由 m = n，得到 a m = a n
（4）如果 0.2x=5 那么x=_.
随堂练习：
1.填空并说出是根条性质及怎 样变形（改变式子的形式）
（4）如果 0.2x=5, 那么x=_25_. 答：根据等式性质2，两
边都乘以5。
练习2： 以下等式变形，正确的是（ B）
① 由x = y，得到 x＋5 ＝ y＋5
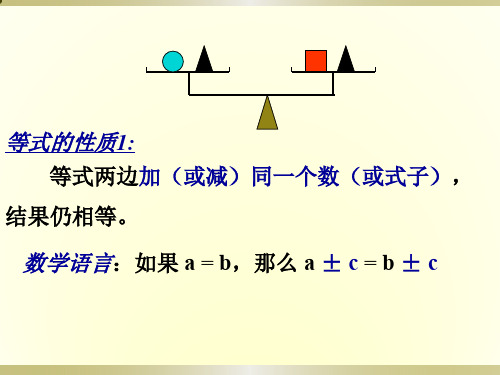
等式的性质1:
等式两边加（或减）同一个数（或式子）， 结果仍相等。
数学语言：如果 a = b，那么 a ± c = b ± c
等式的性质2：
等式两边乘同一个数（或式子），或除以同 一个非0的数（或式子）结果仍相等。
数学语言：如果 a = b，那么 a c = b c
如果
a
=
b，那么
a c
bc（c≠ 0）
习惯上，我们写为x=8.
归纳总结
1、等式的两条性质； ① 如果 a = b，那么 a ± c = b ± c ② 如果 a = b，那么 a c = b c 如果 a = b，那么 a b（c≠ 0）
cc
2、解一元一次方程的实质就是利用等式的 性质求出未知数的值
② 若 －x = y，根据_等__式_的__性__质__2_，得到 x =_－__y_ 。
随堂练习： 1.填空并说出是根据等式的哪 条性质及怎样变形（改变式子 的形式） （1）如果3x+7=8，那么
3x=8－______.
随堂练习： 1.填空并说出是根据性质及怎 样变形（改变式子的形式） （1）如果3x+7=8那么 3x=8－_7_;
② 由 2 a +1 = b+1，得到 2 a = b
③ 由 m = n，得到 a m = a n
数学等式的定义和性质
数学等式的定义和性质第一部分：等式的定义：含有等号的式子叫做等式(数学术语)。
形式：把相等的两个数(或字母表示的数)用“=”连接起来。
等式可分为矛盾等式和条件等式。
矛盾等式就是左右两边不相等的"等式"。
也就是不成立的等式,比如5+2=8,实际上5+2=7,所以5+2=8是一个矛盾等式.有些式子无法判断是不是矛盾等式,比如x-9=2,只有x=11时这个等式才成立(这样的等式叫做条件等式),x11时,这个等式就是矛盾等式。
第二部分：等式的性质：1.等式两边同加上(或减去)同一个数或同一个整式，所得结果仍是等式。
即若a=b，则am=bm。
2.等式两边同乘以(或除以)同一个数(除数不能为零)，所得结果仍是等式。
即若a=b，则am=bm，(m0)。
3.等式具有传递性。
若a1=a2,a2=a3,a3=a4,……an=an,那么a1=a2=a3=a4=……=an4.等式两边同时乘方(或开方)，两边依然相等若a=b 那么有a^c=b^c 或(c 次根号a)=(c次根号b)5.等式的对称性(若a=b，则b=a)。
等式的性质是解方程的基础，很多解方程的方法都要运用到等式的性质。
如移项，运用了等式的性质1;去分母，运用了等式的性质2。
运用等式的性质，涉及除法时，要注意转换后，除数不能为0，否则无意义。
拓展：1：等式两边同时被一个数或式子减，结果仍相等。
如果a=b，那么c-a=c-b2：等式两边取相反数，结果仍相等。
如果a=b，那么-a=-b3：等式两边不等于0时，被同一个数或式子除，结果仍相等。
如果a=b0，那么c/a=c/b4：等式两边不等于0时，两边取倒数，结果仍相等。
如果a=b0，那么1/a=1/b第三部分：例题：方程3x-4=1+2x，移项，得3x-2x=1+4，也可以理解为方程两边同时()A.加上(-2x+4)B.减去(-2x+4)C.加上(2x+4)D.减去(2x+4)已知：|a|=3，b2=4，ab0，求a-b的值.解答过程：根据等式的基本性质1，方程3x-4=1+2x的两边同时加上(-2x+4)，可得：3x-4+(-2x+4)=1+2x+(-2x+4)，即3x-2x=1+4.故选A.。
3.1.2等式的性质
b+2变成b+2+4=b+6
(2)3x=2x+5 由2x+5变成5
3x变成3x-2x
(3) 1 x=5 由 1 x变成x
2
2
5变成5×2=10
(4)5m=2n 由5m变成m
2n变成2n÷5= 2 n
5
栏目索引
3.1.2 等式的性质
栏目索引
答案 (1)b+6 (2)2x (3)10 (4) 2 n
栏目索引
7.用适当的数或式子填空,使变形后仍是等式,并说明是根据哪一个性质
得到的.
(1)若3x+5=2,则3x=2-
;
(2)若-4x= 1 ,则x=
.
3
解析 (1)5.根据等式的性质1,方程两边都减5.
(2)- 1 .根据等式的性质2,方程两边都除以-4.
12
3.1.2 等式的性质
栏目索引
1.已知由- 1 x=6可得x=-24,下列变形方法:①方程两边同乘- 1 ;②方程两
题型二 利用等式的性质对已知等式进行变形
例2 利用等式的性质在横线上填上适当的数或式子,并说明变形的根
据以及是怎样变形的.
(1)如果2x-3=-5,则2x=
,x=
;
(2)如果5x+2=2x-4,则3x=
,x=
;
(3)如果 1 x=2x-3,则- 5 x=
,x=
.
3
3
分析 首先观察等式的左边是如何由上一步变形得到的,确定变形的依
=1,且6÷ 14
=-24; 14
÷(-4)≠1,所以②③正确,①④错误.
3.1.2 等式的性质
等式的性质-完整版课件
【跟踪训练】
1.解方程并验:6x+3=2-7x.
解：两边减3，得 -6x＝-7x-1 两边加7x，得 x=-1.
检验：把x=－1代入方程：
左边=－6×（－1）＋3=9；
右边=2－7×（－1）＝9. 左边=右边，
所以x＝-1是原方程的解.
2. 已知 3 a4m 与 15a 5+3m是同类项，求m的值.
下列方程变形是否正确？如果正确，说明变形的根据； 如果不正确，说明理由. （1）由x=y，得x+3=y+3
依据：等式性质1：等式两边同时加上3.
（２）由a=b，得a－6=b＋6
左边减6，右边加6，运算符号不一致.
（３）由m=n,得m-2x2=n-2x2
依据：等式性质1：等式两边同时减去2x2.
（４）由2x=x-5，得2x+x=-5
量．请你判断：1个砝码A与
个砝码C的质量相等．
【解析】由题意的A=B+C，A+B=3C，解得A=2C，即1 个砝码A与2个砝码C的质量相等. 答案：2
a b4，.如果a=b, 且
cc
则c应满足的条件是_c_≠__0___.
5.解方程
（1）4x - 2 = 2 x=1
1
（2） x + 2 = 6 x=8
8
解：由题意得，4m=5+3m,解得m=5. 3.请同桌（加、减、乘、除各举一例，除 号用分数表示）.
1.填空并在括号内注明利用了等式的哪条性质.
（1）如果5+x=4，那么x=____（ （2）如果-2x=6，那么x=____ (
）
-1 ) 等式的性质1
等号
a
b
+
等式的基本性质
图1
a
= bb
图1
a
bb
图1
a
bb
图1
a
bb
a
bb
平衡的天平两边同时增加 同样的物品，天平仍然保持平衡。
图1
a
bb
图2
１个花盆和 3 个花瓶同样重。
天平保持平衡的道理1:
平衡的天平两边同时增加 或减少 同样的物品，天平仍然保持平衡。
等式的基本性质1: 等式的两边同时加上或减去同一个数， 左右两边仍然相等。
如果a＝b，那么 a＋c＝b＋c a－c＝b－c
图3
χ
yy
2个
2个
图4
１个排球和 3 个皮球同样重。
天平保持平衡的道理2:
平衡的天平两边物品同时扩大或缩小相 同的倍数，天平保持平衡。
等式的基本性质3: 等式的两边同时乘或除以同一个数 （0除外），左右两边仍然相等。
如果a＝b，那么 a×c＝b×c a÷c＝b÷c (c≠0)
两边拿掉（ 1 ）个苹果，天平仍保持平衡。 一把香蕉和（ 5 ）个苹果同样重。
6只樱桃和( 3)个草莓同样重， ( 2)只樱桃和1个草莓同样重。
填空:在○中填符号，□中填适当的数。
如果a=b, 那么a+0.6=b○+0□.6
a○- 13□=b-
1 3
a×2.5=b○×□2.5
a○÷□6 =b÷6
② 如果χ-48=26.8， 那么χ-48+48=26.8○+□48
③ 如果χ+2.1=10.5， 那么 3（χ+2.1）=10.5○X□3
填空:在○中填符号，□中填Байду номын сангаас当的数。
如果х+15= 48，那么
a
= bb
图1
a
bb
图1
a
bb
图1
a
bb
a
bb
平衡的天平两边同时增加 同样的物品，天平仍然保持平衡。
图1
a
bb
图2
１个花盆和 3 个花瓶同样重。
天平保持平衡的道理1:
平衡的天平两边同时增加 或减少 同样的物品，天平仍然保持平衡。
等式的基本性质1: 等式的两边同时加上或减去同一个数， 左右两边仍然相等。
如果a＝b，那么 a＋c＝b＋c a－c＝b－c
图3
χ
yy
2个
2个
图4
１个排球和 3 个皮球同样重。
天平保持平衡的道理2:
平衡的天平两边物品同时扩大或缩小相 同的倍数，天平保持平衡。
等式的基本性质3: 等式的两边同时乘或除以同一个数 （0除外），左右两边仍然相等。
如果a＝b，那么 a×c＝b×c a÷c＝b÷c (c≠0)
两边拿掉（ 1 ）个苹果，天平仍保持平衡。 一把香蕉和（ 5 ）个苹果同样重。
6只樱桃和( 3)个草莓同样重， ( 2)只樱桃和1个草莓同样重。
填空:在○中填符号，□中填适当的数。
如果a=b, 那么a+0.6=b○+0□.6
a○- 13□=b-
1 3
a×2.5=b○×□2.5
a○÷□6 =b÷6
② 如果χ-48=26.8， 那么χ-48+48=26.8○+□48
③ 如果χ+2.1=10.5， 那么 3（χ+2.1）=10.5○X□3
填空:在○中填符号，□中填Байду номын сангаас当的数。
如果х+15= 48，那么
等式与不等式的基本性质
等式与不等式的基本性质在数学中，等式和不等式是两个基本的数学概念。
它们有着各自独特的性质和应用。
本文将讨论等式和不等式的基本性质，并且展示它们在解决实际问题中的应用。
一、等式的基本性质等式是表示两个表达式相等的数学陈述。
在等式中，左边的表达式被称为等号的左部，右边的表达式被称为等号的右部。
等号将左部和右部连接在一起。
1. 反身性：等式两边互相等于自身。
例如，x = x 是一个满足反身性的等式。
2. 对称性：等式两边可以互相交换。
例如，如果 a = b，那么 b = a。
3. 传递性：如果 a = b，b = c，则有 a = c。
这意味着等式具有传递性。
4. 相等性原理：如果两个对象是相等的，那么它们的任何性质都是相等的。
这是等式的重要性质。
5. 合并性质：对于任何数 a 和 b，如果 a = b，则 a + c = b + c，其中c 是任意数。
等式在代数中扮演着非常重要的角色。
通过解方程，我们可以确定未知数的值，从而解决各种实际问题。
二、不等式的基本性质不等式是表示两个表达式大小关系的数学陈述。
根据大小关系，不等式可以分为大于（>）、小于（<）、大于等于（≥）、小于等于（≤）等形式。
1. 传递性：如果 a > b，b > c，则有 a > c。
不等式也具有传递性。
2. 反身性：不等式的反身性是指a ≥ a 或a ≤ a 总是成立的。
3. 加法性质：对于任何数 a、b 和 c，如果a ≥ b，则a + c ≥ b + c。
同样地，如果a ≤ b，则a + c ≤ b + c。
4. 乘法性质：对于任何数 a、b 和 c，如果a ≥ b 且 c > 0，则a * c ≥b * c。
同样地，如果a ≤ b 且c < 0，则a * c ≤ b * c。
不等式的性质在解决各种实际问题中非常有用。
例如，在优化问题中，我们可以使用不等式来确定最大值或最小值。
三、等式与不等式的应用等式和不等式在各个领域都有广泛的应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、设置问题，导入新课
你能用估算的方法求下列方程的解吗？
(1) x 2 5
很简单，就是 x 3
1 (2) x 5 4 3
到底是什么呢？
探究等式性质1
探究等式性质1
探究等式性质1性质1
探究等式性质1
探究等式性质1
探究等式性质1
例2：利用等式的性质解下列方程
(1) x 7 26
解：两边减7，得
x 7 7 26 7
于是
x 19
小试牛刀 1、利用等式的性质解下列方程并检验
(1) x 5 6 解：两边加5，得 x 55 65 于是 x 11 检验：把 x 11代入 方程 x 5 6，得： 左边 11 5 6 右边 所以 x 11 是方程的解
小结：
学习完本课之后你有什么收获？
1、等式的性质1？ 用字母怎样表示？
2、解方程最终必须将方程 化作什么形式？
作业：
课本P85,4
x 1 y 3 x 5a y 5a
( ) × ( )
已知y+4=2，下列等式成立吗？根据是什么？ （1）y=2-4 解： （2）4=2-y （3）y=2-y
（1）成立，根据等式的性质1，等式两边都减去4 （2）成立，根据等式的性质1，等式两边都减去y
（3）不成立，根据等式的性质1
3.1.2 等式的性质
1. 什么叫做一元一次方程？ 方程两边都是整式，只含有一个未知数， 并且未知数的指数是一次的方程叫一元一次 方程。 2. 下列各式中，哪些是一元一次方程？ （1）7+8=15 （2）x+3=8 （3）3x-1 （5）2x-y=3x+1 （4）x=0 （ 6） 3 x 2 1 5
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
等式性质1： 等式两边加（或减）同一个数（或式子），结果 仍相等。 c b ____ c 如果 a b，那么 a ___
练一练：判断对错，对的请说出根据什么？错 的请说出为什么。
1) 如果 x y ，那么 2) 如果 x y，那么