10-6 静电场的环路定理 电势能
合集下载
静电场的环路定理 电势
(8-22)
静电场的环路定理 电势
式中，Uab为静电场中任意两点 a、b间的电势差，也称为电压.式（ 8-22）表明，静电场中a、b两点的 电势之差等于把单位正电荷从a点沿 任意路径移到b点电场力所做的功.电 势差是绝对的.
静电场的环路定理 电势
四、 电势的计算 1. 点电荷电场的电势
设在真空中有一点电荷q，其周围的电场分布为
(8- 21)
式（8-21
a的电势在数值上等
于把单位正电荷从a点沿任意路径移到无限远电场力所做的功.在
许多实际问题中，也常选地球为电势零点.
电势是标量，在国际单位制中，电势的单位为伏特（V）.
静电场的环路定理 电势
2. 电势差
从电场力做功的角度引入电势能的概念，由式(8-19) 和式(8-20)可以看出，电势能Wa不仅与a点的电场性质有 关，还与试验电荷q0有关，因而不能用来描述电场中某场 点的性质.但是，人们发现电势能与试验电荷q0的比值与试 验电荷q0无关，仅与a点电场的性质有关.因此，用电势描 述电场的能量特征.a、b两点的电势分别用Va、Vb表示.由 式（8-18），定义
dW=F·dl=q0E·dl=q0Edlcosθ
静电场的环路定理 电势
式中，θ为E与dl的夹角.由图8-20可以看出，元位移dl在电场力 方向的投影为dlcosθ=dr，则元功可写成
静电场的环路定理 电势
既然每个点电荷的电场力对q0所做 的功都与路径无关，那么它们的代数和 也必然与路径无关.由此可以得到以下结 论：在任意带电体的电场中，电场力对 试验电荷q0所做的功只与试验电荷q0及 其始末位置有关，而与路径无关.
静电场的环路定理 电势
2. 电势叠加原理
设场源电荷是由分布在有限区域内的点电荷系q1、q2、q3、 …、qn组成，根据场强叠加原理，任一点P处的场强等于各个点电 荷在该点产生场强的矢量和，即
静电场的环路定理 电势
式中，Uab为静电场中任意两点 a、b间的电势差，也称为电压.式（ 8-22）表明，静电场中a、b两点的 电势之差等于把单位正电荷从a点沿 任意路径移到b点电场力所做的功.电 势差是绝对的.
静电场的环路定理 电势
四、 电势的计算 1. 点电荷电场的电势
设在真空中有一点电荷q，其周围的电场分布为
(8- 21)
式（8-21
a的电势在数值上等
于把单位正电荷从a点沿任意路径移到无限远电场力所做的功.在
许多实际问题中，也常选地球为电势零点.
电势是标量，在国际单位制中，电势的单位为伏特（V）.
静电场的环路定理 电势
2. 电势差
从电场力做功的角度引入电势能的概念，由式(8-19) 和式(8-20)可以看出，电势能Wa不仅与a点的电场性质有 关，还与试验电荷q0有关，因而不能用来描述电场中某场 点的性质.但是，人们发现电势能与试验电荷q0的比值与试 验电荷q0无关，仅与a点电场的性质有关.因此，用电势描 述电场的能量特征.a、b两点的电势分别用Va、Vb表示.由 式（8-18），定义
dW=F·dl=q0E·dl=q0Edlcosθ
静电场的环路定理 电势
式中，θ为E与dl的夹角.由图8-20可以看出，元位移dl在电场力 方向的投影为dlcosθ=dr，则元功可写成
静电场的环路定理 电势
既然每个点电荷的电场力对q0所做 的功都与路径无关，那么它们的代数和 也必然与路径无关.由此可以得到以下结 论：在任意带电体的电场中，电场力对 试验电荷q0所做的功只与试验电荷q0及 其始末位置有关，而与路径无关.
静电场的环路定理 电势
2. 电势叠加原理
设场源电荷是由分布在有限区域内的点电荷系q1、q2、q3、 …、qn组成，根据场强叠加原理，任一点P处的场强等于各个点电 荷在该点产生场强的矢量和，即
第 2 章 电势
四、电势梯度 例题
五、电势能
1.定义
静电场是保守场，可引进静电势能的概念。检验
电荷 q0 在静电场中从 a 点移到 b 点电场力作正
功，电势能减少。
定义电势能增量Δ W
W Wb Wa dA
L rb ra
E P mgh
q0 E dl
b a
x2 r 2
r
O
R
x
P
dS
4 0 x 2 r 2
S
dS 2rdr R 2 rdr ( x 2 R2 x) 0 4 0 x 2 r 2 2 0
三、电势叠加原理 讨论
(1) x R时 R2 1 1 R2 2 ( x R ) x(1 2 ) 2 x(1 ) 2 x 2 x R2 x 2x R2 R2 Q (x x) 2 0 2x 40 x 40 x
rb
ra
E dl
q0 (b a )
五、电势能 定义电势能
W q0
即：一个电荷在电场中某点的电势能等于它的电 量与电场中该点电势的乘积。 一般取 r→∞ 时为势能零点，则空间任一点的电 势能为
W q0
r
E dl
五、电势能
2.注意
（1）电势能是属于系统的，为场源电荷和电荷
第 2 章
电势
一、静电场环路定理 二、电势差和电势 三、电势叠加原理 四、电势梯度 五、电势能 六、静电场的能量
一、静电场环路定理
1.静电场力所作的功
与引力场相类似，静电场也是保守场，静电力
是保守力，即静电力作功与具体路径无关。 点电荷电场： dA q0 E dl q0 cos1 dl q E b E e 2 r 40 r q0 Edr
电磁学知识点归纳
电磁学知识点归纳1.库仑定律：描述电荷之间相互作用的定律。
对于电荷q1和q2，它们之间的库仑力的大小与它们的电荷量成正比，与它们之间的距离的平方成反比。
方向沿从q1指向q2的方向。
2.高斯定理：描述电场与电荷分布之间的关系。
在真空中，电场通过一个封闭曲面的通量与该曲面内部的自由电荷量成正比。
在介质中，电通量密度通过一个封闭曲面的通量与该曲面内部的电荷量成正比。
3.点电荷的电场：描述点电荷在空间中产生的电场。
对于点电荷q，它在距离r处产生的电场的大小与1/r^2成反比，方向沿径向。
4.无限大均匀带电平面：描述一个无限大的带电平面所产生的电场。
在平面两侧，电场强度大小相等，方向相反，大小与平面上的电荷密度成正比，与距离平面的距离成反比。
5.电势与电势能：描述电场在空间中的分布所产生的电势。
电势在某一点的数值等于单位正电荷在该点所具有的电势能。
电势能是电荷在电场中移动所具有的能量。
6.静电场的环路定理：描述静电场为保守场的特点。
在一个闭合回路中，电场沿路径做功的总和等于回路内电势能的变化量。
7.均匀带电球面的电场和电势：描述一个均匀带电球面所产生的电场和电势。
在球面内部，电场强度大小与距离球心的距离成反比，方向沿径向。
在球面外部，电场强度大小与距离球心的距离平方成反比，方向沿径向。
8.导体静电平衡的特点：描述导体在静电平衡时的特点。
导体内部电场强度为零，导体表面的电场强度方向垂直于导体表面，导体是一等势体，导体表面的电场强度大小与表面附近处的电荷面密度成正比，导体内部无净余电荷，净余电荷只能分布在导体的表面。
9.电容的定义式：描述电容的定义式。
电的电容只与两导体的形状、大小、相对位置及周围介质有关，与电荷量和电势差无关。
10.常见电的电容：描述常见电的电容计算公式。
孤立导体球的电容与球半径成正比，平板电的电容与板间距成反比，球形电的电容与球半径成正比，柱形电的电容与柱长的自然对数成正比。
11.电容的串并联：描述电容的串联和并联。
静电场的环路定理静电场力的功电势能
静电场力的功
02
电场力的定义
电场力是电荷在电场中受到的 力，其大小和方向由电场强度
和电荷的乘积决定。
电场力的大小为 F=qE，其 中 F 是电场力，q 是电荷量，
E 是电场强度。
电场力的方向与电场强度的方 向相同，即由正电荷指向负电
荷。
电场力做功的计算
电场力做功可以通过积分计算，即 W=∫F·dr，其中 W 是电场力做的功， F 是电场力，dr 是位移矢量。
在匀强电场中，电场力做功可以通过 W=qEd计算，其中 W 是电场力做 的功，q 是电荷量，E 是电场强度，d 是位移。
在非匀强电场中，需要计算电场力在路径上的积分来计算电场力做的功。
电场力做功的特点
01
电场力做功与路径无关，只与初末位置的电势差有关。
02
电场力做功是标量，没有方向。
03
电场力做功的过程是能量转化的过程，可以转化为其他形式 的能量。
电势能
03
电势能的定义
电势能是指电荷在电场中由于位置差 异而具有的能量。
电势能是电荷与电场共同具有的能量， 其大小由电场强度和电荷量共同决定。
电势能是相对的，与零电势点的选择 有关。
电势能的变化规律
1
电场力做功与路径无关，只与初末位置有关。
2
电场力做正功，电势能减少；电场力做负功，电 势能增加。
3
静电力做功与电荷的运动路径无关，只与初末位 置有关。
电势能与电场力的关系
01
电场力做功等于电势能的减少量。
02
电势能的变化量等于电场力做的功。
03 电势能与电场力做功的关系是能量守恒定律在静 电场中的具体表现。
THANKS.
静电场的环路定理、静 电场力的功、电势能
高中物理竞赛初级讲义 电学电势及电势能
电势叠加原理：任意带电体电场中某点的电势，等于带电体上各部分电荷单独存在时，在该点产生电势的代数和。
半径为R、电荷为q的均匀带电球壳内外，距球心r处的电势：
【例1】试求电偶极子周围的电势分布．
【例2】试求均匀带电圆环轴线上电势和电场分布。设圆环半径为R，电荷线密度为η。
【例3】半径为R的半球形薄壳，其表面均匀分布面电荷密度为σ的电荷，求该球开口处圆面上任一点的电势．
【例7】如图所示，AB=2l，OCD是以B为中心，l为半径的半圆。A点有正点电荷q，B点有负点电荷-q。
（1）把单位正电荷从O点沿OCD移到D点，电场力对它作了多少功？
（2） 把单位负电荷从D点沿AB的延长线移到无穷远，电场力对它作了多少功？
（3）电荷q均匀分布在半球面ACB上，球面半径为R，CD为通过半球顶点C和球心O的轴线，如图所示．P、Q为CD轴线上相对O点对称的两点，已知P点的电势为φP，试求Q点的电势φQ．
【例6】有人设想了一种静电场：电场的方向都垂直于纸面并指向纸里，电场强度的大小自左向右逐渐增大，如图所示．这种分布的静电场是否可能存在？试述理由．
电势差：电场中两点电势的差值叫电势差。
匀强电场中，沿场强方向两点间的电势差：
2.等势面
等势面：静电场中电势相同的点组成的面叫等势面。
判断电势高低的方法：
等量异种点电荷和等量同种点电荷连线上与中垂线上场强及电势的变化规律
3.电势的计算
（1）由定义 ，B点为电势零点，一般为无穷远处
（2）点电荷的电势： ，其中r是场点到电荷q的距离。
电磁学第3讲电势及电势能
一、电势能
1.静电场的环路定理
静电场力是保守力，静电场是保守场。
静电场的环路定理：静电场中场强沿场力对电荷所做功等于电荷电势能的改变量：
半径为R、电荷为q的均匀带电球壳内外，距球心r处的电势：
【例1】试求电偶极子周围的电势分布．
【例2】试求均匀带电圆环轴线上电势和电场分布。设圆环半径为R，电荷线密度为η。
【例3】半径为R的半球形薄壳，其表面均匀分布面电荷密度为σ的电荷，求该球开口处圆面上任一点的电势．
【例7】如图所示，AB=2l，OCD是以B为中心，l为半径的半圆。A点有正点电荷q，B点有负点电荷-q。
（1）把单位正电荷从O点沿OCD移到D点，电场力对它作了多少功？
（2） 把单位负电荷从D点沿AB的延长线移到无穷远，电场力对它作了多少功？
（3）电荷q均匀分布在半球面ACB上，球面半径为R，CD为通过半球顶点C和球心O的轴线，如图所示．P、Q为CD轴线上相对O点对称的两点，已知P点的电势为φP，试求Q点的电势φQ．
【例6】有人设想了一种静电场：电场的方向都垂直于纸面并指向纸里，电场强度的大小自左向右逐渐增大，如图所示．这种分布的静电场是否可能存在？试述理由．
电势差：电场中两点电势的差值叫电势差。
匀强电场中，沿场强方向两点间的电势差：
2.等势面
等势面：静电场中电势相同的点组成的面叫等势面。
判断电势高低的方法：
等量异种点电荷和等量同种点电荷连线上与中垂线上场强及电势的变化规律
3.电势的计算
（1）由定义 ，B点为电势零点，一般为无穷远处
（2）点电荷的电势： ，其中r是场点到电荷q的距离。
电磁学第3讲电势及电势能
一、电势能
1.静电场的环路定理
静电场力是保守力，静电场是保守场。
静电场的环路定理：静电场中场强沿场力对电荷所做功等于电荷电势能的改变量：
静电场的环路定理 电场的电势(势函数)：静电场的保守性意味着,对静电场来说,存在着一个由电场中各点位
9-6 电势
物理学教程 （第二版）
三 电势的叠加原理
点电荷系 E Ei
i
VA E dl Ei dl
A
iA
q1
q2 q3
r1 r2 r3
E3
E2
A
E1
VA
VAi
i
i
qi
4π 0ri
电荷连续分布
VP
dq
4π 0r
dqqdrqP
dV
dE
第九章 静电场
9-6 电势
第九章 静电场
9-6 电势
物理学教程 （第二版）
此标量函数（电势）在 A、B 两点的数值之差等 于从A到B移动单位正电荷时静电场力所做的功.
E dl
( EpB
EpA )
AB
q0 q0
q0
E dl AB
(VB
VA )
A
B E
B 点电势
VB
EpB
q0
A 点电势
VA
EpA q0
VA AB E dl VB （ VB为参考电势，值任选）
由
V外 (r)
Q
4π 0r
可得
V (R)
Q
4π 0R
V内
或
V内(r)
R r
E1
dr
R
E2
dr
Q
4π 0R
Q
V外 (r) 4π 0r
Q
V内(r) 4π 0R
V
Q
4 π 0R
oR
Q
4π 0r物理中能量单位 1eV 1.602 1019 J
第九章 静电场
9-6 电势
物理学教程 （第二版）
二 点电荷的电势
大学物理10.4静电场的环路定理电势能.ppt
q1
q2
qi qn
带电体对q0 做功与路径无关 结论 静电场力做功只与始末位置有关，与路径无关，所以静 电力是保守力，静电场是保守力场。
二、静电场的环路定理
在静电场中，沿闭合路径移动q0，电场力做功
b
Aab q0E dl
L1
q0 由 a 点经 L1 到 达 b 点所做的功
b
a
a(L1) q0E dl b(L2 ) q0E dl
验一个电场不是静电场。 b c d a
E dl a E dl b E dl c E dl d E dl
b
d
a E1dl c E2dl
E1ab E2 cd 0 不是静电场
a
b
E
d
c
(2) 环路定理表明静电场电力线不能闭合（无旋场）。 (3) 静电场是无旋场，可引进电势能。
单个点电荷产生的电场rrqq4barrd1200???0al?dbabaqel????11400barrqq???lr?d?rqqbarr?4300???balbrardl?rd?qe??q0点电荷对q0做功与路径无关dr?l??drr?cosd?rl?r?r?d?r?dr?rr????0al?balqe?bqe?dbabaqel????012d?neel??????????01020alal?al?dddbbnlqelqel????????????????结论静电场力做功只与始末位置有关与路径无关所以静电力是保守力静电场是保守力场
例 如图所示, 在带电量为 Q 的点电荷所产生的静电场中，
有一带电量为 q 的点电荷
求 q 在 a 点和 b 点的电势能
解 • 选无穷远为电势能零点
Q
qQ 1
静电场的环路定理、电势
R2
3
)2
=……
例3：求无限长均匀带电直线的电场中的电势 分布。
解：选取B点为电势零点，B点距带电直导 线为 rB 。
B B
U E dl
dr
p
p 2 0r
2 0 ln r 2 0 ln r0 2 0 ln r C
rp
Q rB B
☆当电荷分布扩展到无穷远时，电势零点不能 再选在无穷远处。
a
b
a
a、b两点的电势差等于将单位正电荷从a点移
到b时，电场力所做的功。
电势和电势能的区别：
电势是电场的属性，与试验电荷无关； 电势能是属于电荷和电场系统所共有。
注意:
1、电势是相对量，电势零点的选择是任意的。 对于有限带电体而言,电势零点的选择在无限 远点;对于仪器而言电势零点选择在底板上.
2、两点间的电势差与电势零点选择无关。
六、电势的计算
1、点电荷电场中的电势
q • r0
•P
距q为r（P点）的场强为
q
E 4 0r 2 r0
r
由电势定义得：uP
P
E • dl
q
r
4
0r
2
dr
q
4 0r
讨论：
➢大小
q 0 u 0 r u r u最小 q 0 u 0 r u r u最大
就等于把它从该点移到零势能处静电场力所作的功
五、电势、电势差
定义电势
ua
Wa q0
E dl
a
Wa q0 E dl
a
单位正电荷在该点 所具有的电势能
单位正电荷从该点到无穷远 点(电势零)电场力所作的功
定义电势差 ua ub
电场中任意两点 的 电势之差（电压）
大学物理电场的环路定理及电势的计算
0
qr
3
(r R ) (r R )
4 0 r
E
令 U 0 ，沿径向积分
1 r
2
U外
P
E 外 d r q 1 r
o
4
r
qr dr
0
r
3
R
r
4 0 r
U外
q 4 0 r
E dr
R
1 r
R
a
E dl
零势点
Ecosdl
a
注意： • 选取零势点的原则：使场中电势分布有确定值 一般,场源电荷有限分布:选 U 0 场源电荷无限分布:不选 U 0 许多实际问题中选 U 地 球 0
[例一] 点电荷 q 场中的电势分布
r E
o
P
解： E
L L
静电场中任意闭合路径
静电场环路定理
E dl 0
L
路径上各点的总场强
静电场强沿任意闭合路径的线积分为零.反映了 静电场是保守力场.
凡保守力都有与其相关的势能，静电场是有势场.
三. 电势能 W
由 A保 E P W
b
A静 电 力 q 0
a
E dl (W b W a ) W a W b
dq 4 0 r
dU
4 r d r
2
4 0 r
rd r 0
R2
由叠加原理：
r
R2
R1
o P
U
dU
静电场环路定理电势能和电势.pptx
V
dV
1dq
Q440r0
r
Q
dq
Q
4 0 R2 x 2
(解毕 )
第23页/共43页
x a
x V (x) dr R o Qr
4 0R
o
x
课堂练习 求均匀带电园盘( R, σ )轴线上电势分布。
提示： 建立坐标系，取元，如图所示。
选∞处为电势零点，则：
dV 2dqrdr 4 0 r 2 x 2
q
r
r
r
4
q
0 r 2
dr
aq r
r 10V
E
8V 6V
V (r )
q
4 0r
( 球对称分布 )
等势面分布
第14页/共43页
课堂练习 求半径为R均匀带电 Q 的球面电势分布。
解 选∞处为电势零点，则：
V (r) r E dr
0
E(r) Q
4 0r 2
(r R) (r R)
r
4
即：电势 V 的叠加为标量叠加，而 叠加，后者运算较繁。
的叠加却为矢量
E
第13页/共43页
E
☻由于静电场的保守特性，
b
V与a积分路a 径E无 dr
关，可选取一合理的路径进行积分。
例 求点电荷 q 的电势分布。
解 选∞处为电势零点，则：
V (r)
E dr
E dr cos 0
(r (r)
R)
E
dr
R
E
dr
E dr
r
r
R
V (r) 0
Q
R 4 0r2
dr
cos
0
Q
08.3静电场的环路定理、电势
E a E b
b
a
u 3
u 2 u 1
2.电势梯度 电势梯度 单位正电荷从 a到 b电场力的功 到 电场力的功
u+d +u
E•d = Ec sθ l =u−(u+d ) l o d u Ec sθ l =− u o d d
在 l E d 方向上的分量 电场强度沿某 一方向的分量 一般
u
E l
n
a
b
l 由电势定义得 u =∫ E•d =∫ P
r
∞
4 ε0r π
d = r
q 4 ε0r π
讨论 大小
q>0 u>0 r ↑ u↓ r → u 小 ∞ 最 q<0 u<0 r ↑ u↑ r → u 大 ∞ 最
为球心的同一球面上的点电势相等 对称性 以q为球心的同一球面上的点电势相等
点电荷系的电势 由电势叠加原理， 的电势为 由电势叠加原理，P的电势为
单位正电荷在该点 所具有的电势能
∞
W = ∫q E•d l a 0
a
∞
单位正电荷从该点到无穷远 电势零)电场力所作的功 点(电势零 电场力所作的功 电势零
定义电势差 a b 定义电势差 u −u 电场中任意两点 的 电势之差（电压） 电势之差（电压）
u =u −u =∫ E•d −∫ E•d =∫ E•d l l l ab a b
d q −q A =u −u =0−( ) + oc o c 4 03R 4 0R a πε πε b c q +q 0 −q = 6 0R πε R R R
② 将单位负电荷由 ∞ O电场力所作的功
A O =u −u =0 o ∞ ∞
功、电势差、电势能之间的关系 电势差、
b
a
u 3
u 2 u 1
2.电势梯度 电势梯度 单位正电荷从 a到 b电场力的功 到 电场力的功
u+d +u
E•d = Ec sθ l =u−(u+d ) l o d u Ec sθ l =− u o d d
在 l E d 方向上的分量 电场强度沿某 一方向的分量 一般
u
E l
n
a
b
l 由电势定义得 u =∫ E•d =∫ P
r
∞
4 ε0r π
d = r
q 4 ε0r π
讨论 大小
q>0 u>0 r ↑ u↓ r → u 小 ∞ 最 q<0 u<0 r ↑ u↑ r → u 大 ∞ 最
为球心的同一球面上的点电势相等 对称性 以q为球心的同一球面上的点电势相等
点电荷系的电势 由电势叠加原理， 的电势为 由电势叠加原理，P的电势为
单位正电荷在该点 所具有的电势能
∞
W = ∫q E•d l a 0
a
∞
单位正电荷从该点到无穷远 电势零)电场力所作的功 点(电势零 电场力所作的功 电势零
定义电势差 a b 定义电势差 u −u 电场中任意两点 的 电势之差（电压） 电势之差（电压）
u =u −u =∫ E•d −∫ E•d =∫ E•d l l l ab a b
d q −q A =u −u =0−( ) + oc o c 4 03R 4 0R a πε πε b c q +q 0 −q = 6 0R πε R R R
② 将单位负电荷由 ∞ O电场力所作的功
A O =u −u =0 o ∞ ∞
功、电势差、电势能之间的关系 电势差、
环路定理 电势能差 电势差
q
dl r
r dr F
E
电场力的功只与始末位置有关，而与路径无关。 2.任意带电体系的场 对于由多个静止点电荷组成的系统或静止的连续带 电体，可看成是由无数电荷元组成。
由场强叠加原理可得到电场强度的线积分（移动单 位电荷的功）为：
3
b
aபைடு நூலகம்
b E dl ( E1 E2 En ) dl a b b b E1 dl E2 dl En dl Aab
a
电场力是保守力
5
二、电势能和电势
电场力是保守力，可引入势能的概念。 1.电势能差
b
q0 a
E
设在静电场中，将检验电荷 q0 从 a 点沿任意路径移动 到 b 点，电场力作功为Aab。 定义: 电荷 q0 在静电场中a 、b两点间的电势能差定义为， q0从 a 点沿任意路径移动到 b 点的过程中， Wa - Wb等于电场力所作 的作功Aab 电势能差（势能增量的负值）等于保守力所作的功。
•对无限带电体不宜选无穷远为电势零点。此时只有 电势的相对值（即电势差）有意义。
4.电势能与电势的区别：W 可正可负，取决于 q 和 q0 ； U只取决于场源电荷 q 。
10
另一方面： 当已知电势分布时，可由电势差求出点电荷在电 场中移动的过程中电场力所做的功：
Aab q0
b
a
E dl q0 (U a U b )
a
式中：Wa、Wb是电荷q0分别在a点和b点时,q0与电场所组成的系统 的静电势能。
b
2.电势能
电势能也是一个相对的量，若选择一个零势能 点作为参考。 若令 W 0, 即选定b点为电势能零点。 b 则，电荷q0在此系统的电场中a点的电势能为：
静电场的环路定理和电势
若令 E p(b) 0
(0)
(0)
Ep(a)
(a)
F dl
q0
E dl
(a)
3 电势
定义：把一个单位正电荷从静电场中 P1点移到 P2 点，电场力作的功等于 P1点到P2点电势的减量。
P1
P2
两点之间的电势差， 并不仅由这两点处的电场决定， 它取决于电场的分布。
设 P2为电势为零的参考点，2 =0
对无限大电荷分布， 选有限远 的适当点为电势零点。
实际上：常选大地或机壳的公共线 为电势零点。
例1：求点电荷 q 的电势分布。
【解】 利用电势定义（积分法）
取无限远为电势零点,
()
E dl ( p)
r
q
4 π 0r 2
dr
q
4 π0r
0
q
r
P
∞
r dl
q> 0 r
q< 0
--------点电荷的电势公式
取某一距离直线为 r0 的 P0点的电势为零。
任一点 P 的电势
P0
rP
Edl P
P P0
P’
P0
Edl Edl
P
P
r0
r0
0
dr
r 2 π0r
rP
P’
r0
> 0
0 r0
r0
dr
r 2 π0r
P0
r > r0 的点，电势为负,
r = r0 的点，电势为零,
由场强叠加原理
可以证明：
任意点电荷系或连续带电体的静电场也是保守力场。
常用下式表示静电场 的保守性：
……称为静电场的环路定理
电势叠加原理
a
a
路径上各点的总场强
例：点电荷 q 场中的电势分布
o
rr
P
r E
解：
r E
=
r qr
4πε 0 r 3
q
U
∝1 r
令
U
U
=
∞=
∞r ∫E⋅
0
r dl
沿径向积分
rr
=
∞
∫
qr
⋅
dr
P
r 4πε r3
0
∞
=∫
qdr
=
q
r 4πε r2 4πε r
0
0
o
r
电势叠加原理
例1.
解：
简例
2. 连续分布电荷的电场中的电势
=
q
4πε0(R2 +
x )2
1 2
例3.
带电薄圆盘
解：
例4.
带电薄球壳
例5.求均匀带电球壳腔内任意点电势
已知： R1, R2 , ρ
求：U P
R2
ρ
r o R1
解：将带电球壳视为许多均匀带
P
dr
电球面的集合，
取半径 r ，厚 dr 的球壳为电荷元：dq = ρ ⋅ 4πr2 ⋅dr
令 U ∞ = 0 ，dq 在腔内产生的电势：
dU = dq = ρ ⋅ 4πr 2dr = ρrdr
4πε 0 r
4πε 0 r
ε0
∫ ∫ 由叠加原理：U =
dU
=
R2 ρ rdr ε R1 0
=
ρ 2ε 0
( R2 2
−
R12 )
即：腔内各点等势
解：
等势面 等势面
静电场的环路定理
a ( L2 )
b
a ( L1 )
v v b q0 E ⋅ dl − ∫
v v q0 E ⋅ dl
环路定理
=0
∫
L
v v E ⋅ dl = 0
该定理还可表达为：电场强度的环流等于零。 该定理还可表达为：电场强度的环流等于零。 根据保守力的定义，任何力场， 根据保守力的定义，任何力场，只要其场强的环流 为零，该力场就叫保守力场 势场。 保守力场或 为零，该力场就叫保守力场或势场。可以引入相应 的势能，即电势能。 的势能，即电势能。
q 4πε 0 x
•从电荷分布求场强，再由场强分布求电势 从电荷分布求场强， 从电荷分布求场强
U P = ∫ E • d r （场强积分法） 场强积分法）
P ∞
例4 求均匀带电球面的电场中电势的分布 解 由高斯定理可以求的球面内外的场强分布为
+ P1 + + + + +
2
r <R r ≥R
对球外一点P 对球外一点
二 电势
某点电势电W 之比只取决于电场， 某点电势电 a与q0之比只取决于电场，定义电该 点的电势 单位：伏特（ ） 电势. 点的电势. 单位：伏特（V） 电势电
W a = q0 ∫
"0"
a
v E ⋅ dl
电势
WA VA = q0
=∫
"0"
A
v E⋅ E⋅ dl
由上式可以看出, 由上式可以看出,静电场中某点的电势在数值上 等于单位正电荷放在该点处时的电势能, 等于单位正电荷放在该点处时的电势能,也等于单位 正电荷从该点经任意路径到电势零点处(无穷远处) 正电荷从该点经任意路径到电势零点处(无穷远处) 时电场力所做的功。 时电场力所做的功。
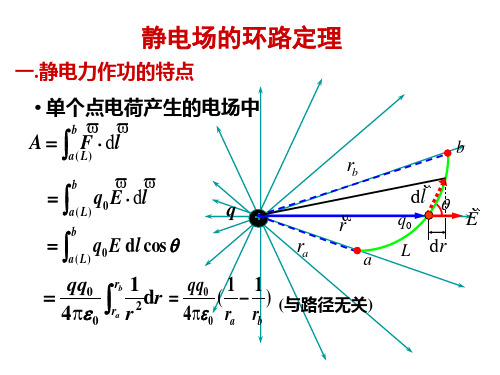
b
a ( L1 )
v v b q0 E ⋅ dl − ∫
v v q0 E ⋅ dl
环路定理
=0
∫
L
v v E ⋅ dl = 0
该定理还可表达为：电场强度的环流等于零。 该定理还可表达为：电场强度的环流等于零。 根据保守力的定义，任何力场， 根据保守力的定义，任何力场，只要其场强的环流 为零，该力场就叫保守力场 势场。 保守力场或 为零，该力场就叫保守力场或势场。可以引入相应 的势能，即电势能。 的势能，即电势能。
q 4πε 0 x
•从电荷分布求场强，再由场强分布求电势 从电荷分布求场强， 从电荷分布求场强
U P = ∫ E • d r （场强积分法） 场强积分法）
P ∞
例4 求均匀带电球面的电场中电势的分布 解 由高斯定理可以求的球面内外的场强分布为
+ P1 + + + + +
2
r <R r ≥R
对球外一点P 对球外一点
二 电势
某点电势电W 之比只取决于电场， 某点电势电 a与q0之比只取决于电场，定义电该 点的电势 单位：伏特（ ） 电势. 点的电势. 单位：伏特（V） 电势电
W a = q0 ∫
"0"
a
v E ⋅ dl
电势
WA VA = q0
=∫
"0"
A
v E⋅ E⋅ dl
由上式可以看出, 由上式可以看出,静电场中某点的电势在数值上 等于单位正电荷放在该点处时的电势能, 等于单位正电荷放在该点处时的电势能,也等于单位 正电荷从该点经任意路径到电势零点处(无穷远处) 正电荷从该点经任意路径到电势零点处(无穷远处) 时电场力所做的功。 时电场力所做的功。
10静电场2(环路定理、电势)
2
P 1
3.关系：E q V P 0
W EP1 EP2 q0U12
二、点电荷电场的电势 在点电荷的电场中任取一点P，由电势的定义来 计算P的电势：
V
P
E dr E dr
P
q
P
q 40 r
2
P
dr
q 40 r
r
E dr
积分路径选为沿径向的直线 在正点电荷的电场中，电势为正，随r的增大电 势逐渐减小；在负点电荷的电场中，电势为负，随 r的增大电势逐渐增大。并且，在点电荷的电场中， 电势也呈球对称分布。
2．在电场中任一点，电势沿不同方向的空间 变化率不相等。 当 0 时，l 沿着 E 的方向，变化率有最 大值： dV E max dl
即沿某一方向的电势的空间变化率最大， 此最大值称为该点的电势梯度，其方向是 该点附近电势升高最快的方向。
E
三、电势能 静电场力是保守力，可引入电势能的概念。 静电场力做功等于电势能的减少。 在静电场中，试验电荷由点 P 运动到点 P2， 1 则电场力做功为： P W q0 E dr EP EP
2
P 1
1
2
P E P1 、 P2 即分别为 q0 在 P 、 2 点的电势能。 E 1
则有： 1 V2 V
P2
P 1
E dr
1.单位：V， V 1J / C 1 2.通常选取无穷远处或大地为电势零点，则有： EP V E dr P q0
即P点的电势等于场强沿任意路径从P点到 无穷远处的线积分。
电势的值随电势零点选取的不同而不同， 是相对的；而两点的电势差是绝对的，与 电势零点无关。 P U12 V1 V2 E dr
P 1
3.关系：E q V P 0
W EP1 EP2 q0U12
二、点电荷电场的电势 在点电荷的电场中任取一点P，由电势的定义来 计算P的电势：
V
P
E dr E dr
P
q
P
q 40 r
2
P
dr
q 40 r
r
E dr
积分路径选为沿径向的直线 在正点电荷的电场中，电势为正，随r的增大电 势逐渐减小；在负点电荷的电场中，电势为负，随 r的增大电势逐渐增大。并且，在点电荷的电场中， 电势也呈球对称分布。
2．在电场中任一点，电势沿不同方向的空间 变化率不相等。 当 0 时，l 沿着 E 的方向，变化率有最 大值： dV E max dl
即沿某一方向的电势的空间变化率最大， 此最大值称为该点的电势梯度，其方向是 该点附近电势升高最快的方向。
E
三、电势能 静电场力是保守力，可引入电势能的概念。 静电场力做功等于电势能的减少。 在静电场中，试验电荷由点 P 运动到点 P2， 1 则电场力做功为： P W q0 E dr EP EP
2
P 1
1
2
P E P1 、 P2 即分别为 q0 在 P 、 2 点的电势能。 E 1
则有： 1 V2 V
P2
P 1
E dr
1.单位：V， V 1J / C 1 2.通常选取无穷远处或大地为电势零点，则有： EP V E dr P q0
即P点的电势等于场强沿任意路径从P点到 无穷远处的线积分。
电势的值随电势零点选取的不同而不同， 是相对的；而两点的电势差是绝对的，与 电势零点无关。 P U12 V1 V2 E dr
高二物理竞赛静电场的环路定理电势能课件
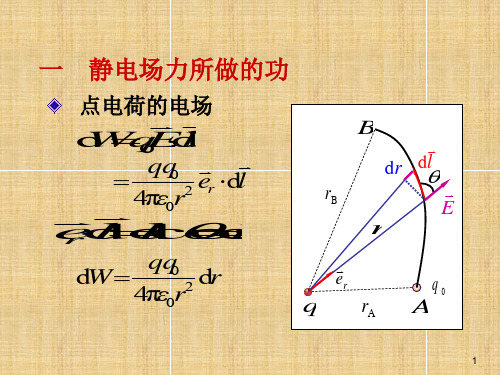
5
A q 0 E B d l E p A E p B ( E p B E p A )
令 EpB 0
EpAAq B0Edl
A E pA
BE pB E源自试验电荷q0在电场中某点的电势能，在 数值上等于把它从该点移到零势能处静电场 力所作的功.
6
1 真空中一半径为R的半圆细环，均匀带 电Q. 设无穷远处为电势零点，求圆心O处 的电势U0 . 若将一带电荷量为q的点电荷从 无穷远处移到圆心O处，求电场力做的功W.
结论: W仅与q0的始末 位置有关，与路径无关.
B
rB
dr
dl
E
r
er
q0
q rA A
2
任意带电体的电场（点电荷的组合）
EEi
i
Wq0
Edl
l
i
q0 lEi dl
结论：静电场力做功，与路径无关.
3
二 静电场的环路定理
q Edlq Edl 整个带电球层在球0心处产生的电势为
0
2静电试场用线静不电构场成的闭环合A 路曲定线B 理. 证明C，电场线
解：在球内取半径为r、厚为dr的薄球壳，该壳内所包
含的电荷为 dqdVA4 rr2dr
在半径为r的球面内包含的总电荷为
q dV r4A3d rrA4r
V
0
以该球面为高斯面，由高斯定理得
E 1•d s E 14 r2 A4/r0
s
10
• 所以
E1A2r/40 (r≤R) 方向沿径向，A>0时向外, A<0 时向里 在球体外作一半径为r的同心高斯球面，由高斯定理
空腔是等势区，各点电势均为V .
•在球层内取半径为r→r＋dr的薄球层．其电荷为
大学物理74yy 功,环路定理,电势
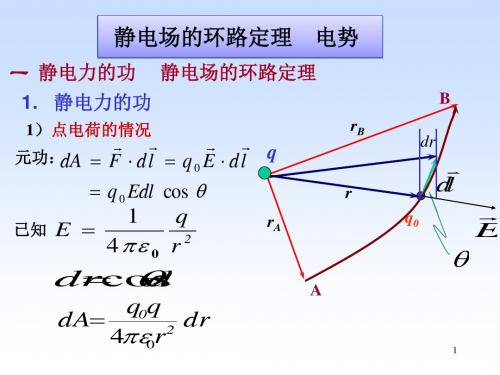
dq
4 0r
电势-----迭加原理
dq dV
r
p
dVP
VP
QdVP
dq
Q40r
12
▲5. 电势计算例题：（两种基本方法）
1.场强积分法（由定义求）
〈1〉由电势定义
〈2〉确定 E 分布
VA
WA q0
"0" A
Edl
〈3〉选零势点和 便于计算的积分路径 若路径上各段E 的表达式不同，应分段积分。
4
二、电势能 电势
1、电势能
A保EPW
设WA 和 WB 分别表示试探电荷 q 0 在起点A和终点B处的电势能
A A B W ( W B W A ) W A W B
B
B B A
A A BAF d l q 0AE d l WA
WB
q
ra
1
40
r2 dr
Q 4πε0
q ra
6
2、电势
"0"
W Aq0 A Edl
WA
"0"
Edl
q0
A
定义A 点的电势VA：
比值与试探电荷无关, 反 映了电场在 A 点的性质.
VA
WA q0
"0" A
Edl
注意：
1、电势零点与电势能零点选取规则相同 2、电势描述电场的性质，与试探电荷无关 3、电势是标量，可正可负，单位：V，伏特
求：沿线、距离一端 a 米处的电势。
0 P 解：
ddQx
a x
dV
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
任意带电体的电场（点电荷的组合） 点电荷的组合）
E = ∑ Ei
i
W = q0 ∫ E ⋅ dl = ∑ q 0 ∫l E i ⋅ d l
l
i
结论：静电场力做功，与路径无关. 结论：电势能
二
q0
静电场的环路定理
∫ E ⋅ dl = q ∫ E ⋅ dl
5
1010-6 静电场的环路定理 电势能
∫ q E ⋅ dl
A 0
B
= EpA − EpB = −( EpB − EpA )
B EpB
令 EpB = 0
E pA = ∫
EP =0 A
q 0 E ⋅ dl
A E pA
E
试验电荷q 在电场中某点的电势能， 试验电荷 0在电场中某点的电势能，在 数值上等于把它从该点移到零势能处静电场 力所作的功. 力所作的功.
0 ABC ADC
B
D
C
q0 ( ∫ E ⋅ dl + ∫ E ⋅ dl ) = 0
ABC CDA
E
∫ E ⋅ dl
l
=0
A
结论： 结论：沿闭合路径一 电场力作功为零. 周，电场力作功为零
静电场是保守场
4
1010-6 静电场的环路定理 电势能
三
电势能
静电场是保守场， 电场是保守场， 保守场 B 静电场力是保守力 保守力. 静电场力是保守力 EpB 静电场力所做的功就 E 等于电荷电势能增量 等于电荷电势能增量 A E pA 的负值. 负值 WAB = EpA − EpB = −( EpB − EpA ) 电场力做正功，电势能减少. 电场力做正功，电势能减少.
qq0 dW = dr 2 4 πε0 r
qq 0 rB dr W = ∫rA r 2 4 πε 0 qq 0 1 1 = ( − ) 4 πε0 rA rB
B
l dr dθ
rB
E
r
结论: 仅与 仅与q 结论: W仅与 0的始末 位置有关 有关， 位置有关，与路径无关.
er
q0
q
rA
A
2
1010-6 静电场的环路定理 电势能
6
1010-6 静电场的环路定理 电势能
一
静电场力所做的功
点电荷的电场
dW = q0 E ⋅ dl qq0 = e ⋅ dl 2 r 4 πε0 r
B
l dr dθ
rB
er ⋅ dl = dl cos θ = dr qq0 dW = dr 2 4 πε0 r
E
r
er
q0
q
rA
A
1
1010-6 静电场的环路定理 电势能