大学物理练习题静电场的环路定理电势

合集下载

63静电场环路定理电势

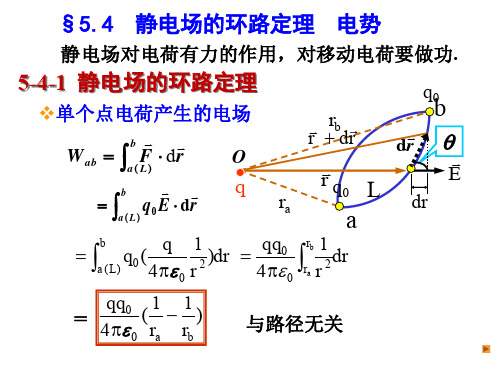
E2
q1
4 0 r 2
R1 r R2
E3
q1 +q2
40r 2
r R2
q1 II
I R1
R2 •
III
rE
P•
III区：U3
E dl
P
q2 q1 II III
E3 dr E3dr
r
r
I R1
R2 •
r
q1 q2
4 0 r 2
dr
q1 q2
40r
rr
P• P•
R2
II区： U3
R r
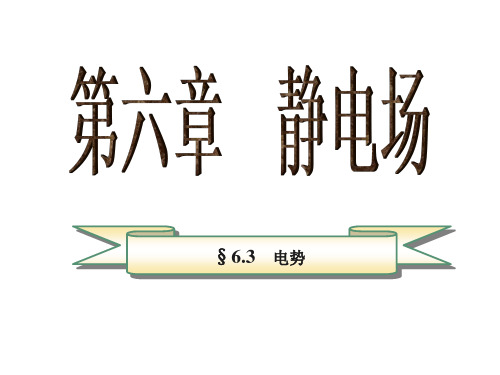
Q
4 0 R3
rdr
Q
R 4 0r 2 dr
Q
8 0 R
Qr 2
8 0 R3
Q
4 0 R
Q (3R 2 r 2 )
8 0 R3
o rp R
rp
路径的线积分为零（电场强度的环流为
零）
3. 电势能比重力做功保守力重力势能
较静电场力做功保守力电势能
静电场力对电荷所做功等于电荷电势能增量的负值
B
WAB A q0E • dl EpB EpA
令 B点为电势能零点，则可得任一点 A
的电势能
0
E p A
q0
E • dl
E dl
P
E dr
E2dr
E3dr
r
r
R2
R2 r
q1
4 0 r 2
dr
R2
q1 q2
4 0 r 2
dr
1
4 0
( q1 r
q2 R2
)
I区：
U3
E dl

6-3 静电场的环路定理和电势

V(r>R)

1
4 0
q r
练习在点电荷 +2q 的电场中，如果取图中P点处为电势零点，则 M点的电势为
2q P M
a
a
（A） q
2π 0a
（C）
q
8π
0
a
q
（B）
4π 0a
（D） q
4π 0a
练习在点电荷q的电场中，选取以q为中心，R为半径的球面上一点P处作电势零点，则与点电荷q距离为r的P’点电势为
A

（D）电场力作的功 W 0
电势的求解方法
（1）利用电势叠加原理
VP
dq
4π0r
使用条件：有限大带电体且选无限远处为电势零点.
（2）利用电势的定义
V 0点
VA E dl
A
使用条件：场强分布已知或很容易确定.
均匀带电球面：
V( r R )

1
4 0
q R
四电势
1、电势
VA

EpA q0

E dl
AB
(VB 0)
q0
A
B E
物理意义：描述电场能的性质，某点的电势在数值上等于将单位正电荷从该点沿着任意路径移到零势能点时电场力所做的功.
B
电势差（电压）：U AB VA VB
E dl
A
WAB q0 (VA VB ) (EPB EPA)
位置有关，与路径无关.
B
dr
dl
q0
E

二静电场的环路定理

q0 E dl q0 E dl

09-4静电场的环路定理和电势

P

r0

2 π 0r
dr
r
o VA 0 P r r0

2 π0
ln
r0 r
r
关于静电场的实验定律和定理的关系：静电场静止电荷
库仑定律
F12 q1q 2 4 π 0 r12
2
激发
高斯定理
e 12

1 E dS
S
0 （ S 内）

qi
平方反比律
-15
J C
1.6 10
-19
5 10 V
4
计算一个电子伏特（eV）的能量
一个电子在电场中经过电势差为1V的两点时，电场力对它做的功
W qU
1.60 10
19
C 1V 1.60 10
19
J
一个电子伏特的能量
电子伏特是近代物理学中能量单位，虽然它也出现 “伏特”这个名称，但它并非电压的单位，而是能量的单位
A B
A
AB两点之间的电势差等于场强由A点到B点的线积分
把电荷q从A点移动到B点，电场力做的功 B B WAB qE dl q E dl qU AB
A A
Wba 8 10
15
J
Wab qU ab q(Va Vb )
Vb 8 10
在负电荷形成的电场中，任一点的电势均为负，且离点电荷越远的点，电势越高
A A2 A3 1
点电荷系电场的电势 V A E dl
A
q1
q2 r2
r1
E3
场强的叠加原理

大学物理习题参考解答上静电场环路定理_电势能_电势和电势差

02. 如图所示， CDEF 是一矩形，边长分别为 l 和 2l 。在 DC 延长线上 CA l 处的 A 点有点电荷 q ，在 CF 的中点 B 点有点电荷 q ，若使单位正电荷从 C 点沿 CDEF 路径运动到 F 点，则电场
力所作的功等于：
【D】
(A)
q 4ol
5 1； 5l
(B)
q 4ol
三判断题
09. 静电场中某点电势值的正负取决于电势零点的选取。
【对】
10. 在已知静电场分布的条件下，任意两点 P1 和 P2 之间的电势差决定于 P1 和 P2 两点的位置。【对】
11. 正电荷在电势高的地方，电势能也一定高。 12. 电场强度的方向总是指向电势降落最快的方向。
【对】【对】
1 4 0
4 r12 r1
1 4 0
4 r22 r2
0

——
r1 ' r2 0
XCH
第3页
20XX-3-24
大学物理教程_上_习题集参考解答
r1 r2
—— 外球面带负电
外球面应放掉电荷： Q Q Q Q 4 r22 4 r22
Q
(1
r1 r2
)
4
r22
将 r1 10 cm and r2 20 cm ， 8.85 109C / m2 代入上式得到：
13. 静电场的保守性体现在电场强度的环流等于零。
【对】
四计算题
14. 如图所示， AB 2L ， OCD 是以 B 为中心 L 为半径的半圆， A 和 B 两处分别有正负电荷 q 和 q ，试问：
1) 把单位正电荷从 O 沿 OCD 移动到 D ，电场力对它作了多少功？
XCH

高等物理静电场环路定理

a
a 20

V Edl Edr pp
p
R
z
1q
y

4 0 r
xz

2 ) 定义法:

1
Vp

4 0r
dq
q

qx
x 40(R2x2)3/2dx

q 4
0
1 (R2 x2)1/2
x
o q

4 0 R2 x2
特例:
★若x = 0，
得：Vp

q
40R
W A B q 0 A B E d l E p A E p B ( E p B E p A )
试探电荷q o 在电场中某一点的静电势能在数值上等于把试探电荷q o 由该点移到零势能点静电力所作的功。若选 B 点为电势能零点，则
B
E P A q 0A E d l q 0A B E d l
E内 0
p
R
q
z
x
z

4 0 R2 x2
V 0
场强分布
电势分布
q
例题2均匀带电球面内外的电势分布。带电量为Q，球面半径为R
。
解∶由高斯定理得：
p
E外

1 4 0
Q r2
1 V
40
dV
r
1）对球内的一点P，其电势为:
r
r dWFdlq0Edl
Q
p

VEdr drrC

q0Q
1 (1)
20 20
4 0 r ra
2、电势、电势差：
V dV （1）、定义：
电势的物理意义：

【大学物理】静电场的环路定理电势等势面电势梯度

r r r r－ r l cos
r

r
r+
q l
q+
3. 连续分布电荷电场中的电势利用电势叠加原理：
dV
dq
dq VP 4 π 0 r
r
P
使用此公式的前提条件为有限大带电体且选无限远处为电势零点；积分是对整个带电体的积分。 E 利用电势定义式： dl “ 0 ” P
qr E1 3 4 π 0 R
r
q E2 2 4 π 0 r
V1 E1dr E 2 dr
r R
R

q R

R
r
qr q dr dr 3 2 R 4 π r 4 π 0 R 0
2
q q q (3 R r ) 2 2 (R r ) 3 8 π 0 R 4 π 0 R 8 π 0 R
与路径无关
a
dr
任意带电体系产生的电场
任意带电体系都可以看成电荷系 q1、q2、…，移动q0，静电力所作功为: b b q E •b dr W F dr 0
ab
q0 a• q0 ( E1 E 2 E n ) dr a( L) n b q 0 E i d r ＝ qi q0 ( 1 1 ) a( L) i 1 rbi i 4 0 rai
注意：
• 电势能的零点可以任意选取，但是在习惯上，当场源电荷为有限带电体时，通常把电势能的零点选取在无穷远处。这时，空间a点的电势能：
E pa

a
q0 E dl
• 电势能为电场和位于电场中的电荷这个系统所共有。

静电学03环路定理和电势

带电
a
板
VP
Vpq
Vp板
a qdx
a/2 4 π0x2
a ( ) d x a / 2 20
q ( 1 1) a q a 4 π 0 a / 2 a 20 2 4 π 0a 40
例用静电场的环路定理证明电力线如图分布的电场不可能是静电场。
D C
AB
证明在电场中作扇形环路 ABCDA，
PB
vv E dl UB
令 UB 0
UP
rB
v E
drv
r
rB r
2π 0r
er
dr
ln rB 2π 0 r
oB
rB
r
P
r
例. 电荷分布如图所示，设 q >0, >0，求P点电势
能否选无限远处为电势零点？
q•
可统一选大平板处 P0 点电势为零，
无
P
p0
限大均
匀
a /2
1. 点电荷的电势：V q
4π 0 r
2. 点电荷系的电势：(q1,q2,…qn)
V
n
Vi
i
n i
qi
4π 0 ri
3.电荷连续分布带电体, 场中 P 点电势：
dq
V 4π0r
线电荷分布 dq dl 面电荷分布 dq dS
体电荷分布 dq dV
例求半径为R的均匀球面电荷q的电场强度和电势分布？
2
dr
q
4π 0 r
VA
E dr
A
A (E1 E2 En ) dr
A E1 dr A E2 dr
A En dr
VA
n

静电场的环路定理、电势

R2
3
)2
=……
例3：求无限长均匀带电直线的电场中的电势分布。
解：选取B点为电势零点，B点距带电直导线为 rB 。
B B
U E dl
dr
p
p 2 0r
2 0 ln r 2 0 ln r0 2 0 ln r C
rp
Q rB B
☆当电荷分布扩展到无穷远时，电势零点不能再选在无穷远处。
a
b
a
a、b两点的电势差等于将单位正电荷从a点移
到b时，电场力所做的功。
电势和电势能的区别：
电势是电场的属性，与试验电荷无关；电势能是属于电荷和电场系统所共有。
注意:
1、电势是相对量，电势零点的选择是任意的。对于有限带电体而言,电势零点的选择在无限远点;对于仪器而言电势零点选择在底板上.
2、两点间的电势差与电势零点选择无关。
六、电势的计算
1、点电荷电场中的电势
q • r0
•P
距q为r（P点）的场强为
q
E 4 0r 2 r0
r
由电势定义得：uP
P
E • dl
q
r
4
0r
2
dr
q
4 0r
讨论：
➢大小
q 0 u 0 r u r u最小 q 0 u 0 r u r u最大
就等于把它从该点移到零势能处静电场力所作的功
五、电势、电势差
定义电势
ua
Wa q0
E dl
a
Wa q0 E dl
a
单位正电荷在该点所具有的电势能
单位正电荷从该点到无穷远点(电势零)电场力所作的功
定义电势差 ua ub
电场中任意两点的电势之差（电压）

所有分类环路定理电势能电势

所有分类环路定理电势能电势
Wq0a b Ed clo s
dcl o s dr
Wq0ab Edr
点电荷的场
q
Wq0ab 410rq2dr
q0q 1 1
40 ra rb
b
rb
dl r
ra
q0 a
dr F
E
W q0q 1 1
40 ra rb
电场力的功只与始末位置有关，而与路径无关，电场力为保守力，静电场为保守场。
电场力是保守力，可引入势能的概念。
引力是保守力，作功为
W 引[Gm1 rm b2(Gm1 rm a2)]
取无穷远为零势能点，则引力势能为：
电场力作功
Ep
G m1m2 r
W q0q 1
40 ra
r1b (4q0q0rb
q0q )
40ra
1.电势能Ep
定义：单位：焦耳，J
EP
q0q
40r
为点电荷电势能（选无穷远为零势能点）
r
r
r
0R E2dr d l/d /r/E / 高斯面
R410 rq2dr
q
4 0 R
•II区：球壳外电势
II
rR
选无穷远为电势 0 点，
U2 r E2dl
I
qo RE
r
r
r
rE2dr d l/d /r/E / 高斯面
1
r 40
rq2dr
q
4 0 r
II
I
qoR
II
I
qoR
qE
4 0 R 2
qV 4 0 R
oR
r oR
r
例3 如图，两个同心的均匀带电球壳，半径分别

08.3静电场的环路定理、电势

E a E b
b
a
u 3
u 2 u 1
2.电势梯度电势梯度单位正电荷从 a到 b电场力的功到电场力的功
u+d +u
E•d = Ec sθ l =u−(u+d ) l o d u Ec sθ l =− u o d d
在 l E d 方向上的分量电场强度沿某一方向的分量一般
u
E l
n
a
b
l 由电势定义得 u =∫ E•d =∫ P
r
∞
4 ε0r π
d = r
q 4 ε0r π
讨论大小
q>0 u>0 r ↑ u↓ r → u 小 ∞ 最 q<0 u<0 r ↑ u↑ r → u 大 ∞ 最
为球心的同一球面上的点电势相等对称性以q为球心的同一球面上的点电势相等
点电荷系的电势由电势叠加原理，的电势为由电势叠加原理，P的电势为
单位正电荷在该点所具有的电势能
∞
W = ∫q E•d l a 0
a
∞
单位正电荷从该点到无穷远电势零)电场力所作的功点(电势零电场力所作的功电势零
定义电势差 a b 定义电势差 u −u 电场中任意两点的电势之差（电压）电势之差（电压）
u =u −u =∫ E•d −∫ E•d =∫ E•d l l l ab a b
d q −q A =u −u =0−( ) + oc o c 4 03R 4 0R a πε πε b c q +q 0 −q = 6 0R πε R R R
② 将单位负电荷由 ∞ O电场力所作的功
A O =u −u =0 o ∞ ∞
功、电势差、电势能之间的关系电势差、

《大学物理》作业3

《大学物理》作业 No. 3环路定理电势班级 ____________ 学号 ___________ 姓名 ____________ 成绩 ________说明：字母为黑体者表示矢量一、选择题1.关于静电场中某点电势值的正负，下列说法中正确的是： [ ] (A) 电势值的正负取决于置于该点的试验电荷的正负;(B) 电势值的正负取决于电场力对试验电荷作功的正负;(C) 电势值的正负取决于电势零点的选取;(D) 电势值的正负取决于产生电场的电荷的正负。

2. 真空中一半径为R 的球面均匀带电Q ，在球心O 处有一带电量为q 的点电荷，如图所示。

设无穷远处为电势零点，则在球内离球心O 距离为r 的P 点处电势为： [ ] (A)rq 04πε (B))(410RQ r q +πε (C)r Q q 04πε+ (D))(410RqQ r q -+πε 3. 在带电量为－Q 的点电荷A 的静电场中，将另一带电量为q 的点电荷B 从a 点移到b 点，a 、b 两点距离点电荷A 的距离分别为r 1和r 2，如图所示。

则在电荷移动过程中电场力做的功为 [ ] (A))11(4210r r Q --πε； (B) )11(4210r r qQ -πε； (C))11(4210r r qQ --πε； (D) )(4120r r qQ--πε。

4.以下说法中正确的是[ ] (A) 沿着电力线移动负电荷,负电荷的电势能是增加的；(B) 场强弱的地方电位一定低,电位高的地方场强一定强； (C) 等势面上各点的场强大小一定相等；(D) 初速度为零的点电荷, 仅在电场力作用下,总是从高电位处向低电位运动； (E) 场强处处相同的电场中,各点的电位也处处相同.二、填空题 1．电量分别为q 1, q 2, q 3的三个点电荷位于一圆的直径上, 两个在圆周上,一个在圆心.如图所示. 设无穷远处为电势零点，圆半径为R ，则b 点处的电势U = .-• • • q 1 q 2q 3 RO b2．如图所示，在场强为E 的均匀电场中，A 、B 两点间距离为d ，AB 连线方向与E 的夹角为α. 从A 点经任意路径到B 点的场强线积分l E d ⎰⋅AB= .3．如图所示, BCD 是以O 点为圆心,以R 为半径的半圆弧,在A 点有一电量为-q 的点电荷,O 点有一电量为+q 的点电荷. 线段BA = R .现将一单位正电荷从B 点沿半圆弧轨道 BCD 移到D 点，则电场力所作的功为 .三、计算题1.电量q 均匀分布在长为l 2的细杆上，求：（1）在杆延长线上与杆较近端距为a 处的电势；（2）在杆中垂线上与杆距为a 处的电势。

环路定理电势能差电势差

q
dl r
r dr F
E

电场力的功只与始末位置有关，而与路径无关。 2.任意带电体系的场对于由多个静止点电荷组成的系统或静止的连续带电体，可看成是由无数电荷元组成。
由场强叠加原理可得到电场强度的线积分（移动单位电荷的功）为：
3

b
aபைடு நூலகம்
b E dl ( E1 E2 En ) dl a b b b E1 dl E2 dl En dl Aab
a
电场力是保守力
5
二、电势能和电势
电场力是保守力，可引入势能的概念。 1.电势能差
b
q0 a
E
设在静电场中，将检验电荷 q0 从 a 点沿任意路径移动到 b 点，电场力作功为Aab。定义: 电荷 q0 在静电场中a 、b两点间的电势能差定义为， q0从 a 点沿任意路径移动到 b 点的过程中， Wa - Wb等于电场力所作的作功Aab 电势能差（势能增量的负值）等于保守力所作的功。
•对无限带电体不宜选无穷远为电势零点。此时只有电势的相对值（即电势差）有意义。
4.电势能与电势的区别：W 可正可负，取决于 q 和 q0 ； U只取决于场源电荷 q 。
10
另一方面：当已知电势分布时，可由电势差求出点电荷在电场中移动的过程中电场力所做的功：
Aab q0
b
a
E dl q0 (U a U b )
a
式中：Wa、Wb是电荷q0分别在a点和b点时,q0与电场所组成的系统的静电势能。
b
2.电势能
电势能也是一个相对的量，若选择一个零势能点作为参考。若令 W 0, 即选定b点为电势能零点。 b 则，电荷q0在此系统的电场中a点的电势能为：

环路定理电场强度的线积分静电场的环流为零电势环路定理

环路定理电场强度的线积分电势静电场的环流为零环路定理其实是我们熟悉的静电场是保守力场的另一种数学描述形式. 有了高斯定理和环路定理, 静电场就有了一个完整的描述.例题 17-4-1 圆环均匀带电,半径为R,电量为q,求轴线上的电势.xRr = R2 + z2zzyϕ=14πε 0ηdl∫L r=4πε 01 R2+z2∫Ldq=q4πε0 R2 + z2例题 17-4-2 求半径为R总电量为q的均匀带电球在球内外的电势分布.∞解:由例题17-3-1,可知电场强度分布为E=⎧ qr⎪⎪⎪⎨4πεq0rR3 ⎪⎩ 4πε0r3, ,r<R r>R取参考点为无穷远,电势为ϕ(r) = ∫r∞ E ⋅ dlPrR路径选为沿径向(图中橙色线), 场点在球外时,电势为ϕ(r)=∫r∞qdr4πε0r 2=q4πε0r场点在球内时，电势为ϕ(r)=∫rRqrdr4πε 0 R 3+∫R∞4πqεd0rr 2=q (3 −8πε 0 Rr2 R2)六.电场线规定电场线上每一点的切线方向与该点的E的方向一致.-qq-q2q三个点电荷位于等边三角形的顶点上, 电荷大小都为 q .从中心附近的电场的方向可以简单的看出, 位于中心的点电荷处于不稳定平衡. 定性上看黑色虚线所示球面上的通量为零.电场线的三条性质：(1)电场线始于正电荷或无穷远,终于负电荷或无穷远,在无电荷处不中断.q-qS1S2S3规定过任一面元的Ｅ通量与通过该面元的电场线数目成正比，则电场线的疏密程度能反映电场强度大小．(2)电场线不相交, 否则试探点电荷受力有两个可能的方向.(3)电场线不闭合.七.等势面空间中电势相等的点的集合构成了等势面.点电荷的等势面等势面与电场强度处处正交. 作业: 17-13, 17-14, 17-15《费曼物理学讲义》 R. P. Feynman第二卷是关于电磁学的.。

《大学物理》静电场练习题及答案

《大学物理》静电场练习题及答案一、简答题1、为什么在无电荷的空间里电场线不能相交?答案：由实验和理论知道，静电场中任一给定点上，场强是唯一确定的，即其大小和方向都是确定的．用电场线形象描述静电场的空间分布时，电场线上任一点的切线方向表示该点的场强方向．如果在无电荷的空间里某一点上有几条电场线相交的话，则过此交点对应于每一条电场线都可作出一条切线，这意味着交点处的场强有好几个方向，这与静电场中任一给定点场强具有唯一确定方向相矛盾，故无电荷的空间里电场线不能相交．2、简述静电场中高斯定理的文字内容和数学表达式。

答案：在真空中的静电场内，通过任意封闭曲面的电通量等于该封闭曲面所包围的所有电荷电量的代数和的01ε倍。

0ε∑⎰=⋅内S SqS d E3、写出静电场的环路定理，并分别说明其物理意义。

答案：静电场中，电场强度的环流总是等于零(或0l=⋅⎰l d E)，静电场是保守场。

4、感生电场与静电场有哪些区别和联系?5、在电场中某一点的电场强度定义为0q F E=.若该点没有试验电荷，那么该点的电场强度又如何? 为什么?答案：电场中某一点的电场强度是由该电场自身性质所决定，与这一点有无试验电荷没有任何关系。

6、在点电荷的电场强度公式中，如果0→r ，则电场强度E 将趋于无限大。

对此，你有什么看法? 答案：这表明，点电荷只是我们抽象出来的一个物理模型，当带电体较小而作用距离较大时使用点电荷模型较为方便、精确。

但当作用距离r 很小时，点电荷模型的误差会变大，这时我们不能再用点电荷的电场强度公式而要采用更精确的模型。

二、选择题1、如图所示，两个同心均匀带电球面，内球面半径为1R 、带有电荷1Q ，外球面半径为2R 、带有电荷2Q ，则在外球面外面、距离球心为r 处的P 点的场强大小E 为 ( A ) A 、20214r Q Q επ+B 、()()2202210144R r Q R r Q -π+-πεε C 、()2120214R R Q Q -+επ D 、2024r Q επ2、A 和B 为两个均匀带电球体，A 带电荷q +，B 带电荷q -，作一与A 同心的球面S 为高斯面，如图所示。

浙江农林大学环路定理电势电势梯度习题

四计算题1、两点电荷1q =1.5×10-8C ，2q =3.0×10-8C ，相距1r =42cm ，要把它们之间的距离变为2r =25cm ，需作多少功（填写A 、B 、C 或D ，从下面的选项中选取）A 、-6.55×10-6 JB 、-4.55×10-6 JC 、-6.55×10-4 JD 、-8.55×10-6 J 答案：A 解: ⎰⎰==⋅=22210212021π4π4d d r r r r q q r r q q r F A εε )11(21r r -61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J2、如图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功．A 、-6.55×10-6 JB 、-4.55×10-6 JC 、-6.55×10-4 JD 、-8.55×10-6 J 答案：A解: 如图所示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-=3、如图所示，有三个点电荷1Q 、2Q 、3Q 沿一条直线等间距分布，已知其中任一点电荷所受合力均为零，且1Q ＝3Q ＝Q 。

求在固定1Q 、3Q 的情况下，将2Q 从点O 移到无穷远处外力所作的功． A 、208Q dπε B 、204Q dπεC 、202Q d πε D 、20Q d πε答案：A解由题意1Q 所受合力为零，即0)2(4420312021=+d Q Q d Q Q πεπε 解得Q Q Q 414132-=-=将2Q 从点O 移到无穷远处外力所作的功，等于电荷2Q 在点O 的电势能。

4.3 静电场的环路定理、电势(2)

q > 0, U > 0 q < 0, U < 0
上页下页
2.点电荷系的电势点电荷系的电势设有点电荷系
UA = ∫ =∫
∞ A
v v E ⋅ dr
q1，q 2，⋅ ⋅ ，q n ⋅
q1 q2 q3
A
∞
A
(
r v v v E1 + E2 + ⋅ ⋅ ⋅ + En ⋅ dr
)
v r2 v r3
v r1
上页下页
3.连续带电体的电势连续带电体的电势
设连续带电体由无穷多个电荷元组成，每个电荷元视为点电荷，
dq在P处产生电势为：
dU p =
dq 4πε 0 r
dq 4πε 0 r
整个带电体在P处产生的电势为：
U p = ∫ dU p = ∫
q
++ d q = ρ d V ++ + v dq +++ r + +++ +++ ++ q P
∞ v ∞ Q v Q dr = 或U 外 ( r ) = ∫ E 2 ⋅ d r = ∫ 2 r 4π ε 0r r 4 π ε 0r
上页下页
（4） r < R ）
Q Q 由 U 外 (r ) = 可得 U ( R ) = = U内 4 πε 0 r 4 πε 0 R Q Rv v ∞v v 或 U 内 (r ) = ∫ E1 ⋅ dr + ∫ E2 ⋅ dr = r R 4π ε 0R
上页下页
四.电势
EPA 仅与位置有关，而与电荷无关。由于仅与位置有关，而与电荷无关。 q0

电磁学练习题(环路定理电势)

环路定理电势－选择题1．下列关于场强和电势的关系的说法中，正确的是：()A 已知某点的场强E ，就可以确定该点电势U ；()B 已知某点的电势U ，就可以确定该点场强E ；()C 在某空间内的场强不变，则U 也一定不变； ()D 在等势面上，场强E 不一定处处相等。

答案：()D下列关于静电场的说法中，正确的是：()A 电势高的地方场强就大； ()B 带正电的物体电势一定是正的；()C 场强为零的地方电势一定为零； ()D 电场线与等势面一定处处正交。

答案：()D在均匀电场中各点，下列诸物理量中：(1)电场强度、(2)电势、(3)电势梯度，哪些是大小相等的?()A (1)、(2)、(3)都相等； ()B (1)、(2)相等；()C (1)、(3)相等； ()D (2)、(3)相等。

答案：()C图中实线为某电场中的电场线，虚线表示等势面，由图可看出：()A ,A B C A B C E E E U U U >>>>； ()B ,A B C A B C E E E U U U <<<<；()C ,A B C A B C E E E U U U >><<； ()D ,A B C A B C E E E U U U <<>>答案：()D关于静电场的保守性的叙述可以表述为：()A 静电场场强沿任一曲线积分时，只要积分路径是某环路的一部分，积分结果就一定为零；()B 静电场场强沿任意路径的积分与起点和终点的位置有关，也要考虑所经历的路径；()C 当点电荷q 在任意静电场中运动时，电场力所做的功只取决于运动的始末位置而与路径无关。

()D 静电场场强沿某一长度不为零的路径做积分，若积分结果为零，则路径一定闭合。

答案：()C静电场中，电场线为平行直线的区域内()A 场强E 处处相同，电势U 可以存在不同； ()B 场强E 可以处处不同，电势U 可以处处相同；()C 场强E 可以处处不同，电势U 可以处处不同； ()D 场强E 处处相同，电势U 也处处相同。

7-4静电场环路定理电势1

*关于电势的讨论： ①电势是反映电场性质的量，与q0 无关。 ②电势和电势能一样具有相对意义。
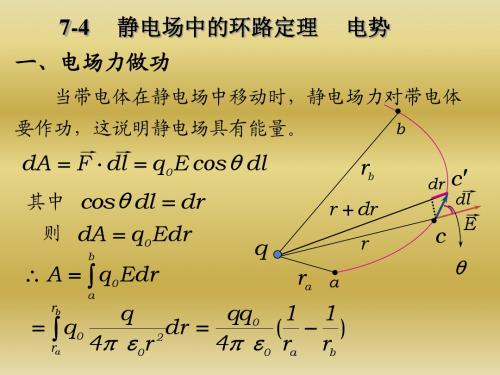
③电势是标量，单位为伏特。
2、电势差（电压）电场中两点的电势差：
Aab E dl E dl E dl q0 a b a 即： Aab q0U ab
b
U ab U a U b
U 0
[例]求一均匀带电球面的电势。已知：q , R 。
① r≤ R

(球内任意一点)
R
U E dl E内 dl E 外 dl
r r
R
q
+ +
+
+
0 q

q 4 πε r 0
+
R
dr 2
+ +
+ +
R
+
r .P
+
+ + +
+ +
4 πε R 0
二、静电场的环路定理 q0 E dl q0 E dl
q0 ( E dl
ABC
l
ABC
E dl ) 0
CDA
ADC
B
D
C
E
E dl 0
A
结论：沿闭合路径一周，电场力作功为零.
3
静电场是保守场
因此可以引入势能的概念
*关于电势差的讨论： ①电势差具有绝对意义，和参考点的选择无关。 ②Uab等于将单位正电荷从a 点沿任意路径移至b 点电场力所作的功。
五、电势的计算
1、点电荷电场的电势