锐角三角函数复习课件公开课.ppt
合集下载
锐角三角函数课件

$sin 30^circ = frac{1}{2}$
45度角的余弦值
$cos 45^circ = frac{sqrt{2}}{2}$
30度角的余弦值
$cos 30^circ = frac{sqrt{3}}{2}$
60度角的正弦值
$sin 60^circ = frac{sqrt{3}}{2}$
45度角的正弦值
在工程学中的应用
结构设计
在建筑和机械设计中,锐角三角 函数用于计算结构件的角度和长
度。
控制系统
在控制系统的设计中,锐角三角函 数用于描述系统的传递函数和稳定 性。
信号处理
在信号处理中,锐角三角函数用于 频谱分析和滤波器的设计。
05
特殊角度的三角函数值
30度、45度、60度的三角函数值
30度角的正弦值
正切函数的图像在每 一个开区间(π/2+kπ, π/2+kπ), k∈Z内都是递增的。
04
锐角三角函数的应用
在几何学中的应用
01
02
03
计算角度
锐角三角函数可以帮助我 们计算出特定角度的三角 形的角度,例如直角三角 形中的锐角。
计算边长
通过已知的角度和边长, 我们可以使用锐角三角函 数来计算其他边的长度。
04
90度角的余弦值
$cos 90^circ = 0$
06
习题与解答
习题
题目1
已知直角三角形中,一个锐角为 30°,邻边长为3,求对边长。
题目2
在直角三角形中,已知一个锐角 为45°,斜边长为5,求邻边长。
题目3
已知直角三角形中,一个锐角为 60°,对边长为6,求斜边长。
答案与解析
01
45度角的余弦值
$cos 45^circ = frac{sqrt{2}}{2}$
30度角的余弦值
$cos 30^circ = frac{sqrt{3}}{2}$
60度角的正弦值
$sin 60^circ = frac{sqrt{3}}{2}$
45度角的正弦值
在工程学中的应用
结构设计
在建筑和机械设计中,锐角三角 函数用于计算结构件的角度和长
度。
控制系统
在控制系统的设计中,锐角三角函 数用于描述系统的传递函数和稳定 性。
信号处理
在信号处理中,锐角三角函数用于 频谱分析和滤波器的设计。
05
特殊角度的三角函数值
30度、45度、60度的三角函数值
30度角的正弦值
正切函数的图像在每 一个开区间(π/2+kπ, π/2+kπ), k∈Z内都是递增的。
04
锐角三角函数的应用
在几何学中的应用
01
02
03
计算角度
锐角三角函数可以帮助我 们计算出特定角度的三角 形的角度,例如直角三角 形中的锐角。
计算边长
通过已知的角度和边长, 我们可以使用锐角三角函 数来计算其他边的长度。
04
90度角的余弦值
$cos 90^circ = 0$
06
习题与解答
习题
题目1
已知直角三角形中,一个锐角为 30°,邻边长为3,求对边长。
题目2
在直角三角形中,已知一个锐角 为45°,斜边长为5,求邻边长。
题目3
已知直角三角形中,一个锐角为 60°,对边长为6,求斜边长。
答案与解析
01
中考数学锐角三角函数(共56张PPT)

二、填空题
(1)求旋转木马E处到出口B处的距离; (2)求海洋球D处到出口B处的距离.(结果保留整数)
解:(1) ∵AE=80,∠BAE=30°,∠ABE =90°, ∴BE=AEsin30°=80× =40(m). 答:旋转木马E处到出口B处的距离为40 m.
(2) ∵∠CED=∠AEB,∠DCE=∠ABE =90°,
∴∠D=∠BAE=30°.
∵CD=34 m,
∴DE=
=
=
(m).
∴DB=BE+DE=
≈40+
≈79(m).
答:海洋球D处到出口B处的距离为79 m.
二、填空题
11. 小明在某次作业中得到如下结果: sin27°+ sin283°≈0.122+0.992=0.9945; sin222°+ sin268°≈0.372+0932=1.0018; sin229°+ sin261°≈0.482+0.872=0.9873; sin237°+ sin253°≈0.602+0.802=1.0000;
二、填空题
9. (2017北京)计算:4cos30°+
原式=4× +1-
+2
=
+1- +2=3.
-
+
.
10.(2017湘潭)某游乐场部分平面图如图Z2816所示,点C,E,A在同一直线上,点D,E,B在 同一直线上,测得A处与E处的距离为80 m, C处与D处的距离为34 m,∠C=90°,∠ABE =90°,∠BAE=30°. (2≈1.4,3≈1.7)
图Z28-7
A.
m
B.
m
《锐角三角函数》课件

锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
锐角的三角函数PPT

余弦函数的符号为cos,表示为cos(θ), 其中θ为锐角。
02
余弦函数的图像是一条周期为2π的余弦 曲线,表示在直角三角形中,邻边的长 度与斜边的长度的比值在[-1,1]之间周 期性变化。
04
正切函数的定义
01
正切函数:tan(θ) = sin(θ) / cos(θ)
02
正切函数的定义域:(0, π/2)
余弦函数的值域:[-1, 1]
余弦函数的图像:一个周期为2π的周 期函数,图像关于y轴对称
余弦函数的奇偶性:偶函数,f(x) = f(-x)
余弦函数的单调性:在[0, π/2]上是 增函数,在[π/2, π]上是减函数
余弦函数的导数:f'(x) = -sin(x)
正切函数的性质
01
02
03
04
05
值域:正弦函数的值域是[-1, 1]
奇偶性:正弦函数是奇函数, 即f(x) = -f(-x)
周期性:正弦函数的周期是 2π,即f(x + 2π) = f(x)
最值:正弦函数的最大值是1, 最小值是-1
图像:正弦函数的图像是一 条正弦曲线,关于原点对称
余弦函数的性质
定义:余弦函数是直角三角形中的一 个角与对边和斜边的比值
03
正切函数的值域:(0, ∞)
04
正切函数的图像:在平 面直角坐标系中,正切 函数的图像是一条以原 点为中心的对称曲线, 在y轴右侧的部分为单调 递增,在y轴左侧的部分 为单调递减。
Part Two
锐角三角函数的性 质
正弦函数的性质
定义:正弦函数是直角三角 形中的一个角(锐角)的正 弦值与对边长度的比值
06
正切函数是锐 角三角函数中 的一种,表示 在一个直角三 角形中,对边 (opposite) 的长度与邻边 (adjacent) 的长度之比。
第16讲锐角三角函数复习课件(共42张PPT)

解:原式= 3+ 2× 22+ 3--3-2 3+1= 3+1+ 3 +3-2 3+1=5.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
4.在△ABC 中,若|cos A-12|+(1-tan B)2=0,则∠C 的
度数是
(C )
A.45°
B.60°
C.75°
D.105°
5.式子 2cos 30°-tan 45°- (1-tan 60°)2的值是
∵CE=EF,∴CAEC=
m= 5m
55,
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
∴tan∠CAE= 55. 解法二:∴在 Rt△ABC 中,
tan
B=ABCC=
2m = 5m
2, 5
在 Rt△EFB 中,EF=BF·tan B=2m,∴CE=EF=2m,
5
5
2m
∴在 Rt△ACE 中,tan∠CAE=CAEC=2m5= 55,
∴tan∠CAE= 55.
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
7.如图5-16-4,在Rt△ABC中, ∠C=90°,∠A=30°,E为线段AB上 一点且AE∶EB=4∶1,EF⊥AC于F, 连结FB,则tan∠CFB的值等于 ( C )
3 A. 3
53 C. 3
23 B. 3 D.5 3
大师导航 归类探究 自主招生交流平台 思维训练
第五章 解直角三角形
第16讲 锐角三角函数
全效优等生
全效优等生
大师导航 归类探究 自主招生交流平台 思维训练
月球有多远? 如图,如果从地球上A点看, 月球S刚好在地平线上(即AS和地 球半径OA垂直),而同时从地球上B点看,S刚好在天顶处(即S 在地球半径OB的延长线上),那么∠S就叫做月球S的地平视 差,根据一个天体的地平视差,可以算出这个天体的距离. ∠S可以从∠AOB算出,而∠AOB可以从地球上A,B两点 的经纬度算出. 月球S的地平视差(∠S),就是从月球S看来,垂直于视线 (SA)的地球半径(OA)所对的角.
公开课《锐角三角函数复习》课件

(3)已知 tan( ∠A+20°)= 3 ,求锐角A . (4)在△ABC中, ∠ B、 ∠ C均为锐角,且
1 3 0 sin B + cos C 2 2
2
,求∠A的度数。
第21课时┃锐角三角函数及其应 用 突|破|点|2 特殊角的三角函数值的计算
例 2 [2017·烟台]在 Rt△ABC 中,∠C=90°,AB=2,BC= 3, A 1 则 sin =Leabharlann _______. 2 2b
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
第22课时┃锐角三角函数
例 1 【2018· 原创】如图 22-2,在 Rt△ABC 中,∠BAC =90°,AD⊥BC 于点 D,判断正误:
图 22-2 AD (1)sinB= ;( √ ) AB AD (3)sinB= ;( × ) AC AC (2)sinB= ;( BC CD (4)sinB= .( AC √
B
一.锐角三角函数的概念
对边与斜边的比叫做∠A 正弦:把锐角A的__________ a 的正弦,记作 sin A c A 邻边与斜边的比叫做∠A的 余弦:把锐角A的__________ 余弦,记作 cos A b
c
c
a
b
C
对边与邻边的比叫做∠A的 正切:把锐角A的__________ a 正切,记作 tan A
1. 巩固三角函数的概念,巩固用直角三角形边之 比来表示某个锐角的三角函数. 2. 熟记30°,45°, 60°角的三角函数值.会计 算含有特殊角的三角函数的值,会由一个特殊 锐角的三角函数值,求出它的对应的角度. 3.掌握直角三角形的边角关系,会运用勾股定理, 直角三角形的两锐角互余及锐角三角函数解直 角三角形. 4.会用解直角三角形的有关知识解决简单的实际 问题.
1 3 0 sin B + cos C 2 2
2
,求∠A的度数。
第21课时┃锐角三角函数及其应 用 突|破|点|2 特殊角的三角函数值的计算
例 2 [2017·烟台]在 Rt△ABC 中,∠C=90°,AB=2,BC= 3, A 1 则 sin =Leabharlann _______. 2 2b
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.
第22课时┃锐角三角函数
例 1 【2018· 原创】如图 22-2,在 Rt△ABC 中,∠BAC =90°,AD⊥BC 于点 D,判断正误:
图 22-2 AD (1)sinB= ;( √ ) AB AD (3)sinB= ;( × ) AC AC (2)sinB= ;( BC CD (4)sinB= .( AC √
B
一.锐角三角函数的概念
对边与斜边的比叫做∠A 正弦:把锐角A的__________ a 的正弦,记作 sin A c A 邻边与斜边的比叫做∠A的 余弦:把锐角A的__________ 余弦,记作 cos A b
c
c
a
b
C
对边与邻边的比叫做∠A的 正切:把锐角A的__________ a 正切,记作 tan A
1. 巩固三角函数的概念,巩固用直角三角形边之 比来表示某个锐角的三角函数. 2. 熟记30°,45°, 60°角的三角函数值.会计 算含有特殊角的三角函数的值,会由一个特殊 锐角的三角函数值,求出它的对应的角度. 3.掌握直角三角形的边角关系,会运用勾股定理, 直角三角形的两锐角互余及锐角三角函数解直 角三角形. 4.会用解直角三角形的有关知识解决简单的实际 问题.
锐角三角函数复习课件九年级中考复习

误的是( A )
A.sin B=
1
3
1
C.tan B=
2
B.sin C=
2 5
5
D.sin2B+sin2C=1
3
8.如图,点 A(x,4)在第一象限,OA 与 x 轴所夹的锐角为 α,cos α= ,
5
则 tan α 的值为( A
A.
4
3
B.
3
4
C.
5
4
)
D.
4
5
3
9.在 Rt△ABC 中,∠C=90°,若 sin A= ,则 cos B 的值是( B )
B
2- 3
2+ 3 2-
=23.类比这种方法,计算
tan
22.5°的
3
)
B. 2-1
C. 2
1
D.
2
14.在如图所示的网格中,小正方形的边长为1,点A,B,C,D都在
格点上,
AB与CD相交于点O,则∠AOC的正切值是( A )
A.
C.
2
3
3
5
3
B.
2
5
D.
3
(1)cos260°+sin260°=
1 ;
cos45°
(2)
-
tan 45°= 0 ;
sin45°
3
(3)1-2sin 30°cos 30°= 1- 2
.
练习题
1.在△ABC 中,∠A=105°,∠B=45°,tan C 的值是
3
3
.
2.在Rt△ABC中,∠C=90°,若△ABC的三边都缩小5倍,则sin
是( D )
《锐角三角函数》(九年级下册数学)公开课获奖课件百校联赛一等奖课件

B
C A
这个问题能够归结为: 在 Rt△ABC 中,∠C=90°,∠A=30°,BC=35 m, 求 AB.
在上面旳问题中,假如出 水口旳高度为 50 m,那么需要 准备多长旳水管?
D B' B
am 50 m 35 m
A
C C' E
思索:由这些成果,你能得到什么结论?
结论: 在直角三角形中,假如一种锐角旳度数是30°, 那么不论三角形旳大小怎样,这个角旳对边与斜
第二十八章
28.1 锐角三角函数(1)
新知探究
比萨斜塔 1350 年落成时就已倾斜,其塔顶中心点 偏离垂直中心线 2.1 m.至今,这座高 54.5 m 旳斜塔仍 巍然挺立.
你能用“塔身中心线 与垂直中心线所成旳角θ” 来描述比萨斜塔旳倾斜程 度吗?
比萨斜塔 1350 年落成时就已倾斜,其塔顶中心点偏 离垂直中心线 2.1 m.至今,这座高 54.5 m 旳斜塔仍巍然 挺立.
你能用“塔身中心线与垂直中心线所成旳角θ”来描 述比萨斜塔旳倾斜程度吗?
2.1 m 垂直中心线
塔顶中心点 54.5 m 塔身中心线
θ
问题探究
为了绿化荒山,某地打算从位于山脚下旳机井房沿着 山坡铺设水管,在山坡上修建一座扬水站,对坡面旳绿地 进行喷灌.现测得斜坡与水平面所成角旳度数是 30°, 为 使出水口旳高度为 35 m,需要准备多长旳水管?
在图中 ∠A旳对边记作a ∠B旳对边记作b ∠C旳对边记作c
例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB旳值.
求sinA就 是要拟定∠A 旳对边与斜
边旳比;求 sinB就是要 拟定∠B旳对 边与斜边旳 比
解:(1)在Rt△ABC中,
AB AC2 BC2 42 32 5
C A
这个问题能够归结为: 在 Rt△ABC 中,∠C=90°,∠A=30°,BC=35 m, 求 AB.
在上面旳问题中,假如出 水口旳高度为 50 m,那么需要 准备多长旳水管?
D B' B
am 50 m 35 m
A
C C' E
思索:由这些成果,你能得到什么结论?
结论: 在直角三角形中,假如一种锐角旳度数是30°, 那么不论三角形旳大小怎样,这个角旳对边与斜
第二十八章
28.1 锐角三角函数(1)
新知探究
比萨斜塔 1350 年落成时就已倾斜,其塔顶中心点 偏离垂直中心线 2.1 m.至今,这座高 54.5 m 旳斜塔仍 巍然挺立.
你能用“塔身中心线 与垂直中心线所成旳角θ” 来描述比萨斜塔旳倾斜程 度吗?
比萨斜塔 1350 年落成时就已倾斜,其塔顶中心点偏 离垂直中心线 2.1 m.至今,这座高 54.5 m 旳斜塔仍巍然 挺立.
你能用“塔身中心线与垂直中心线所成旳角θ”来描 述比萨斜塔旳倾斜程度吗?
2.1 m 垂直中心线
塔顶中心点 54.5 m 塔身中心线
θ
问题探究
为了绿化荒山,某地打算从位于山脚下旳机井房沿着 山坡铺设水管,在山坡上修建一座扬水站,对坡面旳绿地 进行喷灌.现测得斜坡与水平面所成角旳度数是 30°, 为 使出水口旳高度为 35 m,需要准备多长旳水管?
在图中 ∠A旳对边记作a ∠B旳对边记作b ∠C旳对边记作c
例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB旳值.
求sinA就 是要拟定∠A 旳对边与斜
边旳比;求 sinB就是要 拟定∠B旳对 边与斜边旳 比
解:(1)在Rt△ABC中,
AB AC2 BC2 42 32 5
锐角三角函数复习.ppt
又BC-CD=BD
解得x=6
∴CD=6
A
B
C
D
例题解析
(2) BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中z x xk
问题2 要解一个直角三角形,除一个直角的已知元素外,还需要几个元素?为什么这些元素中至少要有一条边?试给出可以求解直角三角形的两个条件.
A
B
C
D
问题3 如果题中给出的图形不是直角三角形而是一个综合图形,我们用什么方法进行处理,就能把它转化为可以解的直角三角形?
问题4 你认为需要具备哪些知识、掌握哪些方法,就能较顺利地解决有关实际问题?请总结实际问题的一般步骤和注意点.
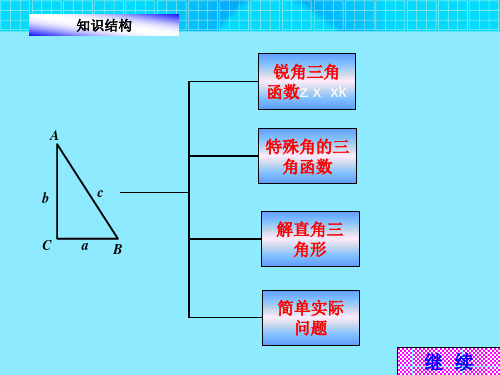
锐角三角 函数z x xk
特殊角的三 角函数
解直角三 角形
简单实际 问题
c
a
b
A
B
C
知识
特殊角的三 角函数
2
1
30°
1
1
45°
2
1
60°
30°+ 60°= 90°
返 回
解直角 三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数 关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
返 回
简单实 际问题
数学模型
直角三角形
等腰梯形
组合图形
等腰三角形
构建
解
作高转化为直角三角形
解
返 回
问题1 已知:如同,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=3,CD= ,怎样求sinA和cos∠BCD的值?怎样求∠B的正切值?
已知:如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求:(1)DC的长;(2)sinB的值.
解得x=6
∴CD=6
A
B
C
D
例题解析
(2) BC=BD+CD=4+6=10=AD
在Rt△ACD中
在Rt△ABC中z x xk
问题2 要解一个直角三角形,除一个直角的已知元素外,还需要几个元素?为什么这些元素中至少要有一条边?试给出可以求解直角三角形的两个条件.
A
B
C
D
问题3 如果题中给出的图形不是直角三角形而是一个综合图形,我们用什么方法进行处理,就能把它转化为可以解的直角三角形?
问题4 你认为需要具备哪些知识、掌握哪些方法,就能较顺利地解决有关实际问题?请总结实际问题的一般步骤和注意点.
锐角三角 函数z x xk
特殊角的三 角函数
解直角三 角形
简单实际 问题
c
a
b
A
B
C
知识
特殊角的三 角函数
2
1
30°
1
1
45°
2
1
60°
30°+ 60°= 90°
返 回
解直角 三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数 关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
返 回
简单实 际问题
数学模型
直角三角形
等腰梯形
组合图形
等腰三角形
构建
解
作高转化为直角三角形
解
返 回
问题1 已知:如同,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AD=3,CD= ,怎样求sinA和cos∠BCD的值?怎样求∠B的正切值?
已知:如图,在△ABC中,∠C=90°,点D在BC上,BD=4,AD=BC,cos∠ADC= ,求:(1)DC的长;(2)sinB的值.
锐角三角函数复习课件公开课

锐角三角函数复习课件公 开课
欢迎来到锐角三角函数复习课件公开课! 在本课程中,我们将回顾锐角三角 函数的基本概念,常见公式,性质和图像,解三角方程,以及一些实际应用。
锐角三角函数的基本概念
锐角三角函数是用于描述锐角三角形中角度和边长之间关系的函数。包括正弦、余弦和正切等函 数。
1 正弦函数
描述角的对边与斜边之间的关系。
总结和回顾
在本课程中,我们回顾了锐角三角函数的基本概念、常见公式、性质和图像。学习了如何利用锐角三角 函数求解三角方程,并了解了一些实际应用。希望你已经对锐角三角函数有了更深入的理解!
锐角三角函数在直角三角形的图像中不断变化,并呈现出一些特殊的性质。
单位圆
单位圆是用于可视化锐角三角 函数图像和特殊性质的工具。
正弦函数
正弦函数是一条波浪形曲线, 用于描述周期性变化。
余弦函数
余弦函数是一条类似正弦函数 的波浪形曲线,但相位差90度。
利用锐角三角函数求解三角方程
锐角三角函数可以用于解决涉及三角函数的方程,从而求得角度的值。
2 余弦函数
描述角的邻边与斜边之间的关系。
3 正切函数
描述角的对边与邻边之间的关系。
常见的锐角三角函数公式
锐角三角函数有一些常见的公式用于计算和简化角度的计算。
倍角和半角公式
• 正弦和余弦的倍角和半角公式。 • 正切的双角和半角公式。
和差公式
• 正弦和余弦的和差公式。 • 正切的和差公式。
锐角三角函数的性质和图像
1
方程转化
将方程转化为以三角函数为未知数的
方程求解
2
方程。
利用三角函数的运算特性和解方程的
方法求解得出角度的值。
3
验证解
欢迎来到锐角三角函数复习课件公开课! 在本课程中,我们将回顾锐角三角 函数的基本概念,常见公式,性质和图像,解三角方程,以及一些实际应用。
锐角三角函数的基本概念
锐角三角函数是用于描述锐角三角形中角度和边长之间关系的函数。包括正弦、余弦和正切等函 数。
1 正弦函数
描述角的对边与斜边之间的关系。
总结和回顾
在本课程中,我们回顾了锐角三角函数的基本概念、常见公式、性质和图像。学习了如何利用锐角三角 函数求解三角方程,并了解了一些实际应用。希望你已经对锐角三角函数有了更深入的理解!
锐角三角函数在直角三角形的图像中不断变化,并呈现出一些特殊的性质。
单位圆
单位圆是用于可视化锐角三角 函数图像和特殊性质的工具。
正弦函数
正弦函数是一条波浪形曲线, 用于描述周期性变化。
余弦函数
余弦函数是一条类似正弦函数 的波浪形曲线,但相位差90度。
利用锐角三角函数求解三角方程
锐角三角函数可以用于解决涉及三角函数的方程,从而求得角度的值。
2 余弦函数
描述角的邻边与斜边之间的关系。
3 正切函数
描述角的对边与邻边之间的关系。
常见的锐角三角函数公式
锐角三角函数有一些常见的公式用于计算和简化角度的计算。
倍角和半角公式
• 正弦和余弦的倍角和半角公式。 • 正切的双角和半角公式。
和差公式
• 正弦和余弦的和差公式。 • 正切的和差公式。
锐角三角函数的性质和图像
1
方程转化
将方程转化为以三角函数为未知数的
方程求解
2
方程。
利用三角函数的运算特性和解方程的
方法求解得出角度的值。
3
验证解
《锐角三角函数》PPT教学课件(第2课时)

1
∠ 的对边 =
= .
2
斜边
A
可得 AB=2BC=70m,即需要准备70m长的水管.
C
知识讲解
1.正弦
如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计
算∠A的对边与斜边的比
A
BC
AB
,你能得出什么结论?
即在直角三角形中,当一个锐角等于45°
时,不管这个直角三角形的大小如何,这
数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦
、余弦和正切,记号中习惯省去“∠”;
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且在直角
三角形中sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角
切比3,分子根号别忘添.
30°,45°,60°角的正切值可以看成是 3, 9 , 27.
当A、B为锐角时,
若A≠B,则
sinA≠sinB,
cosA≠cosB,
tanA≠tanB.
知识讲解
注意
1.从函数角度理解∠A的锐角三角函数:把∠A看成自
变量,其取值范围是0°<∠A<90°,sinA,cosA,
在Rt△ABC中,如果锐角A确定,
那么∠ A 的对边与斜边的比、邻
边与斜边的比都是一个定值.
B
斜
边
A
∠A的邻边
∠A的对边
┌
C
知识讲解
归纳:
在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜
边的比值是一个常数,与直角三角形的大小无关.
28章锐角三角函数全章ppt课件

问题(1)当梯子与地面所成的角a为75°时,梯子顶端与地面的 距离是使用这个梯子所能攀到的最大高度.
问题(1)可以归结为:在Rt △ABC中,已知∠A=75°,斜
边AB=6,求∠A的对边BC的长.
B
由 sin A BC 得 AB
BC AB sin A 6sin 75
由计算器求得 sin75°≈0.97
α
A
C
所以 BC≈6×0.97≈5.8
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的 角a的问题,可以归结为:在Rt△ABC中,已知AC=2.4,斜边AB=6, 求锐角a的度数
由于
B
cos a AC 2.4 0.4
AB 6
tan A BC 8k 8 AC 15k 15
例题示范
例3: 如图,在Rt△ABC中,∠C=90° B
1.求证:sinA=cosB,sinB=cosA
2.求证:tan A sin A ;tan A 1
cos A
tan B
3.求证:sin2 A cos2 A 1
A
C
sin2 A sin A sin A
如图,Rt△ABC中,直角边AC、BC小于斜边AB,
sin A BC <1
AB
sin B AC AB
<1
A
C
所以0<sinA <1, 0<sinB <1, 如果∠A < ∠B,则BC<AC , 那么0< sinA <sinB <1
探究
精讲
如图,在Rt△ABC中,∠C= 90°,当锐角A确定时,∠A 的对边与斜边的比就随之确 定,此时,其他边之间的比 是否也确定了呢?为什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水平距离BC为30m,在A点测得D点的仰角∠EAD为45°, 在B点测得D点的仰角∠CBD为60°,求这两座建筑物的 高度(结果保留根号)
F
16
解直角三角形的实际应用------求距离问题
例2:如图,海岛A四周20海里周围内为暗礁 区,一艘货轮由东向西航行,在B处见岛A在 北偏西60˚,航行24海里到C,见岛A在北偏西 30˚,货轮继续向西航行,有无触礁的危险?
例2
300
12
三、解直角三角形
知识梳理:
a b c (1)三边之间的关系 22
2(勾股定理)
A
(2)两锐角之间的关系
∠A+∠B=90°
b
(3)边角之间的关系
sin
A
A的对边 斜边
a c
sin
B
B的对边 斜边
b c
C
cos
A
A的邻边 斜边
b c
cos B
B的邻边 斜边
A
A的邻边 斜边
b c
⑶正切
tan
A
A的对边 A的邻边
a b
A
b
c
Ca
B
8
直击中考 考点一:锐角三角函数的定义及简单应用
例1:在正方形网格中,∠α的位置如图所示,则
sinα的值为( B) .
A1 B 2C 3 D 3
2
2
2
3
9
直击中考 考点一:锐角三角函数的定义及简单应用
例2、(1)(2016乐山)在Rt△ABC中,若
• 是啊,如果你优秀,你便拥有了大把的选 择机会,否则你只能被迫谋生。
3
当你抱怨自己已经很辛苦的时候,请看看在西部 的那些穷孩子,他们饭吃不饱,衣穿不暖,冻着 脚丫,啃着窝窝头的情形,请你对比一下那些透 支着体力却依旧食不果腹的打工者!
4
• 当你想要放弃了,一定要想想那些睡得比你晚、 起得比你早、跑得比你卖力、天赋还比你高的牛 人,他们早已在晨光中跑向那个你永远只能眺望 的远方。
• 所以,请不要在最能吃苦的时候选择安逸,没有 谁的青春是在红地毯上走过。从来就没有什么天 生的幸运,一切全都靠背后日复一日、年复一年 辛劳的耕耘,努力。
5
努力到无能为力,拼搏到感动自 己,你的人生终将闪耀。
6
锐角三角函数
7
一.锐角三角函数的定义
⑴正弦
sin
A
A的对边 斜边
a c
⑵余弦
cos
23
14
直击中考
考点三:解直角三角形
例2:(2016.内高)如图,测量河宽AB(假
设河的两岸平行),在C点测得∠ACB=30°,
D点测得∠ADB=60°,又CD=60m,则河宽AB
为
m(结果保留根号)
15
四、解直角三角形的实际应用
直击中考: 考点四:解直角三角形的实际应用------求高度问题
例1(2017.新疆)如图,甲、乙为两座建筑物,它们之间的
N1
N
A
D
C
B
17
小结:
说一说这节课你有什么收获?
1,锐角三角函数的定义
2,特殊角的三角函数值 3,解直角三角形 4,解直角三角形的应用
常用的思想方法 和辅助线的作法
18
作业:中考总复习P126 1---3题
19
(2018•新疆)如图,在数学活动课上,小丽为了 测量校园内旗杆AB的高度,站在教学楼的C处测得 旗杆底端B的俯角为45°,测得旗杆顶端A的仰角 为30°.已知旗杆与教学楼的距离BD=9m,请你帮 她求出旗杆的高度(结果保留根号).
∠C=90°,AB=2BC,则sinB的值为(
)
A、 1 B、 2
C、 3 D、1
C
2
2
2
B
c a
A
bC
10
二、特殊角的三角函数值
锐角a
三角函数 sin a cos a tan a
30°
1 2 3 2
3 3
45°
2 3
11
直击中考 考|. 点二:特殊角三角函数值
例1
450 -
吃 苦 在 前,享 受 在 后 -----------冲刺中考
1
马云在《不吃苦,你要 青春干嘛》这篇演讲中这 样说到“当你不去拼一份 奖学金,不去过没试过的 生活,整天挂着QQ,刷着 微博,逛着淘宝,玩着网 游,干着我80岁都能做的 事,你要青春干嘛?”
2
• 著名作家龙应台在给儿子安德烈的一封信 中这样写到:我要求你读书用功,不是因 为我要你跟别人比成就,而是因为,我希 望你将来拥有更多选择的权利,选择有意 义、有时间的工作,而不是被迫谋生。
a c
tan
A
A的对边 A的邻边
a b
tan B
B的对边 B的邻边
b a
c
a
B
13
直击中考 考点三:解直角三角形
例1:(2014•新疆)如图,在Rt△ABC中, ∠C=90°,∠B=37°,BC=32,则AC=-----(参考数据:sin37°≈0.60,cos37°≈0.80, tan37°≈0.75)
如图,某校数学兴趣小组为测得校园里旗杆 AB的高度,在操场的平地上选择一点C,测 得旗杆顶端A的仰角为30°,再向旗杆的方 向前进16米,到达点D处(C、D、B三点在 同一直线上),又测得旗杆顶端A的仰角为 45°,请计算旗杆AB的高度(结果保留根号 )
22
(2017.乌鲁木齐)一艘渔船位于港口A的北偏东 60°方向,距离港口20海里B处,它沿北偏西37° 方向航行至C处突然出现故障,在C处等待救援, B,C之间的距离为10海里,救援船从港口A出发 20分钟到达C处,求救援的艇的航行速 度.(sin37°≈0.6,cos37°≈0.8, ≈1.732,结 果取整数)
20
一艘渔船位于港口A的北偏东60°方向,距离港口 20海里B处,它沿北偏西37°方向航行至C处突然 出现故障,在C处等待救援,B,C之间的距离为10 海里,救援船从港口A出发20分钟到达C处,求救 援的艇的航行速度.(sin37°≈0.6, cos37°≈0.8, ≈1.732,结果取整数
)
21
F
16
解直角三角形的实际应用------求距离问题
例2:如图,海岛A四周20海里周围内为暗礁 区,一艘货轮由东向西航行,在B处见岛A在 北偏西60˚,航行24海里到C,见岛A在北偏西 30˚,货轮继续向西航行,有无触礁的危险?
例2
300
12
三、解直角三角形
知识梳理:
a b c (1)三边之间的关系 22
2(勾股定理)
A
(2)两锐角之间的关系
∠A+∠B=90°
b
(3)边角之间的关系
sin
A
A的对边 斜边
a c
sin
B
B的对边 斜边
b c
C
cos
A
A的邻边 斜边
b c
cos B
B的邻边 斜边
A
A的邻边 斜边
b c
⑶正切
tan
A
A的对边 A的邻边
a b
A
b
c
Ca
B
8
直击中考 考点一:锐角三角函数的定义及简单应用
例1:在正方形网格中,∠α的位置如图所示,则
sinα的值为( B) .
A1 B 2C 3 D 3
2
2
2
3
9
直击中考 考点一:锐角三角函数的定义及简单应用
例2、(1)(2016乐山)在Rt△ABC中,若
• 是啊,如果你优秀,你便拥有了大把的选 择机会,否则你只能被迫谋生。
3
当你抱怨自己已经很辛苦的时候,请看看在西部 的那些穷孩子,他们饭吃不饱,衣穿不暖,冻着 脚丫,啃着窝窝头的情形,请你对比一下那些透 支着体力却依旧食不果腹的打工者!
4
• 当你想要放弃了,一定要想想那些睡得比你晚、 起得比你早、跑得比你卖力、天赋还比你高的牛 人,他们早已在晨光中跑向那个你永远只能眺望 的远方。
• 所以,请不要在最能吃苦的时候选择安逸,没有 谁的青春是在红地毯上走过。从来就没有什么天 生的幸运,一切全都靠背后日复一日、年复一年 辛劳的耕耘,努力。
5
努力到无能为力,拼搏到感动自 己,你的人生终将闪耀。
6
锐角三角函数
7
一.锐角三角函数的定义
⑴正弦
sin
A
A的对边 斜边
a c
⑵余弦
cos
23
14
直击中考
考点三:解直角三角形
例2:(2016.内高)如图,测量河宽AB(假
设河的两岸平行),在C点测得∠ACB=30°,
D点测得∠ADB=60°,又CD=60m,则河宽AB
为
m(结果保留根号)
15
四、解直角三角形的实际应用
直击中考: 考点四:解直角三角形的实际应用------求高度问题
例1(2017.新疆)如图,甲、乙为两座建筑物,它们之间的
N1
N
A
D
C
B
17
小结:
说一说这节课你有什么收获?
1,锐角三角函数的定义
2,特殊角的三角函数值 3,解直角三角形 4,解直角三角形的应用
常用的思想方法 和辅助线的作法
18
作业:中考总复习P126 1---3题
19
(2018•新疆)如图,在数学活动课上,小丽为了 测量校园内旗杆AB的高度,站在教学楼的C处测得 旗杆底端B的俯角为45°,测得旗杆顶端A的仰角 为30°.已知旗杆与教学楼的距离BD=9m,请你帮 她求出旗杆的高度(结果保留根号).
∠C=90°,AB=2BC,则sinB的值为(
)
A、 1 B、 2
C、 3 D、1
C
2
2
2
B
c a
A
bC
10
二、特殊角的三角函数值
锐角a
三角函数 sin a cos a tan a
30°
1 2 3 2
3 3
45°
2 3
11
直击中考 考|. 点二:特殊角三角函数值
例1
450 -
吃 苦 在 前,享 受 在 后 -----------冲刺中考
1
马云在《不吃苦,你要 青春干嘛》这篇演讲中这 样说到“当你不去拼一份 奖学金,不去过没试过的 生活,整天挂着QQ,刷着 微博,逛着淘宝,玩着网 游,干着我80岁都能做的 事,你要青春干嘛?”
2
• 著名作家龙应台在给儿子安德烈的一封信 中这样写到:我要求你读书用功,不是因 为我要你跟别人比成就,而是因为,我希 望你将来拥有更多选择的权利,选择有意 义、有时间的工作,而不是被迫谋生。
a c
tan
A
A的对边 A的邻边
a b
tan B
B的对边 B的邻边
b a
c
a
B
13
直击中考 考点三:解直角三角形
例1:(2014•新疆)如图,在Rt△ABC中, ∠C=90°,∠B=37°,BC=32,则AC=-----(参考数据:sin37°≈0.60,cos37°≈0.80, tan37°≈0.75)
如图,某校数学兴趣小组为测得校园里旗杆 AB的高度,在操场的平地上选择一点C,测 得旗杆顶端A的仰角为30°,再向旗杆的方 向前进16米,到达点D处(C、D、B三点在 同一直线上),又测得旗杆顶端A的仰角为 45°,请计算旗杆AB的高度(结果保留根号 )
22
(2017.乌鲁木齐)一艘渔船位于港口A的北偏东 60°方向,距离港口20海里B处,它沿北偏西37° 方向航行至C处突然出现故障,在C处等待救援, B,C之间的距离为10海里,救援船从港口A出发 20分钟到达C处,求救援的艇的航行速 度.(sin37°≈0.6,cos37°≈0.8, ≈1.732,结 果取整数)
20
一艘渔船位于港口A的北偏东60°方向,距离港口 20海里B处,它沿北偏西37°方向航行至C处突然 出现故障,在C处等待救援,B,C之间的距离为10 海里,救援船从港口A出发20分钟到达C处,求救 援的艇的航行速度.(sin37°≈0.6, cos37°≈0.8, ≈1.732,结果取整数
)
21
