c++用递归的方法编写函数求Fibonacci级数
fibonacci数列递归算法的实现,集合全排列问题递归算法的实现,整数划分问题递归算

Fibonacci数列、集合全排列和整数划分问题Fibonacci数列Fibonacci数列是一个由0和1开始,每个后续数字等于前两个数字之和的数列。
以下是Fibonacci数列的递归算法实现:// 递归实现Fibonacci数列function fibonacci(n) { if (n <= 1){ return n; } return fibonacci(n - 1) + fibonacci(n - 2);}集合全排列集合全排列问题是指给定一个集合,求该集合中元素的全排列。
以下是集合全排列的递归算法实现:// 递归实现集合全排列function permute(arr, start = 0) { if (start === arr.length) { console.log(arr); // 输出当前排列 } for (let i = start; i < arr.length; i++) { // 交换当前元素与起始位置元素 [arr[start], arr[i]] = [arr[i], arr[start]]; permute(arr, start + 1); // 递归调用下一次排列 [arr[start],arr[i]] = [arr[i], arr[start]]; // 恢复当前元素与起始位置元素的交换 }}整数划分整数划分问题是指将一个整数拆分成多个正整数的和,求所有的划分方式。
以下是整数划分的递归算法实现:// 递归实现整数划分function partition(n, max, prefix = []) { if (n === 0) { console.log(prefix); // 输出当前划分 } for (let i = Math.min(max, n); i >= 1; i--) { partition(n - i, i, [...prefix, i]); // 递归调用下一次划分 }}。
c++实验报告【范本模板】

面向对象程序设计(C++)实验报告指导老师:***学生:吴健班级:软131学号:*********目录实验一、VC6.0环境入门与简单程序设计实验报告 (3)实验二、函数的应用实验报告 (7)实验三、类与对象实验报告 (14)实验四、C++程序结构实验报告 (22)实验五、数组、指针与字符串实验报告 (26)实验六、继承和派生实验报告 (33)实验七、多态性实验报告 (42)实验八、面向对象综合实验实验报告 (48)实验一、VC6.0环境入门与简单程序设计实验报告系软件工程班级 131 学号 139074164 姓名吴健同组者指导教师柯栋梁一、实验目的:1、熟悉VC++6.0开了环境并编写简单的C++程序。
3、使用C++语言编写简单的输入输出程序。
4、使用VC++6.0的DEBUG调试功能:单步执行、设置断点、观察变量值。
二、实验内容:1、使用VC++建立一个标准C++程序,编译、运行如下程序:#include<iostream〉Int main(){Cout〈<”Hello World!\n";Cout<<”Welcome to C++!\n";}2、编程计算图形的面积。
程序可计算圆形、长方形、正方形等的面积,运行时首先提示用户选择图形类型,然后根据不同图形类型,输入相关参数计算其面积,并将其显示出来.3、使用DEBUG功能观察任务2程序运行中变量值的变化情况.三、实验要求:1、任务1要求熟悉VC++开发环境,并能够使用其建立第一个C++程序.2、实验前要做好充分准备,包括程序清单、调试步骤、调试方法,以及对程序结果的分析等。
四、实验报告:1.程序运行截图2.面积计算1、程序说明。
用if -else语句进行选择程序功能,while语句实现功能的循环实现程序如下:#include〈iostream>#include〈cmath〉using namespace std;int main(){cout〈<”1计算圆面积”<〈endl〈<"2计算矩形面积"<〈endl〈<"3计算正方形面积”〈〈endl<<"4退出"〈〈endl<<"请选择相应功能代码:”;int x; //x对应编号cin〉>x;double area;while(x!=4){if(x==1){double r;cout〈〈"半径:";cin〉>r;area=3。
fibonacci数列递归算法

fibonacci数列递归算法Fibonacci数列是指从0和1开始,后面的每一项都是前面两项的和。
即数列的第n项为Fn = Fn-1 + Fn-2,其中F1 = 0,F2 = 1、递归算法是一种特殊的算法,它通过在函数内部调用自己来解决问题。
下面将详细介绍Fibonacci数列的递归算法。
递归算法的核心思想是将一个大问题分解为更小的子问题,然后通过递归调用来解决子问题,最终得到最终的解。
对于Fibonacci数列来说,递归算法可以通过以下方式实现:1. 首先定义一个递归函数fibonacci(n),用于计算第n个Fibonacci数。
函数的输入参数是整数n,输出结果是第n个Fibonacci数的值。
2.在函数内部,我们需要处理递归结束的情况。
当n=1时,返回0;当n=2时,返回1、这是因为F1=0,F2=13. 如果n大于2,则需要进行递归调用。
我们通过调用fibonacci(n-1)和fibonacci(n-2)来计算第n-1和n-2个Fibonacci数的值。
4. 最后,将第n-1和n-2个Fibonacci数的值相加,即可得到第n个Fibonacci数的值。
下面是具体的递归算法实现:```pythondef fibonacci(n):if n == 1:return 0elif n == 2:return 1else:return fibonacci(n-1) + fibonacci(n-2)```这个递归函数可以计算任意位置的Fibonacci数。
例如,fibonacci(6)将返回8,因为第6个Fibonacci数为8递归算法的优点是思路清晰,易于理解和实现。
但它也存在一些问题。
首先,递归算法的复杂度较高,计算时间较长。
这是因为在计算第n个Fibonacci数时,需要重复计算很多次前面的Fibonacci数。
其次,由于递归调用会占用大量的系统资源,当n很大时,递归算法可能导致堆栈溢出的问题。
斐波那契数列递归和非递归的方式

斐波那契数列递归和非递归的方式
斐波那契数列是一个非常经典的数列,它的定义如下:
F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2) (n>=2)
递归方式求斐波那契数列的时间复杂度较高,因为它会重复计算很多次,导致算法效率低下。
而非递归方式求斐波那契数列的时间复杂度要低很多。
下面我们来介绍一下斐波那契数列的递归和非递归的求解方式。
1. 递归方式
递归方式求解斐波那契数列代码如下:
```
int fibonacci(int n)
{
if(n==0) return 0;
if(n==1) return 1;
return fibonacci(n-1) + fibonacci(n-2);
}
```
这种方法的时间复杂度是指数级别的,因为每个数都要计算一遍,所以效率极低。
2. 非递归方式
非递归方式求解斐波那契数列代码如下:
```
int fibonacci(int n)
{
if(n==0) return 0;
if(n==1) return 1;
int a = 0, b = 1, c;
for(int i=2; i<=n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
```
这种方法的时间复杂度是O(n),效率要比递归方式高很多。
综上所述,非递归方式求解斐波那契数列要比递归方式高效得多,我们在实际的程序开发中应该尽量采用非递归方式。
递归求fabonacci数列c语言

递归求fabonacci数列c语言Fibonacci数列,相信大家都不陌生。
大名鼎鼎的斐波那契数列,在数学上和计算机科学领域都有着广泛的应用。
在这里,我们来学习一下如何用C语言递归求解Fibonacci数列。
什么是Fibonacci数列?Fibonacci数列,又称为斐波那契数列,是一个非常著名的数学数列。
它的定义如下:F(0)=0F(1)=1F(n)=F(n-1)+F(n-2)(n>=2)也就是说,每个数都是前两个数之和。
Fibonacci数列前几项依次为:0、1、1、2、3、5、8、13、21、34、55、89……递归求解Fibonacci数列在C语言中,Fibonacci数列的递归求解其实非常简单。
我们只需要定义一个函数,在函数体内部递归调用即可。
以下是递归求解Fibonacci数列的C语言代码:```cint Fib(int n){if(n == 0) // 当n等于0时,Fibonacci数列的第一项为0return 0;else if(n == 1) // 当n等于1时,Fibonacci数列的第二项为1return 1;else // 当n大于等于2时,按照公式递归计算return Fib(n-1) + Fib(n-2);}```以上代码中,我们定义了一个名为Fib的函数,接受一个整数类型的参数n。
在函数体内部,我们使用了C语言中的if-else结构,根据n的值判断返回什么值。
当n等于0时,Fibonacci数列的第一项为0,返回0;当n等于1时,Fibonacci数列的第二项为1,返回1;否则,按照公式递归调用Fib函数计算Fibonacci数列的第n项。
在主函数中,我们可以调用Fib函数输出Fibonacci数列的前十项:```cint main(){int n = 10; // 输出Fibonacci数列的前十项for(int i=0; i<n; ++i)printf("%d ", Fib(i));printf("\n");return 0;}```输出的结果如下:0 1 1 2 3 5 8 13 21 34以上就是用C语言递归求解Fibonacci数列的方法。
斐波那契数列python递归算法

斐波那契数列python递归算法
斐波那契数列是一个非常经典的计算机科学问题,它指的是从数字1开始,依次包含1和2的整数序列,每个数字等于前两个数字之和。
在这种情况下,它的算法是比较简单的,我们可以使用递归的方法来求解斐波那契数列。
在Python中可以使用如下代码:
def Fibonacci(n):
if n <= 0:
return 0
elif n == 1:
return 1
else:
return Fibonacci(n-1) + Fibonacci(n-2)
# Driver program
print ("Fibonacci series")
for i in range(10):
print (Fibonacci(i))
Fibonacci函数是一个递归函数,该函数可以根据给定的项数,计算斐波那契数列中每一项的值。
实现上,我们可以使用递归函数先判断当前是否为0或1,如果是,则直接返回结果,否则递归调用自身,在函数的返回语句中将前两项的值相加,返回值即为斐波那契数列的对应项的值。
最后我们可以完成一下程序,以此来验证我们的实现是否正确:
输出的结果表明,我们的实现正确无误,即结果正确。
斐波那契数列_记忆化递归c++

斐波那契数列_记忆化递归c++一、简介斐波那契数列是一个经典的数学序列,由0和1开始,之后的每个数字都是前两个数字的和。
这个数列在数学、计算机科学、经济学等领域都有广泛的应用。
记忆化递归是一种有效的算法,可以大大提高斐波那契数列的计算效率。
二、问题描述斐波那契数列的递归算法非常耗时,因为它会重复计算相同的子序列。
记忆化递归则通过缓存已计算的结果,避免重复计算,从而大大提高了效率。
三、算法实现以下是使用C语言实现记忆化递归的斐波那契数列的代码:```c#include <stdio.h>#include <stdlib.h>long long fibonacci(int n) {if (n <= 1) {return n;}long long *cache = malloc(n * sizeof(long long));if (!cache) {return -1; // 处理内存分配错误}for (int i = 0; i < n; i++) {cache[i] = fibonacci(i - 1);}return cache[n - 1]; // 返回缓存中的结果}```这段代码首先检查输入的数字是否小于或等于1,如果是,则直接返回该数字。
否则,它使用动态内存分配创建一个缓存数组,用于存储已计算的结果。
然后,它使用递归调用 `fibonacci` 函数来计算前 `n-1` 个斐波那契数,并将结果存储在缓存数组中。
最后,它返回缓存数组中第 `n-1` 个元素的值,即所需的斐波那契数。
四、使用示例以下是一个使用上述代码的简单示例:```cint main() {int n = 10; // 请求计算前10个斐波那契数long long result = fibonacci(n);printf("斐波那契数列前%d项为:%lld\n", n, result);return 0;}```运行这段代码将输出前n个斐波那契数。
递归求斐波那契数列的时间复杂度

递归求斐波那契数列的时间复杂度
斐波那契数列是一种非常常见的数列,其中每个数字是前两个数字的和,例如:0、1、1、2、3、5、8、13、21、34……以此类推。
如果要使用递归方法求斐波那契数列的第n个数字,其时间复杂度会是多少呢?
首先,使用递归方法求解斐波那契数列的代码如下所示:
```
int fibonacci(int n) {
if (n == 0 || n == 1) {
return n;
} else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
```
这段代码比较简单,当n等于0或1时,返回n本身;否则,递归调用fibonacci(n-1)和fibonacci(n-2)的结果之和。
接下来,我们分析一下这段代码的时间复杂度。
很明显,每一次递归调用都会产生两个新的递归调用,也就是说,如果我们要求斐波那契数列的第n个数字,就需要递归调用n次。
而每一次递归调用都会产生两个新的递归调用,这样的话,递归树的深度将会是指数级别的,因此,这段代码的时间复杂度为O(2^n)。
实际上,由于递归树的每个节点都会被重复计算,因此,这个算法的效率很低,而且当n比较大的时候,效率会变得非常非常低。
因此,如果要求斐波那契数列的第n个数字,最好使用非递归的方法,例如采用循环实现。
这样的话,时间复杂度为O(n),效率会高得多。
递归法求斐波那契数列

递归法求斐波那契数列1 斐波那契数列斐波那契数列是一个普遍存在的数学现象,它可以在许多自然界形成中找到答案。
斐波那契数列是指由数字1,1,2,3,5,8,13,21,34等等组成的数列,每个数字(从第三个数字开始)都是前面两个数字的和。
它被称为“斐波那契数列”,因为每个数字都是前两个数字之和,由数学家莱昂纳多·斐波那契发现的。
2 递归法求解斐波那契数列递归法是一种重复调用自身的程序设计方法。
事实上,它是一种非常强大的算法,因为它可以分解复杂的问题。
对于斐波那契数列,我们可以使用递归法,这种法则可以将一个较大的问题简化为规模更小的问题。
求解斐波那契数列的算法的基本思想是找到递推式,即F(n)=F(n-1)+F(n-2),其中n是斐波那契数列的项数,F(n-1)是斐波那契数列中第n-1项,F(n-2)是斐波那契数列中第n-2项。
从这一递归式中可以看出,求解斐波那契数列的第n项,我们可以先求解其前两项,然后加起来。
3 递归法求解斐波那契数列的算法伪代码:- 设置F(0)=0,F(1)=1;- 若n==0或n==1时,直接返回 n;- 若n>1,则 F(n)=F(n-1)+F(n-2);- 返回 F(n)。
4 应用斐波那契数列有许多应用,如蛇爬楼梯、计算兔子繁衍、求解计算机算法时间复杂度等等,这些都得益于斐波那契数列的递归性质以及其蕴含的数学规律。
有时候,你可以使用诸如数学归纳法等方法来解决斐波那契数列相关的题目。
但是,要有效的解决这种复杂的问题,还需要使用计算机科学的方法,比如递归算法。
5 结论总之,斐波那契数列是一种普遍存在的数学现象,它的应用非常广泛,其中最有用的是可以用来解决复杂的数学问题。
要有效地解决这种问题,可以使用递归法来求解斐波那契数列。
用数组求斐波那契数列

用数组求斐波那契数列用数组求斐波那契数列斐波那契数列是指依次每个数等于前两个数之和的数列,其前几项为1,1,2,3,5,8,13……本文将介绍使用数组的方法来求解斐波那契数列。
一、使用递归来求解斐波那契数列最简单的方法莫过于使用递归来求解斐波那契数列了,但是递归的方法存在严重的效率问题,当时数组较大时递归的深度会非常大,导致程序性能极差。
代码如下:```pythondef fibonacci(n):if n<2:return nreturn fibonacci(n-1)+fibonacci(n-2)```上述代码使用了递归的方法求解斐波那契数列,当n小于2时直接返回n,否则分别递归求解前两个数之和。
二、使用数组来求解斐波那契数列由于递归产生的性能问题,我们可以使用更加高效的方法来求解斐波那契数列——使用数组。
代码如下:```pythondef fibonacci(n):if n<2:return narr=[0]*narr[0]=1arr[1]=1for i in range(2,n):arr[i]=arr[i-1]+arr[i-2]return arr[n-1]```上述代码使用了数组来求解斐波那契数列,当n小于2时直接返回n,否则创建一个长度为n的数组,设置前两个数分别为1和1,然后循环依次求解数组中每个数的值即可。
三、使用动态规划来求解斐波那契数列动态规划是一种常用的算法,本章节将介绍如何使用动态规划来求解斐波那契数列。
代码如下:```pythondef fibonacci(n):if n<2:return narr=[0]*narr[0]=1arr[1]=1for i in range(2,n):arr[i]=arr[i-1]+arr[i-2]return arr[n-1]```上述代码使用了动态规划来求解斐波那契数列,当n小于2时直接返回n,否则创建一个长度为n的数组,设置前两个数分别为1和1,然后循环依次求解数组中每个数的值即可。
c语言数组求斐波那契数列第n项

C语言是一种广泛应用于计算机编程领域的编程语言,它具有高效、快速、灵活等优点,因此在对性能要求较高的应用中得到广泛应用。
而斐波那契数列是一个非常经典的数学问题,该问题的解决方法也是程序员面试中常见的问题之一。
本文将通过C语言数组的方式来求解斐波那契数列的第n项。
一、斐波那契数列的定义和特点1.1 斐波那契数列的定义斐波那契数列是一个典型的递归数列,其定义如下:F(0) = 0, F(1) = 1,F(n) = F(n-1) + F(n-2) (n>=2)1.2 斐波那契数列的特点斐波那契数列具有以下特点:1)数列中的每一项都是前两项之和;2)数列的前几个数为:0, 1, 1, 2, 3, 5, 8, 13, 21, ...3)数列的增长速度非常快,因此在实际应用中需要注意数值溢出的问题。
二、使用C语言数组求解斐波那契数列第n项2.1 算法思路使用C语言数组求解斐波那契数列的第n项,可以利用数组来存储前两项的值,然后根据递推式依次计算后续的值,直到计算到第n项为止。
2.2 算法实现下面是使用C语言数组求解斐波那契数列第n项的代码实现:```c#include <stdio.h>int fibonacci(int n){int fib[n+1];int i;fib[0] = 0;fib[1] = 1;for (i = 2; i <= n; i++){fib[i] = fib[i-1] + fib[i-2];}return fib[n];}int m本人n(){int n;printf("请输入要求解的斐波那契数列的项数:");scanf("d", n);printf("第d项的斐波那契数为:d\n", n, fibonacci(n));return 0;}```2.3 算法分析该算法使用数组fib来存储斐波那契数列的前几项,然后从第3项开始通过循环计算后续的值,直到计算到第n项为止。
递归求斐波那契数列的时间复杂度

递归求斐波那契数列的时间复杂度
斐波那契数列是一个经典的数列,其定义为:前两项为1,之后每一项都是前两项的和。
即:1,1,2,3,5,8,13,21,34,……
递归求解斐波那契数列是一种常见的方法,其实现如下:
int fibonacci(int n) {
if (n <= 2) {
return 1;
}
else {
return fibonacci(n - 1) + fibonacci(n - 2);
}
}
这段代码的时间复杂度是多少呢?我们可以通过递归树的方式
来分析。
当n=5时,递归树如下所示:
f(5)
/
f(4) f(3)
/ /
f(3) f(2) f(2) f(1)
/
f(2) f(1)
我们可以发现,在计算f(5)的过程中,我们需要计算f(4)和f(3)。
而计算f(4)的过程中,又需要计算f(3)和f(2)。
因此,递归树的深度为n,且每个节点都会递归两次。
因此,当n越大时,递归树的节点数将呈指数级增长,即其时间复杂度为O(2^n)。
这意味着,当我们要计算一个较大的斐波那契数列时,递归方法将非常低效。
我们应该使用其他方法,如迭代或矩阵快速幂,来计算斐波那契数列。
斐波那契级数与递推数列的程序实现

斐波那契级数与递推数列的程序实现斐波那契数列是一个典型的递推数列,它以递推的方式定义,即每一项都是前两项的和。
斐波那契数列的定义如下:F(0)=0F(1)=1F(n)=F(n-1)+F(n-2)(n>=2)以下是斐波那契数列的一个常见的递归实现:```def fibonacci_recursive(n):if n == 0:return 0elif n == 1:return 1else:return fibonacci_recursive(n-1) + fibonacci_recursive(n-2) ```这个递归实现十分直观,但是其时间复杂度为O(2^n),效率较低。
由于递归实现中存在大量的重复计算,我们可以使用动态规划的思想,通过记录已经计算过的项来避免重复计算,从而提高效率。
以下是斐波那契数列的动态规划实现:def fibonacci_dp(n):fib = [0] * (n+1)fib[0] = 0fib[1] = 1for i in range(2, n+1):fib[i] = fib[i-1] + fib[i-2]return fib[n]```在动态规划实现中,我们使用一个长度为n+1的数组来保存已经计算过的斐波那契数列的项,避免了重复计算。
除了递归和动态规划,还可以使用迭代的方式来实现斐波那契数列。
迭代实现避免了递归的函数调用和动态规划中的数组,从而节省了空间,提高了效率。
以下是斐波那契数列的迭代实现:```def fibonacci_iterative(n):if n == 0:return 0elif n == 1:return 1fib1 = 0fib2 = 1for i in range(2, n+1):fib = fib1 + fib2fib1 = fib2fib2 = fibreturn fib2```迭代实现中,我们使用了两个变量fib1和fib2来保存前两项的值,通过迭代更新它们来计算后面的项。
C语言中斐波那契数列的三种实现方式(递归、循环、矩阵)
C语⾔中斐波那契数列的三种实现⽅式(递归、循环、矩阵)⽬录⼀、递归⼆、循环三、矩阵《剑指offer》⾥讲到了⼀种斐波那契数列的 O(logN) 时间复杂度的实现,觉得挺有意思的,三种⽅法都记录⼀下。
⼀、递归⼀般来说递归实现的代码都要⽐循环要简洁,但是效率不⾼,⽐如递归计算斐波那契数列第n个元素。
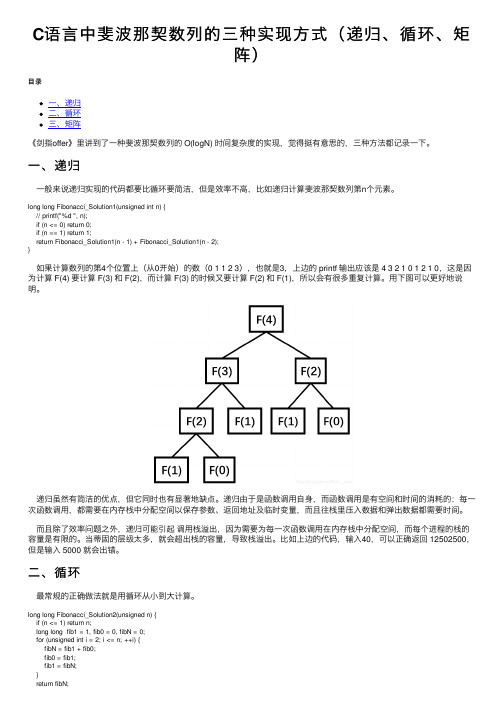
long long Fibonacci_Solution1(unsigned int n) {// printf("%d ", n);if (n <= 0) return 0;if (n == 1) return 1;return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);}如果计算数列的第4个位置上(从0开始)的数(0 1 1 2 3),也就是3,上边的 printf 输出应该是 4 3 2 1 0 1 2 1 0,这是因为计算 F(4) 要计算 F(3) 和 F(2),⽽计算 F(3) 的时候⼜要计算 F(2) 和 F(1),所以会有很多重复计算。
⽤下图可以更好地说明。
递归虽然有简洁的优点,但它同时也有显著地缺点。
递归由于是函数调⽤⾃⾝,⽽函数调⽤是有空间和时间的消耗的:每⼀次函数调⽤,都需要在内存栈中分配空间以保存参数、返回地址及临时变量,⽽且往栈⾥压⼊数据和弹出数据都需要时间。
⽽且除了效率问题之外,递归可能引起调⽤栈溢出,因为需要为每⼀次函数调⽤在内存栈中分配空间,⽽每个进程的栈的容量是有限的。
当蒂固的层级太多,就会超出栈的容量,导致栈溢出。
⽐如上边的代码,输⼊40,可以正确返回 12502500,但是输⼊ 5000 就会出错。
⼆、循环最常规的正确做法就是⽤循环从⼩到⼤计算。
long long Fibonacci_Solution2(unsigned n) {if (n <= 1) return n;long long fib1 = 1, fib0 = 0, fibN = 0;for (unsigned int i = 2; i <= n; ++i) {fibN = fib1 + fib0;fib0 = fib1;fib1 = fibN;}return fibN;}或者下边这种long long Fibonacci_Solution2(unsigned n) {if (n <= 1) return n;long long a = 0, b = 1;for (unsigned int i = 2; i <= n; ++i) {b = a + b;a =b - a;}return b;}三、矩阵数中提到了⼀种 O(logN) 时间复杂度的算法,就是利⽤数学公式计算。
递归函数求斐波那契数列

递归函数求斐波那契数列
斐波那契数列是一种经典的数列,它的前两项为0和1,之后的每一项都是前两项之和。
即F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2)。
递归函数是一种函数调用自身的方法,可以用来求解斐波那契数列。
定义一个递归函数fib(n),它的功能是求解斐波那契数列的第n 项。
当n等于0或1时,直接返回n;否则,返回fib(n-1)+fib(n-2)。
在实际应用中,递归函数的效率并不高。
因为每次调用函数都会新开辟一段栈空间,占用额外的内存。
因此在求解斐波那契数列时,如果n很大,递归函数可能会导致程序崩溃。
为了避免这种情况,我们可以使用循环的方式来实现斐波那契数列的求解。
具体步骤如下:
1. 定义两个变量a和b,分别表示斐波那契数列的前两项。
2. 用一个循环从2到n,每次将a和b的和赋值给b,将b的值赋给a。
3. 循环结束后,变量b的值就是斐波那契数列的第n项。
使用循环的方式求解斐波那契数列的效率更高,因为它不需要额外开辟栈空间,也不会导致程序崩溃。
- 1 -。
python递归求斐波那契数列

python递归求斐波那契数列斐波那契数列是指每个数都是由前两个数相加得到的数列,即从第三项开始,每一项都等于前两项之和。
数列的前两项通常为0和1。
在python中,我们可以使用递归的方式来求解斐波那契数列。
递归是一种非常常用的解决问题的方法,它是通过将问题划分成更小的子问题来解决的。
我们定义一个函数fibonacci,该函数接受一个整数n作为参数,用于指定要计算的斐波那契数列的长度。
函数内部通过递归的方式来计算斐波那契数列。
```pythondef fibonacci(n):if n <= 0:return []elif n == 1:return [0]elif n == 2:return [0, 1]else:fib_list = fibonacci(n-1)fib_list.append(fib_list[-1] + fib_list[-2])return fib_list```在上述代码中,我们首先判断n的值,如果n小于等于0,则返回一个空列表。
如果n等于1,则返回一个只包含0的列表。
如果n 等于2,则返回一个包含0和1的列表。
这三种情况是递归的终止条件。
如果n大于2,则递归调用fibonacci函数,传入n-1作为参数,得到一个长度为n-1的斐波那契数列fib_list。
然后将fib_list 的最后两个数相加,并将结果添加到fib_list中,最后返回fib_list。
接下来,我们可以调用fibonacci函数来计算斐波那契数列。
例如,我们可以计算前10项斐波那契数列。
```pythonn = 10fib_list = fibonacci(n)print(fib_list)```运行上述代码,将得到以下输出结果:```[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]```从输出结果可以看出,前10项斐波那契数列依次为0, 1, 1, 2, 3, 5, 8, 13, 21, 34。
递归法求斐波那契数列第n项

递归法求斐波那契数列第n项斐波那契数列是数学中一个著名的数列,它的定义是:前两项为0和1,从第三项起,每一项都等于前两项之和。
用数学公式表示为:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2)。
斐波那契数列可以用递归的方法来求解。
递归是一种将一个大问题分解成更简单的子问题的方法,通过不断地调用自身来解决问题。
对于斐波那契数列,可以使用递归算法来计算第n项的值。
要求斐波那契数列的第n项,可以先考虑递归的终止条件,即边界条件。
根据斐波那契数列的定义,前两项为0和1,因此当n为0或1时,直接返回0或1即可。
这是一个递归的终止条件,可以作为递归算法的基准情况。
当n大于1时,需要计算第n项的值。
根据斐波那契数列的定义,第n项等于前两项之和,因此可以通过递归调用求解第n-1项和第n-2项的值,然后将两者相加得到第n项的值。
具体递归的表达式为:F(n)=F(n-1)+F(n-2)。
递归算法的思想是将大问题分解成更小的子问题,然后通过不断地调用自身来解决子问题。
在这个过程中,递归算法会不断地调用自身,直到达到终止条件。
然后从最小的子问题开始,逐步解决更大的子问题,最终解决整个问题。
递归算法的实现需要注意两个问题:递归的终止条件和递归表达式的正确性。
递归的终止条件是确定的,就是当n为0或1时,直接返回0或1;递归表达式的正确性是基于斐波那契数列的定义的,通过不断地调用自身求解子问题,并将子问题的解合并得到整个问题的解。
递归算法的效率并不高。
由于递归算法会进行多次重复计算,因此在计算较大的斐波那契数列时,会出现严重的效率问题。
例如,计算F(50)时就需要进行大量的重复计算,造成了很大的时间消耗。
为了提高效率,可以使用动态规划的方法来解决斐波那契数列的问题。
动态规划是一种将大问题分解成更小的子问题,并保存子问题的解以供重复使用的方法。
通过动态规划,可以避免重复计算,提高算法的效率。
动态规划方法的基本思想是,首先确定递推关系式,然后根据递推关系式计算每个子问题的解,最后根据子问题的解计算整个问题的解。
使用递归算法求斐波那契数列的第n项

使用递归算法求斐波那契数列的第n项使用递归算法求解斐波那契数列的第n项是一个经典的数学问题。
斐波那契数列是指从0和1开始,后一项是前两项之和的数列。
数学表达式可以表示为:Fn = Fn-1 + Fn-2,其中n表示数列的项数。
递归算法是一种通过调用自身函数来解决问题的方法。
在求解斐波那契数列的第n项时,可以利用递归算法的特性,将问题不断拆分为更小的子问题,直到最终达到基本情况。
为了使用递归算法求解斐波那契数列的第n项,首先需要定义一个递归函数。
这个函数接受一个整数n作为参数,表示要求解的斐波那契数列的第n项。
然后,通过判断n的值,确定是否已经达到基本情况。
当n等于0或1时,斐波那契数列的第n项分别为0和1,即F0=0,F1=1。
这是递归算法的基本情况,可以直接返回结果。
当n大于1时,可以通过递归调用自身函数来求解斐波那契数列的第n项。
具体思路是,先递归求解第n-1项和第n-2项,然后将两者相加得到第n项的值。
下面是使用递归算法求解斐波那契数列的第n项的示例代码:```pythondef fibonacci(n):if n == 0:return 0elif n == 1:return 1else:return fibonacci(n-1) + fibonacci(n-2)```通过上述递归函数,我们可以很方便地求解斐波那契数列的任意一项。
例如,要求解斐波那契数列的第10项,可以调用`fibonacci(10)`,得到结果55。
然而,尽管递归算法简洁明了,但也存在一些问题。
递归算法的时间复杂度较高,随着n的增大,计算量呈指数级增加。
这是因为递归算法需要重复计算相同的子问题,造成了重复的工作量。
此外,递归算法还会占用较多的内存空间,因为每次递归调用都需要在栈中保存一些临时变量。
为了解决递归算法的效率问题,可以考虑使用迭代算法来求解斐波那契数列。
迭代算法通过循环的方式,逐步计算每一项的值,避免了重复计算和大量的函数调用。
