大学物理-旋转矢量
旋转矢量法在简谐振动中的应用探讨

旋转矢量法在简谐振动中的应用探讨摘要:结合旋转矢量法的理论依据探究旋转矢量法在简谐振动中的应用,探究结果发现:旋转矢量法的理论依据是两个振幅相等,频率相同的简谐振动,相位差等于π/2,沿垂直方向的合成就是圆周运动;而旋转矢量法可计算简谐振动的矢端速度与加速度、相位与初相位、运动时间间隔及合振动。
关键词:旋转矢量法;简谐振动;应用0.旋转矢量法旋转矢量法[1],也叫匀速圆周运动法,参考圆法,用其方法来解决简谐振动中的问题,相对来说比较简单。
如图1,做一个圆周,以O为原点,向右为正方向建立坐标轴,根据题目条件确定半径位置,要观察的是半径的端点在x轴上的投影的位置,如果速度为正,半径端点一定处于x轴下方,反之在x轴上方,比如,t=0时,质点正经过平衡位置向正方向运动,那么这个半径端点就是在原点正下方,即端点的投影刚好在原点[2]。
而以O为原点的旋转向量A的端点与在x 轴上的投影点的运动为简谐振动。
图1 旋转矢量图2 相位差为π/2互相垂直简谐振动的合成1.简谐振动矢量法的理论依据互相垂直相同频率简谐振动的合成[3],现将分振动的运动学方程表示为,,质点既沿Ox轴又沿Oy轴运动,实际上是在Oxy平面上运动。
从上面方程消去t,得合振动的轨迹方程:=。
当相位差为时,,表明合振动的轨迹为以x和y为轴的椭圆,如图2所示这里又可分为两种情况,时,x方向的振动比y方向的振动超前,即,当某一瞬时,则x=0,y=A2,即质点在图2(a)中的P点,经过很短时间后略大于零,y将略小于A2,为正,而略大于,x将为负,故质点运动到第二象限,即质点沿椭圆逆时针运动。
反之,时,y方向的振动比x方向的振动超前,质点沿椭圆顺时针方向运动,如图2(b)。
以上两分运动中,若=且相位差为,则其合运动轨迹方程褪化为圆。
两个振幅相等,频率相同的简谐振动,相位差等于沿互相垂直方向合成的为圆周运动;反推理可得,圆周运动亦能分解为两互相垂直的同振幅同频率的简谐振动。
大学物理-11第十一讲简谐振动、振动能量、旋转矢量法

14
例:边长l的立方体木块浮于静水中,浸入水中部分 的高度为b。今用手将木块压下去,放手让其开始运 动。忽略水的阻力,证明木块作谐振动。 解:以水面为原点建立坐标OX。
任意时刻 F浮水(bx)l2g mgF浮ma
水 b l2g水 l2(bx)gm a
力使 减小.
mgsinmldd2t2
很小,sin mg
ml
d2
dt2
l m
f mg
d 2
dt 2
g
l
0
角谐振动
解为 0cos(t)
g T 2 l
l
g
12
例:如图所示装置,轻弹簧k =50N/m,滑轮 M =1kg,
半径 R =0.2m,物体 m =1.5kg。若将物体由平衡位置
X
P
xAcos(t)
◆可用该旋转矢量末端的投影点 P 的运动来表示简 谐振动。
16
旋转矢量法的应用
1.确定初位相 ●由初始位置 x0 确定旋转矢量两个可能的位置。 (特殊情况下只有一个位置) ●根据初始速度方向,由旋转矢量两个可能的位 置中确定初始位置,从而找出初相.。
A
Ox
17
例:确定下列情况的初位相 (a) 已知 t = 0 时,x = -A。 (b) 已知 t = 0时,x = 0,且向 x 轴正方向运动。 (c) 已知 t = 0,x = -A/2,且向 x 轴负方向运动。 (d) 已知 t = 0,x = -A/2,且向 x 轴正方向运动。
13
d2x dt2
k x0 m(1/2)m
d2x dt 2
大学物理B(Ⅱ)旋转矢量

t 0.667s
x
A
00 7.5 A 2
A v
t0
例 一简谐运动的运动
曲线如图所示,求振动周
期.
t(s) t 0
A A2 0 A x
t 7.5
2π T T
t 7.5s
T 18s
例 已知谐振动的 A 、T ,求 1)如图简谐运动方
A'
44
因为 v0 0 ,由旋转矢量图可知 ' π 4
x Acos(t ) 0.0707cos(6.0t π)
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向 Ox轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
A/2 t ta
A 0 A x
t0
π ( π) 2π
3 33
tb
T
2π
T 3
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
旋转矢量表示法B版

1 2
⎞ ⎟ ⎠
−
π⎤
3
⎥ ⎦
=
2 π
⎡ 2π ⎢⎣ 3
−
π⎤ 3 ⎥⎦
=
2 3
=
0.667(s)
四、相图(phase diagram)
利用相图描述非线性动力学的方 法是19世纪末法国数学家亨利·庞加 莱(H.Poincare)发明的.
现以坐标和速度为坐标轴定义一 个平面, 称为相平面. 系统的一个运 动状态对应于相平面上的一个点, 称 为相点. 当系统的运动状态发生变化 时, 相点在相平面内运动, 相点的轨 迹则称为相图.
A 端投影:
x = A cos(ωt + ϕ )
与简谐运动方程完全相同, 所以投影点的运动为简谐运动.
二、初相位
ϕ = π平衡位置 2
旋转矢量表示法
π <ϕ <π 2
ϕ
ϕ=π
负向最大
π 0<ϕ<
2
x ϕ=0
正向最大
π < ϕ < 3π 2
3π < ϕ < 2π 2
ϕ = 3π 平衡位置 2
初相位讨论
大学物理
振动学基础
第3讲 旋转矢量表示法
旋转矢量表示法
旋转矢量表示法
一、旋转矢量表示法(参考圆法)
是研究简谐运动规律时所采用的直观的几何描述方法.
自 Ox 轴原点作矢量 A , 其模等 于振幅. A 绕 O点逆时针旋转, 角 速度为ω (其数值即为简谐运动的 角频率) , 则 A 称为旋转振幅矢量. 设初始时刻 t = 0 时 A 与 x 轴夹角 等于初相位 ϕ , 经过时间 t , A 与 x 轴夹角等于相位ω t +ϕ .
1-1 简谐运动方程及旋转矢量

热力学基础 f ( P,V , T ) C
气体动理论 k N 0
量子物理
E = h
xPx h
1 2 1 mv f(v)dv kT 2 2 h E , p h
第九章
振动
Chapter 9 Vibration
String theory: Theory of everything
2. 简谐运动的运动学分析 运动方程 x A cos(t )
(1)描述简谐运动的基本物理量 A——振幅
ω——角频率
T——周期 ν——频率 ωt +φ——相位
A A
x
T
o
t
初相:表示物体在初 始时刻的振动状态。
v A sin( t )
a A cos(t )
l
FT m
g l
o
Acos(t )
问题:
P
Simple Harmonic Motion (SHM)
5. 简谐运动的两个实例——单摆和复摆 (2)复摆 5
o
d 2 转动正向 2 sin 0 dt
2
lc
*
C
P
( C点为质心)
mglc J
3. 旋转矢量法
简谐运动 平衡位置 振幅 角频率 初相 相位 位移 旋转矢量 圆心
A
t
o
x
半径 角速度
初始角度 t时刻的夹角
半径在x轴上的投影
例1 已知某简谐运动的振动曲线如图所示, 位移的单位为cm,时间单位为s,则此简谐振 动的
振幅 A= 角频率
2 cm
4 rad s 1 3
大学物理旋转矢量

极坐标表示法
极坐标与平面角
旋转矢量在极坐标系中由一个起点、一个长度和一个平面角唯一确定。平面角表示矢量旋转的方向和角度。
旋转矢量的运算
在极坐标系中,可以通过加减、数乘等运算得到新的旋转矢量。
直角坐标表示法
直角坐标与平面矢量
旋转矢量在直角坐标系中由三个分量唯一确定,这三个分量表示矢量在x、y、z轴上的投影。
结论总结
总结实验结果,得出结论,并指出实验的局限性和未来改进的方向 。
THANKS
感谢观看
旋转矢量的积分
当一个旋转矢量在某区间内进行积分时,其 结果为该区间内所有点处的切线方向与该区 间内所有点处的速度方向一致的点所组成的
线段。
04
旋转矢量在物理中的应用
角动量守恒定律
角动量定义
物体的转动惯量和转动半径的乘积称为角动量。
角动量守恒定律
在没有外力矩作用的情况下,物体的角动量保持不变。
旋转矢量表示
旋转矢量的应用领域
物理学
旋转矢量在物理学中广泛应用于描述物体的 旋转运动,如刚体的转动、电磁场的旋涡等 。
工程学
在机械工程、航空航天等领域,旋转矢量可以用于 分析物体的动态平衡、稳定性等问题。
电子技术
在电子技术中,旋转矢量可以用于描述信号 的相位、频率等参数,以及进行数字信号处 理。
02
旋转矢量的表示方法
03
旋转矢量的运算规则
加法运算规则
平行四边形法则
当两个旋转矢量相加时,以两个矢量的末端 为起点,分别画出平行四边形的两个相邻边 ,连接对角线,得到的结果是两个旋转矢量 相加后的矢量。
三角形法则
当两个旋转矢量相加时,以一个矢量的起点 为起点,画另一个矢量的平行线,得到的结 果是两个旋转矢量相加后的矢量。
北京化工大学 普通物理学 1-3旋转矢量

2 ϕ =π − = π 3 3
π
∆ϕ = ω∆t
1 – 3
旋转矢量
第1章 机械振动 章
例3:已知两个简谐振动曲线如图所示,其中 为振 :已知两个简谐振动曲线如图所示,其中A为振 幅,x1 的相位比 x2 的相位超前 。
x
x1
A
A − 2
x2
t
1 – 3
旋转矢量
第1章 机械振动 章
x2
∆ϕ
0
x
3 ∆ϕ = π − = π 4 4
由旋转矢量图可知
1 – 3
旋转矢量
第1章 机械振动 章
A (2)求物体从初位置运动到第一次经过 处时的 2 速度; 速度;
解
x = A cos(ωt + ϕ ) = A cos( ω t )
A
x 1 cos( ω t ) = = A 2 π 5π ωt = 或 3 3 π 由旋转矢量图可知 ω t = 3
∆t = t 2 − t1 =
∆ϕ
x a A
A2
ω
b
v
π ∆ϕ = 3
tb
o
t
−A
−A
0
∆ϕ A ta A
2
x
π 3 1 ∆t = T = T 2π 6
1 – 3旋转矢量第1章 机械振动 章2)对于两个同频率的简谐运动,相位差表示它 对于两个同频率的简谐运动, 的简谐运动 们时间步调上的差异。(解决振动合成问题 步调上的差异。(解决振动合成问题) 们时间步调上的差异。(解决振动合成问题)
x1 = A1 cos(ωt + ϕ1 ) x2 = A2 cos(ωt + ϕ 2 )
∆ϕ = (ωt + ϕ 2 ) − (ωt + ϕ1 )
大学物理12机械振动2

A
x x−t 图
T
ω v = − A ω sin( ω t + ϕ )
π = Aω cos(ωt +ϕ + ) 2 2 a = − A ω cos( ω t + ϕ )
= Aω cos(ωt +ϕ + π)
2
T=
2π
取ϕ = 0
− Aω
v v −t图 Aω o T
l = l0 1− (v / c)2
在飞船B上测得飞船 相对于飞船 的速度: 在飞船 上测得飞船A相对于飞船 的速度: 上测得飞船 相对于飞船B的速度
v = l / ∆t = (l0 / ∆t) 1−(v / c)
解得:v = l0 / ∆t 1 + (l0 / c∆t )
2
2
= 2.68 ×10
8
∆φ > π 3π 称振动( )落后于振动( ) φ2 −φ1 > 0 例:φ2 −φ1= 2 称振动(2)落后于振动(1) 2π − ∆φ
分别作出四种情况的矢量图! 分别作出四种情况的矢量图!
2 4
∆ϕ21 = (ω t + ϕ2 ) - (ω t + ϕ1) = ϕ2 - ϕ1
φ2 −φ1 < 0 例:φ2 −φ1= − 3π称振动(2)超前振动(1) 2π + ∆φ 称振动( )超前振动( )
90
v am
ω
0
ω t+ϕ
·
x
1、用旋转矢量方法确定初相位ϕ: 、 要求条件: 的关系, 要求条件:已知 x0 与A的关系,初速度的方向。 的关系 初速度的方向。 例1: 已知一物体做简谐振动。1)x0=(1/2)A且向位移的 : 已知一物体做简谐振动。 ) 且向位移的 且向位移的正方向运动。 负方向运动; ) 且向位移的正方向运动 负方向运动; 2)x 0= 0且向位移的正方向运动。试求 两种情况下的初相。 两种情况下的初相。 ϕ = π/3
大学物理 旋转矢量(一)

大学物理旋转矢量(一)引言概述:在大学物理的学习中,旋转矢量(一)是一个重要的知识点。
旋转矢量是描述物体在空间中旋转运动的工具,它具有方向和大小,并可以表示绕定轴进行的旋转。
本文将围绕旋转矢量展开讨论,依次讲解旋转矢量的基本概念、旋转轴和角速度、刚体的定点转动、角动量和力矩、以及旋转的动力学方程。
一、旋转矢量的基本概念1. 旋转的定义与描述2. 旋转角度的表示方法3. 旋转矢量的含义与性质4. 旋转矩阵的使用及推导5. 旋转矢量与坐标系的转换二、旋转轴和角速度1. 旋转轴的定义与求解2. 旋转轴的方向确定方法3. 角速度的概念与计算4. 角速度的单位及数值表达5. 转动矢量与角速度的关系三、刚体的定点转动1. 定点转动的定义与特点2. 转动惯量的概念与计算3. 定点转动的动力学方程4. 定点转动的动力学矢量关系5. 刚体定点转动现象的实例分析四、角动量和力矩1. 角动量的概念与性质2. 角动量的计算与单位3. 力矩的定义与计算4. 力矩的性质与作用5. 角动量和力矩的关系及应用五、旋转的动力学方程1. 旋转的动力学定律与原理2. 牛顿第二定律在旋转运动中的应用3. 旋转的动力学方程的推导过程4. 动力学方程与运动学方程的对应关系5. 旋转动力学方程实际问题的解析解和数值解总结:通过本文的介绍,我们对大学物理中的旋转矢量有了更深入的认识。
我们了解到旋转矢量的基本概念、旋转轴和角速度的计算方法、刚体的定点转动特性、角动量和力矩的关系,以及旋转的动力学方程的应用。
这些知识将有助于我们理解旋转运动的本质和规律,为进一步的学习和研究打下了基础。
大学物理 旋转矢量(两篇)2024

引言概述:在大学物理学中,旋转矢量(二)是一个重要的概念。
它在描述物体旋转和角动量时发挥着关键作用。
本文将详细阐述旋转矢量的相关内容,包括其定义、性质以及在实际应用中的应用案例等。
正文内容:一、旋转矢量的定义1.旋转矢量的概念和来源2.旋转矢量的数学表示和坐标系选择3.旋转矢量的物理意义和几何解释4.旋转矢量与旋转矩阵的关系5.旋转矢量的性质和基本运算法则二、旋转矢量的旋转定理1.旋转矢量的定义和旋转方向2.旋转定理的几何解释和物理意义3.旋转定理的数学推导和证明4.旋转定理的应用案例:刚体的旋转运动5.旋转定理的实验验证和实际应用三、旋转矢量的角动量1.角动量的定义和物理性质2.角动量的计算方法和表达式3.角动量守恒定律和旋转矢量的关系4.角动量的变化和影响因素5.角动量对物体运动轨迹的影响和解释四、旋转矢量的应用案例1.旋转矢量在力学和动力学问题中的应用2.旋转矢量在电磁学和光学问题中的应用3.旋转矢量在量子力学和粒子物理学问题中的应用4.旋转矢量在天体力学和宇宙学问题中的应用5.旋转矢量在工程和技术领域中的实际应用五、旋转矢量的拓展与发展1.旋转矢量的局限性和扩展性2.旋转矢量在现代物理学和数学中的发展趋势3.旋转矢量在计算机图形学和虚拟现实领域中的应用4.旋转矢量的研究方法和实验手段5.旋转矢量相关学科和概念的比较和关联总结:旋转矢量作为大学物理学的重要内容,在描述物体旋转和角动量时具有不可替代的作用。
本文从旋转矢量的定义、性质和旋转定理开始,详细阐述了其在实际应用中的案例和应用领域。
同时,展望了旋转矢量的拓展与发展,以及与其他学科和概念的比较与关联。
通过对旋转矢量的深入研究和理解,有助于我们更好地理解物体的旋转规律和角动量的变化,为解决各种实际问题提供了强有力的工具和方法。
引言概述:旋转矢量是大学物理中一个重要概念,它在描述物体或系统的旋转运动中起到了关键作用。
本文将从基本概念出发,分析旋转矢量的定义、性质和应用,并探讨其在物理学中的重要性。
11-1简谐振动旋转矢量表示法
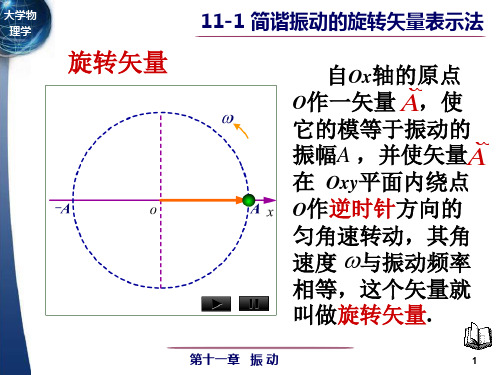
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
第十一章 振 动
3
大学物 理学
1111-1 简谐振动的旋转矢量表示法
ω
t =t
ωt + ϕ
v A
x
o
x = A cos(ωt + ϕ )
以 o 为原 v 点旋转矢量 A 的端点在 x 轴 上的投影点的 运动为简谐运 动.
x1 = A1 cos(ωt + ϕ1 ) x2 = A2 cos(ωt + ϕ 2 )
∆ϕ = (ωt + ϕ 2 ) − (ωt + ϕ1 )
∆ϕ = ϕ 2 − ϕ1
第十一章 振 动
10
大学物 理学
1111-1 简谐振动的旋转矢量表示法
∆ϕ = ϕ 2 − ϕ1
∆ϕ = 0 同步
∆ϕ = ±π 反相 ∆ϕ为其它
简谐运动, (1)对同一简谐运动,相位差可以给出 ) 同一简谐运动 两运动状态间变化所需的时间. 两运动状态间变化所需的时间.
x1 = A cos(ωt1 + ϕ )
x2 = A cos(ωt 2 + ϕ )
∆ϕ = (ωt2 +ϕ) −(ωt1 +ϕ)
∆t = t2 −t1 = ∆ϕ
ω
第十一章 振 动
x = 0.104m v = −0.188m / s 2 a = −1.03m / s
A
− 0.12 −0.06
t 时刻
x/m
0.12
起始时刻
15
o
π − 3
0.06
A
第十一章 振 动
ω
大学物 理学
旋转矢量法描述简谐波

( 4 ) 矢 端加速 度在 Y轴上 投影 的负 值 即是该 质
点 的加 速度.
( 5 ) 该 质点动 能与 势能 的 比值
Ek
图 1
, MP\
E 一\ O P/
对 于第 5点 , 由于位 于 5 C处 的质点 做类 简 谐振
如图 1为 旋转 矢 量 图 , 矢端 沿 圆周运 动 的 角速
摘 要 : 采 用 旋 转 矢 量 法 将 简 谐 波 的时 间性 与 空 间性 , 各质点的能量 、 相位 、 位移 、 速 度 以及 加 速 度 均 反 映 到 矢 量 图中, 并利用该方法探究同方向 、 同频 率 波 的 合 成 问 题 , 直 观 地 反 映 合 成 波 的相 关 性 质 .
【 例 1 】一 平 面简 谐 波沿 z轴 正 向传 播 , 已知 距
[ Al s i n ( 一 h + 1 ) +
A2 s i n( 一 疋 r + 2 )s i no a o z ( 1 5 )
波 源 z一 2 m 处 的质点 M 在 t :2 s 时刻 , 向下 运动 且 相位为 , 波长 为 6 0 m, 周期 为 3 s . 求:
y — y1 + 2 ( 1 4 )
式( 1 2 ) 、 ( 1 3 ) 代 人式 ( 1 4 ) 整理, 得
一
所 以
[ A1 c o s ( 一 妇 十 1 ) + A 2 c o s ( 一 + 2 ) ] o o s  ̄ 0 t 一
鲁 E 一 ( \ / O P ) 。
^
为波 长. 其 波上各 质点 的位移 、 速度 、 加速 度 等
学习简谐 波 的过程 中, 对 波 的相 位 、 时间性 与空 间性
4.3 简谐振动的旋转矢量法

2
大学物理
第一版
4.3 简谐振动的旋转矢量法
t t
A
o
t
x
以o 为原点 旋转矢量 A 的 端点在 x轴上的 投影点的运动为 简谐运动.
x A cos(t )
3
大学物理
第一版
4.3 简谐振动的旋转矢量法
x A cos(t )
以o 为原点 的端 旋转矢量 A 点在 x 轴上的投 影点的运动为简 谐运动.
讨论
相位差:表示两个相位之差
(1)对同一简谐运动,相位差可以给出两运 动状态间变化所需的时间.
x1 Acos( )
t t 2 t1
x2 Acos( t2 )
9
大学物理
第一版
4.3 简谐振动的旋转矢量法
vm A
A
x A cos(t )
v a
v A sin(t )
x a A 2 n
a A 2 cos( t )
7
大学物理
第一版
4.3 简谐振动的旋转矢量法
3
用旋转矢量图画简谐运动的
xt 图
8
大学物理
第一版
4.3 简谐振动的旋转矢量法
0.08
17
大学物理
第一版
4.3 简谐振动的旋转矢量法
法二
t
时刻
t
π3 π3
起始时刻
x/m
0.08
0.08 0.04
o
0.04
π π 2 1 rad s t 0.667 s t 3 2 3
18
大学物理
大学物理学教学中初相位的求解——旋转矢量法

大学物理学教学中初相位的求解——旋转矢量法
初相位的求解作为理论物理学中一个重要的内容经常被大学物理学教学中提及,相比较传统的三角函数法,旋转矢量法作为一种新的数学计算方式正逐步在各个大学物理教学中得到应用,本文将以此方式进行初相位的求解及应用。
旋转矢量法是一种计算变换位置、旋转之间关系的重要方法,可以把旋转视为矢量,这种矢量可以是旋转轴向量乘以旋转角度的形式。
在计算初相位时,可以利用旋转矢量的相加、相减,从而得出相应的位置、角度变换及旋转信息,从而解决初相位求解问题。
旋转矢量法具体应用于初相位求解时如下:
(1)以坐标系0-A,以A点为原点,以X轴为横轴,以Y轴为纵轴。
(3)从A点到B点的位移量为Rb,定义α角为旋转量,此旋转的旋转轴向量为:
U=(X`Y`Z`)。
(5)根据位移量Ra和α角,计算出旋转矢量:〖R_b〗^α=(X^`Y^`Z^`)。
(6)由计算出的旋转矢量〖R_b〗^α和位移量Ra,求出从A点到B点的旋转量Φ:Φ=〖R_a〗^α+Ra,Φ即为A点到B点的初相位。
(9)根据计算出的β角得出从A点到B点的旋转量γ:γ=β- α。
以上就是应用旋转矢量法求出初相位的步骤,3D旋转的运算角度可以根据同理求出。
传统的三角函数法只能表示2D的运算,而旋转矢量法则不仅可以求出2D的运算,还可以求出3D的运算,可以用来解决复杂的初相位求解问题。
总之,旋转矢量法作为一种基于几何的运算方式,其优点可以体现在于它融合几何和代数在一起,能够有效解决复杂多轴的位移、角度变换及旋转运算的问题,可以有效求解初相位问题。
从而为进一步的理论物理数学研究打下基础。
大学物理(工科) 4—1 简谐运动、旋转矢量简谐运动的合成

2
tan1( v0 ) 注意: 确定 的象限 x0
二、简谐运动的描述
x Acos(t )
1.解析法(由振动表达式)
A, T, , x, v, a
2.曲线法(由振动曲线)
x
x Acos(t )
A
►确定振幅A;
o
►确定周期T,ω;
►确定φ
-A
T
t
•根据图像判断速度的正负用斜率 •利用初始条件确定几个φ,再利用速度正负判断保留φ
3、掌握描述简谐波的各物理量及各量间的关系;
4、理解机械波产生的条件. 掌握由已知质点的简谐 运动方程得出平面简谐波的波函数的方法. 理解波函 数的物理意义. 了解波的能量传播特征及能流、能流密 度概念.
匀速直线运动
直线运动
匀变速直线运动
学
变速直线运动
过 的
变加速直线运动
运
动 形
平抛运动
式
抛体运动
例4.2: 已知一简谐振动的曲线如图所示,写出振动方程。
x (cm)5
6
2
3
p
O 1
t(s)
解: 已知振动方程表达式为:x Acos(t ),v Asin(t )
► 定振幅: A=0.06m
►定初相
x0 0.06cos 0.03
cos 0.5
利用斜率判断0时刻速度方向 0 0
晶格点阵
§4—1 简谐运动、旋转矢量、简谐运动的能量
一、简谐运动动力学 1.模型
2.定义 ►受力:F=-kx
►动力学微分方程:
d2 dt
x
2
2
x
0
令 2 k
m
►运动方程: x(t)=Acos( t + )
大学物理-旋转矢量
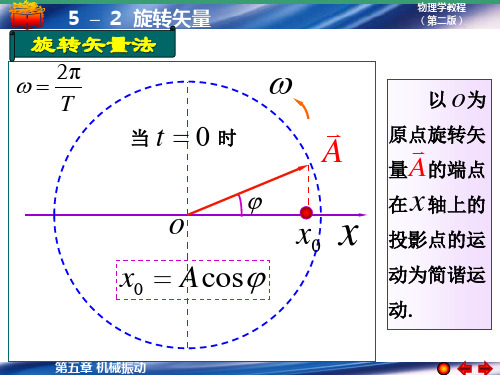
t 0 x0 A v0 0
A A cos cos 1
x o A
y
x
A
A
o
xo
A
物理学教程 (第二版)
l
t
第五章 机械振动
5 – 2 旋转矢量
4.初始条件
x
t 0
o
x0 0
v0 0
0 A cos cos 0
/ 2 , 3 / 2
y
x
3 A
o
2
x
以 o为 原点 旋转矢 量A的端点
x 在 轴上的
投影点的运 动为简谐运 动.
第五章 机械振动
5 – 2 旋转矢量
物理学教程 (第二版)
x Acos(t )
旋 转 矢量 A的
x 端点在
轴上的投 影点的运 动为简谐 运动.
第五章 机械振动
5 – 2 旋转矢量
y vm t π
2
t
0
an
a v
m 0.01kg o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
F kx m 2x 1.70103 N
第五章 机械振动
5 – 2 旋转矢量
物理学教程 (第二版)
(2)由起始位置运动到 x 0.04m 处所需要
A
x
物理学教程 (第二版)
vm A an A 2
x Acos(t )
v A cos(t π )
2
a A2 cos(t )
第五章 机械振动
5 – 2 旋转矢量
用旋转矢量表示简谐运动初相
1.初始条件 t 0 x0 A v0 0
大学物理学教学中初相位的求解_旋转矢量法

· 118·
安庆师范学院学报( 自然科学版)
2012 年
[ 1]李振美. 类比教学法在操作系统核心内容教学中的应用 —以进程管理为例[ J]. 中国科教创新导刊, 2010 ( 31 ) : 73. [ 2]彭宗举, 2007 ( 2 ) : 123 - 124. 沈明圻, 赵一呜. 类比教学法在操作系统教学中的应用研究[J]. 高等理科教育, [ 3]伍一 等. C 语言程序设计与实训教程[M]. 北京: 清华大学出版社 2007. [ 4]夏宽理, . 北京: 中国铁道出版社 2006. 赵子正. C 语言程序设计[M] [ 5]包振宇, M] . 北京: 北京交通大学出版社 2009. 孙干. C 语言程序设计[ [ 6]苏小红, M]. 北京: 高等教育出版社 2011. 王宇颖, 孙志岗 等. C 语言程序设计[
2π 3π π π π t + ) ; 同理可求得 ⑵ 的初相位( 图 3 ) 为 φ = - - =- ( 注: 这里初相位的范围取 T 3 2 4 4 3π 7π 2π 3π + 2π = ), t - )。 相应的简谐振动表达式 x = Acos( 4 4 T 4
( - π, , π] 也有教材取 φ = -
图5
图6
根据此性质可很方便地求得波形图中各点的振动特点 。 本题中给出波向右传播而波源点 O 在波峰 6 ( a ) , O 。 的左侧见图 故 点向下振动 因坐标原点的初始位置在原点或平衡位置 , 这表明坐标原点初始位 置在平衡位置且沿负向运动。 因而利用旋转矢量法( 图 6 ( b) ) 可很方便地确定 O 点的初相位为 φ = 所以 O 点的简谐振动方程为 y = Acos( ωt + φ) = 0 . 04cos( 0 . 8 πt + y( x, t) = 0 . 04cos[ 0 . 8 π( t - π ), 相应的波动方程为 2 π , 2
大学物理第三讲:8.1.3旋转矢量法

5 / 4或 3 / 4
已知:A1 A2 5cm;
x/cm
1 / 2;2
t/s
1合振动的振幅:A 求: 2 ? 合振动的初相位:
2 A12 A2 ;
o
8-18 已知两个同方向、同频率的简谐振动如下:
x1 5 102 cos(10t 3 / 5)
作 业:
1、仔细阅读教材; 2、请你做题8-18;
预 习:
1、§8-2 简谐振动的合成
2、§8-3 阻尼振动 受迫振动、共振
16
谢谢大家!
欢迎大家多提宝贵意见!
2015.10.10
17
18
813旋转矢量法一简谐振动与旋转矢量的关系二旋转矢量的长处三应用举例四小结作业预习??简谐振动可用一旋转矢量a来表示??0t0a?x?t?0tta?ox??????taxcos一简谐振动与旋转矢量的关系??简谐振动与一旋转矢量a的对应关系1旋转矢量a的长度为简谐振动的振幅4旋转矢量a作逆时针匀速运动角速度2为t0时的相位初相位3t为t时刻的相位5旋转矢量a的末端在参考坐标轴上的投影点的运动即代表质点做简谐振动
x2 6 102 cos(10t / 5)
x3 7 102 cos( 10t )SI
求: 问值为何值时, x1 x2的振幅最大?
问值为何值时, x2 x3的振幅最小?
解:
A1
A3
x1 , x3
A3
x2 , x3
15
A2
小 结:
1、旋转矢量法 2、利用旋转矢量解题
相消 (2k 1 ) 2
2k 3 / 5时,x1 x2的振幅最大 Amax A1 A2
用旋转矢量法求受迫振动的振幅和初相

P H ASE OF FO R CED VIBRATI O N BY R OTATING VECTO RXu You w en Xu D i yu( D epa r t ment of Physics , S ichua n Vocatio n al and Technical College , S ui n i n g , S ichuan 629000)Abstract A cco r d i n g to t h e dyna m ic a n d ki n e matic equatio n s of fo r ced vi b ratio n , t h e a mp li2 t u de a n d i n itial p h a s e of fo rce d vi b ratio n a r e o b t a i n ed .K ey Words fo rced vi b ratio n ; ro t a ti n g vecto r ; a m p lit u de ; i n itial p ha s e系统在周期性外力作用下被强迫进行的振动,称为受迫振动. 受迫振动是工程技术中常见的振动. 研究受迫振动具有很大的意义. 求解受迫振动达到稳定状态时的振幅和初相, 一般书籍[ 1~6 ] 都是通过求解受迫振动的动力学方程而得出的,本文用旋转矢量法求受迫振动的振幅和初相.图 1受迫振动的动力学方程旋转矢量受迫振动所受的作用力有:准弹性力- k x 、如图1 所示,从O x坐标轴的原点O , 作一矢量 A ,其长度A 等于谐振动的振幅; t = 0 时 A 与O x 轴夹角等于初相φ; 并使 A 以大小等于谐振动角频率ω的角速度, 沿逆时针方向匀速转动, 这个矢量A 就称为旋转矢量.旋转矢量法是直观地研究谐振动的几何方法. 它不仅可以帮助人们形象地了解谐振动各物理量的含义及其相互关系, 而且便于对谐振动进谐激励力F0 co sωt 、与速度成反比的阻尼力- cv 因此,作受迫振动物体所受的合力为+ F0 co sωt -F = - k x由牛顿第二定律,得cv2md x= - k x + F0 co sωt - cv2d t2d x= - k x +F0sωt - c v∴d t2m m m取ω2 = k/ m ,2β= c/ m , f 0 = F0 / m ,并注意v =d x,0 d t代入上式得受迫振动的动力学方程为d2 x d x2+ 2βd t+ ω0 x = f 0 co sωt(1)d t2这是一个非齐次的常系数二阶微分方程.它的通解为A 0e -βt co s( 0 - β2 t + φ0 )ω2+ A c o s(ωt - δ)x =经过足够长的时间后, 其中第一项解减弱到可以忽略不计,只有第二项是振幅不变的振动.因此,受迫振动达到稳定状态时的运动学方程为[ 7]图 2作H G ⊥O G,在Rt △O G H 中,x = A c o s(ωt - δ)(2)F2 = ( B - D) 2 + C2式中A 是受迫振动稳态时的振幅;角频率等于简谐激励的角频率ω;δ是稳态响应与简谐激励的相差, 即受迫振动的初相. 式(2) 表示稳定状态的受迫振动是一个与简谐激励力同频率的简谐振动.f 2(ω2ω2 ) 2( βω) 2即=0 A - A + 2 A= A2 [ (ω2ω2 ) 2β2ω20 - + 4 ]βωA2βωC 2t a nδ===ω2 2 2 20 A -ω Aω0- ωB - D于是得受迫振动的振幅A 和初相δ分别为f 0用旋转矢量法求受迫振动的振幅和初相 A =(ω20- ω2 ) 2 + 4β2ω22βω由式( 2) 得δ= a r ct a nω2 2- ωd2 x= - ω A c o s(ωt - δ)2由此可知, 用旋转矢量法求受迫振动的振幅和初相,比用解微分方程的方法求解直观简单得多, 充分显示了用旋转矢量描述谐振动的优越性其实,任何谐振量都可以用旋转矢量来描述. 因此, 只要用得上旋转矢量法, 就要尽量应用它.d t2= ω2 A c o s[π+ (ωt - δ) ]2βd x = - 2βωA si n(ωt - δ)( 3)d tπ+ (ωt - δ)= 2βωA co s( 4)2参考文献ω20 x =ω0 A c o s(ωt - δ)2 (5)令B =ω2 A 、C = 2βωA 、D = ω2 A 、F = f 0 , 则式(3) 、0 [ 1 ] 赵景员, 王淑贤. 力学[ M ] . 北京: 人民教育出版社, 1979 .470~473赵凯华, 罗蔚茵. 力学[ M ] . 北京: 高等教育出版社, 1995 .273~275张三慧. 波动与光学[ M ]第2 版. 北京: 清华大学出版社,2000 . 24~25马文蔚,解希顺等. 物理学( 下册)[ M ] 第4 版. 北京:高等教育出版社,1999 . 30~31卢德馨. 大学物理学[ M ] . 北京: 高等教育出版社, 1998 .142~143刘克哲. 物理学(上卷) [ M ] 第2 版. 北京: 高等教育出版社,1999 . 155~156周圣源,黄伟民. 高工专物理学[ M ] . 北京: 高等教育出版社,1996 . 61 ,75( 4) 、( 5) 与式( 1) 的右边变为d2 x[ 2 ]= D co s[π+ (ωt - δ) ](6)d t2[ 3 ]π+ (ωt - δ)2βd x = C co s(7)2d t[ 4 ]ω20 x = B c o s(ωt - δ)( 8)(9)f 0 co sωt = F co sωt[ 5 ]将式(6) 、(7) 、(8) 、(9) 代入式(1) ,并用旋转矢量B 、C、D 、F 表示各谐振量, 则有F = B + C + D并且C ⊥B , D ⊥C.旋转矢量图如图2 所示.[ 6 ][ 7 ]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x oA
y
x
A
A 0
o
x
o
l
t
2.初始条件
x
t 0
o
l
x0 0
v0 0
y
x
0 A cos
cos 0
A
o
A
2
x
o
t
/ 2 , 3 / 2
v0 A sin 0, sin 0 取 / 2
3.初始条件
t 0
x
l
x0 A v0 0
o A
y
x
A A cos
A 处时的
速度;
2
(3)如果物体在 x 0.05m 处时速度不等于零,
而是具有向右的初速度 v0 0.30m s,1 求其运动方程.
x/m
o 0.05
解 (1) x Acos(t )
k 0.72N m1 6.0s1
m
0.02kg
A 0.05m
由旋转矢量图可知 0
x Acos(t )
(3)如果物体在 x 0.05m 处时速度不等于零,
而是具有向右的初速度 v0 0.30m s,1 求其运动方程.
解 x Acos(t )
6.0s1
A
x02
v02
2
0.0707m
o π 4 x A'
由旋转矢量图可知 π 4
x Acos(t ) 0.0707cos(6.0t π)
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
y vm t π
2
t
0
an A
a v x
vm A an A 2
x Acos(t )
v A cos(t π )
2
a A2 cos(t )
用旋转矢量表示简谐运动初相
1.初始条件 t 0 x0 A v0 0
A A cos
4
例2 一质量为 0.01kg 的物体作简谐运动,其振
幅为 0.08m,周期为 4s ,起始时刻物体在 x 0.04m
处,向Ox 轴负方向运动(如图).试求
(1)t 1.0s 时,物体所处的位置和所受的力;
v
x/m
0.08 0.04 o 0.04 0.08
解 A 0.08m
2π π s1
A
cos 1
A
o
xo
t
A
4.初始条件
x
t 0
l
o
x0 0
v0 0
y
x
0 A cos
3 A
cos 0
o
2
x
o
A
t
/ 2 , 3 / 2
v0 A sin 0, sin 0 取 3 / 2
讨论 ➢ 相位差:表示两个相位之差 .
1)对同一简谐运动,相位差可以给出两运动状
0.04 0.08cos(π t π) 23
t 0.667s
解法二
t 时刻
t
π3 π3
0.08 0.04 o 0.04
起始时刻
x/m
0.08
t π
3
π s1
2
t 0.667s
旋转矢量法
2π
T
当t 0时
A
o
x0 x
x0 Acos
以 o为 原点 旋转矢 量A的端点
x 在 轴上的
投影点的运
动为简谐运
动.
2π
T
t t 时
A
t
o
x x0 x
x Acos(t )
以 o为 原点 旋转矢 量A的端点
x 在 轴上的
投影点的运
动为简谐运
动.
旋 转 矢量 A的
x 端点在
态间变化所需的时间. (t2 ) (t1 )
x Acos(t1 )
x Acos(t2 )
xa Ab
t
t2
t1
Ab
A2
o
A
v
π
t
A
t π 3 T 1 T
0
A 2
Aa
A
x
3
2π 6
2)对于两个同频率的简谐运动,相位差表示它 们间步调上的差异.(解决振动合成问题)
x1 A1 cos(t 1) x2 A2 cos(t 2 )
(t 2 ) (t 1) 2 1
0同步 x
π 反相
x
超前
为其它
落后
x
o
o
o
t
t
t
例1 如图所示,一轻弹簧的右端连着一物体,弹
簧的劲度系数 k 0.72N m1,物体的质量 m 20g.
(1)把物体从平衡位置向右拉到 x 0.05m 处停
下后再释放,求简谐运动方程; (2)求物体从初位置运动到第一次经过
T2
A 0.08m
2π π s1
T2
t 0, x 0.04m 代入 x Acos(t )
0.04 0.08cos
π
3
v0 0
π
3
A
π3
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
m 0.01kg
v
x/m
0.08 0.04 o 0.04 0.08
x 0.08cos(π t π ) 23
t 1.0s 代入上式得 x 0.069m
F kx m 2x 1.70103 N
(2)由起始位置运动到 x 0.04m 处所需要
的最短时间.
v
x/m
0.08 0.04 o 0.04 0.08
法一 设由起始位置运动到 x 0.04m 处所
需要的最短时间为 t
0.05cos6.0t m
oAx
(2)求物体从初位置运动到第一次经过 A 处时) Acos(t)
cos(t) x 1
A2
t π 或 5π
33
由旋转矢量图可知 t π
3
v A sint
A
o A Ax
2
0.26m s1 (负号表示速度沿 Ox轴负方向)
