2.2空间向量的运算 课件(北师大版选修2-1)
合集下载
北师版数学选修2-1课件:第2章 2 空间向量的运算
【答案】 B
上一页
返回首页
下一页
→ → → 3.在空间四边形ABCD中,连接AC,BD,则AB+BC+CD为________. 【解析】 【答案】 → → → → → → AB+BC+CD=AC+CD=AD. → AD
上一页
返回首页
下一页
4.若空间向量a,b满足|a|=|b|=1,a与b的夹角为60° ,求a· a+a· b=_____.
【答案】 C
上一页
返回首页
下一页
→ → → → (2)化简(AB-CD)-(AC-BD)=________.
→ -CD → )-(AC → -BD →) 【自主解答】 法一:(AB → -CD → -AC → +BD → =AB → → → → =AB+DC+CA+BD → +BD → )+(DC → +CA →) =(AB → +DA → =0. =AD
下一页
→ +D → →= 2.如图221所示,在平行六面体ABCDA1B1C1D1中,AA C - BB 1 1 1 1 ( )
图221 → A.AB 1 → C.AD
上一页
→ B.DC → D.BA
返回首页 下一页
【解析】
→ → → → → → → → → → AA1+D1C1-BB1=AA1+A1B1+B1B=AB1+B1B=AB=DC.
上一页 返回首页 下一页
减法
空间向量a与一个实数λ的乘积是一个 向量,记作λa,满足: 空间向量 ①|λa|=|λ||a| 的数乘 ②当λ>0时,λa与a方向 相同 ; 当λ<0时,λa与a方向 相反; 当λ=0时,λa= 0
①λa=aλ(λ∈R) ②λ(a+b)= λa+λb (λ+μ)a=λa+μa (λ∈R,μ ∈R) ③(λμ)a= λ(μa) (λ∈R,μ ∈R).
2.2《空间向量的运算》线上课程课件-北师大版高中数学选修2-1

02 新知讲授
一、空间向量的加、减法
1. 如图,设a和b是空间两个向量,过一
点O,作a和b的相等向量 OA和OB ,根据平
面向量加法的平行四边形法则,平行四边
形的对角线OC对应的向量就是a与b的和,
记作a+b.
a-b
2. 与平面向量类似,a与b的差定义为 a+(-b),记作a-b,其中-b是b的相反向量.
1.三角形法则和平行四
1.由于对两个法则不熟悉而
边形法则的应用;
造成对和、差向量的方向与
2.数乘向量要抓住它的
1.向量的加减法;
大小判断错误;
定义,从大小与方向两方
2.空间向量的数乘;
2.由于忽视了共线定理中的
面来理解;
3.空间向量的数量积.
b≠0,而造成解题错误;
3.数量积可以类比平面
3.在求数量积时,不能正确
江西省中小学2020年秋季学期线上课程——北师大版高中数学选修2-1
第二章:空间向量与立体几何 2. 空间向量的运算
01 新课导入
代数主要是研究运算的一门学科,它在中学数学中 占有非常重要的地位。随着对代数学习的深入,运算对 象在不断地拓展,对运算规律的理解也在不断地加深。 向量是代数研究最重要的对象之一。它不仅可以进行加 减运算,与实数结合进行数乘运算,而且还可以进行内 积(也就是向量的数量积)等运算。
③ (a·b)=( a)·b ( R ).
结论:
(1) a a a;
(2) a b a b 0;
(3) cos
a, b
a a
b b
(a 0, b 0).
2.向量a的单位向量
对于任意一个非零向量a,我们把
高中数学北师大版选修2-1 2.2.1空间向量的线性运算 课件(30张)

§2 空间向量的运算
-1-
第1课时 空间向量的线性运算
-2-
第1课时 空间向量的线性运算
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
1.会用图形说明空间向量加法、减法、数乘向量及它们的运算 律. 2.能运用空间向量的运算意义及运算律解决简单的立体几何问 题.
-8-
第1课时 空间向量的线性运算
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
【做一做 2】 给出下列命题: ① 在空间中, 零向量一定没有方向;
②若 ABCD-A'B'C'D'为平行六面体, 则������������ = ������' ������' ; ③若 ABCD-A'B'C'D'为长方体, 则������������ + ������������ + ������������' = ������������' + ������' ������' .
UBIAODAOHANG HISHI SHULI IANLIБайду номын сангаасTOUXI
UITANGYANLIAN
3.运算律 空间向量加法和减法的运算律与平面向量的运算律相同,表示如 下: (1)结合律 (a+b)+c=a+(b+c); (2)交换律 a+b=b+a. 说明:空间向量的加法、减法运算满足平行四边形法则或三角形 法则,并且空间向量的加法满足交换律和结合律.
-1-
第1课时 空间向量的线性运算
-2-
第1课时 空间向量的线性运算
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
1.会用图形说明空间向量加法、减法、数乘向量及它们的运算 律. 2.能运用空间向量的运算意义及运算律解决简单的立体几何问 题.
-8-
第1课时 空间向量的线性运算
M 目标导航 Z 知识梳理 D典例透析 S随堂演练
UBIAODAOHANG HISHI SHULI IANLI TOUXI
UITANGYANLIAN
【做一做 2】 给出下列命题: ① 在空间中, 零向量一定没有方向;
②若 ABCD-A'B'C'D'为平行六面体, 则������������ = ������' ������' ; ③若 ABCD-A'B'C'D'为长方体, 则������������ + ������������ + ������������' = ������������' + ������' ������' .
UBIAODAOHANG HISHI SHULI IANLIБайду номын сангаасTOUXI
UITANGYANLIAN
3.运算律 空间向量加法和减法的运算律与平面向量的运算律相同,表示如 下: (1)结合律 (a+b)+c=a+(b+c); (2)交换律 a+b=b+a. 说明:空间向量的加法、减法运算满足平行四边形法则或三角形 法则,并且空间向量的加法满足交换律和结合律.
2.2 空间向量的运算 课件(北师大选修2-1)
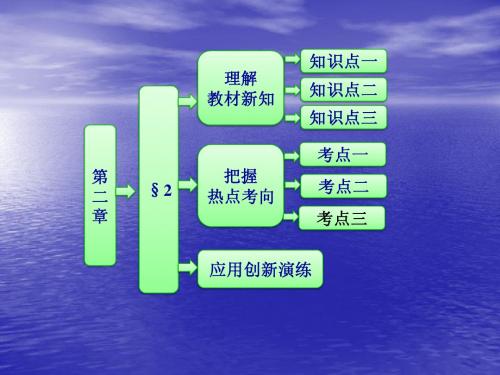
[精解详析]
∵E,H 分别是 AB,AD 的中点,
∴EH = AH -AE 1 1 = AD - AB 2 2 1 = (AD -AB ) 2 1 = BD . 2
2 2 又∵CF=2FB,CG=2GD,∴ C F = C B ,C G = C D .
λa的模是a的
模的 |λ| 倍
(3)空间向量的数乘运算律:
①交换律:λa= aλ (λ∈R); λa+λb ,
②分配律:λ(a+b)=
(λ+μ)a=λa+μ a(λ∈R,μ∈R); ③结合律:(λμ)a= λ(μa) (λ∈R,μ∈R). (4)定理:空间两个向量a与b(b≠0)共线的充分必要条件 是存在实数λ,使得 a=λb .
b=0 ; ②a⊥b ⇔ a·
a· b ③cos〈a,b〉= |a||b| (a≠0,b≠0.)
a (4)对任意一个非零向量, |a| 叫作向量 a 的单位向量, 把
记作 a0.a0 与 a 同 方向.
与平面向量类似,空间向量的加减、数乘、数量积运算 有如下特点 1.空间向量的加减法满足平行四边形和三角形法则,结 果仍是一个向量. 2.空间向量的数乘运算,结果仍是一个向量,方向取决 于λ的正负,模为原向量模的|λ|倍.
设 a,b,c 是任意空间向量,类比平面向量的数量 积,回答以下问题. 问题 1:由 a· b=0,一定能推出 a=0 或 b=0 吗?
π 提示:不一定,也可能〈a,b〉= . 2
问题 2:由 a· b=a· 能得到 b=c 吗? c
提示:不一定.
问题 3:(a· b)c=a(b· c)成立吗?
提示:不一定.
2
高中数学第二章空间向量与立体几何2.2空间向量的运算课件北师大版选修2_1

= 12 + 1×1×cos 60°- 2×1×1×cos 60°+ 1×1×cos 60°+12-2×1×1×cos 60° =1.
讲课堂互动讲义
空间向量的线性运算 已知空间四边形 OABC, M,N 分别是对边 OA、BC 的中点, 点 G 在 MN 上,且 MG=2GN,如 图,设O→A=a,O→B=b,O→C=c, 试用 a,b,c 表示向量O→G.
如图.
(2)减法法则 与平面向量类似,a与b的差定义为_a_与__-__b_的___ __和__向__量___,记作a-b,其中-b是b的相反向 量.
(3)运算律 交换律:a+b=__b_+__a_b+a; 结合律:(a+b)+c=__a_+__(_b_+__c)__.
[强化拓展]
(1)空间向量的加减法与平面向量的加减法完全相
[强化拓展] (1)因为空间任意两个向量都是共面的,所以空间向 量共线定理与平面向量共线定理是相同的;定理中 b≠0 不可丢掉,否则实数 λ 不一定存在,且不一 定唯一.如:a≠0,b=0,则 λ 不存在;a=b=0, 则 λ 不唯一. (2)在 a=λb 中,对于确定的 λ 与 b,a=λb 可以表 示空间中与 b 平行且长度为|λb|的所有的向量.
4.空间向量的数量积
λ(a·b)
b·a a·b+a·c
(1)若 a,b 是非零向量,则 a⊥b⇔a·b
两个 =0. 向量 (2)若 a 与 b 同向,则 a·b=|a|·|b|; 数量 若反向,则 a·b=-|a|·|b|. 积的 特别地:a·a=|a|2 或|a|= a·a. 性质 (3)若 θ 为 a,b 的夹角,则 cos θ=|aa|··b|b|.
2.射线 AB、AC、AD 不共面, 连接 BC、CD、DB,分别取 AB、BC、CD、DA 的中点 E、 F、G、H,试判断四边形 EFGH 的图形形状,并用向量的方法 证明.
讲课堂互动讲义
空间向量的线性运算 已知空间四边形 OABC, M,N 分别是对边 OA、BC 的中点, 点 G 在 MN 上,且 MG=2GN,如 图,设O→A=a,O→B=b,O→C=c, 试用 a,b,c 表示向量O→G.
如图.
(2)减法法则 与平面向量类似,a与b的差定义为_a_与__-__b_的___ __和__向__量___,记作a-b,其中-b是b的相反向 量.
(3)运算律 交换律:a+b=__b_+__a_b+a; 结合律:(a+b)+c=__a_+__(_b_+__c)__.
[强化拓展]
(1)空间向量的加减法与平面向量的加减法完全相
[强化拓展] (1)因为空间任意两个向量都是共面的,所以空间向 量共线定理与平面向量共线定理是相同的;定理中 b≠0 不可丢掉,否则实数 λ 不一定存在,且不一 定唯一.如:a≠0,b=0,则 λ 不存在;a=b=0, 则 λ 不唯一. (2)在 a=λb 中,对于确定的 λ 与 b,a=λb 可以表 示空间中与 b 平行且长度为|λb|的所有的向量.
4.空间向量的数量积
λ(a·b)
b·a a·b+a·c
(1)若 a,b 是非零向量,则 a⊥b⇔a·b
两个 =0. 向量 (2)若 a 与 b 同向,则 a·b=|a|·|b|; 数量 若反向,则 a·b=-|a|·|b|. 积的 特别地:a·a=|a|2 或|a|= a·a. 性质 (3)若 θ 为 a,b 的夹角,则 cos θ=|aa|··b|b|.
2.射线 AB、AC、AD 不共面, 连接 BC、CD、DB,分别取 AB、BC、CD、DA 的中点 E、 F、G、H,试判断四边形 EFGH 的图形形状,并用向量的方法 证明.
2.空间向量及其加减运算-北师大版高中数学选修2-1PPT全文课件

例题
例 已知平行A 六B面 CD 体 A'B'C'D',化简下 列向量表达式化 ,简 并结 标果 出的向量
⑵ABADAA';
起点相同的三个不共面 向量之和,等于以这三 个向量为棱的平行六面 体的以公共起点为起点
的对角线所示向量
D’ A’
D
C’ B’
C
A
B
2 . 空 间 向量 及其加 减运算 -北师大 版高中 数学选 修2-1 PPT全文 课件【 完美课 件】
b
加法交换律:
A
a
B
abba
加法结合律:
向量减法的三角形法则
(ab)ca(bc)
4.推广:
(1)首尾相接的若干向量之和, 等于由起始向量的起点指向末尾向量的终点的 向量; A 1A 2A 2A 3A 3A 4 A n 1A nA1 A n
(2)首尾相接的若干向量若构成一个封闭图 形,则它们的和为: 零向量
A1
A n1
A2
An
2 . 空 间 向量 及其加 减运算 -北师大 版高中 数学选 修2-1 PPT全文 课件【 完美课 件】
A3
A4
2 . 空 间 向量 及其加 减运算 -北师大 版高中 数学选 修2-1 PPT全文 课件【 完美课 件】
例题
例 已知平行A 六B面 CD 体 A'B'C'D',化简下 列向量表达式化 ,简 并结 标果 出的向量
在这里,空间向量的加减法运算性质 完全和平面向量的运算性质一样!
2 . 空 间 向量 及其加 减运算 -北师大 版高中 数学选 修2-1 PPT全文 课件【 完美课 件】
问题 2.空间向量及其加减运算-北师大版高中数学选修2-1PPT全文课件【完美课件】
高中数学 2.2 空间向量的运算课件 北师大版选修21

空间向量的线性运算
如图 2-2-1 已知三棱锥 A-BCD,E、F 分别
是 BC、CD 的中点,化简下列各表达式.
(1)A→B+B→C+C→D;
(2)A→B+12B→D+12B→C;
(3)A→F-12A→B-12A→C.
图 2-2-1
【思路探究】 结合图形特点,利用空间向量的线性运 算法则进行化简.
空间两个向量 a 与 b(b≠0)共线的充要条件是存在实数
λ,使得 a=λB.
单位向量
【问题导思】 在平面向量中,与 a 共线的单位向量有几个,分别是什 么? 【提示】 有 2 个,分别是|aa|与-|aa|.
对于任意一个非零向量 a,我们把|aa|叫作向量 a 的单位向 量,记作 a0,a0 与 a同方向 .
2 空间向量的运算
教师用书独具演示
●三维目标 1.知识与技能 (1)理解空间向量的概念,掌握其表示方法. (2)能用图形说明空间向量加法、减法、数乘向量及它们 的运算律. (3)能用空间向量的运算意义及运算律解决立体几何中的 简单问题.
2.过程与方法 通过对空间向量的运算的学习,了解并初步把握空间向 量的运算意义及运算律解决立体几何中的简单问题的方法. 3.情感、态度与价值观 培养学生知识迁移的能力,渗透数形结合思想.
【解】 (1)∵A→B+A→D=A→C,
∴
A→1O-
1 2
A→B
-12
A→D=
A→1O-
12(A→B+
A→D)
=A→1O-
1 2
A→C
=
A→1O-A→O=A→1A. (2)E→O=E→D+D→O=23D→1D+12D→B=23D→1D+12(D→A+A→B)=23
A→1A+12D→A+12A→B=12A→B-12A→D-23A→A1.
2.2《空间向量的运算》课件(北师大版选修2-1)
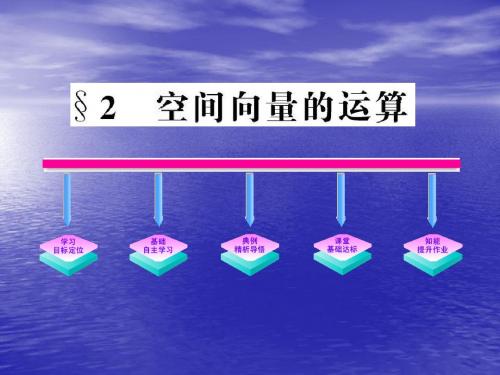
何值时BP·CQ的值最大?并求出这个最大值.
【解题提示】把BP·CQ化成关于θ的函数关 系式,再求函数最值.
【解析】
学习目标定位
基础自主学习
典例精析导悟
课堂基础达标
知能提升作业
一、选择题(每题4分,共16分) 1.下列命题中不正确的是(
(A)| 0 |=0 (C)| a |2= a 2
)
(B) a - a =0 (D) a - a = 0 【解析】选B. a - a = 0 ≠0
【解题提示】正确地画出辅助线,利用向量共线定理求
解.
【解析】EF与AD+BC共线.连接AC,取AC中点G,连接EG,FG,
∴GF= 1 AD,EG= 1 BC.
2 1 2 2 1 1 BC= (AD+BC). 2 2
又∵GF,EG,EF共面,
∴EF=GF+EG= AD+
即EF与AD+BC共线.
8.已知空间四边形OABC各边及对角线长都相等,E,F分别为
AB,OC的中点,求异面直线OE与BF夹角的余弦值.
【解析】如图,设OA= a ,OB= b ,OC= c ,且| a |=| b |=| c |=1, 易知∠AOB=∠BOC=∠AOC= , 3
则 a · b = b·c = c·a = . 2
1
9.(10分)如图,在Rt△ABC中,已知BC=a,若长为 2a的线段PQ以点A为中点,问PQ与BC的夹角θ 取
二、填空题(每题4分,共8分) 5.化简:
(1)
=_____________;
(2)平行六面体A)AB-AC+BC-BD-DA =CB+BC-(BD+DA) =0 -BA =AB
《2.2 空间向量的运算》课件-优质公开课-北师大选修2-1精品

b≠0,则存在唯一实数x使a=xb;②若存在 唯一实数λ,使a=λb,则a∥b.
• 判定两向量共线的关键是找到实数λ.运用② 证明直线平行还需说明a(或b)上有一点不在 b(或a)上.
• 运用②证明三点共线,还需说明a与b有公共 点.
• 5.数量积
• 由于空间任意两个向量都可转化为共面向量, 所以空间两个向量的夹角的定义和取值范围、 两个向量垂直的定义和表示及向量的模的概 念和表示等,都与平面向量相同.
重点难点点拨
• 本节重点:向量的线性运算及运算律、数量 积.
• 本节难点:向量的线性运算及运算律、数量 积.
知能自主梳理
1.空间向量加减法的定义 如图,设 a 和 b 是空间两个向量,过 一点 O 作 a 和 b 的相等向量O→A和O→B,根 据平面向量加法的平行四边形法则,平行 四边形的对角线 OC 对应的向量O→C就是 a 与 b 的和,记作 a+b. a 与 b 的差定义为 a+(-b),记作 a-b,其中-b 是 b 的 相反向量.
• 与平面上两个向量的数量积一样,空间两个 向量的数量积也具有如下性质.
• ①a⊥b⇔a·b=0.用于判断两向量是否垂 直.
• ②|a|2=a·a用于求向量的模.
• ③|a·b|≤|a||b|用于判断或证明不等式.
• 6.向量中应该重视的问题
• ①空间向量的加法、减法、数乘向量的意义 及运算律与平面向量类似,这些运算不但适 合学过的代数运算律,而且很多性质与实数 性质相同.
④a·b=0⇒/ a=0 或 b=0,a=0 时,一定有 a·b=0. ⑤三个不为零的实数 a、b、c,有(ab)c=a(bc)成立,但对 于三个向量 a、b、c,(a·b)·c≠a·(b·c),因为 a·b 是一个实数,(a·b)c 是与 c 共线的向量,而 a(b·c)是与 a 共线的向量,a 与 c 却不一 定共线.
• 判定两向量共线的关键是找到实数λ.运用② 证明直线平行还需说明a(或b)上有一点不在 b(或a)上.
• 运用②证明三点共线,还需说明a与b有公共 点.
• 5.数量积
• 由于空间任意两个向量都可转化为共面向量, 所以空间两个向量的夹角的定义和取值范围、 两个向量垂直的定义和表示及向量的模的概 念和表示等,都与平面向量相同.
重点难点点拨
• 本节重点:向量的线性运算及运算律、数量 积.
• 本节难点:向量的线性运算及运算律、数量 积.
知能自主梳理
1.空间向量加减法的定义 如图,设 a 和 b 是空间两个向量,过 一点 O 作 a 和 b 的相等向量O→A和O→B,根 据平面向量加法的平行四边形法则,平行 四边形的对角线 OC 对应的向量O→C就是 a 与 b 的和,记作 a+b. a 与 b 的差定义为 a+(-b),记作 a-b,其中-b 是 b 的 相反向量.
• 与平面上两个向量的数量积一样,空间两个 向量的数量积也具有如下性质.
• ①a⊥b⇔a·b=0.用于判断两向量是否垂 直.
• ②|a|2=a·a用于求向量的模.
• ③|a·b|≤|a||b|用于判断或证明不等式.
• 6.向量中应该重视的问题
• ①空间向量的加法、减法、数乘向量的意义 及运算律与平面向量类似,这些运算不但适 合学过的代数运算律,而且很多性质与实数 性质相同.
④a·b=0⇒/ a=0 或 b=0,a=0 时,一定有 a·b=0. ⑤三个不为零的实数 a、b、c,有(ab)c=a(bc)成立,但对 于三个向量 a、b、c,(a·b)·c≠a·(b·c),因为 a·b 是一个实数,(a·b)c 是与 c 共线的向量,而 a(b·c)是与 a 共线的向量,a 与 c 却不一 定共线.
2020北师大版高中数学选修2-1 教师课件:第二章 空间向量的运算
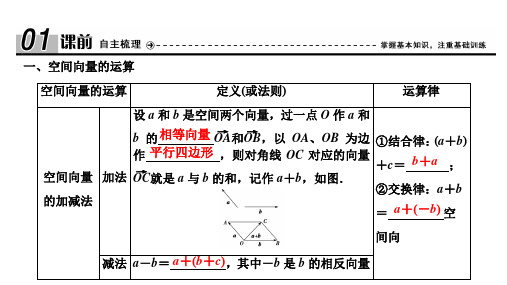
1.已知空间四边形 ABCD,如图,连接 AC,BD,设 M,G 分别是 BC,CD 的中点, 化简下列各表达式: (1)A→B+B→C+C→D; (2)A→B+12(B→D+B→C); (3)A→G-12(A→B+A→C).
解析:(1)A→B+B→C+C→D=A→C+C→D=A→D. (2)A→B+12(B→D+B→C)=A→B+12B→C+12B→D =A→B+B→M+M→G=A→G. (3)A→G-12(A→B+A→C)=A→G-A→M=M→G.
一、空间向量的运算
空间向量的运算
定义(或法则)
运算律
设 a 和 b 是空间两个向量,过一点 O 作 a 和
b 的 相等向量 O→A和O→B,以 OA、OB 为边 ①结合律:(a+b)
空间向量
加法
作 平行四边形 ,则对角线 OC 对应的向量 O→C就是 a 与 b 的和,记作 a+b,如图.
+c=
b+a
[解析] M,N 分别是 AC,BF 的中点,而四边形 ABCD,ABEF 都是平行四边形. 所以M→N=M→A+A→F+F→N=12C→A+A→F+12F→B. 又因为M→N=M→C+C→E+E→B+B→N=-12C→A+C→E-A→F-12F→B, 所以12C→A+A→F+12F→B=-12C→A+C→E-A→F-12F→B. 所以C→E=C→A+2A→F+F→B=2(M→A+A→F+F→N). 所以C→E=2M→N. 所以C→E与M→N共线.
空间向量的运算
定义(或法则)
运算律
与数量 积有关 的结论
①|a|= a·a ; ②a⊥b⇔a·b= 0 ; ③cos〈a,b〉=|aa|·|bb|(a≠0,b≠0)
二、共线向量基本定理
空间两个向量 a 与 b(b≠0)共线的充要条件是存在实数 λ,使得 a=λb .
2019-2020高中北师版数学选修2-1 第2章 §2 空间向量的运算课件PPT

D.|a·b|≤|a||b|
D [|a|·a是与a共线的向量,a2是实数,故A错误;
(a·b)2=
|a|2·|b|2·cos2〈a,b〉≠a2·b2,故B错误; (a·b)c与c共线,a(b·c)
与a共线,故C错误; |a·b|=||a|·|b|·cos〈a,b〉|≤|a|·|b|,故D正
确.]
栏目导航
() ()
[答案] (1)× (2)× (3)√ (4)√
栏目导航
2.化简P→M-P→N+M→N所得的结果是( )
A.P→M
B.N→P
C.0
D.M→N
C [因为P→M-P→N+M→N=N→M+M→N=0.]
栏目导航
3.下列式子中正确的是( A.|a|·a=a2 C.(a·b)c=a(b·c)
) B.(a·b)2=a2·b2
第二章 空间向量与立体几何
§2 空间向量的运算
栏目导航
学习目标:1.会用图形说明空间向量加法、减法、数乘向量及 它们的运算律.(重点) 2.会利用两个空间向量共线的充要条件解决 有关问题.(难点) 3.能够利用空间向量的数量积的定义求两个向量 的数量积.(重点)
栏目导航
自主预习 探新知
栏目导航
1.空间向量的运算
栏目导航
(2)如图,在平行六面体ABCD-A1B1C1D1中,设 A→A1 =a, A→B = b, A→D =c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c 表示以下各向量:
①A→P;②A→1N;③M→P+N→C1.
栏目导航
0 [(1)法一:(A→B-C→D)-(A→C-B→D)=A→B-C→D-A→C+B→D=A→B +D→C+C→A+B→D=(A→B+B→D)+(D→C+C→A)=A→D+D→A=0.
D [|a|·a是与a共线的向量,a2是实数,故A错误;
(a·b)2=
|a|2·|b|2·cos2〈a,b〉≠a2·b2,故B错误; (a·b)c与c共线,a(b·c)
与a共线,故C错误; |a·b|=||a|·|b|·cos〈a,b〉|≤|a|·|b|,故D正
确.]
栏目导航
() ()
[答案] (1)× (2)× (3)√ (4)√
栏目导航
2.化简P→M-P→N+M→N所得的结果是( )
A.P→M
B.N→P
C.0
D.M→N
C [因为P→M-P→N+M→N=N→M+M→N=0.]
栏目导航
3.下列式子中正确的是( A.|a|·a=a2 C.(a·b)c=a(b·c)
) B.(a·b)2=a2·b2
第二章 空间向量与立体几何
§2 空间向量的运算
栏目导航
学习目标:1.会用图形说明空间向量加法、减法、数乘向量及 它们的运算律.(重点) 2.会利用两个空间向量共线的充要条件解决 有关问题.(难点) 3.能够利用空间向量的数量积的定义求两个向量 的数量积.(重点)
栏目导航
自主预习 探新知
栏目导航
1.空间向量的运算
栏目导航
(2)如图,在平行六面体ABCD-A1B1C1D1中,设 A→A1 =a, A→B = b, A→D =c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c 表示以下各向量:
①A→P;②A→1N;③M→P+N→C1.
栏目导航
0 [(1)法一:(A→B-C→D)-(A→C-B→D)=A→B-C→D-A→C+B→D=A→B +D→C+C→A+B→D=(A→B+B→D)+(D→C+C→A)=A→D+D→A=0.
高中数学选修2-1北师大版 空间向量的运算 课件(42张)

在进行向量的加减法运算时要牢记加减法的运算法则,最终的表 达方式是唯一的,但在具体的解题过程中,注意封口多边形法则的应
用,只要形成封闭图形即可,在解题过程中注意灵活选择.
1.已知空间四边形 ABCD,如图,连接 AC,BD,设 M,G 分别是 BC,CD 的中点,化简下列各表达式: → +BC → +CD →; (1)AB 1 → → → (2)AB+2(BD+BC); 1 → → → (3)AG-2(AB+AC).
研重点 究疑点 1.提示:由数量积的定义知 a· b=|a||b|cos〈a,b〉是一个数,从 而(a· b)· c 与 c 共线,又 a· (b· c)=(b· c)· a 是与 a 共线的一个向量,所以 (a· b)· c=a· (b· c)不一定成立. 2.提示:不是.由 a=λb 可得出 a,b 共线.而由 a,b 共线不一 定能得到 a=λb,如当 b=0,a≠0 时. 3.D 向量 a,b 不一定是共线向量,因此,当 a,b 不共线时, a0,b0 也不共线,此时 a0,b0 不相等,故 A,C 错误;向量与数量不 能比较,故 B 错;单位向量的模都是 1,因此|a0|=|b0|.故选 D.A.a0=b0C. Nhomakorabea0,b0共线
B.a0=1
D.|a0|=|b0|
→ -AB → +BC → 化简后 4.在正方体 ABCDA1B1C1D1 中,向量表达式DD 1 的结果是( → A.BD 1 → C.B 1D ) → B.D 1B → D.DB 1
5.若 a,b 均为非零向量,则 a· b=|a||b|是 a,b 共线的( A.充分不必要条件 C.充要条件 B.必要不充分条件 D.既不充分又不必要条件
空间向量的线性运算
→ =a,OB → =b,OC → =c, [例 1] 如图所示,在四面体 OABC 中,OA → 和OE →. D 为 BC 的中点,E 为△ABC 的重心,试用 a、b、c 表示向量OD
高中数学(北师大版)选修21第2章空间向量的运算PPT课件

第二章 2.2 第1课时
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-1
[正解] 命题①为假命题,因为A→B、C→D两个向量所在的直线 可能没有公共点,所以四点不一定在一条直线上;命题②为真命 题,因为A→B、A→C两个向量所在的直线有公共点 A,所以三点共线.故 填②.
[答案] ② [总结反思] 我们所研究的向量为自由向量,所以平行向量就 是共线向量,但是向量所在的直线却不一定共线,也有可能平行, 关键是看这两个向量有没有公共点,如果没有公共点,那么对应 的两条直线平行;如果有公共点,那么对应的两条直线重合.
[分析] 要判断C→E与M→N是否共线,只需判断是否存在实数 x, 使C→E=xM→N,若存在,则C→E与M→N共线,否则M→N与C→E不共线.
第二章 2.2 第1课时
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-1
[解析] M,N 分别是 AC,BF 的中点,而四边形 ABCD,ABEF 都是平行四边形,
[ 答 案 ] C
[解析] A→B与B→C两向量平行,且有一个公共点,所以三点共
线.
第二章 2.2 第1课时
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-1
向量共线 如图所示,四边形 ABCD,ABEF 都是平行四边形, 且不共面,M、N 分别是 AC、BF 的中点,判断C→E与M→N是否共线?
所以M→N=M→A+A→F+F→N=12C→A+A→F+12F→B. 又因为M→N=M→C+C→E+E→B+B→N=-12C→A+C→E-A→F-12F→B, C→E-(12C→A+A→F+12F→B)=C→E-M→N. 所以C→E=2M→N. 所以C→E与M→N共线.
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-1
[正解] 命题①为假命题,因为A→B、C→D两个向量所在的直线 可能没有公共点,所以四点不一定在一条直线上;命题②为真命 题,因为A→B、A→C两个向量所在的直线有公共点 A,所以三点共线.故 填②.
[答案] ② [总结反思] 我们所研究的向量为自由向量,所以平行向量就 是共线向量,但是向量所在的直线却不一定共线,也有可能平行, 关键是看这两个向量有没有公共点,如果没有公共点,那么对应 的两条直线平行;如果有公共点,那么对应的两条直线重合.
[分析] 要判断C→E与M→N是否共线,只需判断是否存在实数 x, 使C→E=xM→N,若存在,则C→E与M→N共线,否则M→N与C→E不共线.
第二章 2.2 第1课时
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-1
[解析] M,N 分别是 AC,BF 的中点,而四边形 ABCD,ABEF 都是平行四边形,
[ 答 案 ] C
[解析] A→B与B→C两向量平行,且有一个公共点,所以三点共
线.
第二章 2.2 第1课时
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修2-1
向量共线 如图所示,四边形 ABCD,ABEF 都是平行四边形, 且不共面,M、N 分别是 AC、BF 的中点,判断C→E与M→N是否共线?
所以M→N=M→A+A→F+F→N=12C→A+A→F+12F→B. 又因为M→N=M→C+C→E+E→B+B→N=-12C→A+C→E-A→F-12F→B, C→E-(12C→A+A→F+12F→B)=C→E-M→N. 所以C→E=2M→N. 所以C→E与M→N共线.
最新-高中数学 22《空间向量的运算》课件 北师大版选修2-1 精品

A1A2 A2 A3 A3A4 . An1An An A1 0
⑶两个向量相加的平行四边形法则在空间仍然成立 .
例1已知平行六面体 ABCD A' B'C' D(' 如图),化简下列
向量表达式,并标出化简结果的向量
⑴AB BC;
⑵AB AD AA';
⑶AB AD 1 CC' 2
⑷ 1 (AB AD AA' ). 3
推论:空间一点P位于平面MAB内的充分必要条件是存在
有序实数对x、y,使 MP =xMA+y MB
或对空间任一点O,有OP= OM +x MA +y MB ①
平面MAB内,点P对应的实数对(x,y)是唯一的,①式 叫做平面MAB的向量表达式。
例2、对空间任一点O和不共线的三点A、B、C,试问满足 向量关系式
OP OA t a ① 其中向量a叫做直线l的方向向量。
OP OA t AB OP (1 t)OA tOB ②
①或②式都叫做空间直线的向量参数方程
4.共面向量
(1)概念:已知平面α与 a向量,作 OA a ,如 果直线OA平行于平面α或在α内,那么我们说向量 a 平行于平面α,记作 a ∥α。
OP =x OA+y OB +ZOC (其中x+y+z=1)
的四点P、A、B、C是否共面
例3、已知平行四边形ABCD,从平面AC外一点O引向量
OE=k OA ,OF =kOB ,OG =kOC ,OH OD
=k ,求证: ⑴四点E、F、G、H共面;
⑵平面EG∥平面AC。
O
D
C
A
Bபைடு நூலகம்
H
⑶两个向量相加的平行四边形法则在空间仍然成立 .
例1已知平行六面体 ABCD A' B'C' D(' 如图),化简下列
向量表达式,并标出化简结果的向量
⑴AB BC;
⑵AB AD AA';
⑶AB AD 1 CC' 2
⑷ 1 (AB AD AA' ). 3
推论:空间一点P位于平面MAB内的充分必要条件是存在
有序实数对x、y,使 MP =xMA+y MB
或对空间任一点O,有OP= OM +x MA +y MB ①
平面MAB内,点P对应的实数对(x,y)是唯一的,①式 叫做平面MAB的向量表达式。
例2、对空间任一点O和不共线的三点A、B、C,试问满足 向量关系式
OP OA t a ① 其中向量a叫做直线l的方向向量。
OP OA t AB OP (1 t)OA tOB ②
①或②式都叫做空间直线的向量参数方程
4.共面向量
(1)概念:已知平面α与 a向量,作 OA a ,如 果直线OA平行于平面α或在α内,那么我们说向量 a 平行于平面α,记作 a ∥α。
OP =x OA+y OB +ZOC (其中x+y+z=1)
的四点P、A、B、C是否共面
例3、已知平行四边形ABCD,从平面AC外一点O引向量
OE=k OA ,OF =kOB ,OG =kOC ,OH OD
=k ,求证: ⑴四点E、F、G、H共面;
⑵平面EG∥平面AC。
O
D
C
A
Bபைடு நூலகம்
H
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
互相平行或重合,则这些向量叫做共线向
量或平行向量
a平行于b,记作a∥b
(2)共线向量定理: 对空间任意两个向量a、b(b≠0),a∥b的充要条 l 件是存在实数λ ,使a=λ b。 P
a
A B
推论:如果l为经过已知点A且平行于已知向量a的直线, 那么对任一点O,点P在直线l上的充要条件是存在实数t,满 足等式 OP OA t ① a 其中向量a叫做直线l的方向向量。 OP OA t AB OP (1 t )OA tOB ② ①或②式都叫做空间直线的向量参数方程
D
S
·
A
C
P·
A B
R·
B
D C
G C
D
A
· Q
B
⑵平面EG∥平面AC。
O
D A H
C B G
E
F
小结:1、空间向量的概念 2、空间向量的运算 3 、共线向量(平行向量)的概念及空 间向量共线的充要条件 4、共面向量的概念及向量共面的充要 条件
作业
1.如图是正方体,P、Q、R、S分别是所在棱的中点,求证: 这四个点共面
。
.2.如图设A是△BCD所在平面外的一点,G是△BCD的重 1 心。求证: AG ( AB AC AD) 3
D' 例1已知平行六面体 ABCD A' B' C '(如图),化简下列向 量表达式,并标出化简结果的向量
⑴AB BC;
⑵AB AD AA';
1 ⑶ AB AD CC ' 2
1 ⑷ ( AB AD AA' ). 3
3.共线向量(平行向量)
(1)概念:如果表示空间向量的有向线段所在的直线
O A
a
α
a
(2)共面向量定理 如果两个向量 a b不共线,则向量 、 面的充要条件是,存在实数对x、y,使
与向量 、共 p ab
p=x a +y b
推论:空间一点P位于平面MAB内的充分必要条件是存在有 MP 序实数对x、y,使 =x MA MB +y OP OM +x +y ① 或对空间任一点O,有 = MB MA
2.空间向量的运算 结论:空间向量的加法、减法、数乘向量的定义与平面 向量的运算一样
OB量) OP λa ( R)
运算律:⑴加法交换律: a b b a ⑵加法结合律:(a b) c a (b c)
空间向量及其运算
一、复习 1、平面向量的概念
2、平面向量的加减和数乘运算
1.空间向量的概念 在空间,我们把具有大小和方向的量叫做向量
注意:⑴空间的平移就是一个向量。平移实际就是点 到点的一次变换,因此我们说空间任意两个向 量是共面的 ⑵向量一般用有向线段表示。同向等长的有向线段 表示同一或相等的向量。 ⑶空间的两个向量可用同一平面内的两条有向线段来 表示
平面MAB内,点P对应的实数对(x,y)是唯一的,①式叫 做平面MAB的向量表达式。
例2、对空间任一点O和不共线的三点A、B、C,试问满足向 量关系式 +y OP =x OA OB+Z OC(其中x+y+z=1) 的四点P、A、B、C是否共面
例3、已知平行四边形ABCD,从平面AC外一点O引向量 , OE=k OA , OF =k OB ,OG =k OC , OH =k OD 求证: ⑴四点E、F、G、H共面;
( a b ) a b ⑶数乘分配律:
空间向量加法的运算律要注意以下几点: ⑴首尾相接的若干向量之和,等于由起始向量的起点 指向末尾向量的终点的向量.即:
A1 A2 A2 A3 A3 A4 An1 An A1 An
⑵首尾相接的若干向量若构成一个封闭图形,则它们 的和为零向量.即: A1 A2 A2 A3 A3 A4 An1 An An A1 0 . ⑶两个向量相加的平行四边形法则在空间仍然成立.
O
4.共面向量
a (1)概念:已知平面α 与 a 向量,作 OA ,如果 直线OA平行于平面α 或在α 内,那么我们说向量 平 a a 行于平面α ,记作 ∥α 。
通常我们把平行于同一平面的向量,叫做共面向量说 明:⑴空间任意两个向量总是共面的; ⑵空间任意三个向量不一定共面; ⑶空间四边形ABCD中 AD AC AB 、 、 不共面。
量或平行向量
a平行于b,记作a∥b
(2)共线向量定理: 对空间任意两个向量a、b(b≠0),a∥b的充要条 l 件是存在实数λ ,使a=λ b。 P
a
A B
推论:如果l为经过已知点A且平行于已知向量a的直线, 那么对任一点O,点P在直线l上的充要条件是存在实数t,满 足等式 OP OA t ① a 其中向量a叫做直线l的方向向量。 OP OA t AB OP (1 t )OA tOB ② ①或②式都叫做空间直线的向量参数方程
D
S
·
A
C
P·
A B
R·
B
D C
G C
D
A
· Q
B
⑵平面EG∥平面AC。
O
D A H
C B G
E
F
小结:1、空间向量的概念 2、空间向量的运算 3 、共线向量(平行向量)的概念及空 间向量共线的充要条件 4、共面向量的概念及向量共面的充要 条件
作业
1.如图是正方体,P、Q、R、S分别是所在棱的中点,求证: 这四个点共面
。
.2.如图设A是△BCD所在平面外的一点,G是△BCD的重 1 心。求证: AG ( AB AC AD) 3
D' 例1已知平行六面体 ABCD A' B' C '(如图),化简下列向 量表达式,并标出化简结果的向量
⑴AB BC;
⑵AB AD AA';
1 ⑶ AB AD CC ' 2
1 ⑷ ( AB AD AA' ). 3
3.共线向量(平行向量)
(1)概念:如果表示空间向量的有向线段所在的直线
O A
a
α
a
(2)共面向量定理 如果两个向量 a b不共线,则向量 、 面的充要条件是,存在实数对x、y,使
与向量 、共 p ab
p=x a +y b
推论:空间一点P位于平面MAB内的充分必要条件是存在有 MP 序实数对x、y,使 =x MA MB +y OP OM +x +y ① 或对空间任一点O,有 = MB MA
2.空间向量的运算 结论:空间向量的加法、减法、数乘向量的定义与平面 向量的运算一样
OB量) OP λa ( R)
运算律:⑴加法交换律: a b b a ⑵加法结合律:(a b) c a (b c)
空间向量及其运算
一、复习 1、平面向量的概念
2、平面向量的加减和数乘运算
1.空间向量的概念 在空间,我们把具有大小和方向的量叫做向量
注意:⑴空间的平移就是一个向量。平移实际就是点 到点的一次变换,因此我们说空间任意两个向 量是共面的 ⑵向量一般用有向线段表示。同向等长的有向线段 表示同一或相等的向量。 ⑶空间的两个向量可用同一平面内的两条有向线段来 表示
平面MAB内,点P对应的实数对(x,y)是唯一的,①式叫 做平面MAB的向量表达式。
例2、对空间任一点O和不共线的三点A、B、C,试问满足向 量关系式 +y OP =x OA OB+Z OC(其中x+y+z=1) 的四点P、A、B、C是否共面
例3、已知平行四边形ABCD,从平面AC外一点O引向量 , OE=k OA , OF =k OB ,OG =k OC , OH =k OD 求证: ⑴四点E、F、G、H共面;
( a b ) a b ⑶数乘分配律:
空间向量加法的运算律要注意以下几点: ⑴首尾相接的若干向量之和,等于由起始向量的起点 指向末尾向量的终点的向量.即:
A1 A2 A2 A3 A3 A4 An1 An A1 An
⑵首尾相接的若干向量若构成一个封闭图形,则它们 的和为零向量.即: A1 A2 A2 A3 A3 A4 An1 An An A1 0 . ⑶两个向量相加的平行四边形法则在空间仍然成立.
O
4.共面向量
a (1)概念:已知平面α 与 a 向量,作 OA ,如果 直线OA平行于平面α 或在α 内,那么我们说向量 平 a a 行于平面α ,记作 ∥α 。
通常我们把平行于同一平面的向量,叫做共面向量说 明:⑴空间任意两个向量总是共面的; ⑵空间任意三个向量不一定共面; ⑶空间四边形ABCD中 AD AC AB 、 、 不共面。
