2013年青岛大学考研真题827信号与系统
青岛大学信号与系统第八章离散时间系统的z域分析

则
Z [an x(n)] X ( z ) a
z , Rx1 a Rx2
特别地 Z [(1)n x(n)] X (z) , Rx1 z Rx2
例:Z
[cos(0n)u(n)]
z(z cos0 ) z2 2z cos0 1
, z 1
Z
[ n cos(0n)u(n)]
z
(z
cos0 )
2
2
nu(n)
z
d dz
z
z 1
(z
z 1)2
n2u(n)
z
d dz
(z
z 1)2
z(z 1) (z 1)3
X (z) 1 [ z z(z 1)] z2 2 (z 1)2 (z 1)3 (z 1)3
, z 1
(四)序列指数加权( z 域尺度变换)
若 Z [x(n)] X (z) , Rx1 z Rx2
X (z) Z [x(nT )] x(nT )zn n
2T 0 T 3T
t
L [xs (t)] z esT Z [x(nT )]
z
esT
r eT
T 2
s
z re j s j
T—— 抽样间隔,
s
2
T
——
抽样角频率
z平面和 s平面的映射关系:
1. s平面原点 ( 0, 0) j
x(1) (n)
0
n
x(n 1)u(n) x(n 1)u(n 1)
x(0) (n 1)
0
n
x(n 1)u(n) x(n 1)u(n 1) x(1) (n) x(n 1)u(n) x(n 1)u(n 1) x(0) (n 1) x(n 2)u(n) x(n 2)u(n 2) x(2) (n) x(1) (n 1) x(n 2)u(n) x(n 2)u(n 2) x(0) (n 2) x(1) (n 1)
青岛大学2020年827信号与系统

信号与信息处理专业硕士入学考试大纲
考试科目代码及名称:827信号与系统
一、考试要求
掌握连续时间信号与系统分析的基本理论,掌握离散信号分析、离散时间系统设计的基本理论和方法,具备从事实际信号分析与处理工作的基本能力。
二、考试内容
(1)信号的运算和分解
(2)连续线性时不变系统的时域经典分析
(3)系统模型与系统框图
(4)单位冲激响应与卷积
(5)傅里叶变换与采样定理
(6)拉普拉斯变换与连续系统的s域分析
(7)系统函数与频率响应
(8)信号无失真传输、调制与解调
(9)离散时间系统的时域经典分析
(10)序列的z变换与离散傅里叶变换
三、试卷结构(题型分值)
1.本科目满分为150分,考试时间为180分钟。
2.题型结构
(1)选择题:占总分的16%
(2)填空题: 占总分的16%
(3)计算题:占总分的68%
四、参考书目
《信号与系统引论》,郑君里应启珩杨为理,高等教育出版社,出版时间2018-12-10。
青岛大学考研专业课真题——信号与系统 2007年 (附带答案及评分标准)

科目代码: 827 科目名称: 信号与系统 (共 12 页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效Ⅰ、填空题(共14题,每题3分,共42分)1.积分=-'+⎰∞∞-dt t t )1()2(2δ 。
2.如图1所示,)(t f 为原始信号,)(1t f 为变换信号,则)(1t f 的表达式为 (用)(t f 表示)。
3.若正弦序列0sin()n ω的周期10N =,则0ω的最小取值为0ω= 。
4. 给定微分方程、起始状态、激励信号分别为()2()3()d d r t r t e t dtdt+=、(0)0r -=、()()e t u t =,则(0)r += 。
5.已知)4()()()(--==n u n u n h n x ,则卷积和序列)()()(n h n x n y *=共有 个非零取值。
6.单边拉氏变换21()(2)F s s =+对应的原函数为=)(t f 。
7.图2所示因果周期矩形脉冲的拉氏变换()F s = 。
8.序列||1()2n x n ⎛⎫= ⎪⎝⎭的z 变换及其收敛域为 。
图12 0 )(t f 2t 1 3)(1t f 2t-4 -2图22TT )(t ft1T 2…科目代码: 827 科目名称: 信号与系统 (共 12 页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效9.若象函数2()(1)z F z z =-,1z <,则原序列=)(n f 。
10.调幅信号26()(100)cos(10)f t Sa t t ππ=⋅的频带宽度为 Hz 。
11.若离散线性时不变系统的单位样值响应()()2(1)3(2)(3)h n n n n n δδδδ=+---+-,则单位阶跃响应()g n 的序列波形为。
12.若某线性时不变离散时间系统的单位样值响应为)(2)1(3)(n u n u n h n n -+--=,则该系统是(因果/非因果、稳定/非稳定)系统。
陈后金《信号与系统》(第2版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)

图2-2
3.有一离散时间信号
(1)画出
(2)求序列 学]
使之满足
解:(1)
又 比较上述两式可得: 故如图2-3所示。
[电子科技大
图2-3
4.已知 如图2-4(a),画出
和
的波形。[北
京理工大学]
解:将 反转得 如图2-4(b)所示,将它们相加、减得 ,波形如图2-4(c)、(d)所示。
图2-4 5.已知f(t)的波形如图2-5所示,令r(t)=tu(t)。
大学]
图1-2 解:因为:
故:
y2(t)的波形如图1-3所示。
图1-3 3.将如图1-4(a)、(b)所示的连续信号展成如下形式:
给出信号
最简单的解析表达形式。[北京航空航天大学]
图1-4
解:(a)该信号可分为两段:
和
可化简为
故
,即:
(b)该信号可分为三段: 可化简为 故
,即
4.求
的值。[北京航空航天大学2006研]
,应该与齐次解有关,即系统的特征根为-1和-3,故特征方程应为 ,即a0=4,a1=3。
(2)设系统对激励 rzs(t),则
的零输入响应和零状态响应分别为rzi(t)和
由于
,则由线性时不变系统的微分特性可知
同时,设系统的单位冲激响应为h(t),则由线性时不变系统的叠加性 可知
由式(1)、式(2),并设
陈后金《信号与系统》(第2版)配 套模拟试题及详解
第一部分 名校考研真题 第1章 信号与系统分析导论 一、选择题
1.方程 天大学2007研] A.线性时不变 B.非线性时不变 C.线性时变 D.非线性时变 E.都不对 【答案】B
描述的系统是( )。[北京航空航
信号与系统 第二章习题 王老师经典解法(青岛大学)小白发布
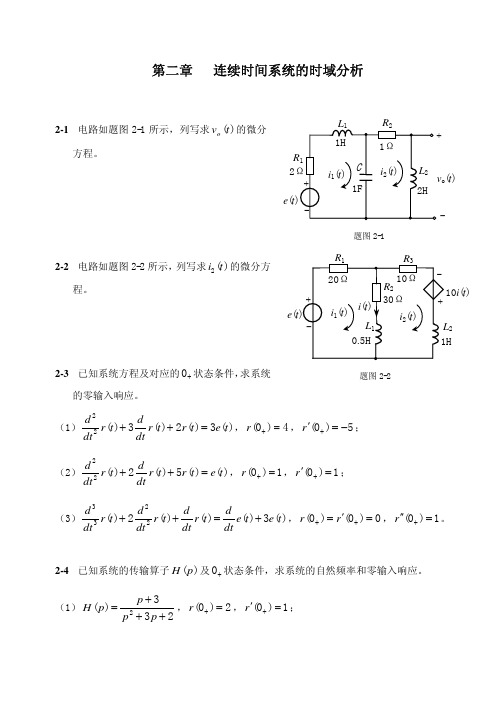
2-16 已知 f1 (t ) =
画出下列各卷积的波形。 (1) s1 (t ) = f1 (t ) ∗ f 2 (t ) ; (2) s2 (t ) = f1 (t ) ∗ f 2 (t ) ∗ f 2 (t ) ; (3) s3 (t ) = f1 (t ) ∗ f 3 (t ) 。
2-17 求题图 2-17 所示电路在 e(t ) = (1 + 2e
第二章
连续时间系统的时域分析
2-1 电路如题图 2-1 所示,列写求 vo (t ) 的微分 方程。
L1 1H R1 2Ω + e(t) i 1 (t )
R2 1Ω + L2 2H 题图 2-1
C
1F
i 2 (t )
vo(t)
2-2 电路如题图 2-2 所示, 列写求 i2 (t ) 的微分方 程。
题图 2-18
−2 t
− 1)U (t ) , 试利用卷积的性质求题
1 0 -1
e2(t)=tU(t) 1 t 0
e3(t)
t 0 1
2-19 一线性时不变的连续时间系统,其初始状态一定,当输入 e1 (t ) = δ (t ) 时,其全响应
r1 (t ) = −3e − tU (t ) ; 当 输 入 e2 (t ) = U (t ) 时 , 其 全 响 应 r2 (t ) = (1 − 5e − t )U (t ) 。 求 当 输 入 e(t ) = tU (t ) 时的全响应。
2-14 计算卷积 f (t ) = f 1 (t ) ∗ f 2 (t ) ,其中 f1 (t ) = sgn(t − 1) , f 2 (t ) = e 2-15 求下列卷积 (1) f1 (t ) = e
2013年青岛大学考研真题816高等代数

青岛大学2013年硕士研究生入学考试试题科目代码:816 科目名称:高等代数(共2页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、(15分)设432432()242,()22f x x x x x g x x x x x =+−−−=+−−−,求(),()u x v x 使()()()()((),()).u x f x v x g x f x g x +=二、(15分).证明:方程组11112211211222221122n n n n n n nn n na x a x a xb a x a x a x b a x a x a x b +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯对任何12,,,n b b b ⋯都有解的充分必要条件是系数矩阵的行列式0ij a ≠.三、(20分),a b 取什么值时,线性方程组1234512345234512345132322635433x x x x x x x x x x a x x x x x x x x x b++++=⎧⎪+++−=⎪⎨+++=⎪⎪+++−=⎩有解?在有解的情形,求一般解.四、(20分)设,A B 为n n ×矩阵,证明:如果0AB =,那么()()rank A rank B n +≤.五、(20分)设A 是一个n 阶矩阵,证明:1)A 是反对称矩阵当且仅当对任一个n 维向量X ,有0=′A X X .2)如果A 是对称矩阵,且对任一个n 维向量X 有0=′A X X ,那么0=A .六、(20分)设n ααα,...,,21是n 维线性空间V 的一组基,A 是一个n×s 矩阵,且An s ),...,,(),...,,(2121αααβββ=证明:),...,,(21s L βββ的维数等于A 的秩.七、(20分)设321,,εεε,4ε是四维线性空间V 的一组基,已知线性变换A 在这组基下的矩阵为⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛−−−21225521312112011)求A 在基42112εεεη+−=,4443343222,,3εηεεηεεεη=+=−−=下的矩阵;2)求A 的核与值域;3)在A 的核中选一组基,把它扩充为V 的一组基,并求A 在这组基下的矩阵;4)在A 的值域中选一组基,把它扩充为V 的一组基,并求A 在这组基下的矩阵.八、(20分)设V 是复数域上的n 维线性空间,而线性变换A 在基n εεε,...,,21下的矩阵是一若尔当块.证明:1)V 中包含1ε的A -子空间只有V 自身;2)V 中任一非零A -子空间都包含n ε;3)V 不能分解成两个非平凡的A -子空间的直和.。
信号与系统第二章_连续时间系统时域分析(青岛大学)

n
rzi (t) Azikekt k 1
(b)
r(k zi
)
(0
)
r(k) (0 )
k 0,1,L ,(n 1)
系数Azik可直接由 r(k) (0 ) 来确定。
例:已知描述某二阶LTI连续时间系统的动态方程
d2 dt 2
r(t)
5
d dt
r(t)
6r(t)
e(t)
起始状态 r(0 ) 1,r(0 ) ,2激励信号
(t)
2
p3
5
2p p2
5
p
3
e(t)
2
d3 dt3
vo
(t)
5
d2 dt 2
vo
(t)
5
d dt
vo
(t)
3vo
(t)
2
d dt
e(t)
总结: (1)引入算子符号后,RLC 电路可借助纯电阻电路的分析方法;
(2)是否可消去公共因子的原则:微分方程的阶数应等于电路 阶数(独立储能元件的个数)。
§2.3 微分方程的经典解法 r(t) rh (t) rp (t)
r(0 ) r(0 ) 1
(4)由 0状态确定待定系数
r(t) A1et A2e2t 0.5e3t
rr((00))
A1 A1
A2 0.5 1 2A2 1.5
3
A1 A2
5.5 5
全响应 r(t) 5.5et 5e2t 0.5e3t ,t 0
(一)经典法求解微分方程步骤:
r(t) 0 u(t) r(0 ) r(0 )
代入
d2 dt 2
r(t)
3
d dt
r(t)
2013年华科824信号与系统真题与答案

因为一个信号的偶部是偶函数,奇部是奇函数,一个奇函数和一个偶函数的乘积是奇函数, 所以 xe [n]xo [n] 是奇函数,所以
n
x [n]x [n] 0
e o
即:
n
x 2 [n]
n
xe 2 [n] xo 2 [n] 。
由初值定理可知:
yzs [0] lim Yzs (z) 2 (当然你也可以逆变换先求出 yzs [n] 不过这样要复杂些)
z
由题可知 yzi [0]
8 4 12 22 y[0] y zi [0] y zs [0] 3 15 5 5
9、左边序列 x[n] 的 Z 变换 X (z)
当 W= 时, 6、傅里叶变换分析法与拉氏变换分析法一样,可用来分析不稳定的 LTI 系统。 【考查重点】 :主要考查傅里叶变换和拉氏变换的适用范围 【答案解析】 :F 对于单位冲激响应不满足绝对可积条件的系统是不存在频率响应的,也即不存在傅里叶变 换,所以傅里叶分析方法不能来分析不稳定的系统。 7、 根据 BIBO 稳定性准则, 一个稳定的连续时间 LTI 系统的所有极点一定位于虚轴的左侧。 【考查重点】 :这是第九章的考点,主要考查系统稳定性和零极点位置的关系。 【答案解析】 :F 一个稳定的连续时间 LTI 系统的收敛域一定包括虚轴, 即使所有极点都在虚轴左侧, 但如果 是非因果系统,它的收敛域只会在虚轴左侧,不会包括虚轴,这样的系统还是不稳定的。所
华中科技大学招收2013年硕士学位研究生入学考试试题 (答案与解析)
一、 填空题(每空 3 分)
1、已知一零初始状态的 LTI 系统在输入 x1 (t) u (t) 激励下的响应为 y1 (t) 4e2t u(t) ,那 么在输入 x2 (t) tu (t) 激励下的响应为 。
高分子考研真题,青岛大学12-17年

腈纶纤维,除加入丙烯腈作主要单体外,还常加入丙烯酸甲酯和
衣康酸辅助单体与其共聚。试说明它们对产品性能的影响。
12. 甲基丙烯酸甲酯于 10℃进行乳液聚合,试从下列引发剂体系
中选取合适的引发剂
(1)BPO (2)AIBN (3)(NH4)S2O8 (4)
K2S2O8
(5)HOOH+Fe2+ (6)(N
10)茂金属催化剂
二. 问答题(每题 10 分, 共 120 分) 1. 在自由基聚合反应中,何种条件下会出现反应自动加速现象?解 释其产生的原因。 2. 用光气法合成的聚碳酸酯分子量可以较大,该产物经洗涤净化等 过程后,在造粒过程中有时发生分子量显著降低的情况。请分析 造成上述情况的主要原因和应采取的防止措施。 3. 苯乙烯分别在乙苯,异丙苯,苯,甲苯四种溶剂中进行自由基聚 合,除溶剂种类不同外,其它条件皆相同,请问所得聚合物之分 子量由小到大的顺序是怎样的?解释之。 4. 以 n-C4H9Li 为引发剂,分别以硝基甲烷和四氢呋喃为溶剂,在相 同条件下使异戊二烯聚合。判断在不同溶剂中聚合速度的大小顺 序,并说明其原因。 5. 要合成分子链中有以下特征基团的聚合物,应选用那类单体,并 通过何种反应聚合而成? 1) –CH22) –NH-CO-, 3) –NH-CO-O4) –NH-CO-HN5) –OCH2CH2-
1
各步基元反应的反应式。
7. 请指出下列烯类单体适于何种机理聚合:自由基聚合、阳离子聚
合、阴离子聚合。 o. r& ^5 n4
CH2=CHC6H5,CH2=C(CH3)2 ,CF2=CF2 ,CH2=C(CN)COOR,
CH2=CHCl +
8. 给出聚酰亚胺合成时所用原料,合成反应式及聚合物的主要特性
2013年青岛大学考研真题825自动控制理论
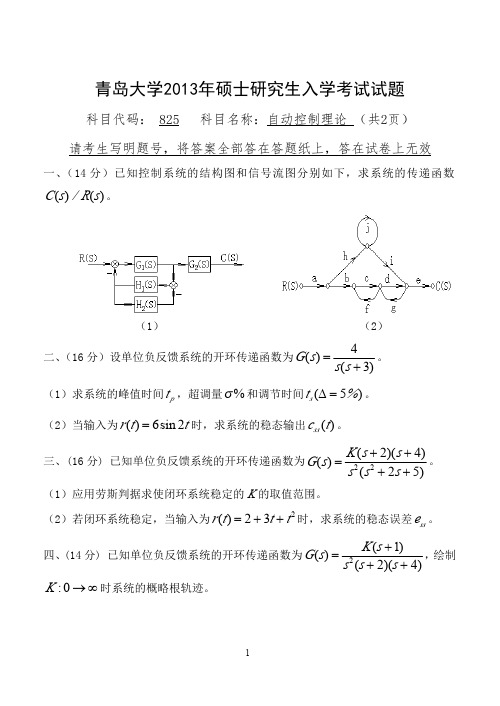
,绘制其开环对
数幅频渐近特性曲线。
七 、( 14 分 ) 已 知 离 散 系 统 的 结 构 图 如 下 , 其 中 T = 1s , G(s) = 1 , s +1
H (s) = 2 。 求 系 统 的 闭 环 脉 冲 传 递 函 数 Φ(z) 并 判 断 其 稳 定 性 。( s+2
Z( 1 ) s+a
K
。利用描述函数法分别判断 K=2 和 K=10
A+2
s(s + 1)(s + 2)
时闭环系统的运动特性。
2
十、(16 分)给定系统的动态方程如下,判断该系统的可控性和可观测性。
⎡−1 −2 −2⎤ ⎡2⎤
ẋ
=
⎢ ⎢
0
−1
1
⎥ ⎥
x
+
⎢⎢0 ⎥⎥
u,
⎢⎣ 1 0 −1⎥⎦ ⎢⎣1⎥⎦
y = [1 1 0]x
=
z
z − e−aT
, e−1
= 0.3697,
e −2
=
0.1353 ,
e −3
= 0.0498 )
八、(14 分)已知非线性系统的微分方程为 ̇ẋ + 4ẋ + 3x + x2 = 0,求系统的奇点并
判断其类型。 九、(16 分)已知非线性系统的结构如图所示,其中非线性环节的描述函数为
N (A) = 2A + 1 , G(s) =
1
ቤተ መጻሕፍቲ ባይዱ
五、(16 分) 已知单位负反馈系统的开环传递函数为 G(s) =
10
。
s(s +1)(s + 2)
(1)绘制系统的开环幅相曲线,并应用奈氏判据判断闭环系统的稳定性。
2013年青岛大学考研真题852概论及数据统计

青岛大学2013年硕士研究生入学考试试题科目代码:科目名称:概率论及数理统计(2)(共2页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、解释概念(20分)1)概率的古典概型与几何概型2)大数定律与中心极限定理3)点估计与区间估计4)相关分析与回归分析二、计算题(20分)某工厂有四条流水线生产同一种产品,该四条流水线的产量分别占总产量的10%,20%,30%,40%,又这四条流水线的次品率依次为5%,4%,3%,2%,问:1)现从出厂产品中任取一件,问恰好取到次品的概率为多少?2)在出厂产品中随机地取一件产品发现是次品,为进行产品质量追溯,此次品出自第1条流水线生产的概率是多少?三、计算题(20分)一人驾车从城中甲地到乙地,途中经过若干交通路口,设他在每个路口遇“红灯”的概率均为0.4,试求:1)此人过5个路口仅遇到一次“红灯”的概率;2)此人第5次过路口才遇到“红灯”的概率;3)此人第5次过路口已是第3次遇“红灯”的概率。
四、计算题(20分)已知ηζ,相互独立,且()()21~,~ληλζP P ,1)求ηζξ+=的分布2)泊松分布是否满足可加性?五、计算题(10分)ξ服从参数为p 的几何分布:()p q k P k 1−==ξ,,...2,1=k ,求ξξD E ,。
并给出ξD 与ξE 的关系。
六、证明题(20分)若对连续型随机变量ξ,有)0(>+∞<r E rξ,证明:r rE p εξεξ≤>)(并验证切比雪夫不等式成立。
七、计算题(20分)设总体ξ~),(2σµN ,2,σµ为未知参数,(n ξξξ,...,,21)是来自总体ξ的一个样本,问:1)2,σµ的矩估计;2)2,σµ的极大似然估计;3)讨论上述两种估计的无偏性。
八、计算题(20分)某省进行的公务员录取考试中,申论平均成绩为75.6分,标准差为7.4分。
某岗位报考考生共50名,测得平均申论统考成绩为78分,试问该岗位报考考生的申论成绩与全省申论统考成绩有无显著差异?(96.10.050.975==u ,α)。
2013年青岛大学考研真题912计算机专业基础综合

青岛大学2013年硕士研究生入学考试试题科目代码:912科目名称:计算机技术专业基础综合(共9页)请考生写明题号,将答案全部答在答题纸上,答在试卷上无效一、单项选择题(共20小题,每题1分,共20分)1.计算机网络的目标是实现()。
A.数据处理B.信息传输与数据处理C.文献查询D.资源共享与信息传输2.若某通信链路的数据传输速率是1200bps,采用16相位调制,则该链路的波特率是()。
A.4800波特B.600波特C.300波特D.9600波特3.下列描述不正确的是()。
A.每个数据报在传输过程中独立地选择路由B.数据报方式在传输数据前不建立电路呼叫C.同一源节点发出的数据报按发出的顺序到达目的站节点D.每个数据报的传输是独立的,与其他数据报无关4.在子网192.168.128.0/29中,能够收到目的地址为192.168.128.7的IP分组的最大主机数是()。
A.0B.4C.6D.85.关于TCP和UDP协议区别的描述,错误的是()。
A.UDP协议比TCP协议的安全性差B.TCP协议是面向连接的,而UDP是无连接的C.UDP协议要求对方发出的每个数据包都要确认D.TCP协议可靠性高,UDP则需要应用层保证数据传输的可靠性6.主机A与主机B之间已经建立一个TCP连接,主机A向主机B发送了3个连续的TCP段,分别包含300字节、400字节和500字节的有效载荷,第三段的序号为900。
若主机B仅正确接收第1和第3段,则主机B发给主机A的确认序号是()。
A.300B.500C.1200D.14007.在OSI参考模型中,自下而上第一个提供端到端服务的层次是()。
A.数据链路层B.传输层C.会话层D.应用层8.在无噪声情况下,若某个通信链路的带宽为6kHz,采用16个相位,每个相位4种振幅的QAM调制技术,则该通信链路的最大数据传输速率是()。
A.72kbpsB.48kbpsC.96kbpsD.24kbps9.一个TCP连接总是以1KB的最大段长发送TCP段,发送方有足够多的数据要发送。
【青岛大学2012年考研专业课真题】信号与系统2012
4
科目代码: 827 科目名称: 信号与系统 (共
4
页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
e(t ) e3t u(t ) ,则 r (0 )
。
9 .若可逆系统的单位冲激响应为 h(t ) ,其逆系统的单位冲激响应为 hI (t ) ,则
h(t ) hI (t )
。
10.图 3 所示以 f (t ) 为输入, g (t ) 为输出的对 调幅波进行相干解调的系统是 (线性/非线性) 、 的。 (时变/时不变)
f (t )
低通滤波
g (t )
cos(0t )
图3
二、 (15 分)计算图 4 所示矩形脉冲信号 h(t ) 和半波正弦脉冲信号 e(t ) 的卷积积 分 r (t ) h(t ) e(t ) ,并画出 r (t ) 的波形。
f e (t ) =
, f o (t ) =
。 。
Hz ,
3.若正弦序列 sin(0 n) 的周期 N 10 ,则 0 的最小取值为 0 4.周期矩形脉冲信号 f (t ) 如图 1 所示,则该信号的谱线间隔为 直流分量为 。
1 … -10 -1 0 1 图1 10
f (t )
…
t
5.频谱函数 F () j sgn() 的傅里叶逆变换 f (t ) 6 .图 2 所示因果周期信号的拉氏变换 F ( s) 为 。
f (t )
1 0 1 2 3
图2
。 ,对应的收敛域
4
5
6
t
1 7.序列 ( ) n u (n) 的 z 变换 X ( z ) 2
8.给定微分方程、起始状态、激励信号分别为
青岛大学信号与系统考研真题2009—2011年

(15 分)15.电路如题图 15 所示, t 0 时开关 K 处于“1”的位置而且已经达 到稳态;当 t 0 时开关 K 由“1”转向“2”。
2 K i(t) R1 1
1
+
+
4V
2V
-
-
C 1F
L 1H 4
3
R2
2
题图 15
(1)试画出开关动作后的复频域等效电路; (2)求响应电流 i(t) 在 t 0 内的表达式。
青岛大学 2009 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统 (共 4 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
Ⅰ、填空题(共 11 题,每空格 3 分,共 33 分)
1.对冲激偶信号 (t) , (t)dt
,
(t
t0
)
f
(t)dt
。
2.时间函数 f (t) etu(t) 的傅里叶变换 F ( )
(3) 在题图 17 所示的解调过程中,试确定 A 、1 、2 之值,使得 y(t) g(t) 。
f (t)
A
y(t )
1 1
cos(2t)
题图 17
(20 分)18.已知离散时间系统的差分方程为 y(n) 0.81y(n 2) x(n) 0.81x(n 2)
(1)求系统函数 H (z) ,画出零、极点分布图; (2)求频率响应 H (e j ) ,粗略绘出幅频响应曲线,判断系统具有何种滤波特性; (3)求系统的单位样值响应 h(n) ,画出 h(n) 的波形; (4)以使用最少数量的单位延时器为条件,画出系统的仿真框图。
u(t)
则下列说法正确的是(
)。
信号与系统 第一章_绪论(青岛大学)小白发布

∫
∞
−∞ ∞
Sa (t )dt = π Sa 2 (t )dt = π
∫
−∞
另外一个类似的函数:
sin π t sinc( t ) = πt
§1.3 信号的运算
(一)对自变量进行的运算: 移位、反褶与尺度 对自变量进行的运算: 移位、 1. 移位: f (t ) → f (t ± t0 ) 移位:
t
t
t
sin (Ωt ) + sin (8 Ωt )
× sin ( Ωt ) sin (8 Ωt )
t
t
反相点
§1.4 阶跃信号与冲激信号 奇异信号: 奇异信号:
(一)单位斜变信号tu(t) (二)单位阶跃信号 u(t) (三)单位冲激信号δ (t) (四)冲激偶信号δ ' (t)
(一)单位斜变信号tu(t)
(3) cos(3n − )
当 当
2π
2π
π
ω0
为有理数时, 为周期序列; 为有理数时,sin(ω0n) 为周期序列; 为无理数时, 为非周期序列。 为无理数时,sin(ω0n) 为非周期序列。
2π 为无理数, 为无理数, 3
非周期序列
4
ω0
4.能量(有限)信号与功率(有限)信号 能量(有限)信号与功率(有限)
2.信号的传输、 2.信号的传输、交换和处理 信号的传输
信号传输(Transmission)
——古代烽火传送边疆警报 ——击鼓、信鸽、旗语等 击鼓、信鸽、 ——电信号传输(19世纪开始): 电信号传输( 世纪开始 世纪开始):
1837年莫尔斯发明了电报 年莫尔斯发明了电报 1876年贝尔发明了电话 年
青岛大学概率论及数理统计2013年考研真题考研试题硕士研究生入学考试试题

1青岛大学2013年硕士研究生入学考试试题科目代码:619科目名称:概率论及数理统计(共3页)请考生写明题号,将答案答在答题纸上,答在试卷上无效
一、概念题(每题8分共40分)
1、基本事件(8分)
2、概率的公理化定义(8分)
3、全概率公式(8分)
4、概率密度函数的基本性质(8分)
5、特征函数(8分)
二、填充题(每题4分共20分)
1、(4分)设A 和B 是相互独立的随机事件,()0.5p A =,()0.7p B =,则()p A B =∪。
2、(4分)随机变量ξ的数学期望()5E ξ=,标准差()2σξ=,则2()E ξ=。
3、(4分)设随机变量X 在区间(0,2)上服从均匀分布,则随机变量2Y X =在区间(0,4)上的概率密度为()Y f y =。
4、(4分)甲盒中有2个白球和3个黑球,乙盒中有3个白球和2个黑球,今从每个盒中各取2个球,发现它们是同一颜色的,则这颜色是黑色的概率为___________。
5、(4分)设总体X 的概率密度为
⎪⎩⎪⎨⎧<<+=其它,
0,10,)1()(x x x f θθ1−>θ.n X X X ,,,21⋯是来自X 的样本,则未知参数θ的极大似然估计量为_________。
三、选择题(每题3分共15分)
1、设A 、B 、C 为三个事件,()0P AB >且(|)1P C AB =,则有
(A)()()()1P C P A P B ≤+−(B)()()
P C P A B ≤∪(C)()()()1P C P A P B ≥+−(D)()()
P C P A B ≥∪。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. 1 ,σ > 1 B. 1 ,σ < 1 C.
1− s
1− s
1 ,σ < 1 D. 1 ,σ > 1
s −1
s −1
f (t)
g (t )
2
2
5. 序 列 x(n) = 2δ (n +1) − δ (n) + 3δ (n − 2) 的 z
02 t
-2 0 2 t
图3
变换的收敛域为(
)。
A. z > 0
青岛大学 2013 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统 (共 6 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
青岛大学 2013 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统(共 3 页) 请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
R2 两 端 , 为 使 v2 (t) 较 v1(t) 无 失 真 , R1 、 R2 、 C1 、 C2 应 满 足 的 关 系
为
。
三、(15 分)计算图 6 所示脉冲函数 f1(t) 和 f2 (t) 的卷积积分 f (t) = f1(t) ∗ f2 (t) ,
并画出 f (t) 的波形。
f1 (t ) 1
性的是(
)。
n
A. y(n) = ∑ x(k)
k =−∞
C. y(n) = x(n) sin(2π n + π ) 76
B. y(n) = 2x(n) + 3 D. y(n) = [x(n)]2
8.下列系统函数描述的因果线性时不变离散时间系统中,构成全通网络的是
(
)。
A. H (z) = z − 0.5 z + 0.5
f2 (t) 2
-1 0 1
t 01
图6
t
3
青岛大学 2013 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统 (共 6 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
四、(15 分) 格状网络如图 7 所示。
R1
+
+
(1)求电压转移函数 H (s) = V2 (s) ,在 s 平面上绘出 v1(t) C1
Hz。
Hz , 其 调 幅 信 号
4. s 平面的虚轴映射到 z 平面是___
_,实轴映射到 z 平面是
。
5.写出图 4 所示信号流图描述的连续时间系统的微分方程 R1
e(t) 1
5
1p 1p -5
-6
14 r(t)
图4
+ C1
v1(t)
C2
-
图5
。
+ R2 v2(t)
-
6. 图 5 所示电路为由电阻 R1 、 R2 组成的分压器,分布电容 C1 、 C2 并接于 R1 、
dt 2
dt
dt
起始状态 r(0− ) = 1 、 r′(0− ) = 2 ,激励 e(t) = e−tu(t) ,求:
(1)零输入响应 rzi (t) ; (2)零状态响应 rzs (t) ; (3)全响应 r(t) 。
六、(18 分)因果离散时间系统如图 8 所示。
+
1
∑
E
+
(1)选择合适的状态变量,列写状态方程和 x(n)
2 1
在(
)处。
A. n = 0
B. n = 1
01 2 3
n
C. n = 2
D. n = 3
图2
4. 信号 etu(−t) 的拉氏变换及收敛域为(
)。
1
青岛大学 2013 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统 (共 6 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
-4 -2 0 t
A. f (−2t + 1) 2
B. f (− 1 t +1) 2
C. f (−2t +1)
D. f (− 1 t + 1) 22
3.离散序列 x1(n) = u(n) − u(n − 2) , x2 (n) 如图 2 所示,
x2(n) 3
则卷积和序列 y(n) = x1(n) ∗ x2 (n) 的最大取值发生
B. H (z) = z + 2 z Ʊ 0.5 z+2
D. H (z) = z + 0.5 z − 0.5
2
青岛大学 2013 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统 (共 6 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效 二、填空题(每空格 3 分,共 24 分)
1/2
输出方程(化为矩阵方程形式);
1/4
(2)判断系统的稳定性;
+
+
1
∑
E
+
(3)列写出系统的差分方程。
2
图8
七、(18 分)描述某因果离散时间系统的差分方程为
y(n)
2
4
青岛大学 2013 年硕士研究生入学考试试题
科目代码: 827 科目名称: 信号与系统 (共 6 页)
请考生写明题号,将答案全部答在答题纸上,答在试卷上无效
1.当ω 0 满足
条件时,正弦序列 sin(ω 0n) 才是周期序列。
2.给定微分方程、起始状态、激励信号分别为
d dt
r(t)
+
r(t)
=
2
d dt
e(t)
、
r(0−
)
=
0
、
e(t) = u(t) ,则 r(0+ ) =
。
3 . 信 号 f1(t) = Sa(100πt) 的 频 带 宽 度 为 f2 (t) = f1(t) ⋅ cos(106πt) 的频带宽度为
B. z < ∞
C. 0 < z < ∞ D. 整个 z 平面
6.若图 3 所示信号 f (t) 的傅里叶变换为 F (ω ) = R(ω ) + jX (ω ) ,则信号 g(t) 的傅
里叶变换 G(ω) 为(
)。
A. 1 R(ω ) 2
B. R(ω )
C. jX (ω )
D. 2R(ω )
7.以下描述系统的各方程中, x(n) 为激励, y(n) 为响应,则具有线性时不变特
C2 v2(t)
V1 ( s)
-
R2
-
H (s) 的零、极点分布图;
图7
(2)在网络参数 R1、 R2 、 C1 、 C2 满足什么条件时可构成全通网络, 给出此条 件下的 H (s) 。
五、(16 分)描述某连续时间系统的微分方程为
d2
d
d
r(t) + 3 r(t) + 2r(t) = e(t) + 3e(t)
一、单项选择题(每题 3 分,共 8 题,24 分)
∞
∑ 1. 序列和 δ (k ) 等于(
)。
k =−∞
A. ∞ B. u(n) C. (n +1)u(n)
D. 1
2.图 1 所示 f (t) 为原始信号, f1(t) 为变换信号,则 f1(t) 的表达式为(
)。
f (t) 2
0 12 3
t
图1
f1 (t ) 2
