2010北约 高校自主招生数学试题及解答
2010复旦交大清华北大自主招生数学试题

O x O xO x则该多面体的体积为______________A. 32个;B. 30个;C.28个;D.26个7、给定平面向量(1,1),那么,平面向量(231-,231+)是将向量(1,1)经过________. A .顺时针旋转60°所得;B .顺时针旋转120°所得;C .逆时针旋转60°所得;D .逆时针旋转120°所得;8、在直角坐标系Oxy 中已知点A 1(1,0),A 2(1/2,3/2),A 4(−1,0),A 5(−1/2,−3/2)和A6(1/2, −3/2).问在向量−−→−ji A A (i,j=1,2,3,4,5,6,i≠j)中,不同向量的个数有_____.A.9个;B.15个;C.18个;D.30个 9、对函数f:[0,1]→[0,1],定义f 1(x)=f(x),……,f n (x) =f(f n−1(x)),n=1,2,3,…….满足f n (x)=x的点x ∈[0,1]称为f 的一个n−周期点.现设⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤=121,22,210,2)(x x x x x f 问f 的n−周期点的个数是___________.A.2n 个;B.2n 2个;C.2n 个;D.2(2n −1)个.10、已知复数z 1=1+3i ,z 2=−3+3i ,则复数z 1z 2的幅角__________. A.13π/12;B.11π/12;C.−π/4;D.−7π/12.11、设复数βαβαcos sin ,sin cos i w i z +=+=满足z w =3/2,则sin(β−α)=______. A.±3/2;B.3/2,−1/2;C. ±1/2;D.1/2,−3/2.12、已知常数k 1,k 2满足0<k 1<k 2,k 1k 2=1.设C 1和C 2分别是以y=±k 1(x−1)+1和y=±k 2(x−1)+1为渐近线且通过原点的双曲线.则C 1和C 2的离心率之比e 1/e ·等于_______.A.222111k k ++; B.212211k k ++ C.1 D.k 1/k 213、参数方程0,)cos 1()sin (>⎩⎨⎧-=-=a t a y t t a x 所表示的函数y=f(x)是____________.A .图像关于原点对称;B .图像关于直线x=π对称;C .周期为2aπ的周期函数D .周期为2π的周期函数.14、将同时满足不等式x−ky−2≤0,2x+3y−6≥0,x+6y−10≤0 (k>0)的点(x,y)组成集合D 称为可行域,将函数(y+1)/x 称为目标函数,所谓规划问题就是求解可行域中的点(x,y)使目标函数达到在可行域上的最小值.如果这个规划问题有无穷多个解(x,y),则k 的取值为_____.A.k≥1;B.k≤2C.k=2;D.k=1.15、某校有一个班级,设变量x 是该班同学的姓名,变量y 是该班同学的学号,变量z 是该班同学的身高,变量w 是该班同学某一门课程的考试成绩.则下列选项中正确的是________.A. y 是x 的函数;B. z 是y 的函数;C. w 是z 的函数;D. w 是x 的函数.16、对于原命题“单调函数不是周期函数”,下列陈述正确的是________. A. 逆命题为“周期函数不是单调函数”; B. 否命题为“单调函数是周期函数”; C. 逆否命题为“周期函数是单调函数”; D. 以上三者都不正确17、设集合A={(x,y)|log a x+log a y>0},B={(x,y)|y+x<a}.如果A∩B=∅,则a 的取值范围是_______A .∅;B .a>0,a≠1;C .0<a≤2, a≠1D .1<a≤218、设计和X 是实数集R 的子集,如果点x 0∈R 满足:对任意a>0,都存在x ∈X 使得0<|x−x 0|<a ,则称x 0为集合X 的聚点.用Z 表示整数集,则在下列集合(1){n/(n+1)|n ∈Z, n≥0}, (2) R\{0}, (3){1/n|n ∈Z, n≠0}, (4)整数集Z 中,以0为聚点的集合有_____.A .(2), (3);B .(1), (4);C .(1), (3);D .(1), (2), (4)19、已知点A(−2,0),B(1,0),C(0,1),如果直线kx y =将三角形△ABC 分割为两个部分,则当k=______时,这两个部分得面积之积最大?A .23-B .43-C .34-D .32- 20、已知x x x x f 2cos 3cos sin )(+=,定义域⎥⎦⎤⎢⎣⎡=ππ127,121)(f D ,则=-)(1x f_____A .π12123arccos 21+⎪⎪⎭⎫ ⎝⎛-xB .π6123arccos 21-⎪⎪⎭⎫ ⎝⎛-x C .π12123arcsin 21+⎪⎪⎭⎫ ⎝⎛--x D .π6123arcsin 21-⎪⎪⎭⎫ ⎝⎛-x 21、设1l ,2l 是两条异面直线,则直线l 和1l ,2l 都垂直的必要不充分条件是______ A .l 是过点11l P ∈和点22l P ∈的直线,这里21P P 等于直线1l 和2l 间的距离 B .l 上的每一点到1l 和2l 的距离都相等 C .垂直于l 的平面平行于1l 和2l D .存在与1l 和2l 都相交的直线与l 平行22、设ABC−A’B’C’是正三棱柱,底面边长和高都为1,P 是侧面ABB ’A’的中心,则P到侧面ACC’A’的对角线的距离是_____A .21 B .43 C .814 D .82323、在一个球面上画一组三个互不相交的圆,成为球面上的一个三圆组.如果可以在球面上通过移动和缩放将一个三圆组移动到另外一个三圆组,并且在移动过程中三个圆保持互不相交,则称这两个三圆组有相同的位置关系,否则就称有不同的位置关系.那么,球面上具有不同的位置关系的三圆组有______A .2种B .3种C .4种D .5种24、设非零向量()()()321321321,,,,,,,,c c c c b b b b a a a a ===为共面向量,),,(31x x x x x = 是未知向量,则满足0,0,0=⋅=⋅=⋅x c x b x a的向量x 的个数为_____A .1个B .无穷多个C .0个D .不能确定 25、在Oxy 坐标平面上给定点)1,2(),3,2(),2,1(C B A ,矩阵⎪⎪⎭⎫⎝⎛-112k 将向量,,分别变换成向量',',',如果它们的终点',','C B A 连线构成直角三角形,斜边为''C B ,则k 的取值为______A .2±B .2C .0D .0,−2 26、设集合A,B,C,D 是全集X 的子集,A∩B≠∅,A∩C≠∅.则下列选项中正确的是______. A.如果B D ⊂或C D ⊂,则D∩A≠∅;B.如果A D ⊂,则C x D∩B≠∅,C x D∩C≠∅;C.如果A D ⊃,则C x D∩B=∅,C x D∩C=∅;D.上述各项都不正确.27、已知数列{}n a 满足21=a 且n a n ⎧⎫⎨⎬⎩⎭是公比为2的等比数列,则∑==nk k a 1______A .221-+n n B .22)1(1+-+n n C .)1(22-+n n n D .n n n 22)1(+-28、复平面上圆周2211=+--iz z 的圆心是_______ A .3+i B .3−i C .1+i D .1−i29.已知C 是以O 为圆心、r 为半径的圆周,两点P 、P *在以O 为起点的射线上,且满足|OP|∙|OP *|=r 2,则称P 、P *关于圆周C 对称.那么,双曲线22x y -=1上的点P(x,y)关于单位圆周C':x 2+y 2=1的对称点P *所满足的方程是(A)2244x y x y -=+ (B)()22222x y x y -=+ (C)()22442x y x y -=+(D)()222222x y x y-=+30、经过坐标变换⎩⎨⎧+-=+=θθθθcos sin 'sin cos 'y x y y x x 将二次曲线06532322=-+-y xy x 转化为形如1''2222=±by a x 的标准方程,求θ的取值并判断二次曲线的类型_______A .)(6Z k k ∈+=ππθ,为椭圆 B .)(62Z k k ∈+=ππθ,为椭圆C .)(6Z k k ∈-=ππθ,为双曲线D .)(62Z k k ∈-=ππθ,为双曲线31、设k, m, n 是整数,不定方程mx+ny=k 有整数解的必要条件是____________ A. m,n 都整除k ; B. m,n 的最大公因子整除k ; C. m,n,k 两两互素; D. m,n,k 除1外没有其它共因子2010年五校合作自主选拔通用基础测试 数学试题 适用高校:清华大学、上海交通大学等五校 一、选择题1.设复数2()1a i w i+=+,其中a 为实数,若w 的实部为2,则w 的虚部为( ) (A)32- (B)12- (C)12 (D)322.设向量,a b ,满足||||1,==⋅=a b a b m ,则||+a tb ()t R ∈的最小值为( ) (A)2(C)13. 无试题4. 无试题5.在ABC ∆中,三边长,,a b c ,满足3a c b +=,则tan tan 22A C的值为( ) (A)15 (B)14 (C)12 (D)236.如图,ABC ∆的两条高线,AD BE 交于H ,其外接圆圆心为O ,过O 作OF 垂直BC 于F ,OH 与AF 相交于G ,则OFG ∆与GAH ∆面积之比为( )(A)1:4 (B)1:3 (C)2:5 (D)1:2O H G FEDCBA7.设()e (0)axf x a =>.过点(,0)P a 且平行于y 轴的直线与曲线:()C y f x =的交点为Q ,曲线C 过点Q 的切线交x 轴于点R ,则PQR ∆的面积的最小值是( )(A)1 (C)e2(D)2e 48.设双曲线2212:(2,0)4x y C k a k a -=>>,椭圆2222:14x y C a +=.若2C 的短轴长与1C 的实轴长的比值等于2C 的离心率,则1C 在2C 的一条准线上截得线段的长为( )(A) (B)2 (C) (D)49.欲将正六边形的各边和各条对角线都染为n 种颜色之一,使得以正六边形的任何3个顶点作为顶点的三角形有3种不同颜色的边,并且不同的三角形使用不同的3色组合,则n 的最小值为( )(A)6 (B)7 (C)8 (D)910.设定点A B C D 、、、是以O 点为中心的正四面体的顶点,用σ表示空间以直线OA 为轴满足条件()B C σ=的旋转,用τ表示空间关于OCD 所在平面的镜面反射,设l 为过AB 中点与CD 中点的直线,用ω表示空间以l 为轴的180°旋转.设στ表示变换的复合,先作τ,再作σ.则ω可以表示为( )(A)στστσ (B)στστστ (C)τστστ (D)στσστσ 二、解答题11.在ABC ∆中,已知22sin cos 212A BC ++=,外接圆半径2R =. (Ⅰ)求角C 的大小;(Ⅱ)求ABC ∆面积的最大值.12.设A B C D 、、、为抛物线24x y =上不同的四点,,A D 关于该抛物线的对称轴对称,BC 平行于该抛物线在点D 处的切线l .设D 到直线AB ,直线AC 的距离分别为12,d d ,已知12d d +=.(Ⅰ)判断ABC ∆是锐角三角形、直角三角形、钝角三角形中的哪一种三角形,并说明理由;(Ⅱ)若ABC ∆的面积为240,求点A 的坐标及直线BC 的方程.O(Ⅱ)一般地,设正n 棱锥的体积V 为定值,试给出不依赖于n 的一个充分必要条件,使得正n 棱锥的表面积取得最小值.14.假定亲本总体中三种基因型式:,,AA Aa aa 的比例为:2:u v w (0,0,0,21)u v w u v w >>>++=且数量充分多,参与交配的亲本是该总体中随机的两个.(Ⅰ)求子一代中,三种基因型式的比例;(Ⅱ)子二代的三种基因型式的比例与子一代的三种基因型式的比例相同吗?并说明理由.15.设函数()1x m f x x +=+,且存在函数()1(,0)2s t at b t a ϕ==+>≠,满足2121()t s f t s-+=. (Ⅰ)证明:存在函数()(0),t s cs d s ψ==+>满足2121()s t f s t +-=; (Ⅱ)设113,(),1,2,.n n x x f x n +===证明:1123n n x --≤.2010年名牌大学自主招生考试试题(3)适用高校:清华大学、上海交通大学等五校(样题)一、选择题(每题5分,共25分)1.函数y=32cos sin cos x x x +-的最大值为 (A)2827 (B)3227 (C)43 (D)40272.已知a 、b 、c 、d 是实数,az bcz dω+=+, 且当Imz>0时,In ω>0.则 (A)ad+bc>0; (B)ad+bc <0; (C)ad−bc >0; (D)ad−bc<0.3.甲、乙、丙、丁等七人排成一排,若要求甲在中间,乙丙相邻,且丁不在两端,则不同的排法共有( )(A)24种; (B)48种; (C)96种; (D)120种4.己知F 为抛物线y 2=2px 的焦点,过点F 的直线l 与该抛物线交于A 、B 两点,l 1、l 2分别是该抛物线在A 、B 两点处的切线,l 1、l 2相交于点C ,设|AF|=a ,|BF|=b ,则|CF|=(C)2a b+;5.设θ是三次多项式f(x)=x 3−3x +10的一个根,且α=222θθ+-,若h(x)是一个有理系数的二次多项式,满足条件()h αθ=.则h(0)= (A)−2; (B)2; (C)12-; (D)12二、解答题(本大题共55分)1.(本题15分)己知f(x)是定义在R 上的奇函数,且当x <0时,f(x)单调递增,f(−1)=0.设函数()2sin cos 2x x m x m ϕ=+-,集合M=()|0,,02m x x πϕ⎧⎫⎡⎤∈<⎨⎬⎢⎥⎣⎦⎩⎭对任意的,N=()|0,,[]02m x f x πϕ⎧⎫⎡⎤∈<⎨⎬⎢⎥⎣⎦⎩⎭对任意的,求MN.2.(本题20分)甲、乙、丙、丁等4人相互传球,第一次由甲将球传出,每次传球时,传球者将球等可能地传给另外3人中的任何1人.(l)经过2次传球后,球在甲乙两人手中的概率各是多少?(2)经过n 次传球后,球在甲手中的概率记为p n (n=1,2,…) ,试求1n P +与n P 的关系式,并求n P 的表达式及lim n n P →∞3.(本题20分)设p 、q 是一元二次方程x 2+2ax−1=0(a>0)的两个根.其中p >0,令y 1=p−q,yn+1=2n y −2,n=1,2,…,证明:11212111lim ......n n y y y y y y →∞⎛⎫+++⎪⎝⎭=p. 2010年北京大学、香港大学、北京航空航天大学三校联合自主招生考试试题(数学部分)1.(仅文科做)02απ<<,求证:sin tan ααα<<.(25分) 2.AB 为边长为1的正五边形边上的点.证明:AB(25分)3.AB 为21y x =-上在y 轴两侧的点,求过AB 的切线与x 轴围成面积的最小值.(25分)4.向量OA 与OB 已知夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ 在0t 时取得最小值,问当0105t <<时,夹角的取值范围.(25分)5.(仅理科做)存不存在02x π<<,使得sin ,cos ,tan ,cot x x x x 为等差数列.(25分)。
2010高考数学全国卷1(题题详细解析)

绝密★启用前2010年普通高等学校招生全国统一考试及答案第I 卷一.选择题 (1)复数3223i i+=-(A)i (B)i - (C)12-13i (D) 12+13i1.A 【命题意图】本小题主要考查复数的基本运算,重点考查分母实数化的转化技巧.【解析】32(32)(23)694623(23)(23)13i i i i i i ii i +++++-===--+.(2)记cos(80)k -︒=,那么tan 100︒=A.21k k- B. -21k k- C.21k k- D. -21k k-2.B 【命题意图】本小题主要考查诱导公式、同角三角函数关系式等三角函数知识,并突出了弦切互化这一转化思想的应用. 【解析】222sin 801cos 801cos (80)1k=-=--=-,所以tan 100tan 80︒=-2sin 801.cos 80k k-=-=-(3)若变量,x y 满足约束条件1,0,20,y x y x y ≤⎧⎪+≥⎨⎪--≤⎩则2z x y =-的最大值为(A)4 (B)3 (C)2 (D)13.B 【命题意图】本小题主要考查线性规划知识、作图、识图能力及计算能力.【解析】画出可行域(如右图),由图可知,当直线l 经过点A(1,-1)时,z 最大,且最大值为m ax 12(1)3z =-⨯-=.0x y += 1Oy x =y20x y --=xA 0:20l x y -=2-2A(4)已知各项均为正数的等比数列{n a },123a a a =5,789a a a =10,则a a a=(A) 52(B) 7 (C) 6 (D) 424.A 【命题意图】本小题主要考查等比数列的性质、指数幂的运算、根式与指数式的互化等知识,着重考查了转化与化归的数学思想.【解析】由等比数列的性质知31231322()5a a a a a a a === ,37897988()a a a a a a a ===10,所以132850a a =,所以13336456465528()()(50)52a a a a a a a a a =====(5)353(12)(1)x x +-的展开式中x 的系数是(A) -4 (B) -2 (C) 2 (D) 45.B 【命题意图】本小题主要考查了考生对二项式定理的掌握情况,尤其是展开式的通项公式的灵活应用,以及能否区分展开式中项的系数与其二项式系数,同时也考查了考生的一些基本运算能力.【解析】35533(12)(1)(16128)(1)x x x x x x x +-=+++-故353(12)(1)x x +-的展开式中含x的项为333551()1210122C x xC x x x ⨯-+=-+=-,所以x的系数为-2.(6)某校开设A 类选修课3门,B 类选择课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有 (A) 30种 (B)35种 (C)42种 (D)48种6.A 【命题意图】本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想.【解析】:可分以下2种情况:(1)A 类选修课选1门,B 类选修课选2门,有1234C C 种不同的选法;(2)A 类选修课选2门,B 类选修课选1门,有2134C C 种不同的ABC DA 1B 1C 1D 1 O选法.所以不同的选法共有1234C C +2134181230C C =+=种.(7)正方体ABCD-1111A B C D 中,B 1B 与平面AC 1D 所成角的余弦值为 A23B33C 23D637.D 【命题意图】本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D 到平面AC 1D 的距离是解决本题的关键所在,这也是转化思想的具体体现.【解析】因为BB 1//DD 1,所以B 1B 与平面AC 1D 所成角和DD 1与平面AC 1D 所成角相等,设DO ⊥平面AC1D ,由等体积法得11D A C D D A C DV V --=,即111133A C D A C D S D O S D D ∆∆⋅=⋅.设DD 1=a,则12211133sin 60(2)2222AC D S AC AD a a ∆==⨯⨯=,21122A C D S A D C D a ∆==.所以1312333AC DAC DS D D aD O a S a∆∆===,记DD 1与平面AC1D 所成角为θ,则13sin 3D O D D θ==,所以6cos 3θ=.(8)设a=3log 2,b=In2,c=125-,则A a<b<c Bb<c<a C c<a<b D c<b<a8.C 【命题意图】本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用. 【解析】 a=3log 2=21log 3, b=In2=21log e,而22log 3log 1e >>,所以a<b,c=125-=15,而2252log 4log 3>=>,所以c<a,综上c<a<b.(9)已知1F 、2F 为双曲线C:221x y -=的左、右焦点,点p 在C 上,∠1F p 2F =060,则P 到x 轴的距离为 (A)32(B)62(C) 3 (D) 69.B 【命题意图】本小题主要考查双曲线的几何性质、第二定义、余弦定理,考查转化的数学思想,通过本题可以有效地考查考生的综合运用能力及运算能力.【解析】不妨设点P 00(,)x y 在双曲线的右支,由双曲线的第二定义得21000||[()]12a P F e x a e x x c=--=+=+,22000||[)]21aPF e x ex a x c=-=-=-.由余弦定理得 cos ∠1F P 2F =222121212||||||2||||P F P F F F P F P F +-,即cos 0602220000(12)(21)(22)2(12)(21)x x x x ++--=+-,解得2052x =,所以2200312y x =-=,故P 到x 轴的距离为06||2y =(10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b 的取值范围是 (A)(22,)+∞ (B)[22,)+∞ (C)(3,)+∞ (D)[3,)+∞10.A 【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 222a a=+>,从而错选A,这也是命题者的用苦良心之处.【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a=,所以a+2b=2a a+又0<a<b,所以0<a<1<b ,令2()f a a a=+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞).(11)已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为俩切点,那么PA PB ∙的最小值为 (A) 42-+(B)32-+(C) 422-+ (D)322-+11.D 【命题意图】本小题主要考查向量的数量积运算与圆的切线长定理,着重考查最值的求法——判别式法,同时也考查了考生综合运用数学知识解题的能力及运算能力. 【解析】如图所示:设PA=PB=x (0)x >,∠APO=α,则∠APB=2α,APO=21x +,21sin 1xα=+,||||cos 2P A P B P A P B α∙=⋅ =22(12sin )x α-=222(1)1x x x -+=4221x x x -+,令PA PB y ∙= ,则4221x xy x -=+,即42(1)0x y x y -+-=,由2x 是实数,所以2[(1)]41()0y y ∆=-+-⨯⨯-≥,2610y y ++≥,解得322y ≤--或322y ≥-+.故min ()322PA PB ∙=-+.此时21x =-.(12)已知在半径为2的球面上有A 、B 、C 、D 四点,若AB=CD=2,则四面体ABCD 的体积的最大值为 (A)233(B)433(C) 23 (D)83312.B 【命题意图】本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过球这个载体考查考生的空间想象能力及推理运算能力.【解析】过CD 作平面PCD ,使AB ⊥平面PCD,交AB 与P,设点P 到CD 的距离为h ,则有A B C D 11222323V h h =⨯⨯⨯⨯=四面体,当直径通过AB 与CD 的中点时,22max 22123h =-=,故max 433V =.第Ⅱ卷二.填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上. (注意:在试题卷上作答无效)(13)不等式2211x x +-≤的解集是 .13.[0,2] 【命题意图】本小题主要考查根式不等式的解法,利用平方去掉根号是解根式不等式的基本思路,也让转化与化归的数学思想体现得淋漓尽致. 解析:原不等式等价于2221(1),10x x x ⎧+≤+⎨+≥⎩解得0≤x ≤2.(14)已知α为第三象限的角,3cos 25α=-,则tan(2)4πα+= .14.17-【命题意图】本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.12x =y=1xy aO12x =-414a y -=2y x x a=-+【解析】因为α为第三象限的角,所以2(2(21),2(21))(k k k Z απππ∈+++∈,又3c o s 25α=-<0, 所以2(2(21),2(21))()2k k k Z παπππ∈++++∈,于是有4sin 25α=,sin 24tan 2cos 23ααα==-,所以tan(2)4πα+=41tantan 2134471tantan 2143παπα-+==--+.(15)直线1y =与曲线2y x x a =-+有四个交点,则a 的取值范围是 .15.(1,5)4【命题意图】本小题主要考查函数的图像与性质、不等式的解法,着重考查了数形结合的数学思想.【解析】如图,在同一直角坐标系内画出直线1y =与曲线2y x x a =-+,观图可知,a 的取值必须满足1,4114a a >⎧⎪⎨-<⎪⎩解得514a <<.(16)已知F 是椭圆C 的一个焦点,B 是短轴的一个端点,线段BF 的延长线交C 于点D ,且BF 2FD =uu r uur,则C 的离心率为 . 16.23【命题意图】本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径. 【解析】如图,22||BF b c a =+=,作1D D y ⊥轴于点D 1,则由BF 2FD =uu r uur,得1||||2||||3O F BF D D BD ==,所以133||||22D D O F c ==,即32D c x =,由椭圆的第二定义得2233||()22ac cFD e a ca=-=-又由||2||BF FD =,得232c c a a=-,整理得22320c a ac -+=.xO yBF1DD两边都除以2a ,得2320e e +-=,解得1()e =-舍去,或23e =.三.解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分10分)(注意:在试题卷上作答无效............) 已知A B C V 的内角A ,B 及其对边a,b 满cot cot a b a A b B +=+,求内角C .17. 【命题意图】本小题主要考查三角恒等变形、利用正弦、余弦定理处理三角形中的边角关系,突出考查边角互化的转化思想的应用.【解析】(18)(本小题满分12分)(注意:在试题卷上作答无效.........).投到某杂志的稿件,先由两位初审专家进行评审.若能通过两位初审专家的评审, 则予以录用;若两位初审专家都未予通过,则不予录用;若恰能通过一位初审专家的评 审,则再由第三位专家进行复审,若能通过复审专家的评审,则予以录用,否则不予录 用.设稿件能通过各初审专家评审的概率均为0.5,复审的稿件能通过评审的概率为0.3. 各专家独立评审.(I)求投到该杂志的1篇稿件被录用的概率;(II)记X 表示投到该杂志的4篇稿件中被录用的篇数,求X 的分布列及期望. 【命题意图】本题主要考查等可能性事件、互斥事件、独立事件、相互独立试验、分布列、数学期望等知识,以及运用概率知识解决实际问题的能力,考查分类与整合思想、化归与转化思想.【解析】(18)解:(Ⅰ)记 A 表示事件:稿件能通过两位初审专家的评审; B 表示事件:稿件恰能通过一位初审专家的评审; C 表示事件:稿件能通过复审专家的评审; D 表示事件:稿件被录用. 则 D=A+B·C,()0.50.50.25,()20.50.50.5P A P B P C=⨯==⨯⨯== ()()P D P A B C=+=()()P A P B C + =()()()P A P B P C + =0.25+0.5×0.3 =0.40.(Ⅱ)~(4,0.4)X B ,其分布列为: 4(0)(10.4)0.1296,P X ==-= 134(1)0.4(10.4)0.3456,P X C ==⨯⨯-= 2224(2)0.4(10.4)0.3456,P X C ==⨯⨯-= 334(3)0.4(10.4)0.1536,P X C ==⨯⨯-=4(4)0.40.0256.P X === 期望40.4 1.6E X =⨯=.(19)(本小题满分12分)(注意:在试题卷上作答无效.........) 如图,四棱锥S-ABCD 中,SD ⊥底面ABCD ,AB//DC ,AD ⊥DC ,AB=AD=1,DC=SD=2,E 为棱SB 上的一点,平面EDC ⊥平面SBC .(Ⅰ)证明:SE=2EB ;(Ⅱ)求二面角A-DE-C 的大小 .【命题意图】本小题主要考查空间直线与直线、直线与平面、平面与平面的位置关系,二面角等基础知识,考查空间想象能力、推理论证能力和运算能力. (19) 【解析】解法一:(Ⅰ)连接BD,取DC 的中点G ,连接BG,由此知 1,DG GC BG ===即A B C ∆为直角三角形,故B C B D ⊥.又ABCD,BC SD SD ⊥⊥平面故,所以,BC ⊥⊥平面BDS,BC DE .作BK ⊥EC,EDC SBC K ⊥为垂足,因平面平面,(Ⅱ) 由225,1,2,,SA SD AD AB SE EB AB SA =+===⊥知22121,AD =133AE SA AB ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭又. 故AD E ∆为等腰三角形.取ED 中点F,连接A F ,则226,3AF D E AF AD D F⊥=-=.连接F G ,则//,FG EC FG DE ⊥.所以,A F G ∠是二面角A D E C --的平面角. 连接AG,AG=2,2263FG D G D F=-=,2221cos 22AF FG AGAFG AF FG+-∠==-,所以,二面角A D E C --的大小为120°.解法二:以D 为坐标原点,射线D A 为x 轴的正半轴,建立如图所示的直角坐标系D xyz -,由,m D E m D C⊥⊥,得m D E⊥=,0m DC⊥=故20,20 111x y zyλλλλλ++==+++.令2x=,则(2,0,)mλ=-.(20)(本小题满分12分)(注意:在试题卷上作答无效.........) 已知函数()(1)ln 1f x x x x =+-+.(Ⅰ)若2'()1xf x x ax ≤++,求a 的取值范围; (Ⅱ)证明:(1)()0x f x -≥ .【命题意图】本小题主要考查函数、导数、不等式证明等知识,通过运用导数知识解决函数、不等式问题,考查了考生综合运用数学知识解决问题的能力以及计算能力,同时也考查了函数与方程思想、化归与转化思想. 【解析】20.解: (Ⅰ)11()ln 1ln x f x x x xλ+'=+-=+,()l n 1x f x x x '=+, 题设2()1xf x x ax '≤++等价于ln x x a -≤.令()ln g x x x =-,则1()1g x x'=-当01x <<,'()0g x >;当1x ≥时,'()0g x ≤,1x =是()g x 的最大值点,()(1)1g x g =-≤ 综上,a 的取值范围是[)1,-+∞.(Ⅱ)有(Ⅰ)知,()(1)1g x g =-≤即ln 10x x -+≤.当01x <<时,()(1)ln 1ln (ln 1)0f x x x x x x x x =+-+=+-+≤; 当1x ≥时,()l n (l n 1f x x x x x =+-+ 1l n (l n 1)x x x x=++- 11ln (ln 1)x x x x=--+0≥所以(1)()0x f x -≥(21)(本小题满分12分)(注意:在试题卷上作答无效.........) 已知抛物线2:4C y x =的焦点为F ,过点(1,0)K -的直线l 与C 相交于A 、B 两点,点A 关于x 轴的对称点为D . (Ⅰ)证明:点F 在直线BD 上;(Ⅱ)设89F A F B = ,求B D K ∆的内切圆M 的方程 .【命题意图】本小题为解析几何与平面向量综合的问题,主要考查抛物线的性质、直线与圆的位置关系,直线与抛物线的位置关系、圆的几何性质与圆的方程的求解、平面向量的数量积等知识,考查考生综合运用数学知识进行推理论证的能力、运算能力和解决问题的能力,同时考查了数形结合思想、设而不求思想.【解析】(21)解:设11(,)A x y ,22(,)B x y ,11(,)D x y -,l 的方程为1(0)x my m =-≠.(Ⅱ)由①知,21212(1)(1)42x x m y m y m +=-+-=- 1212(1)(1) 1.x x m y m y =--=因为 11(1,),FA x y =-uu r 22(1,)FB x y =-uur,212121212(1)(1)()1484FA FB x x y y x x x x m ⋅=--+=-+++=-uu r uur故 28849m -=,解得 43m =±所以l 的方程为3430,343x y x y ++=-+=又由①知 2214(4)4473y y m -=±-⨯=±故直线BD 的斜率21437y y =±-,因而直线BD 的方程为3730,3730.x y x y +-=--=因为KF 为BK D ∠的平分线,故可设圆心(,0)(11)M t t -<<,(,0)M t 到l 及BD 的距离分别为3131,54t t +-. 由313154t t +-=得19t =,或9t =(舍去),故 圆M 的半径31253t r +==.所以圆M 的方程为2214()99x y -+=.(22)(本小题满分12分)(注意:在试题卷上作答无效.........) 已知数列{}n a 中,1111,n na a c a +==-.(Ⅰ)设51,22n n c b a ==-,求数列{}n b 的通项公式;(Ⅱ)求使不等式13n n a a +<<成立的c 的取值范围 .【命题意图】本小题主要考查数列的通项公式、等比数列的定义、递推数列、不等式等基础知识和基本技能,同时考查分析、归纳、探究和推理论证问题的能力,在解题过程中也渗透了对函数与方程思想、化归与转化思想的考查. 【解析】(Ⅱ)12211,1, 2.a a c a a c ==->>由得 用数学归纳法证明:当2c >时1n n a a +<. (ⅰ)当1n =时,2111a c a a =->,命题成立;。
“北约”自主招生数学试题及解答(2010-2012)

2010年“北约”自主招生数学试题及解答1.(仅文科做)02απ<<,求证:sin tan ααα<<. 【解析】 不妨设()sin f x x x =-,则(0)0f =,且当02x π<<时,()1cos 0f x x '=->.于是()f x 在02x π<<上单调增.∴()(0)0f x f >=.即有sin x x >. 同理可证()tan 0g x x x =->.(0)0g =,当02x π<<时,21()10cos g x x '=->.于是()g x 在02x π<<上单调增。
∴在02x π<<上有()(0)0g x g >=。
即tan x x >。
注记:也可用三角函数线的方法求解.2.AB 为边长为1的正五边形边上的点.证明:AB(25分) 【解析】 以正五边形一条边上的中点为原点,此边所在的直线为x 轴,建立如图所示的平面直角坐标系.⑴当,A B 中有一点位于P 点时,知另一点位于1R 或者2R 时有最大值为1PR ;当有一点位于O 点时,1max AB OP PR =<;⑵当,A B 均不在y 轴上时,知,A B 必在y 轴的异侧方可能取到最大值(否则取A 点关于y 轴的对称点A ',有AB A B '<).不妨设A 位于线段2OR 上(由正五边形的中心对称性,知这样的假设是合理的),则使AB 最大的B 点必位于线段PQ 上.且当B 从P 向Q 移动时,AB 先减小后增大,于是max AB AP AQ =或;对于线段PQ 上任意一点B ,都有2BR BA ≥.于是22max AB R P R Q == 由⑴,⑵知2max AB R P =.不妨设为x .下面研究正五边形对角线的长.IHG F E 1111x x-1如右图.做EFG ∠的角平分线FH 交EG 于H . 易知5EFH HFG GFI IGF FGH π∠=∠=∠=∠=∠=. 于是四边形HGIF 为平行四边形.∴1HG =. 由角平分线定理知111EFEH x FG x HG ===-.解得x =3.AB 为21y x =-上在y 轴两侧的点,求过AB 的切线与x 轴围成面积的最小值.(25分)【解析】 不妨设过A 点的切线交x 轴于点C ,过B 点的切线交x 轴于点D ,直线AC 与直线BD 相交于点E .如图.设1122(,),(,)B x y A x y ,且有222211121,1,0y x y x x x =-=->>.由于2y x '=-,于是AC 的方程为2222x x y y =--;① BD 的方程为1122x x y y =--. ②联立,AC BD 的方程,解得121221(,1)2()y y E x x x x ---. 对于①,令0y =,得222(,0)2y C x -;对于②,令0y =,得112(,0)2y D x -. 于是221212121222112222y y x x CD x x x x --++=-=-. 121(1)2ECD S CD x x ∆=-.不妨设10x a =>,20x b -=>,则 2222111111()(1)(22)44ECD a b S ab a b a b ab a b a b∆++=++=+++++1111()(2)(2)44a b ab ab ab ab=+++⋅++≥ ③0s >,则有331111111(2)(.....)223399ECD S s s s s s s s s ∆=++=++++++ 6个 9个1243691616111116)]8()29s s s ⋅⋅[⋅(⋅()=⋅≥3218)3=⋅(= ④又由当12x a x b s ==-==时,③,④处的等号均可取到.∴min ()ECD S ∆ 注记:不妨设311()(2)2g s s s s=++,事实上,其最小值也可用导函数的方法求解. 由2211()(32)2g s s s '=+-知当2103s <<时()0g s '<;当213s <时()0g s '>.则()g s 在(0,上单调减,在)+∞上单调增.于是当s =时()g s 取得最小值. 4.向量OA 与OB 已知夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ在0t 时取得最小值,问当0105t <<时,夹角的取值范围.(25分) 【解析】 不妨设OA ,OB 夹角为α,则1,2OP t OQ t =-=,令 222()(1)42(1)2cos g t PQ t t t t α==-+-⋅-⋅2(54cos )(24cos )1t t αα=++--+. 其对称轴为12cos 54cos t αα+=+.而12()54x f x x +=+在5(,)4-+∞上单调增,故12cos 1154cos 3αα+-+≤≤. 当12cos 1054cos 3αα++≤≤时,012cos 1(0,)54cos 5t αα+=∈+,解得223αππ<<. 当12cos 1054cos αα+-<+≤时,()g t 在[0,1]上单调增,于是00t =.不合题意. 于是夹角的范围为2[,]23ππ.5.(仅理科做)存不存在02x π<<,使得sin ,cos ,tan ,cot x x x x 为等差数列.(25分) 【解析】 不存在;否则有(cos sin )(cos sin )cos sin cot tan sin cos x x x x x x x x x x-+-=-=, 则cos sin 0x x -=或者cos sin 1sin cos x x x x+=.若cos sin 0x x -=,有4x π=.而此时1,122不成等差数列;若cos sin 1sin cos x x x x+=,有2(sin cos )12sin cos x x x x =+.解得有sin cos 1x x =. 而11sin cos sin 2(0,]22x x x =∈,矛盾!2011年“北约”自主招生数学试题及解答2012年“北约”自主招生数学试题及解答《自主招生》三大系列《全国重点高校自主招生备考指南·高一、高二基础版》从从高高一一开开始始行行动动起起来来!!⊙专为高一、高二学生设计,细致分析自主招生关键信息,深入讲解自主招生备考方略。
北约自主招生数学题及解答

北约自主招生数学题及解答∎1、已知平行四边形的其中两条边长分别是3和5,一条对角线长是6,求另一条对角线的长。
解:由对角线的平方和等于四边的平方和:所以36+x 2=2(9+25),x 2=32,∴x=4√2。
∎2求过抛物线y =2x 2−2x −1,y =−5x 2+2x +3交点的直线方程。
解:{y =2x 2−2x −1y =−5x 2+2x +3,{5y =10x 2−10x −52y =−10x 2+4x +6,7y=−6x+1,∴6x+7y −1=0为所求。
∎3、等差数列a 1,a 2,⋯满足a 3=−13,a 7=3,这个数列的前n 项和为S n ,数列S 1,S 2,⋯中哪一项最小,并求出这个最小值。
解:d=a 7−a 37−3=164=4,∴a 1=−21,S n =2n 2−23n ,当n=234,即n=6时S n 最小,最小为−66。
∎4、∆ABC 的三边a,b,c 满足a+b ≥2c ,A,B,C 为∆ABC 的内角,求证:C ≤60°。
解:ab ≤(a+b 2)2,cosC=a 2+b 2−c 22ab=(a+b)2−2ab−c 22ab≥(a+b)2−c 2(a+b)22−1=1−2c 2(a+b)2≥1−2c 24c 2=12,所以C ≤60°。
∎ 5、是否存有四个正实数,它们的两两乘积分别是2,3,5,6,10,16?解:设存有四个正实数分别为a<b<c<d ,依题意:ab=2,ac=3,ad=5,bc=6,bd=10,cd=16,∴a 2bc =6,∴a =1,b=2,c=3,d=5,而cd=15≠16,故不存有。
或解:∵abcd=32,而(abcd)3=1800×16,不满足,故不存有。
∎6、C 1和C 2是平面上两个不重合的固定圆,C 是该平面上的一个动圆,C 和C 1,C 2都相切,则C 的圆心的轨迹是何种曲线?说明理由。
北约自主招生考数学试卷分析

10.(2013年5题)
S n1 4a n 2 设数列 a 满足 a1 1, 前 n 项和为 S n , 求 a 2013 .
n
点评:数列综合题,是高等数学极限与级数理论 的基础。
11.(2013年6题)
模长为1的复数 x, y, z 满足 x y z 0 , 求
xy yz zx x yz .
2013 复数 数论 2014 三角函数 数论
三角函数 不等式 数列 不等式
从上面可以看出来,“北约”近两年的自主招 生的考点的大方向是不变的。基本上就是三角函 数、不等式、数列、排列组合、几何等几大模块。 而且2014年的北约考试基本上可以看做是2013年 的北约考试的“平行削弱版”,甚至可能相较于 某些省份的高考题并没有难太多。
2.(2014年第2题)
10个人分成3组,一组4人,另外两组各3人, 求共有几种分法。
点评:排列组合基础题型,分组问题,比去年难度小。
3.(2013年第2题)
在6×6的棋盘中停放着3个红色車和3个黑色車,每一 行、 每一列都只有一个車,共有多少种停放方法? 点评:排列组合近两年都考,它是数理统计的必备 知识。
i 1 n
, 求证:
n i 12 xi 源自 2 1 .
n
点评:不等式是高考也是自主招生考试的重 点,对学生逻辑推理的能力要求高。
6.(2012年第9题,最后一题)
求证:对于任意的正整数n , (1 2 ) n 必可表示 成 s s 1 的形式,其中 s N . 点评:本题运算量不大,但有较高的思维要求。
7.(2011年第7题,最后一题)
求: f ( x) | x 1 | | 2 x 1 | | 2011 x 1 | 的最小值. 点评:含绝对值的函数或不等式历来是高考、 竞赛和自主招生考式的重点内容。
2011年---2013“北约”、“华约”自主招生数学试题

2011年“北约”13校联考自主招生数学试题2012年北约自主招生数学试题1、求x 的取值范围使得12)(-+++=x x x x f 是增函数;2、求1210272611=+-+++-+x x x x 的实数根的个数;3、已知0)2)(2(22=+-+-n x x m x x 的4个根组成首项为41的等差数列,求n m -;4、如果锐角ABC ∆的外接圆的圆心为O ,求O 到三角形三边的距离之比;5、已知点)0,2(),0,2(B A -,若点C 是圆0222=+-y x x 上的动点,求ABC ∆面积的最小值。
6、在2012,,2,1Λ中取一组数,使得任意两数之和不能被其差整除,最多能取多少个数?7、求使得a x x x x =-3sin sin 2sin 4sin 在),0[π有唯一解的a ; 8、求证:若圆内接五边形的每个角都相等,则它为正五边形;9、求证:对于任意的正整数n ,n )21(+必可表示成1-+s s 的形式,其中+∈N s2012年自主招生北约联考数学试题解答2013年北约自主招生数学试题解析12312为两根的有理系数多项式的次数最小是多少?解析:显然,多项式23()(2)(1)2f x x x ⎡⎤=---⎣⎦2和312-于是知,2和312为两根的有理系数多项式的次数的最小可能值不大于5. 若存在一个次数不超过4的有理系数多项式432()g x ax bx cx dx e =++++,其两根分别为和1,,,,a b c d e不全为0,则:420(42)(2020a c eg a c e b db d++=⎧=++++=⇒⎨+=⎩(1(7)(232(630g a b c d e a b c d a b c=-+----+++++702320a b c d ea b c d+---=⎧⇒⎨+++=⎩即方程组:420(1)20(2)70(3)2320(4)630(5)a c eb da b c d ea b c da b c++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩,有非0有理数解.由(1)+(3)得:110a b c d++-=(6)由(6)+(2)得:1130a b c++=(7)由(6)+(4)得:13430a b c++=(8)由(7)-(5)得:0a=,代入(7)、(8)得:0b c==,代入(1)、(2)知:0d e==.于是知0a b c d e=====,与,,,,a b c d e不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x和1-和1为两根的有理系数多项式的次数最小为5.2.在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车占一格,共有几种停放方法?解析:先从6行中选取3行停放红色车,有36C种选择.最上面一行的红色车位置有6种选择;最上面一行的红色车位置选定后,中间一行的红色车位置有5种选择;上面两行的红色车位置选定后,最下面一行的红色车位置有4种选择。
2008-2011北京大学(北约)自主招生数学试题(全附答案)
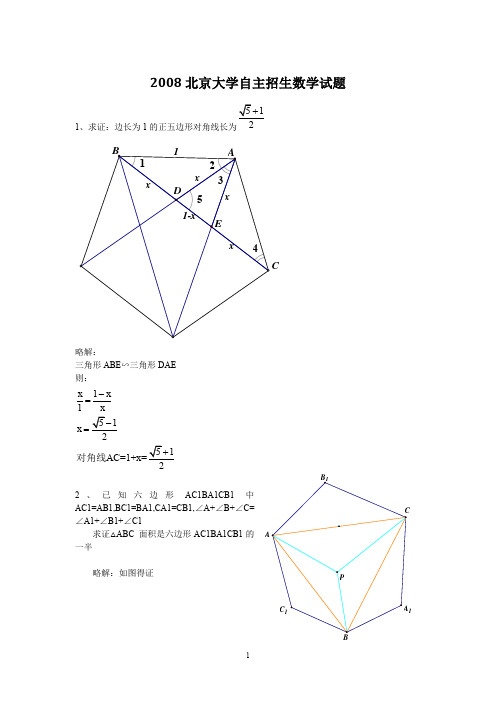
5
答案: 1、 不妨设角 ADC 为 a,那么角 ABC=π-a。 由余弦定理可得 AC=根号(9+16-24cosa)=根号(1+4+4cosa) 从而可解出 cosa=5/7.即有 sina=2(根号 6)/7. 代入 cosa=5/7,可得 AC=根号(55/7). 所以圆的半径就是 AC/2sina. 2、设 13=a1+md,25=a1+nd,41=a1+kd. 那么我们可得 a1+(m+499(k+m-2n))d=2009. 而实际上这道题是有漏洞的,因为 (m+499(k+m-2n))可能是负的,也就是当这是递减的等差数列的时候,那么 2009 就不在这个 数列中了。 3、 挺简单,设 a=tanx+(根 3),b=cotx+(根号 3),假设均为有理数。 那么由(a-(根号 3) ) (b-(根号 3) )=1 可得(a+b)根号 3=ab+2.若 a+b 非零,除过来就矛盾了。 所以必有 a+b=0,此时 ab+2 也是 0. 显然与 a,b 是有理数矛盾。 4、b=0 的时候可知得有|a|≤1.,此时 a+b≤1.下面考虑 b 不等于 0 的情况。 代入+1 和-1 后得出的式子可以化成|a|≤b+1.....(1)(必有 b≥-1) 对称轴的位置是 x=-a/4b.当对称轴在[-1,1]外的时候 那么 1≤|-a/4b|≤(b+1)/4|b|. 分类讨论后就可以得出 b≤1/3.此时 a+b≤b+1+b≤5/3. 若对称轴在[-1,1]内,则可得 a^2≤8(b-b^2)......(2) 这里注意到(b+1)^2-8(b-b^2)=(3b-1)^2≥0.故只需要(2)式成立,就必有 (1)式也成立。此时用柯西不等式 (a+b-1/2)^2≤(a^2+8(b-1/2)^2)(1+1/8)≤9/4 那么就有了 a+b≤2.等号成立的充要条件是 a=4/3,b=2/3,易验证这是成立的. 比较三种情况,显然 2 是 a+b 的最大值, 5、设优秀有 a 人,及格 b 人,不及格 c 人。 则 a+b+c=333 ① 6a+4b+0c≤1000(这里都取各层次里的最少人,故用小于等于) 即 6a+4b≤1000 即 3a+2b≤500 由①得 2a+2b=666-2c 即 a+666-2c≤500 即 a+166≤2c 若 a≥167 则这 167 人至少共解出 167*6=1002 道题,矛盾 故 a≤166 故 a+166≤166+166≤2c 即 c≥166 所以 c≥166≥a 即不及格得人数大于等于优秀的人数
2010年北京高考数学(理科)试题与答案

2010年普通高等学校招生全国统一考试数 学(理)本试卷分第Ⅰ卷和第Ⅱ卷两部分。
第Ⅰ卷1至2页、第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效,考试结束后,将本试卷和答题卡。
第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1) 集合2{03},{9}P x Z x M x R x =∈≤<=∈≤,则P M I =(A) {1,2} (B) {0,1,2} (C){x|0≤x<3} (D) {x|0≤x ≤3}(2)在等比数列{}n a 中,11a =,公比1q ≠.若12345m a a a a a a =,则m=(A )9 (B )10 (C )11 (D )12(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为(4)8名学生和2位第师站成一排合影,2位老师不相邻的排法种数为(A )8289A A (B )8289A C (C ) 8287A A (D )8287A C(5)极坐标方程(ρ-1)(θπ-)=0(ρ≥0)表示的图形是(A )两个圆 (B )两条直线(C )一个圆和一条射线 (D )一条直线和一条射线(6)若a ,b 是非零向量,“a ⊥b ”是“函数()()()f x xa b xb a =+⋅-为一次函数”的(A )充分而不必要条件 (B )必要不充分条件(C )充分必要条件 (D )既不充分也不必要条件(7)设不等式组 110330530x y x y x y 9+-≥⎧⎪-+≥⎨⎪-+≤⎩表示的平面区域为D ,若指数函数y=x a 的图像上存在区域D 上的点,则a 的取值范围是(A )(1,3] (B )[2,3] (C ) (1,2] (D )[ 3, +∞](8)如图,正方体ABCD-1111A B C D 的棱长为2,动点E 、F 在棱11A B 上,动点P ,Q 分别在棱AD ,CD 上,若EF=1,1A E=x ,DQ=y ,D P=z(x,y,z大于零),则四面体PE FQ的体积 (A)与x,y,z都有关(B)与x有关,与y,z无关(C)与y有关,与x,z无关(D)与z有关,与x,y无关第II 卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
[高考]2009、2010清华北大自主招生试题
![[高考]2009、2010清华北大自主招生试题](https://img.taocdn.com/s3/m/bb933beeba4cf7ec4afe04a1b0717fd5360cb29a.png)
2009北京大学自主招生语数外物化试题(理科)时间:2009-11-06 作者:来源:网络资源一数学1 圆内接四边形ABCD,AB=1,BC=2,CD=3,DA=4。
求圆半径。
2 已知一无穷等差数列中有3项:13,25,41。
求证:2009为数列中一项。
3 是否存在实数x使tanx+(根3)与cotx+(根3)为有理数?4 已知对任意x均有acosx+bcos2x>=-1恒成立,求a+b的最大值5 某次考试共有333名学生做对了1000道题。
做对3道及以下为不及格,6道及以上为优秀。
问不及格和优秀的人数哪个多?二英语1 单选20道,四级难度,20分。
2 阅读两篇,四级难度,10道,40分。
第一篇是关于“ideal body”的,第二篇是关于“materialism”的。
3 英译汉3句,比较简单,20分4 汉译英4句,仍然简单,20分三. 语文1 基础(1)写两个成语,然后曲解,6分。
(2)改病句:1我们都有一个家,名字叫中国。
2素胚勾勒出青花笔锋浓转淡。
6分(3)对联:博雅塔前人博雅(博雅塔为北大一风景),8分2 翻译古文一篇300字左右的文不加点的文言文,要求翻译全文(20分)书杜袭喻繁钦语后[1]·(清)林纾吴人之归,有绮其衣者[2],衣数十袭[3],届时而易之。
而特居于盗乡,盗涎而妇弗觉[4],犹日炫其华绣于丛莽之下[5],盗遂杀而取之。
盗不足论,而吾甚怪此妇知绮其衣,而不知所以置其身。
夫使托身于荐绅之家[6],健者门焉,严扃深居,盗乌得取?唯其濒盗居而复炫其装[7],此其所以死耳。
天下有才之士,不犹吴妇之绮其衣乎?托非其人,则与盗邻,盗贪利而耆杀[8],故炫能于乱邦,匪有全者。
杜袭喻繁钦曰:“子若见能不已[9],非吾徒也。
”钦卒用其言,以免于刘表之祸[10]。
呜呼!袭可谓善藏矣,钦亦可谓善听矣。
不尔,吾未见其不为吴妇也。
3 大阅读,20分阅读理解是一篇选自鲁迅《野草》的文章,要求指出很多意像的象征意义求乞者我顺着剥落的高墙走路,踏着松的灰土。
清北学长精心打造——北约自主招生数学模拟试题及参考答案(四)

绝密★启用前清北学长精心打造——北约自主招生数学模拟试题(四)考试范围:xxx ;考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、考号等信息<br/>2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(5*6=30分)1.已知函数()()432,,,f x x ax bx cx d a b c d =++++为实常数的图象经过三点12,2A ⎛⎫ ⎪⎝⎭,13,3B ⎛⎫ ⎪⎝⎭,14,4C ⎛⎫ ⎪⎝⎭,则()()15f f +的值等于() A .0B .1C .265D .252.已知函数()122,x f x -=-关于x 的方程()()220f x f x k -+=,下列四个命题中是假.命题的是()A .存在实数k ,使得方程恰有2个不同的实根;B .存在实数k ,使得方程恰有4个不同的实根;C .存在实数k ,使得方程恰有6个不同的实根;D .存在实数k ,使得方程恰有8个不同的实根;3.函数f 定义在正整数有序对的集合上,并满足(,),(,)(,),f x x x f x y f y x ==()(,)(,)x y f x y yf x x y+=+,则(14,52)f 的值为( )A .364B .182C .91D .无法计算4.二次函数c bx ax y ++=2的图象的一部分如图,则a 的取 值范围是 ( )A .01<≤-aB .1->aC .01<<-aD .1-≤a5.关于x 、y 的方程20071111=++xy y x 的正整数解(x ,y )的个数为( )A .16B .24C .32D .486.设圆O 1和圆O 2是两个定圆,动圆P 与这两个定圆都相切,则圆P 的圆心轨迹不可能是 ( )第II 卷(非选择题)二、填空题(6*6=36分)7.定义: 区间[](),c d c d <的长度为d c -. 已知函数3log y x =的定义域为[],a b , 值域为[]0,2,则区间[],a b 长度的最大值与最小值的差等于________.8.设na 是(3+x )n的展开式中x 项的系数(n=2, 3, 4,… ), 则当n >100时,223a +333a +…+nn a 3的整数部分的值为.9. 平面上给定ΔA 1A 2A 3及点p 0,定义A s =A s-3,s ≥4,构造点列p 0,p 1,p 2,…,使得p k+1为绕中心A k+1顺时针旋转1200时p k 所到达的位置,k=0,1,2,…,若p 1986=p 0.则ΔA 1A 2A 3为 三角形。
北京大学2010年数学分析试题及解答

|Pn(x) − Pm(x)| < ε.
因为 I 为无穷区间, 因此当 n > m ⩾ Nε 时, |Pn(x) − Pm(x)| 为常数. 设
|PNε (x) − Pn(x)| = cn, n > N,
于是 {cn} 为有界数列, 必有收敛子列 {cnk }∞ k=1, 设
结合 |PNε (x) − Pnk (x)| = cnk , 令 k → ∞ 得
2ε
∫1
3 + |t − t0| η0
∫1
0
xt0+θ(t−t0)(ln x)2
η0
xa(ln x)2 · f (x) dx
· f (x) dx
η0
θ ∈ (0, 1)
因此存在正数 δ <
ε
{∫ 1 , 其中 M = max
3M
η0
xa(ln x)2 · f (x)
} dx, 1 . 当 |t − t0| < δ 时, 就有
ε
{∫ A0 , 其中 M = max
3M
0
xb(ln x)2 · f (x)
} dx, 1 . 当 |t − t0| < δ 时, 就有
|J2(t) − J2(t0)| < ε.
这说明 J2(t) 在 [a, b] 上连续, 由 [a, b] 的任意性知 J2(t) 在 (−1, 1) 上连续. 因此 J(t) = J1(t) + J2(t) 在 (−1, 1) 上连续.
ε <,
∀t ∈ [a, b].
A
3
于是 ∀t, t0 ∈ [a, b]
∫ +∞
∫ +∞
|J2(t) − J2(t0)| =
“北约”“华约”自主招生数学模拟试题带答案.doc

2014年“北约”“华约”自主招生模拟试题数学(满分150分)第一部分:填空题(共5小题 每题10分)1. 若tan 2α=,则224sin 3sin cos 5cos αααα--= 1 .2. 在复数集C 内,方程22(5)60x i x --+=的解为 .3. 设8219)22015()22015(+++=x ,求数x 的个位数字.4. 设{|100600,}A n n n N =≤≤∈,则集合A 中被7除余2且不能被57整除的数的个数为______70_______.5. 设P 是抛物线2440y y x --=上的动点,点A 的坐标为(0,1)-,点M 在直线PA 上, 且分PA 所成的比为2:1,则点M 的轨迹方程是 9y ²-12x-4=0 . 第二部分:解答题(共5小题 每题20分)1设集合()12log 32A x x ⎧⎫⎪⎪=-≥-⎨⎬⎪⎪⎩⎭,21a B x x a ⎧⎫=>⎨⎬-⎩⎭.若A B ≠∅,求实数a 的取值范围-1≤a <0或0<a ≤32. 为了搞好学校的工作,全校各班级一共提了P )(+∈N P 条建议.已知有些班级提出了相同的建议,且任何两个班级都至少有一条建议相同,但没有两个班提出全部相同的建议.求证该校的班级数不多于12-P 个3. 设平面向量(3,1)a =-,13(,2b =.若存在实数(0)m m ≠和角((,))22ππθθ∈-, 使向量2(tan 3)c a b =+-,tan d ma b θ=-+,且c d ⊥.(I)求函数()m f θ=的关系式; (II)令tan t θ=,求函数()m g t =的极值.4. 已知双曲线的两个焦点分别为1F ,2F ,其中1F 又是抛物线24y x =的焦点,点A (1,2)-, B (3,2)在双曲线上.(I)求点2F 的轨迹方程; (II)是否存在直线y x m =+与点2F 的轨迹有且只 有两个公共点?若存在,求实数m 的值,若不存在,请说明理由.5. 已知a ,b 均为正整数,且,sin )(),20(2sin ,2222θπθθn b a A b a ab b a n n ⋅+=<<+=>其中求证:对一切*N ∈n ,n A 均为整数参考答案一、 选择题1. 由tan 2α=,得sin 2cos αα=,有22sin 4cos αα=,即221cos 4cos αα-=. 则21cos 5α=,原式=222216cos 6cos 5cos 5cos 1αααα--==. 2. 设x a bi =+,,a b R ∈,代入原方程整理得22(2256)(45)0a b a b ab a b i --+-++-=有2222560450a b a b ab a b ⎧--+-=⎨+-=⎩,解得11a b =⎧⎨=⎩或3232a b ⎧=⎪⎪⎨⎪=-⎪⎩,所以1x i =+或3322x i =-. 3. 直接求x 的个位数字很困难,需将与x 相关数联系,转化成研究其相关数. 【解】令])22015()22015[(,)22015()22015(82198219+++=+-+-=y x y 则 ])22015()22015[(8219-+-+,由二项式定理知,对任意正整数n.)2201515(2)22015()22015(22 +⋅⋅+=-++-n n n n n C 为整数,且个位数字为零.因此,x y +是个位数字为零的整数.再对y 估值, 因为2.0255220155220150=<+=-<, 且1988)22015()22015(-<-, 所以.4.02.02)22015(201919<⨯<-<<y 故x 的个位数字为9.【评述】转化的思想很重要,当研究的问题遇到困难时,将其转化为可研究的问题.4. 解:被7除余2的数可写为72k +. 由100≤72k +≤600.知14≤k ≤85.又若某个k 使72k +能被57整除,则可设72k +=57n . 即5722877n n k n --==+. 即2n -应为7的倍数. 设72n m =+代入,得5716k m =+. ∴14571685m ≤+≤. ∴m =0,1.于是所求的个数为70.5. 设点P 00(,)x y ,M (,)x y ,有0203x x +⨯=,02(1)3y y +⨯-=,得03x x =,032y y =+ 而2000440y y x --=,于是得点M 的轨迹方程是291240y x --=.二、 解答题1. 解:{}13A x x =-≤<,()(){}30B x x a x a =--<. 当0a >时,{}03B x a x a =<<<,由AB ≠∅得03a <<; 当0a <时,{}30B x a x a =<<<,由A B ≠∅得1a >-; 当0a =时,{}20B x x =<=∅,与AB ≠∅不符. 综上所述,()()1,00,3a ∈-2. 证明:假设该校共有m 个班级,他们的建议分别组成集合m A A A ,,,21 。
北京大学(北约)2010~2014自主招生试题及答案(全)

2014年北京大学自主招生数学试题1. 圆心角为3π的扇形面积为6π,求它围成圆锥的表面积. 2. 将10个人分成3组,一组4人,两组每组3人,共有几种分法. 3. 2()2()(),(1)1,(4)733a b f a f b f f f ++===,求()2014f . 4.2()lg(2)f x x ax a =-+的值域为R ,求a 的取值范围.5. 已知1x y +=-,且,x y 都为负实数,求1xy xy+的取值范围. 6. 22()arctan14x f x C x +=+-在11,44⎛⎫- ⎪⎝⎭上为奇函数,求C 的值. 一、求证:tan3Q ∉二、已知实系数二次函数()f x 与()g x ,()()f x g x =和()()30f x g x +=有两重根,()f x 有两相异实根,求证:()g x 没有实根.三、1213,a a a 是等差数列,{}113i j k M a a a i j k =++≤<<≤,问:7160,,23是否同在M 中,并证明你的结论.四、()01,2,,i x i n >=,且11n i i x ==∏,求证1)1)nn i i x =≥∏.答案1.π7; 2.2100; 3.4027)2024(12)(=⇒-=f x x f ; 4.1 00≥≤⇒≥∆a or a ;5.⎪⎭⎫⎢⎣⎡+∞,417;6.2arctan 0)0(-=⇒=C f 一、求证:Q ∉︒3tan解:若Q aab Q a ∈-=︒=⇒∈=︒2126tan 3tan ,Q ab b a c ∈-+=︒=⇒19tan Q bc cb d ∈-+=︒=⇒115tan 52518tan 41518sin 2-=︒⇒-=︒ 于是Q d d ∈-=⇒=-=︒233215tan ,从而矛盾。
二.实系数二次函数)(),(x g x f ,)()(x g x f =和0)()(3=+x g x f 有两重根,)(x f 有两相异根,求证:)(x g 无实数根。
北约自主招生能力测试数学试题(含参考答案

综合性大学自主选拔录取联合考试自然科学基础——理科试卷数学部分(北约)一、选择题(每小题8分,合计48分)1.圆心角为3π的扇形的面积为6π,则它围成的圆锥的表面积为( B ).A .B .7πC .D .解:由2166S R ππ==扇形得6R =,由263r ππ=⨯得1r =,故它围成的圆锥的表面积为267r πππ+=.2.将10个人分为3组,一组4人,另两组各3人,共有( C )种分法.A .1070B .2014C .2100D .4200解:433106321002C C C N ==. 3.已知2()2()()33a b f a f b f ++=,(1)1f =,(4)7f =,则(2014)f =( A ). A .4027 B .4028 C .4029 D .4030 解:421(4)2(1)(2)()333f f f f +⨯+===,124(1)2(4)(3)()533f f f f +⨯+===,猜想*()21()f n n n N =-∈,假设()21f n n =-对3(1)n k k ≤≥都成立,则(31)3(1)2(1)2(31)1f k f k f k +=+-=+-,(32)3(2)2(2)2(32)1f k f k f k +=+-=+-,(33)3(3)2(3)2(33)1f k f k f k +=+-=+-,所以*()21()f n n n N =-∈.4.若2()lg(2)f x x ax a =-+的值域为R ,则a 的取值范围是( D ).A .01a ≤≤B .C .D .0a ≤或1a ≥解:由题知,{}2(0,)2y y x ax a +∞⊆=-+,故2(2)40a a ∆=--≥,解得:0a ≤或1a ≥.5.已知1x y +=-,且x 、y 均为负实数,则1xy xy+有( B ). A .最大值174 B .最小值174 C .最大值174- D .最小值174-解:1()()x y =-+-≥104xy <≤,而函数1()f t t t=+在(0,1)上单调递减,在(1,)+∞单调递增,故1()()4f xy f ≥,即1174xy xy +≥,当且仅当12x y ==-时取等号. 6.已知22()arctan14x f x C x +=+-在(,)44ππ-上为奇函数,则C =( B ). A .0 B .arctan 2- C .arctan 2 D .不存有解:由()0f x =得arctan(2)arctan 2C =-=-,此时()()f x f x +-22arctan14x x +=-22arctan 214x C x -+++4arctan()2arctan 203=--=,故arctan 2C =-符合题意.二、解答题(每题18分,共72分)7.证明:0tan3R ∉.证明:设0tan 3Q ∈,则0tan 6tan12tan 24tan 30tan(624)Q Q Q Q ∈⇔∈⇔∈⇔=+∈,这与0tan 303Q =矛盾. 8.已知实系数二次函数()f x 和()g x ,若方程()()f x g x =和3()()0f x g x +=都只有一个偶重根,方程()0f x =有两个不等的实根,求证:方程()0g x =没有实根. 解:设2()f x ax bx c =++,2()g x dx ex f =++,0ad ≠,所以2()4()()b e a d c f -=--,2(3)4(3)(3)b e a d c f +=++,所以223124b e ac df +=+,又240b ac ->,所以22()44(4)0g x e df b ac ∆=-=--<,所以方程()0g x =没有实根.9.已知1a ,2a ,…,13a 成等差数列,{}113i j k M a a a i j k =++≤<<≤,问:0,72,163是否能够同时在M 中?并证明你的结论.解:设该数列的公差为d ,∴p ∃,q ,*r N ∈,130a pd +=,173()2a p q d ++=,1163()3a p q r d +++=,∴2111q r =,∴21q ≥,11p ≥,又0123p ≥++=,∴35p q r ++≥, 又12111033p q r ++≤++=,与上式矛盾,故0,72,163不能够同时在M 中.10.i x (1i =,2,…,n )为正实数,且11nii x==∏,求证:1)1)nn i i x =≥∏.解:由AM GM -不等式得:11(n i n =≥,11(ni n =≥两式相加得:1≥,故1)1)nn i i x =≥∏.。
2008-2011北京大学(北约)自主招生数学试题(全附答案)

形
=
舞ACBABA慧CB麓AC =/缓二C
。,
。/
l/
Dk
:::.?日 \、E。.・。
\I,・’
,‘1
.。.
BA 。,
。
口2丁,62丁,
.al一口2
bI—b2
B A +£ A B C +£C .,二 C
即证{一(口I+口2+bI+62)一(口l+d2+口,+
a 口l a 口2
2丁+口,
2丁一口'
【百189】+1=13分,而北方最高分的最大值为6+n
万方数据
14
中’?善i:.7(200s年第2期・高中版)
南方球队内部比赛总得分CⅢ2
,12
・解题研究・
=136,
一l=11分<13分,
.・.
冠军在南方队
北方球队内部比赛总得分c2=28,
北方胜南方得分=30—28=2, 北方球队最高得分=7+2=9, 因为9×17=153<270, 所以南方球队中至少有一支得分超过9分. 冠军在南方球队中.综上所述,冠军是一支南方 球队. 点评这道试题要注意突破口的选择,也需要 耐心和比较强的推理、分析能力. 5.(理科)0一xyz坐标系内xoy平面系内0≤,,≤ 2一石2绕),轴旋转一周构成一个不透光立体在点 (1,0,1)设置一光源,在xoy平面内有一以原点为圆 心的圆c被光照到的长度为2霄,求曲线C上未被照 到的长度.
c:+。+n(肛+9)≥召,c:≤A,
即3n2—22n一36。<0.
‘.・
’B=9A,
.・.c:+9+n(,l+9)≥B=9A1>9c:,
(1)
,’2
又总分为乞Ⅲ有10I乞小钴厶(1)得厅=6或8.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、解答题 1.(文)02
απ
<<
,求证:sin tan ααα<< 2.AB 为边长为1的正五边形边上的点.证明:AB
3. AB 为21y x =-上在y 轴两侧的点,求过AB 的切线与x 轴围成面积的最小值
4. 已知OA 与OB 夹角,1OA =,2OB =,(1)OP t OA =-,OQ tOB =,01t ≤≤.PQ 在0t 时取得最小值,问当01
05
t <<时,夹角的取值范围 5.(理)存不存在02
x π
<<,使得sin ,cos ,tan ,cot x x x x 为等差数列. ##Answer##
1.【简解】不妨设()sin f x x x =-,则(0)0f =,且当02
x π
<<时,()1cos 0f x x '=->.于是()f x 在02
x π
<<
上单调增.∴()(0)0f x f >=.即有sin x x >. 同理可证()tan 0g x x x =->. (0)0g =,当02x π<<
时,21()10cos g x x '=->.于是()g x 在02
x π<<
上单调增。
∴在02
x π
<<
上有()(0)0g x g >=。
即tan x x >。
2.【解析】以正五边形一条边上的中点为原点,此边所在的直线为x 轴,建立如图所示的平面直角坐标系.
⑴当,A B 中有一点位于P 点时,知另一点位于1R 或者2R 时有最大值为1PR ;当有一点位于O 点时,1max AB OP PR =<;
⑵当,A B 均不在y 轴上时,知,A B 必在y 轴的异侧方可能取到最大值(否则取A 点关于y 轴的对称点A ',有AB A B '<).
不妨设A 位于线段2OR 上(由正五边形的中心对称性,知这样的假设是合理的),则使AB 最大的B 点必位于线段PQ 上.
且当B 从P 向Q 移动时,AB 先减小后增大,于是max AB AP AQ =或; 对于线段PQ 上任意一点B ,都有2BR BA ≥.于是22max AB R P R Q == 由⑴,⑵知2max AB R P =.不妨设为x .
下面研究正五边形对角线的长.如图.做EFG ∠的角平分线FH 交EG 于H .
I H G
F
E 11
1
1x x-1
易知5
EFH HFG GFI IGF FGH π
∠=∠=∠=∠=∠=. 于是四边形HGIF 为平行四边形.∴1HG =.
由角平分线定理知111EF EH x FG
x HG =
==-
.解得x =3.【解析】不妨设过A 点的切线交x 轴于点C ,过B 点的切线交x 轴于点D ,直线AC 与直线BD 相交于点E .如图.设1122(,),(,)B x y A x y ,且有222211121,1,0y x y x x x =-=->>. 由于2y x '=-,于是AC 的方程为2222x x y y =--;①
BD 的方程为1122x x y y =--. ②
联立,AC BD 的方程,解得121221(,1)2()y y E x x x x ---.对于①,令0y =,得2
2
2(,0)2y C x -;
对于②,令0y =,得1
1
2(,0)2y D x -.于是221212121222112222y y x x CD x x x x --++=
-=-. 121
(1)2
ECD S CD x x ∆=-.不妨设10x a =>,20x b -=>,则
2222111111
()(1)(22)44ECD a b S ab a b a b ab a b a b
∆++=++=+++++
1111
()(2)(2)44a b ab ab ab ab
=+++⋅++≥ ③
0s >,则有336
9
1111111(2)(.....)223399ECD S s s s s s s s s
∆=++=++++++
124
3
691616111116)]8()2
9
s s s ⋅
⋅[⋅(⋅()=⋅≥3218)3=⋅( ④
又由当12x a x b s ==-=时,③,④处的等号均可取到. ∴min ()ECD S ∆=
4.【简解】不妨设OA ,OB 夹角为α,则1,2OP t OQ t =-=,令
2
22()(1)42(1)2cos g t PQ t t t t α==-+-⋅-⋅2(54cos )(24cos )1t t αα=++--+.
其对称轴为12cos 54cos t αα+=+.而12()54x f x x +=+在5(,)4-+∞上单调增,故12cos 1
154cos 3
αα+-+≤≤.
当12cos 1054cos 3αα++≤≤时,012cos 1(0,)54cos 5t αα+=∈+,解得223αππ<<
. 当12cos 1054cos α
α
+-<+≤
时,()g t 在[0,1]上单调增,于是00t =.不合题意.
于是夹角的范围为2[,]23
ππ
.
5.【简解】不存在;否则有(cos sin )(cos sin )
cos sin cot tan sin cos x x x x x x x x x x
-+
-=-=,
则cos sin 0x x -=或者cos sin 1sin cos x x
x x
+=
.
若cos sin 0x x -=,有4
x π
=
.而此时1,122不成等差数列;
若cos sin 1sin cos x x x x
+=,有2(sin cos )12sin cos x x x x =+.解得有sin cos 1x x =
而11
sin cos sin 2(0,]22
x x x =∈,矛盾!。
