5.1.1相交线同步练习题
(整理)新人教版初中数学七年级下册单元同步练习试题全册

5.1.1-2相交线、垂线检测题一、填空1.如图,直线AB,CD 相交于O,OE 平分∠AOD,FO ⊥OD 于O,∠1=40°,则∠2=•___ __,∠4=______.421D CAB (5)OFE D C A B NM(6)O FE(第1题图) (第2题图)2.如图,AB ⊥CD 于O,EF 为过点O 的直线,MN 平分∠AOC,若∠EON=100•°,•那么 ∠EOB=________,∠BOM=________.3.如图,AB 是一直线,OM 为∠AOC 的角平分线,ON 为∠BOC 的角平分线,则OM,ON 的位置关系是_______.4.直线外一点与直线上各点连结的线段中,以_________为最短.5.从直线外一点到这条直线的________叫做这点到直线的距离.C AB NM(7)DCA B(8)O(第3题图) (第7题图) (第8题图)6.经过直线外或直线上一点,有且只有______直线与已知直线垂直.7.如图,要证BO ⊥OD,请完善证明过程,并在括号内填上相应依据:∵AO ⊥CO,∴∠AOC=__________(___________).又∵∠COD=40°(已知),∴∠AOD=_______.•∵∠BOC=∠AOD=50°(已知),∴∠BOD=_______, ∴_______⊥_______(__________).8. 如图,点B 到AC 的距离是线段_________的长度,_________是线段BC 到A 的距离二、选择9.下列语句正确的是( )A.相等的角为对顶角B.不相等的角一定不是对顶角C.不是对顶角的角都不相等D.有公共顶点且和为180°的两个角为邻补角10.两条相交直线与另外一条直线在同一平面内,它们的交点个数是( ) A.1 B.2 C.3或2 D.1或2或311.如图10,PO ⊥OR,OQ ⊥PR,能表示点到直线(或线段)的距离的线段有( ) A.1条 B.2条 C.3条 D.5条(10)PQDCAB(11)O D C AB(12)FE (第11题图) (第12题图) (第14题图)12.如图,OA ⊥OB,OC ⊥OD,则( )A.∠AOC=∠AODB.∠AOD=∠DOBC.∠AOC=∠BODD.以上结论都不对 13.下列说法正确的是( )A.在同一平面内,过已知直线外一点作这条直线的垂线有且只有一条B.连结直线外一点和直线上任一点,使这条线段垂直于已知直线C.作出点P 到直线的距离D.连结直线外一点和直线上任一点的线段长是点到直线的距离 14.如图,与∠C 是同旁内角的有( ). A.2 B.3 C.4 D.5 15.下列说法正确的是( ).A.两条直线相交成四个角,如果有三个角相等,那么这两条直线垂直.B.两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直.C.两条直线相交成四个角,如果有一对对顶角互余,那么这两条直线垂直.D.两条直线相交成四个角,如果有两个角互补,那么这两条直线垂直. 16.如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是( )A. 12(∠1+∠2)B. 12∠1C. 12(∠1-∠2)D.12∠2三、作图题17、如图,按要求作出:(1)AE ⊥BC 于E; (2)AF ⊥CD 于F;(3)连结BD,作AG ⊥BD 于G.18、如下左图,一辆汽车在直线形的公路AB 上由A 向B 行驶,M 、N 分别是位于公路AB 两侧的村庄,(1)现在公路AB 上修建一个超市C ,使得到M 、N 两村庄距离最短,请在图中画出点C (2)设汽车行驶到点P 位置时离村庄M 最近;行驶到点Q 位置时,距离村庄N 最近,请在图中公路AB 上分别画出P 、Q 两点的位置。
人教版七年级数学下册 5.1.1相交线 同步练习题含答案

相交线一、单选题1.如图,对于直线A B,线段C D,射线E F,其中能相交的图是()A.B.C.D.2.如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是()A.25°B.35°C.45°D.55°3.如图,点O在直线A B上,射线O C平分∠D O B.若∠COB=35°,则∠A O D等于( ).A.35°B.70°C.110°D.145°4.如图,∠1=100°,∠2=145°,那么∠3=().A.55°B.65°C.75°D.85°5.如图,直线A B、C D相交于点O,且∠AOD+∠BOC=100°,则∠A O C是( )A.150°B.130°C.100°D.90°6.如图,直线AB,CD 交于O,EO⊥AB于O,∠1与∠3的关系是()A.互余B.对顶角C.互补D.相等7.如图所示,∠1和∠2是对顶角的是()A.B.C.D.8.下面四个图形中,∠1与∠2是邻补角的是( )A.B.C.D.9.如图,下列各组角中,互为对顶角的是()A.∠1和∠2B.∠1和∠3C.∠2和∠4D.∠2和∠5 10.10.如图所示,下列判断正确的是( )A.图⑴中∠1和∠2是一组对顶角B.图⑵中∠1和∠2是一组对顶角C.图⑶中∠1和∠2是一对邻补角D.图⑷中∠1和∠2互为邻补角二、填空题11.如图所示,AB∥CD,EF 与AB,CD 相交,EF 与AB 交于点,EF 与CD 交于.12.两条直线相交,只有个交点.13.平面内四条直线共有三个交点,则这四条直线中最多有条平行线.14.探究题:(1)三条直线相交,最少有个交点,最多有个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有个交点,最多有个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有个交点,最多有个交点,对顶角有对,邻补角有对.三、解答题15.平面上两条直线相交于一点,三条直线俩两相交,每个交点都不经过第三条直线.(1)5 条直线的交点为个.(2)请探索n条直线的交点个数.16.如图所示,已知直线 AB 和CD 相交于点 O,OM 平分∠BOD,∠MON=90°,∠AOC=50°.(1)求∠AON的度数.(2)写出∠DON的余角.17.如图,直线A B与C D相交于点O,∠A O C∶∠A O D=1∶2.求∠B O D的度数.18. 如图,三条直线 A B ,C D ,E F 交于一点,若∠1=30°,∠2=70°,求∠3 的度数.答案1.B2.D3.C4.B5.B6.A7.C8.D9.A10.D11.MN 12. 1.13.三14.(1)1,3;(2)1,6;(3)1,n (n 1) 2,n(n-1),2n(n-1)15.(1)如图所示:我们发现:2 条直线相交有 1 个交点;3 条直线相交有 1+2=3 个交点;4 条直线相交有 1+2+3=6 个交点,则 5 条直线的交点为 1+2+3+4=10;n(n 1)(2)图(n):1+2+3+…+n-1=.216.(1)∵∠AOC+∠AOD=∠AOD+∠BOD=180°,∴∠BOD=∠AOC=50°,∵OM 平分∠BOD,∴∠BOM=∠DOM=25°,又由∠MON=90°,∴∠AON=180°﹣(∠MON+∠BOM)=180°﹣(90°+25°)=65°;(2)由∠DON+∠DOM=∠MON=90°知∠DOM 为∠DON 的余角,∵∠AON+∠BOM=90°,∠DOM=∠MOB,∴∠AON+∠DOM=90°,∴∠NO D+∠BOM=90°,故∠DON 的余角为:∠DOM,∠BOM .17.由邻补角的性质,得∠A OC+∠AO D=180°.由∠A O C∶∠A O D=1∶2,得∠A O D=2∠A O C,∠AOC+2∠AOC=180°,解得∠AOC=60°.由对顶角相等,得∠B O D=∠A O C=60°.故答案为:60°.18.解:如图,∵∠4=∠2=70°(对顶角相等),∴∠3=180°-∠1-∠4=180°-30°-70°=80°.。
(精校版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案

(直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(直打版)人教版七年级下册第五章相交线与平行线5.1相交线同步练习题含答案(word版可编辑修改)的全部内容。
初一数学人教版七年级下册第五章 相交线与平行线5.1 相交线同步练习题1. 下列说法中正确的是( )A.不相等的角一定不是对顶角B.互补的两个角是邻补角C.互补且有一条公共边的两个角是邻补角D.两条直线相交所成的角是对顶角2. 下列说法正确的是( )A.在同一平面内,过直线外一点向该直线画垂线,垂足一定在该直线上B.在同一平面内,过线段或射线外一点向该线段或射线画垂线,垂足一定在该线段或射线上C.过线段或射线外一点不一定能画出该线段或射线的垂线D.过直线外一点与直线上一点画的一条直线与该直线垂直3. 已知∠α和∠β的对顶角,若∠α=60°,则∠β的度数为( )A.30° B.60° C.70° D.150°4。
如图,直线AB,CD相交于点O,因为∠1+∠3=180°,∠2+∠3=180°,所以∠1=∠2,其推理依据是( )A.同角的余角相等 B.对顶角相等C.同角的补角相等 D.等角的补角相等5. 如图,OB⊥CD于点O,∠1=∠2,则∠2与∠3的关系是( )A.∠2=∠3 B.∠2与∠3互补C.∠2与∠3互余 D.不能确定6。
新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)

新人教版七年级数学下册全册教案附同步练习及单元测试卷(含答案)第五章相交线与平行线5.1.1相交线教学目标:1.理解对顶角和邻补角的概念,能在图形中辨认.2.掌握对顶角相等的性质和它的推证过程.3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.重点:在较复杂的图形中准确辨认对顶角和邻补角.难点:在较复杂的图形中准确辨认对顶角和邻补角.教学过程一、创设情境,引入课题先请同学观察本章的章前图,然后引导学生观察,并回答问题.学生活动:口答哪些道路是交错的,哪些道路是平行的.教师导入:图中的道路是有宽度的,是有限长的,而且也不是完全直的,当我们把它们看成直线时,这些直线有些是相交线,有些是平行线.相交线、平行线都有许多重要性质,并且在生产和生活中有广泛应用.所以研究这些问题对今后的工作和学习都是有用的,也将为后面的学习做些准备.我们先研究直线相交的问题,引入本节课题.二、探究新知,讲授新课1.对顶角和邻补角的概念学生活动:观察上图,同桌讨论,教师统一学生观点并板书.【板书】∠1与∠3是直线AB、CD相交得到的,它们有一个公共顶点O,没有公共边,像这样的两个角叫做对顶角.学生活动:让学生找一找上图中还有没有对顶角,如果有,是哪两个角?学生口答:∠2和∠4再也是对顶角.紧扣对顶角定义强调以下两点:(1)辨认对顶角的要领:一看是不是两条直线相交所成的角,对顶角与相交线是唇齿相依,哪里有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;二看是不是有公共顶点;三看是不是没有公共边.符合这三个条件时,才能确定这两个角是对顶角,只具备一个或两个条件都不行.(2)对顶角是成对存在的,它们互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角.2.对顶角的性质提出问题:我们在图形中能准确地辨认对顶角,那么对顶角有什么性质呢?学生活动:学生以小组为单位展开讨论,选代表发言,井口答为什么.【板书】∵∠1与∠2互补,∠3与∠2互补(邻补角定义),∴∠l=∠3(同角的补角相等).注意:∠l与∠2互补不是给出的已知条件,而是分析图形得到的;所以括号内不填已知,而填邻补角定义.或写成:∵∠1=180°-∠2,∠3=180°-∠2(邻补角定义),∴∠1=∠3(等量代换).学生活动:例题比较简单,教师不做任何提示,让学生在练习本上独立完成解题过程,请一个学生板演。
人教版七年级数学下册第五章5.1.1相交线同步检测试题合集(共4套)

5.1.1 相交线班级:___________ 姓名:___________ 得分:___________一、填空题(每小题6分,共30分)1.下面四个图形中,∠1与∠2是对顶角的图形()A.甲B.乙C.丙D.丁2.已知∠α和∠β是对顶角,若∠α=30°,则∠β的度数为()A.30°B.60°C.70°D.150°3.下列说法中:①对顶角相等;②相等的角是对顶角;③互补的两个角是邻补角;④邻补角一定互补;⑤两条相交直线形成的四个角中,同一角的两邻补角一定是对顶角.其中说法正确的个数是()A. 2个B. 3个C. 4个D. 5个4.如图所示,三条直线AB、CD、EF相交于一点O,则∠AOE+∠DOB+∠COF等于()A. 150°B. 180°C. 210°D. 120°第4题图第5题图5.如图,直线AB,CD交于点O.射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于()A.38°B.104°C.142°D.144°二、填空题(每小题6分,共30分)6.如图,A、B、O在同一条直线上,如果OA的方向是北偏西24030',那么OB的方向是东偏南.第6题图第7题图7.如图,直线AB、CD交于点O,射线OM平分∠AOC,若∠BOC=1040,,则∠COM =.8.如图所示,其中共有________对对顶角.甲21丙12丁21乙12第8题图第10题图9.三条直线两两相交,则交点有_________个.10.如图,直线AB、CD相交于点O,∠EOC=70°,OA平分∠EOC,则∠BOD=.三、解答题(每小题20分,共40分)11.如图所示,三条直线AB、CD、EF相交于点O,∠AOF=3∠FOB,∠AOC=90°,求∠EOC 的度数.12.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的4倍.求:(1)∠AOD、∠BOD的度数;(2)∠BOE的度数.参考答案【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
5_1_1相交线 (分层作业)【2023春人教版七下数学精品备课】 解析版

5.1 相交线第1课时相交线参考答案与试题解析夯基训练知识点1 邻补角1.识别邻补角应同时满足以下三条:①有公共_____________;②有一条公共边;③两角的另一边_____________.1.【答案】①顶点③分别互为反向延长线2.邻补角是指( )A.和为180°的两个角B.有公共顶点且互补的两个角C.有一条公共边且相等的两个角D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角2.【答案】D3.下列选项中,∠1与∠2互为邻补角的是( )3.【答案】D解:根据邻补角的定义是有公共顶点且有一条公共边,另一边互为反向延长线的两个角,故选项D正确。
4.如图,∠1的邻补角是( )A.∠BOCB.∠BOE和∠AOFC.∠AOFD.∠BOC和∠AOF4.【答案】B解:根据邻补角的定义,与∠1有公共顶点且有一条公共边,另一边互为反向延长线的角为∠BOE和∠AOF,故选项B正确。
5.如图,∠α的度数等于( )A.135°B.125°C.115°D.105°5.【答案】A解:根据邻补角的性质可知。
6.如图所示,直线AB和CD相交所成的四个角中,∠1的邻补角是________.6.【答案】∠2和∠4解析:根据邻补角的概念判断:有一个公共顶点、一条公共边,另一边互为延长线.∠1和∠2、∠1和∠4都满足有一个公共顶点和一条公共边,另一边互为延长线,故为邻补角.故答案为∠2和∠4.方法总结:邻补角的定义包含了两层含义:相邻且互补.但需要注意的是:互为邻补角的两个角一定互补,但互补的角不一定是邻补角.知识点2 对顶角及其性质7识别对顶角应同时满足:①有公共___________;②两个角的两边___________.7.【答案】①顶点②分别互为反向延长线8.如图,小强和小丽一起玩跷跷板,横板AB绕O上下转动,当小强从A到A'的位置时,∠AOA'=45°,则∠BOB'的度数为___________,理由是___________.8.【答案】45°;对顶角相等9.如图,直线AB,CD相交于点O,则∠1 ∠2,根据的是;∠2+∠3= ,根据的是.9.【答案】=;对顶角相等;180°;邻补角的定义10.下列语句正确的是( )A.顶点相对的两个角是对顶角B.有公共顶点并且相等的两个角是对顶角C.两条直线相交,有公共顶点的两个角是对顶角D.两条直线相交,有公共顶点且没有公共边的两个角是对顶角10.【答案】D解:A错误,如图①,∠1与∠2的顶点相对,但∠1与∠2不是对顶角;B错误,如图②,∠1与∠2有公共顶点,且∠1=∠2,但∠1与∠2不是对顶角;C错误,如图③,∠1与∠2是两条直线相交且有公共顶点的角,但∠1与∠2不是对顶角;D正确.11.下列图形中∠1与∠2互为对顶角的是( )11.解析:观察∠1与∠2的位置特征,只有C中∠1和∠2同时满足有公共顶点,且∠1的两边是∠2的两边的反向延长线.故选C.方法总结:判断对顶角只看两点:①有公共顶点;②一个角的两边分别是另一个角的两边的反向延长线.12.如图,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.12.解析:根据对顶角的性质,可得∠AOC与∠BOD的关系,根据OA平分∠COE,可得∠COE 与∠AOC的关系,根据邻补角的性质,可得答案.解:由对顶角相等得∠AOC=∠BOD=42°.∵OA平分∠COE,∴∠COE=2∠AOC=84°.由邻补角的性质得∠DOE=180°-∠COE=180°-84°=96°.方法总结:解决此类问题的关键是在图中找出对顶角和邻补角,根据两种角的性质找出已知角和未知角之间的数量关系.题型总结题型1 利用对顶角的性质求角13.如图,直线AB,CD,EF相交于点O,如果∠AOC=65°,∠DOF=50°.(1)求∠BOE的度数;(2)通过计算∠AOF的度数,你发现射线OA有什么特殊性吗?13.解:(1)因为∠AOC=65°,所以∠BOD=∠AOC=65°.又因为∠BOE+∠BOD+∠DOF=180°,∠DOF=50°,所以∠BOE=180°-65°-50°=65°.(2)因为∠AOF=∠BOE=65°,且∠AOC=65°,所以∠AOF=∠AOC,所以射线OA是∠COF的平分线.题型2 利用邻补角及对顶角的性质求角(方程思想)14.补全解答过程:如图,已知直线AB,CD相交于点O,OA平分∠EOC,若∠EOC∶∠EOD=2∶3,求∠BOD的度数.解:由∠EOC∶∠EOD=2∶3,设∠EOC=2x°,则∠EOD=3x°.因为∠EOC+∠____________=180°(____________),所以2x+3x=180,解得x=36.所以∠EOC=72°.因为OA平分∠EOC(已知),所以∠AOC=12∠EOC=36°.因为∠BOD=∠AOC(____________),所以∠BOD=____________.14.EOD;平角的定义(邻补角的性质);对顶角相等;36°15.如图,直线AC,EF相交于点O,OD是∠AOB的平分线,OE在∠BOC内,∠BOE=12∠EOC,∠DOE=72°,求∠AOF的度数.15.解析:因为已知量与未知量的关系较复杂,所以想到列方程解答,根据观察可设∠BOE =x,则∠AOF=∠EOC=2x,然后根据对顶角和邻补角找到等量关系,列方程.解:设∠BOE=x,则∠AOF=∠EOC=2x.∵∠AOB与∠BOC互为邻补角,∴∠AOB=180°-3x.∵OD平分∠AOB,∴∠DOB=12∠AOB=90°-32x.∵∠DOE=72°,∴90°-32x+x=72°,解得x=36°.∴∠AOF=2x=72°.方法总结:在相交线中求角的度数时,就要考虑使用对顶角相等或邻补角互补.若已知关系较复杂,比如出现比例或倍分关系时,可列方程解决角度问题.拓展培优拓展角度1 利用邻补角的性质求折叠中的角(折叠法)16.将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD的大小.16.解:由折叠的性质可知∠ABC=∠A'BC,∠EBD=∠E'BD,所以∠A'BC=12∠ABE',∠E'BD=12∠EBE'.由∠ABE'与∠EBE'互为邻补角,得∠ABE'+∠EBE'=180°,因此∠CBD=∠A'BC+∠E'BD=12∠ABE'+12∠EBE'=12(∠ABE'+∠EBE')=90°点拨:此题运用了折叠法,解题时关键要弄清折叠前后哪些角对应相等.拓展角度2 利用邻补角及对顶角的定义进行计数(基本图形法)17.下列各图中的直线都相交于一点.(1)(2)若n 17.解:(1)2;6;12;4;12;24(2)对顶角共有n(n-1)对,邻补角共有2n(n-1)对.技巧解:巧数图形中对顶角或邻补角的对数:(1)在复杂图形中数对顶角或邻补角的对数时,我们一般先确定图形中包含有几个两条直线相交的基本图形;(2)在每个基本图形中有2对对顶角、4对邻补角,从而计算出所有对顶角、邻补角的对数. 拓展角度3 与对顶角有关的探究问题18.我们知道:两直线交于一点,对顶角有2对;三条直线交于一点,对顶角有6对;四条直线交于一点,对顶角有12对……(1)10条直线交于一点,对顶角有________对;(2)n(n ≥2)条直线交于一点,对顶角有________对.18.解析:(1)仔细观察计算对顶角对数的式子,发现式子不变的部分及变的部分的规律,得出结论,代入数据求解.如图①,两条直线交于一点,图中共有()4244-⨯=2对对顶角;如图②,三条直线交于一点,图中共有()6264-⨯=6对对顶角;如图③,四条直线交于一点,图中共有()8284-⨯=12对对顶角……按这样的规律,10条直线交于一点,那么对顶角共有()202204-⨯=90(对).故答案为90;(2)利用(1)中规律得出答案即可.由(1)得n(n ≥2)条直线交于一点,对顶角的对数为()2n 224n -=n(n -1).故答案为n(n -1).方法总结:解决探索规律的问题,应全面分析所给的数据,特别要注意观察符号的变化规律,发现数据的变化特征.。
《新课程课堂同步练习册人教版七年级下册数学》参考答案

《新课程课堂同步练习册人教版七年级下册数学》参考答案§5.1.1相交线一、选择题1.C 2.D 3.B 4.D二、填空题1.∠AOD、∠AOC或∠BOD 2.145°3.135°4.35°三、解答题1.解:(图7)因为∠2=30°,所以∠1=30°(对顶角相等)又,所以∠3=2∠1=60°所以∠4=∠3=60°(对顶角相等)2.解:(图8)(1)因为,又(对顶角相等)所以因为所以所以(对顶角相等)(2)设则,由+=180°,可得,解得,所以3.解:(图9)AB、CD相交于O 所以∠AOD与∠BOD互为邻补角所以∠AOD+∠BOD=180°,又OE是∠AOD的平分线,所以∠1=∠AOD,同理∠2=∠BOD所以∠1+∠2=∠AOD+∠BOD=(∠AOD+∠BOD)=×180°=90°即∠EOF的度数为90°§5.1.2垂线一、选择题1.D 2. B 3.C二、填空题1.不对2.40°3.互相垂直4.180°三、解答题1.答:最短路线为线段AB,设计理由:垂线段最短.2.解:由题意可知∠1+∠2=90°,又∠1-∠2=54°所以2∠1=144°所以∠1=72°,所以∠2=90°-∠1=18°3.解:(图7)(1)因为,所以,又,所以,所以,又是的平分线,所以==45°(2)由(1)知==45°,所以=90°所以与互相垂直.§5.1.3同位角、内错角、同旁内角一、选择题1.D 2.B 3.B 4.C二、填空题1.AB内错角2. AB 、CD 、AD 3. DE 、BC 、AB 、同位角4.同位角、内错角、同旁内角三、解答题1.答:∠ABC与∠ADE构成同位角,∠CED与∠ADE构成内错角,∠A、∠AED分别与∠ADE构成同旁内角;∠ACB与∠DEA构成同位角,∠BDE与∠DEA构成内错角,∠A、∠ADE分别与∠DEA构成同旁内角.2.答:图中共有5对同旁内角,它们分别是:∠ABC 与∠BAC、∠ABC与∠BAD、∠ACB与∠BAC 、∠ACB与∠CAE、∠ABC与∠ACB3.答:∠1与∠2是直线AC截直线AE、BD形成的同位角;∠2与∠3是直线BD截直线AC、DE形成的内错角;∠3与∠4是直线BD截直线AC、DE形成的同旁内角.§5.2.1平行线一、选择题1.D 2.C 3.A 4..A二、填空题1.2.相交3.经过直线外一点,有且只有一条直线与这条直线平行.三、解答题1.略2.(1)略(2)a//c§5.2.2平行线的判定(一)一、选择题1.B 2.C 3..C 4.A二、填空题1.∠4,同位角相等,两直线平行;∠3,内错角相等,两直线平行.2.∠1,∠BED 3.答案不唯一,合理就行4.70°三、解答题1.答:,因为∠1=50°,所以∠2=130°(邻补角定义),又∠3=130°,所以∠2=∠3,所以(内错角相等,两直线平行)2.(图1)答:AB∥CD,因为∠1=∠2,且∠1+∠2=90°,所以∠1=∠2=45°,因为∠3=45°,所以∠2=∠3,所以AB∥CD§5.2.2平行线的判定(二)一、选择题1.C 2.A 3.A 4.D二、填空题1.∠2 内错角相等,两直线平行;∠4 同旁内角互补,两直线平行2.BC//AD;BC//AD;∠BAD;∠BCD(或∠3+∠4);3. AB//CD 同位角相等,两直线平行;∠C,内错角相等,两直线平行;∠BFE,同旁内角互补,两直线平行.三、解答题1.答:AB//CD AD//BC,因为∠A+∠B=180°所以AD//BC (同旁内角互补,两直线平行),又∠A=∠C,所以∠C +∠B=180°,所以AB//CD(同旁内角互补,两直线平行)2.解:AB//CD,∵∠APC=90°∴∠1+∠2=90°,∵AP、CP分别是∠BAC和∠ACD的平分线,∴∠BAC=2∠1,∠ACD=2∠2,∴∠BAC+∠ACD=2∠1+2∠2=2(∠1+∠2)=180°∴AB//CD(同旁内角互补,两直线平行)§5.3.1 平行线的性质(一)一、选择题1.C 2.C 3.C二、填空题1. 50° 2. 25° 3. 60三、解答题1.已知;垂直的性质;等量代换,同位角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.2.解:延长BA交CE于点F,因为AB//CD,∠C=52°,所以∠EFB=∠C=52°(两直线平行,同位角相等),又∠E=28°,所以∠FAE=180°―∠E―∠C =100°所以∠EAB=80°(邻补角定义)§5.3.1 平行线的性质(二)一、选择题1.D 2.A 3.B 4.D二、填空题1. 80° 2. 65° 3. 90°三、解答题1.解:延长梯形玉片图形的两腰及下底,构造出玉片原图如图8所示,∵AD//BC,∴∠1+∠A=180°∠2+∠D=180°(两直线平行,同旁内角互补)又∠A=115°,∠D=100°,∴∠1 =180°-∠A=65°∠2 =180°-∠D=80°即梯形玉片另外两个角的度数分别是65°、80°.2.解:∵∠END=50°(已知)又AB//CD,(已知)∴∠BMF+∠END =180°(两直线平行,同旁内角互补),又∵MG平分∠BMF(已知)∴,而AB//CD(已知)∴∠1=∠BMG=65°(两直线平行,内错角相等)§5.3.2 命题、定理一、选择题1.A 2.D 3.C二、填空题1.如果两个角是对顶角,那么它们相等;2.“题设:一个三角形是直角三角形,结论:它的两个锐角互余.”3.如∠A=50°∠B=60°则∠A+∠B>90°(答案不唯一,只要写出两个角,它们的和大于或等于均可;但不写∠A+∠B≥90°.)4.①③④三、解答题1. (1) 答:在同一个平面内,如果两条直线都和第三条直线垂直,那么这两条直线互相平行.这个命题是真命题.(2) 答:如果两个角是同旁内角,那么这两个角互补.这个命题是假命题. (3) 答:如果几个角相等,那么它们的余角相等;或者,如果几个角是等角的余角,那么这几个角相等.这个命题是真命题.2.(1)答:是命题,题设是:两直线平行线被第三条直线所截;结论是:内错角相等.(2)答:不是命题.(3)答:不是命题.(4)答:是命题,题设是:两个角互为邻补角;结论是:这两个角的平分线互相垂直.或者,题设是:两条射线是两个互为邻补角的角的平分线;结论是:这两条角平分线互相垂直.3.答:这个说法是正确的,根据题意作出右图,如图所示.则有AB//CD,EP是∠BEF的平分线,FP是∠DFE的平分线.∵AB//CD∴∠BEF+∠DFE=180°(两直线平行,同旁内角互补)又∵EP与FP分别是∠BEF与∠DFE的平分线,∴∠BEF=2∠2∠DFE=2∠1,∴2∠2 +2∠1=180°,∴∠1 +∠2=90°,∴∠P=90°∴EP⊥FP,即“两条平行线被第三条直线所截,则同旁内角的角平分线互相垂直.”说法正确.§5.4平移 (一)一、选择题1.D 2.A 3.A二、填空题1. 5cm 2.2 3.形状与大小相等4.70°、 50°、 60°、60°三、解答题1.图略2.(如图5),相等的线段:,,;相等的角:,,;平行的线段:,,3.答:线段AB平移成线段EF、HG与CD;线段AE可以由线段BF、CG或DH平移得到;FG不能由AE或EF平移得到.§5.4平移 (二)一、选择题1.D 2.B 3.D 4.C二、填空题1.60°、8cm 2.一只小鸟 3.36平方单位 4.16cm三、解答题1.图略2.解:由楼梯侧面可以知道,可将楼梯水平方向的线段向下平移到线段AC上,将楼梯竖直方向的线段向右平移到线段BC上则所需地毯总长度刚好等于线段AC加上线段BC 的长,即6+2.8=8.8米,其面积为8.8×2=17.6 m2,所以购买地毯至少需要17.6×50=880元.3.解:当AB在线段CD上向上或向下平移时, S1·S4 =S2 ·S3因为S1 =AP·PC,S4 =DP·BP;S2=DP·AP,S3=BP·PCS1·S4=AP·PC·DP·BP, S2 ·S3=DP·AP·BP·PC所以S1 ·S4 =S2·S第6章平面直角坐标系§6.1.1有序数对一、选择题1. D2. C3. A4. A二、填空题1.两2.(5,6)2.组4号3. (9,12) ,不同4.(19,110)三、解答题 1.(1).B(4,0) C(6,0) D(7,2) E(6,3)(2).8 2.3个格.3.解:如图所示的是最短路线的6种走法.一、选择题1.D2.B3.B4.C二、填空题1.二三y轴上2. 有序数对横坐标纵坐标3.负数负数正数4. 72三、解答题1.略 2.图略 3.略§6.1. 2平面直角坐标系(二)一、选择题1.A2.B3.A4.C二、填空题 1.二三(-1,-2)2. 三四(1,-2)3.(0,0)纵横 4. 72三、解答题1.略 2. 解:因为a2+1 0,-1-b2 0,所以点A在第四象限. 3.(1) a=1,b=3(2) a= - 3, b=1§6.2.1用坐标表示地理位置一、选择题1.B2.D3.C二、填空题1.∠BOA ∠COA2.110 3.正北三、解答题1. 正北,两家距离100米.2.图略.小玲家(-150,100),小敏家(200,300),小凡家(-300,150).3.解:李哲在湖心亭,丁琳在望春亭,张瑞在游乐园.图略.他们三人到望春亭集合,三人所行路程之和最短.§6.2.2用坐标表示平移一、选择题1.B2.D3.A4.D二、填空题1.(5,-3)(3,-6)2.(0,0)3.不变4.(-1,-2)三、解答题 1.A′(2,3),B′(1,0),C′(5,1).2.(1)略(2)四边形ABCD的面积为6.5.第七章三角形§7.1.1 三角形的边一、选择题1、C 2 、B 3、 B二、填空题1、8 4 △BOC 、△BEC、△BDC 、△ABC 2、 5cm,7cm或6cm,6cm3、24、否因为任意两线段之和都大于第三条,这三条线段围成一个三角形.三、解答题1、不相信.这位同学的身高约1.65米,腿长大约不超过1米,根据三角形两边之和大于第三边,步子的长不可能有2米远.2、若小明家,小华家,学校位置在同一条直线上,S=1m 或5m;若三者不在同一直线上,根据三角形三边关系知1 S 5;所以S的范围为1m≤S ≤5m.3、因为a、b、c为△ABC的三边,所以a+b-c ≥0,b-c-a≤0 ,c-a-b≤0.原式=a+b-c-(b-c-a)+(c-a-b)= a+b-c -b+c+a+c-a-b= a-b+c§7.1.2三角形的高、中线与角平分线一、选择题1 、B 2、 C 3、D二、填空题1、ADBE 2、6 cm 40° 3、钝角 4、AD BC ∠ADB ∠ADC三、解答题1、解:△ABD 的周长=AB+AD+BD,△ACD 的周长=AC+AD+CD因为AD是△ABC的中线,所以 BD=CD,△ABD与△ACD 的周长之差= AB -AC=8-5=3(cm)2、如右图:3、解:AD=2CE.因为,而 AB=2BC所以AD=2CE§7.1.3 三角形的稳定性一、选择题1、A 2、 A 3 A二、填空题1、三角形具有稳定性2、三角形具有稳定性3、三角形具有稳定4、三角形具有稳定三、简答题1、答案不唯一.2、答案不唯一.3、答案不唯一.§7.2.1三角形的内角一、选择题1、D 2 、C 3 、 A二、填空题1、20°60° 100° 2、60°3、40°或100°4、40°三、简答题1、解:设∠A=x°,则∠B=15°+ x°,∠C=15°+ x°+ 45°=60°+ x°因为∠A+∠B +∠C=180°,所以x°+15°+ x°+60°+ x°=180°,解得x=35,∠C=95°2 、解:因为∠C+∠1+∠2=180°, ∠C+∠B+∠A=180°所以∠1+∠2=60°+50°=110°3解:在△ABC中,∠BAC=180°-∠B-∠C=180°-65°-45°=70°,因为AE是∠BAC的角平分线,所以∠BAE=∠BAC=×70°=35°.因为AD⊥BC,所以∠ADB=90°. 在△ABD中, ∠BAD=180°-65°-90°=25°所以∠DAE=∠BAE -∠BAD=35°-25°=10°§7.2.2三角形的外角一、选择题1、A 2D 3 B二、填空题1、105° 2、 85°3、 80° 4、165三、简答题1、如图,根据三角形的一个外角等于与它不相邻的两个内角的和,知:∠1=∠B+∠D,∠2=∠A+∠C,而∠1+ ∠2+∠E=180°,所以∠A+∠B+∠C+∠D+∠E=180°2、因为DF⊥AB,所以∠BFD =90°在△BFD中,∠B=180°-∠D-∠BFD =180°-45°-90°=45°,在△ABC中, ∠BCA=180°-∠A-∠B=180°-40°-45°=95°3、∠AEB>∠CED.理由:根据三角形的一个外角大于与它不相邻的任何一个内角,知∠AEB >∠ACB ,∠ACB >∠CED,所以∠AEB >∠CED.§7.3.1 多边形一、选择题1 、A. 2 、B 3、B二、填空题1、(n-3)(n-2);2、120°; 3、8 ;4、 433三、简答题1、图略2、180°×3=540°3、因为360°÷30°=12,所以他一共左转了12次,12×10=120,一共走了120米.§7.3.2 多边形的内角和一、选择题1 、C 2、 D 3、D二、填空题1、900 ; 2、8; 3、135 ;4、 90°、90°、120°、60°三、简答题1、因为多边形的外角和等于360 o,360o ÷72o=5,所以该多边形的边数为5;五边形内角和为(5-2)×180°=540°.2、设该正多边形的一个外角为x,则每一个内角为(x +60°),相邻的内角与外角互补,所以(x+60°)+x=180°,解得x=60°,即每个外角为60°,因为多边形的外角和等于360°,360°÷60°=6,所以这个多边形的边数为6.3、因为多边形的内角和都是180°的倍数,且每个外角的范围是大于0°小于180°,1340°=180°×7﹢80°,所以这个多边形的边数为7﹢2=9,这个外角的度数为80°§7.4课题学习镶嵌一、选择题1 、C 2、A 3、A二、填空题1、3 ; 2、3 3、4或5 4、12三、解答题1、不能.因为正十边形的内角和为(0-2)180°=1440°,1440°÷10=144°,144°的整数倍得不到360°所以用正十边形不能铺满地面.2、能,需要6个;也能,需要4个.3、正方形和正八边形组合能镶嵌成平面图案.因为正方形的每个内角为90°,正八边形的每个内角为135°,90°+2×135°=360°,所以正方形和正八边形组合能镶嵌成平面图案;用正方形和正六边形不能镶嵌成平面图案.因为找不到正整数m、n,使得,所以不能.第8章二元一次方程组§8.1二元一次方程组一、选择题 1.B2.B3.A二、填空题1.2.2,-13. 无数,无数;4.三、解答题 1.解:设小华买了x千克香蕉,y千克苹果,依题意可得2.解:设这个学校有x个班,这批图书有y本,依题意可得3.解:设甲原来有羊x只,乙原来有羊y只,依题意可得§8.2消元——二元一次方程组的解法(一)一、选择题1.C 2.B 3.A二、填空题1.-1 2. , 3. 1,4 4.7,2三、解答题1.(1)(2)(3)(4)2. 这个学生有中国邮票216张,外国邮票109张.§8.2消元——二元一次方程组的解法(二)一、选择题1.C 2.D 3.B二、填空题1.2.3. 4,-14.-16三、解答题1.(1)(2)(3)(4)。
5.1.1相交线

在我们的生活的世界中,蕴涵着大 量的相交线和平行线,
这节课我们就来学习相交线所成的角
注意观察用剪刀剪布时剪把手张 角的变化与剪刀张角是怎样变化的
如果把剪刀的构造看作是两条相交的 直线,以上就关系到两条直线相交所 成的角的问题,
画直线AB、CD相交于点O A
1
2 4
O
D
3
C
B
练习:下列说法对不对 1.邻补角可以看成是平角被过它顶点的一 条射线分成的两个角 2.邻补角是互补的两个角,互补的 两个角是邻补角 3.对顶角相等,相等的两个角是对顶角
[练习]课本P9-1,2
例题:如图,直线a,b相交, 1 求
2 , 3, 4
40
的度数
巩固练习 教科书5页练习 已知,如图 AOC 35 , COF 80 求: AOD 和 DOF 的度数
,
[作业]课本 P 10-7,8
一判断题 1如果两个角有公共顶点和一条公共过,而且 这两个角互为补角,那么它们互为邻补角( )
2两条直线相交,如果它们所成的邻补角相等, 那么一对对顶角就互补( ) 二填空题
如图,直线AB、CD、EF相交于点O, AOE
的对顶角是 若
,
,
COF
的邻补角是
130
AOC
:AOE
=
=2:3, EOD
则 BOC
初中数学同步训练必刷题(人教版七年级下册5

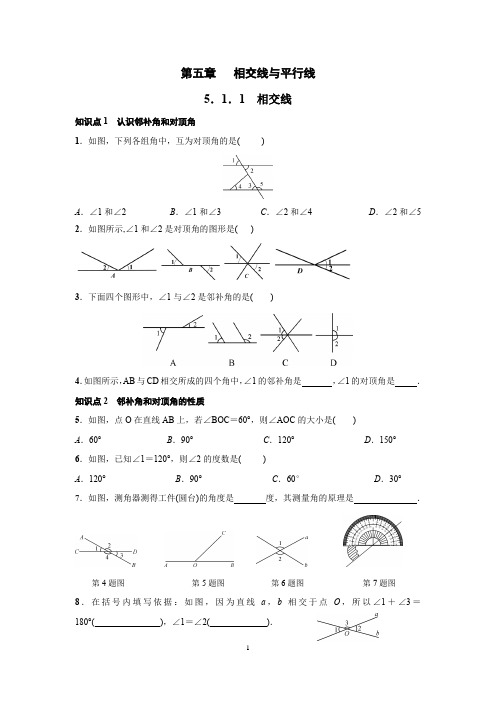
初中数学同步训练必刷题(人教版七年级下册5.1.1 相交线)一、单选题1.(2022七下·承德期末)下列四个图形中,∠1与∠2是对顶角的是()A.B.C.D.2.(2022七上·南海期中)直线AB和直线CD相交于点O,若∠AOC=40°,则∠BOC等于()A.140°B.60°C.40°D.160°3.(2022七下·崇川期末)如图,直线AB与CD相交于点O,∠AOC:∠AOD=2:3,则∠BOD等于()A.36°B.72°C.60°D.75°(4.(2022九上·南宁开学考)如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC 的度数是()A.115°B.125°C.135°D.145°5.(2022七下·承德期末)如图,小明手持手电筒照向地面,手电筒发出的光线CO与地面AB形成了两个角,∠BOC=8∠AOC,则∠BOC的度数是()A.160°B.150°C.120°D.20°6.(2022七下·延庆期末)如图,直线AB,CD相交于点O,如果∠1=35°,那么∠2的度数是()A.35°B.55°C.145°D.165°7.(2022七下·钦州期末)如图,直线AB,CD,EO相交于点O,已知OA平分∠EOC,若∠EOC:∠EOD =2:3,则∠BOD的度数为()A.40°B.37°C.36°D.35°8.(2022七下·东明期末)如图,直线AB、CD相交于点O,且∠AOC+∠BOD=110°,则∠AOD的度数为()A.125°B.120°C.110°D.100°9.(2022七下·青县期末)如图,直线AB、CD相交于点O,下列描述一定正确的是()A.∠1和∠2互为对顶角B.∠1和∠3互为邻补角C.∠1=∠2D.∠1=∠310.(2022七下·江油期中)如图,直线AB、CD相交于O,OA平分∠EOC,若∠EOC=70°,那么∠BOD 的度数是()A.30°B.35°C.45°D.40°二、填空题11.(2022七下·五常期末)若∠1和∠2是对顶角,∠1=36°,则∠2的度数是度.12.(2022七下·大连期末)如图,∠1与∠2是对顶角,∠1=α+10°,∠2=40°,则α=°.13.(2022七下·富川期末)如图,直线AB,CD相交于点O,OE是∠AOD的平分线,若∠BOD=40°,则∠COE的度数为.14.(2022七下·榆林期末)若∠1与∠2是对顶角,∠3与∠2互余,且∠3=37∘,则∠1的度数为°. 15.(2022七下·雨花期末)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.若∠AOC=76°,则∠BOF的度数为°.16.(2022七下·义乌开学考)如图,点O 在直线AB 上,过点O 作射线OC,若∠AOC=53°17′28″,则∠BOC 的度数是.17.(2021七下·涿鹿期末)在同一平面内的三条直线,它们的交点个数可能是.18.(2021七下·玉林期末)如图,两直线交于点O,若∠3=3∠2,则∠1的度数是.19.(2021七下·孝义期中)如图是某城市一座古塔底部平面图,在不能进入塔内测量的情况下,学习兴趣小组设计了如图所示的一种测量方案,学习兴趣小组认为测得∠COD的度数就是∠AOB的度数.其中的数学原理是.20.(2021七下·滦南期末)小明用一副三角板自制对顶角的“小仪器”,第一步固定直角三角板ABC,并将边AC延长至点P,第二步将另一块三角板CDE的直角顶点与三角板ABC的直角顶点C 重合,摆放成如图所示,延长DC至点F,∠PCD与∠ACF就是一组对顶角,若∠ACF=30∘,则∠PCD=,若重叠所成的∠BCE=n∘(0∘<n<90∘),则∠PCF的度数.三、解答题21.(2022七下·中山期末)如图,直线AB,CD相交于点O,OE平分∠BOC,OF∠CD,若∠BOE=72°,求∠AOF的度数.22.(2022七下·韩城期中)如图,直线AB,CD相交于点O,∠BOC=125°,∠AOE=∠BOD,求∠DOE的度数.23.(2022七下·河源期中)如图,直线a,b相交于点O,已知3∠1−∠2=100°,求∠3的度数.24.(2021七下·南沙期中)如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.25.(2022七下·黄州期中)如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,∠DOF=90°.(1)求∠DOE的度数;(2)求∠EOF的度数.26.(2021七下·瑶海期末)如图,直线AB,CD和EF相交于点O,(1)写出∠AOC,∠BOF的对顶角;(2)如果∠AOC=70°,∠BOF=20°,求∠BOC和∠DOE的度数.27.(2021七下·武昌期中)如图,直线MD、CN相交于点O,OA是∠MOC内的一条射线,OB是∠NOD 内的一条射线,∠MON=70°.(1)若∠BOD=12∠COD,求∠BON的度数;(2)若∠AOD=2∠BOD,∠BOC=3∠AOC,求∠BON的度数.28.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分,(1)直接写出图中∠AOC的对顶角为, ∠BOE的邻补角为;(2)若,且=2:3,求的度数.答案解析部分1.【答案】C【知识点】对顶角及其性质【解析】【解答】解:对顶角指的是有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,所以:A 、两角没有公共顶点,不符合题意;B 、两角也是只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意;C 、两角有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角,符合题意;D 、两角只有一条边互为反向延长线,另一条边没有互为反向延长线,不符合题意; 故答案为:C .【分析】有一个公共顶点,并且一个角的两边是另一个角两边的反向延长线的两个角是对顶角,据此逐一判断即可.2.【答案】A 【知识点】邻补角【解析】【解答】解:∵∠AOC=40°,∴∠BOC=180°-∠AOC=180°-40°=140°, 故答案为:A .【分析】利用邻补角求出∠BOC 的度数即可。
寒假预习《5.1.1 相交线》课时检测卷精选 2021-2022学年人教版数学七年级下册(含答案)

寒假预习《5.1.1 相交线》同步测试培优卷精选 2021-2022学年人教版数学七年级下册(含答案)一、精心选一选1. 根据语句“直线1l与直线2l相交,点M在直线1l上,直线2l不经过点M.”画出的图形是()A.B.C.D.2. 下列各图中,∠1和∠2是对顶角的是( )A.B.C.D.3. 如图,对顶角量角器中α∠的度数为()A.120°B.60°C.90°D.50°4. 下面各图中∠1和∠2是对顶角的是()A.B.C .D .5. 如图,直线AB ,CD 交于点O ,射线OM 平分∠AOD ,若∠BOD=760,则∠BOM等于( )A .B .C .D .6. 两条直线相交于一点,则共有对顶角的对数为( )A .1对B .2对C .3对D .4对7. 如图所示,直线AB ,CD 交于点O ,射线OM 平分AOC ∠.若38AOM ∠=︒,则BOC∠等于( )A .104︒B .144︒C .106︒D .136︒8. 如图,直线AB ,CD 相交于点O ,OE AB ⊥,垂足为点O ,若50BOD ∠=︒,则COE∠的度数为( )A .40°B .45°C .50°D .55°9. 下列结论中错误的是( )A .连接两点的线段叫两点之间的距离B .两点之间,线段最短C .同角的补角相等D .两点确定一条直线二、细心填一填10. 如图,两条直线AB ,CD 交于点O ,射线OM 是∠AOC 的平分线,若∠BOD =80°,则∠BOM 的度数是__.11. 如图是一把剪刀,若∠AOB+∠COD=60°,则∠BOD=____°.12. 如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC,则∠BOD=________.13. 若∠α=70°,则它的补角是________.14. 如图,直线AB、CD相交于点O,OE平分∠BOD,若∠AOD-∠DOB=60°,则∠EOB=___.15. 已知,如图,直线AB、CD相交于O,OE平分∠BOD且∠AOE=150°,∠AOC的度数为______.16. 如图,直线AB、CD相交于点O,135∠=︒,则直线AB与直线CD的夹角是BOC______︒.17. 如图,直线AB和OC相交于点O,∠AOC=100°,则∠1=_______度.18. 如图,直线AB CD 、相交于O 点,OE AB ⊥.(1)2∠和3∠互为___角; 1∠和3∠互为_______角;2∠和4∠互为___角. (2)若125∠=︒,那么2∠=_________;3BOE ∠=∠-∠______=_______︒-____︒=___︒;4∠=∠_____1-∠=__︒-____︒=______︒.三、用心做一做19. 如图,直线AB 、CD 相交于点O ,DOE BOD ∠∠=,OF 平分AOE ∠,20BOD ∠︒=.(1)求AOE ∠的度数;(2)求COF ∠的度数.20. 如图所示,已知∠AOC=160°,OC 平分∠BOD ,OE 平分∠AOD ,求∠BOE 的度数.21. 如图,直线BC 与MN 相交于点O ,AO ⊥BC ,OE 平分∠BON ,若∠EON=20°.求∠AOM 和∠NOC 的度数.22. 如图,已知DM 平分ADC ∠,BM 平分ABC ∠,且27A ∠=︒,33M ∠=︒,求C ∠的度数.23. 已知O 为直线AB 上一点,射线OD 、OC 、OE 位于直线AB 上方,OD 在OE 的左侧,120AOC ∠=︒,DOE α∠=.(1)如图1,70α=︒,当OD 平分AOC ∠时,求EOB ∠的度数.(2)如图2,若2DOC AOD ∠=∠,且80α<︒,求EOB ∠(用α表示). (3)若90α=︒,点F 在射线OB 上,若射线OF 绕点O 顺时针旋转n ︒(0180n <<︒),2FOA AOD ∠=∠,OH 平分EOC ∠,当120FOH ∠=︒时,求n 的值.24. 如图,要测得两堵墙形成的∠AOB 的度数,但人不能进入围墙,请你写出两种不同的测量方法,并说明几何道理.参考答案一、精心选一选1. D【分析】利用直线2l 不经过点M 可判断A ,利用点M 在直线1l 上,不在直线2l 上可判断B ,利用点M 在直线1l 外可判断C ,根据直线1l 与直线2l 相交,点M 在直线1l 上,直线2l 不经过点M 可判断D .【详解】解:A .直线2l 不经过点M ,故本选项不合题意;B .点M 在直线1l 上,不在直线2l 上,故本选项不合题意;C .点M 在直线1l 外,故本选项不合题意;D .直线1l 与直线2l 相交,点M 在直线1l 上,直线2l 不经过点M ,故本选项符合题意;答案:D .【点睛】本题考查根据语句画图问题,掌握画图的基本语句是解题关键. 2. B【分析】根据对顶角的定义对各图形判断即可.【详解】解:A 、∠1和∠2不是对顶角,故选项错误;B 、∠1和∠2是对顶角,故选项正确;C 、∠1和∠2不是对顶角,故选项错误;D 、∠1和∠2不是对顶角,故选项错误.故选B .【点睛】本题考查了对顶角的定义,是基础题,熟记概念并准确识图是解题的关键. 3. B【分析】根据量角器的读数以及的对顶角相等即可求得α∠的度数.【详解】由图可知α∠的对顶角为60︒,根据对顶角相等,则α∠的度数为60︒, 故选B .【点睛】本题考查了量角器的使用,对顶角相等,理解对顶角相等是解题的关键. 4. C【解析】【分析】根据对顶角的定义对各选项分析判断后利用排除法求解.【详解】A 、∠1和∠2不是对顶角,故A 错误;B 、∠1和∠2不是对顶角,故B 错误;C 、∠1和∠2是对顶角,故C 正确;D 、∠1和∠2不是对顶角,是邻补角,故D 错误.故选:C .【点睛】本题考查了对顶角、邻补角,熟记概念并准确识图是解题的关键.5. C【解析】角平分线定义,对顶角的性质,补角的定义.由∠BOD=760,根据对顶角相等的性质,得∠AOC=760,根据补角的定义,得∠BOC=1040.由射线OM 平分∠AOD ,根据角平分线定义,∠COM=380.∴∠BOM=∠COM +∠BOC=1420.故选C .6. B如图,直线AB、CD相交于一点O,图中的∠AOD和∠BOC,∠AOC和∠BOD 是对顶角,共计2对.故选B.7. A【分析】根据2∠的度数,利用平角的定义计算即可.∠=∠AOC AOM计算AOC【详解】∵OM平分AOC∠,38∠=︒,AOM∴∠=∠=⨯︒=︒,AOC AOM223876∴∠=︒-∠=︒-︒=︒.BOC AOC180********故选:A.【点睛】本题考查了角的平分线,平角的定义,熟记角的定义,平角的定义是解题的关键.8. A【分析】根据对顶角相等得到AOC∠的度数.∠,再根据作余角定义,求COE【详解】解:∵50⊥∠=∠=,OE ABAOC BOD︒∴90905040∠=︒-∠=︒-︒=︒,COE AOC故选:A.本题考查了对顶角的性质和互为余角的性质,熟悉相关性质并能进行计算是解题的关键.9. A【分析】根据两点之间的距离,同角的余角或补角相等,两点确定一条直线,线段的性质即可判断.【详解】解:A、连接两点的线段的长度叫两点之间的距离,故错误;B、两点之间,线段最短,故正确;C、同角的补角相等,故正确;D、两点确定一条直线,故正确;故选A.【点睛】本题考查了对余角或补角,直线的性质,线段的性质的理解和运用,知识点有:同角的余角或补角相等,两点确定一条直线,两点之间线段最短二、细心填一填10. 140°【分析】先根据对顶角相等得出∠AOC=80°,再根据角平分线的定义得出∠COM,最后解答即可.【详解】解:∵∠BOD=80°,∴∠AOC=80°,∠COB=100°,∵射线OM是∠AOC的平分线,∴∠COM=40°,∴∠BOM=40°+100°=140°,故答案为:140°.【点睛】此题考查对顶角和角平分线的定义,关键是得出对顶角相等.11. 150【分析】根据对顶角相等得到∠AOB的度数,再根据邻补角的定义即可得出结论.【详解】∵∠AOB=∠COD,∠AOB+∠COD=60°,∴∠AOB=∠COD=30°,∴∠BOD=180°-∠AOB=180°-30°=150°.故答案为150°.【点睛】本题考查了对顶角相等和邻补角的定义.求出∠AOB的度数是解题的关键.12. 35°【详解】试题分析:∵∠EOC=70°,OA平分∠EOC,∴∠AOC=12∠EOC=12×70°=35°,∴∠BOD=∠AOC=35°.故答案为35°.点睛:本题考查了角平分线的定义,对顶角相等的性质,熟记定义并准确识图是解题的关键.13. 110°.【详解】试题分析:根据定义∠α的补角度数是180°﹣70°=110°.故答案是110°.考点:余角和补角.14. 30°【详解】∵∠AOD-∠BOD=60°,∴∠AOD=∠BOD+60°,∵AB为直线,∴∠AOD+∠BOD=∠AOB=180°,∴∠BOD+60°+∠BOD=180°,∴∠BOD=60°,∵OE平分∠BOD,∴∠EOB=30°故答案为: 30°.15. 60°【解析】根据两直线相交,对顶角相等,可推出∠AOC=∠DOB,又根据OE平分∠BOD,x,∠AOE=150°,可求∠AOC.设∠AOC=x, ∠AOD=180°-x,∠DOE=12x,解:设∠AOC=x, ∠AOD=1800-x,∠AOC=∠DOB,OE平分∠BOD,∠DOE=12x=150°,x=60°, ∠AOC=60°∵∠AOE=150°,∴180°-x+ 12故答案为60°“点睛”本题主要考查对顶角的性质以及角平分线的定义,邻补角,解决问题的关键是用方程思想解题.16. 45【分析】先根据邻补角的定义求出∠AOC,再根据直线的夹角为锐角解答.【详解】解:∵∠BOC=135°,∴∠AOC=180°-∠BOC=180°-135°=45°,∴直线AB与直线CD的夹角是45°.故答案为:45.【点睛】本题考查了邻补角的定义,要注意直线的夹角是锐角.17. 80.【解析】试题分析:由邻补角互补,得∠1=180°﹣∠AOC=180°﹣100°=80°,故答案为80.考点:对顶角、邻补角.18. 余余邻补25 2 90 25 65 AOB180 25155根据余角、补角、邻补角、平角的定理计算求解即可.【详解】解:∵OE AB ⊥,∴90AOE EOB ==︒∠∠,∴2390=+︒∠∠,1390∠+∠=︒,∴2∠和3∠互为余角; 1∠和3∠互为余角;∵24180∠+∠=︒且有公共边,∴2∠和4∠互为邻补角;∵125∠=︒,1∠和2∠互为对顶角,∴1225∠=∠=︒,32BOE ∠=∠-∠=90︒-25︒=65︒;4∠=∠AOB 1-∠=180︒-25︒=155︒.故答案为:余;余;邻补;25︒;2;90;25;65;AOB ;180;25;155.【点睛】本题考查的是余角和补角、对顶角和邻补角的概念,如果两个角的和等于90°(直角),就说这两个角互为余角,如果两个角的和等于180°(平角),就说这两个角互为补角.三、用心做一做19. (1)140︒;(2)90︒【分析】(1)因为DOE BOD =∠,求出∠BOE ,得出AOE ∠;(2)利用180COF DOE EOF ∠=︒-∠-∠,从而求出COF ∠的度数.【详解】解:(1)20BOD ∠=︒,DOE BOD ∠=∠,202040BOE ∴∠=︒+︒=︒,18040140AOE ∴∠=︒-︒=︒;(2)20DOE ∠=︒,111407022EOF AOE ∠=∠=⨯︒=︒, 180207090COF ∴∠=︒-︒-︒=︒.本题考查了平角的性质、对顶角、角平分线的性质,解题的关键是根据题意得出各角之间的关系.20. 110°【分析】先利用平角的概念求出∠BOC的度数,然后利用角平分线的定义即可求出∠BOD的度数和∠EOD的度数,最后利用∠BOE=∠EOD+∠BOD即可求解.【详解】∵∠AOC=160°,∠AOC+∠BOC=180°,∴∠BOC=180°-160°=20°.∵OC平分∠BOD,∴∠BOD=2∠BOC=40°.又∵∠AOD+∠BOD=180°,∴∠AOD=180°-40°=140°.∵OE平分∠AOD,∴∠EOD=12∠AOD=70°,∴∠BOE=∠EOD+∠BOD=70°+40°=110°.【点睛】本题主要考查角平分线的定义,平角的定义和角的和与差,掌握角平分线的定义是解题的关键.21. 50AOM︒∠=,140NOC︒∠=.【解析】【分析】要求∠AOM的度数,可先求它的余角.由已知∠EON=20°,结合角平分线的概念,即可求得∠BON.再根据对顶角相等即可求得;要求∠NOC的度数,根据邻补角的定义即可.【详解】解:∵OE平分∠BON,∴∠BON=2∠EON=2×20°=40°,∴∠NOC=180°-∠BON=180°-40°=140°,∠MOC=∠BON=40°,∵AO ⊥BC ,∴∠AOC=90°,∴∠AOM=∠AOC-∠MOC=90°-40°=50°,所以∠NOC=140°,∠AOM=50°. 【点睛】结合图形找出各角之间的关系,利用角平分线的概念,邻补角的定义以及对顶角相等的性质进行计算.22. 39C ∠=︒.【分析】根据角平分线的性质及对顶角相等可求得,2C M A ∠=∠-∠,然后再利用已知条件及角的和差计算求解即可.【详解】解:如图所示:设BC 与MD 的交点为E DM 平分ADC ∠,BM 平分ABC ∠21CDQ ∴∠=∠,22ABQ ∠=∠在CDQ ∆与ABQ ∆中,CQD AQB ∠=∠2122C A ∴∠+∠=∠+∠①在CDE ∆与MBE ∆中,CED MEB ∠=∠12C M ∴∠+∠=∠+∠②用2⨯-②①得:2C M A ∠=∠-∠27A ∠=︒,33M ∠=︒2332739C ∴∠=⨯︒-︒=︒故39C∠=︒【点睛】角平分线的性质及对顶角相等、角的和差计算是本题的考点,根据题意求得2C M A∠=∠-∠是解题的关键.23. (1)50°;(2)140EOBα∠=︒-;(3)168或72.【分析】(1)利用角平分线的定义和邻补角的定义求得∠BOC和∠EOC,再利用角的和差即可求得∠BOE;(2)先根据已知数量关系求得∠DOE,再利用角的和差即可得出结论;(3)设BOF n∠=︒,分①若DOE∠在AOC∠的内部,②当DOE∠在射线OC的两侧时两种情况,利用角的和差列出方程求解即可.【详解】解:(1)∵120AOC∠=︒,OD平分AOC∠,∴60AOD DOC∠=∠=︒,60BOC∠=︒,又70DOEα∠==︒,∴706010COE∠=︒-︒=︒,∴6050BOE COE∠=︒-∠=︒;(2)∵120AOC∠=︒,2DOC AOD∠=∠,∴1403AOD AOC∠=∠=︒,80DOC∠=︒,60BOC∠=︒,∴80EOCα∠=︒-,∴6080140 EOB BOC EOCαα∠=∠+∠=︒+︒-=︒-;(3)①如图,若DOE∠在AOC∠的内部设BOF n∠=︒则依题意有:()11118090222AOD FOA n n ∠=∠=︒-︒=︒-︒, ∵120AOC ∠=︒,90DOE α∠==︒,∴1209030AOD EOC AOC DOE ∠+∠=∠-∠=︒-︒=︒,又∵OH 平分EOC ∠,∴()113022EOH EOC AOD ∠=∠=︒-∠111309030224n n ⎛⎫=︒-︒+︒=︒-︒ ⎪⎝⎭, 又120FOH ∠=︒,∴1118090903012024n n n ︒-︒+︒-︒+︒+︒-︒=︒,∴168n =;②当DOE ∠在射线OC 的两侧时如图设BOF n ∠=︒,则依题意有119022AOD AOF n ∠=∠=︒-︒,∵120AOC ∠=︒,90DOE α∠==︒,∴190120602COE AOD n ∠=∠+︒-︒=︒-︒,又OH 平分EOC ∠,∴113024EOH EOC n ∠=∠=︒-︒,又120FOH ∠=︒,∴1130909012042n n n ⎛⎫︒+︒-︒+︒-︒-︒=︒ ⎪⎝⎭, ∴72n =,∴综上所述OF 顺时针旋转的角度为168或72.【点睛】本题考查邻补角的有关计算,角平分线的有关计算,角的和差,一元一次方程的应用.(3)中能分类讨论画出图形,结合图形利用角的和差列出方程是解题关键.24. 见解析【分析】根据邻补角和对顶角的性质进行设计即可.【详解】方法一:如图所示,延长AO至C,测量∠BOC的度数,根据邻补角的性质得:∠AOB=180°-∠BOC,即可求解;方法二:如图所示,分别延长AO,BO,测量∠COD的度数,根据对顶角相等得:∠AOB=∠COD,即可求解.【点睛】本题考查邻补角和对顶角的实际应用,熟记基本定义和性质并灵活运用是解题关键.。
5.1相交线习题

(D)(C)(B)(A)22211121《5.1相交线》练习题班级 姓名 得分一:填空、选择题(每题5分)1、直线AB 、CD 相交于点O ,若∠AOC=50度,则∠∠BOD= 。
2、如右图,直线AB 与CD 相交于点O ,射线OE 平分∠已知∠AOD=40度,则∠COE= ,∠BOD= 3、若∠1与∠2是对顶角,∠3与∠2互余,且∠3=60那么∠1= 。
4、若∠1与∠2是对顶角,且∠1与∠2互余,则∠1=__ ___5、如图,直线AB 、CD 交于点O ,则 (1)若∠1+∠3=68度,则∠1= 。
(2)若∠2:∠3=4:1,则∠2= 。
(3)若∠2-∠1=100度,则∠3= 。
第5题6、下列各图中,∠1和∠2是对顶角的是( )7、已知直线AB 、CD 相交于点O ,则与∠AOC 互补的角有( )A 、1个B 、2个C 、3个D 、4个 第7题 8、如图,三条直线两两相交,其中对顶角共有( ) A 、3对 B 、4对 C 、5对 D 、6对9、下列说法错误的是 ( ) 第9题A 、对顶角的平分线成一个平角B 、对顶角相等C 、相等的角是对顶角D 、对顶角的余角相等 10、如右图,直线AB 、CD 交于点O ,OE 、OF 是过O 点 的两条射线,其中构成对顶角的是( ) A 、∠AOF 与 ∠DOE B 、∠EOF 与∠BOEC 、∠BOC 与∠AOD D 、∠COF 与∠BOD321O DBCA ODCBAOF EDCB AEDOCBA321OFE D CB A11、下列说法中正确的个数有 ( )(1)直线外一点与直线上各点连接的所有线中垂线段最短。
(2)画一条直线的垂线段可以画无数条。
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直。
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离。
A 、1个 B 、2个 C 、3个 D 、4个12、如图2-28,∠1与∠2不能构成同位角的图形是 ( )13、如图2-29,图中共有同旁内角( )A .2B .3C .4D .514、如图2-30,与∠1构成同位角的共有 ( )A .1个B .2个C .3个D .4个三:解答题(每题10分)15、如图,直线AD 和BE 相交于O 点,OC ⊥AD ,∠COE=70度,求∠AOB 的度数。
人教版七年级下册数学5.1.1相交线与平行线练习题(含答案)
第五章相交线与平行线5.1.1相交线知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( )3.下面四个图形中,∠1与∠2是邻补角的是( )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是,∠1的对顶角是.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( )A.120° B.90° C.60°D.30°7.如图,测角器测得工件(圆台)的角度是度,其测量角的原理是.第4题图第5题图第6题图第7题图8.在括号内填写依据:如图,因为直线a,b相交于点O,所以∠1+∠3=180°( ),∠1=∠2( ).AB9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是___________,∠EOC 的对顶角是___________②∠AOC 的邻补角是_________________,∠BOE 的邻补角是__________________. ③若∠AOC=50°,求∠BOD ,∠COB 的度数. 解:∵∠AOC=50° ∴∠BOD=__________=________( ); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠________( )=180°-________°=________°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.【综合训练】11.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( )A .62°B .118°C .72°D .59°第12题图 第13题图14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x = . 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为 . 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD=__________=________( );∵OE 平分∠AOD ∴∠AOE=21___________( ) ∵∠AOD+∠AOC=180°∴∠AOD=180°-∠________( )=_________________________=___________ ∠AOE=____________.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.20.探究题:(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有 个交点,最多有 个交点,对顶角有 对,邻补角有 对.OE DC BA第五章相交线与平行线5.1.1相交线答案知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( A )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( C )3.下面四个图形中,∠1与∠2是邻补角的是( D )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2,∠4,∠1的对顶角是∠3.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( C )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( A )A.120° B.90° C.60°D.30°AB 7.如图,测角器测得工件(圆台)的角度是40度,其测量角的原理是对顶角相等.8.在括号内填写依据:如图,因为直线a ,b 相交于点O , 所以∠1+∠3=180°(邻补角互补), ∠1=∠2(对顶角相等).9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是_∠BOC__,∠EOC 的对顶角是__∠DOF___ ②∠AOC 的邻补角是_∠AOD____,∠BOE 的邻补角是___∠AOE__. ③若∠AOC=50°,求∠BOD ,∠COB 的度数.解:∵∠AOC=50°∴∠BOD=_∠AOC_=_50°(对顶角相等); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠AOC (邻补角互补) =180°- 50° = 130°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.解:因为OA 平分∠EOC ,∠EOC =70°, 所以∠AOC =12∠EOC =35°.所以∠BOD =∠AOC =35°. 【综合训练】11.下列说法正确的有( B )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( C )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( A )A .62°B .118°C .72°D .59° 14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x=40或80. 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为135°. 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=140°.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD= ∠AOC = 120° (对顶角相等); ∵OE 平分∠AOD∴∠AOE=21∠AOD∵∠AOD+∠AOC=180°∴∠AOD=180°-∠AOC (邻补角互补)=180°-120°= 60° ∠AOE= 30°.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.解:因为∠AOE =∠BOE ,且∠AOE +∠BOE =180°, 所以∠AOE =∠BOE =90°. 因为∠DOE =50°,所以∠DOB =∠BOE -∠DOE =40°.因为OB 平分∠DOF ,所以∠DOF =2∠DOB =80°.OE DCBA19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数. 解:设∠1=∠2=x °,则∠3=8x °. 由∠1+∠2+∠3=180°,得 10x =180.解得x =18. 所以∠1=∠2=18°. 所以∠4=∠1+∠2=36°. 20.探究题:(1)三条直线相交,最少有1个交点,最多有3个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有1个交点,最多有6个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有1个交点,最多有n (n -1)2个交点,对顶角有n(n -1)对,邻补角有2n(n -1)对.解:(1)图略,对顶角有6对,邻补角有12对. (2)图略,对顶角有12对,邻补角有24对.。
《5.1相交线》练习题

(D)(C)(B)(A)22211121《5.1相交线》练习题一1、下列各图中,∠1和∠2是对顶角的是( )2、已知直线AB 、CD 相交于点O ,则与∠AOC 互补的角有 ( ) A 、1个 B 、2个 C 、3个 D 、4个3、如图,三条直线两两相交,其中对顶角共有 ( ) A 、3对 B 、4对 C 、5对 D 、6对4、如图,直线AB 、CD 交于点O ,OE 、OF 是过O 点的两条射线,其中构成对顶角的是 ( )A 、∠AOF 与 ∠DOEB 、∠EOF 与∠BOEC 、∠BOC 与∠AOD D 、∠COF 与∠BOD5、下列说法错误的是 ( )A 、对顶角的平分线成一个平角B 、对顶角相等C 、相等的角是对顶角D 、对顶角的余角相等 6、如图,直线AB 与CD 相交于点O ,∠AOD+∠BOC=236度,则∠AOC 的度数为 ( )A 、72度B 、62度C 、124度D 、144度 7、如图,点A 到直线CD 的距离是指哪条线段长 ( )A 、ACB 、CDC 、AD D 、BD 8、在“同一平面内,过一点有且只有一条直线与已知直线垂直”中这一点的位置 ( )A 、在直线的上方B 、在直线的下方C 、在直线上D 、可以任意位置9、下列说法中正确的个数有 ( ) (1)直线外一点与直线上各点连接的所有线中垂线段最短。
(2)画一条直线的垂线段可以画无数条。
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直。
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离。
A 、1个 B 、2个 C 、3个 D 、4个10、如图2-27,∠BAC 和∠ACD 是( )A .同位角B .同旁内角C .内错角D .以上结论都不对O F E D CBA ODCBADABC11、如图2-28,∠1与∠2不能构成同位角的图形是 ( )12、如图2-29,图中共有同旁内角 对A .2B .3C .4D .513、如图2-30,与∠1构成同位角的共有 ( )A .1个B .2个C .3个D .4个 14、如图2-31,下列判断正确的是 [ ]A .4对同位角,4对内错角,2对同旁内角B .4对同位角、4对内错角,4对同旁内角C .6对同位角,4对内错角,4对同旁内角D .6对同位角,4对内错角,2对同旁内角15、如图,直线AB 、CD 相交于点O ,若∠AOC=50度,则∠BOC= ,∠AOD= ∠BOD= 。
人教版初中数学七年级下册第五章第一节《5.1相交线》同步练习题(含答案)

人教版初中数学七年级下册第五章第一节《 5.1相交线》同步练习题(含答案)5.1《相交线》同步练习题、选择题(每小题只有一个正确答案) 1 •如图所示,/ 1与/2不是同位角的是()A.2 .在同一平面内,下列说法中,错误的是 A. 过两点有且只有一条直线B. 过一点有无数条直线与已知直线平行C. 过直线外一点有且只有一条直线与已知直线平行D. 过一点有且只有一条直线与已知直线垂直3 .已知:0A 丄 0C , / AOB :/ AOC , 2 : 3,则/ BOC 的度数为( ),A. 30 °B.60 °C. 150 °D.30。
或 150 °4.如图,点A 到线段BC 所在直线的距离是线段()A. / 1和/ 3是同位角B. / 1和/ 5是同位角C. / 1和/ 2是同旁内角D. / 5和/6是内错角6 .两条直线相交所构成的四个角中:①有三个角都相等;②有一对对顶角互补;③有 一个角是直角;④有一对邻补角相等.其中能判定这两条直线垂直的有 ( ) A. 1个 B. 2个 C. 3个 D. 4个7 .平面上三条直线两两相交最多能构成对顶角的对数是( A. 7 B. 6 C. 5 D. 4二、填空题8.如图,直线a 与b 相交于点 0,直线c 丄b ,且垂足为0,若/仁35 °,则/2= ______________D.A. AC 的长度B. AD 的长度C. AE 的长度5. 如图所示,下列说法错误的是()D. AB 的长度9 .如图,计划把河水引到水池 A 中,先作AB 丄CD ,垂足为B ,然后沿AB 开渠,能使 所开的渠道最短,这样设计的依据是 _______________10 .两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x) °,则 x= _________11 .如图,在平面内,两条直线 l i , 12相交于点0,对于平面内任意一点 M ,若p , q 分 别是点M 到直线11,12的距离,则称(p, q)为点M 的距离坐标”.根据上述规定, 距离 坐标”是(2,1的点共有 _____________________ 个.三、解答题13 .如图,直线 AB, CD 相交于点 0, / BOE=90°,OF 平分/ AOD / COE=20°,求/ BOD 与/ DOF 的度数.BC D(1)/ 1和/ 3是直线 被直线 所截得的 (2)/ 1和/ 4是直线 被直线 所截得的 (3)/ B 和/2是直线被直线 所截得的 (4)/ B 和/4是直线被直线所截得的12 .看图填空:人教版初中数学七年级下册第五章第一节《 5.1相交线》同步练习题(含答案)14 .在同一平面内三条直线交点有多少个? 甲:同一平面三直线相交交点的个数为 0个,因为a , b ,c 如图(1)所示.乙:同一平面内三条直线交点个数只有 1个,因为a , b,c 交于同一点0,如图(2)所示.以上说法谁对谁错?为什么?15 .已知,如图,直线AB 和CD 相交于点 0, / C0E 是直角,0F 平分/ AOE, / COF=34°, 求/ A0C和/ BOD 的度数.16 .探究题:(I)(1) 三条直线相交,最少有____ 个交点;最多有 _____ 个交点,画出图形,并数出图形中的对顶角和邻补角的对数;(2) 四条直线相交,最少有____ 个交点;最多有 _______ 个交点,画出图形,并数出图形中的对顶角和邻补角的对数;(3) 依次类推,n条直线相交,最少有________ 个交点;最多有_______ 个交点,对顶角有对,邻补角有__________ 对.参考答案I. B2. B3. D4. B5. B6. D7. B8. 55°9•垂线段最短10. 40 或80II. 4,12. 解析:根据同旁内角、同位角及内错角的概念可得:(1) / 1和/3是直线AB、BC被直线AC所截得的同旁内角;(2) / 1和/ 4是直线AB, BC被直线AC所截得的同位角;(3) / B和/ 2是直线AB, AC被直线BC所截得的同位角;(4) / B和/4是直线AC, BC被直线AB所截得的内错角•13. / BOD=70°, / DOF=55°解:•••/ COE=20°,Z BOE=90°,•••/ BOD=180°, 20°, 90° =70°,•••/ AOD—180°, 70° =110°,•/ OF 平分/ AOD ,1• / DOF=-/AOD=55°,•••/ BOD=70°,Z DOF=55°.14. 甲,乙说法都不对,各自少了三种情况,具体见解析解析:甲、乙说法都不对,都少了三种情况.a// b,c与a,b相交如图(1);a,b,c两两相交如图(2),所以三条直线互不重合,交点有0个或1个或2个或3个,共四种情况15. / AOC=22 , / BOD=22 .解析:,,COE=90 , , COF=34 ,,,EOF= COE , COF=56°,,OF是,AOE的平分线,,,AOE=2, EOF=112°,,,AOC=112°, 90 ° =22 ° ,,,BOD和,AOC是对顶角,,,BOD=22°,16. (1)1,3,画图见解析,对顶角有6对,邻补角有12对;(2)1,6, 画图见解析,对顶角有12对,邻补角有24对;(3)1, n n 1,n(n —1),2 n(n —1).2分析:当直线同交于一点时,只有一个交点;当直线两两相交,且不过同一点时,交点个数2最多;根据对顶角与邻补角的定义找出即可.;1三条直线相交,最少有 1个交点,最多有3个交点,如图:对顶角:6对,邻补角:12对;;2四条直线相交,最少有 1个交点,最多有6个交点,如图:对顶角:12对,邻补角:24对;n n 1(3) n 条直线相交,最少有 1个交点,最多有 个交点,对顶角有 n (n - 1)对,2邻补角有2n (n - 1)对. 丄,“宀,n n 1故答案为:(1) 1, 3 ; (2) 1, 6; (3) 1, , n ( n- 1), 2n (n - 1).2。
最新人教版七年级数学下册《5.1相交线》同步练习(含答案)

最新人教版七年级数学下册《5.1相交线》同步练习(含答案)相交线与平行线 5.1 相交线同步练习一、单选题(共10题;共30分)1.如图所示,∠1和∠2是对顶角的图形有( )A. 1个B. 2个C. 3个D. 4个 2.如图,下列说法不正确的是()A. ∠1和∠2是同旁内角B. ∠1和∠3是对顶角C. ∠3和∠4是同位角 D. ∠1和∠4是内错角3.如图所示,∠1和∠2是对顶角的是() A.B.C.D.4.下列说法中正确的个数为()①两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直;②两条直线相交成四个角,如果有一个角是直角,那么这两条直线垂直;③一条直线的垂线可以画无数条;④在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直. A. 1 B. 2 C. 3 D. 4 5.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为()A. 75°B. 15°C. 105°D. 165° 6.如图所示,下列说法错误的是()A. ∠A和∠B是同旁内角B. ∠A和∠3是内错角C. ∠1和∠3是内错角 D. ∠C和∠3是同位角7.如图,三条直线相交于点O.若CO⊥AB,∠1=56°,则∠2等于()A. 30°B. 34°C. 45°D. 56° 8.在下列语句中,正确的是().A. 在平面上,一条直线只有一条垂线;B. 过直线上一点的直线只有一条; C. 过直线上一点且垂直于这条直线的直线有且只有一条;D. 垂线段就是点到直线的距离 9.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有 ( )A. 1个B. 2个C. 3个D. 4个 10.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是()①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.A. ①②③B. ①②④C. ①③④D. ②③④二、填空题(共10题;共30分)11.如图,CD相交于点O,EO⊥AB,直线AB,垂足为点O,若∠AOD=132°,则∠EOC=________12.如图,OA平分∠COE,已知直线AB与CD相交于点O,若∠DOE=70°,则∠BOD=________.13.如图,∠1和∠2是________角,∠2和∠3 是________角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交线同步练习题
一、选择题:(每小题3分,共15分)
1.如图所示,∠1和∠2是对顶角的图形有( )
12
12
1221
A.1个
B.2个
C.3个
D.4个
2.如图1所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )
A.150°
B.180°
C.210°
D.120°
O F E
D C B A
(1)
3.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角
一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个
B.2个
C.3个
D.4个
4.如图2所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,
则∠AOC•的度数为( ) A.62° B.118° C.72° D.59°
60︒
30︒34l 3
l 2l 1
12
(2)
5.如图3所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°;
B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°;
D.∠1=∠3=90°,∠2=60°,∠4=30°
O
D C B A
(3)
二、填空题:(每小题2分,共16分)
1. 如图4所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
34D
C B A
12
(4)
2.如图4所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.
3.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC
的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.
O F
E
D C B
A
4.如图6所示,已知直线AB,CD 相交于O,OA 平分∠EOC,∠EOC=70°,则∠
BOD=•______.
O E
D C B A
5.对顶角的性质是______________________.
6.如图7所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.
O D C
B A
1
2
7.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•
则∠EOB=______________. O E
D C B A
8.如图9所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部
分,• 且∠BOE:∠EOD=2:3,则∠EOD=________.
O E
D
C
B
A
三、训练平台:(每小题10分,共20分)
1. 如图所示,AB,CD,EF 交于点O,∠1=20°,∠BOC=80°,求∠2的度数.
O F
E D C B
A 1
2
2. 如图所示,L 1,L 2,L 3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
34l 3
l 2
l 1
12
=。
