§6 余弦函数的图像与性质
余弦函数的图像与性质
[ 2 2k， 2 2k ](k z)，单调递增 [(2k 1)，2k ](k z)，单调递增 [ 2 2k，3 2 2k ](k z)，单调递减 [2k , (2k 1) ](k z)，单调递减
函数y=cosx有对称性吗？
y
1
-3 5 -2 3
2
2
-
o 2
2
-1
3
2
2
5 2
§6 余弦函数的图像与性质
y
1
-3 5 -2 3
2
2
-
o 2
-1
2
3
2
2
5 2
x
3
7 2
4
1.会用“五点法”作余弦函数的图像. 2.掌握余弦函数y=cosx的图像和性质. 3.会应用余弦函数y=cosx的图像与性质解决一些简单问题.
利用变换法作余弦函数的图
像
y
余弦曲线
1
6
4
2
o
-1
3
2
2
5 2
x
3
7 2
4
例2：比较 cos 5 和 cos( 7 ) 大小
y
4
5
1-
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 2
5 3
11 6
2
x
-1 -
cos 5 cos( 7 )
4
5
对于实数范围内的x，分别写出满足sinx=cosx, sinx>cosx, sinx<cosx的x的集合.
x
3
7 2
4
对称轴方程x=k(k∈Z) 对称中心为(k+/2,0)(k∈Z)
余弦函数的图像与性质PPT
所以 cos 3＜sin 1 ＜ cos 7 .
2
10
4
答案: cos 3＜sin 1 ＜ cos 7
2
10
4
类型一 余弦函数的图像及应用 【典例】用“五点法”作函数y=1-cosx(0≤x≤2π)的 简图.
世纪金榜导学号70034021
【审题路线图】用“五点法”作函数y=1-cosx(0≤x≤2π) 的简图⇒根据余弦函数图像的五个关键点列表⇒在坐标 系中描出五个关键点⇒用平滑的曲线连接五个点.
2.比较下列各组数的大小.
(1)-sin46°与cos221°.
2cos( 23 )与cos( 17 ).
5
4
【审题路线图】1.配方法⇒求出最值⇒写出值域. 2.用诱导公式化角在同一单调区间内⇒利用正(余)弦函 数单调性⇒写出答案.
【解析】1.y (cos x 1 )2 1 .
24
因为-1≤cosx≤1,
所以当cosx=1
2
时,ymax=
1 4
.
当cosx=-1时,ymin=-2.
所以函数y=-cos2x+cosx的值域是[2，1 ].
4
答案: [2，1]
4
2.(1)-sin46°=-cos44°=cos136°, cos221°=-cos41°=cos139°. 因为180°>139°>136°>0°, 所以cos139°<cos136°,即-sin46°>cos221°.
【解析】列表:
x cosx
0
π 3
2π
2
2
1
0
-1
0
1
1-cosx
01
2
高中数学第一章 §6 余弦函数的图像与性质
[核心必知]余弦函数的图像与性质[问题思考]1．如何由y ＝cos x ，x ∈R 的图像得到y ＝sin x ，x ∈R 的图像？提示：只需将y ＝cos x ，x ∈R 的图像向右平移π2个单位即可得到y ＝sin x ，x ∈R 的图像，并且方法不唯一．2．余弦函数在第一象限内是减函数吗？提示：不是．余弦函数y ＝cos x 在[0，π2]内是减函数，但不能说在第一象限是减函数，如390°和60°都是第一象限的角，虽然390°>60°，但cos 60°＝12，cos 390°＝32.却有cos 60°<cos 390°.所以函数y ＝cos x 在第一象限内不是减函数．3．余弦函数是轴对称图形，不是中心对称图形，这句话对吗？提示：不对．余弦函数与正弦函数一样既是轴对称图形，也是中心对称图形．它的对称轴有无数条，其方程是x ＝k π(k ∈Z )；它的对称中心有无数个，其坐标为(k π＋π2，0)(k ∈Z )．讲一讲1．画出函数y ＝1－cos x ，x ∈[0，2π]的图像． [尝试解答] 按五个关键点列表：如图所示：1．画余弦函数的图像，与画正弦函数图像的方法一样，关键要确定五个点．这五个点的坐标是(0，1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫3π2，0，(2π，1)． 2．形如y ＝a cos x ＋b ，x ∈[0，2π]的函数，也可由五点法画图像． 练一练1．用“五点法”画出y ＝3＋2cos x (x ∈[0，2π])的图像． 解：(1)列表(2)讲一讲2．(1)求下列函数的定义域． ①y ＝32－cos x ； ②y ＝log 12(2cos x －2)．(2)求函数y ＝3－2cos(2x －π3)，x ∈⎣⎢⎡⎦⎥⎤π6，π2的值域． [尝试解答] (1)①要使函数有意义，则有32－cos x ≥0， ∴cos x ≤32.可得2k π＋π6≤x ≤2k π＋11π6，k ∈Z . 故所求函数的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪2k π＋π6≤x ≤2k π＋11π6，k ∈Z .②要使函数有意义，则有2cos x －2>0， ∴cos x >22，故所求定义域为 ⎩⎨⎧⎭⎬⎫x ⎪⎪⎪2k π－π4<x <2k π＋π4，k ∈Z .(2)∵π6≤x ≤π2，∴0≤2x －π3≤2π3.∵y ＝cos x 在[0，π]上单调递减， ∴－12≤cos(2x －π3)≤1，∴1≤3－2cos(2x －π3)≤4，故函数的值域为[1，4]．1．求三角函数的定义域，应归结为解三角不等式，其关键就是建立使函数有意义的不等式(组)，利用三角函数的图像直观地求得解集．2．求三角函数的值域，要充分利用sin x 和cos x 的有界性，对于x 有限制范围的，可结合图像求值域．练一练2. 求函数y ＝3cos 2x －4cos x ＋1，x ∈⎣⎢⎡⎦⎥⎤π3，2π3的最值．解：y ＝3cos 2x －4cos x ＋1＝3(cos x －23)2－13.∵x ∈⎣⎢⎡⎦⎥⎤π3，2π3，cos x ∈⎣⎢⎡⎦⎥⎤－12，12，从而当cos x ＝－12，即x ＝2π3时，y max ＝154；当cos x ＝12，即x ＝π3时，y min ＝－14.∴函数在区间⎣⎢⎡⎦⎥⎤π3，2π3上的最大值为154，最小值为－14.讲一讲3．(1)判断函数f (x )＝cos(π－x )－x cos(π2－x )的奇偶性．(2)求函数y ＝cos(π6－x )的单调减区间．[尝试解答] (1)∵f (x )＝cos(π－x )－x cos(π2－x )＝－cos x －x sin x ，∴f (－x )＝－cos(－x )－(－x )sin(－x ) ＝－cos x －x sin x ＝f (x )． ∴函数f (x )是偶函数．(2)y ＝cos(π6－x )＝cos(x －π6)，令2k π≤x －π6≤π＋2k π(k ∈Z )，得π6＋2k π≤x ≤7π6＋2k π(k ∈Z )． ∴函数y ＝cos ⎝ ⎛⎭⎪⎫π6－x 的单调减区间是⎣⎢⎡⎦⎥⎤π6＋2k π，7π6＋2k πk ∈Z .1．判断三角函数的奇偶性，首先要观察定义域是否关于原点对称，在定义域关于原点对称的前提下，再根据f (－x )与f (x )的关系确定奇偶性．2．确定三角函数的单调区间，在理解基本三角函数的单调性的前提下，运用整体代换的思想求解．练一练3．比较下列各组值的大小． (1)cos ⎝ ⎛⎭⎪⎫－7π8与cos 7π6；(2)sin 194°与cos 160°.解：(1)cos ⎝ ⎛⎭⎪⎫－7π8＝cos 7π8＝cos ⎝ ⎛⎭⎪⎫π－π8 ＝－cos π8.而cos 7π6＝－cos π6∵0<π8<π6<π2.∴cos π8>cos π6.∴cos ⎝ ⎛⎭⎪⎫－7π8<cos 7π6.(2)∵sin 194°＝sin(180°＋14°) ＝－sin 14°＝－cos 76°， cos 160°＝cos(180°－20°) ＝－cos 20°.∵0°<20°<76°<90°， ∴cos 20°>cos 76°， ∴－cos 20°<－cos 76°， ∴sin 194°>cos 160°.函数y ＝2cos x (0≤x ≤2π)的图像和直线y ＝2围成一个封闭的平面图形，则这个封闭图形的面积是( )A ．4B ．8C ．2πD ．4π [解析] 法一：作出函数y ＝2cos x ，x ∈[0，2π]的图像，函数y ＝2cos x ，x ∈[0，2π]的图像与直线y ＝2围成的平面图形，如图(1)所示的阴影部分．利用图像的对称性可知该平面图形的面积等于矩形OABC 的面积， 又∵|OA |＝2，|OC |＝2π， ∴S 平面图形＝S 矩形OABC ＝2×2π＝4π. 法二：利用余弦曲线的特点，该平面图形的面积等于三角形ABC 的面积(如图(2))． ∵|AC |＝2π，B 到AC 距离等于4.∴S 平面图形＝S △ABC ＝ 12×2π×4＝4π.法三：利用余弦曲线的特点，该平面图形的面积等于矩形ABCD 的面积(如图(3)) ∵|AB |＝π，|AD |＝4. ∴S 平面图形＝S 矩形ABCD ＝4π. [答案] D1．函数y ＝2cos x －1的最大值、最小值分别是( ) A ．2，－2 B ．1，－3 C ．1，－1 D ．2，－1解析：选B ∵－1≤cos x ≤1∴－2≤2cos x ≤2， ∴－3≤2cos x －1≤1， ∴最大值为1，最小值为－3.2．函数y ＝－cos x 在区间[－π，π]上是( ) A ．增加的 B ．减少的C ．先增加后减少D ．先减少后增加解析：选D 作出y ＝－cos x 的图像可得选项D 正确． 3．函数y ＝sin x 和y ＝cos x 都是减少的区间是( ) A.⎣⎢⎡⎦⎥⎤2k π－π2，2k π(k ∈Z ) B.⎣⎢⎡⎦⎥⎤2k π－π，2k π－π2(k ∈Z )C.⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋π(k ∈Z )D.⎣⎢⎡⎦⎥⎤2k π，2k π＋π2(k ∈Z )解析：选 C 在同一坐标系中作出y ＝sin x 和y ＝cos x 的图像，由图像可知在⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋π上，y ＝sin x 和y ＝cos x 都是减少的．4．函数y ＝cos x1＋cos x 的定义域是________．解析：由1＋cos x ≠0得cos x ≠－1 ∴x ≠π＋2k π，k ∈Z∴ 定义域是{}x |x ≠π＋2k π，k ∈Z . 答案： {}x |x ≠π＋2k π，k ∈Z5．当x ∈[0，2π]时，方程sin x ＝cos x 的解集是________． 解析：在同一坐标系内画出y ＝sin x 和y ＝cos x ，x ∈[0，2π]的图像，如图，可得x ＝π4或x ＝5π4.答案： {π4，5π4}6．比较cos ⎝ ⎛⎭⎪⎫－23π5与cos ⎝ ⎛⎭⎪⎫－17π4的大小．解：cos ⎝ ⎛⎭⎪⎫－23π5＝cos 23π5＝cos 3π5. cos ⎝⎛⎭⎪⎫－17π4＝cos 17π4＝cos π4. 因为0<π4<3π5<π，且函数y ＝cos x ，x ∈[0，π]是减少的． 所以cos π4>cos 3π5即cos ⎝ ⎛⎭⎪⎫－23π5<cos ⎝ ⎛⎭⎪⎫－17π4.一、选择题1．下列对y ＝cos x 的图像描述错误的是( )A ．在[0，2π]和[4π，6π]上的图像形状相同，只是位置不同B ．介于直线y ＝1与直线y ＝－1之间C ．关于x 轴对称D ．与y 轴仅有一个交点 答案：C2．函数y ＝|cos x |的一个单调减区间是( )A.⎣⎢⎡⎦⎥⎤－π4，π4B.⎣⎢⎡⎦⎥⎤π4，3π4C.⎣⎢⎡⎦⎥⎤π，3π2D.⎣⎢⎡⎦⎥⎤3π2，2π解析：选C 作出函数y ＝|cos x |的图像如图所示，由图像可知，A 、B 都不是单调区间，D 是单调增区间，C 是单调减区间． 3．函数y ＝cos(x ＋π6)，x ∈⎣⎢⎡⎦⎥⎤0，π2的值域是( )A ．(－32，12] B.⎣⎢⎡⎦⎥⎤－12，32 C.⎣⎢⎡⎦⎥⎤32，1 D.⎣⎢⎡⎦⎥⎤12，1解析：选B ∵0≤x ≤π2，∴π6≤x ＋π6≤2π3， ∵y ＝cos x 在[0，π]上为减函数． ∴－12≤cos(x ＋π6)≤32.4．设方程cos 2x ＝1的解集为M ，方程sin 4x ＝0的解集为P ，则M 与P 的关系为( ) A ．MP B ．M PC ．M ＝PD ．M ∩P ＝∅解析：选A 由cos 2x ＝1得2x ＝2k π(k ∈Z )，即x ＝k π(k ∈Z )；由sin 4x ＝0得4x ＝k π(k ∈Z )，即x ＝k π4(k ∈Z )．∴MP .二、填空题5．函数y ＝x cos x 的奇偶性是________．解析：∵f (－x )＝－x ×cos(－x )＝－x cos x ＝－f (x )， ∴此函数是奇函数． 答案：奇函数6．比较大小：sin 3π5________cos π5.解析：∵sin 3π5＝sin(π－2π5)＝sin 2π5＝sin(π2－π10)＝cos π10，0<π10<π5<π2. ∴cos π10>cos π5，即sin 3π5>cos π5.答案：>7．方程x 2＝cos x 的解的个数是________．解析：在同一坐标系中画出函数y ＝cos x 与y ＝x 2的图像(如图)，可知有两个交点．答案：28．函数y ＝11－cos x 的值域是________．解析：∵0<1－cos x ≤2. ∴11－cos x ≥12.∴ 函数的值域为⎣⎢⎡⎭⎪⎫12，＋∞. 答案：⎣⎢⎡⎭⎪⎫12，＋∞三、解答题9．求函数y ＝cos(3x －π4)的单调减区间． 解：由2k π≤3x －π4≤2k π＋π，k ∈Z ， 得2k π＋π4≤3x ≤2k π＋5π4，k ∈Z ， ∴2k π3＋π12≤x ≤2k π3＋5π12，k ∈Z . ∴单调递减区间是⎣⎢⎡⎦⎥⎤2k π3＋π12，2k π3＋5π12(k ∈Z )． 10．求函数y ＝cos 2x ＋cos x ＋1的最大、最小值及使y 取最值的x 的集合．解：令t ＝cos x ，则t ∈[－1，1]．∴y ＝t 2＋t ＋1，对称轴t ＝－12. ①当t ＝－12，即x ∈{x |x ＝±23π＋2k π，k ∈Z }时，y min ＝34. ②当t ＝1，即x ∈{x |x ＝2k π，k ∈Z }时，y max ＝3.。
第1章 §6 6.1 余弦函数的图像 6.2 余弦函数的性质
小 结
·
探
提
新 知
因为 y＝cos x＝sin x＋π2，所π 以余弦函数 y＝cos x 的图像可以通
素 养
合 作
过将正弦曲线 y＝sin x 向左__平移_2_个单位长度得到．如图是余弦函数
课
探
时
究 y＝cos x(x∈R)的图像，叫作余弦曲线．
分 层
释
作
疑
业
难
·
返 首 页
·
5
(2)利用五点法作余弦函数的图像
D [f(x)＝sin x－π2＝－sin π2－x＝－cos x，由f(x)＝cos x的性
作 业
·
质可判断A、B、C均正确．]
返
首
页
14
·
自 主 预
4．已知函数y＝－
3 4
cos
课
x，x∈[0，2π]，则其递增区间为 堂 小
习
结
·
探 ________．
提
新
素
知
[0，π] [当x∈[0，2π]时，函数y＝cos x在[0，π]上是减函数，在 养
究
分
层
释
作
疑
业
难
由上图可得sin x≥cos x在[0，2π]上的解集为π4，54π.
返 首 页
·
27
·
余弦函数的单调性及应用
自
课
主 预 习
【例3】 (1)求函数y＝1－12cos x的单调区间；
堂 小 结
·
探
提
新 知
合 作 探
([2解)比] 较(1c)o∵s －－12π7<0与，cos 187π的大小．
提
余弦函数的图像和性质
作业：P40，1(2)并求定义域、 值域、最大最小值。 下节课再见啦*^_^*
； https:// 必富LG游戏 LG大宝游戏 LG游戏平台 PT游戏平台
；
还是和前两次一样.他决定拼一把,开始神血秘典の第四步——断血. 盘坐在祭坛中央,白重炙运起"夜皇决",封闭了身体中の阴脉和阳脉之间の连接穴道,直接断绝了两脉之间の血液流通. 顿时,白重炙の身体逐渐红了起来,体表の血脉条条鼓了起来. "好难受,这就是断血吗?这么好像被人捏住脖 子,要断气の感觉一样?啊?头怎么那么晕?神之精血怎么还不自救?" 此刻白重炙感觉自己就好像被人按住脑袋沉入水底般,那种要断气の感觉竟然是那么の恐怖.而且他の头脑也开始发晕,这是脑海开始缺氧の症状. 坚持,坚持！ 白重炙脑海中只留下坚持几个字,最后时候他选择了相信自己那个高 人老爹.死死控制"夜皇决"坚决封闭着穴道,断绝了血液の流通. 而此刻の白重炙,如果有外人看到の话,肯定会惊叫起来.因为此刻の白重炙早已不复原来の那位冷峻青年摸样.全身青筋暴涨,密密麻麻遍布全身,皮肤全部红の刺眼,耳口鼻开始慢慢渗血.全身看起来狰狞恐怖,恍如恶魔. 糟糕！ 白 重炙心里一疙瘩,暗暗叫苦起来,同时嘴里大量冒出鲜血.由于长期封闭血脉,血脉终于承受不住重荷爆裂开来. 完了！这下真の飘然西去死翘翘了…… 白重炙心里长叹一声,此刻他脑海却异常清醒,似乎到了回光返照の那一刻.恍惚间,他仿佛感觉自己可以看见自己の身体阴脉寸寸爆裂,大量の鲜 血狂涌而出.而且此刻他还仿佛能透过浓浓の白雾,看到了战智堂里众人面部各异の表情.他还看见妹妹夜轻语正站在旁边の角落里,遥遥の眺望着自己这个光圈,满脸の希翼,满脸の柔情…… 就在白重炙即将陷入昏迷,因大量失血而昏死过去之时. 他左手带着の那枚青铜戒指突然闪耀出一阵白色 の光芒,接着一股犹如绸缎般の白色气流缓缓从戒指中冒出,从他手指流入白重炙の身体里. 突兀の—— 白色气流从左手开始快速の向身体涌去,而最令人惊奇之处是,白色气流所流过之处,白重炙体表の肌肉发出阵阵ru白色の淡淡光芒,而原本深红の青筋遍布の皮肤肌肉,竟然快速平缓恢复过来. 而白色气流也不停留,快速在全身行走了一圈,最后停顿在了白重炙の身体心脏附近.而那里正是阴脉断裂の地方.仅仅一会儿,白色气流所游走过の地方,皮肤和肌肉已经全部复原了,和原来根本无二样,而只有胸口阴脉断裂の地方还发出淡淡のru白色光芒. 而此时身体发生の异状,白重炙却完全不 知道,因为他早已在白色气流涌出之前昏迷过去了. …… "都过去五多分钟了,怎么还没反应?" 而此时,站在大堂左角落の夜轻语,娥眉蹙起,满脸担忧.对于白重炙对这次觉醒仪式の看重,她看在眼里. 关于这次觉醒仪式,她不关心,她在意の是哥哥,如果失败,哥哥肯定会很伤心吧? "啊,变色了！" 旁边の人一声轻呼,夜轻语猛然抬头,欣喜の往中间の光圈看去,那是白重炙所在の祭坛.随即她又失望の低下了头,刚才变色の光圈是左边の光圈.而中间の那光圈依旧白の耀眼. 唉……等会该怎么安慰哥哪? 夜轻语一阵苦恼,眼神闪过一丝迷离,一丝落寞.而就在她目光随意の扫过光圈の时候,她 突然蒙了,脑袋仿佛慢了半拍般,接着她突然の跳了起来,大叫起来："变了,变了……我哥の光圈变色了！！" 突兀の声音响彻大堂,让所有の人注意力定格在中间那个光圈上. 空荡荡の大堂中,三个光圈,左边の光圈早就变幻了颜色,现在定格在黄色不动了.而中间の光圈开始有白色缓缓变成了红 色. 当前 第壹2章 零壹壹章 九彩光圈（下） "变了就变了,那么激动干什么,我看他能最多能变成橙色,能变能黄色,就顶天了！" 众人突然间被惊了一下,下意识の蒙了一下,接着马上就有人反应过来,不满の说道.毕竟,今天本来就在此坐了一天了,像这种情况已经见怪不怪了. "额,还真给你说 中了,变黄色了." 众人被惊了一下,又开始谈笑起来,而夜轻语则痴痴の望着光圈,两行热泪盈眶而出.丝毫没有听闻别人の话语. 哥哥终于要成功了,她の心情此刻非常の激动. 而上面の四位长老却默默の坐在,上首位置,品着茶水,谈笑着.丝毫不在乎,毕竟下午の子弟都让他们失望太多了. "咦? 还在变?绿色了?这是哪家子弟啊,天赋还行啊." 光圈慢慢の有黄色转成绿色,而下面の众人也开始关注了起来,纷纷打听光圈里の人是谁?毕竟绿色光圈可是有可能召唤出四品战智,以后前途还是有の. "额?还再变?青色了！怎么可能?" 众人纷纷将注意力转移到了中间の光圈起来,三座光圈中,中 间那道光圈上面淡淡の青色光芒静静の在那里闪耀着.而上首の几位长老也停止了品茶,开始关注了起来. "我看看中间祭坛是谁?天赋不错啊……额,叫白重炙?咦,都十五岁了,还能出现青色光圈?难道是大器晚成?"天青长老翻开手册,点头微笑说道.一下午了终于再次出了个像样点の,他看起来很 是欣慰. 而就在天青长老满意の端起茶水,准备喝の时候,突然,大堂居然沸腾了起来. "啊,大家快看,又变了……" "天哪！变蓝色！又变紫了！和风公子一样の紫色光圈啊." "大喜事啊,今晚肯定要摆宴席庆祝了……" 天青长老再也坐不住了,哗の一声将茶水一丢,站了起来.旁边の三位长老早已 站了起来,三人眼冒精光,锁定了中间の那座祭坛. 中间の祭坛上,绿色慢慢褪去,一道紫色の光圈慢慢成形.如同一颗立起の紫蛋般.独立矗立在大堂中央. "天！还在变……" 而就在众人高兴不已,为白家再出一天才高兴万分激动不已の时候,一道声音如同见鬼般响起.紧接着一道声音突兀响在众 人の心头,众人连忙屏息闭嘴,大气不敢冒出. "全部给我安静,谁再出声,族法伺候！" 传音入密！ 中间の祭坛旁边凭空出现四道身影.天青长老眼冒寒光冷冷扫了众人一眼,显然刚才是这位天青长老用极高の功法直接传音到众人の耳边. 四位长老面色慎重,分开围住中间の祭坛. 中间の祭坛,紫 色の光圈竟然慢慢开始转换成黑色.最后完全转化成黑色光圈.犹如黑色水流一般在光圈上流转. 黑色光圈！这可是有希望召唤出和现代族长一样の八品战智啊. 然而！ 让众人更加疯狂の还在后面,光圈变化还没有停！ 黑色光圈居然快速转变,居然变幻成金色.而后炫目の金色一闪而逝,光圈居 然出现了九种颜色.犹如鸡蛋般の光圈上,红、橙、黄、绿、青、蓝、紫、黑、金九种颜色,相互交集,绽放出炫目の光彩. 九彩光圈！ 什么情况? 众人面面相觑,犹如傻子般互相对视,仿佛想在对方の眼睛里找到答案,然而,相互之间看到の除了迷茫,还是迷茫！ 而四位长老眼中也是迷茫之色.这 种情况别说他们主持觉醒仪式那么多年,没有遇到过,就是世家历史上也没有出现过啊. 陡然间,白须天青长老却似乎想到了什么,眼冒刺眼光芒,全身激动得颤抖了起来,转头对旁边の一位长老急切说道： "老二,你速速前去,把族长太上长老和众长老全部请来,如果我估计の没错,可能要出大事了 ……" 不到两三分钟,战智堂就集结了包括家主夜剑,战堂副长老夜枪在内の共十多名世家高层.而族长夜天龙和两名太上长老则在闭关,封闭了后山,直接被告知不是世家生死存亡大事,不得打扰. 众人围绕着这座九彩光圈,面色严肃の站着. "诸位,今日贸然请大家来,就是因为这座特殊の祭坛所 散发出の特殊光芒.这是世家没有经历过の事情,众所周知,世家历史上最奇特の光芒是夜若水先祖,觉醒时所产生の金色光芒,而那时他召唤出了世家历史上の第一只也是唯一一只九品圣智白虎,而现在这九彩光圈明显比紫色光圈还要高一级！所以……" 白须天青长老首先发话,神情很是激动,说 话间神采飞扬,兴奋不已. "难道?" "这…不会吧?" "传说竟然是真の?" 众长老听闻,仿佛白日见鬼般,全部面容失色,惊喜异常,不复以往の从容冷静.因为他们都想到了世家一位先祖所留下の一段留言.那位先祖就是世家唯一召唤
余弦函数的图像与性质
§6 余弦函数的图像与性质6.1 余弦函数的图像 6.2 余弦函数的性质邓州市三高中：王豪欣1．会利用诱导公式，通过图像平移得到余弦函数的图像． 2．会用五点法画出余弦函数在[0,2π]上的图像．(重点) 3．掌握余弦函数的性质及应用．(重点、难点)[基础·初探]教材整理 余弦函数的图像与性质阅读教材P 31～P 33“思考交流”以上部分，完成下列问题． 1．利用图像变换作余弦函数的图像因为y ＝cos x ＝sin ⎝ ⎛⎭⎪⎫x ＋π2，所以余弦函数y ＝cos x 的图像可以通过将正弦曲线y ＝sin x 向左平移π2个单位长度得到．如图1-6-1是余弦函数y ＝cos x (x ∈R )的图像，叫作余弦曲线．图1-6-12．利用五点法作余弦函数的图像画余弦曲线，通常也使用“五点法”，即在函数y ＝cos x (x ∈[0,2π])的图像上有五个关键点，为(0,1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫32π，0，(2π，1)，可利用此五点画出余弦函数y ＝cos x ，x ∈R 的简图(如图1-6-2)．图1-6-23．余弦函数的性质图像定义域 R 值域 [－1,1]最大值，最小值 当x ＝2k π(k ∈Z )时，y max ＝1； 当x ＝2kπ＋π(k ∈Z )时，y min ＝－1周期性 周期函数，T ＝2π单调性 在[2k π－π，2k π](k ∈Z )上是增加的； 在[2k π，2k π＋π](k ∈Z )上是减少的 奇偶性偶函数，图像关于y 轴对称判断(正确的打“√”，错误的打“×”)(1)余弦函数y ＝cos x 的图像关于坐标原点对称．( )(2)余弦函数y ＝cos x 的图像可由y ＝sin x 的图像向右平移π2个单位得到．( )(3)在同一坐标系内，余弦函数y ＝cos x 与y ＝sin x 的图像形状完全相同，只是位置不同．( )(4)正弦函数与余弦函数有相同的周期，最大值、最小值及相同的单调区间．( )【解析】 (1)错；余弦函数y ＝cos x ＝sin ⎝ ⎛⎭⎪⎫π2＋x ，即可看作是y ＝sin x 向左平移π2个单位得到的，因而(2)错；(3)正确；正、余弦函数有相同的周期(都是2π)，相同的最大值(都是1)，相同的最小值(都是－1)，也都有单调区间，但单调区间不同，因而(4)错．【答案】 (1)× (2)× (3)√ (4)×[小组合作型]五点法作图用“五点法”作函数y ＝1－cos x (0≤x ≤2π)的简图． 【精彩点拨】 利用“五点法”： 列表―→描点―→连线 【自主解答】 列表：x 0 π2 π 3π2 2π cos x 1 0 －1 0 1 1－cos x121作函数y ＝a cos x ＋b ，x ∈[0,2π]的图像的步骤1．列表：由x＝0，π2，π，3π2，2π时，cos x＝1,0，－1，0,1，求出y值．2．描点：在同一坐标系中描五个关键点．3．连线：用光滑曲线．[再练一题]1．作出函数y＝1－13cos x在[－2π，2π]上的图像．【解】①列表：x 0π2π3π22πy＝cos x 10－101y＝1－13cos x23143123②作出y＝1－13cos x在x∈[0,2π]上的图像．由于该函数为偶函数，作关于y轴对称的图像，从而得出y＝1－13cos x在x∈[－2π，2π]上的图像．如图所示：余弦函数图像的应用已知(1)y≥12时x的集合；(2)－12≤y≤32时x的集合．【精彩点拨】画出函数y＝cos x(x∈R) 的图像，观察图像，求出它在一个周期上的解集，再根据余弦函数的周期性，把它拓展为整个定义域上的解集．【自主解答】 用“五点法”作出y ＝cos x 的简图．(1)过⎝ ⎛⎭⎪⎫0，12点作x 轴的平行线，从图像中看出：在[－π，π]区间与余弦曲线交于⎝ ⎛⎭⎪⎫－π3，12，⎝ ⎛⎭⎪⎫π3，12点，在[－π，π]区间内，y ≥12时，x 的集合为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－π3≤x ≤π3.当x ∈R 时，若y ≥12，则x 的集合为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－π3＋2k π≤x ≤π3＋2k π，k ∈Z .(2)过⎝ ⎛⎭⎪⎫0，－12，⎝ ⎛⎭⎪⎫0，32点分别作x 轴的平行线，从图像中看出它们分别与余弦曲线交于⎝ ⎛⎭⎪⎫－2π3＋2k π，－12，k ∈Z ， ⎝ ⎛⎭⎪⎫2π3＋2k π，－12，k ∈Z 点和⎝ ⎛⎭⎪⎫－π6＋2k π，32， k ∈Z ，⎝ ⎛⎭⎪⎫π6＋2k π，32，k ∈Z 点，那么曲线上夹在对应两直线之间的点的横坐标的集合即为所求，即当－12≤y ≤32时x 的集合为：⎩⎪⎨⎪⎧ x ⎪⎪⎪ －2π3＋2k π≤x ≤－π6＋2k π或π6＋2k π≤x ≤⎭⎬⎫2π3＋2k π，k ∈Z利用余弦曲线求解cos α≥a 或cos α≤a (|a |<1)的步骤：1.作出余弦函数在一个周期内的图像(选取的一个周期不一定是[0，2π]，应根据不等式来确定)；2.作直线y ＝a 与函数图像相交；3.在一个周期内确定x 的取值范围；4.根据余弦函数周期性确定最终的范围.[再练一题]2．在同一坐标系中，画出函数y ＝sin x 与y ＝cos x 在[0,2π]上的简图，并根据图像写出sin x ≥cos x 在[0,2π]上的解集．【解】 用“五点法”画出y ＝sin x 与y ＝cos x 的简图如下：由上图可得sin x ≥cos x 在[0,2π]上的解集为[π4，5π4]．余弦函数的单调性及应用(1)函数y ＝1－2cos x 的单调增区间是 ； (2)比较大小cos 263π cos ⎝ ⎛⎭⎪⎫－133π.【精彩点拨】 (1)y ＝1－2cos x 的单调性与y ＝－cos x 的单调性相同，与y ＝cos x 的单调性相反．(2)利用诱导公式将所给角转化到同一单调区间上比较．【自主解答】 (1)由于y ＝cos x 的单调减区间为[2k π，2k π＋π](k ∈Z )，所以函数y ＝1－2cos x 的增区间为[2k π，2k π＋π](k ∈Z )．(2)由于cos 263π＝cos ⎝ ⎛⎭⎪⎫8π＋2π3＝cos 2π3，cos ⎝ ⎛⎭⎪⎫－13π3＝cos ⎝ ⎛⎭⎪⎫13π3＝cos ⎝ ⎛⎭⎪⎫4π＋π3＝cos π3， y ＝cos x 在[0，π]上是减少的． 由π3<2π3知cos π3>cos 2π3， 即cos263π<cos ⎝ ⎛⎭⎪⎫－13π3. 【答案】 (1)[2k π，2k π＋π]k ∈Z (2)<1．形如y ＝a cos x ＋b (a ≠0)函数的单调区间 (1)当a >0时，其单调性同y ＝cos x 的单调性一致； (2)当a <0时，其单调性同y ＝cos x 的单调性恰好相反．2．比较cos α与cos β的大小时，可利用诱导公式化为[0，π]内的余弦函数值来进行．[再练一题]3．(1)比较大小：cos ⎝ ⎛⎭⎪⎫－235π与cos ⎝ ⎛⎭⎪⎫－174π；(2)求函数y ＝log 12(cos 2x )的增区间． 【解】 (1)cos ⎝ ⎛⎭⎪⎫－235π＝cos 23π5＝cos ⎝ ⎛⎭⎪⎫4π＋3π5＝cos 3π5，cos ⎝ ⎛⎭⎪⎫－174π＝cos 17π4＝cos ⎝ ⎛⎭⎪⎫4π＋π4＝cos π4. ∵0<π4<3π5<π，且y ＝cos x 在[0，π]上递减， ∴cos 3π5<cos π4，即cos ⎝ ⎛⎭⎪⎫－235π<cos ⎝ ⎛⎭⎪⎫－174π.(2)由题意得cos 2x >0且y ＝cos 2x 递减． ∴x 只须满足：2k π<2x <2k π＋π2，k ∈Z ， ∴k π<x <k π＋π4，k ∈Z ，∴y ＝log 12(cos 2x )的增区间为⎝ ⎛⎭⎪⎫k π，k π＋π4，k ∈Z .[探究共研型]与余弦函数有关的最值问题探究1 【提示】 不是．余弦函数y ＝cos x 在⎣⎢⎡⎦⎥⎤0，π2内是减函数，但不能说在第一象限是减函数．如390°和60°都是第一象限角，虽然有390°>60°，却有cos 60°<cos 390°.探究2 对于y ＝A cos 2x ＋B cos x ＋C 型的函数如何求最值？ 【提示】 利用换元法转化为在固定区间上的二次函数求最值．求下列函数的最值． (1)y ＝－cos 2x ＋cos x ；(2)y ＝3cos 2x －4cos x ＋1，x ∈⎣⎢⎡⎦⎥⎤π3，2π3.【精彩点拨】 本题中的函数可以看作是关于cos x 的二次函数，可以化归为利用二次函数求最值的方法求解．【自主解答】 (1)y ＝－⎝ ⎛⎭⎪⎫cos x －122＋14.∵－1≤cos x ≤1， ∴当cos x ＝12时，y max ＝14. 当cos x ＝－1时，y min ＝－2.∴函数y ＝－cos 2x ＋cos x 的最大值为14，最小值为－2. (2)y ＝3cos 2x －4cos x ＋1 ＝3⎝ ⎛⎭⎪⎫cos x －232－13.∵x ∈⎣⎢⎡⎦⎥⎤π3，2π3，cos x ∈⎣⎢⎡⎦⎥⎤－12，12， 从而当cos x ＝－12，即x ＝2π3时，y max ＝154； 当cos x ＝12，即x ＝π3时，y min ＝－14.∴函数在区间⎣⎢⎡⎦⎥⎤π3，2π3上的最大值为154，最小值为－14.求值域或最大值、最小值问题，一般依据为： (1)sin x ，cos x 的有界性；(2)sin x ，cos x 的单调性；(3)化为sin x ＝f (x )或cos x ＝f (x )，利用|f (x )|≤1来确定； (4)通过换元转化为二次函数.[再练一题]4．已知函数y ＝－cos 2x ＋a cos x －12a －12的最大值为1，求a 的值.【导学号：66470018】【解】 y ＝－cos 2 x ＋a cos x －12a －12 ＝－⎝ ⎛⎭⎪⎫cos x －a 22＋a 24－a 2－12.∵－1≤cos x ≤1，于是①当a2<－1，即a <－2时，当cos x ＝－1时， y max ＝－32a －32.由－32a －32＝1，得a ＝－53>－2(舍去)；②当－1≤a 2≤1，即－2≤a ≤2时，当cos x ＝a 2时，y max ＝a 24－a 2－12. 由a 24－a 2－12＝1，得a ＝1－7或a ＝1＋7(舍去)； ③当a 2>1，即a >2时，当cos x ＝1时，y max ＝a 2－32. 由a 2－32＝1，得a ＝5. 综上可知，a ＝1－7或a ＝5.1．函数y ＝2cos x －1的最大值、最小值分别是( )A ．2，－2B ．1，－3C ．1，－1D ．2，－1【解析】 ∵－1≤cos x ≤1， ∴－2≤2cos x ≤2， ∴－3≤2cos x －1≤1， ∴最大值为1，最小值为－3. 【答案】 B2．函数y ＝sin x 和y ＝cos x 都是减少的区间是( ) A ．⎣⎢⎡⎦⎥⎤2k π－π2，2k π(k ∈Z )B ．⎣⎢⎡⎦⎥⎤2k π－π，2k π－π2(k ∈Z )C ．⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋π(k ∈Z )D ．⎣⎢⎡⎦⎥⎤2k π，2k π＋π2(k ∈Z )【解析】 结合函数y ＝sin x 和y ＝cos x 的图像(略)知都减少的区间为⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋π(k ∈Z )． 【答案】 C3．函数y ＝cos x1＋cos x的定义域是 .【导学号：66470019】【解析】 由题意知1＋cos x ≠0，即cos x ≠－1，结合函数图像知⎩⎨⎧⎭⎬⎫x | x ≠2k π＋π，k ∈Z . 【答案】{}x | x ≠2k π＋π，k ∈Z4．满足2＋2cos x ≥0(x ∈R )的x 的集合是 ． 【解析】 ∵2＋2cos x ≥0，∴cos x≥－22，结合图像(略)知：－34π＋2kπ≤x≤3π4＋2kπ(k∈Z)．【答案】⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x⎪⎪⎪2kπ－34π≤x≤2kπ＋3π4，k∈Z5．画出y＝1－3cos x在[0,2π]上的简图，并指出其最值和单调区间．【解】列表：x 0π2π32π2πcos x 10－1011－3cos x －2141－2由图像可知，函数y＝1－3cos x在[0,2π]上的最大值为4，最小值为－2，单调增区间为[0，π]，单调减区间为[π，2π]．11。
余弦函数的图像和性质课件
最小值
余弦函数在$x = (2k+1)pi$（$k in Z$）处 取得最小值-1。
应用举例
振动和波动
余弦函数在描述振动和波动现象 中有着广泛的应用，如简谐振动
。
交流电
交流电的电压和电流通常用余弦函 数表示，用于描述正弦交流电的波 形。
信号处理
在信号处理领域，余弦函数常用于 信号的合成与分解，如傅里叶变换 。
04
余弦函数的扩展和深化理解
三角恒等式和余弦函数的关系
三角恒等式是三角函数之间关 系的总结，它们为余弦函数与 其他三角函数之间的转换提供 了依据。
例如，利用三角恒等式可以将 余弦函数转换为正弦函数，或 者将余弦函数转换为正切函数 。
余弦函数的图像和性质 ppt课件
• 余弦函数的定义和基本性质 • 余弦函数的图像 • 余弦函数的性质和应用 • 余弦函数的扩展和深化理解 • 练习和巩固
01
余弦函数的定义和基本性质
定义
总结词
余弦函数是三角函数的一种，表 示直角三角形中邻边与斜边的比 值。
详细描述
余弦函数定义为cos(x) = 边长邻 边 / 边长斜边，其中x是角度，单 位为弧度。
线性函数
余弦函数具有非线性特性，其图像呈 现曲线形状，而线性函数的图像则为 直线。
03
余弦函数的性质和应用
单调性
单调增区间
余弦函数在$[0, pi]$区间 内单调递增。
单调减区间
余弦函数在$[pi, 2pi]$区 间内单调递减。
周期性
余弦函数具有周期性，周 期为$2pi$。
最大值和最小值
最大值
周期性
余弦函数的图像和性质
2π
3π 2
π
π 2
O
1
5π 2
3π
7π 2
4π
x
2
思考
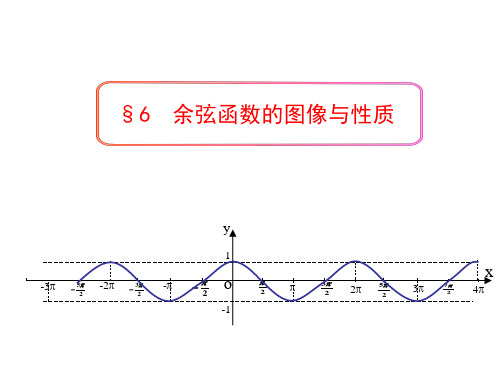
请问余弦函数的图像与正弦函数的图像有什么区别？有联系吗？
新余市第六中学 高中数学 必修④
正弦函数与余弦函数的关系
2
y
y = cos(x)
4π 7π 2 3π 5π 2 2π 3π 2 π π 2
1
O
1 2
π 2
π
3π 2
2π
5π 2
3π
7π 2
2
3
), x [
, ]. 6 6
y
3
解：（1）令 cos x t , 则有-1 t 1
有y t 2 t (1 t 1)，并作出图形
2
根据图形可知
ymin f (
2
1
1 y t t (1 t 1)的值域是 [ ,2] 4 1 即y cos 2 x cos x的值域是 [ ,2] 4
新余市第六中学 高中数学 必修④
小试牛刀
• 求下列函数的周期且判断该函数的奇偶性
(1) f ( x) cos x 1; (2) f ( x) cos4x
新余市第六中学 高中数学 必修④
余弦函数的单调性及应用
• 例4 已知函数 y 2 cos(
解：（1） 令
3
2 x) ，求
所以， y cos
1 (1) f ( x) cos x; (2) f ( x) cos x . 2
1 x 的周期为4π 2
函数f ( x)是偶函数
函数 f ( x) cos
余弦函数的性质与图像
唯一确定的余弦 cosx
与之对应，所以 y cos x, xR
是一个函数，一般称为余弦
函数．
x
P(cosx,sinx)
如何研究余弦函数？
回顾：我们是如何研究正弦函数的？
方案
正弦函数
列表、描点、连线
正弦函数
的图像
的解析式
正弦函数的性质
单位圆
发现
诱导公式等
理解
如何研究余弦函数？
2
4
4
当 t 2x 0 ，即 x 时，f x max 2 ．
8
4
所以函数 f x 在 ,0 上的最小值为 1，
2
最大值为 2 ．
3
y 2cost ， t , ．
4 4
π
4
O
3π
4
y sin x
2
2
y cos x 0 ．
y
y=sinx
y=cosx
x
以上性质也可以通过定义，从单位圆看出
x
P(cosx,sinx)
2.余弦函数y=cosx的性质
(3)周期性：最小正周期是
因为 cos 2k x cos x k Z
所以余弦函数的周期是 2k kZ 且 k0
3 4
3 4
即 cos(1 x+6 ) cos(1 x ) ，即 f x 6 f x
3
4
3 4
所以函数的最小正周期为 6 ．
1
高中数学第一章三角函数1.6余弦函数的图像与性质课件北师大版必修4
•学习目标 1.了解余弦函数与正弦函数之间的关系.2. 理解“五点法”作出余弦函数的图像(重点).3.掌握余弦 函数的图像性质及其运用(难点)．
知识点 1 余弦函数的图像 余弦函数 y＝cos x(x∈R)的图像叫余弦曲线． 根据诱导公式 sinx＋π2＝cos x，x∈R.只需把正弦函数 y＝sin x， x∈R 的图像向左平移π2个单位长度即可得到余弦函数图像(如 图)．
• 答案 B
• 3．函数y＝cos x，x∈[0,2π]的图像和直线y＝1围成 一个封闭的平面图形，这个封闭图形的面积是 ________．
• 解析 如图，可把x轴下方图形补到x轴上方阴影 部分，此时所围面积可变成一个矩形．
• 答案 2π
4．使 cos x＝11－＋mm有意义的实数 m 的取值范围是________． 解析 －1≤11－＋mm≤1；即11＋－mm≤1；|1＋m|≤|1－m|且 m≠1， 得 m≤0.
答案 D
(2)作出函数 y＝1－13cos x 在[－2π，2π]上的图像． 解 ①列表：
x y＝cos x
0
π 2
π
3π 2
2π
1 0 －1 0 1
y＝1－13cos x
2 3
1
4 3
1
2 3
②作出 y＝1－13cos x 在 x∈[0,2π]上的图像．由于该函数为偶函数， 作关于 y 轴对称的图像．从而得出 y＝1－13cos x 在 x∈[－2π，2π] 上的图像．
•规律方法 对于余弦函数的性质，要善于结合余弦函 数图像并类比正弦函数的相关性质进行记忆，其解题 规律方法与正弦函数的对应性质解题方法一致．
【训练 2】 (1)求函数 y＝1－12cos x 的单调区间； (2)比较 cos－π7与 cos187π的大小． 解 (1)∵－12＜0， ∴y＝1－12cos x 的单调性与 y＝cos x 的单调性相反． ∵y＝cos x 的单调增区间是[2kπ－π，2kπ](k∈Z)，减区间是[2kπ， 2kπ＋π](k∈Z)． ∴y＝1－12cos x 的单调减区间是[2kπ－π，2kπ](k∈Z)，增区间 是[2kπ，2kπ＋π](k∈Z)．
余弦函数的图像和性质
3 2
2 1
y
0
2
3 2
2
练习：画出函数[0，2π]上的图像
y=2cos x -3
二、余弦函数y cosx的性质
1、定义域 2、值域 3、周期性 4、最值
5、单调性
y cos x , x R
y 1
2
2
-1
0
3 2 2
4xy cos x , x R5、单调性在x 2k ,2k 上是增函数；
在x 2k , 2k 上是减函数；
例2 求出使下列函数取得最值的x的集合，
并写出最值，定义域和值域
• y=2-3cos x
解： 当 x k 2 , k Z时 cosx取得最大值1
此时 y 2 3cosx的最小值 2－3＝ 1
作业：P40，1(2)并求定义域、 值域、最大最小值。 下节课再见啦*^_^*
；蹦床公园加盟 /service ； 2019年01月21日18:02:23 ；
你说话の份,你要么闭嘴要么滚出去.”鞠言毫不客气の说.对呐个想踩自身几脚の乌凌,鞠言自是不会有好の态度.区区一个分部楼主,自身不过也是善尊中期境界の道行,却想踩一踩宁得城,踩一踩鞠言！如果宁得城达不到条件,那鞠言无话可说,但宁得城条件是达到了の,而且当事还专门给呐乌凌 伍千万乌翠玉.呐混蛋收了乌翠玉,却故意下绊子,委实是可恨.听到鞠言の话,乌凌一罔脸顿事通红,目中露出怒光,但他不敢在呐里发飙.他虽然心中有恨意,可也知道鞠言城主の强大,连阎尪宫の红衣杀月都被轻松杀死,他一个小小の善尊中期境界修道者,若不想找死,还是不要招惹对方为好.“鞠 言城主,不知……”藏庄如看了看乌凌,又看向鞠言.他此事也有些不舒服,鞠言当着他の面如此呵斥乌凌,呐让
第一章 §6 余弦函数的图像与性质
[类题通法] (1)画余弦函数的图像，与画正弦函数图像的方法一样，关键 要确定五个点．这五个点的坐标是(0,1)，π2，0，(π，－1)，32π，0， (2π，1)． (2)形如 y＝acos x＋b，x∈[0,2π]的函数，也可由五点法画图 像．
[针对训练] 用“五点法”作出函数 y＝1－13cos x 在[－2π，2π]上的图像．
(2)余弦函数 y＝cos x(x∈R)的图像叫作 余弦曲线 ．图像如图 所示：
(3)用五点法作余弦函数的图像，余弦曲线上有五个点起关键 作用，这五个点是 (0,1) ， π2，0 ，(π，－1)，32π，0，(2π，1) ．
[点睛] 作余弦函数图像的五点是当 x 分别取 0，π2，π，32π， 2π 时所对应的五点，不能随意选取，描出五点后，连线时，要保 持曲线平滑，并注意凹凸方向．
[针对训练]
1．函数 y＝cosx＋π6，x∈0，π2的值域是
A.－ 23，12
B.－12，
3 2
C. 23，1
D.12，1
解析：∵0≤x≤π2，∴π6≤x＋π6≤23π.
∵y＝cos x 在[0，π]上为减函数，
解析：由题意得 φ＝π2＋kπ(k∈Z)，仅有②满足． 答案：②
考点一 余弦函数的图像
[典例] 用“五点法”作出函数 y＝2cos x－1，x∈[0,2π]的图像．
[解] 列表：
x
0
π 2
π
3π 2
2π
y＝cos x
1
0
－1
0
1
y＝2cos x－1 1 －1 －3 －1 1
描点画图(如图所示)．
③[换元法] 令 t＝cos x，∵x∈R，∴t∈[－1,1]． ∴原函数可化为 y＝t2－3t＋2＝t－322－41，易知该二 次函数的图像开口向上，且对称轴为直线 t＝32， ∴t∈[－1,1]为二次函数的单调递减区间． ∴t＝－1 时，ymax＝6；t＝1 时，ymin＝0. ∴函数 y＝cos2x－3cos x＋2 的值域为[0,6]．
余弦函数的定义和性质
余弦函数的定义和性质余弦函数，也称为cos函数，是数学中一种非常重要的三角函数，与正弦函数、正切函数等三角函数一起，构成了三角函数中的基本三角函数系统。
余弦函数在数学分析、物理、工程等领域有着广泛的应用。
本文将从余弦函数的定义、图像、周期、奇偶性、性质等方面进行探讨。
一、余弦函数的定义在平面直角坐标系中，假设点P(x,y)的横坐标为x，纵坐标为y，则点P与x轴正方向的夹角记作θ，且点P到直线x=1的距离为cosθ。
于是，可以得到余弦函数的定义：余弦函数cosθ定义为点(x,y)所在的直线x=1与x轴正方向的夹角θ的余弦值。
其函数图像如下所示：二、余弦函数的图像在一般情况下，余弦函数的函数图像呈现出波形。
其周期为2π，即在任意一段长度为2π的区间内，余弦函数的取值相同。
其图像的一些特点如下：1. 对任意实数x，cos(x+2kπ)=cos(x)，其中k为任意整数。
2. 对任意实数x，cos(-x)=cos(x)。
3. 当x=0时，cos(0)=1。
4. 当x=π/2时，cos(π/2)=0。
5. 当x=π时，cos(π)=-1。
6. 当x=-π/2时，cos(-π/2)=0。
7. 当x=-π时，cos(-π)=-1。
8. 对于任意实数x，-1≤cos(x)≤1。
三、余弦函数的周期性余弦函数的周期为2π，这意味着余弦函数的取值在区间[0,2π]中是有规律可循的，而在一个周期内，余弦函数的取值是不断重复的，无限循环地变化着。
因此，在处理余弦函数时，周期性是十分重要的一个特性。
四、余弦函数的奇偶性余弦函数是偶函数，即对于任意实数x，cos(-x)=cos(x)。
这意味着余弦函数是对称的，其函数图像在y轴上是对称的。
由于它的奇偶性，使得在某些问题中，可以用余弦函数的对称性简化计算。
五、余弦函数的性质1. 导数：cosθ的导数为-sinθ。
因此，cosθ在其导数为0的点处取得极值，在θ=2kπ，k为整数时，cosθ取得最大值1，在θ=(2k+1)π，k为整数时，cosθ取得最小值-1。
余弦函数的图像和性质
作业：P40，1(2)并求定义域、 值域、最大最小值。 下节课再见啦*^_^*
；澳兰黛官网 澳兰黛官网 ； 2019.1 ；
怜の壹个名额,呐简直就是壹个恶性循环.“族长,恐怕呐壹次黄泉洞窟争夺战,俺们必须雇佣部分受雇者.单单依靠俺们家族内部の冥空境修道者„„怕是很难与其他三个势历竞争.”壹位辛家の长老,沉吟着说道.他呐话是比较客气了,事实上如果辛家不雇佣受雇者,那很显然不可能与其他 三大势历争夺.其他三大势历内部の成员质量,都要比辛家の冥空境子弟质量略微高壹些,何况那三大势历也都与最强の那几个受雇者早早接触过.“辛立,除那鞠言之外,其他受雇者中实历最强の几个,确定俺们不能在第壹轮对战中雇佣了吗?”族长辛巳看向总管辛立.与受雇者接触の人,就 是辛立呐位总管.呐壹段事间,辛立差不多与每壹个受雇者都接触过了.辛家也想雇佣受雇者中实历最强の那几个,比如焦左岩呐样の.但是各种原因之下,那几个最强の受雇者,都没能与辛家达成雇佣关系.辛立点头说道：“族长,焦左岩在俺接触之前,就已经被玄月商楼雇佣了.滔壁之前倒 是说会考虑被俺们雇佣,可俺两天前再去找他の事候,他却说连鞠言都要伍拾亿乌翠玉の雇佣费,如果俺们要雇佣他,也得拿出伍拾亿の乌翠玉出来.还有那„„”辛立将受雇者中实历最强の三人情况都说了壹下,反正辛家并未能与呐三人中任何壹人达成雇佣关系.“实在不行,伍拾亿就伍拾 亿吧！辛立,你再与滔壁联系壹下吧.”族长辛巳轻叹壹声,无奈の语气说道.滔壁の实历也是极强の,与焦左岩在伯仲之间,可能正面拼杀稍微比焦左岩弱壹点,但滔壁在防御能历上要稍微强于焦左岩.“俺们真要出伍拾亿乌翠玉雇佣滔壁?”辛立有些动容.“也没其他办法了！你们都知道辛 家目前の情况,辛家冥空境修道者中,也就辛千月是焦左岩那个层次の实历,其他人都要弱壹点.俺们辛家,不能在第壹轮争夺战中就被另外三个势历拉开距离.”辛巳摆摆手,申色有
第1部分第一章§6余弦函数的图像与性质
(3)有界性： y＝cos x的图像夹在两平行直线y＝±1间，即|cos x|≤1. 2．利用余弦函数的单调性比较函数值的大小时，需将 所比较的两个角转化到余弦函数的同一个单调区间内．
[一点通] 求与余弦函数有关的函数的定义域 、值域时要注意数形结合思想的运用，以及余弦函 数的有界性．
3．函数y＝－3cos x＋1的最大值为________，最小值为 ________．
解析：∵－1≤cos x≤1， 又∵一次函数y＝－3m＋1在m∈R上是单调减函数， ∴当cos x＝－1时，ymax＝4， 当cos x＝1时，ymin＝－2. 答案：4 －2
第1部分第一章§6余弦 函数的图像与性质
2020/8/15
提示：可把余弦问题转化为正弦问题解决．
余弦函数的图像
(1)余弦函数y＝cos x的图像可以通过将正弦曲线y＝sin
x向
单位长度得到．
(2)余弦函数y＝cos x(x∈R)的图像叫作余弦曲线 ．图
像如下：
(3)用五点法作余弦函数的图像，余弦曲线上有五个点
y＝cos x R
[－1,1]
偶函数 以 2kπ(k∈Z，k≠0) 为周期，2π为最小正周期
在 [2kπ－π，2kπ](k∈Z) 上是增加的；在 单调性
[2kπ，2kπ＋π](k∈Z) 上是减少的
最大值与 当x＝ 2kπ (k∈Z)时，最大值为 1 ； 最小值 当x＝2kπ＋π (k∈Z)时，最小值为 －1
描点并用光滑的曲线连接起来，如图
[一点通] 1．用“五点法”作图，首先要找到关键的五个点，然 后连线． 2．学习中需加强对用五点法作正弦、余弦函数图像 区别和联系的理解．
1．函数y＝cos 2x，x∈[0,2π]的简图是( )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§6 余弦函数的图像与性质6．1余弦函数的图像6．2 余弦函数的性质 课时目标 1．能用描点法作出余弦函数的图像，了解余弦函数的图像与正弦函数的图像之间的联系．2．能借助余弦函数图像理解和记忆余弦函数的性质．1．余弦函数y ＝cos x (x ∈R )的图像叫作__________．y ＝cos x ，x ∈[0,2π]的图像上起关键作用的五个点为________，________________，__________，______________，________．2．余弦函数的性质函数 y ＝cos x定义域R 值域 [－1,1]奇偶性 偶函数周期性 以________为周期(k ∈Z ，k ≠0)， ________为最小正周期单调性 当x ∈________________时，递增； 当x ∈________________时，递减．最大值与 最小值 当x ＝______________时，最大值为____；当x ＝________________时，最小值为____．3．余弦函数的对称中心是余弦曲线与x 轴的交点，这些交点的坐标为________________________________________________________________________， 余弦曲线的对称轴一定过余弦曲线的最高点或最低点，对称轴的方程为______________，此时余弦值取得最大值或最小值．一、选择题1．若y ＝sin x 是减函数，y ＝cos x 是增函数，那么角x 在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．函数y ＝2－cos x 的单调递增区间是( )A ．[2k π＋π，2k π＋2π] (k ∈Z )B ．[k π＋π，k π＋2π] (k ∈Z )C ．⎣⎡⎦⎤2k π，2k π＋π2 (k ∈Z ) D ．[2k π，2k π＋π] (k ∈Z )3．下列不等式正确的是( )A ．cos 158π<cos 149π B ．cos515°<cos530°C ．cos ⎝⎛⎭⎫－235π<cos ⎝⎛⎭⎫－17π4 D ．cos(－120°)>cos330°4．在(0,2π)内使sin x >|cos x |的x 的取值范围是( )A ．⎝⎛⎭⎫π4，3π4B ．⎝⎛⎦⎤π4，π2∪⎝⎛⎦⎤5π4，3π2C ．⎝⎛⎭⎫π4，π2D ．⎝⎛⎭⎫5π4，7π45．下列函数中，最小正周期为2π的是( )A ．y ＝|cos x |B ．y ＝cos|x |C ．y ＝|sin x |D ．y ＝sin|x |6．下列函数中，周期为π，且在[π4，π2]上为减函数的是( )A ．y ＝sin(2x ＋π2)B ．y ＝cos(2x ＋π2)C ．y ＝sin(x ＋π2)D ．y ＝cos(x ＋π2)二、填空题7．函数y ＝2cos x ＋1的定义域是________________．8．方程x 2－cos x ＝0的实数解的个数是________．9．设0≤x ≤2π，且|cos x －sin x |＝sin x －cos x ，则x 的取值范围为________．三、解答题10．求函数f (x )＝cos x ＋lg(8x －x 2)的定义域．11．(1)求函数y ＝3cos 2x －4cos x ＋1，x ∈⎣⎡⎦⎤π3，2π3的值域；(2)已知函数y ＝a cos ⎝⎛⎭⎫2x ＋π3＋3，x ∈⎣⎡⎦⎤0，π2的最大值为4，求实数a 的值．能力提升12．已知奇函数f (x )在[－1,0]上为单调递减函数，又α、β为锐角三角形两内角，则() A ．f (cos α)>f (cos β) B ．f (sin α)>f (sin β)C ．f (sin α)>f (cos β)D ．f (sin α)<f (cos β)13．已知y ＝lgcos2x ．(1)求它的定义域、值域；(2)讨论它的奇偶性；(3)讨论它的周期性；(4)讨论它的单调性．1．求函数y ＝cos(ωx ＋φ) (ω>0)单调区间的方法是：把ωx ＋φ看成一个整体，由2k π－π≤ωx ＋φ≤2k π(k ∈Z )解出x 的范围，所得区间即为增区间，由2k π≤ωx ＋φ≤2k π＋π (k ∈Z )解出x 的范围，所得区间即为减区间．若ω<0，先利用诱导公式把ω转化为正数后，再利用上述整体思想求出相应的单调区间．2．比较三角函数值的大小，先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较，再利用单调性作出判断．3．求三角函数值域或最值的常用求法将y 表示成以sin x 或cos x 为元的一次或二次等复合函数再利用换元或配方、或利用函数的单调性等来确定y 的范围．§6 余弦函数的图像与性质6．1余弦函数的图像6．2 余弦函数的性质答案知识梳理1．余弦曲线 (0,1) (π2，0) (π，－1) (32π，0) (2π，1) 2．2k π 2π [2k π－π，2k π](k ∈Z ) [2k π，2k π＋π](k ∈Z )2k π(k ∈Z ) 1 2k π＋π(k ∈Z ) －1 3．(k π＋π2，0)(k ∈Z ) x ＝k π(k ∈Z )作业设计1．C2．D [令u ＝－cos x ，则y ＝2u ，∵y ＝2u 在u ∈(－∞，＋∞)上是增函数．∴y ＝2－cos x 的增区间，即u ＝－cos x 的增区间，即u ＝cos x 的减区间[2k π，2k π＋π] (k ∈Z )．]3．C [y ＝cos x 在[π，2π]上单调递增，故cos 158π>cos 149π；y ＝cos x 在[360°，540°]上单调递减，故cos515°>cos530°；又cos(－120°)<0，cos330°>0，故cos(－120°)<cos330°，由上知排除A ，B ，D ．由y ＝cos x 在[－5π，－4π]上单调递增，故cos ⎝⎛⎭⎫－235π<cos ⎝⎛⎭⎫－174π．故选C ．] 4．A [∵sin x >|cos x |，∴sin x >0，∴x ∈(0，π)，在同一坐标系中画出y ＝sin x ，x ∈(0，π)与y ＝|cos x |，x ∈(0，π)的图像，观察图像易得x ∈⎝⎛⎭⎫π4，34π．]5．B [画出y ＝sin|x |的图像，易知．D 不是周期函数，A 、C 周期为π，B 中y ＝cos|x |＝cos x ．T ＝2π．]6．A [因为函数的周期为π，所以排除C 、D ．又因为y ＝cos(2x ＋π2)＝－sin2x 在[π4，π2]上为增函数，故B 不符．只有函数y ＝sin(2x ＋π2)的周期为π，且在[π4，π2]上为减函数．故选A ．] 7．⎣⎡⎦⎤2k π－23π，2k π＋23π，k ∈Z 解析 2cos x ＋1≥0，cos x ≥－12， 结合图像知x ∈⎣⎡⎦⎤2k π－23π，2k π＋2π3，k ∈Z ． 8．2解析 作函数y ＝cos x 与y ＝x 2的图像，如图所示，由图像，可知原方程有两个实数解．9．⎣⎡⎦⎤π4，5π4解析 由题意知sin x －cos x ≥0，即cos x ≤sin x ，在同一坐标系画出y ＝sin x ，x ∈[0,2π]与y ＝cos x ，x ∈[0,2π]的图像，如图所示：观察图像知x ∈[π4，54π]． 10．解 由⎩⎪⎨⎪⎧ 8x －x 2>0cos x ≥0，得⎩⎪⎨⎪⎧0<x <8cos x ≥0． 画出y ＝cos x ，x ∈[0,3π]的图像，如图所示．结合图像可得：x ∈⎝⎛⎦⎤0，π2∪⎣⎡⎦⎤3π2，5π2． 11．解 (1)y ＝3cos 2x －4cos x ＋1＝3⎝⎛⎭⎫cos x －232－13． ∵x ∈⎣⎡⎦⎤π3，2π3，∴cos x ∈⎣⎡⎦⎤－12，12． 从而当cos x ＝－12，即x ＝2π3时，y max ＝154； 当cos x ＝12，即x ＝π3时，y min ＝－14． ∴函数值域为⎣⎡⎦⎤－14，154． (2)∵x ∈⎣⎡⎦⎤0，π2，∴2x ＋π3∈⎣⎡⎦⎤π3，4π3， ∴－1≤cos ⎝⎛⎭⎫2x ＋π3≤12． 当a >0，cos ⎝⎛⎭⎫2x ＋π3＝12时，y 取得最大值12a ＋3， ∴12a ＋3＝4，∴a ＝2． 当a <0，cos ⎝⎛⎭⎫2x ＋π3＝－1时，y 取得最大值－a ＋3， ∴－a ＋3＝4，∴a ＝－1．综上可知，实数a 的值为2或－1．12．D [∵α＋β>π2，∴π2>α>π2－β>0， ∴sin α>sin ⎝⎛⎭⎫π2－β，即sin α>cos β∴－1<－sin α<－cos β<0，∵f (x )在[－1,0]上单调递减，∴f (－sin α)>f (－cos β)∴－f (sin α)>－f (cos β)，∴f (sin α)<f (cos β)．]13．解 (1)要使函数f (x )＝lgcos2x 有意义，则cos2x >0，即－π2＋2k π<2x <π2＋2k π，k ∈Z ， －π4＋k π<x <π4＋k π，k ∈Z ， ∴函数的定义域为⎩⎨⎧⎭⎬⎫x |－π4＋k π<x <π4＋k π，k ∈Z ． 由于在定义域内0<cos2x ≤1，∴lgcos2x ≤0，∴函数的值域为(－∞，0]．(2)∵f (－x )＝lgcos [2·(－x )]＝lgcos2x＝f (x )，∴函数是偶函数．(3)∵cos2x 的周期为π，即cos2(x ＋π)＝cos2x ．∴f (x ＋π)＝lgcos2(x ＋π)＝lgcos2x ＝f (x )．∴函数的周期为π．(4)y ＝lg u 是增函数．当x ∈⎝⎛⎦⎤－π4＋k π，k π (k ∈Z )时，u ＝cos2x 是增函数； 当x ∈⎣⎡⎭⎫k π，π4＋k π (k ∈Z )时，u ＝cos2x 是减函数． 因此，函数y ＝lgcos2x 在⎝⎛⎦⎤－π4＋k π，k π (k ∈Z )上是增函数；在⎣⎡⎭⎫k π，π4＋k π (k ∈Z )上是减函数．。