九年级数学直线和圆的位置关系
初中数学直线和圆的位置关系知识点总结

初中数学直线和圆的位置关系知识点总结直线和圆的位置关系是初中数学中的一个重要知识点,它涉及到点、线、圆之间的相对位置关系。
我们可以通过以下几个方面来总结这一知识点:1.判定圆和直线的位置关系:a.直线包含于圆内:当直线上的所有点都在圆内时,称直线包含于圆内。
此时,直线与圆的交点为无穷个(无限多个)。
b.直线与圆相交:当直线和圆有一个或两个交点时,称直线与圆相交。
相交的情况还可以细分为相离相交、相切相交和截割相交。
-相离相交:直线和圆相切于两个点,相交与标准的两个正数圆相交;-相切相交:直线和圆相交于一个点,直线切圆;-截割相交:直线和圆相交于两个点,直线截割圆;c.直线与圆相离:当直线上的所有点都不在圆内时,称直线与圆相离。
此时,直线与圆的交点为零个。
d.直线与圆重合:当直线上的所有点都在圆上时,称直线与圆重合。
2.圆心与直线间的距离:a.圆心到直线的距离:圆心到直线的距离等于圆心到直线的垂直距离,垂直距离是圆心到直线的最短距离。
b.两圆心间的距离:两个圆心之间的直线距离等于两个圆相切时的直线距离。
3.判断点与直线的位置关系:a.点在直线上:当一个点恰好在直线上时,称这个点在直线上。
b.点在直线上方:当一个点位于直线的上方时,称这个点在直线上方。
c.点在直线下方:当一个点位于直线的下方时,称这个点在直线下方。
4.判断点与圆的位置关系:a.点在圆内:当一个点位于圆内时,称这个点在圆内。
b.点在圆上:当一个点正好位于圆上时,称这个点在圆上。
c.点在圆外:当一个点位于圆外时,称这个点在圆外。
5.判断直线与圆相交的条件:a.直线与圆有交点的条件:直线和圆有交点当且仅当直线的距离小于圆的半径。
b.直线与圆相切的条件:直线和圆相切当且仅当直线的距离等于圆的半径。
6.判断两圆的位置关系:a.内离:两圆的圆心之间的距离大于两个圆的半径之和,此时两个圆的内部没有共同点。
b.相离:两圆的圆心之间的距离等于两个圆的半径之和,此时两个圆相切于外公切点。
九年级数学人教版(上册)第1课时 直线和圆的位置关系

12.在 Rt△ABC 中,∠C=90°,AC=3,BC=4,以点 C 为 圆心,r 为半径作圆.若⊙C 与线段 AB 有且只有一个交点,则 r 的 取值满足3<r≤4 或 r=152 .
13.如图,P 为正比例函数 y=32x 图象上的一个动点,⊙P 的半 径为 3,设 P(x,y).
(1)求⊙P 与直线 x=2 相切时点 P 的坐标. 解:当⊙P 与直线 x=2 相切时,得 |x-2|=3,即 x-2=±3, ∴x=5 或 x=-1, 即点 P 的坐标为(5,125)或(-1,-32).
7.如图,在 Rt△ABC 中,∠C=90°,AB=4 cm,BC=2 cm. 判断以点 C 为圆心,下列 r 为半径的⊙C 与 AB 的位置关系.
(1)r=1.5 cm. 解:过点 C 作 CD⊥AB,垂足为 D. 在 Rt△ABC 中, ∵AB=4 cm,BC=2 cm, ∴AC=2 3 cm.
知识点 3 由数量关系判断直线和圆的位置关系
4.已知⊙O 的直径为 12 cm,圆心到直线 l 的距离 5 cm,则直
线 l 与⊙O 的公共点的个数为(A )
A.2
B.1
C.0
D.不确定
5.如图,∠O=30°,C 为 OB 上一点,且 OC=6,以点 C 为 圆心,半径为 3 的圆与 OA 的位置关系是(C )
(2)直接写出⊙P 与直线 x=2 相交、相离时 x 的取值范围.
解:当⊙P 与直线 x=2 相交时,x 的取值范围为-1<x<5; 当⊙P 与直线 x=2 相离时,x 的取值范围为 x<-1 或 x>5.
14.以坐标原点 O 为圆心,1 为半径作圆,若直线 y=-x+b
与⊙O 相交,则 b 的取值范围是(B )
北师大版数学九年级下册3.6《直线和圆的位置关系》教案1

北师大版数学九年级下册3.6《直线和圆的位置关系》教案1一. 教材分析北师大版数学九年级下册3.6《直线和圆的位置关系》是本节课的主要内容,这部分内容是在学生已经掌握了直线、圆的基本性质的基础上进行学习的。
通过学习直线和圆的位置关系,可以让学生更好地理解直线和圆之间的相互关系,为后续学习圆的方程和解决实际问题打下基础。
二. 学情分析九年级的学生已经具备了一定的数学基础,对直线和圆的基本性质有了初步的了解。
但是,对于直线和圆的位置关系的理解和应用还有一定的困难。
因此,在教学过程中,需要引导学生通过观察、思考、探究,从而理解直线和圆的位置关系,并能够运用到实际问题中。
三. 教学目标1.让学生理解直线和圆的位置关系,并能够运用到实际问题中。
2.培养学生的观察能力、思考能力和探究能力。
3.培养学生的合作意识和交流能力。
四. 教学重难点1.直线和圆的位置关系的理解和应用。
2.如何引导学生通过观察、思考、探究来理解直线和圆的位置关系。
五. 教学方法1.观察法:通过观察直线和圆的位置关系,让学生直观地理解直线和圆的位置关系。
2.讨论法:引导学生通过小组讨论,共同探究直线和圆的位置关系。
3.练习法:通过适量的练习,让学生巩固对直线和圆的位置关系的理解。
六. 教学准备1.准备一些直线和圆的图片,用于导入和呈现。
2.准备一些练习题,用于巩固和拓展。
七. 教学过程1.导入(5分钟)通过展示一些直线和圆的图片,让学生观察并思考直线和圆之间的相互关系。
引导学生提出问题,激发学生的学习兴趣。
2.呈现(10分钟)通过PPT或者黑板,呈现直线和圆的位置关系的定义和性质。
引导学生理解直线和圆的位置关系,并能够运用到实际问题中。
3.操练(10分钟)让学生进行一些实际的操作,例如画出给定直线和圆的位置关系,或者找出给定直线和圆的位置关系。
通过操作,让学生加深对直线和圆的位置关系的理解。
4.巩固(10分钟)让学生做一些练习题,巩固对直线和圆的位置关系的理解。
九年级数学直线和圆的位置关系

高档题型解析及思路拓展
例题3
解析
思路拓展
已知直线$l_{1}$和圆$O_{1}$相切于点 $P$,直线$l_{2}$过点$P$且与圆 $O_{1}$相交于另一点$Q$,求直线 $l_{2}$的方程。
由于直线$l_{1}$和圆$O_{1}$相切于点 $P$,因此点$P$是切点,且直线 $l_{1}$在点$P$处的切线斜率与直线 $l_{2}$的斜率相等。我们可以通过求 出点$P$的坐标和切线斜率,再利用点 斜式求出直线$l_{2}$的方程。
若直线与圆相切,则直线到圆心的距 离等于半径,由此可求出切线方程。
直线与圆的交点坐标
联立直线方程和圆方程求解,可得交 点坐标。若有两个交点,则它们关于 圆心对称。
02
直线与圆的位置关系分类
相离关系
定义
直线与圆没有公共点,称为相离。
判定方法
通过比较圆心到直线的距离与圆的 半径大小来判断。若圆心到直线的 距离大于圆的半径,则直线与圆相 离。
直线与圆的交点个数
通过观察图形或计算,确定直线与圆的交点个数。若有两个交点,则直线与圆 相交;若有一个交点,则直线与圆相切;若没有交点,则直线与圆相离。
综合应用举例
解法一
联立直线l和圆C的方程,消去一 个未知数得到一个一元二次方程 。根据判别式的值判断位置关系 。
解法二
计算圆心(a,b)到直线l的距离d,根 据d与半径r的大小关系判断位置关 系。
圆的性质
圆上任意一点到圆心的距 离等于半径;圆的任意弦 所对的圆周角等于弦所对 圆心角的一半。
圆的切线
与圆有且仅有一个交点的 直线称为圆的切线,切线 与半径垂直。
直线与圆的交点问题
直线与圆的位置关系
直线与圆的切线问题
初三数学直线和圆的位置关系

初三数学直线和圆的位置关系一.直线和圆的位置关系:①相交:直线和圆有两个公共点,这时说这条直线和圆相交;这条直线叫做圆的割线;②相切:直线和圆有唯一公共点,这时说这条直线和圆相切;这条直线叫做圆的切线,这个点叫做切点.③相离:直线和圆没有公共点,这时说这条直线和圆相离.二.直线和圆的位置关系的判定:(1)定理:若⊙O的半径为R,圆心到直线l 的距离为d. 则直线l与⊙O相交d﹤R;直线l与⊙O相切 d =R;直线l与⊙O相离d﹥R;(2)“圆心到直线的距离d和半径R的数量关系”与“直线和圆的位置关系”之间的对应与等价关系列表如下:例1、1.在Rt△ABC中,∠C=,AC=3cm,AB=6cm,以点C为圆心,与AB边相切的圆的半径为_________cm.2.如图,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移_________cm时与⊙O相切.3.已知⊙O的直径为6cm,如果直线l上的一点C到圆心的距离为3cm,则直线l与⊙O的位置关系是_________.4.⊙O的半径为R,圆心O到直线l的距离d与R是方程x2-6x+9=0的两个实数根,则直线l和⊙O的位置关系是_________.三.切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线;2.切线的性质:①切线垂直于过切点的半径;②切线和圆心的距离等于半径;③经过圆心且垂直于切线的直线必过切点;④经过切点垂直于切线的直线必过圆心.综上所述,在解决有关圆的切线的问题,连接圆心和切点的线段是最常见的辅助线.四、切线长的定义及切线长定理过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长,如图所示,PA,PB 是⊙O的两条切线,A,B为切点,线段PA,PB的长即为点P到⊙O的切线长.切线长定理:过圆外一点所画的圆的两条切线长相等.例2、如图,AB是⊙O的直径,BC切⊙O于点B,AD∥CO.求证:CD是⊙O的切线.1、⊙O的半径为R,直线l和⊙O有公共点,若圆心到直线l的距离是d,则d与R的大小关系是()A.d>RB.d<RC.d≤RD.d≥R2、点A为直线l上任一点,过A点与直线l相切的圆有()个.A.1 B.2C.不存在 D.无数个3、在Rt△ABC中,∠A=,BA=12,CA=5,若以A为圆心,5为半径作圆,则斜边BC与⊙A的位置关系是()A.相交 B.相离C.相切 D.不确定4、等边△ABC的边长为6,点O为△ABC的外心,以O为圆心,为半径的圆与△ABC的三边()A.都相交B.都相离C.都相切D.不确定5、两个同心圆的半径分别为3cm和5cm,作大圆的弦MN=8cm,则MN与小圆的位置关系是()A.相交 B.相切C.相离D.无法判断6、如图,在直角坐标系中,⊙O的半径为1,则直线与⊙O的位置关系是()A.相离 B.相交C.相切 D.以上三种情形都有可能7、下列说法正确的是()A.垂直于切线的直线必过切点B.垂直于半径的直线是圆的切线C.圆的切线垂直于经过切点的半径D.垂直于切线的直线必经过圆心8、已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm的长为半径作圆,则这个圆与斜边所在的直线的位置关系是()A.相交 B.相切C.相离 D.不能确定9、如右上图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为()10、如下图,AB是⊙O的直径,点D在AB的延长线上,过点D作⊙O的切线,切点为C,若∠A=25°,∠D=__________.11、如图,⊙O的半径为1,圆心O在正三角形的边AB上沿图示方向移动,当⊙O移动到与AC相切时,OA=__________.12、设⊙O的半径为R,⊙O的圆心到直线的距离为d,若d、R是方程x2-6x+m=0的两根,则直线l 与⊙O相切时,m的值为__________.13、已知∠ABC=60°,点O在∠ABC的平分线上,OB=5cm,以O为圆心,2cm为半径作⊙O,则⊙O与BC的位置关系是__________.14、如图,Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,DB的长为半径作⊙D.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.15、如图,以边长为4的正△ABC的BC边为直径作⊙O与AB相交于点D,⊙O的切线DE交AC于E,EF⊥BC,点F是垂足,求EF的长.16、如图,PA是⊙O的切线,切点是A,过点A作AH⊥OP于点H,交⊙O于点B.求证:PB是⊙O的切线.17、如图,已知AB是⊙O的直径,AB=2,∠BAC=30°,点C在⊙O上,过点C与⊙O相切的直线交AB 的延长线于点D,求线段BD的长.1.弧长公式:n°的圆心角所对的弧长l公式不要死记硬背,可依比例关系很快地随手推得:2.扇形面积公式:(1)和含n°圆心角的扇形的面积公式同样不要死记硬背,可依比例关系很快地随手推得:.(2)将弧长公式代入扇形面积公式中,立即得到用弧长和半径表示的扇形面积公式:。
直线和圆的位置关系第1课时课件初中数学北师版九年级下册

切线性质 圆的切线垂直于经过切点的半径.
几何符号表达: ∵直线l是⊙O 的切线,A是切点. ∴直线l ⊥OA.
O
A
l
学习目标
自主学习
合作探究
当堂检测
课堂总结
探究三:切线的性质定理的证明
问题提出:如何证明切线的性质定理呢?
问题探究: 证法1:反证法. 小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
相交
(5) ? .O 相交
注意:直线是可 以无限延伸的.
学习目标
自主学习
合作探究
当堂检测
课堂总结
探究二:用数量关系判断直线与圆的位置关系
问题1:同学们用直尺在圆上移动的过程中,除了发现公共点的个数产生了 变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识: 点到直线的距离是指从直线外一点(A)到直线
C
O
A
D
学习目标
自主学习
合作探究
当堂检测
课堂总结
方法总结:
利用切线的性质解题时,常需连接辅助线,一般连接圆心与 切点,构造直角三角形,再利用直角三角形的相关性质解题.
学习目标
自主学习
பைடு நூலகம்
合作探究
当堂检测
课堂总结
练一练: 4.如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
解:连接OB,则∠OBP=90°. 设⊙O的半径为r,则OA=OB=r, OP=OA+PA=2+r.
在Rt△OBP中, OB2+PB2=PO2,即r2+42=(2+r)2. 解得 r=3, 即⊙O的半径为3.
九年级数学直线与圆的位置关系

点和圆的位置关系有几种?
A B C
点到圆心的距离为d, 圆的半径为r,则: 点在圆外 点在圆上 点在圆内 d>r; d=r; d<r.
直线与圆的位置关系
(地平线)
● ● ●
O
● ●
O
O
a(地平线)
O
O
一、直线与圆的位置关系
(用公共点的个数来区分)
特点: 直线和圆没有公共点, 叫直线和圆相离 特点: 直线和圆有惟一的公共点, 叫做直线和圆相切。 C
C
x
A
图形 直线与圆的 位置关系
.O r d ┐ l
.o d r ┐ l .
A
. B
.O d r ┐ . lC
相离
0 d>r
相切
1 d=r
相交பைடு நூலகம்
2 d<r
公共点的个数
圆心到直线的距离 d 与半径 r 的关系
公共点的名称 直线名称
切点
切线
已知⊙O的半径r=7cm,直线l1 // l2, 且l1与⊙O相切,圆心O到l2的距离为9cm. 求l1与l2的距离m.
.A
.A
.B
这时的直线叫切线
惟一的公共点叫切点。 特点: 直线和圆有两个公共点, 叫做直线和圆相交。
a(地平线)
观察太阳落山的照片,在太阳落山的过程中,太阳与 地平线(直线a)经历了哪些位置关系的变化?
看图判断直线l与 ⊙O的位置关系
(1) (2)
· O · O
l
(3) l l
· O
相离
相交
相切
课堂练习:
2、已知⊙O的半径为5cm, 圆心O与直线AB的距 离为d, 根据条件填写d的范围: 1)若AB和⊙O相离, 则 d > 5cm ; ; 2)若AB和⊙O相切, 则 d = 5cm
人教版初中数学九年级上册第24章圆知识复习第二部分点和圆、直线和圆的位置关系

*有兴趣的同学可以尝试证明: (1)如图,正五角星中AC=a, 求该五角星外接圆的直径.(用三角函数表示) (2)圆内接四边形两组对边乘积之和等于两条对角线 的乘积。(提示:构造相似形)
(3)若圆内接四边形的对角线互相垂直,则过对角线 的交点所作任一边的垂线将对边平分. A
B
E
•
O
C
D
中考试题精选
O• 5 A 4P B
【及时巩固】
7、如图,AB是ʘO的直径,AC是弦,∠CAB=30º, 过C点作ʘO的切线交AB的延长线于D,如果 OD=12cm,那么ʘO的半径为 6 .
C
30º • 60º 30º
AO
BD
【及时巩固】
8、如图,PB、PC分别切ʘO于B、C两点,A 是ʘO上一点,∠CAB=50º,则∠P等于 80º .
6、如图,△ABC内接于⊙O,AB的延长线 与过C点的切线GC相交于点D,BE与AC相 交于点F,且CB=CE.求证:(1)BE∥DG; (2)CB2-CF2=BF·FE.
A
O•
E
FB
G CD
中考试题精选
7、如图,PC为⊙O的切线,C为切点, PAB是过O点的割线,CD⊥AB于点D,
若 tan B 1,PC=10cm,求△BCD的面积. 2
A
对应的一个基本图
E O• C D
P
形,其中有很多关
系,你能找出多少?
B
弦切角:圆的切线和过切点的弦所夹的角。 P
O•
O•
B
A
M
(5)弦切角定理:弦切角等于它所夹的弧所对 的圆周角.
推论:如果两个弦切角所夹的弧相等,那么 这两个弦切角也相等.
(6)和三角形各边都相切的圆叫三角形的内切圆。 内切圆的圆心是三角形的内心(即三角形三内角 平分线的交点)。各边都和圆相切的三角形叫圆 的外切三角形。
直线与圆的位置关系-2020-2021学年九年级数学上册同步课堂帮帮帮(苏科版)(解析版)

直线与圆的位置关系知识点一、直线与圆的位置关系直线与圆有三种位置关系,如下所示:判定直线与圆的位置关系通常有以下两种方法:(1)根据直线与圆的公共点的个数判断;(2)根据圆心到直线的距离与半径的大小关系判断. 知识点二、切线的判定定理与切线的性质定理1. 切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.如图所示,OA 的一条半径,直线l 经过点A 且OA ⊥l ,则l 的切线.判定一条直线是否是圆的切线共有以下三种方法:(1)定义法:当直线与圆有且只有一个公共点时,直线与圆相切;(2)数量关系法:当圆心到直线的距离等于半径时,直线与圆相切;(3)判定定理法:经过半径的外端,并且垂直于这条半径的直线是圆的切线.2.切线的性质定理:圆的切线垂直于经过切点的半径.如图所示:直线l的切线,切点为点A,则OA⊥l.例:如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是的切线.(2)若PB=6,DB=8,求⊙O的半径.【解答】(1)见解析;(2)3【解析】(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,∴∠OBP=∠E=90°,∵OB为圆的半径,∴PB为圆O的切线;(2)在Rt△PBD中,PB=6,DB=8,根据勾股定理得,∵PD与PB都为圆的切线,∴PC=PB=6,∴DC=PD﹣PC=10﹣6=4,在Rt△CDO中,设OC=r,则有DO=8﹣r,根据勾股定理得:(8﹣r)2=r2+42,解得:r=3,则圆的半径为3.知识点三、三角形的内切圆1.定义:与三角形各边都相切的圆叫做三角形的内切圆.三角形内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2.性质:三角形的内心就是三角形三条内角平分性的交点,内心到三角形各边的距离相等,任意三角形的内心都在三角形的内部.3.三角形的内切圆的作法:作三角形任意两个内角平分线,它们的交点就是内切圆的圆心,过圆心向任意一条边作垂线,垂线段的长度就是内切圆的半径.补充:三角形外心与内心对比:例:直角三角形的两条直角边分别为8和15,那么这个直角三角形最大能容纳一个直径为几的圆?【解答】6【解析】如图所示:由勾股定理可求出三角形斜边AB=17,设三角形的内切圆的半径为r即,解得半径,则直径为6.知识点四、切线长及切线长定理1.切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长;2.切线长定理:过圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.外一点P引两条切线PA、PB,切点分别为A、B,连接OA、OB、AB,延长PO并延长交圆于点E,则:①垂直:OA⊥PA,OB⊥PB,OD⊥AB;②全等:△OAP≌△OBP,△OCA≌△OCB,△ACP≌△BCP;③弧相等:.巩固练习一.选择题1.如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠C=65°,则∠P的度数为()A.50°B.65°C.70°D.80°【解答】A【解析】连接OA 、OB ,∵PA 、PB 是⊙O 切线, ∴PA ⊥OA ,PB ⊥OB , ∴∠PAO =∠PBO =90°,∵∠P +∠PAO +∠AOB +∠PBO =360°, ∴∠P =180°﹣∠AOB , ∵∠ACB =65°,∴∠AOB =2∠ACB =130°, ∴∠P =180°﹣130°=50°, 故选A .2.平面直角坐标系中,⊙P 的圆心坐标为(﹣4,﹣5),半径为5,那么⊙P 与y 轴的位置关系是( ) A .相交 B .相离 C .相切 D .以上都不是【解答】A【解析】∵⊙P 的圆心坐标为(﹣4,﹣5), ∴⊙P 到y 轴的距离d 为4 ∵d =4<r =5 ∴y 轴与⊙P 相交 故选A .3.三角形的三边长分别为6,8,10,则它的边与半径为2的圆的公共点个数最多为( ) A .3 B .4 C .5 D .6【解答】B【解析】∵62+82=100,102=100, ∴三角形为直角三角形,设内切圆半径为r ,则12(6+8+10)r =12×6×8, 解得r =2,所以应分为五种情况:当一条边与圆相离时,有0个交点,当一条边与圆相切时,有1个交点,当一条边与圆相交时,有2个交点,当圆为三角形内切圆时,有3个交点,当两条边与圆同时相交时,有4个交点,故公共点个数可能为0、1、2、3、4个.∴则它的边与半径为2的圆的公共点个数最多为4个,故选B.4.如图,AB是圆O的直径.点P是BA延长线上一点,PC与圆O相切,切点为C,连接OC,BC,如果∠P =40°,那么∠B的度数为()A.40°B.25°C.35°D.45°【解答】B【解析】∵PC与圆O相切,切点为C,∴OC⊥PC,∴∠OCP=90°,∵∠P=40°,∴∠POC=90°﹣∠P=90°﹣40°=50°,∵OB=OC,∴∠B=∠OCB,∵∠POC=∠B+∠C,∠POC=25°.∴∠B=12故选B.5.如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA=PB;②OP⊥AB;③四边形OAPB有外接圆;④M是△AOP外接圆的圆心.其中正确说法的个数是()A.1 B.2 C.3 D.4【解答】C【解析】∵PA,PB是⊙O的两条切线,A,B为切点,∴PA=PB,所以①正确;∵OA=OB,PA=PB,∴OP垂直平分AB,所以②正确;∵PA,PB是⊙O的两条切线,A,B为切点,∴OA⊥PA,OB⊥PB,∴∠OAP=∠OBP=90°,∴点A、B在以OP为直径的圆上,∴四边形OAPB有外接圆,所以③正确;∵只有当∠APO=30°时,OP=2OA,此时PM=OM,∴M不一定为△AOP外接圆的圆心,所以④错误.故选C.6.如图,点D是△ABC中BC边的中点,DE⊥AC于E,以AB为直径的⊙O经过D,连接AD,有下列结论:AC;④DE是⊙O的切线.其中正确的结论是()①AD⊥BC;②∠EDA=∠B;③OA=12A.①②B.①②③C.②③D.①②③④【解答】D【解析】∵AB是⊙O直径,∴∠ADB=90°,∴AD⊥BC,选项①正确;连接OD,如图,∵D为BC中点,O为AB中点,∴DO为△ABC的中位线,∴OD∥AC,又DE⊥AC,∴∠DEA=90°,∴∠ODE=90°,∴DE为圆O的切线,选项④正确;又OB=OD,∴∠ODB=∠B,∵AB为圆O的直径,∴∠ADB=90°,∵∠EDA+∠ADO=90°,∠BDO+∠ADO=90°,∴∠EDA=∠BDO,∴∠EDA=∠B,选项②正确;由D为BC中点,且AD⊥BC,∴AD垂直平分BC,AB,∴AC=AB,又OA=12AC,选项③正确;∴OA=12则正确的结论为①②③④.故选D.7.如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A'B'C'D'的边A'B'与⊙O相切,切点为E,边CD'与⊙O相交于点F,则CF的长为()A.2.5 B.1.5 C.3 D.4【解答】D【解析】如图,连接OE并延长交CF于点H,∵矩形ABCD 绕点C 旋转得矩形A 'B 'C 'D ', ∴∠B ′=∠B ′CD ′=90°,A ′B ′∥CD ′,BC =B ′C =4,∵边A 'B '与⊙O 相切,切点为E , ∴OE ⊥A ′B ′,∴四边形EB ′CH 是矩形, ∴EH =B ′C =4,OH ⊥CF ,∵AB =5,∴OE =OC =12AB =52, ∴OH =EH ﹣OE =32,在Rt △OCH 中,根据勾股定理,得CH =√OC 2−OH 2=√(52)2−(32)2=2,∴CF =2CH =4. 故选D .8.如图,△ABC 内接于⊙O ,BD 切⊙O 于点B ,AB =AC ,若∠CBD =40°,则∠ABC 等于( )A .40°B .50°C .60°D .70°【解答】D【解析】∵BD 切⊙O 于点B , ∴∠DBC =∠A =40°, ∵AB =AC , ∴∠ABC =∠C ,∴∠ABC =(180°﹣40°)÷2=70°.故选D.9.如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA 的值是()A.32B.23C.12D.34【解答】A【解析】∵PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D,∴AC=EC,DE=DB,PA=PB∵△PCD的周长等于3,∴PA+PB=3,∴PA=32.故选A.10.如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=()A.6 B.7 C.8 D.9【解答】D【解析】∵PB,PD是⊙O的割线,∴PA•PB=PC•PD,∵PA=2,PC=CD=3,∴2PB=3×6解得:PB=9.故选D.11.如图,这条花边中有4个圆和4个正三角形,且这条花边的总长度AB为4,则花边上正三角形的内切圆半径为()A.√33B.23√3C.1 D.√3【解答】A【解析】如图,选择一个等边三角形和其内切圆,圆O是等边三角形ACE的内切圆,圆O切三角形的边CE于点D,∵这条花边的总长度AB为4,∴CE=2,连接OC,AD,则AD过点O,∴CD=DE=12CE=1,∵△ACE是等边三角形,∴∠ACE=60°,∵圆O是等边三角形ACE的内切圆,∴∠OCD=30°,∴OD=CD•tan30°=√33.∴花边上正三角形的内切圆半径为√33.故选A.二.填空题12.在矩形ABCD中,AB=6,BC=8,点O在对角线AC上,圆O的半径为2,如果圆O与矩形ABCD的各边都没有公共点,那么线段AO长的取值范围是.【解答】103<AO<203【解析】在矩形ABCD中,∵∠D=90°,AB=6,BC=8,∴AC=10,如图1,设⊙O与AD边相切于E,连接OE,则OE⊥AD,∴OE∥CD,∴△AOE∽△ACD,∴OECD =AOAC,∴AO10=26,∴AO=103,如图2,设⊙O与BC边相切于F,连接OF,则OF⊥BC,∴OF∥AB,∴△COF∽△CAB,∴OCAC =OFAB,∴OC10=26,∴OC=103,∴AO=203,∴如果圆O与矩形ABCD的各边都没有公共点,那么线段AO长的取值范围是103<AO<203,故答案为103<AO<203.13.如图,⊙O的半径为6cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s 的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为时,BP与⊙O相切.【解答】2秒或10秒【解析】连接OP∵当OP⊥PB时,BP与⊙O相切,∵AB=OA,OA=OP,∴OB=2OP,∠OPB=90°;∴∠B=30°;∴∠O=60°;∵OA=6cm,=2π,弧AP=60π×6180∵圆的周长为:12π,∴点P运动的距离为2π或12π﹣2π=10π;∴当t=2秒或10秒时,有BP与⊙O相切.故答案为2秒或10秒.14.在Rt△ABC中,∠C=90°,AC=BC,若以点C为圆心,以2cm长为半径的圆与斜边AB相切,那么BC的长等于.【解答】2√2cm【解析】过C点作CD⊥AB于D,如图,∵⊙C与AB相切,∴CD为⊙C的半径,即CD=2,∵∠C=90°,AC=BC,∴∠B=45°,∴△CDB为等腰直角三角形,∴BC=√2CD=2√2(cm).故答案为2√2cm.15.如图,在矩形ABCD中,已知AB=6,BC=4,以CD为直径作⊙O,将矩形ABCD绕点C旋转,使所得矩形A′B′C′D′的边A′B′与⊙O相切,切点为M,边CD′与⊙O相交于点N,则CN的长为.【解答】4√2【解析】连接OM,延长MO交CD于点G,作OH⊥B′C于点H,则∠OMB′=∠OHB′=90°,∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′,∴∠B′=∠B′CD′=90°,AB=CD=6,BC=B′C=4,∴四边形OMB′H和四边形MB′CG都是矩形,OE=OD=OC=3,∴B′H=OM=3,∴CH=B′C﹣B′H=1,∴CG=B′M=OH=√OC2−CH2=2√2,∵四边形MB′CG是矩形,∴∠OGC=90°,即OG⊥CD′,∴CN=2CG=4√2,故答案为4√2.16.如图,正方形ABCD的边长为8,E为AB中点,F为BC边上的动点,连接EF,以点F为圆心,EF长为半径作⊙F.当⊙F与AD边相切时,CF的长为.【解答】8﹣4√3【解析】当⊙F与直线AD相切时.设切点为K,连接FK,如图:则FK⊥AD,四边形FKDC是矩形.∴FE=FK=CD=2BE,∴BE=4,FE=8,在Rt△FBE中,FB=√FE2−BE2=√82−42=4√3,∴CF=BC﹣FB=8﹣4√3.故答案为8﹣4√3.17.一个菱形的周长是20cm,两对角线之比是4:3,则该菱形的内切圆的半径是cm.【解答】125【解析】如图所示:菱形ABCD,对角线AC,BD,可得菱形内切圆的圆心即为对角线交点,设AB与圆相切于点E,可得OE⊥AB,∵一个菱形的周长是20cm,两对角线之比是4:3,∴AB=5cm,设BO=4x,则AO=3x,故(4x)2+(3x)2=25,解得:x=1,则AO=3,BO=4,故EO•AB=AO•BO,解得:EO=12.5.故答案为12518.以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点F,交AB边于点E,若△CDE的周长为12,则直角梯形ABCE周长为.【解答】14【解析】设AE的长为x,正方形ABCD的边长为a,∵CE与半圆O相切于点F,∴AE=EF,BC=CF,∵EF+FC+CD+ED=12,∴AE+ED+CD+BC=12,∵AD=CD=BC=AB,∴正方形ABCD的边长为4;在Rt△CDE中,ED2+CD2=CE2,即(4﹣x)2+42=(4+x)2,解得:x=1,∵AE+EF+FC+BC+AB=14,∴直角梯形ABCE周长为14.故答案为14.19.如图,在△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=.【解答】1【解析】在△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理,得AB=5,如图,设△ABC的内切圆与三条边的切点分别为D、E、F,连接OD、OE、OF,∴OD⊥AB,OE⊥BC,OF⊥AC,∵∠C=90°,∴四边形EOFC是矩形,根据切线长定理,得CE=CF,∴矩形EOFC是正方形,∴CE=CF=r,∴AF=AD=AC﹣FC=3﹣r,BE=BD=BC﹣CE=4﹣r,∵AD+BD=AB,∴3﹣r+4﹣r=5,解得r=1.则△ABC的内切圆半径r=1.故答案为1.20.已知△ABC的三边a、b、c满足b+|c﹣3|+a2﹣8a=4√b−1−19,则△ABC的内切圆半径=.【解答】1【解析】∵b+|c﹣3|+a2﹣8a=4√b−1−19,∴|c﹣3|+(a﹣4)2+(√b−1−2)2=0,∴c=3,a=4,b=5,∵32+42=25=52,∴c2+a2=b2,∴△ABC是直角三角形,∠ABC=90°,设内切圆的半径为r,根据题意,得S△ABC=12×3×4=12×3×r+12×4×r+12×r×5,∴r=1,故答案为1.21.如图,在Rt△AOB中,OB=2√3,∠A=30°,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O 的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为.【解答】2√2【解析】连接OP、OQ,作OP′⊥AB于P′,∵PQ是⊙O的切线,∴OQ⊥PQ,∴PQ=√OP2−OQ2=√OP2−1,当OP最小时,线段PQ的长度最小,当OP⊥AB时,OP最小,在Rt△AOB中,∠A=30°,=6,∴OA=OBtanA在Rt△AOP′中,∠A=30°,OA=3,∴OP′=12∴线段PQ长度的最小值=√32−1=2√2,故答案为2√2.三.解答题22.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,过点A和点D的圆,圆心O在线段AB上,⊙O交AB于点E,交AC于点F.(1)判断BC与⊙O的位置关系,并说明理由;(2)若AD=8,AE=10,求BD的长.【解答】(1)BC与⊙O相切,理由见解析;(2)BD=1207【解析】(1)BC与⊙O相切,理由:连接OD,∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠ODA=∠CAD,∴OD∥AC,∵∠C=90°,∴∠ODC=90°,∴OD⊥BC,∵OD为半径,∴BC是⊙O切线;(2)连接DE,∵AE是⊙O的直径,∴∠ADE=90°,∵∠C=90°,∴∠ADE=∠C,∵∠EAD=∠DAC,∴△ADE∽△ACD,∴AEAD =ADAC,10 8=8AC,∴AC =325,∴CD =√AD 2−AC 2=√82−(325)2=245, ∵OD ⊥BC ,AC ⊥BC ,∴OD ∥AC ,∴△OBD ∽△ABC ,∴OD AC=BD BC , ∴5325=BD BD+245, ∴BD =1207.23.如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为H ,P 是CD 延长线上一点,DE ⊥AP ,垂足为E ,∠EAD =∠HAD .(1)求证:AE 为⊙O 的切线;(2)已知PA =2,PD =1,求⊙O 的半轻和DE 的长.【解答】(1)见解析;(2)DE 的长为35,⊙O 的半径为32 【解析】(1)证明:连接AO 并延长交⊙O 于点M ,连接MD ,如图,∵AB ⊥CD ,∴AD̂=BD ̂, ∴∠M =∠BAD ,∵∠EAD =∠HAD .∴∠M =∠EAD ,∵AM 为直径,∴∠ADM =90°,∴∠M +∠MAD =90°,∴∠EAD +∠MAD =90°,即∠MAE =90°,∴AM ⊥AE ,∴AE 为⊙O 的切线;(2)∵∠EAD =∠HAD ,DH ⊥AH ,DE ⊥AE ,AD =AD ,∴△AHD ≌△AED (AAS )∴DE =DH ,AH =AE ,设DE =x ,AH =y ,则DH =x ,AE =y ,∵∠EPD =∠HPA ,∠PED =∠PHA =90°,∴Rt △PED ∽Rt △PHA ,∴DE AH =PE PH =PD PA ,即x y =2−y 1+x =12, ∴解得x =35,y =65,即DE 的长为35,AH =65,设圆的半径为r ,则OH =r −35, 在Rt △OAH 中,(r −35)2+(65)2=r 2,解得r =32, 即⊙O 的半径为32.答:⊙O 的半轻和DE 的长分别为:32,35.24.如图,AB 是⊙O 的直径,AB =6,OC ⊥AB ,OC =5,BC 与⊙O 交于点D ,点E 是BD ̂的中点,EF ∥BC ,交OC 的延长线于点F .(1)求证:EF 是⊙O 的切线;(2)CG∥OD,交AB于点G,求CG的长.【解答】(1)见解析;(2)CG=173【解析】证明:(1)连接OE,交BD于H,∵点E是BD̂的中点,OE是半径,∴OE⊥BD,BH=DH,∵EF∥BC,∴OE⊥EF,又∵OE是半径,∴EF是⊙O的切线;(2)∵AB是⊙O的直径,AB=6,OC⊥AB,∴OB=3,∴BC=√OB2+OC2=√9+25=√34,∵S△OBC=12×OB×OC=12×BC×OH,∴OH=√34=15√3434,∵cos∠OBC=OBBC =BHOB,∴√34=BH3,∴BH=9√3434,∴BD=2BH=9√3417,∵CG∥OD,∴ODCG =BDBC,∴3CG =9√3417√34,∴CG=173.25.如图,△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC,AB,AC切于点D,E,F,求AE,BD 和CF的长.【解答】AE=4,BD=9,CF=5【解析】设AE=x,∵△ABC的内切圆分别和BC,AB,AC切于点D,E,F,∴AF=AE=x,BE=BD,CD=CF,而BE=BA﹣AE=13﹣x,CF=CA﹣AF=9﹣x,∴BD=13﹣x,CD=9﹣x,而BD+CD=BC,∴13﹣x+9﹣x=14,解得x=4,∴AE=4,BD=9,CF=5.26.已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.(1)若PA=6,求△PCD的周长.(2)若∠P=50°求∠DOC.【解答】(1)△PCD的周长=12;(2)∠COD=65°【解析】(1)连接OE,∵PA、PB与圆O相切,∴PA=PB=6,同理可得:AC=CE,BD=DE,△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;(2)∵PA PB与圆O相切,∴∠OAP=∠OBP=90°∠P=50°,∴∠AOB=360°﹣90°﹣90°﹣50°=130°,在Rt△AOC和Rt△EOC中,{OA=OEOC=OC,∴Rt△AOC≌Rt△EOC(HL),∴∠AOC=∠COE,同理:∠DOE=∠BOD,∠AOB=65°.∴∠COD=1227.已知PA、PB、DE是⊙O的切线,切点分别为A、B、F,PO=13cm,⊙O的半径为5cm,求△PDE的周长.【解答】24cm【解析】连接OA,则OA⊥PA.在直角三角形APO中,PO=13cm,OA=5cm,根据勾股定理,得AP=12cm.∵PA、PB、DE是⊙O的切线,切点分别为A、B、F,∴PA=PB,DA=DF,EF=EB,∴△PDE的周长=2PA=24cm.28.如图,⊙O是梯形ABCD的内切圆,AB∥DC,E、M、F、N分别是边AB、BC、CD、DA上的切点.(1)求证:AB+CD=AD+BC;(2)求∠AOD的度数.【解答】(1)见解析;(2)∠AOD=90°【解析】(1)证明:∵⊙O切梯形ABCD于E、M、F、N,由切线长定理:AE=AN,BE=BM,DF=DN,CF=CM,∴AE+BE+DF+CF=AN+BM+DN+CM,∴AB+DC=AD+BC;(2)连OE、ON、OM、OF,∵OE=ON,AE=AN,OA=OA,∴△OAE≌△OAN,∴∠OAE=∠OAN.同理,∠ODN=∠ODF.∴∠OAN+∠ODN=∠OAE+∠ODE.又∵AB∥DC,∠EAN+∠CDN=180°,×180°=90°,∴∠OAN+∠ODN=12∴∠AOD=180°﹣90°=90°.。
中考数学直线与圆的位置关系专题含答案
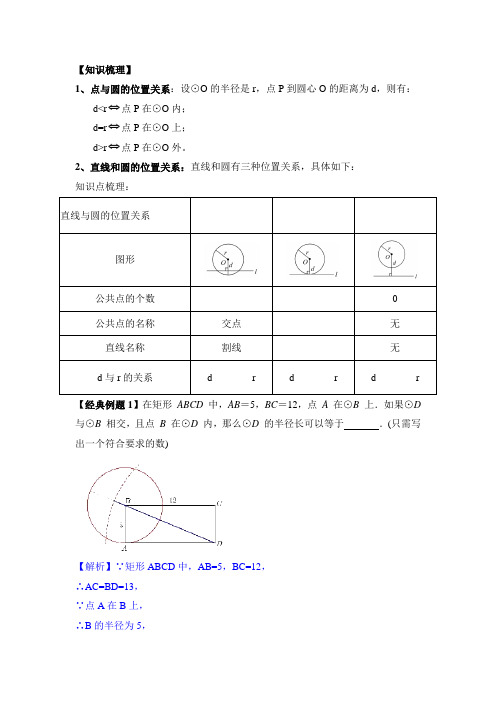
【知识梳理】1、点与圆的位置关系:设⊙O的半径是r,点P到圆心O的距离为d,则有:d<r⇔点P在⊙O内;d=r⇔点P在⊙O上;d>r⇔点P在⊙O外。
2、直线和圆的位置关系:直线和圆有三种位置关系,具体如下:知识点梳理:直线与圆的位置关系______ ______ ______ 图形公共点的个数______ ______ 0公共点的名称交点______ 无直线名称割线______ 无d与r的关系d________r d________r d________r 【经典例题1】在矩形ABCD 中,AB=5,BC=12,点 A 在⊙B 上.如果⊙D 与⊙B 相交,且点 B 在⊙D 内,那么⊙D 的半径长可以等于.(只需写出一个符合要求的数)【解析】∵矩形ABCD中,AB=5,BC=12,∴AC=BD=13,∵点A在B上,∴B的半径为5,∵如果D与B相交,∴D的半径R满足8∵点B在D内,∴R>13,∴14符合要求,故答案为:14(答案不唯一).练习1-1在公园的O处附近有E,F,G,H四棵树,位置如图所示(图中小正方形的边长均相等).现计划修建一座以O为圆心,OA为半径的圆形水池,要求池中不留树木,则E,F,G,H四棵树中需要被移除的为 ()A.E,F,GB.F,G,HC.G,H,ED.H,E,F练习1-2已知☉O的直径等于12,圆心O到直线l的距离恰好为一元二次方程2x2-10x+3=0的两根的和,那么直线l和☉O的位置关系是.练习1-3如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=23.将⊙P沿着与y轴平行的方向平移,使⊙P与x轴相切,则平移距离为_____.练习1-4(20上海中考)如图,在矩形ABCD 中,AB=6,BC=8,点O 在对角线AC 上,⊙O 的半径为2,如果⊙O 与矩形ABCD 的各边都没有公共点,那么线段AO 长的取值范围是 .320310<<x练习1-5如图,已知矩形ABCD 中,AB=2,BC=32,O 是AC 上一点,AO=m ,且O 的半径长为1,求:(1)线段AB 与O 没有公共点时m 的取值范围。
人教版九年级数学上册:24.2.2 直线和圆的位置关系

P
4cm l
A
P 4cm
l A
O .
直线和圆没有公共点,
O
叫做直线和圆相离 .
l
我指你答
快速判断下列各图中直线与圆的位置关系.
.O1
.O2
l
.O
l
.O
.O
l
l
小组合作探究
2.直线和圆的位置关系 — 数量特征
d:圆心到直线的距离 r :半径
Or
d
l
直线 l 和⊙O相交
d<r
O
r
d
直线 l 和⊙O相切
l
O r
d
l
直线 l 和⊙O相离
d=r d>r
知识要点
判定直线与圆的位置关系的方法有__两__种: (1)根据定义,由_直__线___与__圆__的__公__共__点__ 的个数来判断; (2)根据性质,由_圆__心__到__直__线__的__距__离__与__半__径__ 的关系来判断. (在实际应用中,常采用第二种方法判定)
我问你答
分别请三位同学提问以下1、2、3中的 其中一项内容,让 其他同学回答另两项内容。
1、直线和圆位置关系, 2、公共点个数, 3、d与r的关系,
挑战一:我会说,我来说
1、已知⊙O的半径为5cm,O到直线a的距离为 3cm,则⊙O与直线a的位置关系是_相__交__.直线a 与⊙O的公共点个数是_两__个_.
●
●
O
O
(地平线)
●
O
a(地平线)
九年级数学 点与圆、直线与圆、圆与圆的位置关系

九年级数学 点与圆、直线与圆、圆与圆的位置关系1、点与圆的位置关系有 种,若圆的半径为r ,点P 到圆心的距离为d 。
则:点P 在圆内⇔ ;点P 在圆上⇔ ;点P 在圆外⇔ 。
2、过三点的圆:⑴过同一直线上三点 作圆,过 三点,有且只有一个圆;⑵三角形的外接圆:经过三角形各顶点的圆叫做三角形的 ,外接圆的圆心叫做三角形的 ,这个三角形叫做这个圆的 。
⑶三角形外心的形成:三角形 的交点, 相等。
1、直线与圆的位置关系有 种:○1当直线和圆有两个公共点时,叫做直线和圆 ,这时直线叫圆的 线,; ○2当直线和圆有唯一公共点时,叫做直线和圆 ,这时直线叫圆的 线; ○3当直线和圆没有公共点时,叫做直线和圆 ,这时直线叫圆的 线。
2、设⊙O 的半径为r ,圆心O 到直线l 的距离为d ,则:直线l 与⊙O 相交r d _____⇔直线l 与⊙O 相切r d _____⇔直线l 与⊙O 相离r d _____⇔3、 切线的性质和判定:⑴性质定理:圆的切线垂直于经过切点的 。
【谈重点】根据这一定理,在圆中遇到切线时,常常连接圆心和切点,即可得垂直关系。
⑵判定定理:经过半径的 且 这条半径的直线是圆的切线。
【谈重点】在切线的判定中,当直线和圆的公共点标出时,用判定定理证明。
当公共点未标出时,一般可证圆心到直线的距离d=r 来判定相切。
4、 切线长定理:⑴切线长定义:在经过圆外一点的圆的切线上,这点和切点之间 的长叫做这点到圆的切线长。
⑵切线长定理:从圆外一点引圆的两条切线,它们的 相等,并且圆心和这一点的连线平分 的夹角5、 三角形的内切圆:⑴与三角形各边都 的圆,叫做三角形的内切圆,内切圆的圆心叫做三角形的 ;⑵三角形内心的形成:是三角形 的交点;(3)内心的性质:到三角形各 的距离相等,内心与每一个顶点的连接线平分 。
【谈重点】三类三角形内心都在三角形若△ABC三边为a、b、c面积为s,内切圆半径为r,则s= ,若△ABC为直角三角形,则r=考点一:切线的性质例题1已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连结AE,交CD于点F.(1)若⊙O的半径为8,求CD的长;(2)证明:PE=PF;(3)若PF=13,sinA=513,求EF的长.对应训练1.如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.(1)求证:AB=AC;(2)若AD=4,cos∠ABF=45,求DE的长.考点二:切线的判定例题2如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=63cm.(1)求证:AC是⊙O的切线;(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)对应训练2.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.(1)求证:AC是⊙O的切线:(2)若BF=8,DF=40,求⊙O的半径r.知识点三、圆和圆的位置关系圆和圆的位置关系有种,若⊙O1半径为R,⊙O 2半径为r,圆心距为d;○1当⊙O 1 与⊙O 2 外离⇔;○2当⊙O 1 与⊙O 2 外切⇔;○3当⊙O 1 与⊙O2相交⇔;○4当⊙O 1 与⊙O2内切⇔;○5当⊙O 1 与⊙O 2内含⇔。
九年级数学直线和圆的位置关系

6.5cm 6.5cm
O·
O·
d=6.5cm
O·
d=4.5cm
A
M
B
N d=4.5cm< r = 6.5cm
d=8cm
解 (1) 圆心距
D 直线与圆相交, 直线与圆相切,
有两个公共点; (2)圆心距 d=6.5cm = r = 6.5cm
有一个公共点;
(3)圆心距 d=8cm>r = 6.5cm 没有公共点. 直线与圆相离,
d
.Or
.B
.A
l
直线与圆的位置关系的识别与特征
1、直线与圆相离 < => d>r 2、直线与圆相切 < => d=r 3、直线与圆相交 < => d<r
H.
相切
.O
d
. C
r .D
l
相交
d
Or
. E .F
总结:
判定直线 与圆的位置关系的方法有____ 两种:
直线 与圆的公共点 (1)根据定义,由________________
B
A
A M B
O
3、直线l上的一点到圆心O的距离等于⊙O的半径,则 直线l与⊙O( ).
A、相离;B、相切;C、相交;D、相切或相交。
思考题:已知点A的坐标为(1,2),⊙A的半径为3.
(1)若要使⊙A与y轴相切,则要把⊙A向右平移几个单 位?此时,⊙A与x轴、⊙A与点O分别有怎样的位置关系? 若把⊙A向左平移呢?
A
B
知识回顾: 1、什么叫点到直线的距离?
直线外一点到这条直线 的 a 垂线段的长度叫点到直线 的距离。
.E
.
D 2、连结直线外一点与直线上所有点
初中数学 如何判断一条直线与圆的位置关系

初中数学如何判断一条直线与圆的位置关系
判断一条直线与圆的位置关系有几种情况:相离、相切、相交。
下面我将详细介绍这些情况以及判断的方法:
1. 直线与圆相离:
当直线与圆没有交点时,它们被认为是相离的。
判断直线与圆相离的方法有两种:-计算直线到圆心的距离,如果距离大于圆的半径,则直线与圆相离。
-判断直线与圆的方程是否满足不相交的条件。
2. 直线与圆相切:
当直线与圆有且仅有一个交点时,它们被认为是相切的。
判断直线与圆相切的方法有两种:
-计算直线到圆心的距离,如果距离等于圆的半径,则直线与圆相切。
-判断直线与圆的方程是否满足切线的条件。
3. 直线与圆相交:
当直线与圆有两个交点时,它们被认为是相交的。
判断直线与圆相交的方法有两种:-计算直线与圆心的距离,如果距离小于圆的半径,则直线与圆相交。
-判断直线与圆的方程是否满足相交的条件。
在判断直线与圆的位置关系时,可以使用以下工具和方法:
-距离公式:计算直线到圆心的距离可以使用距离公式来求解。
-圆的方程:圆的方程可以用来判断直线与圆的位置关系。
需要注意的是,判断直线与圆的位置关系时,可以结合使用上述方法,以确保准确判断它们之间的关系。
以上是关于判断直线与圆的位置关系的方法和步骤的介绍。
希望以上内容能够满足你对直线与圆位置关系的了解。
人教版九年级数学上册《直线和圆的位置关系》圆PPT精品课件

情景2:用砂轮磨刀时擦出的火花,:是沿着什么方向飞出的?
知识回顾
推进新课
回顾直线与圆相切:
切线
切点
判断直线和圆相切
有哪两种办法?
.
.O
直线与圆
相切
新知探究
切线具有的性质
1. 定义法:
和圆有且只有一个公共点
的直线是圆的切线.
2. 数量关系法(d=r ):
圆心到直线的距离等于
半径的直线是圆的切线.
一不可: (1)直线经过半径的外端; (2)直线与这半径垂直.
归纳
切线的判定方法
判断一条直线是圆的切线的 三种方法
O
1.定义法:与圆有唯一公共点的直线是圆的切线;
l
A
2.数量关系法:圆心到这条直线的距离等于半径,
即d=r;
3.判定定理:经过半径的外端且垂直于这条半径
O r
d
l
A
O
的直线是圆的切线.
又AP=AC,所以∠P=∠ACP=30°,
所以∠OAP=∠AOC-∠P=90°.
所以OA⊥PA,所以PA是⊙O的切线.
人教版 数学 九年级上册
直线和圆的位置关系
第3课时
学习目标
1.掌握切线长的定义及切线长定理.
2. 运用切线长定理进行计算与证明.
复习引入
问题1
在同一个平面内,有一点 和⊙,过点 能否作
1
• ∴MN= 2 OM=2.5cm.
• 所以(1)⊙M与直线OA相离,因为r<MN.
• (2)⊙M与直线OA相交,因为r>MN.
• (3)⊙M与直线OA相切,因为r=MN.
综合应用
• 6.已知⊙O的半径为 2 ,直线l与点O的距离为d,
九年级上册数学第四单元必备知识点:直线和圆的位置关系

九年级上册数学第四单元必备知识点:直线
和圆的位置关系
直线和圆的位置关系:相交、相切、相离
当直线和圆相交时,d
当直线和圆相切时,d=r;反过来,当d=r时,直线和圆相切。
当直线和圆相离时,dgt;r;反过来,当dgt;r时,直线和圆相离。
切线的性质定理:圆的切线垂直于过切点的直径
切线的判定定理:经过直径的一端,并且垂直于这条直径的直线是圆的切线。
切线长:在经过圆外一点的圆的切线上,这点到切点之间的线段的长叫做这点到圆的切线长。
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和圆外这点的连线平分两条切线的夹角。
欢迎大家去阅读由小编为大家提供的九年级上册数学第四单元必备知识点,大家好好去品味了吗?希望能够帮助到大家,加油哦!
(必备)初三年级上册数学第二单元知识:二次函数
第一学期九年级数学第一单元核心知识点梳理:因式分解法。
九年级数学直线和圆的位置关系

点和圆的位置关系
A d3 d2 C
d1
O
r
B
数量特征
点A在圆内
点B在圆上 点C在圆外
d1 r d2 r
d3 r
24.1直线和圆的位置关系
如果把点换成一条直线,直 线和圆又有哪几种位置关系?
尝试活动
请同学们在纸上画一个圆,把直尺边缘看成一条直线, 任意移动直尺,观察有几种位置关系?
直线和圆有三种位置关系 O O O 相切 相交 (1)相交:直线与圆有两个公共点时,叫做直线和圆相交。 这时直线叫做圆的割线。 相离
r 2 .4 r 2 .4
; ;
A
点 悟
D
C B
当圆心到 直线的距离一 定时,圆与直 线的位置关系 由这个圆的半 径大小确定。
练习3:
如图,已知∠AOB=300,M为OB上一点,且OM=5cm, 以M为圆心,以 r 为半径的圆与直线OA有怎样的位置关系? 为什么? A (1) r =2cm; N (2) r =4cm; (3) r =2.5cm。 B O 解 : 过M作MN⊥OA于N M ∵ ∠AOB=300 ∴MN=
练习2:
在 Rt△ABC 中,∠C = 90°,AC = 3 , AB = 5 , 以 C 为圆心, r 为半径作圆,那么: (1)直线AB与⊙ C相离时, r 的取值范围是 0 r 2.4 ; (2)直线AB与⊙ C相切时, r 的取值范围是 (3)直线AB与⊙ C相交时, r 的取值范围是
公共点个数
圆心到直线距离 d 与半径 r 关系 公共点名称 直线名称
2
d<r
相切 1 d=r
相离 0 d>r 无 无
交点
割线
九年级数学直线和圆的位置关系

2、切线的性质定理:圆的切线垂直于经过 切点的半径. 几何语言: ∵AB是⊙O的切线,E为切点 ∴AB⊥OE (常用的辅助线是连接圆心和切点)
将这一性质定理做个推广, 若一条直线满足: ①过圆心,②过切点,③垂直于切线; 则由任意两个当条件,都可以推出另一个结论. 具体来说,就是: ①切线垂直于经过切点的半径; ②过圆心且垂直于切线的直线 必过切点; ③过切点且垂直于切线的直线 必过圆心
身进京纵强贼(5) “年夜,苏家女眷,一定会跟从前一样出去。”宝音道,“你们也先收拾着,省得措手不及。”“ ,您亲口到老太太面前 去求么?”乐韵问宝音,手抚着辫梢。辫上还扎着白绳。她的爹爹,病榻上辗转三年,终于死了。乐韵可以请假回去守孝,宝音一定会准,但 乐韵没请。“他受苦这么些年,死了倒也是解脱。”乐韵道,“他在时,我尽了孝。他走了,我也觉得解脱。要我回去守着,我一个人寂寂的, 说不定倒伤心了。我不去守。”她只是个小丫头,没人会责备她不遵制、未丁忧,宝音只道:“留在府里,便留着。戴孝,便当为四姨娘、七 戴了。”那是!明蕙死在寺中,虽是庶女,好歹是宗谱中 ,且是未嫁的,明蕙的生母刘四姨娘又是宝音庶母,宝音服大功,大老爷都要为她们 服缌麻 。所谓“大功”、“小功”,是“五服”中的等级,各各用的布料、穿的时间等不同。那些生麻布、熟麻布,缝边、不缝边,原是几代 前的祖制,穿起来烦难得很,齐衰以下那些亲属关系,要劳烦礼部的学士专门按古书度算的。再说,制度里竟没规定父母为孩子穿什么。莫非 姑舅们都一片白晃晃了,伤心的父母们好意思满身红艳艳绿莹莹黄澄澄紫幽幽的坐着么?再再说,制度里一穿就好几个月、好几年的,一家里 有多少亲属呀?都照这个服法,满朝百姓都白茫茫一片了,天子要是瞅一眼,猛古丁还当自己死了,大伙儿服国丧哪!这也太不吉利了。所以 至前朝,有贤人出来说,父母对子女,也可着丧服,只按子女对父母的本服减等而服,又道,制度里虽规定那几年、几个月,实则只需大略过 了一段时间,即可以麻换葛、衣服换布条,意思意思什么的就完了。至本朝百载而下,礼纲益驰,若非至近尊亲,市井中大部分平常人也就含 糊着穿个白色粗布、系个白条过去罢了,官府也不来管。明蕙是庶女,刘四姨娘也只是个姨娘,本也可按“大部分平常人”办理,但这一次, 老太太发了话,大家都按制着服。连老太太、大老爷,也尊前贤说的“按本服减等而服”。幸而明蕙娘儿俩辈份低,诸人为她们,穿个丧服也 罢了,依制“不杖”,就是不必扶个孝杖表示自己哀毁逾恒形销骨立,否则,一府人顿时的扶起白杖来,不知道的还当这儿闹瘟疫了……嗯哼, 总之既服着丧,更不适合大过年的出门了!一家白花花,给乡亲们洗眼睛不是?宝音却坚定道:“我们会出门的。”飘儿帘下通禀:“四 来 访!”宝音眼神微妙的一变:“请!”明秀进来,穿着小功的细缘边熟麻衣,人瘦了一圈,因不是为明蕙哀伤,而是为唐静轩,神情却仍端 庄——甚至比先前更端庄了。她对宝音道:“笙妹妹,年夜之时,我们还照往常出门罢?”一干丫头都崇拜的望着宝音:铁口直断!这也太强 了!丫头们钦
九年级数学直线和圆的位置关系

(2) 当 r = 2.4cm时, 有 d = r, 因此C和AB相切.
(3) 当 r = 3cm时, 有 d < r, 因此C和AB相离.
(四) 课堂练习
一 判断题
1. 直线上一点到圆的距离大于半径 , 则直线与圆相离 ( ) 2. 直线上一点到圆的距离等于半径,则直线与圆相切( ) 3. 直线上一点到圆的距离小于半径,则直线与圆相交( )
直 线 和 圆 的 位 置 关 系
直线和圆的位置关系
教学内容:
1 直线和圆的三种位置关系及有关定义 2 直线和圆的位置关系的性质与判定 3 例题讲述
4 课堂练习
5 内容小结
6 课后作业布置
l
一 ) 直 线 和 圆 的 位 置 关 系
(
1.直线和圆的位置关系有三种(从直线与圆 公共点的个数) 2.用图形表示如下:
B D B A D B D
C
C
A
(1)
C
A
(2)
(3)
解:过C作CD⊥AB,垂足为D(如上图).在RtABC中,根据勾股定理
得:AB=5cm. 再根据三角形的面积公式有 CD· AB=AC· BC,
∴CD•5=3Х4 ∴CD=2.4cm 即圆心C到AB的距离d=2.4cm.
(1) 当 r = 2cm时, 有 d > r, 因此C和AB相离.
1
M
B
(五) 内容小节
一 直线和圆的位置关系有三种
相离 相切 相交
二 直线和圆位置关系的性质与判定 ( r与d的数量大小关系)
① 直线L和O相离
(性质)
(判定) (性质) (判定) (性质) (判定)
d>r
②
直线L和O相切
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第31课直线和圆的位置关系
知识点:
直线和圆的位置关系、切线的判定和性质、三角形的内切圆、切线长定理、弦切角的定理、相交弦、切割线定理
大纲要求:
1.掌握直线和圆的位置关系的性质和判定;
2.掌握判定直线和圆相切的三种方法并能应用它们解决有关问题:(1)直线和圆有唯一公共点;(2)d=R;(3)切线的判定定理 (应用判定定理是满足一是过半径外端,二是与这半径垂直的二个条件才可判定是圆的切线)
3.掌握圆的切线性质并能综合运用切线判定定理和性质定理解决有关问题:(1)切线与圆只有一个公共点;(2)圆心到切线距离等于半径;(3)圆的切线垂直于过切点的半径;(4) 经过圆心且垂直于切线的直线必过切点;(5)经过切点且垂直于切线的直线必过圆心;(6)切线长定理;(7) 弦切角定理及其推论。
4,掌握三角形外切圆及圆外切四边形的性质及应用;
5.注意:(1)当已知圆的切线时,切点的位置一般是确定的,在写条件时应说明直线和圆相切于哪一点,辅助线是作出过确定的半径;当证明直线是圆的切线时,如果已知直线过圆上某一点则可作出这一点的半径证明直线垂直于该半径;即为“连半径证垂直得切线”;若已知条件中未明确给出直线和圆有公共点时,则应过圆心作直线的垂线,证明圆心到直线的距离等于半径,即为:“作垂直证半径得切线”。
(2) 见到切线要想到它垂直于过切点的半径;若过切点有垂线则必过圆心;过切点有弦,则想到弦切角定理,想到圆心角、圆周角性质,可再联想同圆或等圆弧弦弦心距等的性质应用。
(3)任意三角形有且只有一个内切圆,圆心为这个三角形内角平分线的交点。
考查重点与常用题型:
1.判断基求概念,基本定理等的证误。
在中考题中常以选择填空的形式考查形式对基本概念基求定理的正确理解,如:已知命题:(1)三点确定一个圆;(2)垂直于半径的直线是圆的切线;(3)对角线垂直且相等的四边形是正万形;(4)正多边形都是中心对称图形;(5)对角线相等的梯形是等腰梯形,其中错误的命题有 ( )
(A)2个 (B)3个 (C)4个 (D)5个
2.证明直线是圆的切线。
证明直线是圆的切线在各省市中考题中多见,重点考查切线的判断定理及其它圆的一些知识。
证明直线是圆的切线可通过两种途径证明。
3.论证线段相等、三角形相似、角相等、弧相等及线段的倍分等。
此种结论的证明重点考查了金等三角形和相似三角形判定,垂径定理及其推论、圆周角、圆心角的性质及切线的性质,弦切角等有关圆的基础知识。
考点训练:
1.如图⊙O切AC于B,AB=OB=3,BC= 3 ,则∠AOC的度数为()
(A)90 °(B)105°(C)75°(D)60°
2.O是⊿ABC的内心,∠BOC为130°,则∠A的度数为()
(A)130°(B)60°(C)70°(D)80°
3.下列图形中一定有内切圆的四边形是()
(A)梯形(B)菱形(C)矩形(D)平行四边形
4.PA 、PB 分别切⊙O 于A 、B ,∠APB=60°,PA=10,则⊙O 半径长为( )
(A )103 3 (B )5 (C )10 3 (D )5 3 5.圆外切等腰梯形的腰长为a ,则梯形的中位线长为
6.如图⊿ABC 中,∠C=90°,⊙O 分别切AB 、BC 、AC 于D 、E 、F ,AD=5cm ,BD=3cm ,则⊿ABC 的面积为
7.如图,MF 切⊙O 于D ,弦AB ∥CD ,弦AD ∥BF ,BF 交⊙O 于E , 40m CD ︒=, 80m
AB ︒=,则∠ADM = °,∠AGB= °,∠BAE= °。
8.PA 、PB 分别切⊙O 于A 、B ,AB=12,PA=313 ,则四边形OAPB 的面积为
9.如图,AB 是⊙O 直径,EF 切⊙O 于C ,AD ⊥EF 于D ,求证:AC 2=AD ·AB 。
10.如图,AB 是⊙O 的弦,AB=12,PA 切⊙O 于A ,PO ⊥AB 于C ,PO=13,求PA 的长。
解题指导:
1. 如图⊿ABC 中∠A =90°,以AB 为直径的⊙O 交BC 于D ,E 为AC 边中点,求证:DE 是⊙O
的切线。
2.如图,AB是⊙O直径,DE切⊙O于C,AD⊥DE,BE⊥DE,求证:以C为圆心,CD为半径的圆C和AB相切。
3.如图,梯形ABCD中,AD∥BC,AB=CD,⊙O分另与AB、BC、CD、AD相切于E、F、G、H,求证:⊙O直径是AD,BC的比例中项。
4.已知:AB是⊙O的直径,AC和BD都是⊙O切线,CD切⊙O于E,EF⊥AB,分别交AB,AD 于E、G,求证:EG=FG。
独立训练:
1.已知点M到直线L的距离是3cm,若⊙M与L相切。
则⊙M的直径是;若⊙M的半径是3.5cm,则⊙M与L的位置关系是;若⊙M的直径是5cm,则⊙M与L的位置是。
2.RtΔABC中,∠C=90°,AC=6,BC=8,则斜边上的高线等于;若以C为圆心作与AB相切的圆,则该圆的半径为r=;若以C为圆心,以5为半径作圆,则该圆与AB的位置关系是。
3.设⊙O的半径为r,点⊙O到直线L的距离是d,若⊙O与L至少有一个公共点,则r与d 之间关系是。
4.已知⊙O的直径是15 cm,若直线L与圆心的距离分别是①15 cm;②③7.5 cm;③5 cm 那么直线与圆的位置关系分别是;;。
5.已知:等腰梯形ABCD外切于为⊙O,AD∥BC,若AD=4,BC=6,AB=5,则⊙O的半径的长为。
6.已知:PA、PB切⊙O于A、B,C是弧AB上一点,过点C的切线DE交PA于D,交PB于E,ΔPDE 周长为。
7.已知:PB是⊙O的切线,B为切点,OP交⊙O于点A,BC⊥OP,垂足为C ,OA=6 cm,OP =8 cm,则AC的长为cm。
8.已知:ΔABC内接于⊙O,P、B、C在一直线上,且PA2=PB•PC,求证:PA是⊙O的切线。
9.已知:PC切⊙O于C,割线PAB过圆心O,且∠P =40°,求∠ ACP度数。
10已知:过⊙O一点P,作⊙O切线PC,切点C,PO交⊙O于B,PO延长线交⊙O于A,CD⊥AB,垂足为D,求证:(1)∠DCB=∠PCB (2)CD:BD=PA:CP。
