2018年全国各地高考数学试题及解答分类汇编大全(16概率、随机变量及其分布) 精品
2018年全国各地高考数学(理科试卷及答案)

2018年高考数学理科试卷(江苏卷)数学Ⅰ一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位......置上... 1.已知集合{}8,2,1,0=A ,{}8,6,1,1-=B ,那么=⋂B A .2.若复数z 满足i z i 21+=⋅,其中i 是虚数单位,则z 的实部为 .3.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 .4.一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为 .5.函数()1log 2-=x x f 的定义域为 .6.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 .7.已知函数()⎪⎭⎫ ⎝⎛<<-+=222sin ππϕx x y 的图象关于直线3π=x 对称,则ϕ的值是 .8.在平面直角坐标系xOy 中,若双曲线()0,012222>>=-b a by a x 的右焦点()0,c F 到一条渐近线的距离为c 23,则其离心率的值是 . 9.函数()x f 满足()()()R x x f x f ∈=+4,且在区间]2,2(-上,()⎪⎪⎩⎪⎪⎨⎧≤<-+≤<=02,2120,2cos x x x xx f π,则()()15f f 的值为 .10.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .11.若函数()()R a ax x x f ∈+-=1223在()+∞,0内有且只有一个零点,则()x f 在[]1,1-上的最大值与最小值的和为 .12.在平面直角坐标系xOy 中,A 为直线x y l 2:=上在第一象限内的点,()0,5B ,以AB为直径的圆C 与直线l 交于另一点D .若0=⋅CD AB ,则点A 的横坐标为 .13.在ABC ∆中,角C B A 、、所对的边分别为c b a 、、,120=∠ABC ,ABC ∠的平分线交AC 于点D ,且1=BD ,则c a +4的最小值为 .14.已知集合{}*∈-==Nn n x x A ,12|,{}*∈==N n x x B n,2|.将B A ⋃的所有元素从小到大依次排列构成一个数列{}n a ,记n S 为数列{}n a 的前n 项和,则使得112+>n n a S 成立的n 的最小值为 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在平行六面体1111ABCD A B C D -中,1111,AA AB AB B C =⊥. 求证:(1)11AB A B C 平面∥; (2)111ABB A A BC ⊥平面平面.16.(本小题满分14分)已知,αβ为锐角,4tan 3α=,5cos()αβ+=.(1)求cos2α的值; (2)求tan()αβ-的值.17.(本小题满分14分)某农场有一块农田,如图所示,它的边界由圆O 的一段圆弧MPN (P 为此圆弧的中点)和线段MN 构成.已知圆O 的半径为40米,点P 到MN 的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD ,大棚Ⅱ内的地块形状为CDP △,要求,A B 均在线段MN 上,,C D 均在圆弧上.设OC与MN 所成的角为θ.(1)用θ分别表示矩形ABCD 和CDP △的面积,并确定sin θ的取值范围;(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(本小题满分16分)如图,在平面直角坐标系xOy 中,椭圆C 过点1(3,)2,焦点12(3,0),(3,0)F F ,圆O 的直径为12F F .(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标;②直线l 与椭圆C 交于,A B 两点.若OAB △,求直线l 的方程.19.(本小题满分16分)记(),()f x g x ''分别为函数(),()f x g x 的导函数.若存在0x ∈R ,满足00()()f x g x =且00()()f x g x ''=,则称0x 为函数()f x 与()g x 的一个“S 点”.(1)证明:函数()f x x =与2()22g x x x =+-不存在“S 点”; (2)若函数2()1f x ax =-与()ln g x x =存在“S 点”,求实数a 的值;(3)已知函数2()f x x a =-+,e ()xb g x x=.对任意0a >,判断是否存在0b >,使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”,并说明理由.20.(本小题满分16分)设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项为1b ,公比为q 的等比数列. (1)设110,1,2a b q ===,若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围;(2)若*110,,a b m q =>∈∈N ,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,,1n m =+均成立,并求d 的取值范围(用1,,b m q 表示).数学Ⅱ(附加题)21.【选做题】本题包括 A 、B 、C 、D 四小题,请选定其中两小题,并在相应的答题区域内...................作答...若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4—1:几何证明选讲](本小题满分10分)如图,圆O 的半径为2,AB 为圆O 的直径,P 为AB 延长线上一点,过P 作圆O 的切线,切点为C .若23PC = BC 的长. B .[选修4—2:矩阵与变换](本小题满分10分)已知矩阵2312⎡⎤=⎢⎥⎣⎦A . (1)求A 的逆矩阵1-A ;(2)若点P 在矩阵A 对应的变换作用下得到点(3,1)P ',求点P 的坐标. C .[选修4—4:坐标系与参数方程](本小题满分10分)在极坐标系中,直线l 的方程为πsin()26ρθ-=,曲线C 的方程为4cos ρθ=,求直线l被曲线C 截得的弦长.D .[选修4—5:不等式选讲](本小题满分10分)若x ,y ,z 为实数,且x +2y +2z =6,求222x y z ++的最小值.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.学科#网22.(本小题满分10分)如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.(1)求异面直线BP与AC1所成角的余弦值;(2)求直线CC1与平面AQC1所成角的正弦值.23.(本小题满分10分)设*n ∈N ,对1,2,···,n 的一个排列12n i i i ,如果当s <t 时,有s t i i >,则称(,)s t i i 是排列12n i i i 的一个逆序,排列12n i i i 的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记()n f k 为1,2,···,n 的所有排列中逆序数为k 的全部排列的个数. (1)求34(2),(2)f f 的值;(2)求(2)(5)n f n ≥的表达式(用n 表示).数学Ⅰ试题参考答案一、填空题:本题考查基础知识、基本运算和基本思想方法.每小题5分,共计70分. 1.{1,8}2.23.904.8 5.[2,+∞) 6.310 7.π6-8.2 9.2210.4311.–312.313.914.27二、解答题15.本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系,考查空间想象能力和推理论证能力.满分14分.证明:(1)在平行六面体ABCD -A 1B 1C 1D 1中,AB ∥A 1B 1. 因为AB ⊄平面A 1B 1C ,A 1B 1⊂平面A 1B 1C , 所以AB ∥平面A 1B 1C .(2)在平行六面体ABCD -A 1B 1C 1D 1中,四边形ABB 1A 1为平行四边形. 又因为AA 1=AB ,所以四边形ABB 1A 1为菱形, 因此AB 1⊥A 1B .又因为AB 1⊥B 1C 1,BC ∥B 1C 1, 所以AB 1⊥BC .又因为A 1B ∩BC =B ,A 1B ⊂平面A 1BC ,BC ⊂平面A 1BC , 所以AB 1⊥平面A 1BC . 因为AB 1⊂平面ABB 1A 1, 所以平面ABB 1A 1⊥平面A 1BC .16.本小题主要考查同角三角函数关系、两角和(差)及二倍角的三角函数,考查运算求解能力.满分14分. 解:(1)因为,,所以. 因为,所以, 因此,. (2)因为为锐角,所以.4tan 3α=sin tan cos ααα=4sin cos 3αα=22sin cos 1αα+=29cos 25α=27cos22cos 125αα=-=-,αβ(0,π)αβ+∈又因为,所以, 因此.因为,所以, 因此,.17.本小题主要考查三角函数的应用、用导数求最值等基础知识,考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.满分14分. 解:(1)连结PO 并延长交MN 于H ,则PH ⊥MN ,所以OH =10. 过O 作OE ⊥BC 于E ,则OE ∥MN ,所以∠COE =θ, 故OE =40cos θ,EC =40sin θ,则矩形ABCD 的面积为2×40cos θ(40sin θ+10)=800(4sin θcos θ+cos θ), △CDP 的面积为12×2×40cos θ(40–40sin θ)=1600(cos θ–sin θcos θ). 过N 作GN ⊥MN ,分别交圆弧和OE 的延长线于G 和K ,则GK =KN =10. 令∠GOK =θ0,则sin θ0=14,θ0∈(0,π6). 当θ∈[θ0,π2)时,才能作出满足条件的矩形ABCD , 所以sin θ的取值范围是[14,1). 答:矩形ABCD 的面积为800(4sin θcos θ+cos θ)平方米,△CDP 的面积为 1600(cos θ–sin θcos θ),sin θ的取值范围是[14,1). (2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3,设甲的单位面积的年产值为4k ,乙的单位面积的年产值为3k (k >0), 则年总产值为4k ×800(4sin θcos θ+cos θ)+3k ×1600(cos θ–sin θcos θ) =8000k (sin θcos θ+cos θ),θ∈[θ0,π2). 设f (θ)= sin θcos θ+cos θ,θ∈[θ0,π2), 则222()cos sin sin (2sin sin 1)(2sin 1)(sin 1)f θθθθθθθθ=--=-+-=--+′. 令()=0f θ′,得θ=π6, 当θ∈(θ0,π6)时,()>0f θ′,所以f (θ)为增函数; 5cos()5αβ+=-225sin()1cos ()5αβαβ+=-+=tan()2αβ+=-4tan 3α=22tan 24tan 21tan 7ααα==--tan 2tan()2tan()tan[2()]1+tan 2tan()11ααβαβααβααβ-+-=-+==-+当θ∈(π6,π2)时,()<0f θ′,所以f (θ)为减函数, 因此,当θ=π6时,f (θ)取到最大值. 答:当θ=π6时,能使甲、乙两种蔬菜的年总产值最大. 18.本小题主要考查直线方程、圆的方程、圆的几何性质、椭圆方程、椭圆的几何性质、直线与圆及椭圆的位置关系等知识,考查分析问题能力和运算求解能力.满分16分. 解:(1)因为椭圆C的焦点为12(),F F -,可设椭圆C 的方程为22221(0)x y a b a b +=>>.又点1)2在椭圆C 上,所以2222311,43,a ba b ⎧+=⎪⎨⎪-=⎩,解得224,1,a b ⎧=⎪⎨=⎪⎩ 因此,椭圆C 的方程为2214x y +=.因为圆O 的直径为12F F ,所以其方程为223x y +=.(2)①设直线l 与圆O 相切于0000(),,(00)P x y x y >>,则22003x y +=, 所以直线l 的方程为0000()x y x x y y =--+,即0003x y x y y =-+. 由220001,43,x y x y x y y ⎧+=⎪⎪⎨⎪=-+⎪⎩,消去y ,得222200004243640()x y x x x y +-+-=.(*) 因为直线l 与椭圆C 有且只有一个公共点,所以222222000000()()(24)(44364820)4x x y y y x ∆=--+-=-=. 因为00,0x y >,所以001x y ==. 因此,点P的坐标为. ②因为三角形OAB,所以1 2AB OP ⋅=AB . 设1122,,()(),A x y B x y ,由(*)得001,2x =,所以2222121()()x B y y x A =-+- 222000222200048(2)(1)(4)x y x y x y -=+⋅+.因为22003x y +=,所以22022016(2)32(1)49x AB x -==+,即42002451000x x -+=, 解得22005(202x x ==舍去),则2012y =,因此P的坐标为.综上,直线l的方程为y =+19.本小题主要考查利用导数研究初等函数的性质,考查综合运用数学思想方法分析与解决问题以及逻辑推理能力.满分16分.解:(1)函数f (x )=x ,g (x )=x 2+2x -2,则f ′(x )=1,g ′(x )=2x +2. 由f (x )=g (x )且f ′(x )= g ′(x ),得 222122x x x x ⎧=+-⎨=+⎩,此方程组无解, 因此,f (x )与g (x )不存在“S ”点.(2)函数21f x ax =-(),()ln g x x =, 则12f x ax g x x'='=(),(). 设x 0为f (x )与g (x )的“S ”点,由f (x 0)与g (x 0)且f ′(x 0)与g ′(x 0),得200001ln 12ax x ax x ⎧-=⎪⎨=⎪⎩,即200201ln 21ax x ax ⎧-=⎪⎨=⎪⎩,(*) 得01ln 2x =-,即120e x -=,则1221e 22(e )a -==. 当e2a =时,120e x -=满足方程组(*),即0x 为f (x )与g (x )的“S ”点.因此,a 的值为e2.(3)对任意a >0,设32()3h x x x ax a =--+.因为(0)0(1)1320h a h a a =>=--+=-<,,且h (x )的图象是不间断的,所以存在0x ∈(0,1),使得0()0h x =,令03002e (1)x x b x =-,则b >0.函数2e ()()xb f x x a g x x=-+=,,则2e (1)()2()x b x f x x g x x -=-=′,′. 由f (x )与g (x )且f ′(x )与g ′(x ),得22e e (1)2xx b x a x b x x x ⎧-+=⎪⎪⎨-⎪-=⎪⎩,即00320030202e e (1)2e (1)2e (1)x x xx x x a x x x x x x x ⎧-+=⋅⎪-⎪⎨-⎪-=⋅⎪-⎩(**) 此时,0x 满足方程组(**),即0x 是函数f (x )与g (x )在区间(0,1)内的一个“S 点”.因此,对任意a >0,存在b >0,使函数f (x )与g (x )在区间(0,+∞)内存在“S 点”. 20.本小题主要考查等差和等比数列的定义、通项公式、性质等基础知识,考查代数推理、转化与化归及综合运用数学知识探究与解决问题的能力.满分16分. 解:(1)由条件知:. 因为1||n n a b b -≤对n =1,2,3,4均成立, 即对n =1,2,3,4均成立, 即11,1d 3,32d 5,73d 9,得. 112(,)n n n a n d b -=-=1 12|()1|n n d ---≤≤≤≤≤≤≤≤7532d ≤≤因此,d 的取值范围为.(2)由条件知:.若存在d ,使得1||n n a b b -≤(n =2,3,···,m +1)成立,即,即当时,d 满足. 因为,则,从而,,对均成立.因此,取d =0时,1||n n a b b -≤对均成立.下面讨论数列的最大值和数列的最小值(). ①当时,, 当时,有,从而.因此,当时,数列单调递增,故数列的最大值为. ②设,当x >0时,, 所以单调递减,从而<f (0)=1.当时,, 因此,当时,数列单调递减,故数列的最小值为. 因此,d 的取值范围为.75[,]32111(1),n n n a b n d b b q -=+-=1111 |1|2,3,,(1())n b n d b q b n m -+--≤=+2,3,,1n m =+1111211n n q q b d b n n ---≤≤--q ∈112n m q q -<≤≤11201n q b n --≤-1101n q b n ->-2,3,,1n m =+2,3,,1n m =+12{}1n q n ---1{}1n q n --2,3,,1n m =+2n m ≤≤111 2222111()()()n n n n n n n n q q nq q nq n q q q n n n n n n -------+--+-==---112mq <≤2n m q q ≤≤1() 20n n n n q q q ---+>21n m ≤≤+12{}1n q n ---12{}1n q n ---2m q m-()()21x f x x =-ln 21(0(n )l 22)x f x x '=--<()f x ()f x 2n m ≤≤111112111()()()nn n q q n n f q n n n n --=≤-=<-21n m ≤≤+1{}1n q n --1{}1n q n --mq m11(2)[,]m mb q b q m m-数学Ⅱ(附加题)参考答案21.【选做题】A .[选修4—1:几何证明选讲]本小题主要考查圆与三角形等基础知识,考查推理论证能力.满分10分. 证明:连结OC .因为PC 与圆O 相切,所以OC ⊥PC .又因为PC =OC =2,所以OP .又因为OB =2,从而B 为Rt △OCP 斜边的中点,所以BC =2. B .[选修4—2:矩阵与变换]本小题主要考查矩阵的运算、线性变换等基础知识,考查运算求解能力.满分10分. 解:(1)因为2312⎡⎤=⎢⎥⎣⎦A ,det()221310=⨯-⨯=≠A ,所以A 可逆, 从而1-A 2312-⎡⎤=⎢⎥-⎣⎦. (2)设P (x ,y ),则233121x y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,所以13311x y -⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A , 因此,点P 的坐标为(3,–1). C .[选修4—4:坐标系与参数方程]本小题主要考查曲线的极坐标方程等基础知识,考查运算求解能力.满分10分. 解:因为曲线C 的极坐标方程为=4cos ρθ, 所以曲线C 的圆心为(2,0),直径为4的圆. 因为直线l 的极坐标方程为πsin()26ρθ-=,则直线l 过A (4,0),倾斜角为π6, 所以A 为直线l 与圆C 的一个交点. 设另一个交点为B ,则∠OAB =π6. 连结OB ,因为OA 为直径,从而∠OBA =π2,所以π4cos6AB ==因此,直线l 被曲线C截得的弦长为. D .[选修4—5:不等式选讲]本小题主要考查柯西不等式等基础知识,考查推理论证能力.满分10分. 证明:由柯西不等式,得2222222()(122)(22)x y z x y z ++++≥++. 因为22=6x y z ++,所以2224x y z ++≥, 当且仅当122x y z ==时,不等式取等号,此时244333x y z ===,,, 所以222x y z ++的最小值为4.22.【必做题】本小题主要考查空间向量、异面直线所成角和线面角等基础知识,考查运用空间向量解决问题的能力.满分10分.学科%网解:如图,在正三棱柱ABC −A 1B 1C 1中,设AC ,A 1C 1的中点分别为O ,O 1,则OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,以1,{},OB OC OO 为基底,建立空间直角坐标系O −xyz .因为AB =AA 1=2,所以1110,1,0,,0,1,0,0,1,())()()2,,0,1,2)()A B C A B C --.(1)因为P 为A 1B 1的中点,所以1,2)2P -,从而131(,,2)(0,2,222),BP AC ==--,故111||||cos ,|||||5BP AC BP AC BP AC ⋅-===⋅.因此,异面直线BP 与AC 1所成角的余弦值为.(2)因为Q 为BC 的中点,所以1,0)2Q ,因此33(,0)22AQ =,11(0,2,2),(0,0,2)AC CC ==.设n =(x ,y ,z )为平面AQC 1的一个法向量,则10,0,AQ AC ⎧⎪⎨⎪⎩⋅=⋅=n n 即30,2220.y y z +=⎪+=⎩ 不妨取1,1)=-n ,设直线CC 1与平面AQC 1所成角为θ,则111||sin |cos |,|||CCCC CC |θ==⋅⋅==n n n ,所以直线CC 1与平面AQC 1所成角的正弦值为.23.【必做题】本小题主要考查计数原理、排列等基础知识,考查运算求解能力和推理论证能力.满分10分.解:(1)记()abc τ为排列abc 的逆序数,对1,2,3的所有排列,有(123)=0(132)=1(213)=1(231)=2(312)=2(321)=3ττττττ,,,,,,所以333(0)1(1)(2)2f f f ===,.对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置. 因此,4333(2)(2)(1)(0)5f f f f =++=.(2)对一般的n (n ≥4)的情形,逆序数为0的排列只有一个:12…n ,所以(0)1n f =. 逆序数为1的排列只能是将排列12…n 中的任意相邻两个数字调换位置得到的排列,所以(1)1n f n =-.为计算1(2)n f +,当1,2,…,n 的排列及其逆序数确定后,将n +1添加进原排列,n +1在新排列中的位置只能是最后三个位置. 因此,1(2)(2)(1)(0)(2)n n n n n f f f f f n +=++=+. 当n ≥5时,112544(2)[(2)(2)][(2)(2)][(2)(2)](2)n n n n n f f f f f f f f ---=-+-++-+…242(1)(2)4(2)2n n n n f --=-+-+⋯++=, 因此,n ≥5时,(2)n f =222n n --.绝密★启用前2018年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页,150分。
(精品word)2018年高考试题(卷)分类汇编-概率统计
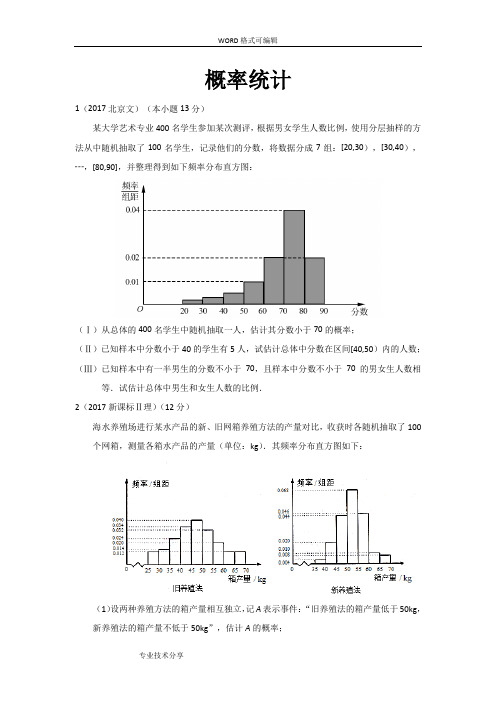
概率统计1(2017北京文)(本小题13分)某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.2(2017新课标Ⅱ理)(12分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:(3).附:,22()()()()()n ad bc K a b c d a c b d -=++++3(2017天津理)(本小题满分13分)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为111,,234. (Ⅰ)设X 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X 的分布列和数学期望; (Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率. 4(2017新课标Ⅲ理数)(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:以最高气温位于各区间的频率代替最高气温位于该区间的概率。
2018全国各地高考数学试题汇编附解析

2018全国各地高考数学试题汇编(附解析)2018年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ1.已知集合{0,1,2,8}B=-,那么A B=▲.A=,{1,1,6,8}[答案]{1,8}2.若复数z满足i12iz⋅=+,其中i是虚数单位,则z的实部为▲.[答案]23.已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为▲.[答案]904.一个算法的伪代码如图所示,执行此算法,最后输出的S的值为▲.[答案]85.函数()f x=的定义域为▲.[答案][)∞+,26.某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 ▲ . [答案]1037.已知函数sin(2)()22y x ϕϕππ=+-<<的图象关于直线3x π=对称,则ϕ的值是 ▲ . [答案]6-π8.在平面直角坐标系xOy 中,若双曲线22221(0,0)x y a b a b-=>>的右焦点(c,0)F 到一条渐近线,则其离心率的值是 ▲ . [答案]29.函数()f x 满足(4)()()f x f x x +=∈R ,且在区间(2,2]-上,cos ,02,2()1||,20,2x x f x x x π⎧<⎪⎪=⎨⎪+<⎪⎩≤-≤ 则((15))f f 的值为 ▲ .[答案]2210.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 ▲ .[答案]3411.若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点,则()f x 在[1,1]-上的最大值与最小值的和为 ▲ . [答案]-312.在平面直角坐标系xOy 中,A 为直线:2l y x =上在第一象限内的点,(5,0)B ,以AB 为直径的圆C 与直线l 交于另一点D .若0AB CD ⋅=,则点A 的横坐标为 ▲ . [答案]313.在ABC △中,角,,A B C 所对的边分别为,,a b c ,120ABC ∠=︒,ABC ∠的平分线交AC 与点D ,且1BD =,则4a c +的最小值为 ▲ . [答案]914.已知集合*{|21,}A x x n n ==-∈N ,*{|2,}n B x x n ==∈N .将A B 的所有元素从小到大依次排列构成一个数列{}n a .记n S 为数列{}n a 的前n 项和,则使得112n n S a +>成立的n 的最小值为 ▲ . [答案]2715.在平行六面体1111ABCD A B C D -中,1111,AA AB AB B C =⊥. 求证:(1)11AB A B C 平面∥; (2)111ABB A A BC ⊥平面平面.[答案]16.已知,αβ为锐角,4tan 3α=,cos()αβ+=. (1)求cos2α的值; (2)求tan()αβ-的值. [答案]17.某农场有一块农田,如图所示,它的边界由圆O的一段圆弧MPN(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.先规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为CDP△,要求,A B 均在线段MN上,,C D均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和CDP△的面积,并确定sinθ的取值范围;(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4:3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.[答案]18.如图,在平面直角坐标系xOy 中,椭圆C 过点1)2,焦点12(F F ,圆O 的直径为12F F .(1)求椭圆C 及圆O 的方程;(2)设直线l 与圆O 相切于第一象限内的点P .①若直线l 与椭圆C 有且只有一个公共点,求点P 的坐标;②直线l 与椭圆C 交于,A B 两点.若OAB △,求直线l 的方程.[答案]19.记(),()f x g x ''分别为函数(),()f x g x 的导函数.若存在0x ∈R ,满足00()()f x g x =且00()()f x g x ''=,则称0x 为函数()f x 与()g x 的一个“S 点”.(1)证明:函数()f x x =与2()22g x x x =+-不存在“S 点”; (2)若函数2()1f x ax =-与()ln g x x =存在“S 点”,求实数a 的值;(3)已知函数2()f x x a =-+,e ()x b g x x=.对任意0a >,判断是否存在0b >,使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”,并说明理由. [答案]20.设{}n a 是首项为1a ,公差为d 的等差数列,{}n b 是首项为1b ,公比为q 的等比数列.(1)设110,1,2a b q ===,若1||n n a b b -≤对1,2,3,4n =均成立,求d 的取值范围;(2)若*110,,a b m q =>∈∈N ,证明:存在d ∈R ,使得1||n n a b b -≤对2,3,,1n m =+均成立,并求d 的取值范围(用1,,b m q 表示). [答案]2018 年普通高等学校招生全国统一考试(全国I卷)文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
高三数学-2018年高考数学全国统一考试概率统计分类解析 精品
2018年普通高等学校招生全国统一考试数学分类解析—概率统计一.选择题:1. (安徽理)(10).设两个正态分布2111()(0)N μσσ>,和2222()(0)N μσσ>,的密度函数图像如图所示。
则有( A ) A .1212,μμσσ<<B .1212,μμσσ<>C .1212,μμσσ><D .1212,μμσσ>>2.(福建理)(5)某一批花生种子,如果每1粒发牙的概率为45,那么播下4粒种子恰有2粒发芽的概率是 (B )A.16625 B.96625 C.192625D.2566253. (福建文)(5)某一批花生种子,如果每1粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是 (C )A.12125 B.16125 C.48125 D.961254. (广东理)(3).某校共有学生2000名,各年级男、女生人数如表1.已知在全校 学生中随机抽取1名,抽到二年级女生的概率是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( C ) A .24 B .18 C .16 D .125.(湖南理) 4.设随机变量ζ服从正态分布N (2,9) ,若P (ζ>c+1)=P (ζ<c -)1,则c =(B)A.1B.2C.3D.46. (江西文)(11).电子钟一天显示的时间是从00:00到23:59,每一时刻都由四个数字组成,则一天中任一时刻显示的四个数字之和为23的概率为 (C )A .1180 B .1288 C .1360D .14807. (辽宁理文)(7).4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( C ) A.13 B.12 C.23 D.348.(山东理)(7)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为(B ) (A )511(B )681 (C )3061(D )40819.(山东理) (8)右图是根据《山东统计年整2018》中的资料作成的1997年至2018年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2018年我省城镇居民百户家庭人口数的平均数为(B )(A )318.6 (B )318.6 (C)318.6 (D)301.6 10.(山东文)9.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( B )AB C .3D .8510.(陕西文)(3).某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为( C ) A .30 B .25 C .20 D .15 11.(重庆理)(5)已知随机变量ζ服从正态分布N (3,a 2),则P (3)ζ<=(D )(A)15(B)14(C)13(D)1212. (重庆文)(5)某交高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是(D )(A)简单随机抽样法(B)抽签法7420136203851192(C)随机数表法 (D)分层抽样法13.(重庆文)(9)从编号为1,2,…,10的10个大小相同的球中任取4个,则所取4个球的最大号码是6的概率为 (B )(A)184(B)121(C)25(D)35二.填空题:1.(广东文) (11).为了调查某厂工人生产某种产品的能力,随机抽查 了20位工人某天生产该产品的数量.产品数量的分组区间为[)45,55,[)[)[)55,65,65,75,75,85, [)85,95由此得到频率分布直方图如图,则这20名工人中一天生产该产品数量在[)55,75的人数是 13 .2.(海南宁夏理文)(16).从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm ),结果如下:甲品种:271 273 280 285 285 287 292 294 295 301 318 318 318 318 310 314 319 323 325 325 328 331 334 337 352乙品种:284 292 295 318 318 318 312 313 315 315 316 318 318 320 322 322 324 327 329 331 333 336 337 343 356 由以上数据设计了如下茎叶图根据以上茎叶图,对甲、乙两品种棉花的纤维长度作比较,写出两个统计结论: ① ;3 127 7 5 5 0 28 4 5 4 2 29 2 5 8 7 3 3 1 30 4 6 79 4 0 31 2 3 5 5 6 8 8 8 5 5 3 32 0 2 2 4 7 9 7 4 1 33 1 3 6 734 3 2 35 6甲乙② .以下任填两个:(1).乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度). (2).甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散.(或:乙品种棉花的纤维长度较甲品种棉花的纤维长度更集中(稳定).甲品种棉花的纤维长度的分散程度比乙品种棉花的纤维长度的分散程度更大). (3).甲品种棉花的纤维长度的中位数为318mm ,乙品种棉花的纤维长度的中位数为318mm . (4).乙品种棉花的纤维长度基本上是对称的,而且大多集中在中间(均值附近).甲品种棉花的纤维长度除一个特殊值(352)外,也大致对称,其分布较均匀.3. (湖北文)11.一个公司共有1 000名员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为50的样本,已知某部门有200名员工,那么从该部门抽取的工人数是 10 . 4.(湖北文)14.明天上午李明要参加奥运志愿者活动,为了准时起床,他用甲、乙两个闹钟叫醒自己,假设甲闹钟准时响的概率是0.80,乙闹钟准时响的概率是0.90,则两个闹钟至少有一准时响的概率是 0.98 .5. (湖南理)15.对有n (n ≥4)个元素的总体{1,2,3,…,n }进行抽样,先将总体分成两个子总体{1,2,…,m }和{m +1、m +2,…,n }(m 是给定的正整数,且2≤m ≤n -2),再从每个子总体中各随机抽取2个元素组成样本,用P i j 表示元素i 和f 同时出现在样本中的概率,则P 1m =4()m n m -;所有P if (1≤i <j ≤)n 的和等于 6 .6. (湖南文)(12)从某地区15000位老人中随机抽取500人,其生活能否自理的情况如下表所示:则该地区生活不能自理的老人中男性比女性约多____60____人。
2018年全国各地高考数学分类汇编word版含答案14-概率

2018年全国各地高考数学分类汇编word版含答案14-概率一、选择题(共6小题;共30分)1. 从名男同学和名女同学中任选人参加社区服务,则选中的人都是女同学的概率为A. B. C. D.2. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于的偶数可以表示为两个素数的和”,如.在不超过的素数中,随机选取两个不同的数,其和等于的概率是A. B. C. D.3. 如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形的斜边,直角边,.的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为,,,则A. B. C. D.4. 设,随机变量的分布列是则当在内增大时,A. 减小B. 增大C. 先减小后增大D. 先增大后减小5. 若某群体中的成员只用现金支付的概率为,既用现金支付也用非现金支付的概率为,则不用现金支付的概率为A. B. C. D.6. 某群体中的每位成员使用移动支付的概率都为,各成员的支付方式相互独立,设为该群体的位成员中使用移动支付的人数,,,则A. B. C. D.二、填空题(共2小题;共10分)7. 某兴趣小组有名男生和名女生,现从中任选名学生去参加活动,则恰好选中名女生的概率为.8. 有编号互不相同的五个砝码,其中克、克、克砝码各一个,克砝码两个.从中随机选取三个,则这三个砝码的总质量为克的概率是(结果用最简分数表示).三、解答题(共5小题;共65分)9. 已知某校甲、乙、丙三个年级的学生志愿者人数分别为,,.现采用分层抽样的方法从中抽取名同学去某敬老院参加献爱心活动.(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(2)设抽出的名同学分别用,,,,,,表示,现从中随机抽取名同学承担敬老院的卫生工作.(ⅰ)试用所给字母列举出所有可能的抽取结果;(ⅱ)设为事件“抽取的名同学来自同一年级”,求事件发生的概率.10. 电影公司随机收集了电影的有关数据,经分类整理得到下表:电影类型第一类第二类第三类第四类第五类第六类电影部数好评率好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.(1)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;(2)随机选取部电影,估计这部电影没有获得好评的概率;(3)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加,哪类电影的好评率减少,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)11. 电影公司随机收集了电影的有关数据,经分类整理得到如表:电影类型第一类第二类第三类第四类第五类第六类电影部数好评率好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.假设所有电影是否获得好评相互独立.(1)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;(2)从第四类电影和第五类电影中各随机选取部,估计恰有部获得好评的概率;(3)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等.用“”表示第类电影得到人们喜欢,“”表示第类电影没有得到人们喜欢().写出方差,,,,,的大小关系.12. 某工厂的某种产品成箱包装,每箱件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为,且各件产品是否为不合格品相互独立.(1)记件产品中恰有件不合格品的概率为,求的最大值点.(2)现对一箱产品检验了件,结果恰有件不合格品,以()中确定的作为的值.已知每件产品的检验费用为元,若有不合格品进入用户手中,则工厂要对每件不合格品支付元的赔偿费用.(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为,求;(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?13. 已知某单位甲、乙、丙三个部门的员工人数分别为,,.现采用分层抽样的方法从中抽取人,进行睡眠时间的调查.(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?(2)若抽出的人中有人睡眠不足,人睡眠充足,现从这人中随机抽取人做进一步的身体检查.(i)用表示抽取的人中睡眠不足的员工人数,求随机变量的分布列与数学期望;(ii)设为事件“抽取的人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件发生的概率.答案第一部分1. D2. C3. A4. D5. B6. B第二部分7.8.第三部分9. (1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为,由于采用分层抽样的方法从中抽取名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取人,人,人.(2)(ⅰ)从抽出的名同学中随机抽取名同学的所有可能结果为,,,,,,,,,,,,,,,,,,,,,共种.(ⅱ)由(Ⅰ),不妨设抽出的名同学中,来自甲年级的是,,,来自乙年级的是,,来自丙年级的是,,则从抽出的名同学中随机抽取的名同学来自同一年级的所有可能结果为,,,,,共种.所以,事件发生的概率为.10. (1)设事件为选取的电影是获得好评的第四类电影,基本事件总数为,事件中包含的基本事件个数为,所以.(2)设事件为选取的电影获得好评,则事件包含的基本事件个数为,则,,所以电影未获得好评的概率为.(3)第五类电影好评率增加,第二类电影好评率减少,可使得获得好评的电影总数与样本中电影总部数的比值最大.11. (1)电影公司收集电影有(部),获得好评第四类电影有(部),所以随机选取部电影是获得好评的第四类电影概率为.(2)设事件:第四类获得好评,;事件:第五类获得好评,;事件:恰有部获得好评,(3).12. (1)件产品中恰有件不合格品的概率为.因此令,得.当时,;当时,.所以的最大值点为.(2)由()知,.(i)令表示余下的件产品中的不合格品件数,依题意知,,即.所以.(ii)如果对余下的产品作检验,则这一箱产品所需要的检验费为元.由于,故应该对余下的产品作检验.13. (1)由已知,甲、乙、丙三个部门的员工人数之比为,由于采用分层抽样的方法从中抽取人,因此应从甲、乙、丙三个部门的员工中分别抽取人,人,人.(2)(i)随机变量的所有可能取值为,,,..所以,随机变量的分布列为随机变量的数学期望.(ii)设事件为“抽取的人中,睡眠充足的员工有人,睡眠不足的员工有人”;事件为“抽取的人中,睡眠充足的员工有人,睡眠不足的员工有人”,则,且与互斥,由(i)知,,,故.所以,事件发生的概率为.。
2018年全国各地高考数学试题及解答分类汇编大全(15 概率、统计、统计案例、推理与证明)

2018年全国各地高考数学试题及解答分类汇编大全 (15概率、统计、统计案例、推理与证明)一、选择题1.(2018全国新课标Ⅰ文、理)某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是( ) A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半1。
答案:A解答:由图可得,A 选项,设建设前经济收入为x ,种植收入为0.6x .建设后经济收入则为2x ,种植收入则为0.3720.74x x ⨯=,种植收入较之前增加.另解:假设建设前收入为a ,则建设后收入为2a ,所以种植收入在新农村建设前为60%a ,新农村建设后为37%2a ⋅;其他收入在新农村建设前为4%a ⋅,新农村建设后为5%2a ⋅,养殖收入在新农村建设前为30%a ⋅,新农村建设后为30%2a ⋅ 故不正确的是A.2.(2018全国新课标Ⅱ文)从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为( )A .0.6B .0.5C .0.4D .0.32.【答案】D【解析】设2名男同学为1A ,2A ,3名女同学为1B ,2B ,3B ,从以上5名同学中任选2人总共有12A A ,11A B ,12A B ,13A B ,21A B ,22A B ,23A B ,12B B ,13B B ,23B B 共10种可能,选中的2人都是女同学的情况共有共12B B ,13B B ,23B B 三种可能则选中的2人都是女同学的概率为30.310P ==,故选D .3.(2018全国新课标Ⅲ文)若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( )A .0.3B .0.4C .0.6D .0.73.答案:B解答:由题意10.450.150.4P =--=.故选B.二、填空1.(2018江苏)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 ▲ .1.【答案】90【解析】由茎叶图可知,5位裁判打出的分数分别为89,89,90,91,91,故平均数为8989909191905++++=.2.(2018江苏)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为 ▲ .2.【答案】310【解析】从5名学生中抽取2名学生,共有10种方法,其中恰好选中2名女生的方法有3种,因此所求概率为310.3. (2018上海)有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是______(结果用最简分数表示)4.(2018全国新课标Ⅲ文)某公司有大量客户,且不同年龄段客户对其服务的评价有较大差异.为了解客户的评价,该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样,则最合适的抽样方法是________. 14.答案:分层抽样解答:由题意,不同龄段客户对其服务的评价有较大差异,故采取分层抽样法.三、解答题1.(好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.(1)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率; (2)随机选取1部电影,估计这部电影没有获得好评的概率;(3)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加01.,哪类电影的好评率减少01.,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)1.【答案】(1)0025.;(2)0814.;(3)增加第五类电影的好评率,减少第二类电影的好评率. 【解析】(1)由题意知,样本中电影的总部数是140503002008005102000+++++=.第四类电影中获得好评的电影部数是20002550⨯=.,故所求概率为5000252000=..(2)设“随机选取1部电影,这部电影没有获得好评”为事件B .没有获得好评的电影共有14006500830008520007580008510091628⨯+⨯+⨯+⨯+⨯+⨯=......部.由古典概型概率公式得()162808142000P B ==..(3)增加第五类电影的好评率,减少第二类电影的好评率.2.(2018北京理)设n 为正整数,集合A =12{|(,,,),{0,1},1,2,,}n k t t t t k n αα=∈=.对于集合A 中的任意元素12(,,,)n x x x α=和12(,,,)n y y y β=,记M (αβ,)=111122221[(||)(||)(||)]2n n n n x y x y x y x y x y x y +--++--+++--.(Ⅰ)当n =3时,若(1,1,0)α=,(0,1,1)β=,求M (,αα)和M (,αβ)的值;(Ⅱ)当n =4时,设B 是A 的子集,且满足:对于B 中的任意元素,αβ,当,αβ相同时,M (αβ,)是奇数;当,αβ不同时,M (αβ,)是偶数.求集合B 中元素个数的最大值;(Ⅲ)给定不小于2的n ,设B 是A 的子集,且满足:对于B 中的任意两个不同的元素,αβ,M (αβ,)=0.写出一个集合B ,使其元素个数最多,并说明理由.2(共14分)解:(Ⅰ)因为α=(1,1,0),β=(0,1,1),所以M (α,α)=12 [(1+1−|1−1|)+(1+1−|1−1|)+(0+0−|0−0|)]=2,M (α,β)=12[(1+0–|1−0|)+(1+1–|1–1|)+(0+1–|0–1|)]=1.(Ⅱ)设α=(x 1,x 2,x 3,x 4)∈B ,则M (α,α)= x 1+x 2+x 3+x 4. 由题意知x 1,x 2,x 3,x 4∈{0,1},且M (α,α)为奇数, 所以x 1,x 2,x 3,x 4中1的个数为1或3.所以B ⊆{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}. 将上述集合中的元素分成如下四组:(1,0,0,0),(1,1,1,0);(0,1,0,0),(1,1,0,1);(0,0,1,0),(1,0,1,1);(0,0,0,1),(0,1,1,1).经验证,对于每组中两个元素α,β,均有M (α,β)=1. 所以每组中的两个元素不可能同时是集合B 的元素. 所以集合B 中元素的个数不超过4.又集合{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}满足条件, 所以集合B 中元素个数的最大值为4.(Ⅲ)设S k =( x 1,x 2,…,x n )|( x 1,x 2,…,x n )∈A ,x k =1,x 1=x 2=…=x k –1=0)(k =1,2,…,n ),S n +1={( x 1,x 2,…,x n )| x 1=x 2=…=x n =0}, 则A =S 1∪S 1∪…∪S n +1.对于S k (k =1,2,…,n –1)中的不同元素α,β,经验证,M (α,β)≥1. 所以S k (k =1,2 ,…,n –1)中的两个元素不可能同时是集合B 的元素. 所以B 中元素的个数不超过n +1.取e k =( x 1,x 2,…,x n )∈S k 且x k +1=…=x n =0(k =1,2,…,n –1).令B =(e 1,e 2,…,e n –1)∪S n ∪S n +1,则集合B 的元素个数为n +1,且满足条件. 故B 是一个满足条件且元素个数最多的集合.3.(2018江苏)设*n ∈N ,对1,2,···,n 的一个排列12n i i i ,如果当s <t 时,有s t i i >,则称(,)s t i i 是排列12n i i i 的一个逆序,排列12n i i i 的所有逆序的总个数称为其逆序数.例如:对1,2,3的一个排列231,只有两个逆序(2,1),(3,1),则排列231的逆序数为2.记()n f k 为1,2,···,n 的所有排列中逆序数为k 的全部排列的个数.(1)求34(2),(2)f f 的值;(2)求(2)(5)n f n ≥的表达式(用n 表示).3.【答案】(1)2,5;(2)5n ≥时,()2222n n n f --=.【解析】(1)记()abc τ为排列abc 的逆序数,对1,2,3的所有排列,有()123=0τ,()132=1τ,()213=1τ,()231=2τ,()312=2τ,()321=3τ,所以()301f =,()()33122f f ==.对1,2,3,4的排列,利用已有的1,2,3的排列,将数字4添加进去,4在新排列中的位置只能是最后三个位置.因此,()()()()433322105f f f f =++=.(2)对一般的()4n n ≥的情形,逆序数为0的排列只有一个:12n ,所以()01n f =.逆序数为1的排列只能是将排列12n 中的任意相邻两个数字调换位置得到的排列,所以()11n f n =-.为计算()12n f +,当1,2,…,n 的排列及其逆序数确定后,将1n +添加进原排列,1n +在新排列中的位置只能是最后三个位置.因此,()()()()()122102n n n n n f f f f f n +=++=+.当5n ≥时,()()()()()()()()11254422222222n n n n n f f f f f f f f ---=-+-++-+⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦()()()24212422n n n n f --=-+-+++=,因此,5n ≥时,()2222n n n f --=.4.(2018天津文)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动. (Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i )试用所给字母列举出所有可能的抽取结果;(ii )设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率. 4.【答案】(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人;(2)①答案见解析;②521.【解析】(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.(2)①从抽出的7名同学中随机抽取2名同学的所有可能结果为{},A B ,{},A C ,{},A D ,{},A E ,{},A F ,{},A G ,{},B C ,{},B D ,{},B E ,{},B F ,{},B G ,{},C D ,{},C E ,{},C F ,{},C G ,{},D E ,{},D F ,{},D G ,{},E F ,{},E G ,{},F G ,共21种.②由(1),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{},A B ,{},A C ,{},B C ,{},D E ,{},F G ,共5种. 所以,事件M 发生的概率为()521P M =.5.(2018全国新课标Ⅰ文)某家庭记录了未使用节水龙头50天的日用水量数据(单位:m 3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:((2)估计该家庭使用节水龙头后,日用水量小于0.35 m 3的概率;(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)5.答案:略 解答:(1)(2)由题可知用水量在[0.3,0.4]的频数为10,所以可估计在[0.3,0.35)的频数为5,故用水量小于30.35m 的频数为1513524+++=,其概率为240.4850P ==.(3)未使用节水龙头时,50天中平均每日用水量为: 31(0.0510.1530.2520.3540.4590.55260.657)0.50650m ⨯+⨯+⨯+⨯+⨯+⨯+⨯=, 一年的平均用水量则为30.506365184.69m ⨯=. 使用节水龙头后,50天中平均每日用水量为: 31(0.0510.1550.25130.35100.45160.555)0.3550m ⨯+⨯+⨯+⨯+⨯+⨯=, 一年的平均用水量则为30.35365127.75m ⨯=, ∴一年能节省3184.69127.7556.94m -=.6.(2018全国新课标Ⅱ文、理) 下图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y 与时间变量t 的两个线性回归模型.根据2000年至2016年的数据(时间变量t 的值依次为1,2,,17)建立模型①:ˆ30.413.5yt =-+;根据2010年至2016年的数据(时间变量t 的值依次为1,2,,7)建立模型②:ˆ9917.5yt =+. (1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值; (2)你认为用哪个模型得到的预测值更可靠?并说明理由.6.【答案】(1)模型①226.1亿元,模型②2565.亿元;(2)模型②,见解析. 【解析】(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为 30.413.5192ˆ26.1y=-+⨯=(亿元). 利用模型②,该地区2018年的环境基础设施投资额的预测值为 ˆ9917592565y =+⨯=..(亿元). (2)利用模型②得到的预测值更可靠.理由如下: (i )从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线30.413.5y t =-+上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型ˆ99175y t =+.可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.(ii )从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.7.(2018全国新课标Ⅲ文、理)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m ,并将完成生产任务所需时间超过m 和不超过m(3附:22()()()()()n ad bc K a b c d a c b d -=++++,2()0.0500.0100.0013.8416.63510.828P K k k ≥.7.答案:见解析解答:(1)第一种生产方式的平均数为184x =,第二种生产方式平均数为274.7x =,∴12x x >,所以第一种生产方式完成任务的平均时间大于第二种,∴第二种生产方式的效率更高.(2)由茎叶图数据得到80m =,∴列联表为(3)222()40(151555)10 6.635()()()()20202020n ad bc K a b c d a c b d -⨯-⨯===>++++⨯⨯⨯,∴有99%的把握认为两种生产方式的效率有差异.。
2018年高考试题分类汇编(统计与概率)

2018年高考试题分类汇编(统计与概率)考点1 简单计数1.(2018·浙江卷)从1,3,5,7,9中任取2个数字,从0,2,4,6中任取2个数字,一共可以组成____个没有重复数字的四位数.(用数字作答)2.(2018·全国卷Ⅰ理科)从2位女生,4位男生中选3位参加科技比赛,且至少有1位女生入选,则不同的选法共有种.(用数字填写答案)考点2 随机事件的概率考法1古典概型1. (2018·全国卷Ⅱ文科)从2名男同学和3名女同学中任选2人参加社区服务,则选中的两人都是女同学的概率为A.0.6 B.0.5 C.0.4 D.0.32.(2018·全国卷Ⅱ理科)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是“每个大于2的偶数可以表示成两个素数的和”.例如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是A.112B.114C.115D.1183.(2018·江苏卷)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为.4.(2018·上海卷)有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是_ __.(结果用最简分数表示)5.(2018·天津卷文科)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用,,,,,,A B C D E F G表示,现从中随机抽取2名同学承担敬老院的卫生工作.(1)试用所给字母列举出所有可能的抽取结果;(2)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.考法2 几何概型1.(2018·全国卷Ⅰ文理)下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB ,AC .ABC ∆的三边所围成的区域记为Ⅰ,黑色区域记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为1p ,2p ,3p ,则A.12p p =B. 13p p =C. 23p p =D. 123p p p =+考法3 互斥事件与相互独立事件 1.(2018·全国卷Ⅲ文科)某群中的成员只用现金支付的概率为0.45,既用现金也用非现金支付的概率为0.15,则不用现金支付的概率为A .0.3B .0.4C . 0.6D .0.72.(2018·全国卷Ⅲ理科)某群中的每位成员使用移动支付的概率都为p ,各成 员的支付方式互相独立,设X 为该群体的10位成员中使用移动支付的人数, 2.4DX =,(4)p X =<(6)p X =,则p =A .0.7B .0.6C .0.4D .0.3考点3 统计初步考法1 抽样方法1.(2018·全国卷Ⅲ文科)某公司有大量客户,且不同年龄段客户对其服务的平价有较大的差异.为了解客户的平价,该公司准备进行抽样调查,可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样,则最适合的抽样方法为 . 考法2 统计图表1.(2018·江苏卷)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为 .2.(2018·全国卷Ⅰ文理)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解高该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:4% 6% 30% 60% 养殖收入 其他收入 第三产业收入 种植收入 建设前经济收入构成比例5% 28% 30% 37% 养殖收入 其他收入 第三产业收入 种植收入 建设后经济收入构成比例 8 9 9 9 0 1 1则下面结论中不正确的是A.新农村建成后,种植收入减少B.新农村建成后,其他收入增加一倍以上C.新农村建成后,养植收入增加一倍D.新农村建成后,养植收入与第三产业收入的总和超过了经济收入的一半考点4 统计与概率考法1 分布列、期望、方差1.(2018·天津卷理科)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(Ⅰ)应从甲、乙、丙三个部门的员工中分别抽取多少人?(Ⅱ)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(1)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;(2)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.2.(2018·全国卷Ⅰ理科)某工厂的某种产品成箱包装,每箱200件,每箱产品在交付用户之前要对产品作检验,如检验出不合格产品,则更换为合格产品.检验时,先从这箱产品种任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为(01)<<,且各件产品是否为不合格产品互相独立.p p(Ⅰ)记20件产品中恰有2件不合格品的概率为()p.f p的最大值f p,求()0(Ⅱ)现对一箱产品检验了20件,结果恰有2件不合格品,以(Ⅰ)中确定的p0作为p的值.已知每件产品的检验费为2元,若有不合格品进入用户手中,则工厂要对每件不合格产品支付25元的赔偿费用.(1)若不对该产箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X,求EX;(2)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?3.(2018·北京卷文科)电影公司随机收集了电影的有关数据,经分类整理得到下表:好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(Ⅱ)随机选取1部电影,估计这部电影没有获得好评的概率;(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)4.(2018·北京卷理科)好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.假设所有电影是否获得好评相互独立.(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(Ⅱ)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率;(Ⅲ)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用“1k ξ=”表示第k 类电影得到人们喜欢,“0k ξ=”表示第k 类电影没有得到人们喜欢(1,2,3,4,5,6k =).写出方差1D ξ,2D ξ,3D ξ,4D ξ,5D ξ,6D ξ的大小关系.考法2 线性回归分析1.(2018·全国卷Ⅱ文理)下图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图,为了预测该地区2018年的环境基础设施投资额,建立了y 与时间变量t 的两个线性回归模型.根据2000年至2016的数据(时间变量t 的值依次为1,2,,17 )建立模型① 30.413.5y t =-+;根据2010年至2016的数据(时间变量t 的值依次为1,2,,7 )建立模型② 9917.5y t =+.(Ⅰ)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值; (Ⅱ)你认为哪个模型的预测值更可靠?并说明理由.考法3 用样本估计总体1.(2018·全国卷Ⅰ文科)某家庭记录了未使用节水龙头50天的日用水量数据(单位:3m )和使用节水龙头50天的日用水量数据,得到频率分布表如下:(Ⅰ)在答题卡上作出使用了节水龙头50天的日用水量频率分布直方图: (Ⅱ)估计该家庭使用了节水龙头后,日用水量小于3(Ⅲ)估计该家庭使用了节水龙头后,一年 能节省多少水?(一年按365天计算,同一 组中的数据以这组数据所在区间的中点的值 作代表.) 2000 2001 2002 20032004 2005 2006 2008 2007 2009 2010 2012 2014 2013 2015考法4 独立性检验1.(2018·全国卷Ⅲ文理)某工厂为了提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20名工人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min )绘制了如下茎叶图:(Ⅰ)根据茎叶图判断哪种生产方式的效率更高?并说明理由.(Ⅱ)求40名工人完成生产任务所需的时间的中位数m , 并将完成生产任务所(Ⅲ)根据(Ⅱ)中列联表,能否有99%把握认为两种生产方式的效率有差异?附:22()()()()()n ad bc K a b c d a c b d -=++++第一种生产方式 第二种生产方式 8 8 7 6 5 5 6 8 9 0 1 2 2 3 4 5 6 6 8 1 4 4 5 09 9 7 6 2 9 8 7 7 6 5 4 3 3 2 2 1 1 0 0。
2018年全国各地高考数学试题及解答分类汇编大全(16 随机变量及其分布)

2018年全国各地高考数学试题及解答分类汇编大全(16概率、随机变量及其分布 正态分布)一、选择题1.(2018浙江)设0<p <1则当p 在(0,1)内增大时,A .D (ξ)减小 B .D (ξ)增大C .D (ξ)先减小后增大D .D (ξ)先增大后减小1..答案:D解答:111()0122222p p E p x -=???+, 22211113()()()()222222p p D p p p x -=?+?+?22111()422p p p =-++=--+,所以当p 在(0,1)内增大时,()D x 先增大后减小,故选D.2.(2018全国新课标Ⅲ理)某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10位成员中使用移动支付的人数, 2.4DX =,()()46P X P X =<=,则p =( )A .0.7B .0.6C .0.4D .0.32.答案:B解答:由~(10,)X B p ,∴10(1)2.4D X p p =-=,∴21010 2.40p p -+=,解之得120.4,0.6p p ==,由(4)(6)P X P X =<=,有0.6p =.二、填空三、解答题1.(2018假设所有电影是否获得好评相互独立.(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率; (Ⅱ)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率;(Ⅲ)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用“1k ξ=”表示第k 类电影得到人们喜欢,“0k ξ=”表示第k 类电影没有得到人们喜欢(k =1,2,3,4,5,6).写出方差1D ξ,2D ξ,3D ξ,4D ξ,5D ξ,6D ξ的大小关系.1.【答案】(1)概率为0025.;(2)概率估计为035.;(3)142536D D D D D D ξξξξξξ>>=>>. 【解析】(1)由题知,样本中电影的总部数是140503002008005102000+++++=,第四类电影中获得好评的电影部数是20002550⨯=..故所求概率为5000252000=..(2)设事件A 为“从第四类电影中随机选出的电影获得好评”, 事件B 为“从第五类电影中随机选出的电影获得好评”.故所求概率为()()()()()()()()()11P AB AB P AB P AB P A P B P A P B +=+=-+-. 由题意知,()P A 估计为025.,()P B 估计为02.. 故所求概率估计为0250807502035⨯+⨯=...... (3)142536D D D D D D ξξξξξξ>>=>>.2.(2018天津理)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(I )应从甲、乙、丙三个部门的员工中分别抽取多少人?(II )若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查. (i )用X 表示抽取的3人中睡眠不足的员工人数,求随机变量X 的分布列与数学期望; (ii )设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A 发生的概率. 2.【答案】(1)从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人. (2)①答案见解析;②.【解析】(1)由已知,甲、乙、丙三个部门的员工人数之比为3∶2∶2, 由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人. (2)(1)随机变量X 的所有可能取值为0,1,2,3.()()34337C C 0,1,2,3C k kP X k k -⋅===.随机变量X 的数学期望()0123353535357E X =⨯+⨯+⨯+⨯=. (2)设事件B 为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”; 事件C 为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”, 则A B C =,且B 与C 互斥,由(1)知,()()2P B P X ==,()()1P C P X ==, 故()()()627()1P A P B C P X P X ===+==. 所以,事件A 发生的概率为67.。
2018全国高考数学统计与概率专题(附答案解析)

2018全国高考真题数学统计与概率专题(附答案解析)1.(全国卷I,文数、理数第3题.5分)某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半答案:A2.(全国卷I,文数19题.12分)某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:未使用节水龙头50天的日用水量频数分布表日用水量[)00.1,[)0.10.2,[)0.20.3,[)0.30.4,[)0.40.5,[)0.50.6,[)0.60.7,频数 1 3 2 4 9 26 5使用了节水龙头50天的日用水量频数分布表日用水量[)00.1,[)0.10.2,[)0.20.3,[)0.30.4,[)0.40.5,[)0.50.6,频数 1 5 13 10 16 5 (1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)【答案解析】解:(1)(2)根据以上数据,该家庭使用节水龙头后50天日用水量小于0.35m3的频率为0.2×0.1+1×0.1+2.6×0.1+2×0.05=0.48,因此该家庭使用节水龙头后日用水量小于0.35m 3的概率的估计值为0.48. (3)该家庭未使用节水龙头50天日用水量的平均数为11(0.0510.1530.2520.3540.4590.55260.655)0.4850x =⨯+⨯+⨯+⨯+⨯+⨯+⨯=. 该家庭使用了节水龙头后50天日用水量的平均数为21(0.0510.1550.25130.35100.45160.555)0.3550x =⨯+⨯+⨯+⨯+⨯+⨯=. 估计使用节水龙头后,一年可节省水3(0.480.35)36547.45(m )-⨯=. 3.(全国卷I ,理数20题12分)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品,检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为()01p p <<,且各件产品是否为不合格品相互独立.(1)记20件产品中恰有2件不合格品的概率为()f p ,求()f p 的最大值点0p ; (2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的0p 作为p 的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.(i )若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为X ,求EX ;(ii )以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?【答案解析】(1)20件产品中恰有2件不合格品的概率为221820()C (1)f p p p =-.因此 2182172172020()C [2(1)18(1)]2C (1)(110)f p p p p p p p p '=---=--.令()0f p '=,得0.1p =.当(0,0.1)p ∈时,()0f p '>;当(0.1,1)p ∈时,()0f p '<. 所以()f p 的最大值点为00.1p =. (2)由(1)知,0.1p =.(i )令Y 表示余下的180件产品中的不合格品件数,依题意知(180,0.1)YB ,=+.X Y=⨯+,即402520225X Y所以(4025)4025490=+=+=.EX E Y EY(ii)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元.由于400EX>,故应该对余下的产品作检验.4.(全国卷Ⅱ,文数5题.5分)从2名男同学和3名女同学中任选2人参加社区服务,则选中2人都是女同学的概率为A.0.6 B.0.5C.0.4D.0.3【答案】D5.(全国卷Ⅱ,文数、理数18题.12分)下图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图.为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2,,17)建立模型①:ˆ30.413.5y t=-+;根据2010年至2016年的数据(时间变量t的值依次为1,2,,7)建立模型②:ˆ9917.5=+.y t(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;(2)你认为用哪个模型得到的预测值更可靠?并说明理由.【答案解析】解:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为y=–30.4+13.5×19=226.1(亿元).利用模型②,该地区2018年的环境基础设施投资额的预测值为y=99+17.5×9=256.5(亿元).(2)利用模型②得到的预测值更可靠.理由如下:(i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=–30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型y=99+17.5t 可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.(ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.6.(全国卷Ⅱ,理数5题.5分)从2名男同学和3名女同学中任选2人参加社区服务,则选中2人都是女同学的概率为A.0.6 B.0.5 C.0.4 D.0.3【答案】A7.(全国卷Ⅲ,文数5题.5分)若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为A.0.3 B.0.4 C.0.6 D.0.7【答案】B8.(全国卷Ⅲ,文数、理数18题.12分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m 和不超过m的工人数填入下面的列联表:超过m不超过m第一种生产方式第二种生产方式(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?附:22()()()()()n ad bcKa b c d a c b d-=++++,2()0.0500.0100.0013.8416.63510.828P K kk≥.【答案解析】解:(1)第二种生产方式的效率更高.理由如下:(i)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.(ii)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的效率更高.(iii)由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.(iv)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.学科%网以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分. (2)由茎叶图知7981802m +==. 列联表如下:超过m 不超过m第一种生产方式 15 5 第二种生产方式515(3)由于2240(151555)10 6.63520202020K ⨯-⨯==>⨯⨯⨯,所以有99%的把握认为两种生产方式的效率有差异.9.(北京卷,文数17题,13分)电影公司随机收集了电影的有关数据,经分类整理得到下表: 电影类型 第一类 第二类 第三类 第四类 第五类 第六类 电影部数 140 50 300 200 800 510 好评率0.40.20.150.250.20.1好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(Ⅱ)随机选取1部电影,估计这部电影没有获得好评的概率;学科*网(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)【答案解析】(Ⅰ)由题意知,样本中电影的总部数是140+50+300+200+800+510=2000. 第四类电影中获得好评的电影部数是200×0.25=50, 故所求概率为500.0252000=. (Ⅱ)方法一:由题意知,样本中获得好评的电影部数是 140×0.4+50×0.2+300×0.15+200×0.25+800×0.2+510×0.1 =56+10+45+50+160+51=372.故所求概率估计为37210.8142000-=. 方法二:设“随机选取1部电影,这部电影没有获得好评”为事件B .没有获得好评的电影共有140×0.6+50×0.8+300×0.85+200×0.75+800×0.8+510×0.9=1628部.由古典概型概率公式得16280.8142)00(0P B ==. (Ⅲ)增加第五类电影的好评率, 减少第二类电影的好评率. 10.(北京卷,理数17题,12分)电影公司随机收集了电影的有关数据,经分类整理得到下表:好评率是指:一类电影中获得好评的部数与该类电影的部数的比值. 假设所有电影是否获得好评相互独立.(Ⅰ)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(Ⅱ)从第四类电影和第五类电影中各随机选取1部,估计恰有1部获得好评的概率; (Ⅲ)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用“1k ξ=”表示第k 类电影得到人们喜欢,“0k ξ=”表示第k 类电影没有得到人们喜欢(k =1,2,3,4,5,6).写出方差1D ξ,2D ξ,3D ξ,4D ξ,5D ξ,6D ξ的大小关系.【答案解析】解:(Ⅰ)由题意知,样本中电影的总部数是140+50+300+200+800+510=2000, 第四类电影中获得好评的电影部数是200×0.25=50. 故所求概率为500.0252000=. (Ⅱ)设事件A 为“从第四类电影中随机选出的电影获得好评”, 事件B 为“从第五类电影中随机选出的电影获得好评”. 故所求概率为P (AB AB +)=P (AB )+P (AB )=P (A )(1–P (B ))+(1–P (A ))P (B ). 由题意知:P (A )估计为0.25,P (B )估计为0.2. 故所求概率估计为0.25×0.8+0.75×0.2=0.35. (Ⅲ)1D ξ>4D ξ>2D ξ=5D ξ>3D ξ>6D ξ. 11.(天津卷,文数,15题,13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(Ⅱ)设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i )试用所给字母列举出所有可能的抽取结果;(ii )设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率.【答案解析】本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识.考查运用概率知识解决简单实际问题的能力.满分13分. (Ⅰ)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.(Ⅱ)(i )解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种.(ii )解:由(Ⅰ),不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种. 所以,事件M 发生的概率为P (M )=521. 12.(天津卷,理数,16题,13分)已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16. 现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.(I )应从甲、乙、丙三个部门的员工中分别抽取多少人?(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.【答案解析】本小题主要考查随机抽样、离散型随机变量的分布列与数学期望、互斥事件的概率加法公式等基础知识.考查运用概率知识解决简单实际问题的能力.满分13分.学.科网(Ⅰ)解:由已知,甲、乙、丙三个部门的员工人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7人,因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(Ⅱ)(i)解:随机变量X的所有可能取值为0,1,2,3.P(X=k)=34337C CCk k-⋅(k=0,1,2,3).所以,随机变量X的分布列为随机变量X的数学期望11218412 ()0123353535357E X=⨯+⨯+⨯+⨯=.(ii)解:设事件B为“抽取的3人中,睡眠充足的员工有1人,睡眠不足的员工有2人”;事件C为“抽取的3人中,睡眠充足的员工有2人,睡眠不足的员工有1人”,则A=B∪C,且B与C互斥,由(i)知,P(B)=P(X=2),P(C)=P(X=1),故P(A)=P(B∪C)=P(X=2)+P(X=1)=67.所以,事件A发生的概率为67.13.(江苏卷,3题,5分)已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为__________.【答案解析】答案:90解析:8989909191905++++=14.(浙江卷,7题,4分)设0<p<1,随机变量ξ的分布列是ξ0 1 2P12p-122p 则当p在(0,1)内增大时,A.D(ξ)减小B.D(ξ)增大C.D(ξ)先减小后增大D.D(ξ)先增大后减小【答案】D第11 页共11 页。
【高三数学试题精选】2018年高考真题理科数学概率归类汇编

2018年高考真题理科数学概率归类汇编5 P(c)=1- P= ,解得P= ………………………………4 分(2)由题意,P( =0)=P( =1)=P( =2)=P( =3)=所以,随机变量的概率分布列为0123P故随机变量X的数学期望为E =0 ……………………12分[点评]本小题主要考查相互独立事,独立重复试验、互斥事、随机变量的分布列、数学期望等概念及相关计算,考查运用概率知识与方法解决实际问题的能力10.【2018高考湖北理20】(本小题满分12分)根据以往的经验,某工程施工期间的降水量X(单位)对工期的影响如下表降水量X工期延误天数 02610历年气象表明,该工程施工期间降水量X小于300,700,900的概率分别为03,07,09 求(Ⅰ)工期延误天数的均值与方差;(Ⅱ)在降水量X至少是的条下,工期延误不超过6天的概率【答案】(Ⅰ)由已知条和概率的加法式有,所以的分布列为0261003040201于是,;故工期延误天数的均值为3,方差为(Ⅱ)由概率的加法式,又由条概率,得故在降水量X至少是的条下,工期延误不超过6天的概率是11【2018高考江苏25】(10分)设为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,;当两条棱平行时,的值为两条棱之间的距离;当两条棱异面时,.(1)求概率;(2)求的分布列,并求其数学期望.【答案】解(1)若两条棱相交,则交点必为正方体8个顶点中的一个,过任意1个顶点恰有3条棱,∴共有对相交棱。
∴ 。
(2)若两条棱平行,则它们的距离为1或,其中距离为的共有6对,∴ ,。
∴随机变量的分布列是∴其数学期望。
【考点】概率分布、数学期望等基础知识。
【解析】(1)求出两条棱相交时相交棱的对数,即可由概率式求得概率。
(2)求出两条棱平行且距离为的共有6对,即可求出,从而求出(两条棱平行且距离为1和两条棱异面),因此得到随机变量的分布列,求出其数学期望。
2018年高考数学全国卷试题答案解析(6套)

中,最短路径的长度为
5
A. 【答案】B
B.
C.
D. 2
【解析】分析:首先根据题中所给的三视图,得到点 M 和点 N 在圆柱上所处的位置,点 M 在上底面上,点 N 在下底面上,并且将圆柱的侧面展开图平铺,点 M、N 在其四分之一的 矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果. 详解:根据圆柱的三视图以及其本身的特征, 可以确定点 M 和点 N 分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的 长方形的对角线的端点处, 所以所求的最短路径的长度为 ,故选 B.
【答案】B 【解析】分析:首先利用余弦的倍角公式,对函数解析式进行化简,将解析式化简为 ,之后应用余弦型函数的性质得到相关的量,从而得到正确选项. 详解:根据题意有 所以函数 且最大值为 的最小正周期为 ,故选 B. , ,
点睛: 该题考查的是有关化简三角函数解析式, 并且通过余弦型函数的相关性质得到函数的 性质,在解题的过程中,要注意应用余弦倍角公式将式子降次升角,得到最简结果. 9. 某圆柱的高为 2,底面周长为 16,其三视图如右图.圆柱表面上的点 在正视图上的对 应点为 ,圆柱表面上的点 在左视图上的对应点为 ,则在此圆柱侧面上,从 到 的路径
2018 年高考全国卷数学试题答案解析
目录
文科 全国一卷 全国二卷 全国三卷 2-18 19-35 36-47
理科 全国一卷 全国二卷 全国三卷 48-66 67-80 81-96
1
全国卷 1 ቤተ መጻሕፍቲ ባይዱ科数学试题解析
1. 已知集合 A. 【答案】A 【解析】 分析: 利用集合的交集中元素的特征, 结合题中所给的集合中的元素, 求得集合 中的元素,最后求得结果. 详解:根据集合交集中元素的特征,可以求得 2. 设 A. 0 B. ,则 C. D. ,故选 A. B. , C. D. ,则
2018年全国各地高考数学试题及解答分类汇编大全(04 导数及其应用)

则曲线 y 2ln x 在点 1,0 处的切线的斜率为 k f 1 2 , 则所求切线方程为 y 0 2 x 1 ,即 y 2x 2 .
4.(2018 全国新课标Ⅱ理)曲线 y 2 ln(x 1) 在点 (0, 0) 处的切线方程为__________.
4.【答案】 y 2x
x
,1
1
1,1a
f x
0
f x
Z
极大值
]
f x 在 x 1处取得极大值,不合题意. ③当 x1 x2 ,即 a 1时, f x , f x 随 x 的变化情况如下表:
x
,1 a
1 a
1 a
,1
f x
0
1 a 0 极小值
1 0
1 a
,
Z
1,
f x
Z
极大值
]
极小值
Z
f x 在 x 1处取得极小值,即 a 1满足题意.
1 x
1)2 k 1
4
16
0 ,得 h(x) 有两个极值点 x1, x2 (x1 x2 ) ,
∴
1 x1
1 4
,∴ 0
x1
16 .
可知 h(x) 在 (0, x1) 递增, (x1, x2 ) 递减, (x2 , ) 递增,
∴ h(x1) kx1
x1
ln x1
a
( 2
1 x1
1) x1
(1)证明:函数 f (x) x 与 g(x) x2 2x 2 不存在“S 点”;
(2)若函数 f (x) ax2 1与 g(x) ln x 存在“S 点”,求实数 a 的值; (3)已知函数 f (x) x2 a ,g(x) bex .对任意 a 0 ,判断是否存在 b 0 ,使函数 f (x) 与 g(x)
2018年全国各地高考数学试题及解答分类汇编大全(16随机变量及其分布)

2018年全国各地高考数学试题及解答分类汇编大全 (16概率、随机变量及其分布 正态分布)一、选择题则当p 在(0, 11..答案:D解答:E(x) =0? 1 -p 1? 1 2? p p+ 1 ,1-222 23) D(x): p?(p y + 1? (p 1、2 )+舟?(2 2 2 2 2 2 2 1 -(p- 1 2 1_ - p + p + 4 _ ' 1) +2,所以当p 在(0,1)内增大时,D (x )先增大后减小,故选 D.2. ( 2018全国新课标川理) 某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10位成员中使用移动支付的人数, DX =2.4 , P X =4 ::: P X =6 ,则 p =()A . 0.7B . 0.6C . 0.4D . 0.32.答案:B解答:由 X ~ B(10,p) ,••• DX =10p(1 - pH 2.4 ,••• 10p 2 -10p 2.4= 0,解之得口 =0.4,p 2 =0.6,由 P(X =4) :: P(X =6),有 p =0.6.二、 填空 三、 解答题假设所有电影是否获得好评相互独立.(I )从电影公司收集的电影中随机选取 1部,求这部电影是获得好评的第四类电影的概率; (n )从第四类电影和第五类电影中各随机选取 1部,估计恰有1部获得好评的概率; (川)假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等,用“ 1=1 ”表示第k 类电影得到人们喜欢,“ I =0”表示第k 类电影没有得到人们喜欢(k=1, 2, 3, 4, 5, 6).写出方差D ^ , D © , D-3, D © , D 冷,D 绪的大小关系.1. ( 2018浙江)设A • D (3减小C •D ( 3)先减小后增大 B • D (E )增大 D • D ( 3)先增大后减小第1页(共2页)1. 【答案】(1)概率为 0.025 ; (2)概率估计为 0.35 ; (3)D ! . D ; -D ^D 5 D 3 D 6 • 【解析】(1)由题知,样本中电影的总部数是 140 50 300 - 200 800 51^2000 , 第四类电影中获得好评的电影部数是 200 0.25 =50 .故所求概率为50=0 025 .2000(2)设事件A 为从第四类电影中随机选出的电影获得好评”,事件B 为 从第五类电影中随机选出的电影获得好评 ”.故所求概率为 P AB AB = P AB P AB 二 P A 1「P B ]厂门一P A P B .由题意知,P A 估计为0.25 , P B 估计为0.2 . 故所求概率估计为 0.25 0.8 0.75 0.2 =0.35 . (3) D ! D 4 D 2 = D 5 D 3 D 6 .2. ( 2018天津理)已知某单位甲、乙、丙三个部门的员工人数分别为 样的方法从中抽取 7人,进行睡眠时间的调查.(I) 应从甲、乙、丙三个部门的员工中分别抽取多少人?(II) 若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这 身体检查•(i )用X 表示抽取的3人中睡眠不足的员工人数,求随机变量(ii )设A 为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工” ,求事件A 发生的概率•2.【答案】(1)从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.t(2 [①答案见解析;②-.7【解析】(1)由已知,甲、乙、丙三个部门的员工人数之比为3 : 2 : 2,由于采用分层抽样的方法从中抽取 7人, 因此应从甲、乙、丙三个部门的员工中分别抽取3人,2人,2人.(2) (1)随机变量X 的所有可能取值为 0, 1 , 2, 3.c k c 3»P X =k 二 4C 33 k =0,1,2,3 .随机变量X 的数学期望E X =0丄,1 122183 —二12.35 35 35 35 7(2)设事件B 为抽取的3人中,睡眠充足的员工有 1人,睡眠不足的员工有 2人”; 事件C 为 抽取的3人中,睡眠充足的员工有 2人,睡眠不足的员工有 1人”, 则A =B C ,且B 与C 互斥,由(1)知,P B ]=P X =2 , P C 产P X =1 ,6故 P A =P(B C) =P X =2 P X =1 =~ . 所以,事件 A 发生的概率为-.724, 16, 16.现采用分层抽 7人中随机抽取3人做进一步的 X 的分布列与数学期望;第2页(共2页)。
2018--2020年高考数学试题分类汇编概率及答案详解

2018—2020年高考数学试题分类汇编概率一、选择题.1、(2018年浙江高考数学理科7)设0<p<1,随机变量ξ的分布列是ξ0 1 2P则当p在(0,1)内增大时,()A.D(ξ)减小 B.D(ξ)增大 C.D(ξ)先减小后增大 D.D(ξ)先增大后减小解:设0<p<1,随机变量ξ的分布列是E(ξ)=0×+1×+2×=p+;方差是D(ξ)=×+×+×=﹣p2+p+=﹣+,∴p∈(0,)时,D(ξ)单调递增;p∈(,1)时,D(ξ)单调递减;∴D(ξ)先增大后减小.故选:D.2、(2018年高考数学全国卷1理科3)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是()A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半解:设建设前经济收入为a,建设后经济收入为2a.A项,种植收入37×2a﹣60%a=14%a>0,故建设后,种植收入增加,故A项错误.B项,建设后,其他收入为5%×2a=10%a,建设前,其他收入为4%a,故10%a÷4%a=2.5>2,故B项正确.C项,建设后,养殖收入为30%×2a=60%a,建设前,养殖收入为30%a,故60%a÷30%a=2,故C项正确.D项,建设后,养殖收入与第三产业收入总和为(30%+28%)×2a=58%×2a,经济收入为2a,故(58%×2a)÷2a=58%>50%,故D项正确.故选:A.3、(2018年高考数学全国卷1文科3)某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是()A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4、(2018年高考数学全国卷1理科10)如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为I,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则()A.p1=p2 B.p1=p3 C.p2=p3 D.p1=p2+p3解:如图:设BC=a,AB=c,AC=b,∴a2=b2+c2,∴SⅠ=×4bc=2bc,SⅢ=×πa2﹣2bc,SⅡ=×πc2+×πb2﹣SⅢ=×πc2+×πb2﹣×πa2+2bc=2bc,∴SⅠ=SⅡ,∴P1=P2,故选:A.5、(2018年高考数学全国卷2理科8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是()A.B.C.D.解:在不超过30的素数中有,2,3,5,7,11,13,17,19,23,29共10个,从中选2个不同的数有=45种,和等于30的有(7,23),(11,19),(13,17),共3种,则对应的概率P==,故选:C.6、(2018年高考数学全国卷2文科5)从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为()A.0.6 B.0.5 C.0.4 D.0.3解:从2名男同学和3名女同学中任选2人参加社区服务,共有C52=10种,其中全是女生的有C32=3种,故选中的2人都是女同学的概率P==0.3,7、(2018年高考数学全国卷3理科8)某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X 为该群体的10位成员中使用移动支付的人数,DX=2.4,P (x=4)<P (X=6),则p=( ) A .0.7 B .0.6 C .0.4 D .0.3解:某群体中的每位成员使用移动支付的概率都为p ,看做是独立重复事件,满足X ~B (10,p ), P (x=4)<P (X=6),可得,可得1﹣2p <0.即p.因为DX=2.4,可得10p (1﹣p )=2.4,解得p=0.6或p=0.4(舍去). 故选:B .8、(2018年高考数学全国卷3文科5)若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为( ) A .0.3 B .0.4 C .0.6 D .0.7解:某群体中的成员只用现金支付,既用现金支付也用非现金支付,不用现金支付,是互斥事件, 所以不用现金支付的概率为:1﹣0.45﹣0.15=0.4. 故选:B .9、(2019年高考全国I 卷文科6)某学校为了解1 000名新生的身体素质,将这些学生编号为1,2,…,1 000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是 A .8号学生 B .200号学生C .616号学生D .815号学生答案:C解析:组距为10,所以选出号码为等差数列,公差为10,故选C10、(2019年高考全国I 卷理科6)我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是A .516B .1132C .2132D .1116答案:A解析:一共有6426=种可能,其中满足恰有3个阳爻的有2036=C 种,概率为1656420=故选A 11、(2019年高考全国II 卷文科4)生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为 A .23B .35 C .25D .15答案:B解析:设5只兔子为A,B,C,D,E,其中A,B,C 为测量过指标的取出3只所有情况:ABC 、ABD 、ABE 、ACD 、ACE 、ADE 、BCD 、BCE 、BDE 、CDE 共10种满足条件的有6种:ABD 、ABE 、ACD 、ACE 、BCD 、BCE 故概率为53=p 故答案选B 12、(2019年高考全国II 卷理科5)演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是A .中位数B .平均数C .方差D .极差 答案:A解析:9个数的中位数与去掉两个数后的7个数的中位数相同.故答案选A13、(2019年高考全国III 卷文科3)两位男同学和两位女同学随机排成一列,则两位女同学相邻的概率是A .16B .14C .13D .12答案:D解析:两位男生和两位女生排成一列,共有44A 种站法,其中两位女生相邻的站法共有3322A A 种,所以两位女生相邻的概率是21123412312443322=⨯⨯⨯⨯⨯⨯⨯=A A A 。
2018高考数学小题精练+B卷及解析:专题(16)概率及解析 含答案

2018高考数学小题精练+B 卷及解析:专题(16)概率及解析 专题(16)概率1.甲从正方形四个顶点中任意选择两个顶点连成直线,乙也从该正方形四个顶点中任意选择两个顶点连成直线,则所得的两条直线相互垂直的概率是( ) A .318 B . 418 C . 518 D . 618【答案】C【解析】甲共得6条,乙共得6条,共有6×6=36(对),其中垂直的有10对,∴1053618P ==.本题选择C 选项.2.如图,大正方形的面积是34,四个全等直角三角形围成一个小正方形,直角三角形的较短边长为3,向大正方形内抛一枚幸运小花朵,则小花朵落在小正方形内的概率为( )A .117 B . 217 C . 317 D . 417【答案】B点睛:数形结合为几何概型问题的解决提供了简捷直观的解法.用图解题的关键:用图形准确表示出试验的全部结果所构成的区域,由题意将已知条件转化为事件A 满足的不等式,在图形中画出事件A 发生的区域,据此求解几何概型即可.3.在棱长为a 的正方体中随机地取一点P ,则点P 与正方体各表面的距离都大于3a的概率为 ( )A .127 B . 116 C . 19 D . 13【答案】A【解析】符合条件的点P 落在棱长为3a的正方体内,根据几何概型的概率计算公式得P =333a a ⎛⎫ ⎪⎝⎭=127. 故选A .4.现有10个数,它们能构成一个以1为首项, 3-为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是( ) A .35 B . 45 C . 712 D . 12【答案】A【解析】由题意成等比数列的10个数为:1,−3,(−3)2,(−3)3…(−3)9,其中小于8的项有: 1,−3,(−3)3,(−3)5,(−3)7,(−3)9共6个数这10个数中随机抽取一个数,则它小于8的概率是63105p ==. 本题选择A 选项.5.用随机数法从100名学生(男生30人)中抽取10人,则某女生被抽到的可能性为( ) A .B .C .D .【答案】D【解析】按比例女生有可能抽到人,则女生被抽到的概率是,故选D .6.若正方形ABCD 边长为4,E 为四边上任意一点,则AE 的长度大于5的概率等于( ) A .132 B . 78 C . 38 D . 18【答案】D【方法点睛】本题題主要考查“长度型”的几何概型,属于中档题. 解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与长度有关的几何概型问题关鍵是计算问题题的长度以及事件的长度;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本裏件对应的区域测度把握不准导致错误 ;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.7.在区间 [-2,3]上任取一个数x ,则函数()f x =有意义的概率为A .25 B . 35 C . 45 D . 15【答案】D【解析】函数()f x =有意义的概率,即240x -≥, 24x ≥, x 2≥,又x ∈ [-2,3],所以x ∈ [2,3],所以函数()f x =有意义的概率为()321325-=--.故选:D8.已知一只蚂蚁在边长为4的正三角形内爬行,则此蚂蚁到三角形三个顶点的距离均超过1的概率为( ) A . 3112π-B . 3124π-C . 312πD . 324π 【答案】B点睛:对于几何概型的计算,首先确定事件类型为几何概型并确定其几何区域(长度、面积、体积或时间),其次计算基本事件区域的几何度量和事件A 区域的几何度量,最后计算()P A .9.先后抛掷三枚均匀的壹角、伍角、壹元硬币,则出现两枚正面,一枚反面的概率是( ) A .38 B . 58 C . 12 D . 13【答案】A【解析】先后抛掷三枚均匀硬币共有8中情况,其中两正一反共有3种情况,所求概率为38. 故选A .10.已知在数轴上0和3之间任取一实数x ,则使“2log 1x <”的概率为( ) A .14B .18C .23D .112【答案】C考点:几何概型.11.点P 在边长为1的正方形ABCD 内运动,则动点P 到顶点A 的距离1||<PA 的概率为( ) A .41 B .21C .4πD .π【答案】C 【解析】试题分析:如图可知41412ππ==R P .故正确选项为C .考点:几何概型.【思路点晴】本题主要考查的是几何概型求概率,属基础题.解几何概型的试题,一般先求出实验的基本事件构成的区域长度(或面积或体积或弧度),再求出事件A 构成的区域长度(或面积或体积或弧度),最后代入几何概型的概率公式即可,几何概型的概率公式为()积或弧度)的区域长度(面积或体试验的全部结果所构成面积或体积或弧度)构成事件的区域长度(=A P .12.取一根长度为5m 的绳子,拉直后在任意位置剪断,那么剪得两段的长度都不小于2m 的概率为( ) A .12B .13C .14D .15【答案】D 【解析】试题分析:两边各留下2m ,中间剩下1m ,所以两段的长度都不小于2m 的概率为15. 考点:几何概型.专题19 概率1.设,m n 分别是先后抛掷一枚骰子得到的点数,则方程20x mx n ++=有实根的概率为( ) A .1936 B . 1136 C . 712 D . 12【答案】A本题选择A 选项.2.市场调查发现,大约的人喜欢在网上购买家用小电器,其余的人则喜欢在实体店购买家用小电器。
2018年各地高考数学文科分类汇编——统计与概率

(全国1卷3)3.棊地国经过一年的新农科建设,农柑的经洛收入霜九了一倍.实现韶话.打吏蚱地了解谨地区农 村的经济隨人变化情况.统计f 该地区新农村建设前后农村的经济q 夂人构咸比例.得到如下饼團:则~F 面结论申不正葫的是( )A. 新农柑建设后.神栢收入碱少B. 新农村建设后.苴他I 攵入増加了一管以上 c.新农村建设涪:养殖收入増加-—倍D-新农荷建设后・养话收入皆幫三产业收人的忌和超过了经济收人的一半^-―=1的〜焦点为(戈』),则亡的知涪( (i~ 4〃【解析】由图可得,A 选项,设建设前经挤收入为厂种植收入为06匚建设后经济收人则为2x .勺 0.37x lx = 0.74x ,(全国1卷19)仪〔口分〕某家庭记录了未使用节水九头旳天的日冃水量数据〔鱼也 m 打刘使用了节水龙头刘 天的日用术量数堀,得到频数分布裏如口日屈 水量[0. 0.1) [0二 0.2)[0.2, 03) [0.3, 0.41[0.4, 0.5)'0.5. 0,6) [0© 0.7, 频数349265日用 水量 |0,0.1, [0.1, 022)[D.2 r 03)[03, 0.4} [0一4, 0 <)[0.5. 0.6)频数151310165'iT fL < ft Hi :七粗 雄设显冷牧入杓底:〕答案:⑴在答题卡上作出使用了节水龙头勿天的日用水 量数据的颉率分布直方因匕 ①估计该家庭使坤节水龙头后.FI 用水量小干 0=5诵概率I(3)估计诩冢庭使用节水龙头后,一年能节省多少水? (—年按365天计算,问一组中的数据次这组数摇所在区间巾点的14作代表•)⑼執〔】)如圉;(2)由題可知用水量在[03,0.41的敘數打10,所臥可估计在[03,0.35)的颉数为5,枚用水量小于0.3勺沪的频数为1 + 5 + 13 + 5 = 24.其槪率为G )未使用节水提头吋,兄天中平均每日用水量为’—(0.05xl-015<3 + 0卫,兀2 + 0一3,冷4十山4、只9十(1巾》;2& + 04勺><7)二0」0・沪,一年的平均用戒量则为0.506 <365 =184.69/??. 使用节水龙头肓,“天中平均每日用水量为:—(O.O?xl-0.1?i <5-OJ?xl3 + 0J5 <10 + 0 4?xl6+0.55x 5)= 0,35w?3 , 50—年的平均用水量则为0.35x365 = 127.75;??, /. 一年能节省 1S4.69-127.75 = 5G.9W.0 0.1G_3 DJ. 0J g AJ6 村曲水0:答案:盯■*・■”(全国2卷5)从2名男同学和3名女同学中任选2人参加社区服务,则选中2人都是女同学的概率为A • 0.6B • 0.5 C. 0.4 D. 0.3答案:D解析:从2名男生和3名女生中任选丄人肆加社区腹务,共有*个基本事件,选中的2人都是女生包括3个基本事件.其概率是"=0氏故选£硏・16(全国2卷18)下图是某地区2000年至2016年环境基础设施投资额y (单位:亿元)的折线图.240220200J8OJ60140120100SO604020为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2丄,17 )建立模型①:? 30.4 13.5t ;根据2010年至2016年的数据(时间变量t的值依次为1,2丄,7 )建立模型②:? 99 17.5t.(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;(2)你认为用哪个模型得到的预测值更可靠?并说明理由.答案:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为$ = - 30.4+13.5 X 19=226亿元)•利用模型②,该地区2018年的环境基础设施投资额的预测值为§=99+17.5 X 9=256.5亿元).(2)利用模型②得到的预测值更可靠.理由如下:(i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=-30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型§=99+17.5t可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.(ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.(全国3卷5)5.若果胖体屮的成诞只川现金支付的概率为站久联用现金支忖也用菲现金支村的概率为0.15,则不用现企支付的概举为k.0.3 B. 04 C. 06 D. 07答案:B(全国3卷14)14?某公司脊尢量客户二^冋龄段客户对其服务的评价有较大差昇.为『解客户的评价.谨公冠备进行捕样调査*可供选抒的抽林方注冇简吊飯机捕梓,分恳抽样和系统抽样.则最件适的抽样答案:分层抽样(全国3卷18)某□ 旳理咼宅产效率.幵展技术创靳沽动・提山『定威臬念生产任务的荫种新的生产方式.为比较两种生产方式的效率・选取40窘工人,将他们随机分成两组,粵组的人’第一俎工人用第一种生产方式.笫•.组匸人屮弟一側主兰疗貳.根橢匚人完咸主产任势的工作时何(单陆mm」绘制『如下茎叶图;鹉一种咔产方式鸽二种十产方盍»6S 5 6 H Q01223 456G89 7 6 27r3 214』,2 110 0◎0'1>咆离苹叶国判断哪种生产方式的效率更高?井说叩理由'(2)求40 人完成生产任务所需时冏的中垃養e・并将完咸生产任务所需时谢JBitm和不趙过ill的工人数車入卜一而胸列联农:超过m第-种生产方式苗一种左产方亢竹'根撫<2)中的列表.能否有夕珈前把掘认为两种生产方式的效率有英:只?pfK1 >k) 0 050 0.010 0 001~k 3 &41 6 635 10 SC&(i+b)(c +(i)(a +c)(b I d)答案:IS.谓:(1』第二神主产疔式的效率史届-理由如卜:<1)rti拆叶乌叮知;用箒一种牛产厅弍的I】人中.仃巧%的丁.人完成牛产仆务所需时仙孕少曲分瞅曲第:种牛产方式的工人中,件巧%的工人完成住产任务所需时阊至劣西分瞅丙此第二种牛产方式的效率更高.⑹由訓图可知!用第种生严方氏的工人充感生产任务所霜耐间的申位竝为85 5分钟.m 笫二种生产方武的丄人完成生产任势所■时间的中位数为73 $分榊+因此第一种生产方式的效率更高*(»0山茎叶图可却:用第」种生产力式的工人克成生产任务平均斯需时间高于旳井件;用第二种生产方式的工人完成生产任务平灼所需时间低于S0分4札凶此第二种生产方式的效率更高*(珂〕由茎叶圏可知;用第一种主严方式的工人完成生产任存所需时同分布在^8 k的最裁’关]苇蛊大锁呈対称仆布:用笫一种生产方丈前丁人完虑生产任务所需时间好布音戟7 I的吊芥.芫]些了上孜気融称分布.只用两种朱产方式的工人立成牛.产作务所需时何分布的区间相同.故可以认为用第…种工卢方式克成生严任务新需的时何比用第一种生产启式充成生产任务所需的时间更少,因此第二种牛.4庁式的做率更高.以上幣出了4科理曲.考生象出其中任藝一科毀其雜舎理理由均可褂分,7^ + 31由墓肝图知nr上f帥.•j列联表如S:m「心贰所处叩的把握认册种牛心式呗率於⑺由于疋「好评率是指:一类电影中获得好评的部数与该类电影的部数的比值^(I)从电影公司收集的电影中随机选取1部,求这部电影是获得好评的第四类电影的概率;(n)随机选取1部电影,估计这部电影没有获得好评的概率;(川)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加0.1,哪类电影的好评率减少0.1,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)答案:C I >由题意知,样本中电彭的总制数是140+50H-3O(K200-^00+510^00.第四类电豹中漲得妊评的电豹部数杲200/0J5=50.50故陽求槪率拘^ = 0D廿.2005(II )方法一:由题意知“样不中铁潯好评的电戟部数是140>=&.4-5卸0J!十加十十勺軟0.1=5&-10-45+SO-160+51372故所求舉至皆计为I—=0.814.2000方法二;设杯随机选取1部电虽紅这部电影没有寢得好评”拘事件玄滾有戏得好评的电黒共有UO M O.MD K0.S+3OO K O.85-2M N O.75+1O0W D.8+51O X(>.Q-162S部1 JC7P由古典探型粧至公式得P(B) - ——= 0 S14.2000GH) J§加第五类电影的好评率,减少第二类电彭的好评率.(天津卷15)(15)(本小题满分13分)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240, 160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.(I) 应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?(II) 设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.(i) 试用所给字母列举出所有可能的抽取结果;(ii) 设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.答案:(I)解:由已知,甲、乙、丙三个年级的学生志愿者人数之比分别为3:2:2, 由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的志愿者中分别抽取3人,2人,2人.(II)(i)解:从抽取的7名同学中随机抽取2名同学的所有可能结果为A, B,AC,A, D,A,E, AF,AG,B,C,B, D,B, E,B, F,B, G,C, D,C, E,C, F,C,G,D, E,D, F,D, G,E, F,E, G,F,G,共21 种.(ii)解:由(I),不妨设抽出的7名同学中,来自甲年级的是A, B, C,来自乙年级的是D,E,来自丙年级的是F,G,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为A, B , AC , B, C , D, E , F,G ,共5种.5所以,事件M发生的概率P(M)—.21。
2018年高考试题(卷)分类汇编概率统计

.概率统计1( 2017 北京文)(本小题13 分)某大学艺术专业400 名学生参加某次测评,依据男女学生人数比率,使用分层抽样的方法从中随机抽取了100 名学生,记录他们的分数,将数据分红7 组: [20,30 ), [30,40 ),┄, [80,90],并整理获得以下频次散布直方图:(Ⅰ)从整体的400 名学生中随机抽取一人,预计其分数小于70 的概率;(Ⅱ)已知样本中分数小于40 的学生有 5 人,试预计整体中分数在区间[40,50 )内的人数;(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70 的男女生人数相等.试预计整体中男生和女生人数的比率.2(2017 新课标Ⅱ理)(12 分)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对照,收获时各随机抽取了100个网箱,丈量各箱水产品的产量(单位:kg).其频次散布直方图以下:( 1)设两种养殖方法的箱产量互相独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,预计 A 的概率;( 2)填写下边列联表,并依据列联表判断能否有99%的掌握以为箱产量与养殖方法有关:箱产量< 50kg箱产量≥ 50kg旧养殖法新养殖法( 3)依据箱产量的频次散布直方图,求新养殖法箱产量的中位数的预计值(精准到0.01 ).附:,K2n( ad bc)2(a b)(c d )(a c)(b d )3( 2017 天津理)(本小题满分13 分)从甲地到乙地要经过 3 个十字路口,设各路口信号灯工作互相独立,且在各路口碰到红灯的概率分别为1,1,1.2 3 4(Ⅰ)设 X 表示一辆车从甲地到乙地碰到红灯的个数,求随机变量X 的散布列和数学希望;(Ⅱ)如有 2 辆车独立地从甲地到乙地,求这 2 辆车共碰到 1 个红灯的概率.4( 2017 新课标Ⅲ理数)(12 分)某商场计划按月订购一种酸奶,每日进货量同样,进货成本每瓶 4 元,售价每瓶 6 元,未售出的酸奶降价办理,以每瓶 2 元的价钱当日所有办理完.依据早年销售经验,每日需求量与当日最高气温(单位:℃)有关.假如最高气温不低于25,需求量为 500瓶;假如最高气温位于区间 [20 , 25),需求量为 300 瓶;假如最高气温低于20,需求量为200 瓶.为了确立六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下边的频数散布表:最高气温[10 ,15)[15 , 20)[20 , 25)[25 , 30)[30 , 35)[35 , 40)天数216362574以最高气温位于各区间的频次取代最高气温位于该区间的概率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年全国各地高考数学试题及解答分类汇编大全(16概率、随机变量及其分布)一、选择题:1.(2018福建文)某一批花生种子,如果每一粒发芽的概率为45,那么播下3粒种子恰有2粒发芽的概率是( C )A.12125B.16125 C.48125D.961252.(2018福建理)某一批花生种子,如果每1粒发牙的概率为45, 那么播下4粒种子恰有2粒发芽的概率是(B )A.16625B.96625C.192625D.2566253.(2018安徽理)设两个正态分布2111()(0)N μσσ>,和2222()(0)N μσσ>,的密度函数图像如图所示。
则有( A )A . 1212,μμσσ<<B .1212,μμσσ<>C .1212,μμσσ><D .1212,μμσσ>>4. (2018湖南理)设随机变量ξ服从正态分布(2,9)N ,若(1)(1)P c P c ξξ>+=<-,则c = ( B . )A.1B.2C.3D.4 4.【答案】B4.【解析】2(2,3)N ⇒ 12(1)1(1)(),3c P c P c ξξ+->+=-≤+=Φ 12(1)(),3c P c ξ--<-=Φ31()()1,33c c --∴Φ+Φ= 311()()1,33c c --⇒-Φ+Φ=解得c =2, 所以选B.5.(2018江西文、理)电子钟一天显示的时间是从00∶00到23∶59,每一时刻都由四个数字组成,则一天中任一时刻显示的四个数字之和为23的概率为( C ) A .1801 B .2881 C .3601 D .4801 5.C .一天显示的时间总共有24601440⨯=种,和为23总共有4种,故所求概率为1360.6.(2018辽宁文、理) 4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( C ) A .13B .12C .23D .347.(2018山东理)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为( B ) (A )511(B )681 (C )3061(D )40818. (2018重庆理)已知随机变量ζ服从正态分布N (3,a 2),则P (ζ<3=(D ) (A)15(B)14(C)13(D)129. (2018重庆文)从编号为1,2,…,10的10个大小相同的球中任取4个,则所取4个球的最大号码是6的概率为( B )(A)184 (B)121 (C)25(D)35二、填空题:1.(2018江苏) 一个骰子连续投2 次,点数和为4 的概率121. 1.【解析】本小题考查古典概型.基本事件共6×6 个,点数和为4 的有(1,3)、(2,2)、(3,1)共3 个,故316612P ==⨯ 【答案】1122.在平面直角坐标系xoy 中,设D 是横坐标与纵坐标的绝对值均不大于2 的点构成的区域, E 是到原点的距离不大于1 的点构成的区域,向D 中随机投一点,则落入E 中的概率__16π . 2.【解析】本小题考查古典概型.如图:区域D 表示边长为4 的正方形的内部(含边界),区域E 表示单位圆及其内部,因此.214416P ππ⨯==⨯【答案】16π3.明天上午李明要参加奥运志愿者活动,为了准时起床,他用甲、乙两个闹钟叫醒自己,假设甲闹钟准时响的概率是0.80,乙闹钟准时响的概率是0.90,则两个闹钟至少有一准时响的概率是 0.98 .4.(2018上海文)在平面直角坐标系中,从六个点:(00)(20)(11)(02)(22)A B C D E ,,,,,,,,,中任 取三个,这三点能构成三角形的概率是45(结果用分数表示).5.(2018上海理)在平面直角坐标系中,从六个点:A(0,0)、B(2,0)、C(1,1)、D(0,2)、E(2,2)、F(3,3)中任取三个,这三点能构成三角形的概率是 34. (结果用分数表示)三、解答题: 1.(2018安徽文)在某次普通话测试中,为测试汉字发音水平,设置了10张卡片,每张卡片印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音“g ”.(Ⅰ)现对三位被测试者先后进行测试,第一位被测试者从这10张卡片总随机抽取1张,测试后放回,余下2位的测试,也按同样的方法进行。
求这三位被测试者抽取的卡片上,拼音都带有后鼻音“g ”的概率。
(Ⅱ)若某位被测试者从10张卡片中一次随机抽取3张,求这三张卡片上,拼音带有后鼻音“g ”的卡片不少于2张的概率。
1.解:(1)每次测试中,被测试者从10张卡片中随机抽取1张卡片上,拼音带有后鼻音“g ”的概率为310,因为三位被测试者分别随机抽取一张卡片的事件是相互独立的,因而所求的概率为333271*********⨯⨯=(2)设(1,2,3)i A i =表示所抽取的三张卡片中,恰有i 张卡片带有后鼻音“g ”的事件,且其相应的概率为(),i P A 则127323107()40C C P A C == , 3333101()120C P A C == 因而所求概率为23237111()()()4012060P A A P A P A +=+=+= 2.(2018安徽理)为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。
某人一次种植了n 株沙柳,各株沙柳成活与否是相互独立的,成活率为p ,设ξ为成活沙柳的株数,数学期望3E ξ=,标准差σξ(Ⅰ)求n,p 的值并写出ξ的分布列; (Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率 2. (1)由233,()(1),2E np np p ξσξ===-=得112p -=,从而16,2n p == ξ的分布列为ξ 01 23456P164664 1564 2064 1564 664164(2)记”需要补种沙柳”为事件A, 则()(3),P A P ξ=≤ 得16152021(),6432P A +++== 或 156121()1(3)16432P A P ξ++=->=-=3.(2018北京文)甲、乙等五名奥运志愿者被随机地分到A ,B ,C ,D 四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加A 岗位服务的概率; (Ⅱ)求甲、乙两人不在同一个岗位服务的概率.3.解:(Ⅰ)记甲、乙两人同时参加A 岗位服务为事件E A ,那么P (E A )=.401442333-A C A即甲、乙两人同时参加A 岗位服务的概率是.401(Ⅱ)记甲、乙两个同时参加同一岗位服务为事件E ,那么P (E )=.101442344=A C A所以,甲、乙两人不在同一岗位服务的概率是P (E )=1-P (E )=.109 4.(2018北京理)甲、乙等五名奥运志愿者被随机地分到A B C D ,,,四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加A 岗位服务的概率; (Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量ξ为这五名志愿者中参加A 岗位服务的人数,求ξ的分布列.4.解:(Ⅰ)记甲、乙两人同时参加A 岗位服务为事件A E ,那么3324541()40A A P E C A ==,即甲、乙两人同时参加A 岗位服务的概率是140.(Ⅱ)记甲、乙两人同时参加同一岗位服务为事件E ,那么4424541()10A P E C A ==,所以,甲、乙两人不在同一岗位服务的概率是9()1()10P E P E =-=.(Ⅲ)随机变量ξ可能取的值为1,2.事件“2ξ=”是指有两人同时参加A 岗位服务, 则235334541(2)4C A P C A ξ===.所以3(1)1(2)P P ξξ==-==,ξ的分布列是5. (2018福建文)三人独立破译同一份密码,已知三人各自译出密码的概率分别为111,,543,且他们是否破译出密码互不影响。
(1)求恰有二人破译出密码的概率;(2)“密码被破译”与“密码未被破译”的概率那个大?说明理由。
5.解:记“第i 个人破译出密码”为事件(1,2,3)i A i =,则:123111(),(),()543P A P A P A === (1)设“恰好二人破译出密码”为事件B,则有:1231231233()()()()20P B P A A A P A A A P A A A =⋅⋅+⋅⋅+⋅⋅=(2)设“密码被破译”为事件C ,“密码未被破译”为事件D ,则有:1234322()()()()5435P D P A P A P A =⋅⋅=⋅⋅= , 3()1()5P C P D =-= ()()P C P D > 所以密码被破译的概率大6.(2018福建理)某项考试按科目A 、科目B 依次进行,只有当科目A 成绩合格时,才可继续参加科 目B 的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证 书.现某人参加这项考试,科目A 每次考试成绩合格的概率均为23,科目B 每次考试 成绩合格的概率均为12.假设各次考试成绩合格与否均互不影响. (Ⅰ)求他不需要补考就可获得证书的概率;(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求ξ的数学期望E ξ.6.本小题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题/解愉问题的能力.满分12分.解:设“科目A 第一次考试合格”为事件A ,“科目A 补考合格”为事件A 2;“科目B 第一次考试合格”为事件B ,“科目B 补考合格”为事件B .(Ⅰ)不需要补考就获得证书的事件为A 1·B 1,注意到A 1与B 1相互独立,则1111211()()()323P A B P A P B =⨯=⨯= . 答:该考生不需要补考就获得证书的概率为13. (Ⅱ)由已知得,ξ=2,3,4,注意到各事件之间的独立性与互斥性,可得1112(2)()()P P A B P A A ξ==+2111114.3233399=⨯+⨯=+=112112122(3)()()()P P A B B P A B B P A A B ξ==++2112111211114,3223223326693=⨯⨯+⨯⨯+⨯⨯=++=12221212(4)()()P P A A B B P A A B B ξ==+12111211111,3322332218189=⨯⨯⨯+⨯⨯⨯=+= 故4418234.9993E ξ=⨯+⨯+⨯=答:该考生参加考试次数的数学期望为83.7. (2018广东文)某初级中学共有学生2000名,各年级男、女生人数如下表. 已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19 . (1)求x 的值;(2)现用分层抽样的方法在全校抽取48名学生, 问应在初三年级抽取多少名?(3)已知245,245≥≥z y ,求初三年级中女生比男生多的概率。
