福建省华安县第一中学2017-2018学年高二下学期期末考试 数学(理) Word版含答案
2017-2018学年高二数学下学期期末考试试题理(2)

数学试卷(理数)时间:120分钟总分:150分一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知为实数,,则的值为A.1B.C.D.2.“”是“直线和直线平行”的A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件3.下列说法正确的是A.一个命题的逆命题为真,则它的逆否命题一定为真B.“”与“”不等价C.“若,则全为”的逆否命题是“若全不为0,则”D.一个命题的否命题为假,则它的逆命题一定为假4.若,,,,则与的大小关系为A. B. C. D.5.已知命题及其证明:(1)当时,左边,右边,所以等式成立;(2)假设时等式成立,即成立,则当时,,所以时等式也成立.由(1)(2)知,对任意的正整数等式都成立.经判断以上评述A.命题,推理都正确B.命题正确,推理不正确C.命题不正确,推理正确D.命题,推理都不正确6.椭圆的一个焦点是,那么等于A.B.C.D.7.设函数(其中为自然对数的底数),则的值为A. B. C. D.8.直线(为参数)被曲线截得的弦长是A. B. C. D.9.已知函数在上为减函数,则的取值范围是A. B. C. D.10.一机器狗每秒前进或后退一步,程序设计师让机器狗以前进步,然后再后退步的规律移动,如果将此机器狗放在数轴的原点,面向数轴的正方向,以步的距离为个单位长,令表示第秒时机器狗所在位置的坐标.且,那么下列结论中错误的是A. B.C. D.11.已知A、B、C、D四点分别是圆与坐标轴的四个交点,其相对位置如图所示.现将沿轴折起至的位置,使二面角为直二面角,则与所成角的余弦值为A.B.C.D.12.点在双曲线上,、是这条双曲线的两个焦点,,且的三条边长成等差数列,则此双曲线中等于A.3B.4C.5D.6二、填空题(每小5分,满分20分)13.若,则__________.14.在三角形ABC中,若三个顶点坐标分别为,则AB边上的中线CD的长是__________.15.已知F1、F2分别是椭圆的左右焦点,A为椭圆上一点,M为AF1中点,N为AF2中点,O为坐标原点,则的最大值为__________.16.已知函数,过点作函数图象的切线,则切线的方程为。
2017高二下期末考

华安一中2016-2017学年下学期期末考高二英语试题(考试时间:120分钟总分:150分)第Ⅰ卷(共100分请涂在答题卡上)第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.15.C.£9.18.答案是B1. Where did the woman leave her hat?A. In a taxi.B. In a restaurant.C. In a car.2. What is the local time right now?A. 7:15.B. 11:15.C. 9:15.3. What are the speakers discussing?A. Whether to go to France.B. What to do in France.C. How to go to France.4. Why is the girl upset?A. Her family is about to leave.B. Her mother is out of work.C. She has no friends now.5. What was the weather like in the Lake District on holiday?A. Snowy.B. Rainy.C. Sunny.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段材料。
每段材料后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段材料前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
2017-2018学年(新课标)最新福建省高二下学期期末考试数学(理)试题及解析-精品试题

2017-2018学年福建省高二数学下学期期末模拟测试一、选择题1.复数131ii -++=( )A .2+iB .2-i C1+2iD .1- 2i2. 二项式5)12(x x -的展开式中含21x 项的系数为( )A .10B .10-C 40D .40-3.某次数学成绩ξ~())0(,902>σσN ,显示()6.011070=≤≤ξp ,则()=<70ξP ( )A .2.0B .3.0C .1.0D .5.04.右表是降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对应数据,根据表中提供的数据,可求出y 关于x的线性回归方程ˆy0.70.35x =+,则表中m 的值为 A .3 B .3.15 C .4 D .4.55.2013年第12届全国运动会将在沈阳举行,某校4名大学生申请当,,A B C 三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务A 比赛项目,则不同的安排方案共有 A .20种B .24种C .30种D .36种6.二项式1(n x-的展开式中含有4x 的项,则正整数n 的最小值是A .4B .6C .8D . 12 7.在右图所示的电路中,5只箱子表示保险匣,箱中所示数值表示通电时保险丝被切断的概率,当开关合上时,电路畅通的概率是 A .3629 B .720551C .7229D .144298.若(x +1)5=a 0+a 1(x -1)+a 2(x -1)2+…+a 5(x -1)5,则a 0=( )A .32B .1 C-1 D .-32 9.函数()4x e x f -=π的部分图象大致是( )x3 4 5 6 y2.5m44.510.用数学归纳法证明(1)(2)n n)213(21)n n n n +++=⋅⋅-(,从k 到1k +,左边需要增乘的代数式为 ( ) A .21k + B .2(21)k + C .211k k ++ D .231k k ++ 11. 已知随机变量η=8--ξ,若ξ~B(10,0.6),则Eη,Dη分别是( ) A .6和2.4 B .2和2.4 C .2和5.6 D .6和5.614. 某电视台连续播放6个广告,分别是三个不同的商业广告和三个不同的公益广告,要求最后播放的不能是商业广告,且任意两个公益广告不能连续播放,则不同的播放方式有( ). A. 36种 B. 108种 C. 144种 D. 720种15.设定义在R 上的函数()f x 是最小正周期为2π的偶函数,()f x '是()f x 的导函数,当[]0,x π∈时,0()1f x <<;当(0,)x π∈且2x π≠时 ,()()02x f x π'->,则函数()sin y f x x =-在[2,2]ππ-上的零点个数为( )A .2B .4C .5D .8第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,满分25分.请把答案填在答题纸的相应位置.三、解答题:本大题共4小题,共50分.解答应写出文字说明,证明过程或演算步骤. 21.(本题满分14分)(1)(本小题满分7分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为sin 3πρθ⎛⎫-= ⎪⎝⎭曲线C 的参数方程为1cos ,sin x αy α=+⎧⎨=⎩(α为参数,0απ≤≤).(Ⅰ)写出直线l 的直角坐标方程; (Ⅱ)求直线l 与曲线C 的交点的直角坐标.(2)(本小题满分7分)选修4-5:不等式选讲已知,,a b c R +∈,且3a b c ++=,222a b c ++的最小值为M . (Ⅰ)求M 的值;(Ⅱ)解关于x 的不等式|4||1|x x M +--≥. 22.(本题满分12分)已知函数33)(23+-=x kx x f(1)当k=0时,求函数)(x f 的图像与直线1-=x y 所围封闭图形的面积; (2)当k>0时,求函数)(x f 的单调区间。
福建省华安县第一中学高二数学下学期期末考试试题理

福建省华安县第一中学高二数学下学期期末考试试题理时间:120分钟满分:150分一、选择题(每小题5分,共12小题60分) 1、已知全集,,,则图中阴影部分表示的集合是( )A.B. C. D.2、0.20.32已知0.2,,,则()log20.2a b c ===A.<<a b cB.<c<b aC.<a<b cD.<c<a b3、设则“”是“”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件4、抛物线上有一点,它的横坐标是,它到焦点的距离是,则抛物线的方程为( )A. B. C.D.5、函数的单调递增区间是( )A. B. C. D.6、函数满足,那么函数的图象大致为( )A. B. C. D.7、已知,且,则的值是( ) A.B.C.D.8、定义在上的偶函数满足对任意的(),有,则( )A. B. C.D.9、已知函数有极大值和极小值,则的取值范围( )A. B.C.D.10、若点是曲线上任一点,则点到直线的最小距离是( ) A.B.C.D.11、已知双曲线的左支上一点M 到右焦点F2的距离为18,N 是线段MF2的中点,O 是坐标原点,则|ON|等于( ) A.4B.2C.1D.12、已知定义在上的函数是其导数,且满足,则不等式(其中e 为自然对数的底数)的解集为 ( )A.B.C.D.二、填空题(每小题5分,共4小题20分)13、若的离心率为,则实数等于__________.14、若是奇函数,则__________.15、已知直线是曲线的切线,则__________.16、若函数的图像与轴有三个不同的交点,则实数的取值范围是__________.三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)17、已知函数在,处都取得极值.(1)求,的值(2)函数的单调区间;18、已知函数,.(1)当时,解不等式.(2)若对于恒成立,求实数的取值范围.19、在极坐标系中,曲线的极坐标方程为,以极点为坐标原点,极轴为轴的正半轴,取相同的单位长度建立平面直角坐标系,直线的参数方程为(为参数).(1)求曲线的直角坐标方程和直线的普通方程;(2)设,直线与曲线交于,两点,求的值.20、如图,四边形为正方形,平面,,. (1)证明:平面平面;(2)求二面角的余弦值.21、已知椭圆的长轴长为,且点在椭圆上.(1)求椭圆的方程;(2)过椭圆右焦点斜率为的直线交椭圆于,两点,若,求直线的方程.22、已知函数.(1)讨论的单调性;(2)若函数在上有零点,求的取值范围.2018-2019下学期高二数学理科期末试卷卷答案解析第1题答案C第1题解析图中阴影部分表示的集合,由,,则,则.第2题答案B第3题答案A第3题解析由于不等式的解集为则可推出反之不成立,所以“”是“”的充分而不必要条件.故选第4题答案A第4题解析由题意知,,∴,∴抛物线方程为.故选A.第5题答案A第5题解析因为,所以,解得:.第6题答案C第6题解析∵,∴,解得,∴,∴当时,函数单调递增,且;当时,函数单调递减. 第7题答案B第7题解析由得到,,且,代入到得:,即,等价于,所以,又,则,故选第8题答案A第8题解析根据题意得:在上单调递增,在上单调递减;又是偶函数,所以选A.第9题答案A第9题解析因为函数有极大值和极小值,故方程有两不等实根,即,,由,可得或.第10题答案A第10题解析,,所以点为,到直线的最小距离是.第11题答案A第11题解析解答:根据题意作出示意图,如图所示;由双曲线的定义,可得,又,;因为N是线段MF2的中点,O是坐标原点,所以.第12题答案A第12题解析设,则, ∵,∴,则,∴在上为增函数∵,∴,又∵,∴,∴,故选A.第13题答案83第14题答案第14题解析,,所以,即,故.第15题答案第15题解析,则,依题意可得存在,使得且,所以,即,解得.第16题答案第16题解析,所以当和时,,单调递增,当时,,单调递减,极大值,极小值,的图像与轴有三个不同的交点,所以,得.第17题答案略第17题解析(1),∵,∴,,联立解得,.,(2)∴,令, 解得.∴函数的单调递减区间为.第18题答案见解析第18题解析(1)时,不等式为,等价于或或,解得,或或,∴,∴不等式的解集是.(2)由绝对值的三角不等式得, ∵对于恒成立,∴,解得或.∴实数的取值范围为.第19题答案见解析第19题解析(1)曲线的直角坐标方程为,直线的普通方程为.(2)易知点在直线上. 将直线的参数方程(为参数)代入曲线的直角坐标方程,化简得,设点,对应的参数分别为,,则,,所以.第20题答案(1)略;(2)第20题解析如图,以D为坐标原点,线段DA的长为单位长,射线DA,DP,DC为x,y,z轴的正半轴建立空间直角坐标系D-xyz.(1)证明:依题意有Q(1,1,0),C(0,0,1),P(0,2,0).则所以.即PQ⊥DQ,PQ⊥DC.又DQ∩DC=D,故PQ⊥平面DCQ.又PQ⊂平面PQC,所以平面PQC⊥平面DCQ.(2)依题意有B(1,0,1),,,设是平面PBC的一个法向量,则,因此可取.设是平面PBQ的一个法向量,则,可取.所以,由图可知,二面角为钝二面角,故二面角的余弦值为.第21题答案略第21题解析(1)由题意,设椭圆方程为,又点在椭圆上,可得, 则椭圆的方程为.(2)由(1)知,,,椭圆右焦点坐标为,则直线的方程为,由,由于直线过椭圆右焦点,可知,设,,则,,, 所以,由,即,可得,即,所以直线的方程为.第22题答案(1)见解析;(2).第22题解析(1)因为,所以.①当时,因为,所以在上单调递增;②当时,令,解得或.令,解得,则在,上单调递增;在上单调递减.(2)因为,所以,在上有零点,等价于关于的方程在上有解, 即在上有解.因为,所以.令,则.令,,解得;令,,解得, 则在上单调递减,在上单调递增,因为,,所以,则,,故的取值范围为.。
福建省华安县第一中学2017_2018学年高二英语下学期期末考试试题-含答案 师生通用

华安一中2017-2018学年第二学期期末考高二英语试卷(考试时间:120分钟总分:150分)第Ⅰ卷 (共100分)第一部分听力(共两节,满分30分)第一节 (共5小题;每小题l.5,满分7.5)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.How will the woman get to Glasgow?A. By train.B. By plane.C. By car.2. What does the man mean?A. The refrigerator is too heavy.B. He can’t help the woman.C. He needs to see a doctor.3. What does the man think of the lecture?A. Interesting.B. New.C. Boring.4.When will the speakers leave for the zoo?A. At 8:15.B. At 9:45.C. At 10:30.5. What are the speakers mainly talking about?A. A competition.B. A classmate.C. A team.第二节 (共15小题;每小题l.5,满分22.5)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. What makes the woman get her achievement?A. The teamwork.B. Her experience.C. Her leadership.7. How has the woman changed after the project?A. She is more competitive about her career.B. She is no longer afraid of new challenges.C. She is willing to help people in trouble.听第7段材料,回答第8、9题。
福建省华安县17学年高二数学下学期期末考试试题理

2016-2017学年高二下学期期末考理科数学试卷(时间:120分钟 总分:150分)一、选择题(共12小题,每小题5分,满分60分) 1.在复平面内,复数32i 1i--对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2.已知随机变量),,0(~2σξN 若,023.0)3(=>ξP 则=≤≤-)33(ξP ( ) A .0.477 B .0.628 C .0.954 D .0.9773.若n=22xdx ⎰,则(x ﹣)n的展开式中常数项为( )A .B . ﹣C .D . ﹣4.甲、乙两人独立地解决同一个问题,甲能解决这个问题的概率是P 1,乙能解决这个问题的概率是P 2,那么至少有一人能解决这个问题的概率是( ) A . P 1+P 2 B . P 1P 2 C . 1﹣P 1P 2 D . 1﹣(1﹣P 1)(1﹣P 2) 5.随机变量ξ~B (n ,P ),E ξ=15,D ξ=11.25,则n=( ) A . 60 B . 55 C . 50 D . 45 6.6个人排成一排,其中甲、乙不相邻的排法种数是( ) A . 288 B . 480 C . 600 D . 6407.在比赛中,如果运动员A 胜运动员B 的概率是23,那么在五次比赛中运动员A 恰有三次获胜的概率是( ) A.40243 B.80243 C.110243 D.202438.已知x >0,由不等式x+≥2=2,x+=≥3=3,…,可以推出结论:x+≥n+1(n ∈N *),则a=( )A . 2nB . 3nC . n 2D . n n9.某产品40件,其中有次品数3件,现从中任取2件,则其中至少有一件次品的概率是( ) A .0.146 2 B .0.153 8 C .0.996 2 D .0.853 810.已知抛物线22y px =(0)p >,过其焦点且斜率为-1的直线交抛物线于,A B 两点,若线段AB 的中点的横坐标为3,则该抛物线的准线方程为( )A .1x =B .2x =C .1x =-D .2x =- 11.已知椭圆C :+=1(a >b >0)的离心率为,与双曲线x 2﹣y 2=1的渐近线有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C 的方程为( )A .+=1 B .+=1 C . +=1 D . +=1二、填空题(共4小题,每小题5分,满分20分)13.曲线y=x 3+x 在点(1,)处的切线与坐标轴围成的三角形面积为 .14.如图所示,直线kx y =分抛物线2y x x =-与x 轴所围成图形为面积相等的两部分,则实数k 的值为 . 15.若函数sin ()cos a xf x x-=在区间ππ(,)63上单调递增,则实数a 的取值范围是 .16.已知f (x )=x 3﹣x 2+2x+1,x 1,x 2是f (x )的两个极值点,且0<x 1<1<x 2<3,则实数a 的取值范围为 .三、解答题(共6小题,满分70分) 17.(本小题满分10分)在平面直角坐标系中,以原点为极点,x 轴为极轴建立极坐标系,曲线1C 的方程为sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数),曲线2C 的极坐标方程为2:cos sin 1C ρθρθ+=,若曲线1C 与2C 相交于A 、B 两点. (1)求||AB 的值;(2)求点(1,2)M -到A 、B 两点的距离之积.18.(本小题满分12分)为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下资料: 日期 4月1日 4月7日 4月15日 4月21日 4月30日 温差x/℃ 10 11 13 12 8 发芽数y/颗 23 25 30 26 16(Ⅰ)从这5天中任选2天,记发芽的种子数分别为m ,n ,求事件“m ,n 均不小于25”的概率.(Ⅱ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出y 关于x 的线性回归方程y bx a =+.(参考公式:=,=﹣)19.(本小题满分12分)“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由;(下面的临界值表供参考)(参考公式:))()()(()(22d b c a d c b a bc ad n K ++++-=其中d c b a n +++=)(2)现计划在这次场外调查中按年龄段分层抽样选取6名选手,并抽取3名幸运选手,求3名幸运选手中在20~30岁之间的人数的分布列和数学期望.20.(本小题满分12分)三棱锥被平行于底面ABC 的平面所截得的几何体如图所示,截面为111A B C ,90BAC ∠=,1A A ^平面ABC,1A A =,AB =2AC =,111AC =,12BD DC =. (Ⅰ)证明:BC ⊥平面1A AD ;A 1 A C 1B 1BDC(Ⅱ)求二面角1A CC B --的余弦值.21.(本小题满分12分)已知椭圆C :()2222+10a x y a b b=>>的左焦点F 10),F 2是它的右焦点,点M 是椭圆C 上一点,△MF 1F 2的周长等于4+2. (1)求椭圆C 的方程;(2)过定点P (0,2)作直线l 与椭圆C 交于不同的两点A ,B ,且OA ⊥OB (其中O 为坐标原点),求直线l 的方程.22.(本小题满分12分)已知函f (x )=ax 2﹣e x(a ∈R ). (Ⅰ)a=1时,试判断f (x )的单调性并给予证明; (Ⅱ)若f (x )有两个极值点x 1,x 2(x 1<x 2). (i ) 求实数a 的取值范围; (ii )证明:()1e12f x -<<- (注:e 是自然对数的底数)2016-2017学年高二下期末考理科数学答题卷13、 14、 15、 16、 三、解答题:2016-2017学年高二下期末考理科数学试卷参考答案及评分标准二、填空题:本大题共4小题,每小题5分,共20分13、14、12- 15、[2,)+∞ 16、(3,)三、解答题:本大题共6小题,共70分.17解: (1) 曲线1C 的普通方程为2212x y +=,2:cos sin 1C ρθρθ+=, 则2C 的普通方程为10x y +-=,则2C 的参数方程为:()122x t y ⎧=--⎪⎪⎨⎪=+⎪⎩为参数……………………2分代入1C 得23140t +=,12AB t t =-==………………………… 6分(2) 12143MA MB t t ==. ……………………10分 18解:(Ⅰ)用数组(m ,n )表示选出2天的发芽情况, m ,n 的所有取值情况有:(23,25),(23,30),(23,26),(23,16),(25,30), (25,26),(25,16),(30,26),(30,16),(30,26),共有10个 设“m ,n 均不小于25”为事件A , 则包含的基本事件有(25,30),(25,26),(30,26) 所以P (A )=,故m ,n 均不小于25的概率为;……………………………….6分(Ⅱ)由数据得=12,=27,3•=972,x i y i =977,x i 2=434,32=432.由公式,得==,=27﹣×12=﹣3.所以y 关于x 的线性回归方程为=x ﹣3.............12分 19解:(1)706.23804010020)10301070(1202>=⨯⨯⨯⨯-⨯=k有%90的把握认为猜对歌曲名称与否和年龄有关……………4分(2)设3名选手中在20~30岁之间的人数为ξ,可能取值为0,1,2,………5分 20~30岁之间的人数是2人……………6分51)0(3634===C C P ξ,53)1(361224===C C C P ξ,51)2(362214===C C C P ξ………10分…………11分()1=ξE ……………………12分20解:(Ⅰ)以AB 、AC 、AA 1分别为x 轴、y 轴、z 轴建立空间直角坐标系 则11(000)0)(020)(00A B C A C ,,,,,,,,,,:1:2BD DC =,13BD BC \=.D \点坐标为2033÷ç÷ç÷ç÷ç桫,,.\22033AD 骣÷ç÷=ç÷ç÷ç桫,,,1(220)(00BC AA =-=,,,.10BC AA =,0BC AD =,1BC AA \^,BC AD ^,又1A A AD A =,BC \^平面1A AD ……………………………….5分(Ⅱ)BA ^平面11ACC A ,取(20)AB ==,m 为平面11ACC A 的法向量, 设平面11BCC B 的法向量为()l m n =,,n,则100BC CC ==,n n .200m m ìï-+=ï\íï-+=ïî,,l n \==,,如图,可取1m =,则3=÷,,n ,22010cos 5(2)??<>==+,m n …………12分21解:(1)∵椭圆C :=1的左焦点F 1的坐标为(﹣,0),F 2是它的右焦点,点M 是椭圆C 上一点,△MF 1F 2的周长等于4+2,∴,解得a=2,b=1, ∴椭圆C 的方程为..............4分(2)当直线l 的斜率不存在时,不满足题意.当直线l 的斜率存在时,设直线l 的方程为y=kx ﹣2,A (x 1,y 1),B (x 2,y 2),联立,得(1+4k 2)x 2﹣16kx+12=0,△=(﹣16k )2﹣48(1+4k 2)>0, 由根与系数关系得x 1+x 2=,x 1•x 2=,..............8分∵y 1=kx 1﹣2,y 2=kx 2﹣2,∴y 1y 2=k 2x 1•x 2﹣2k (x 1+x 2)+4. ∵OA ⊥OB ,∴x 1x 2+y 1y 2=0,∴(1+k 2)x 1x 2﹣2k (x 1+x 2)+4=0,∴﹣+4=0,解得k=±2,∴直线l的方程是y=2x﹣2或y=﹣2x﹣2...............12分22解:(Ⅰ)当a=1时,f(x)=x2﹣e x,f(x)在R上单调递减.事实上,要证f(x)=x2﹣e x在R上为减函数,只要证明f′(x)≤0对∀x∈R恒成立即可,设g(x)=f′(x)=2x﹣e x,则g′(x)=2﹣e x,当x=ln2时,g′(x)=0,当x∈(﹣∞,ln2)时,g′(x)>0,当x∈(ln2,+∞)时,g′(x)<0.∴函数g(x)在(﹣∞,ln2)上为增函数,在(ln2,+∞)上为减函数.∴f′(x)max=g(x)max=g(ln2)=2ln2﹣2<0,故f′(x)<0恒成立所以f(x)在R上单调递减;..............4分(Ⅱ)(i)由f(x)=ax2﹣e x,所以,f′(x)=2ax﹣e x.若f(x)有两个极值点x1,x2,则x1,x2是方程f′(x)=0的两个根,故方程2ax﹣e x=0有两个根x1,x2,又因为x=0显然不是该方程的根,所以方程有两个根,设,得.若x<0时,h(x)<0且h′(x)<0,h(x)单调递减.若x>0时,h(x)>0.当0<x<1时h′(x)<0,h(x)单调递减,当x>1时h′(x)>0,h(x)单调递增.要使方程有两个根,需2a>h(1)=e ,故且0<x1<1<x2.故a 的取值范围为...............8分(ii)证明:由f′(x1)=0,得:,故,x1∈(0,1)=,x1∈(0,1)设s(t)=(0<t<1),则,s(t)在(0,1)上单调递减故s(1)<s(t)<s(0),即...............12分- 11 -。
2017届福建省漳州市华安一中高三高考模拟理科数学试题及答案 精品 精品

2017年高中毕业班质量检测理科数学试卷理科数学备课组(完卷时间:120分钟;满分:150分)第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知集合M ={(x ,y )|x +y =2},N ={(x ,y )|x -y =4},那么集合M ∩N 为( )(A).x =3,y =-1 (B).(3,-1)(C).{3,-1} (D).{(3,-1)}2.a 为正实数,i 为虚数单位,|a +i i|=2,则a =( ) (A)2 (B) 3 (C) 2(D)13.运行下面的程序:当输入168,72时,输出的结果是( )(A)168 (B)72 (C)36 (D)244. 已知命题p : n ∈N ,2n >1 000,则 非p 为( )(A) n ∈N ,2n ≤1 000 (B) n ∈N ,2n >1 000(C) n ∈N ,2n <1 000 (D) n ∈N ,2n ≥1 0005. 已知等比数列{an}的前n 项积为∏n,若8843=⋅⋅a a a ,则∏9=( ).A.512B.256C.81D.166. 如图,设向量(3,1)OA = ,(1,3)OB = ,若OC =λOA +μOB ,且λ≥μ≥1,则用阴影表示C 点所有可能的位置区域正确的是( )7. 函数f (x )的部分图象如图所示,则f (x )的解析式可以是( ).A.f (x )=x +sin xB.x x x f cos )(=C.f (x )=x cos xD.)23)(2()(ππ--=x x x x f8.定义:离心率的椭圆为“黄金椭圆”, 已知E : + =1(a>b>0)的一个焦点为F(c,0)(c>0),则E22x a 22y b为“黄金椭圆”是“a 、b 、c 成等比数列”的( )(A)既不充分也不必要条件 (B)充分且必要条件(C)充分不必要条件 (D)必要不充分条件9函数 ()x 231f x ()x 2-=- 的零点所在的区间为( )(A)(0,1) (B)(1,2) (C)(2,3)(D)(3,4)10.已知函数f(x)=x3+bx2+cx+d(b 、c 、d 为常数),当x ∈(0,1)时取得极大值,当x ∈(1,2)时取极小值,则22)3()21(-++c b 的取值范围是( ).A.()5,237B.)5,5(C.)25,437(D.(5,25)第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分11. 从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有________种.12. 若 展开式中第6项的系数最大,则不含x 的项等3n 21(x )x+于____________.13. 若直线20x y -+=与圆22C:(3)(3)4x y -+-=相交于A 、B 两点,则CA CB ⋅ 的值为14. 若某几何体的三视图(单位:cm)如图所示,则此几何体的侧面积=_________cm 2.15.已知函数1(1)sin 2,[2,21)2(),()(1)sin 22,[21,22)2n n x n x n n f x n N x n x n n ππ+⎧-+∈+⎪⎪=∈⎨⎪-++∈++⎪⎩ ,若数列{am}满足))(2(+∈=N m m f a m ,且{}m a 的前m 项和为m S ,则20142006S S -= .三、解答题:本大题共六个小题,共80分.解答应写出文字说明、证明过程和演算步骤.16. (13分) 某同学参加语文、数学、英语3门课程的考试.假设该同学语文课程取得优秀成绩的概率为错误!未找到引用源。
2017-2018学年(新课标)最新福建省福州高二下学期期末考试数学(理)试题及解析-精品试题

2017-2018学年福建省福州市高二下学期期末检测(理)3.独立性检验的临界值表:一、选择题(本大题共8小题,每小题5分,共40分。
每题有且只有一个选项是正确的,请把答案填在答卷相应位置上)1.已知随机变量ξ的数学期望E ξ=0.05且η=5ξ+1,则Eη等于A. 1.15B. 1.25C. 0.75D. 2.52. 某射击选手每次射击击中目标的概率是0.8,如果他连续射击5次,则这名射手恰有4次击中目标的概率是A.40.80.2⨯B.445C 0.8⨯C.445C 0.80.2⨯⨯D. 45C 0.80.2⨯⨯3.6个人排成一排,其中甲、乙不相邻的排法种数是A.288B.480C.600D.6404.一工厂生产的100个产品中有90个一等品,10个二等品,现从这批产品中抽取4个,则其中恰好有一个二等品的概率为A .41004901C C -B .4100390110490010C C C C C + C .4100110C C D .4100390110C C C5. 已知服从正态分布2(,)N μσ的随机变量在区间(,)μσμσ-+,(2,2)μσμσ-+和(3,3)μσμσ-+内取值的概率分别为68.3%,95.4%和99.7%。
某校高一年级1000名学生的某次考试成绩服从正态分布2(90,15)N ,则此次成绩在(60,120)范围内的学生大约有A.997B.972C.954D.683人6.某车间加工零件的数量x 与加工时间y 的统计数据如下表:现已求得上表数据的回归方程ˆˆy bx a =+中的b 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为A .84分钟B .94分钟C .102分钟D .112分钟7. 先后抛掷红、蓝两枚骰子,事件A :红骰子出现3点,事件B :蓝骰子出现的点数为奇数,则(|)P A B =A.61B.31C.21D.365 8.甲、乙、丙、丁四个人排成一行,则乙、丙两人位于甲同侧的排法总数是A.16B.12C.8D.6二、填空题(本大题共4小题,每小题5分,共20分)9. 6名同学坐成一排,其中甲、乙必须坐在一起的不同坐法是________种.10.若5(1)ax -展开式中各项系数和为32,其中a R ∈,该展开式中含2x 项的系数为_________. 11.已知某一随机变量X 的概率分布列如下,且E (X )=7,求D (X ) . 12.给出下列结论:(1)在回归分析中,可用相关指数R 2的值判断模型的拟合效果,R 2越大,模型的拟合效果越好; (2)某工产加工的某种钢管,内径与规定的内径尺寸之差是离散型随机变量;(3)随机变量的方差和标准差都反映了随机变量的取值偏离于均值的平均程度,它们越小,则随机变量偏离于均值的平均程度越小;(4)甲、乙两人向同一目标同时射击一次,事件A :“甲、乙中至少一人击中目标”与事件B :“甲,乙都没有击中目标”是相互独立事件。
2017-2018学年高二年级数学期末试卷(理数)含答案

2.若 x 2m2 3 是 1 x 4 的必要不充分条件,则实数 m 的取值范围是( )
10.已知函数 f x 1 x3 1 mx2 4x 3 在区间 1,2上是增函数,则实数 m 的取值范围是(
32
A . 3,3
B . ,3 3, C . ,1 1,
,则满足
11.已知函数
f
x
3|x1| , x2 2x
x 1,
0, x
0
若关于
x
的方程 f
x2
a
1f
x
a
0有
7
个不
等实根,则实数 a 的取值范围是(
)
A . 2,1
B .2,4
C . 2,1
D . ,4
12.
已知函数
A . loga c logb c B . logc a logc b C . a c bc
D . ca cb
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是 9.已知函数 f x 2 xm 1 为偶函数,记 a f log0.5 3 , b f log2 5 , c f 2m,则
由题设知
,
则
解得 的横坐标分别是 则 有 又
,又 于是
, ,
,
,即 l 与直线 平行, 一定相交,分别联立方
设
是平面
的法向量,则
,即
。
对任意
,要使
与
的面积之比是常数,只需 t 满足
可取
,故,所以 与平面
20. (1)依题意可得
所成角的正弦值为 ---------12 分 ,
福建省华安一中2018-2019学年高二下学期期末考试 数学(理) Word版含答案
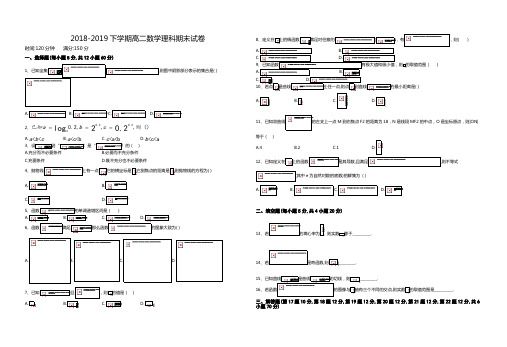
2018-2019下学期高二数学理科期末试卷时间:120分钟满分:150分一、选择题(每小题5分,共12小题60分)1、已知全集,,,则图中阴影部分表示的集合是( )A. B. C. D.2、0.20.32已知0.2,,,则()log20.2a b c===A.<<a b c B.<c<baC.<a<bc D.<c<ab3、设则“”是“”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件4、抛物线上有一点,它的横坐标是,它到焦点的距离是,则抛物线的方程为( )A. B.C.D.5、函数的单调递增区间是()A.B.C.D.6、函数满足,那么函数的图象大致为( )A.B. C. D.7、已知,且,则的值是()A.B.C.D.8、定义在上的偶函数满足对任意的(),有,则()A.B.C.D.9、已知函数有极大值和极小值,则的取值范围()A.B.C.D.10、若点是曲线上任一点,则点到直线的最小距离是( )A.B. C. D.11、已知双曲线M到右焦点F2的距离为18,N是线段MF2的中点,O是坐标原点,则|ON|等于()A.4B.2C.1D.12、已知定义在上的函数是其导数,且满足,则不等式(其中e为自然对数的底数)的解集为( )A. B. C.D.二、填空题(每小题5分,共4小题20分)13、若的离心率为,则实数等于__________.14、若是奇函数,则__________.15、已知直线是曲线的切线,则__________.16、若函数轴有三个不同的交点,则实数的取值范围是__________.三、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)17、已知函数在,处都取得极值. (1)求,的值 (2)函数的单调区间;18、已知函数,.(1)当时,解不等式.(2)若对于恒成立,求实数的取值范围.19、在极坐标系中,曲线的极坐标方程为,以极点为坐标原点,极轴为轴的正半轴,取相同的单位长度建立平面直角坐标系,直线的参数方程为(为参数). (1)求曲线的普通方程; (2)设,直线与曲线交于,两点,求的值.20、如图,四边形为正方形,平面,,.(1)证明:平面平面; (2)求二面角的余弦值.21、已知椭圆的长轴长为且点在椭圆上.(1)求椭圆的方程; (2)过椭圆右焦点斜率为的直线交椭圆于,两点,若,求直线的方程.22、已知函数.(1)讨论的单调性;(2)若函数在上有零点,求的取值范围.2018-2019下学期高二数学理科期末试卷卷答案解析第1题答案C第1题解析则第2题答案B第3题答案A第3题解析.故选第4题答案A第4题解析A.第5题答案A第5题解析第6题答案C第6题解析,,,.第7题答案B第7题解析,故选第8题答案A第8题解析A.第9题答案A第9题解析等实根,第10题答案A第10题解析所以点第11题答案A第11题解析N是线段MF2的中点,O是坐标原点,所以第12题答案A第12题解析则上为增函数故选A. 第13题答案83第14题答案第14题解析即第15题答案第15题解析第16题答案递增,,轴有三个不同的交点,第17题答案 略第17题解析∴联立解得.,第18题答案见解析 第18题解析,(2)∴实数第19题答案见解析第19题解析 (1)曲线直线(2)易知点在直线上.将直线的参数方程(为参数)代入曲线的直角坐标方程,化简得设点,,,第20题答案 (1)略; (2第20题解析如图,以D 为坐标原点,线段DA 的长为单位长,射线DA ,DP ,DC 为x,y ,z 轴的正半轴建立空间直角坐标系D-xyz.(1)证明:依题意有Q(1,1,0),C(0,0,1),P(0,2,0).即PQ⊥DQ,PQ⊥DC.又DQ∩DC=D ,故PQ⊥平面DCQ.又PQ ⊂平面PQC ,所以平面PQC⊥平面DCQ. (2)依题意有B(1,0,1)PBC 的一个法向量,的一个法向量,第21题答案 略第21题解析 (1),(2)由(1),所以直线第22题答案 (1)见解析;第22题解析(1),在上单调递增;,;.(2)在上有零点,等价于关于的方程在上有解,在上有解.,则,,解得;令,,解得,在上单调递减,在上单调递增,,,则,,故的取值范围为。
福建省华安县第一中学高二数学下学期期末考试试题文(含解析)

福建省华安县第一中学高二数学下学期期末考试试题文(含解析)一、选择题(在每小题给出的四个选项中只有一项是符合题目要求的) 1.复数1iz i-=在复平面上对应的点位于 ( ) A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】C 【解析】 【详解】1i z i-=2(1)1i ii i -==--. 所以在复平面上对应的点位于第三象限,故选C.2.有一段演绎推理:“对数函数log a y x =是增函数,已知0.5log y x =是对数函数,所以0.5log y x =是增函数”,结论显然是错误的,这是因为( )A. 大前提错误B. 小前提错误C. 推理形式错误D. 非以上错误【答案】A 【解析】 【分析】根据演绎推理的结构特点可判断出该推理大前提错误.【详解】因为log a y x =不一定是增函数(当01a <<时是减函数,当1a >时才是增函数),故演绎推理的大前提是错误的,故选A.【点睛】为了保证演绎推理得到的结论是正确的,则需大前提正确,小前提需蕴含再大前提中,这样得到的结论才是正确的.3.若集合A ={x |x (x -1)<2},且A ∪B =A ,则集合B 可能是( ) A. {-1,2} B. {0,2} C. {-1,0} D. {0,1}【答案】D 【解析】 【分析】由已知计算A ,结合B A ⊆,由此能求出集合B 的可能结果.【详解】解:集合{|(1)2}{|12}A x x x x x =-<=-<<,且A B A ⋃=,故B A ⊆,{|12}B x x ∴⊂-<<,结合选项知集合B 可能是{0,1}. 故选:D . 【点睛】本题考查集合关系,是基础题.4.已知a R ∈,则“11a<”是“1a >”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件【答案】B 【解析】 【详解】或,所以是的必要非充分条件,故选B.考点:充分必要条件5.函数f(x)=log 2x +2x -1的零点必落在区间( )A. (18,14)B. (14,12) C. (12,1)D. (1,2)【答案】C 【解析】 【详解】f(18)=-154<0,f(14)=-52<0,f(12)=-1<0,f(1)=1>0,f(2)=4>0, ∴函数零点落在区间(12,1)上,故选C.6.已知 5.10.9m =,0.90.95.1,log 5.1n p ==,则这三个数的大小关系是( )A. m<n<pB. m<p<nC. p<m<nD. p<n<m【答案】C 【解析】 【分析】利用指数函数与对数函数的性质即可比较大小.【详解】设函数f (x )=0.9x ,g (x )=5.1x ,h (x )=log 0.9x 则f (x )单调递减,g (x )单调递增,h (x )单调递减 ∴0<f (5.1)=0.95.1<0.90=1,即0<m <1 g (0.9)=5.10.9>5.10=1,即n >1h (5.1)=log 0.95.1<log 0.91=0,即p <0 ∴p<m <n 故选:C .【点睛】本题考查对数值比较大小,可先从范围上比较大小,当从范围上不能比较大小时,可借助函数的单调性数形结合比较大小.属基础题7.观察下列算式:122=,224=,328=,4216=,5232=,6264=,,72128=,82256=……用你所发现的规律可得20192的末位数字是( ) A. 2B. 4C. 6D. 8【答案】D 【解析】 【分析】通过观察可知,末尾数字周期为4,据此确定20192的末位数字即可.【详解】通过观察可知,末尾数字周期为4,201945043=⨯+,故20192的末位数字与32末尾数字相同,都是8.故选D . 【点睛】归纳推理是由部分到整体、由特殊到一般的推理,由归纳推理所得的结论不一定正确,通常归纳的个体数目越多,越具有代表性,那么推广的一般性命题也会越可靠,它是一种发现一般性规律的重要方法.8.如图所示,5组数据(),x y 中去掉()3,10D 后,下列说法错误的是( )A. 残差平方和变大B. 相关系数r 变大C. 相关指数2R 变大D. 解释变量x 与预报变量y 的相关性变强 【答案】A 【解析】 【分析】由散点图知,去掉(3,10)D 后,y 与x 的线性相关加强,由相关系数r ,相关指数2R 及残差平方和与相关性的关系得出选项.【详解】解:由散点图知,去掉(3,10)D 后,y 与x 的线性相关加强,且为正相关, 所以r 变大,2R 变大,残差平方和变小. 故选:A .【点睛】本题考查刻画两个变量相关性强弱的量:相关系数r ,相关指数2R 及残差平方和,属于基础题.9.已知()f x 是定义在(,)-∞+∞上的偶函数,且在(,0]-∞上是增函数,设4(log 7)a f =,12(log 3)b f =,1.6(2)c f =,则,,a b c 的大小关系是( )A. c a b <<B. b c a <<C. c b a <<D. a b c <<【答案】C 【解析】 【分析】利用对数和指数幂的运算性质,结合函数单调性和奇偶性的性质是解决本题的关键. 【详解】解:()f x 是定义在(,)-∞+∞上的偶函数,1222(log 3)(log 3)(log 3)b f f f ∴==-=,22442log 4log 3log 9log 71=>=>>, 1.6122>, 1.6420log 7log 32<<<,在(-∞,0]上是增函数,∴在[0,)+∞上为减函数,则 1.642(log 7)(log 3)(2)f f f >>,即c b a <<, 故选:C .【点睛】本题主要考查大小比较,根据函数的奇偶性和单调性之间的关系以及对数的运算性质是解决本题的关键,属于基础题.10.定义在R 上的奇函数()f x 满足:(1)(1)f x f x +=-,且当10x -<<时,()21xf x =-,则2(log 20)f =( ) A.14B. 14-C. 15-D.15【答案】D 【解析】由()()11f x f x +=-可知函数()f x 是周期为2的周期函数,所以()()()()()()22log 52222241log 202log 5log 5log 522log 521155f f f f f -⎛⎫=+==-=--=--=--=⎪⎝⎭,故选D.11.函数2()(3)ln f x x x =-⋅的大致图象为( )A. B.C. D.【答案】C 【解析】 函数()()23ln f x xx =-⋅是偶函数,排除,A D ,选项,()23ln 0x x -⋅=,当0x >时,解得1x =,或3x =是函数()()23ln f x xx =-⋅在0x >时的两个零点,当1x e=时,2211113ln 30f e e e e ⎛⎫⎛⎫⎛⎫=-⋅=-< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,可得选项B 不正确,故选C.【方法点晴】本题通过对多个图象的选择考查函数的的图象与性质,属于中档题.这类题型也是近年高考常见的命题方向,该题型的特点是综合性较强较强、考查知识点较多,但是并不是无路可循.解答这类题型可以从多方面入手,根据函数的定义域、值域、单调性、奇偶性、特殊点以及0,0,,x x x x +-→→→+∞→-∞时函数图象的变化趋势,利用排除法,将不合题意的选项一一排除.12.已知函数()22,?52,x x a f x x x x a+>⎧=⎨++≤⎩,若函数()()2g x f x x =-恰有三个不同的零点,则实数a 的取值范围是 A. [)1,1- B. [)1,2- C. [)2,2- D. []0,2【答案】B 【解析】由题意可得()22,?32,x x a g x x x x a -+>⎧=⎨++≤⎩恰有三个不同的零点,如图所示,12a -≤<本题选择B选项.二、填空题(将答案填入答卷指定位置).13.函数1()f x xx=-+在1[2,]3--上的最大值是_____【答案】3 2【解析】【分析】求导数,确定函数的单调性,即可得解.【详解】解:1y x x=-+,1[2,]3--2110y x∴'=--<,∴函数1y x x=-+在1[2,]3--上单调递减,2x∴=-时,函数1y x x=-+在1[2,]3--上的最大值为32,故答案为:32.【点睛】本题考查运用导数研究函数的单调性,属于基础题.14.函数()212log2y x x=-的单调递减区间是______________. 【答案】()2,+∞【解析】【分析】令22t x x =-,根据复合函数单调性的判断方法,考虑该函数在()(),02,-∞+∞的增区间即可.【详解】函数的定义域为()(),02,-∞+∞,令22t x x =-,则原函数可分解为:12log y t =,22t x x =-,其中()2,x ∈+∞,22t x x =-在()2,+∞为增函数,在(),0-∞上为减函数,故()212log 2y x x =-的减区间为()2,+∞,填()2,+∞.【点睛】本题考查与对数有关的复合函数的单调性,注意先考虑函数的定义域,再利用“同增异减”求内函数相应的单调区间即可.15.函数2()(1)5f x x a x =--+在区间1(,1)2上为增函数,则(2)f 的取值范围是 ______.【答案】[)7,+∞ 【解析】 【分析】根据函数()()215f x x a x =--+在区间1,12⎛⎫ ⎪⎝⎭上为增函数,可得2a ≤,从而可得()21127f a =-≥.【详解】函数()()215f x x a x =--+在区间1,12⎛⎫ ⎪⎝⎭上为增函数,由于函数图象(抛物线)开口向上, 所以其对称轴12a x -=或与直线12x =重合或位于直线12x =的左侧, 即应有1122a -≤,解得2a ≤, 所以()21127f a =-≥,即()2f 的取值范围是[)7,+∞,故答案为[)7,+∞.【点睛】本题主要考查二次函数的图象与性质,重点考查二次函数的对称轴的位置与单调性,意在考查数形结合思想的应用以及灵活应用所学知识解决问题的能力,属于中档题.16.若函数()326f x x x m =-++的极大值为12,则实数m =____.【答案】﹣20 【解析】 【分析】根据已知对函数求导使得导函数等于0,验证函数在这两个数字左右两边的导函数值,看出在4x =处取得极大值,代入得到结果.【详解】解:函数326+y x x m =-+的极大值为12,23120y x x ∴'=-+=,0x ∴=,4x =,∴函数在(0,4)上单调递增,在(4,)+∞上单调递减,故4x =为极大值点,649612m ∴-++=, 20m ∴=-故答案为:20-.【点睛】本题考查函数的极值的应用,解题的关键是看出函数在哪一个点取得极大值,代入求出结果,属于基础题.三.解答题(解答应写出文字说明,推理过程或演算步骤)17.某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(其中16名女员工,14名男员工)的得分,如下表:(Ⅰ)现求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:合计30(Ⅱ)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?参考数据:0.10 0.050 0.025 0.010 0.0012.7063.841 5.024 6.635 10.828参考公式:【答案】(1)见解析(2)见解析【解析】试题分析:(1)由题意完成列联表即可;(2)由题意计算可得:()22301211348.571 6.63515151614K⨯-⨯=≈>⨯⨯⨯故能在犯错不超过1﹪前提下,认为该企业员工“性别”与“工作是否满意”有关。
福建省华安县第一中学高二数学下学期期末考试试题理(2021年整理)

福建省华安县第一中学2017-2018学年高二数学下学期期末考试试题理编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(福建省华安县第一中学2017-2018学年高二数学下学期期末考试试题理)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为福建省华安县第一中学2017-2018学年高二数学下学期期末考试试题理的全部内容。
2017—2018学年华安一中高二年下学期末试卷数学理科考试时间:120分钟;注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(每题5分,共60分,在每小题给出的四个选项中只有一项是符合题目要求的) 1.已知复数z 满足()13i z i +=+, i 为虚数单位,则z 等于( )A 。
1122i - B. 1122i + C 。
1i - D 。
1i +2、已知事件A 发生的概率为830,事件B 发生的概率为930,事件A 、B 同时发生的概率为630,若事件B 已经发生,则此时事件A 也发生的概率为A .89B .34C .15D .233.随机变量()2~9,X N σ, (6)0.2P X <=,则(912)P X <<=( ) A 。
0.9974 B 。
0.4987 C 。
0.4 D 。
0.3 4.()203sin x x dx π+⎰=( )A. 2318π- B 。
2318π+ C. 214π- D 。
312π+5.某产品的广告费用x 与销售额y 的统计数据如下表:根据上表中的数据可以求得线性回归方程^^y b x a =+中的b 为6.6,据此中模型预报广告费用为10万元时销售额为( )A .66.4万元B .66.2万元C .66.8万元D .67.6万元6.从1,2,3,4,5,6,7,8,9这九个数中,随机取出3个不同的数,这3个数的和是偶数的概率是( ) A.1121 B. 1021 C. 59 D. 497.已知2()2(1)f x x x f '=+⋅,则(0)f '等于( )A. 0 B 。
2017—2018学年度第二学期期末考试高二数学理科(带答案

2017—2018学年度第二学期期末考试高二数学(理)试题一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合A={4,5,7,9},B={3,4,7,8,9},全集U A B =U ,则集合)(B A C U I 中的元素共有( ) A .3个 B. 4个C.5个D.6个2. 复数3223ii+=-( ) A.1 B.1-C.iD.i -3.已知)1,1(),2,(a n a m -=-=,且n m //,则a=( ) A .﹣1B .2或﹣1C .2D .﹣24. 在区间[]1,1-上随机选取一个实数x ,则事件"210"x -< 的概率为( )A .12B .34C .23D .145. 已知tan a =4,cot β=13,则tan(a+β)=( )A.711B.711-C. 713D.713-6.在6)2(y x -的展开式中,含24y x 的项的系数是( ) A .15 B .-15C .60D . -607.执行如图所示的程序框图,若输入的a 为2,则输出 的a 值是( )A. 2B. 1C.21D.1-8. 设非零向量a 、b 、c 满足c b a c b a =+==|,|||||,则>=<b a ,( ) A.150°B.120°C.60°D.30°9. 甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有( ) A.150种B.180种C.300种D.345种10.下列四个结论中正确的个数是(1)对于命题,:0R x p ∈∃使得0120≤-x ,则,:R x p ∈∀⌝都有012>-x ; (2)已知),2(~2σN X ,则 (2)0.5P X >=(3)已知回归直线的斜率的估计值是2,样本点的中心为(4,5),则回归直线方程为32ˆ-=x y; (4)“1≥x ”是“21≥+xx ”的充分不必要条件. A .1B .2C .3D .411.正方体1111ABCD A B C D -中,若1D AC △外接圆半径为26,则该正方体外接球的表面积为( ) A.2πB.8πC.12πD.16π12.已知奇函数()f x 的导函数为()f x ',当0x ≠时,()()0f x f x x'+>,若11(),()a f b ef e e e==--,()1c f =,则,,a b c 的大小关系正确的是( ) A .a b c << B .b c a << C .c a b << D .a c b <<二、填空题:本题共4小题,每小题5分,共20分。
福建省华安一中高二数学下学期期末考试试卷 理-人教版高二全册数学试题

华安一中2014—2015学年高二年下学期期末考(理科)数学试 卷第Ⅰ卷(选择题50分)一、选择题:(本大题共10小题,每小题5分,共50分)1、已知i 是虚数单位,若i(x +y i)=3+4i ,x ,y ∈R ,则复数x +y i 的模是 ( )A .5B .3C .4D .22、某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系,运用2⨯2列联表进行独立性检验,经计算K 2=11.069,则所得到的统计学结论为:有多大把握认为“学生性别与支持该活动有关系” ( ) P(K 2≥k 0) 0.100 0.050 0.025 0.010 0.001 k 。
2.7063.8415.0246.63510.828A .0.1%B .1%C .99%D .99.9%3、在极坐标系中,点⎝ ⎛⎭⎪⎫2,π3到圆ρ=4cos θ的圆心的距离为( )A. 3 B .2 C. 1+π29D.4+π294.若复数z ii z+=(i 为虚数单位)的复数Z 为( ) 11.22A i + 11.22B i -+ 11.22C i - 11.22D i -- 5.直线4y x =与曲线3y x =在第三象限内围成的封闭图形的面积为( ) A 22B 42C 2D 46、某校为了丰富学生们的课外活动分别成立A 、B 、 C 兴趣小组,现有甲,乙,丙、丁四名同学报名参加,每人仅参加一个兴趣小组,每个兴趣小组至少有一人报名,则不同的报名方法有( )A . 12种B . 24种C . 36种D . 72种7、“1a =”是“5(1)ax +的展开式的各项系数之和为32”的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件8、若某公司从五位大学毕业生A 、B 、C 、D 、E 中录用三人,这五人被录用的机会均等,则A 或B 被录用的概率为( )A .B .C .D .9.若4(1)(1)x m ++的展开式中的x 的奇次幂项的系数和为64,则m 的值( )A. 3B. 5C.7D.910已知函数f (x )=|x -2|+1,g (x )=kx ,若方程f (x )=g (x )有两个不相等的实根,则实数k 的取值范围是( )A. 3(,1)2B. 1(0,)2C. (1,2)D. (2,+∞) 第Ⅱ卷(非选择题100分)二.填空题(本大题共5小题,每小题4分,共20分)11、设随机变量ξ服从正态分布(2,9)N ,若(1)(1)P c P c ξξ>+=<-,则c = . 12、⎝ ⎛⎭⎪⎫12x -2y 5的展开式中x 3y 2的系数是 (用数字作答)。
福建省华安一中、长泰一中等四校2017-2018学年高二数学下学期第一次联考试题(4月)试题 理

福建省华安一中、长泰一中等四校2017-2018学年高二数学下学期第一次联考试题(4月)试题 理(考试时间:120分钟 总分:150分)★友情提示:要把所有答案都写在答题卷上,写在试卷上的答案无效。
一、选择题(每题5分,共60分,在每小题给出的四个选项中只有一项是符合题目要求的)1.设复数i i z 510)2(-=+⋅(i 为虚数单位),则z 的共轭复数z 为( )A .i 43+-B .i 43+C .i 43--D .i 43-2.函数13)(3+-=x x x f 在闭区间[-3,0]上的最大值、最小值分别是( )A. 1,-1B. 9,-19C. 1,-17D. 3,-173.已知复数ii i z --=1)43((i 为虚数单位),则在复平面内,复数z 对应的点位于( ) A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限4.曲线x x y +=221在点(2,4)处的切线与坐标轴围成的三角形面积为( ) A 、32 B 、2 C 、1 D 、34 5.已知直线1+=x y 与曲线)ln(a x y +=相切,则a 的值为( )A. 2B. 1C. 3D. 06.设函数()()10312f x x =-,则()1f '等于( )A. 0B. 1-C. 60D. 60-7.若x x x f 5)(3-=,且)2(f a '=则⎰-=-aa dx x a 22( ) A. π49 B. 249π C. 3686 D. 0 8.由曲线3x y =与3x y =所围成的封闭图形的面积为( ) A.21 B. 2 C. 1 D. 32 9.函数223)(a bx ax x x f +--=在1=x 处有极值10,则点()b a ,坐标为( )A. ()3,3-B. ()11,4-C. ()3,3-或()11,4-D.不存在10.对于函数f (x ),若∀a ,b ,c ∈R ,f (a ),f (b ),f (c )都是某一三角形的三边长, 则称f (x )为“可构造三角形函数”.以下说法正确的是( )A.f (x )=1(x ∈R )不是“可构造三角形函数”B.“可构造三角形函数”一定是单调函数C.)(11)(2R x x x f ∈+=是“可构造三角形函数” D.若定义在R 上的函数f (x )的值域是],[e e (e 为自然对数的底数),则f (x )一定是“可构造三角形函数”11.下列图中阴影部分面积与复数4)1)(83(i z --=(i 为虚数单位)的模相同的是( ).12.函数()f x 的导函数为'()f x ,对任意的实数x ,都有)(2)(x f x f >'成立,则( )A .)3ln 21(2)2ln 21(3f f <B .)3ln 21(2)2ln 21(3f f > C .)3ln 21(3)2ln 21(2f f < D .)3ln 21(3)2ln 21(2f f < 二、填空题(每小题5分,共20分,.将答案填入答卷指定位置).13.曲线22)(2-+=x x x f 在0P 处的切线平行于直线20185+=x y ,则点0P 坐标为_______.14.已知曲线方程)(31)(23R a ax x x f ∈-=,若对任意实数m ,直线0:=++m y x l 都不是曲线)(x f y =的切线,则实数a 的取值范围是_______15.若三角形内切圆的半径为r ,三边长为a b c ,,,则三角形的面积等于1()2S r a b c =++,根据类比推理的方法,若一个四面体的内切球的半径为R ,四个面的面积分别是1234S S S S ,,,,则四面体的体积V =____________________________.16.如图所示,第n 个图形是由正2n +边形拓展而来(1,2,n =),则第n 个图形共有____个顶点.三、解答题。
2017-2018学年福建省华安县第一中学高二下学期期末考试物理试题 解析版

“华安一中” 2017-2018学年下学期期末考高二物理试题一、选择题(本题共13小题,共48分。
其中1-10小题为单选题,每小题3分;11-13为多项选择题,每小题6分,多选题有错选不得分,漏选得3分。
)1. 弹簧振子在光滑水平面上做简谐运动,在振子向平衡位置运动的过程中( )A. 振子所受的回复力逐渐增大B. 振子的加速度逐渐减小C. 振子的速度逐渐减小D. 振子的位移逐渐增大【答案】B【解析】试题分析:振子向平衡位置运动的过程中,位移减小,根据F=-kx可知,振子所受回复力逐渐减小,选项AB错误;根据牛顿第二定律可知,振子加速度逐渐减小,选项D正确;质点的速度逐渐增大,选项C错误;故选D.考点:简谐振动的规律.2. 变压器铁芯是用薄硅钢片叠压而成,而不是采用一整块硅钢,这是因为()A. 增大涡流,提高变压器效率B. 减小涡流,提高变压器效率C. 增大铁芯中的电阻,以产生更多的热量D. 减小铁芯中的电阻,以减小发热量【答案】B【解析】试题分析:涡流越大电能的损耗就越多,所以变压器的铁芯是利用薄硅钢片叠压而成的,而不是采用一整块硅钢是为了减小涡流,减少电能的损耗,增大电阻就可以使回路中电流减小,热效应减少。
所以BD正确,AC错误;故答案选BD考点:考查涡流的应用点评:把块装金属置于随时间变化的磁场中或让它在磁场中运动时,金属块内将产生感应电流。
这种电流在金属块内自成闭合回路,很像水的漩涡,因此叫做涡电流简称涡流。
整块金属的电阻很小,所以涡流常常很强。
如变压器的铁心,当交变电流穿过导线时,穿过铁心的磁通量不断随时间变化,它在副线圈产生感应电动势,同时也在铁心中产生感应电动势,从而产生涡流。
这些涡流使铁心大量发热,浪费大量的电能,效率很低。
但涡流也是可以利用的,在感应加热装置中,利用涡流可对金属工件进行热处理。
大块的导体在磁场中运动或处在变化的磁场中,都要产生感应电动势,形成涡流,引起较大的涡流损耗。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年华安一中高二年下学期末试卷数学理科考试时间:120分钟;注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(每题5分,共60分,在每小题给出的四个选项中只有一项是符合题目要求的)1.已知复数z 满足()1i z i +=, i 为虚数单位,则z 等于( )A.1122i - B. 1122i + C. 1i - D. 1i + 2、已知事件A 发生的概率为830,事件B 发生的概率为930,事件A 、B 同时发生的概率为630,若事件B 已经发生,则此时事件A 也发生的概率为A .89B .34C .15D .233.随机变量()2~9,X N σ, (6)0.2P X <=,则(912)P X <<=( ) A. C. 0.4 D. 0.34( )A. 2318π-B. 2318π+C.214π- D. 312π+ 5.某产品的广告费用x 与销售额y 的统计数据如下表:根据上表中的数据可以求得线性回归方程^^y b x a =+中的b 为6.6,据此中模型预报广告费用为10万元时销售额为( )A .66.4万元B .66.2万元C .66.8万元D .67.6万元6.从1,2,3,4,5,6,7,8,9这九个数中,随机取出3个不同的数,这3个数的和是偶数的概率是( ) A.1121 B. 1021 C. 59 D. 497.已知2()2(1)f x x x f '=+⋅,则(0)f '等于( )A. 0B. 2C. – 4D. –28.函数2(21)y x =+在1=x 处的导数值是( )A. 8 B .6 C .12 D .109.甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为a ,再由乙猜甲刚才想的数字,把乙猜的数字记为b ,且0,1,29{}a b ∈⋯、,,.若||1a b ≤-,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为( )A .950 B .750 C .925D . 257 10.若1()n x x+的展开式的二项式系数之和为64,则展开式的常数项为( )A 、20B 、10C 、40D 、3011.将石子摆成如图的梯形形状.称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2 018项与5的差,即52018-a =( )A. 1 012×2 018B. 1 012×2 017C. 2 020×2 016D. 2 020×2 01512.已知f (x )为定义在),0(+∞错误!未找到引用源。
上的可导函数,且错误!未找到引用源。
恒成立,则不等式()0)(12<-x f f x 的解集为( ). A. (0,1) B. (1,2) C. 错误!未找到引用源。
D. 错误!未找到引用源。
第II 卷(非选择题)二、填空题(每小题5分,共20分,.将答案填入答卷指定位置). 13、曲线2ln y x =在(1,0)处的切线方程为 14.42)2(--x x 展开式中错误!未找到引用源。
项的系数为______.15.已知函数2(x)sin 1xf x e =++,其导函数记为/(x)f ,则)2018()2018()2018()2018(-'-'+-+f f f f 的值为______.16.定义在()1,-+∞上的函数()f x 满足x x f co s 1)(+>', ()01f =,则不等式()sin 1f x x x >++的解集为__________.三、解答题(本大题共6小题,满分70分,解答应写出文字说明,推理过程或演算步骤) 17.(本小题满分12分)已知函数()2xf x e x ax =--.(1)若函数()f x 的图象在0x =处的切线方程为2y x b =+,求,a b 的值; (2)若函数()f x 在R 上是增函数, 求实数a 的最大值. 18.(本小题满分12分)桌面上有两颗均匀的骰子(6个面上分别标有数字1,2,3,4,5,6).将桌面上骰子全部抛掷在桌面上,然后拿掉那些朝上点数为奇数的骰子,如果桌面上没有了骰子,停止抛掷,如果桌面上还有骰子,继续抛掷桌面上的剩余骰子. 记抛掷两次之内(含两次)去掉的骰子的颗数为X .(Ⅰ)求(0)P X =;(Ⅱ)求X 的分布列及期望 E X ().19.(本小题满分12分)近年来我国电子商务行业迎来发展的新机遇.2016年“618”期间,某购物平台的销售业绩高达516亿元人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.(1)选完成关于商品和服务评价的22⨯列联表,再判断能否在犯错误的概率不超过0.001的前提下(即有99.9%的把握),认为商品好评与服务好评有关?(即有99.9%的把握认为商品好评与服务好评有关?)(2)若将频率视为概率,某人在该购物平台上进行的3次购物中,设对商品和服务全为好评的次数为随机变量X :①求对商品和服务全为好评的次数X 的分布列; ②求X 的数学期望和方差.2K 的观测值:()()()()()2n ad bc k a b c d a c b d -=++++(其中n a bc d =+++)关于商品和服务评价的22⨯列联表:20.(本小题满分14分)已知函数()()ln 1f x x x =+-. (1)求()f x 的单调区间;(2)若k Z ∈,且()311f x x k x ⎛⎫-+>- ⎪⎝⎭对任意1x >恒成立,求k 的最大值.21.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xoy 中,直线l的参数方程为132x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以原点为极点,x 轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρθ=. (1)写出圆C 的直角坐标方程;(2)点p 为直线l 上一动点,当p 到圆心C 的距离最小时,求点p 的直角坐标.22.(本小题满分10分) 选修4—5:不等式选讲. 已知函数()|||5|f x x a x =-+-.(1)若不等式()3f x ≥恒成立,求a 的取值范围;(2)当2a =时,求不等式2()815f x x x -+≥的解集.17-18学年高二下学期期末试卷数学理科参考答案1.C 2.D 3.D 4.B . 5.B 6.A 7.C 8.C 9.D 10.A 11.B 12.A 13.22y x =- 14.32 15.2 16.),0(+∞ 17.(1)()()'2,'01x f x e x a f a =--∴=-.―――――2分于是由题知12a -=,解得1a =-.―――――――3分()()2,01x f x e x x f ∴=-+∴=,于是120b =⨯+,解得1b =.――――――5分(2)由题意()'0f x ≥即20x e x a --≥恒成立,2x a e x ∴≤- 恒成立, 设()2xh x e x =-,则()'2xh x e =-.――――――7分―――――――10分()()min ln 222ln 2,22ln 2,h x h a a∴==-∴≤-∴的最大值为22ln 2-.――――12分18.(Ⅰ) 11111(=0)=222216P x ⨯⨯⨯= …… 4分 (Ⅱ)122122211113(1)()()()()P X C C ==+=………8分………………… 12分19.(1)由题意可得关于商品和服务评价的22⨯列联表如下:――――――3分()222008010407011.11110.8281505012080K ⨯⨯-⨯=≈>⨯⨯⨯,故能在犯错误的概率不超过0.001的前提下,认为商品好评与服务好评有关 ――――――6分 (2)①每次购物时,对商品和服务全为好评的概率为25,且X 的取值可以是0,1,2,3.其中()()()31233327235423360;1;2= 5125551255512P X P X C P X C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫======== ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭;()333238355125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,X 的分布列为:――――――――10分②由于23,5XB ⎛⎫⎪⎝⎭,则()()2622183,31555525E X D X ⎛⎫=⨯==⨯⨯-= ⎪⎝⎭――――12分20.(1)函数定义域为()1,-+∞,――――――1分 且()1111x f x x x -=-='∴++当()1,0x ∈-时, ()0f x '>即()f x 在区间()1,0-上是增函数,―――――3分当()0,+∞时, ()0f x '<,即()f x 在区间()0,+∞上是减函数―――――5分()f x ∴的单调递增区间为()1,0-,单调递减区间为()0,+∞.―――――6分(2)由()311f x x k x ⎛⎫-+>-⎪⎝⎭变形,得()3ln 11x x x k x ⎛⎫--+>- ⎪⎝⎭―――――7分 整理得ln 30x x x kx k +-+>,―――――8分令()()ln 3,ln 2g x x x x kx k g x x k =+-+=+'∴-,1ln 0x x >∴>若2k ≤时, ()0g x '>恒成立,即()g x 在区间()1,+∞上递增, 由()1110,120222g k k k >∴+>∴>-∴-<≤ 又k Z k ∈∴的最大值为2.―――――11分若2k >由2ln 20k x k x e -+->∴>,由2ln 201k x k x e -+-<∴<<,即()g x 在()21,k e -上单调递减,在区间()2,k e -+∞上单调递增,所以()g x 在区间()1,+∞上有最小值,为()223k k g e k e --=-于是转化为230(2)k k e k -->>恒成立,求k 的最大值 令()()2233x x h x x eh x e --=-∴=-',当2ln3x >+时, ()()0,h x h x '<单调递减 当22ln3x <<+时, ()()0,h x h x '>单调递增.()h x ∴在2ln3x =+处取得最大值.1ln3232ln34<<∴<+<,()()1130,2ln333ln30h h e=->+=+> ()()234120,5150h e h e =->=-<, 4,k k ∴≤∴的最大值为4.―――――14分21.(1)由错误!未找到引用源。
