浙江省磐安县第二中学高一数学 集合 单元测试
浙江省磐安县第二中学高一数学 测试题

浙江省磐安县第二中学高一数学 测试题2.方程x 2-px +6=0的解集为M ,方程x 2+6x -q =0的解集为N ,且M ∩N ={2},那么p +q 等于A.21B.8C.6D.73. 下列四个函数中,在(0,+∞)上为增函数的是A.f (x )=3-xB.f (x )=x 2-3xC.f (x )=-错误!未找到引用源。
D.f (x )=-| x |4.函数f (x )=x 2+2(a -1)x +2在区间(-∞,4]上递减,则a 的取值范围是A.[-3,+∞]B.(-∞,-3)C.(-∞,5]D.[3,+∞)5. 下列四个函数中,与y =x 表示同一函数的是A.y =(错误!未找到引用源。
)2B.y =错误!未找到引用源。
C.y =错误!未找到引用源。
D.y =错误!未找到引用源。
6. 函数y =错误!未找到引用源。
+1(x ≥1)的反函数是A.y =x 2-2x +2(x <1)B.y =x 2-2x +2(x ≥1)C.y =x 2-2x (x <1)D.y =x 2-2x (x ≥1)7. 已知函数f (x )=错误!未找到引用源。
的定义域是一切实数,则m 的取值范围是A.0<m ≤4B.0≤m ≤1C.m ≥4D.0≤m ≤48.某商场对顾客实行购物优惠活动,规定一次购物付款总额:(1)如果不超过200元,则不给予优惠;(2)如果超过200元但不超过500元,则按标价给予9折优惠;(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折 优惠.某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款是A.413.7元B.513.7元C.546.6元D.548.7元9. 二次函数y =ax 2+bx 与指数函数y =(错误!未找到引用源。
)x 的图象只可能是错误!未找到引用源。
10. 已知函数f (n )=错误!未找到引用源。
高一集合测试试题及答案

高一集合测试试题及答案一、选择题(每题4分,共40分)1. 集合A={1,2,3},集合B={2,3,4},则A∩B的元素个数是()。
A. 1B. 2C. 3D. 42. 集合A={1,2,3,4},集合B={4,5,6,7},则A∪B的元素个数是()。
A. 6B. 7C. 8D. 93. 集合A={x|x^2-1=0},则A的元素是()。
A. {-1, 0}B. {-1, 1}C. {0, 1}D. {-1, 0, 1}4. 集合A={1,2,3},集合B={x|x∈A},则B是()。
A. 空集B. 单元素集合C. 有限集合D. 无限集合5. 集合A={x|x是奇数},集合B={x|x是偶数},则A∩B是()。
A. {0}B. {1}C. 空集D. {2, 4, 6, ...}6. 集合A={x|x^2-4=0},则A的元素是()。
A. {-2, 2}B. {-2, 0, 2}C. {-2, 2, 4}D. {-2, 2, -4}7. 集合A={x|x^2-9=0},则A的元素是()。
A. {-3, 3}B. {-3, 0, 3}C. {-3, 3, 9}D. {-3, 0, 9}8. 集合A={1,2,3},集合B={x|x∈A且x是偶数},则B是()。
A. {1, 3}B. {2}C. {1, 2, 3}D. 空集9. 集合A={x|x是自然数},集合B={x|x是正整数},则A∪B是()。
A. AB. BC. 空集D. {0, 1, 2, 3, ...}10. 集合A={x|x^2-4x+4=0},则A的元素是()。
A. {-2, 2}B. {-2, 0, 2}C. {-2, 2, 4}D. {2}二、填空题(每题4分,共20分)1. 集合A={1,2,3},集合B={2,3,4},则A∩B=______。
2. 集合A={x|x^2-1=0},则A=______。
3. 集合A={x|x^2-4=0},则A=______。
浙江省磐安县第二中学高一数学 基础题

1. 用描述法表示下列集合:(1) 二次函数42+-=x y 的值域(2) 反比例函数x y 1=的定义域(3) 不等式x x 2325+≥-的解集2. 已知集合{},52≤≤-=x x A {}102<<=x x B ,求B A B A ,,B C A C R R ,.3. 求下列函数的定义域:(1)23)(-=x x x f (2)x x f =)((3)34)(--=x x x g (4)x x g 17.0)(=(5)y=x 2log (6)y=x )21(1-4在同一直角坐标系中画出函数y=x 2,y=x )21(的图象,并观察两个函数的图象关于哪个坐标轴对称。
5.画出函数y=x 2log 与函数x y 21log =的图象,并观察这两个函数的图象关于哪个坐标轴对称。
6.已知1)1(2+-=+x x x f ,求)5(),2(f f 的值高一数学基础题(2)1. 计算:(1))3()6)(2(31212132a b a b a -÷ (其中a,b 均大于0)(2)322a a a ⋅ (a>0)(3)2lg 5lg ln ++e(4))15log 5(log )21log 2(log 3355-++(5)2log 5log 4log 3log 5432⋅⋅⋅(6)81log 2log 2334+2. 画出下列函数的图象,并根据图象求下列函数的值域:(1)43+=x y (2)13+=x y(3)y=862+-x x(4)32)(2-+-=x x x f (5)13-=x y (6)2log 3+=x y3. 若14log 3=x ,求xx -+44的值。
4. 若1052==b a ,求b a 11+的值5. 设xx a y a y 22131,-+==,其中1,0≠>a a 且,确定x 为何值时,有:(1)21y y = (2)21y y >6. 已知1)21()(,43)(2-=-+=xx g x x x f ,求这两个函数的零点7.用定义证明函数1)(+-=x x f 在R 上是减函数。
高一数学集合单元测试卷

高一数学集合单元测试卷一、选择题(每题5分,共40分)1. 下列对象能构成集合的是()A. 很大的数。
B. 聪明的人。
C. 小于10的正整数。
D. 某班跑得快的同学。
2. 设集合A = {xx^2 - 3x + 2 = 0},则集合A中的元素为()A. 1,2.B. -1,-2C. 1,-2D. -1,2.3. 已知集合A={1,2,3},B = {2,3,4},则A∩ B=()A. {1,2,3,4}B. {2,3}C. {1,4}D. varnothing4. 若集合A={xx > 1},B={xx < 3},则A∪ B=()A. {x1 < x < 3}B. {xx > 1}C. {xx < 3}D. R5. 设全集U={1,2,3,4,5},集合A = {1,2,3},则∁_U A=()A. {4,5}B. {1,2,3}C. {2,3,4,5}D. {1,4,5}6. 已知集合A={x - 1,B={x0,则A∩ B=()A. {x1 < x < 0}B. {x0 < x < 2}C. {x2 < x < 3}D. {x1 < x < 3}7. 若集合M={xx = 3k - 2,k∈ Z},N={xx = 3l+1,l∈ Z},则M与N的关系是()A. M = NB. M⊂neqq NC. N⊂neqq MD. M∩ N=varnothing8. 集合A={xx^2 - 5x + 6 = 0},集合B={xax - 1 = 0},若B⊆ A,则a的值为()A. (1)/(2)或(1)/(3)B. (1)/(2)或(1)/(3)或0C. (1)/(3)D. (1)/(2)二、填空题(每题5分,共20分)1. 集合{1,2,3}的所有子集个数为______。
2. 已知集合A = {xx < - 1或x > 3},B={xx < a},若A∪ B = A,则a的取值范围是______。
高中集合单元测试题及答案

高中集合单元测试题及答案一、选择题(每题3分,共30分)1. 集合A={1,2,3},集合B={2,3,4},那么A∩B等于:A. {1}B. {2,3}C. {4}D. {1,2,3,4}2. 对于任意集合A和B,下列哪个表达式是正确的:A. A∪B = B∪AB. A∩B = B∩AC. A∪B = A∩BD. 所有选项都正确3. 如果集合C={x|x>5},那么C的补集C'等于:A. {x|x≤5}B. {x|x<5}C. {x|x≥5}D. {x|x=5}4. 集合{1,2,3}与{2,3,4}的并集是:A. {1,2,3}B. {2,3}C. {1,2,3,4}D. {4}5. 集合{1,2,3}与{2,3,4}的差集是:A. {1}C. {4}D. {1,4}6. 集合{1,2,3}的幂集包含多少个元素?A. 2^3B. 3^2C. 3^3D. 4^37. 集合{1,2,3}的子集个数是:A. 3B. 4C. 7D. 88. 集合{1,2,3}的真子集个数是:A. 3B. 4C. 6D. 79. 如果A={1,2},B={2,3},那么A∪B∩C={3},C可能是什么?A. {1,3}B. {2,3}C. {3}D. 所有选项都正确10. 集合{1,2,3}的对称差集与{2,3,4}是:A. {1,4}B. {1,2,3,4}D. {1,4,5}二、填空题(每题2分,共10分)11. 集合A={x|x是小于10的正整数},A的元素有________个。
12. 如果A={1,2,3},B={3,4,5},那么A∩B={________}。
13. 集合A={x|x是偶数},B={x|x是奇数},则A∪B=________。
14. 如果A={1,2,3},B={2,3,4},那么A⊆B是________(填“真”或“假”)。
15. 集合{1,2,3}的幂集的元素个数是________。
浙江省磐安县第二中学高一数学 基础练习题(1)

浙江省磐安县第二中学高一数学 基础练习题(1)1. 将下列集合用区间来表示:(1){}1}≥x x (2)⎭⎬⎫⎩⎨⎧〉+-021|x x x (3){}83|≤≤x x3.若集合A={}0)1(|2=+-+b x a x x 中仅有一个元素a,求a+b 的值4.求下列函数的定义域。
(1)1)(-=x x f (2)211)(+-+=x x x g (3)xxy 244--= (4))5(log )()2(x x f x -=-5.求下列函数的值域:(1))50(642≤≤+-=x x x y (2)1391++=+x xy(3))2(log 55.0≥+=x x y (4)y=x 1)21(6.求下列函数的单调区间:(1)|1|+=x y (2)xx y 22)31(-= (3))4(log 22x x y +=7.判断下列函数的奇偶性:(1)x x x f +=3)( (2)⎪⎩⎪⎨⎧<-≥-=)0(21)0(12)(x x x f xx(3)xxx f -+=55lg )( (4)1212)(-+=x x x f8.已知函数f(x)是R 上的偶函数,且当)0,(-∞∈x 时,)1()(3x x x f +=,求当),0(+∞∈x 时,f(x)的解析式。
9.设)(x f 在R上是偶函数,在区间(-0,∞)上递增,且有)123()12(22+-<++a a f a a f ,求a 的取值范围10.若函数1)(2--=x ax x f 只有一个零点,求实数a 的取值范围。
11.若函数b ax x x f ++=2)(有两个零点-2,3,求a,b 的值。
12.函数53)(3+--=x x x f 的零点大致所在的区间为( )A.(1,2)B.(-2,-1)C.(0,1)D.(-1,0)13.将进货单价为8元的商品按10元一个销售,每天可卖出100个,若每涨价1元,则日销售量减少10元,为获得最大利润,则此商品当日销售应定为每个多少钱?14.画出1×2×3×4×5×6的程序框图。
浙江省金华市磐安县第二中学2020-2021学年高一上学期10月月考数学试题

浙江省金华市磐安县第二中学2020-2021学年高一上学期10月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.设全集为R ,集合{}02A x x =<<,{}1B x x =≥,则()R A B =( ) A .{}01x x <≤ B .{}01x x << C .{}12x x ≤< D .{}02x x << 2.下列集合中表示同一集合的是( )A .{(3,2)}M =,{(2,3)}N =B .{2,3}M =,{3,2}N =C .{(,)1}M x y x y =+=∣,{1}N y x y =+=∣ D .{2,3}M =,{(2,3)}N =3.设集合{}20A x x x =-=,则集合A 的真子集的个数为( )A .1B .2C .3D .4 4.设R x ∈,则“12x >”是“2210x x +->”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 5.设x y ,为正数,则14(x y )()x y ++的最小值是( ) A .8 B .9 C .12 D .156.已知集合{}|11A x x =->,{}1023B =-,,,,则()U A B =( ) A .{}0,1,2 B .{}0,2 C .{}1,3-D .{}1,0,1,2,3- 7.设A 、B 为两个互不相同的集合.命题:P x A B ∈⋂;命题:q x A ∈或x B ∈.则p 是q 的( )条件.A .充分且必要B .充分非必要C .必要非充分D .非充分且非必要8.不等式x 2﹣2x ﹣3<0的解集为( )A .{x |﹣1<x <3}B .∅C .RD .{x |﹣3<x <1}9.命题“x R ∀∈,210x x -+≥”的否定是( )A .x R ∀∈,210x x -+<B .x R ∀∈,210x x -+≤C .0x R ∃∈,20010x x -+<D .0x R ∃∈,20010x x -+≤10.已知234,a b +=则48a b +的最小值为( )A .2B .4C .8D .16二、多选题11.已知集合{0,1,2}A =,{,2}B a =,若B A ⊆,则a =( )A .0B .1C .2D .0或1或2 12.已知0,0,1a b a b >>+=,则下列结论中一定成立的是( )A .22a b +的最小值是12B .1ab ab+的最小值是2CD .49a b+的最小值是25三、双空题 13.设集合{}1,0,2A =-,则集合A 的子集有__________个,若集合{}|,2B x x A x A =∈-∉且则B =_________.14.已知集合2|Ax x x ,集合{|124}x B x =<<,则集合A 的子集个数为________;A B =__________15.已知A ⊆B ,则“x∈A”是“x∈B”的________条件,“x∈B”是“x∈A”的________条件.(填“充分”或“必要”)16.函数()21f x x x =+-(x >1)的最小值是______;取到最小值时,x =______.四、填空题17.已知集合(){}|40A x x x =->,{}0,1,5B =,则A B =________.18.已知集合{}{}2320,3A x x x B x x a =-+≤=-<.若A B ⊆,则实数a 的取值范围是__________.19.若关于x 的不等式210mx mx +->的解集为∅,则实数m 的取值范围为 .五、解答题20.请解决下列问题:(1)设,,{1,},{1,}a b R P a Q b ∈==--,若P Q =,求-a b 的值;(2)已知集合{|0},{|12}A x x a B x x =<<=<<,若B A ⊆,求实数a 的取值范围. 21.已知命题p :2430x x -+≤,命题q :()222100x x a a -+-<>. (1)当4a =时,p q ∧为真命题,求x 的取值范围;(2)若q ⌝是p ⌝的充分不必要条件,求实数a 的取值范围.22.南康某服装厂拟在2020年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m 万件与年促销费用(04)x x ≤≤万元满足131m x =-+.已知2020年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2020年该产品的利润y 万元表示为年促销费用x 万元的函数;(2)该服装厂2020年的促销费用投入多少万元时,利润最大?23.解关于x 的不等式ax 2-(2a +3)x +6>0(a ∈R ).参考答案1.B【分析】根据补集、交集的定义即可求出.【详解】解:{|02}A x x =<<,{|1}B x x =,{|1}R B x x ∴=<,(){|01}R A B x x ∴=<<.故选:B .【点睛】本题主要考查交集的运算法则,补集的运算法则等知识,意在考查学生的转化能力和计算求解能力.2.B【分析】利用集合的定义和元素的三个性质,对A 、B 、C 、D 四个选项进行一一判断;【详解】A.M 、N 都是点集,()3,2与()2,3是不同的点,则M 、N 是不同的集合,故错误;B.2,3M ,{}3,2N =,根据集合的无序性,集合M ,N 表示同一集合,故正确;C.{}(,)1M x y x y =+=∣,M 集合的元素表示点的集合,{}1N y x y =+=∣,N 表示直线1x y +=的纵坐标,是数集,故不是同一集合,故错误;D.2,3M 集合M 的元素是两个数字2,3,{}(2,3)N =,集合N 的元素是一个点()2,3,故错误;故选:B.【点睛】本题主要考查集合的定义及元素的性质,属于基础题.3.C【分析】可用列举法列出所有真子集即可.【详解】由题可解集合{}0,1A =,则集合A 的真子集有∅、{}0、{}1.故选:C .【点睛】本题考查集合的真子集,可用列举法或公式计算即可,易错点为列举法容易忽略空集,属于基础题.4.A【详解】由题意得,不等式2210x x +->,解得1x <-或12x >, 所以“12x >”是“2210x x +->”的充分而不必要条件, 故选A .考点:充分不必要条件的判定.5.B【分析】将式子整理成符合基本不等式的形式,利用基本不等式求得最小值.【详解】()1444145x y x x y x y y y x y x ⎛⎫++=+++=++ ⎪⎝⎭,x y 为正数 40x y ∴>,0y x>44x y y x ∴+≥=(当且仅当4x y y x =,即2x y =时取等号) ()14549x y x y ⎛⎫∴++≥+= ⎪⎝⎭本题正确选项:B【点睛】本题考查利用基本不等式求解和的最小值问题,属于基础题.6.B【分析】求解集合A ,然后根据补集的运算求解U A ,再根据集合的交集的运算,即可求解. 【详解】 由题意{}|11{|0A x x x x =->=<或2}x >,所以{|02}U A x x =≤≤, 所以(){}0,2U A B ⋂=.故选:B【点睛】本题考查了绝对值不等式的求解,以及集合的混合运算问题,属于基础题.7.B【详解】命题:P x A B ∈⋂成立,但是命题:q x A ∈或x B ∈一定成立,所以p 是q 的充分条件; 命题:q x A ∈或x B ∈成立,但是命题:P x A B ∈⋂不一定成立,所以p 是q 的非必要条件. 故答案为B8.A【解析】分析:利用二次不等式的解法,求解即可.详解:x 2﹣2x ﹣3=0,可得方程的解为:x=﹣1,x=3.不等式x 2﹣2x ﹣3<0的解集为:{x|﹣1<x <3}.故选A .点睛:本题考查一元二次不等式的解法,考查基本求解能力.9.C【分析】根据全称命题的否定:改变量词,否定结论,可得出结论.【详解】命题“x R ∀∈,210x x -+≥”为全称命题,其否定为“0x R ∃∈,20010x x -+<”.故选:C.【点睛】本题考查全称命题否定的改写,要注意量词和结论的变化,属于基础题.10.C【解析】2348228.a b a b +=+≥===故选C11.AB【分析】由B A ⊆,则{0,2}B =或{1,2}B =,再根据集合相等求出参数的值;【详解】解:由B A ⊆,可知{0,2}B =或{1,2}B =,所以0a =或1.故选:AB.【点睛】本题考查根据集合的包含关系求参数的值,属于基础题.12.ACD【分析】 由22211()22a b a b +≥+=可判断A ; 由已知得210()24a b ab +<≤=,由22211(1)2a b ab ab ab ab ab+-+==+,可判断B ;由22()2a b ≤+=可判断C ; 由494949()()13b a a b a b a b a b+=++=++,可判断D . 【详解】222110,0,1,(),22a b a b a b a b >>+=∴+≥+=所以A 中结论一定成立, 由已知得210()24a b ab +<≤=,222211(1)11724(1)244a b ab ab ab ab ab +-∴+==+≥-+=,所以B 中的结论是错误的,由22()2a b ≤+=≤,所以C 中的结论是成立的,由已知得494949()()131325b a a b a b a b a b+=++=++≥+=,所以D 中的结论是成立的, 故选:ACD.【点睛】本题考查基本不等式的应用,运用注意基本不等式所需满足的条件,属于基础题. 13.8 {-1}【分析】(1)可以写出集合A 的所有子集,从而得出集合A 子集的个数;(2)根据条件x∈A,且2﹣x ∉A ,即可求出集合B .【详解】A={﹣1,0,2}的子集为:∅,{﹣1},{0},{2},{﹣1,0},{﹣1,2},{0,2},{﹣1,0,2},共8个;∵x∈A,且2﹣x ∉A ;∴B={﹣1}.故答案为(1). 8 (2). {-1}.【点睛】考查列举法和描述法表示集合的概念,子集的定义及求法,找子集时不要漏了空集. 14.4 {}1【分析】求出集合A 、B ,即可求出集合A 的子集个数及A B .【详解】 {}2A x x x =={}0,1=,{}124x B x =<<{}02x x =<<,故集合A 的子集个数为224N ==,A B {}1=.故答案为:4;{}1【点睛】本题考查交集及其运算,考查了子集,属于基础题.15.充分 必要【分析】由充分条件和必要条件的定义可以判断.【详解】因为A ⊆B ,即A 是B 的子集,所以如果有x∈A,即x 是集合A 的元素,那么一定有x∈B,即x 是集合B 的元素,根据充分条件的定义可知,“x∈A”是“x∈B”的充分条件,同时x∈B”是“x∈A”的必要条件.【点睛】本题考查充分条件和必要条件的定义,关键是理解定义,属于基础题.16.1 12 【分析】由题知10x ->,又由()2111f x x x =-++-,结合基本不等式即可求解. 【详解】∵1x >,∴10x ->,由基本不等式可得()121111f x x x ≥==-++-,当且仅当211x x -=-即1x =1.故答案为:1;1【点睛】本题主要考查了利用基本不等式求解最值,考查学生的运算求解能力.17.{5}【分析】先求解集合A ,再根据交集的定义求解即可.【详解】(,0)(4,)A =-∞⋃+∞,所以{5}A B =.故答案为:{5}【点睛】本题考查了集合的交集运算,属于基础题.18.()1,-+∞【分析】解一元二次不等式即可求出集合A ,进而求出{}3B x x a =<+,再根据A B ⊆,即可列出不等式,从而求出a 的取值范围.【详解】 解:由题可知,{}{}232012A x x x x x =-+≤=≤≤, {}{}33B x x a x x a =-<=<+,由于A B ⊆,则32a +>,解得:1a >-,所以实数a 的取值范围为()1,-+∞.故答案为:()1,-+∞.【点睛】本题考查根据集合间的包含关系求参数的取值范围,涉及一元二次不等式的解法,属于基础题.19.[4,0]-【解析】试题分析:当0m =时,不等式变形为10->,解集为∅,符合题意;当0m ≠时,依题意可得20{4040m m m m <⇒-≤<∆=+≤, 综上可得40m -≤≤.考点:一元二次不等式.【易错点睛】本题主要考查不等式中的一元二次不等式问题,难度一般.有很多同学做此题时直接考虑为一元二次不等式,其二次函数应开口向下且与x 轴至多有一个交点,而忽略二次项系数为0时的情况导致出现错误.当二次项系数含参数时一定要讨论是否为0,否则极易出错.20.(1)0a b -=(2)2a ≥【分析】(1)直接根据集合相等得到答案.(2)根据集合的包含关系得到2a ≥得到答案.【详解】(1)由于P Q =,所以1a =-,且1b -=,0a b ∴-=.(2){|0},{|12}A x x a B x x =<<=<<,且B A ⊆,2a ∴≥如图所示.【点睛】本题考查了根据集合相等和集合的包含关系求参数,意在考查学生的理解能力.21.(1)13x ≤≤(2)[)2,+∞【分析】(1)解一元二次不等式分别可得集合A 、B ,代入4a =可确定集合B ,由p q ∧为真命题可知两个命题均为真命题,即可解不等式组求得x 的取值范围;(2)根据逆否命题的性质由题意可得p 是q 的充分不必要条件,即可由集合的关系确定a 的取值范围.【详解】命题p :2430x x -+≤,解得13x ≤≤,令[]1,3A =.命题q :()222100x x a a -+-<>),解得11a x a -≤≤+,令[]1,1B a a =-+. (1)当4a =时,[]3,5B =-,因为p q ∧为真命题,所以p 真q 真,则13,35,x x ≤≤⎧⎨-≤≤⎩所以13x ≤≤.(2)因为q ⌝是p ⌝的充分不必要条件,即p 是q 的充分不必要条件,所以集合A 是集合B 的真子集,所以11,13,a a -≤⎧⎨+≥⎩解得2a ≥. 经检验2a =满足题意,所以a 的取值范围为[)2,+∞.【点睛】本题考查了一元二次不等式解法,由复合命题真假确定参数的取值范围,逆否命题的性质应用,由充分不必要关系确定参数的取值范围,属于基础题.22.(1)1656([0,4])1y x x x =--∈+;(2)3万元. 【分析】(1)根据题意,结合已知条件,列出函数关系即可;(2)对函数进行配凑,使之可用基本不等式,即可求得利润的最大值.【详解】(1)由题意知:每件产品的销售价格为8162m m+⨯, 8162(816)816m y m m x m x m+∴=⋅⨯-++=+- 181631x x ⎛⎫=+-- ⎪+⎝⎭ 16561x x =--+([0,4])x ∈;(2)由16165657(1)574911y x x x x ⎡⎤=--=-++≤-=⎢⎥++⎣⎦, 当且仅当1611x x =++,即3x =时取等号. 故该服装厂2020年的促销费用投入3万元时,利润最大.【点睛】本题考查分式函数模型的应用,涉及用基本不等式求最值,属综合基础题.23.详见解析【分析】首先讨论不等式的类型:(1)a =0时,是一次不等式;(2)a ≠0时,是一元二次不等式,然后讨论a 的符号,再讨论两根3a与2的大小.【详解】原不等式可化为:(ax﹣3)(x﹣2)>0;当a=0时,化为:x<2;当a>0时,化为:(x3a-)(x﹣2)>0,①当3a>2,即0<a32<时,解为:x3a>或x<2;②当3a=2,即a32=时,解为:x≠2;③当3a<2,即a32>时,解为:x>2或x3a<,当a<0时,化为:(x3a-)(x﹣2)<0,解为:3a<x<2.综上所述:当a<0时,原不等式的解集为:(3a,2);当a=0时,原不等式的解集为:(﹣∞,2);当0<a32<时,原不等式的解集为:(﹣∞,2)∪(3a,+∞);当a32=时,原不等式的解集为:(﹣∞,2)∪(2,+∞);当a32>时,原不等式的解集为:(﹣∞,3a)∪(2,+∞)【点睛】(1)解一元二次不等式时,当二次项系数为负时要先化为正,再根据判别式符号判断对应方程根的情况,然后结合相应二次函数的图象写出不等式的解集.(2)解含参数的一元二次不等式,要把握好分类讨论的层次,一般按下面次序进行讨论:首先根据二次项系数的符号进行分类,其次根据根是否存在,即判别式的符号进行分类,最后当根存在时,再根据根的大小进行分类.。
浙江省磐安县第二中学高一数学4月月考试题

2017—2018学年高一年级数学4月考卷一、单选题(本大题共10小题,每题4分,共40分。
)1.已知集合()2{|lg 43}A x y x x ==--,集合{|21}x B x =<,则A B ⋂= ( )A. {|0}x x <B. {|40}x x -<<C. {|41}x x -<<D. {|1}x x <2.在等比数列{}n a 中,5145a a =,则891011a a a a = ( )A .10B .25C .50D .753.已知向量()1,2a =, ()1,0b =, ()3,4c =,若λ为实数, ()//a b c λ+,则λ=( ) A. 2 B. 1 C. 12 D. 144.设S n 是等差数列{a n }的前n 项和,已知a 2=3,a 6=15,则S 7等于( ) A. 13 B. 50 C. 49 D. 635.函数的零点所在的区间是( ). A. B. C. D.6.已知a ,b ,c 是△ABC 三边之长,若满足等式(a+b ﹣c )( a+b+c )=ab ,则∠C 的大小为( )A .60° B.90° C.120° D.150°7.设()f x 是定义在R 上的奇函数,当0x ≤时, ()232f x x x =-,则()1f = ( ) A. 5 B. 1 C. -1 D. -58.已知数列{}n a 是等差数列,若91130a a +<,10110a a ⋅<,且数列{}n a 的前n 项和n S 有最大值,那么n S 取得最小正值时n 等于A .20B .17C .19D .219.△ABC 中已知下列条件:①b =3,c =4,B =30°;②a =5,b =8,A =30°;③c =6, b =3,B =60°;④c =9,b =12,C =60°.其中满足上述条件的三角形有两解的是 ( )A. ①②B. ①④C. ①②③D. ③④ 10.数列{},{}n n a b 满足1,(1)(2)n n n a b a n n ==++,则{}n b 的前10项之和A .14B .712C .34D .512二、填空题(本大题共7小题,多空题每题6分,单空题每空4分,共36分。
浙江省磐安县第二中学高一数学 集合 单元测试

3.下列八个关系式①{0}=φ ②φ=0 ③φ⊆{φ} ④φ∈{φ} ⑤{0}⊇φ ⑥0∉φ ⑦φ≠{0} ⑧φ≠{φ}其中正确的个数( )(A )4 (B )5 (C )6 (D )7 4.下列语句:(1)0与{0}表示同一个集合;(2)由1,2,3组成的集合可表示为{1,2,3}或{3,2,1};(3)方程(1)(1)(2)0x x x ---=的所有解的集合可表示为{1,1,2}; (4)集合{54<<x x }是有限集,正确的是( )(A )只有(1)和(4) (B )只有(2)和(3) (C )只有(2) (D )以上语句都不对5.设集合A={2,3},B={2,3,4},C={3,4,5}则A B C =() ( )A .{2,3,4}B .{2,3,5}C .{3,4,5}D .{2,3,4,5}6.设A 、B 是全集U 的两个子集,且A ⊆B ,则下列式子成立的是( ) (A )C U A ⊆C U B (B )C U A C U B=U (C )AC U B=φ (D )C U AB=φ7.设,,若,则实数的取值范围是( )(A )(B )(C )(D )8.函数21)(--=x x x f 的定义域为( ) A .[1,2)∪(2,+∞) B .(1,+∞) C .[1,2) D .[1,+∞) 9.函数f (x )= 2(1)xx x ⎧⎨+⎩,0,0x x ≥< ,则(2)f -=( ) A. 1 B .2 C. 3 D.410.集合A={x Z k k x ∈=,2} B={Z k k x x ∈+=,12} C={Z k k x x ∈+=,14}又,,B b A a ∈∈则有( )(A )(a+b )∈ A (B) (a+b) ∈B (C)(a+b) ∈ C (D) (a+b) ∈ A 、B 、C 任一个 11.图中阴影部分表示的集合是( )A. )(B C A UB. B A C U )(C. )(B A C UD. ()U C A B12.若{1,2,3,a}∪{3,2a }={1,2,3,a },则a 的取值集合为A .{0,±1}B .{0,-1,-2}C .{-1,- 2}D .{0,-1,-2,2} 13.若M={Z n x n x ∈=,2},N={∈+=n x n x ,21Z},则M ⋂N 等于( ) (A )φ (B ){φ} (C ){0} (D )Z 14.下列各式中,正确的是( ) (A )2}2{≤⊆x x (B )∅{12<>x x x 且}(C ){Z k k x x ∈±=,14}},12{Z k k x x ∈+=≠ (D ){Z k k x x ∈+=,13}={Z k k x x ∈-=,23} 15.设U={1,2,3,4,5},A ,B 为U 的子集,若AB={2},(C U A )B={4},(C U A )(C U B )={1,5},则下列结论正确的是( ) (A )3B A ∉∉3, (B )3B A ∈∉3, (C )3B A ∉∈3, (D )3B A ∈∈3, 16.下列各组函数中,表示同一函数的是( )A .0,xy x y x== B .1,112-=+⨯-=x y x x yC .2,y x y x ==D .2)(|,|x y x y ==17.设M ={x |-2≤x ≤2},N ={y |0≤y ≤2},函数f (x )的定义域为M ,值域为N ,ABU则f (x )的图象可以是( )18.若U 、φ分别表示全集和空集,且(C U A )B ⊆A ,则集合A 与B 必须满足( ) (A)φ (B)A=φ (C)B=φ (D)A=U 且A ≠B二、填空题(17×2=34分)1. 在直角坐标系中,坐标轴上的点的集合可表示为2. 若A={1,4,x},B={1,x 2}且A B=B ,则x=3集合{1,2,3}的子集有 个,写出它的非空真子集4.设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(C U A )(C U B )= 5方程2560x x -+=的解集可表示为方程组的解集可表示为⎩⎨⎧=-=+0231332y x y x6 若{}21,,0,,b a a a b a ⎧⎫=+⎨⎬⎩⎭,则20112012a b +的值为7.设集合A={23≤≤-x x },B={x 1212+≤≤-k x k },且A ⊇B ,则实数k 的取值范围是 。
浙江省金华市磐安县第二中学高中数学1.1集合的运算检测题1无答案新人教A版必修1

集合的基本运算(一)基础训练 1.设集合A={1,2},B={1,2,3},C={2,3,4}则=C B A )(( )( A ) {1,2,3} ( B ) {1,2,4} ( C ) }4,3,2{ ( D ) }4,3,2,1{ 2.满足条件M{1}={1,2,3}的集合M 的个数( )A.1 B.2 C.3 D.4 3.已知全集U R =,则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩(Venn )图是( )4.设A={x|x>-2},B={x|x<0},则A ∩ B.=A B=5.设A={x ︱-2<x<-1},B={x ︱-3<x<3}, A B= A B=6.设A={x ︱3x-1>0,x ∈R},B={x ︱5-2x>0, x ∈R },则A B=________________.7.(1)设A={奇数}、B={偶数},则A ∩Z= ,B ∩Z= ,A ∩B=(2)设A={奇数}、B={偶数},则A ∪Z= ,B ∪Z= ,A ∪B=___;__________,__________}250|{}31|{}24|{)3(==≥≤=≤≤-=≤≤-=C B A C B A x x x C x x B x x A 那么,或,,集合8. 若集合A={x -2<x <1},B={x 0<x<2},求集合A ∩B ,A B ⋃能力提升:1满足A ∪{1,2}={1,2,3,4}的集合A 的个数是( ) A. 7 B. 6 C. 5 D. 4 2.设集合A={x ︱x ≤1},B={x ︱x>p },要使∅=B A ,则p 应满足的条件是( ) A .P>1 B.P ≥1 C.P<1 D.P ≤1 3.已知集合M ⊆{4,7,8},且M 中至多有一个偶数,则这样的集合共有( ); A 3个 B 4个 C 6个 D 5个 4.设集合}21|{<≤-=x x A ,}|{a x x B <=,若AB ≠∅,则a 的取值范围是( ) (A )2a < (B )2a >- (C )1a >- (D ) a ≤-1<25.已知集合}06{2=-+=x x x M ,}01{=-=mx x N ,若M N ⊆,则实数m 的取值构成的集合为_______________.__________}21|{}2|{.6=∈+=∈=B A Z m m B Z n n A ,则,集合7.设P 、Q 为两个非空实数集合,定义集合},|{Q b P a b a Q P ∈∈+=+,若},5,2,0{=P }6,2,1{=Q ,则P +Q 中元素的个数是_______________.8.已知M={1},N={1,2},设A={(x ,y )|x ∈M ,y ∈N},B={(x ,y )|x ∈N ,y ∈M},则A ∩B=______________.A ∪B=______________.9.A={2,3,a 2+4a+2},B={0,7,a 2+4a-2,2-a},且A B ={3,7},求B10.A={x|a ≤x ≤a+3},B={x|x <-1或x >5} , 分别求出满足下列条件的a 的取值范围 :(1) A ∩B=∅ (2) A ∩B=A11.已知方程20x bx c ++=有两个不等的实根1x ,2x ,设C={1x ,2x },A={1,3,5,7,9},B={1,4,7,10},若A C=∅, CB=C,试求b 、c 的值。
磐安县第二中学2018-2019学年高一数学10月月考试题

浙江省磐安县第二中学2018—2019学年高一数学10月月考试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟。
学校:___________姓名:___________班级:___________考号:___________题号一二三总分得分分卷I一、选择题(共10小题,每小题5.0分,共50分)1。
有以下四个集合:(1){x|x2-2x+1=0};(2){-1,2};(3){(-1,2)};(4){边长为3,4的三角形}.其中为单元素集合的是( )A.(3)(4)B.(1)(3)C.(1)(3)(4)D.(2)(4)2。
“booknote”中的字母构成一个集合,该集合的元素个数是( )A.5B.6C.7D.83.已知A={x|<-1},B={x|x2-4x-m≥0},若A B,则实数m 的取值范围是()A.m≥0B.m≤-3C.-3≤m≤0D.m≤-3或m≥04。
下列各式中是函数的个数为()①y=1;②y=x2;③y=1-x;④y=+.A.4B.3C.2D.15。
已知函数f(x)的定义域为[-3,4],在同一坐标系下,函数f(x)的图象与直线x=3的交点个数是()A.0B.1C.2D.0或16.函数y=的定义域为()A.(-∞,1)B.(-∞,0)∪(0,1]C.(-∞,0)∪(0,1)D.[1,+∞)7.已知函数y=f(x)的定义域为{x|a≤x≤b},则函数y=f(x+a)的定义域为( )A.{x|a≤x≤b}B.{x|2a≤x≤a+b}C.{x|0≤x≤b-a}D.{x|0≤x≤a+b}8。
函数y=的值域为( )A.∪B.(-∞,2)∪(2,+∞)C.RD.∪9。
已知f(x-1)=x2+4x-5,则f(x)等于()A.x2+6xB.x2+8x+7C.x2+2x-3D.x2+6x-1010。
已知f(x)=则不等式x+(x+2)·f(x+2)≤5的解集是()A.[-2,1]B.(-∞,-2]C.D.分卷II二、填空题(共4小题,每小题5。
浙江省磐安县第二中学高一数学同步训练 立体几何
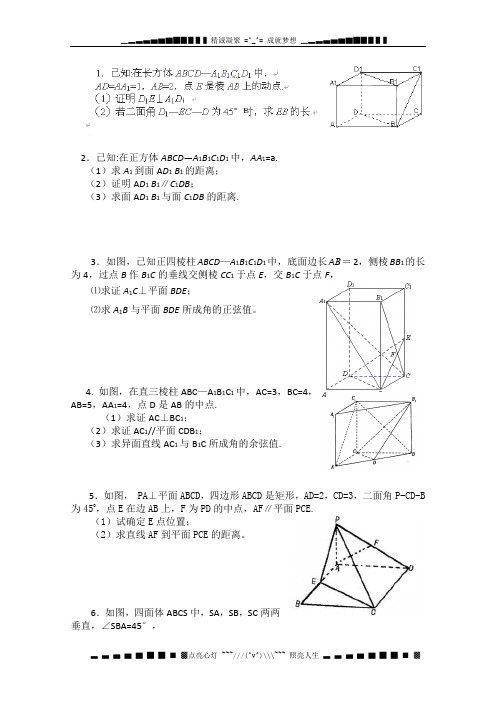
2.已知:在正方体ABCD—A1B1C1D1中,AA1=a.(1)求A1到面A D1 B1的距离;(2)证明A D1 B1∥C1DB;(3)求面A D1 B1与面C1DB的距离.3.如图,已知正四棱柱ABCD—A1B1C1D1中,底面边长A B=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F,⑴求证A1C⊥平面BDE;⑵求A1B与平面BDE所成角的正弦值。
4. 如图,在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.(1)求证AC⊥BC1;(2)求证AC1//平面CDB1;(3)求异面直线AC1与B1C所成角的余弦值.5.如图, PA⊥平面ABCD,四边形ABCD是矩形,AD=2,CD=3,二面角P-CD-B 为450,点E在边AB上,F为PD的中点,AF∥平面PCE.(1)试确定E点位置;(2)求直线AF到平面PCE的距离。
6.如图,四面体ABCS中,SA,SB,SC两两垂直,∠SBA=45°,ABCHSM∠SBC=60°,M 为AB 的中点. (1)求证CSM ⊥ABC ;(2)求SC 与平面ABC 所成角的正弦值。
7.如图,在底面是菱形的四棱锥P —ABC D中,∠ABC=600,PA=AC=a , PB=PD=a 2,点E 是PD 的中点.(1)证明PA ⊥平面ABCD ,PB ∥平面EAC ;(2)求以AC 为棱,EAC 与DAC 为面的二面角θ8.如图,在底面是直角梯形的四棱锥P ABCD -中,AD ∥BC ,∠ABC =90°, 且∠ADC =arcsin55,又PA ⊥平面ABCD ,AD =3AB =3PA =3。
D9. 如图,直三棱柱ABC-A 1B 1C 1中,AB ⊥AC,D 、E 分别为AA 1、B 1C 的中点,DE ⊥平面BCC 1(Ⅰ)证明:AB=AC(Ⅱ)设二面角A-BD-C 为60°,求B 1C 与平面BCD 所成的角的大小A CBAB1C1DE。
浙江省磐安县第二中学2020-2021学年高一10月竞赛数学试卷 Word版含答案

2019-2020学年磐安二中高一数学10月月考卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第I 卷(选择题)一、单选题(本大题共12小题,每小题5分,共60分)1.设全集为R ,集合{}02A x x =<<,{}1B x x =≥,则()R A B = A .{}01x x <≤B .{}01x x <<C .{}12x x ≤<D .{}02x x << 【答案】B【解析】 分析:由题意首先求得R C B ,然后进行交集运算即可求得最终结果.详解:由题意可得:{}|1R C B x x =<,结合交集的定义可得:(){}01R A C B x ⋂=<<.本题选择B 选项.点睛:本题主要考查交集的运算法则,补集的运算法则等知识,意在考查学生的转化能力和计算求解能力.2.下列集合中表示同一集合的是( )A .{(3,2)}M =,{(2,3)}N =B .{2,3}M =,{3,2}N =C .{(,)1}M x y x y =+=∣,{1}N y x y =+=∣ D .{2,3}M =,{(2,3)}N =【答案】B【解析】【分析】利用集合的定义和元素的三个性质,对A 、B 、C 、D 四个选项进行一一判断;【详解】A.M 、N 都是点集,()3,2与()2,3是不同的点,则M 、N 是不同的集合,故错误;B.2,3M ,{}3,2N =,根据集合的无序性,集合M ,N 表示同一集合,故正确;C.{}(,)1M x y x y =+=∣,M 集合的元素表示点的集合,{}1N y x y =+=∣,N 表示直线1x y +=的纵坐标,是数集,故不是同一集合,故错误;D.2,3M集合M 的元素是两个数字2,3,{}(2,3)N =,集合N 的元素是一个点()2,3,故错误;故选:B.【点睛】本题主要考查集合的定义及元素的性质,属于基础题.3.设集合{}20A x x x =-=,则集合A 的真子集的个数为( )A .1B .2C .3D .4 【答案】C【解析】【分析】可用列举法列出所有真子集即可.【详解】由题可解集合{}0,1A =,则集合A 的真子集有∅、{}0、{}1.故选:C .【点睛】本题考查集合的真子集,可用列举法或公式计算即可,易错点为列举法容易忽略空集,属于基础题. 4.设R x ∈,则“12x >”是“2210x x +->”的( ) A .充分而不必要条件 B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】A【解析】【分析】【详解】由题意得,不等式2210x x +->,解得1x <-或12x >, 所以“12x >”是“2210x x +->”的充分而不必要条件, 故选A .考点:充分不必要条件的判定.5.设,x y 为正数, 则()14x y x y ⎛⎫++ ⎪⎝⎭的最小值为 ( ) A .6B .9C .12D .15 【答案】B【解析】【分析】 整理后可用基本不等式求最小值.【详解】()14455549x y x y x y y x x ⎛⎫++=++≥+=+= ⎪⎝⎭, 当且仅当2y x =时等号成立,故最小值为9,选B.【点睛】本题考查不等式的应用,属于容易题.6.已知集合A ={x||x −1|>1},B ={−1,0,2,3},则(C U A)∩B =( )A .{0,1,2}B .{0,2}C .{−1,3}D .{−1,0,1,2,3}【答案】B【解析】【分析】求解集合A ,然后根据补集的运算求解C U A ,再根据集合的交集的运算,即可求解.【详解】由题意A ={x||x −1|>1}={x|x <0或x >2},所以C U A ={x|0≤x ≤2},所以(C U A)∩B ={0,2},故选B.【点睛】本题主要考查了绝对值不等式的求解,以及集合的混合运算问题,其中解答总正确求解集合A ,准确利用集合的运算是解答的关键,着重考查了推理与计算能力,属于基础题.7.设A 、B 为两个互不相同的集合.命题:P x A B ∈⋂;命题:q x A ∈或x B ∈.则p 是q 的( )条件.A .充分且必要B .充分非必要C .必要非充分D .非充分且非必要【答案】B【解析】【详解】命题:P x A B ∈⋂成立,但是命题:q x A ∈或x B ∈一定成立,所以p 是q 的充分条件; 命题:q x A ∈或x B ∈成立,但是命题:P x A B ∈⋂不一定成立,所以p 是q 的非必要条件. 故答案为B8.不等式x 2﹣2x ﹣3<0的解集为( )A .{x |﹣1<x <3}B .∅C .RD .{x |﹣3<x <1}【答案】A【解析】分析:利用二次不等式的解法,求解即可.详解:x 2﹣2x ﹣3=0,可得方程的解为:x=﹣1,x=3.不等式x 2﹣2x ﹣3<0的解集为:{x|﹣1<x <3}.故选:A .点睛:本题考查一元二次不等式的解法,考查基本求解能力.9.命题“x R ∀∈,210x x -+≥”的否定是( )A .x R ∀∈,210x x -+<B .x R ∀∈,210x x -+≤C .0x R ∃∈,20010x x -+<D .0x R ∃∈,20010x x -+≤【答案】C【解析】【分析】根据全称命题的否定:改变量词,否定结论,可得出结论.【详解】命题“x R ∀∈,210x x -+≥”为全称命题,其否定为“0x R ∃∈,20010x x -+<”.故选:C.【点睛】本题考查全称命题否定的改写,要注意量词和结论的变化,属于基础题.10.已知234,a b +=则48a b +的最小值为( )A .2B .4C .8D .16【答案】C【解析】2348228.a b a b +=+≥===故选C二、多选题11.已知集合{0,1,2}A =,{,2}B a =,若B A ⊆,则a =( )A .0B .1C .2D .0或1或2【答案】AB【解析】【分析】由B A ⊆,则{0,2}B =或{1,2}B =,再根据集合相等求出参数的值;【详解】解:由B A ⊆,可知{0,2}B =或{1,2}B =,所以0a =或1.故选:AB.【点睛】本题考查根据集合的包含关系求参数的值,属于基础题.12.已知0,0,1a b a b >>+=,则下列结论中一定成立的是( ) A .22a b +的最小值是12 B .1ab ab+的最小值是2CD .49a b+的最小值是25 【答案】ACD【解析】【分析】由22211()22a b a b +≥+=可判断A ; 由已知得210()24a b ab +<≤=,由22211(1)2a b ab ab ab ab ab+-+==+,可判断B ;由22()2a b ≤+=可判断C ; 由494949()()13b a a b a b a b a b+=++=++,可判断D . 【详解】222110,0,1,(),22a b a b a b a b >>+=∴+≥+=所以A 中结论一定成立, 由已知得210()24a b ab +<≤=,222211(1)11724(1)244a b ab ab ab ab ab +-∴+==+≥-+=,所以B 中的结论是错误的,由22()2a b ≤+=≤,所以C 中的结论是成立的,由已知得494949()()131325b a a b a b a b a b+=++=++≥+=,所以D 中的结论是成立的, 故选:ACD.【点睛】本题考查基本不等式的应用,运用注意基本不等式所需满足的条件,属于基础题.第II 卷(非选择题)请点击修改第II 卷的文字说明三、双空题13.设集合{}1,0,2A =-,则集合A 的子集有__________个,若集合{}|,2B x x A x A =∈-∉且则B =_________.【答案】8 {-1}【解析】【分析】(1)可以写出集合A 的所有子集,从而得出集合A 子集的个数;(2)根据条件x∈A,且2﹣x ∉A ,即可求出集合B .【详解】A={﹣1,0,2}的子集为:∅,{﹣1},{0},{2},{﹣1,0},{﹣1,2},{0,2},{﹣1,0,2},共8个;∵x∈A,且2﹣x ∉A ;∴B={﹣1}.故答案为(1). 8 (2). {-1}.【点睛】考查列举法和描述法表示集合的概念,子集的定义及求法,找子集时不要漏了空集.14.已知集合{}2A |x x x ==,集合{|124}x B x =<<,则集合A 的子集个数为________;A B ⋂=__________【答案】4, {}1【解析】【分析】求出集合A 、B ,即可求出集合A 的子集个数及A B ⋂.【详解】{}2A x x x ==={}0,1,{}124x B x =<<={}02x x <<,故集合A 的子集个数为224N ==,A B ⋂={}1【点睛】本题并集及其运算,考查了子集与真子集,求集合的交集的基础题.15.已知A ⊆B ,则“x∈A”是“x∈B”的________条件,“x∈B”是“x∈A”的________条件.(填“充分”或“必要”)【答案】充分 必要【解析】【分析】由充分条件和必要条件的定义可以判断.【详解】因为A ⊆B ,即A 是B 的子集,所以如果有x∈A,即x 是集合A 的元素,那么一定有x∈B,即x 是集合B 的元素,根据充分条件的定义可知,“x∈A”是“x∈B”的充分条件,同时x∈B”是“x∈A”的必要条件.【点睛】本题考查充分条件和必要条件的定义,关键是理解定义,属于基础题.16.函数()21f x x x =+-(x >1)的最小值是______;取到最小值时,x =______.【答案】1 1【解析】【分析】由已知可知x -1>0,由y =x +21x -=x -1+21x -+1,结合基本不等式即可求解. 【详解】∵x >1,∴x -1>0,由基本不等式可得y =x +21x -=x -1+21x -+1≥1,当且仅当x -1=21x -即x =12时,函数取得最小值1.故答案为1;1+【点睛】 本题主要考查了利用基本不等式求解最值,属于基础试题.四、填空题17.已知集合{}(4)0A x x x =-,{}0,1,5B =,则AB =________.【答案】{5} 【解析】【分析】【详解】解析:(,0)(4,)A =-∞⋃+∞,{5}A B =.18.已知集合{}{}2320,3A x x x B x x a =-+≤=-<.若A B ⊆,则实数a 的取值范围是__________.【答案】()1,-+∞【解析】【分析】解一元二次不等式即可求出集合A ,进而求出{}3B x x a =<+,再根据A B ⊆,即可列出不等式,从而求出a 的取值范围.【详解】 解:由题可知,{}{}232012A x x x x x =-+≤=≤≤, {}{}33B x x a x x a =-<=<+,由于A B ⊆,则32a +>,解得:1a >-,所以实数a 的取值范围为()1,-+∞.故答案为:()1,-+∞.【点睛】本题考查根据集合间的包含关系求参数的取值范围,涉及一元二次不等式的解法,属于基础题. 19.若关于x 的不等式210mx mx +->的解集为∅,则实数m 的取值范围为 .【答案】[4,0]-【解析】试题分析:当0m =时,不等式变形为10->,解集为∅,符合题意;当0m ≠时,依题意可得20{4040m m m m <⇒-≤<∆=+≤,综上可得40m -≤≤.考点:一元二次不等式.【易错点睛】本题主要考查不等式中的一元二次不等式问题,难度一般.有很多同学做此题时直接考虑为一元二次不等式,其二次函数应开口向下且与x 轴至多有一个交点,而忽略二次项系数为0时的情况导致出现错误.当二次项系数含参数时一定要讨论是否为0,否则极易出错.五、解答题20.请解决下列问题:(1)设,,{1,},{1,}a b R P a Q b ∈==--,若P Q =,求-a b 的值;(2)已知集合{|0},{|12}A x x a B x x =<<=<<,若B A ⊆,求实数a 的取值范围.【答案】(1)0a b -=(2)2a ≥【解析】【分析】(1)直接根据集合相等得到答案.(2)根据集合的包含关系得到2a ≥得到答案.【详解】(1)由于P Q =,所以1a =-,且1b -=,0a b ∴-=.(2){|0},{|12}A x x a B x x =<<=<<,且B A ⊆,2a ∴≥如图所示.【点睛】本题考查了根据集合相等和集合的包含关系求参数,意在考查学生的理解能力.21.已知命题p :2430x x -+≤,命题q :()222100x x a a -+-<>. (1)当4a =时,p q ∧为真命题,求x 的取值范围;(2)若q ⌝是p ⌝的充分不必要条件,求实数a 的取值范围.【答案】(1)13x ≤≤(2)[)2,+∞【解析】【分析】(1)解一元二次不等式分别可得集合A 、B ,代入4a =可确定集合B ,由p q ∧为真命题可知两个命题均为真命题,即可解不等式组求得x 的取值范围;(2)根据逆否命题的性质由题意可得p 是q 的充分不必要条件,即可由集合的关系确定a 的取值范围.【详解】命题p :2430x x -+≤,解得13x ≤≤,令[]1,3A =.命题q :()222100x x a a -+-<>),解得11a x a -≤≤+,令[]1,1B a a =-+. (1)当4a =时,[]3,5B =-,因为p q ∧为真命题,所以p 真q 真,则13,35,x x ≤≤⎧⎨-≤≤⎩ 所以13x ≤≤.(2)因为q ⌝是p ⌝的充分不必要条件,即p 是q 的充分不必要条件,所以集合A 是集合B 的真子集,所以11,13,a a -≤⎧⎨+≥⎩解得2a ≥. 经检验2a =满足题意,所以a 的取值范围为[)2,+∞.【点睛】本题考查了一元二次不等式解法,由复合命题真假确定参数的取值范围,逆否命题的性质应用,由充分不必要关系确定参数的取值范围,属于基础题.22.南康某服装厂拟在2020年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)m 万件与年促销费用(04)x x ≤≤万元满足131m x =-+.已知2020年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格定为每件产品年平均成本的2倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2020年该产品的利润y 万元表示为年促销费用x 万元的函数;(2)该服装厂2020年的促销费用投入多少万元时,利润最大?【答案】(1)1656([0,4])1y x x x =--∈+;(2)3万元. 【解析】【分析】(1)根据题意,结合已知条件,列出函数关系即可;(2)对函数进行配凑,使之可用基本不等式,即可求得利润的最大值.【详解】(1)由题意知:每件产品的销售价格为8162m m+⨯, 8162(816)816m y m m x m x m+∴=⋅⨯-++=+- 181631x x ⎛⎫=+-- ⎪+⎝⎭ 16561x x =--+([0,4])x ∈;(2)由16165657(1)574911y x x x x ⎡⎤=--=-++≤-=⎢⎥++⎣⎦, 当且仅当1611x x =++,即3x =时取等号. 故该服装厂2020年的促销费用投入3万元时,利润最大.【点睛】本题考查分式函数模型的应用,涉及用基本不等式求最值,属综合基础题.23.解关于x 的不等式ax 2-(2a +3)x +6>0(a ∈R ).【答案】详见解析【解析】【分析】首先讨论不等式的类型:(1)a =0时,是一次不等式;(2)a ≠0时,是一元二次不等式,然后讨论a 的符号,再讨论两根3a与2的大小. 【详解】原不等式可化为:(ax ﹣3)(x ﹣2)>0;当a =0时,化为:x <2;当a>0时,化为:(x3a-)(x﹣2)>0,①当3a>2,即0<a32<时,解为:x3a>或x<2;②当3a=2,即a32=时,解为:x≠2;③当3a<2,即a32>时,解为:x>2或x3a<,当a<0时,化为:(x3a-)(x﹣2)<0,解为:3a<x<2.综上所述:当a<0时,原不等式的解集为:(3a,2);当a=0时,原不等式的解集为:(﹣∞,2);当0<a32<时,原不等式的解集为:(﹣∞,2)∪(3a,+∞);当a32=时,原不等式的解集为:(﹣∞,2)∪(2,+∞);当a32>时,原不等式的解集为:(﹣∞,3a)∪(2,+∞)【点睛】(1)解一元二次不等式时,当二次项系数为负时要先化为正,再根据判别式符号判断对应方程根的情况,然后结合相应二次函数的图象写出不等式的解集.(2)解含参数的一元二次不等式,要把握好分类讨论的层次,一般按下面次序进行讨论:首先根据二次项系数的符号进行分类,其次根据根是否存在,即判别式的符号进行分类,最后当根存在时,再根据根的大小进行分类.。
浙江省磐安县第二中学高一数学同步训练 (文)三角函数基础练习卷(二)

三角函数相关公式:二倍角公式:sin 2α=cos 2α= = = tan 2α= 半角公式:sin 2α=cos2α= tan 2α= 注意:二倍角与半角的概念是相对的,半角公式本质上也就是二倍角公式。
一、选择题1、)619sin(π-的值等于………………( ) A 、21 B 、21- C 、23 D 、23- 2、已知a = 200sin ,则 160tan 等于( )A 、21a a --B 、21a a -C 、a a 21--D 、aa 21- 3、已知1sin()43πα-=,则cos()4πα+的值等于……………………………………( )A B . C .13 D .13- 4、若角0600的终边上有一点()a ,4-,则a 的值是……………………………………( )A 34B 34-C 34±D 3 5、若sin()cos cos()sin αβααβα---35=,那么2cos β的值为……………( ) A 、725 B 、1825 C 、725- D 、1825-6、110sin ) A 、1 B 、2 C 、4 D 、147、已知35sin ,αα=是第二象限角,且1tan()αβ+=,则tan β的值为……( )A 、-7B 、7C 、34-D 、348、若270360α︒<<︒,则化简式子) A 、sin 2αB 、cos 2αC 、sin 2α- D 、cos 2α-9、已知tan α、tan β是方程2x ++40=的两根,且(,)22ππαβ∈-、,则αβ+等于……………………………………( )A 、3π B 、23π- C 、3π或23π- D 、3π-或23π10、函数⎪⎩⎪⎨⎧≥<<-π=-0,01),sin()(12x e x x x f x ,若 2)()1(=+a f f ,则a 的所有可能值为( )(A )1 (B )22,1-(C )22- (D )22,1 二、填空题11、α的终边与6π的终边关于直线x y =对称,则α= 。
浙江省磐安县第二中学高一数学同步训练 (文)三角函数基础练习卷(一)

___姓名__________学号__________三角函数相关公式:诱导公式口诀:两角和差公式:sin()αβ+=sin()αβ-=cos()αβ+=cos()αβ-=tan()αβ+=tan()αβ-=注意:把握题目中各角度与结构之间的联系,以决定所需运用的公式。
一、选择题 1 02120sin 等于……………………( ) A 23± B 23 C 23- D 21 2、已知α为第三象限角,则2α所在的象限是A .第一或第二象限B .第二或第三象限C .第一或第三象限D .第二或第四象限3 已知4sin 5α=,并且α是第二象限的角,那么tan α的值等于…………………( ) A 43- B 34- C 43 D 34 4 设sin 2cos3tan 4a =则…………( )A 0a >B 0a <C 0a =D a 值不存在5.如果A 为锐角,21)sin(-=+A π,那么 =-)cos(A π……………………………( ) A .21- B .21 C .23- D .23 6.已知==ααcos ,32tan则…………( ) A .54 B .-54 C .154 D .-537.=+-)12sin 12)(cos 12sin 12(cos ππππ( )A .23-B .21-C .21 D .23 8. 给出下列各函数值:①)1000sin(0-;②)2200cos(0-;③)10tan(-;④917tan cos 107sinπππ 其中符号为负的有…( ) A ① B ② C ③ D ④ 9.22sin 2cos 1cos 2cos 2⋅=+αααα………………( ) A .tan α B .tan 2α C . 1 D .12 10.已知3tan =α,23παπ<<,那么ααsin cos -的值是……………………( ) A 231+-B 231+-C 231-D 231+ 二、填空题11 设扇形的周长为8cm ,面积为24cm ,则扇形的圆心角的弧度数是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省磐安县第二中学高一数学 集合 单元测试
3.下列八个关系式①{0}=φ ②φ=0 ③φ⊆{φ} ④φ∈{φ} ⑤{0}⊇φ ⑥0∉φ ⑦
φ≠{0} ⑧φ≠{φ}其中正确的个数( )
(A )4 (B )5 (C )6 (D )7 4.下列语句:(1)0与{0}表示同一个集合;(2)由1,2,3组成的集合可表示为{1,2,3}或{3,2,1};(3)方程(1)(1)(2)0x x x ---=的所有解的集合可表示为{1,1,2}; (4)集合{54<<x x }是有限集,正确的是( )
(A )只有(1)和(4) (B )只有(2)和(3) (C )只有(2) (D )以上语句都不对
5.设集合A={2,3},B={2,3,4},C={3,4,5}则A B C =() ( )
A .{2,3,4}
B .{2,3,5}
C .{3,4,5}
D .{2,3,4,5}
6.设A 、B 是全集U 的两个子集,且A ⊆B ,则下列式子成立的是( ) (A )C U A ⊆C U B (B )C U A C U B=U (C )A
C U B=φ (
D )C U A
B=φ
7.设,
,若,则实数的取值范围是( )
(A )
(B )
(C )
(D )
8.函数2
1
)(--=
x x x f 的定义域为( ) A .[1,2)∪(2,+∞) B .(1,+∞) C .[1,2) D .[1,+∞)
9.函数f (x )= 2(1)x
x x ⎧⎨+⎩
,0,0x x ≥< ,则(2)f -=( )
A. 1 B .2 C. 3 D.4
10.集合A={x Z k k x ∈=,2} B={Z k k x x ∈+=,12} C={Z k k x x ∈+=,14}又
,,B b A a ∈∈则有( )
(A )(a+b )∈ A (B) (a+b) ∈B (C)(a+b) ∈ C (D) (a+b) ∈ A 、B 、C 任一个 11.图中阴影部分表示的集合是( )
A. )(B C A U
B. B A C U )(
C. )(B A C U
D. ()U C A B
12.若{1,2,3,a}∪{3,2a }={1,2,3,a },则a 的取值集合为
A .{0,±1}
B .{0,-1
} C .{-1,- 2} D .{0,-1
} 13.若M={Z n x n x ∈=
,2},N={∈+=n x n x ,2
1
Z},则M ⋂N 等于( ) (A )φ (B ){φ} (C ){0} (D )Z 14.下列各式中,正确的是( ) (A )2}2{≤⊆x x (B )
∅
{12<>x x x 且}
(C ){Z k k x x ∈±=,14}},12{Z k k x x ∈+=≠ (D ){Z k k x x ∈+=,13}={Z k k x x ∈-=,23} 15.设U={1,2,3,4,5},A ,B 为U 的子集,若A B={2},(C U A )
B={4},(C U A )(C U B )
={1,5},则下列结论正确的是( ) (A )3B A ∉∉3, (B )3B A ∈∉3, (C )3B A ∉∈3, (D )3B A ∈∈3, 16.下列各组函数中,表示同一函数的是
( )
A .0,x
y x y x
== B .1,112-=+⨯-=
x y x x y
C
.,y x y ==D .2)(|,|x y x y ==
17.设M ={x |-2≤x ≤2},N ={y |0≤y ≤2},函数f (x )的定义域为M ,值域为N ,
则f (x )的图象可以是( )
18.若U 、φ分别表示全集和空集,且(C U A )B ⊆A ,则集合A 与B 必须满足( ) (A)φ (B)A=φ (C)B=φ (D)A=U 且A ≠B 二、填空题(17×2=34分)
1. 在直角坐标系中,坐标轴上的点的集合可表示为
2. 若A={1,4,x},B={1,x 2
}且A B=B ,则x=
3集合{1,2,3}的子集有 个,写出它的非空真子集
4.设U={0,1,2,3,4},A={0,1,2,3},B={2,3,4},则(C U A )(C U B )= 5方程2560x x -+=的解集可表示为 方程组的解集可表示为⎩⎨
⎧=-=+0
2313
32y x y x
6 若{}
21,,0,,b a a a b a ⎧⎫=+⎨⎬⎩
⎭
,则20112012a b +的值为
7.设集合A={23≤≤-x x },B={x 1212+≤≤-k x k },且A ⊇B ,则实数k 的取值范围是 。
8.设全集U={x x 为小于20的非负奇数},若A (C U B )={3,7,15},
(C U A )
B={13,17,19},又(C U A )
(C U B )=φ,则A
B=
9.设U={三角形},M={直角三角形},N={等腰三角形},则M N= M N= C U M=
C U N= C U (M N )=
10.设全集为⋃,用集合A 、B 、C 的交、并、补集符号表图中的阴影部分。
(1) (2) (3)
三、解答题
1.设全集U={1,2,3,4},且A={x x 2
-5x+m=0,x ∈U}若C U A={1,4},求m 的值。
(4分)
2.已知集合A={a 2
,a+1,-3},B={a-3,2a-1,a 2
+1},若A B={-3},求实数a 。
(6分)
3.设全集U={x x *,5N x ∈≤且},集合A={x 052=+-q x x },B={x x 2
+px+12=0},且(C U A )
B={1,4,3,5},求实数P 、q 的值。
(6分)
4.设A={x }01)1(2{,042
2
2
=-+++==+a x a x x B x x ,其中x ∈R,如果A B=B ,求实数
a 的取值范围。
(7分)
5. 已知集合{}{}|3,|15A x a x a B x x x =≤≤+=≤->或,
(1)若A B =∅,求实数a 的取值范围;
(2)若A B ≠∅,求实数a 的取值范围。
(7分)。
