3-2向量组的线性相关性
3-2向量组的线性关系

是否线性相关。 因为
例5. 当向量组含两个非零向量时,
设
与 线性相关
证明: 使得
与
若
对应分量成正比
与
线性相关,则存在不全为零的数
或
或
即
与
的对应分量成比例.
20
例如
对应分量不成比例,
线性无关。
对应分量成比例, 几何上说向量 共线。
线性相关。
21
例6. 求证含有零向量的向量组必线性相关,
证明: 设向量组 取数 必有 则此向量组必定线性相关。 中,
第二步将
代入
得齐次线性方程组。
30
有
第三步根据方程组的解来判别线性相关还是线性无关: 线性相关。 方程组有非零解,则称向量组 方程组只有零解,则称向量组 线性无关。 下面介绍利用矩阵的秩来判别向量组的线性相关性 的方法。 这是判别向量组线性相关性的主要方法。
31
线性相关 (无关) 有非零解 (只有零解) ) 秩 A m (秩 A m 此定理是证明向量组线性相关性的基本方法。 推论1 当m=n时,即向量个数=分量个数时, 线性相关(线性无关) 向量组构成行列式的值为零,即 A 0. ( A 0). 推论2 设n 维向量组中含有m个向量, 当m>n 时, 此向量组必定线性相关。
组合,即存在不全为0的数
由于
不全为0, 线性相关.
则
41
向量 这说明
可由
线性表示, 线性相关;
而向量组 e1 , e2 ,, en 中任一向量都不能被 其他向量线性表示,其线性无关。
一个向量组中有没有某个向量可由其余向量 线性表示, 这是向量组的一种属性,称为向量组的 线性相关性。
3-2-1 向量组的线性相关性

向量组的线性相关性是一个最难掌握的 内容,需下苦功夫学好。
一、n维向量组的线性相关性
m个具有相同维数的向量称为向量组。
定义2.1 给 定 向 量 组A :1,2 ,,m ,如 果 存 在 不
全 为 零 的 数c1 , c2 ,, cm使
c11 c2 2 cm m 0 则称向量组A是线性相关的,否则称它线性无关. 当向量组线性无关时,也称该向量组为线性无关 (向量)组,简称无关组
其 中p为 实 数 。
例3
设
向
量
组
1
,
2
,
线
3
性
无
关
,
1
1
2,
2 2 3 , 3 3 1 , 试 证 向 量 组1 , 2 , 3
线性无关。
证 设有数x1 , x2 , x3使得
即 x11 x2 2 x3 3 0
x11 2 x2 2 3 x3 3 1 0 x1 x3 1 x1 x2 2 x2 x3 3 0
1
,
2
,
,
唯
m
一
地
线
性
表
示
。
向量组与矩阵
n维行向量组 i ai1 , ai2 ,, ain ,(i 1,2,, m), 可以
构成一个矩阵
a
11
a
A
21am1a12 a22am2a1 j a2 j
amj
a
1n
1
a2n
amn
2
m
A称
为
由n维
行
向
量
组1
,
2
,,
所
m
构
向量组的线性相关性(2)
ar线性
证 用反证法. 若 a1 ,a2 , ar , a r 1线性相关, 则有不全为
k1a1 k2a2
否则 (kr 1 0)
kr 1ar 1 0 其中 kr 不能为零, 1
若 kr 1 0
k1 k2
k1a1 k2a2
ar 1
kr 0
(Ⅰ)
(Ⅱ)
α1α 2
β1β2
αr
βs
若(Ⅰ)中每一个向量都能由向量组(Ⅱ)线性表示,则称 向量组(Ⅰ)可由向量组(Ⅱ)线性表示. 若向量组(Ⅰ) 与向量组(Ⅱ)可以互相线性表示,则称 向量组(Ⅰ)与向量组(Ⅱ)等价. 向量组之间的等价关系具有以下性质:
① 反身性 ② 对称性 ③ 传递性
例 证
设n维向量组α1 , α 2 , , α n 与e1 ,e2 ,
行 向 量
n
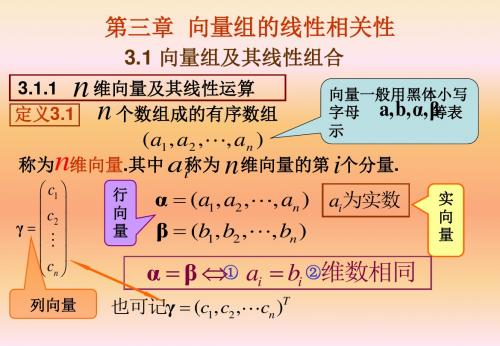
(a1 , a2 ,, an )
α (a1 , a2 , β (b1 , b2 ,
, an ) ai为实数 , bn )
cn )
T
实 向 量
① a b ②维数相同 α β i iFra bibliotek列向量
也可记γ (c1, c2 ,
规定:行向量与列向量都按矩阵的运算规则进行运算. 因 此,n维列向量与 n 维行向量总看成是两个不同的向量
则 (k1 k3 , k1 2k2 3k3 , k1 5k2 6k3 ) 0
1 D1 1 0 2 5 1 3 6
亦即
0
这是关于 k1 , k2 , k3 的齐次方程组
据定 理1.4 有非 零解
即有不全为零的数 k1 , k2 , k3 ,使 从而向量组
k1a1 k2a2 k3a3 0 也可直接求解得 , k1 1, k2 1, k3 1, 即 a1 + a2 - a3 = 0
3-2向量组的线性相关与线性无关

的线性组合 解 设存在四个数 x1 , x2 , x3 , x4 ,使得
β = x1α1 + x2α 2 + x3α 3 + x4α 4
即
1 1 1 1 1 2 1 1 −1 =x +x −1 + x3 + x4 1 2 1 1 −1 1 −1 1 1 −1 −1 1
亦即( x1 + x 3 )α 1 + ( x1 + x 2 )α 2 + ( x 2 + x 3 )α 3 = 0, 线性无关, 因 α 1,α 2,α 3 线性无关,故有
x 1 + x 3 = 0, x 1 + x 2 = 0, x + x = 0. 2 3
1 0 1 由于 1 1 0 = 2 ≠ 0 0 1 1
全为零的数 k1 , k 2 ,L , k m 使 r r r r k1α 1 + k 2α 2 + L + k mα m = 0
则称向量组A是线性相关的,否则称它线性无关. 是线性相关的,否则称它线性无关. 1. α 1 , α 2 , L , α n 线性无关 ⇔ 只有当 k1 = L = k n = 0时 ,
才有 k1α 1 + k 2α 2 + L + k nα n = 0 成立 .
2. 对于任一向量组 , 不是线 性无关就是线性相关 .
3.向量组只包含一个向量α 时, 若α = 0 则 α 线性相关, 若α ≠ 0, 则 α 线性无关 .
4.包含零向量的任何向量 组是线性相关的 .
5.对于含有两个向量的向 量组, 它线性相关的 充要条件是两向量的分 量对应成比例 .
3-2向量的线性相关性

构成一个m n矩阵
1T T 2 B T m
线性方程组的向量表示
a11 x1 a12 x 2 a1n x n b1 , a 21 x1 a 22 x 2 a 2 n x n b2 , a m 1 x1 a m 2 x 2 a mn x n bm .
x1b1ห้องสมุดไป่ตู้ x2b2 x3b3 0
即 x1 1 2) x2 ( 2 3 ) x3 ( 3 1 ) 0, (
亦即 x1 x3 ) 1 ( x1 x2 ) 2 ( x2 x3 ) 3 0, ( 因 1, 2, 3线性无关,故有 x1 x 3 0, 方程组只有零解1 x2 x3 0, x x1 x 2 0, 所以向量组 1 , b2 , b3线性无关 b . x x 0. 2 3
有解;
定义2 设 有 两 个 向 量 组 A : 1 , 2 , , m 及B : 1 , 2 , , s .
若B组 中 的 每 个 向 量 都 能 向 量 组 线 性 表 示 , 则 由 A 称 向 量 组 能 由 向 量 组 线 性 表 示. 若 向 量 组 与 向 B A A 量 组B能 相 互 线 性 表 示 , 则 这 两 个向量组等价, 称
向量组 a1, a 2 ,, a n 称为矩阵A的列向量组.
类似地, 矩阵A (aij )mn 又有m个n维行向量
a11 a12 a 21 a 22 A ai1 ai 2 a m1 am 2
T 1 T 2
a1 n a2n a in a mn
3-2-2向量组的线性相关性的判定

即, 表示式是唯一的.
设
a11 a21 as1 a12 a22 as 2 1 , 2 , , s a1n a2 n asn
a s1 a11 a21 a a a 12 22 s2 1 , 2 , , s asn a1n a2 n b b b 1 2 s
证明 由已知, 存在不全为零的数k1,k2 , …,kr, l ,使
k11+k22+ …+krr+l =0 若l =0, 则k11+k22+ …+krr=0, 矛盾. 所以l 0, 于是
β α1 α2 αr
k1 l k2 l kr l
若有: =k11+k22+ …+krr=l11+l22+ …+lrr 则有: 所以: (k1 l1)1+(k2 l2)2+ …+(krl1)r=0 k1 l1=k2 l2= …=k+ …+kss=0, 故 k1=k2= …=kr=0 所以1, 2,…, s 线性无关.
不妨设k10, 则有: α1
k2 k1
α2 α3 αs
k3 k1 ks k1
充分性:不妨设1可由2, …,s线性表示, 即存在一组 数k2,,…,ks使: 1=k22+ …+kss , 于是有 1+k22+ …+kss =0
3.向量组的线性相关性与线性方程组的解

3.向量组的线性相关性与线性方程组的解§3.1 线性方程组解的判定1.定理3.1:n 元线性方程组AX=b ,其中A=(a 12a 12a 1n a 21a 22a 2na m1a m2a mn),x=( x 1x 2??x n ) ,b=( b 1b 2??b m )(1)无解的充要条件是R(A)<R(A,b);(2)有惟一解的充要条件是R(A)=R(A,b)=n ,(3)有无穷多解的充要条件是R(A)=R(A,b)<n.注:(1)R(A,b)先化为行阶梯形,判别。
有解时再化为行最简形求解。
(2)R(A)=m 时,AX=b 有解。
(3)R(A)=r 时,有n-r 个自由未知量,未必是后面n-r 个。
2.定理3.2:n 元线性方程组AX=0(1)有惟一解(只有零解)的充要条件是R(A)=n ; (2)有无穷多解(有非零解)充要条件是R(A)<n .注:(1)m <n,AX=0必有非零解。
3.定理3.3:矩阵方程AX=B 有解的充要条件是R(A)=R(A,B) 求解线性方程组例1. {4x 1+2x 2?x 3=23x 1?x 2+2x 3 =1011x 1+3x 2 =8例2. {2x 1+x 2?x 3+x 4 =14x 1+2x 2?2x 3+x 4=22x 1+x 2 ?x 3?x 4 =1例3. 求解齐次线性方程组{3x 1+ 4x 2?5x 3+ 7x 4 =02x 1?3x 2+3x 3? 2x 4 =04x 1+11x 2?13x 3+16x 4=07x 1?2x 2+ x 3+ 3x 4 =0例4.写出一个以X=C 1(2?310)+C 2(?2401)为通解的齐次线性方程组。
例5(每年).(1)λ取何值时,非齐次线性方程组{ λx 1+x 2+x 3=1x 1+λx 2+x 3=λx 1+x 2+λx 3=λ2(1)有惟一解;(2)无解;(3)有无穷多组解?并在有无穷多组解时求出通解.(2)非齐次线性方程组{x 1+x 2+2x 3=02x 1+x 2+ax 3=13x 1+2x 2+4x 3=b当a,b 取何值时,(1)有惟一解;(2)无解;(3)有无穷多组解?并求出通解.例5(12/13学年).设A=(λ110λ?1011λ), b=(a11),已知Ax=b 存在两个不同的解:(1)求λ,a;(2)求Ax=b 的通解。
3.2向量3-3向量组的线性相关性

b11 b12 b1n
(c1,c2,,cn)(1,2,,s)b21
b22
b2n
bs1 ks2 ksn
线性代数课件 hty
19
同时C的 ,行向量B组 的能 行由 向量组,线 A 性 为这一表示的 :系数矩阵
1T 2T mT
3.当没有明确说明是行向量还是列向量时, 都当作列向量.
线性代数课件 hty
5
解析几何
三、向量空间
向量
(n3)
线性代数
既有大小又有方向的量
坐
有次序的实数组成的数组
几何形象: 可随意 平行移动的有向线段
标
代数形象: 向量的 坐标表示式
系 aT(a 1,a2, ,an)
线性代数课件 hty
6
解析几何
线性代数课件 hty
22
五、线性相关性的概念
定义3 给定向 A:量 1,组 2,,m,如果存在
全为零k1,的 k2, 数 ,km使
k11k22kmm0
则称向量组A是线性相关的,否则称它线性无关.
注意 1若 . 1,2, ,n线性无 ,则关 只有 1 n 0时 ,才有
类似,A 若 经矩 初阵 等列B变 ,A 换 则 的变 列向量 B的 组列 与向量 . 组等价
线性代数课件 hty
21
对方程组A的各个方程做线性运所算得到的 一个方程就称为方程A组的一个线性组合;若方 程组B的每个方程都是方程A组的线性组合,就 称方程组B能由方程组A线性表示,这时方程组 A的解一定是方程组 B的解;若方程组A与方程组 B能相互线性表示,就这称两个方程组等价,等 价的方程组一定同.解
线性代数课件 hty
13
定义1 给定向 A:量 1,2, 组 ,m ,对于任
3-2 向量组的线性相关性

一、解的判定定理 二、方程组的求解
顾
Henan Agricultural University
结束
第二节 向量组的线性相关性
• • • • 一、n 维向量的定义及线性运算 二、向量组的线性相关性的定义 三、向量组的线性相关性的判定 四、向量组的线性相关性的系列性质
Henan Agricultural University
即
x1(a1+a2)+x2(a2+a3)+x3(a3+a1)=0, 亦即 (x1+x3)a1+(x1+x2)a2+(x2+x3)a3=0. 因为a1, a2, a3线性无关, 故有
x1+ x3 =0 x1+ x2 =0 . x2 + x3 =0
Henan Agricultural University
1 2 4 1 2 4 r 1 0 2 r r 0 −5 −5 ~ 0 1 1 ~ 0 1 1 , ~0 3 3 0 0 0 0 0 0 0 −9 −9 0 0 0 0 0 0 所以R(a1, a2, b1)=R(a1, α2), 从而方程组有解, 即b1可由a1, a2线 性表示, 且存在x1=2, x2=1, 使2a1+a2=b1. 定理1 定理 向量b能由向量组A: a1, a2, ⋅⋅⋅, am线性表示的充分必要条 件是矩阵A=(a1, a2, ⋅⋅⋅, am)与矩阵B=(a1, a2, ⋅⋅⋅, am, b)的秩相等, 即R(A)=R(B). 1 2 4 2 −1 3 T T T (a1 , a2 , b ) = 1 −1 1 −1 3 1 11
例5 已知向量组a1, a2, a3线性无关, b1=a1+a2, b2=a2+a3, b3=a3+a1, 试证向量组b1, b2, b3线性无关. 证法二 把已知的三个向量等式写成一个矩阵等式
向量组线性相关性

向量组线性相关性向量组线性相关性是数学中一个重要的概念,它可以在许多应用中使用,包括统计和线性代数。
它表明了两个变量是如何相互影响的,并且可以用来解释不同情况下变量之间的线性关系。
因此,了解这个概念对推断变量之间的关系非常重要。
在这篇文章中,我们将详细讨论向量组线性相关性的定义、特性和应用。
首先,我们将介绍什么是向量组,包括它的结构、特性和如何表示。
接下来,我们将讨论线性相关性的定义,它的两个重要特性,即相关系数和回归线。
最后,我们将讨论向量组线性相关性的应用,特别是在统计学中,它可以用来推断和预测数据集之间的关系。
首先,让我们来看看什么是向量组。
它是一组由单位矢量组成的数值,它们被称为标量。
向量组由坐标轴上的点组成,这些点的特性取决于它们的大小和关系。
例如,在二维空间中,每一个矢量都可以用它的横坐标和纵坐标来表示,这两个坐标是矢量的分量。
此外,矢量的大小是按照它们两个坐标的积来表示的,这个大小可以用简单的乘法计算,也可以用更复杂的三角函数计算。
其次,我们来讨论线性相关性。
线性相关性是指在两个变量之间存在线性关系的能力。
它可以用相关系数来表示。
相关系数是一个指标,表示两个变量的相关性。
它的值介于-1和1之间,-1表示完全负相关,1表示完全正相关,0表示无关。
因此,通过计算相关系数,可以了解两个变量之间的线性关系。
此外,另一个重要的线性相关性特性是回归线。
回归线是一条拟合两个变量之间线性关系的直线,它可以用来推测两个变量之间的关系。
通过画出回归线,可以更清楚地了解两个变量之间的关系,例如它们之间是线性相关还是非线性相关。
最后,我们来看看向量组线性相关性的应用。
它主要应用于统计学,用来推断和预测数据集之间的关系。
它也可以用来了解变量之间的线性依赖性,以及变量的趋势及其变化。
此外,它还可以用来帮助预测未来,因为它可以用来推断不同数据集之间的相关性。
总之,向量组线性相关性是一个非常重要的概念,它可以帮助我们了解变量之间的关系,推断不同数据集之间的关系,以及预测未来。
线性代数:3.2 向量的线性相关性

,
是线性无关的.
n
例:判断向量组
1 1, a, a2, a3 ,2 1, b, b2, b3 , 4 1, c, c2, c3 ,4 1, d, d 2, d 3
线性相关还是线性无关。(a, b, c, d各不相同)
考虑齐次线性方程组
x1 x2 x3 x4 0 ax1 bx2 cx3 dx4 0 a2 x1 b2 x2 c2 x3 d 2 x4 0 a3 x1 b3 x2 c3 x3 d 3 x4 0 其系数行列式是范德蒙德行列式
即齐次线性方程组有非零解,
所以向量 1,2 ,3 线性相关。
而向量 1,2 对应分量不成比例,所以线性无关。
例: 已知向量组 1 , 2 , 3 线性无关,
1 1 2, 2 2 3,3 3 1
试证 : 1 , 2 , 3线性无关.
证明: 设 k11 k2 2 k3 3 0 k1(1 2 ) k2 ( 2 3 ) k3 ( 3 1 ) 0
设 k11 k22 l11 l22
两式相减得
kmm lmm
(k1 l1 )1 (k2 l2 )2 (km lm )m 0
因为1,2 ,,m线性无关,
所以系数k1 l1 0, k2 l2 0,, km lm 0, 于是有ki li , i 1, 2, , m.
k11 k22 kmm 0
不妨设ki 0,于是
i
k1 ki
1
ki 1 ki
i 1
ki 1 ki
i 1
即i可由其余m-1个向量线性表示。
km ki
m
(充分性)设i可由其余m 1个向量线性表示, 即i l11 li1 i1 li1 i1 lmm
于是l11 l i1 i1 (1) i l i1 i1 lm m 0
线性代数3-2

定理3 改变向量的个数时,部分相关,整体也相关; 整体无关,部分也无关.
定理4 同步改变向量的分量顺序时,线性相关性不变. 定理5 改变向量的维数时,低维无关,高维也无关;
高维相关,低维也相关.
定理6 向量组 a1, a2 , , an 线性相关的充分必要条
证 设 A1 组为 A 组的最大无关组,B1 组为 B 组 的最大无关组,则 A1 组、B1 组中所含的向量 个数分别为 r1,r2 .
因为 A 组能由 B 组线性表示,故 A1 组也能由 B1 组线性表示.(请思考为什么?)
于是由引理知 r1≤ r2 .
证毕
定理7的若干推论
推论 1 等价的向量组有相同的秩.
m
am1
am 2
a1 s
1
a2 s
2
ams
s
⑶传递性 若A组与B组等价,B组与C组等价, 则A组与C组等价.
证 (不妨设为行向量情形)
因 A 组与 B 组等价,故存在矩阵 K1、T1, 使得 A=K1B,B=T1A, 又 B 组与 C 组等价,故存在矩阵 K2、T2 , 使得 B=K2C,C=T2B, 于是有 A= K1K2C,C=T2T1A, 即 A 与 C 等价.
矩阵:
b11 b12
( c1 , c2 ,
, cn ) (1,2 ,
,
s
)
b21
b22
bs1 bs2
b1n
b2n
bsn
同时,C的行向量组能由B的行向量组线性表示, A
3-2向量组间的线性关系

α1i α 2i i =12,L m βi = M i =12,L m , , , , αri α r+1,i
x β1 + x2β2 + x3β3 =θ 1 x (α +α2) + x2(α2 +α3) + x3(α3 +α ) =θ 1 1 1
x +x =0 1 2 x2 +x3 =0
x 1
+x3 =0 1 0 1 1 0 1
1 1 0= 0 1 − = 2 1 0 1 1 0 1 1 x = x2 = x3 =0 1
第二节 向量的线性相关性
第三章
一、线性相关与线性无关的概念 二、向量组的线性相关性的判别 三、线性组合与线性表示 四、向量的等价 五、向量组的最大线性无关组
1
一、线性相关与线性无关的概念
, 定义1 定义1 设 A:α1,α2 ,Lαm
如果存在一组不全为 如果存在一组不全为0的数 存在一组不全为0
为n元向量组, 元向量组
线性无关。 β , β , β线性无关。
1 2 3
22
方程组只有零解, 从而 方程组只有零解,
证明二: 证明二:
1 0 1 β , β2, β3 ) =(α ,α2,α3 ) 1 1 0 ( 1 1 0 1 1 记 做 B= A C
从而 R(B)= R(A), ( ) ( ),
+2x4 =0 x 1 x +2x =0 得同解方程组 2 4 x3 −x4 =0 2x x =− 4 1 方程组的解 为任意实数) 2x x2 =− 4 令 x4 = k (k 为任意实数) x =x 3 4
3.1 3.2向量及向量组的线性相关性

, 2
a22
,, s
a2s
ar1
ar2
ars
则 k11 k22 kss k11 k22 kss
k11
k2 2
ks s
a11
k1
a21
a12
k2
a22
a1s
ks
a2s
k1a11 k1a21
k2a12 ksa1s
k2a22 ksa2s
ars
k1ar1
k2ar 2
ksa1s 0
ksa2s
0
ksars
0
ksa2s 0
ksa1s
0
ksars
0
a11
a12
a1s
1
a21
,
2
a22
, s
a2s
,
ar1
ar2
ars
ka11
ka12
ka1s
1
a21
通常用希腊字母α, β, γ等表示.
说明
①行向量也是1×n的行矩阵,列向量也是n×1的列矩阵; ②行向量可看作是列向量的转置; ③为统一起见,以后所讨论的向量均指列向量.
分量全为零的向量称为零向量, 记作θ ---读作“西塔”
二、向量的运算
如: (a1, a2 , , an )T , (b1, b2 , , bn )T 定义2. 若向量 和 对应的分量分别相等,即ai=bi ,i=1,2,…,n
a22
,
a1s
s
a2
s
,
a11
a21
a12
a22
a1s
a2s
ar1
ar
线性代数各章学习要点3

第3章n维向量和线性方程组向量是线性代数的重点内容之一,也是难点,对逻辑推理有较高的要求。
本章从研究向量的线性关系(线性组合、线性相关与线性无关)出发,然后讨论向量组含最多的线性无关向量的个数,即引出向量组的秩和最大无关组,最后,应用向量空间的理论研究线性方程组的解的结构。
无论是证明、判断、还是计算,关键在于深刻理解本章的基本概念,搞清楚其相互关系,并会灵活应用。
3. 1 n维向量及其运算定义(n维向量)由数域F中的n个数a-i,a2/ , a n组成的有序数组-■ - ( a i, a2, , a n)a2耳一称为数域F上的一个n维向量,前者称为行向量,后者称为列向量,其中a1, a2 / ,a n称为向量的分量(或坐标)。
分量是实(复)数的向量称为实(复)向量。
如果没有特殊的声明,以下所讨论指数域F上的向量。
行向量可以看成行矩阵,列向量看成列矩阵,向量的运算规定按矩阵的运算法则进行。
以下讨论的向量,再没有指明是行向量还是列向量时,都当作列向量。
设有向量■■ = (a i,a2,…,a n),- - (b1 ,b2 / , b n )则向量相等的定义为- a i = b i (i=1,2,…,n)向量的加法定义为a + P =(a i +b i a? +b2 …a* +b n T数乘向量的定义为k:(「k)二(ka i,ka2, ,ka n)T向量的加法以及数乘运算统称为向量的线性运算,它满足下列8条运算规律(其中:■,'-,为n维向量,k,l为常数):(1)二:+:= :+=;)( :• - ) ( - );(3)存在零向量0= ( 0,0,…,0 ) T,使得〉+0= ;(4)存在:-的负向量-二=(_a i,_a2,…,-a n)T,使得〉+ (-二)=0;(5)仁• = :•;(6)k(l : )=(kl):-;(7)k(: + 1 )=k +k :;(8)(k+l)用=k : +1 :;如果记矩阵A = (a j )m n的第j列向量为:a i ja2jQ j = : , (j=1,2,…,n)貝一则由向量的线性运算,可将方程组Ax=b写成下列形式:论一:* - X2J2…'x n J n二 b而齐次线性方程组A X=0则可写成向量形式:Xv 1 ■ X2: 2 …• X n: n = 03. 2向量组的线性相关性定义(线性组合)设宀,:^,…,〉m是一组n维向量,k1, k2/ ,k m是一组常数,则称向量kr 1 k2: 2 k m: m为向量〉1,〉2,i,〉m的一个线性组合,并称k1,k2 / , k m为该线性组合的系数。
线性代数课件:3-2向量组的线性相关性

定理3.2.2 若向量组α1,α2, …,αm无关, 而α1,α2, …,αm, β 线性相关,则β可由α1,α2, …,αm,线性表出,而且表法唯一。
证 由向量组α1,α2, …,αm, β线性相关, 即存在一组不全为零的数k1,k2, …,km,k使得
k11 k22 kmm k 0.
例3.2.4设向量组α1,α2,α3,α4的线 性无关,证明:
(1)设向量组α1- α3,2α1-α2,2α3-α2线 性相关;
(2)设向量组α1- α2,α2-α3,α3+α1线性 无关。
证(1)设
k1(1 3 ) k2(21 2 ) +k3 (23 2 ) 0 (3.2.4) 即
(k1 2k2 )1 (k2 k3 ) 2 (k1 2k3 )3 0 。
怎样用代数方式表示平行四边形法则?
§3.2 向量组的线性相关性 3.2.1 向量组的线性相关与线性无关 3.2.2 向量组线性相关性的判别法 3.2.3 向量组的线性相关性的一些性质
3.2.1 向量组的线性相关与线性无关 定义3.2.1 设α1 , α2 , … , αm, β都是
数域P上的n维向量,如果存在数域P上的 数k1,k2, …,km,使得
Very important!
设n维向量 1 1,0,,0,
2 0,1,,0 ,n 0,0,,1
则任何一个n维向量α=(a1,a2,…,an) ,都可 由ε1,ε2, …,εn线性表出:
a11 a2 2 an n
我们称ε1,ε2, …,εn为基本单位向量。
定义3.2.2 设α1,α2, …,αm是数域P上 的m个n维向量,如果存在数域P上的m 个不全为零的数k1,k2, …,km,使得
3-2向量组的线性相关性

上页 下页 返回 结束
证明 存在性 ∵ α1,α2, ,αm, β线性相关
∴ 存在不全为 0的k1, k2 , , km , k, 使得 k1α 1+k2α 2+ + kmα m+kβ = 0
3
推论1: 设两个 n 维向量组 A : α1 , , αr ,与B : β1 , , βs , 若向量组A 能由向量组B线性表示, 且 r > s,则向量组 A必线性相关. (如果个数多的向量组能由个数少的向 向量组线性表示,则个数多的向量组必线性相关)
推论2: 设两个 n 维向量组 A : α1 , , αr ,与B : β1 , , βs , 若此两个向量组等价且皆线性无关,则 r = s . (等价的线性无关向量组所含向量个数相同)
⎪⎩ x2 + x3 = 0
由于此方程组的系数行 列式
1 01 1 1 0 =2≠0
011
故方程组只有零解 x1 = x2 = x3 = 0,
所以
向量Байду номын сангаасβ1
,
β
2
,
β
线性无关
3
.
注 若向量组坐标没给出,则用定义做.
上页 下页 返回 结束
二、向量组线性相关性的判定
P67例5
定理1(判别法一)
n个n维向量所组成的向量组 α1,α 2,
1
⎥ ⎥
;
⎢⎣ 3 ⎥⎦
⎢⎣−5⎥⎦
⎢⎣ 2 ⎥⎦
解: 因为向量个数等于向量维数,
1 0 −1 1 0 0 ∴ −2 2 1 = −2 2 −1 = 5 ≠ 0
3-2向量的线性相关性

线性表示, 故向量 β 可由向量组 α1 ,α2 ,α3 线性表示,且
β = α1 + 0α2 +α3 .
例 4 设β = (2, 8, 2, 0) ,
T
α1 = (1, 2, 2, 3) , T α2 = ( 2, 4, 4, 6) , α3 = (1, 0, 3, 6)T
例如基本单位向量组 ε 1 = (1,0,L,0) ,ε 2 = (0,1,L,0) ,L, T ε n = (0,0,L ,1) 和α 1 = (1,0,L ,0)T , α 2 = (1,1,L ,0 )T ,L,
T T
等价。 α n = (1,1,L ,1) 等价。
T
4 例 设有两个向量组 (Ι)α1 , α2 ,L, α ( ) 1 , β2 ,L, β ΙΙ β s t 并设 ( A 并设 = α1 , α2 ,L, α )和B = β1 , β2 ,L, β ), ( s t 是 存在t ΙΙ × 能由( (Ι)能由( )线性表出的充要条件 :存在ts矩 A=BC 阵C,使得 C,使得 使得
AX = β
如果方程组中的 x1 , x2 ,L, xn 分别用 代入后, c1 , c2 ,L, cn 代入后, 可以使每个方程都变成恒等 式,则称有序数组 c1 , c2 ,L, cn 为方程组的一个 解,向量 ------------ X = (c1 , c2 ,L, cn )T 为方程组的一个解向量 方程组的所有解( 解向量。 为方程组的一个解向量。方程组的所有解(或 解集。 解向量)组成的集合,称为该方程组的解集 解向量)组成的集合,称为该方程组的解集。
由3个2维向量组成的向量组线性相关

由3个2维向量组成的向量组线性相关3个2维向量组线性相关是指,一组由3个2维向量组成的向量之间存在线性关系,即它们的线性组合可以表示为它们的标量积。
3个2维向量组线性相关是比较常见的,它们可以用投影和变换来实现,也可以用线性代数的方法来分析。
首先,我们简单地介绍一下什么是一个2维向量。
2维向量就是一条直线,由长度和方向(也可以称为角度)组成。
在数学中,它可以被表示为一个有两个分量的有序对,即(x,y)。
其中的x和y分量分别表示向量的横向长度和纵向长度。
其中,x为横向长度,即从原点((0,0))沿着向量右侧的长度;y为纵向长度,即从原点((0,0))沿着向量上部的长度。
接下来,我们可以用数学语言来描述什么是3个2维向量组线性相关。
假设,给定一组3个2维向量,即:A(x1,y1),B(x2,y2),C(x3,y3)。
若这3个2维向量之间存在线性关系,即,它们的线性组合可以用标量积来表示,则称这3个向量组线性相关。
如果这3个2维向量组中存在2个或2个以上的向量平行,则该组向量不存在线性相关性,只有当所有3个2维向量都不能表示为两个或两个以上的向量的线性组合时,才可以称为线性相关。
此外,3个2维向量组线性相关可以用几种方式来实现和分析。
投影法是一种比较简单的方法,它将3个2维向量映射到一个新的空间中,以形成一个新的“坐标系”,由新的“坐标系”可以更容易地确定3个2维向量之间的线性关系。
另一种是变换法,利用线性代数,将3个2维向量变换到一个新的基准空间,并利用新的基准空间来检验3个2维向量之间的线性关系。
最后,我们来看下3个2维向量组线性相关在实际中的一些应用。
由于3个2维向量构成的空间是一个简单的,它在很多领域都有应用。
比如在科学研究领域,它可以用来描述粒子的线性组合、在几何分析领域,它可以用来解决复杂的角度关系问题等;又如在技术制造方面,它可以用来表示组件的定位关系;在信息技术领域,它可以用来描述向量之间的线性关系等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 -1 -1
ö ÷ ÷ ÷
,a
5
=
æ ç ç ç
-1 1 2
ö ÷ ÷, ÷
ç÷ ç ÷ ç ÷
ç÷ ç÷
è2ø è 4 ø è 0 ø
è6ø è3ø
判别下列向量组的线性相关性 .
(1)a1 ,a2; (2)a1 ,a2 ,a3; (3)a1 ,a2 ,a3 ,a4; (4)a1 ,a2 ,a3 ,a4 ,a5 (5)a1 ,a2 ,a3 ,a5
çæ b1 ÷ö
则b1 = ç a2 ÷, b2 = ç b2 ÷也线性无关.
çè a3 ÷ø
çè b3 ÷ø
设k1b1 + k2b2 = 0
Þ
ïíìkk11aa12
+ +
k2b1 k2b2
= =
0 0
Þ k1a1 + k2a2 = 0
ïîk1a3 + k2b3 = 0
Þ
k1
=
k2
=
0(a1
,
a
线性无关
3 -5 2 3 -5 5
\
α 1
,
α 2
,
α 3
线性无关
é1 ù
é2ù
é-1ù
é1 ù
(2)
α 1
=
êê-2úú
,
α 2
=
ê ê
2
ú ú
,
α 3
=
ê ê
0
ú ú
,
α 4
=
ê ê
2
ú ú
êë 1 úû
êë-5úû
êë 1 úû
êë-2úû
解: 因为向量个数大于向量维数,
\
α 1
,
α 2
,
α 3
,
α 4
αT = a1e1T +a 2 e2T +L+anenT
如:α
=
é2ù êë3úû,
基本向量组为
e1
=
é1ù êë0úû , e2
=
é0ù êë1úû
α = 2e1 + 3e2
线性方程组的向量表示
ì a11 x1 + a12 x2 + L + a1n xn = b1,
ïï í ï
a21 x1 + a22 x2 + L + a2n xn = b2 , LLLLLLLLLLLLLL
线性相关
4
则(l1 - l1 )a 1+(l2 - l2 )a 2+L + (lm - lm )a m= 0
Q
a1
,a
2
,
L,
a
线性无关
m
\ li = li (i = 1,2,L, m)
考虑
a
1
,
a
2线性相关,则a1
,
a
2
,
a
呢
3
?
上页 下页 返回 结束
P53定理3.2
定理4(判别法三) A : a1,a2 ,L,am线性相关,则B : a1,a2 ,L,am ,am+1 L,an 也线性相关;反之,B线性无关,则A也线性无关.
若k = 0, 则 存在不全为0的k1, k2,L, km , 使得
k1a 1+k2a 2+L + kma m= 0
这与
a
1
,
a
2
,
L,
a
线性无关矛盾
m
\
k
¹ 0,
b
=
-
k1 k
a
1-
k2 k
a
2-L
-
km k
a
m
上页 下页 返回 结束
唯一性
若 b = l1a 1+l2a 2+L + lma m, b = l1a 1+l2a 2+L + lma m
证明
çæ 1 ÷ö a1 = ç0÷ ,
çè 0 ÷ø
çæ 0÷ö a2 = ç1÷ ,
çè 0÷ø
çæ 0÷ö a3 = ç0÷
çè 1÷ø
令k1a1 + k2a2 + k3a 3 = 0
即
æ ç ç
k1 k2
ö ÷ ÷
=
æ ç ç
0 0
ö ÷ ÷
çè k3 ÷ø çè 0 ÷ø
\ k1 = k2 = k3 = 0
如
a1
=
éa1 êëa2
ù ú, û
a
2
=
éb1 ù
êëb2
ห้องสมุดไป่ตู้ú û
线性无关,
éa1 ù
éb1 ù
则
b1
=
ê ê
a2
úú,
b
2
=
êêb2
ú ú
êëa3 úû
êëb3 úû
线性无关
上页 下页 返回 结束
3
证明 证
若a1
=
ççèæ
a1 a2
÷÷øö, a 2
=
ççèæ
b1 b2
÷÷øö线性无关,
çæ a1 ÷ö
1
三、线性相关与线性无关
①
1. 定义3 对于向量组A : a1 ,a 2 ,L ,a m ,如果存在不
P52定义3.10 P53定义3.11
全为零的数k1 , k2 ,L, km使 ② k1a1 + k2a2 + L + kmam = 0
则称向量组A是线性相关的,否则称它线性无关.
如 2a1 - a2 - a3 = 0 Þ a1,a2,a3线性相关.
2
)
Þ
b1,
b
线性无关
2
上页 下页 返回 结束
P55 推论3.3
定理6(判别法五)
当m
>
n时,
任意m个n维向量a 1 ,
a
2
,L,a
必线性相关
m
.
例3
设a1
=
æ ç ç ç
1 0 3
ö ÷ ÷ ÷
,a
2
=
æ ç ç ç
2 -1 0
ö ÷ ÷ ÷
,
a
3
=
æ ç ç ç
-3 1 2
ö ÷ ÷÷,a4
=
æ ç ç ç
2. 两向量线性相关 Û 两向量的分量对应成比例
如
α
=
é1ù
ê ë
t
ú û
,
β
=
é ê ë
2t 1
ù ú û
,
则当
t=
±
1 2
时,
α与 β线性相关。
3. 两个向量线性相关的几何意义是两向量共线; 三个向量线性相关的几何意义是三向量共面.
P53例3.6
定理3
向量组
a
1
,a
2
,L,a
线性无关,且向量组
m
故方程组只有零解 x1 = x2 = x3 = 0,
所以向量组b1
,
b
2
,
b
线性无关
3
.
注 若向量组坐标没给出,则用定义做.
上页 下页 返回 结束
四、向量组线性相关性的判定
P56 引理3.2
定理1(判别法一)
n个n维向量所组成的向量组
a
1
,
a
2
,
L
,
a
线性相关
n
Û
向量组
a
1
,
a
2
,
L
,
a
所对应的方阵的行列式
β 1
+
k2
β 2
+Lks
β s
,
则向量α是向量组A : β1, β2 ,L, βs的一个线性组合, 这时
称向量α可由向量组A
:
β 1
,
β 2
,L
,
β
s线性表示.
如:α
=
é3ù êë4úû,
β1
=
é1ù êë1úû
,
β2
=
é1ù êë2úû
α = 2 β1 + β2
注 (1) 若a = kb , 则a与b成比例 . (分量成比例)
解:(1), (2),(5)无关,(3),(4)相关
上页 下页 返回 结束
练 研究下列向量组的线性相关性
é1 ù
é0ù
é-1ù
(1)
α 1
=
ê ê
-2
ú ú
,
α 2
=
ê ê
2
ú ú
,
α 3
=
ê ê
1
ú ú
;
êë 3 úû
êë-5úû
êë 2 úû
解: 因为向量个数等于向量维数,
1 0 -1 1 0 0 \ -2 2 1 = -2 2 -1 = 5 ¹ 0
(2) 零向量是任一向量的线性组合.
O = 0×a1 + 0 ×a2 +L+ 0 ×am
(3)向量组中每一个向量都可由该向量组线性表示.
a1 = 1×a1 + 0 ×a2 + 0 ×a3
(4) 任一n维向量 αT = (a1 , a 2 ,Lan ) 都是基本 向量组 e1T = (1, 0,L, 0), e2T = (0,1,L, 0), enT = (0, 0,L,1) 的线性组合:
a1,a 2 ,L,a m (m
³
2)线性无关
