铁路既有线路的整体拟合整正
高速铁路线路的拟合处理与精度分析

高速铁路线路的拟合处理与精度分析第一章:引言高速铁路在现代交通中担任着不可替代的作用,通过铁路行车时,铁路线路的拟合处理和精度分析,是确保铁路安全和稳定性的重要手段。
第二章:高速铁路线路的拟合处理高速铁路的铁路线路在拟合过程中,需要考虑以下四点内容:2.1 高速铁路线路的轨距设计铁路两条钢轨的距离,即轨距被设计为1435mm,遵循此轨距设计,可以保证高速铁路车辆的稳定性和行车安全。
2.2 高速铁路线路的线性拟合高速铁路线路的线性拟合是指通过采集地表高程等数据,利用线性回归分析方法,得出铁路线路的拟合直线方程,以最小化误差,提高拟合精度。
2.3 高速铁路线路的曲线拟合高速铁路线路中,一些区域存在曲线路段,为保证车辆的稳定性和行车安全,需要对曲线路段进行拟合处理。
曲线拟合主要包括圆前后倾和超高曲线等拟合方式。
2.4 高速铁路线路的交点拟合高速铁路线路中的接口和交点,需要进行拟合处理,通过拟合处理得出正确的交点位置,以最大程度减小车辆运行跳跃和停顿等现象,提高铁路行车安全性。
第三章:高速铁路线路拟合精度分析3.1 高速铁路线路拟合精度分析的方法高速铁路线路拟合精度分析方法可以采用精度对比法、精度分析图法等多种方法。
其中,在方法选择上应根据实际情况和需要确定最适合的方法,以检验铁路线路拟合精度。
3.2 高速铁路线路拟合精度分析的实现高速铁路线路拟合精度分析的实现可以通过编程实现,在实际的拟合数据中进行验证,通过与拟合标准进行对比,确定标准和实际拟合数据之间的误差,以评估拟合精度。
同时,可采用GIS等多种工具软件进行实现加大拟合精度的保证。
第四章:结论高速铁路线路拟合处理和精度分析,是保证高速铁路安全和稳定性的重要手段。
通过轨距设计、线性拟合、曲线拟合和交点拟合等方式,可提高铁路线路的拟合精度。
同时,采用精度对比法、精度分析图法等方法,对拟合处理结果进行精确评估和分析。
总的来说,通过铁路线路拟合处理和精度分析,可有效提高高速铁路行车安全、稳定和舒适性,对于现代化交通的发展起到至关重要的推动作用。
附带曲线的定位与整正

TNTl z yP(yz)G (z y )F (缝中)曲外股工作边K 外xM O'WU V Q 直内股工作边线路中线88ααH z yR 外D 基准=5 000X zy X O单位:mm附带曲线的定位与整正■ 刘彪1 概述陇海线属于我国6大繁忙干线之一,有着车流密度大、年通过总质量大等特点。
列车通过站场侧线股道的频率高,对道岔和附带曲线的冲击大,近年来,伴随着陇海线天兰段设备全面的提升,当客车径路更换无缝线路后,附带曲线成为站场的薄弱地段。
如何整正既有线的岔后附带曲线,特别是在高铁站场中附带曲线的整正,成为工务技术人员研究的共同课题。
附带曲线又名岔后连接曲线[1],是由道岔侧向引出,连接道岔和股道且与道岔导曲线成反向的曲线,且附带曲线应满足以下规定[2-3]:(1)平行股道的线间距不大于5.2 m;(2)辙叉根端至附带曲线始点的夹直线长度不应短于7.5 m,特殊地段不短于6.0 m;(3)半径不得小于该组道岔的导曲线半径,但也不宜大于导曲线半径的1.5倍;(4)设置超高不应大于15 mm,顺坡率不得大于2‰;(5)轨距加宽与一般曲线地段相同,按不大于2‰递减;(6)可不设缓和曲线,但其长度不得小于20 m。
2 利用双向定位法精确定位附带曲线2.1 几何框架及各关键控制点要利用双向定位法准确定位附带曲线,需要道岔的图摘 要:整正既有线的岔后附带曲线,特别是高铁站场中附带曲线的整正,成为工务技术人员的共同课题。
现有整治方法有绳正法、坐标法与直股支距法,其中直股支距法应用较为普遍,但经过多年实践,此计算方法误差较大,整正效果不理想。
在直股支距法基础上提出双向定位法,以附带曲线外股工作边为对象,详细计算附带曲线起点位置G、每个测点在岔后直内股钢轨上的支距H 和水平投影横距差△X ,从而准确定位附带曲线的每个测点位置,达到整正附带曲线的目的。
详细阐述双向定位法的具体推理及作业过程,同时介绍破桩法和整桩法2种不同附带曲线正矢点的布置方法。
既有线能力加强及改建设计习题解答

既有线能力加强及改建设计习题参考解答8-1 改善运营条件(改善平、纵面、道口、轨道加强等),为什么可以提高既有线的通过能力或输送能力?结合通过能力及输送能力的计算公式简要说明。
参考答案:答:改善运营条件包括改善平、纵面,改善和加强道口,加强轨道等,其中平纵面的改善包括加大曲线半径、延长缓和曲线、缓建最大坡度、延长到发线有效长等措施。
(1)改善运营条件对通过能力的提高。
单线通过能力的计算公式为HB F W T 1440t t t t T N +++-=,双线的为LTt t T N +-=1440(半自动闭塞)或IT N T-=1440(自动闭塞)。
由这些计算公式可知,提高通过能力的关键是缩短列车在区间的运行时分,而缩短运行时分的方法有改善信联闭设施、缩短站间距、提高列车的旅行速度。
加大曲线半径、延长缓和曲线、缓建最大坡度、改善道口、加强轨道等都能提高列车的运行速度,自然就能提高通过能力。
(2)改善运营条件对输送能力的提高。
输送能力的计算公式为β6jH 10· 365G N C =,其中G j =G ×K J ,而[]Z Z Z L L L KH KH KH K K H )()()(· 1N N N N N N μεμεμεεα-+-+-+-+=。
也就是说可以提高通过能力和牵引吨数来提高输送能力。
由前面论述已知改善运营条件能提高通过能力,而提高牵引吨数的措施中就包括延长到发线、降低最大坡度、加强轨道等改善运营条件的措施,所以改善运营条件能提高通过能力。
8-2 简述既有铁路能力加强中,提高通过能力的措施。
参考答案:答:提高通过能力的措施有行车组织措施、改换信联闭装置、增设车站和线路所和增建第二线及其过渡措施。
行车组织措施包括缩短控制区间的运行图周期、采用特种运行图、减少旅客列车扣除系数等。
采用较完善的信号、连锁、闭塞装置,可使列车在车站上交会、越行的作业时间缩短,从而提高通过能力。
铁路曲线整正教学

步骤九、曲线拨量优化
如所得拨量太大,不宜 拨动,可以采用“对称调整 正矢”方法,将拨量调整得 小些。
如上例中: 所计算的最大拨量为-84mm, 现需拨量小,以最大拨量点 为中心(表中第12点)在该 点前段和后段分别将正矢作 对称调整。如需将负的半拨 量调小,在前段用“上减下 加”,后段用“上加下减”。 (如将正的半拨量调小时, 可在前段用“上加下减”, 后段用“上减下加”。)
长。
渐伸线原理
渐伸线的特性
渐伸线的法线M3N3,M 2N2,…就是对应点上
的原曲线切线;
渐伸线上任意两点曲率半
径之差(M3N3-M2N2),等 于对应点上圆曲线弧长
(N3N2)。
曲线上任一点拨动时都
曲线拨动假设
沿渐伸线方向;
曲线拨动前后,其长 度不变。
拨量计算
n 点沿拨前曲线An上各点的切线方向展开, 则n点所走过的轨迹 n n '' 称为n点的渐伸 线,其长度为En 。 同样拨后曲线段 An’ 的渐伸线为n’ n '' ,长度为En’ 。
实测正矢 104 103 106 105 102 102 101 83 60 36 21 4
步骤一、计算曲线的理论正矢并检验合格情况
根据公式计算计划正矢填入表格 查表,容许偏差为“5、10、15” 检查缓曲现场正矢与理论正矢差 检查圆曲线正矢连续差 检查圆曲最大正矢与最小正矢差
步骤二、编制计划正矢
划 正 矢
f
f'1230 Nhomakorabea0f0′
1 f1
f1′
2 f2
f2′
3 f3
f3′
4┇ ┇
┇┇
┇┇
┇┇
n fn
基于遗传算法的既有铁路曲线整正优化设计

快还将 降低砂 浆 与钢 筋 的 黏结 强 度 。 因此 , 芯 升 温 板
速度 不 宜超 过 1 0℃/ 。第 三 , 工 艺 上解 决 , 化 混 h 从 优
应 力 施 工 关 键 技 术 [ ] 铁 道 建 筑 ,0 0 3 :0 8 . J. 21 ()8—1
[ ] 恩 龙 . R SI 无 砟 轨 道 板 制 造 技 术 [ ] 建 筑 机 械 技 术 3张 C T I型 J.
与 管 理 ,0 8 6 :0 9 . 2 0 ( ) 9 —4
但是 考虑 到升温 速度决 定着 残余 变形 的大小 及脱模 强
度, 升温越 快 , 需临 界 初始 结 构 强 度 也越 高 , 温 过 所 升
[] 4 中华 人 民共 和 国铁 道 部 . 技 基 [ 0 8 7 科 2 0 ] 4号 客 运 专 线 铁 路双块式轨枕无砟轨道双块 式混凝土轨 枕暂行 技术条件 [ ] s.
铁 2 1 年 第 3期 01
道
建
筑
Ra l y Eng n e i iwa i e rng
文 章 编 号 :0 3 19 (0 1 0 — 1 10 10 —9 5 2 1 )3 0 1 —3
基 于遗传 算 法 的既 有 铁 路 曲线整 正 优 化 设 计
孙 晓丽 , 蒋红 斐 , 石 星
水拌合 混凝 土 , 道板芯 部温 度不 超过 5 轨 5℃ 。但 是 笔
者也 发现 了一些 问题并 提 出相 应改 进措施 。 1 在静停 期和 升温 期 , 块温 度 和板 芯 温 度 不 能 ) 试 很好一 致 。由于入模 后影 响板 芯温 度的 因素 除了模 板 之外还 有环境 温度 、 周边 混凝 土温度 场等 , 控制 系统应 将 所有影 响 因素一并 加 以考 虑 , 而对 电加 热量 进 行 进 实时调 节 , 控制 水 温 。从 而达 到 试块 温 度 自动 与构 件 芯 部温度 相一致 , 现试 块 与 轨 道板 构 件 同条件 养 护 实
铁路既有曲线整正测量方法

V O1 1 O . .5 N 3
S p. 0 e 2 02
铁 路 既 有 曲 线 整 正 测 量 方 法
匡 华 云
( 阳铁 路 工 程 学 校 湖 南 衡 阳 衡 4 10 ) 2 0 1
摘 要 : 出 了全 站 仪 任 意 点 设 站 测 量 既 有 曲 线 上 点 的 坐 标 的 方 法 , 曲 线 整 正 中 的 半 径 选 择 , 和 曲 线 长 给 对 缓 度 选 配 , 距 计 算 方 法 进 行 了探 讨 , 论 的 方 法 及 推 导 的 公 式 可 以 直 接 应 用 于 既 有 曲 线 整 正 作 业 。 拨 讨
KUANG a — y n Hu — u
( n y n ala n ie r g sh o , n y n 4 1 0 ia He g a g R i y E gn ei c o l He g a g,2 0 1Chn ) w n
Absr c Th s a e e l t h t o f h w o u e t e l cr n c — ttl— sa in i sr me t p a e t ta t i p p r d a s wi t e me h d o o t s h ee to i h oa tto n tu n , l c d a a y p i t t e e mi e t o r n ts o ont fp i t n o e ae a l y c r aur i e. tas t d e h r b- n o n ,o d tr n he c o dia e fp i s o o ns o p rt d r iwa u v t e ln I o su id te p o l
c r e a l s te c ve a l a h u e v co , i h c n b ie t s d i e t c to r fo e ae u - u v s wela h ur s wel st e c r e t r wh c a e d r c l u e n r ci a in wo k o p rt d c r v y i f v t r i e。 au e ln
铁路既有曲线整正计算中基于坐标法的渐伸线误差分析研究

Absr c : ta t App y n he r lv ntkn wl d fg o e r l i g t e e a o e ge o e m t y,we a l s d t e t or f c m p i g t e a l a e O— na y e h he y o o utn h loc t d C or i t s i c or a e wih t r c lni g d s a e a d t e t or fc l ultn h nv l t lo a e e s n d na e n a c d nc t he ta k i n it nc n h he y o ac a i g t e i o u e a l c t d v r i e
( . h o fCii En ne rn 1 Sc o l vl gi e ig。 S u h s ioo g Unv riy, Ch n du61 0 I, Chn o o t we tJa tr ie st eg 03 ia;
2 S h o fCii En ie rn , La z o ioo g Un v riy , La z o 3 0 0, Chn ) . c o lo vl gn eig n h u Ja tn ie st nh u7 0 7 ia
关 键 词 : 曲线 整 正 ;渐 伸 线 ;偏 角法 ;坐 标 法 ;拨 后 正 矢
中 图分 类 号 : 1 . 2 U2 6 4 6 文 献标 志码 :A d i1 . 9 9 ji n 1 O — 3 0 2 1 . 4 0 4 o :0 3 6 /.s . O 18 6 . 0 2 0 . 1 s
applyingtherelevantknowledgeofgeometryweanalysedthetheoryofcomputingtheallocatedcoordinatesinaccordancewiththetrackliningdistanceandthetheoryofcalculatingtheinvoluteallocatedversinewithformulasweproposedamethodforconvertingdatameasuredbythedeflectionanglemethodintothereleantdataessentialtothecoordinatemethodadoptingthesameradiusofcurveandthesamelengthoftransitioncurvewecomputedthetrackliningdistancesandallocatedversineswiththedeflectionangleandcoordinatemethodsrespectivelycomparingtheresultsofthetwomethodswefoundoutthemagitudesandlawoferrorofthetrackliningdistanceandallocatedversineoftheinvolutemethodanalyticalresultsindicateasfollowerrorsofthetrackliningdistanceandallocatedversineareallrelatedtothesizeofthedeflectionanglethecalculationaccuracycanmeetthebasicrequirementsofcurverealignmentkeywords铁路既有曲线整正计算中基于坐标法的渐伸线误差分析研究83上述文章都详细论文利用现场测得首先利用偏角法通过优化计其对应的最优半径和缓和曲线料转化为坐标法所需要的曲线半径及缓和曲线长度条然后利用公式计算出偏角li120sini1sini1arcsin20i1180li20sini1sin20sini120sini1为i1lcosilisiniyi为各计算点转化5712yj的偏角法优化出的曲线半坐标法即可计算出各测点zhhy在偏角法的测
基于三次样条曲线的铁路既有曲线整正方法

本文在分析三次样条曲线表示铁路既有 曲线平 面线形 时产生 的误差 组成 及影 响因素 的基础 上 ,提
出 1 既有 曲线 的整正方 法 。 种
1 三次样条 曲线表示铁路既有 曲线平 面线形 的理论可行性
目前 ,理论 较为成熟 的 曲线拟合 方法有 L — a
gag 多项 式 插 值 、分 段 低 次 Hemi rn e r t 项 式 插 e多
求得 △ 。 j 变换 R, , L 的值 即可求得它们对 aL和 z
2 三次样条 曲线拟合铁路 既有 曲线平
面线形 的误差组成
铁 路 既有 曲线 的平面 整正 需要 曲线上 一 系列有
拟合 误差 的影 响 。
序离散测量点数据。依据这些离散的测点数据估计
整条 既有 曲线线 形属 于逆 向工 程 曲线重构 中的拟合 问题¨ 。 曲线 重构 误差 ( 合误差 )反 映 曲线 的拟 6 ] 拟
要来 自数学模 型产 生的拟合误差和既有曲线变形产 生的拟合误 差。既有 曲线参 数对拟合误 差影 响的分析结果表 明:数学模型产生的既有 曲线 曲率 、一阶导数 和点 位拟合误 差随既有 曲线半径 的增 大而减 小,三者的最大值 随 着既有曲线缓和曲线长度 的增大有先降后增的趋势 ,既 有曲线 的总 转角对三 者的影 响较小 ,可忽略不计 。既 有 曲线变形产生的既有曲线点位拟合误差近似等于既有 曲线 的变形量 。在此 基础上 ,提 出 1种能够得 到既有 曲线 上任意一点拨距量的整 正方法 ,并利用 VC ++6 o软件编制相关计算程序 ,且用实例 验证 了此方法 的实用性 。 . 关键词 :三次样条 曲线 ;拟合误差分 析;既有线 ;平面线形 ;既有 曲线 ;整正方法
中 图 分 类 号 :U 1 . 3. 22322 文 献 标 识 码 :A
曲线整正

工程项目部二零一二年二月二日铁路曲线一般包括圆曲线和缓和曲线两部分,是为线路转向设置的,它是线路的薄弱环节。
铁路既有曲线在经过长期运营后,其平面线型和曲线要素会发生变化,容易出现晃车病害,所以应加强曲线检查和整修,保持其良好状态。
(一)定义:1. 当列车因地势地形影响,由一个方向转向另一个方向时,列车不可能在两直线成折角的线路上运行,必须在两直线间用一定长度的弧线来连接,这种改变列车折角运行而连接两直线间的弧线成为平面曲线。
分为两种,一种是圆曲线,另一种是带缓和曲线的圆曲线。
(三)圆曲线测量曲线轨道方向整正曲线正式为保证曲线轨道平面位置的正确和圆顺,当现场正式与计划正式超过容许偏差标准时,应及时进行整正。
圆与矢的关系:在圆曲线上两点间拉一直线,此直线段叫做弦。
弦上任意点到圆曲线上的垂直距离叫正式(或矢距),在弦中央点对应的矢距叫正矢,R=半径AB=弦AC.CB=半弦FG=矢距CD=正矢(二)结构状态检查为及时掌握线桥设备的技术状态,防止出现较大的结构损伤,建立了全面的线桥设备结构状态检查制度,根据设备的类型等具体情况,制订了相应的检查周期。
①每月对道岔结构全面检查一遍;②每季对联结零件全面检查一遍;③每季对无缝线路钢轨位移全面观测一遍;④每季对拱桥、结合梁桥和其他重要桥涵设备全面检查一遍;⑤每半年对桥面全面检查一遍;⑥每年对所有桥涵设备全面检查一遍;⑦对严重病害地段和薄弱处所应经常检查、观测。
⑧对无砟轨道结构定期全面检查,尤其对轨道板、乳化沥青砂浆、底座板等结构出现的裂缝、掉块、预埋套管失效、碎裂等要重点检查。
(三)沉降区域观测为全面掌握京津城际铁路的沉降变化情况,探索其对动车组运行安全和线桥设备质量的影响,制订了京津城际铁路沉降观测和定期分析制度,对京津城际铁路的沉降变化进行了全面监控。
①铁道部第三勘察设计院在承担全线三维精测网的复测、管理的基础上,增加全线高程代用网复测、三处沉降区域的设标网和轨面高程测量等工作,并对数据进行统计分析。
既有铁路曲线整正平差算法

αx l 0 αyl0
(7)
直点) ,圆曲线半径和缓和曲线长度 ;还需要根据 平差计算得到的观测值的改正值来确定整正拨距 量。
3. 1 特征点识别
整体平差之前要初步识别曲线的特征点 ,传 统的方法是按照直线 、缓和曲线 、圆曲线的曲率变 化规律结合曲率图进行判断 。理论上直线段曲率 应为零 ,缓和曲线段的曲率变化为定值 ,圆曲线曲 率为定值 ,曲率变化为零 。对铁路而言 ,直缓点 、 缓圆点 、圆缓点 、缓直点往往产生错动 ,如图 3 所 示 。一般情况下 ,特征点不易判断准确 ,为此 ,可 采用稳健估计方法[4 ] 进行特征点识别 。首先根 据曲率图大致判定哪一段属于直线段 、缓和曲线 或圆曲线段 ,初步识别后 ,分别建立曲线误差方 程 ,采用稳健估计进行处理 ,不属于该曲线类型的 点在稳健估计时自动删除 。
图 2 缓和曲线 Fig. 2 Transition curve
任何一段铁路曲线均由上述 3 种线形组合而
成 ,均可由式 (2) 、式 (4) 和式 (6) 建立总的误差方
程
V = AδX + l
(8)
对于由直线 —缓和曲线 —圆曲线 —缓和曲线
—直线组成的典型铁路曲线段 , 每个直线段有参
数 k1 , k2 , x i ;圆曲线段有参数圆心坐标 ( x 0 , y0) 、 圆心半径 R 及圆心角φi ;每个缓和曲线段有参数 缓和曲线总长度 l0 、缓和曲线上每点的缓和曲线 长度 li 。一条典型曲线上若有 n 个点 , 则平差中 有 2 n 个观测值 , n + 9 个未知参数 。
标系 xB y , XO Y 为线路工程坐标系 , 则缓和曲线
在局部坐标系 xB y 中的参数方程为
xi
绳正法整正铁路曲线探讨

绳正法整正铁路曲线探讨作者:张玉龙来源:《科学与财富》2013年第05期摘要:铁路曲线整正,是把已变形的不规则曲线中线,拨正到接近于既有线路平面的正确位置。
目前,既有铁路曲线整正方法主要是绳正法。
针对绳正法在整正曲线过程中存在的问题,提出了在计算过程中如何调整正矢的方法,确保原有曲线的设计要素,进而保证曲线的圆顺度,确保列车安全、平稳的运行。
关键词:整正曲线绳正法现场正矢计划正矢铁路曲线轨道在列车的动力作用下,特别是横向水平力的作用下,可产生变形,其中最常见的变形形式是曲线轨道方向的变化,结果轨道不能保持原设计的圆顺度。
为了保证行车的平稳与安全,有必要进行定期的检查,并及时整正曲线使曲线轨道恢复到原来的设计位置,保持曲线轨道良好的圆顺度。
《铁路线路修理规则》中规定:线路直线地段轨向不良,可用目测方法拨正。
曲线地段轨向不良,可用绳正法测量、计算与拨正。
绳正法,就是利用曲线上的正矢与曲线的关系,改正正矢,使之恢复原有的设计曲率,并通过相应的拨量,把它拨正到原来的设计位置。
一、绳正法整正曲线的方法及步骤用绳正法进行曲线整正主要分为量、算、拨三个步骤。
这三个步骤是互相衔接、互相关联的,一个步骤发生了错误,都直接影响曲线整正的质量。
1、量是在现场量取曲线上测点的正矢。
测量现场正矢是曲线整正计算前的准备工作,这项工作虽然简单,但非常重要,其准确度直接关系到接下来的计算工作,并影响到拨正后曲线的圆顺程序。
因此,应从主观和客观两方面入手,力求减小误差、提高精度。
测量正矢时要求做到:“三不”,“三要”和“两准确”。
“三不”是:在大风情况下不测;弦线拉的时紧时松用力不一致时不测;弦线未放在轨面下16mm处不测。
“三要”是:要用细而光滑弹性小且坚实的弦线;要在板尺、弦线、视觉三垂直时读数;要先压除线路鹅头,反弯,消灭接头支嘴时再测。
“两准确”是:读数要准确,记录要准确。
2、算是计算出整正曲线的拨道量。
计算曲线各测点拨道量时,经常会出现计划正矢总和与现场实测正矢总和不一致情况以及正矢差累计不为零的情况;传统的做法是调整计划正矢消除以上两种不一致的情况。
绳正法整正铁路曲线探讨

《 铁路线路修理规贝 J l 》 中规定: 线路直线地段轨 向不 良, 可用 目测方法拨 正 曲线地段轨 向不 良, 可用绳正法测量、 计算 与拨正 。 绳正法, 就是利用曲 线上 的正矢与 曲线 的关系 , 改正正矢, 使之恢 复原 有的设计 曲率 , 并通过相 应的拨量 , 把它拨正到原来的设计位置。 绳正法 整正 曲线 的方法及步骤 用绳正法进行曲线整正主要分为量 、 算、 拨三个步骤。这三 个步 骤是互 相衔接、 互相关联的, 一个步骤发生了错误 , 都直接影响曲线整正 的质量 。 1 、 量是在现 场量取 曲线上测点的正矢。测量现场正矢是曲线整 正计算
正法在整 正曲线过程 中存在 的问题 , 提 出了在 计算过程 中如何调整 正矢 的方法 , 确 保原有 曲线 的设计要素 , 进而 保证 曲线 的圆顺 度, 确保列车 安全、 平稳
的运行 。
关键 词: 整正 曲线 绳正法 现场正矢 计划正矢
铁路 曲线轨道在列车的动力作用下, 特 别是横 向水平力的作用 下, 可产 生变形 , 其中最常见 的变形形式是 曲线轨道 方向的变化, 结果轨道不 能保持 原设计 的圆顺度。为了保证行车的平稳与安全 , 有必要进行定期 的检查, 并 及时整正 曲线使 曲线轨道恢复到原来的设计位置,保持曲线轨道 良好 的圆
全、 平 稳 运 行 的 重 要 环节 。
、
前 的准备工作 , 这项工作虽然简单 , 但非常重 要, 其准 确度直接关系到接 下 来的计算工作, 并影 响到拨正后 曲线的圆顺程序 。因此, 应从主观和 客观两 方面入手, 力求 减小误差、 提高精度。 测量正矢时要求做 到: “ 三不” , “ 三要 ” 和‘ 两准 确” 。 “ 三不 ” 是: 在大风情况下不测 ; 弦线拉 的时紧 时松用 力不一致 时不测 ;
项目教学-铁路曲线整正

f1 f23 1 20.6 20.6mm f 2 f 21 2 20.6 41.2mm
f5(HY)=f19= fc-fs/6=100mm
步骤三、计算正矢差
正矢差=现场正矢-计划正矢 正矢差的合计数为零
步骤四、计算差累计
“斜加平写”, 这一列的合计数为终点的半拨量, 应当为0, 因而需要对计划正矢进一步修正。
的弦线,两端拉紧并贴靠轨道外轨内侧轨顶面下16mm处,
在弦线中点准确量出弦线至外轨内侧的距离。(读数的精度
上,一般要按四舍五入取整到毫米。测量3次,取其平均值。)
现场实测正矢要求
“三不”
1. 在大风情况下 不测; 2. 弦线拉的时紧 时松、用力不 一致时不测; 3. 弦线未放在轨 面下16mm处不 测。
50000 50000 f 100 (mm ) R 500
fc=100mm 注:fc 表示圆曲线的正矢。
测点在缓和曲线始、终点上的正矢计算
“缓和曲线正矢递增率”,用 fs 表示
f0(ZH) = fs/6 f1 = f s f2 = 2fs … fn(HY)= fc-fs/6 fn+1 = fc
“三要”
1. 要有细而光滑 坚实的弦线; 2. 要在板尺、弦 线、视觉三垂 直时读数; 3. 要事先压除鹅 头,消灭接头 支嘴后再测。
“两准确”
1. 读数准确; 2. 记录准确。
该项工作是计算前的准备工作,虽然简单,但非常重要,其准确度 影响到拨正后曲线的圆顺。因此,力求减小误差、提高精度。
曲线测点分桩示意图
2
i 0
i n 1 j i
f
j 0
结论:第n点的渐伸线长度En,等于到前一点(n-1)为止的正矢 累计的合计数的两倍。
既有线平面拟合及优化方法研究

其 中, i 为 测 点编 号 , m为 总测 点数 , △ 为第 i 个 测 点 的拨量 , 值 为正 表 明测 点在拟 合 曲线 内侧 , 反 之在 外 侧 。
_ 厂 = ∑ 。 △ 2 = 厶 m 。 [ J( x , - X o ) + 一 I 1 o ) 。 一R ] _ ∑ 。 [ 厂 _ ) 2 + 广 ) z 斗 一2 R \ / ( ] c ) 2 + 广y 0 ) 刁
理论, 并 且置镜 点可 以在轨 道外 , 短直 线边 可 以通 过 多测量 点 内业拟 合得到 , 可靠 性高 。 因此 推荐
理 论上 圆 曲线段 各等分 点正矢相 等 , 缓和 曲线 段 各等 分点 正矢成 比例变 化 , 直 线段 正矢 为零 。但
实际 上 由于 既有 线运 营影 响使 得 线路 产 生变 形或
到 设计质 量 、 工程 品质和 车辆运 营安 全“ 。 目前 既有线 计算 方法主 要有两类 , 一类 是基于
( 1 )
渐 伸线 原理发展起 来 的方法 , 如矢距 法 、 偏角 法 、 绳
正 法等 ; 另一类 是坐标 法 乜 。由于渐伸 线法 具有理
论 不严 , 计 算工作 量大 , 误差难 以控制 , 对测 量要求
拟合功能和矩阵计算功能应用到数值计 算中, 利用雅克比迭代思想求解 了Z H , H Y, Y H, H Z等既有线曲
线要 素 。
【 关键 词】 既有线 拟合
最 小二乘
拨量 计算
里程范 围 , 为后 续分段 拟合求 解直线 、 缓和 曲线 、 圆
在 既有 线 改造 和 新线 接轨 设 计 中 ,既有 线测 量、 拨量计 算及 参数拟 合都 是十分重 要而繁 琐 的工
铁路既有曲线整正方法的探讨

铁路既有曲线整正方法的探讨摘要:阐述了三种铁路曲线整正常用的方法以及这三种方法的优缺点及使用情况进行讨论。
关键词:铁路曲线整正缓和曲线一、背景铁路既有曲线在经过长期运营后,其平面线型会发生变化,已非缓和曲线和圆曲线所组成的标准线型,具体表现为曲线的偏角、半径、缓和曲线长度等线型参数与最初的设计值不符。
陇海线小半径曲线多,更加明显。
要得到这些发生变化后的参数,对它进行整正,将已变形的曲线恢复到标准线型,只有先对既有曲线进行测量,然后依据某种理论在测量数据的基础上推算出曲线的平面线型参数,最终得出将曲线恢复为标准线型的曲线拨量。
目前铁路曲线常用的整正方法主要有绳正法(正矢法)、偏角法、坐标法。
本文将针对这三种主要方法进行探讨。
二、三种整正方法的原理及算法1、绳正法(正矢法)绳正法是铁路曲线日常养护维修的主要方法之一。
现在日常维修中采用的一般方法是简易拨道法,即测量完曲线正矢后,计算拨量时只考虑正矢超限的几个点,对这几个点的曲线正矢进行调整。
简易拨道法测量、计算简单方便。
当简易法把曲线越拨越乱时,再用渐伸线法对整条曲线进行全面整正。
该方法的原理及计算都比较简单,现以以下曲线为例进行说明。
该计算表通过现场测量出的曲线正矢,计算出曲线的实际半径及各点计划正矢,进而得出曲线的整正拨量。
2、偏角法[1]偏角法是也是一种比较常用的测量方法,它是利用经纬仪测出曲线各观测点的偏角,然后根据渐伸线原理来进行既有曲线的计算。
利用渐伸线原理计算拨量的步骤①测量渐伸线长(根据偏角计算的渐伸线长度)按下式计算:Ek+j=Ek+(∑βk+γj)lj (1)式中Ek+j:第k置镜点后第j测点的测量渐伸线长,k∈{1,2···m},j∈ {1,2,···n}Σβk:第k置镜点的累计偏角γj:第j测点的偏角lj:第j测点到其置镜点的里程差②渐伸线函数的一阶导数是曲线的角函数,二阶导数是曲线的曲率函数,所以可以根据测量渐伸线长利用差分法来估算曲线的线型参数。
铁路轨道复合不平顺的分析与整治

轨道复合不平顺的分析与整治轨道复合不平顺是指铁路轨道同一地点存在多种病害或相邻地点存在连续多处同一种病害。
轨道复合不平顺比轨道单项不平顺对行车安全威胁性更大,对于此类病害应引起高度重视,特别是在铁路第六次提速区段,建议将此类病害提级处理,即一级病害按二级及以上病害处理;二级病害按三级及以上病害处理。
迄今为止,我国铁路尚未对轨道复合不平顺规定过安全标准值,但是因其对行车安全威胁性大,有必要对其加以探讨。
轨道复合不平顺的形式很多,按照引起机车车辆横向力、垂向力复合方式不同,分为逆相位复合不平顺、顺相位复合不平顺、谐波振动复合不平顺等主要三种形式。
一、轨向、水平逆相位复合不平顺当存在轨道方向不平顺引起的车辆横向力与轨道水平不平顺引起的车辆横向力作用一致时(如图1所示:方向为正,水平为负),为轨道轨向、水平逆相位复合不平顺,对列车运行安全威胁最大。
图1 轨向与水平逆相位复合不平顺示意图1、轨道方向复合复合不平顺的计算公式如下:△y = ∣y―1.4△ h∣(公式1)式中:△y ---方向不平顺复合值y ----- 方向不平顺值△h --- 水平不平顺值2、轨道轨向、水平逆相位复合不平顺对行车安全指标的影响我们直接引用西南交通大学翟婉明教授著《车辆—轨道耦合动力学》对此项病害的计算结果(见表1)。
需要说明的是,这里选用的是一个波长为10米的方向不平顺,对应波长为12.5米的水平不平顺的逆相位复合不平顺。
表1:轨道复合不平顺对行车安全指标的影响表中:△h ----水平不平顺值y ----- 方向不平顺值P ------ 轮轨垂向作用力Q ------ 轮轴横向水平力Q/P ------ 脱轨系数△P/P ----轮重减载率a cy--------- 方向不平顺引起的水平加速度a c△h ------- 水平不平顺引起的水平加速度从表中可以看出,对轨道水平和方向逆相位复合不平顺安全限值起主控作用的动力学系数是轮重减载率,将轮重减载率静态指标控制为≤0.60,准静态指标控制为≤0.65,动态指标控制为≤0.80,脱轨系数动态指标控制为≤0.80。
铁路曲线整正教学

现场实测正矢要求
“三不”
1. 在大风情况下 不测;
2. 弦线拉的时紧 时松、用力不 一致时不测;
3. 弦线未放在轨 面下16mm处不 测。
“三要”
1. 要有细而光滑 坚实的弦线;
2. 要在板尺、弦 线、视觉三垂 直时读数;
3. 要事先压除鹅 头,消灭接头 支嘴后再测。
缓和曲线的正 矢与
计算正矢差 (mm)
圆曲线正 矢
连续差 (mm)
6
12
圆曲线正矢 最大
最小值差 (mm)
18
5
10
15
4
8
12
3
6
9
R>800 Vmax≤120 km/h
3
6
9
Vmax >120km/h
2
4
6
即我们平常所说的“三、六、九”
现场正矢测量图片
现场实测正矢方法
先在曲线上每10m设测点(用弦代替弧),再用一根20m长 的弦线,两端拉紧并贴靠轨道外轨内侧轨顶面下16mm处, 在弦线中点准确量出弦线至外轨内侧的距离。(读数的精度
fc
10 2 2R
1000
50000 R
(mm )
算例一
圆曲线正矢计算
已知: 曲线半径
解:
R=500m, 弦长20m,
f 50000 50000 100(mm)
R
500
计算: 圆曲线的正矢值。
fc=100mm 注:fc 表示圆曲线的正矢。
测点在缓和曲线始、终点上的正矢计算
“缓和曲线正矢递增率”,用 fs 表示
“两准确”
北方地区铁路 曲线轨道方向的整正
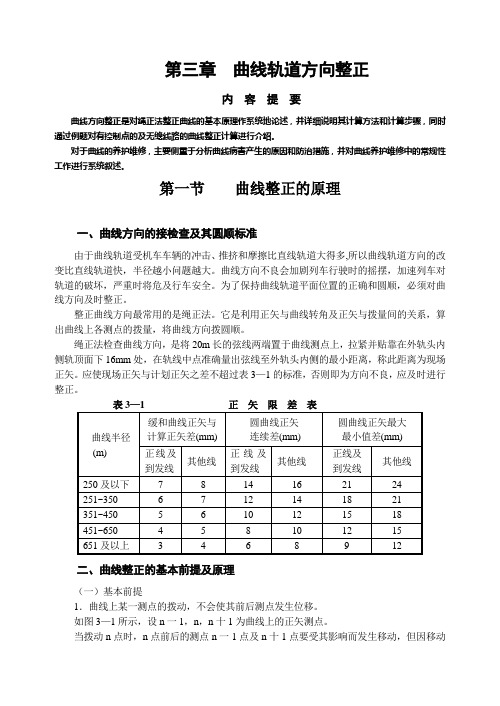
第三章曲线轨道方向整正内容提要曲线方向整正是对绳正法整正曲线的基本原理作系统地论述,并详细说明其计算方法和计算步骤,同时通过例题对有控制点的及无缝线路的曲线整正计算进行介绍。
对于曲线的养护维修,主要侧重于分析曲线病害产生的原因和防治措施,并对曲线养护维修中的常规性工作进行系统叙述。
第一节曲线整正的原理一、曲线方向的接检查及其圆顺标准由于曲线轨道受机车车辆的冲击、推挤和摩擦比直线轨道大得多,所以曲线轨道方向的改变比直线轨道快,半径越小问题越大。
曲线方向不良会加剧列车行驶时的摇摆,加速列车对轨道的破坏,严重时将危及行车安全。
为了保持曲线轨道平面位置的正确和圆顺,必须对曲线方向及时整正。
整正曲线方向最常用的是绳正法。
它是利用正矢与曲线转角及正矢与拨量间的关系,算出曲线上各测点的拨量,将曲线方向拨圆顺。
绳正法检查曲线方向,是将20m长的弦线两端置于曲线测点上,拉紧并贴靠在外轨头内侧轨顶面下16mm处,在轨线中点准确量出弦线至外轨头内侧的最小距离,称此距离为现场正矢。
应使现场正矢与计划正矢之差不超过表3—1的标准,否则即为方向不良,应及时进行整正。
二、曲线整正的基本前提及原理(一)基本前提1.曲线上某一测点的拨动,不会使其前后测点发生位移。
如图3—1所示,设n一1,n,n十1为曲线上的正矢测点。
当拨动n点时,n点前后的测点n一1点及n十1点要受其影响而发生移动,但因移动甚小,可假设其不动。
由于测点间距愈大,拨量愈小,此前提的可靠性愈高。
所以,在整正曲线计算中,应适当限制拨量,以保证质量。
2.曲线上某一测点向外或向内有一拨量,则其相邻两测点的正矢将相应减小或增大此拨量的一半。
如图3—1所示,当n 点向外的拨量为e n 时 ,其前后两测点的正矢f n+1及f n-1将各减少2ne 。
反之,其前后两测点的正矢将各增加2n e。
因此,若n -1点的拨量为e n+1,n 点的拨量为e n , n+1点的拨量为e n+1,则n 点拨量后的正矢为:⎪⎭⎫⎝⎛+-+=+-211/n n n n ne e ef f(3—1)(二)基本原理1.曲线整正前后,应保持曲线两端直线方向不变。
铁路既有曲线整正计算方法研究

铁路既有曲线整正计算方法研究刘永孝;张咏军【摘要】将偏角法实测数据转化为坐标法需要的坐标数据,分别用偏角法和坐标法计算各自的拔距值,并将两拨距值进行对比分析,从而得出渐伸线法计算的误差大小.同时通过计算两种方法的拨后正矢,分析其差值的规律,进而得出了一些有益的结论,对曲线整正计算方法的改进有一定的借鉴意义.【期刊名称】《铁道建筑》【年(卷),期】2010(000)011【总页数】4页(P116-119)【关键词】曲线整正;渐伸线;偏角法;坐标法【作者】刘永孝;张咏军【作者单位】兰州交通大学,土木工程学院,兰州,730070;兰州交通大学,土木工程学院,兰州,730070【正文语种】中文【中图分类】U216.42+6在既有线平面改建及日常线路的大、中维修中,多根据外业测得的曲线正矢、偏角及测点坐标来确定使该曲线保持圆顺所需要的曲线半径、缓和曲线长度,进而计算出各计算点的拨道量[1]。
铁路曲线整正常用的计算方法有三种,即偏角法、绳正法、坐标法。
其中偏角法和绳正法是基于渐伸线原理进行计算的,计算结果有一定的近似性,对外业施测和内业计算有相应要求,在一定条件下是满足测量和计算精度要求的[2] 。
而坐标法具有理论严密、公式推求准确、测量计算成果精度高等优点[3] 。
在这些拨道计算方法中,以往都是将它们独自分隔开来,并且分析渐伸线误差及适用范围时,都采用了理论分析方法,很少针对实测数据进行对比研究。
本文针对同一条曲线,选用相同的曲线参数,将这三种方法结合起来,研究它们之间的转化公式,计算出各自的拨量值,同时将它们的计算结果进行对比,分析出利用渐伸线整正曲线的误差大小及规律。
1 曲线整正计算方法间的转化关系分析1.1 偏角法转坐标法如图1所示γi-1=180°-(βi-1 -αi-1)根据余弦定理有式中αi——i测点的累计偏角;βi-1——i-1 测点与后一测点 i的 20 m 的弦与水平线形成的夹角;图1 曲线计算示意Ei——i点的渐伸线长度;γi-1——i-1 点的视距线与 i-1 测点与后一测点i的20 m的弦线间的夹角; li——各计算点与置镜点的距离,也就是视距。
整正及增改建既有铁路曲线方法

整正及增改建既有铁路曲线方法
李伟
【期刊名称】《铁道勘察》
【年(卷),期】2005(031)004
【摘要】总结了既有曲线常用的测设方法,介绍整体优化坐标法的理论和优化方法,以及全站仪任意点置镜极坐标法测量既有曲线的工作方法和数据处理软件.
【总页数】3页(P37-39)
【作者】李伟
【作者单位】中铁郑州勘察设计咨询院有限公司,河南,郑州,450052
【正文语种】中文
【中图分类】U2
【相关文献】
1.关于铁路曲线整正拨道量修正新方法的探讨 [J], 廖显军
2.既有铁路曲线整正计算中的计划正矢计算方法的研究 [J], 刘永孝;刘学毅;李斌;代丰
3.基于遗传算法的既有铁路曲线整正优化设计 [J], 孙晓丽;蒋红斐;石星
4.全站仪整体优化坐标法整正及增改建铁路既有曲线 [J], 何恩祥;白存仓
5.局部铁路曲线拨量整正的计算方法 [J], 廖显军
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
交通世界TRANSPOWORLD收稿日期:2018-05-10作者简介:席海鹏(1981—),男,工程师,从事铁路设计相关工作。
铁路既有线路的整体拟合整正席海鹏1,王国辉1,马华宇2(1.中铁工程设计咨询集团有限公司郑州设计院,河南郑州450000;2.河南建筑职业技术学院,河南郑州450000)摘要:既有线拟合整正一直以来是困扰铁路养护维修、既有线改造的一类老问题,目前针对曲线的最小二乘法拟合算法及程序都比较成熟,但大部分停留在依据原有线路设计资料基础上对单条曲线进行拟合整正。
很少有算法或程序在没有任何既有线路原设计资料的基础上,仅通过测量的离散点数据,对整条既有线路进行整体优化整正。
鉴于此,通过数学最小二乘法对缺少原有设计资料的既有线路整体拟合整正进行探讨,最后利用京广铁路某段实测数据进行实验。
实验结果表明,拟合整正后对全线的拨道量的改善率达到了51.7%,提高了工务养护的技术水平,保证了列车运行安全性。
关键词:精密测量控制网;数据处理;曲线偏角中图分类号:U212文献标识码:A1线路养护的必要性京广铁路作为我国南北运输的主要通道,在客货运输中起着国民经济大动脉的作用。
某段线路在经过铁路5次大提速技改后,首次实现了既有线客货混跑铁路客车最高时速250km/h 。
在这个区段既有时速70~80km/h 的货车,又有时速120~250km/h 的客车。
车辆密度很大,这样就对线路的养护提出了更高的要求。
然而传统的养护手段绳正法不能控制整个线路的平面走向,往往会出现线路偏离设计位置的情况。
再加上施工方法带来的一些问题,其中部分线路直线部分不直,曲线部分不圆顺。
为了保证列车运行安全性以及高速客车乘客对舒适度的要求,提速地段建立高精度整体控制网,对既有线路进行统一的复测、整正[1]。
既有线路中线测量获得的离散点群,如何找到最合理的线路的直线部分、曲线部分、缓和曲线部分的准确分界点,以及在保证全部拨道量最小的前提下,对直线部分、缓和曲线部分、圆曲线部分分别进行优化拟合对于线路的整体拟合整正至关重要。
本文基于最小二乘法实现了对整条线路的拟合整正,可以最大程度地接近既有线路,改善传统工务养护手段,提高工务养护的技术水平。
2数据采集2.1布设精密测量控制网首先根据既有线路工程或后期养护改造等级需要整体建立相应精度的各等级精密测量控制网,布设控制网精度必须满足后期测量精度的要求,一般要求平面坐标系采用工程独立坐标系统。
2.2离散点测量首先采用钢尺量距对既有线路进行百尺标量测,用于标记测量离散点位置关系。
依托建立的精密测量控制网及百尺标对既有线路进行现状测量,测量精度应满足后期拟合整正计算的精度需求。
一般要求在直线段部分测量离散点间距≤50m ,曲线段离散点间距≤20m ,桥梁、涵洞、道岔、短夹直线、小偏角曲线等相应位置根据工程需要相应加桩[2]。
3数据处理3.1离散点数据整体分段3.1.1离散点曲率半径计算离散点从起始里程开始采用式(1)上3个点计算一个外接圆曲率半径,获得一组里程与曲率半径相对应的数据。
r12(1)式(1)中:()x 1-y 1,()x 2-y 2,()x 3-y 3分别为试样上标记的3点坐标;k 1=x 1-x 2y 1-y 2,k 2=x 3-x 2y 3-y 2。
3.1.2曲率半径图绘制根据计算所得曲率半径及相应里程绘制曲率半径图(见图1),根据图1对离散点进行直线、曲线、直线的划15总473期2018年第23期(8月中)分。
此部分可以人工干预手动划分段落,也可以设置筛选条件实现电脑段落自动划分。
3.2数据的分段拟合整正3.2.1直线部分的最小二乘法拟合整正直线部分根据分离出来的直线段落离散点坐标,根据经验组成线性方程f ()y =ay +b ,其中a ,b 为待定常数,最理想的情况是选取能使直线x =ay +b 经过选取段落中的各个离散点坐标的a ,b 。
但在实际上这是不可能的,因为这些点经过运营磨耗、养护维修、测量误差等原因,坐标本来就不在同一条直线上。
因此,只能要求选取使f ()y =ay +b 在y 0,y 1,y 2,⋯,y i 处的函数值与实测数据x 0,x 1,x 2,⋯,x i 相差都很小的a ,b ,就是要使偏差x i -f (y i )()i =0,1,2,⋯,i 都很小。
为达到这一要求,在求和时,因为偏差有正有负,可能互相抵消,为了避免这种情形,可对偏差取绝对值再求和,使∑i =1n ||x i -f ()y i 很小。
为了方便分析和计算,选取常数a ,b ,使M =∑i =1n||x i -()ay i +b 2最小来保证每个偏差的绝对值都很小,也就是采用最小二乘法来解决。
上述问题可通过求方程组的解来解决,见式(2):ìíîïïïïa ∑i =0n y 2i +b ∑i =0n y i =∑i =0nx i y i a ∑i =0n y i +(i +1)b =∑i =0nx i(2)解得拟合直线方程系数a ,b ,从而确定理论最优直线方程。
以上直线部分的最优化理论拟合整正方法,在实际应用中往往存在一定的局限性,因既有线路存在建设初期测量精度以及后期维修改造造成的大型结构、构筑物中心坐标并不在拟合理论直线上,因此在直线拟合时应加入人工干预成分,通过指定固定点来确定直线方程,甚至为了达到最小化工程量的目的,可把长直线切断加入大半径曲线。
3.2.2曲线偏角的确定根据离散点数据分段方法确定的曲线部分的拟合,首先要确定曲线的偏角。
首先,应在两端直线部分拟合出最优方程;然后,根据两端直线最优方程确定两端直线的坐标方位角;最后,根据两端直线的坐标方位角求解曲线偏角。
3.2.3曲线部分的最小二乘法拟合整正曲线部分的拟合首先采用与上述离散点整体分段类似的方法,绘制曲线部分曲率图,根据曲率图把曲线部分划分为缓和曲线部分、圆曲线部分、缓和曲线部分,圆曲线部分采用相应的最小二乘拟合法确定最优曲线半径,缓和曲线长结合曲线段落划分及曲线半径选配最合适长度。
3.2.4实测数据拟合整正实验本文采用京广高铁某段100km 的数据按照以上方法进行拟合整正,表1给出了部分数据拟合前和拟合后的对比结果,表中数据是里程和对应的拨道量。
从表1可看出,通过上述拟合整正对原始拨道量有了明显的改善[3]。
图1曲率半径图拟合前数据828100.00828200.00828300.30828400.50828500.00828600.20828700.30828800.00828900.10828920.40828940.00828960.40828980.10-0.003-0.012-0.018-0.015-0.007-0.008-0.0050.0000.0060.0530.0660.0790.082828980.10829000.30829020.00829040.31829060.13829080.00829102.19829120.00829140.50829160.31829181.88829200.38829222.000.0820.0800.0720.0740.0710.0230.0400.0030.0050.0060.0040.0100.01拟合后数据828100.00828200.00828300.30828400.50828500.00828600.20828700.30828800.00828900.10828920.40828940.00828960.40828980.10-0.003-0.011-0.017-0.014-0.005-0.007-0.0030.0020.0080.0050.0060.0080.006828980.10829000.30829020.00829040.30829060.10829080.00829102.20829120.00829140.50829160.30829181.90829200.40829222.000.0060.0120.0120.005-0.005-0.011-0.009-0.007-0.0040.0040.0090.0100.004表1拟合整正前后拨道量对比表16交通世界TRANSPOWORLD对全线的拨道量进行了统计,统计中因为拨道量有正负之分,为避免拨道量相互抵消,对拨道量进行了取绝对值求和,拟合前拨道量总和为2.136m,拟合后拨道量总和为1.031m。
然后采用式(3)计算了拟合后拨道量的改善率,拟合后拨道量改善51.7%。
x=A-BA×100%(3)计算结果证明,采用上述拟合整正方法对全线拨道量有了极大的改善。
4结语综上所述,本文详细研究了既有铁路整体优化拟合流程,并具体介绍了既有线直线部分最小二乘法拟合整正的原理。
基于京广铁路100km的实测数据,对既有铁路拟合整正进行实验,实验结果表明,采用整体优化拟合对既有线拟合整正有较大的改善,在基本不动既有铁路设施的前提下,本着整体拨道量最小的目标,改造了既有营运铁路直线不直、曲线不圆顺的不良现状,使提速路段列车运行更安全,乘客更舒适,对今后改善传统的工务养护手段具有重大意义。
参考文献:[1]候茂盛.基于最优化理论的既有铁路曲线整正方法研究及应用[D].兰州:兰州交通大学,2015.[2]吴清华.基于绝对坐标的轨道线路拟合整正方法研究[D].长沙:中南大学,2012.[3]潘学英.关于座标法计算铁路既有曲线软件的研制与探讨[J].北京测绘,2001(3):20-23.(编辑:唐勍勍)(上接第14页)形视距指标的计算方法,确定不同路线规划要求下的行车视距需要满足的标准。
相关分析和总结,可以为高速公路立体交叉设计中的路线指标检验和改进提供参考。
参考文献:[1]田兆丰.山区互通立交的视距检查方法[J].公路与汽运,2013(2):89-91.[2]王华,孙绿松.设计阶段互通立交安全性评价中若干问题的探讨[J].公路交通科技(应用技术版),2009(8):224-225.[3]尹和山.高速公路互通式立交路线视距指标研究[J].工程与建设,2017,31(1):81-82.[4]包泮旺.识别视距对互通式立体交叉主线形指标选用的影响的研究[J].公路,2011(8):134-137.(编辑:唐勍勍)17。
