第二节可测函数的收敛性续19316

合集下载

可测函数的收敛性46189PPT资料31页

(1k)
m(N 1n NE[|fnf|])0
()
从m 而 E 时当 0 ， ,有
关于N 单调减小
N l im m (n N E [fn | f| ]) m (N l （ in m N E [fn | f| ] ） ) m (N 1 n N E [fn | f| ]) 0
依测度收敛
0 ,有 l n i m m [f|n E f| ] 0
0 , 0 , N 0 , n N , 有 m E [ |f n f | ]
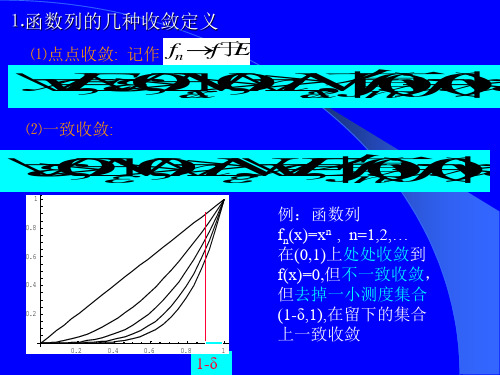
2.几乎处处收敛(x)=xn
0.6
0.4
0.2
0.2
0.4
0.6
k 1 N 1 n N
f n ( x ) 不收敛 f ( x ) : 1 k 1 , N 1 , n N , 使 |f n ( x ) f ( x ) | 1 k
引理：设mE<+∞，fn ，f在E上几乎处处有限且可测，
若 f n fa . e . 于 E ，则 0 ,有 N l i m m ( n N E [ |fn f| ] ) 0
依测度收敛并不指出函数列在哪个点上的收敛，其要点在于误差超过σ的点所成的集的测度应随n趋于无穷而趋于零，而不论点集的位置状态如何
不依测度收敛
0,使m 得 [E |fnf|]不收0敛于
0 , 0 , N 0 , n N , 使得 m E [ |f n f | ]
0.8
1
1-δ
例：函数列fn(x)=xn 在(0,1)上处处收敛到 f(x)=0,但不一致收敛，但去掉一小测度集合
(1-δ,1),在留下的集合上一致收敛, 即几乎一致收敛.
定理2.2 叶果洛夫(Egoroff)定理

级数的收敛性判定与计算

级数的收敛性判定与计算级数是数学中一种特殊的数列求和形式。

在数学分析中，我们通常关心的是级数的收敛性判定与计算。

本文将介绍几种常见的级数收敛性判定方法，并以例子详细说明其计算过程。

一、级数的收敛性判定在讨论级数的收敛性之前，先来了解一下级数的定义。

设有数列{an}，则数列{an}的和称为级数，用Σan表示。

1.正项级数收敛判定如果对于数列{an}的每一项都有an≥0且数列{an}的部分和序列{s1, s2, s3, ...}有上界，则称Σan为正项级数。

关于正项级数的收敛性，有以下判定定理：（1）Cauchy准则：正项级数Σan收敛当且仅当对任意ε>0，存在N∈N，当n>N时，对任意的m>n，有|sm-sn|<ε。

（2）比较判别法：若存在正数c，当n>N时，对任意的m>n，有an≤cn，则正项级数Σan收敛。

（3）极限判别法：如果lim(n→∞)(an+1/an)=l，其中l>0或l=+∞，则正项级数Σan与Σan收敛或发散。

2.交错级数收敛判定若级数Σ(-1)^(n-1)an的一般项是由正项和负项构成的交错形式，则称之为交错级数。

关于交错级数的收敛性，有以下判定定理：（1）莱布尼茨判别法：对于交错级数Σ(-1)^(n-1)an，若满足an≥0、an递减（即an+1≤an）且lim(n→∞)an=0，则交错级数Σ(-1)^(n-1)an收敛。

3.绝对收敛和条件收敛对于级数Σan，若级数Σ|an|收敛，则称Σan为绝对收敛级数；若Σan收敛而Σ|an|发散，则称Σan为条件收敛级数。

二、级数的计算在判断级数的收敛性后，有时我们还需要计算级数的和。

以下是几种常见的级数计算方法。

1.等差级数等差级数是指数列项的差值为常数的级数。

对于等差级数Σa+(n-1)d，其求和公式为Sn=(n/2)[2a+(n-1)d]，其中n为项数，a为首项，d为公差。

2.几何级数几何级数是指数列项的比值为常数的级数。

§ 3.2 可测函数的收敛性

83§3.2 可测函数的收敛性教学目的使学生对可测函数序列的几乎处处收敛性, 依测度收敛性和几乎一致收敛性及它们的之间蕴涵关系有一个全面的了解.本节要点本节引进的几种收敛是伴随测度的建立而产生的新的收敛性. 特别是依测度收敛是一种全新的收敛, 与熟知的处处收敛有很大的差异. Egorov 定理和Riesz 定理等揭示了这几种收敛之间的关系. Riesz 定理在几乎处处收敛和较难处理的依测度收敛之间架起了一座桥梁.设),,(µF X 是一测度空间. 以下所有的讨论都是在这一测度空间上进行的. 先介绍几乎处处成立的概念.几乎处处成立的性质设)(x P 是一个定义在E 上与x 有关的命题. 若存在一个零测度集N , 使得当N x ∉时)(x P 成立(换言之, })(:{不成立x P x N ⊂), 则称P (关于测度µ)在E 上几乎处处成立. 记为)(x P a.e.−µ, 或者)(x P a.e.在上面的定义中, 若)(x P 几乎处处成立, 则集})(:{不成立x P x 包含在一个零测度集内. 若})(:{不成立x P x 是可测集, 则由测度的单调性知道.0}))(:({=不成立x P x µ 特别地, 当测度空间),,(µF X 是完备的时候如此.例1 设给定两个函数f 和g . 若存在一个零测度集N , 使得当N x ∉时),()(x g x f = 则称f 和g 几乎处处相等, 记为g f = a.e.例2 设f 为一广义实值函数. 若存在一个零测度集N, 使得当N x ∉时,+∞<f 则称f 是几乎处处有限的, 记为+∞<f , a.e.注1 设f 是几乎处处有限的可测函数, 则存在一零测度集N, 使得当N x ∉时.+∞<f 令.~c N fI f = 则f ~是处处有限的可测函数并且 a.e..~f f =因此, 在讨论几乎处处有限的可测函数的性质时, 若在一个零测度集上改变函数的值不影响该性质, 则不妨假定所讨论的函数是处处有限的.注意, f 几乎处处有限与 a.e.M f ≤是不同的概念. a.e.M f ≤表示84存在一个零测度集N , 使得f 在c N 上有界. 显然 a.e.M f ≤蕴涵f 几乎处处有限. 但反之不然. 例如, 设),10(1)(≤<=x xx f .)0(+∞=f 则f 在)1,0(上关于L 测度是几乎处处有限的, 但在)1,0(中并不存在一个L 零测度集N 和,0>M 使得在N −)1,0(上, .)(M x f ≤ 初学者常常在这里发生误解, 应当引起注意.可测函数的几种收敛性和定义在区间上的函数列的一致收敛一样, 可以定义在任意集上的函数列的一致收敛性. 设E 是X 的子集. )1(,≥n f f n 定义在E 上的函数. 若对任意0>ε, 存在,0>N 使得当N n ≥时, 对一切E x ∈成立,)()(ε<−x f x f n 则称}{n f 在E 上一致收敛于f , 记为..un f f n →定义1 设}{n f 为一可测函数列, f 为一可测函数.(1) 若存在一个零测度集N , 使得当N x ∉时, 有)()(lim x f x f n n =∞→, 则称}{n f 几乎处处收敛于f , 记为f f n n =∞→lim a.e., 或f f n → a.e.. (2) 若对任给的0>ε, 总有.0})({lim =≥−+∞→εµf f n n则称}{n f 依测度收敛于f , 记为.f f n → µ(3) 若对任给的0>δ, 存在可测集δE , δµδ<)(E , 使得}{n f在c E δ上一致收敛于f , 则称}{n f 几乎一致收敛于f , 记为n nf lim =f a.un., 或 f f n → a..un..容易证明, 若将两个a.e.相等的函数不加区别, 则上述几种极限的极限是唯一的. 例如, 若,a.e.f f n → g f n → a.e., 则g f = a.e.. 其证明留作习题.例3 设))),,0[(),,0([m +∞+∞M 为区间),0[∞+上的Lebesgue 测度空间. 其中)),0[(+∞M 是),0[∞+上的L 可测集所成的σ-代数, m 是1R 上的L 测度在),0[∞+上的限制. 令85.1),(1)(),1(≥−=n x I x f n n n则对任意,0>x ).(0)(∞→→n x f n 当0=x 时)(x f n 不收敛于0. 但,0})0({=m 因此在),0[∞+上.0a.e. → n f 由于对,21=ε ).(,0)),[]1,0([})21({/+∞→ → +∞=+∞∪=≥n n n m f m n 因此}{n f 不依测度收敛于0. 这个例子表明在一般情况下, 几乎处处收敛不一定能推出依测度收敛.例4 设)]),1,0[(],1,0[(m M 是]1,0[上的Lebesgue 测度空间. 令.1,)(≥=n x x f n n则对任意0>δ, }{n f 在]1,0[δ−上一致收敛于0.由于δδ=−])1,1((m 可以任意小, 因此0a..un. → n f . 又显然.0a.e. → n f例5 设)]),1,0[(],1,0[(m M 是]1,0[上的Lebesgue 测度空间. 令.1,,,1,1[≥=−=n n i ni n i A i n L 将}{i n A 先按照n 后按照i 的顺序重新编号记为}{n E . 显然.0)(→n E m 令)()(x I x f n E n =, 1≥n ,.0)(=x f对任意0>ε, 由于.,0)(})({∞→→=≥−n E m f f m n n ε故}{n f 依测度收敛于f . 但}{n f 在]1,0[上处处不收敛. 事实上, 对任意]1,0[0∈x , 必有无穷多个n E 包含0x , 也有无穷多个n E 不包含0x . 故有无穷多个n 使得,1)(0=x f n 又有无穷多个n 使得.0)(0=x f n 因此}{n f 在0x 不收敛. 这个例子表明依测度收敛不能推出几乎处处收敛. 例3和例4表明, 依测度收敛和几乎处处收敛所包含的信息可能相差很大.几种收敛性之间的关系为叙述简单计, 以下我们设所讨论的函数都是实值可测函数. 但以下结果对几乎处处有限的可测函数也是成立的由(见注1的说明).引理2 设+∞<)(X µ. 若.a.e.f f n → 则对任意0>ε有86.0)}{(lim =≥−∞=∞→U n i i n f f εµ 证明设0>ε是一给定的正数. 任取X x ∈, 若对任意,1≥n 存在,n i ≥ 使得.)()(ε≥−x f x f i 则)()(x f x f n 不收敛于. 这表明IU ∞=∞=≥−1}{n n i i f fε)}.()(:{/x f x f x n → ⊂由于,a.e.f f n → 因此由上式知道.0}{1=≥−∞=∞=IU n n i i f f εµ 由于+∞<)(X µ, 由测度的上连续性, 我们有0}{}{lim 1=≥−= ≥−∞=∞=∞=∞→IU U n n i i n i i n f f f f εµεµ. ■ 容易证明, 若,a..un.f f n → 则f f n → a.e.(其证明留作习题). 下面的定理表明当+∞<)(X µ时, 其逆也成立.定理3 (叶戈洛夫)若+∞<)(X µ, 则f f n → a.e.蕴涵.a..un.f f n →证明设+∞<)(X µ, .a.e.f f n → 由引理2 , 对任意0>ε, 有.0}{lim =≥−∞=∞→U n i i n f f εµ 于是对任意的0>δ和自然数1≥k , 存在自然数k n 使得.2}1{k n i i k k f f δµ< ≥−∞=U 令.}1{1U U ∞=∞=≥−=k n i i kk f f E δ 由测度的次可数可加性我们有 .2}1{)(11δδµµδ=≤ ≥−≤∑∑∞=∞=∞=k k k n i i k k f f E U 往证在c E δ上, }{n f 一致收敛于f . 事实上, 由De Morgan 公式得87.1,}1{}1{1≥<−⊂<−=∞=∞=∞=k k f f k f f E kk n i i k n i i c I I I δ (1) 对任意0>ε, 取k 足够大使得.1ε<k则由(1)式知道, 当k n i ≥时对一切c E x δ∈, 有.1)()(ε<<−kx f x f i 即在c E δ上}{n f 一致收敛于f . 这就证明了f f n → a..un.. 定理证毕. 注 2 在叶戈洛夫定理中, 条件+∞<)(X µ不能去掉. 例如, 若令),()(),[x I x f n n +∞= .1≥n 则}{n f 在1R 上处处收敛于0. 但容易知道}{n f 不是几乎一致收敛于0.定理4 若+∞<)(X µ, 则f f n → a.e.蕴涵.f f n → µ证明设+∞<)(X µ, .a.e.f f n → . 由引理2 , 对任意0>ε有.0}{lim =≥−∞=∞→U n i i n f f εµ 由测度的单调性立即得到()≤≥−∞→}{lim εµf f n n .0}{lim =≥−∞=∞→U n i i n f f εµ 即.f f n → µ ■ 本节例3表明, 在定理4中, 条件+∞<)(X µ不能去掉.定理5 (Riesz)若,f f n → µ 则存在}{n f 的子列}{k n f , 使得.a.e.f f k n →证明设.f f n → µ 对任意0>ε和0>δ, 存在1≥N , 使得当Nn ≥时, 有δεµ<≥−})({f f n .于是对任意自然数1≥k , 存在自然数k n , 使得.21})1({k n k f f k <≥−µ (2)88我们可适当选取k n 使得L ,2,1,1=<+k n n k k . 往证.a.e.f f k n → 令L I ,2,1,}1{=<−=∞=i k f f E ik n i k . 对任意i E x ∈, 当i k ≥时, .1)()(kx f x f k n <− 这表明}{k n f 在i E 上收敛于f . 令.1U ∞==i i E E 则}{k n f 在E 上收敛于f . 往证.0)(=c E µ 由De Morgan 公式, 我们有.}1{11I IU ∞=∞=∞=≥−==i i i k n c i c k f f E E k 利用(2)容易得到.1)(1≤c E µ 因此由测度的上连续性并且利用(2), 我们有.021lim })1({lim }1{lim )(=≤≥−≤ ≥−=∑∑∞=∞→∞=∞→∞=∞→i k k i ik n i ik n i ck f f k f f E k k µµµU 这就证明了.a.e.f f k n → ■定理6 设+∞<)(X µ. 则f f n → µ当且仅当}{n f 的任一子列}{k n f 都存在其子列}{k n f ′, 使得).(a.e.∞→′ → ′k f f k n证明必要性(此时不需设+∞<)(X µ). 设.f f n → µ 显然}{n f 的任一子列}{k n f 也依测度收敛于 f. 由定理 5 , 存在}{k n f 的子列}{k n f ′, 使得).(a.e.∞→′ → ′k f f k n充分性. 用反证法. 若}{n f 不依测度收敛于f , 则存在,0>ε 使得.0}({/ → ≥−εµf f n 于是存在0>δ和}{n f 的子列}{kn f , 使得 .})({δεµ≥≥−f f kn 由此知}{k n f 的任何子列}{k n f ′都不能依测度收敛于f . 由定理4, }{k n f ′也不89能a.e.收敛于f . 这与定理所设的条件矛盾. 故必有.f f n → µ ■定理5和定理6给出了依测度收敛和几乎处处收敛的联系. 利用这种联系, 常常可以把依测度收敛的问题转化为几乎处处的问题. 而几乎处处收敛是比较容易处理的.例 6 设)1(,,,≥n g f g f n n 是有限测度空间),,(µF X 上的几乎处处有限的可测函数, ,f f n → µ .g g n → µ 又设h 是2R 上的连续函数. 则).,(),(.g f h g f h n n → µ特别地, .fg g f n n → µ证明不妨设)1(,,,≥n g f g f n n 都是处处有限的. 设),(k k n n g f h 是),(n n g f h 的任一子列. 由定理6, 存在}{k n f 的子列}{k n f ′使得).(a.e.∞→′ → ′k f f k n 同理存在}{k n g ′的子列, 不妨仍记为}{k n g ′, 使得).(a.e.∞→′ → ′k g g k n 既然h 是连续的, 因此有).,(),( a.e.g f h g f h k k n n → ′′这表明),(n n g f h 的任一子列),(k k n n g f h , 都存在其子列),(k k n n g f h ′′使得).,(),( a.e.g f h g f h k k n n → ′′ 再次应用定理6, 知道).,(),(.g f h g f h n n → µ 特别地, 若取,),(xy y x h = 则得到.fg g f n n → µ ■小结本节介绍了几乎处处收敛, 依测度收敛和几乎一致收敛, 它们是伴随测度的建立而产生的新的收敛性.几种收敛性之间有一些蕴涵关系. 其中最重要的是Egorov 定理和Riesz 定理.利用Riesz 定理,可以把较难处理的依测度收敛的问题化为几乎处处收敛的问题.习题习题三, 第18题—第28题.。

可测函数列常见的几种收敛

可测函数列常见的几种收敛摘要：本文介绍了可测函数列常见的几种收敛：一致收敛、几乎一致收敛、几乎处处收敛、依测度收敛等以及它们之间的关系．关键字：可测函数列；一致收敛；几乎一致收敛；几乎处处收敛；依测度收敛前言在数学分析中我们知道一致收敛是函数列很重要的性质，比如它能保证函数列的极限过程和(R)积分过程可交换次序等．可是一般而言函数列的一致收敛性是不方便证明的，而且有些函数列在其收敛域内也不一定是一致收敛的，如文中所给的例2函数()f x 在收敛域[0,1]内不一致收敛，但对于一个0δ>当0δ→时在[0,]δ内一致收敛，这不见说明了一致收敛的特殊性，也验证了我们平时常说的“矛盾的同一性和矛盾的斗争性是相联系的、相辅相成的”[1]1 可测函数列几种收敛的定义1.1 一致收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集E 上的实值函数．若对于0,ε∀>存在,K N +∈使得对于,k K x E ∀≥∀∈都有()()k f x f x ε-<则称}{()k f x 在E 上一致收敛到()f x ．记作： u k f f −−→(其中u 表示一致uniform)．1.2 点点收敛若函数列12(),(),(),,(),k f x f x f x f x 在点集D E ⊂上每一点都收敛，则称它在D 上点点收敛．例1 定义在[0,1]E =上的函数列1(),1k f x kx=+则()k f x 在E 上点点收敛到函数 1,0,()0,0 1.x f x x =⎧=⎨<≤⎩ 而且还能看出{()}k f x 在[]0,1上不一致收敛到()f x ，但对于0,{()}k f x δ∀>在[,1]δ上一致收敛到()f x ．1.3 几乎一致收敛[3]设E 是可测集，若0,,E E δδ∀>∃⊂使得(\),m E E δδ<在E δ上有u k f f −−→则称{()}k f x 在E 上几乎一致收敛与()f x ，并记作...a u k f f −−→(其中a.u ．表示几乎一致almost uniform) ．例2 定义在[]0,1E =上的函数()k k f x x =在[]0,1上收敛却不一致收敛．但是只要从[]0,1的右端点去掉任一小的一段使之成为[]()0,10,0δδδ->→则{()}k f x 在此区间上就一致收敛，像这样的收敛我们就可以称之为在[]0,1E =上几乎一致收敛与0．1.4 几乎处处收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集n E R ⊂上的广义实值函数．若存在E 中点集Z ，有()0,m Z =及对于每一个元素\x E Z ∈，有lim ()()k x f x f x →∞= 则称{()}k f x 在E 上几乎处处收敛与()f x ，并简记为,.[]k f f a e E →或..a e k f f −−→若上文的例1也可以称之为在[]0,1上几乎处处收敛与()f x ．1.5 依测度收敛例3在[0,1)上构造函数列{()}k f x 如下：对于k N +∈，存在唯一的自然数i 和j ，使得2,i k j =+其中02,i j ≤≤令1[,)22()(),1,2,,[0,1).i i k j j f x x k x χ+==∈任意给定的0[0,1),x ∈对于每一个自然数i ，有且仅有一个j ，使得01[,)22i i j j x +∈．数列0{()}f x 中有无穷多项为1，有无穷多项为0．由此可知，函数列{()}k f x 在[0,1)上点点不收敛．因此仅考虑点收敛将得不到任何信息．然而仔细观察数列0{()}k f x 虽然有无穷多个1出现，但是在“频率”意义下，0却也大量出现．这一事实可以用点集测度语言来刻画．只要k 足够大，对于01,ε<≤点集{[0,1)()0}{[0,1)()1}1[,)22k k i ix f x x f x j j ε∈-≥=∈=+= 的测度非常小．事实上 1({[0,1)()0})2k i m x f x ε∈-≥=．这样对于任给的0,δ>总可以取到0,k 也就是取到0,i 使得当0k k >时，有({[0,1)()0})1k m x f x εδ∈-<>-其中02i δ-<．这个不等式说明，对于充分大的h ，出现0的“频率”接近1．我们将把这样一种现象称为函数列{()}k f x 在区间[0,1)上依测度收敛到零函数，并将抽象出以下定义[3]：设12(),(),(),,(),k f x f x f x f x 是可测集E 上几乎处处有限的可测函数．若对于任意给定的0,ε>有lim (())0,k x m E f f ε→∞->= 则称{()}k f x 在E 上依测度收敛到函数()f x ，记为.m k f f −−→2 可测函数列几种收敛的关系2.1 点点收敛与一致收敛的关系由上述定义我们可以知道u k f f −−→，必有{()}k f x 点点收敛于()f x ．如例1．反之则不一定成立，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则()f x 也是可测函数．2.2 几乎处处收敛与一致收敛的关系由定义可知有一致收敛必几乎处处收敛....()a u a e k k f f f f −−→⇒−−→．反之则不然，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则极限函数()f x 也是可测函数．应用：从数学分析我们知道一致收敛的函数列对于求极限运算和(R)积分运算、微分运算与(R)积分运算等可以交换次序．2.3 几乎处处收敛与一致收敛的关系叶果洛夫(E ΓopoB )定理[5]：设(),{}n m E f <∞是E 上一列a.e ．收敛于一个a.e ．有限的函数f 的可测函数，则对于任意的0δ>，存在子集E E δ⊂，使{}n f 在E δ上一致收敛，且(\)m E E δδ<．注定理中“()m E <∞”不可去掉如：例4定义在(0,)E =+∞的函数列1,(0,]()(1,2,).0,(,)m x m x m x m f ∈⎧==⎨∈+∞⎩ 则m f 在(0,)+∞上处处收敛于1，但对于任何正数δ及任何可测集E δ，当时(\)m E E δδ<时，m f 在E δ上不一致收敛于1．这是因为，当时(\)m E E δδ<时，E δ不能全部含于(0,]m 中，必有(,)m E m x δ∈+∞ ，于是有()0m m x f =．sup ()1()11m m m x E f x f x δ∈-≥-=所以()m x f 在E δ上不一致收敛与1，也即定理中“()m E <∞”不可去掉[4]．由定义我们知道一致收敛必是几乎处处收敛的，反之则不成立．但它们又有密切的关系，即使上述定理告诉我们几乎处处收敛“基本上”是一致收敛的(在除去一个测度为任意小集合的子集上)．应用由上述定理我们还可以得到“鲁津定理”：设()f x 是E 上a.e ．有限的可测函数，则对于任意的0δ>，存在闭子集E F δ⊂，使()f x 在F δ上是连续函数，且(\)m E F δδ<．也就是说：在E 上a.e ．有限的可测函数“基本上”是连续的(在除去一个测度为任意小集合的子集上)．也即我们可以用连续函数来逼近a.e ．有限的可测函数．2.4几乎处处收敛与依测度收敛的关系例5 取(0,1]E =，将E 等分，定义两个函数：(1)111,(0,]2()10,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩， (1)210,(0,]2()11,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩．然后将(0,1]四等分、八等分等等．一般的，对于每个n ，作2n 个函数：()11,(,]22()1,2,,2.10,(,]22n n n n j n j j x x j j j x f -⎧∈⎪⎪==⎨-⎪∉⎪⎩ ．我们把(),1,2,,2{}n j x j f = ，先n 按后按j 的顺序逐个的排成一列：(1)(1)()()()12122(),(),,(),(),,(),n n n n x f x f x f x f x f (1)()()n j x f 在这个序列中是第22n j N -+=个函数．可以证明这个函数列是依测度收敛于零的．这是因为对于任何的0σ>，()0[]n j f E σ-≥或是空集(当1σ>)，或是1,22(]n n j j - (当01σ<≤)，所以 ()102([])n j n f m E σ-≥≤ (当时1σ>时，左端为0)．由于当2(1,2,,2.)2n n j j N -+== 趋于∞时n →∞，由此可见()([0])0lim n j N m E f σ→∞-≥=，也即()()0m n j x f −−→．但是函数列(1)在上的任何一点都不收敛．事实上，对于任何点0(0,1]x ∈，无论n 多么大，总存在j ，使01(,]22n n j j x -∈，因而()0()1n j x f =，然而()10()0n j x f +=或()10()0n j x f -=，换言之，对于任何0(0,1]x ∈，在()0(){}n j x f 中必有两子列，一个恒为1，另一个恒为0．所以序列(1)在(0,1]上任何点都是发散的．这也就说明依测度收敛的函数列不一定处处收敛，也就是说依测度收敛不能包含几乎处处收敛，但仍有：黎斯(F ．Riesz) [5] 设在E 上{}n f 测度收敛于f ，则存在子列{}i n f 在E 上a.e ．收敛于f ．例6 如例4，当()1()m x n f →→∞当x E ∈．但是当01σ<<时，1[](,)m f E m σ-≥=+∞且(,)m m +∞=∞．这说明}{n f 不依测度收敛于1．这个例子又说明了几乎处处收敛也不包含依测度收敛，但是有下述关系：勒贝格(Lebesgue) [5] 设mE <∞，{}n f 是E 上a.e ．有限的可测函数列， {}n f 在E 上a.e ．收敛于a.e ．有限的函数f ，则()()m n x f x f −−→．此定理中的“mE <∞”不可去掉，原因参看例1．定理也说明在的在的条件mE <∞下，依测度收敛弱于几乎处处收敛．有以上定理黎斯又给出了一个用几乎处处收敛来判断依测度收敛的充要条件：设mE <∞，{}n f 是E 上的可测函数列，那么{}n f 依测度收敛于f 的充要条件是：{}n f 的任何子列{}k n f 中必可找到一个几乎处处收敛于f 的子序列．证明（必要性）由于{}n f 依测度收敛于f ，由定义知道这时{}n f 的的任何子序列{}k n f 必也依测度收敛于f ，由黎斯定理可知{}k n f 中必存在几乎处处收敛于f 的子序列．（充分性）如果{}n f 不依测度收敛于f ，即存在一个0σ>，使得()n f f m E σ-≥不趋于0．因此必有子序列{}k n f ，使得(())0.lim kn k m E f f a σ→∞-≥=> 这样{}k n f 就不可能再有子序列几乎处处收敛于f 了，否则由勒贝格定理知将有{}k n f 依测度收敛于f ，即(())0.lim kn k m E f f σ→∞-≥= 这与上式矛盾，所以{}n f 依测度收敛于f ．应用依测度收敛在概率统计中有重要的意义，如例3；它也是证明中心极限定理的重要依据，由中心极限定理我们可以知道用一个正态分布来模拟一个样本容量较大的样本的概率分布，从而简化了大样本概率分布的处理和计算[7]．结束语：上述定义中的各种收敛的极限函数都是唯一的，而且从本文还可以知道一致收敛是最强的收敛，它蕴含了点点收敛、几乎处处收敛、依测度收敛等上述几种收敛．各种收敛都有不同的意义，在各种实践中作用也各不同．参考文献：[1]马克思主义基本原理概论教材编写课题组．马克思主义基本原理概论[M]．高等教育出版社，2009,7[2] 华东师范大学数学系．数学分析(第三版)[M]．高等教育出版社，2001,6．[3] 郭懋正．实变函数与泛函分析[M]．北京大学出版社，2005,2[4] 柳藩，钱佩玲．实变函数论与泛函分析[M]．北京师范大学出版社，1987．[5] 程其襄，张奠宙，魏国强等．实变函数与泛函分析既基础[M]．高等教育出版社，2003,7．[6] 夏道行，严绍宗等复旦大学数学系主编．实变函数与应用泛函分析基础[M]．上海科学技术出版社．1987．[7] 茆诗松，程依明，濮晓龙．概率论与数理统计教程[M]．高等教育出版社，2004,7．。

可测函数列常见的几种收敛

可测函数列常见的几种收敛摘要：本文介绍了可测函数列常见的几种收敛：一致收敛、几乎一致收敛、几乎处处收敛、依测度收敛等以及它们之间的关系．关键字：可测函数列；一致收敛；几乎一致收敛；几乎处处收敛；依测度收敛前言在数学分析中我们知道一致收敛是函数列很重要的性质，比如它能保证函数列的极限过程和(R)积分过程可交换次序等．可是一般而言函数列的一致收敛性是不方便证明的，而且有些函数列在其收敛域内也不一定是一致收敛的，如文中所给的例2函数()f x 在收敛域[0,1]内不一致收敛，但对于一个0δ>当0δ→时在[0,]δ内一致收敛，这不见说明了一致收敛的特殊性，也验证了我们平时常说的“矛盾的同一性和矛盾的斗争性是相联系的、相辅相成的”[1]1可测函数列几种收敛的定义1.1一致收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集E 上的实值函数．若对于0,ε∀>存在,K N +∈使得对于,k K x E ∀≥∀∈都有()()k f x f x ε-<则称}{()k f x 在E 上一致收敛到()f x ．记作：u k f f −−→(其中u 表示一致uniform)． 1.2点点收敛若函数列12(),(),(),,(),k f x f x f x f x 在点集D E ⊂上每一点都收敛，则称它在D 上点点收敛．例1定义在[0,1]E =上的函数列1(),1k f x kx =+则()k f x 在E 上点点收敛到函数 1,0,()0,0 1.x f x x =⎧=⎨<≤⎩ 而且还能看出{()}k f x 在[]0,1上不一致收敛到()f x ，但对于0,{()}k f x δ∀>在[,1]δ上一致收敛到()f x ．1.3几乎一致收敛[3]设E 是可测集，若0,,E E δδ∀>∃⊂使得(\),m E E δδ<在E δ上有u k f f −−→则称{()}k f x 在E 上几乎一致收敛与()f x ，并记作...a u k f f −−→(其中a.u ．表示几乎一致almost uniform)．例2定义在[]0,1E =上的函数()k k f x x =在[]0,1上收敛却不一致收敛．但是只要从[]0,1的右端点去掉任一小的一段使之成为[]()0,10,0δδδ->→则{()}k f x 在此区间上就一致收敛，像这样的收敛我们就可以称之为在[]0,1E =上几乎一致收敛与0．1.4几乎处处收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集n E R ⊂上的广义实值函数．若存在E 中点集Z ，有()0,m Z =及对于每一个元素\x E Z ∈，有lim ()()k x f x f x →∞= 则称{()}k f x 在E 上几乎处处收敛与()f x ，并简记为,.[]k f f a e E →或..a e k f f −−→ 若上文的例1也可以称之为在[]0,1上几乎处处收敛与()f x ．1.5依测度收敛例3在[0,1)上构造函数列{()}k f x 如下：对于k N +∈，存在唯一的自然数i 和j ，使得2,i k j =+其中02,i j ≤≤令1[,)22()(),1,2,,[0,1).i i k j j f x x k x χ+==∈任意给定的0[0,1),x ∈对于每一个自然数i ，有且仅有一个j ，使得01[,)22i i j j x +∈．数列0{()}f x 中有无穷多项为1，有无穷多项为0．由此可知，函数列{()}k f x 在[0,1)上点点不收敛．因此仅考虑点收敛将得不到任何信息．然而仔细观察数列0{()}k f x 虽然有无穷多个1出现，但是在“频率”意义下，0却也大量出现．这一事实可以用点集测度语言来刻画．只要k 足够大，对于01,ε<≤点集{[0,1)()0}{[0,1)()1}1[,)22k k i ix f x x f x j j ε∈-≥=∈=+= 的测度非常小．事实上1({[0,1)()0})2k i m x f x ε∈-≥=．这样对于任给的0,δ>总可以取到0,k 也就是取到0,i 使得当0k k >时，有({[0,1)()0})1k m x f x εδ∈-<>-其中02i δ-<．这个不等式说明，对于充分大的h ，出现0的“频率”接近1．我们将把这样一种现象称为函数列{()}k f x 在区间[0,1)上依测度收敛到零函数，并将抽象出以下定义[3]：设12(),(),(),,(),k f x f x f x f x 是可测集E 上几乎处处有限的可测函数．若对于任意给定的0,ε>有 lim (())0,k x m E f f ε→∞->= 则称{()}k f x 在E 上依测度收敛到函数()f x ，记为.m k f f −−→ 2可测函数列几种收敛的关系2.1点点收敛与一致收敛的关系由上述定义我们可以知道u k f f −−→，必有{()}k f x 点点收敛于()f x ．如例1．反之则不一定成立，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则()f x 也是可测函数．2.2几乎处处收敛与一致收敛的关系由定义可知有一致收敛必几乎处处收敛....()a u a e k k f f f f −−→⇒−−→．反之则不然，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则极限函数()f x也是可测函数．应用：从数学分析我们知道一致收敛的函数列对于求极限运算和(R)积分运算、微分运算与(R)积分运算等可以交换次序．2.3几乎处处收敛与一致收敛的关系叶果洛夫(E ΓopoB )定理[5]：设(),{}n m E f <∞是E 上一列a.e ．收敛于一个a.e ．有限的函数f 的可测函数，则对于任意的0δ>，存在子集E E δ⊂，使{}n f 在E δ上一致收敛，且(\)m E E δδ<．注定理中“()m E <∞”不可去掉如：例4定义在(0,)E =+∞的函数列1,(0,]()(1,2,).0,(,)m x m x m x m f ∈⎧==⎨∈+∞⎩ 则m f 在(0,)+∞上处处收敛于1，但对于任何正数δ及任何可测集E δ，当时(\)m E E δδ<时，m f 在E δ上不一致收敛于1．这是因为，当时(\)m E E δδ<时，E δ不能全部含于(0,]m 中，必有(,)m E m x δ∈+∞，于是有()0m m x f =． sup ()1()11m m m x E f x f x δ∈-≥-=所以()m x f 在E δ上不一致收敛与1，也即定理中“()m E <∞”不可去掉[4]．由定义我们知道一致收敛必是几乎处处收敛的，反之则不成立．但它们又有密切的关系，即使上述定理告诉我们几乎处处收敛“基本上”是一致收敛的(在除去一个测度为任意小集合的子集上)．应用由上述定理我们还可以得到“鲁津定理”：设()f x 是E 上a.e ．有限的可测函数，则对于任意的0δ>，存在闭子集E F δ⊂，使()f x 在F δ上是连续函数，且(\)m E F δδ<．也就是说：在E 上a.e ．有限的可测函数“基本上”是连续的(在除去一个测度为任意小集合的子集上)．也即我们可以用连续函数来逼近a.e ．有限的可测函数．2.4几乎处处收敛与依测度收敛的关系例5取(0,1]E =，将E 等分，定义两个函数：(1)111,(0,]2()10,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩， (1)210,(0,]2()11,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩．然后将(0,1]四等分、八等分等等．一般的，对于每个n ，作2n 个函数：()11,(,]22()1,2,,2.10,(,]22n n n n j n j j x x j j j x f -⎧∈⎪⎪==⎨-⎪∉⎪⎩．我们把(),1,2,,2{}n j x j f =，先n 按后按j 的顺序逐个的排成一列：(1)(1)()()()12122(),(),,(),(),,(),n n n n x f x f x f x f x f (1)()()n j x f 在这个序列中是第22n j N -+=个函数．可以证明这个函数列是依测度收敛于零的．这是因为对于任何的0σ>，()0[]n j f E σ-≥或是空集(当1σ>)，或是1,22(]n n j j -(当01σ<≤)，所以 ()102([])n j n f m E σ-≥≤ (当时1σ>时，左端为0)．由于当2(1,2,,2.)2n n j j N -+==趋于∞时n →∞，由此可见()([0])0lim n j N m E f σ→∞-≥=，也即()()0m n j x f −−→．但是函数列(1)在上的任何一点都不收敛．事实上，对于任何点0(0,1]x ∈，无论n 多么大，总存在j ，使01(,]22n n j j x -∈，因而()0()1n j x f =，然而()10()0n j x f +=或()10()0n j x f -=，换言之，对于任何0(0,1]x ∈，在()0(){}n j x f 中必有两子列，一个恒为1，另一个恒为0．所以序列(1)在(0,1]上任何点都是发散的．这也就说明依测度收敛的函数列不一定处处收敛，也就是说依测度收敛不能包含几乎处处收敛，但仍有：黎斯(F ．Riesz)[5]设在E 上{}n f 测度收敛于f ，则存在子列{}i n f 在E 上a.e ．收敛于f ．例6 如例4，当()1()m x n f →→∞当x E ∈．但是当01σ<<时，1[](,)m f E m σ-≥=+∞且(,)m m +∞=∞．这说明}{n f 不依测度收敛于1．这个例子又说明了几乎处处收敛也不包含依测度收敛，但是有下述关系：勒贝格(Lebesgue)[5]设mE <∞，{}n f 是E 上a.e ．有限的可测函数列，{}n f 在E 上a.e ．收敛于a.e ．有限的函数f ，则()()m n x f x f −−→．此定理中的“mE <∞”不可去掉，原因参看例1．定理也说明在的在的条件mE <∞下，依测度收敛弱于几乎处处收敛．有以上定理黎斯又给出了一个用几乎处处收敛来判断依测度收敛的充要条件：设mE <∞，{}n f 是E 上的可测函数列，那么{}n f 依测度收敛于f 的充要条件是：{}n f 的任何子列{}k n f 中必可找到一个几乎处处收敛于f 的子序列．证明（必要性）由于{}n f 依测度收敛于f ，由定义知道这时{}n f 的的任何子序列{}k n f 必也依测度收敛于f ，由黎斯定理可知{}k n f 中必存在几乎处处收敛于f 的子序列．（充分性）如果{}n f 不依测度收敛于f ，即存在一个0σ>，使得()n f f m E σ-≥不趋于0．因此必有子序列{}k n f ，使得(())0.lim kn k m E f f a σ→∞-≥=> 这样{}k n f 就不可能再有子序列几乎处处收敛于f 了，否则由勒贝格定理知将有{}k n f 依测度收敛于f ，即(())0.lim kn k m E f f σ→∞-≥= 这与上式矛盾，所以{}n f 依测度收敛于f ．应用依测度收敛在概率统计中有重要的意义，如例3；它也是证明中心极限定理的重要依据，由中心极限定理我们可以知道用一个正态分布来模拟一个样本容量较大的样本的概率分布，从而简化了大样本概率分布的处理和计算[7]．结束语：上述定义中的各种收敛的极限函数都是唯一的，而且从本文还可以知道一致收敛是最强的收敛，它蕴含了点点收敛、几乎处处收敛、依测度收敛等上述几种收敛．各种收敛都有不同的意义，在各种实践中作用也各不同．参考文献：[1]马克思主义基本原理概论教材编写课题组．马克思主义基本原理概论[M]．高等教育，2009,7[2]华东师X 大学数学系．数学分析(第三版)[M]．高等教育，2001,6．[3]郭懋正．实变函数与泛函分析[M]．大学，2005,2[4]柳藩，钱佩玲．实变函数论与泛函分析[M]．师X 大学，1987．[5]程其襄，X 奠宙，魏国强等．实变函数与泛函分析既基础[M]．高等教育，2003,7．[6]夏道行，严绍宗等复旦大学数学系主编．实变函数与应用泛函分析基础[M]．某科学技术．1987．[7]茆诗松，程依明，濮晓龙．概率论与数理统计教程[M]．高等教育，2004,7．。

三角函数的级数展开与收敛性

三角函数的级数展开与收敛性在数学中，三角函数是研究角度和周期性现象的重要工具。

在很多实际问题中，利用三角函数的级数展开可以提供简洁的数学模型，并且通过分析其收敛性可以得到有用的结论。

本文将介绍三角函数的级数展开以及相应的收敛性。

一、正弦函数的级数展开与收敛性正弦函数是三角函数中最常见的函数之一，它可以通过无穷级数来表示。

正弦函数的级数展开称为正弦级数，其形式为：sin(x) = x/1! - x^3/3! + x^5/5! - x^7/7! + ...其中，n!表示n的阶乘，x为自变量。

正弦级数是一个交错级数，交错级数的收敛性可以通过判断其通项趋于零且绝对值递减来确定。

在正弦级数中，当自变量x为有界值时，其通项趋于零且绝对值递减，所以正弦级数在有限区间内绝对收敛。

另外，正弦函数具有周期性，所以正弦级数在整个实数范围内也收敛。

二、余弦函数的级数展开与收敛性余弦函数是另一个常见的三角函数，它也可以通过无穷级数来表示。

余弦函数的级数展开称为余弦级数，其形式为：cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...同样地，余弦级数也是一个交错级数。

与正弦级数类似，余弦级数在有界区间内绝对收敛，在整个实数范围内也收敛。

通过分析其通项趋于零且绝对值递减可以得出结论。

三、其他除了正弦函数和余弦函数，其他常见的三角函数如正切函数、余切函数、正割函数和余割函数等也可以通过级数展开表示。

这些函数的级数展开形式各不相同，但原则上可以利用类似的收敛性分析方法来确定其收敛性。

需要注意的是，有些三角函数的级数展开并不在整个实数范围内收敛，而只在特定的区间内部分收敛。

这时，需要根据具体问题来确定收敛的范围，以保证结果的准确性和可靠性。

四、应用举例三角函数的级数展开在数学和物理等领域有广泛的应用。

例如，在计算机图形学中，可以利用正弦级数展开来生成复杂的图形和动画效果；在信号处理中，可以利用三角函数的级数展开来对信号进行分析和重构；在电路分析和控制系统设计中，也可以利用三角函数的级数展开来建立数学模型和分析系统的稳定性等。

可测函数列的收敛性

目录摘要 (1)关键词 (1)Abstract (1)Keywords (1)前言 (1)1.可测函数列几种收敛的定义 (1)1.1 一致收敛 (1)1.2 点点收敛 (1)1.3 几乎一致收敛 (2)1.4 几乎处处收敛 (2)1.5 依测度收敛 (2)2.可测函数列几种收敛的关系 (3)2.1 点点收敛与一致收敛的关系 (3)2.2 点点收敛与几乎处处收敛的关系 (3)2.3 几乎处处收敛与一致收敛的关系 (3)2.4 几乎处处收敛与几乎一致收敛的关系 (3)2.5几乎处处收敛与依测度收敛的关系 (4)参考文献 (6)可测函数列的收敛性摘要:本文介绍了可测函数列常见的几种收敛:一致收敛、几乎一致收敛、几乎处处收敛、依测度收敛等,以及它们之间的关系.关键字:可测函数列;一致收敛;几乎一致收敛;几乎处处收敛;依测度收敛.Convergence of Measurable Function SequenceAbstract :This article introduces several common convergences of the measurable functionsequence :uniform convergence ,almost uniform convergence,almost everywhere converge- nce,convergence in measure and the relations about them .Key words :Measurable functions ;Uniform convergence ;Almost uniform convergence ; Almost everywhere convergence ;Convergence in measure前言在数学分析中我们知道,一致收敛是函数列很重要的性质,它能保证极限过程和一些运算的可交换性.但一般而论,一个收敛的函数列在其收敛域上是不一定一致收敛的.其实这一现象在某种意义下是带有普遍性的.1.可测函数列几种收敛的定义1.1一致收敛设()()()() ,,,,,21x f x f x f x f k 是定义在点集E 上的实值函数.若对于0>∀ε存在0>εN ,使得对于εN n ≥∀,E x ∈∀都有()(),ε<-x f x f k则称}{()k f x 在E 上一致收敛到()f x .记作:uk f f −−→(其中u 表示一致收敛).1.2点点收敛若函数列()()()() ,,,,,21x f x f x f x f k 在点集D E ⊂上每一点都收敛,则称它在D 上点点收敛．即E x ∈∀,0>∀ε,()0,>∃x N ε,对()x N n ,ε≥∀, 有()()ε<-x f x f k ,记作 f f k →于E ．例1 定义在[0,1]E =上的函数列1(),1k f x kx=+则()k f x 在E 上点点收敛到函数 ()⎩⎨⎧<<==.10,0,0,1x x x f 而且还能看出{()}k f x 在[]0,1上不一致收敛到()f x ,但对于0,{()}k f x δ∀>在[,1]δ上一致收敛到()f x . 1.3几乎一致收敛设E 是可测集,若0,,E E δδ∀>∃⊂使得(\),m E E δδ<且在E δ上有uk f f −−→,则称{()}k f x 在E 上几乎一致收敛与()f x ,并记作...a u k f f −−→(其中..u a 表示几乎一致收敛).即去掉某个零测度集,在剩下的集合上一致收敛.例2 定义在[]0,1E =上的函数()k k f x x =在[]0,1上收敛却不一致收敛.但是只要从[]0,1的右端点去掉任意小的一段成为[]()0,10,0δδδ->→,则{()}k f x 在其上就一致收敛了,像这样的收敛我们就可以称之为在[]0,1E =上几乎一致收敛于0. 1.4几乎处处收敛设()()()() ,,,,,21x f x f x f x f k 是定义在点集n E R ⊂上的广义实值函数.若存在E 中点集Z ,有()0,m Z =及对于每一个元素\x E Z ∈有lim ()()k x f x f x →∞=,则称{()}k f x 在E 上几乎处处收敛于()f x ,并简记为..,e a f f k →于E 或..a e k f f −−→即去掉某个零测度集,在剩下的集合上处处收敛.上文的例1也可以称之为在[]0,1上几乎处处收敛于()f x . 1.5依测度收敛设{}n f 是q R E ⊂上的一列..e a 有限的可测函数,若有E 上..e a 有限的可测函数()x f 满足下列关系:对任意0>σ有[]0lim =≥-σf f mE n n,则称函数列{}n f 依测度收敛于f ,记为:()()x f x f n ⇒.改用N -ε说法:对任意0>ε及0>σ,存在正数()σε,N ∃,使()σε,N n ≥时,[]εσ<≥-f f mE n .依测度收敛用文字叙述,就是说,如果事先给定一个（误差）0>σ,不论这个σ有多么小,使得()()x f x f n -大于σ的点x 虽然可能很多,但这些点所成之集合的测度随着n 无限增大而趋于零.从而可知,不依测度收敛的定义为:0>∃σ,使得[]σ≥-f f mE n 不收敛于0,即0>∃σ,0>∃ε, 对0>∀N 都N n ≥∃,使得[]εσ≥≥-f f mE n .2.可测函数列几种收敛的关系2.1点点收敛与一致收敛的关系由上述定义我们可以知道uk f f −−→,必有{()}k f x 点点收敛于()f x ,如例1,反之则不一定成立.2.2点点收敛与几乎处处收敛的关系由定义易知,点点收敛必几乎处处收敛,反之则不然. 2.3几乎处处收敛与一致收敛的关系由定义可知,一致收敛必几乎处处收敛....()a u a e k k f f f f −−→⇒−−→,反之则不然,如例2.而且还可以得到:若{()}k f x 是可测集E 上的可测函数列,则极限函数()f x 也是可测函数.2.4几乎处处收敛与几乎一致收敛的关系叶果洛夫(E ΓopoB )定理设(),{}n m E f <∞是E 上一列..e a 收敛于一个..e a 有限的函数f 的可测函数,则对于任意的0δ>,存在子集E E δ⊂,使{}n f 在E δ上一致收敛,且(\)m E E δδ<.注定理中“()m E <∞”不可去掉.如例3 定义在(0,)E =+∞的函数列()(]()⎩⎨⎧=∞∈∈=.,2,1,,,0,,0,1 n n x n x x f n显然n f 在(0,)+∞上处处收敛于1,但对于任何正数δ及任何可测集E δ,当(\)m E E δδ<时,n f 在E δ上不一致收敛于1,这是因为,当(\)m E E δδ<时,E δ不能全部含于(]n ,0中,必有()∞⋂∈,n E x n δ,于是有()0=n n x f .()().111sup =-≥-∈n n x n E x x f f δ所以()x f n 在E δ上不一致收敛于1,也即定理中“()m E <∞”不可去掉.由定义我们知道,一致收敛必是几乎处处收敛的,反之则不成立.但它们又有密切的关系,即上述定理告诉我们几乎处处收敛是“基本上”一致收敛 (在除去一个测度为任意小集合的子集上一致收敛)的.应用由上述定理我们还可以得到“鲁津定理”:设()f x 是E 上..e a 有限的可测函数,则对于任意的0δ>,存在闭子集E F δ⊂,使()f x 在F δ上是连续函数,且(\)m E F δδ<.简言之:在E 上..e a 有限的可测函数是“基本上连续” (在除去一个测度任意小集合的子集上连续)的函数,则我们可以用连续函数来逼近..e a 有限的可测函数. 2.5几乎处处收敛与依测度收敛的关系例4 依测度收敛而处处不收敛的函数列取(0,1]E =,将E 等分,定义两个函数:()()⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛∈⎥⎦⎤⎝⎛∈=.1,21,0,21,0,111x x x f ()()⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛∈⎥⎦⎤ ⎝⎛∈=.1,21,1,21,0,012x x x f 然后将(0,1]四等分、八等分,等等.一般地,对每个n ,作2n 个函数:()().2,,2,1.2,21,0,2,21,1n n n n n n j j j j x j j x x f =⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛-∉⎥⎦⎤ ⎝⎛-∈=我们把(){}n n i j f 2,,2,1, =先按n 后按j 的顺序逐个的排成一列:(1)(1)()()()12122(),(),,(),(),,(),nn n n x f x f x f x f x f(1)()()n j x f 在这个序列中是第22n j N -+=个函数.可以证明这个函数序列是依测度收敛于零的.这是因为对于任何的0σ>,()0[]n j f E σ-≥或是空集(当1σ>),或是1,22(]n n j j - (当01σ<≤),所以()102([])n j nf m E σ-≥≤(当时1σ>时,左端为0). 由于当2(1,2,,2.)2n n j j N -+== 趋于∞时,n →∞,由此可见()[]()00lim =≥-∞→σn j n f E m ,即()().0⇒x f n j但是函数列(1)在](1,0上的任何一点都不收敛.事实上,对任何点0(0,1]x ∈,无论n 多么大,总存在j ,使01(,]22n nj jx -∈,因而()0()1n j x f =,然而()10()0n j x f +=或()10()0n j x f -=,换言之,对任何0(0,1]x ∈,在()0(){}n j x f 中必有两个子列,一个恒为1,另一个恒为零,所以序列(1)在(0,1]上任何点都是发散的.这也就说明依测度收敛的函数列不一定处处收敛,也就是说依测度收敛不能包含几乎处处收敛.但仍有里斯(F.Riesz):设在E 上{}n f 测度收敛于f ,则存在子列{}i n f 在E 上..e a 收敛于f .例5 如例3,显然()()∞→→n x f n 1,当x E ∈.但是当01σ<<时,[]()+∞=≥-,1n f E n σ,且()∞=+∞,n m .这说明}{n f 不依测度收敛于1.这个例子又说明了一个..e a 的函数列也可以不是依测度收敛的,但是有下述关系: 勒贝格(Lebesgue)设mE <∞,{}n f 是E 上..e a 有限的可测函数列, {}n f 在E 上..e a 收敛于..e a 有限的函数f ,则()()x f x f n ⇒.此定理中的“mE <∞”不可去掉（例1）.定理也说明在的在的条件mE <∞下,依测度收敛弱于..e a 收敛.由以上勒贝格(Lebesgue)定理又可得出一个用几乎处处收敛来判断依测度收敛的充要条件,即:设mE <∞,{}n f 是E 上的可测函数列,那么{}n f 依测度收敛于f 的充要条件是:{}n f 的任何子函数列{}k n f 中必可找到一个几乎处处收敛于f 的子序列.证明（必要性）由于{}n f 依测度收敛于f ,知道这时{}n f 的的任何子序列{}k n f 必也依测度收敛于f ,由里斯定理可知{}k n f 中必存在几乎处处收敛于f 的子序列.（充分性）用反证法,即如果{}n f 不依测度收敛于f ,则存在一个0σ>,使得()n f f m E σ-≥不趋于0.则必有子序列{}kn f ,使得(())0.lim kn k m E f f a σ→∞-≥=>又由已知,在E 上必存在{}k n f 的子列几乎处处收敛于f ,又mE <∞,由勒贝格定理知将有{}k n f 依测度收敛于f ,即(())0.lim k n k m E f f σ→∞-≥=这与上式矛盾,所以{}n f 依测度收敛于f .注上述定义中的各种收敛的极限函数都是唯一的,而且从本文还可以知道一致收敛是最强的收敛,它蕴含了点点收敛、几乎处处收敛、依测度收敛等上述几种收敛.各种收敛都有不同的意义,在各种实践中作用也各不同.参考文献:[1] 华东师范大学数学系.数学分析[M] (第三版).北京:高等教育出版社,2010.[2] 程其襄,张奠宙,魏国强等.实变函数与泛函分析基础[M] (第三版).北京:高等教育出版社,2010.6.。

测函数列三种收敛性的区别与联系解析

目录1．前言 (1)2．概念 (1)2.1 几乎处处收敛 (1)2.2 几乎一致收敛 (1)2.3 依测度收敛 (2)3．三种收敛性之间的区别 (2)3.1 存在可测函数列几乎处处收敛而不依测度收敛 (2)3.2 存在可测函数列依测度收敛而不几乎处处收敛 (2)3.3 存在可测函数列几乎处处收敛而不几乎一致收敛 (4)4．三种收敛性的充要条件 (4)4.1 几乎处处收敛的充要条件 (4)4.2 几乎一致收敛的充要条件 (4)4.3 依测度收敛的充要条件 (6)5．三种收敛性之间的联系 (6)5.1 几乎一致收敛与几乎处处收敛 (6)5.2 依测度收敛与几乎处处收敛 (8)5.3 依测度收敛与几乎一致收敛 (10)5.4 三种收敛之间的关系图： (11)6．结论 (11)7．致谢 (12)8．参考文献 (13)n f 可测函数列三种收敛性的区别与联系摘要：对于可测集合E 上的几乎处处有限的可测函数列n f 来说有三种常见类型的收敛：几乎处处收敛，几乎一致收敛和依测度收敛。

本文首先介绍可测函数列三种收敛的概念，并讨论几乎处处收敛，几乎一致收敛和依测度收敛三者之间的关系。

这几种概念是伴随测度的建立而产生的新的收敛性，相对其他两种收敛性来说，依测度收敛的收敛条件是比较弱的，与熟知的处处收敛有很大的差异。

Egorov 定理、Riesz 定理和Lebesgue 定理等揭示了这几种收敛之间的关系。

关键词：几乎处处收敛几乎一致收敛依测度收敛中图分类号：O 17Difference and Connection between Three Types of Convergence of Measurable Function SequenceJiang Zhong (Tutor ：You Xuexiao)(Department of Mathematics, Hubei Normal University, Huangshi Hubei435002,China)Abstract : For the measurable function sequencewhich is finite almost everywhere on the measurable set E ,there are three types of common convergence: convergence almost everywhere, convergence almost uniform and convergence in measurable. This article has first described the concepts of those three types of convergence, and then discussed the relationship among convergence almost everywhere,convergence almost uniform and convergence in measurable . Those concepts are the new convergence,which are arised with the establishment of measure. Comparing with the other twotypes of convergence, the conditions of convergence inmeasurable are relatively weak, and has large differencewith the well-known convergence almost everywhere. TheEgorov theorem, Riesz theorem and Lebesgue theorem and soon reveal the relationship among these types of convergence.Keywords: Convergence almost everywhere Convergence almost uniform Convergence in measurable可测函数列三种收敛性的区别与联系蒋忠（指导教师，游雪肖）（湖北师范学院数学与应用数学湖北黄石 435002）1．前言本文介绍了几乎处处收敛、几乎一致收敛与依测度收敛，它们是伴随测度的建立而产生的新的收敛性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

再由Lebesgue定理（mE ）,得fnkij gnkij fg 于E，
这与（*）式矛盾，所以 fn gn f g于E
注：上述结果的证明也可通过依测度收敛的等价描述证明任取 {fn gn} 的子列{fnk gnk} ，找 {fnk gnk} 的子列 {fnki gnki} 使得 f g nki nki fg a.e.于E
条件mE<+∞对(3)来说不可少
例
设
fn
(x)
x
1 n
,
f (x) x, 则fn f于E
但
f
2 n
不依测度收敛于f
2于R
注：令
gn (x)
x n
,
g(x)
0
，则 gn不依测度收敛于g
对0
1,
有
lim
n
mE[|gn
g|
]
lim m(n， )
n
依测度收敛的等价描述令mE<+∞，则 fn f于E 对{fn} 的任意子列 {fnk} ,存在{fnk}的子列 {fnki} ，使得 fnki f a.e.于E
第四章可测函数
第四节依测度收敛
1. 依测度收敛的定义及例子
例1：依测度收敛但处处不收敛的函数列例2：几乎处处收敛但不依测度收敛的函数列
2. Riesz定理及勒贝格定理
Riesz定理若 fn f于E ,则必有{fn}的子列 {fnk} ，使得 fnk f a.e.于E
3. 收敛间的关系
（3）证明
若fnf于E,gng于E,则fngn fg于E
证明：假设 fn gn f g于E 不成立，则
0, 0, N 0, n N , 使E[|fngn fg| ]
故 0, 0,和一自然数列{nk}, 使E[| fnk gnk fg| ] （*）
由fnk f于E,知存在{ fnk }的子列{ fnki }，使fnki f a.e.于E 由gnki g于E,知存在{gnki }的子列{gnkij }，使gnkij g a.e.于E 从而f g nkij nkij fg a.e.于E，
(2) fn gn f g于E
(3) fn gn f g于E
注：(1),(2),(4)当mE=+∞
(4) | fn || f | 于E 时,也成立；条件mE<+∞
对(3)来说不可少.
（2）的证明：设 {fn} 与 {gn} 是E上几乎处处有限的可测函数
列, fn (x) f (x) 于E，gn (x) g(x) 于E, 则
m(E
FnБайду номын сангаас)
1 n
0(n
0)
即gn (x) f (x)于E
再由Riesz定理，存在{gn(x)} 的子列 {gni(x)}
使gni(x)→f(x) a.e.于E，
令 fi (x) gni (x) ，即得我们所要的结果。
fn (x) gn (x) f (x) g(x) 于E
证明：由于 | ( fn (x) gn (x)) ( f (x) g(x)) || fn (x) f (x) | | gn (x) g(x) |
0, mE mE mE 故
[|( fn gn )( f g )| ]
[| fn f |2 ]
fn f a.e.于E
子列
叶果洛夫
Riesz定理
逆定理
Lebesgue定理
叶果洛夫定理 mE<+∞
mE<+∞
fn f于E
子列
fn f a.u.于E
⒋依测度收敛的性质（唯一性和四则运算）
定理：令mE<+∞ ， fn f于E, gn g于E ，则 (1) 若又有 fn h于E , 则f(x)=h(x) a.e.于E。
[|gn g|2 ]
令n ，即得 mE 0 [|( fn gn )( f g )| ]
所以fn (x) gn (x) f (x) g(x)于E
注:(1),(4)的证明类似，只要利用|| fn (x) | | f (x) ||| fn (x) f (x) |
| f (x) h(x) || ( fn (x) f (x)) ( fn (x) h(x)) || fn (x) f (x) | | fn (x) h(x) |
例对 E=R1 上的a.e.有限的可测函数f(x)，一定存在 E上的连续函数列{fi(x)}使fi(x)→f(x) a.e.于E
证明：由鲁津定理的推论知
1 n
, 闭集F
n
E，及E上的连续函数gn
(x)
使在Fn上gn (x)
f (x)且m(E Fn )
1 n
从而
0, mE[|gn f | ]
证明：（必要性）任取 {fn}的子列 {fnk} ，
由于 fn f于E 当然有 fnk f于E
由Riesz定理知，存在 {fnk}的子列 {fnki} ，
使得 fnki f a.e.于E
反之：假设 fn f于E 不成立，则
0, 使mE[| fn
f
|
不收敛于
]
0
充分性
即 0, 0, N 0, n N , 使mE[| fn f | ]
故存在 {fn}的子列 {fnk} ，使得
mE [| fnk f | ] (k 1, 2,3, )
显然 {fnk}的任何子列 {fnki}都不依测度收敛与f，再由Lebesgue定理(mE<+∞)的逆否命题知，显然 {fnk}的任何子列 {fnki}都不几乎处处收敛与f ，
这与条件矛盾，从而fn f于E