可测函数列常见的几种收敛.docx

合集下载

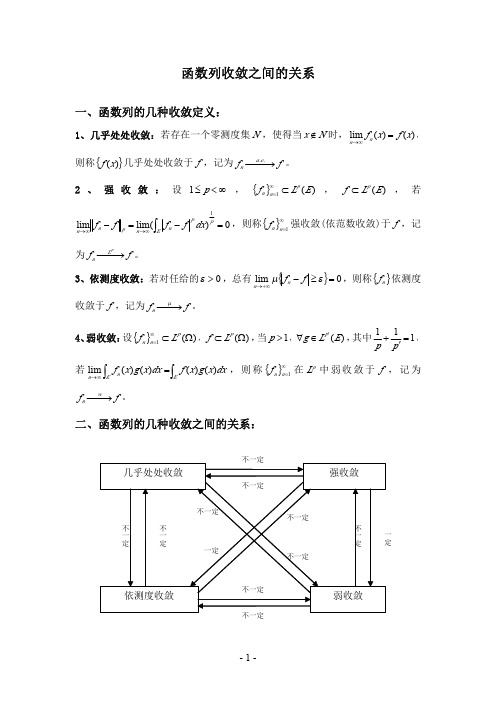
函数列收敛之间的关系

(x)
=
⎪⎪1 ⎨
⎪0
⎪⎩
x
∈
⎛ ⎜
⎝
j −1 ,
2n
j 2n
⎥⎦⎤,
x ∉ ⎜⎛ ⎝
j −1 ,
2n
j 2n
⎥⎦⎤,
( j = 1,2,⋯,2n )
{ } 把
f
( j
n)
,
j
=
1,2,⋯,2 n
先按 n 后按 j 的顺序逐个地排成一列：
f (1) 1
(
x)
，
f
( 1
2)
(
x),⋯,
f1(n) (x) ，
(x)
是从左边数起的第
i
个小区间上恒等于
1，而在其他地方恒等
于 0。
一般地，将 [0,1]分为 k 等分，定义第 k 组的第 i 个函数为，令
f1(x) =
f (1) 1
(
x)
，
f 2 (x) = f1(2) (x)
，
f3 (x) =
f
(2) 2
(
x)
，
f4 (x) =
f (3) 1
(
x)
，
f5 (x) =
>
0，
{ } lim mE
n→∞
x
fn (x) −
f (x)
≥σ
= 0 ，所以 fn (x) ⇒ f (x) = 0 ， x ∈ [0,1]。但是若取
g(x) = 1， x ∈ [0,1]，则 g(x) ∈ Lp (E) 。而
1
1
1
∫ ∫ ∫ lim
n→∞
0
fn (x)g(x)dx
=

§ 3.2 可测函数的收敛性

83§3.2 可测函数的收敛性教学目的使学生对可测函数序列的几乎处处收敛性, 依测度收敛性和几乎一致收敛性及它们的之间蕴涵关系有一个全面的了解.本节要点本节引进的几种收敛是伴随测度的建立而产生的新的收敛性. 特别是依测度收敛是一种全新的收敛, 与熟知的处处收敛有很大的差异. Egorov 定理和Riesz 定理等揭示了这几种收敛之间的关系. Riesz 定理在几乎处处收敛和较难处理的依测度收敛之间架起了一座桥梁.设),,(µF X 是一测度空间. 以下所有的讨论都是在这一测度空间上进行的. 先介绍几乎处处成立的概念.几乎处处成立的性质设)(x P 是一个定义在E 上与x 有关的命题. 若存在一个零测度集N , 使得当N x ∉时)(x P 成立(换言之, })(:{不成立x P x N ⊂), 则称P (关于测度µ)在E 上几乎处处成立. 记为)(x P a.e.−µ, 或者)(x P a.e.在上面的定义中, 若)(x P 几乎处处成立, 则集})(:{不成立x P x 包含在一个零测度集内. 若})(:{不成立x P x 是可测集, 则由测度的单调性知道.0}))(:({=不成立x P x µ 特别地, 当测度空间),,(µF X 是完备的时候如此.例1 设给定两个函数f 和g . 若存在一个零测度集N , 使得当N x ∉时),()(x g x f = 则称f 和g 几乎处处相等, 记为g f = a.e.例2 设f 为一广义实值函数. 若存在一个零测度集N, 使得当N x ∉时,+∞<f 则称f 是几乎处处有限的, 记为+∞<f , a.e.注1 设f 是几乎处处有限的可测函数, 则存在一零测度集N, 使得当N x ∉时.+∞<f 令.~c N fI f = 则f ~是处处有限的可测函数并且 a.e..~f f =因此, 在讨论几乎处处有限的可测函数的性质时, 若在一个零测度集上改变函数的值不影响该性质, 则不妨假定所讨论的函数是处处有限的.注意, f 几乎处处有限与 a.e.M f ≤是不同的概念. a.e.M f ≤表示84存在一个零测度集N , 使得f 在c N 上有界. 显然 a.e.M f ≤蕴涵f 几乎处处有限. 但反之不然. 例如, 设),10(1)(≤<=x xx f .)0(+∞=f 则f 在)1,0(上关于L 测度是几乎处处有限的, 但在)1,0(中并不存在一个L 零测度集N 和,0>M 使得在N −)1,0(上, .)(M x f ≤ 初学者常常在这里发生误解, 应当引起注意.可测函数的几种收敛性和定义在区间上的函数列的一致收敛一样, 可以定义在任意集上的函数列的一致收敛性. 设E 是X 的子集. )1(,≥n f f n 定义在E 上的函数. 若对任意0>ε, 存在,0>N 使得当N n ≥时, 对一切E x ∈成立,)()(ε<−x f x f n 则称}{n f 在E 上一致收敛于f , 记为..un f f n →定义1 设}{n f 为一可测函数列, f 为一可测函数.(1) 若存在一个零测度集N , 使得当N x ∉时, 有)()(lim x f x f n n =∞→, 则称}{n f 几乎处处收敛于f , 记为f f n n =∞→lim a.e., 或f f n → a.e.. (2) 若对任给的0>ε, 总有.0})({lim =≥−+∞→εµf f n n则称}{n f 依测度收敛于f , 记为.f f n → µ(3) 若对任给的0>δ, 存在可测集δE , δµδ<)(E , 使得}{n f在c E δ上一致收敛于f , 则称}{n f 几乎一致收敛于f , 记为n nf lim =f a.un., 或 f f n → a..un..容易证明, 若将两个a.e.相等的函数不加区别, 则上述几种极限的极限是唯一的. 例如, 若,a.e.f f n → g f n → a.e., 则g f = a.e.. 其证明留作习题.例3 设))),,0[(),,0([m +∞+∞M 为区间),0[∞+上的Lebesgue 测度空间. 其中)),0[(+∞M 是),0[∞+上的L 可测集所成的σ-代数, m 是1R 上的L 测度在),0[∞+上的限制. 令85.1),(1)(),1(≥−=n x I x f n n n则对任意,0>x ).(0)(∞→→n x f n 当0=x 时)(x f n 不收敛于0. 但,0})0({=m 因此在),0[∞+上.0a.e. → n f 由于对,21=ε ).(,0)),[]1,0([})21({/+∞→ → +∞=+∞∪=≥n n n m f m n 因此}{n f 不依测度收敛于0. 这个例子表明在一般情况下, 几乎处处收敛不一定能推出依测度收敛.例4 设)]),1,0[(],1,0[(m M 是]1,0[上的Lebesgue 测度空间. 令.1,)(≥=n x x f n n则对任意0>δ, }{n f 在]1,0[δ−上一致收敛于0.由于δδ=−])1,1((m 可以任意小, 因此0a..un. → n f . 又显然.0a.e. → n f例5 设)]),1,0[(],1,0[(m M 是]1,0[上的Lebesgue 测度空间. 令.1,,,1,1[≥=−=n n i ni n i A i n L 将}{i n A 先按照n 后按照i 的顺序重新编号记为}{n E . 显然.0)(→n E m 令)()(x I x f n E n =, 1≥n ,.0)(=x f对任意0>ε, 由于.,0)(})({∞→→=≥−n E m f f m n n ε故}{n f 依测度收敛于f . 但}{n f 在]1,0[上处处不收敛. 事实上, 对任意]1,0[0∈x , 必有无穷多个n E 包含0x , 也有无穷多个n E 不包含0x . 故有无穷多个n 使得,1)(0=x f n 又有无穷多个n 使得.0)(0=x f n 因此}{n f 在0x 不收敛. 这个例子表明依测度收敛不能推出几乎处处收敛. 例3和例4表明, 依测度收敛和几乎处处收敛所包含的信息可能相差很大.几种收敛性之间的关系为叙述简单计, 以下我们设所讨论的函数都是实值可测函数. 但以下结果对几乎处处有限的可测函数也是成立的由(见注1的说明).引理2 设+∞<)(X µ. 若.a.e.f f n → 则对任意0>ε有86.0)}{(lim =≥−∞=∞→U n i i n f f εµ 证明设0>ε是一给定的正数. 任取X x ∈, 若对任意,1≥n 存在,n i ≥ 使得.)()(ε≥−x f x f i 则)()(x f x f n 不收敛于. 这表明IU ∞=∞=≥−1}{n n i i f fε)}.()(:{/x f x f x n → ⊂由于,a.e.f f n → 因此由上式知道.0}{1=≥−∞=∞=IU n n i i f f εµ 由于+∞<)(X µ, 由测度的上连续性, 我们有0}{}{lim 1=≥−= ≥−∞=∞=∞=∞→IU U n n i i n i i n f f f f εµεµ. ■ 容易证明, 若,a..un.f f n → 则f f n → a.e.(其证明留作习题). 下面的定理表明当+∞<)(X µ时, 其逆也成立.定理3 (叶戈洛夫)若+∞<)(X µ, 则f f n → a.e.蕴涵.a..un.f f n →证明设+∞<)(X µ, .a.e.f f n → 由引理2 , 对任意0>ε, 有.0}{lim =≥−∞=∞→U n i i n f f εµ 于是对任意的0>δ和自然数1≥k , 存在自然数k n 使得.2}1{k n i i k k f f δµ< ≥−∞=U 令.}1{1U U ∞=∞=≥−=k n i i kk f f E δ 由测度的次可数可加性我们有 .2}1{)(11δδµµδ=≤ ≥−≤∑∑∞=∞=∞=k k k n i i k k f f E U 往证在c E δ上, }{n f 一致收敛于f . 事实上, 由De Morgan 公式得87.1,}1{}1{1≥<−⊂<−=∞=∞=∞=k k f f k f f E kk n i i k n i i c I I I δ (1) 对任意0>ε, 取k 足够大使得.1ε<k则由(1)式知道, 当k n i ≥时对一切c E x δ∈, 有.1)()(ε<<−kx f x f i 即在c E δ上}{n f 一致收敛于f . 这就证明了f f n → a..un.. 定理证毕. 注 2 在叶戈洛夫定理中, 条件+∞<)(X µ不能去掉. 例如, 若令),()(),[x I x f n n +∞= .1≥n 则}{n f 在1R 上处处收敛于0. 但容易知道}{n f 不是几乎一致收敛于0.定理4 若+∞<)(X µ, 则f f n → a.e.蕴涵.f f n → µ证明设+∞<)(X µ, .a.e.f f n → . 由引理2 , 对任意0>ε有.0}{lim =≥−∞=∞→U n i i n f f εµ 由测度的单调性立即得到()≤≥−∞→}{lim εµf f n n .0}{lim =≥−∞=∞→U n i i n f f εµ 即.f f n → µ ■ 本节例3表明, 在定理4中, 条件+∞<)(X µ不能去掉.定理5 (Riesz)若,f f n → µ 则存在}{n f 的子列}{k n f , 使得.a.e.f f k n →证明设.f f n → µ 对任意0>ε和0>δ, 存在1≥N , 使得当Nn ≥时, 有δεµ<≥−})({f f n .于是对任意自然数1≥k , 存在自然数k n , 使得.21})1({k n k f f k <≥−µ (2)88我们可适当选取k n 使得L ,2,1,1=<+k n n k k . 往证.a.e.f f k n → 令L I ,2,1,}1{=<−=∞=i k f f E ik n i k . 对任意i E x ∈, 当i k ≥时, .1)()(kx f x f k n <− 这表明}{k n f 在i E 上收敛于f . 令.1U ∞==i i E E 则}{k n f 在E 上收敛于f . 往证.0)(=c E µ 由De Morgan 公式, 我们有.}1{11I IU ∞=∞=∞=≥−==i i i k n c i c k f f E E k 利用(2)容易得到.1)(1≤c E µ 因此由测度的上连续性并且利用(2), 我们有.021lim })1({lim }1{lim )(=≤≥−≤ ≥−=∑∑∞=∞→∞=∞→∞=∞→i k k i ik n i ik n i ck f f k f f E k k µµµU 这就证明了.a.e.f f k n → ■定理6 设+∞<)(X µ. 则f f n → µ当且仅当}{n f 的任一子列}{k n f 都存在其子列}{k n f ′, 使得).(a.e.∞→′ → ′k f f k n证明必要性(此时不需设+∞<)(X µ). 设.f f n → µ 显然}{n f 的任一子列}{k n f 也依测度收敛于 f. 由定理 5 , 存在}{k n f 的子列}{k n f ′, 使得).(a.e.∞→′ → ′k f f k n充分性. 用反证法. 若}{n f 不依测度收敛于f , 则存在,0>ε 使得.0}({/ → ≥−εµf f n 于是存在0>δ和}{n f 的子列}{kn f , 使得 .})({δεµ≥≥−f f kn 由此知}{k n f 的任何子列}{k n f ′都不能依测度收敛于f . 由定理4, }{k n f ′也不89能a.e.收敛于f . 这与定理所设的条件矛盾. 故必有.f f n → µ ■定理5和定理6给出了依测度收敛和几乎处处收敛的联系. 利用这种联系, 常常可以把依测度收敛的问题转化为几乎处处的问题. 而几乎处处收敛是比较容易处理的.例 6 设)1(,,,≥n g f g f n n 是有限测度空间),,(µF X 上的几乎处处有限的可测函数, ,f f n → µ .g g n → µ 又设h 是2R 上的连续函数. 则).,(),(.g f h g f h n n → µ特别地, .fg g f n n → µ证明不妨设)1(,,,≥n g f g f n n 都是处处有限的. 设),(k k n n g f h 是),(n n g f h 的任一子列. 由定理6, 存在}{k n f 的子列}{k n f ′使得).(a.e.∞→′ → ′k f f k n 同理存在}{k n g ′的子列, 不妨仍记为}{k n g ′, 使得).(a.e.∞→′ → ′k g g k n 既然h 是连续的, 因此有).,(),( a.e.g f h g f h k k n n → ′′这表明),(n n g f h 的任一子列),(k k n n g f h , 都存在其子列),(k k n n g f h ′′使得).,(),( a.e.g f h g f h k k n n → ′′ 再次应用定理6, 知道).,(),(.g f h g f h n n → µ 特别地, 若取,),(xy y x h = 则得到.fg g f n n → µ ■小结本节介绍了几乎处处收敛, 依测度收敛和几乎一致收敛, 它们是伴随测度的建立而产生的新的收敛性.几种收敛性之间有一些蕴涵关系. 其中最重要的是Egorov 定理和Riesz 定理.利用Riesz 定理,可以把较难处理的依测度收敛的问题化为几乎处处收敛的问题.习题习题三, 第18题—第28题.。

常见的收敛和发散函数的例子

常见的收敛和发散函数的例子收敛和发散是数学中重要的概念。

收敛函数是指一个数列或序列在趋近于某个特定值时稳定而缓慢的变化，反之，发散函数是指在趋近于某个特定值时，却以无限快的速度变化。

在数学中，一些收敛和发散的函数有着非常重要的应用和意义。

下面，我们来看一些常见的收敛和发散函数的例子。

1.收敛函数1.1幂级数函数幂级数函数是由一系列单项式组成的无穷级数。

具有良好的收敛性质。

一个幂级数在某一点处收敛的充分必要条件是：此点到所有单项式的“起点”所组成的类似于圆盘的区域都包含在幂级数的收敛区域内。

1.2柯西序列柯西序列是指在数列中，当误差越来越小时，相邻两个数之间的距离也越来越小。

柯西序列的收敛性，是根据误差、距离的特征来决定的。

在实数系中，柯西序列必有极限值。

1.3一次函数一次函数是一个非常常见的函数形式，其值由自变量某与常数a和b的线性组合所决定。

一次函数有着稳定的收敛性质，也就是说，当某逐渐增大时，y也会按着规律逐渐增大，但是这个过程是有限制的，不能无限增大。

2.发散函数2.1阶乘函数阶乘函数是一个非常特殊的函数，其值为n!，也就是从1到n的所有整数的乘积。

阶乘函数是一个非常快速的函数，其在n趋近于无穷大时，会发散至正无穷大。

2.2双曲函数双曲函数是一组涉及指数的函数，类似于正弦和余弦函数，但是它们有着更快速的增长速度。

当变量趋向于无穷大，双曲函数会发散至正无穷大。

2.3余弦函数余弦函数是一种周期性函数，其值由正弦函数相移90度后的值得到。

余弦函数在某些情况下，当自变量趋向于某些特定的值时，会发散。

在数学中，收敛和发散的函数广泛应用于数学分析、微积分、复变函数等领域。

无论是理论研究还是实际应用，都需要对这些函数的性质和特征进行深入的研究。

可测函数列常见的几种收敛

可测函数列常见的几种收敛摘要：本文介绍了可测函数列常见的几种收敛：一致收敛、几乎一致收敛、几乎处处收敛、依测度收敛等以及它们之间的关系．关键字：可测函数列；一致收敛；几乎一致收敛；几乎处处收敛；依测度收敛前言在数学分析中我们知道一致收敛是函数列很重要的性质，比如它能保证函数列的极限过程和(R)积分过程可交换次序等．可是一般而言函数列的一致收敛性是不方便证明的，而且有些函数列在其收敛域内也不一定是一致收敛的，如文中所给的例2函数()f x 在收敛域[0,1]内不一致收敛，但对于一个0δ>当0δ→时在[0,]δ内一致收敛，这不见说明了一致收敛的特殊性，也验证了我们平时常说的“矛盾的同一性和矛盾的斗争性是相联系的、相辅相成的”[1]1可测函数列几种收敛的定义1.1一致收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集E 上的实值函数．若对于0,ε∀>存在,K N +∈使得对于,k K x E ∀≥∀∈都有()()k f x f x ε-<则称}{()k f x 在E 上一致收敛到()f x ．记作：u k f f −−→(其中u 表示一致uniform)． 1.2点点收敛若函数列12(),(),(),,(),k f x f x f x f x 在点集D E ⊂上每一点都收敛，则称它在D 上点点收敛．例1定义在[0,1]E =上的函数列1(),1k f x kx =+则()k f x 在E 上点点收敛到函数 1,0,()0,0 1.x f x x =⎧=⎨<≤⎩ 而且还能看出{()}k f x 在[]0,1上不一致收敛到()f x ，但对于0,{()}k f x δ∀>在[,1]δ上一致收敛到()f x ．1.3几乎一致收敛[3]设E 是可测集，若0,,E E δδ∀>∃⊂使得(\),m E E δδ<在E δ上有u k f f −−→则称{()}k f x 在E 上几乎一致收敛与()f x ，并记作...a u k f f −−→(其中a.u ．表示几乎一致almost uniform)．例2定义在[]0,1E =上的函数()k k f x x =在[]0,1上收敛却不一致收敛．但是只要从[]0,1的右端点去掉任一小的一段使之成为[]()0,10,0δδδ->→则{()}k f x 在此区间上就一致收敛，像这样的收敛我们就可以称之为在[]0,1E =上几乎一致收敛与0．1.4几乎处处收敛[3]设12(),(),(),,(),k f x f x f x f x 是定义在点集n E R ⊂上的广义实值函数．若存在E 中点集Z ，有()0,m Z =及对于每一个元素\x E Z ∈，有lim ()()k x f x f x →∞= 则称{()}k f x 在E 上几乎处处收敛与()f x ，并简记为,.[]k f f a e E →或..a e k f f −−→ 若上文的例1也可以称之为在[]0,1上几乎处处收敛与()f x ．1.5依测度收敛例3在[0,1)上构造函数列{()}k f x 如下：对于k N +∈，存在唯一的自然数i 和j ，使得2,i k j =+其中02,i j ≤≤令1[,)22()(),1,2,,[0,1).i i k j j f x x k x χ+==∈任意给定的0[0,1),x ∈对于每一个自然数i ，有且仅有一个j ，使得01[,)22i i j j x +∈．数列0{()}f x 中有无穷多项为1，有无穷多项为0．由此可知，函数列{()}k f x 在[0,1)上点点不收敛．因此仅考虑点收敛将得不到任何信息．然而仔细观察数列0{()}k f x 虽然有无穷多个1出现，但是在“频率”意义下，0却也大量出现．这一事实可以用点集测度语言来刻画．只要k 足够大，对于01,ε<≤点集{[0,1)()0}{[0,1)()1}1[,)22k k i ix f x x f x j j ε∈-≥=∈=+= 的测度非常小．事实上1({[0,1)()0})2k i m x f x ε∈-≥=．这样对于任给的0,δ>总可以取到0,k 也就是取到0,i 使得当0k k >时，有({[0,1)()0})1k m x f x εδ∈-<>-其中02i δ-<．这个不等式说明，对于充分大的h ，出现0的“频率”接近1．我们将把这样一种现象称为函数列{()}k f x 在区间[0,1)上依测度收敛到零函数，并将抽象出以下定义[3]：设12(),(),(),,(),k f x f x f x f x 是可测集E 上几乎处处有限的可测函数．若对于任意给定的0,ε>有 lim (())0,k x m E f f ε→∞->= 则称{()}k f x 在E 上依测度收敛到函数()f x ，记为.m k f f −−→ 2可测函数列几种收敛的关系2.1点点收敛与一致收敛的关系由上述定义我们可以知道u k f f −−→，必有{()}k f x 点点收敛于()f x ．如例1．反之则不一定成立，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则()f x 也是可测函数．2.2几乎处处收敛与一致收敛的关系由定义可知有一致收敛必几乎处处收敛....()a u a e k k f f f f −−→⇒−−→．反之则不然，如例2．而且还可以得到若{()}k f x 是可测集E 上的可测函数列，则极限函数()f x也是可测函数．应用：从数学分析我们知道一致收敛的函数列对于求极限运算和(R)积分运算、微分运算与(R)积分运算等可以交换次序．2.3几乎处处收敛与一致收敛的关系叶果洛夫(E ΓopoB )定理[5]：设(),{}n m E f <∞是E 上一列a.e ．收敛于一个a.e ．有限的函数f 的可测函数，则对于任意的0δ>，存在子集E E δ⊂，使{}n f 在E δ上一致收敛，且(\)m E E δδ<．注定理中“()m E <∞”不可去掉如：例4定义在(0,)E =+∞的函数列1,(0,]()(1,2,).0,(,)m x m x m x m f ∈⎧==⎨∈+∞⎩ 则m f 在(0,)+∞上处处收敛于1，但对于任何正数δ及任何可测集E δ，当时(\)m E E δδ<时，m f 在E δ上不一致收敛于1．这是因为，当时(\)m E E δδ<时，E δ不能全部含于(0,]m 中，必有(,)m E m x δ∈+∞，于是有()0m m x f =． sup ()1()11m m m x E f x f x δ∈-≥-=所以()m x f 在E δ上不一致收敛与1，也即定理中“()m E <∞”不可去掉[4]．由定义我们知道一致收敛必是几乎处处收敛的，反之则不成立．但它们又有密切的关系，即使上述定理告诉我们几乎处处收敛“基本上”是一致收敛的(在除去一个测度为任意小集合的子集上)．应用由上述定理我们还可以得到“鲁津定理”：设()f x 是E 上a.e ．有限的可测函数，则对于任意的0δ>，存在闭子集E F δ⊂，使()f x 在F δ上是连续函数，且(\)m E F δδ<．也就是说：在E 上a.e ．有限的可测函数“基本上”是连续的(在除去一个测度为任意小集合的子集上)．也即我们可以用连续函数来逼近a.e ．有限的可测函数．2.4几乎处处收敛与依测度收敛的关系例5取(0,1]E =，将E 等分，定义两个函数：(1)111,(0,]2()10,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩， (1)210,(0,]2()11,(,1]2x x x f ⎧∈⎪⎪=⎨⎪∈⎪⎩．然后将(0,1]四等分、八等分等等．一般的，对于每个n ，作2n 个函数：()11,(,]22()1,2,,2.10,(,]22n n n n j n j j x x j j j x f -⎧∈⎪⎪==⎨-⎪∉⎪⎩．我们把(),1,2,,2{}n j x j f =，先n 按后按j 的顺序逐个的排成一列：(1)(1)()()()12122(),(),,(),(),,(),n n n n x f x f x f x f x f (1)()()n j x f 在这个序列中是第22n j N -+=个函数．可以证明这个函数列是依测度收敛于零的．这是因为对于任何的0σ>，()0[]n j f E σ-≥或是空集(当1σ>)，或是1,22(]n n j j -(当01σ<≤)，所以 ()102([])n j n f m E σ-≥≤ (当时1σ>时，左端为0)．由于当2(1,2,,2.)2n n j j N -+==趋于∞时n →∞，由此可见()([0])0lim n j N m E f σ→∞-≥=，也即()()0m n j x f −−→．但是函数列(1)在上的任何一点都不收敛．事实上，对于任何点0(0,1]x ∈，无论n 多么大，总存在j ，使01(,]22n n j j x -∈，因而()0()1n j x f =，然而()10()0n j x f +=或()10()0n j x f -=，换言之，对于任何0(0,1]x ∈，在()0(){}n j x f 中必有两子列，一个恒为1，另一个恒为0．所以序列(1)在(0,1]上任何点都是发散的．这也就说明依测度收敛的函数列不一定处处收敛，也就是说依测度收敛不能包含几乎处处收敛，但仍有：黎斯(F ．Riesz)[5]设在E 上{}n f 测度收敛于f ，则存在子列{}i n f 在E 上a.e ．收敛于f ．例6 如例4，当()1()m x n f →→∞当x E ∈．但是当01σ<<时，1[](,)m f E m σ-≥=+∞且(,)m m +∞=∞．这说明}{n f 不依测度收敛于1．这个例子又说明了几乎处处收敛也不包含依测度收敛，但是有下述关系：勒贝格(Lebesgue)[5]设mE <∞，{}n f 是E 上a.e ．有限的可测函数列，{}n f 在E 上a.e ．收敛于a.e ．有限的函数f ，则()()m n x f x f −−→．此定理中的“mE <∞”不可去掉，原因参看例1．定理也说明在的在的条件mE <∞下，依测度收敛弱于几乎处处收敛．有以上定理黎斯又给出了一个用几乎处处收敛来判断依测度收敛的充要条件：设mE <∞，{}n f 是E 上的可测函数列，那么{}n f 依测度收敛于f 的充要条件是：{}n f 的任何子列{}k n f 中必可找到一个几乎处处收敛于f 的子序列．证明（必要性）由于{}n f 依测度收敛于f ，由定义知道这时{}n f 的的任何子序列{}k n f 必也依测度收敛于f ，由黎斯定理可知{}k n f 中必存在几乎处处收敛于f 的子序列．（充分性）如果{}n f 不依测度收敛于f ，即存在一个0σ>，使得()n f f m E σ-≥不趋于0．因此必有子序列{}k n f ，使得(())0.lim kn k m E f f a σ→∞-≥=> 这样{}k n f 就不可能再有子序列几乎处处收敛于f 了，否则由勒贝格定理知将有{}k n f 依测度收敛于f ，即(())0.lim kn k m E f f σ→∞-≥= 这与上式矛盾，所以{}n f 依测度收敛于f ．应用依测度收敛在概率统计中有重要的意义，如例3；它也是证明中心极限定理的重要依据，由中心极限定理我们可以知道用一个正态分布来模拟一个样本容量较大的样本的概率分布，从而简化了大样本概率分布的处理和计算[7]．结束语：上述定义中的各种收敛的极限函数都是唯一的，而且从本文还可以知道一致收敛是最强的收敛，它蕴含了点点收敛、几乎处处收敛、依测度收敛等上述几种收敛．各种收敛都有不同的意义，在各种实践中作用也各不同．参考文献：[1]马克思主义基本原理概论教材编写课题组．马克思主义基本原理概论[M]．高等教育，2009,7[2]华东师X 大学数学系．数学分析(第三版)[M]．高等教育，2001,6．[3]郭懋正．实变函数与泛函分析[M]．大学，2005,2[4]柳藩，钱佩玲．实变函数论与泛函分析[M]．师X 大学，1987．[5]程其襄，X 奠宙，魏国强等．实变函数与泛函分析既基础[M]．高等教育，2003,7．[6]夏道行，严绍宗等复旦大学数学系主编．实变函数与应用泛函分析基础[M]．某科学技术．1987．[7]茆诗松，程依明，濮晓龙．概率论与数理统计教程[M]．高等教育，2004,7．。

可测函数列的几种收敛性关系

可测函数列的几种收敛性关系段胜忠;杨国翠【摘要】对可测函数列的几种收敛性的定义和性质进行归纳和总结,讨论他们之间的关系,并给出相应的证明,从而使各种收敛之间的关系更加明了.【期刊名称】《保山学院学报》【年(卷),期】2014(033)005【总页数】3页(P12-14)【关键词】可测函数列;一致收敛;几乎处处收敛;依测度收敛;强收敛;弱收敛【作者】段胜忠;杨国翠【作者单位】保山学院数学学院,云南保山678000;保山学院数学学院,云南保山678000【正文语种】中文【中图分类】O13可测函数列的一致收敛、几乎处处收敛、依测度收敛、强收敛、弱收敛是经典实变函数和泛函分析理论中几种重要的收敛关系。

本文的目的在于对可测函数列的几种收敛性的相互关系给出总结和证明，从而为偏微分方程研究中所使用的弱收敛方法提供理论依据。

定义1.1设fn(x)(n=1,2,3…)，f(x)均为定义在可测集Ω上的几乎处处有限的可测函数，若满足，则称{fn(x)}在Ω上一致收敛于f(x)，记为定义1.2设{fn(x)}是定义在可测集Ω上的一列可测函数，若存在Ω中的点集E，满足m(E)，∀x∈Ω\E，则称{fn(x)}在Ω上几乎处处收敛于f(x)，记为fn(x)→f(x),a.e.于Ω。

定义1.3设{fn(x)}是定义在可测集Ω上的一列可测函数，若∀σ＞0有0，则称函数列{fn(x)}在Ω上依测度收敛于f(x)，记为fn(x)⇒f(x)。

定义1.4设fn(n=1，2，3…)，f∈Lp(Ω)，若当n→∞时，有||fn-f||→0，则称fn强收敛于f，记为定义1.5设fn(n=1,2,3…)，f∈Lp(Ω)，若对每一个g∈Lq(Ω)（q为p的共轭数），当n→∞时，有则称fn弱收敛于f，记为fn(x)（1）一致收敛与几乎处处收敛的关系若函数列fn(x)一致收敛于f(x)，则几乎处处收敛于f(x)。

逆命题一般不成立。

例如函数列fn(x)=xn(n=1,2,3…)在Ω=［0,1］上几乎处处收敛于零,但并不一致收敛于零。

各种函数列收敛的总结

各种函数列收敛的总结利用余项准则证明函数列一致收敛1. 证明Sn(x)=xn,n=1,2,..., 在[0,b](0<b<1) 上一致收敛.2. 证明函数列fn(x)=(1−x)xn,n=1,2,⋯, 在[0,1] 一致收敛.利用余项准则证明函数列非一致收敛1. 证明Sn(x)=xn,n=1,2,..., 在[0,1] 上非一致收敛.2. 函数列gn(x)=(1−xn)x,n=1,2,⋯, 在[0,1] 上非一致收敛.3. 证明函数列fn(x)=xn−x2n, n=1,2,⋯, 在[0,1] 上非一致收敛.4. 设函数列fn(x)=nx(1−x)n,n=1,2,⋯, 证明: (1) 在[0,1] 上收敛; (2) 在[0,1] 上非一致收敛,但在[α,1](α>0 上非一致收敛,但在[α,1) 上一致收敛 ;(3)limn→∞∫01fn(x)dx=∫01limn→∞fn(x)dx.5. 设函数列fn(x)=n(xn−x2n),n=1,2,⋯,x∈[0,1]. (1) 求函数列fn(x) 的极限函数;(2)证明fn(x) 非一致收敛;(3)验证极限运算与积分运算不能交换顺序.含有参数函数列一致收敛1. 设fn(x)=ncx(1−x2)n,n=1,2,⋯, 讨论函数列fn(x) 在[0,1] 上的一致收敛性.2. 讨论函数列fn(x)=ncxe−nx,n=1,2,⋯,x∈[0,1] 的一致收敛性.3. 讨论函数列在指定区间上的一致收敛性:fn(x)=x(ln⁡n)αnx,n=1,2,⋯,x∈[0,+∞).4. 讨论函数列在指定区间上的一致收敛性:fn(x)=cnx1+ncnx2(c>0) ,n=1,2,⋯(1)x∈(−∞,+∞),(2)x ∈(−∞,)(,+∞)已知f(x) 连续利用闭区间连续则有界或可积必有界证明{gn(f(x)) }一致收敛1. 设f(x) 在[0,1] 上连续, f(1)=0. 证明： {f(x)xn } 在[0,1] 上一致收敛.2. 设f(x) 在[12,1] 上连续.证明：收敛的充要条件是f(1)=0.3. 设f(x) 在[0,π2] 上连续.证明： (2) {sinn⁡xf(x)} 在[0,π2] 上一致收剑的充要条件是f(π2)=0.4. 若f(x) 在[a,b] 连续, f(x)>0,gn(x)=f(x)n,n=1,2,⋯. 证明 :gn(x) 在[a,b] 上一致收敛于 1.5. 设函数f0(x) 在[a,b] 上可积,且fn(x)=∫axfn−1(t)dt, x∈[a,b],n=1,2,⋯, 证明 :{fn(x)} 在[a,b] 上一致收剑于0.6. 设u0(x) 在[a,b] 上连续,G(x,t) 在闭X 域[a,b]×[a,b] 上连续, 对∀x∈[a,b], 设un(x)=∫axG(x,y)un−1(y)dy,n,证明：{un(x)} 在[a,b] 上一致收剑于0.已知{fn(x)}递推式证明一致收敛1. 设x⩽f1(x)⩽x,fn(x)=xfn−1(x),x∈[0,1], n=1,2,⋯. 证明:(1) {fn(x)} 为单调有界数在(2)$fn(x)$在[0,1]$ 上一致收敛.与cosx 有关的函数列一致收敛求解下列各题.1. 设fn(x)=cosn⁡x,n=1,2,⋯,x∈[0,π2]. (1) 求极限函数f(x); (2) fn(x) 在[0,π2] 上是否一致收敛? (3) 是否有limn→∞∫0π2fn(x)dx=∫0π2f(x)dx.2. 设fn(x)=cos⁡x+cos2⁡x+⋯+cosn⁡x,n=1,2,⋯, 当x∈(0,π2) 时 , 求limn→∞fn(x) ,并讨论{fn(x)} 在[0,π2] 上的一致收敛性利用f(x) 连续则一致连续证明函数列一致收敛1. 设f(x) 在[0,1] 连续,令fn(t)=∫0Tf(xn)dx,t∈[0,1], n=1,2,⋯, 证明函数列 {fn(t)} 在[0,1] 上一致收敛于g(t)=tf(0)函数列为差商形式且极限函数与导数有关1. 设函数f(x) 在(a,b+1) 上有连续导数(ab), 令fn(x)=n(f(x+1n)−f(x)),x∈(a,b+1)n=1,2,⋯证明：(1) 函数列内闭一致收敛于f′(x) ,(2)2. 设f∈C1(I), I 是有界闭区间, Fn(x)=n[f(x+1n)−f(x)]. 证明:函数列 {Fn(x)} 在I 上一致收敛.如果I 是有界开区间,问 {Fn(x)} 在I 上是否一致收敛？3. 设函数f(x) 在(−∞,+∞) 上有连续导函数f′(x), 且fn(x)=en(f(x+e−n)−f(x))n=1,2,⋯.证明:函数列{fn(x)}在任一有限区间区间(a,b) 内一致收敛于f′(x) .4. 设函数f(x) 在(a,b) 上有连续导函数,定义Fn(x)=n2[f(x+1n)−f(x−1n)]x∈[a,b], n=1,2,⋯. 证明:函数列 {fn(x)}在(a,b) 处处收敛且内闭一致收敛.5. 设函数f(x) 在[0,M+1] 上连续, 记fn(x)=n(∫0x+1nf(t)dt−∫0xf(t)dt)x∈[0,M]. .证明:函数列{fn(x)} 在[0,M] 上一致收敛于f(x) .6. 设函数f(x) 在(−∞,+∞) 上连续,定义fn(x)=n2∫−1n1nf(x+t)dt,n=1,2,⋯,x∈[a,b] n=1,2⋯. 证明:函数列{fn(x)}在任何闭区间[a,b] 一致收敛于f(x) .分段函数非一致收敛的证明1. 设fn(x)=1−nx,0 证明函数列在(0,1) 上非一致收敛，但limn→∞∫01fn(x)dx=∫01limn→∞fn(x)dx.利用函数列一致收敛Cauchy 收敛准则证明复合函数列一致收敛1. 设f(x) 在[0,1] 连续, fn(t)=∫0tf(xn)dx,t∈[0,1], n=1,2,⋯, 证明函数列 {fn(t)} 在[0,1] 一致收敛于g(t)=tf(0).2. 设函数f(x,y) 在闭区域[a,A]×[b,B] 上连续,函数列{φn(x)} 在[a,A] 上一致收剑,且b⩽φn(x)⩽B. 证明:函数列Fn(x)=f(x,φn(x)),n=1,2,⋯, 在[a,A] 上一致收敛.3. 设函数f(x,y) 在闭区域[a,b]×[c,d] 上连续, 函数列{φn(x)} 在 [a, b] 上一致收剑,且a⩽φn(x)⩽b, 函数列{ψn(x)} 在[a,b] 上一致收敛,且c⩽ψn(x)⩽d. 证明 : 函数列Fn(x)=f(φn(x),ψn(x)),n=1,2,⋯, 在[a,b] 上一致收剑.4. 设函数f(x,y) 在闭X 域[x0−a,x0+a]×[y0−b,y0+b] 上连续，函数列 {φn(x)} 在[x0−a,x0+a] 上一致收剑φ(x), 且y0−b⩽φn(x)⩽y0+b. 证明：limn→∞∫x0xf(t,φn(t))dt=limn→∞∫x0xf(t,φ(t))dt.已知函数列一致收敛且每一项一致收敛证明极限函数一致连续1. 设函数列 {fn(x)} 在区间I 上一致收签于f(x) .证明:若每个fn(x) 在I 上一致连续,则f(x) 在I 上一致连续.2. 设函数项级数∑n=1∞un(x) 在I 上一致收签于s(x), 如果每个un(x) 在I 上一致连续,证明s(x) 在I 上一致连续.3. 设函数列 {fn(x)} 在区间[a,b] 上连续,在(a,b) 上一致收剑于f(x) .证明: f(x) 在[a,b] 上一致连续.4. 设un(x) 在[a,b] 上连续,∑n=1∞un(x) 在(a,b) 上一致收签于s(x). 证明: (1)∑n=1∞un(x) 在x=a,x=b 收剑;(2)∑n=1∞un(x) 在[a,b] 连续 ; (3)f(x)=∑n=1∞un(x) 在[a,b] 上一致连续.5. 设fn(x),n=1,2,⋯, 为R 上的一致连续函数,且limn→∞fn(x)=f(x), ∀x∈R1, 问 :f(x) 是否为连续函数？若答案为“是”,请给出证明;若答案为“否”,请给出反例.等度连续6. 设函数列{fn(x)}在区间[a,b] 上连续, {fn(x)} 在[a,b] 上一致收剑于f(x) .证明: {fn(x)} 在[a,b] 上等度连续 (即∀ε>0,∃δ>0, 当∀x′,x′′∈[a,b], |x′−x′′|<δ时, 对任意自然数n 有|fn(x′)−fn(x′′)|<ε利用反证法证明1. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x) ,且每个函数连续,假定每个fn(x) 在[a,b] 上不处处为负.证明f(x) 在[a,b] 上不处处为负.2. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续,若每个fn(x) 在[a,b] 上均有零点.证明f(x) 在[a,b] 上至少有一个零点.3. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续,若∫abfn(x)dx⩾0n=1,2,⋯, 证明至少存在一点x0∈[a,b] 使得f(x0)⩾0.与零点有关的问题1. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续,若f(x) 在[a,b] 上无零点,证明:(1) 当n 充分大时, fn(x) 在[a,b] 也无零点. (2) 证明: {1fn(x)} 在[a,b] 一致收敛于1f(x). {xn}与函数列复合得到新函数列证明1. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x), 且每个函数连续, {xn}⊂[a,b] 且limn→∞xn=x0 . 证明: limn →∞fn(xn)=f(x0).(2) 设{Sn(x)}是函数项级数∑k=1∞uk(x) 的前n 项部分和函数列,每个Sn(x) 在[a,b] 上连续,且. ∑k=1∞uk(x) 在[a,b] 上一致收剑于S(x). 又{xn} ⊂[a,b] 且limn→∞xn=x0. 证明: limn→∞Sn(xn)=S(x0).3. 设函数列 {fn(x)} 在区间[a,b] 上一致收剑于f(x) ,且每个函数连续,若存在xn∈[a,b] 有limn→∞fn(xn)=A.证明:存在x0∈[a,b] 使f(x0)=A.已知函数列{fn(x)}一致收敛且函数列极限是数列{an}证明数列{an}收敛1. 设连续函数列 {fn(x)} 在U(x0,δ)(δ>0) 内一致收敛,且limx→xnfn(x)=an,n∈N. 证明 {an}收敛.(南开大学 2002)利用反证法证明函数列在闭区间端点发散导致闭区间非一致收敛1. 设fn(x) 在[a,b] 上连续,且{fn(b)} 发散.证明: {fn(x)} 在[a,b] 上非一致收敛.2. 设un(x) 在[a,b] 连续,且∑n=1∞un(x) 在x=b 发散.证明∑n=1∞un(x) 在[a,b) 非一致收敛.3. 设 {Sn(x)} 在x=c 上左连续,且 {Sn(c)} 发散.证明:在任何开区间(c−δ,c)(δ>0) 内 {Sn(x)} 非一致收敛.4. 设每个un(x) 在x=c 连续,但∑n=1∞un(x) 在x=c 发散,则∀δ>0,∑n=1∞un(x) 在(c,c+δ) 上均非一致收敛.讨论∑n=1∞1(sin⁡x+cos⁡x)n 在(0,π2) 内是否一致收敛.5. 设un(x) 在(a,b] 上连续, ∑n=1∞un(x) 在(a,b) 上收敛,根据∑n=1∞un(b) 的敛散性, 讨论∑n=1∞un(x) 在(a,b) 上的一致敛散性.6. 设hn(x) 在[a,b) 连续,且fn(x)⩽hn(x)⩽gn(x),∀x ∈[a,b). 若级数∑n=1∞fn(x) 和∑n=1∞gn(x) 在(a,b) 上收敛,级数∑n=1∞hn(a) 发散,证明: (1) 级数∑n=1∞hn(x) 在(a,b) 上收敛; (2) 级数∑n=1∞hn(x) 在(a,b) 上非一致收敛.7. 设un(x) 在[a,b] 上连续,∑n=1∞un(x) 在(a,b) 上一致收敛,证明: ∑n=1∞un(a),∑n=1∞un(b) 收敛.已知函数列一致收敛且每个函数列有界证明极限函数有界和函数列一致有界1. 设函数列 {fn(x)} 在[a,b] 上一致收敛于f(x), 且.每个fn(x) 在[a,b] 有界.证明: 回极限函数f(x) 在[a,b] 有界;(2) 函数列 {fn(x)} 在[a,b] 一致有界,且limn→∞supa∈x<bfn(x)=supa<x<bf(x)2. 设函数列{fn(x)} 在区间[a,b] 上连续,且一致收敛于f(x), 若∀x∈[a,b],f(x)>0. 证明: ∃N,δ>0, 使得∀x∈[a,b],n>N 时有fn(x)>δ.3. 设函数列 {fn(x)} 在I 上一致收敛于f(x), 且存在数列{an }使得∀x∈I, 总有|fn(x)|⩽an 证明:f(x) 在I 上有界.复合函数一致收敛1. 设fn(x),n=1,2,⋯, 在[a,b] 上连续,且{fn(x)} 在[a,b] 上一致收敛于f(x) ,证明:(1) ∃M>0, 使得∀n⩾1,∀x∈[a,b] 有|fn(x)|⩽M,|f(x)|⩽M;(2) 若g(x) 在(−∞,+∞) 内连续,则g(fn(x)) 在[a,b] 上一致收敛于g(f(x)) .2. 设f(x)=∑n=0∞anxn 的收敛半径为R=+∞, 令fn(x)=∑k=0nakxk, 证明: {f(fn(x)) }在[a,b] 上一致收敛于f(f(x)) ,其中[a,b] 为任一有穷闭区间.3. 设f(u) 在区间J 上一致连续,函数列 {gn(x)} 在 I 上一致收敛于 g(x), 当x∈I 时, g(x)∈J ,且存在正整数N,使得n>N 及x∈I 时gn(x)∈J ,证明{f(gn(x))} 在I 上一致收敛于f(g(x)) .已知两个函数列分别一致收敛且极限函数有界证明函数列之积一致收敛1. 设函数列 {fn(x)} 与 {gn(x)} 在区间I 上分别一致收敛于f(x),g(x). 假定f(x) 与g(x) 都在I 上有界,证明: (1){fn(x)gn(x)} 在区间I 上一致收敛于f(x)g(x) (2) 如果 {f∗n(x)} 与 {g∗n(x)} 在区间 I 上分别收敛于f(x) 与g(x) ,能否保证必有f∗n(x)g∗n(x)} 在区间I 上一致收敛于 f(x)g(x),请说明理由. (3) 举例说明:对(1) 中的结论，“f(x) 与g(x) 在I 上有界”条件不可去.2. 设函数列 {fn(x)} 与 {gn(x)} 在(−∞,+∞) 上有界连续,且分别一致收敛于f(x) 与g(x) 证明: {fn(x)gn(x)} 在(−∞,+∞) 上一致收敛于f(x)g(x) .如果{fn(x)},{gn(x)} 在(−∞,+∞) 上不是有界函数列,举例说明上述结论不一定成立.3. 设函数列 {fn(x)} 与 {gn(x)} 在区间[a,b] 上分别一致收敛于f(x) 与g(x), 假定存在正数{Mn} 使|fn(x)|⩽Mn,|gn(x)|⩽Mn,x∈[a,b],n=1,2,3,⋯, 证明: {fn(x)gn(x)} 在区间I 上一致收敛于f(x)g(x) .4. 设函数列 {fn(x)} 与 {gn(x)} 在区间[a,b] 上分别一致收敛于f(x) 与g(x) . 证明:函数列max {fn(x),gn(x)} 在区间I 上一致收敛于max {f(x),g(x)}.与反常积分结合1. 设fn(x),n=1,2,⋯, 在[a,+∞) 上连续,且反常积分∫a+∞fn(x)dx 关于n 一致收签.又对任意M>a,{fn(x)}在[a,M] 上一致收敛于f(x),证明：(1)∫a+∞f(x)dx 收敛(2) limn→∞∫a+∞fn(x)dx=∫a+∞f(x)dx.与二重积分结合1. 设连续函数序列 {fn(x,y)} 在有界闭区域 D 上一致收剑于f(x,y), 证明: ∬Df(x,y)dxdy=limn→∞∬Dfn(x,y)dxdy。

可测函数的收敛性43994

⑶几乎处处收敛: everywhere）
记作
fn
f
a.e.于E
E[ fn f ] 0
(almost
即：去掉某个零测度集，在留下的集合上处处收敛
⑷几乎一致收敛:记作 fn f a.u.于E (almost uniformly)
即：去掉某个小（任意小）测度集，在留下的集合上一致收敛
0, 可测子集e E, me ,
对0
1,
有
lim
n
mE[|
f
n
f
|
]
lim m(n， )
n
所以{fn(x)}在R+上不依测度收敛于1，另外{fn}不几乎一致收敛于1
fn不几乎一致收敛于f 0,可测子集e E, me , 0,N 0, n N, x E e,使 | fn (x) f (x) |
即：去掉任意小（适当小）测度集，在留下的集合上仍不一致收敛
近似地说一致连续是函数图象陡的程度能有个控制
1 0.8
0.6 fn(x)=xn
0.4 0.2
0.2
0.4
0.6
0.8
1
1 0.8
fn(x)=xn
0.6 0.4 0.2
0.2
0.4
0.6
0.8
1
1-δ
例：函数列
fn(x)=xn , n=1,2,… 在(0,1)上处处收敛到 f(x)=0,但不一致收敛，但去掉一小测度集合 (1-δ,1),在留下的集合上一致收敛
依测度收敛
0,
有 lim n
mE[| fn
f
|
]
0
0, 0, N 0, n N , 有mE[| fn f | ]

可测函数列的收敛性

目录摘要 (1)关键词 (1)Abstract (1)Keywords (1)前言 (1)1.可测函数列几种收敛的定义 (1)1.1 一致收敛 (1)1.2 点点收敛 (1)1.3 几乎一致收敛 (2)1.4 几乎处处收敛 (2)1.5 依测度收敛 (2)2.可测函数列几种收敛的关系 (3)2.1 点点收敛与一致收敛的关系 (3)2.2 点点收敛与几乎处处收敛的关系 (3)2.3 几乎处处收敛与一致收敛的关系 (3)2.4 几乎处处收敛与几乎一致收敛的关系 (3)2.5几乎处处收敛与依测度收敛的关系 (4)参考文献 (6)可测函数列的收敛性摘要:本文介绍了可测函数列常见的几种收敛:一致收敛、几乎一致收敛、几乎处处收敛、依测度收敛等,以及它们之间的关系.关键字:可测函数列;一致收敛;几乎一致收敛;几乎处处收敛;依测度收敛.Convergence of Measurable Function SequenceAbstract :This article introduces several common convergences of the measurable functionsequence :uniform convergence ,almost uniform convergence,almost everywhere converge- nce,convergence in measure and the relations about them .Key words :Measurable functions ;Uniform convergence ;Almost uniform convergence ; Almost everywhere convergence ;Convergence in measure前言在数学分析中我们知道,一致收敛是函数列很重要的性质,它能保证极限过程和一些运算的可交换性.但一般而论,一个收敛的函数列在其收敛域上是不一定一致收敛的.其实这一现象在某种意义下是带有普遍性的.1.可测函数列几种收敛的定义1.1一致收敛设()()()() ,,,,,21x f x f x f x f k 是定义在点集E 上的实值函数.若对于0>∀ε存在0>εN ,使得对于εN n ≥∀,E x ∈∀都有()(),ε<-x f x f k则称}{()k f x 在E 上一致收敛到()f x .记作:uk f f −−→(其中u 表示一致收敛).1.2点点收敛若函数列()()()() ,,,,,21x f x f x f x f k 在点集D E ⊂上每一点都收敛,则称它在D 上点点收敛．即E x ∈∀,0>∀ε,()0,>∃x N ε,对()x N n ,ε≥∀, 有()()ε<-x f x f k ,记作 f f k →于E ．例1 定义在[0,1]E =上的函数列1(),1k f x kx=+则()k f x 在E 上点点收敛到函数 ()⎩⎨⎧<<==.10,0,0,1x x x f 而且还能看出{()}k f x 在[]0,1上不一致收敛到()f x ,但对于0,{()}k f x δ∀>在[,1]δ上一致收敛到()f x . 1.3几乎一致收敛设E 是可测集,若0,,E E δδ∀>∃⊂使得(\),m E E δδ<且在E δ上有uk f f −−→,则称{()}k f x 在E 上几乎一致收敛与()f x ,并记作...a u k f f −−→(其中..u a 表示几乎一致收敛).即去掉某个零测度集,在剩下的集合上一致收敛.例2 定义在[]0,1E =上的函数()k k f x x =在[]0,1上收敛却不一致收敛.但是只要从[]0,1的右端点去掉任意小的一段成为[]()0,10,0δδδ->→,则{()}k f x 在其上就一致收敛了,像这样的收敛我们就可以称之为在[]0,1E =上几乎一致收敛于0. 1.4几乎处处收敛设()()()() ,,,,,21x f x f x f x f k 是定义在点集n E R ⊂上的广义实值函数.若存在E 中点集Z ,有()0,m Z =及对于每一个元素\x E Z ∈有lim ()()k x f x f x →∞=,则称{()}k f x 在E 上几乎处处收敛于()f x ,并简记为..,e a f f k →于E 或..a e k f f −−→即去掉某个零测度集,在剩下的集合上处处收敛.上文的例1也可以称之为在[]0,1上几乎处处收敛于()f x . 1.5依测度收敛设{}n f 是q R E ⊂上的一列..e a 有限的可测函数,若有E 上..e a 有限的可测函数()x f 满足下列关系:对任意0>σ有[]0lim =≥-σf f mE n n,则称函数列{}n f 依测度收敛于f ,记为:()()x f x f n ⇒.改用N -ε说法:对任意0>ε及0>σ,存在正数()σε,N ∃,使()σε,N n ≥时,[]εσ<≥-f f mE n .依测度收敛用文字叙述,就是说,如果事先给定一个（误差）0>σ,不论这个σ有多么小,使得()()x f x f n -大于σ的点x 虽然可能很多,但这些点所成之集合的测度随着n 无限增大而趋于零.从而可知,不依测度收敛的定义为:0>∃σ,使得[]σ≥-f f mE n 不收敛于0,即0>∃σ,0>∃ε, 对0>∀N 都N n ≥∃,使得[]εσ≥≥-f f mE n .2.可测函数列几种收敛的关系2.1点点收敛与一致收敛的关系由上述定义我们可以知道uk f f −−→,必有{()}k f x 点点收敛于()f x ,如例1,反之则不一定成立.2.2点点收敛与几乎处处收敛的关系由定义易知,点点收敛必几乎处处收敛,反之则不然. 2.3几乎处处收敛与一致收敛的关系由定义可知,一致收敛必几乎处处收敛....()a u a e k k f f f f −−→⇒−−→,反之则不然,如例2.而且还可以得到:若{()}k f x 是可测集E 上的可测函数列,则极限函数()f x 也是可测函数.2.4几乎处处收敛与几乎一致收敛的关系叶果洛夫(E ΓopoB )定理设(),{}n m E f <∞是E 上一列..e a 收敛于一个..e a 有限的函数f 的可测函数,则对于任意的0δ>,存在子集E E δ⊂,使{}n f 在E δ上一致收敛,且(\)m E E δδ<.注定理中“()m E <∞”不可去掉.如例3 定义在(0,)E =+∞的函数列()(]()⎩⎨⎧=∞∈∈=.,2,1,,,0,,0,1 n n x n x x f n显然n f 在(0,)+∞上处处收敛于1,但对于任何正数δ及任何可测集E δ,当(\)m E E δδ<时,n f 在E δ上不一致收敛于1,这是因为,当(\)m E E δδ<时,E δ不能全部含于(]n ,0中,必有()∞⋂∈,n E x n δ,于是有()0=n n x f .()().111sup =-≥-∈n n x n E x x f f δ所以()x f n 在E δ上不一致收敛于1,也即定理中“()m E <∞”不可去掉.由定义我们知道,一致收敛必是几乎处处收敛的,反之则不成立.但它们又有密切的关系,即上述定理告诉我们几乎处处收敛是“基本上”一致收敛 (在除去一个测度为任意小集合的子集上一致收敛)的.应用由上述定理我们还可以得到“鲁津定理”:设()f x 是E 上..e a 有限的可测函数,则对于任意的0δ>,存在闭子集E F δ⊂,使()f x 在F δ上是连续函数,且(\)m E F δδ<.简言之:在E 上..e a 有限的可测函数是“基本上连续” (在除去一个测度任意小集合的子集上连续)的函数,则我们可以用连续函数来逼近..e a 有限的可测函数. 2.5几乎处处收敛与依测度收敛的关系例4 依测度收敛而处处不收敛的函数列取(0,1]E =,将E 等分,定义两个函数:()()⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛∈⎥⎦⎤⎝⎛∈=.1,21,0,21,0,111x x x f ()()⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛∈⎥⎦⎤ ⎝⎛∈=.1,21,1,21,0,012x x x f 然后将(0,1]四等分、八等分,等等.一般地,对每个n ,作2n 个函数:()().2,,2,1.2,21,0,2,21,1n n n n n n j j j j x j j x x f =⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤ ⎝⎛-∉⎥⎦⎤ ⎝⎛-∈=我们把(){}n n i j f 2,,2,1, =先按n 后按j 的顺序逐个的排成一列:(1)(1)()()()12122(),(),,(),(),,(),nn n n x f x f x f x f x f(1)()()n j x f 在这个序列中是第22n j N -+=个函数.可以证明这个函数序列是依测度收敛于零的.这是因为对于任何的0σ>,()0[]n j f E σ-≥或是空集(当1σ>),或是1,22(]n n j j - (当01σ<≤),所以()102([])n j nf m E σ-≥≤(当时1σ>时,左端为0). 由于当2(1,2,,2.)2n n j j N -+== 趋于∞时,n →∞,由此可见()[]()00lim =≥-∞→σn j n f E m ,即()().0⇒x f n j但是函数列(1)在](1,0上的任何一点都不收敛.事实上,对任何点0(0,1]x ∈,无论n 多么大,总存在j ,使01(,]22n nj jx -∈,因而()0()1n j x f =,然而()10()0n j x f +=或()10()0n j x f -=,换言之,对任何0(0,1]x ∈,在()0(){}n j x f 中必有两个子列,一个恒为1,另一个恒为零,所以序列(1)在(0,1]上任何点都是发散的.这也就说明依测度收敛的函数列不一定处处收敛,也就是说依测度收敛不能包含几乎处处收敛.但仍有里斯(F.Riesz):设在E 上{}n f 测度收敛于f ,则存在子列{}i n f 在E 上..e a 收敛于f .例5 如例3,显然()()∞→→n x f n 1,当x E ∈.但是当01σ<<时,[]()+∞=≥-,1n f E n σ,且()∞=+∞,n m .这说明}{n f 不依测度收敛于1.这个例子又说明了一个..e a 的函数列也可以不是依测度收敛的,但是有下述关系: 勒贝格(Lebesgue)设mE <∞,{}n f 是E 上..e a 有限的可测函数列, {}n f 在E 上..e a 收敛于..e a 有限的函数f ,则()()x f x f n ⇒.此定理中的“mE <∞”不可去掉（例1）.定理也说明在的在的条件mE <∞下,依测度收敛弱于..e a 收敛.由以上勒贝格(Lebesgue)定理又可得出一个用几乎处处收敛来判断依测度收敛的充要条件,即:设mE <∞,{}n f 是E 上的可测函数列,那么{}n f 依测度收敛于f 的充要条件是:{}n f 的任何子函数列{}k n f 中必可找到一个几乎处处收敛于f 的子序列.证明（必要性）由于{}n f 依测度收敛于f ,知道这时{}n f 的的任何子序列{}k n f 必也依测度收敛于f ,由里斯定理可知{}k n f 中必存在几乎处处收敛于f 的子序列.（充分性）用反证法,即如果{}n f 不依测度收敛于f ,则存在一个0σ>,使得()n f f m E σ-≥不趋于0.则必有子序列{}kn f ,使得(())0.lim kn k m E f f a σ→∞-≥=>又由已知,在E 上必存在{}k n f 的子列几乎处处收敛于f ,又mE <∞,由勒贝格定理知将有{}k n f 依测度收敛于f ,即(())0.lim k n k m E f f σ→∞-≥=这与上式矛盾,所以{}n f 依测度收敛于f .注上述定义中的各种收敛的极限函数都是唯一的,而且从本文还可以知道一致收敛是最强的收敛,它蕴含了点点收敛、几乎处处收敛、依测度收敛等上述几种收敛.各种收敛都有不同的意义,在各种实践中作用也各不同.参考文献:[1] 华东师范大学数学系.数学分析[M] (第三版).北京:高等教育出版社,2010.[2] 程其襄,张奠宙,魏国强等.实变函数与泛函分析基础[M] (第三版).北京:高等教育出版社,2010.6.。

判断收敛的方法范文

判断收敛的方法范文在数学中，收敛是指序列或级数逐渐接近一些确定的极限值的过程。

判断一个序列或级数是否收敛，是数学中一个重要的问题，本文将介绍一些判断序列和级数收敛的方法。

首先，我们来讨论判断数列收敛的方法。

一、有界性判定法：如果数列{an}是一个有界数列，即存在一个正数M，使得对于数列中的所有项，都有，an， < M，那么这个数列收敛。

证明：设数列{an}收敛于A，那么对于任意正数ε，存在正整数N，使得当n>N时，有，an - A，< ε。

取ε = 1，那么存在正整数N1，使得当n>N1时，有，an - A， < 1另一方面，根据三角不等式，有，an， - ，A，≤ ，an - A，所以当n>N1时，有，an， - ，A， < 1令M = max{，a1，, ，a2，, ..., ，aN1 - 1，, ，A， + 1}，则对于数列中的任意项an，都有，an， < M，即数列{an}是一个有界数列。

二、单调性判定法：如果数列{an}单调递增且有上界（即有界），或者数列{an}单调递减且有下界，那么这个数列收敛。

证明：我们以第一种情况为例，即数列{an}单调递增且有上界。

设数列{an}的上界为M，即对于数列中的所有项，都有an ≤ M。

由于{an}是一个单调递增数列，所以对于任意正数ε，存在正整数N，使得当n>N时，有an ≥ an - 1结合上述两个不等式，有M ≥ an ≥ an - 1，所以当n>N时，有an - 1 ≤ M。

令A = sup{an ，n ∈ N}，则由最小上界性质可知，A ≤ M。

另一方面，对于任意正数ε，存在正整数N1，使得当n>N1时，有an - A < ε。

另一方面，对于任意正整数n，有an ≤ M，所以an - A ≤ M - A。

由于ε是任意正数，所以我们可以令ε = M - A，那么存在正整数N2，使得当n>N2时，有an - A < M - A。

测函数列三种收敛性的区别与联系解析

目录1．前言 (1)2．概念 (1)2.1 几乎处处收敛 (1)2.2 几乎一致收敛 (1)2.3 依测度收敛 (2)3．三种收敛性之间的区别 (2)3.1 存在可测函数列几乎处处收敛而不依测度收敛 (2)3.2 存在可测函数列依测度收敛而不几乎处处收敛 (2)3.3 存在可测函数列几乎处处收敛而不几乎一致收敛 (4)4．三种收敛性的充要条件 (4)4.1 几乎处处收敛的充要条件 (4)4.2 几乎一致收敛的充要条件 (4)4.3 依测度收敛的充要条件 (6)5．三种收敛性之间的联系 (6)5.1 几乎一致收敛与几乎处处收敛 (6)5.2 依测度收敛与几乎处处收敛 (8)5.3 依测度收敛与几乎一致收敛 (10)5.4 三种收敛之间的关系图： (11)6．结论 (11)7．致谢 (12)8．参考文献 (13)n f 可测函数列三种收敛性的区别与联系摘要：对于可测集合E 上的几乎处处有限的可测函数列n f 来说有三种常见类型的收敛：几乎处处收敛，几乎一致收敛和依测度收敛。

本文首先介绍可测函数列三种收敛的概念，并讨论几乎处处收敛，几乎一致收敛和依测度收敛三者之间的关系。

这几种概念是伴随测度的建立而产生的新的收敛性，相对其他两种收敛性来说，依测度收敛的收敛条件是比较弱的，与熟知的处处收敛有很大的差异。

Egorov 定理、Riesz 定理和Lebesgue 定理等揭示了这几种收敛之间的关系。

关键词：几乎处处收敛几乎一致收敛依测度收敛中图分类号：O 17Difference and Connection between Three Types of Convergence of Measurable Function SequenceJiang Zhong (Tutor ：You Xuexiao)(Department of Mathematics, Hubei Normal University, Huangshi Hubei435002,China)Abstract : For the measurable function sequencewhich is finite almost everywhere on the measurable set E ,there are three types of common convergence: convergence almost everywhere, convergence almost uniform and convergence in measurable. This article has first described the concepts of those three types of convergence, and then discussed the relationship among convergence almost everywhere,convergence almost uniform and convergence in measurable . Those concepts are the new convergence,which are arised with the establishment of measure. Comparing with the other twotypes of convergence, the conditions of convergence inmeasurable are relatively weak, and has large differencewith the well-known convergence almost everywhere. TheEgorov theorem, Riesz theorem and Lebesgue theorem and soon reveal the relationship among these types of convergence.Keywords: Convergence almost everywhere Convergence almost uniform Convergence in measurable可测函数列三种收敛性的区别与联系蒋忠（指导教师，游雪肖）（湖北师范学院数学与应用数学湖北黄石 435002）1．前言本文介绍了几乎处处收敛、几乎一致收敛与依测度收敛，它们是伴随测度的建立而产生的新的收敛性。

几种收敛函数的介绍

几种收敛函数的介绍在数学中，收敛函数是一类重要的函数，它们在其中一种极限意义下趋向于一些确定的值。

收敛函数在数学分析、数值计算和工程学科中都有广泛的应用。

下面我将为您介绍几种常见的收敛函数。

1.序列的收敛函数：序列是函数的一个特殊情况，它是一组按照一定顺序排列的数。

一个序列收敛到一些数，意味着当序列的项无限接近于该数时，序列的极限存在。

例如，序列1，1/2，1/3，1/4，...的极限是0，即这个序列收敛于0。

数学中有许多序列的收敛函数，如调和序列、等差数列和等比数列等。

2.函数列的一致收敛函数：函数列是指一组按照一定顺序排列的函数。

函数列的一致收敛就意味着当序列的项无限接近于一些函数时，函数列的极限存在且与该函数无关。

一致收敛函数在数学中有广泛的应用，例如在数值计算中用于逼近数值解。

函数列的一致收敛函数能够保持原始序列的收敛性质，其定义与序列的收敛函数类似。

3.幂级数的收敛函数：幂级数是一种特殊的级数，它是形如∑(a_n*x^n)的级数，其中a_n是系数序列，x是变量。

幂级数的收敛函数是指当幂级数的所有项无限接近于一些函数时，该函数在给定区间上收敛。

幂级数的收敛函数在数学分析和物理学中具有广泛的应用，例如在函数逼近、微积分和物理模型建立等方面。

4.泰勒级数的收敛函数：泰勒级数是一种特殊的幂级数，它是一个函数在其中一点附近展开成多项式的形式。

泰勒级数的收敛函数是指当泰勒级数的所有项无限接近于一些函数时，该函数在给定区间上收敛。

泰勒级数的收敛函数在数学分析和物理学中有广泛的应用，例如在函数逼近、微积分和物理模型建立等方面。

5.紧收敛函数：紧收敛函数是指对于一个给定的度量空间，其中任意序列都有子序列收敛于该函数。

紧收敛函数在函数空间理论、泛函分析和拓扑学等领域中具有重要的应用。

紧收敛函数是一种强收敛函数，能够保持原始序列的所有收敛性质。

总结起来，收敛函数是数学中一类重要的函数，它们在序列、函数列、幂级数和紧收敛函数等方面具有广泛的应用。

收敛函数_精品文档

收敛函数1. 引言在数学中，收敛函数是一类非常重要的函数，它们在数学分析、实数理论以及其他领域中扮演着重要的角色。

本文将介绍什么是收敛函数，它们的定义以及一些典型的例子和性质。

同时，我们还将讨论收敛函数的应用以及它们在数学和实际问题中的意义。

2. 收敛函数的定义在数学中，给定一个函数序列{fn(x)}，如果对于任意的x0，都存在一个数列{an}，使得fn(x0)在n趋于无穷大时收敛到x0，那么我们称函数序列{fn(x)}在点x0处收敛。

换句话说，对于任意给定的误差ε，存在一个正整数N，使得当n>N时，|fn(x0) - x0| < ε。

3. 收敛函数的例子3.1 线性收敛函数线性函数是一种最简单的函数类型，它的图像是一条直线。

在数学中，我们称线性函数为收敛函数，因为它们具有收敛到零的特性。

例如，y = x是一个线性函数，它的图像是一条通过原点的直线。

当x趋向于无穷大时，y也趋向于无穷大，但是它们之间的差值在不断减小，最终收敛于零。

3.2 幂函数幂函数是一类常见的函数类型，它们具有形如y = x^n的形式。

当幂函数的幂指数大于1时，它们可以是收敛函数。

例如，y = x^2是一个典型的收敛函数，因为当x趋向于无穷大时，y也趋向于无穷大，但是它们之间的差值在不断减小，最终收敛于零。

4. 收敛函数的性质4.1 收敛函数的极限对于一个收敛函数fn(x)，它在点x0处的极限等于x0。

换句话说，lim┬(n→∞)⁡〖fn(x0) = x0〗。

4.2 收敛函数的一致收敛性如果一列函数{fn(x)}在定义域D上的每一个点处都收敛，并且收敛的极限也是一个定义在D上的函数f(x)，那么我们称函数序列{fn(x)}在D上一致收敛于f(x)。

4.3 收敛函数的连续性如果一个函数序列{fn(x)}在某个点x0处收敛，并且在该点的极限f(x0)存在，那么我们称f(x)在x0处是连续的。

5. 收敛函数的应用收敛函数在数学中具有广泛的应用。

完全收敛性与可测函数序列几种收敛性的关系

显然，， ∞时，当ｌ一由上式结论可得。又由引理２１可知完全收敛性强于几乎处处收敛性。（）
２主要结果
利用完全收敛性强于几乎一致收敛性给出了可测函数序列依测度收敛的另一个刻画。
定理ｌ设（ｌ／均为实值可测函数，）当且仅当对（）），（吖的任何子列（）存在其子列（）厶，，使得，ｃ，一 ∞）吖．（．证明充分性：根据完全收敛性强于几乎一致收敛性以及引理２３，（）结论得证。必要性：设一．（）（）令为的一子列，仍有一／则。由依测度收敛的下义，在（）存的子列
ｌ（［ — ￡）０ｉ＿ＪｆｍＵＪ］＝．
（）３吖，当且仅当对（）的任何子列（）存在其子列（，，ａ姗．（一 ∞），，，使）吖．，七．
【收稿日期］２ｒ１０ｔ］ — ７ｘ一１
（）３设－ｉｔ，存在子列（）使吖＋，则，
由完全收敛的定义可以得到这样的结论：
引理３完全收敛性强于几乎一致收敛性。事实上，由引理ｌ２以及完全收敛的定义，Ｖｅ（）对＞０有
（１ — ｌｅ）（１ — ｌ￡）Ｕ［ｆ］ｓ［ｆ］
维普资讯
第２卷第２７期
Ｖ１２Ｎｏ２ｏ．７．
长春师范学院学报（自然科学版）
ＪｒａｏＣａｇｈｎＮｒａＵｉｒｔ（ａｒ．ｃｎｅｏｎｌｆｈｎｅｕｏｌｎｅｉＮｔａＳｉｃ｝ｕｍｖｓｙｕ１ｅ

第4章《可测函数列的几种收敛性》习题解答

第4章可测函数列的几种收敛性习题4.14.1设f 是广义实值可测函数，A 为零测集，则0A fI = a.e. 证明若cA ω∈，则()()0A fI ωω=①，这表明{}0cA A fI ⊂=，等价地说，{}0A fI ≠A ⊂．注意到A 为零测集，于是可测集{}0A fI ≠也为零测集，故0A fI = a.e.4.2举例说明：命题4.2及性质4.4中的条件“μ是完备测度”去掉后结论都未必成立．解设{}1,2,3Ω=，{}{}{},1,2,3,=∅Ω ，(){}()1,20μμ∅==，{}()3μ()1μ=Ω=．因为{}1∉ ，所以μ非上的完备测度．定义()()120f f ==，()33f =；()11g =，()22g =，()33g =，显然，f 为 -可测，f g = a.e.，但g 非 -可测，所以命题4.2的结论不成立．f ，g 如上定义，取n f f ≡，1n ≥，我们有n f g → a.e.，尽管诸n f 都是 -可测函数，可是没有性质4.4的结论．4.3设f 和g 都是广义实值可测函数，（1）若f g = a.e.，则f g ++= a.e.，且f g --= a.e.；（2）若f g ≤ a.e.，则fg ++≤ a.e.，且f g --≥ a.e.证明由f 和g 都是广义实值可测函数，命题3.16及命题3.14知，{}f g ≠，{}f g >，{}fg ++≠，{}f g --≠，{}f g ++>，{}f g --<等均为可测集．（1）假设{}f g ω∈=，那么()()()()00f f g g ωωωω++=∨=∨=，()()()()()()00f f g g ωωωω--=-∧=-∧=，这表明{}{}f g fg ++=⊂=，{}{}f g f g --=⊂=，它们分别等价于{}f g ++≠①因为f 取广义实值，所以可能出现()f ω=∞，而此时()0A I ω=，但致使0⋅∞这种无意义情形发生的集合是一个零测集，并不影响往后的结论，故规定00⋅∞=．{}f g ⊂≠，{}{}f g f g --≠⊂≠．因为f g = a.e.，所以()0f g μ≠=，于是()0f g μ++≠=，()0f g μ--≠=，由此得所需结论．（2）假设{}f g ω∈≤，那么()()()()00f f g g ωωωω++=∨≤∨=，()()()()()()00f f g g ωωωω--=-∧≥-∧=，这表明{}{}f g fg ++≤⊂≤，{}{}f g f g --≤⊂≥，它们分别等价于{}f g ++>{}f g ⊂>，{}{}f g f g --<⊂>．因为f g ≤ a.e.，所以()0f g μ>=，于是()0f g μ++>=，()0f g μ--<=，由此得所需结论．4.4设广义实值函数f ，g ，h 满足g f h ≤≤，若g ，h 都可测，且g h = a.e.，则f a.e.可测．证明因为g h = a.e.，所以∃N ∈ ，()0N μ=，使得()()g h ωω=，c N ω∈．于是当cN ω∈时，()()fh ωω=，从而fh = a.e.，故f a.e.可测．4.5证明：几乎处处相等的随机变量具有相同的概率分布．证明设X Y = a.e.，则()B ∀∈ ，我们有()(){}{}(){}{}()X P A P X A P X A X Y P X A X Y =∈=∈⋂=+∈⋂≠ {}{}(){}{}()()()Y P X A X Y P Y A X Y P Y A P A =∈⋂==∈⋂==∈=，这就证明了X Y P P =，即X 与Y 具有相同的概率分布．4.6设(),,μΩ 是(),,μΩ 的完备化测度空间（见定理2.22），试证：对任意的 -可测函数f ，必存在一个 -可测函数g ，使得f g =μ-a.e.证明设f 为 -可测函数，则对任意的r ∈ ，有{}f r <∈ ，故{}f r <可以写成{}r r f r A N <=⋃，其中r A ∈ ，r N μ∈ ．由μ 的定义，对每个r N ，∃r M ∈ ，满足r r N M ⊂，且()0r M μ=．记r r M M ∈=⋃ ，则M ∈ ，满足()0M μ=．定义()()0,,,,M g f M ωωωω∈⎧⎪=⎨∉⎪⎩ 则{}{}(){}(){}(){}()0c c g r M g r M g r M r M fr <=⋂<⋃⋂<=⋂<⋃⋂<，注意到{}0M r ⋂<∈ ，{}()c c c r r r M f r M A N M A ⋂<=⋂⋃=⋂∈ ，所以，对任意的r ∈ ，{}g r <∈ ．再由习题3.4得g 为 -可测函数，且f g =μ-a.e.4.7证明：{}01111i kn k nm n k n ff f f m εε∞∞∞∞∞>=====⎧⎫⋃⋂⋃-≥=⋃⋂⋃-≥⎨⎬⎩⎭．证明设()(){}01kn k nff εωωωε∞∞>==∈⋃⋂⋃-≥，则0ε∃>，使得()(){}1k n k nf f ωωωε∞∞==∈⋂⋃-≥．任取满足1mε≤的m ∈ ，则有 ()()11k n k nf f m ωωω∞∞==⎧⎫∈⋂⋃-≥⎨⎬⎩⎭，故111k m n k nf f m ω∞∞∞===⎧⎫∈⋃⋂⋃-≥⎨⎬⎩⎭．反过来，设111k m n k nf f m ω∞∞∞===⎧⎫∈⋃⋂⋃-≥⎨⎬⎩⎭，则m ∃∈ ，使得 11k n k nf f m ω∞∞==⎧⎫∈⋂⋃-≥⎨⎬⎩⎭．任取满足1mε≤的0ε>，则有 ()(){}1k n k nf f ωωωε∞∞==∈⋂⋃-≥，故()(){}01kn k nff εωωωε∞∞>==∈⋃⋂⋃-≥．4.8定理4.5中的“ε≥”可改为“ε>”，即“{}10k n k n f f με∞∞==⎛⎫⋂⋃-≥= ⎪⎝⎭，0ε∀>”⇔“{}10k n k n f f με∞∞==⎛⎫⋂⋃->= ⎪⎝⎭，0ε∀>”．证明 “⇒”是显然的，下面证明“⇐”．因为{}11kk m ff f f m εε∞=⎧⎫-≥=⋂->-⎨⎬⎩⎭．所以0ε∀>，对任意满足010m ε->的0m ∈ ，都有 {}1111k k n k n n k n m f f f f m μεμε∞∞∞∞∞=====⎛⎫⎧⎫⎛⎫⋂⋃-≥=⋂⋃⋂->-⎨⎬ ⎪ ⎪⎝⎭⎩⎭⎝⎭1010k n k n f f m με∞∞==⎛⎫⎧⎫≤⋂⋃->-= ⎪⎨⎬⎩⎭⎝⎭，故{}10k n k n f f με∞∞==⎛⎫⋂⋃-≥= ⎪⎝⎭，0ε∀>，这完成了充分性的证明． 4.9（1）（a.e.收敛的唯一性）若..a e n f f →且..a e n f g →，则f g = a.e.；（2）若f g = a.e.且..a e n f f →，则..a e n f g →．证明（1）由..a e n f f →知，存在1N ∈ ，且()10N μ=，使得 ()()n f fωω→，1c N ω∈，由..a e n f g →知，存在2N ∈ ，且()20N μ=，使得()()n f g ωω→，2cN ω∈．令12N N N =⋃，则N ∈ ，()0N μ=，且()()n f fωω→，()()n f g ωω→，c N ω∈，于是，()()fg ωω=，c N ω∈，即fg = a.e.（2）若f g = a.e.且..a e n f f →，如前面证明所示，N 和1N 分别是使f g = a.e.和..a e n f f →成立的例外集，则()()f g ωω=，()()n f f ωω→，()1cN N ω∈⋃，于是，()()n f g ωω→，()1cN N ω∈⋃，故..a e n f g →．4.10设{},,1n A A n ≥⊂ ，则（1）..0n a e A I →⇔()lim 0n n A μ→∞=；（2）..n a e A A I I →⇔A ，lim n n A →∞，lim n n A →∞这三个集合中两两仅相差一个零测集．证明（1）由定理4.5，..0n a e A I →⇔{}10k A n k n I με∞∞==⎛⎫⋂⋂≥= ⎪⎝⎭，0ε∀> ⇔{}110k A n k nI μ∞∞==⎛⎫⋂⋂== ⎪⎝⎭⇔10k n k n A μ∞∞==⎛⎫⋂⋂= ⎪⎝⎭⇔()lim 0n n A μ→∞=．（2）仍由定理4.5，..n a e A A I I →⇔{}10k A A n k n I I με∞∞==⎛⎫⋂⋂-≥= ⎪⎝⎭，0ε∀> ⇔{}110k A A n k n I I μ∞∞==⎛⎫⋂⋂-== ⎪⎝⎭．由习题1.13知k k A A A A I I I ∆-=，故..n a e A A I I →⇔10k n k n A A μ∞∞==⎛⎫⋂⋂∆= ⎪⎝⎭⇔()()lim lim 0n n n n A A A A μ→∞→∞⎛⎫-⋃-= ⎪⎝⎭ ⇔()lim 0n n A A μ→∞-=且()lim 0n n A A μ→∞-=⇔A ，lim n n A →∞，lim n n A →∞这三个集合中两两仅相差一个零测集，最后一步只需注意lim lim n n n n A A →∞→∞⊂．习题4.24.11（1）（几乎一致收敛的唯一性①）若.un.a n f f →且.un.a n f g →，则f g = a.e.；（2）若f g = a.e.且.un.a n f f →，则.un.a n f g →．①几乎一致收敛的极限在a.e.意义下是唯一的．证明（1）0ε∀>，有{}22n n f g f f f g εεε⎧⎫⎧⎫-≥⊂-≥⋃-≥⎨⎬⎨⎬⎩⎭⎩⎭，故由定理4.13，当n →∞时，()0022n n f g f f f g εεμεμμ⎛⎫⎛⎫≤-≥≤-≥+-≥→ ⎪ ⎪⎝⎭⎝⎭，即()0f g με-≥=．于是()()111100n n f g f g f g f g n n μμμμ∞∞==⎛⎫⎧⎫⎛⎫≠=->=⋃-≥≤-≥=∑⎨⎬ ⎪ ⎪⎩⎭⎝⎭⎝⎭，这就证明了f g = a.e.（2）若f g = a.e.且.un.a n f f →，则再由定理4.13，{}k k n f g με∞=⎛⎫⋃-≥ ⎪⎝⎭{}{}{}{}{}{}k k k n k n f g f g f g f g μεμε∞∞==⎛⎫⎛⎫=⋃-≥⋂=+⋃-≥⋂≠ ⎪ ⎪⎝⎭⎝⎭{}{}{}{}0k k k n k n f f f g f f μεμε∞∞==⎛⎫⎛⎫=⋃-≥⋂=≤⋃-≥→ ⎪ ⎪⎝⎭⎝⎭，故.un.a n f g →．4.12设()[][]()(),,0,1,0,1,μλΩ=⋂ ，令()n n f x x =，1n ≥，()0,01,1,1,x f x x ≤<⎧=⎨=⎩则.un.a n f f →，但n f f ．证明 01ε∀<<，因为{}))()1k k n k n f f λελλ∞∞==⎛⎫⎛⎫⋃-≥=⋃==- ⎪ ⎪⎝⎭⎝⎭所以{}lim 0k n k n f f λε∞→∞=⎛⎫⋃-≥= ⎪⎝⎭，由推论4.13知.un.a n f f →．可是，因为[]()()[)0,10,1sup sup 10n n x x f x f x x ∈∈-==→，所以n f f ．4.13若存在0n ε→，使级数()1n n n f f με∞=-≥<∞∑，则.un.a n f f →．证明 0ε∀>，由0n ε→知，存在N ∈ ，当n N ≥时，有n εε≤．故当n N ≥时，{}()()k k k k k n k n k nf f f f f f μεμεμε∞∞∞===⎛⎫⋃-≥≤-≥≤-≥ ⎪⎝⎭∑∑，从而{}lim 0k n k n f f με∞→∞=⎛⎫⋃-≥= ⎪⎝⎭，再由推论4.13知.un.a n f f →．习题4.34.14定义4.19中的“ε≥”可改为“ε>”，即“()lim 0nn ff με→∞-≥=，0ε∀>”⇔“()lim 0n n f f με→∞->=，0ε∀>”．证明 “⇒”是显然的，下面证明“⇐”．因为{}11n n m f f f f m εε∞=⎧⎫-≥=⋂->-⎨⎬⎩⎭，所以0ε∀>，对任意满足010m ε->的0m ∈ ，都有 ()11n n m f f f f m μεμε∞=⎛⎫⎧⎫-≥=⋂->-⎨⎬ ⎪⎩⎭⎝⎭01n f f m με⎛⎫≤->- ⎪⎝⎭，故由01lim 0n n f f m με→∞⎛⎫->-= ⎪⎝⎭得()lim 0n n f f με→∞-≥=，0ε∀>，这就完成了充分性的证明．4.15（1）（依测度收敛的唯一性①）若n f f μ→且n f g μ→，则f g = a.e.；（2）若f g = a.e.且n f f μ→，则n f g μ→．证明（1）0ε∀>，有{}22nn f g ff fg εεε⎧⎫⎧⎫-≥⊂-≥⋃-≥⎨⎬⎨⎬⎩⎭⎩⎭，故当n →∞时，()022n n f g f f f g εεμεμμ⎛⎫⎛⎫-≥≤-≥+-≥→ ⎪ ⎪⎝⎭⎝⎭，即()0f g με-≥=．于是()()111100n n f g f g f g f g n n μμμμ∞∞==⎛⎫⎧⎫⎛⎫≠=->=⋃-≥≤-≥=∑⎨⎬ ⎪ ⎪⎩⎭⎝⎭⎝⎭，这就证明了f g = a.e.（2）若f g = a.e.且n f f μ→，则由(){}{}(){}{}()n n n f g f g f g f g f g μεμεμε-≥=-≥⋂=+-≥⋂≠{}{}()()0nn ff fg f f μεμε=-≥⋂=≤-≥→知n f g μ→．4.16②设{},1n A n ≥⊂ ，则0n A I μ→⇔()lim 0n n A μ→∞=．证明 0n A I μ→⇔lim00nA n Id μ→∞-=⎰⇔()lim 0n n A μ→∞=．4.17设μ是() 上的计数测度，12,,,f f f 都是上的实值函数，则n f f μ→⇔..a un n f f →．证明 “⇒”．若n f f μ→，则0ε∀>，()lim 0nn ff με→∞-≥=．注意到μ为计数测① 依测度收敛的极限在a.e.意义下是唯一的． ②本题应该与习题4.10比较．度，所以当n 充分大时，{}nff ε-≥=∅，进而{}k k nf f ε∞=⋃-≥=∅，故{}l i m 0k n k n f f με∞→∞=⎛⎫⋃-≥= ⎪⎝⎭，这表明..a un n f f →． “⇐”．这是因为..a un n f f →⇒{}lim 0k n k n f f με∞→∞=⎛⎫⋃-≥= ⎪⎝⎭，0ε∀> ⇒()lim 0n n f f με→∞-≥=，0ε∀>⇒n f f μ→．4.18若n f f μ→，则lim lim n n n n f f f →∞→∞≤≤ a.e.证明设n f f μ→，则由推论4.18知，存在{},1n f n ≥的子列{},1k n f k ≥，使得k n f f → a.e.,于是lim liminf liminf limsup limsup lim k k n k n k n n n k nn k nn n n n k nk nf f f f f f f →∞≥→∞≥→∞→∞→∞→∞≥≥=≤==≤= a.e.4.19设{},,1n f f n ≥和{},,1n g g n ≥都是可测函数列，n f f μ→，n g g μ→．（1）n f f μ→；（2）n n af bg af bg μ+→+；（3）当μ有限时，22nf f μ→，n n f g fg μ→，n n f fg gμ→（诸0n g ≠ a.e.且0g ≠ a.e.）．证明（1）取一元一致连续函数()h x x =，由定理4.22（ⅰ）得()()n h f h f μ→，即n f f μ→．（2）取二元一致连续函数()1212,h x x ax bx =+，由定理 4.22（ⅰ）得(),n n h f g(),h f g μ→，即n n af bg af bg μ+→+．（3）取一元连续函数()2h x x =，由定理4.22（ⅱ）得()()n h f h f μ→，即22nf f μ→；取二元连续函数()1212,h x x x x =，由定理4.22（ⅱ）得()(),,n n h f g h f g μ→，即n n f g fg μ→；取二元连续函数()1122,x h x x x =，由定理4.22（ⅱ）得()(),,n n h f g h f g μ→，即n n f fg gμ→．4.20设μ为有限测度，则n f f μ→⇔11n n f ff fμ→++．证明 “⇒”取连续函数()1xg x x=+，由定理4.22（ⅱ）即得． “⇐”取连续函数()1xg x x=-，由定理4.22（ⅱ）即得．。

可测函数列的几种收敛的关系

可测函数列的几种收敛的关系
1. 一致收敛：如果函数列 {fn(x)} 对于任意给定的ε > 0，都存
在一个 N，使得当 n > N 时，对于任意的 x ∈ E，都有|fn(x) − f(x)| < ε，则称函数列 {fn(x)} 在 E 上一致收敛于 f(x)，记作
fn(x) → f(x) (x ∈ E)。

一致收敛意味着收敛速度足够快，也意
味着极限函数与原函数的交换次序是可以进行的。

2. 逐点收敛：如果对于任意的 x ∈ E，函数列 {fn(x)} 都收敛
于 f(x)，即lim_n→∞ fn(x) = f(x)，则称函数列 {fn(x)} 逐点收
敛于 f(x)，也叫点态收敛。

3. 均方收敛：如果对于任意的ε > 0，有lim_n→∞ ∫[a,b] |fn(x)
− f(x)|² dx = 0，则称函数列 {fn(x)} 在 [a,b] 上均方收敛于 f(x)，记作 fn(x) ⇀ f(x) (a ≤ x ≤ b)。

均方收敛意味着收敛速度足够快，但是极限函数与原函数的交换次序一般是不可进行的。

4. 平均收敛：如果对于任意的ε > 0，有lim_n→∞ ∫[a,b] |fn(x)
− f(x)| dx = 0，则称函数列 {fn(x)} 在 [a,b] 上平均收敛于 f(x)，记作 fn(x) ⟶f(x) (a ≤ x ≤ b)。

平均收敛比逐点收敛更强，但是
收敛速度可能不够快。