2019年高考数学一轮复习专题1.1集合的概念及其基本运算(练)理
高考数学一轮复习 1.1 集合的概念与运算

2.如果集合 A 中含有 n 个元素,则集合 A 有 2n 个子集,2n-1 个真子集. 3.正确理解交、并、补集的含义是解决集合的运算问题的关键.数轴和 Venn 图是进行集合交、并、补运算的有力工具.
12
核心考点
(4)空集: 不含任何元素的集合
叫做空集,记作: ⌀
.
规定:空集是 任何集合的子集 .
4
知识梳理
双击自测
知识梳理
-5-
3.集合的基本运算
并集
符号 表示
A∪B
图形 表示
交集 A∩B
补集
设全集为 U,集合 A 的 补集∁UA
含义
A∪
B={x|x∈A,或 x∈B}
A∩B={x|x∈A,且 x∈B}
∁UA={x|x∈U,且 x∉ A}
-13-
考点一
考点二
考点三
考点一集合的基本概念
1.设集合 A={1,2,3},B={4,5},M={x|x=a+b,a∈A,b∈B},则 M 中元素的
个数为( )
A.3
B.4
C.5
D.6
关闭
由题意知 x=a+b,a∈A,b∈B,则 x 的可能取值为 5,6,7,8.因此,集合 M 共有 4 个元素.故选 B.
关闭
B
13 解析 答案
核心考点
-14-
考点一
考点二
考点三
2.若集合 A={x∈R|ax2+ax+1=0}中只有一个元素,则 a=( )
(6)设全集为 R,函数 y= 1-������2的定义域为 M,则∁RM={x|x>1,或 x<1}.( )
2019高考数学一轮复习第一章集合与常用逻辑用语1.1集合的概念及运算练习理
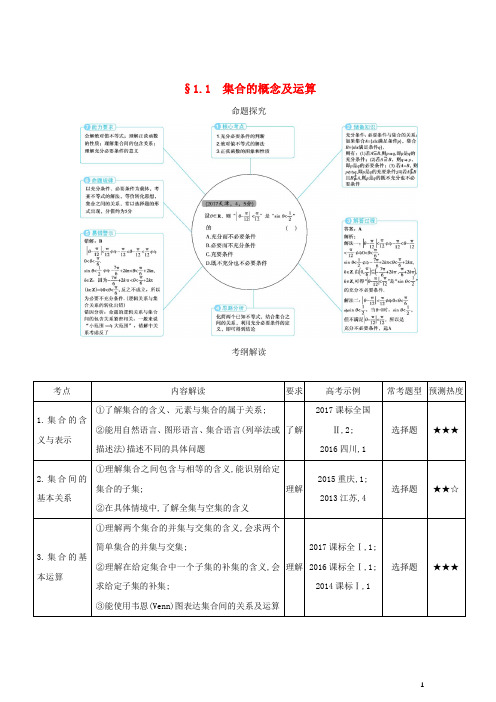
§1.1集合的概念及运算命题探究考纲解读分析解读 1.理解、掌握集合的表示方法,能够判断元素与集合、集合与集合之间的关系.2.能够正确处理含有字母的讨论问题,掌握集合的交、并、补运算和性质.3.要求具备数形结合的思想意识,会借助Venn图、数轴等工具解决集合运算问题.4.命题以集合的运算为主,其中基本知识和基本技能是高考的热点.5.本节在高考中分值为5分左右,属于中低档题.五年高考考点一集合的含义与表示1.(2017课标全国Ⅱ,2,5分)设集合A={1,2,4},B={x|x2-4x+m=0}.若A∩B={1},则B=( )A.{1,-3}B.{1,0}C.{1,3}D.{1,5}答案 C2.(2016四川,1,5分)设集合A={x|-2≤x≤2},Z为整数集,则集合A∩Z中元素的个数是( )A.3B.4C.5D.6答案 C3.(2013山东,2,5分)已知集合A={0,1,2},则集合B={x-y|x∈A,y∈A}中元素的个数是( )A.1B.3C.5D.9答案 C4.(2017江苏,1,5分)已知集合A={1,2},B={a,a2+3}.若A∩B={1},则实数a的值为. 答案 1考点二集合间的基本关系1.(2015重庆,1,5分)已知集合A={1,2,3},B={2,3},则( )A.A=BB.A∩B=⌀C.A⫋BD.B⫋A答案 D2.(2013江苏,4,5分)集合{-1,0,1}共有个子集.答案8考点三集合的基本运算1.(2017课标全国Ⅰ,1,5分)已知集合A={x|x<1},B={x|3x<1},则( )A.A∩B={x|x<0}B.A∪B=RC.A∪B={x|x>1}D.A∩B=⌀答案 A2.(2017课标全国Ⅲ,1,5分)已知集合A={(x,y)|x2+y2=1},B={(x,y)|y=x},则A∩B中元素的个数为( )A.3B.2C.1D.0答案 B3.(2017天津,1,5分)设集合A={1,2,6},B={2,4},C={x∈R|-1≤x≤5},则(A∪B)∩C=()A.{2}B.{1,2,4}C.{1,2,4,6}D.{x∈R|-1≤x≤5}答案 B4.(2017山东,1,5分)设集合M={x||x-1|<1},N={x|x<2},则M∩N=()A.(-1,1)B.(-1,2)C.(0,2)D.(1,2)答案 C5.(2016课标全国Ⅱ,2,5分)已知集合A={1,2,3},B={x|(x+1)(x-2)<0,x∈Z},则A∪B=()A.{1}B.{1,2}C.{0,1,2,3}D.{-1,0,1,2,3}答案 C6.(2016天津,1,5分)已知集合A={1,2,3,4},B={y|y=3x-2,x∈A},则A∩B=()A.{1}B.{4}C.{1,3}D.{1,4}答案 D7.(2014课标Ⅰ,1,5分)已知集合A={x|x2-2x-3≥0},B={x|-2≤x<2},则A∩B=()A.[-2,-1]B.[-1,2)C.[-1,1]D.[1,2)答案 A教师用书专用(8—24)8.(2017北京,1,5分)若集合A={x|-2<x<1},B={x|x<-1或x>3},则A∩B=()A.{x|-2<x<-1}B.{x|-2<x<3}C.{x|-1<x<1}D.{x|1<x<3}答案 A9.(2017浙江,1,5分)已知集合P={x|-1<x<1},Q={x|0<x<2},则P∪Q=()A.(-1,2)B.(0,1)C.(-1,0)D.(1,2)答案 A10.(2017山东,1,5分)设函数y=的定义域为A,函数y=ln(1-x)的定义域为B,则A∩B=()A.(1,2)B.(1,2]C.(-2,1)D.[-2,1)答案 D11.(2016课标全国Ⅲ,1,5分)设集合S={x|(x-2)(x-3)≥0},T={x|x>0},则S∩T=()A.[2,3]B.(-∞,2]∪[3,+∞)C.[3,+∞)D.(0,2]∪[3,+∞)答案 D12.(2016北京,1,5分)已知集合A={x||x|<2},B={-1,0,1,2,3},则A∩B=()A.{0,1}B.{0,1,2}C.{-1,0,1}D.{-1,0,1,2}答案 C13.(2016浙江,1,5分)已知集合P={x∈R|1≤x≤3},Q={x∈R|x2≥4},则P∪(∁R Q)=( )A.[2,3]B.(-2,3]C.[1,2)D.(-∞,-2]∪[1,+∞)答案 B14.(2016山东,2,5分)设集合A={y|y=2x,x∈R},B={x|x2-1<0},则A∪B=()A.(-1,1)B.(0,1)C.(-1,+∞)D.(0,+∞)答案 C15.(2015课标Ⅱ,1,5分)已知集合A={-2,-1,0,1,2},B={x|(x-1)(x+2)<0},则A∩B=()A.{-1,0}B.{0,1}C.{-1,0,1}D.{0,1,2}答案 A16.(2015天津,1,5分)已知全集U={1,2,3,4,5,6,7,8},集合A={2,3,5,6},集合B={1,3,4,6,7},则集合A∩∁U B=( )A.{2,5}B.{3,6}C.{2,5,6}D.{2,3,5,6,8}答案 A17.(2015福建,1,5分)若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( )A.{-1}B.{1}C.{1,-1}D.⌀答案 C18.(2015四川,1,5分)设集合A={x|(x+1)(x-2)<0},集合B={x|1<x<3},则A∪B=()A.{x|-1<x<3}B.{x|-1<x<1}C.{x|1<x<2}D.{x|2<x<3}答案 A19.(2015广东,1,5分)若集合M={x|(x+4)(x+1)=0},N={x|(x-4)(x-1)=0},则M∩N=()A.{1,4}B.{-1,-4}C.{0}D.⌀答案 D20.(2014课标Ⅱ,1,5分)设集合M={0,1,2},N={x|x2-3x+2≤0},则M∩N=()A.{1}B.{2}C.{0,1}D.{1,2}答案 D21.(2014辽宁,1,5分)已知全集U=R,A={x|x≤0},B={x|x≥1},则集合∁U(A∪B)=()A.{x|x≥0}B.{x|x≤1}C.{x|0≤x≤1}D.{x|0<x<1}答案 D22.(2014浙江,1,5分)设全集U={x∈N|x≥2},集合A={x∈N|x2≥5},则∁U A=( )A.⌀B.{2}C.{5}D.{2,5}答案 B23.(2015江苏,1,5分)已知集合A={1,2,3},B={2,4,5},则集合A∪B中元素的个数为.答案 524.(2016江苏,1,5分)已知集合A={-1,2,3,6},B={x|-2<x<3},则A∩B=.答案{-1,2}三年模拟A组2016—2018年模拟·基础题组考点一集合的含义与表示1.(2018广东茂名化州二模,1)设集合A={-1,0,1},B={x|x>0,x∈A},则B=( )A.{-1,0}B.{-1}C.{0,1}D.{1}答案 D2.(2017河北冀州第二次阶段考试,1)若集合A={x|x2-7x<0,x∈N*},则集合B=中元素的个数为( )A.1B.2C.3D.4答案 D考点二集合间的基本关系3.(2018四川成都龙泉一中月考,2)已知集合A=,B={x|ax+1=0},且B⊆A,则a的取值组成的集合为( )A.{-3,2}B.{-3,0,2}C.{3,-2}D.{3,0,-2}答案 D4.(2017河南南阳、信阳等六市一模,1)已知集合A={(x,y)|y-=0},B={(x,y)|x2+y2=1},C=A∩B,则C的子集的个数是( )A.0B.1C.2D.4答案 C考点三集合的基本运算5.(2018豫南豫北第二次联考,1)已知集合A={y|y=2x},B={x|y=},则A∩B=()A.{y|y>1}B.{y|y≥1}C.{y|y>0}D.{y|y≥0}答案 B6.(2018江西重点中学第一次联考,1)已知集合M=,则∁R M=( )A.{x|-1<x<1}B.{x|-1<x≤1}C.{x|x<-1或x≥1}D.{x|x≤-1或x≥1}答案 C7.(2017广东惠州第三次调研,1)已知全集U=R,集合A={1,2,3,4,5},B={x∈R|x≥2},则图中阴影部分所表示的集合为( )A.{0,1,2}B.{0,1}C.{1,2}D.{1}答案 D8.(2017河南濮阳第二次检测,13)已知集合A={-1,a},B={3a,b},若A∪B={-1,0,1},则a= .答案0B组2016—2018年模拟·提升题组(满分:35分时间:20分钟)一、选择题(每小题5分,共30分)1.(2018广东茂名化州二模,1)若集合A={0,1},B={y|y=2x,x∈A},则(∁R A)∩B=()A.{0}B.{2}C.{2,4}D.{0,1,2}答案 B2.(2018吉林榆树第一高级中学第三次模拟,1)设全集U={1,3,5,6,9},A={3,6,9},则图中阴影部分表示的集合是( )A.{1,3,5}B.{1,5,6}C.{6,9}D.{1,5}答案 D3.(2018四川南充一诊,2)已知集合A={(x,y)|y=f(x)},B={(x,y)|x=1},则A∩B中的元素有( )A.1个B.1个或2个C.至多1个D.可能2个以上答案 C4.(2017湖南永州二模,2)已知集合P={x|-1≤x≤1},M={a},若P∩M=⌀,则a的取值范围是( )A.(-∞,-1]B.[1,+∞)C.[-1,1]D.(-∞,-1)∪(1,+∞)答案 D5.(2017河北唐山摸底,1)已知集合A⊆{1,2,3,4,5},且A∩{1,2,3}={1,2},则满足条件的集合A的个数为( )A.2B.4C.8D.16答案 B6.(2016江西南昌十所省重点中学二模,2)设集合A=,B={x|y=ln(x2-3x)},则A∩B中元素的个数是( )A.1B.2C.3D.4答案 A二、填空题(共5分)7.(2017江西九江地区七校联考,14)设A,B是非空集合,定义A⊗B={x|x∈A∪B且x∉A∩B},已知M={y|y=-x2+2x,0<x<2},N={y|y=2x-1,x>0},则M⊗N= .答案∪(1,+∞)C组2016—2018年模拟·方法题组方法1 与集合元素有关问题的解题方略1.(2016湖南衡阳八中一模,1)已知集合A={0,1},B={z|z=x+y,x∈A,y∈A},则集合B的子集个数为( )A.3B.4C.7D.8答案 D方法2 集合间的基本关系的解题方法2.(2017河北衡水中学七调,1)已知集合A={x|log2x<1},B={x|0<x<c},若A∪B=B,则c的取值范围是( )A.(0,1]B.[1,+∞)C.(0,2]D.[2,+∞)答案 D3.(2018河北衡水中学模拟,13)已知含有三个实数的集合既可表示成,又可表示成{a2,a+b,0},则a2 017+b2 017等于.答案-1方法3 集合的基本运算的解题方法4.(2017安徽淮北第二次模拟,2)已知全集U=R,集合M={x|x+2a≥0},N={x|log2(x-1)<1},若集合M∩(∁U N)={x|x=1或x≥3},那么a的取值为( )A.a=B.a≤C.a=-D.a≥答案 C5.(人教A必1,一,1-1A,7,变式)设全集U={x∈N|x≤8},集合A={1,3,7},B={2,3,8},则(∁U A)∩(∁U B)=( )A.{1,2,7,8}B.{4,5,6}C.{0,4,5,6}D.{0,3,4,5,6}答案 C方法4 求解集合新定义问题的技巧6.(2018陕西西安长安质检,2)若x∈A,且∈A,则称A是伙伴关系集合,集合M=的所有非空子集中具有伙伴关系的集合的个数是( )A.31B.7C.3D.1答案 B7.(2017湖北武昌一模,1)设A,B是两个非空集合,定义集合A-B={x|x∈A,且x∉B}.若A={x∈N|0≤x≤5},B={x|x2-7x+10<0},则A-B=( )A.{0,1}B.{1,2}C.{0,1,2}D.{0,1,2,5}答案 D。
高考数学一轮复习专题1.1集合的概念及其基本运算(测)(2021年整理)

(浙江专版)2019年高考数学一轮复习专题1.1 集合的概念及其基本运算(测)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((浙江专版)2019年高考数学一轮复习专题1.1 集合的概念及其基本运算(测))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(浙江专版)2019年高考数学一轮复习专题1.1 集合的概念及其基本运算(测)的全部内容。
第01节 集合的概念及其基本运算班级__________ 姓名_____________ 学号___________ 得分__________一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【2018年新课标I 卷文】已知集合,,则A. B 。
C 。
D 。
【答案】A【解析】分析:利用集合的交集中元素的特征,结合题中所给的集合中的元素,求得集合中的元素,最后求得结果。
详解:根据集合交集中元素的特征,可以求得,故选A.2。
【2017天津文】设集合{1,2,6},{2,4},{1,2,3,4}A B C ===,则()A B C = (A ){2}(B){1,2,4}(C ){1,2,4,6}(D ){1,2,3,4,6} 【答案】B【解析】由题意可得:{}(){}1,2,4,6,1,2,4A B A B C =∴=.本题选择B 选项.3.【2018届浙江省嘉兴市高三上期末】已知集合{|1}P x x =<, {}0Q x x =,则( ) A 。
P Q ⊆ B 。
Q P ⊆ C. P ⊆ R C Q D 。
R C P Q ⊆ 【答案】D【解析】R C P =[1,)+∞∴ R C P Q ⊆,选D.4.【2018届浙江省嵊州市高三上期末】已知集合2{|1}A x x =≤, {}21B =-,,则A B ⋂=( ) A. {}1 B. {}21-, C. {|11}x x -≤≤ D. {|211}x x x =--≤≤,或 【答案】A【解析】 {}2|1A x x =≤ {}=|11x x -≤≤, {}21B =-,, {}1A B ∴⋂=,故选A.5.【2018届浙江省杭州市高三上期末】设集合{|22}A x x =+≤, []0,4B =,则()R C A B ⋂=( ) A 。
高考数学一轮复习讲练测专题1.1集合的概念及其基本运算(讲)理(含解析)

1},专题1.1集合的概念及其基本运算(讲)【辭析】由已知得^ = {1,4}.当口 = <时.A = [3],则討二〔12*卜・4厂直=0,当也=1时,J = ;L3j ; 则JU5 = {1.3r 4} p = 当a = 4时.^ = {4.3}, = (1,3.4}, -40-8={4}.当疽产1,戊戸吳。
否4时…儿丘二卩”丸好,JO^ =0,综上所述,当a = 3时—儿P = {1S4齐AClB^Qi 当应"时,血JH"4}, /仃丘二{1»当*4时,则加UE 二口34、“5={4}f 当口工1, 口产3, a 芦4时I dl-再三卜 B =0.2.【2015高考天津,理1】已知全集U 1,2,3,4,5,6,7,8 ,集合A 2,3,5,6,集合B 1,3,4,6,7则集合AI ejB () (A )2,5( B )3,6 (C ) 2,5,6 ( D ) 2,3,5,6,8【答案】A【赭斤】^5 = (2,5,8}_所以二冷5},故选九3. 【云南省玉溪一中 2015届高三上学期第一次月考试卷】设集合B {(x, y) y 3x },则A B 的子集的个数是( )A. 4 B. 3C. 2D. 1【答案】A1.【课本典型习题,P12第3题】设集合Ax(x a)(x 3) 0,a R , Bx(x 4)(x 1) 0 ,AUB , AI B .【答案】当a 3时,AU B 1,3,4 , AI B ;当a 1 时,AU B1,3,4,AI B 1 ;当 a时,贝U AU B 1,3,4 , AIB 4 ;当 a 1 ,a 3, a 4时, AU B1,3,4, a , AI B【课前小测摸底细】求4{(“)話【解析】篥會話为橢區|兰+匸=1上的昌集合卫为扌無心煎i' = 丁上的点,由于指纹函数恒过点(Q1)・16 -4* 斗由于点121在椭圆兰十二“曲内部,因此扌旨数函数与椭圆有2个交点.,的子篥的个数次F =4个,16 4故答累为扎4. 【基础经典试题】集合M ={y | y= x2—1, x R},集合N={x|y= 9 x2, x R},则MIN等于( )A. {t|0 t 3} B . {t|—1 t 3} C . {(- . 2,1),( .2,1) D •【答案】B【鱷析】■・」=/—in —h 二対=[—h +工)・又丫)=嗣-》匸9 - ? > 0 +/■[- 3,3]. ■- M A -V = [-l(3].5. 【改编自2012年江西卷理科】若集合A={— 1,1}, B= 0,2,则集合{z|z= x+ y, x A, y B}中的元素的非空子集个数为()A. 7 B . 6 C . 5 D . 4【答案】A【鋒析】由已知得,集台V尸K+F送用ye ^={-1.1.3}-所以其非空子集个数冷2为二7,故选【考点深度剖析】高考对集合知识的考查要求较低,均是以小题的形式进行考查,一般难度不大,要求考生熟练掌握与集合有关的基础知识•纵观近几年的高考试题,主要考查以下两个方面:一是考查具体集合的关系判断和集合的运算•解决这类问题的关键在于正确理解集合中元素所具有属性的含义,弄清集合中元素所具有的形式以及集合中含有哪些元素•二是考查抽象集合的关系判断以及运算•【经典例题精析】考点1集合的概念K【1-1 】若a, b R,集合{1 , a b, a 0,-,b,求b a的值_____________________ .a【答案】2iy【解析】由d d+方卫}=0—血可知“山则只能卄庄0,则有以下对应关爲CJ - b = 0.b—=c ab = 1.Jl_2【1-2】已知集合A={x|x+ m好4 = 0}为空集,则实数m的取值范围是()A. ( —4, 4) B . [ —4, 4] C . ( —2, 2) D . [ —2, 2]【答案】A【解析】依题意知一元二次方程F十ww十4二0无解,^flzA A= w;_16 < 0(解得一4€楞羔4.故选A.【1-3】已知A={a+ 2, (a+ 1)2, a2+ 3a+ 3},若1€ A,则实数a构成的集合B的元素个数是()A. 0 B . 1 C . 2 D . 3【答案】B丽析】若口则1,代入集合」」得川={1"1},与集合元责的互异性若S+1F=1,帶住=0或一2,代入集合4帰/=匸切}或去{0二1},后■看与集合的互异性矛盾,故尸0 符合要求J若/+3卄3=1,则尸—诫-拿代人黑皆出得沪{山1}或看•戶{轴助都与集合的互异性相矛盾, 無上可如只有口二。
2019版高考数学:§1.1 集合的概念及运算

2019年4月28日
梅花三麓专业文档
18
5.(2017天津,1,5分)设集合A={1,2,6},B={2,4},C={1,2,3,4},则(A∪B)∩C= ( )
A.{2}
B.{1,2,4}
C.{1,2,4,6} D.{1,2,3,4,6}
答案 B 本题考查集合的运算. 由题意知A∪B={1,2,4,6},∴(A∪B)∩C={1,2,4},故选B.
答案 A 本题考查集合的并集. A∪B={1,2,3}∪{2,3,4}={1,2,3,4}.故选A.
2019年4月28日
梅花三麓专业文档
5
5.(2014课标Ⅱ,1,5分,0.866)已知集合A={-2,0,2},B={x|x2-x-2=0},则A∩B= ( ) A.⌀ B.{2} C.{0} D.{-2} 答案 B ∵集合A={-2,0,2},B={x|x2-x-2=0}={2,-1},∴A∩B={2},故选B.
2019年4月28日
梅花三麓专业文档
22
9.(2016山东,1,5分)设集合U={1,2,3,4,5,6},A={1,3,5},B={3,4,5},则∁U(A∪B)= ( ) A.{2,6} B.{3,6} C.{1,3,4,5} D.{1,2,4,6} 答案 A ∵A∪B={1,3,4,5},∴∁U(A∪B)={2,6},故选A.
2019年4月28日
梅花三麓专业文档
23
10.(2016浙江,1,5分)已知全集U={1,2,3,4,5,6},集合P={1,3,5},Q={1,2,4},则(∁UP)∪Q= ( ) A.{1} B.{3,5} C.{1,2,4,6} D.{1,2,3,4,5} 答案 C ∵U={1,2,3,4,5,6},P={1,3,5},∴∁UP={2,4,6},∵Q={1,2,4},∴(∁UP)∪Q={1,2,4,6}.
2019-2020年高考数学大一轮总复习 1.1集合与集合的运算课时作业 理

2019-2020年高考数学大一轮总复习 1.1集合与集合的运算课时作业理A级训练(完成时间:10分钟)1.(xx·四川)已知集合A={x|(x+1)(x-2)≤0},集合B为整数集,则A∩B=()A.{-1,0} B.{0,1}C.{-2,-1,0,1} D.{-1,0,1,2}2.(xx·全国)设集合U={1,2,3,4,5},集合A={1,2},则∁U A=()A.{1,2} B.{3,4,5}C.{1,2,3,4,5} D.∅3.(xx·广西)设集合M={1,2,4,6,8},N={1,2,3,5,6,7},则M∩N中元素的个数为()A.2 B.3C.5 D.74.已知集合A={x|x2-x-2<0},B={x|-1<x<1},则()A.A B B.B AC.A=B D.A∩B=∅5.已知集合A={0,1},满足条件A∪B={2,0,1,3}的集合B共有()A.2个B.2个C.3个D.4个6.设集合U={x|x<5,x∈N*},M={x|x2-5x+6=0},则∁U M=()A.{1,4} B.{1,5}C.{2,3} D.{3,4}7.已知全集U=R,则正确表示集合M={0,1,2}和N={x|x2+2x=0}关系的韦恩(Venn)图是()A. B.C. D.8.集合A={x∈R||x-2|≤5}中的最小整数为________.9.(xx·重庆)设全集U={n∈N|1≤n≤10},A={1,2,3,5,8},B={1,3,5,7,9},则(∁U A)∩B =________.10.若集合A={-1,3},集合B={x|x2+ax+b=0},且A=B,求实数a,b.B 级训练(完成时间:15分钟)1.[限时1分钟,达标是( )否( )]设全集U =R ,M ={x |x (x +3)<0},N ={x |x <-1},则图中阴影部分表示的集合为( )A .{x |x ≥-1}B .{x |-3<x <0}C .{x |x ≤-3|D .{x |-1≤x <0}2.[限时1分钟,达标是( )否( )](xx·江西)若集合A ={x ∈R |ax 2+ax +1=0}其中只有一个元素,则a =( )A .4B .2C .0D .0或43.[限时1分钟,达标是( )否( )]已知集合M ={x ||x -4|+|x -1|<5},N ={x |a <x <6},且M ∩N =(2,b ),则a +b =( )A .6B .7C .8D .94.[限时1分钟,达标是( )否( )](xx·上海)已知互异的复数a ,b 满足ab ≠0,集合{}a ,b ={}a 2,b 2,则a +b =________.5.[限时3分钟,达标是( )否( )]已知集合A ={x |6x +1≥1,x ∈R },B ={x |x 2-2x -m <0},若A ∩B ={x |-1<x <4},则实数m 的值为________.6.[限时4分钟,达标是( )否( )]已知集合A ={-4,2a -1,a 2},B ={a -5,1-a,9},分别求适合下列条件的a 的值.(1)9∈(A ∩B );(2){9}=A ∩B .[限时4分钟,达标是( )否( )]设A ={x |x 2-8x +15=0},B ={x |ax -1=0}.(1)若a =15,试判定集合A 与B 的关系; (2)若B ⊆A ,求实数a 组成的集合C .C 级训练(完成时间:8分钟)1.[限时4分钟,达标是( )否( )](xx·广东)设集合A ={(x 1,x 2,x 3,x 4,x 5)|x i ∈{-1,0,1},i =1,2,3,4,5},那么集合A 中满足条件“1≤|x 1|+|x 2|+|x 3|+|x 4|+|x 5|≤3”的元素个数为( )A .60B .90C .120D .1302.[限时4分钟,达标是( )否( )](xx·揭阳一模)定义一个集合A 的所有子集组成的集合叫做集合A 的幂集,记为P (A ),用n (A )表示有限集A 的元素个数,给出下列命题:①对于任意集合A ,都有A ∈P (A );②存在集合A ,使得n [P (A )]=3;③用∅表示空集,若A ∩B =∅,则P (A )∩P (B )=∅;④若A ⊆B ,则P (A )⊆P (B );⑤若n (A )-n (B )=1,则n [P (A )]=2×n [P (B )].其中正确的命题个数为( )A .4B .3C .2D .1第一章 集合与简易逻辑第1讲 集合与集合的运算【A 级训练】1.D 解析:A ={x |(x +1)(x -2)≤0}={x |-1≤x ≤2},又集合B 为整数集,故A ∩B ={-1,0,1,2},故选D.2.B3.B 解析:因为M ={1,2,4,6,8},N ={1,2,3,5,6,7},所以M ∩N ={1,2,6},即M ∩N中元素的个数为3.故选B.4.B 解析:A ={x |x 2-x -2<0}={x |-1<x <2},则B A .5.D 解析:因为A ={0,1},且A ∪B ={2,0,1,3},所以B 可能为{2,3}或{2,3,0}或{2,3,1}或{2,0,1,3},则满足条件的集合B 共有4个.6.A 解析:U ={1,2,3,4},M ={x |x 2-5x +6=0}={2,3},所以∁U M ={1,4}.7.A 解析:N 为x 2+2x =0的解集,解x 2+2x =0可得,x =0或-2,则N ={-2,0},M ∩N ={0}≠∅.8.-3 解析:由|x -2|≤5,得-5≤x -2≤5,即-3≤x ≤7,所以集合A 中的最小整数为-3.9.{7,9} 解析:因为全集U ={n ∈N |1≤n ≤10},A ={1,2,3,5,8},B ={1,3,5,7,9},所以∁U A ={4,6,7,9},所以(∁U A )∩B ={7,9},故答案为{7,9}.10.解析:因为A =B ,所以B ={x |x 2+ax +b =0}={-1,3}.所以⎩⎪⎨⎪⎧-a =-1+3=2b =-1×3=-3,解得a =-2,b =-3. 【B 级训练】1.D 解析:M ={x |x (x +3)<0}={x |-3<x <0},由图象知,图中阴影部分所表示的集合是M ∩(∁U N ),又N ={x |x <-1},所以∁U N ={x |x ≥-1}.所以M ∩(∁U N )=[-1,0).2.A解析:当a=0时,方程为1=0不成立,不满足条件,当a≠0时,Δ=a2-4a =0,解得a =4.3.B 解析:由集合M 中的不等式,解得0<x <5,所以M ={x |0<x <5},因为N={x |a <x <6},且M ∩N =(2,b ),所以a =2,b =5,则a +b =2+5=7.4.-1 解析:第一种情况:a =a 2,b =b 2,因为ab ≠0,所以a =b =1,与已知条件矛盾,不符;第二种情况:a =b 2,b =a 2,所以a =a 4⇒a 3=1,所以a 2+a +1=0,即a +b =-1.5.8 解析:由6x +1≥1,得x -5x +1≤0,所以-1<x ≤5,所以A ={x |-1<x ≤5}. 因为A ∩B ={x |-1<x <4},所以有42-2×4-m =0,解得m =8.此时B ={x |-2<x <4},符合题意,故实数m 的值为8.6.解析:(1)因为9∈(A ∩B ),所以9∈A 且9∈B .所以2a -1=9或a 2=9,所以a =5或a =-3或a =3.经检验a =5或a =-3符合题意.所以a =5或a =-3.(2)因为{9}=A ∩B ,所以9∈A 且9∈B ,由(1)知a =5或a =-3.当a =-3时,A ={-4,-7,9},B ={-8,4,9},此时A ∩B ={9};当a =5时,A ={-4,9,25},B ={0,-4,9},此时A ∩B ={-4,9},不合题意.综上知a =-3.7.解析:由x 2-8x +15=0,得x =3或x =5.所以A ={3,5}.(1)当a =15时,由15x -1=0,得x =5.所以B ={5},所以B A . (2)因为A ={3,5}且B ⊆A ,所以,若B =∅,则方程ax -1=0无解,有a =0;若B ≠∅,则a ≠0,由方程ax -1=0,得x =1a ,所以1a =3或1a =5,即a =13或a =15.所以C ={0,13,15}. 【C 级训练】1.D 解析:由题目中“1≤|x 1|+|x 2|+|x 3|+|x 4|+|x 5|≤3”考虑x 1,x 2,x 3,x 4,x 5的可能取值,设A ={0},B ={-1,1},分为①有2个取值为0,另外3个从B 中取,共有方法数:C 25×23;②有3个取值为0,另外2个从B 中取,共有方法数:C 35×22;③有4个取值为0,另外1个从B 中取,共有方法数:C 45×2.所以总共方法数是C 25×23+C 35×22+C 45×2=130,即元素个数为130.故选D.2.B 解析:由P (A )的定义可知①正确,④正确,设n (A )=n ,则n [P (A )]=2n ,所以②错误,若A ∩B =∅,则P (A )∩P (B )={∅},③不正确;n (A )-n (B )=1,即A 中元素比B 中元素多1个,则n [P (A )]=2×n [P (B )],⑤正确,故选B..。
2019-2020年高考数学一轮复习专题1.1集合的概念及其基本运算测(I)

2019-2020年高考数学一轮复习专题1.1集合的概念及其基本运算测(I)班级__________ 姓名_____________ 学号___________ 得分__________一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【xx 天津文】设集合{1,2,6},{2,4},{1,2,3,4}A B C ===,则(A )(B )(C )(D )【答案】【解析】由题意可得:{}(){}1,2,4,6,1,2,4A B A B C =∴=U U I .本题选择B 选项.2. 【xx 安徽黄山二模】已知集合{}()()R 2,1,0,1,2,{|120}A B x x x =--=-+≥ð,则( )A. B. C. D.【答案】B3. 设集合,为整数集,则集合中元素的个数是( )A .3B .4C .5D .6 【答案】C【解析】由题意得,则,故中元素的个数是个,故选C.4. 【xx 中原名校三模】集合,{}22|2,N x x y x R =+=∈,则( )A .B .C .D .【答案】B【解析】由,得,所以集合,由,得,所以,故选B.5.【xx 陕西汉中二模】已知集合{}2{|320},30A x x x B x x =-+<=-,则( )A. B. C. D.【答案】C【解析】因为{|12},{|3}A x x B x x =<<=<,则,应选答案C 。
6.已知集合{}{}1,2,3,4,5,2,4,6P Q ==,若,则的子集个数为( )A .5B .4C .3D .2【答案】B【解析】由题意,它的子集有个.故选B .7.设和是两个集合,定义集合或且.若, (){}22Q x |y log x 2x 15==--,那么等于( )A.-1,4]B.(-∞,-1]∪4,+∞)C.(-3,5)D.(-∞,-3)∪-1,4]∪(5,+∞)【答案】D8.已知集合,{}2|540,B x x x x Z =-+<∈,若,则等于( )A .2B .3C .2或3D .2或4 【答案】C【解析】由已知可得,由于,则或,故选C.9.设集合,,则满足且的集合S 的个数是( )A .57B .56C .49D .8 【答案】B【解析】集合的个数为.10.【xx 陕西师范附属二模】集合, ,则( )【答案】D【解析】依题意(){}3,3,1,0,1,2,3P Q =-=-,故.二、填空题:本大题共7小题,共36分.11.【改编自xx 北京西城区5月模拟】已知集合, (){|20}B x R x x =∈⋅-<,那么 【答案】 【解析】集合, (){|20}={|02}B x R x x x x =∈⋅-<<<,所以.12.设集合,,,则实数的值为 .【答案】【解析】因为,所以13.【改编自xx 福建漳州5月质检】已知集合{}{}10,2101A x x B =+=--,,,,则【答案】{-2,-1}14.已知集合,,若,,则 . 【答案】-5 【解析】因为2{|20}(,1)(2,)P y y y =-->=-∞-+∞U ,所以,因此为方程两根,即13,1323 5.a b a b -=-+-⨯=⇒+=--=-15.已知集合,,若,则实数的取值范围为_______.【答案】【解析】{}{}{}242,1,A x y x x x x B x a x a A B B B A ==-=-≤≤=<<+=∴⊆Q I16. 已知,{|2135}B x a x a =+≤≤-,,则的取值范围为________.【答案】【解析】17.【改编自xx 江西4月质检】已知集合, ,若全集为实数集,则 .【答案】【解析】()(){}()11R 355log 412,4,48,,2,22x A x x B x A B -⎧⎫⎪⎪⎛⎫⎛⎤=--===+∞∴⋂=⎨⎬ ⎪ ⎥⎝⎭⎝⎦⎪⎪⎩⎭Q ð,故. 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.【xx 山西孝义模考】已知,22{|2(1)10}B x x a x a =+++-=,其中.如果,求实数的取值范围.【答案】【解析】,解得,∴.∵,∴或.∴224(1)4(1)0a a ∆=+--≤,解得.但是:时,,舍去.∴实数的取值范围是.19.已知集合{|12},{|3}A x x B x m x m =≤≤=≤≤+.(1)当时,求;(2)若,求实数的取值范围.【答案】(1),(2).20.若集合A ={x|-2≤x≤5},B ={x|m +1≤x≤2m-1},且B ⊆A ,求m 的可取值组成的集合.【答案】【解析】当,即时,,满足;若,且满足,如图所示,则121,12,215,m m m m +≤-⎧⎪+≥-⎨⎪-≤⎩即2,3,3,m m m ≥⎧⎪≥-⎨⎪≤⎩∴.故或,即所求集合为.21.已知函数的定义域为集合,集合,集合.(1)求;(2)若 (),求的值.【答案】(1).(2)=1.【解析】(1)由题意得=.,=,∴.(2)由题意得=,∴,∵, ∴,∴,又∵, ∴=1.22.已知{}0232≤+-∈=x x R x A ,{}02242≥-⋅-∈=a a R x B x x .(Ⅰ)当时,求;(Ⅱ)若,求实数的取值范围.【答案】(Ⅰ)1,2];(Ⅱ) -2,1].【解析】(Ⅰ)由题得, 所以a=1时,。
2019年高考数学一轮总复习 专题1.1 集合的概念及其运算练习(含解析)理.doc

2019年高考数学一轮总复习 专题1.1 集合的概念及其运算练习(含解析)理真题回放1. 【2017高考新课标2理数】设集合{}1,2,4A =,{}240x x x m B =-+=。
若{}1AB =,则B =( )A.{}1,3-B.{}1,0C.{}1,3D.{}1,5 【答案】C 【解析】 试题分析:由{}1AB =得1B ∈,即1x =是方程240x x m -+=的根,所以140,3m m -+==,{}1,3B =,故选C 。
【考点】 交集运算,元素与集合的关系【考点解读】集合中元素的三个特性中的互异性对解题影响较大,特别是含有字母的集合,在求出字母的值后,要注意检验集合中的元素是否满足互异性。
两个防范:一是不要忽视元素的互异性;二是保证运算的准确性。
2. 【2017高考新课标1卷理】已知集合A ={x |x <1},B ={x |31x<},则A .{|0}AB x x =< B .A B =RC .{|1}A B x x =>D .AB =∅【答案】A【考点】集合的运算,指数运算性质.【考点解读】集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理.3. 【2017高考新课标3理数】已知集合A ={}22(,)1x y x y +=│,B ={}(,)x y y x =│,则A B 中元素的个数为A .3B .2C .1D .0【答案】B【解析】试题分析:集合中的元素为点集,由题意,结合A 表示以()0,0 为圆心, 为半径的单位圆上所有点组成的集合,集合B 表示直线y x = 上所有的点组成的集合,圆221x y += 与直线y x = 相交于两点()1,1 ,()1,1-- ,则AB 中有两个元素。
故选B 。
【考点】 交集运算;集合中的表示方法。
【考点解读】求集合的基本运算时,要认清集合元素的属性(是点集、数集或其他情形)和化简集合,这是正确求解集合运算的两个先决条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第01节集合的概念及其基本运算
A基础巩固训练
1.【2018湖北5月押题】设集合,,则下列结论正确的是()
A. B. C. D.
【答案】B
【名师点睛】集合的基本运算的关注点
(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图.
2.【2018浙江5月考试】已知集合,,若,则
A. B. C.
D.
【答案】B
【解析】分析:由可得是方程的两根,再根据韦达定理列方程求解即可.
详解:,
由,可得是方程得两根,
由韦达定理可得,即,故选B.
【名师点睛】集合的基本运算的关注点:
(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提;(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决;
(3)注意划归思想的应用,常常转化为方程问题以及不等式问题求解.
3.【2018云南玉溪一模】已知集合,,
则的元素个数为()
A. B. C. D.
【答案】B
【名师点睛】本题考查了两个集合的交点个数问题,主要注意两个集合都为点集,所以交集的个数也就是两个方程的解的个数,因此可以通过方程思想来解,属于简单题.
4.【2018三明一中模拟】设集合,,则()
A. B. C. D.
【答案】D
【解析】分析:化简集合,根据交集的定义计算.
详解:因为集合,
化简,
所以,故选D.
【名师点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合且属于集合的元素的集合.
5.【2018浙江台州模拟】设全集是实数集,或,,则
()
A. B. C. D.
【答案】C
【解析】分析:首先解一元二次不等式,求得集合N,应用补集的定义求得集合M,再结合交集定义求得
,从而求得结果.
详解:由于,所以,,所以
,故选C.
【名师点睛】该题考查的是有关集合的运算的问题,在解题的过程中,需要明确集合的运算法则,注意对应集合中元素的特征,从而求得结果.
B能力提升训练
1.【2018安庆一中模拟】已知全集,集合,,则下图中阴影部分所表示的集合为( )
A. B. C. D.
【答案】B
【解析】分析:求出函数的值域可得集合,解不等式可得集合,然后可求出
.
详解:由题意得,.
∴.图中阴影部分所表示的集合为,∴.故选B.
【名师点睛】本题考查函数值域的求法、不等式的解法和集合的运算,解答的关键是正确理解图中阴影部分所表示的集合的含义.
2.【2018河北衡水押题】已知集合,,则()
A. B. C. D.
【答案】B
【解析】分析:首先根据分式不等式的解法以及指数不等式,化简集合A,B,之后根据交集的定义写出.
详解:集合,,则
,故选B.
【名师点睛】该题考查的是有关集合的运算问题,在解题的过程中,需要先将集合中的元素确定,之后再根据集合的交集中元素的特征,求得结果.
3.【2018河南押题】已知集合,,则()
A. B. C. D.
【答案】C
【解析】分析:由题意首先求得集合Q 和集合,然后进行交集运算即可求得最终结果. 详解:因为,, 所以
.即
.
本题选择C 选项.
【名师点睛】本题主要考查集合的交并补混合运算及其应用,意在考查学生的转化能力和计算求解能力. 4.【2018广东江门一模】已知
,
,若
,则实数
的取值范围是 . 【答案】
【名师点睛】解答本题注意两点:一是弄清两个集合的含义,二是要借助数形结合的方法解决问题.解题时将两集合间的包含关系转化为圆与直线相离或相切处理,然后根据圆心到直线的距离大于或等于半径来解决.
5.【2018内蒙古呼和浩特一模】已知集合
,集合
,集合
,
若A B C ⋃⊆,则实数m 的取值范围是______________. 【答案】1,12⎡⎤
-⎢⎥⎣⎦
【解析】由题意, {|12}A B x x ⋃=-<< ,
∵集合{|1
0}C x mx A B C =+⋃⊆>, , ①111102022
m x m m m m -
∴-≥∴≥-∴-≤<,<,,,<; ②m 0= 时,成立;
③1101101m x m m m m -
∴-≤-∴≤∴≤>,>,,,<, 综上所述, 112m -≤≤, 故答案为1
12
m -≤≤.
C 思维拓展训练 1.【2018郑州模拟】已知全集,集合
,
,
则
中元素的个数是( )
A .0
B .1
C .2
D .3 【答案】D
【名师点睛】集合的基本运算的关注点
(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提. (2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决. (3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn 图. 2.【2018重庆二诊】设集合()()(){
}
22
,|3sin 3cos 1,A x y x y R ααα=
+++=∈,
(){},|34100B x y x y =++=,记P A B =⋂,则点集P 所表示的轨迹长度为( )
A ....【答案】D
【解析】由题意得圆()()2
2
3sin 3cos 1x y αα+++=的圆心()3sin ,3cos αα--在圆229x y +=上,当α变
化时,该圆绕着原点转动,集合A 表示的区域是如图所示的环形区域.
由于原点()0,0到直线34100x y ++=的距离为
2d ==,所以直线34100x y ++=恰好与圆环
的小圆相切.
所以P A B =⋂表示的是直线34100x y ++=截圆环的大圆2216x y +=所得的弦长.
故点集P 所表示的轨迹长度为=D .
【名师点睛】解答本题的关键是正确理解题意,弄懂集合A 和P A B =⋂的含义,然后将问题转化为求圆的弦长的问题处理,在圆中求弦长时要用到由半径、弦心距和半弦长构成的直角三角形,然后利用勾股定理求解.
3.【2018福建莆田模拟】设非空集合
满足:当
时,有
.给出如下三个命题:①
若,则; ②若,则;③若,则.其中正确命题的个数是
A .0
B .1
C .2
D .3 【答案】D
【解析】分析:先根据非空集合满足:当
时,有
得到
且
,然后对三
个命题一一进行验证即可. 详解:由定义设非空集合,
满足
时,有
知,符合定义的参数的值,
一定大于等于或小于等于,惟如此才能保证时,
有
即
,符合条件的的值一定大于等于,小于等于,
惟如此才能保证打时,有即
,正对各个命题进行判断: 对于①
,故必有
,可得
;
②,则,解之可得,
对于③,若,则,解之得,
正确命题有个,故选D .
【名师点睛】本题主要考查元素与集合、不等式的解法以及转化与划归思想的应用,属于难题.转化与划归思想解决高中数学问题的一种重要思想方法,是中学数学四种重要的数学思想之一,尤其在解决知识点较多以及知识跨度较大的问题发挥着奇特功效,大大提高了解题能力与速度.运用这种方法的关键是将题设条件研究透,这样才能快速找准突破点.以便将问题转化为我们所熟悉的知识领域,进而顺利解答,希望同学们能够熟练掌握并应用于解题当中.本题中,将集合问题转化为不等式问题是解题的根据.
4.【2018上海普陀二模】设集合1|,2x
M y y x R ⎧⎫⎪⎪⎛⎫
==∈⎨⎬ ⎪⎝⎭⎪⎪⎩⎭
,
()()()1|1112,121N y y x m x x m ⎧⎫⎛⎫
==+-+--≤≤⎨⎬ ⎪-⎝⎭⎩⎭
,若N M ⊆,则实数m 的取值范围是
_________. 【答案】()1,0-
【解析】 1|,2x
M y y x R ⎧⎫⎪⎪⎛⎫
==∈⎨⎬ ⎪⎝⎭⎪⎪⎩⎭
()0,=+∞, N M ⊆,
()()()111121y x m x m ⎛⎫∴=+-+-- ⎪-⎝⎭在[]1,2 上恒为正,设()111f x m ⎛⎫
=+ ⎪-⎝⎭
()()()112x m x -+--,则()()10
{ 20f f >>,即10
{ 1
10
1
m m ->+>-,得11
{ 1,0m m m -<<><,即10m -<<,实数m 的取值范围是()1,0-,故答案为()1,0-.
5.【2018河北邯郸一模】已知集合1
{|}2
M x x =≥-, 32
{|310}A x M x x a =∈-+-=,
{|20}B x M x a =∈--=,若集合A B ⋃的子集的个数为8,则a 的取值范围为__________.
【答案】51,11,28⎡⎫⎛
⎫-
-⋃-⎪ ⎪⎢⎣⎭⎝
⎭
【名师点睛】
对于方程解的个数(或函数零点个数)问题,可利用函数的值域或最值,结合函数的单调性、草图确定其中参数范围.从图象的最高点、最低点,分析函数的最值、极值;从图象的对称性,分析函数的奇偶性;从图象的走向趋势,分析函数的单调性、周期性等.。
