运输问题-数学模型及其解法
运输问题模型

。
目标可以减少,说明当前
解不是最优解
闭回路法调整
选x22进基,找到闭回路
x12 5-
x14 1 +
x22 +
x24 5-
X22最多增加5
x12 5-5 x22 + 5
x14 1 +5 x24 5-5
X22进基,x12和x24经过调整同时变成 零。但是要注意只有一个变量出基。
例如:令x12出基
B1
B2
B3
B4
产量
A1 A2 A3 销量
× 2
3 1
× 8
3 ,0
×
9
10
×
3
4
4
4
2
8
4,0
79 2 5,2 5 7,3 6
B1
B2
B3
B4
产量
A1 A2 A3 销量
×
×
2
9
10
7
3
×
×
2
1
3
4
2
×
4
8
4
2
5
3 ,0
8
4,0 6,4
9 5,2,0 7,3
B1
B2
B3
B4
产量
A1 A2 A3 销量
7
-1
2
5
1
3
4
2
7
3
4
3
8
4
2
5
3 ,0
8,5 4,0 6,4,0
9,5 5,2,0 7,3,0
重新计算检验数
A1 u1=0
A2 u2=-5
A3 u3=-5 销量
B1
初二数学运输问题

初二数学运输问题
摘要:
一、初二数学运输问题简介
1.运输问题的背景和实际意义
2.初二数学运输问题的基本内容
二、运输问题的基本模型和解决方法
1.基本模型:产销平衡模型
2.基本解决方法:线性规划
三、初二数学运输问题在生活中的应用
1.货物运输调度
2.交通路线规划
3.资源分配优化
四、初二数学运输问题的拓展思考
1.运输问题的变形和扩展
2.运输问题与其他数学领域的关联
正文:
初二数学运输问题涉及到货物运输、交通路线规划等实际问题,通过数学方法对其进行建模和求解,具有重要的实际意义。
运输问题属于线性规划的一个子领域,主要研究如何在满足一定约束条件的前提下,使得目标函数达到最优值。
运输问题的基本模型是产销平衡模型,即在多个产地和销地之间进行货物
运输,要求满足供需平衡和运输容量约束。
解决运输问题的基本方法是线性规划,将问题转化为求解线性方程组,通过计算得到最优解。
在生活中,初二数学运输问题有着广泛的应用。
例如,在货物运输调度中,通过运输问题的求解,可以有效地安排运输车辆的行驶路线和货物装载方案,提高运输效率。
在交通路线规划中,运输问题可以帮助我们找到最佳的道路使用方案,减少交通拥堵。
此外,运输问题还可以应用于资源分配优化等方面。
初二数学运输问题作为线性规划的一个实际应用,可以帮助学生更好地理解线性规划的基本思想和方法。
通过对运输问题的拓展思考,学生可以尝试解决一些变形和扩展的运输问题,进一步锻炼自己的数学思维能力。
运筹学运输问题

当出现检验数<0,证明原初始方案或改 进方案还不是最优→如何进行基变量的 调入调出?
给检验数<0的非基变量赋值,越大 越好。但要考虑产销平衡问题。
11
8、运输问题的校验方法2 —位势法
利用行位势和列位势两类数据,将检验数与 单位运价联系起来
12
检 验 数 方 程
13
λ
= c – u – v ij ij i j
A、位势法求检验数的步骤
第一步:根据最小元素法或Vogel法确定的初始运量表做 一表格,将基变量(或运量)数据替换成与之对应的单位 运价;(或对单位运价表进行修改,只保留与基变量对应的运价信
息)
第二步:在右侧增加一列,下侧增加一行,用于填写位势 数据。右侧表示行位势ui(i=1,2...m),下侧表示列位 势vj(j=1,2...n); 第三步:对于基变量对应的单位运价处,ui+vj=cij。随便 确定任一个位势,即可求解全部行和列位势; 第四步:在非基变量对应的空格处,计算检验数λij=cij(ui+vj)。并将检验数填入检验数表中; 第五步:判断检验数λij是否大于0,如是,则表示较优。 如不是,则需要调整基变量。 第六步:基变量的调整采用闭回路法进行。
收点 发点 9
B1
4
B2
1
B3
11
B4 -1
10 5
发量
偶 点 0 减 , 2 奇 点 加 5
A1
14 ③奇点 9 18 1 A2 x x 1 9 11 6 8 0 A3 1 3 x 14 ②偶点 12 2
11 21 22 31
x 3 2
x 6 7
5
13
偶点④
9
3运输问题及其解法

m
n
m
(3.1-4)
将后 n 个约束相加,得
∑∑ xij = ∑ b j ,
j =1 i =1 j =1 m n
m
n
(3.1-5)
因为,
(3.1-4)式与(3.1-5)式是相同的.由此可见,这 m + n 个约束 ∑ ai = ∑ b j ,所以,
i =1 j =1
不是独立的.我们可以证明:当所有的 ai , b j 都大于零时,任何 m + n − 1 个约束都是相互独立 的.即,系数矩阵 A 的秩 r ( A) = m + n − 1 ,事实上,
位(称为需求量), 设 cij (i = 1, 2,L , m, j = 1, 2,L , n) 为由产地 Ai 运往销地 B j 的单位运费, xij 为从 Ai 调往 B j 的物资数量,试问如何调运,求能使总运费最小. 为了清楚起见,通常将上述数据列在一张表上,该表称为运输表(见表3.1-1).
初看起来,最小元素法十分合理,但是,有时按某一最小单位运价优先安排物品调运时, 却可能导致不得不采用运费很高的其他供销点对,从而使整个运输费用增加.对每一个供应地 或销售地, 均可由它到各销售地或到各供应地的单位运价中找出最小单位运价和次小单位运价, 并称这两个单位运价之差为该供应地或销售地的罚数.若罚数的值不大,当不能按最小单位运 价安排运输时造成的运费损失不大;反之,如果罚数的值很大,不按最小运价组织运输就会造 成很大损失,故应尽量按最小单位运价安排运输,元素差额法就是基于这种考虑提出来的. 现结合上例说明这种方法: 首先计算运输表中每一行和每一列的次小单位运价和最小单位运价之间的差值,并分别称 之为行罚数和列罚数;将算出的行罚数填入位于运输表右侧行罚数栏的左边第一列的相应格子 中,列罚数填人位于运输表下边列罚数栏的第一行的相应格子中. A1 行中的次小和最小单位运 价分别为8和6,故其行罚数为2, B1 列中次小单位运价和最小单位运价分别为9和8,故其列罚 数为1,如此进行,可计算出 A1 , A2 , A3 的行罚数分别为2,2和4, B1 , B2 , B3 , B4 列的列罚数分别 为1,3,3,2.在这些罚数中最大者为4(在表4.2 - 6中用小圆圈标出),它位于 A3 行,由于在
运筹学第3章:运输问题-数学模型及其解法

整数规划模型
01
整数规划模型是线性规划模型 的扩展,它要求所有变量都是 整数。
02
整数规划模型适用于解决离散 变量问题,例如车辆路径问题 、排班问题等。
03
在运输问题中,整数规划模型 可以用于解决车辆调度、装载 等问题,以确保运输过程中的 成本和时间效益达到最优。
混合整数规划模型
混合整数规划模型是整数规划和线性规划的结合,它同时包含整数变量和 连续变量。
运筹学第3章:运输问题-数学模 型及其解法
目录
• 引言 • 运输问题的数学模型 • 运输问题的解法 • 运输问题的应用案例 • 结论
01 引言
运输问题的定义与重要性
定义
运输问题是一种线性规划问题,主要 解决如何将一定数量的资源(如货物 、人员等)从起始地点运送到目标地 点,以最小化总运输成本。
总结词
资源分配优化是运输问题在资源管理 领域的应用,主要解决如何将有限的 资源合理地分配到各个部门或项目, 以最大化整体效益。
详细描述
资源分配优化需要考虑资源的数量、 质量、成本等多个因素,通过建立运 输问题的数学模型,可以找到最优的 资源分配方案,提高资源利用效率, 最大化整体效益。
05 结论
运输问题的发展趋势与挑战
生产计划优化
总结词
生产计划优化是运输问题在生产领域的应用,主要解决如何合理安排生产计划, 满足市场需求的同时降低生产成本。
详细描述
生产计划优化需要考虑原材料的采购、产品的生产、成品的销售等多个环节,通 过建立运输问题的数学模型,可以找到最优的生产计划和调度方案,提高生产效 率,降低生产成本。
资源分配优化
发展趋势
随着物流行业的快速发展,运输问题变得越来越复杂,需要更高级的数学模型和算法来 解决。同时,随着大数据和人工智能技术的应用,运输问题的解决方案将更加智能化和
运筹学运输问题-图文

销地 B1
B2
...
Bn
产量
产地
A1
X11 X12
...
X1n
a1
A2
X21 X22
...
X2n
a2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Am
Xm1 Xm2
...
Xmn
am
销量
b1
b2
...
bn
则运输问题的数学模型如下:
产销平衡表
销地 B1
B2
...
Bn
产量
产地
A1
a1
A2
a2
.
.
.
.
.
.
Am
am
销量
b1
b2
...
bn
单位运价表
销地
B1
B2
...
Bn
产地
A1
c11
c12
...
c1n
A2
c21
c22
...
c2n
.
.
.
.
.
.
.
.
.
.
.
.
Am
cm1
cm2
...
cmn
❖ 若总产量等于总销量(产销平衡),试确定总运费最省 的调运方案。
Table14 检验数表
销地
B1
B2
B3
B4
产地
A1
运筹学运输问题解析

2. 典型的运输问题:
cij
a1 a2 …
am
A1
A2 … Am
B1
b1
B2
…
b2 … bn
Bn
求最小运费的运输方案
销地 产地 A1
B1
c11 c21
B2
c12 c22
…
Bn
c1n c2n
产量
a1
A2
… Am
a2
…
cm1 b1 b2
cm2 …
cmn bn
am
销量
销地 产地
B1
B2
…
Bn
产量
A1
ij
j =1, 2, …,n
xij 0
产销平衡问题为等式约束。 产销平衡问题中各产地产量之和与各销 售地点的销量之和相等。
二、运输问题数学模型的特点: 1. 运输问题一定有最优解;
2. 运输问题约束条件的系数矩阵:
x11 +x12+x13 x11
x12
xij 0
x21+x22+x23 + x21 +x22 x13 +x23
min Z cij xij
i 1 j 1
2
3
x
j 1
2
3
ij
ai
bj
i=1,2
x
i 1
ij
j =1, 2, 3
xij 0
典型运输问题的数学模型
min Z cij xij
i 1 j 1
m
n
x
x
i 1
n
j 1 m
ij
ai
bj
i=1,2,…,m
运输问题

运输问题1 运输问题提出运输问题是社会经济生活和军事活动中经常出现的优化问题。
在经济建设和国防建设中,经常遇到煤、钢铁、木材、粮食、武器装备等物资的调运问题。
如何制定调运方案,将物资运往指定地点,而且实现运输成本最小,即为运输问题。
运输问题是在1941年美国学者希奇柯克(Hitchcock )在研究生产组织和铁路运输方面的线性规划问题时提出的。
运输问题的提出,不仅可以求出物资的合理调运方案,其他类型的问题也都可以经过变换后转为运输问题来进行求解。
Hitchcock 运输问题如下:在m 个补给仓库处,分别有补给物品12,,,m a a a 个单位,这些物品要分发给n 个消费仓库,各消费仓库的需要量分别为12,,,n b b b 个单位。
从第i 个补给仓库到第j 个消费仓库运输一个单位的物品成本为ij c 元。
假设物品的总补给量等于总需求量,求使总运输成本最小的分配方案。
2 运输问题数学模型运输问题的一般提法: 有m 个生产地12,,,m A A A ,可供应某种物质,其产量分别为12,,,m a a a ,另有n 个销售地12,,,n B B B ,其销售量分别为12,,,n b b b ,从i A 到j B 运输单位物资的运价为ij c 。
问应如何组织调运,使调运方案的总运费最小。
建立数学模型:设从i A 到j B 的发运量为ij x ,则从i A 运出的物质总量应不大于i a ,ij x 应满足:1,1,2,,niji j xa i m =≤=∑ (1)同理运到j B 的物质总量应不大于j b ,ij x 应满足:1,1,2,,mijj i xb j n =≤=∑ (2)总运输成本为:11m nij ij i b Z c x ===∑∑(3)可建立运输问题的一般数学模型如下:11min mnij ij i b Z c x ===∑∑11..,1,2,,,1,2,,0&nij i j mijj i ij ij s t x a i m xb j n x x Z==≤=≤=≥∈∑∑(4)特别地,当11mni j i j a b ===∑∑时,称为产销平衡运输问题,也简称运输问题,其数学模型如下:1111min ..,1,2,,,1,2,,0&mnij iji b nij i j mijj i ij ij Z c x s t x a i m xb j nx x Z=========≥∈∑∑∑∑ (5)但在现实生活中多为产销不平衡运输问题,即产大于销:11m ni j i j a b ==≤∑∑,或销大于产:11mni ji j a b==≥∑∑。
运输问题的数学模型详细讲解,有案例+多种方法

m ( 3 1) x ij b j j 1,2, , n i 1 n s .t . x ij a i i 1,2, , m j 1 x 0 ij m n 其中,ai和bj满足: ai b j 称为产销平衡条件。
2、流向图
流向图:
在交通图上表示物资流向的图被称为流向 图。在图中每个发点吨数全部运完,每个 收点所需吨数均已满足。
2、流向图
发点A到收点B的 运输量,用括号 括起。
2、流向图
关于流向图的一些规定 箭头必须表示物资运输的方向 流量写在箭头的旁边,加小括号。 流向不能直接跨越路线上的收点、发点、 交叉点 任何一段弧上最多只能显示一条流向!即 同一段弧上的多条流向必须合并。 除端点外,任何点都可以流进和流出
2 4 6 4 B4
(2)
B5
4 2
8 B3
(8)
4
B2
(8) (1)
4 6 7 A1
3
5 8 A2
图 4-10
第三步:补上丢掉的边,检查有无迂回。 圈 B5B4B3A2 的 圈 长 =4+4+5+8=21, 内 圈长= 4+4+5=13>21/2,有迂回,所 以流向图不是最优流向图。需要调整。
约束方程式中共mn个变量,m+n个约束。
上述模型是一个线性规划问题。但是其结构很特殊, 特点如下: 1.变量多(mn个),但结构简单。
x11 x12 x1n x 21 x 22 x 2 n x m 1 x m 2 x mn 1 1 1 1 1 1 技术系数矩阵 A 1 1 1 1 1 1 1 1 1 1 1 1 m行 n行
数学建模---第四章-运输问题

p , p , , p i1 j1 i2 j2
ir jr
是线性相关的.
推论 1 若变量组对应的列向量组线性无关,则该变 量组一定不包含闭回路.
Go on
性质 1 的证明
Proof : 由直接计算可知
p p p p i1 j1
i1 j2
i2 j2
从理论上讲,运输问题也可用单纯形法来求解, 但是由于运输问题数学模型具有特殊的结构,存在一 种比单纯形法更简便的计算方法 —— 表上作业法, 用表上作业法来求解运输问题比用单纯形法可节约计 算时间与计算费用.但表上作业法的实质仍是单纯形法
§1 运输问题及其数学模型
§1 运输问题及其数学模型
一、运输问题的数学模型
A3 55
6
3
10 4
10
bj 5500 25 10 15
§2 运输问题的表上作业法 2、最小元素法 规则:优先安排单位运价最小的产地与销地之间的运输
任务. Note : 在某行(或列)填入最后一个数时,如果行和 列同时饱和,规定只划去该行(或列)
z 10 40 5 25 3 5 110
设某种物资共有 m 个产地 A1,A2,…,Am,各 产地的产量分别是a1,a2 ,…,am;有n 个销地 B1, B2,…,Bn ,各销地的销量分别为b1,b2,…,bn .
假定从产地Ai(i =1,2,…,m)向销地Bj(j =1, 2,…,n)运输单位物资的运价是cij,问怎样调运才能 使总运费最小?
j 1
i 1, 2, , m
m
xij bj
i 1
j 1, 2, , n
xij 0 i 1, 2, , m; j 1, 2, , n xij 0 i 1, 2, , m; j 1, 2, , n
运输问题数学建模

该系数矩阵中每列只有两个元素为1,其余的都为零。
2.m+n个约束中有一个是多余的(因为其间含有一个平衡关系 式 ) ai bj 所以R(A)=m+n-1,即解的mn个变量中基变量为m+n-1个。
二、 表上作业法
运输问题仍然是线性规划问题,可以用线性规划 法中的单纯形法来解决。但是:
1. 运输问题所涉及的变量多,造成单纯形表太大;
例3.1
某公司从三个产地A1、A2、A3 将物品运往四个
销地B1、B2、B3、B4,各产地的产量、各销地的销量和各产 地运往各销地每件物品的运费如下表3-4所示
销地 产地 A1 A2 A3 销量 B1 3 1 7 3 B2 11 9 4 6 B3 3 2 10 5 B4 10 8 5 6 产量 7 4 9 20(产销平 衡)
销量,这样的运输问题称为产销平衡的运输问题。 (2)
a b
i 1 i j 1
m
n
j
。即运输问题的总产量不等于总
销量,这样的运输问题的数学模型
若用xij表示从Ai到Bj的运量,那么在产销平衡的条件下, 要求得总运费最小的调运方案,数学模型为:
m in z cij x ij
教学要求:
1 .掌握运输问题的数学模型、系数矩阵特殊形 式 2 .掌握用西北角法、最小元素法求初始基可行 解 3 .掌握回路、位势法求解过程和表上作业法求 解运输问题过程
一、 运输问题及其数学模型
问题的提出:
在经济建设中,经常碰到物资调拨中的运输问题。 例如 煤、钢材、粮食、木材等物资,在全国都有若干 生产基地,分别将这些物资调到各消费基地去,应如 何制定调运方案,使总的运输费用最少?
A2
运输问题—数学模型及其解法

余保留在新的基础解中 退化较严重时,可能会出现多次迭代只有值为 0 的基变量在
转移。此时,一要耐心,二要正确选择出变量
踏石法迭代中需注意的问题:
1、错误地将分配表中基变量的解代入到运费表中 2、不能正确画闭合回路 3、初始解退化,未能补足基变量的个数。因此在位势法中 多次令某个 ui 或 vj 为 0; 4、在位势法中只能令一个 ui 或 vj 为 0;若不能求出全部 ui 和 vj ,说明基变量未选够数或未选对
3.3.3 关于退化问题
1、初始解退化。即所求初始基变量的个数少于 m+n1。必须
补足基变量的个数,否则不能正常解出 m+n个 ui 和 vj
所补基变量的值为 0 ,补充的原则:(1)尽量先选运费小的实变量;
(2)补充后不能有某个基变量独占一行一列
12
3.3.3 关于退化问题
2、迭代过程中出现退化
❖ 共有m+n1个基变量xij ,因此可得m+n1个等式 ui+vj=wij ❖ m+n1个等式只能解出 m+n1个 ui 和 vj ,而一共有m+n
个 ui 和 vj ,但可令任一个ui 或 vj =0,从而解出其它 m+n1个的值;这就是位势法 ❖ 令 zij= ui + vj ,其相当原问题xij的机会费用 ❖ 若对所有非基变量有 zij wij 0,即 ui + vj wij,表明当 前ui 和 vj 是对偶问题的可行解,由互补松弛定理可知当前 m+n1个基变量xij 是最优解,否则 ❖ 从 zij wij > 0 中找最大者,对应 xij 就是入变量
运输问题模型

运输问题摘要运输问题是运筹学的一个分支,是线性规划的特殊形式。
它研究的是如何在一个大宗物资调运中,制定出一个由若干个产地将物资根据已知的运输交通网运到各个销售地的方案,使得总运费最小。
物流是整个物流活动中核心,运输管理是物流活动的统筹规划和管理的一重要部分,对运输环节进行规划和优化,对提高物流活动的运行效率有重要意义。
本文通过对运输问题模型和求解方法的研究,在产销平衡的条件下,运用不同的软件Excel、Lingo、和Matlab等对运输问题进行求解,同时对内点法求解运输问题进行了研究,最终在计算机上得以实现。
通过研究得出结果如下:(1)三个软件Excel、Lingo和Matlab在求解简单的运输问题,其结果表上作业法求解的结果是一样的。
(2)在进行比较复杂的运输问题求解时,Excel出现可变单元格过多而无法进行继续求解,而Lingo和Matlab的求解结果相同,在时间耗费上差异不大,在内存占用上Matlab比Lingo的大。
(3)根据内点法的原理和方法进行研究,编写出对运输问题进行求解的代码,并实现求解。
关键词:运输问题表上作业法Excel Lingo Matlab 内点法Study on the Solution and Practice of the Model of LogisticsTransportion ProblemAbstractTransportion problem is a branch of Operations Research,it is a special form of linear programming. It researchs how to build a program that in a bulk material dispatching to delivered all these materials based on the known traffic network to all sales from a number of producer, bringing the total freight minimum. Logistics is the core of the logistics activities, transportation management is an important part of overall planning and management in the logistics activities. Planning and management the transport link is very important for improving the efficiency of logistics activities.Based on the study of the transportion model and its solution, under the conditions of production and marketing balance, used different software such as Excel, Lingo, Matlaband so on to solve the transportion problem, and also studied the solving of the transportion problem by using the internal point method, and eventually can be achieved in the computer. Through the results of the study are as follows:(1)Threesoftware, Excel, Lingo, and Matlab in solving a simple transportation problems, the result and result of suing Tabular method were the same.(2) When solved the more complex transportation problem, Excel appears too much variable to solve, however the results of using Lingo and Matlab is the same, and little difference in time spenting and in the memory footprint Matlab is larger than the Lingo .(3) Based on the study of the principles and methods of interior point method, to write a program to solve the transportion problem.Keywords: The Transportation Problems Tabular Method Excel LingoMatlab Interior Point Method目录第一章绪论......................................................................... 错误!未指定书签。
运输问题

B2 5 4 6 4 1
B3 33 7 5 3 2
B4 发量 4 5 8 4 1 4 6 3 13
hi 1 0 1
收点 发点 A1 A2 A3 收量 kj
B1 6 42 7 2 2
B2 5 4 6 4 1
B3 33 7 5 3 2
B4 发量 4 5 8 4 1 4 6 3 13
hi 1 0 1
收点 发点 A1 A2 A3 收量 kj
3
B 4 5 8 4 1
4
发 量 4 6 3 13
hi 1 1 2
收 量 kj
收 点 发 点 A1 A A
2 3
B 6 42 7 2 2
1
B 5 4 63 4 1
2
B 33 7 5 3 2
3
B 4 5 8 4 1
4
发 量 4 6 3 13
hi 1 1 2
收 量 kj
收 点 发 点 A1 A A
2 3
B 收 点 发 点 A1 6 A A
2 3 1
B 5 4 6
2
B 3 3 7 5
3
B 4 5 8
4
发 量 4 6 3
4 7 2
收 量
4
3
4
13
(2)再从最小元素开始(4) 即A1优先满足B4 1个单位, A1 已经满足,划去A1行,
B 收 点 发 点 A1 6 A A
2 3 1
B 5 4 6
2
B 3 3 7 5
2
c
12
…
… …
n
c
1n
产量
1
a
a
1
2
… m
销量
c
21
运筹学 第3章 运输问题
第三章运输问题在生产实际中,经常需要将某种物资从一些产地运往一些销地,因而存在如何调运使总的运费最小的问题。
这类问题一般可用线性规划模型来描述,当然可以用单纯形法求解。
但由于其模型结构特殊,学者们提供了更为简便和直观的解法—-表上作业法。
此外,有些线性规划问题从实际意义上看,并非运输问题,但其模型结构类似运输问题,也可以化作运输问题进行求解。
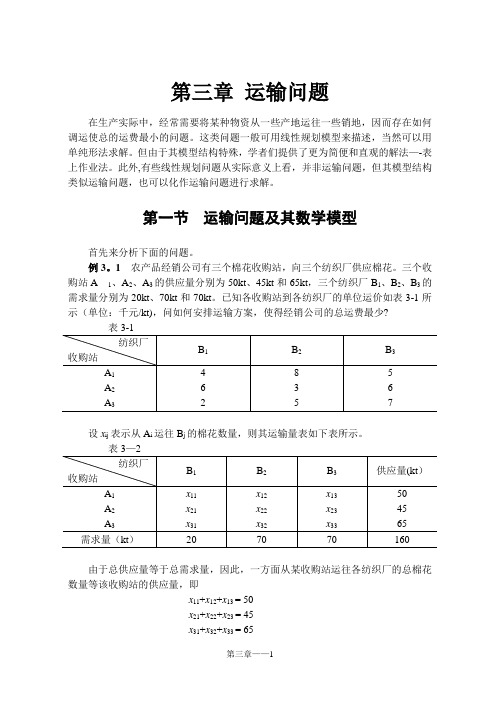
第一节运输问题及其数学模型首先来分析下面的问题。
例3。
1农产品经销公司有三个棉花收购站,向三个纺织厂供应棉花。
三个收购站A1、A2、A3的供应量分别为50kt、45kt和65kt,三个纺织厂B1、B2、B3的需求量分别为20kt、70kt和70kt。
已知各收购站到各纺织厂的单位运价如表3-1所示(单位:千元/kt),问如何安排运输方案,使得经销公司的总运费最少?设x ij表示从A i运往B j的棉花数量,则其运输量表如下表所示。
表3—2由于总供应量等于总需求量,因此,一方面从某收购站运往各纺织厂的总棉花数量等该收购站的供应量,即x11+x12+x13 = 50x21+x22+x23 = 45x31+x32+x33 = 65另一方面从各收购站运往某纺织厂的总棉花数量等该纺织厂的需要量,即x 11+x 21+x 31 = 20 x 12+x 22+x 32 = 70 x 13+x 23+x 33 = 70因此有该问题的数学模型为min f= 4x 11+8x 12+5x 13+6x 21+3x 22+6x 23+2x 31+5x 32+7x 33x 11+x 12+x 13 = 50 x 21+x 22+x 23 = 45 x 31+x 32+x 33 = 65 x 11+x 21+x 31 = 20 x 12+x 22+x 32 = 70 x 13+x 23+x 33 = 70x ij ≥0,i=1,2,3;j=1,2,3 生产实际中的一般的运输问题可用以下数学语言描述。
数学建模中优化模型之运输问题

A B C
d
e f 需量
70 40 80 × 40 × × 0 60 30 90 90 30 -20 -15 -65 25 0 50 20 100 60 50 × -50 × 60 50 0 20 20 70 20 × × -15 30 20 20 0 15 × 60 30 × × 90 100 20 15 0 × 90 × × × 90 90 120 120 120 运费——5550
14
4
5
2
5
7
7 9
6
8
9
13
10
6 6
u2=-2
-11
v1=10 v2=6
13
v4=0
u3=6
v3=4
单位费用变化:5-(10+6)=-11
对偶变量法(13)
1 6 1 8 2 5 3 7 2 5 3 3 4 u1=-4
14
4
5
2
5
7
7 9
6
8
9
13
10
6 6
v3=4
u2=-2
-11
v1=10
-3
14 8
9
13
10
6
6
u2=-2
6
v3=4
13
v4=0
u3=6
u2+v3=c23
u2=-2
对偶变量法(5)
1 6 1 8 2 5 3 v1 v2=6 7 2 5 3 3 u1 4 2 7 4
14 8
9
13
10
6
6
u2=-2
6
v3=4
13
v4=0
u3=6
u2+v2=c22
第三章 运输问题 — 数学模型及其解法

0 2 0
2 2 0 0
0 1 2 1
0
0 10
列 标 记
4 0 2 0
2 2 0 0
(0) 1 2 1
0 * 0
0 1
打
破 4
僵
局
(0) 2 0*
2 2 0 0
(0) 1 2 1
0 * 0*
0 1
逐 行
4
1 当第i个工人分配去做第j项任务 xij 0 当第i个工人未分配去做第j项任务
i, j 1,2, , m
• 运输问题是任务分配问题的松弛问题 • 任务分配问题不但是整数规划,而且是01规划 • 任务分配问题有2m个约束条件,但有且只有m个非零解,
是自然高度退化的 • 任务分配是两部图的匹配问题,有著名的匈牙利算法 下面介绍一种适合手算的算法(出自清华教科书)
mm
min f ( x) aij xij
i1 j1
m
xij
1
i 1,2, ,m
imj11xij 1 j 1,2, , m
xij 0,1
1
任务分配问题的数学模型
模型中:xij 为第 i 个工人分配去做第 j 项任务; aij 为第 i 个工人为完成第 j 项任务时的工时消耗; {aij}mm 称为效率矩阵
0 1 0
3 0 1
2 2 2
2 1 3
换
0 1 0
3 0 1
2 2 2
1
0 2
第二步:检查覆盖所有零元素一个未标记的零,对其加( )标记,将 ( )标记元素同行同列上其它的零打上*标记。若该行有二个以上 未标记的零,暂不标记,转下一行检查,直到所有行检查完;
第七章-运输问题

运产们费地单办得价到运新销 输的地量 综合表B1格:
B2
B3
产 量 (件)
A1
6
4 x11
6 x12
x13
200
A2 销 量 (件)
6
5 x21
5 x22
x23
300
150
150
200
500 500
•
min f = 6x11+ 4x12+ 6x13+ 6x21+ 5x22+ 5x23
s. t.
x11+ x12 + x13 = 200
法
销地
产地
B1
A1
3
A2
1
3
A3
7
销量
30
4 0,
x21
6 =x11200,
x22
=x013,x23
200 = 200。
A2
6
5 x21
5 x22
x23
300
销 量 (件)
150
150
200
500 500
•
§7.1 运输问题的模型
1.一般运输问题的线性规划模型
假设 A1,A2,… ,Am 表示某物资的 m 个产地; B1,B2,… ,Bn 表示某物资的 n 个销地;
•
例.喜庆食品公司有三个生产面包的分厂A1,A2,A3,
有§四个7.销2售运公司输B问1,题B的2,表B3上,B作4,业其法各分厂每日的产
量、各销售公司每日的销量以及各分厂到各销售公司的 单位运价如表所示,在表中产量与销量的单位为吨,运 价的单位为百元/吨。问该公司应如何调运产品在满足各 销点的需求量的前提下总运费最少?
