高一数学测试题A卷及答案
高一数学下学期(人教A版A卷)-(考试版)(范围:必修第二册第6、7、8章)

2022-2023学年高一下学期期中考前必刷卷数学(考试时间:120分钟试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:必修第二册第6、7、8章。
5.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,第1~8题只有一项符合题目要求,第9~12题有多项符合题目要求。
全部选对的得5分,选对但不全的得2分,有选错的得0分。
1.在ABC 中,点D 是线段BC (不包括端点)上的动点,若=+AB xAC y AD ,则()A .1x >B .1y >C .1x y +>D .1xy >2.欧拉公式i s co in s i x e x x +=(i )是由瑞士著名数学家欧拉发现的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里非常重要,被誉为“数学中的天桥”.根据欧拉公式可知,i 3e π表示的复数位于复平面中的()A .第一象限B .第二象限C .第三象限D .第四象限3.已知向量()()1,,,2a k b k →→==,若a →与b →方向相同,则k 等于()A .1B .C .D4.ABC 中,若1,2,30a c B ︒===,则ABC 的面积为()A .12B .2C .1D 5.设复数z 满足|2|1z i -=,在复平面内z 对应的点到原点距离的最大值是()A .1BC D .36.已知在锐角ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,π3A =,则222b c a +的取值范围是()A .5,34⎛⎤⎥⎝⎦B .(]0,3C .5,24⎛⎤ ⎥⎝⎦D .5,23⎛⎤ ⎥⎝⎦7.已知在ABC 中,2B A =,ACB ∠的平分线CD 把三角形分成面积比为4:3的两部分,则cos A =()A .3B .3C .13D .238.设O 为ABC 所在平面内一点,满足2730OA OB OC --=,则ABC 的面积与BOC 的面积的比值为()A .2.5B .3C .3.5D .49.已知复数122z i =-,则下列结论正确的有()A .1z z ⋅=B .2z z=C .31z =-D .2020122z i =-+10.下列命题中正确的是:()A .两个非零向量a ,b ,若a b a b -=+ ,则a 与b 共线且反向B .已知0c ≠ ,且a c b c ⋅=⋅ ,则a b=C .若()3,4OA =- ,()6,3OB =- ,()5,3OC m m =---,ABC ∠为锐角,则实数m 的取值范围是34m >-D .若非零a ,b 满足a b a b ==- ,则a 与a b +的夹角是30︒11.如图所示设,Ox Oy 是平面内相交成2πθθ⎛⎫≠ ⎪⎝⎭角的两条数轴,12,e e 分别是与x ,y 轴正方向同向的单位向量,则称平面坐标系xOy 为θ反射坐标系,若12OM xe ye =+,则把有序数对(),x y 叫做向量OM 的反射坐标,记为(),OM x y = .在23πθ=的反射坐标系中,()()12,21a b ==- ,,.则下列结论中,正确的是()A .()1,3a b -=-B .a =C .a b⊥D .a 在b 上的投影向量为714- 12.在南方不少地区,经常看到一种用木片、竹篾或苇蒿等材料制作的斗笠,用来遮阳或避雨,有一种外形为圆锥形的斗笠,称为“灯罩斗笠”,不同型号的斗笠大小经常用帽坡长(母线长)和帽底宽(底面圆直径长)两个指标进行衡量,现有一个“灯罩斗笠”,帽坡长20厘米,帽底宽关于此斗笠,下列说法正确的是()A .斗笠轴截面(过顶点和底面中心的截面图形)的顶角为120︒B .过斗笠顶点和斗笠侧面上任意两母线的截面三角形的最大面积为平方厘米C .若此斗笠顶点和底面圆上所有点都在同一个球上,则该球的表面积为1600π平方厘米二、填空题:本题共4小题,共2013.若点A (-2,0),B (3,4),C (2,a )共线,则a =________.14.在四边形ABCD 中,(1,2)AC = ,(4,2)BD =-,则该四边形的面积为________15.如图,在四面体A BCD -中,AC BD a ==,AC 与BD 所成的角为60°,M 、N 分别为AB 、CD 的中点,则线段MN 的长为______.16.如图,在ABC 中,已知2AB =,6AC =,60BAC ∠=︒,2BC BM =,3AC AN =,线段AM ,BN 相交于点P ,则MPN ∠的余弦值为___________.三、解答题:本题共6小题,共70分。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(60)

高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1.设某项试验成功的概率是失败的概率的2倍,用随机变量X描述1次试验的成功次数,则P(X=0)等于( )A.0B.12C.13D.232.若∣a⃗∣=1,∣b⃗⃗∣=2,且(a⃗+b⃗⃗)⊥a⃗,则a⃗与b⃗⃗的夹角θ=( )A.π3B.−π3C.2π3D.2π3或−π33.已知i为虚数单位,若复数z满足z(1−i)=1+i,则z=( )A.i B.−12i C.1D.124.在复平面内,复数z1=3−i,z2=−1+2i对应的两点间的距离为( )A.2B.3C.4D.55.甲、乙两名同学在高考前的5次模拟考中的数学成绩如茎叶图所示,记甲、乙两人的平均成绩分别为x,y,下列说法正确的是( )A.x<y,且乙比甲的成绩稳定B.x>y,且乙比甲的成绩稳定C.x<y,且甲比乙的成绩稳定D.x>y,且甲比乙的成绩稳定6.复数z(1−i)=i(i为虚数单位),则z的共轭复数在复平面上对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限7.设a⃗=(32,sinα),b⃗⃗=(cosα,13),且a⃗∥b⃗⃗,则锐角α为( )A.45∘B.30∘C.75∘D.60∘8.已知实数a∈[−3,3],则复数z=a+i2−i在复平面内对应的点位于第二象限的概率为( )A.512B.12C.712D.349. 下列叙述中,错误的一项为 ( ) A .棱柱中两个互相平行的平面一定是棱柱的底面 B .棱柱的各个侧面都是平行四边形 C .棱柱的两底面是全等的多边形 D .棱柱的面中,至少有两个面相互平行10. 在 △ABC 中,a =5,b =3,则 sinA:sinB 的值是 ( ) A . 53B . 35C . 37D . 57二、填空题(共6题) 11. 思考辨析 判断正误两条直线无公共点,则这两条直线平行.( )12. 已知非零向量 a ⃗,b ⃗⃗ 满足 ∣a ⃗∣=∣∣a ⃗−b ⃗⃗∣∣,则 (a ⃗−12b ⃗⃗)⋅b ⃗⃗= .13. 设两个非零向量 a ⃗ 与 b ⃗⃗ 不共线.若 ka ⃗+b ⃗⃗ 与 a ⃗+kb ⃗⃗ 共线,则 k = .14. 已知 (a −i )2=2i ,其中 i 是虚数单位,那么实数 a = .15. 若复数 z 满足 2z +z =3−2i ,其中 i 为虚数单位,则 z = .16. 已知 O 为 △ABC 内一点,OA ⃗⃗⃗⃗⃗⃗+2OB ⃗⃗⃗⃗⃗⃗+3OC ⃗⃗⃗⃗⃗⃗=0⃗⃗,则 S△ABC S △AOC= .三、解答题(共6题)17. 一个盒子里装有完全相同的十个小球,分别标上 1,2,3,⋯,10 这 10 个数字,现随机地抽取两个小球,如果: (1)小球是不放回的; (2)小球是有放回的.分别求两个小球上的数字为相邻整数的概率.18. 正六边形 ABCDEF 中,O 是其中心,设 AB ⃗⃗⃗⃗⃗⃗=m ⃗⃗⃗,AF ⃗⃗⃗⃗⃗⃗=n ⃗⃗,用 m ⃗⃗⃗,n ⃗⃗ 表示 AD ⃗⃗⃗⃗⃗⃗,BD ⃗⃗⃗⃗⃗⃗⃗.19. 如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上,并记组成该“钉”的四条线段的公共点为 O ,钉尖为 A i (i =1,2,3,4).(1) 设OA1=a(a>0),当A1,A2,A3在同一水平面内时,求OA1与平面A1A2A3所成角的大小(结果用反三角函数值表示).(2) 若该“钉”的三个端尖所确定的三角形的面积为3√2cm2,要用某种线型材料复制100枚这种“钉”(损耗忽略不计),共需要该种材料多少米?⃗⃗⃗⃗⃗⃗对应的复数是1+2i,向量20.复平面内有A,B,C三点,点A对应的复数是2+i,向量BA⃗⃗⃗⃗⃗⃗对应的复数是3−i,求点C在复平面内的坐标.BC21.已知过球面上三点A,B,C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,求球面面积与球的体积.22.定义:对于两个非零向量p⃗和q⃗,如果存在不全为零的常数α,β,使αp⃗+βq⃗=0⃗⃗,那么称p⃗和q⃗是线性相关的,否则称p⃗和q⃗是线性无关的.已知a⃗=3i⃗−4j⃗,a⃗+b⃗⃗=4i⃗−3j⃗,试判断a⃗与b⃗⃗的线性关系(相关还是无关),并证明你的结论.答案一、选择题(共10题)1. 【答案】C【知识点】事件的关系与运算2. 【答案】C【解析】因为(a⃗+b⃗⃗)⊥a⃗,所以(a⃗+b⃗⃗)⋅a⃗=a⃗2+a⃗⋅b⃗⃗=1+2cosθ=0,解得cosθ=−12,又θ∈[0,π],所以θ=2π3.【知识点】平面向量的数量积与垂直3. 【答案】A【解析】由z(1−i)=1+i,得z=1+i1−i =(1+i)2(1−i)(1+i)=2i2=i.【知识点】复数的乘除运算4. 【答案】D【解析】在复平面内,复数z1=3−i,z2=−1+2i对应的两点的坐标分别为(3,−1),(−1,2),则两点间的距离为∣z2−z1∣=√(−1−3)2+[2−(−1)]2=5.【知识点】复数的加减运算、复数的几何意义5. 【答案】A【解析】由题,x=15×(101+102+105+114+138)=112,y=15×(108+118+117+124+123)=118,所以x<y,由茎叶图可知,乙的成绩更集中,故乙比甲的成绩稳定.【知识点】样本数据的数字特征6. 【答案】C【解析】因为z=i1−i =i(1+i)(1−i)(1+i)=−1+i2=−12+12i,所以z=−12−12i,对应点为(−12,−12),在第三象限.【知识点】复数的几何意义、复数的乘除运算7. 【答案】A【知识点】平面向量的数乘及其几何意义8. 【答案】A【解析】 z =a+i2−i =(a+i )(2+i )(2−i )(2+i )=2a+(a+2)i+i 24−i 2=2a−1+(a+2)i5,由于点位于第二象限, 所以 {2a −1<0,a +z >0,则 −2<a <12, P =∣∣12−(−2)∣∣∣3−(−3)∣=512.【知识点】复数的乘除运算、复数的几何意义9. 【答案】A【解析】在A 中,棱柱中两个互相平行的平面不一定是棱柱的底面, 例如正六棱柱的相对侧面互相平行,故A 错误;在B 中,由棱柱的定义知棱柱的各个侧面都是平行四边形,故B 正确; 在C 中,由棱柱的定义知棱柱的两底面是互相平行且全等的多边形,故C 正确; 在D 中,棱柱的定义是,有两个面互相平行,其余各面都是四边形, 相邻的公共边互相平行,有这些面围成的几何体是棱柱,由此得到D 正确. 【知识点】棱柱的结构特征10. 【答案】A【解析】根据正弦定理,得 sinAsinB =ab =53. 【知识点】正弦定理二、填空题(共6题) 11. 【答案】 ×【知识点】直线与直线的位置关系12. 【答案】 0【知识点】平面向量的数量积与垂直13. 【答案】 ±1【解析】因为 ka ⃗+b ⃗⃗ 与 a ⃗+kb⃗⃗ 共线,所以存在实数 λ,使 ka ⃗+b ⃗⃗=λ(a ⃗+kb ⃗⃗),即 (k −λ)a ⃗=(λk −1)b⃗⃗. 又 a ⃗,b ⃗⃗ 是两个不共线的非零向量,所以 k −λ=λk −1=0. 消去 λ,得 k 2−1=0,所以 k =±1. 【知识点】平面向量的数乘及其几何意义14. 【答案】 −1【解析】 a 2−2ai −1=a 2−1−2ai =2i ,a =−1. 【知识点】复数的乘除运算15. 【答案】 1−2i【解析】设 z =a +bi (a,b ∈R ), 则 z =a −bi , 因为 2z +z =3−2i ,所以 2a +2bi +a −bi =3−2i , 所以 3a =3,b =−2, 解得 a =1,b =−2, 所以 z =1−2i .【知识点】复数的加减运算16. 【答案】 3【解析】如图所示,取 BC 的中点 D ,AC 的中点 E ,连接 OD ,OE , 则OA ⃗⃗⃗⃗⃗⃗+2OB ⃗⃗⃗⃗⃗⃗+3OC ⃗⃗⃗⃗⃗⃗=(OA⃗⃗⃗⃗⃗⃗+OC ⃗⃗⃗⃗⃗⃗)+2(OB ⃗⃗⃗⃗⃗⃗+OC ⃗⃗⃗⃗⃗⃗)=2OE⃗⃗⃗⃗⃗⃗+4OD ⃗⃗⃗⃗⃗⃗⃗=0⃗⃗,所以 OE⃗⃗⃗⃗⃗⃗=−2OD ⃗⃗⃗⃗⃗⃗⃗, 所以 D ,O ,E 三点共线, 所以 DE ⃗⃗⃗⃗⃗⃗=32OE ⃗⃗⃗⃗⃗⃗, 又 DE 为 △ABC 的中位线,BA ⃗⃗⃗⃗⃗⃗=2DE ⃗⃗⃗⃗⃗⃗, 所以 BA⃗⃗⃗⃗⃗⃗=3OE ⃗⃗⃗⃗⃗⃗. 设在 △ABC 和 △AOC 中,AC 边上的高分别为 ℎ1,ℎ2,则 ℎ1=3ℎ2, 所以 S△ABC S △AOC=3.【知识点】平面向量的数乘及其几何意义三、解答题(共6题)17. 【答案】从十个小球中随机抽取两个小球,记事件 A 为“两个小球上的数字为相邻整数”,其所有可能的结果为 (1,2),(2,3),(3,4),(4,5),(5,6),(6,7),(7,8),(8,9),(9,10),(2,1),(3,2),(4,3),(5,4),(6,5),(7,6),(8,7),(9,8),(10,9),共 18 种.(1)如果小球是不放回的,按抽取顺序记录结果 (x,y ),则 x 有 10 种可能,y 有 9 种可能,共有 90 种可能的结果, 因此,事件 A 的概率是 1890=15.(2)如果小球是有放回的,按抽取顺序记录结果 (x,y ),则 x 有 10 种可能,y 有 10 种可能,共有 100 种可能的结果, 因此,事件 A 的概率是 18100=950. 【知识点】古典概型18. 【答案】 AD ⃗⃗⃗⃗⃗⃗=2AO ⃗⃗⃗⃗⃗⃗=2(m ⃗⃗⃗+n ⃗⃗),BD ⃗⃗⃗⃗⃗⃗⃗=BA ⃗⃗⃗⃗⃗⃗+AD ⃗⃗⃗⃗⃗⃗=m ⃗⃗⃗+2n ⃗⃗.【知识点】平面向量的数乘及其几何意义19. 【答案】(1) 根据题意,可知组成该种钉的四条线段长必相等,且两两所成的角相等,A 1,A 2,A 3,A 4 两两连接后得到的四面体 A 1A 2A 3A 4 为正四面体,延长 A 4O 交平面 A 1A 2A 3 于 B ,则 A 4B ⊥平面A 1A 2A 3,连接 A 1B ,则 A 1B 是 OA 1 在平面 A 1A 2A 3 上的射影, 所以 ∠OA 1B 即为 OA 1 与平面 A 1A 2A 3 所成角. 设 A 1A 4=l , 则 A 1B =√33l . 在 Rt △A 4A 1B 中,A 1A 42=A 1B 2+A 4B 2,即 l 2=(√33l)2+(a +√a 2−(√33l)2)2,所以 l =2√63a , 故 A 1B =√33×2√63a =2√23a ,cos∠OA 1B =A 1B OA 1=2√23(其中 0<∠OA 1B <π2),所以 ∠OA 1B =arccos2√23, 故 OA 1 与平面 A 1A 2A 3 所成角的大小为 arccos 2√23.(2) 12A 1A 22⋅√32=3√2,根据(1)可得 A 1A 2=2√63a ,所以 a =√2724cm ,1100⋅100⋅(4a )=4a =2√2164m . 答:复制 100 枚这种“钉”,共需材料 2√2164米.【知识点】棱锥的结构特征、线面角20. 【答案】因为 AC⃗⃗⃗⃗⃗⃗=BC ⃗⃗⃗⃗⃗⃗−BA ⃗⃗⃗⃗⃗⃗, 所以 AC⃗⃗⃗⃗⃗⃗ 对应的复数为 (3−i )−(1+2i )=2−3i , 设 C (x,y ),则 (x +yi )−(2+i )=2−3i ,所以 x +yi =(2+i )+(2−3i )=4−2i , 故 x =4,y =−2.所以点 C 在复平面内的坐标为 (4,−2). 【知识点】复数的加减运算、复数的几何意义21. 【答案】如图设球心为 O ,球的半径为 R ,作 OO 1⊥平面ABC 于点 O 1,则 OA =OB =OC =R ,且 O 1 是 △ABC 的外心,设 M 是 AB 的中点, 因为 AC =BC , 所以 O 1∈CM , 所以 O 1M ⊥AB , 设 O 1M =x ,则 O 1A =√22+x 2,O 1C =CM −O 1M =√62−22−x . 又 O 1A =O 1C ,所以 √22+x 2=√62−22−x ,解得 x =7√24. 所以 O 1A =O 1B =O 1C =9√24.在 Rt △OO 1A 中,O 1O =R 2,∠OO 1A =90∘,OA =R , 由勾股定理得 (R 2)2+(9√24)2=R 2,解得 R =3√62, 所以 S 球=4πR 2=54π,V 球=43πR 3=27√6π. 【知识点】球的表面积与体积22. 【答案】线性无关.对照定义,可求得 α=β=0.【知识点】平面向量的数乘及其几何意义。
人教A版高一数学必修第一册全册复习训练题卷含答案解析(48)

人教A 版高一数学必修第一册全册复习训练题卷(共30题)一、选择题(共10题)1. 已知 a =1.70.3,b =0.31.7,c =log 0.31.7,则 a ,b ,c 的大小关系为 ( ) A . a <b <c B . c <b <a C . c <a <b D . b <a <c2. 已知 m ∈R ,“函数 y =2x +m −1 有零点”是“函数 y =log m x 在 (0,+∞) 上为减函数”的 ( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件3. 已知 sin (α+β)=14,sin (α−β)=13,则 tanα:tanβ= ( )A . −17B . 17C . −7D . 74. 根据统计,一名工人组装第 x 件某产品所用的时间(单位:分钟)为 f (x )=√x x <A√Ax ≥A (A ,c为常数),已知工人组装第 4 件产品用时 30 min ,组装第 A 件产品用时 15 min ,那么 c 和 A 的值分别是 ( ) A . 75,25 B . 75,16 C . 60,25 D . 60,165. 已知函数 f (x )={ln (x +1)+m,x ≥0ax −b +1,x <0(m <−1),对于任意 s ∈R ,且 s ≠0,均存在唯一实数 t ,使得 f (s )=f (t ),且 s ≠t ,若关于 x 的方程 ∣f (x )∣=f (m2) 有 4 个不相等的实数根,则 a 的取值范围是 ( ) A . (−4,−2) B . (−1,0)C . (−2,−1)D . (−4,−1)∪(−1,0)6. 已知 a >0 且 a ≠1,下列说法中正确的是 ( ) ①若 M =N ,则 log a M =log a N ; ②若 log a M =log a N ,则 M =N ; ③若 log a M 2=log a N 2,则 M =N ; ④若 M =N ,则 log a M 2=log a N 2. A .①③B .②④C .②D .①②③④7.定义在(−1,1]上的函数f(x)满足f(x)+1=1f(x+1),当x∈[0,1]时,f(x)=x,若函数g(x)=∣∣f(x)−12∣∣−mx−m+1在(−1,1]内恰有3个零点,则实数m的取值范围是( )A.(32,+∞)B.(32,258)C.(32,2516)D.(23,34)8.实数α,β为方程x2−2mx+m+6=0的两根,则(α−1)2+(β−1)2的最小值为( )A.8B.14C.−14D.−2549.若a>b>0,c<d<0,则一定有( )A.ac −bd>0B.ac−bd<0C.ad>bcD.ad<bc10.一个半径为R的扇形,它的周长是4R,则这个扇形所含弓形的面积为( )A.12R2B.12R2Ssin1cos1C.12(1−sin1cos1)R2D.(1−sin1cos1)R2二、填空题(共10题)11.已知△ABC中,sin(A+B)=45,cosB=−23,则sinB=,cosA=.12.函数y=lg(x2+2x−a)的定义域为R,则实数a的取值范围是.13.已知函数y=f(x)是定义在R上的以3为周期的奇函数,且f(2)=0,则方程f(x)=0在区间(0,6)内零点的个数的最小值是个.14.一个驾驶员喝了少量酒后,血液中的酒精含量迅速上升到0.3mg/mL,在停止喝酒后,血液中的酒精含量以每小时25%的速度减少.为了保障交通安全,规定驾驶员血液中的酒精含量不得超过0.09mg/mL,那么这个驾驶员至少要经过小时才能开车.(精确到1小时,参考数据lg2≈0.30,lg3≈0.48)15.将函数y=√4+6x−x2−2(x∈[0,6])的图象绕坐标原点逆时针方向旋转角θ(0≤θ≤α),得到曲线C.若对于每一个旋转角θ,曲线C都是一个函数的图象,则tanα的最大值为.16.设集合A为含有三个元素的集合,集合B={z∣z=x+y,x,y∈A,x≠y},若B={log 26,log 210,log 215},则集合 A = .17. 已知 p:∣x −4∣>6,q:x 2−2x +1−a 2>0(a >0),若 p 是 q 的充分不必要条件,则实数 a的取值范围为 .18. 已知 α 为第二象限角,sinα+cosα=12,则 cos2α= .19. 定义在 R 上的函数 f (x ) 满足 f (x +2)=f (x )−2,当 x ∈(0,2] 时,f (x )={x 2−x −6,x ∈(0,1]−2x−1−5,x ∈(1,2],若 x ∈(−6,−4] 时,关于 x 的方程 af (x )−a 2+2=0(a >0) 有解,则实数 a 的取值范围是 .20. 已知函数 f (x )={x +2x −3,x ≥1lg (x 2+1),x <1,则 f(f (−3))= ,f (x ) 的最小值是 .三、解答题(共10题)21. 已知一扇形的周长为 40 cm ,当它的半径和圆心角取何值时,能使扇形的面积最大,最大面积是多少?22. 已知实数 a ,b 是常数,函数 f (x )=(√1+x +√1−x +a)(√1−x 2+b).(1) 求函数 f (x ) 的定义域,判断函数的奇偶性,并说明理由;(2) 若 a =−3,b =1,设 t =√1+x +√1−x ,记 t 的取值组成的集合为 D ,则函数 f (x )的值域与函数 g (t )=12(t 3−3t 2)(t ∈D ) 的值域相同.试解决下列问题:(i )求集合 D ;(ii )研究函数 g (t )=12(t 3−3t 2) 在定义域 D 上是否具有单调性?若有,请用函数单调性定义加以证明:若没有,请说明理由.并利用你的研究结果进一步求出函数 f (x ) 的最小值.23. 对于定义域为 R 的函数 g (x ),若存在正常数 T ,使得 cosg (x ) 是以 T 为周期的函数,则称g (x ) 为余弦周期函数,且称 T 为其余弦周期.已知 f (x ) 是以 T 为余弦周期的余弦周期函数,其值域为 R .设 f (x ) 单调递增,f (0)=0,f (T )=4π. (1) 验证 g (x )=x +sin x3 是以 6π 为周期的余弦周期函数;(2) 设 a <b ,证明对任意 c ∈[f (a ),f (b )],存在 x 0∈[a,b ],使得 f (x 0)=c ;(3) 证明:“u 0 为方程 cosf (x )=1 在 [0,T ] 上的解,”的充要条件是“u 0+T 为方程 cosf (x )=1 在区间 [T,2T ] 上的解”,并证明对任意 x ∈[0,T ],都有 f (x +T )=f (x )+f (T ).24. 已知函数 f (x )=(sinx +cosx )2+2cos 2x −1.(1) 求 f (x ) 的最小正周期;(2) 求 f (x ) 在 [0,π2] 上的单调区间.25. 已知函数 f (x )=a +b x (b >0,b ≠1) 的图象过点 (1,4) 和点 (2,16).(1) 求 f (x ) 的表达式; (2) 解不等式 f (x )>(12)3−x2;(3) 当 x ∈(−3,4] 时,求函数 g (x )=log 2f (x )+x 2−6 的值域.26. 已知函数 f (x ) 的定义域为 D ,若对任意的 x 1∈D ,都存在 x 2∈D ,满足 f (x 1)=1f (x 2),则称函数 f (x ) 为“L 函数”.(1) 判断函数 f (x )=sinx +32,x ∈R 是否为“L 函数”,并说明理由;(2) 已知“L 函数”f (x ) 是定义在 [a,b ] 上的严格增函数,且 f (a )>0,f (b )>0,求证:f (a )⋅f (b )=1.27. 记函数 f (x ) 的定义域为 D ,如果存在实数 a ,b 使得 f (a −x )+f (a +x )=b 对任意满足a −x ∈D 且 a +x ∈D 的 x 恒成立,则称 f (x ) 为 Ψ 函数. (1) 设函数 f (x )=1x −1,试判断 f (x ) 是否为 Ψ 函数,并说明理由; (2) 设函数 g (x )=12x +t ,其中常数 t ≠0,证明 g (x ) 是 Ψ 函数;(3) 若 ℎ(x ) 是定义在 R 上的 Ψ 函数,且函数 ℎ(x ) 的图象关于直线 x =m (m 为常数)对称,试判断 ℎ(x ) 是否为周期函数?并证明你的结论.28. 已知函数 f (x ) 和 g (x ) 的图象关于原点对称,且 f (x )=x 2+2x .(1) 求函数 g (x ) 的解析式;(2) 若 ℎ(x )=g (x )−λf (x )+1 在区间 [−1,1] 上是增函数,求实数 λ 的取值范围.29. 解答题.(1) 已知 cosα=17,cos (α+β)=−1114,α,β 都是锐角,求 cosβ 的值;(2) 已知 π2<β<α<34π,cos (α−β)=1213,sin (α+β)=−35,sin2α.30.用五点法作出下列函数在[−2π,0]上的图象.(1) y=1−sinx;(2) y=sin(π+x)−1.答案一、选择题(共10题) 1. 【答案】B【知识点】指数函数及其性质、对数函数及其性质2. 【答案】B【解析】若函数 y =f (x )=2x +m −1 有零点,则 f (0)=1+m −1=m <1, 当 m ≤0 时,函数 y =log m x 在 (0,+∞) 上为减函数不成立,即充分性不成立,若 y =log m x 在 (0,+∞) 上为减函数,则 0<m <1,此时函数 y =2x +m −1 有零点成立,即必要性成立,故“函数 y =2x +m −1 有零点”是“函数 y =log m x 在 (0,+∞) 上为减函数”的必要不充分条件. 【知识点】指数函数及其性质、充分条件与必要条件、对数函数及其性质3. 【答案】C【解析】 sin (α+β)=sinαcosβ+cosαsinβ=14,sin (α−β)=sinαcosβ−cosαsinβ=13, 所以 sinαcosβ=724,cosαsinβ=−124,所以 tanα:tanβ=sinαcosβcosαsinβ=−7. 【知识点】两角和与差的正切4. 【答案】D【知识点】函数的模型及其实际应用5. 【答案】A【解析】由题意可知 f (x ) 在 [0,+∞) 上单调递增,值域为 [m,+∞),因为对于任意 s ∈R ,且 s ≠0,均存在唯一实数 t ,使得 f (s )=f (t ),且 s ≠t , 所以 f (x ) 在 (−∞,0) 上是减函数,值域为 (m,+∞), 所以 a <0,且 −b +1=m ,即 b =1−m . 因为 ∣f (x )∣=f (m2) 有 4 个不相等的实数根,所以 0<f (m2)<−m ,又 m <−1,所以 0<am 2<−m ,即 0<(a2+1)m <−m ,所以 −4<a <−2,所以则 a 的取值范围是 (−4,−2).【知识点】对数函数及其性质、函数的零点分布6. 【答案】C【解析】对于①,当 M =N ≤0 时,log a M ,log a N 都没有意义,故不成立; 对于②,log a M =log a N ,则必有 M >0,N >0,M =N ,故成立;对于③,当 M ,N 互为相反数且不为 0 时,也有 log a M 2=log a N 2,但此时 M ≠N ,故不成立; 对于④,当 M =N =0 时,log a M 2,log a N 2 都没有意义,故不成立. 综上,只有②正确. 【知识点】对数的概念与运算7. 【答案】C【解析】当 x ∈(−1,0) 时,x +1∈(0,1),f (x )=1f (x+1)−1=1x+1−1,若函数 g (x )=∣∣f (x )−12∣∣−mx −m +1 在 (−1,1] 内恰有 3 个零点,即方程 ∣∣f (x )−12∣∣−mx −m +1=0 在 (−1,1] 内恰有 3 个根,也就是函数 y =∣∣f (x )−12∣∣ 与 y =mx +m −1 的图象有三个不同交点,作出函数图象如图:由图可知,过点 (−1,−1) 与点 (−13,0) 的直线的斜率为 32;设过点 (−1,1),且与曲线 y =1x+1−1−12=−3x−12(x+1) 相切的切点为 (x 0,y 0), 则 yʹ∣x=x 0=−1(x 0+1)2=y 0−1x0−(−1), 又因为 y 0=−3x 0−12(x 0+1),解得 {x 0=−15,y 0=−14,则切点为 (−15,−14).所以切线的斜率为 k =1+14−1−(−15)=−2516,由对称性可知,过点 (−1,−1) 与曲线 ∣∣f (x )−12∣∣ 在 (−1,0) 上相切的切线的斜率为 2516.所以使函数 y =∣∣f (x )−12∣∣与 y =mx +m −1 的图象有三个不同交点的 m 的取值范围为(32,2516).【知识点】函数的零点分布、利用导数求函数的切线方程8. 【答案】A【解析】因为 Δ=(2m )2−4(m +6)≥0, 所以 m 2−m −6≥0, 所以 m ≥3 或 m ≤−2.而(α−1)2+(β−1)2=α2+β2−2(α+β)+2=(α+β)2−2αβ−2(α+β)+2=(2m )2−2(m +6)−2(2m )+2=4m 2−6m −10=4(m −34)2−494,因为 m ≥3,或 m ≤−2,所以当 m =3 时,(α−1)2+(β−1)2 的最小值为 8,故选A . 【知识点】函数的最大(小)值9. 【答案】D【解析】因为 c <d <0,所以 0<−d <−c , 又 0<b <a ,所以 −bd <−ac ,即 bd >ac , 又因为 cd >0,所以 bdcd >accd ,即 bc >ad . 【知识点】不等式的性质10. 【答案】D【解析】 l =4R −2R =2R ,α=lR =2R R=2,可得:S 扇形=12lR =12×2R ×R =R 2,可得:S 三角形=12×2Rsin1×Rcos1=sin1⋅cos1⋅R 2,可得:S弓形=S扇形−S三角形=R2−sin1⋅cos1⋅R2 =(1−sin1cos1)R2.【知识点】弧度制二、填空题(共10题)11. 【答案】√53;6+4√515【知识点】两角和与差的余弦12. 【答案】a<−1【知识点】函数的定义域的概念与求法、对数函数及其性质13. 【答案】7【知识点】函数的零点分布、函数的周期性14. 【答案】5【解析】设经过n小时后才能开车,由题意得0.3(1−0.25)n≤0.09,所以(34)n≤0.3,所以nlg34≤lg310<0,所以n≥lg3−1lg3−2lg2=0.48−10.48−0.6=133,解得n≥133,故至少经过5小时才能开车.故答案为:5.【知识点】函数模型的综合应用15. 【答案】23【解析】将函数变形为方程,可得(x−3)2+(y+2)2=13,x∈[0,6],y≥0,其图象如图所示.过点O作该图象所在圆M的切线OA,将该函数的图象绕原点逆时针旋转时,其最大的旋转角为∠AOy,此时曲线C都是一个函数的图象,因为k OA=−1k OM =32,所以tan∠AOy=23.【知识点】函数的相关概念16. 【答案】 {1,log 23,log 25}【解析】设 A ={a,b,c }(a <b <c ),则 {a +b =log 26,b +c =log 215,c +a =log 210,所以 a +b +c =log 230,所以 a =1,b =log 23,c =log 25, 所以 A ={1,log 23,log 25}. 【知识点】元素和集合的关系17. 【答案】 0<a ≤3【知识点】充分条件与必要条件18. 【答案】 −√74【解析】因为 sinα+cosα=12,所以 1+2sinαcosα=14,所以 2sinαcosα=−34,则 (cosα−sinα)2=1−2sinαcosα=74. 又因为 α 为第二象限角,所以 cosα<0,sinα>0, 则 cosα−sinα=−√72,所以cos2α=cos 2α−sin 2α=(cosα+sinα)(cosα+sinα)=12×(−√72)=−√74. 【知识点】二倍角公式19. 【答案】 1≤a ≤√2【解析】因为函数 f (x ) 满足 f (x +2)=f (x )−2,所以若 x ∈(−6,−4] 时,则 x +2∈(−4,−2],x +4∈(−2,0], 若 x +6∈(0,2],即若 x ∈(−6,−5] 时, 则 x +2∈(−4,−3],x +4∈(−2,−1], 若 x +6∈(0,1],则f (x )=2+f (x +2)=4+f (x +4)=6+f (x +6)=6+(x +6)2−(x +6)−6=x 2+11x +30,若 x ∈(−5,−4] 时,则 x +2∈(−3,−2],x +4∈(−1,0], 若 x +6∈(1,2],则 f (x )=2+f (x +2)=4+f (x +4)=6+f (x +6)=6−2x+6−1−5=1−2x+5,由 af (x )−a 2+2=0(a >0) 得 af (x )=a 2−2(a >0), 即 f (x )=a −2a (a >0).作出函数 f (x ) 在 x ∈(−6,−4] 的图象如图. 在函数的值域为 −1≤f (x )≤0, 由 −1≤a −2a≤0,得 {a −2a ≥−1,a −2a ≤0,即 {a 2+a −2≥0,a 2−2≤0, 即 {a ≥1 或 a ≤−2,−√2≤a ≤√2,因为 a >0,所以 1≤a ≤√2.【知识点】函数的零点分布20. 【答案】 0 ; 2√2−3【解析】因为 f (−3)=lg [(−3)2+1]=lg10=1,所以 f(f (−3))=f (1)=1+2−3=0.当x ≥1 时,x +2x −3≥2√x ⋅2x −3=2√2−3,当且仅当 x =2x ,即 x =√2 时等号成立,此时 f (x )min =2√2−3<0;当 x <1 时,lg (x 2+1)≥lg (02+1)=0,此时 f (x )min =0.所以f(x)的最小值为2√2−3.【知识点】函数的最大(小)值、分段函数三、解答题(共10题)21. 【答案】设扇形的圆心角为θ(0<θ<2π),半径为r,弧长为l,面积为S,则l+2r=40,所以l=40−2r.S=12lr=12(40−2r)r=20r−r2=−(r−10)2+100.所以当r=10cm时,扇形的面积最大,最大值为100cm2,此时θ=lr =40−2×1010=2.【知识点】弧度制22. 【答案】(1) 因为实数a,b是常数,函数f(x)=(√1+x+√1−x+a)(√1−x2+b),所以由{1+x≥0,1−x≥0,1−x2≥0.解得−1≤x≤1.所以函数的定义域是[−1,1].对于任意x∈[−1,1],有−x∈[−1,1],且f(−x)=(√1+(−x)+√1−(−x)+a)(√1−(−x)2+b)=(√1−x+√1+x+a)(√1−x2+b)=f(x),即f(−x)=f(x)对x∈[−1,1]都成立.(又f(x)不恒为零)所以,函数f(x)是偶函数.(该函数是偶函数不是奇函数也可以)(2) 因为a=−3,b=1,所以f(x)=(√1+x+√1−x−3)(√1−x2+1).设t=√1+x+√1−x(−1≤x≤1),则t2=2+2√1−x2.所以0≤√1−x2≤1,2≤t2≤4(t≥0),即√2≤t≤2.所以D=[√2,2].于是,g(t)=12(t3−3t2)的定义域为D=[√2,2].对于任意的t1,t2∈D,且t1<t2,有g(t1)−g(t2)=12[t13−3t12−(t23−3t22)]=12[(t1−t2)(t12+t1t2+t22)−3(t1−t2)(t1+t2)]=12(t1−t2)[(t12−2t1)+(t22−2t2)+(12t1t2−t1)+(12t1t2−t2)]=12(t1−t2)[t1(t1−2)+t2(t2−2)+12t1(t2−2)+12t2(t1−2)].又t1>0,t2>0,t1−t2<0,且t1−2≤0,t2−2≤0(这里二者的等号不能同时成立),所以12(t1−t2)[t1(t1−2)+t2(t2−2)+12t1(t2−2)+12t2(t1−2)]>0,即g(t1)−g(t2)>0,g(t1)>g(t2).所以函数g(t)在D上是减函数.所以(g(t))min =g(2)=12×(23−3×22)=−2.又因为函数f(x)的值域与函数g(t)=12(t3−3t2)的值域相同,所以函数f(x)的最小值为−2.【知识点】函数的值域的概念与求法、函数的奇偶性23. 【答案】(1) g(x)=x+sin x3,所以cosg(x+6π)=cos(x+6π+sin x+6π3)=cos(x+sin x3)=cosg(x),所以g(x)是以6π为周期的余弦周期函数.(2) 因为f(x)的值域为R;所以存在x0,使f(x0)=c;又c∈[f(a),f(b)],所以f(a)≤f(x0)≤f(b),而f(x)为增函数;所以a≤x0≤b;即存在x0∈[a,b],使f(x0)=c;(3) 若u0+T为方程cosf(x)=1在区间[T,2T]上的解;则:cosf(u0+T)=1,T≤u0+T≤2T;所以cosf(u0)=1,且0≤u0≤T;所以u0为方程cosf(x)=1在[0,T]上的解;所以“u0为方程cosf(x)=1在[0,T]上得解”的充分条件是“u0+T为方程cosf(x)=1在区间[T,2T]上的解”;下面证明对任意x∈[0,T],都有f(x+T)=f(x)+f(T):①当x=0时,f(0)=0,所以显然成立;②当x=T时,cosf(2T)=cosf(T)=1;所以f(2T)=2k1π,(k1∈Z),f(T)=4π,且2k1π>4π,所以k1>2;(1)若k1=3,f(2T)=6π,由(2)知存在x0∈(0,T),使f(x0)=2π;cosf(x0+T)=cosf(x0)=1⇒f(x0+T)=2k2π,k2∈Z;所以f(T)<f(x0+T)<f(2T);所以4π<2k2π<6π;所以2<k2<3,无解;(2)若k1≥5,f(2T)≥10π,则存在T<x1<x2<2T,使得f(x1)=6π,f(x2)=8π;则T,x1,x2,2T为cosf(x)=1在[T,2T]上的4个解;但方程cosf(x)=1在[0,2T]上只有f(x)=0,2π,4π,3个解,矛盾;(3)当k1=4时,f(2T)=8π=f(T)+f(T),结论成立;③当x∈(0,T)时,f(x)∈(0,4π),考查方程cosf(x)=c在(0,T)上的解;设其解为f(x1),f(x2),⋯,f(x n),(x1<x2<⋯<x n);则f(x1+T),f(x2+T),⋯,f(x n+T)为方程cosf(x)=c在(T,2T)上的解;又f(x+T)∈(4π,8π);而f(x1)+4π,f(x2)+4π,⋯,f(x n)+4π∈(4π,8π)为方程cosf(x)=c在(T,2T)上的解;所以f(x i+T)=f(x i)+4π=f(x i)+f(T);所以综上对任意x∈[0,T],都有f(x+T)=f(x)+f(T).【知识点】Asin(ωx+ψ)形式函数的性质、二倍角公式24. 【答案】(1) 由已知得,f(x)=sin2x+cos2x+1=√2sin(2x+π4)+1.函数的最小正周期T=2π2=π.(2) 由2kπ−π2≤2x+π4≤2kπ+π2(k∈Z)得,kπ−3π8≤x≤kπ+π8(k∈Z),又x∈[0,π2],所以x∈[0,π8],所以f(x)的单调递增区间为[0,π8],由2kπ+π2−≤2x+π4≤2kπ+3π2(k∈Z)得,kπ+π8≤x≤kπ+5π8(k∈Z),又x∈[0,π2],所以x∈[π8,π2 ],所以f(x)的单调递减区间为[π8,π2 ].【知识点】Asin(ωx+ψ)形式函数的性质25. 【答案】(1) 由题意知 {4=a +b,16=a +b 2,解得 {a =0,b =4 或 {a =7,b =−3(舍去), 所以 f (x )=4x . (2) f (x )>(12)3−x2,所以 4x>(12)3−x2,所以 22x >2x 2−3, 所以 2x >x 2−3, 解得 −1<x <3,所以不等式的解集为 (−1,3). (3) 因为g (x )=log 2f (x )+x 2−6=log 24x +x 2−6=2x +x 2−6=(x +1)2−7,因为 x ∈(−3,4],所以当 x =−1 时,g (x )min =−7, 当 x =4 时,g (x )max =18,所以函数 g (x )=log 2f (x )+x 2−6 的值域为 [−7,18].【知识点】函数的解析式的概念与求法、指数函数及其性质、函数的值域的概念与求法26. 【答案】(1) 不是; (2) 反证法,略.【知识点】Asin(ωx+ψ)形式函数的性质27. 【答案】(1) f (x ) 的定义域为 {x∣ x ≠0}.设 f (x )=1x −1 是为 Ψ 函数,则存在实数 a ,b ,使得 f (a −x )+f (a +x )=b 对任意满足 a −x ∈D 且 a +x ∈D 的 x 恒成立, 即 1a−x +1a+x −2=b ,所以 (b +2)(a 2−x 2)=2a 恒成立,所以 a =0,b =−2. 所以存在 a =0,b =−2,使得 f (a −x )+f (a +x )=b 对任意 x ≠±a 恒成立. 所以 f (x )=1x −1 是 Ψ 函数.(2) 若 g (a +x )+g (a −x )=12a−x +t +12a+x +t =b 恒成立, 则 2a+x +2a−x +2t =b (2a+x +t )(2a−x +t ) 恒成立, 即 (1−bt )(2a+x +2a−x )=b (22a +t 2)−2t 恒成立,所以 1−bt =0,b (22a +t 2)−2t =0,又 t ≠0,所以 b =1t ,a =log 2∣t∣. 所以存在实数 a ,b 使得 g (x ) 是 Ψ 函数.(3) 因为函数 ℎ(x ) 的图象关于直线 x =m (m 为常数)对称, 所以 ℎ(m −x )=ℎ(m +x ),所以当 m ≠a 时, ℎ(x +2m −2a )=ℎ[m +(x +m −2a )]=ℎ[m −(x +m −2a )]=ℎ(2a −x )=ℎ(a +(a −x )),又 ℎ(a +x )+ℎ(a −x )=b ,所以 ℎ(a +(a −x ))=b −ℎ[a −(a −x )]=b −ℎ(x ),所以 ℎ(x +2m −2a )=b −ℎ(x ),ℎ(x )=b −ℎ(x +2m −2a )=ℎ(x +2m −2a +2m −2a )=ℎ(x +4m −4a ).所以 ℎ(x ) 为周期函数,周期为 4m −4a .若 m =a ,则 ℎ(a −x )=ℎ(a +x ),且 ℎ(a −x )=b −ℎ(a +x ), 所以 ℎ(a +x )=b2,显然 ℎ(x ) 是周期函数. 综上,ℎ(x ) 是周期函数.【知识点】函数的对称性、函数的周期性、幂函数及其性质、指数函数及其性质28. 【答案】(1) g (x )=−x 2+2x ,(2) ℎ(x )=−(1+λ)x 2+2(1−λ)x +1,当 λ=−1 时,ℎ(x )=4x +1 在 [−1,1] 上显然为增函数,当 λ≠−1 时,可得 {1+λ>0,1−λ1+λ≥1, 或 {1+λ>0,1−λ1+λ≤−1,⇒−1<λ≤0 或 λ<−1,综上所述,所求 λ 的取值范围是 λ=−1 或 −1<λ≤0 或 λ<−1,即 λ≤0.【知识点】函数的解析式的概念与求法、函数的单调性29. 【答案】(1) 由题知,sinα=4√37,sin (α+β)=5√314,所以,cosβ=cos (α+β−α)=cos (α+β)cosα+sin (α+β)sinα=12. (2) 因为 0<α−β<π4,cos (α−β)=1213,所以 sin (α−β)=513,因为 π<α+β<3π2,sin (α+β)=−35,所以 cos (α+β)=−45,所以 sin2α=sin [(α−β)+(α+β)]=sin (α−β)cos (α+β)+cos (α−β)sin (α+β)=−5665. 【知识点】两角和与差的正弦、两角和与差的余弦30. 【答案】(1) 找出关键的五个点,列表如下: x −2π−3π2−π−π2y =sinx 010−10y =1−sinx10121描点作图,如图所示.(2) 由于 y =sin (x +π)−1=−sinx −1,找出关键的五个点,列表如下: x −2π−3π2−π−π20y =sinx 010−10y =−sinx −1−1−2−10−1描点作图,如图所示. 【知识点】正弦函数的图象。
人教A版高一数学必修第一册全册复习测试题卷含答案解析(56)

人教A 版高一数学必修第一册全册复习测试题卷3(共30题)一、选择题(共10题)1. 下列命题中真命题的个数是 ( ) ①函数 y =sinx ,其导函数是偶函数;②“若 x =y ,则 x 2=y 2”的逆否命题为真命题; ③“x ≥2”是“x 2−x −2≥0”成立的充要条件;④命题 p:“存在 x 0∈R ,x 02−x 0+1<0”,则命题 p 的否定为:“对任意的 x ∈R ,x 2−x +1≥0”. A . 0 B . 1 C . 2 D . 32. 已知定义在实数集 R 上的偶函数 f (x ) 满足 f (x +1)=f (x −1),且当 x ∈[0,1] 时,f (x )=x 2,则关于 x 的方程 f (x )=12∣x ∣ 在 [−1,2] 上根的个数是 ( ) A . 2 B . 4 C . 6 D . 83. 设函数 f (x ) 的定义城为 A ,如果对于任意的 x 1∈A ,都存在 x 2∈A ,使得 f (x 1)+f (x 2)=2m (其中 m 为常数)成立,则称函数 f (x ) 在 A 上“与常数 m 相关联”.给定函数:① y =1x ;② y =x 3;③ y =(12)x;④ y =lnx ;⑤ y =cosx +1,则在其定义域上与常数 1 相关联的所有函数是 ( ) A .①②⑤ B .①③ C .②④⑤ D .②④4. 若不等式x 2+mx +1>0的解集为R ,则m 的取值范围是( ) A .RB .(−2,2)C .(−∞,−2)∪(2,+∞)D .[−2,2]5. 已知 0<a <1,则方程 a ∣x∣=∣log a x ∣ 的实根个数为 ( ) A . 2 B . 3 C . 4 D .与 a 的值有关6. 集合 {x ∈N ∗∣ x −2<3} 的另一种表示形式是 ( ) A . {0,1,2,3,4} B . {1,2,3,4} C . {0,1,2,3,4,5} D . {1,2,3,4,5}7. 要得到函数 y =cos2x 的图象,只需将函数 y =cos (2x −π) 的图象 ( )A .向左平移 π3个单位长度B .向右平移 π3个单位长度C .向左平移 π6 个单位长度D .向右平移 π6 个单位长度8. 给出下列命题:①如 a >b ,则 ac 2>bc 2; ② sinx +1sinx ≥2; ③ x 2+2+1x 2+2≥2;④若 a >b >0,则 a −1a >b −1b ; ⑤若 x ≥0,则 t =2x x 2+1的最大值为 1.以上命题正确命题的个数为 ( ) A . 4 B . 3 C . 2 D . 19. 已知函数 f (x )={∣2x −1∣,x ≤1log 2(x −1),x >1,若 f (x 1)=f (x 2)=f (x 3)(x 1,x 2,x 3 互不相等)则x 1+x 2+x 3 的取值范围是 ( ) A . (0,8) B . (1,3) C . (3,4] D . (1,8]10. k 为整数,化简 sin [(k+1)π+θ]⋅cos [(k+1)π−θ]sin (kπ−θ)⋅cos (kπ+θ)的结果是 ( )A . ±1B . −1C . 1D . tanθ二、填空题(共10题)11. 方程 ∣∣cos (x +π2)∣∣=∣log 18x ∣ 的解的个数为 (用数字作答).12. 已知 k 为常数,函数 f (x )={x+2x+1,x ≤0∣lnx ∣,x >0,若关于 x 的方程 f (x )=kx +2 有且只有四个不同解,则实数 k 的取值构成的集合为 .13. 已知函数 f (x )={∣log 2x ∣,0<x <2sin (π4x),2≤x ≤10,若存在实数 x 1,x 2,x 3,x 4 满足 x 1<x 2<x 3<x 4,且 f (x 1)=f (x 2)=f (x 3)=f (x 4),则 x 1x 2+x 3+x 4= .14. 已知函数 f (x )=∣∣∣sinx1x 131∣∣∣,若 f (a )=2021,则 f (−a )= .15. 已知 tanα,tanβ 是一元二次方程 x 2+3√3x +4=0 的两根,α,β∈(−π2,0),则 cos (α+β)= .16. 已知函数 f (x )={∣x 2+5x +4∣,x ≤0,2∣x −2∣,x >0,若函数 y =f (x )−a∣x∣ 恰有 4 个零点,则实数 a的取值范围为 .17. 如图,是我国古代数学家赵爽的弦图,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为 4,大正方形的面积为 100,直角三角形中较小的锐角为 α,则 tanα= .18. 若函数 f (x )={−x +6,x ≤23+log a x,x >2(a >0 且 a ≠1)的值域为 [4,+∞),则 f (1)= ;实数a 的取值范围为 .19. 已知命题 p :∃x ∈R ,ax 2+2ax +1≤0,若命题 p 为假命题,则实数 a 的取值范围是 .20. 已知函数 f (x )={log 2(−x ),x <0x −2,x ≥0,若函数 g (x )=a −∣f (x )∣ 有四个零点 x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则 ax 1x 2+x 3+x 4a的取值范围是 .三、解答题(共10题)21. 已知命题 p :集合 M ={x∣ x <−3或x >5},q :集合 N ={x∣ −a ≤x ≤8}.(1) 若 M ∩N ={x∣ 5<x ≤8},求实数 a 的取值范围; (2) 若 p 是 q 的充分不必要条件,求实数 a 的取值范围.22. 已知函数 f (x )=ln (x −1+a ).(1) 设 f −1(x ) 是 f (x ) 的反函数.当 a =1 时,解不等式 f −1(x )>0;(2) 若关于 x 的方程 f (x )+ln (x 2)=0 的解集中恰好有一个元素,求实数 a 的值;(3) 设 a >0,若对任意 t ∈[12,1],函数 f (x ) 在区间 [t,t +1] 上的最大值与最小值的差不超过 ln2,求 a 的取值范围.23. 已知函数 f (x ) 的定义域为 D ,值域为 f (D ),即 f (D )={y∣ y =f (x ),x ∈D }.若 f (D )⊆D ,则称 f (x ) 在 D 上封闭.(1) 试分别判断函数 f (x )=2017x +log 2017x ,g (x )=x 2x+1 在 (0,1) 上是否封闭,并说明理由. (2) 函数 f (x )=√x +1+k 的定义域为 D =[a,b ],且存在反函数 y =f −1(x ).若函数 f (x )在 D 上封闭,且函数 f −1(x ) 在 f (D ) 上也封闭,求实数 k 的取值范围.(3) 已知函数 f (x ) 的定义域是 D ,对任意 x ,y ∈D ,若 x ≠y ,有 f (x )≠f (y ) 恒成立,则称 f (x ) 在 D 上是单射.已知函数 f (x ) 在 D 上封闭且单射,并且满足 f n (D )⫋D ,其中 f n+1(x )=f(f n (x )),(n ∈N ∗),f 1(x )=f (x ).证明:存在 D 的真子集 D n ⫋D n−1⫋⋯⫋D 3⫋D 2⫋D 1⫋D ,使得 f (x ) 在所有 D i (i =1,2,3,⋯n ) 上封闭.24. 设函数 f (x ) 的定义域为 D ,若存在正实数 a ,使得对于任意 x ∈D ,有 x +a ∈D ,且f (x +a )>f (x ),则称 f (x ) 是 D 上的“a 距增函数”.(1) 判断函数 f (x )=2x −x 是否为 (0,+∞) 上的“1 距增函数”?说明理由;(2) 写出一个 a 的值,使得 f (x )={x +2,x <0√x x ≥0 是区间 (−∞,+∞) 上的“a 距增函数”;(3) 已知函数 f (x ) 是定义在 R 上的奇函数,且当 x >0 时,f (x )=∣x −a ∣−a .若 f (x ) 为R 上的“2021 距增函数”,求 a 的取值范围.25. 已知关于 x 的方程 x 2−2x +a =0.当实数 a 为何值时,(1) 方程的一个根大于 1,另一个根小于 1?(2) 方程的一个根在区间 (−1,1) 内,另一个根在区间 (2,3) 内? (3) 方程的两个根都大于零?26. 解答:(1) 函数 y =log 2(x −1) 的图象是由 y =log 2x 的图象如何变化得到的? (2) 在下边的坐标系中作出 y =∣log 2(x −1)∣ 的图象.(3) 设函数 y =(12)x与函数 y =∣log 2(x −1)∣ 的图象的两个交点的横坐标分别为 x 1,x 2,设M =x 1x 2−2(x 1+x 2)+4,请判断 M 的符号.27. 已知 −π<x <0,且 cos (π2+x)−cosx =−15.(1) 求 sinx −cosx 的值; (2) 求 tanx 的值.28. 已知函数 f (x )=sin (π2−x)sinx −√3cos 2x .(1) 求 f (x ) 的最小正周期和最大值; (2) 讨论 f (x ) 在 [π6,2π3] 上的单调性.29. 已知二次函数 y =x 2−(a +1a)x +1.(1) 当 a =12 时,求关于 x 的不等式 y ≤0 的解集; (2) 若 a >0,求关于 x 的不等式 y ≤0 的解集.30. 设 x >y >0,求证:x 2x y 2y >(xy )x+y .答案一、选择题(共10题) 1. 【答案】D【解析】①正确;因为函数 y =sinx ,所以 yʹ=cosx 是偶函数;②正确;因为命题“若 x =y ,则 x 2=y 2”是真命题,所以其逆否命题也是真命题;③错误;当 x ≥2 时,x 2−x −2=(x +1)(x −2)≥0 成立;当 x 2−x −2=(x +1)(x −2)≥0 时,有 x ≥2 或 x ≤−1.④正确;依据特称命题的否定的格式可知正确.【知识点】命题的概念与真假判断、全(特)称命题的概念与真假判断、全(特)称命题的否定2. 【答案】B【知识点】函数的奇偶性、函数的零点分布、函数的周期性3. 【答案】D【解析】若在其定义域上与常数 1 相关联,则满足 f (x 1)+f (x 2)=2. ① y =1x 的定义域为 {x∣ x ≠0},由 f (x 1)+f (x 2)=2 得 1x 1+1x 2=2,即1x 2=2−1x 1,当 x 1=12时,2−1x 1=2−2=0,此时1x 2=0 无解,不满足条件;② y =x 3 的定义域为 R ,由 f (x 1)+f (x 2)=2 得 (x 1)3+(x 2)3=2,即 x 2=√2−x 133唯一,满足条件;③ y =(12)x 定义域为 R ,由 f (x 1)+f (x 2)=2 得 (12)x 1+(12)x 2=2,即 (12)x 2=2−(12)x 1,当 x 1=−2 时,(12)x 2=2−(12)x 1=2−4=−2,无解,不满足条件;④ y =lnx 定义域为 {x∣ x >0},由 f (x 1)+f (x 2)=2 得 lnx 1+lnx 2=2,得 lnx 1x 2=2, 即 x 1x 2=e 2,x 2=e 2x 1,满足唯一性,满足条件;⑤ y =cosx +1 的定义域为 R ,由 f (x 1)+f (x 2)=2 得 cosx 1+cosx 2=2,得 cosx 2=2−cosx 1,当 x 1=π3 时,cosx 2=2−cosx 1=2−0=2,无解,不满足条件.故满足条件的函数是②④.【知识点】余弦函数的性质、对数函数及其性质、幂函数及其性质、指数函数及其性质4. 【答案】B【解析】【分析】利用一元二次不等式的解法即可得出.【解析】解:∵不等式x 2+mx +1>0的解集为R ,∴△=m 2−4<0,解得−2<m <2. ∴m 的取值范围是(−2,2). 故选:B .【点评】熟练掌握一元二次不等式的解法是解题的关键.5. 【答案】A【解析】设y1=a∣x∣,y2=∣log a x∣,分别作出它们的图象如图所示.由图可知,有两个交点,故方程a∣x∣=∣log a x∣有两个根.【知识点】函数零点的概念与意义6. 【答案】B【解析】由x−2<3,得x<5,又x∈N∗,所以x=1,2,3,4,即集合的另一种表示形式是{1,2,3,4},故选B.【知识点】集合的表示方法7. 【答案】C【解析】y=cos(2x−π3)=cos2(x−π6)的图象,向左平移π6个单位长度可得函数y=cos2x的图象.【知识点】三角函数的图象变换8. 【答案】C【知识点】均值不等式的应用9. 【答案】C【解析】设f(x1)=f(x2)=f(x3)=a,作出函数f(x)的图象与直线y=a,如图.由图可知0<a≤1,不妨设x1<x2<x3,则x1+x2=1,log2(x3−1)=a,因此x3=2a+1,故x1+x2+x3=2+2a,又0<a≤1,所以1<2a≤2,因此3<x1+x2+x3≤4.【知识点】函数的零点分布10. 【答案】B【解析】当k为偶数时,设k=2n,n∈Z,则原式=sin[(2n+1)π+θ]⋅cos[(2n+1)π−θ]sin(2nπ−θ)⋅cos(2nπ+θ)=sin(π+θ)⋅cos(π−θ)−sinθ⋅cosθ=−sinθ⋅(−cosθ)−sinθ⋅cosθ=−1.当k为奇数时,设k=2n+1,n∈Z,则原式=sin[(2n+2)π+θ]⋅cos[(2n+2)π−θ]sin[(2n+1)π−θ]⋅cos[(2n+1)π+θ]=sin[2(n+1)π+θ]⋅cos[(2n+1)π−θ]sin(π−θ)⋅cos(π+θ)=sinθ⋅cosθsinθ⋅(−cosθ)=−1.综上,原式的值为−1.【知识点】诱导公式二、填空题(共10题)11. 【答案】12【知识点】对数函数及其性质、函数的零点分布、Asin(ωx+ψ)形式函数的性质12. 【答案】{1e3}∪(−e,−1)【解析】作函数y=f(x)和y=kx+2的图象,如图所示,两图象除了(0,2)还应有3个公共点,当k≥0时,直线应与曲线y=f(x)(x>1)相切,设切点(x0,lnx0),则切线斜率为k=1x0,又 k =lnx 0−2x 0,则 1x 0=lnx 0−2x 0,解得 x 0=e 3,此时 k =1e 3,当 k <0 时,当 y =kx +2 与曲线 y =x+2x+1相切于点 (0,2) 时,函数 y =f (x ) 和 y =kx +2的图象只有三个公共点,不符合题意,此时 k =−1,当 −1<k <0 时,函数 y =f (x ) 和 y =kx +2 的图象只有三个公共点,不符合题意, 当直线 y =kx +2 与 y =f (x )(0<x <1)相切时,两图象只有三个公共点, 设切点 (x 0,−lnx 0),则切线的斜率 k =−1x 0,又 k =−lnx 0−2x 0,则 −1x 0=−lnx 0−2x 0,解得 x 0=e −1,此时 k =−e 不符合题意, 当 k <−e 时,两图象只有两个公共点,不合题意, 而当 −e <k <−1 时,两图象有 4 个公共点,符合题意, 所以实数 k 的取值范围是 {1e 3}∪(−e,−1).【知识点】函数的零点分布、利用导数求函数的切线方程13. 【答案】 13【解析】作出函数 y =f (x ) 的图象如图所示:由于 f (x 1)=f (x 2)=f (x 3)=f (x 4),则 x 1,x 2,x 3,x 4 可视为直线 y =k 与曲线 y =f (x ) 有四个交点时,四个交点的横坐标.由图象可知,∣log 2x 1∣=∣log 2x 2∣,由于 0<x 1<1<x 2<2,则 log 2x 1<0,log 2x 2>0, 所以,−log 2x 1=log 2x 2,即 log 2x 1+log 2x 2=log 2(x 1x 2)=0,得 x 1x 2=1, 由图象知,曲线 y =sin πx 4(2≤x ≤10) 的图象关于直线 x =6 对称,所以,x 3+x 4=12, 因此,x 1x 2+x 3+x 4=13, 故答案为 13.【知识点】函数的零点分布14. 【答案】 −2021【解析】 f (x )=sinx −x 13,为奇函数, 所以 f (−a )=−f (a )=−2021. 【知识点】函数的奇偶性15. 【答案】 −12【知识点】两角和与差的正切、两角和与差的余弦16. 【答案】(1,2)【解析】考查函数 y =f (x ) 图象与 y =a ∣x ∣ 图象的交点的情况,根据图象,得 a >0. 当 a =2 时,函数 y =f (x ) 与 y =a ∣x ∣ 图象有 3 个交点; 当 y =a ∣x ∣(x ≤0) 图象与 y =∣x 2+5x +4∣ 图象相切时,在整个定义域内,函数 y =f (x ) 图象与 y =a ∣x ∣ 图象有 5 个交点,此时,由 {y =−ax,y =−x 2−5x −4, 得 x 2+(5−a )x +4=0.由 Δ=0,解得 a =1 或 a =9(舍去).故当 1<a <2 时,函数 y =f (x ) 与 y =a ∣x ∣ 图象有 4 个交点.【知识点】函数零点的概念与意义、函数图象17. 【答案】 34【解析】由题意得大正方形的边长为 10,小正方形的边长为 2, 所以 2=10cosα−10sinα, 即 cosα−sinα=15 ⋯⋯ ①, 两边同时平方得 (cosα−sinα)2=125,即 cos 2α+sin 2α−2sinαcosα=125,又因为 cos 2α+sin 2α=1, 所以 2sinαcosα=2425, 所以(cosα+sinα)2=cos 2α+sin 2α+2sinαcosα=1+2425=4925,已知 α 为锐角,所以 cosα+sinα=75 ⋯⋯ ②, 由①②得 cosα=45,sinα=35,所以 tanα=34.【知识点】同角三角函数的基本关系18. 【答案】 5 ; (1,2]【知识点】函数的值域的概念与求法19. 【答案】 [0,1)【解析】因为“∃x ∈R ,ax 2+2ax +1≤0”为假命题, 所以其否定“∀x ∈R ,ax 2+2ax +1>0”为真命题. 当 a =0 时,显然成立;当 a ≠0 时,ax 2+2ax +1>0 恒成立可化为:{a >0,4a 2−4a <0,解得 0<a <1.综上实数 a 的取值范围是 [0,1).【知识点】全(特)称命题的概念与真假判断20. 【答案】 [4,+∞)【知识点】函数的零点分布三、解答题(共10题)21. 【答案】(1) −5≤a≤3.(2) a≥3.【知识点】交、并、补集运算、充分条件与必要条件22. 【答案】(1) 当a=1时,f(x)=ln(x−1+1),由y=ln(x−1+1)得x−1+1−=e y,所以x=1e y−1,因为f−1(x)是f(x)=ln(x−1+a)的反函数,所以f−1(x)=1e x−1,x≠0,由f−1(x)>0得1e x−1>0,所以:e x−1>0,解得:x>0,即不等式f−1(x)>0的解集为{x∣ x>0};(2) 方程f(x)+ln(x2)=0即ln(x−1+a)+ln(x2)=0,所以x+ax2=1,① a=0,则x=1,经过验证,满足关于x的方程f(x)+ln(x2)=0的解集中恰好有一个元素;② a≠0时,(i)若Δ=1+4a=0,解得a=−14,代入x+ax2=1,解得x=2,经过验证,满足关于x的方程f(x)+ln(x2)=0的解集中恰好有一个元素;(ii)若Δ=1+4a>0,则a>−14;当a>0时由1x +a>0解x>0或x<−1a,即方程f(x)+ln(x2)=0的解要在(−∞,−1a)∪(0,+∞)范围内,解方程x+ax2=1得x=−1±√1+4a2a,因为x=−1+√1+4a2a >2√a2a>0,所以为使关于x的方程f(x)+ln(x2)=0的解集中恰好有一个元素,只需−1−√1+4a2a ≥−1a,即1+√1+4a≤1,显然不成立;当−14<a<0时,由1x+a>0解得:0<x<−1a,即方程f(x)+ln(x2)=0的解要在(0,−1a)范围内,解方程x+ax2=1得x=−1±√1+4a2a,因为a<0,所以−1−√1+4a2a >0,−1+√1+4a2a>0,且−1+√1+4a2a >−1−√1+4a2a,因此只需−1+√1+4a2a <−1a<−1−√1+4a2a,即1−√1+4a2<1<1+√1+4a2,即{−√1+4a<1,√1+4a>1,解得:a>0,与−14<a<0矛盾,也不满足题意;综上,实数a的值为0或−14;(3) 由对数函数的单调性可得y=lnx单调递增,根据幂函数单调性可得y=x−1+a在(0,+∞)上单调递减,因为a>0,t∈[12,1],所以,根据复合函数单调性,可得f(x)=ln(x−1+a)在区间[t,t+1]上单调递减,因此f(x)max=ln(t−1+a),f(x)min=ln(1t+1+a),又函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过ln2,所以ln(t−1+a)−ln(1t+1+a)≤ln2,即(at+1)(t+1)t(at+a+1)≤2,整理得a≥1−tt2+t即a≥1−tt2+t对任意的t∈[12,1]恒成立,令g(t)=1−tt2+t ,t∈[12,1],任取12≤t1<t2≤1,则g (t 1)−g (t 2)=1−t 1t 12+t 1−1−t2t 22+t 2=(1−t 1)(t 22+t 2)−(1−t 2)(t 12+t 1)(t 12+t 1)(t 22+t 2)=(t 22+t 2−t 1t 22−t 1t 2)−(t 12+t 1−t 12t 2−t 1t 2)(t 12+t 1)(t 22+t 2)=(t 2−t 1)(t 2+t 1+1−t 1t 2)(t 12+t 1)(t 22+t 2),因为 12≤t 1<t 2≤1,所以 t 2−t 1>0,t 2+t 1+1−t 1t 2>0,(t 12+t 1)(t 22+t 2)>0,因此 g (t 1)−g (t 2)=(t 2−t 1)(t 2+t 1+1−t 1t 2)(t 12+t 1)(t 22+t 2)>0,即 g (t 1)>g (t 2);所以 g (t )=1−t t 2+t 在 t ∈[12,1] 上单调递减, 所以 g (t )max =g (12)=23,因此,只需 a ≥g (t )max =23,故 a 的取值范围为 [23,+∞).【知识点】对数函数及其性质、函数的最大(小)值、反函数23. 【答案】(1) 因为函数 f (x ) 的定义域为 (0,+∞),值域为 (−∞,+∞),(取一个具体例子也可),所以f (x ) 在 (0,1) 上不封闭. t =x +1∈(1,2),g (x )=ℎ(t )=(t−1)2t=t +1t −2∈(0,12)⊆(0,1),g (x ) 在 (0,1) 上封闭.(2) 函数 f (x ) 在 D 上封闭,则 f (D )⊆D . 函数 f −1(x ) 在 f (D ) 上封闭,则 D ⊆f (D ), 得到:D =f (D ).f (x )=√x +1+k 在 D =[a,b ] 单调递增.则 f (a )=a ,f (b )=b ⇔f (x )=√x +1+k =x 在 [−1,+∞) 两不等实根. g (x )=x 2−(2k +1)x +k 2−1=0({x ≥−1,x ≥k,)故 {(2k +1)2−4(k 2−1)>0,g (−1)≥0,g (k )≥0,2k+12>k,2k+12>−1,解得k∈(−54,−1].另解:⇔f(x)=√x+1+k=x在[−1,+∞)两不等实根.令t=√x+1(t≥0),k+1=t2−t在t∈[0,+∞)有两个不等根,画图,由数形结合可知,k+1∈(−14,0],解得k∈(−54,−1].(3) 如果f(D)=D,则f n(D)=D,与题干f n(D)⫋D矛盾.因此f(D)⫋D,取D1=f(D),则D1⫋D.接下来证明f(D1)⫋D1.因为f(x)是单射,因此取一个p∈D∖D1,则p是唯一的使得f(x)=f(p)的根,换句话说f(p)∉f(D1).考虑到P∈D∖D1,即D1∉D∖{p}.因为f(x)是单射,则f(D1)⫋f(D∖{p})=f(D)∖{f(p)}=D1∖{f(p)}⫋D1.这样就有了f(D1)⫋D1.接着令D n+1=f(D n),并重复上述论证证明D n+1⫋D n.【知识点】函数的值域的概念与求法、指数函数及其性质、反函数24. 【答案】(1) 函数f(x)=2x−x是(0,+∞)上的“1距增函数”,任意x∈(0,+∞),有x+1∈(0,+∞),且2x>1,所以f(x+1)−f(x)=2x+1−(x+1)−(2x−x)=2x−1>0,因此f(x)=2x−x是(0,+∞)上的“1距增函数”.(2) a=10(答案不唯一,不小于4即可)(3) f(x)={∣x−a∣−a,x>0 0,x=0−∣x+a∣+a,x≤0因为f(x)为R上的“2021距增函数”,∪)当x>0时,由定义∣x+2021−a∣−a>∣x−a∣−a恒成立,即∣x+2021−a∣>∣x−a∣恒成立,由绝对值几何意义可得a+a−2021<0,a<20212;∪)当x<0时,分两种情况:当x<−2021时,由定义−∣x+2021+a∣+a>−∣x+a∣+a恒成立,即∣x+2021+a∣<∣x+a∣恒成立,由绝对值几何意义可得−a−a−2021>0,a<−20212;当−2021≤x<0时,由定义−∣x+a∣+a<∣x+2021−a∣−a恒成立,即 ∣x +2021−a ∣+∣x +a ∣≥∣2021−2a ∣>2a 恒成立, 当 a ≤0 时,显然成立, 当 a >0 时,可得 0<a <20214; 综上,a 的取值范围为 (−∞,20214).【知识点】函数的单调性25. 【答案】(1) 已知方程的一个根大于 1,另一个根小于 1,结合二次函数 y =x 2−2x +a 的图象知(图略),当 x =1 时的函数值小于 0,即 12−2+a <0,所以 a <1. 因此 a 的取值范围是 {a∣ a <1}.(2) 由方程的一个根在区间 (−1,1) 内,另一个根在区间 (2,3) 内,结合二次函数 y =x 2−2x +a 的图象知(图略),x 取 −1,3 时函数值为正,x 取 1,2 时函数值为负.即 {1+2+a >0,1−2+a <0,4−4+a <0,9−6+a >0,解得 −3<a <0.因此 a 的取值范围是 {a∣ −3<a <0}.(3) 由方程的两个根都大于零,结合二次函数 y =x 2−2x +a 的图象知(图略),判别式不小于 0,图象的对称轴在 y 轴右侧,且当 x =0 时,函数值为正,即 {Δ=4−4a ≥0,−−22>0,a >0,解得 0<a ≤1.因此 a 的取值范围是 {a∣ 0<a ≤1}. 【知识点】函数的零点分布26. 【答案】(1) 函数 y =log 2(x −1) 的图象是由 y =log 2x 的图象向右平移 1 个单位得到的.(2) 在下边的坐标系中作出 y =∣log 2(x −1)∣ 的图象,如图所示;(3) 设函数 y =(12)x与函数 y =∣log 2(x −1)∣ 的图象的两个交点的横坐标分别为 x 1,x 2, 所以 M =x 1x 2−2(x 1+x 2)+4=(x 1−2)(x 2−2)<0.【知识点】对数函数及其性质、指数函数及其性质、函数的图象变换27. 【答案】(1) 由已知,得 sinx +cosx =15,两边平方得 sin 2x +2sinxcosx +cos 2x =125, 整理得 2sinxcosx =−2425.因为 (sinx −cosx )2=1−2sinxcosx =4925,由 −π<x <0 知,sinx <0,又 sinxcosx =−1225<0, 所以 cosx >0,所以 sinx −cosx <0, 故 sinx −cosx =−75.(2) 故此 sinx =−35,cosx =45, 所以 tanx =−34.【知识点】同角三角函数的基本关系28. 【答案】(1)f (x )=sin (π2−x)sinx −√3cos 2x=cosxsinx −√32(1+cos2x )=12sin2x −√32cos2x −√32=sin (2x −π3)−√32,所以 f (x ) 的最小正周期为 π,最大值为 2−√32.(2) 当 x ∈[π6,2π3] 时,0≤2x −3≤π,所以当 0≤2x −π3≤π2,即 π6≤x ≤5π12时,f (x ) 单调递增,当π2≤2x −π3≤π,即5π12≤x ≤2π3时,f (x ) 单调递减.综上,可知 f (x ) 在 [π6,5π12] 上单调递增,在 [5π12,2π3] 单调递减.【知识点】Asin(ωx+ψ)形式函数的性质29. 【答案】(1) 当 a =12 时,有 x 2−52x +1≤0,即 2x 2−5x +2≤0,解得 12≤x ≤2,故不等式y≤0的解集为{x∣ 12≤x≤2}.(2) y≤0⇔x2−(a+1a )x+1≤0⇔(x−1a)(x−a)≤0,①当0<a<1时,a<1a ,不等式的解集为{x∣ a≤x≤1a};②当a=1时,a=1a=1,不等式的解集为{1};③当a>1时,a>1a ,不等式的解集为{x∣ 1a≤x≤a}.综上,当0<a<1时,不等式的解集为{x∣ a≤x≤1a};当a=1时,不等式的解集为{1};当a>1时,不等式的解集为{x∣ 1a≤x≤a}.【知识点】二次不等式的解法30. 【答案】由x>y>0,x2x y2y>(xy)x+y可等价变形为x2x y2y(xy)x+y >1,即要证(xy)x−y>1.因为xy >1,x−y>0,由幂的基本不等式,可知(xy)x−y>1.【知识点】幂的概念与运算。
人教A版高一数学必修第一册全册复习训练题卷含答案解析(52)
人教A 版高一数学必修第一册全册复习训练题卷(共30题)一、选择题(共10题)1. 已知 a 1,a 2,b 1,b 2 均为非零实数,不等式 a 1x +b 1<0 与不等式 a 2x +b 2<0 的解所组成的集合分别为集合 M 和集合 N ,则“a 1a 2=b 1b 2”是“M =N ”的 ( )A .充分不必要条件B .既不充分也不必要条件C .充要条件D .必要不充分条件2. 下面各组角中,终边相同的是 ( ) A . 390∘,690∘ B . −330∘,750∘ C . 480∘,−420∘D . 3000∘,−840∘3. 若对于任意实数 x 总有 f (−x )=f (x ),且 f (x ) 在区间 (−∞,−1] 上是增函数,则 ( ) A . f (−32)<f (−1)<f (2) B . f (−1)<f (−32)<f (2) C . f (2)<f (−1)<f (−32)D . f (2)<f (−32)<f (−1)4. 函数 f (x )=(x +sinx )cosx 的部分图象大致为 ( )A .B .C.D.5.集合A={x∣ −1<x<3},B={x∣ x2+x−6<0,x∈Z},则A∩B=( )A.(−1,2)B.(−3,3)C.{0,1}D.{0,1,2}6.已知集合A={x∣ 1≤x<3},B={x∣ x2≤4},则A∩B=( )A.{x∣ 1≤x<2}B.{x∣ −2≤x<1}C.{x∣ 1≤x≤2}D.{x∣ 1<x≤2}7.已知cos(π2+α)=√33(−π2<α<π2),则sin(α+π3)=( )A.3√2−√36B.3√2+√36C.√6−36D.√6+368.设集合M={x∈R∣ 0≤x≤2},N={x∈R∣ −1<x<1},则M∩N=( )A.{x∣ 0≤x≤1}B.{x∣ 0≤x<1}C.{x∣ 1<x≤2}D.{x∣ −1<x≤2}9. 式子 a√−1a 经过计算可得 ( ) A . √−a B . √a C . −√a D . −√−a10. 设集合 A ={x∣ −1<x ≤1},B ={−1,0,1,2},则 A ∩B = ( )A . {−1,0,1}B . {−1,0}C . {0,1}D . {1,2}二、填空题(共10题)11. 已知集合 A =(−2,3),B =[−1,4],则集合 A ∩B = .12. 已知 a >0,b >0,则 a 2+4+4ab+4b 2a+2b的最小值为 .13. 若 (3−2m )12>(m +1)12,则实数 m 的取值范围为 .14. 若 cosα=13,则 sin (α−π2)= .15. 若角 α 终边经过点 P (−1,2),则 tanα= .16. 二次函数 y =ax 2+bx +c (x ∈R ) 的部分对应值如表:x−3−2−101234y 60−4−6−6−406则不等式 ax 2+bx +c >0 的解集是 .17. 已知 a >b >0,则 a +4a+b +1a−b 的最小值为 .18. 若 π2<α<π 且 cosα=−13,则 tanα= .19. 如果 α∈(π2,π),且 sinα=45,那么 sin (α+π4)+cos (α+π4)= .20. 已知函数 f (x )=1+∣x∣−x 2(−2<x ≤2).用分段函数的形折表示该函数为 ; 该函数的值域为 .三、解答题(共10题)21.画出下列函数的图象,并根据图象说出函数y=f(x)的单调区间及在每一单调区间上的单调性.(1) y=x2−5x−6;(2) y=9−x2.22.数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.(1) 对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果a>0,且a≠1,M>0,那么log a M n=nlog a M(n∈R).(2) 请你运用上述对数运算性质计算lg3lg4(lg8lg9+lg16lg27)的值.(3) 因为210=1024∈(103,104),所以210的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断20192020的位数.(注:lg2019≈3.305).23.回答下列问题:(1) 将log232=5化成指数式;(2) 将3−3=127化成对数式;(3) 已知log4x=−32,求x;(4) 已知log2(log3x)=1,求x.24.写出下列命题的否定,并判断其否定的真假:(1) p:不论m取何实数,方程x2+mx−1=0必有实根;(2) ∀x,y∈R,x2+y2+2x−4y+5=0.25.已知集合A={x∣2−a≤x≤2+a},B={x∣∣x≤1或x≥4}.(1) 当a=3时,求A∩B;(2) 若A∩B=∅,求实数a的取值范围.26.已知函数f(x)=log a(x+2)−1,其中a>1.(1) 若f(x)在[0,1]上的最大值与最小值互为相反数,求a的值.(2) 若f(x)的图象不经过第二象限,求a的取值范围.27.求2π3的六个三角比的值.28.子集(1)对于两个集合A和B,如果集合A中都属于集合B(若a∈A,则a∈B),那么集合A叫做集合B的子集,记作或,读作“ ”或“ ”.可用文氏图表示为(2)子集的性质:①A⊆A,即任何一个集合是它本身的子集;②∅⊆A,即空集是任何集合的子集.问题:集合A是集合B的子集的含义是什么?,b},Q={0,a+b,b2},且P=Q.求a2018+b2019的值.29.已知集合P={1,ab30.已知集合A={x∣ 1≤x≤2},B={x∣ 1≤x≤a,a≥1}.(1) 若A⫋B,求a的取值范围;(2) 若B⊆A,求a的取值范围.答案一、选择题(共10题) 1. 【答案】D【解析】取 a 1=b 1=1,a 2=b 2=−1,则可得 M =(−∞,−1),N =(−1,+∞),M ≠N ,因此不是充分条件,而由 M =N ,显然可以得到 a 1a 2=b 1b 2,所以是必要条件.故选D .【知识点】充分条件与必要条件2. 【答案】B【解析】因为 390∘=360∘+30∘,690∘=720∘−30∘, 所以 390∘ 与 690∘ 终边不同,A 错误;因为 −330∘=−360∘+30∘,750∘=720∘+30∘, 所以 −330∘ 与 750∘ 终边相同,B 正确; 因为 480∘=360∘+120∘,−420∘=−360∘−60∘, 所以 480∘ 与 −420∘ 终边不同,C 错误;因为 3000∘=2880∘+120∘,−840∘=−720∘−120∘, 所以 3000∘ 与 −840∘ 终边不同,D 错误. 故选B .【知识点】任意角的概念3. 【答案】D【解析】由 f (−x )=f (x ) 可得 f (x ) 为偶函数,且在 (−∞,1] 上单增, 由偶函数性质可知其在区间 [1,+∞) 上, 因为 f (−32)=f (32),f (−1)=f (1), 所以 f (2)<f (−32)<f (−1). 【知识点】函数的单调性4. 【答案】D【解析】因为函数 f (x ) 为奇函数,故排除B ,又因为当 x ∈(0,π2) 时,f (x )>0,当 x ∈(π2,π)时,f (x )<0,故排除C ,A . 【知识点】函数的奇偶性、函数图象5. 【答案】C【解析】 B ={x∣ x 2+x −6<0,x ∈Z }={x∣ −3<x <2,x ∈Z }={−2,−1,0,1},又 A ={x∣ −1<x <3}, 所以 A ∩B ={0,1},故选C .【知识点】交、并、补集运算6. 【答案】C【知识点】二次不等式的解法、交、并、补集运算7. 【答案】A【解析】因为cos(π2+α)=−sinα=√33,所以sinα=−√33,所以−π2<α<0,所以cosα=√63,所以sin(α+π3)=sinαcosπ3+cosαsinπ3 =−√33×12+√63×√32=3√2−√36,故选A.【知识点】两角和与差的正弦8. 【答案】B【解析】因为M={x∈R∣ 0≤x≤2},N={x∈R∣ −1<x<1},所以M∩N={x∣ 0≤x<1}.【知识点】交、并、补集运算9. 【答案】D【解析】因为√−1a 成立,所以a<0,所以a√−1a=−√−a2a=−√−a.故选D.【知识点】幂的概念与运算10. 【答案】C【解析】A∩B={0,1}.【知识点】交、并、补集运算二、填空题(共10题)11. 【答案】[−1,3)【知识点】交、并、补集运算12. 【答案】 4【解析】由a 2+4+4ab+4b 2a+2b=(a+2b )2+4a+2b=(a +2b )+4a+2b ,因为 a >0,b >0, 所以 a +2b >0,4a+2b >0, 所以 (a +2b )+4a+2b≥2√(a +2b )⋅4a+2b=4,当且仅当 a +2b =2 时取等号,即a 2+4+4ab+4b 2a+2b的最小值为 4.【知识点】均值不等式的应用13. 【答案】 [−1,23)【知识点】幂函数及其性质14. 【答案】 −13【知识点】诱导公式15. 【答案】 −2【知识点】任意角的三角函数定义16. 【答案】 (−∞,−2)∪(3,+∞)【知识点】二次不等式的解法17. 【答案】 3√2【解析】 4a+b +1a−b =22a+b +12a−b ≥(2+1)2(a+b )+(a−b )=92a , 所以 a +4a+b +1a−b≥a +92a≥2√a ⋅92a=3√2,当且仅当 {2a+b=1a−b,a =92a,即 a =3√22,b =√22时等号成立.【知识点】均值不等式的应用18. 【答案】 −2√2【知识点】同角三角函数的基本关系19. 【答案】 −3√25【知识点】两角和与差的余弦、两角和与差的正弦20. 【答案】 f(x)={1−x,−2<x ≤01,0<x ≤2; [1,3)【解析】 f (x )=1+∣x∣−x 2(−2<x ≤2),当 −2<x ≤0 时,f (x )=1−x ; 当 0<x ≤2 时,f (x )=1.所以函数 f (x )={1−x,−2<x ≤01,0<x ≤2,函数 f (x ) 的图象如图所示:根据图象,得函数 f (x ) 的值域为 [1,3).【知识点】分段函数、函数的值域的概念与求法三、解答题(共10题) 21. 【答案】(1) 图略.函数 y =x 2−5x −6 在 (−∞,52] 上单调递减,在 [52,+∞) 上单调递增. (2) 函数 y =9−x 2 在 (−∞,0] 上单调递增,在 [0,+∞) 上单调递减. 【知识点】函数的单调性22. 【答案】(1) (a m )n =a mn , log a (a m )n =log a a mn , log a (a m )n =mn ,令 a m =M ,则 m =log a M , 则 log a M n =nlog a M .(2) lg3lg4(lg8lg9+lg16lg27)=lg32lg2(3lg22lg3+4lg23lg3)=34+23=1712. (3) lg20192020=2020lg2019≈2020×3.305=6676.1,所以20192020≈106676.1∈(106676,106677),所以20192020位数为6677.【知识点】对数的概念与运算23. 【答案】(1) 因为log232=5,所以25=32.(2) 因为3−3=127,所以log3127=−3.(3) 因为log4x=−32,所以x=4−32=22×(−32)=2−3=18.(4) 因为log2(log3x)=1,所以log3x=2,即x=32=9.【知识点】对数的概念与运算24. 【答案】(1) ¬p:存在一个实数m,使方程x2+mx−1=0没有实数根.因为该方程的判别式Δ=m2+4>0恒成立,所以¬p为假命题.(2) ¬p:∃x,y∈R,x2+y2+2x−4y+5≠0.因为x2+y2+2x−4y+5=(x+1)2+(y−2)2,当x=0,y=0时,x2+y2+2x−4y+5≠0成立,所以¬p为真命题.【知识点】全(特)称命题的概念与真假判断、全(特)称命题的否定、复合命题的概念与真假判断25. 【答案】(1) 当a=3时,A={x∣−1≤x≤5},B={x∣∣x≤1或x≥4},所以A∩B={x∣∣−1≤x≤1或4≤x≤5}.(2) ①若A=∅,则2−a>2+a,解得a<0,满足A∩B=∅;②若A≠∅,则2−a≤x≤2+a,所以a≥0.因为A∩B=∅,所以{2−a>1,2+a<4,解得0≤a<1.综上,实数a的取值范围是(−∞,1).【知识点】交、并、补集运算26. 【答案】(1) 函数f(x)=log a(x+2)−1的定义域是(−2,+∞).因为a>1,所以f(x)=log a(x+2)−1是[0,1]上的增函数.所以f(x)在[0,1]上的最大值是f(1)=log a3−1;最小值是f(0)=log a2−1.依题意,得log a3−1=−(log a2−1),解得a=√6.(2) 由(1)知,f(x)=log a(x+2)−1是(−2,+∞)上的增函数.在f(x)的解析式中,令x=0,得f(0)=log a2−1,所以,f(x)的图象与y轴交于点(0,log a2−1).依题意,得f(0)=log a2−1≤0.解得a≥2.【知识点】函数的最大(小)值、对数函数及其性质27. 【答案】sin2π3=√32,cos2π3=−12,tan2π3=−√3,cot2π3=−√33,sec2π3=−2,csc2π3=23√3.【知识点】任意角的三角函数定义28. 【答案】(1)任何一个元素;A⊆B;B⊇A;A包含于B;B包含A(2)集合A中的任何一个元素都是集合B中的元素,即由x∈A能推出x∈B.例如{0,1}⊆{−1,0,1},则由0∈{0,1}能推出0∈{−1,0,1}.【知识点】包含关系、子集与真子集29. 【答案】−1.【知识点】集合相等30. 【答案】(1) 若A⫋B,由下图可知,a>2.(2) 若B⊆A,由下图可知,1≤a≤2.【知识点】包含关系、子集与真子集11。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(56)

高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1. 向量 a ⃗=(1,2),b ⃗⃗=(2,λ),且 a ⃗⊥b ⃗⃗,则实数 λ= ( ) A . 3 B . −3 C . 7 D . −12. 袋中共有完全相同的 4 只小球,编号为 1,2,3,4,现从中任取 2 只小球,则取出的 2 只球编号之和是偶数的概率为 ( ) A . 25B . 35C . 13D . 233. 下列命题正确的是 ( ) A .三点确定一个平面B .一条直线和一个点确定一个平面C .圆心和圆上两点可确定一个平面D .梯形可确定一个平面4. 复数 1+i 2= ( ) A . 0B . 2C . 2iD . 1−i5. 已知 ∣a ⃗∣=1,∣b ⃗⃗∣=2,a ⃗ 与 b ⃗⃗ 的夹角为 π3,则 a ⃗⋅b ⃗⃗ 等于 ( ) A . 1B . 2C . 3D . 46. 已知平面向量 a ⃗=(1,x ),b ⃗⃗=(y,1),若 a ⃗∥b ⃗⃗,则实数 x ,y 一定满足 ( ) A .xy −1=0B .xy +1=0C .x −y =0D .x +y =07. 在平行四边形 ABCD 中,A (1,2),B (3,5),AD ⃗⃗⃗⃗⃗⃗=(−1,2),则 AC ⃗⃗⃗⃗⃗⃗+BD ⃗⃗⃗⃗⃗⃗⃗= ( ) A . (−2,4)B . (4,6)C . (−6,−2)D . (−1,9)8. 若 AB ⃗⃗⃗⃗⃗⃗=(1,1),AD ⃗⃗⃗⃗⃗⃗=(0,1),BC ⃗⃗⃗⃗⃗⃗+CD ⃗⃗⃗⃗⃗⃗=(a,b ),则 a +b = ( ) A . −1B . 0C . 1D . 29. 已知直线 a 在平面 γ 外,则 ( ) A . a ∥γ B . a 与 γ 至少有一个公共点 C . a ∩γ=AD . a 与 γ 至多有一个公共点10. 下列四个长方体中,由图中的纸板折成的是 ( )A.B.C.D.二、填空题(共6题)11.思考辨析判断正误当向量的始点在坐标原点时,向量的坐标就是向量终点的坐标.( )12.复数加法与减法的运算法则设z1=a+bi,z2=c+di(a,b,c,d∈R)是任意两个复数,则(1)z1+z2=;(2)z1−z2=.13.利用“斜二测”法作多面体直观图时,需考虑个方向上的尺度.14.若向量a⃗与b⃗⃗的夹角为120∘,且∣a⃗∣=1,∣∣b⃗⃗∣∣=1,则∣∣a⃗−b⃗⃗∣∣=.15.当时,λa⃗=0⃗⃗.16.“直线a经过平面α外一点P”用集合符号表示为.三、解答题(共6题)=bsinA.17.△ABC的内角A,B,C的对边分别为a,b,c,已知asin A+C2(1) 求B;(2) 若△ABC为锐角三角形,且a=2,求△ABC面积的取值范围.18.画出如图水平放置的直角梯形的直观图.19.按图示的建系方法,画出水平放置的正五边形ABCDE的直观图.20. 根据图形用符号表示下列点、直线、平面之间的位置关系.(1) 点 P 与直线 AB ; (2) 点 C 与直线 AB ; (3) 点 M 与平面 AC ; (4) 点 A 1 与平面 AC ; (5) 直线 AB 与直线 BC ; (6) 直线 AB 与平面 AC ; (7) 平面 A 1B 与平面 AC .21. 有 4 条长为 2 的线段和 2 条长为 a 的线段,用这 6 条线段作为棱,构成一个三棱锥.问 a为何值时,可构成一个最大体积的三棱锥,最大值为多少?22. 类似于平面直角坐标系,我们可以定义平面斜坐标系:设数轴 x ,y 的交点为 O ,与 x ,y 轴正方向同向的单位向量分别是 i ⃗,j ⃗,且 i ⃗ 与 j ⃗ 的夹角为 θ,其中 θ∈(0,π2)∪(π2,π).由平面向量基本定理,对于平面内的向量 OP ⃗⃗⃗⃗⃗⃗,存在唯一有序实数对 (x,y ),使得 OP ⃗⃗⃗⃗⃗⃗=xi ⃗+yj ⃗,把 (x,y ) 叫做点 P 在斜坐标系 xOy 中的坐标,也叫做向量 OP⃗⃗⃗⃗⃗⃗ 在斜坐标系 xOy 中的坐标.在平面斜坐标系内,直线的方向向量、法向量、点方向式方程、一般式方程等概念与平面直角坐标系内相应概念以相同方式定义,如 θ=45∘ 时,方程x−24=y−1−5表示斜坐标系内一条过点 (2,1),且方向向量为(4,−5)的直线.),a⃗=(2,1),b⃗⃗=(m,6),且a⃗与b⃗⃗的夹角为锐角,求实数m的取值(1) 若θ=arccos(−13范围;(2) 若θ=60∘,已知点A(2,1)和直线l:3x−y+2=0.①求l一个法向量;②求点A到直线l的距离.答案一、选择题(共10题)1. 【答案】D【解析】由a⃗⊥b⃗⃗,所以有a⃗⋅b⃗⃗=1×2+2×λ=0⇒λ=−1.【知识点】平面向量数量积的坐标运算2. 【答案】C【解析】在编号为1,2,3,4的小球中任取2只小球,则有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6种取法,则取出的2只球编号之和是偶数的有{1,3},{2,4},共2种取法,即取出的2只球编号之和是偶数的概率为26=13,故选:C.【知识点】古典概型3. 【答案】D【解析】由不共线的三点确定一个平面,故A错误;由一条直线和该直线外一点确定一个平面,故B错误;当圆心和圆上两点在圆的直径上,不能说明该三点确定一个平面,故C错误;由于梯形是有一组对边平行的四边形,可得梯形确定一个平面,故D正确.故选:D.【知识点】平面向量的概念与表示4. 【答案】A【解析】因为i2=−1,所以1+i2=0.故选:A.【知识点】复数的乘除运算5. 【答案】A【解析】a⃗⋅b⃗⃗=∣a⃗∣∣b⃗⃗∣cosπ3=1×2×cosπ3=1.【知识点】平面向量的数量积与垂直6. 【答案】A【解析】因为a⃗∥b⃗⃗,所以1×1−xy=0,即xy−1=0.【知识点】平面向量数乘的坐标运算7. 【答案】A【解析】在平行四边形ABCD中,因为 A (1,2),B (3,5),所以 AB⃗⃗⃗⃗⃗⃗=(2,3), 又 AD ⃗⃗⃗⃗⃗⃗=(−1,2), 所以 AC ⃗⃗⃗⃗⃗⃗=AB ⃗⃗⃗⃗⃗⃗+AD ⃗⃗⃗⃗⃗⃗=(1,5),BD ⃗⃗⃗⃗⃗⃗⃗=AD ⃗⃗⃗⃗⃗⃗−AB ⃗⃗⃗⃗⃗⃗=(−3,−1), 所以 AC ⃗⃗⃗⃗⃗⃗+BD ⃗⃗⃗⃗⃗⃗⃗=(−2,4), 故选A .【知识点】平面向量和与差的坐标运算8. 【答案】A【解析】 BC ⃗⃗⃗⃗⃗⃗+CD ⃗⃗⃗⃗⃗⃗=BD ⃗⃗⃗⃗⃗⃗⃗=AD ⃗⃗⃗⃗⃗⃗−AB⃗⃗⃗⃗⃗⃗=(0,1)−(1,1)=(−1,0), 故 a =−1,b =0, 所以 a +b =−1.【知识点】平面向量和与差的坐标运算9. 【答案】D【解析】直线在平面外,故直线与平面相交或直线与平面平行,直线 a 与平面 γ 平行时没有公共点,直线 a 与平面 γ 相交时有一个公共点,故选D . 【知识点】直线与平面的位置关系10. 【答案】A【解析】根据题图中纸板的形状及特殊面的阴影部分可以判断B ,C ,D 不正确,故选A . 【知识点】棱柱的结构特征二、填空题(共6题) 11. 【答案】 √【知识点】平面向量和与差的坐标运算12. 【答案】 (a +c)+(b +d)i ; (a −c)+(b −d)i【知识点】复数的加减运算13. 【答案】三【知识点】直观图14. 【答案】 √3【解析】因为向量 a ⃗ 与 b ⃗⃗ 的夹角为 120∘,∣a ⃗∣=1,∣∣b ⃗⃗∣∣=1,所以 a ⃗⋅b ⃗⃗=∣a ⃗∣∣∣b ⃗⃗∣∣cos120∘=−12,因此 ∣∣a ⃗−b ⃗⃗∣∣=√(a ⃗−b ⃗⃗)2=√∣a ⃗∣2+∣∣b ⃗⃗∣∣2−2a⃗⋅b ⃗⃗=√1+1+1=√3. 【知识点】平面向量的数量积与垂直15. 【答案】 λ=0 或 a ⃗=0⃗⃗【解析】若 λa ⃗=0⃗⃗,则 λ=0 或 a ⃗=0⃗⃗.【知识点】平面向量的数乘及其几何意义16. 【答案】 P ∈a ,P ∉α【知识点】平面的概念与基本性质三、解答题(共6题) 17. 【答案】(1) asinA+C 2=bsinA ,由正弦定理 sinAsinA+C 2=sinBsinA .因为 A ,B ,C 是 △ABC 的内角,sinA ≠0, 所以 sin A+C 2=sinB =sin (π−B )=sin (A +C ), 所以 sinA+C 2=2sinA+C 2cosA+C 2,因为 0<A +C <π, 所以 0<A+C 2<π2.所以 sinA+C 2≠0,cosA+C 2=12,A+C 2=π3,所以 A +C =2π3,B =π−(A +C )=π−2π3=π3(2) 由正弦定理得 asinA =bsinB =csinC =2sinA , 所以 c =2sinC sinA,由三角形内角和知 A +C =120∘, 所以 C =120∘−A , 所以 c =2sin (120∘−A )sinA=√3tanA+1,又 △ABC 为锐角三角形, 所以 120∘−A <90∘ 且 A <90∘, 即 30∘<A <90∘, 又 S △ABC =12acsinB =12ac ×√32=√32c =√32×(√3tanA +1),30∘<A <90∘,因为30∘<A<90∘,所以tanA>√33,得√3tanA <3,即1<√3tanA+1<4,所以S△ABC=√32×(√3tanA+1)∈(√32,2√3).【知识点】正弦定理18. 【答案】(1)在已知的直角梯形OBCD中,以OB所在直线为x轴,垂直于OB的腰OD所在直线为y轴建立平面直角坐标系.画出相应的xʹ轴和yʹ轴,使∠xʹOʹyʹ=45∘,如图①②所示.(2)在xʹ轴上截取OʹBʹ=OB,在yʹ轴上截取OʹDʹ=12OD,过点Dʹ作xʹ轴的平行线l,在l上沿xʹ轴正方向取点Cʹ,使得DʹCʹ=DC.连接BʹCʹ,如图②所示.(3)所得四边形OʹBʹCʹDʹ就是直角梯形OBCD的直观图,如图③所示.【知识点】直观图19. 【答案】画法:(1)在图①中作AG⊥x轴于G,作DH⊥x轴于H.(2)在图②中画相应的xʹ轴与yʹ轴,两轴相交于点Oʹ,使∠xʹOʹyʹ=45∘.(3)在图②中的xʹ轴上取OʹBʹ=OB,OʹGʹ=OG,OʹCʹ=OC,OʹHʹ=OH,yʹ轴上取OʹEʹ=1 2OE,分别过Gʹ和Hʹ作yʹ轴的平行线,并在相应的平行线上取GʹAʹ=12GA,HʹDʹ=12HD.(4)连接AʹBʹ,AʹEʹ,EʹDʹ,DʹCʹ,并擦去辅助线GʹAʹ,HʹDʹ,xʹ轴与yʹ轴,便得到水平放置的正五边形ABCDE的直观图五边形AʹBʹCʹDʹEʹ(如图③).【知识点】直观图20. 【答案】(1) 点P∈直线AB.(2) 点C∉直线AB.(3) 点M∈平面AC.(4) 点A1∉平面AC.(5) 直线AB∩直线BC=点B.(6) 直线AB⊂平面AC.(7) 平面A1B∩平面AC=直线AB.【知识点】点、线、面的位置关系、直线与平面的位置关系、平面与平面的位置关系、直线与直线的位置关系21. 【答案】构成三棱锥,这6条线段作为棱有两种摆放方式.(1)2条长为a的线段放在同一个三角形中.如图所示,不妨设底面 BCD 是一个边长为 2 的正三角形.欲使体积达到最大,必有 BA ⊥底面BCD ,且 BA =2,AC =AD =a =2√2, 此时 V =13×√34×22×2=23√3.(2)2 条长为 a 的线段不在同一个三角形中,此时长为 a 的两条线段必处在三棱锥的对棱,不妨设 AD =BC =a ,BD =CD =AB =AC =2. 取 BC 中点 E ,连接 AE ,DE (见下图).则 AE ⊥BC,DE ⊥BC ⇒BC ⊥平面AED ,V =13S △AED ⋅BC , 在 △AED 中,AE =DE =√4−a 24,AD =a ,S △AED =12a √4−a 24−a 24=12a √4−a 22,所以 V =16a 2√4−a 22=16√a 2a 2(16−2a 2)⋅14,由均值不等式 a 2a 2(16−2a 2)≤(163)3,等号当且仅当 a 2=163时成立,即 a =43√3, 所以此时 V max =16√(163)3⋅14=1627√3.【知识点】棱锥的表面积与体积22. 【答案】(1) 由已知 a ⃗=2i ⃗+j ⃗,b ⃗⃗=mi ⃗+6j ⃗,且 a ⃗⋅b ⃗⃗=2m +6+(12+m )(i ⃗⋅j ⃗)=53m +2>0,得 m >−65;若 a ⃗ 和 b ⃗⃗ 同向,则存在正数 t ,使得 t (2i ⃗+j ⃗)=mi ⃗+6j ⃗, 由 i ⃗ 和 j ⃗ 不平行得,{2t =m t =6 得 m =12.故所求为 m >−65,m ≠12.(2) ①方程可变形为x−01=y−23,方向向量为 d⃗=(1,3), 设法向量为 n ⃗⃗=(a,b ),由 n ⃗⃗⋅d ⃗=0 得 a +3b +12(3a +b )=52a +72b =0, 令 a =−7,b =−5,n ⃗⃗=(−7,5);②取直线 l 上一点 B (0,2),则 BA⃗⃗⃗⃗⃗⃗=(2,−1),所求为 ∣∣BA ⃗⃗⃗⃗⃗⃗⋅n ⃗⃗∣∣∣n⃗⃗∣=∣√(⃗+5j ⃗)2=7√3926.【知识点】直线的点法向式方程(沪教版)、平面向量数量积的坐标运算。
高一数学必修一 第二章一元二次函数、方程和不等式单元测试试卷 (3)

高一数学必修一第二章一元二次函数、方程和不等式单元测试试卷 (3)数学第二章测试卷A卷本试卷满分100分,考试时间80分钟。
一、单项选择题(本大题共5小题,每小题5分,共计25分。
在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案填涂在答题卡相应位置上)1.若$a+b+c=0$,且$a<b<c$,则下列不等式一定成立的是A。
$ab<bc$B。
$ab<ac$XXX<bc$D。
$ab<bc$2.已知正数$a$、$b$满足$\frac{22}{1194}+\frac{a}{b}=1$,则$\frac{a}{b}+\frac{b}{a}$的最小值是A。
6B。
12C。
24D。
363.已知二次函数$f(x)=x^2+bx+c$的两个零点分别在区间$(-2,-1)$和$(-1,0)$内,则$f(3)$的取值范围是A。
$(12,20)$B。
$(12,18)$C。
$(18,20)$D。
$(8,18)$4.若$x>0$,$y>0$,且$\frac{2}{x+1}+\frac{1}{x+2y}=1$,则$2x+y$的最小值为A。
2B。
$\frac{2}{3}$C。
$2+\frac{2}{3}$D。
$3$5.关于$x$的不等式$(ax-1)<x$恰有2个整数解,则实数$a$的取值范围是A。
$-\frac{34}{43}<a\leq-\frac{3}{4}$或$\frac{4}{3}<a\leq\frac{43}{34}$B。
$-\frac{3}{4}<a\leq-\frac{2}{3}$或$\frac{2}{3}<a\leq\frac{3}{4}$C。
$-\frac{34}{43}\leq a<-\frac{3}{4}$或$\frac{4}{3}\leq a<\frac{43}{34}$D。
$-\frac{3}{4}\leq a<-\frac{2}{3}$或$\frac{2}{3}\leq a\leq\frac{3}{4}$二、多项选择题(本大题共2小题,每小题5分,共计10分。
第二章《一元二次函数、方程和不等式》单元测试A卷——高一上学期数学人教A版(2019)必修第一册含答

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第二章《一元二次函数、方程和不等式》单元测试A 卷(答卷时间:40分钟,满分:100分)一、单选题(本题共 7 小题,每小题 5 分,共 35 分.在每小题给出的四个选项中,只有一项符合题目要求)1.已知a b >,c R Î则下列结论正确的是( )A .22a b > B .22ac bc > C .a c b c +>+ D .ac bc<2.若0x >,则1x x +的最小值为( )A .2B .3C .D .43.不等式2230x x --<的解集为( )A .{}|31x x -<< B .{}|13x x -<<C .{}|13x x x <->或D .{}|31x x x <->或4.已知01x <<,则(1)x x -的最大值为( )A .13 B .12 C .14 D .235.已知25,1,4A x B x =+=+则A 和B 的大小关系是( )A .A B > B .A B < C .A B ³ D .无法确定6.已知不等式230ax bx +->的解集为{}|13x x <<,则a b -=( )A .3- B .1- C .3 D .5-7.若1x >,则函数411y x x =-+-取得最小值时x 的值为 ()A .2B .32C .3D .4二、多选题(本题共 3小题,每小题 5 分,共 15 分.在每小题给出的四个选项中,有多个选项符合题目要求,完全正确得5分,选对部分得3分,出现错误选项得0分)8. 设,a b 为任意两个非零实数,那么“不等式11a b<成立”的一个充分不必要条件是 ( )A .0a b <<B .0a b -<C .0a b >>D .a b>9.已知0,0,a b >>下列说法一定成立的是 ( )A .222a b ab +³2a b+£C .a b +> D.22433a a +++()的最小值为410.对于任意实数x ,不等式230x ax -+>恒成立,则实数a 可以是 ( )A .2B .3C .D .4三、填空题(本题共 4小题,每小题 5 分,共 20分,其中14题第一个空2分,第二个空3分)11.不等式201x x ->+的解集是________.12.已知0,a >1,a b +=则a b a a ++的最小值是________.13.设,,a b c R Î则“a b >”是“22ac bc >”的_______________条件.14.已知0,0,m n >>且m 和n 的算术平均数不小于它们的几何平均数,则此不等关系的表达式为______________,8m n +=时,mn 的最大值为____________.四、解答题(本题共 3道大题,每道大题 10分,共 30分.解答应写出必要的文字说明、证明过程或演算步骤.)15.解下列一元二次不等式(1)23100x x -->; (2)22950x x --+>.16.已知,x R Î21,4M x =+N x =,比较M 和N 的大小关系,写出详细过程.17. 若0,a b >>0c d <<求证:(1)11a b<; (2)a c b d->-第二章《一元二次函数、方程和不等式》单元测试A 卷参考答案一、单选题(本题共 7 小题,每小题 5 分,共 35 分.在每小题给出的四个选项中,只有一项符合题目要求)1.C.解析:A 选项中当22()()a b a b a b -=+-无法判断a b +的正负所以无法确定2a 与2b 的大小关系,另外也可以根据不等式的性质中只有满足条件0a b >³,才能得到22a b >因此A 错误;B 选项中当0c =时22ac bc =,0c ¹时22ac bc >,因此B 错误;C 选项中由于a b >,不等式两边同时加上同一实数c ,不等号的方向不变(同向可加性)因此C 正确;D 选项中由于不清楚实数c 的正负,无法通过a b >得到ac 和bc 的大小关系, 故选C.2.A.解析:基本不等式:0,0a b >>2a b +£,当且仅当a b =时等号成立.其中式子2a b +£可变形为a b +³.由于0x >则10x >,因此1x x +³即12x x +³, 当且仅当1x x =即1x =时12x x +=,等号成立,所以1x x +的最小值为2, 故选A.(注意利用基本不等式求最大值或最小值需要满足的条件)3.A.解析:解一元二次方程2230x x --=得1213x x =-=,, 且二次函数223y x x =--的图象开口向上,由此该二次函数的图象如图.通过对该函数图象的观察,得到不等式2230x x --<的解集为{}|13x x -<<, 故选A. (注意借助二次函数与一元二次方程、不等式之间的联系,是求解一元二次不等式的一般性方法).x02a b +£,当且仅当a b =时等号成立.变形得2()2a b ab +£.由01x <<可知0x >,10x ->,则211(1)(24x x x x +--£=,当且仅当1x x =-即12x =时等号成立,所以当12x =时1x x =-有最大值14,故选C.5.C. 分析:比较两项的大小关系,在性质特征不是很明显的情况下通常采用作差法,如果不能直接看出差值与0的大小关系,可将作差的结果进行适当变形,从而得出结论. 解析:22251110442A B x x x x x -=+-+-+=-³()=(),所以0A B -³,因此A B ³,故选C.6.D. 解析:因为不等式230ax bx +->的解集为{}|13x x <<,所以1和3是方程230ax bx +-=的两个解.解法一:将1x =和3x =分别代入230ax bx +-=得{2211303330a b a b +-=+-=g g g g 即{309330a b a b +-=+-=解得{14a b =-=所以5a b -=-,故选D.解法二:方程230ax bx +-=的两个解1和3,说明方程230ax bx +-=是一元二次方程, 0a ¹,则可利用根与系数的关系得到方程组13313ba a +=--´=-ìíî解得{14a b =-=所以5a b -=-,故选D.7.C. 解析:1x >则410,01x x ->>-,所以4141y x x =-+³=-,当且仅当且仅当411x x -=-,即3x =时411y x x =-+-取得最小值4, 所以411y x x =-+-取得最小值时3x =,故选C.二、多选题(本题共 3小题,每小题 5 分,共 15 分.在每小题给出的四个选项中,有多个选项符合题目要求,完全正确得5分,选对部分得3分,出现错误选项得0分)8.AC.思路:题中考查选项中哪几个是“不等式11a b <成立”的充分不必要条件,则该条件成立时可以推出11a b <,而当11a b<成立时无法推出该条件成立.本题考查不等式相关知识,因此注重利用不等式性质及作差法的运用技巧.解析:A 选项,充分性:当0a b <<成立时11a b <也成立,因此充分性成立;必要性:当11a b<成立时无法判断0a b <<成立,因此必要性不成立.所以 “0a b <<”是“不等式11a b<成立”的充分不必要条件. B 选项,充分性:当0a b -<成立时11b a a b ab --=,由于无法确定ab 的符号,因此无法确定11a b<是否成立,因此充分性不成立;必要性:当11a b <成立时110b a a b ab--=<,由于无法确定ab 的符号,无法判断0a b -<成立,因此必要性不成立.所以 “0a b -<”是“不等式11a b<成立”的既不充分也不必要条件.C 选项,充分性:当0a b >>成立时10,ab>利用不等式的性质可知11,a b ab ab >g g 因此11b a >,即11a b <成立,因此充分性成立;必要性:当11a b<成立时无法判断0a b >>成立,因此必要性不成立.所以 “0a b >>”是“不等式11a b<成立”的充分不必要条件. D 选项,充分性:1111,,a b ab b ab a==g g 当a b >成立时由于无法确定1ab 的正负,所以无法确定1a ab g 和1b ab g 的大小关系,即无法确定11a b<成立,因此充分性不成立;必要性:同理当11a b<成立时无法确定a b >成立,因此必要性不成立.所以 “a b >”是“不等式11a b<成立”的既不充分也不必要条件.综上所述可知正确选项为AC.9.AB.解析:因为0,0,a b >>重要不等式222a b ab +³2a b +£均成立,故A,B 正确,当且仅当a b =2a b +=即a b +=,所以a b +>成立,C 错误, 由于2330a +³>,2403a >+则224343a a ++³=+() 当且仅当22433a a =++()成立时等号成立,由于22433a a =++()时21a =-无解,所以22433a a +++()无法取得最小值4,因此D 错误. 综上所述可知正确选项为AB.本题考查对基本不等式的理解及对是否符合利用基本不等式求最值条件的判定能力.10.ABC. 解析:任意实数x ,不等式230x ax -+>恒成立,则函数23y x ax =-+的最小值2min 413041a y ´´-=>´,解得a -<<则选项中满足该条件的实数a 可以是故选ABC.点评:将一元二次不等式恒成立问题转化为函数的最值问题是常见的解题策略,即若0(0)y y ><恒成立则只需min max 0(0)y y ><,这一结论是解决这类问题的关键,也是解决恒成立问题的总的思考方向.三、填空题(本题共 4小题,每小题 5 分,共 20分,其中14题第一个空2分,第二个空3分)11. {}|12x x x <->或解析:本道题考查分式不等式的等价转换.不等式201x x ->+等价于2)(1)0x x -+>(,解得12x x <->或,所以201x x ->+的解集为{}|12x x x <->或,注意解集要写成集合或区间的形式,区间形式将会在下一章学习到.12.2解析:本道题考查基本不等式的构造思维能力和对运用基本不等式求最值方法的掌握.1,a b +=则1=a b a a a a +++,因为10,0a a >>则1=a b a a a a +++³,当且仅当1=a a ,即=1a 时等号成立,因此a b a a++的最小值为2.13.必要不充分条件解析:充分性:,,a b c R Î,当a b >,0c =时2=0c ,22==0ac bc ,因此a b >Þ/22ac bc >,充分性不成立; 必要性:22ac bc >时说明20c ¹,那么一定有20c >,210c >,由不等式的性质可知此时222211ac bc c c>g g ,即a b >,因此22ac bc a b >Þ>必要性成立.综上所述“a b >”是“22ac bc >”的必要不充分条件.14. 第一空:+2m n ³第二空:16解析:0,0,m n >>且m 和n 的算术平均数是+2m n ,m 和n ,因此“m 和n 的算术平均数不小于它们的几何平均数”的符号表达式为+2m n ³+2m n ³变形可知2+(2m n mn £,当且仅当=m n 时等号成立, 8m n +=,mn £28(2=16,所以当且仅当4m n ==时mn 的最大值16.四、解答题(本题共 3道大题,每道大题 10分,共 30分.解答应写出必要的文字说明、证明过程或演算步骤.)15. 解:(1)解一元二次方程2310=0x x --得1=2x -,2=5x 则一元二次函数2=310y x x --的图象如图}5>.(2)不等式22950x x --+>的等价不等式为22+950x x -<解一元二次方程22+95=0x x -得15x =-,21=2x 则22+950x x -<的解集为1|52x x ìü-<<íýîþ即一元二次不等式22950x x --+>的解集为1|52x x ìü-<<íýîþ.方法指导:解一元二次不等式可以从解一元二次方程的根入手,了解一元二次方程与相应二次函数图象的联系,画出二次函数的图象,能根据具体函数图象得到相应一元二次不等式的解集.另外在学习本节课内容之后可以用课堂上推广的一般结论,解决相关问题.注意要明确课本上一般结论的推广过程,理解知识本质,体会数形结合和函数思想的应用,以及具体到抽象,特殊到一般的研究问题的基本方法.16. 分析:比较两项的大小关系,在性质特征不是很明显的情况下通常采用作差法,如果不能直接看出差值与0的大小关系,可将作差的结果进行适当变形,从而得出结论.解:221144M N x x x x -=+-=-+2211222x x =-+g (21=()2x - 因为,x R Î所以21(02x -³所以0M N -³,即M 和N 的大小关系是M N ³.17. 分析:通过观察不难发现两个小问均可采用作差法或利用不等式的性质直接证明.解:(1)0a b >>则10ab>由不等式的性质可知11a b ab ab >g g ,即11b a >,所以11a b<(2)0c d <<则0c d ->->又0a b >>Q ()()a cb d \+->+-ac bd \->-。
2019-2020学年山东省菏泽市高一下学期期末数学试卷(A卷) (解析版)

2019-2020学年山东省菏泽市高一第二学期期末数学试卷(A卷)一、选择题(共8小题).1.在一次抛硬币的试验中,同学甲用一枚质地均匀的硬币做了100次试验,发现正面朝上出现了45次,那么出现正面朝上的频率和概率分别为()A.0.45 0.45B.0.5 0.5C.0.5 0.45D.0.45 0.52.复数z=的虚部为()A.2B.﹣2C.﹣3D.﹣3i3.在某次测量中得到的A样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A、B两样本的下列数字特征对应相同的是()A.平均数B.标准差C.众数D.中位数4.如图是一个正方体的表面展开图,则图中“有”在正方体中所在的面的对面上的是()A.者B.事C.竟D.成5.加强体育锻炼是青少年生活学习中非常重要的组成部分.某学生做引体向上运动,处于如图所示的平衡状态时,若两只胳膊的夹角为60°,每只胳膊的拉力大小均为400N,则该学生的体重(单位:kg)约为()(参考数据:取重力加速度大小为g=10m/s2,≈1.732)A.63B.69C.75D.816.已知向量=(2,3),=(﹣1,2),若m+与﹣2共线,则m的值为()A.﹣2B.2C.D.7.如图所示是一样本的频率分布直方图,样本数据共分3组,分别为[5,10),[10,15),[15,20].估计样本数据的第60百分位数是()A.14B.15C.16D.178.已知正方体ABCD﹣A1B1C1D1棱长为4,P是AA1中点,过点D1作平面α,满足CP⊥平面α,则平面α与正方体ABCD﹣A1B1C1D1的截面周长为()A.4B.12C.8D.8二、多项选择题:本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项符合题目要求,全选对的得5分,选对但不全的得3分,有选错的得0分.9.给出如图所示的三幅统计图,则下列命题中正确的有()A.从折线图能看出世界人口的变化情况B.2050年非洲人口将达到大约15亿C.2050年亚洲人口比其他各洲人口的总和还要多D.从1957年到2050年各洲中北美洲人口增长速度最慢10.在△ABC中,角A、B、C所对的边分别为a、b、c,下列结论正确的是()A.若b2+c2﹣a2>0,则△ABC为锐角三角形B.若A>B,则sin A>sin BC.若b=3,A=60°,三角形面积S=3,则a=D.若a cos A=b cos B,则△ABC为等腰三角形11.在△ABC中,D,E,F分别是边BC,AC,AB中点,下列说法正确的是()A.B.C.若点P是线段AD上的动点,且满足=+,则λ+2μ=1D.若△ABC所在平面内一点P满足=λ()(λ≥0),则点P的轨迹一定通过△ABC的内心12.如图,正方体ABCD﹣A1B1C1D1的棱长为1,动点E在线段A1C1上,F、M分别是AD、CD的中点,则下列结论中正确的是()A.FM∥A1C1B.BM⊥平面CC1FC.存在点E,使得平面BEF∥平面CC1D1DD.三棱锥B﹣CEF的体积为定值三、填空题:本大题共4小题,每小题5分,共20分。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(54)
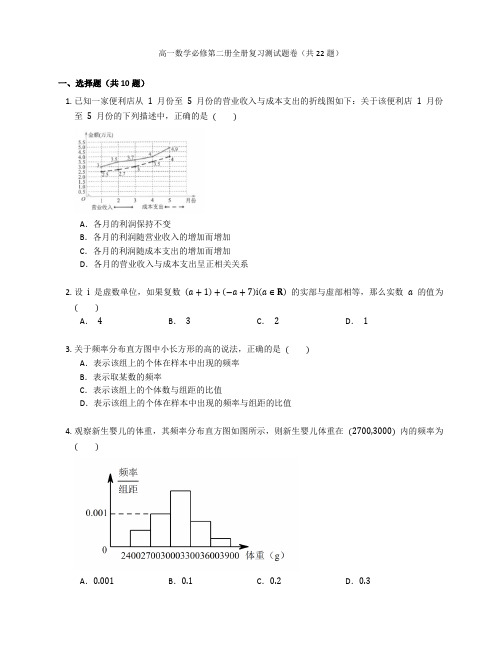
高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1.已知一家便利店从1月份至5月份的营业收入与成本支出的折线图如下:关于该便利店1月份至5月份的下列描述中,正确的是( )A.各月的利润保持不变B.各月的利润随营业收入的增加而增加C.各月的利润随成本支出的增加而增加D.各月的营业收入与成本支出呈正相关关系2.设i是虚数单位,如果复数(a+1)+(−a+7)i(a∈R)的实部与虚部相等,那么实数a的值为( )A.4B.3C.2D.13.关于频率分布直方图中小长方形的高的说法,正确的是( )A.表示该组上的个体在样本中出现的频率B.表示取某数的频率C.表示该组上的个体数与组距的比值D.表示该组上的个体在样本中出现的频率与组距的比值4.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在(2700,3000)内的频率为( )A.0.001B.0.1C.0.2D.0.35. 如果一组数据“x 1,x 2,x 3,x 4,x 5”的平均数是 2,方差是 13,那么另一组数据“3x 1−2,3x 2−2,3x 3−2,3x 4−2,3x 5−2”的平均数和方差分别为 ( ) A . 2,13B . 2,1C . 4,23D . 4,36. 在 △ABC 中,∠BAC =π2,AB =AC =2,P 为 △ABC 所在平面上任意一点,则 PA⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ ) 的最小值为 ( ) A . 1B . −12C . −1D . −27. 已知互相垂直的平面 α,β 交于直线 l ,若直线 m ,n 满足 m ∥α,n ⊥β,则 ( ) A .m ∥lB .m ∥nC .n ⊥lD .m ⊥n8. 复数 i (2−i )= ( ) A . 1+2iB . 1−2iC . −1+2iD . −1−2i9. 若复数 z 满足 z (1+i )=2i ,其中 i 为虚数单位,则 z = ( ) A . 1−iB . 1+iC . −1+iD . −1−i10. 在 △ABC 中,B =30∘,AB =2√3,AC =2,则 △ABC 的面积是 ( )A . √3B . 2√3C . √3 或 2√3D . 2√3 或 4√3二、填空题(共6题) 11. 思考辨析,判断正误.在 △ABC 中,已知两边及夹角时,△ABC 不一定唯一.( )12. 根据党中央关于“精准脱贫”的要求,某市农业经济部门派甲、乙、丙 3 位专家对 A ,B 两个区进行调研,每个区至少派 1 位专家,则甲、乙两位专家均派遣至 A 区的概率为 .13. 已知向量 a =(2,1),b ⃗ =(−1,x ),若 (a +b ⃗ )∥(a −b ⃗ ),则实数 x 的值为 .14. 半径为 3 的球体表面积为 .15. 平面与平面垂直的性质定理:文字语言:两个平面垂直,如果一个平面内有一直线垂直于这两个平面的 ,那么这条直线与另一个平面 .符号语言:α⊥β,α∩β=l,,⇒a⊥β.图形语言:16.若复数z=2+i,其中i为虚数单位,则z在复平面内对应点的坐标为.1−2i三、解答题(共6题)17.已知圆柱的底面直径与高都等于球的直径.求证:(1) 球的表面积等于圆柱的侧面积;.(2) 球的表面积等于圆柱全面积的2318.在静水中划船的速度的大小是每分钟40m,水流速度的大小是每分钟20m,如果一小船从岸边某处出发,沿着垂直于水流的方向到达对岸,则小船的行进方向应指向哪里?19.在△ABC中,内角A,B,C所对的边分别为a,b,c,且满足b2+c2−a2=2bcsin(B+C).(1) 求角A的大小;,求△ABC的面积.(2) 若a=2,B=π320.应用面面平行判断定理应具备哪些条件?21.在北京市“危旧房改造”中,小强一家搬进了回龙观小区.这个小区冬季用家庭燃气炉取暖.为了估算冬季取暖第一个月使用天然气的开支情况,从11月15日起,小强连续八天每天晚上记录了天然气表显示的读数,如下表(注:天然气表上先后两次显示的读数之差就是这段时间内使用天然气的数量):日期15日16日17日18日19日20日21日22日小强的天然气表显示读数(单位:m3)220229241249259270279290妈妈11月15日买了一张面值600元的天然气使用卡,已知每立方米天然气1.70元,请你估算这张卡够小强家用一个月(按30天计算)吗?为什么?22.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.(1) 结合平均数和方差分析谁更优秀;(2) 结合平均数和中位数分析谁的成绩好些;(3) 结合平均数和命中9环及以上的次数分析谁的成绩好些;(4) 从折线图上两人射击命中环数的走势分析谁更有潜力.答案一、选择题(共10题) 1. 【答案】D【知识点】频率分布直方图2. 【答案】B【解析】由题意得 a +1=−a +7,则 a =3.故选B . 【知识点】复数的乘除运算3. 【答案】D【解析】频率分布直方图中小长方形的高是 频率组距,面积表示频率.【知识点】频率分布直方图4. 【答案】D【知识点】频率分布直方图5. 【答案】D【知识点】样本数据的数字特征6. 【答案】C【解析】如图,以直线 AB ,AC 分别为 x ,y 轴建立平面直角坐标系, 则 A (0,0),B (2,0),C (0,2),设 P (x,y ),则 PA⃗⃗⃗⃗⃗ =(−x,−y ),PB ⃗⃗⃗⃗⃗ =(2−x,−y ),PC ⃗⃗⃗⃗⃗ =(−x,2−y ),PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =(2−2x,2−2y ), 所以PA⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ )=−x (2−2x )−y (2−2y )=2x 2−2x +2y 2−2y =2(x −12)2+2(y −12)2−1,当 x =12,y =12 时,PA ⃗⃗⃗⃗⃗ ⋅(PB ⃗⃗⃗⃗⃗ +PC⃗⃗⃗⃗⃗ ) 取得最小值,为 −1. 故选C .【知识点】平面向量数量积的坐标运算7. 【答案】C【解析】由题意知α∩β=l,所以l⊂β,因为n⊥β,所以n⊥l.【知识点】直线与直线的位置关系、点、线、面的位置关系8. 【答案】A【解析】i(2−i)=1+2i.【知识点】复数的乘除运算9. 【答案】B【解析】因为复数z满足z(1+i)=2i,所以z=2i1+i=1+i.【知识点】复数的乘除运算10. 【答案】C【解析】由AB=2√3,AC=2,B=30∘及正弦定理ACsinB =ABsinC得sinC=ABsinBAC=2√3×122=√32.由C为三角形的内角可知C=60∘或120∘.因此A=90∘或30∘.在△ABC中,由AB=2√3,AC=2,A=90∘或30∘,得面积S=12AC⋅AB⋅sinA=2√3或√3.【知识点】正弦定理二、填空题(共6题)11. 【答案】×【知识点】余弦定理12. 【答案】16【解析】该试验所有的样本点为(甲,乙丙),(乙,甲丙),(丙,甲乙),(甲乙,丙),(甲丙,乙),(乙丙,甲)(其中每个样本点表示的都是“派往A区调研的专家、派往B区调研的专家”),共6个,其中甲、乙两位专家均被派遣至 A 区的样本点有 1 个,因此,所求事件的概率为 16. 【知识点】古典概型13. 【答案】 −12【解析】因为 a =(2,1),b⃗ =(−1,x ), 所以 a +b ⃗ =(1,x +1),a −b ⃗ =(3,1−x ), 又 (a +b ⃗ )∥(a −b⃗ ), 所以 1−x −3(x +1)=0, 解得 x =−12.【知识点】平面向量数乘的坐标运算14. 【答案】 36π【知识点】球的表面积与体积15. 【答案】交线;垂直; a ⊂α ; a ⊥l【知识点】平面与平面垂直关系的性质16. 【答案】 (0,1)【知识点】复数的几何意义、复数的乘除运算三、解答题(共6题) 17. 【答案】(1) 略. (2) 略.【知识点】圆柱的表面积与体积、球的表面积与体积18. 【答案】如图所示,设向量 OA⃗⃗⃗⃗⃗ 的长度和方向表示水流速度的大小和方向,向量 OB ⃗⃗⃗⃗⃗ 的长度和方向表示船在静水中速度的大小和方向,以 OA⃗⃗⃗⃗⃗ ,OB ⃗⃗⃗⃗⃗ 为邻边作平行四边形 OACB ,连接 OC . 依题意得 OC ⃗⃗⃗⃗⃗ ⊥OA ⃗⃗⃗⃗⃗ ,∣∣BC ⃗⃗⃗⃗⃗ ∣∣=∣∣OA ⃗⃗⃗⃗⃗ ∣∣=20,∣∣OB ⃗⃗⃗⃗⃗ ∣∣=40,所以 ∠BOC =30∘.故船应向上游且与河岸夹角为 60∘ 的方向行进. 【知识点】平面向量的实际应用问题19. 【答案】(1) 因为 A +B +C =π, 所以 sin (B +C )=sinA , 所以 b 2+c 2−a 2=2bcsinA ,所以b 2+c 2−a 22bc=sinA ,由余弦定理得 cosA =sinA ,可得 tanA =1, 又因为 A ∈(0,π), 所以 A =π4.(2) 根据正弦定理得 b =a sinA ⋅sinB =√6,又 sinC =sin (A +B )=sin (π4+π3)=√6+√24, 所以S △ABC =12absinC =12⋅2⋅√6⋅√6+√24=3+√32.【知识点】余弦定理、正弦定理20. 【答案】①平面 α 内两条相交直线 a ,b ,即 a ⊂α,b ⊂α,a ∩b =P .②两条相交直线 a ,b 都与 β 平行,即 a ∥β,b ∥β. 【知识点】平面与平面平行关系的判定21. 【答案】 300×1.70<600,够用.【知识点】样本数据的数字特征22. 【答案】(1) 根据题意作出统计表:平均数方差中位数命中9环及以上次数甲7 1.271乙75.47.53因为平均数相同,且 s 甲2<s 乙2,所以甲的成绩比乙稳定,甲更优秀.(2) 因为平均数相同,甲的中位数 < 乙的中位数, 所以乙的成绩比甲好.(3) 因为平均数相同,且乙命中 9 环及以上的次数比甲多, 所以乙的成绩比甲好.(4) 因为甲的成绩在平均线附近波动,而乙的成绩整体处于上升趋势,从第 4 次开始射靶的环数没有比甲少的情况发生, 所以乙更有潜力.【知识点】样本数据的数字特征。
高一下数学同步训练:向量及其运算测试(A卷)(附答案)

高一数学同步检测十七 向量及其运算测试(A 卷)说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入答题栏内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.第Ⅰ卷(选择题 共40分)一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,选择一个符合题目要求的选项)1.给出关于平面向量的四个命题: ①a 是非零向量,且a ·b =a ·c ,则b =c ;②|a ·b |=|a |·|b |;③a 、b 是非零向量,a ⊥b ,则|a +b |=|a -b |;④a ,b 是任意两个不共线的非零向量,存在实数p 1、p 2,使得p 1a +p 2b =0,则p 21+p 22=0.以上命题只有两个是正确的,它们是A .③④B .①②C .①③D .②④ 答案:A解析:若a ⊥b ,a ⊥c ,则a ·b =a ·c =0,不一定有b =c ,故①不正确;由a ·b =|a ||b |cosθ,所以|a ·b |=|a ||b ||cosθ|≤|a ||b |.故②不正确.2.设e 1、e 2是两个不共线的向量,则向量a =e 1+λe 2(λ∈R )与向量b =-(e 1-2e 2)共线的充要条件是A .λ=0B .λ=-1C .λ=2D .λ=-2 答案:D解析:因为a ∥b ,所以存在一个实数μ,使a =μb ,即e 1+λe 2=-μ(e 1-2e 2).3.把函数y =2sin2x 的图象按向量a 的方向平移,得到函数y =2sin(2x +π3)+1的图象,则向量a 的坐标为A .(-π3,1)B .(-π6,1)C .(π3,-1)D .(π6,1)答案:B解析:设向量a =(m ,n),在函数y =2sin2x 的图象上任取一点(x 1,y 1),平移后的对应点为(x 0,y 0),4.已知△ABC 的三个顶点A 、B 、C 及平面内一点P ,若,则点P 与△ABC 的位置关系是A .P 在AC 边上B .P 在AB 边上或其延长线上C .P 在△ABC 的内部D .P 在△ABC 的外部答案:A5.如图,已知正六边形P 1P 2P 3P 4P 5P 6,下列向量的数量积中最大的是A.B.C.D.答案:A6.在平行四边形ABCD 中,=13,=14,CE 与BF 相交于G 点,若=a ,=b ,则等于 A.27a +17b B.27a +37b C.37a +17b D.47a +27b 答案:C 解析:如图,7.设向量a =(1,-3),b =(-2,4),c =(-1,-2).若表示向量4a 、4b -2c 、2(a -c )、d 的有向线段首尾相接能构成四边形,则向量d 为A .(2,6)B .(-2,6)C .(2,-6)D .(-2,-6) 答案:D解析:由题意知4a +4b -2c +2(a -c )+d =0, 则(4,-12)+(-6,20)+(4,-2)+d =0, 即(2,6)+d =0,所以d =(-2,-6).8.与向量a =(72,12),b =(12,-72)的夹角相等,且模为1的向量是A .(45,-35)B .(45,-35)或(-45,35)C .(223,-13)D .(223,-13)或(-223,13)答案:B解析:代入验证,知A 、B 、C 、D 模均为1,且|a |=|b |. 设向量e 与a 、b 夹角相等,则a ·e =b ·e ,代入验证即可.9.若点P 分有向线段所成的比为-13,则点B 分有向线段所成的比是A .-32B .-12 C.12 D .3答案:A10.已知向量a =(2,1),a ·b =10,|a +b |=52,则|b |等于 A. 5 B.10 C .5 D .25 答案:C解析:∵50=|a +b |2=|a |2+2a ·b +|b |2 =5+20+|b |2, ∴|b |=5.第Ⅱ卷(非选择题 共60分)二、填空题(本大题共4小题,每小题4分,共16分.答案需填在题中横线上)11.如图,M 、N 是△ABC 的一边BC 上的两个三等分点,若=a ,=b ,则=________.答案:13(b -a )12.若|a |=2,|b |=5,a ·b =-3,则|a +b |=________. 答案:23解析:由|a +b |2=a 2+2a ·b +b 2=22+2×(-3)+52=23,得|a +b |=23. 13.如图,平面内两条相交直线OP 1和OP 2,将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界),若=a+b,且点P 落在第Ⅲ部分,则点(a ,b)在第________象限.答案:四解析:∵P 落在第Ⅲ部分,∴在直线OP 1上的分向量与同向,在直线上的分向量与反向. ∴a>0,b<0,故点(a ,b)在第四象限.14.已知|a |=1,|b |=2,且(λa +b )⊥(2a -λb ),a 与b 的夹角为60°,则λ=________. 答案:-1±3解析:a ·b =|a ||b |cos60°=1×2×12=1.∵(λa +b )⊥(2a -λb ), ∴(λa +b )·(2a -λb )=0,即2λa 2+(2-λ2)a ·b -λb 2=0. ∴λ2+2λ-2=0.解得λ=-1±3.三、解答题(本大题共5小题,共44分.解答应写出文字说明、证明过程或演算步骤) 15.(本小题满分8分)一架执行任务的飞机从A 地按北偏西30°的方向飞行300 km 后到达B 地,然后向C 地飞行,已知C 地在A 地东偏北30°的方向处,且A 、C 两地相距300 km ,求飞机从B 地到C 地飞行的方向及B 、C 间的距离.答案:又因为∠ABC =45°,且A 地在B 地的东偏南60°的方向处,可知C 地在B 地的东偏南15°的方向处.答:飞机从B 地向C 地飞行的方向是东偏南15°,B 、C 两地间的距离为300 2 km.16.(本小题满分8分)如图,▱ABCD 中,M 、N 分别为DC 、BC 的中点,已知=c ,=d ,试用c 、d 表示和.答案:17.(本小题满分9分)求证:平行四边形对角线的平方和等于四边的平方和.答案:证法一:如图,▱ABCD中,求证:AB2+BC2+CD2+DA2=AC2+BD2.①+②得AC2+BD2=2a2+2b2=AB2+BC2+CD2+DA2.故原命题得证.证法二:如图,建立平面直角坐标系,设A(m,n),C(p,0),18.(本小题满分9分)已知a 、b 是两个非零向量,同时满足|a |=|b |=|a -b |,求a 与a +b 的夹角.答案:解法一:根据|a |=|b |,有|a |2=|b |2, 又由|b |=|a -b |,得|b |2=|a |2-2a ·b +|b |2,∴a ·b =12|a |2.而|a +b |2=|a |2+2a ·b +|b |2=3|a |2. 设a 与a +b 的夹角为θ,则解法二:设向量a =(x 1,y 1),b =(x 2,y 2), ∵|a |=|b |,∴x 12+y 12=x 22+y 22.由|b |=|a -b |,得x 1x 2+y 1y 2=12(x 12+y 12).由|a +b |2=2(x 12+y 12)+2·12(x 12+y 12)=3(x 12+y 12),得|a +b |=3·x 12+y 12.设a 与a +b 的夹角为θ,则∴θ=30°.∴△AOB 为正三角形,∠AOB =60°. 于是∠AOC =30°,即a 与a +b 的夹角为30°.19.(本小题满分10分)平面内三点A 、B 、C 共线,=(-2,m),=(n,1),=答案:解:因为A 、B 、C 三点共线,所以=λ.因为=-=(7,-1-m),=-=(n +2,1-m), 所以(7,-1-m)=λ(n +2,1-m), 即7=λ(n +2),1+m =λ(m -1). 所以mn -5m +n +9=0.① 由·=0,得m -2n =0.②由①②得m =6,n =3或m =3,n =32.。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(1)

高一数学必修第二册全册复习测试题卷11(共22题)一、选择题(共10题)1. △ABC 中,若 a =1,c =2,B =60∘,则 △ABC 的面积为 ( ) A . 12B . 1C .√32D . √32. 若书架中放有中文书 5 本,英文书 3 本,日文书 2 本,则抽出一本书为外文书的概率为 ( ) A . 15B . 310C . 25D . 123. 若 θ 为两个非零向量的夹角,则 θ 的取值范围为 ( ) A .(0,π) B .(0,π] C .[0,π) D .[0,π]4. 从一箱产品中随机地抽取一件,设事件 A = { 抽到一等品 },事件 B = { 抽到二等品 },事件 C = { 抽到三等品 } ,且已知 P (A )=0.65,P (B )=0.2,P (C )=0.1.则事件“抽到的是二等品或三等品”的概率为 ( ) A .0.7 B .0.65 C .0.35 D .0.35. 下列关于古典概型的说法中正确的是 ( ) ①试验中所有可能出现的样本点只有有限个; ②每个事件出现的可能性相等; ③每个样本点出现的可能性相等;④若样本点总数为 n ,随机事件 A 包含其中的 k 个样本点,则 P (A )=kn . A .②④ B .③④ C .①④ D .①③④6. 给定一组数据:102,100,103,104,101,这组数据的第 60 百分位数是 ( ) A . 102 B . 102.5 C . 103 D . 103.57. 为比较甲、乙两地某月 14 时的气温情况,随机选取该月中的 5 天,这 5 天中 14 时的气温数据(单位:∘C )如下:甲:2628293131乙:2829303132以下结论:①甲地该月 14 时的平均气温低于乙地该月 14 时的平均气温; ②甲地该月 14 时的平均气温高于乙地该月 14 时的平均气温;③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.其中根据数据能得到的统计结论的编号为( )A.①③B.①④C.②③D.②④8.下列说法正确的是( )A.任何事件的概率总是在(0,1)之间B.频率是客观存在的,与试验次数无关C.随着试验次数的增加,事件发生的频率一般会稳定于概率D.概率是随机的,在试验前不能确定9.用符号表示“点A在直线l上,l在平面α内”,正确的是( )A.A∈l,l∉αB.A⊂l,l⊄αC.A⊂l,l∈αD.A∈l,l⊂α10.半径为2的球的表面积为( )A.4πB.8πC.12πD.16π二、填空题(共6题)11.一家保险公司想了解汽车的挡风玻璃在一年时间里破碎的概率,公司收集了20000部汽车,时间从某年的5月1日到下一年的5月1日,共发现有600部汽车的挡风玻璃破碎,则一部汽车在一年时间里挡风玻璃破碎的概率约为.12.思考辨析 判断正误.( )做100次拋硬币的试验,结果51次出现正面朝上,因此,出现正面朝上的概率是5110013.若空间两个角的两条边分别平行,则这两个角的大小关系是.14.如图所示,在复平面内,网格中的每个小正方形的边长都为1,点A,B对应的复数分别是z1,=.z2,则z2z115.平均数:如果n个数x1,x2,⋯,x n,那么x=叫做这n个数的平均数.16.思考辨析判断正误为了更清楚地反映学生在这学期多次考试中数学成绩情况,可以选用折线统计图.( )三、解答题(共6题)17.如图所示,梯形ABCD中,AD∥BC,且AD<BC,当梯形ABCD绕AD所在直线旋转一周时,其他各边旋转围成了一个几何体,试描述该几何体的结构特征.18.小明是班里的优秀学生,他的历次数学成绩是96,98,95,93,45分,最近一次考试成绩只有45分的原因是他带病参加了考试.期末评价时,怎样给小明评价(90分及90分以上为优秀,75∼90分为良好)?19.类比绝对值∣x−x0∣的几何意义,∣z−z0∣(z,z0∈C)的几何意义是什么?20.如图,在三棱锥P−ABC中,平面PAC⊥平面ABC,∠ACB=90∘,PA=AC=2BC.(1) 若PA⊥PB,求证:平面PAB⊥平面PBC;(2) 若PA与平面ABC所成角的大小为60∘,求二面角C−PB−A的余弦值.21.应用面面平行判断定理应具备哪些条件?22.如图,在四棱锥P−ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,PD=9,E为PA的中点.(1) 求证:DE∥平面BPC.(2) 在线段AB上是否存在一点F,满足CF⊥DB?若存在,试求出此时三棱锥B−PCF的体积;若不存在,请说明理由.答案一、选择题(共10题) 1. 【答案】C【解析】由题得 △ABC 的面积 S =12AB ⋅BC ⋅sin60∘=12×2×1×√32=√32. 【知识点】三角形的面积公式2. 【答案】D【解析】在 10 本书中,中文书 5 本,外文书为 3+2=5 本,由古典概型,在其中抽出一本书为外文书的概率为 510,即 12. 【知识点】古典概型3. 【答案】D【知识点】平面向量的数量积与垂直4. 【答案】D【解析】由题意知事件 A 、 B 、 C 互为互斥事件,记事件 D =“抽到的是二等品或三等品”,则 P (D )=P (B ∪C )=P (B )+P (C )=0.2+0.1=0.3. 【知识点】事件的关系与运算5. 【答案】D【解析】②中所说的事件不一定是样本点,所以②不正确;根据古典概型的特征及计算公式可知①③④正确. 【知识点】古典概型6. 【答案】D【解析】 5×0.6=3,第 60 百分位数是第三与第四个数的平均数, 即103+1042=103.5.【知识点】样本数据的数字特征7. 【答案】B【解析】因为 x 甲=26+28+29+31+315=29,x 乙=28+29+30+31+325=30,所以 x 甲<x 乙.又 s 甲2=9+1+0+4+45=185,s 乙2=4+1+0+1+45=2,所以 s 甲>s 乙,故由样本估计总体可知结论①④正确. 【知识点】样本数据的数字特征8. 【答案】C【解析】不可能事件的概率为 0,必然事件的概率为 1,故A 错误;频率是由试验的次数决定的,故B 错误;概率是频率的稳定值,故C 正确,D 错误. 【知识点】频率与概率9. 【答案】D【解析】点 A 在直线 l 上,表示为 A ∈l ,l 在平面 α 内,表示为 l ⊂α. 【知识点】平面的概念与基本性质10. 【答案】D【解析】因为球的半径为 r =2, 所以该球的表面积为 S =4πr 2=16π. 【知识点】球的表面积与体积二、填空题(共6题) 11. 【答案】 0.03【解析】 P =60020000=0.03.【知识点】频率与概率12. 【答案】 ×【知识点】频率与概率13. 【答案】相等或互补【知识点】直线与直线的位置关系14. 【答案】 −1−2i【解析】由题意,根据复数的表示可知z1=i,z2=2−i,所以z2z1=2−ii=(2−i)⋅(−i)i⋅(−i)=−1−2i.【知识点】复数的乘除运算、复数的几何意义15. 【答案】1n(x1+x2+⋯+x n)【知识点】样本数据的数字特征16. 【答案】√【知识点】频率分布直方图三、解答题(共6题)17. 【答案】如图所示,旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的组合体.【知识点】组合体18. 【答案】小明5次考试成绩从小到大排列为45,93,95,96,98,中位数是95,应评定为“优秀”.【知识点】样本数据的数字特征19. 【答案】∣z−z0∣(z,z0∈C)的几何意义是复平面内点Z到点Z0的距离.【知识点】复数的加减运算20. 【答案】(1) 因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,BC⊂平面ABC,BC⊥AC,所以BC⊥平面PAC,因为PA⊂平面PAC,所以PA⊥BC.又PA⊥PB,PB∩BC=B,所以PA⊥平面PBC,因为PA⊂平面PAB,所以平面PAB⊥平面PBC.(2) 如图,过P作PH⊥AC于点H,因为平面PAC⊥平面ABC,所以PH⊥平面ABC,所以∠PAH=60∘,不妨设PA=2,所以PH=√3,以 C 为原点,分别以 CA ,CB 所在直线为 x 轴,y 轴,以过 C 点且平行于 PH 的直线为 z 轴,建立如图所示的空间直角坐标系,则 C (0,0,0),A (2,0,0),B (0,1,0),P(1,0,√3),因此 AB⃗⃗⃗⃗⃗ =(−2,1,0),AP ⃗⃗⃗⃗⃗ =(−1,0,√3),CB ⃗⃗⃗⃗⃗ =(0,1,0),CP ⃗⃗⃗⃗⃗ =(1,0,√3). 设 n ⃗ =(x 1,y 1,z 1) 为平面 PAB 的一个法向量, 则 {n ⃗ ⋅AB⃗⃗⃗⃗⃗ =0,n ⃗ ⋅AP⃗⃗⃗⃗⃗ =0, 即 {−2x 1+y 1=0,−x 1+√3z 1=0,令 z 1=√3,可得 n ⃗ =(3,6,√3), 设 m ⃗⃗ =(x 2,y 2,z 2) 为平面 PBC 的一个法向量, 则 {m ⃗⃗ ⋅CB⃗⃗⃗⃗⃗ =0,m ⃗⃗ ⋅CP ⃗⃗⃗⃗⃗ =0, 即 {y 2=0,x 2+√3z 2=0,令 z 2=√3,可得 m ⃗⃗ =(−3,0,√3), 所以 cos⟨m ⃗⃗ ,n ⃗ ⟩=4√3×2√3=−14, 易知二面角 C −PB −A 为锐角, 所以二面角 C −PB −A 的余弦值为 14.【知识点】平面与平面垂直关系的判定、利用向量的坐标运算解决立体几何问题、二面角21. 【答案】①平面 α 内两条相交直线 a ,b ,即 a ⊂α,b ⊂α,a ∩b =P .②两条相交直线 a ,b 都与 β 平行,即 a ∥β,b ∥β. 【知识点】平面与平面平行关系的判定22. 【答案】(1) 取 PB 的中点 M ,连接 EM ,CM ,过点 C 作 CN ⊥AB ,垂足为 N ,如图所示. 因为 CN ⊥AB ,DA ⊥AB , 所以 CN ∥DA , 又 AB ∥CD ,所以四边形 CDAN 为矩形, 所以 CN =AD =8,DC =AN =6.在 Rt △BNC 中,BN =√BC 2−CN 2=√102−82=6, 所以 AB =12.因为 E ,M 分别为 PA ,PB 的中点, 所以 EM ∥AB 且 EM =6, 又 DC ∥AB ,且 CD =6, 所以 EM ∥CD 且 EM =CD , 则四边形 CDEM 为平行四边形, 所以 DE ∥CM .因为 CM ⊂平面BPC ,DE ⊄平面BPC ,所以 DE ∥平面BPC .(2) 存在.理由如下:由题意可得 DA ,DC ,DP 两两互相垂直,故以 D 为原点,DA ,DC ,DP所在直线分别为 x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系 Dxyz . 则 D (0,0,0),B (8,12,0),C (0,6,0),所以 DB⃗⃗⃗⃗⃗⃗ =(8,12,0). 假设 AB 上存在一点 F 使 CF ⊥BD ,设点 F 坐标为 (8,t,0)(0≤t ≤12), 则 CF⃗⃗⃗⃗⃗ =(8,t −6,0), 由 CF ⃗⃗⃗⃗⃗ ⋅DB ⃗⃗⃗⃗⃗⃗ =0,得 64+12(t −6)=12t −8=0, 所以 t =23,即 AF =23,故 BF =12−23=343.又 PD =9,所以 V 三棱锥B−PCF =V 三棱锥P−BCF =13×12×343×8×9=136.【知识点】直线与平面平行关系的判定、利用向量的坐标运算解决立体几何问题。
人教版高一数学必修一第一学期期末测试A卷(含答案和解析)

期末测试卷02(本卷满分150分,考试时间120分钟) 测试范围:必修第一册(人教A 版2019)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.设集合}034|{2<+-=x x x A ,}032|{>-=x x B ,则=B A ( )。
A 、)231(,B 、)31(, C 、)323(,D 、)1(∞+,【答案】C【解析】由题意得,}31|{<<=x x A ,}23|{>=x x B ,则)323(,=B A ,故选C 。
2.命题“全等三角形的面积一定都相等”的否定是( )。
A 、全等三角形的面积不一定都相等B 、不全等三角形的面积不一定都相等C 、存在两个不全等三角形的面积相等D 、存在两个全等三角形的面积不相等 【答案】D【解析】命题是省略量词的全称命题,故选D 。
3.已知0>a ,0>b ,且12=+b a ,则ba 11+的最小值为( )。
A 、223+ B 、243+ C 、263+ D 、283+ 【答案】A【解析】∵0>a ,0>b ,∴223221)11)(2(11+≥+++=++=+ab b a b a b a b a , 即最小值为223+,故选A 。
4.已知α为第三象限角,且α=-α2cos 22sin 2,则)42sin(π-α的值为( )。
A 、1027- B 、107- C 、107 D 、1027 【答案】D【解析】由已知得)1(cos 22sin 22-α=-α,则4tan 2=α,由α为第三象限角,得2tan =α,故552sin -=α,55cos -=α,∴1027)2cos 2(sin 22)42sin(=α-α=π-α,故选D 。
5.若函数)2lg()(2a x ax x f +-=的定义域为R ,则实数a 的取值范围为( )。
人教A版高一数学必修第二册全册复习测试题卷含答案解析(52)

高一数学必修第二册全册复习测试题卷(共22题)一、选择题(共10题)1. 在 △ABC 中,∠BAC =60∘,∠BAC 的平分线 AD 交 BC 边于点 D ,已知 AD =2√3,且λAB ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −13AC ⃗⃗⃗⃗⃗ (λ∈R ),则 AB ⃗⃗⃗⃗⃗ 在 AD ⃗⃗⃗⃗⃗ 方向上的投影数量为 ( )A . 1B . 32C . 3D . 3√322. 在 △ABC 中,内角 A ,B ,C 的对边分别为 a ,b ,c .若 3bcosC =c (1−3cosB ),则 c:a = ( ) A . 1:3 B . 4:3 C . 3:1 D . 3:23. 已知 △ABC 中,内角 A ,B ,C 所对的边分别为 a ,b ,c 且 acosC +√32c =b ,若 a =1,√3c −2b =1,则角 B 为 A .π4B .π6C .π3D .π124. 已知向量 a =(2,x ),b ⃗ =(1,2),若 a ∥b ⃗ ,则实数 x 的值为 ( ) A .1B .2C .3D .45. 珠穆朗玛峰是印度洋板块和欧亚板块碰撞挤压形成的.这种挤压一直在进行,珠穆朗玛峰的高度也一直在变化.由于地势险峻,气候恶劣,通常采用人工攀登的方式为珠峰“量身高”.攀登者们肩负高精度测量仪器,采用了分段测量的方法,从山脚开始,直到到达山顶,再把所有的高度差累加,就会得到珠峰的高度.2020 年 5 月,中国珠峰高程测量登山队 8 名队员开始新一轮的珠峰测量工作.在测量过程中,已知竖立在 B 点处的测量觇标高 10 米,攀登者们在 A 处测得到觇标底点 B 和顶点 C 的仰角分别为 70∘,80∘,则 A ,B 的高度差约为 ( )A . 10 米B . 9.72 米C . 9.40 米D . 8.62 米6. 在 △ABC 中,A =120∘,AB =5,BC =7,则 sinB sinC= ( )A . 37B . 35C . 57D . 857. 若 O 为平行四边形 ABCD 的中心,AB ⃗⃗⃗⃗⃗ =2e 1⃗⃗⃗ ,BC ⃗⃗⃗⃗⃗ =3e 2⃗⃗⃗ ,则 32e 2⃗⃗⃗ −e 1⃗⃗⃗ 等于 ( )A . AO ⃗⃗⃗⃗⃗B . BO ⃗⃗⃗⃗⃗C . CO ⃗⃗⃗⃗⃗D . DO⃗⃗⃗⃗⃗⃗8. 在 △ABC 中,AB =2AC =6,BA⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ 2,点 P 是 △ABC 所在平面内的一点,则当 PA ⃗⃗⃗⃗⃗ 2+PB ⃗⃗⃗⃗⃗ 2+PC ⃗⃗⃗⃗⃗ 2 取得最小值时,AP ⃗⃗⃗⃗⃗ ⋅BC ⃗⃗⃗⃗⃗ = ( ) A . 35B . −9C . 7D . −259. 在 △ABC 中,点 D 满足 BD ⃗⃗⃗⃗⃗⃗ =34BC ⃗⃗⃗⃗⃗ ,当点 E 在线段 AD 上移动时,若 AE ⃗⃗⃗⃗⃗ =λAB ⃗⃗⃗⃗⃗ +μAC ⃗⃗⃗⃗⃗ (λ,μ∈R ),则 t =(λ−1)2+μ2 的最小值是 ( ) A .3√1010B .√824C . 910D .41810. 已知 a ,b ⃗ ,c 是三个不共线的向量,a 为给定向量,那么下列叙述中正确的是 ( )A .对任何非零实数 λ 及给定的向量 b ⃗ ,c ,均存在唯一的实数 μ,使得 a =λb ⃗ +μcB .对任何向量 b ⃗ 及给定的非零实数 λ,μ,均存在唯一的向量 c ,使得 a =λb ⃗ +μcC .若 ∣b ⃗ ∣=1,则对任何实数 λ,均存在单位向量 c 和实数 μ,使得 a =λb ⃗ +μcD .若 ∣b ⃗ ∣=1,则对任何实数 μ,均存在单位向量 c 和实数 λ,使得 a =λb ⃗ +μc二、填空题(共6题)11. 已知复数 a+i2−i 为纯虚数,那么实数 a = .12. 如图所示,三棱锥 P −ABC 外接球的半径为 1,且 PA 过球心,△PAB 围绕棱 PA 旋转 60∘后恰好与 △PAC 重合.若 PB =√3,则三棱锥 P −ABC 的体积为 .13. 思考辨析 判断正误频率分布直方图中所有小长方形面积之和为 1.14. 已知向量 a ,b ⃗ 满足 ∣a ∣=2,∣∣b ⃗ ∣∣=3,且已知向量 a,b ⃗ 的夹角为 60∘,(a −c )⋅(b ⃗ −c )=0,则 ∣c ∣ 的最小值是 .15. 已知向量 a =(1,2),b ⃗ =(2,−2),c =(1,λ).若 c ∥(2a +b ⃗ ),则 λ= .16. 在相距 2 km 的 A ,B 两点处测量目标点 C ,若 ∠CAB =75∘,∠CBA =60∘,则 A ,C 两点之间的距离为 .三、解答题(共6题)17. 如图,在五面体 ABCDEF 中,四边形 ABCD 是边长为 2 的正方形,EF ∥平面ABCD ,EF =1,FB =FC ,∠BFC =90∘,AE =√3,H 是 BC 的中点.(1) 求证:FH ∥平面BDE ; (2) 求证:AB ⊥平面BCF ; (3) 求五面体 ABCDEF 的体积.18. 对于任意实数 a ,b ,c ,d ,表达式 ad −bc 称为二阶行列式(determinant ),记作 ∣∣∣ab cd ∣∣∣. (1) 求下列行列式的值:① ∣∣∣1001∣∣∣; ② ∣∣∣1326∣∣∣; ③ ∣∣∣−2510−25∣∣∣;(2) 求证:向量 p =(a,b ) 与向量 q =(c,d ) 共线的充要条件是 ∣∣∣a b cd ∣∣∣=0.(3) 讨论关于 x ,y 的二元一次方程组 {a 1x +b 1y =c 1,a 2x +b 2y =c 2(a 1a 2b 1b 2≠0) 有唯一解的条件,并求出解.(结果用二阶行列式的记号表示)19. 有些同学说:实轴上的点表示实数,虚轴上的点表示虚数,这句话对吗?20. 在 △ABC 中,a ,b ,c 分别是内角 A ,B ,C 的对边,且 A =π6,a =2.(1) 若 B =π4,求 b 的值;(2) 若 △ABC 的面积为 √3,求 △ABC 的周长.21. 已知函数 f (x )=12sin2x −√3cos 2x .(1) 求函数 y =f (x ) 的最小正周期.(2) 在 △ABC 中,角 A ,B ,C 的对边分别为 a ,b ,c ,若锐角 A 满足 f (A )=1−√32,C =π6,c =2,求 △ABC 的面积.22. 在直角 △ABC 中,A =π2,D 为 AC 边上的一点,BD =√3.(1) 若 BC =3,∠BDC =2π3,求 △BDC 的面积.(2) 若 C =π3,求 △BCD 周长 l 的取值范围.答案一、选择题(共10题) 1. 【答案】D【解析】在 AC 上取点 E ,使 AE ⃗⃗⃗⃗⃗ =13AC ⃗⃗⃗⃗⃗ , 连接 DE ,过 D 作 DF ∥AC ,交 AB 于 F ,因为 λAB ⃗⃗⃗⃗⃗ =AD ⃗⃗⃗⃗⃗ −13AC ⃗⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ (λ∈R ),所以 ED ∥AB ,所以四边形 AFDE 为平行四边形, 又 AD 平分 ∠BAC , 所以四边形 AFDE 为菱形. 因为 AD =2√3,∠BAC =60∘, 所以 AE =2,则 AC =6. 设 FB =x , 因为 DF ∥AC , 所以 DFAC =FBAB , 即 26=x 2+x ,解得 x =1, 即 FB =1, 所以 AB =3.所以 AB ⃗⃗⃗⃗⃗ 在 AD ⃗⃗⃗⃗⃗ 方向上的投影数量为 ∣∣AB ⃗⃗⃗⃗⃗ ∣∣⋅cos30∘=3√32.【知识点】平面向量的数量积与垂直2. 【答案】C【解析】由 3bcosC =c (1−3cosB ) 及正弦定理可得 3sinBcosC =sinC (1−3cosB ),化简可得sinC=3sin(B+C).又A+B+C=π,所以sinC=3sinA,所以c:a=sinC:sinA=3:1.【知识点】正弦定理3. 【答案】B【解析】因为acosC+√32c=b,由正弦定理得sinAcosC+√32sinC=sinB=sin(B+C),整理得cosA=√32,所以A=π6,又因为a=1,√3c−2b=1,所以√3sinC−2sinB=sinA=12,即√3sin(5π6−B)−2sinB=12,整理得cos(B+π6)=12,所以B=π6.【知识点】正弦定理4. 【答案】D【解析】向量a=(2,x),b⃗=(1,2),a∥b⃗,可得x=4.【知识点】平面向量数乘的坐标运算5. 【答案】C【解析】根据题意画出如图的模型,则CB=10,∠OAB=70∘,∠OAC=80∘,所以∠CAB=10∘,∠ACB=10∘,所以AB=10,所以在Rt△AOB中,BO=10sin70∘≈9.4(米).【知识点】解三角形的实际应用问题6. 【答案】B【解析】由余弦定理得BC2=AB2+AC2−2⋅AB⋅AC⋅cosA,因此49=25+AC2+5AC,解得AC=3或AC=−8(舍去),因此由正弦定理得sinB sinC=AC AB=35.【知识点】正弦定理、余弦定理7. 【答案】B【解析】由 BA ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ 得 3e 2⃗⃗⃗ −2e 1⃗⃗⃗ =BD ⃗⃗⃗⃗⃗⃗ ,即 2(32e 2⃗⃗⃗ −e 1⃗⃗⃗ )=BD ⃗⃗⃗⃗⃗⃗ =2BO ⃗⃗⃗⃗⃗ .【知识点】平面向量的数乘及其几何意义8. 【答案】B【知识点】平面向量的数量积与垂直9. 【答案】C【解析】如图,设存在实数 m 使得 AE⃗⃗⃗⃗⃗ =mAD ⃗⃗⃗⃗⃗ (0≤m ≤1), 因为AD ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BD⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +34BC ⃗⃗⃗⃗⃗ =AB⃗⃗⃗⃗⃗ +34(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=14AB ⃗⃗⃗⃗⃗ +34AC ⃗⃗⃗⃗⃗ , 所以 AE ⃗⃗⃗⃗⃗ =m (14AB ⃗⃗⃗⃗⃗ +34AC ⃗⃗⃗⃗⃗ )=m 4AB⃗⃗⃗⃗⃗ +3m 4AC ⃗⃗⃗⃗⃗ , 所以 {λ=m 4,μ=3m 4,所以t =(λ−1)2+μ2=(m4−1)2+(3m 4)2=58m 2−m2+1=58(m −25)2+910,当 m =25 时,t 取得最小值,为 910.【知识点】平面向量的分解10. 【答案】B【解析】对于A,由平面向量基本定理可得,有且仅有一对实数λ,μ,使得a=λb⃗+μc成立.故条件中的“对任何非零实数λ”说法不正确.故A错误.对于B,由平面向量基本定理可得结论正确,故B正确.对于C,当λ=0时,a=μc,与题设a,b⃗,c是三个不共线的向量矛盾.故C错误.对于D,当μ=0时,a=λb⃗,与题设a,b⃗,c是三个不共线的向量矛盾.故D错误.【知识点】平面向量的分解二、填空题(共6题)11. 【答案】12【知识点】复数的乘除运算12. 【答案】√38【解析】如图所示,由题意,PA过球心,故取PA中点为O,O即为球心.连接BO,CO,有△PAC由△PAB绕PA轴60∘后重合,故PC=PB,过B作BH⊥PA于H点,同理过C作CH⊥PA于H点,由于r=1,PB=PC=√3,过O点作OG⊥PB于G点,OP=OB=1,故有OG=√(PB2)2−OP2=12⇒∠BPH=π6,即有BH=PB⋅sinπ6=√32,又且∠BHC=60∘,BH=CH,故S△BHC=12×√32×34=3√316,则有V P−ABC=V P−BHC+V A−BHC=13S△BHC(PH+AH)=13×3√316×2=√38,故三棱锥P−ABC的体积为√38.【知识点】棱锥的表面积与体积13. 【答案】 √【知识点】频率分布直方图14. 【答案】√19−√72【解析】如图所示,设 OA ⃗⃗⃗⃗⃗ =a ,OB ⃗⃗⃗⃗⃗ =b ⃗ ,OC ⃗⃗⃗⃗⃗ =c ,由题,得 ∠AOB =π3,∣∣OA ⃗⃗⃗⃗⃗ ∣∣=2,∣∣OB ⃗⃗⃗⃗⃗ ∣∣=3,CA⃗⃗⃗⃗⃗ =a −c ,CB ⃗⃗⃗⃗⃗ =b ⃗ −c ,a ⋅b ⃗ =2×3×cos60∘=3, 又 (a −c )⋅(b ⃗ −c )=0,所以 CA⃗⃗⃗⃗⃗ ⊥CB ⃗⃗⃗⃗⃗ ,则点 C 在以 AB 为直径的圆上, 取 AB 的中点为 M ,则 OM ⃗⃗⃗⃗⃗⃗ =12(OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ ), 设以 AB 为直径的圆与线段 OM 的交点为 E ,则 ∣c ∣ 的最小值是 ∣∣OE ⃗⃗⃗⃗⃗ ∣∣, 因为∣∣OM ⃗⃗⃗⃗⃗⃗ ∣∣=√14(OA⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ )2=12√OA ⃗⃗⃗⃗⃗ 2+2OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ 2=12×√4+2×3+9=√192,又 AB =√OA 2+OB 2−2OA ⋅OB ⋅cos60∘=√4+9−2×2×3×12=√7, 所以 ∣c ∣ 的最小值是 ∣∣OE ⃗⃗⃗⃗⃗ ∣∣=OM −ME =OM −12AB =√19−√72.【知识点】平面向量的数量积与垂直、余弦定理15. 【答案】 12【解析】 2a +b⃗ =2(1,2)+(2,−2)=(4,2), 又因为 c ∥(2a +b ⃗ ), 所以 4×λ−2×1=0, 所以 λ=12.【知识点】平面向量数乘的坐标运算16. 【答案】√6km【知识点】正弦定理三、解答题(共6题)17. 【答案】(1) 连接AC,AC与BD相交于点O,则点O是AC的中点,连接OH,EO,因为H是BC的中点,AB=1.所以OH∥AB,OH=12因为EF∥平面ABCD,EF⊂平面ABFE,平面ABCD∩平面ABFE=AB,所以EF∥AB.因为EF=1,所以OH∥EF,OH=EF.所以四边形EOHF是平行四边形.所以EO∥FH,EO=FH.因为EO⊂平面BDE,FH⊄平面BDE,所以FH∥平面BDE.(2) 证法1:取AB的中点M,连接EM,则AM=MB=1,由(1)知,EF∥MB,且EF=MB,所以四边形EMBF是平行四边形.所以EM∥FB,EM=FB.在Rt△BFC中,FB2+FC2=BC2=4,又FB=FC,得FB=√2.所以EM=√2.在△AME中,AE=√3,AM=1,EM=√2,所以AM2+EM2=3=AE2.所以AM⊥EM.所以AM⊥FB,即AB⊥FB.因为四边形ABCD是正方形,所以AB⊥BC.因为FB∩BC=B,FB⊂平面BCF,BC⊂平面BCF,所以AB⊥平面BCF.证法2:在Rt△BFC中,H为BC的中点,BC=1.所以FH=12AC=√2,EO=FH=1,在△AEO中,AE=√3,AO=12所以AO2+EO2=AE2.所以AO⊥EO.因为 FH ∥EO , 所以 AO ⊥FH .因为 FH ⊥BC ,BC ⊂平面ABCD ,AO ⊂平面ABCD ,AO ∩BC =C , 所以 FH ⊥平面ABCD . 因为 AB ⊂平面ABCD , 所以 FH ⊥AB .因为四边形 ABCD 是正方形, 所以 AB ⊥BC .因为 BC ⊂平面BCF ,FH ⊂平面BCF ,BC ∩FH =H , 所以 AB ⊥平面BCF . (3) 连接 EC ,在 Rt △BFC 中,FH =12BC =1, 所以 EO =FH =1.由(2)知 AB ⊥平面BCF ,且 EF ∥AB , 所以 EF ⊥平面BCF .因为 FH ⊥平面ABCD ,EO ∥FH , 所以 EO ⊥平面ABCD .所以四棱锥 E −ABCD 的体积为 V 1=13⋅EO ⋅S 正方形ABCD =13×1×22=43.所以三棱锥 E −BCF 的体积为 V 2=13⋅EF ⋅S △BCF =13×1×12×(√2)2=13. 所以五面体 ABCDEF 的体积为 V =V 1+V 2=53.【知识点】棱锥的表面积与体积、直线与平面垂直关系的判定、直线与平面平行关系的判定18. 【答案】(1) ① ∣∣∣1001∣∣∣=1;② ∣∣∣1326∣∣∣=1×6−2×3=0;③ ∣∣∣−2510−25∣∣∣=(−2)×(−25)−5×10=0. (2) 若向量 p =(a,b ) 与向量 q =(c,d ) 共线,则 当 q ≠0⃗ 时,有 ad −bc =0,即 ∣∣∣a b c d ∣∣∣=0, 当 q =0⃗ 时,有 c =d =0,即 ∣∣∣a b c d ∣∣∣=ad −bc =0, 所以必要性得证. 反之,若 ∣∣∣a b cd ∣∣∣=0,即 ad −bc =0,当 c ,d 不全为 0 时,即 q ≠0⃗ 时, 不妨设 c ≠0,则 b =adc,所以 p =(a,ad c),因为 q =(c,d ),所以 p =ac q ,所以 p ∥q , 所以向量 p =(a,b ) 与向量 q =(c,d ) 共线,当 c =0 且 d =0 时,q =0⃗ , 所以向量 p =(a,b ) 与向量 q =0⃗ 共线, 充分性得证.综上,向量 p =(a,b ) 与向量 q =(c,d ) 共线的充要条件是 ∣∣∣ab c d ∣∣∣=0. (3) 用 b 2 和 b 1 分别乘上面两个方程的两端,然后两个方程相减,消去 y 得 (a 1b 2−a 2b 1)x =c 1b 2−c 2b 1, ⋯⋯① 同理,消去 x 得 (a 1b 2−a 2b 1)y =a 1c 2−a 2c 1, ⋯⋯② 所以,当 a 1b 2−a 2b 1≠0 时,即 ∣∣∣a 1b 1a 2b 2∣∣∣≠0 时, 由①②可得 x =c 1b 2−c 2b 1a 1b 2−a 2b 1=∣∣∣c 1b 1c 2b 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣,y =a 1c 2−a 2c 1a1b 2−a 2b 1=∣∣∣a 1c 1a 2c 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣, 所以,当 ∣∣∣a 1b 1a 2b 2∣∣∣≠0 时,方程组 {a 1x +b 1y =c 1,a 2x +b 2y =c 2 有唯一解且 x =∣∣∣c 1b 1c 2b 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣,y =∣∣∣a 1c 1a 2c 2∣∣∣∣∣∣a 1b 1a 2b 2∣∣∣. 【知识点】平面向量数乘的坐标运算、二阶行列式19. 【答案】不正确.实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,原点对应的有序实数对为 (0,0),它所确定的复数是 z =0+0i =0,表示的是实数.【知识点】复数的几何意义20. 【答案】(1) 2√2. (2) 4+2√3.【知识点】余弦定理、正弦定理21. 【答案】(1) f (x )=12sin2x −√32cos2x −√32=sin (2x −x3)−√32, T =π.(2) sin (2A −π3)=12,2A −π3=16π, A =π4,C =π6,B =712π, asinA =csinC , a =2√2,S =12acsinB =12×2√2×2×sin 712π=1+√3. 【知识点】Asin(ωx+ψ)形式函数的性质、正弦定理22. 【答案】(1) 由余弦定理得:BC 2=DB 2+DC 2−2DB ⋅DC ⋅cos2π3,即 DC 2+√3DC −6=0,解得 DC =√3,DC =−2√3(舍去).S △BDC =12BD ⋅DC ⋅sin∠BDC =12×√3×√3×sin 2π3=3√34.(2) 在 △BCD 中,C =π3,∠ABC =π6,BD =√3, 设 ∠DBC =α,所以BDsin π3=CD sinα=BC sin(2π3−α),故 CD =2sinα,BC =2sin (α+π3),所以 △BCD 的周长 l =BD +BC +CD =√3+2sinα+2sin (α+π3),即 l =√3+2√3sin (α+π6),因为 α∈(0,π6],所以 l ∈(2√3,3+√3].【知识点】余弦定理、Asin(ωx+ψ)形式函数的性质、正弦定理。
高一数学上学期第一次质检试卷(a卷)(含解析)-人教版高一全册数学试题

2014-2015学年某某省某某市龙河中学高一(上)第一次质检数学试卷(A卷)一、选择题(本大题共12小题,每小题5分,共60分)1.设集合A={x∈Q|x>﹣1},则()A.∅∈A B. C. D.⊈A2.已知全集U={0,1,2,3,4},M={0,1,2},N={2,3},则(∁U M)∩N=()A. {2,3,4} B. {3} C. {2} D. {0,1,2,3,4}3.50名同学参加跳远和铅球测验,跳远和铅球测验成绩分别为及格40人和31人,2项测验成绩均不及格的有4人,2项测验成绩都及格的人数是()A. 35 B. 25 C. 28 D. 154.如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,则 A*B ()A.∁U(A∪B) B. A∪(∁U B) C.(∁U A)∪(∁U B) D.(A∪B)∩∁U(A∩B)5.下列函数中,在区间(0,2)上为增函数的是()A. y=3﹣x B. y=x2+1 C. D. y=﹣|x|6.已知函数f(x)的定义域为(3﹣2a,a+1),且f(x+1)为偶函数,则实数a的值可以是()A. B. 2 C. 4 D. 67.已知函数y=f(x+1)定义域是[﹣2,3],则y=f(x﹣1)的定义域是()A. [0,5] B. [﹣1,4] C. [﹣3,2] D. [﹣2,3]8.若函数f(x)为奇函数,且当x>0时,f(x)=x﹣1,则当x<0时,有()A. f(x)>0 B. f(x)<0 C. f(x)f(﹣x)≤0 D. f(x)﹣f(﹣x)>0 9.函数f(x)的定义域为R+,若f(x+y)=f(x)+f(y),f(8)=3,则f(2)=() A. B. C. D.10.下列所给四个图象中,与所给3件事吻合最好的顺序为()(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再去上学;(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A.①②④ B.④②③ C.①②③ D.④①②11.函数y=f(x)是R上的偶函数,且在(﹣∞,0]上是增函数,若f(a)≤f(2),则实数a的取值X围是()A. a≤2 B. a≥﹣2 C.﹣2≤a≤2 D. a≤﹣2或a≥212.已知函数f(x)=4x2﹣mx+5在区间[﹣2,+∞)上是增函数,则f(1)的X围是() A. f(1)≥25 B. f(1)=25 C. f(1)≤25 D. f(1)>25二、填空题(本大题共4小题,每小题5分,共20分)13.函数y=+的定义域是.14.设函数f(x)=则f[f(﹣1)]的值为.15.已知A有限集合,x∉A,B=A∪{x},若A,B的子集个数分别为a,b,且b=ka,则k=.16.函数f(x)=2x2﹣3|x|的单调减区间是.三、解答题(本大题共6小题,满分70分)17.已知集合A={x|3≤x<10},集合B={x|2x﹣8≥0}.(1)求A∪B;(2)求∁R(A∩B).18.设集合A={a,a2,b+1},B={0,|a|,b}且A=B.(1)求a,b的值;(2)判断函数在[1,+∞)的单调性,并用定义加以证明.19.已知f(x)=x2013+ax3﹣﹣8,f(﹣2)=10,求f(2).20.已知函数f(x)=,x∈[1,+∞).(1)当a=时,判断并证明f(x)的单调性;(2)当a=﹣1时,求函数f(x)的最小值.21.定义在实数R上的函数y=f(x)是偶函数,当x≥0时,f(x)=﹣4x2+8x﹣3.(Ⅰ)求f(x)在R上的表达式;(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).22.已知函数f(x)的定义域为R,对于任意的x,y∈R,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,若f(﹣1)=2.(1)求证:f(x)为奇函数;(2)求证:f(x)是R上的减函数;(3)求函数f(x)在区间[﹣2,4]上的值域.2014-2015学年某某省某某市龙河中学高一(上)第一次质检数学试卷(A卷)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.设集合A={x∈Q|x>﹣1},则()A.∅∈A B. C. D.⊈A考点:元素与集合关系的判断.专题:计算题.分析:先从已知的集合中看出集合中元素的本质属性,再结合元素与集合关系及集合与集合关系对选项进行判断即可.解答:解:∵集合A={x∈Q|x>﹣1},∴集合A中的元素是大于﹣1的有理数,对于A,符号:“∈”只用于元素与集合间的关系,故错;对于B、C、D,因不是有理数,故B对,C、D不对;故选B.点评:本小题主要考查元素与集合关系的判断、常用数集的表示等基础知识,考查符号的运算求解能力.属于基础题.2.已知全集U={0,1,2,3,4},M={0,1,2},N={2,3},则(∁U M)∩N=()A. {2,3,4} B. {3} C. {2} D. {0,1,2,3,4}考点:交、并、补集的混合运算.专题:计算题.分析:利用全集求出M的补集,然后求出与N的交集.解答:解:全集U={0,1,2,3,4},M={0,1,2},N={2,3},则C U M={3,4},所以(C U M)∩N={3}.故选B.点评:本题考查交、并、补集的混合运算,常考题型,基础题.3.50名同学参加跳远和铅球测验,跳远和铅球测验成绩分别为及格40人和31人,2项测验成绩均不及格的有4人,2项测验成绩都及格的人数是()A. 35 B. 25 C. 28 D. 15考点:集合中元素个数的最值.专题:计算题.分析:设两项测验成绩都及格的人数为x人,我们可以求出仅跳远及格的人数;仅铅球及格的人数;既2项测验成绩均不及格的人数;结合全班有50名同学参加跳远和铅球测验,构造方程,可得答案.解答:解:全班分4类人:设两项测验成绩都及格的人数为x人;由跳远及格40人,可得仅跳远及格的人数为40﹣x人;由铅球及格31人,可得仅铅球及格的人数为31﹣x人;2项测验成绩均不及格的有4人∴40﹣x+31﹣x+x+4=50,∴x=25故选B点评:本题考查的知识点是集合中元素个数的最值,其中根据已知对参加测试的学生分为四类,是解答本题的关键.4.如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,则 A*B ()A.∁U(A∪B) B. A∪(∁U B) C.(∁U A)∪(∁U B) D.(A∪B)∩∁U(A∩B)考点: Venn图表达集合的关系及运算.专题:规律型.分析:先判断阴影部分表示元素的性质,再根据交集、并集与补集的意义判定即可.解答:解:∵图中阴影部分表示属于集合A或集合B,且不同时属于A又属于B的元素组成的集合,即表示属于集合(A∪B),且不属于集合(A∩B)的元素组成的集合,故选D.点评:本题考查Venn图表示集合的关系及运算.5.下列函数中,在区间(0,2)上为增函数的是()A. y=3﹣x B. y=x2+1 C. D. y=﹣|x|考点:函数单调性的判断与证明.专题:计算题.分析:根据增函数的定义对A、B、C、D四个选项进行一一判断;解答:解:A、y=3﹣x=﹣x+3,是减函数,故A错误;B、∵y=x2+1,y为偶函数,图象开口向上,关于y轴对称,当x>0,y为增函数,故B正确;C、∵y=,当x>0,为减函数,故C错误;D、当x>0,y=﹣|x|=﹣x,为减函数,故D错误;故选B.点评:此题主要考查函数的单调性的判断与证明,此题考查的函数都比较简单,是一道基础题.6.已知函数f(x)的定义域为(3﹣2a,a+1),且f(x+1)为偶函数,则实数a的值可以是()A. B. 2 C. 4 D. 6考点:函数奇偶性的性质.专题:函数的性质及应用.分析:函数f(x+1)为偶函数,说明其定义域关于“0”对称,函数f(x)的图象是把函数f(x+1)的图象向右平移1个单位得到的,说明f(x)的定义域(3﹣2a,a+1)关于“1”对称,由中点坐标公式列式可求a的值.解答:解:因为函数f(x+1)为偶函数,则其图象关于y轴对称,而函数f(x)的图象是把函数f(x+1)的图象向右平移1个单位得到的,所以函数f(x)的图象关于直线x=1对称.又函数f(x)的定义域为(3﹣2a, a+1),所以(3﹣2a)+(a+1)=2,解得:a=2.故选B.点评:本题考查了函数图象的平移,考查了函数奇偶性的性质,函数的图象关于y轴轴对称是函数为偶函数的充要条件,此题是基础题.7.已知函数y=f(x+1)定义域是[﹣2,3],则y=f(x﹣1)的定义域是()A. [0,5] B. [﹣1,4] C. [﹣3,2] D. [﹣2,3]考点:函数的定义域及其求法.专题:函数的性质及应用.分析:先由函数y=f(x+1)定义域求出函数f(x)的定义域,然后由x﹣1在f(x)的定义域内求函数y=f(x﹣1)的定义域.解答:解:因为y=f(x+1)定义域是[﹣2,3],即x∈[﹣2,3],所以x+1∈[﹣1,4],所以函数f(x)的定义域为[﹣1,4],由﹣1≤x﹣1≤4,得:0≤x≤5,所以函数y=f(x﹣1)的定义域是[0,5].故选A.点评:本题考查了函数定义域及其求法,给出了函数f(x)的定义域为[a,b],求函数f[g (x)]的定义域,让a≤g(x)≤b求解x的X围即可,此题是基础题.8.若函数f(x)为奇函数,且当x>0时,f(x)=x﹣1,则当x<0时,有()A. f(x)>0 B. f(x)<0 C. f(x)f(﹣x)≤0 D. f(x)﹣f(﹣x)>0考点:函数奇偶性的性质.专题:函数的性质及应用.分析:借助于函数为奇函数,当x>0时,f(x)=x﹣1,求解当x<0时,函数解析式,然后,代入各个选项,从而得到正确答案.解答:解:∵函数为奇函数,令x<0,则﹣x>0,∴f(﹣x)=﹣x﹣1,∵f(﹣x)=﹣f(x),∴f(x)=x+1,∴当x<0时,f(x)=x+1,此时,f(x)=x+1的函数值符合不定,因此排除选项A、B,∵f(x)f(﹣x)=﹣(x+1)2≤0成立,∴选项C符合题意,故选:C.点评:本题重点考查函数为奇函数的性质,注意函数的性质的灵活运用,属于中档题.9.函数f(x)的定义域为R+,若f(x+y)=f(x)+f(y),f(8)=3,则f(2)=() A. B. C. D.考点:抽象函数及其应用.专题:计算题.分析:函数f(x)的定义域为R+,若f(x+y)=f(x)+f(y),f(8)=3,令x=y=4,x=y=2,即可求得f(2)的值.解答:解:∵f(x+y)=f(x)+f(y),f(8)=3,∴令x=y=4,则f(8)=2f(4)=3,∴f(4)=,令x=y=2,f(4)=2f(2)=,∴f(2)=.故选B.点评:考查抽象函数及其应用,求抽象函数的有关命题,常采用赋值法求解,属基础题.10.下列所给四个图象中,与所给3件事吻合最好的顺序为()(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再去上学;(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.A.①②④ B.④②③ C.①②③ D.④①②考点:函数的图象.专题:数形结合.分析:根据回家后,离家的距离又变为0,可判断(1)的图象开始后不久又回归为0;由途中遇到一次交通堵塞,可判断中间有一段函数值没有发生变化;由为了赶时间开始加速,可判断函数的图象上升速度越来越快.解答:解:离家不久发现自己作业本忘记在家里,回到家里,这时离家的距离为0,故应先选图象④;回校途中有一段时间交通堵塞,则这段时间与家的距离必为一定值,故应选图象①;最后加速向学校,其距离与时间的关系为二次函数,故应选图象②.故选D.点评:本题考查的知识点是函数的图象,我们分析实际情况中离家距离随时间变化的趋势,找出关键的图象特征,对四个图象进行分析,即可得到答案.11.函数y=f(x)是R上的偶函数,且在(﹣∞,0]上是增函数,若f(a)≤f(2),则实数a的取值X围是()A. a≤2 B. a≥﹣2 C.﹣2≤a≤2 D. a≤﹣2或a≥2考点:奇偶性与单调性的综合.专题:计算题.分析:由已知中函数f(x)是定义在实数集R上的偶函数,根据偶函数在对称区间上单调性相反,结合f(x)上在(﹣∞,0]为单调增函数,易判断f(x)在](0,+∞)上的单调性,根据单调性的定义即可求得.解答:解:由题意,f(x)在(0,+∞)上为单调减函数,从而有或,解得a≤﹣2或a≥2,故选D.点评:本题考查的知识点是函数单调性的应用,其中利用偶函数在对称区间上单调性相反,判断f(x)在(0,+∞)上的单调性是解答本题的关键.12.已知函数f(x)=4x2﹣mx+5在区间[﹣2,+∞)上是增函数,则f(1)的X围是() A. f(1)≥25 B. f(1)=25 C. f(1)≤25 D. f(1)>25考点:函数单调性的性质.专题:计算题.分析:由二次函数图象的特征得出函数f(x)=4x2﹣mx+5在定义域上的单调区间,由函数f(x)=4x2﹣mx+5在区间[﹣2,+∞)上是增函数,可以得出[﹣2,+∞)一定在对称轴的右侧,故可以得出参数m的取值X围,把f(1)表示成参数m的函数,求其值域即可.解答:解:由y=f(x)的对称轴是x=,可知f(x)在[,+∞)上递增,由题设只需≤﹣2⇒m≤﹣16,∴f(1)=9﹣m≥25.应选A.点评:本小题的考点是考查二次函数的图象与二次函数的单调性,由此得出m的取值X围再,再求以m为自变量的函数的值域.二、填空题(本大题共4小题,每小题5分,共20分)13.函数y=+的定义域是{x|x≥﹣1,且x≠2} .考点:函数的定义域及其求法.专题:函数的性质及应用.分析:根据使函数y=+的解析式有意义的原则,构造不等式组,解不等式组可得函数的定义域.解答:解:要使函数y=+的解析式有意义自变量x须满足:解得x≥﹣1,且x≠2故函数y=+的定义域是{x|x≥﹣1,且x≠2}故答案为:{x|x≥﹣1,且x≠2}点评:本题考查的知识点是函数的定义或及其求法,其中根据使函数y=+的解析式有意义的原则,构造不等式组,是解答的关键.14.设函数f(x)=则f[f(﹣1)]的值为 4 .考点:函数的值.专题:计算题.分析:由函数f(x)=,知f(﹣1)=(﹣1)2+1=2,所以f[f(﹣1)]=f (2),由此能求出结果.解答:解:∵函数f(x)=,∴f(﹣1)=(﹣1)2+1=2,∴f[f(﹣1)]=f(2)=22+2﹣2=4,故答案为:4.点评:本题考查分段函数的函数值的求法,是基础题.解题时要认真审题,仔细解答.15.已知A有限集合,x∉A,B=A∪{x},若A,B的子集个数分别为a,b,且b=ka,则k= 2 .考点:并集及其运算.专题:计算题.分析:设A中元素有m个,根据A有限集合,x∉A,B=A∪{x},得到B中元素有(m+1)个,分别表示出子集的个数,即可确定出k的值.解答:解:设集合A中元素为m个,∵A有限集合,x∉A,B=A∪{x},∴B中元素有(m+1)个,∴a=2m,b=2m+1,即b=2a,则k=2.故答案为:2点评:此题考查了并集及其运算,以及子集,弄清题意是解本题的关键.16.函数f(x)=2x2﹣3|x|的单调减区间是(﹣∞,﹣]和[0,] .考点:函数的单调性及单调区间.专题:函数的性质及应用.分析:首先根据题中的已知条件把自变量进行分类,得出分段函数的解析式,进一步画出函数的图象,然后得出单调区间.解答:解:函数f(x)=2x2﹣3|x|=图象如下图所示f(x)减区间为(﹣∞,﹣]和[0,].故答案为:(﹣∞,﹣]和[0,].点评:本题考查的知识点:分段函数的解析式,二次函数的图象以及单调区间的确定,三、解答题(本大题共6小题,满分70分)17.已知集合A={x|3≤x<10},集合B={x|2x﹣8≥0}.(1)求A∪B;(2)求∁R(A∩B).考点:交、并、补集的混合运算.专题:计算题.分析:(1)求解一次不等式化简集合B,然后直接进行并集运算;(2)首先进行交集运算,然后进行补集运算.解答:解:(1)由A={x|3≤x<10},B={x|2x﹣8≥0}={x|x≥4}.∴A∪B={x|3≤x<10}∪{x|x≥4}={x|x≥3}.(2)A∩B={x|3≤x<10}∩{x|x≥4}={x|4≤x<10}.∴∁R(A∩B)={x|x<4或x≥10}.点评:本题考查了交、并、补集的混合运算,是基础的会考题型.18.设集合A={a,a2,b+1},B={0,|a|,b}且A=B.(1)求a,b的值;(2)判断函数在[1,+∞)的单调性,并用定义加以证明.考点:函数单调性的判断与证明;集合的相等.专题:计算题.分析:(1)求,b的值,由于两集合相等,观察发现其对应特征,建立方程求出a,b的值(2)将a,b的值代入,先判断单调性,再用定义法证明即可.解答:解:(1)两集合相等,观察发现a不能为O,故只有b+1=0,得b=﹣1,故b与a对应,所以a=﹣1,故a=﹣1,b=﹣1(2)由(1)得,在[1,+∞)是增函数任取x1,x2∈[1,+∞)令x1<x2,f(x1)﹣f(x2)=﹣=(x1﹣x2)(1﹣)∵1≤x1<x2,∴x1﹣x2<0,又x1x2>1,故1﹣>0∴f(x1)﹣f(x2)=(x1﹣x2)(1﹣)<0∴f(x1)<f(x2)故,在[1,+∞)是增函数点评:本题考查集合相等的概念以及函数单调性的证明方法﹣﹣定义法,解答第二小问时要注意步骤,先判断再证明,注意格式.19.已知f(x)=x2013+ax3﹣﹣8,f(﹣2)=10,求f(2).考点:基本不等式.专题:不等式的解法及应用.分析:利用g(x)=x2013+ax3﹣为奇函数即可得出.解答:解:已知g(x)=x2013+ax3﹣为奇函数,即对g(x)=x2013+ax3﹣有g(﹣x)=﹣g(x),也即g(﹣2)=﹣g(2),f(﹣2)=g(﹣2)﹣8=﹣g(2)﹣8=10,得g(2)=﹣18,∴f(2)=g(2)﹣8=﹣26.点评:本题考查了奇函数的性质,属于基础题.20.已知函数f(x)=,x∈[1,+∞).(1)当a=时,判断并证明f(x)的单调性;(2)当a=﹣1时,求函数f(x)的最小值.考点:函数单调性的性质;函数的最值及其几何意义.专题:函数的性质及应用.分析:(1)当a=时,f(x)==x+2+=x++2.任取x1,x2是[1,+∞)上的任意两个实数,且x1<x2,利用做差法,可判断函数f(x)在[1,+∞)上是增函数.(2)当a=﹣1时,f(x)=x﹣+2.由函数y1=x和y2=﹣在[1,+∞)上都是增函数,可得f(x)=x﹣+2在[1,+∞)上是增函数,故当x=1时,f(x)取得最小值.解答:解:(1)当a=时,f(x)==x+2+=x++2.设x1,x2是[1,+∞)上的任意两个实数,且x1<x2,则f(x1)﹣f(x2)=(x1+)﹣(x2+)=(x1﹣x2)+(﹣)=(x1﹣x2)+=(x1﹣x2)(1﹣)=(x1﹣x2)•.因为1≤x1<x2,所以x1﹣x2<0,x1•x2>0,x1x2﹣>0,所以f(x1)﹣f(x2)<0,即f(x1)<f(x2).所以函数f(x)在[1,+∞)上是增函数.(2)当a=﹣1时,f(x)=x﹣+2.因为函数y1=x和y2=﹣在[1,+∞)上都是增函数,所以f(x)=x﹣+2在[1,+∞)上是增函数.当x=1时,f(x)取得最小值f(1)=1﹣+2=2,即函数f(x)的最小值为2.点评:本题考查的知识点是函数单调性的性质,函数的最值及其几何意义,函数的单调性的证明,是函数单调性与最值的综合应用,难度中档.21.定义在实数R上的函数y=f(x)是偶函数,当x≥0时,f(x)=﹣4x2+8x﹣3.(Ⅰ)求f(x)在R上的表达式;(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).考点:函数奇偶性的性质;二次函数的性质.专题:计算题.分析:(Ⅰ)先根据函数的奇偶性以及x≥0的解析式求出x<0的解析式,因为函数定义在R上,所以函数是分段函数,写出各段的解析式,用大括号连接即可.(Ⅱ)先根据(Ⅰ)中所求函数解析式,求出函数在每段上的最大值,其中最大的就是函数f(x)的最大值,再由函数两段上的图象都是开口向下的抛物线,结合对称轴就可求出函数的单调区间.解答:解:(Ⅰ)设x<0,则﹣x>0,∴f(﹣x)=﹣4(﹣x)2﹣8x﹣3=﹣4x2﹣8x﹣3.又∵f(x)是偶函数,∴f(x)=f(﹣x)=﹣4x2﹣8x﹣3.∴f(x)=(Ⅱ)当x≥0时,f(x)=﹣4x2+8x﹣3,图象为对称轴是x=1,开口向下的抛物线,当x=1时f(x)有最大值为1当x<0时,f(x)=﹣4x2﹣8x﹣3,图象为对称轴是x=﹣1,开口向下的抛物线,当x=﹣1时f(x)有最大值为1∴f(x)的最大值是1.函数单调增区间为(﹣∞,﹣1],和[0,1],单调减区间为[﹣1,0],和[1,+∞)点评:本题主要考查利用函数的奇偶性求分段函数的解析式,以及分段函数的最值,单调区间的求法.22.已知函数f(x)的定义域为R,对于任意的x,y∈R,都有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,若f(﹣1)=2.(1)求证:f(x)为奇函数;(2)求证:f(x)是R上的减函数;(3)求函数f(x)在区间[﹣2,4]上的值域.考点:抽象函数及其应用;函数奇偶性的性质.专题:函数的性质及应用.分析:(1)先利用特殊值法,求证f(0)=0,令y=﹣x即可求证;(2)由(1)得f(x)为奇函数,f(﹣x)=﹣f(x),利用定义法进行证明;(3)由函数为减函数,求出f(﹣2)和f(4)继而求出函数的值域,解答:解:(1)证明:∵f(x)的定义域为R,令x=y=0,则f(0+0)=f(0)+f(0)=2f (0),∴f(0)=0.令y=﹣x,则f(x﹣x)=f(x)+f(﹣x),即f(0)=f(x)+f(﹣x)=0.∴f(﹣x)=﹣f(x),故f(x)为奇函数.(2)证明:任取x1,x2∈R,且x1<x2,则f(x2)﹣f(x1)=f(x2)+f(﹣x1)=f(x2﹣x1).又∵x2﹣x1>0,∴f(x2﹣x1)<0,∴f(x2)﹣f(x1)<0,即f(x1)>f(x2).故f(x)是R上的减函数.(3)∵f(﹣1)=2,∴f(﹣2)=f(﹣1)+f(﹣1)=4.又f(x)为奇函数,∴f(2)=﹣f(﹣2)=﹣4,∴f(4)=f(2)+f(2)=﹣8.由(2)知f(x)是R上的减函数,所以当x=﹣2时,f(x)取得最大值,最大值为f(﹣2)=4;当x=4时,f(x)取得最小值,最小值为f(4)=﹣8.所以函数f(x)在区间[﹣2,4]上的值域为[﹣8,4].点评:本题主要考查了抽象函数及其应用,以及利用函数单调性的定义判断函数的单调性,并根据函数的单调性解函数值不等式,体现了转化的思想,在转化过程中一定注意函数的定义域.。
高一数学 练习题及答案详解 新人教A版必修1

高一数学必修1测试题一、选择题(本大题共10小题,每小题5分,共60分) 1. 下列四个函数中,与y =x 表示同一函数的是A.y =(x )2B.y =33xC.y =2xD.y =x x 22.已知A ={x |y =x ,x ∈R },B ={y |y =x 2,x ∈R },则A ∩B 等于 A.{x |x ∈R } B.{y |y ≥0}C.{(0,0),(1,1)}D.∅ 3.方程x 2-px +6=0的解集为M ,方程x 2+6x -q =0的解集为N ,且M ∩N ={2},那么p +q 等于A.21B.8C.6D.7 4. 下列四个函数中,在(0,+∞)上为增函数的是A.f (x )=3-xB.f (x )=x 2-3x C.f (x )=-11+xD.f (x )=-|x |5.函数f (x )=x 2+2(a -1)x +2在区间(-∞,4]上递减,则a 的取值X 围是A.[-3,+∞]B.(-∞,-3)C.(-∞,5]D.[3,+∞)6. 函数y =1-x +1(x ≥1)的反函数是A.y =x 2-2x +2(x <1)B.y =x 2-2x +2(x ≥1)C.y =x 2-2x (x <1)D.y =x 2-2x (x ≥1)7. 已知函数f (x )=12++mx mx 的定义域是一切实数,则m 的取值X 围是A.0<m ≤4B.0≤m ≤1C.m ≥4D.0≤m ≤48.某商场对顾客实行购物优惠活动,规定一次购物付款总额:(1)如果不超过200元,则不给予优惠;(2)如果超过200元但不超过500元,则按标价给予9折优惠;(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠. 某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款是元元 元元9. 二次函数y =ax 2+bx 与指数函数y =(a b)x的图象只可能是D10. 已知函数f (n )=⎩⎨⎧<+≥-),10)](5([),10(3n n f f n n 其中n ∈N ,则f (8)等于A.2B.4C.6D.711.如图,设a,b,c,d>0,且不等于1,y=a x , y=b x , y=c x ,y=d x在同一坐标系中的图象如图,则a,b,c,d 的大小顺序( ) A 、a<b<c<d B 、a<b<d<c C 、b<a<d<c D 、b<a<c<d12..已知0<a<1,b<-1,函数f(x)=a x+b 的图象不经过:( ) A.第一象限; B.第二象限; C.第三象限; D.第四象限第Ⅱ卷(非选择题 共70分)二、填空题(本大题共4小题,每小题5分,共20分)13.已知f (x )=x 2-1(x <0),则f -1(3)=_______.14.函数)23(log 32-=x y 的定义域为______________ 15.某工厂8年来某产品产量y 与时间t 年的函数关系如下图,则:①前3年总产量增长速度增长速度越来越快; ②前3年中总产量增长速度越来越慢; ③第3年后,这种产品停止生产;④第3年后,这种产品年产量保持不变. 以上说法中正确的是_______.16. 函数y =⎪⎩⎪⎨⎧>+≤<+≤+1)( 5-1),(030),(32x x x x x x 的最大值是_______.三、解答题17. 求函数y =12-x 在区间[2,6]上的最大值和最小值.(10分)18.(本小题满分10分) 试讨论函数f (x )=log a 11-+x x (a >0且a ≠1)在(1,+∞)上的单调性,并予以证明.答案1. BACCB BDCAD BA 二。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
启帆教育数学测试题
一、选择题(每小题6分,总分48分) 1.使奇函数f(x)=sin(2x+θ
θ)在[4
π
-
,0]上为减函数的θ值为( )
A.3
π
-
B.6
π
-
C.
56π D.23
π 2.设函数()sin(2)3
f x x π
=+,则下列结论正确的是( )
A .()f x 的图像关于直线3x π
=对称
B .()f x 的图像关于点(,0)4
π
对称
C .把()f x 的图像向左平移12
π
个单位,得到一个偶函数的图像
D .()f x 的最小正周期为π,且在[0,]6π
上为增函数
3.设)3,1(A ,)3,2(--B ,)7,(x C 若AB ∥,则x 的取值范围是( ) A. 0 B. 3 C. 15 D. 18
4.与向量a=(-5,4)平行的向量是( ) A.(-5k,4k )
B.(-k 5,-k 4)
C.(-10,2)
D.(5k,4k)
5. 二次函数y=ax2+bx 与指数函数y=(a b
)x 的图象只可能是 ( )
6、下列命题中错误的是:( )
A 、如果α⊥β,那么α内一定存在直线平行于平面β;
B 、如果α⊥β,那么α内所有直线都垂直于平面β;
C 、如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;
D 、如果α⊥γ,β⊥γ,α∩β=l,那么l ⊥γ
7、若0.52a =,
πlog 3b =,2log 0.5c =,则( ) A a b c >>
B b a c >>
C c a b >>
D b c a >>
8.已知向量a 与b 不共线,AB =a +k b ,AC =r a +b (k ,r ∈R ),则AB 与AC 共线的条件是( ).
(A )k +r =0 (B )k -r =0 (C )kr +1=0 (D )kr -1=0
二、填空题(每题6分,共30分)
1.已知
3sin()45x π-=
,则sin 2x 的值为 ; 2.阅读下列流程图:
则此流程图表示__________________________算法.
3、已知平行四边形的3个顶点为A(a,b),B(-b,a),C(0,0),则它的第4个顶点D 的坐标是( )
4、
5、 已知A (2,3),B (-1,5),且AC =31AB ,AD =-4
1
AB ,
则CD 中点的坐标是________.
三、解答题(共42分)
1.(14分) 已知函数)0)(2
sin(sin 3sin )(2>++=ωπ
ωωωx x x x f
π的最小正周期为
(1)求);(x f (2)当)(,]2
,12[x f x 求函数时π
π-
∈的值域。
2.(14分)已知函数x x x x f 2cos cos sin 3)(+= (I )写出函数)(x f 的最小正周期和单调递增区间;
(II )若函数)(x f 的图象关于直线0x x =对称,且100<<x ,求0x 的值
3、(14分)
启帆教育数学测试题答案
一. 选择题:DCBA CBAD
二.
填空题:1.
725 2.输出a 、b 、c 当中最小的 3、(a+b,b-a) 4、10
5、(
815,12
37
) 三、解答题
1.解:(1)x x x
x f ωωωcos sin 32
2cos 1)(+-=
2分 .2
1
)62sin(212cos 212sin 23+-=+-=
πωωωx x x 4分 ,0,)(>ωπ且的最小正周期为函数x f
.1,22==∴
ωπω
π
解得
.2
1
)62sin()(+-
=∴π
x x f 6分 (2)].6
5,3[62],2,12[ππππ
π-∈-∴-∈x x 根据正弦函数的图象可得: 当3
,2
6
2π
π
π
=
=
-
x x 即时,
)6
2sin()(π
-
=x x g 取最大值1 8分
当12
,3
6
2π
π
π
-
=-
=-
x x 即时
.2
3
)62sin()(--=取最小值πx x g 10分
,2321)62sin(2321≤+-≤-∴πx 即].2
3
,231[)(-的值域为x f 14分 2.(I )解:2
1
)62sin(2cos 212sin 23cos cos sin 3)(2++=+=
+=
πx x x x x x x f ππ
==
∴22T 由2
26
22
2π
ππ
π
π+
≤+
≤-
k x k )(Z k ∈,得 6
3
π
ππ
π+
≤≤-
k x k )(z k ∈
)(x f ∴的单调递增区间为⎥⎦
⎤
⎢⎣
⎡+
-
6,3
πππ
πk k )(z k ∈ (II ) )(x f 的图象关于直线0x x =对称, 2
6
20π
ππ
+
=+
∴k x 620ππ+=
∴k x )(z k ∈100<<∴x 6
0π
=∴x 3、。
