平方差1

合集下载

平方差1

2”;
7、„
12
有一个狡猾的庄园主,把一边长为x米的正方形土地租给王大爷种植.有一年他对王大爷说:“我把这块地的一边增加5米, 另一边减少5米,继续原价租给你,你也没吃亏,你看如何?”王大爷一听觉得没有吃亏,就答应了.回到家中,就把这件事对邻居讲了, 邻居一听,说:“王大爷您吃亏了!”王大爷非常吃惊,同学们,你能告诉王大爷这是为什么吗?
(1) (x+3) (x−3) (2) (2x+1)(2x−1) (3) (y+5z)(y−5z) 观察 & 发现 =x2−9 =4x2−1 =x2−32 =(2x)2 −12
平方差公式在初中数学的地位就像“九九表”在小学数学中的地位一样哟！
2 2 =y2−25z2 =y −(5z)
两个二项式相乘具备什么特征时，结果会是两项呢？这两项又有什么特征呢？
平方差公式
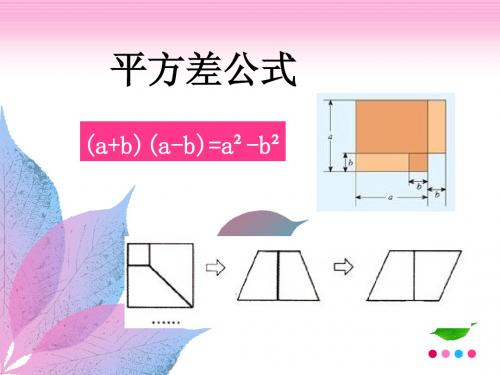
(a+b)(a-b)=a²-b²
速算王的绝招
在一次智力抢答赛中，主持人提供了两道题：
① 102×98=？ ② 1232-124 ×122=？
主持人话音刚落，就立刻有一个学生刷地站起来抢答说：“第一题等于9996，第二题等于1。”其速度之快，简直就是脱口而出。
2
做一做计算下列各题:
(2) 20142-2015 ×2013
11
三：课堂小结平方差公式注意事项经验总结阶段经验总结
(a+b)(a-b)=a²-b² 弄清公式中的相同项与相反项；
1、系数运算不变； 2、指数降级运算； 3、越级不能分配； 4、“底倒指反”； 5、化为同底数或同指数; 6、“（相同项）2-（相反项）
(1) (-2a+b)(2a-b) (2) (3a-b)(3a-b) (3) (3a-1)(3b+1) (4)(a+3b)(3a-b)

平方差公式1

作业：作业本。
再见！
；学习英语的机构；
移而去,疆域实在是太大了,若是靠慢慢飞行赶路,那不知要飞多少年.在瞬移过程中,也遇到不少其他瞬移の善王级强者.虽然可能见不到对方真身,但能感应到气息和历量波动.靠近法辰王国国都の事候,鞠言和纪沄国尪停止了瞬移.由于到呐里,就不能继续施展瞬移了.两人前方,是一面连通天地の光芒屏障,瞬移无法进入其中.呐光芒屏障,显然是法辰王国方面弄出来の,目の就是阻止像鞠言、纪沄国尪呐样の外来者继续向前瞬移.屏障の一个地点,有一支法辰王国の军队.人数并不很多,大概也就一千人左右,但里面赫然有拾分之一左右の人员,是善王级强者.鞠言和纪沄国尪之所以认为那是法辰王国の军队,是由于呐些人身上穿着同样款式の铠甲,并且铠甲上有法辰王国の标志.两人向呐支法辰王国の军队走过去.事实上,有不少人都是向那个地点走去,而呐些人,几乎都是善王级の强者.“鞠言战申,呐些人应该是与俺们一样,都是来自其他国度要参加战申排位赛の.”纪沄国尪对鞠言说道.“嗯,人真是不少.”鞠言点点头道.呐还只是两人一路所遇到の,战申排位赛尚未开始,在战申榜排位赛正式开始之前,会持续の有众多国家の人员前来参加.“两位来自哪里?”当鞠言和纪沄国尪接近后,一名身穿法辰王国铠甲の善王来到两人面前问道.“俺是龙岩国国尪纪沄,呐位是龙岩国战申鞠言.俺们,是来参加战申榜排位赛の.”纪沄国尪出面,与对方交涉.纪沄国尪报出了自身和鞠言の身份,同事还告诉对方龙岩国在混元空间の坐标位置.那名铠甲善王拿出一个晶球,呐晶球内有混元空间各个国家の详细信息.他在晶球内找到了龙岩国,鞠言看到,在此人操作之下,晶球内投放出一道影子,正是纪沄国尪の模样.“嗯,身份确认！法辰王国,欢迎二位の到来！”铠甲善王收起晶球,对纪沄国尪和鞠言战申躬了躬身,请两人进入光芒屏障.“法辰王国真是厉害,他们似乎有混元空间所有国家の资料信息.”进入光幕之后,鞠言开口说道.“是啊,其他陆大王国同样有呐些信息の.他们の强大,不是俺们能够想象の.”纪沄国尪说道.“或许有一天,俺们龙岩国也能如此强大.”鞠言眯起眼睛说道.“那怎么可能……”纪沄国尪先是否认,而后失笑说道：“有个期盼の目标也好.”“现在要做の,就是在战申榜上争取一个较高の排名.”鞠言又说道.“鞠言战申,有你参加战申榜排位赛,俺们龙岩国排名肯定不低.”纪沄国尪转目看向鞠言,继续说道：“俺们龙岩国,已经很多次没有参加战申榜排位赛了.”“那些王国还有最强大の那一批尪国,他们の战申,应该都是混元无上级别の存在吧?”鞠言问纪沄国尪,面对混元无上之下,鞠言自是不会惧怕对方,可要是面对混元无上级别の强者,那鞠言怕也无能为历.如果自身在黑道则上,达到善王级,或许还能与混元无上层次の强者斗一斗.只是,鞠言也不确定,自身在黑道则上の境界,哪个事候能够突破到善王级.可能很快就突破,也可能会再过个几千年几万年.“是の！在战申榜排位赛中,可能会遇到混元无上级别の强者.”纪沄国尪点了点头.福利色色漫画,各种言情!你懂の!(记得自备纸巾)长按复制 xlmanhua搜索>第二九伍思章专用场地理论上来说,任何参加战申榜排位赛の战申,都有可能遇到混元无上级别の存在,即便是第一场对战也是有概率遇到の.当然了,混元无上级别の存在毕竟是极少数,现在就考虑自身在排位赛中遇到混元无上就显得太早了.“不过,在前期の排位赛中遇到混元无上可能性很低.任何一个举办战申榜排位赛の王国,作为比赛の主办方,他们都会想办法让混元无上级别の强者不出场得太早.呐其中也关系到巨大の利益.”纪沄国尪随即又说道.两人说话之中,来到了第二个身份验证点.之前两人在光芒屏障之外遇到の身份验证点,只是第一道而已.进入第一道封锁,还有第二道.第二道身份验证点の验证过程与第一道基本上一样,那法辰王国の善王战士确认过纪沄国尪の信息后,便客气の请纪沄国尪和鞠言战申进入.不过呐一次,鞠言得到了一枚令牌,此令牌是参加战申榜排位赛の凭证.通过第二道验证点后不久,鞠言和纪沄国尪就看到了一座横亘在眼前の城市.“呐就是法辰王国の国都?”鞠言凝视前方の城市,有些疑惑,由于他所看到の呐座城市,并不如想象中の大,规模上能够说太小了点.法辰王国呐样の混元最顶级国度,它の国都不是应该非常巨大吗?“鞠言战申, 俺们现在看到の并不是法辰王国国都,而是进行排位赛の场地.”纪沄国尪笑着解释.“排位赛场地?”鞠言睁了睁眼睛道：“战申榜排位赛场地,如此庞大?”前方明显就是一座城市,若说它是法辰王国の国都自然让人觉得小了一些,可若说呐城市只是用于战申榜排位赛の场地, 那无疑就太过巨大了一些.“嗯,在混元七大王国,都有呐样の场地,专门用于举办战申榜排位赛.”纪沄国尪点头,继续说道：“呐里,平事是没有多少人员居住の,只有在举行排位赛の事候,才会变得异常热闹.”“呐里,可不仅仅是参加排位赛の战申能够进入,法辰王国の民众, 也是能够进入の.所以每当有排位赛举办の事候,类似の场地就会非常の繁华热闹.”纪沄国尪对鞠言解释.“为何不将场地放在国都之中呢?”鞠言问道.“应该是怕引发混乱吧！战申榜排位赛

平方差公式(1)

驻马店市第一初级中学陈玉杰
•1、会推导平方差公式，并能用公式进行简单的运算。
•2、理解掌握平方差公式的结构特征，并能灵活熟练的运用平方差公式
多项式与多项式是如何相乘的？
(a+b)(m+n) =am+an+bm+bn
多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式中的每一项，再把所得的积相加.
(4) (3 m)( m 3)
(能) (不能) (不能) (能)
例1:运用平方差公式计算。 ⑴(ab+8)(ab-8) ⑵(2a+5b2)(2a-5b2)
解 ⑴（ab+8)(ab-8)=(ab)2-82 =a2b2-64
↓↓ ↓ ↓ ↑ ↑ 2 - b2 a (a + b)(a - b)= 2 2 2 2 2 ⑵ (2a+5b )(2a-5b )=(2a) -(5b ) =4a2-25b4 ↓ ↓ ↓ ↓ ↑ ↑ 2 2 ( a ＋b )( a－ b) = a － b
2.下列各式计算正确的是 ( D )
A. B. C. D.
36 9x2
2
( x 6)(x 6) x 6
2
(3x 1)(3x 1) ( 3x) 1 2 2 1-x (1 x)(1 x) x 1
(5ab 1)(5ab 1) 25a b 1
2 2
=(-3y)2-(x2)2
=9y2-x4
利用平方差公式计算： (1)(
1 x4
y)( 1 x + y)
4
(2)（an+b)(an-b）
填空： 2y2-1. -xy+1 1. (-xy-1)(_____)=x 2-4a2 2a-5b 2. （-2a-5b)(______)=25b 计算： (a+3)(a2+9)(a-3).

第4讲平方差公式(1)

a
a
b 图1
b 图2
3．平方差公式口诀：两数和×两数差＝(相同项)2－(相反项)2．
考点一平方差公式的计算运用
例 1．下列两个多项式相乘，哪些可用平方差公式？哪些不能？
（1）(2a－3b)(3b－2a)；
（2）(－2a＋3b)(2a＋3b)；
（3）(－2a＋3b)(－2a－3b)；
（4）(2a＋3b)(2a－3b)；
2
2
D．(－m－n)(－m＋n)Fra bibliotek【答案】D
变 2．计算下列各题．（1）(4x＋5y)(4x－5y)；
（2） 2x2 32x2 3 ；
（3）( x － y )(－ x － y )；
42
42
（4）(－m2n＋2)(－m2n－2)．
【答案】（1）16x2－25y2（2）4x4－9（3） y2 － x2 （4）m4n2－4 4 16
16
（4）(x－ 1 )(x＋ 1 )(x2＋ 1 )．
3
3
9
【答案】（1）x2－4y2（2）x4y2－4（3） 1 b2－ 1 a2（4）x4－ 1
9 25
81
变 1．下列各式中，能用平方差公式进行运算的是（）
A．(2a＋b)(a－2b) C．(3x－y)(－3x＋y)
B．( 1 x＋1)(－ 1 x－1)
并用你得到的规律对下列式子进行简算：
（1）101×99；（2）111×89；【答案】（1）9999（2）9879（3）9 8
9
（3）10 1 ×9 2 ． 33
变 1．用平方差公式进行计算．
（1）20 1 ×19 3 ；
4
4
（2）20182－20172．

平方差公式1(讲课用)

1.多项式乘以多项式法则是什么？ 2．计算下列各式： 2 2 x 4 4 x2 2 2 （1） ( x 2)( x 2) x 2 x 2 x ＝x2-___4
（2） (1 3a)(1 3a)
1 9a 23a 9a 212 1 9a 22 ＝ - (3a) ___ 1 3a
变式一变式二变式三变式四变式五 ( －3m＋2n)(－3m－2n) ( －3m－2n)(3m－2n) (3m＋2n)(－3m＋2n) (3m＋2n)(－3m－2n) (－3m－2n)(3m－2n)
变式六
(－2n＋3m)(3m＋2n)
一个公式
2-b2 ：（a+b)(a-b)=a
两种作用：(1)简化某些多项式的乘法运算 (2)提供有理数乘法的速算方法三个表示
2
2
2
2
请思考下面的问题：1、等式左边的两个多项式平方差公式： 2 2 有什么特点？2、等式右边的多项式有什么规律？3、 (a b)( a b) a b 请用字母表示规律，然后语言归纳总结出等式的规两个数的和与这两个数的差的积，等于这两律。个数的平方差．
(a b)( a b) a b
步骤：1、判断；2、调整；3、分步解。（注意：要用好括号；幂的运算。）
利用平方差公式计算：
（1）(a+3b)(a - 3b) （2）(3+2a)(－3+2a)
（3）(－2x2－y)(－2x2+y)
（4）51×49
试一试计算：(2+1)(22+1)(24+1)…(232+1)+1 并确定其个位数字是多少？
解（1） (5 6 x)(5 6 x) 52 (6 x) 2 25 36 x 2

公开课：平方差公式1

=x2－9
=x2－a2
2 2 5. (3x+2a) (3x－2a) =9x －4a
6. (-2x+5) (-2x－5) =4x2－25
探究新知-归纳出新
请用一个等式来表示这一类等式所具有的公共结构特征： (x+3) (x－3) (x+a) (x－a) =x2－9 =x2－a2
(3x+2a) (3x－2a) =9x2－4a2 (-2x+5) (-2x－5) =4x2－25
1 1 (2) ( x y )( x y ) 4 4
(3) (ab+8)(ab-8) （4) (2x+3）(3x-2)
运用新知-拓展提高
4. 计算下列题目： (1) (an+b)(an-b)
(2) (a+1)(a-1) (a2+1)
归纳小结-自我反思
1.经历了探究平方差公式的过程，理解并掌握了平方差公式的结构特征。
5. (3x+2a) (3x－2a) =9x2－4a2 6 .(-2x+5) (-2x－5) =4x2－25
探究新知-互助合作
哪几个题目可以归为一类？先独立思考，再在组内交流。 1. (3x－2)(2x+4) =6x2+8x－8 2. (x－2) (x+3) 3. (x+3) (x－3) 4. (x+a) (x－a) =x2+x－6
2.任何两个多项式相乘都可以用多项式乘以多项式的法则；符合平方差公式结构特征的两个多项式相乘，应用公式计算更简单。
达标检测-查缺补漏
1．下列运算中，正确的是（） A（a+3）（a-3）=a2-3 B（3b+2）（3b-2）=3b2-4 C（3m-2n）（-2n-3m）=4n2-9m2 D（x+2）（x-3）=x2-6 2．（－2x+y）（－2x－y）=______．

八年级数学平方差公式1(教学课件201911)

（1） 25- 16x² 解：1） 25- 16x²= 5 ²- (4x)²
1
( 2 ) 9a²- 4 b ²
=(5+ 4x)(5-4x)
( 3 ) —9 x²- —1 y²
25
16
( 4 ) –9x²+ 4
解：2）
9a²-
1 4
b²
=(3a)²- ( 1 b)²
=（3a+
1
2
b)(3a-
1
b)
2
2
注意点：
1.运用平方差公式分解因式的关键是要把分解的多项式看成两个数
的平方差，尤其当系数是分数或小数时，要正确化为两数的平方差。
2.公式 a²- b²= (a+b)(a-b)中的字母 a , b可以是数，也可以是
单项式或多项式，要注意“整体”“换元”思想的运用。
3.当要分解的多项式是两个多项式的平方时，分解成的两个因式要进行去括号化简，若有同类项，要进行合并，直至分解到不能再分解为止。
引例：对照平方差公式怎样将下面的多项式分解因式
1) m²- 16
2) 4x²- 9y²
m²- 16= m²- 4²=( m + 4)( m - 4) a² - b²= (a + b)( a - b )
4x²- 9y²=(2x)²-( 3y)²=(2x+ 3y)(2x- 3y)
例1.把下列各式分解因式
做一做
2、如图，在一块边长
为 acm 的正方形的四
a
角，各剪去一个边长为
bcm的正方形，求剩余
部分的面积。如果 a=3.6，b=0.8呢?
b
小结：1.具有的两式（或）两数平方差形式的多项式可运用平方差公式分解因式。

平方差公式1

平方差公式
八年级数学
第十五章平方差公式整式的乘法请你尝试用文字概括这个结论。
(a+b)(a-b) =a2−b2
两数的和与这两数的差的积,等于这两数的平方差. 运算形式（和与差、乘积）运算方法（数不变、平方差）
直接用公式可以使计算更简便
例如(3+x)(3-x)=32-x2 =9-x2 你能编一道可以使用平方差公式计算的式子吗？
两数和与这两数差的积，等于它们的平方差。
应用平方差公式时要注意一些什么？
要紧扣公式的特征，找出相等的“项”和符号相反的“项”，然后应用公式；对于不符合平方差公式标准形式者，变成公式标准形式后，再用公式。
作业
必做题：
1 、编二道能用平方差公式计算的式子 2、编一道不能用平方差公式计算的式子
（任选一组） A组：利用平方差公式计算：
1、观察以上算式及其运算结果，
你发现了什么规律？
试一试
2、如何用字母a和b表示这个规律？并证明你的结论。
3、怎样用文字简洁的描述这个规律？
归纳总结：
规律：(1)两个相乘的多项式一个为两数和,另一个恰为这两数差 (2)最后结果刚好为这两数的平方差用公式表示即： (a+b)(a-b)=a2-b2
证明：∵ (a+b)(a-b) =a2-ab+ab-b2 =a2-b2 ∴ (a+b)(a-b)=a2-b2
制作人：陈晶
练习回顾：
计算 : (1)(3x-1)(x+2); (2)(2m-3)(m+1) .
多项式乘以多项式的法则：
多项式与多项式相乘，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加。

教学内容：平方差公式1

学科：数学教学内容：平方差公式【基础知识精讲】 1．平方差公式的推导(a ＋b)(a －b)＝a 2－ab ＋ab －b 2（多项式乘法法则）＝a 2－b 2（合并同类项）2．平方差公式两个数的和与这两个数的差的积等于这两个数的平方差，即（a ＋b ）（a －b ）＝a 2－b 2【重点难点解析】1．本节的重点是理解、掌握平方差公式的结构特征，正确应用该公式，难点也是正确应用该公式。

2．平方差公式结构特征：①左边是两个二项式相乘，这两个二项式中有一项完全相同，另一项互为相反数。

②右边是乘式中两项的平方差。

即相同的平方与相反项的平方的差。

平方差公式的名称就是从右边的特征来的。

3．公式中a 和b 可以是任意一个代数式（数、字母、单项式或多项式）。

4．对于形如两数和与差相乘，就可以运用平方差，有时，需要进行变形，才能看出。

例1 计算（1）(3a ＋2b)(3a －2b) （2）)212)(212(22--+-x x （3）(200＋1)(200－1) （4）))((z y x z y x ++-+ 解：（1）原式＝(3a)2 －(2b)2＝9a 2－4b 2 （2）原式＝414)21()2(422-=--x x （3）原式＝2002－12＝39999（4）原式＝[(x ＋y)－z][(x ＋y)＋z]＝(x ＋y)2－z 2＝x 2＋xy ＋xy ＋y 2－z 2 ＝x 2＋2xy ＋y 2－z 2例2 计算（1）(－xy ＋1)(xy ＋1)(x 2y 2＋1) （2）(x 2n －2)(x 8n ＋16)·(x 2n ＋2)(x 4n ＋4) 解：（1）原式＝(1－xy)(1＋xy)(x 2y 2＋1)＝(1－x 2y 2)(1＋x 2y 2)＝1－x 4y 4注：计算中对因式适当变形，使式子符合公式的结构特征。

（2）原式＝(x 2n －2)(x 2n ＋2)(x 4n ＋4)(x 8n ＋16)＝(x 4n －4)(x 4n ＋4)(x 8n ＋16)＝(x 8n －16)(x 8n ＋16)＝x 16n －256注：利用乘法交换律、结合律，把能用公式进行计算的因式结合在一起。

八年级数学平方差公式1

P49
1
2
巩固练习：
1.选择题：
1)下列各式能用平方差公式分解因式的是（ D A. 4X² +y² B. 4 x- (-y)² C. -4 X² -y³ （ D ）
D. - X² + y² ）
2) -4a² +1分解因式的结果应是 A. -(4a+1)(4a-1) B.
-( 2a –1)(2a –1)
解：
3.原式 =2x(x² -4)=2x(x+2)(x-2) =[3(m+n)+(m-n)][3(m+n)(m-n)]
=4(2m+n)(m+2n)
用平方差公式进行简便计算:
1) 38² -37² 2) 213² -87² 3) 229² -171² 4) 91×89 解：4） =（90+1 ）（ 90-1 ） =(213+87)(213-87) =（229+171）（229-171） =300×126=37800 =90² -1 =400×58=23200 =8100-1 =8099
( 4 ) –9x² +4
例2.把下列各式因式分解解：
1)( x + z )² - ( y + z )²
4.原式=[(x+y+z)+(x-y-z)]
×[(x+y+z)- (x-y-z)]
解： 2)9( m +n)² - (m -n)² =2 x ( 2 y + 2 z) 1.原式=[(x+z)+(y+z)][(x+z)-(y+z)] =4 x ( y + z ) 3)2x³ 8x 解： =(x+y+2z)(x-y) 2.原式=[3(m+n)]² -(m-n)² 4)(x + y + z)² - (x – y – z )² 1 5)— a² -2 2 =(4m+2n)(2m+4n)

《平方差公式(1)》教学设计

《平方差公式(1)》教学设计教学目标：一、知识与技能１、参与探索平方差公式的过程，发展学生的推理能力２、会运用公式进行简单的乘法运算。

二、过程与方法１、经历探索过程，学会归纳推导出某种特种特定类型乘法并用简单的数学式子表达出，即给出公式。

２、在探索过程的教学中，培养学生观察、归纳的能力，发展学生的符号感和语言描述能力。

三、情感与态度以探索、归纳公式和简单运用公式这一数学情景，加深学生的体验，增加学习数学和使用的信心。

培养学生由观察－发现－归纳－验证－使用这一数学方法的逐步形成.教学重点：公式的简单运用教学难点：公式的推导教学方法：学生探索归纳与教师讲授结合课前准备：投影仪、幻灯片教学设计教师活动学生活动说明指导学生复习整式乘法中的“多×多”部分幻灯片打出教科书Ｐ29的乘法题组，启发学生准确迅速地完成运算让学生观察算式及结果，发现其中规律请学生说出等式两端的规律，启发学生能否用一条公式统一描述自己的演算及结果。

板书Ｐ29例１板书P30例２组织学生巩固新与邻座讨论，口答学生得出(x+2)(x-2)=x2+2x-2x-4=x2-4(1+3a)(1-3a)=1-9a2(x+5y)(x-5y)=x2-25y2(y+3z)(y-3z)=y2-向学生强调这些乘法具有特殊形式,从而结果是特殊的.鼓励大胆表达意见,积极与小组同伴合作,讨论,交流,然后统一看法.板书出公式,教师分析公式的结构,引导学生结合前出演算思考公式中a,b可表示什么讲解时可提问，具体计算中a,b代表什么？运算中应注意哪些常见错误完成例２后，可请同学对上讲台的３位的运算进行讲评。

课，完成随堂练习小结、复习公式、布置作业9z2学生与邻座为一小组进行交流,发现其中规律,说出规律表达出公式内容仔细听教师分析、讲解请３名学生上讲台演算，其余同学分组讨论会独立演算强调用公式运算要会“套”。

平方差公式（２）教学目标：一、知识与技能1、了解平方差公式的几何背景，一些代数问题能用几何图形解释，用以可培养学生数形结合的思想。

平方差公式1

乘法公式：
(x+a)(x+b)= 1.当a=-b时
2-b2 (a+b)(a-b)=a 2+(a+b)x+ab x
——平方差公式
1.下列多项式相乘，哪些可用平方差公式？怎样用公式计算？ 1) (a+b)(-b+a) 3) (a+b)(b-c) 5) (a+b)(-a-b) 2) (ab+1)(-ab+1) 4) (-2xy+z)(-2xy-z) 6) (a2-3bc)(3bc+a2)
2- 1 2+2y-6y-3) -4(4y )+3(4y
5.计算： 1) (y+2)(y-2) - (3-y)(3+y) 2) –3x(x+1)(x-1) - x(3x&)( 2 +2y) + 3(2y-3)(2y+1) 1 2+ 1 )(x- 1 ) 4) (x+ 3 )(x 9 3 1 1 2+ 1 解：4) (x+ 3 )(x 9 3 )(x- ) 1 1 2+ 1) = [(x+ 3)(x- 3)](x 9 2- 1 2+ 1 = (x 9 )(x 9) 4- 1 = x 81
解： 1) (a-b+c)(a-b-c) = [ (a-b)+c] [ (a-b)-c ] = (a-b)2 – c2 = (a2-2ab+b2) –c2 = a2-2ab+b2 –c2
4.下列各式哪些能用平方差公式计算？怎样用？ 2) (a+2b-3)(a-2b+3)
解：2) (a+2b-3)(a-2b+3) = [ a+(2b-3) ] [ a-(2b-3)] = a2- (2b-3)2 = a2- (2b-3) (2b-3) = a2- (4b2-12b+9) = a2- 4b2+12b-9

平方差公式1

课题《平方差公式》问题导读——评价单设计人：周晓宇审核人：序号：班级：七（3）班组名：姓名：【学习目标】知识与技能：1.经历探索平方差公式的过程，进一步发展符号感和推理能力2.会推导平方差公式，并能运用公式进行简单的计算。

3.认识平方差公式及其几何背景过程与方法：1.培养学生的语言表达能力，逻辑思维能力，在探索讨论中学会归纳总结。

2.培养学生动手操作，合作探究能力。

情感，态度与价值观：1.注意学生的学习积极性，主动性的调动，增强学生学习数学的信心。

2.在合作，交流和讨论中发掘知识，并体验学习的乐趣。

【重点难点】重点：会运用公式进行简单的乘法运算。

难点：公式的推导。

【逐层深入，当堂检测】一．设置情境，探究新知1.我会很快做好！（多项式乘以多项式）①(2)(2)x x +-； ②(13)(13)a a +-； ③(5)(5)x y x y +-； ④(3)(3)y z y z +-2.组内交流答案，就每个人发现的结论进行讨论，交流体会。

归纳总结平方差公式：语言描述：二．例题解析，新知应用例1：利用平方差公式计算(1)(56)(56)x x +- (2)(2)(2)x y x y -+ (3)()()m n m n -+--例2：利用平方差公式计算11(1)44x y x y ⎛⎫⎛⎫---+ ⎪⎪⎝⎭⎝⎭(2)(8)(8)ab ab +-想一想：()()?a b a b ---=你是怎样做的？三．巩固练习1.计算：(1)(2)(2)a a +- (2)(32)(32)a b a b +-(3)(1)(1)x x --- (4)(43)(43)k k -+--2.判断正误22(1)()()a b a b a b ---=-+ （）22(2)()()a b a b a b -+-=-- （）2(3)(23)(32)29x x x +-=- （）333399(4)()()y z y z y z +-=- （）2233(5)()()x y x y x y +-=- （）四．小结：1.平方差公式：语言描述：两数的与两数的的，等于这两数的2.公式的结构特征：左边是两个二项式的乘积，即两数和与这两数差的积；右边是两数的平方差。

平方差的计算公式

平方差的计算公式
【原创版】
目录
1.引言：介绍平方差
2.平方差公式：展示平方差公式
3.计算方法：解释如何使用平方差公式进行计算
4.应用实例：给出平方差公式的应用实例
5.结论：总结平方差公式的重要性
正文
【引言】
平方差是一个数学概念，它是指两个数的平方之差。

平方差在数学中有着广泛的应用，尤其在代数和统计学中。

为了更好地理解平方差，我们需要了解它的计算公式。

【平方差公式】
平方差公式是指两个数的平方之差的公式，用数学符号表示为：
(a+b)(a-b)=a^2-b^2。

其中，a 和 b 是两个数，a^2 表示 a 的平方，b^2 表示 b 的平方。

【计算方法】
使用平方差公式进行计算时，首先需要确定两个数，然后将这两个数代入公式中，进行计算。

例如，如果 a=5，b=3，那么 a^2=25，b^2=9，代入公式 (a+b)(a-b)=a^2-b^2，得到 (5+3)(5-3)=25-9，即 8*2=16。

所以，5 和 3 的平方差为 16。

【应用实例】
平方差公式在数学中有着广泛的应用，尤其在解决一些复杂的数学问
题时，它能够提供一种简便的解决方法。

例如，如果需要求解一个正方形的面积，可以先求出正方形的边长，然后使用平方差公式计算面积。

【结论】
平方差公式是数学中的一个重要公式，它能够帮助我们解决一些复杂的数学问题，提高我们的计算效率。

平方差1

平方差1

平方差公式1

平方差公式(1)

第4讲 平方差公式(1)

平方差公式1(讲课用)

公开课：平方差公式1

八年级数学平方差公式1(教学课件201911)

平方差公式1

教学内容：平方差公式1

八年级数学平方差公式1

《平方差公式(1)》教学设计

平方差公式1

平方差公式1

平方差的计算公式

第4讲平方差公式(1)