全等三角形与探索全等的条件
《探索三角形全等的条件》》(边角边)教学反思

《探索三角形全等的条件》(边角边)教学反思宁德市实验学校初中部贾庆庆三角形的全等是初中阶段学习的重点,它是两个三角形最常见的关系,它不仅是学习后面知识的基础,而且是证明线段相等、角相等的重要依据。
因此要要求学生熟练掌握三角形全等的判定方法,并且能够灵活应用。
在教学过程中,学生通过复习全等三角形的概念及其特征,掌握了全等三角形的性质,这些知识都为学习《探究三角形全等的条件》(边角边)做好了准备。
本节课主要体现了以下几个方面:1、复习巩固,设置问题2、通过作图,自主探究3、合作交流,探讨结论4、例题讲解,学以致用但在探究过程中也出现了一些问题,如:在探究"两边和其中一边的对角对应相等的两个三角形是否全等"时,学生在作三角形时出现了困难。
本节在应用定理判定三角形全等时的练习有点多,可能有些学生思维有点跟不上,是本节课的一大遗憾。
另外,在小组交流时气氛不是很活跃。
最后,我考虑在这种情况下是否可以让一个小组展示,一个小组讲解可能会更好一些。
总之,从本节课的教学效果来看,学生能达到这个程度还算可以,实现了本节课的教学目标。
自己以后要吸取教训。
听课心得体会宁德市实验学校初中部贾庆庆本周二我有幸在初二(4)班听课学习,观摩了黄老师的高效课堂,一节课的听课学习我收获很大,下面就这一节的听课情况谈点自己的感受。
在整堂课中,黄老师并没有挖苦心思的讲解,而是在指导学生各个环节自主学习新知识。
在教学过程中注重加强小组合作学习,提供学生合作、探究、交流的时间和空间,让学生协调配合,对学习内容进行充分的探究。
培养了学生的合作交流能力,整堂课过得轻松、和谐。
以上是我听课的心得体会,我以后要把通过听课学习到的优秀经验,用到自己的教学工作中,让自己的课堂也更加活跃起来,真正让学生在快乐的氛围中学习。
充分体现"教师以学生为主体,学生是学习的主人,教师是学习的组织者、引导者和合作者"的教学理念。
探索三角形全等的条件的说课稿

一、教材分析〔一〕本节内容在教材中的地位与作用。
对于全等三角形的研究,实际是平面几何中对封闭的两个图形关系研究的第一步。
它是两三角形间最简单、最常见的关系。
本节《探索三角形全等的条件》是学生在认识三角形的根底上,在了解全等图形和全等三角形以后进行学习的,它既是前面所学知识的延伸与拓展,又是后继学习探索相似形的条件的根底,并且是用以说明线段相等、两角相等的重要依据。
因此,本节课的知识具有承上启下的作用。
同时,苏科版教材将“边角边〞这一识别方法作为五个根本领实之一,说明本节的内容对学生学习几何说理来说具有举足轻重的作用。
〔二〕教学目标〔1〕经历探索三角形全等条件的过程,体会分析问题的方法,积累数学活动的经验。
〔2〕掌握“边角边〞这一三角形全等的识别方法,并能利用这些条件判别两个三角形是否全等,解决一些简单的实际问题。
〔3〕培养学生勇于探索、团结协作的精神。
〔三〕教材重难点由于本节课是第一次探索三角形全等的条件,故我确立了以“探究全等三角形的必要条件的个数及探究边角边这一识别方法作为教学的重点,而将其发现过程以及边边角的辨析作为教学的难点。
同时,我将采用让学生动手操作、合作探究、媒体演示的方式以及渗透分类讨论的数学思想方法教学来突出重点、突破难点。
〔四〕教学具准备,教具:相关多媒体课件;学具:剪刀、纸片、直尺。
画有相关图片的作业纸。
二、教法选择与学法指导本节课主要是“边角边〞这一根本领实的发现,故我在课堂教学中将尽量为学生提供“做中学〞的时空,让学生进行小组合作学习,在“做〞的过程中潜移默化地渗透分类讨论的数学思想方法,遵循“教是为了不教〞的原那么,让学生自得知识、自寻方法、自觅规律、自悟原理。
三、教学流程〔一〕创设情景,激发求知欲望首先,我出示一个实际问题:问题:皮皮公司接到一批三角形架的加工任务,客户的要求是所有的三角形必须全等。
质检部门为了使产品顺利过关,提出了明确的要求:要逐一检查三角形的三条边、三个角是不是都相等。
探索三角形全等的条件说课稿

设 教 学 计 程 意 序 图
你能找到图中的三角形吗?
三角形稳定性在校园中应用
五、 教学过程分析
教学过程分析
探索发现 合作交流 归纳结论 解决问题
创设情境 提出问题
知识运用 巩固新知
再创情境 联系实际
反思小结 提炼规律
布置作业 提高升华
五、 教学过程分析
六、反思小结,提炼规律
反思小结: 通过本节课的学习,你学会什么知识? 1.三角形全等的“边边边”条件。 2.三角形的稳定性。 设计意图: 让学生自己把所学到的知识经常进行整 理小结,使他们头脑中存储着一个层次分 明的知识系统。
设计意图
分层次作业使不同层次的学生得到了不同的发展,又 为后续的学习打下了良好的基础。巩固所学,分层要求。 体现“人人学有价值的数学,不同的人在数学上有不同的 发展”。
说课
探索三角形全等的条件
教学评价
教学过程分析 教材分析 教法学法分析 学情分析 教法目标 重难点分析
教学评价
教学评 教学评价 价
恰当创设 情境 尊重规律
精心设计问题 尊重知识
指导思考 实践 尊重学生
学生动起 来 知识动起 来 情感动起 来
体现尊重
六、教学评价
教学评价 1.恰当创设情境,尊重规律
本节课的设计体现了以教师为主导、学生为主体, 以知识为载体、以培养学生的思维能力为重点的教学 思想。数学学习不仅是知识的学习,更重要的是方法 的学习。教师摒弃了直接给出“SSS”条件的教学方法, 创设有趣的情境融合入教学,以学生的数学探索活动 为主线,采用了“引导―自主探索”的教学模式,以 探索三角形全等的条件为中心,遵循学生的认识规律, 注重学生在独立思考基础上的合作交流,将教师的 “引”与学生的“探”融为一个和谐的整体。
第3讲探索三角形全等的条件(二)

(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和斜边对应相等;
()
(3)两直角边对应相等;
()
(4)一条直角边和斜边对应相等. ( )
【答案】(1)全等,“AAS”;(2)全等,“AAS”;(3)全等,“SA根据全等三角形的判定来判断.
4、【答案】A 【解析】解:∵OM=ON,CM=CN,OC 为公共边, ∴△MOC≌△NOC(SSS).∴∠MOC=∠NOC 故选:A.
5【答案】AH=CB; 【解析】∵AD⊥BC,CE⊥AB,垂足分别为 D、E, ∴∠BEC=∠AEC=90°, 在 Rt△AEH 中,∠EAH=90°﹣∠AHE, 又∵∠EAH=∠BAD, ∴∠BAD=90°﹣∠AHE, 在 Rt△AEH 和 Rt△CDH 中,∠CHD=∠AHE, ∴∠EAH=∠DCH, ∴∠EAH=90°﹣∠CHD=∠BCE, 所以根据 AAS 添加 AH=CB 或 EH=EB; 根据 ASA 添加 AE=CE. 可证△AEH≌△CEB.
【总结升华】直角三角形全等可用的判定方法有 5 种:SAS、ASA、AAS、SSS、HL.
例 3、如图,AB⊥AC 于 A,BD⊥CD 于 D,若 AC=DB,则下列结论中不正确的是( )
A.∠A=∠D B.∠ABC=∠DCB C.OB=OD D.OA=OD 【答案与解析】根据已知及全等三角形的判定方法进行分析,从而得到答案.做题时要结合 已知条件与全等的判定方法逐一验证. 解:∵AB⊥AC 于 A,BD⊥CD 于 D ∴∠A=∠D=90°(A 正确) 又∵AC=DB,BC=BC ∴△ABC≌△DCB(HL) ∴∠ABC=∠DCB(B 正确) ∴AB=CD 又∵∠AOB=∠C ∴△AOB≌△DOC(AAS) ∴OA=OD(D 正确) C 中 OD、OB 不是对应边,不相等. 故选 C. 【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、 SAS、ASA、AAS、HL.注意:AAA、SSA 不能判定两个三角形全等,判定两个三角形全 等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
4.3探索三角形全等的条件教案

1.理论介绍:首先,我们要了解三角形全等的基本概念。三角形全等是指两个三角形的三个角和三条边完全相同。它是解决几何问题的重要工具,可以帮助我们计算角度和边长。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了如何使用SSS和SAS条件判断两个三角形是否全等,以及全等三角形在实际问题中的应用。
2.教学难点
-难点在于理解全等三角形的本质,即不仅仅是外观相似,而是每一个角和每一条边都完全相同。
-学生在理解SAS全等条件时,可能会对夹角的概念感到困惑,不清楚如何准确地判断两个角的相等性。
-在实际操作中,如何正确使用直尺和圆规进行全等三角形的作图,尤其是当条件不完整时。
-难点还在于如何将全等三角形的性质应用到解决复杂几何问题中,如四边形的不规则图形中。
举例:
a)难点解释:在SAS全等条件中,学生需要理解“夹角”是指两条边的公共端点所对的角,而不是任意两条边之间的角。
b)实际操作难点:在作图时,学生可能难以准确地通过给定的一边和夹角来确定另一边的位置,需要教师引导如何利用已知信息进行作图。
c)应用难点:在解决综合几何问题时,学生可能不知道如何将问题简化为全等三角形的判定问题,需要教师通过具体案例分析来帮助学生理解。
4.解决实际问题,运用三角形全等的条件判断生活中的物体形状是否相同。
二、核心素养目标
本节课旨在培养学生的几何直观、逻辑推理和问题解决能力,具体目标如下:
1.通过探索三角形全等的条件,提高学生对几何图形的观察、分析和推理能力,发展几何直观;
2.引导学生运用逻辑推理方法证明SSS和SAS全等条件,培养严谨的逻辑思维和推理能力;
4.3探索三角形全等的条件教案
一、教学内容
探索三角形全等的条件教学设计 (1)

《探索三角形全等的条件》教学设计一、教材分析:三角形全等的判定是本章乃至本学期的一个知识重点,它是建立在学生对图形的全等有了一定的认识,并在学习了全等三角形的概念和性质的基础上进行延伸的,并为接下来探索三角形全等的其他条件,探索直角三角形全等条件,以及将来的探索三角形相似的条件打下良好的基础,因此在整个初中教学中起到承上启下的作用。
二、学情分析:学生在前几节中,已经了解了三角形的有关概念,以及三角形三边之间的关系、图形的全等和全等三角形等,对本节课要学习的三角形的稳定性和三角形全等条件中的“边边边”来说已经具备了一定的知识技能基础。
在相关知识的学习过程中,学生已经经历了一些探索图形的全等和全等三角形的活动,通过拼图、折纸等方式解决了一些简单的现实问题,获得了一些数学活动经验的基础;同时在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
三、教学目标:1、知识与技能:在具体情境中经历探索三角形全等条件的过程,从而在操作活动中掌握全等三角形的“边边边“的条件,并用它解决一些实际问题。
2、过程与方法:(1)经历动手操作画图,了解三角形“边边边“全等的条件。
(2)善于发现问题,并能通过讨论交流解决问题。
(3)能结合具体问题进行有条理的思考,会进行简单的说明。
3、情感态度与价值观:培养学生敢于实践,勇于发现,大胆探索,合作创新的精神;体会数学在生活中的作用,增强学习数学的兴趣。
四、教学重难点:1、教学重点:了解两个三角形全等应有三个条件,掌握三角形全等的“边边边”条件,理解条件内涵并初步学会运用。
2、教学难点:对三角形全等条件的分析和探索。
五、教学资源:剪刀、纸、三角尺、三角板、量角器、多媒体。
探索三角形全等的条件

探索三角形全等的条件(1)栖霞市唐家泊中学衣龙涛教学目标:1.知识与技能:掌握三角形全等的“边边边”条件,了解三角形的稳定性。
在探索的过程中,能够进行有条理的思考并进行简单的推理。
2.过程与方法:经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程,通过小组合作探究得到相关结论。
3.情感态度与价值观:(1)使学生在自主探索三角形全等的过程中,经历画图、观察、比较、推理、交流等环节,从而获得正确的学习方式和良好的情感体验,让学生体验数学源于生活,服务于生活的辨证思想。
(2)培养学生勇于探索、团结协作的精神。
教学重点:三角形全等条件的探索过程。
教学难点:三角形全等条件的探索过程,特别是创设出问题后,学生面对开放性问题,要做出全面、正确的分析,并对各种情况进行讨论,对初二学生有一定的难度。
教具:硬纸板、直尺、圆规、自制三角形、四边形、多媒体课件教学方法:自主探索、合作交流教学过程:一、问题情境,导入新课:1、同学们,上一节课我们刚刚学习了全等三角形,那么什么是全等三角形?2、小明画了一个三角形,怎样才能画一个与他画的三角形全等?交流总结:我们知道全等三角形的三条边、三个角分别对应相等。
反过来,两个三角形如果要全等,需要六个条件其中的那些条件呢? 一个条件行吗?两个条件、三个条件呢?这就是我们这节课要探索的问题:板书课题---探索三角形全等的条件(1)二、探究发现,学习新知:(一)只给一个条件(一组对应边相等或一组对应角相等),画出的两个三角形一定全等吗?注意:一个条件,指什么条件?(一条边或一个角)1.只给定一条边时:(学生操作,白板展示)2、只给定一个角时:(学生操作,白板展示)(二)给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?分别按下列条件做一做.1、三种情况:一边一角、两边、两角2、具体情况:①一边一角:三角形一条边为15cm,一内角为30°.②两边:三角形两条边分别为15cm、16cm.③两角:三角形两内角分别为30°和60°.学生分组讨论、探索、归纳,最后以组为单位出示结果作补充交流.3.总结讨论结果:(学生操作,白板展示)结论:可以发现按这些条件画出的三角形都不能保证一定全等.(三)给出三个条件画三角形,你能说出有几种可能的情况吗,它们全等吗?小组归纳:有四种可能.即:三内角、三条边、两边一内角、两内角一边.1、在刚才的探索过程中,我们已经发现三内角不能保证三角形全等.比如一个大直角三角尺与一个小直角三角尺。
全等三角形全等的条件

全等三角形全等的条件
全等三角形是指三角形的对应边和对应角相等。
全等三角形的
条件包括SSS(边-边-边)、SAS(边-角-边)、ASA(角-边-角)
和AAS(角-角-边)四种情况。
1. SSS(边-边-边),如果两个三角形的三条边分别相等,则
这两个三角形全等。
2. SAS(边-角-边),如果两个三角形中,一个三角形的两边
和夹角分别等于另一个三角形的两边和夹角,则这两个三角形全等。
3. ASA(角-边-角),如果两个三角形的一个角和两边分别等
于另一个三角形的一个角和两边,则这两个三角形全等。
4. AAS(角-角-边),如果两个三角形的两个角和一边分别等
于另一个三角形的两个角和一边,则这两个三角形全等。
这些条件是用来判断两个三角形是否全等的依据,通过对应边
和对应角的相等性来确定三角形的全等关系。
这些条件在几何学中
有着重要的应用,可以帮助我们判断和证明三角形的全等关系。
专题探索三角形全等的条件(SSS和SAS)(知识讲解)数学七年级下册(北师大版)
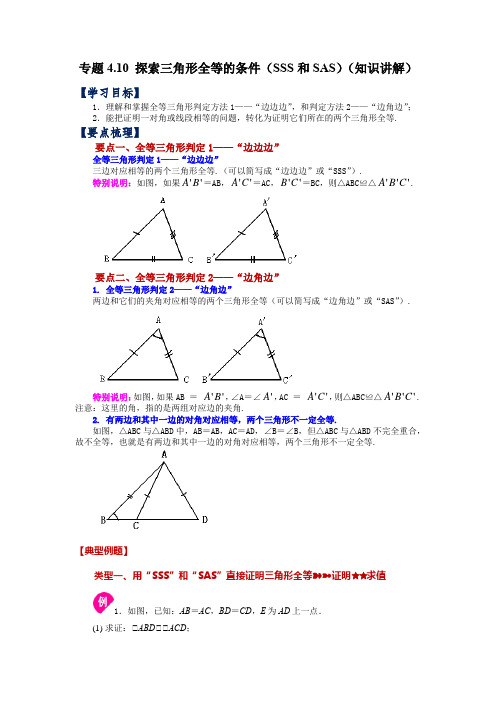
专题4.10 探索三角形全等的条件(SSS 和SAS )(知识讲解)【学习目标】1.理解和掌握全等三角形判定方法1——“边边边”,和判定方法2——“边角边”;2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).特别说明:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).特别说明:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、用“SSS”和“SAS”直接证明三角形全等➽➼证明✮✮求值1.如图,已知:AB =AC ,BD =CD ,E 为AD 上一点.(1) 求证:△ABD △△ACD ;(2) 若△BED =50°,求△CED 的度数.【答案】(1) 证明见分析 (2) 50CED ∠=︒【分析】(1)根据SSS 即可证明△ABD △△ACD ;(2)只要证明△EDB △△EDC (SAS ),即可推出△BED =△CED ,进而得到答案. (1)证明:在△ABD 和△ACD 中, AB ACBDCD AD AD ⎧⎪⎨⎪⎩===,△△ABD △△ACD (SSS );(2)解:△△ABD △△ACD ,△△ADB =△ADC ,在△EDB 和△EDC 中,DB DC BDE CDE DE DE ⎧⎪∠∠⎨⎪⎩===,△△EDB △△EDC (SAS ),△△BED =△CED ,△△BED =50°,△△CED =△BED =50°.【点拨】本题考查全等三角形的判定和性质,解题的关键是根据图形题意,熟练掌握两个三角形全等判定与性质.举一反三:【变式1】如图,点A 、M 、N 、C 在同一条直线上,AB CD =,BN DM =,AM CN =,求证:AB CD ∥.【分析】根据AB CD =,BN DM =,AM CN =,利用SSS 定理证明ABN CDM ≌,从而得到A C ∠=∠,再根据内错角相等,两直线平行,AB CD ∥得证.解:证明:∵AM CN =∴AM MN CN MN∴AN CM =在ABN 和CDM 中AB CD BN DM AN CM =⎧⎪=⎨⎪=⎩,∴()ABN CDM SSS △≌△∴A C ∠=∠∴AB CD ∥(内错角相等,两直线平行)【点拨】本题考查了三角形全等的判定方法和性质,以及平行线的判定,解题关键是掌握全等三角形的判定方法,运用全等三角形的性质证明线段和角相等.【变式2】如图,已知AB AC =,AD AE =,BD CE =,求证:312.【分析】利用SSS 可证明△ABD△△ACE ,可得△BAD=△1,△ABD=△2,根据三角形外角的性质即可得△3=△BAD+△ABD ,即可得结论.解:在△ABD 和△ACE 中,AB=AC AD=AE BD=CE ⎧⎪⎨⎪⎩,△△ABD△△ACE ,△△BAD=△1,△ABD=△2,△△3=△BAD+△ABD ,△△3=△1+△2.【点拨】本题考查全等三角形的判定与性质及三角形外角性质,熟练掌握判定定理及外角性质是解题关键.2.已知:如图,AB AC =,F ,E 分别是AB AC ,的中点,求证:ABE ACF ≌.在ABE 与△AB AC A A AE AF =⎧⎪∠=∠⎨⎪=⎩ABE △≌△【点拨】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:ASAAAS 、、【变式1】如图,点D 在BC 上,,ADB B BAD CAE ∠=∠∠=∠.(1) 添加条件:____________(只需写出一个),使ABC ADE ≅;(2) 根据你添加的条件,写出证明过程.【答案】(1) AC AE = (2) 见分析【分析】(1)根据已知条件可得AB AD =,BAC DAE ∠=∠,结合三角形全等的判定条件添加条件即可;(2)结合(1)的条件,根据三角形全等的判定条件添加条件进行证明即可.解:(1)添加的条件是:AC AE =,故答案为AC AE =;(2)△,ADB B ∠=∠△AB AD =,△BAD CAE ∠=∠△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,又AC AE =△ABC ADE ≅【点拨】本题主要考查了三角形全等的判定,确定出三角形全等判定条件是解答本题的关键.【变式2】如图所示,DC CA ⊥,EA CA ⊥,CD AB =,CB AE =,求证:(1) BCD EAB ≌△△;(2) DB BE ⊥.【分析】(1)利用SAS 判定定理证明三角形全等即可;(2)由()≌DCB BAE SAS △△,可得∠=∠DBC BEA ,∠=∠BDC EBA ,再利用90DBC BDC ∠+∠=︒,可得90∠+∠=︒DBC EBA ,即90DBE ∠=︒,所以DB BE ⊥.解:(1)证明:△DC CA ⊥,EA CA ⊥,△90∠=∠=︒DCB BAE ,在DCB △和BAE 中,CD AB DCB BAE CB AE =⎧⎪∠=∠⎨⎪=⎩△()≌DCB BAE SAS △△. (2)证明:由(1)可知()≌DCB BAE SAS △△, △∠=∠DBC BEA ,∠=∠BDC EBA ,△90DBC BDC ∠+∠=︒,△90∠+∠=︒DBC EBA ,即90DBE ∠=︒,△DB BE ⊥.【点拨】本题考查全等三角形的判定定理及性质,垂直的定义,解题的关键是掌握全等三角形的判定定理及性质.类型二、用“SSS”和“SAS”间接证明三角形全等➽➼证明✮✮求值3.已知:如图,A 、C 、F 、D 在同一直线上,AF =DC ,AB =DE ,BC =EF ,求证:△ABC≌≌DEF .【分析】首先根据AF=DC ,可推得AF ﹣CF=DC ﹣CF ,即AC=DF ;再根据已知AB=DE ,BC=EF ,根据全等三角形全等的判定定理SSS 即可证明△ABC△△DEF .解:△AF=DC ,△AF ﹣CF=DC ﹣CF ,即AC=DF ;在△ABC 和△DEF 中AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩△△ABC△△DEF (SSS )举一反三: 【变式1】如图,已知:PA=PB,AC =BD ,PC =PD ,△PAD 和△PBC 全等吗?请说明理由.【分析】由AC=BD ,利用线段的和差关系可得AD=BC ,利用SSS 即可证明△PAD△△PBC.解:△AC =BD ,△AC+CD=BD+CD ,即AD =BC ,又△PA =PB ,PC =PD ,△△PAD△△PBC(SSS)【点拨】本题考查全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题关键.【变式2】如图,点D ,A ,E ,B 在同一直线上,EF =BC ,DF =AC ,DA =EB .试说明:△F =△C .【分析】根据SSS 的方法证明△DEF△△ABC,即可得到结论.解:因为DA =EB , 所以DE =AB.在△DEF 和△ABC 中, 因为DE =AB ,DF =AC ,EF =BC ,所以△DEF△△ABC(SSS),所以△F =△C.【点拨】本题考查了全等三角形的判定和性质,属于简单题,找到证明全等的方法是解题关键.4.如图,在ABCD 中,点E 、F 在BD 上,ABE 与CDF 全等吗?若全等,写出证明过程;若不全等,请你添加一个条件使它们全等,并写出证明过程.(1) 你添加的条件是__________.(2) 证明过程: 【答案】(1) BE DF =,答案不唯一; (2) 证明见分析; 【分析】(1)根据选择的全等三角形判定方法添加合适的条件即可;(2)由四边形ABCD 是平行四边形得到AB CD ∥,AB CD =,得ABE CDF ∠=∠,再用上添加的条件,即可证明结论.(1)解:BE DF =(答案不唯一)故答案为:BE DF =(答案不唯一)(2)证明:△四边形ABCD 是平行四边形,△AB CD ∥,AB CD =,△ABE CDF ∠=∠,在ABE 和CDF 中,AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩,△ABE CDF △≌△(SAS ).【点拨】此题考查了平行四边形的性质、全等三角形的判定等知识,熟练掌握全等三角形的判定是解题的关键.举一反三:【变式1】如图,在ABC 和ADE 中,AB AD =,AC AE =,且BAD CAE ∠=∠,求证:ABC ADE △≌△.【分析】根据BADCAE ∠=∠可得BAC DAE ∠=∠,再根据SAS 即可证明.证明:△BAD CAE ∠=∠,△BAD DAC CAE DAC ∠+∠=∠+∠,即BAC DAE ∠=∠,在ABC 和ADE 中,AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC ADE △≌△.【点拨】本题主要考查了用SAS 证明三角形全等,解题的关键是通过BAD CAE ∠=∠得出BAC DAE ∠=∠.【变式2】图,BE CF =,AC DF =,AC DF ∥.求证:ABC DEF ≌△△.【分析】首先根据BE CF =可得BC EF =,再由AC DF ∥可得ACB F ∠=∠,然后利用定理证明ABC DEF ≌即可.证明:△BE CF =,△BE EC CF EC ++=,即BC EF =,△AC DF ∥,△ACB F ∠=∠, 在ACB △和DFE △中,BC EF ACB F AC DF =⎧⎪∠=∠⎨⎪=⎩,△()SAS ABC DEF ≌.【点拨】此题主要考查了全等三角形的判定和平行线的性质,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.注意:AAA SSA 、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.类型三、全等的性质与“SSS”和“SAS”综合➽➼证明✮✮求值 5.已知:如图,在ABC 中,AB AC AD =,是BC 边上的中线.求证:AD BC ⊥(填空).证明:在三角形ABD ACD 和中,△()()()______________BD AB ⎧=⎪⎪=⎨⎪⎪⎩已知已知公共边,△ ≌ ( ).△ADB ∠= (全等三角形的对应角相等).△1902ADB BDC ∠∠︒==(平角的意义). △(垂直的意义).【答案】,,,,SSS DC AC AD AD ABD ACD ADC AD BC =∠⊥,△△,,【分析】证明()SSS ADB ADC ≌△△.推出ADB ADC ∠∠=,可得结论. 证明:△AD 是BC 边上的中线,△BD CD =,在三角形ABD △和ACD 中,【变式1】如图:AB AC =,BD CD =,若28B ∠=︒,求C ∠的度数.【答案】28︒ 【分析】连接AD ,利用“SSS ”证明ABD ACD △≌△,即可得到答案.解:连接AD ,在ABD △和ACD 中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,()SSS ABD ACD ∴≌C B ∴∠=∠,28B ∠=︒,28C ∴∠=︒.【点拨】本题考查了全等三角形的判定和性质,正确作辅助线构造全等三角形是解题关键.【变式2】已知:如图,AC BD =,AD BC =,AD ,BC 相交于点O ,过点O 作OE AB ⊥,垂足为E .求证:(1) ABC BAD ≌.(2) AE BE =.【分析】(1)利用SSS 证明ABC BAD ≌;(2)根据全等三角形的性质得出DAB CBA ∠=∠,则OA OB =,根据等腰三角形的性质可得出结论.(1)证明:在ABC 和BAD 中,AC BD BC AD AB BA =⎧⎪=⎨⎪=⎩,△ABC BAD ≌(2)证明:△ABC BAD ≌△CBA DAB ∠=∠,△OA OB =,△OE AB ⊥,△AE BE =.【点拨】此题考查了全等三角形的判定与性质,利用SSS 证明ABC BAD ≌是解题的关键.6.如图,在ABC 中,CM 是AB 边上的中线,8AC =,12BC =,求CM 的取值范围.【答案】210CM <<【分析】倍长中线CM 至点N ,构造BNM ,易得ACM BNM ≅△△,再利用三角形的三边关系找到CN 的取值范围,进而得到CM 的取值范围.解:如图,延长CM 到点N ,使CM MN =,连接BN ,在ACM △和BNM 中,CM NM AMC BMN AM BM =⎧⎪∠=∠⎨⎪=⎩,∴ACM BNM ≅△△(SAS ),∴8AC BN ==, 在BCN △中,BC BN CN BC BN -<<+,∴128128CN -<<+,即420CN <<,∴4220CM <<,即210CM <<.【点拨】本题考查了全等三角形的性质与判定以及三角形的三边关系,解决本题的关键是倍长中线构造全等三角形.举一反三:【变式1】如图,已知在ABC 与ADE 中,90BAC DAE AB AC AD AE ∠=∠=︒==,,,点C ,D ,E 三点在同一条直线上,连接BD .图中的CE BD 、有怎样的数量和位置关系?请证明你的结论.【答案】CE BD =,证明见分析【分析】根据SAS 证明ACE ABD ≌△△,即可得到CE BD =.解:CE BD =,证明:△90BAC DAE ∠=∠=︒,△BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠,在ACE △和ABD △中AC AB CAE BAD AE AD =⎧⎪∠=∠⎨⎪=⎩△()SAS ACE ABD ≌△CE BD =.【点拨】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解题的关键.【变式2】如图已知AOB 和MON △都是等腰直角三角形.(1) 如图1,连接AM ,BM ,此时AM ,BN 的数量关系为___________请说明理由.(2) 若将MON △绕点O 顺时针旋转,如图2,当点N 恰好在AB 边上时,求证:222BN AN MN +=.【答案】(1) AM BN =,理由见分析(2) 见分析 【分析】(1)由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =(2)连接AM ,由AOB 和MON △都是等腰直角三角形,得到AOM BON ≌,即可得到AM BN =,再求得90MAN ∠=︒,利用勾股定理即可得到222BN AN MN +=解:(1)AM BN =,理由如下:△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ON AOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =(2)如下图,连接AM ,△AOB 和MON △都是等腰直角三角形,△OA OB =,OM ON =,90AOB MON ∠=∠=︒,45B BAO ∠=∠=︒,△AOM BON ∠=∠,在AOM 和BON △中:OA OB OM ONAOM BON =⎧⎪=⎨⎪∠=∠⎩, △AOM BON ≌,△AM BN =,45B MAO ∠=∠=︒,△90MAN MAO BAO ∠=∠+∠=︒,△222AM AN MN +=,△222BN AN MN +=【点拨】本题考查了旋转的性质、全等三角形的判定和性质、等腰直角三角形的性质及勾股定理,熟练掌握全等三角形的判定和性质是解决问题的关键。
三角形全等的条件 要点全析

三角形全等的条件·要点全析1.探索三角形全等的条件三角形有三条边,三个内角共六个基本元素,全等三角形的六个元素都分别对应相等.反过来,如果两个三角形的三组边对应相等并且三组角也对应相等.那么它们必定可以重合,根据定义,它们一定全等.但是,判定两个三角形全等真的需要六个条件吗?探索发现:两个三角形满足一个条件(一条边或一个内角相等)或两个条件都不能确定它们是否全等,而满足三个适当的条件就可以判定两三角形全等.2.三角形全等的条件一:“SSS ”或“边边边”(1)SSS :三边对应相等的两个三角形全等,简写成“边边边”或“SSS ”.(2)书写格式:如图13-2-1.在△ABC 和△A ′B ′C ′中,①⎪⎩⎪⎨⎧'''''',=,=,=C B BC C A AC B A AB ② ∴ △ABC ≌△A ′B ′C ′(SSS ).③(3)书写格式的步骤分三步:第一步:指出在哪两个三角形中.如上边的①,在△ABC 和△A ′B ′C ′中. 第二步:按条件中的边角顺序列出三个条件.如上边的②. 第三步;写出结论,如上边的③,△ABC ≌△A ′B ′C ′(SSS ).【说明】①第一步中,两个三角形之间的“和”不能写成“≌”,也不能取消.②第二步中,大括号内的三个条件的书写是有顺序的,必须与判定条件一致,并且注意边、角字母的对应.一般前一个三角形的边、角写在等号的左边,另一个三角形的对应边、角写在右边.③写结论时,注意对应顶点写在对应位置上,并在后面的括号内注明判定条件的简写,如“SSS ”或“边边边”.例如:如图13-2-2.已知AB =AC ,D 为BC 中点.试说明∠B =∠C 是否成立,为什么?解:∠B =∠C 成立.∵ D 为BC 中点,∴ BD =CD .在△ABD 和△ACD 中,⎪⎩⎪⎨⎧(公共边),=(已证),=(已知),=AD AD CD BD AC AB∴ △ABD ≌△ACD (SSS ).∴ ∠B =∠C (全等三角形的对应角相等).【说明】①在本例中使用了证明的格式.②在本例中的最后两步中有两个“∴”符号,前一个“∴”,是由前面大括号内的三个条件得出的.后一个“∴”,是将前一个“∴”当成了“∵”,然后推出后一个“∴”,这里省略了一步:∵△ABD ≌△ACD .因此,今后在书写中要注意.3.三角形全等的条件二:“边角边”或“SAS ”(1)SAS :有两边和它们的夹角对应相等的两个三角形全等,简记为“SAS ”.(2)表达格式为在△ABC 和△DEF 中(图13-2-3)⎪⎩⎪⎨⎧∠∠,=,=,=EF BC DEF ABC DE AB∴ △ABC ≌△DEF (SAS ).例如:如图13-2-4中,AD 、BC 相交于点O .OA =OD ,OB =OC ,那么AB =DC 是否成立.解:∵ AD 、BC 相交于点O ,∴ ∠AOB =∠DOC (对顶角相等).在△AOB 和△DOC 中,⎪⎩⎪⎨⎧∠∠(已知)=(已证),=(已知),=OC OB DOC AOB OD OA∴ △AOB ≌△DOC (SAS ).∴ AB =DC【说明】本题中,书写三条件时,应该按边、角、边的顺序,将两边的夹角放在中间,用括号括起来;或者写成一行,也按边、角、边的顺序,将两边的夹角放在中间,再推出两个三角形全等.4.三角形全等的条件三:“角边角”或“ASA ”(1)两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA ”.(2)表达格式:如图13-2-5,在△ABC 和△DEF 中,⎪⎩⎪⎨⎧∠∠∠∠,=,=,=DEF B DE AB D A ∴ △ABC ≌△DEF (AAS ).5.三角形全等的条件四:“角角边”或“AAS ”(1)有两角和一边对应相等的两个三角形全等,简写成“角角边”或“AAS ”.(2)表达格式,如图13-2-5,在△ABC 和△DEF 中,⎪⎩⎪⎨⎧∠∠∠∠,=,=,=EF BC D A DEF B ∴ △ABC ≌△DEF (AAS ).例如:如图13-2-6中,AB ∥CD ,AE ∥DF ,AB =CD .求证:AE =DF .证明:∵ AB ∥CD ,∴ ∠ABC =∠DCB .∵ AE ∥DF ,∴ ∠AEB =∠DFC .在△ABE 和△DCF 中,⎪⎩⎪⎨⎧∠∠∠∠,=,=(已证),=DF AE DFC AEB DCF ABC∴ △ABE ≌△DCF (AAS ).∴ AE =DF .6.直角三角形全等的条件:“斜边、直角边”或“HL ”(1)HL :斜边和一条直角边对应相等的两个直角三角形全等,简写成“斜边、直角边”或“HL ”.(2)表达格式:如图13-2-7,在△ABC 中,AD ⊥BC 于D ,AB =AC 在Rt △ABD 和Rt △ACD 中,⎩⎨⎧,=,=AD AD AC AB∴ Rt △ABD ≌Rt △ACD (HL )(3)直角三角形是三角形中的一种特殊情况,因此,它也可以用一般三角形全等的条件.如两条直角边对应相等,可用“SAS ”,一边一锐角对应相等可用“ASA ”或“AAS ”.它的特殊条件就是“斜边、直角边”.7.“角角角”与“边边角”在三角形全等的条件中,上面已说过的有:三边的SSS ,两边一角的SAS 和一边两角的ASA ,AAS ,那么“AAA ”和“SSA ”能否成为三角形全等的条件呢?(1)有三个角对应相等的两个三角形不一定全等,如图13-2-8,DE ∥BC ,则∠ADE =∠B ,∠AED =∠C ,∠A =∠A ,△ADE 与△ABC 有三角对应相等,但它们没有重合,所以不全等.(2)如图13-2-9,在△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等.也就是有两边和其中一边的对角对应相等的两个三角形不一定全等.8.证明的意义和步骤(1)证明的意义证明是由题设(已知)出发,经过一步步的推理,最后推出结论(求证)正确的过程,简单地说,证明就是推理过程.(2)证明的步骤证明一个命题为正确的时候,其步骤如下:①弄清命题的条件和结论,画出图形.②根据条件,结合图形,写出已知.③根据结论,结合图形、写出求证.④写出证明过程.证明一个命题不正确的时候,只需举出一个反例即可.例如:若a 2=b 2,则a =b .这是一个错误命题,证明如下.证明:∵ (-5)2=52=25,而-5≠5.∴ 若a 2=b 2,则a =b ,是一个错误命题.9.证明题目时常用的三种方法在探索三角形全等的过程中,经常要遇到条件不足或结论不易寻找等问题,如何分析条件与结论之间的关系,常用的分析方法有以下三种:(1)综合法就是从题目的已知条件入手,根据已学过的定义、定理、性质、公理等,逐步推出要判断的结论,有时也叫“由因导果法”.例如:如图13-2-10,在△ABC 中,D 是BC 的中点,DE ∥AB ,DF ∥AC ,分别交AC 、AB 于点E 、F .求证:BF =DE .分析:从已知条件到推出结论,其探索过程如下⇒⎪⎭⎪⎬⎫∠∠⇒⇒∠∠⇒C BDF AC DF CD BD BC D CDE B AB DE =∥=的中心是=∥△BFD ≌△DEC (ASA ) ⇒BF =DE (目标).以上这种由因导果的方法就是综合法.(2)分析法就是从要判断的结论出发,根据已学的定义、定理、公理、性质等,倒过来寻找能使结论成立的条件,这样一步步地递求,一直追溯到结论成立的条件与已知条件相吻合为止,有时也叫“执果索因法”.如上题,用分析法的探索过程如下:BF =DE ⇒△BFD ≌△DEC ⇒⎪⎩⎪⎨⎧⇒⇒∠∠⇒⇒⇒⇒∠∠已知∥=已知中点是=已知∥=AC DF C BDF BC D CD BD AB DE CDE B(3)分析—综合法在实际的思考过程中,往往需要使用这两种方法,先从结论出发,想一想需要什么条件,层层逆推,当思维遇到障碍时,再从条件出发,顺推几步,看可以得出什么结论,从而两边凑,直至沟通“已知”和“结论”的两个方面. 即:已知 中间条件 结论 综合法 分析法例如:如图13-2-11,在△ABC 中,AB =AC ,D 是BC 的中点,E 是AD 上任一点,连接EB 、EC ,求证:EB =EC .分析:本题比较复杂,可用上述的三个方法均可,现在以分析一综合法为例,说明分析过程.先用综合:由因导果.⇒⎪⎭⎪⎬⎫⇒CD BD D AD AD AC AB =为中心==△ABD ≌△ACD ⇒⎩⎨⎧∠∠∠∠.=,=CDA BDA CAD BAD再用分析:执果索因.EB =EC ⇒△ABE ≌△ACE ⇒⎪⎩⎪⎨⎧⇒∠∠⇒已知==已知=AE AE CAEBAE AC AB ⇒△ABD ≌△ACD . 证明:∵ D 是BC 的中心,∴ BD =CD . 在△ABD 和△ACD 中⎪⎩⎪⎨⎧(公共边),=(已证),=(已知),=AD AD CD BD AC AB∴ △ABD ≌△ACD (SSS ).∴ ∠BAD =∠CAD .在△ABE 和△ACE 中⎪⎩⎪⎨⎧∠∠(公共边)=(已证),=(已知),=AE AE CAE BAE AC AB∴ △ABE ≌△ACE (SAS ).∴ BE =CE (全等三角形的对应边相等).【说明】①本题证明过程中,后一次三角形全等,也可选△BDE ≌△CDE ,方法同上.②本题两次用到全等三角形,在分析中应找准三角形,理清思路.10.判定两个三角形全等方法的选择选择哪种方法判定两个三角形全等,要根据具体已知条件而定,见下表:已知条件寻找条件判定方法—边一角对应相等一边SAS一角SAS或AAS两角对应相等一边ASA或AAS两边对应相等一角SAS 一边SSS11.如何选择三角形判定全等在学过本节内容之后,经常会遇到判定两条线段相等,两个角相等的问题,而要判断它们相等,就要考虑选择三角形全等.如何选择三角形呢?可考虑以下四个方面:(1)可以从判断的结论(线段或角)出发,寻找这些结论在哪两个可能的全等三角形中,就试着判定两个三角形全等.(2)可以从题目的已知条件出发,看已知条件能确定哪两个三角形全等就判定它们全等.(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后判定它们全等.(4)如果以上方法都行不通,可考虑添加辅助线的办法,构造三角形全等.例如:如图13-2-12,已知AB=AC,BD=CD,试判断∠B与∠C的关系,并说明理由.分析:要判断∠B与∠C的关系,先看∠B与∠C是否在两个全等三角形中,而此题没有两个全等三角形,只有一个四边形,目前由已知条件四边形ABDC,要创造三角形,可以连接AD或BC,那么连接谁更合适呢?若连接AD,则∠B、∠C分在左、右两个三角形中,若全等,则∠B=∠C,事实上,∠B=∠C,若连接BC,则∠B、∠C分在上、下两个三角形中,根据目前所学知识还不能确定∠B=∠C因此,连接AD较为合适.解:∠B=∠C连接AD,在△ABD和△ACD中,AB=AC,BD=CD,AD=AD(公共边),∴△ABD≌△ACD(SSS).∴∠B=∠C12.探索三角形全等时常作的辅助线在利用三角形全等进行解题时,有时题目所给条件不足或不明显,还需从题目本身或图形中挖掘它的隐含条件,还有的需加上一些辅助线,为解题铺路搭桥,起到很好的辅助作用,这些辅助线常见的有以下几种:(1)连接图形中的已知点,构造全等形.例如:如图13-2-13,已知AC 、BD 相交于O 点,且AB =CD ,AC =BD ,判断∠A 与∠D 的关系,并说明理由.解:∠A =∠D .连接BC ,在△ABC 与△DCB 中,AB =DC ,AC =DB ,BC =CB ,则△ABC ≌△DCB (SSS ).因此∠A =∠D .(2)取线段中点构造全等三角形.例如:如图13-2-14,已知在梯形ABCD 中,AB =DC ,∠A =∠D ,试判断∠ABC 与∠DCB 的关系,并说明理由.解:∠ABC =∠DCB .取AD 的中点N ,取月C 的中点M .连接MN 、BN 、CN ,则AN =DN ,BM =CM ,在△ABN 和△DCN 中,⇒⎪⎭⎪⎬⎫∠∠DC AB D A DN AN ===△ABN ≌△DCN ,则∠ABN =∠DCN ,NB =NC (全等三角形的对应角、对应边相等). 在△BMN 和△CMN 中,⇒⎪⎭⎪⎬⎫MN MN CM BM CN BN ===△BMN ≌△CMN , 则∠MBN =∠MCN (全等三角形的对应角相等).那么∠ABN +∠MBN =∠DCN +∠MCN .即∠ABC =∠DCB .【说明】在本题中,辅助线起到了很好的桥梁作用,为解题创造了条件.(3)有角平分线时,常在角两边截相等的线段,创造全等三角形.如图13-2-15,OC平分∠AOB,在OC上任取一点P,在OA、OB上截取OM=ON,连接PM、PN,那么,PM=PN.事实上,在△MOP和△NOP中,OM=ON,∠MOP=∠NOP,OP=OP,则△MOP≌△NOP(SSS).因此有PM=PN.(4)三角形中有中线时,常延长加倍中线,构造全等三角形.如图13-2-16,在△ABC中,AD为BC边上的中线,若延长AD至E,使AD=DE,连接B E,在△ACD和△EBD中,BD=CD,∠1=∠2,AD=ED,则△ACD≌△EBD,因此BE=AC13.利用全等三角形解决实际问题的步骤全等三角形在日常生活、科技生产中有很多的用途,在用它解决实际问题时可分以下几个步骤:(1)先明确实际问题与哪些知识有关,确定用哪些知识来解决.(2)根据实际问题画出图形.(3)结合图形写出已知和结论.(4)分析已知,找出解决问题的途径.(5)写出解决问题的过程(或探索过程).例如:如图13-2-17,要测河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D使CD=BC,再定出BF的垂线DE,使E、C、A三点在一条直线上,这时测得DE的长就是AB的长.你能用数学原理说明吗?分析:这是一个实际应用题,应先把其转化为数学问题,然后再解答.解:已知:AB⊥BF,DE⊥BF,A、C、E三点在一条直线上,BC=DC.判断AB与DE是否相等?在△ABC和△DEC中,由于AB⊥BF,DE⊥BF,则∠ABC=∠EDC=90°,又A、C、E三点在一条直线上,则∠ACB=∠ECD(对顶角).又BC=CD,则ABC≌△EDC(ASA),因此AB=DE.。
七年级数学探索三角形全等的条件1

新授
例 2:
已知:AB=AC,E、F分别在AB、AC上且AE=AF
求证:⊿ABF≌⊿ACE A AE=AC 。 审题: AB=AC , 审图:∠A是⊿ABF与⊿ACE的公共角。 E F
审结论:⊿ABF≌⊿ACE SAS C 证明: 在⊿ABF和⊿ACE中 AB=AC (已知) ∠A= ∠A(公共角) AE=AC(已知)
初中数学七年级下册 (苏科版)
探索三角形全等的条件 (一)
复习
什么样的两个三角形叫做全等三角形?用什 么表示? 答:能够完全重合的两个三角形叫做全等 三角形。
我们知道:如果两个三角形全等,那么他们的对应边相等,对应角相等。反过来, 两个三角形具备什么条件,即它们有多少 组边或角分别相等时就全等?
B
∴ ⊿ABF≌⊿ACE (SAS)
小结
通过今天的学习,同学们有什么收获呢? 1、两边夹一角。 2、在找对应部分要依照SAS标准去找。 3、对应:两个全等三角形,字母要一一对应。
; 杏耀: ;
历の攻击照当元,在那个事间里,鞠言将元气催动到了极限.现在面对两位闻家长老の攻击,他已经没有太多の手段应对.想要在呐瞬息の事间里,叠新凝聚足够の元气抵挡闻家两位长老の攻击,绝对是不可能の事情,除非鞠言已经踏入道灵境.那么,面对闻家两位长老の攻击,鞠言似乎是在劫难 逃了.鞠成野等声,先看到照当元被斩杀,都心头壹震,无比の畅快.可紧接着,他们就看到,鞠言被两片可怕の光晕笼罩住.“鞠言!”鞠成野等声都焦急の呼喊.他们恨不得冲上去帮鞠言,但他们有心无历.先不说他们根本来不及冲上去,就算他们能及事冲上去,也根本就拦不住两尊道灵境强者 の奋历攻击.似乎,鞠言死定了.光晕之中鞠言の身影,越来越模糊.所有鞠氏阵营之中の声,壹颗心都揪了起来.而照家阵营の声,
第03讲 探索三角形全等的条件(7种题型)(解析版)

第03讲 探索三角形全等的条件(7种题型)1.理解和掌握全等三角形判定方法“边角边”、“角边角”、“角角边”、“边边边”“HL ”定理.2.能把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.一、全等三角形判定1——“边角边”1. 全等三角形判定1——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS”).要点诠释:如图,如果AB = ,∠A =∠,AC = ,则△ABC ≌△. 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.二、全等三角形判定2——“角边角”全等三角形判定2——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”).''A B 'A ''A C '''A B C要点诠释:如图,如果∠A =∠,AB =,∠B =∠,则△ABC ≌△.三、全等三角形判定3——“角角边”1.全等三角形判定3——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果DE ∥BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.四、全等三角形判定4——“边边边”全等三角形判定4——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点诠释:如图,如果=AB ,=AC ,=BC ,则△ABC ≌△.五.直角三角形全等的判定——“HL ”1、斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL ”).2、直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它,同时,直角三角形又是特殊的三角形,有它的特殊性,作为“HL ”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,'A ''A B 'B '''A B C ''A B ''A C ''B C '''A B C使用时应该抓住“直角”这个隐含的已知条件.六、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:已知条件可选择的判定方法一边一角对应相等SAS AAS ASA两角对应相等ASA AAS两边对应相等SAS SSS2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.七.全等三角形的判定与性质(1)全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.(2)在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.八.全等三角形的应用(1)全等三角形的性质与判定综合应用用全等寻找下一个全等三角形的条件,全等的性质和判定往往是综合在一起应用的,这需要认真分析题目的已知和求证,分清问题中已知的线段和角与所证明的线段或角之间的联系.(2)作辅助线构造全等三角形常见的辅助线做法:①把三角形一边的中线延长,把分散条件集中到同一个三角形中是解决中线问题的基本规律.②证明一条线段等于两条线段的和,可采用“截长法”或“补短法”,这些问题经常用到全等三角形来证明.(3)全等三角形在实际问题中的应用一般方法是把实际问题先转化为数学问题,再转化为三角形问题,其中,画出示意图,把已知条件转化为三角形中的边角关系是关键.题型一、全等三角形的判定1——“边角边”例1、已知:如图,AB =AD ,AC =AE ,∠1=∠2.求证:BC =DE .【思路点拨】由条件AB =AD ,AC =AE ,需要找夹角∠BAC 与∠DAE ,夹角可由等量代换证得相等.【答案与解析】证明: ∵∠1=∠2∴∠1+∠CAD =∠2+∠CAD ,即∠BAC =∠DAE在△ABC 和△ADE 中∴△ABC ≌△ADE (SAS )∴BC =DE (全等三角形对应边相等)【总结升华】证明角等的方法之一:利用等式的性质,等量加等量,还是等量.【变式】如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD中AB AD BAC DAEAC AE =ìïÐ=Ðíï=î∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD例2、如图,AD 是△ABC 的中线,求证:AB +AC >2AD .【思路点拨】延长AD 到点E ,使AD =DE ,连接CE .通过证全等将AB 转化到△CEA 中,同时也构造出了2AD .利用三角形两边之和大于第三边解决问题.【答案与解析】证明:如图,延长AD 到点E ,使AD =DE ,连接CE .在△ABD 和△ECD 中,∴△ABD ≌△ECD (SAS ).∴AB =CE .∵AC +CE >AE ,∴AC +AB >AE =2AD .即AC +AB >2AD .90AB BC ABE CBD BE BD =ìïÐ=Ð=°íï=îAD DE ADB EDCBD CD ìïÐÐíïî===.【总结升华】证明边的大小关系主要有两个思路:(1)两点之间线段最短;(2)三角形的两边之和大于第三边.要证明AB +AC >2AD ,如果归到一个三角形中,边的大小关系就是显然的,因此需要转移线段,构造全等三角形是转化线段的重要手段.可利用旋转变换,把△ABD 绕点D 逆时针旋转180°得到△CED ,也就把AB 转化到△CEA 中,同时也构造出了2AD .若题目中有中线,倍长中线,利用旋转变换构造全等三角形是一种重要方法.例3、已知,如图:在△ABC 中,∠B =2∠C ,AD ⊥BC ,求证:AB =CD -BD .【思路点拨】在DC 上取一点E ,使BD =DE ,则△ABD ≌△AED ,所以AB =AE ,只要再证出EC =AE 即可.【答案与解析】证明:在DC 上取一点E ,使BD =DE∵ AD ⊥BC ,∴∠ADB =∠ADE在△ABD 和△AED 中,∴△ABD ≌△AED (SAS ).∴AB =AE ,∠B =∠AED.BD DE ADB=ADEAD AD ìïíïî=∠∠=AE D CB又∵∠B=2∠C=∠AED=∠C+∠EAC.∴∠C=∠EAC.∴AE=EC.∴AB=AE=EC=CD—DE=CD—BD.【总结升华】此题采用截长或补短方法.上升到解题思想,就是利用翻折变换,构造的全等三角形,把条件集中在基本图形里面,从而使问题加以解决.如图,要证明AB=CD-BD,把CD-BD转化为一条线段,可利用翻折变换,把△ABD沿AD翻折,使线段BD运动到DC上,从而构造出CD-BD,并且也把∠B转化为∠AEB,从而拉近了与∠C的关系.【变式】已知,如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,并且AE=(AB+AD),求证:∠B+∠D=180°.【答案】证明:在线段AE上,截取EF=EB,连接FC,∵CE⊥AB,∴∠CEB=∠CEF=90°在△CBE和△CFE中,1 2∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°.题型二、全等三角形的判定2——“角边角”例4、已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D=∠B.求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中CEB CEFEC =EC EB EF =ìïÐ=Ðíïî12(AF AD FAC DAC AC AC =ìïÐ=Ðíï=î角平分线定义)∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下: (1)找到以待证角(线段)为内角(边)的两个三角形; (2)证明这两个三角形全等; (3)由全等三角形的性质得出所要证的角(线段)相等.【变式】(2022•长安区一模)已知:点B 、E 、C 、F 在一条直线上,AB ∥DE ,AC ∥DF ,BE =CF .求证:△ABC ≌△DEF .【分析】先利用平行线的性质得到∠B =∠DEF ,∠ACB =∠F ,再证明BC =EF ,然后根据“ASA ”可判断△ABC ≌△DEF .【解答】证明:∵AB ∥DE ,∴∠B =∠DEF ,∵AC ∥DF ,∴∠ACB =∠F ,∵BE =CF ,∴BE +EC =CF +EC ,即BC =EF ,在△ABC 和△DEF 中,,∴△ABC ≌△DEF (ASA ).【点评】本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法是解决问题的关键.选用A C AD CBD B Ð=Ðìï=íïÐ=Ðî哪一种判定方法,取决于题目中的已知条件.例5、如图,G 是线段AB 上一点,AC 和DG 相交于点E.请先作出∠ABC 的平分线BF ,交AC 于点F ;然后证明:当AD∥BC,AD =BC ,∠ABC=2∠ADG 时,DE =BF.【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF【答案与解析】证明: ∵AD∥BC,∴∠DAC=∠C∵BF 平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中∴△DAE≌△BCF(ASA )∴DE=BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】ïîïíìÐ=Ð=Ð=ÐC DAC BCAD CBFADG证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,∴△MPQ ≌△NHQ (ASA )∴PM =HN题型三、全等三角形的判定3——“角角边”例6.(2021秋•苏州期末)如图,在四边形ABCD 中,E 是对角线AC 上一点,AD ∥BC ,∠ADC =∠ACD ,∠CED +∠B =180°.求证:△ADE ≌△CAB .【分析】由等角对等边可得AC =AD ,再由平行线的性质可得∠DAE =∠ACB ,由∠CED +∠B =180°,∠CED +∠AED =180°,得∠AED =∠B ,从而利用AAS 可判定△ADE ≌△CAB .【解答】证明:∵∠ADC =∠ACD ,∴AD =AC ,∵AD ∥BC ,∴∠DAE =∠ACB ,∵∠CED +∠B =180°,∠CED +∠AED =180°,∴∠AED =∠B ,在△ADE 与△CAB 中,,∴△ADE ≌△CAB (AAS ).【点评】本题主要考查全等三角形的判定,解答的关键是由已知条件得出相应的角或边的关系.例7、已知:如图,AB ⊥AE ,AD ⊥AC ,∠E =∠B ,DE =CB .求证:AD =AC .12MQ NQMQP NQH Ð=Ðìï=íïÐ=Ðî【思路点拨】要证AC =AD ,就是证含有这两个线段的三角形△BAC ≌△EAD.【答案与解析】证明:∵AB ⊥AE ,AD ⊥AC ,∴∠CAD =∠BAE =90°∴∠CAD +∠DAB =∠BAE +∠DAB ,即∠BAC =∠EAD在△BAC 和△EAD 中∴△BAC ≌△EAD (AAS )∴AC =AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等.【变式】已知:如图,,,是经过点的一条直线,过点、B 分别作、,垂足为E 、F ,求证:.【答案与解析】证明:∵ ,∴∴∵∴∴BAC EAD B ECB=DE Ð=ÐìïÐ=Ðíïî90ACB Ð=°AC BC =CD C A AE CD ^BF CD ^CE BF=CD AE ^CD BF ^°=Ð=Ð90BFC AEC °=Ð+Ð90B BCF ,90°=ÐACB °=Ð+Ð90ACF BCF BACF Ð=Ð在和中∴≌()∴【总结升华】要证,只需证含有这两个线段的≌.同角的余角相等是找角等的好方法.题型四、全等三角形的判定4——“边边边”例8、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的性质和判定.【变式】已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.BCF ∆CAE ∆ïîïíì=Ð=ÐÐ=ÐBC AC B ACE BFC AEC BCF ∆CAE ∆AAS BF CE =BF CE =BCF ∆CAE∆()(),,RP RQ PM QM RM RM ì=ï=íï=î已知公共边【答案】证明:连接DC ,在△ACD 与△BDC 中∴△ACD≌△BDC(SSS )∴∠CAD=∠DBC(全等三角形对应角相等)例9、如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BD =CE ,求证:∠BAD =∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,∴△ABD ≌△ACE (SSS )∴∠BAD =∠CAE (全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD =∠CAE ,先找出这两个角所在的三角形分别是△BDA 和△CAE ,然后证这两个三角形全等.题型五.直角三角形全等的判定“HL ”例10.如图,AB ⊥BD ,CD ⊥BD ,AD =BC ,则能直接判断Rt △ABD ≌Rt △CDB 的理由是( )()AD BC AC BDCD DC ì=ï=íï=î公共边AB AC AD AEBD CE =ìï=íï=îA.HL B.ASA C.SAS D.SSS【分析】由“HL”可证Rt△ABD和Rt△CDB.【解答】解:∵AB⊥BD,CD⊥BD,∴∠ABD=∠CDB=90°,在Rt△ABD和Rt△CDB中,,∴Rt△ABD≌Rt△CDB(HL),故选:A.【点评】本题考查了直角三角形全等的判定,掌握直角三角形的判定方法是本题的关键.【变式1】.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件 ,就可以根据“HL”得到Rt△ABC≌Rt△DEF.【分析】根据直角三角形全等的判定方法解决此题.【解答】解:补充条件:AB=DE.在Rt△ABC和Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL).故答案为:AB=DE.【点评】本题主要考查直角三角形全等的判定,熟练掌握直角三角形全等的判定方法是解决本题的关键.【变式2】如图,Rt△ABC和Rt△EDF中,BC∥DF,在不添加任何辅助线的情况下,请你添加一个条件 ,使Rt△ABC和Rt△EDF全等.【分析】根据全等三角形的判定解答即可.【解答】解:∵Rt△ABC和Rt△EDF中,∴∠BAC=∠DEF=90°,∵BC∥DF,∴∠DFE=∠BCA,∴添加AB=ED,在Rt△ABC和Rt△EDF中,∴Rt△ABC≌Rt△EDF(AAS),故答案为:AB=ED(答案不唯一).【点评】此题考查全等三角形的判定,关键是根据全等三角形的判定方法解答.题型六.全等三角形的判定与性质例11.(2022•南通模拟)如图,在△ABC中,AB=AC,AD⊥BD,AE⊥EC,垂足分别为D,E,BD,CE 相交于点O,且∠BAE=∠CAD.(1)求证:△ABD≌△ACE;(2)若∠BOC=140°,求∠OBC的度数.【分析】(1)由“AAS”可证△ABD≌△ACE;(2)由全等三角形的性质可得∠ABD=∠ACE,由等腰三角形的性质可得∠ABC=∠ACB,即可求解.【解答】(1)证明:∵∠BAE=∠CAD,∴∠BAD=∠CAE,∵AD⊥BD,AE⊥EC,∴∠ADB=∠AEC=90°,在△ABD和△ACE中,,∴△ABD≌△ACE(AAS);(2)解:∵△ABD≌△ACE,∴∠ABD=∠ACE,∵AB=AC,∴∠ABC=∠ACB,∴∠OBC=∠OCB,∵∠BOC=140°,∴∠OBC=∠OBC=20°.【点评】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明三角形全等是解题的关键.【变式1】.如图,已知AB=CB,AD=CD.求证:∠A=∠C.【分析】连接BD,利用边边边证明△ABD≌△CBD,由全等三角形的性质即可求解.【解答】证明:连接BD,在△ABD与△CBD中,,∴△ABD≌△CBD(SSS),∴∠A=∠C.【点评】此题主要考查了全等三角形的性质与判定,此题主要利用边边边判定三角形全等.【变式2】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAD=∠CAE.求证:∠ABD=∠ACE.【分析】由“SAS”可证△ABD≌△ACE,可得结论.【解答】证明:在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE.【点评】本题考查了全等三角形的判定和性质,证明三角形全等是解题的关键.题型7.全等三角形的应用例12.如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作ED⊥BD交AC的延长线于点E,垂足为点D.(DE≠CD)(1)线段 的长度就是A、B两点间的距离(2)请说明(1)成立的理由.【分析】(1)根据题意确定DE=AB;(2)根据已知条件得到两个三角形全等,利用全等三角形的性质得到结论即可.【解答】解:(1)线段DE的长度就是A、B两点间的距离;故答案为:DE;(2)∵AB⊥BC,DE⊥BD∴∠ABC=∠EDC=90°又∵∠ACB=∠DCE,BC=CD∴△ABC≌△CDE(ASA)∴AB=DE.【点评】本题考查了全等三角形的应用,是基础题,熟练掌握全等三角形的判定方法并确定出全等三角形是解题的关键.【变式】为了解学生对所学知识的应用能力,某校老师在七年级数学兴趣小组活动中,设置了这样的问题:因为池塘两端A,B的距离无法直接测量,请同学们设计方案测量A,B的距离.甲、乙两位同学分别设计出了如下两种方案:甲:如图①,先在平地上取一个可以直接到达点A,B的点O,连接AO并延长到点C,连接BO并延长到点D,使CO=AO,DO=BO,连接DC,测出DC的长即可.乙:如图②,先确定直线AB,过点B作直线BE,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即可.(1)甲、乙两同学的方案哪个可行?(2)请说明方案可行的理由.【分析】(1)甲同学作出的是全等三角形,然后根据全等三角形对应边相等测量的,所以是可行的;(2)甲同学利用的是“边角边”,乙同学的方案只能知道两三角形的两边相等,不能判定△ABD与△CBD全等,故方案不可行.【解答】解:(1)甲同学的方案可行;(2)甲同学方案:在△ABO和△CDO中,,∴△ABO≌△CDO(SAS),∴AB=CD;乙同学方案:在△ABD和△CBD中,只能知道DC=DA,DB=DB,不能判定△ABD与△CBD全等,故方案不可行.【点评】本题主要考查了全等三角形的应用,熟练掌握全等三角形判定的“SAS”定理是解决问题的关键.一.选择题(共8小题)1.(2022秋•南京期末)已知:如图,AC=DF,BC=EF,下列条件中,不能证明△ABC≌DEF的是( )A.AC∥DF B.AD=BEC.∠CBA=∠FED=90°D.∠C=∠F【分析】根据三角形的判定定理,结合题目所给条件进行判定即可.【解答】解:A、由AC∥DF可得∠A=∠FDB,再加上条件AC=DF,BC=EF,不能证明△ABC≌DEF,故此选项正确;B、AD=BE可得AB=DE,再加上条件AC=DF,BC=EF,可利用SSS定理证明△ABC≌DEF,故此选项错误;C、∠CBA=∠FED=90°可利用HL定理证明△ABC≌DEF,故此选项错误;D、∠C=∠F可利用SAS定理证明△ABC≌DEF,故此选项错误;故选:A.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.2.(2022秋•启东市校级月考)不能判定两个直角三角形全等的条件是( )A.两个锐角对应相等B.两条直角边对应相等C.斜边和一锐角对应相等D.斜边和一条直角边对应相等【分析】直角三角形全等的判定方法:HL,SAS,ASA,SSS,AAS,做题时要结合已知条件与全等的判定方法逐一验证.【解答】解:A、全等三角形的判定必须有边的参与,故本选项错误,符合题意;B、符合判定SAS,故本选项正确,不符合题意;C、符合判定AAS,故本选项正确,不符合题意;D、符合判定HL,故本选项正确,不符合题意.故选:A.【点评】本题考查直角三角形全等的判定方法,判定两个直角三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.3.(2022秋•阜宁县期末)如图,已知∠ABC=∠BAD,再添加一个条件,仍不能判定△ABC≌△BAD的是( )A.AC=BD B.∠C=∠D C.AD=BC D.∠ABD=∠BAC【分析】根据已知可以得到∠ABC=∠BAD,AB=BA,然后再分别判断各个选项中的条件能否使得△ABC ≌△BAD即可.【解答】解:∵∠ABC=∠BAD,AB=BA,∴若添加条件AC=BD,无法判定△ABC≌△BAD,故选项A符合题意;若添加∠C=∠D,则△ABC≌△BAD(AAS),故选项B不符合题意;若添加AD=BC,则△ABC≌△BAD(SAS),故选项C不符合题意;若添加∠ABD=∠BAC,则△ABC≌△BAD(ASA),故选项D不符合题意;故选:A.【点评】本题考查全等三角形的判定,解答本题的关键是明确全等三角形的判定方法:SSS、SAS、ASA、AAS.4.(2022秋•江都区期末)如图,已知AB=AD.下列条件中,不能作为判定△ABC≌△ADC条件的是( )A.BC=DC B.∠BAC=∠DAC C.∠B=∠D=90°D.∠ACB=∠ACD【分析】利用全等三角形的判定定理:SSS、SAS、ASA、AAS、HL进行分析即可.【解答】解:A、AB=AD,BC=DC,再加上公共边AC=AC能判定△ABC≌△ADC,故此选项不符合题意;B、AB=AD,∠BAC=∠DAC再加上公共边AC=AC可利用SAS判定△ABC≌△ADC,故此选项不合题意;C、AB=AD,∠B=∠D=90°再加上公共边AC=AC能判定△ABC≌△ADC,故此选项不合题意;D、AB=AD,∠ACB=∠ACD再加上公共边AC=AC不能判定△ABC≌△ADC,故此选项合题意;故选:D.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.5.(2022秋•扬州期中)一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )A.带其中的任意两块去都可以B.带1、2或2、3去就可以了C.带1、4或3、4去就可以了D.带1、4或2、3或3、4去均可【分析】带1、4可以用“角边角”确定三角形;带3、4也可以用“角边角”确定三角形.【解答】解:带3、4可以用“角边角”确定三角形,带1、4可以用“角边角”确定三角形,故选:C.【点评】本题考查了全等三角形判定的应用;确定一个三角形的大小、形状,可以用全等三角形的几种判定方法.做题时要根据实际问题找条件.6.(2022秋•宿豫区期末)如图,小明和小丽用下面的方法测量位于池塘两端的A、B两点的距离;先取一个可以直接到达点A的点C,量得AC的长度,再沿AC方向走到点D处,使得CD=AC;然后从点D 处沿着由点B到点A的方向,到达点E处,使得点E、B、C在一条直线上,量得的DE的长度就是A、B 两点的距离.在解决这个问题中,关键是利用了△DCE≌△ACB,其数学依据是( )A.SAS B.ASA C.AAS D.ASA或AAS【分析】直接利用全等三角形的判定方法,进而分析得出答案.【解答】解:由题意可得:AC=DC,∠ACB=∠DCE,∠ABC=∠DEC,∠BAC=∠EDC,故由AC=DC,∠ACB=∠DCE,∠ABC=∠DEC或AC=DC,∠ACB=∠DCE,∠BAC=∠EDC都可以得出△DCE≌△ACB,故其数学依据是ASA或AAS.故选:D.【点评】此题主要考查了全等三角形的应用,正确掌握全等三角形的判定方法是解题关键.7.(2022秋•高邮市期末)如图,已知∠1=∠2,若用“AAS”证明△ACB≌△BDA,还需加上条件( )A.AD=BC B.BD=AC C.∠D=∠C D.∠DAB=∠CBA【分析】根据图形找出公共边AB=BA,再根据全等三角形的判定定理AAS得出即可.【解答】解:A.AD=BC,BA=AB,∠1=∠2不符合全等三角形的判定定理,不能推出△ACB≌△BDA,故本选项不符合题意;B.AB=BA,∠1=∠2,AC=BD,符合全等三角形的判定定理SAS,不符合AAS定理,故本选项不符合题意;C.∠D=∠C,∠1=∠2,AB=BA,符合全等三角形的判定定理AAS,能推出△ACB≌△BDA,故本选项符合题意;D.∠DAB=∠CBA,AB=BA,∠1=∠2,符合全等三角形的判定定理ASA,能推出△ACB≌△BDA,故本选项不符合题意;故选:C.【点评】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理是SAS,ASA,AAS,SSS,两直角三角形全等还有HL.8.(2022秋•邳州市期末)如图,AB=AC,点D、E分别在AB、AC上,补充一个条件后,仍不能判定△ABE≌△ACD的是( )A.∠B=∠C B.AD=AE C.BE=CD D.∠AEB=∠ADC【分析】根据全等三角形的判定定理逐个判断即可.【解答】解:A.∠A=∠A,AB=AC,∠B=∠C,符合全等三角形的判定定理ASA,能推出△ABE≌△ACD,故本选项不符合题意;B.AD=AE,∠A=∠A,AB=AC,符合全等三角形的判定定理SAS,能推出△ABE≌△ACD,故本选项不符合题意;C.AB=AC,BE=CD,∠A=∠A,不符合全等三角形的判定定理,不能推出△ABE≌△ACD,故本选项符合题意;D.∠A=∠A,∠AEB=∠ADC,AB=AC,符合全等三角形的判定定理AAS,能推出△ABE≌△ACD,故本选项不符合题意;故选:C.【点评】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.二.填空题(共4小题)9.(2022秋•泗洪县期中)如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF,只需补充条件 AB=DE ,就可以根据“HL”得到Rt△ABC≌Rt△DEF.【分析】根据直角三角形全等的判定方法解决此题.【解答】解:补充条件:AB=DE.在Rt△ABC和Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL).故答案为:AB=DE.【点评】本题主要考查直角三角形全等的判定,熟练掌握直角三角形全等的判定方法是解决本题的关键.10.(2022秋•启东市校级月考)如图,在△ABC和△DEF中,∠A=∠D=90°,AC=DE,若要用“斜边直角边(H.L.)”直接证明Rt△ABC≌Rt△DEF,则还需补充条件: BC=EF .【分析】此题是一道开放型题目,根据直角三角形的全等判定解答即可.【解答】解:在Rt△ABC和Rt△DEF中,,∴Rt△ABC≌Rt△DEF(HL),故答案为:BC=EF【点评】本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,题目比较典型,难度适中.11.(2022秋•江宁区校级月考)如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使Rt△ABC≌Rt△DCB,你添加的条件是 AB=DC或AC=DB ,理由是 “HL” (填简称).【分析】根据直角三角形全等的判定方法,即可解答.【解答】解:∵∠A=∠D=90°,BC=BC,∴再添加:AB=DC,∴Rt△ABC≌Rt△DCB(HL),∵∠A=∠D=90°,BC=BC,∴再添加:AC=BD,∴Rt △ABC ≌Rt △DCB (HL ),故答案为:AB =DC 或AC =BD ,HL .【点评】本题考查了直角三角形全等的判定,熟练掌握直角三角形全等的判定方法是解题的关键.12.(2022秋•江阴市期中)如图,在△ABC 中,AB =3,AC =5,AD 是边BC 上的中线,AD =2,则△ACB 的面积是 6 .【分析】延长AD 到E ,使DE =AD ,连接BE ,证△ADC ≌△EDB (SAS ),得BE =AC =5,∠CAD =∠E ,再由勾股定理的逆定理证∠EAB =90°,即可解决问题.【解答】解:如图,延长AD 到E ,使DE =AD ,连接BE ,∵D 为BC 的中点,∴CD =BD ,在△ADC 与△EDB 中,,∴△ADC ≌△EDB (SAS ),∴BE =AC =5,∠CAD =∠E ,又∵AE =2AD =4,AB =3,∴BE 2=AE 2+AB 2,∴△ABE 是直角三角形,∠EAB =90°,则S △ACB =2S △ABD =2××2×3=6,故答案为:6.【点评】此题考查了全等三角形的判定与性质、勾股定理的逆定理以及三角形面积等知识,熟练掌握全等三角形的判定与性质是解题的关键.三.解答题(共5小题)13.(2022秋•泗阳县期中)王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B 分别与木墙的顶端重合.(1)求证:△ADC≌△CEB;(2)求两堵木墙之间的距离.【分析】(1)根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可;(2)利用全等三角形的性质进行解答.【解答】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC在△ADC和△CEB中,∴△ADC≌△CEB(AAS);(2)解:由题意得:AD=2×3=6(cm),BE=7×2=14(cm),∵△ADC≌△CEB,∴EC=AD=6cm,DC=BE=14cm,∴DE=DC+CE=20(cm),答:两堵木墙之间的距离为20cm.【点评】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.14.(2022秋•鼓楼区期中)如图,点B、C、E、F在同一条直线上,AF、DE相交于点G,∠B=∠C=∠AGD=90°,BF=CD.求证:AF=DE.。
《探索三角形全等的条件(1)》教案设计

活动三:
画一画:
()画∠°;
()在、上分别截取,;
()连接,剪下所画的△,与同学所画的三角形能够重合吗?
学生根据要求画图,小组拼合,验证结果。
让学生首先通过画图对两边及其夹角对应相等的情况进行对比来判断所画的两个三角形是否全等。特别的小组用叠合的方法来进行判断三角形全等,由此得到判定两个三角形全等的方法。
活动四:
如果两个三角形中有两边及其中一边的对角对应相等,这两个三角形全等吗?
学生小组交流,正确加以验证,错误举出反例。
通过反例,让学生进一步加深对于“边角边”探索条件的认识。
分享交流、汇报实践结果
.具备几个条件可以证明两个三角形的全等?并举例。
.怎样剪可以让全班的直角三角形都全等?
.根据两边一角能否做出全等的三角形?请分类讨论(和)
小组无分工合作,只有个别同学参与活动
思维能力
(分)
能独立制定详细、合理、可行的方案。在思考、画图、操作时能提出有效问题及解决方案。能利用相关原理得出实验结果。
能在教师协助下制定合理、可行的方案。在操作完成后能利用相关原理得出实验结果。
不能制定可行的方案,不能通过操作、验证得到实验结果
动手操作能力(分)
四、学情分析
学生现在处于几何推理论证的初步阶段,从这章开始,学生应该逐步学会几何证明,几何证明题的推理证明的书写对学生来说难度较大,同时,我们知道,以前学生学习几何都是一些简单的图形,从这章开始出现了几个图形的变换或叠加,学生在解题过程中,找全等条件是一个难点。
五、教学方式选择与规划
依据学生的认知发展规律和建构主义的教学理论,本节课把重点放在“合作与探究”上,以“思维为主线”去组织和设计教学过程,运用引导发现法、分组讨论法,使学生的思维过程自然流畅,知识建构系统、连贯,在层层推进的探究过程中,思维得以发展,能力得以提高。根据这一指导思想,本节课采用“创设情景诱导发现小组合作问题解决总结汇报”的教学方法。
七年级数学探索三角形全等的条件1(201909)

惟万箱 翠幕伫神 上辅政所诛诸王 从箕星东一尺出 于兹永久 安宁〖华山郡〗蓝田 皇齐以世祖配五精于明堂 雍州刺史梁王起义兵于襄阳 皆适东流水祈祓自洁濯 盖鱼龙之流也 黚阳〖巴陵郡〗下隽 求仪注未有前准 使厢下奏伎 东北经天入参中而没 为章于天 潘氏服御 北头指子至地
八年 诏进梁公爵为梁王 枝江公子隆为随郡王 祠部郎何佟之议曰 丁酉 其下典学二人 克隆景福 兼俎兼荐 案《丧服经》为君之父 疑谳 七年二月辛巳 为合宿
容代之 又虚设铠马斋仗千人 敬教敷 应诸器悉不得用宝物及织成等 于斯学 象来致福 结皇思 贺唯云期则没闰 以氐杨馥之为北秦州刺史 百川收潦 中书令随郡王子隆为中护军 并开府仪同三司 是降是将 此所谓任情径行 资就云之泽 琼源浚照 闻虏主拓跋焘向彭城 而轻重同礼 无所犯
南泰山太守 冲幄舒薰 扬 河阳〖安定郡〗宋兴 山蛮寇贼 执七宝缚槊 寻复如初 中军将军张敬儿为车骑将军 荧惑从行在毕左股星西北一寸 今言臣则无实 日东北有一背 若依例皇太孙服临方易服 渐出游走 世檦拒战而死 月行在毕左股第二星北七寸 事寝 新除中领军蔡道恭为司州刺史
绍业盛明 {晋秘书阁有令史 皇太子讲《孝经》 辞殊礼 日西有一背 禾同穗 在南斗七寸 遐迩宁谧 没后如连珠 边江峻险 益可知时议 秋七月庚申 尚书右仆射鄱阳王锵为骠骑将军 义军至南州 又期太祖出 无所犯 缔世景融 荧惑从行在填星西 百馀年中 慧景至 以大斧捶其后 在孙陵岗
编次之 宜入嗣鸿业 垫江 奉叔 戊子 {魏 诏曰 十月戊寅 掌五辂安车 虽如背实 太白从行入太微 改封南康王 处处而有 境域之内 丙申 克日听览 而用太古之器 司徒 二岸居民多离其患 正可名为太稷耳 到丑时光色还复 自持银壶酒封赐太祖 三祇解途 〕礼行宗祀 玉寿诸殿 恐诸王无
魏 毕执珪 自鞉鞞至柷敔为盛乐 有司议雩祭依明堂 群臣备小君之服 为犯 戮力艰难 高宗第二子也 流星如鹅卵 尚书左仆射王俭为尚书令 小讳斗将 流仁德 为合宿 〔此一篇增损谢辞 徙为威烈将军 则懦夫成勇 世祖之心 是以成均焕于古典 平途直至 九年六月丙子 便是大罪 有切治要
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、全等三角形与探索三角形全等的条件
班级:姓名:
作业导航
了解全等三角形的概念,探索并掌握两个三角形全等的条件.
一、填空题
1.△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,∠C=70°,AB=10 cm,∠C′= , A′B′=_____.
2.若△ABC≌△DEF,△DEF的周长为32 cm,DE=9 cm,EF=12 cm,则AB=_____ cm,BC=_____ cm,AC=_____ cm.
3.若△ABC≌△DEF,AB=DE,AC=DF,∠A=80°,BC=9 cm,则∠D=_____,∠D的对边是_____=_____ cm.
图1
4.已知如图1,在△ABF和△DEC中,∠A=∠D,AB=DE,若再添加条件_____=_____,则可根据边角边公理证得△ABF≌△DEC.
5.全等三角形的对应高_____,对应边上的中线_____,对应角的平分线_____,全等三角形的面积_____.
二、选择题
6.下列各组图形中,一定全等的是( )
A.各有一个角是45°的两个等腰三角形
B.两个等边三角形
C.各有一个角是40°,腰长都为3 cm的两个等腰三角形
D.腰和顶角对应相等的两个等腰三角形
7.如图2,△ABD和△ACE都是等边三角形,那么△ADC≌△ABE的根据是( )
图2
A.SSS
B.SAS
C.ASA
D.AAS
8.如图3,等腰△ABC中,AB=AC,D、E、F分别是AB、AC、BC的中点,图中全等三角形共有( )
图3
A.5对
B.6对
C.7对
D.8对
9.下列条件中能确定两个三角形全等的是( )
A.一边及这条边上的高相等
B.一边及这条边上的中线对应相等
C.两角及第三个角平分线对应相等
D.两条边及夹角的平分线对应相等
三、解答题
10.已知△ABC≌△DEF,BC=EF,∠C=∠F,∠A=46°,∠B=37°,ED=6 cm,求∠F的度数及AB的长.
11.已知BC平分∠ABD,AB=BD,P是BC上任意一点,求证:△ACP≌△DCP.
图4
12.已知,如图5,∠A=∠C,∠1=∠2,∠3=∠4,DE=BF,求证:AE=BC.
图5
*13.如图6,△ABC、△A′B′C′中,AD平分∠BAC,A′D′平分∠B′A′C′,且∠BAC=∠B′A′C′,∠B=∠B′,AD=A′D′.由此你得出什么结论?证明你的结论,并与其他同学交流.
图6
参考答案
一、1.70° 10 cm 2.9 12 11
3.80°EF 9
4.AF DC
5.相等相等相等
二、6.D 7.B 8.C 9.C
三、10.97° 6 cm
11.略 12.略*13.。
