高三数学专题复习——圆锥曲线(抛物线)
高三数学一轮复习圆锥曲线 抛物线

⑥
x1+x2 x1x2 由⑤⑥得 MA, MB 的交点 M(x0, y0)的坐标为 x0= , y0= , 2 4 因为点 M(x0,y0)在 C2 上,即 x2 0=-4y0,
2 x1 +x2 2 所以 x1x2=- . ⑦ 6
4 由③④⑦得 x = y,x≠0. 3
p [听课记录] 依题意, 设抛物线方程是 y =2px(p>0),则有 2+ = 2
2
3,得 p=2, 故抛物线方程是 y2=4x,点 M 的坐标是(2,± 2 2), |OM|= 22+8=2 3. 答案 B
[规律方法] 1 . 求抛物线的方程一般是利用待定系数法, 即求p但要注意判断标准方程的形式. 2 .研究抛物线的几何性质时,一是注意定义 转化应用;二是要结合图形分析,同时注意平 面几何性质的应用.
[典题导入] (1)(2013·新课标全国Ⅱ高考)设抛物线C: y2 = 2px(p > 0) 的焦点为 F ,点 M 在 C 上, |MF| = 5 ,若以 MF 为直径的圆过点 (0 , 2) ,则 C 的 方程为 ( ) A.y2=4x或y2=8x B . y2 = 2x 或 y2 =8x C.y2=4x或y2=16x D . y2 = 2x 或 y2 =16x
2
当 x1=x2 时,A,B 重合于原点 O,AB 中点 N 为 O,坐标满足 x2 4 = y. 3 4 因此线段 AB 中点 N 的轨迹方程为 x = y. 3
2
[规律方法] 1.设抛物线方程为y2=2px(p>0),直线Ax+ By + C = 0 ,将直线方程与抛物线方程联立, 消去x得到关于y的方程my2+ny+q=0. (1)若m≠0,当Δ>0时,直线与抛物线有两个 公共点; 当Δ=0时,直线与抛物线只有一个公共点; 当Δ<0时,直线与抛物线没有公共点. (2) 若 m = 0 ,直线与抛物线只有一个公共点, 此时直线与抛物线的对称轴平行.
2024数学高考前冲刺题《圆锥曲线(椭圆、双曲线、抛物线)》含答案

黄金冲刺大题06 圆锥曲线(椭圆、双曲线、抛物线)(精选30题)1.(2024·山东·二模)已知椭圆的焦点分别是)()12,F F ,点M 在椭圆上,且124MF MF +=.(1)求椭圆的标准方程;(2)若直线y kx =,A B 两点,且OA OB ⊥,求实数k 的值.2.(2024·江苏南通·模拟预测)在平面直角坐标系xOy 中,设椭圆()2222:10x y C a b a b +=>>1F ,2F 分别是椭圆的左、右焦点,过2F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A ,B 两点,直线2l与C 交于D ,E 两点,且12AF F 的周长是4+(1)求椭圆C 的方程;(2)当32AB DE =时,求ODE 的面积.3.(2024·河北邯郸·二模)已知椭圆C 的中心为坐标原点,对称轴为x 轴、y 轴,且过()2,0,1,M N ⎛ ⎝两点.(1)求C 的方程.(2),A B 是C 上两个动点,D 为C 的上顶点,是否存在以D 为顶点,AB 为底边的等腰直角三角形?若存在,求出满足条件的三角形的个数;若不存在,请说明理由.4.(2024·广东广州·模拟预测)已知椭圆222:1(08x y C b b+=<<,右顶点为E ,上、下顶点分别为12,,B B G是1EB 的中点,且121EB GB ⋅=.(1)求椭圆C 的方程;(2)设过点()4,0D -的直线l 交椭圆C 于点,M N ,点()2,1A --,直线,MA NA 分别交直线4x =-于点,P Q ,求证:线段PQ 的中点为定点.5.(2024·辽宁·二模)平面直角坐标系xOy 中,面积为9的正方形ABCD 的顶点,A B 分别在x 轴和y 轴上滑动,且23OP OA = ,记动点P 的轨迹为曲线Γ.(1)求Γ的方程;(2)过点()4,1E 的动直线l 与曲线Γ交于不同的两点,M N 时,在线段MN 上取点Q ,满足||||||||EM QN QM EN ⋅=⋅.试探究点Q 是否在某条定直线上?若是,求出定直线方程;若不是,说明理由.6.(2024·福建厦门·三模)在直角坐标系xOy 中,已知抛物线2:2(0)C y px p =>的焦点为F ,过F 的直线l 与C 交于,M N 两点,且当l 的斜率为1时,8MN =.(1)求C 的方程;(2)设l 与C 的准线交于点P ,直线PO 与C 交于点Q (异于原点),线段MN 的中点为R ,若3QR ≤,求MNQ △面积的取值范围.7.(2024·浙江丽水·二模)已知抛物线2:4E y x =,点,,A B C 在抛物线E 上,且A 在x 轴上方,B 和C 在x 轴下方(B 在C 左侧),,A C 关于x 轴对称,直线AB 交x 轴于点M ,延长线段CB 交x 轴于点Q ,连接QA .(1)证明:OM OQ为定值(O 为坐标原点);(2)若点Q 的横坐标为1-,且89MB MC ⋅= ,求AQB 的内切圆的方程.8.(2024·江苏苏州·模拟预测)已知点(1,0)A ,(0,1)B ,(1,1)C 和动点(,)P x y 满足2y 是PA PB ⋅ ,PA PC ⋅的等差中项.(1)求P 点的轨迹方程;(2)设P 点的轨迹为曲线1C 按向量31,416a ⎛⎫=- ⎪⎝⎭平移后得到曲线2C ,曲线2C 上不同的两点M ,N 的连线交y 轴于点(0,)Q b ,如果MON ∠(O 为坐标原点)为锐角,求实数b 的取值范围;(3)在(2)的条件下,如果2b =时,曲线2C 在点M 和N 处的切线的交点为R ,求证:R 在一条定直线上.9.(2024·江苏南通·二模)已知双曲线E的渐近线为y =,左顶点为()A .(1)求双曲线E 的方程;(2)直线:l x t =交x 轴于点D ,过D 点的直线交双曲线E 于B ,C ,直线AB ,AC 分别交l 于G ,H ,若O ,A ,G ,H 均在圆P 上,①求D 的横坐标;②求圆P 面积的取值范围.10.(2024·江苏南京·二模)已知抛物线2:2(0)C y px p =>与双曲线2222:1x y E a b-=(0a >,0b >)有公共的焦点F ,且4p b =.过F 的直线1与抛物线C 交于A ,B 两点,与E 的两条近线交于P ,Q 两点(均位于y 轴右侧).(1)求E 的渐近线方程;(2)若实数λ满足1111||||||||OP OQ AF BF λ⎛⎫+=- ⎪⎝⎭,求λ的取值范围.11.(2024·重庆·三模)已知()2,0F ,曲线C 上任意一点到点F 的距离是到直线12x =的距离的两倍.(1)求曲线C 的方程;(2)已知曲线C 的左顶点为A ,直线l 过点F 且与曲线C 在第一、四象限分别交于M ,N 两点,直线AM 、AN 分别与直线12x =交于P ,H 两点,Q 为PH 的中点.(i )证明:QF MN ⊥;(ii )记PMQ ,HNQ ,MNQ 的面积分别为1S ,2S ,3S ,则123S S S +是否为定值?若是,求出这个定值;若不是,请说明理由.12.(2024·河北·二模)已知椭圆()2222:10x y E a b a b +=>>的离心率e =(1)若椭圆E过点(,求椭圆E 的标准方程.(2)若直线1l ,2l 均过点()()*,00,n n P p p a n <<∈N 且互相垂直,直线1l 交椭圆E 于,A B 两点,直线2l 交椭圆E于,C D 两点,,M N 分别为弦AB 和CD 的中点,直线MN 与x 轴交于点(),0n Q t ,设13n np =.(ⅰ)求n t ;(ⅱ)记n a PQ =,求数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和n S .13.(2024·辽宁沈阳·二模)P 为大圆上一动点,大圆半径OP 与小圆相交于点,B PP x '⊥轴于,P BB PP ⊥'''于,B B ''点的轨迹为Ω.(1)求B '点轨迹Ω的方程;(2)点()2,1A ,若点M N 、在Ω上,且直线AM AN 、的斜率乘积为12,线段MN 的中点G ,当直线MN 与y 轴的截距为负数时,求AOG ∠的余弦值.14.(2024·广东佛山·二模)两条动直线1y k x =和2y k x =分别与抛物线()2:20C y px p =>相交于不同于原点的A ,B 两点,当OAB 的垂心恰是C 的焦点时,AB =(1)求p ;(2)若124k k =-,弦AB 中点为P ,点()2,0M -关于直线AB 的对称点N 在抛物线C 上,求PMN 的面积.15.(2024·广东深圳·二模)设抛物线C :22x py =(0p >),直线l :2y kx =+交C 于A ,B 两点.过原点O 作l 的垂线,交直线=2y -于点M .对任意R k ∈,直线AM ,AB ,BM 的斜率成等差数列.(1)求C 的方程;(2)若直线//l l ',且l '与C 相切于点N ,证明:AMN 的面积不小于16.(2024·湖南·一模)已知双曲线2222:1(1)x y C b a a b-=>>的渐近线方程为y =,C 的半焦距为c ,且44244a b c ++=.(1)求C 的标准方程.(2)若P 为C 上的一点,且P 为圆224x y +=外一点,过P 作圆224x y +=的两条切线12,l l (斜率都存在),1l 与C 交于另一点2,M l 与C 交于另一点N ,证明:(ⅰ)12,l l 的斜率之积为定值;(ⅱ)存在定点A ,使得,M N 关于点A 对称.17.(2024·湖南岳阳·三模)已知动圆P 过定点(0,1)F 且与直线3y =相切,记圆心P 的轨迹为曲线E .(1)已知A 、B 两点的坐标分别为(2,1)-、(2,1),直线AP 、BP 的斜率分别为1k 、2k ,证明:121k k -=;(2)若点()11,M x y 、()22,N x y 是轨迹E 上的两个动点且124x x =-,设线段MN 的中点为Q ,圆P 与动点Q 的轨迹Γ交于不同于F 的三点C 、D 、G ,求证:CDG 的重心的横坐标为定值.18.(2024·湖北·二模)已知双曲线P 的方程为()()221,,0,,04x y B a C a -=-,其中()()00002,,,0a D x y x a y >≥>是双曲线上一点,直线DB 与双曲线P 的另一个交点为E ,直线DC 与双曲线P的另一个交点为F ,双曲线P 在点,E F 处的两条切线记为121,,l l l 与2l 交于点P ,线段DP 的中点为G ,设直线,DB DC 的斜率分别为12,k k .(1)证明:12114k k <+≤(2)求GBGC的值.19.(2024·湖北·模拟预测)已知椭圆2212:1x C y a +=和()2222:10x C y a b b +=>>的离心率相同,设1C 的右顶点为1A ,2C 的左顶点为2A ,()0,1B ,(1)证明:12BA BA ⊥;(2)设直线1BA 与2C 的另一个交点为P ,直线2BA 与1C 的另一个交点为Q ,连PQ ,求PQ 的最大值.参考公式:()()3322m n m n m mn n +=+-+20.(2024·山东·二模)已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12,设C 的右焦点为F ,左顶点为A ,过F 的直线与C 于,D E 两点,当直线DE 垂直于x 轴时,ADE V 的面积为92.(1)求椭圆C 的标准方程;(2)连接AD 和AE 分别交圆22(1)1x y ++=于,M N 两点.(ⅰ)当直线DE 斜率存在时,设直线DE 的斜率为1k ,直线MN 的斜率为2k ,求12k k ;(ⅱ)设ADE V 的面积为1,S AMN △的面积为2S ,求12S S 的最大值.21.(2024·山东潍坊·二模)已知双曲线C :()222210,0x y a b a b -=>>的实轴长为2F 到一条渐近线的距离为1.(1)求C 的方程;(2)过C上一点(1P 作C 的切线1l ,1l 与C 的两条渐近线分别交于R ,S 两点,2P 为点1P 关于坐标原点的对称点,过2P 作C 的切线2l ,2l 与C 的两条渐近线分别交于M ,N 两点,求四边形RSMN 的面积.(3)过C 上一点Q 向C 的两条渐近线作垂线,垂足分别为1H ,2H ,是否存在点Q ,满足122QH QH +=,若存在,求出点Q 坐标;若不存在,请说明理由.22.(23-24高三下·湖北武汉·阶段练习)已知抛物线2:=E y x ,过点()1,2T 的直线与抛物线E 交于,A B 两点,设抛物线E 在点,A B 处的切线分别为1l 和2l ,已知1l 与x 轴交于点2,M l 与x 轴交于点N ,设1l 与2l 的交点为P .(1)证明:点P 在定直线上;(2)若PMN ,求点P 的坐标;(3)若,,,P M N T 四点共圆,求点P 的坐标.23.(2024·福建漳州·一模)已知过点()11,0F -的直线l 与圆2F :()22116x y -+=相交于G ,H 两点,GH 的中点为E ,过1GF 的中点F 且平行于2EF 的直线交2G F 于点P ,记点P 的轨迹为C .(1)求轨迹C 的方程.(2)若,A B 为轨迹C 上的两个动点且均不在y 轴上,点M 满足OM OA OB λμ=+(λ,μ∈R ),其中O 为坐标原点,从下面①②③中选取两个作为条件,证明另外一个成立.①点M 在轨迹C 上;②直线OA 与OB 的斜率之积为34-;③221λμ+=.注:若选择不同的组合分别解答,则按第一个解答计分.24.(2024·福建福州·模拟预测)点P 是椭圆E :22221x y a b +=(0a b >>)上(左、右端点除外)的一个动点,()1,0F c -,()2,0F c 分别是E 的左、右焦点.(1)设点P 到直线l :2a x c =的距离为d ,证明2PF d 为定值,并求出这个定值;(2)12PF F △的重心与内心(内切圆的圆心)分别为G ,I ,已知直线IG 垂直于x 轴.(ⅰ)求椭圆E 的离心率;(ⅱ)若椭圆E 的长轴长为6,求12PF F △被直线IG 分成两个部分的图形面积之比的取值范围.25.(2024·福建三明·三模)已知平面直角坐标系xOy 中,有真命题:函数(0,0)ny mx m n x =+≥>的图象是双曲线,其渐近线分别为直线y mx =和y 轴.例如双曲线4y x=的渐近线分别为x 轴和y 轴,可将其图象绕原点O 顺时针旋转π4得到双曲线228x y -=的图象.(1)求双曲线1y x=的离心率;(2)已知曲线22:2E x y -=,过E 上一点P 作切线分别交两条渐近线于,A B 两点,试探究AOB 面积是否为定值,若是,则求出该定值;若不是,则说明理由;(3)已知函数y x =Γ,直线:30l x -=,过F 的直线与Γ在第一象限交于,M N 两点,过,M N 作l 的垂线,垂足分别为,C D ,直线,MD NC 交于点H ,求MNH △面积的最小值.26.(2024·浙江绍兴·二模)已知抛物线C :()220y px p =>的焦点到准线的距离为2,过点()2,2A 作直线交C 于M ,N 两点,点()1,1B -,记直线BM ,BN 的斜率分别为1k ,2k .(1)求C 的方程;(2)求()121232k k k k -+的值;(3)设直线BM 交C 于另一点Q ,求点B 到直线QN 距离的最大值.27.(2024·浙江绍兴·模拟预测)已知抛物线C :22y px =的焦点F ,直线l 过F 且交C 于两点M N 、,已知当3MF NF =时,MN (1)求C 的标准方程.(2)令,02p F ⎛⎫'- ⎪⎝⎭,P 为C 上的一点,直线F P ',FP 分别交C 于另两点A ,B .证明:·1AF PF PF BF '='.(3)过,,A B P 分别作C 的切线123,,l l l , 3l 与1l 相交于D ,同时与2l 相交于E ,求四边形ABED 面积取值范围.28.(2024·河北保定·二模)平面几何中有一定理如下:三角形任意一个顶点到其垂心(三角形三条高所在直线的交点)的距离等于外心(外接圆圆心)到该顶点对边距离的2倍.已知ABC 的垂心为D ,外心为E ,D 和E 关于原点O 对称,()13,0A .(1)若()3,0E ,点B 在第二象限,直线BC x ⊥轴,求点B 的坐标;(2)若A ,D ,E 三点共线,椭圆T :()222210x y a b a b+=>>与ABC 内切,证明:D ,E 为椭圆T 的两个焦点.29.(2024·浙江杭州·模拟预测)设双曲线22:12x C y -=,直线:l y x m =+与C 交于,A B 两点.(1)求m 的取值范围;(2)已知C 上存在异于,A B 的,P Q 两点,使得PA PB QA QB t ⋅=⋅=.(i )当4t =时,求,P Q 到点()2,m m --的距离(用含m 的代数式表示);(ii )当2t =时,记原点到直线PQ 的距离为d ,若直线PQ 经过点(),m m -,求d 的取值范围.30.(2024·湖北·一模)已知椭圆2222:1(0)x y M a b a b+=>>的离心率为12,A ,B 分别为椭圆的左顶点和上顶点,1F 为左焦点,且1ABF(1)求椭圆M 的标准方程:(2)设椭圆M 的右顶点为C 、P 是椭圆M 上不与顶点重合的动点.(i )若点31,2P ⎛⎫⎪⎝⎭,点D 在椭圆M 上且位于x 轴下方,直线PD 交x 轴于点F ,设APF 和CDF 的面积分别为1S ,2S 若1232S S -=,求点D 的坐标:(ii )若直线AB 与直线CP 交于点Q ,直线BP 交x 轴于点N ,求证:2QN QC k k -为定值,并求出此定值(其中QN k 、QC k 分别为直线QN 和直线QC 的斜率).黄金冲刺大题06 圆锥曲线(椭圆、双曲线、抛物线)(精选30题)1.(2024·山东·二模)已知椭圆的焦点分别是)()12,F F ,点M 在椭圆上,且124MF MF +=.(1)求椭圆的标准方程;(2)若直线y kx =,A B 两点,且OA OB ⊥,求实数k 的值.【答案】(1)2214x y +=;【分析】(1)根据所给条件求出,a b ,即可得出椭圆标准方程;(2)联立直线与椭圆方程,根据根与系数的关系及OA OB ⊥,列出方程求k 即可.【详解】(1)设椭圆的标准方程为22221(0)x y a b a b+=>>.由题意可知22224c a a b c ⎧=⎪=⎨⎪=+⎩,解得2,1,a b c ⎧=⎪=⎨⎪=⎩所以椭圆的标准方程为2214x y +=.(2)设()()1122,,,A x y B x y ,如图,联立方程2214y kx x y ⎧=⎪⎨+=⎪⎩,消去y ,得()221440k x +++=,则12122414x x x x k +==+,从而(1212y y kx kx =+()212122k x x x x =+++222414kk-=+,因为,0OA OB OA OB ⊥⋅=,即12120x x y y +=,所以22222424640141414k k k k k --+==+++,解得k =或,经验证知Δ0>,所以k.2.(2024·江苏南通·模拟预测)在平面直角坐标系xOy 中,设椭圆()2222:10x y C a b a b +=>>1F ,2F 分别是椭圆的左、右焦点,过2F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A ,B 两点,直线2l 与C 交于D ,E 两点,且12AF F的周长是4+(1)求椭圆C 的方程;(2)当32AB DE =时,求ODE 的面积.【答案】(1)2214x y +=【分析】(1)由椭圆离心率和焦点三角形的周长,列方程组求出,a b ,得椭圆C 的方程;(2)设直线1l ,2l 的方程,与椭圆联立,利用韦达定理和32AB DE =求出DE 和2l 的方程,再求出O 到直线2l 的距离,可求ODE 的面积.【详解】(1)由题意知,222224a c ca b a c ⎧+=+⎪⎪=⎨⎪=-⎪⎩,解得2,1,a b c ===所以椭圆C 的方程为2214x y +=;(2)若直线1l 的斜率不存在,则直线2l 的斜率为0,不满足32AB DE =,直线1l 的的斜率为0,则12,,A F F 三点共线,不合题意,所以直线1l 的斜率存在且不为0,设直线1l的方程为x my =由2214x my x y ⎧=⎪⎨+=⎪⎩,消去x得2211044m y y ⎛⎫++-= ⎪⎝⎭,设()()1122,,,A x y B x y,则12y y +=1221414y y m =-+,()2241.4m AB m +∴===+同理可得()222214141.1144m m DE m m ⎛⎫+ ⎪+⎝⎭==++,由32AB DE =,得()()2222414134214m m m m++=⋅++,解得22m =,则43DE =,∴直线2l的方程为y x =,∴坐标原点O 到直线2l的距离为d ==1423ODE S =⨯= 即ODE【点睛】方法点睛:解答直线与圆锥曲线的题目时,时常把两个曲线的方程联立,消去x (或y )建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系,涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形,强化有关直线与圆锥曲线联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.3.(2024·河北邯郸·二模)已知椭圆C 的中心为坐标原点,对称轴为x 轴、y 轴,且过()2,0,1,M N ⎛⎝两点.(1)求C 的方程.(2),A B 是C 上两个动点,D 为C 的上顶点,是否存在以D 为顶点,AB 为底边的等腰直角三角形?若存在,求出满足条件的三角形的个数;若不存在,请说明理由.【答案】(1)2214x y +=(2)存在,3个【分析】(1)设椭圆C 的方程为221(0,0,)mx ny m n m n +=>>≠,根据条件得到41314m m n =⎧⎪⎨+=⎪⎩,即可求出结果;(2)设直线DA 为1y kx =+,直线DB 为11y x k=-+,当1k =时,由椭圆的对称性知满足题意;当21k ≠时,联立直线与椭圆方程,求出,A B 的坐标,进而求出AB 中垂线方程,根据条件中垂线直经过点(0,1)D ,从而将问题转化成方程42710k k -+=解的个数,即可解决问题.【详解】(1)由题设椭圆C 的方程为221(0,0,)mx ny m n m n +=>>≠,因为椭圆过()2,0,1,M N ⎛ ⎝两点,所以41314m m n =⎧⎪⎨+=⎪⎩,得到1,14m n ==,所以椭圆C 的方程为2214x y +=.(2)由(1)知(0,1)D ,易知直线,DA DB 的斜率均存在且不为0,不妨设(0)DA k k k =>,1DB k k=-,直线DA 为1y kx =+,直线DB 为11y x k =-+,由椭圆的对称性知,当1k =时,显然有DA DB =,满足题意,当21k ≠时,由22114y kx x y =+⎧⎪⎨+=⎪⎩,消y 得到221()204k x kx ++=,所以2814A k x k =-+,222281411414A k k y k k -=-+=++,即222814(,)1414k k A k k--++,同理可得22284(,44k k B k k -++,所以()2222222222222414(4)14(4)(14)1414888(144)5414ABk k k k k k k k k k k k k k k k k k ----+-+--++===++++++,设AB 中点坐标为00(,)x y ,则2220228812(1)1442(4)(14)k kk k k k x k k -+-++==++,22222022144151442(4)(14)k k k k k y k k --+-++==++,所以AB 中垂线方程为222222215512(1)()(4)(14)1(4)(14)k k k k y x k k k k k -+=--++-++,要使ADB 为AB 为底边的等腰直角三角形,则直AB 中垂线方程过点(0,1),所以222222215512(1)1(0)(4)(14)1(4)(14)k k k k k k k k k -+=--++-++,整理得到42710k k -+=,令2t k =,则2710t t -+=,4940∆=->,所以t 有两根12,t t ,且121270,10t t t t +=>=>,即2710t t -+=有两个正根,故有2个不同的2k 值,满足42710k k -+=,所以由椭圆的对称性知,当21k ≠时,还存在2个符合题意的三角形,综上所述,存在以D 为顶点,AB 为底边的等腰直角三角形,满足条件的三角形的个数有3个.【点睛】关键点点晴:本题的关键在于第(2)问,通过设出直线DA 为1y kx =+,直线DB 为11y x k=-+,联立椭圆方程求出,A B 坐标,进而求出直线AB 的中垂线方程,将问题转化成直线AB 的中垂线经过点(0,1)D ,再转化成关于k 的方程的解的问题.4.(2024·广东广州·模拟预测)已知椭圆222:1(08x y C b b+=<<,右顶点为E ,上、下顶点分别为12,,B B G是1EB 的中点,且121EB GB ⋅=.(1)求椭圆C 的方程;(2)设过点()4,0D -的直线l 交椭圆C 于点,M N ,点()2,1A --,直线,MA NA 分别交直线4x =-于点,P Q ,求证:线段PQ 的中点为定点.【答案】(1)22182x y +=(2)证明见解析【分析】(1)通过椭圆的性质和中点的坐标,然后根据向量的数量积得到等量关系即可求出椭圆的标准方程;(2)设出直线l 的方程并与椭圆方程联立,化简写出根与系数的关系,求得点,P Q 的坐标,进而证得线段PQ 的中点为定点.【详解】(1)由题可得()28,,0a E a = ,()()120,,0,B b B b -,1EB ∴的中点为,22a b G ⎛⎫ ⎪⎝⎭,2221233(,),1,2,2222a b a bEB GB a b b ⎛⎫⋅=-⋅--=-=∴= ⎪⎝⎭ 故椭圆C 的方程为22182x y +=;(2)依题意可知直线l 的斜率存在,设直线l 的方程为()4y k x =+,由()224182y k x x y ⎧=+⎪⎨+=⎪⎩消去y 并化简得()222214326480k x k x k +++-=,由()()422Δ10244146480k k k =-+->,得2111,422k k <-<<.设()(),,,M M N N M x y N x y ,则222232648,1414M N M N k k x x x x k k -+=-=++,依题意可知直线,MA NA 的斜率存在,直线MA 的方程为()1122M M y y x x ++=++,令4x =-,得()2442422M M M M P M M k x x y x y x x -+-----==++()()()2184212424221222M M M M M k x k k x k k k x x x ------+--+===---+++,同理可求得42212Q N k y k x +=---+,()N 4242114242422222P Q M N M k k y y k k k x x x x ⎛⎫++∴+=----=---++ ⎪++++⎝⎭()()4424224M N M N M N x x k k x x x x ++=---+⋅+++()22222232414424242(42)064832241414k k k k k k k k k k -++=---+⋅=--++=⎛⎫-+-+ ⎪++⎝⎭,∴线段PQ 的中点为定点()4,0-.【点睛】方法点睛:对于直线和圆锥曲线相交的问题,我们一般将直线和圆锥曲线联立,利用韦达定理带入计算求解.5.(2024·辽宁·二模)平面直角坐标系xOy 中,面积为9的正方形ABCD 的顶点,A B 分别在x 轴和y 轴上滑动,且23OP OA = ,记动点P 的轨迹为曲线Γ.(1)求Γ的方程;(2)过点()4,1E 的动直线l 与曲线Γ交于不同的两点,M N 时,在线段MN 上取点Q ,满足||||||||EM QN QM EN ⋅=⋅.试探究点Q 是否在某条定直线上?若是,求出定直线方程;若不是,说明理由.【答案】(1)22143x y +=(2)点Q 在定直线上,定直线方程为330x y +-=【分析】(1)设点,,P A B 的坐标,利用平面向量的坐标表示消参得0032x x y ⎧=⎪⎨⎪=⎩,结合正方形面积得Γ的方程;(2)设:14l y kx k =+-,,,Q M N 的坐标,与椭圆联立并根据韦达定理得,M N 横坐标关系,再根据线段乘积关系化为比值关系得01120244x x x x x x --=--,化简得0243kx k+=+,代入直线方程即可0y ,从而求出定直线方程.【详解】(1)设()()()00,,,0,0,P x y A x B y ,由0000222(,0))()333OP OA x y x y ==+=,得0023x x y y ⎧=⎪⎪⎨⎪=⎪⎩,所以032x x y ⎧=⎪⎨⎪=⎩,因为正方形ABCD 的面积为29AB =,即22009x y +=,所以223())92x +=,整理可得22143x y +=,因此C 的轨迹方程为22143x y +=.(2)依题意,直线l 存在斜率,设l :1(4)y k x -=-,即14y kx k =+-,设点()00,Q x y ,()11,M x y ,()22,N x y ()102x x x <<,由22143412y kx kx y =+-⎧⎨+=⎩,消y 得2234(14)12x kx k ++-=,即222(34)8(14)4(14)120k x k k x k ++-+--=,由()()()2222Δ64141634143k k k k ⎡⎤=--+--⎣⎦()()()()()22222216144344834483414k k k k k k ⎡⎤⎡⎤=--+++=+--⎣⎦⎣⎦()()22481282966410k k k k =-++=-++>,k <<所以3k ≠-,可得1228(14)34k k x x k -+=-+,21224(14)1234k x x k --=+,由||||||||EM QN QM EN ⋅=⋅ ,得||||||||QM EM QN EN =,所以01120244x x x x x x --=--,可得222121201228(14)4(14)124234344()28(14)8()834k k k k k x x x x x k k x x k ⎡⎤---⎡⎤--⎢⎥⎢⎥+++-⎣⎦⎣⎦==--+⎡⎤--⎢⎥+⎣⎦()()2222232148142432128128648242432824248k k k k k k k k k k k----+-+-+-+==++-+1632242483k kk k++==++,所以()()200143243914333k k k k ky kx k k k k-++-=+-=+=+++,因为00612393333k kx y k k+-+=+=++,所以点Q 在定直线上,定直线方程为330x y +-=.6.(2024·福建厦门·三模)在直角坐标系xOy 中,已知抛物线2:2(0)C y px p =>的焦点为F ,过F 的直线l 与C 交于,M N 两点,且当l 的斜率为1时,8MN =.(1)求C 的方程;(2)设l 与C 的准线交于点P ,直线PO 与C 交于点Q (异于原点),线段MN 的中点为R ,若3QR ≤,求MNQ △面积的取值范围.【答案】(1)24y x =;(2)(.【分析】(1)先设l 的方程为2px my =+,()11,M x y ,()22,N x y ,联立直线与抛物线方程,结合韦达定理及抛物线定义即可求解;(2)先设出()221,2R m m +,进而可求,P Q 的坐标,可得直线//QR x 轴,求出QR 的范围,再由三角形面积公式即可求解.【详解】(1)不妨先设l 的方程为2px my =+,()11,M x y ,()22,N x y ,代入22y px =,可得2220y mpy p --=,所以122y y mp +=,212y y p =-,则()21212222MN x x p m y y p m p p =++=++=+,由题意可知当斜率为1时,1m =,又8MN =,即228p p +=,解得2p =,所以C 的方程为24y x =;(2)由(1)知2p =,直线l 的方程为1x my =+,抛物线方程24y x =,124y y m +=,124y y =-所以R 的纵坐标1222R y y y m +==,将R 的纵坐标2m 代入1x my =+,得221x m =+,所以R 的坐标()221,2m m +,易知抛物线的准线为=1x -,又因为l 与C 的准线交于点P ,所以P 的坐标21,m ⎛⎫-- ⎪⎝⎭,则直线OP 的方程为2m x y =,把2mx y =代入24y x =,得22y my =,即2y m =或0y =,因为点Q 异于原点,从而Q 的纵坐标为2m ,把2y m =代入2m x y =,得22mx y m ==,所以()2,2Q m m ,因为R 的坐标()221,2m m +,所以R ,Q 的纵坐标相同,所以直线//QR x 轴,且222211QR m m m =+-=+,所以MNQ △面积1212MNQ MRQ NRQ S S S QR y y =+=- ,因为()22212121241616y y y y y y m -=+-=+,所以12y y -==,所以()332222112122MNQS m m QR =+⨯=+= ,因为点Q 异于原点,所以0m ≠,所以210m +>,因为3QR ≤,所以13QR <≤,所以3222QR <≤MNQ △面积的取值范围为(.7.(2024·浙江丽水·二模)已知抛物线2:4E y x =,点,,A B C 在抛物线E 上,且A 在x 轴上方,B 和C 在x 轴下方(B 在C 左侧),,A C 关于x 轴对称,直线AB 交x 轴于点M ,延长线段CB 交x 轴于点Q ,连接QA .(1)证明:OM OQ为定值(O 为坐标原点);(2)若点Q 的横坐标为1-,且89MB MC ⋅= ,求AQB 的内切圆的方程.【答案】(1)1(2)221499x y ⎛⎫-+=⎪⎝⎭【分析】(1)根据已知条件作出图形,设出直线AB 的方程,与抛物线联立,利用韦达定理及直线的点斜式方程即可求解;(2)根据(1)的结论及向量的数量积的坐标表示,进而得出直线AB 的方程,利用直线的斜率公式及直线的点斜式方程,结合角平分线的性质及圆的标准方程即可求解.【详解】(1)设直线AB 的方程为()()()11220,,,,x my t m A x y B x y =+>,则()()11,,,0C x y M t -,由24x my ty x =+⎧⎨=⎩,消去x ,得2440y my t --=,()22Δ1600m t m t =+>⇒+>,所以12124,4y y m y y t +==-,直线BC 的方程为()211121y y y y x x x x ++=--,化简得1221214y y xy y y y y =---,令0y =,得124Q y y x t ==-,所以(),0Q t -因此1OM t OQt==-.(2)因为点Q 的横坐标为1-,由(1)可知,()()1,0,1,0Q M -,设QA 交抛物线于D ,()()()()11221144,,,,,,,A x y B x y C x y D x y -,如图所示又由(1)知,124y y =-,同理可得144y y =,得42y y =-,又()212121211242x x my my m y y m +=+++=++=+,()22212121214416y y y y x x =⋅==,又()()22111,,1,MB x y MC x y =-=-- ,则()()()221121212111444MB MC x x y y x x x x m ⋅=---=-+++=- ,故2844,9m -=结合0m >,得m =所以直线AB的方程为330,x -=又12163y y -===,则141414221214141412443444AD y y y y y y k y y x x x x y y y y ---======--+--,所以直线AD 的方程为3430x y -+=,设圆心(,0)(11)T s s -<<,因为QM 为AQB ∠的平分线,故点T 到直线AB 和直线AD 的距离相等,所以333354s s +-=,因为11s -<<,解得19s =,故圆T 的半径33253s r +==,因此圆T 的方程为221499x y ⎛⎫-+= ⎪⎝⎭.8.(2024·江苏苏州·模拟预测)已知点(1,0)A ,(0,1)B ,(1,1)C 和动点(,)P x y 满足2y 是PA PB ⋅ ,PA PC ⋅的等差中项.(1)求P 点的轨迹方程;(2)设P 点的轨迹为曲线1C 按向量31,416a ⎛⎫=- ⎪⎝⎭平移后得到曲线2C ,曲线2C 上不同的两点M ,N 的连线交y 轴于点(0,)Q b ,如果MON ∠(O 为坐标原点)为锐角,求实数b 的取值范围;(3)在(2)的条件下,如果2b =时,曲线2C 在点M 和N 处的切线的交点为R ,求证:R 在一条定直线上.【答案】(1)23122y x x =-+;(2)0b <或1b >;(3)证明见解析.【分析】(1)根据题意,由平面向量的坐标运算,结合等差中项的定义代入计算,即可得到结果;(2)根据题意,由平移公式可得曲线2C 的方程,然后与直线MN 的方程联立,由平面向量的夹角公式,代入计算,即可得到结果;(3)根据题意,求导可得在点,M N 处的切线方程,联立两条切线方程,代入计算,即可得到结果.【详解】(1)由题意可得(1,)PA x y =-- ,(,1)PB x y =-- ,(1,1)PC x y =--,则22(1)()()(1)PA PB x x y y x y x y ⋅=-⋅-+-⋅-=+--,22(1)(1)()(1)21PA PC x x y y x y x y ⋅=-⋅-+-⋅-=+--+,又2y 是PA PB ⋅ ,PA PC ⋅的等差中项,()()22222212x y x y x y x y y ∴+--++--+=,整理得点(,)P x y 的轨迹方程为23122y x x =-+.(2)由(1)知2131:22C y x x =-+,又31,416a ⎛⎫=- ⎪⎝⎭ ,∴平移公式为34116x x y y ⎧=-⎪⎪⎨⎪=+'⎩'⎪即34116x x y y ⎧=+⎪⎪⎨⎪=-'⎩'⎪,代入曲线1C 的方程得到曲线2C 的方程为:213331164242y x x ''⎛⎫⎛⎫-=+-++ ⎪ ⎪⎝⎭⎝⎭',即2y x ¢¢=.曲线2C 的方程为2y x =.如图由题意可设M ,N 所在的直线方程为y kx b =+,由2y x y kx b⎧=⎨=+⎩消去y 得20x kx b --=,令()11,M x y ,()()2212,N x y x x ≠,则1212x x kx x b +=⎧⎨=-⎩,()()21111,,OM x y x x ∴== ,()()22222,,ON x y x x == ,又MON ∠ 为锐角,cos 0||||OM ONMON OM ON ⋅∴∠=>⋅,即2212120||||x x x x OM ON +>⋅ ,2212120x x x x ∴+>,又12x x b =-,2()0b b ∴-+->,得0b <或1b >.(3)当2b =时,由(2)可得12122x x kx x b +=⎧⎨=-=-⎩,对2y x =求导可得2y x '=,∴抛物线2C 在点,()211,M x x ∴=,()222,N x x 处的切线的斜率分别为12M k x =,22N k x =,∴在点M ,N 处的切线方程分别为()2111:2M l y x x x x -=-,()2222:2N l y x x x x -=-,由()()()211112222222y x x x x x x y x x x x ⎧-=-⎪≠⎨-=-⎪⎩,解得交点R 的坐标(,)x y .满足12122x x x y x x +⎧=⎪⎨⎪=⋅⎩即22k x y ⎧=⎪⎨⎪=-⎩,R ∴点在定直线=2y -上.【点睛】关键点点睛:本题主要考查了曲线的轨迹方程问题以及切线问题,难度较大,解答本题的关键在于联立方程结合韦达定理计算以及转化为坐标运算.9.(2024·江苏南通·二模)已知双曲线E 的渐近线为y =,左顶点为()A .(1)求双曲线E 的方程;(2)直线:l x t =交x 轴于点D ,过D 点的直线交双曲线E 于B ,C ,直线AB ,AC 分别交l 于G ,H ,若O ,A ,G ,H 均在圆P 上,①求D 的横坐标;②求圆P 面积的取值范围.【答案】(1)2213x y -=(2)①⎫⎪⎪⎭;②27π16S >且7π4S ≠【分析】(1)根据渐近线方程及顶点求出,a b 得双曲线方程;(2)①设(),0D t ,由四点共圆可得1AG OH k k ⋅=,根据斜率公式转化为,B C 点坐标表示形式,由直线与双曲线联立得出根与系数的关系,据此化简即可求出t ;②求出G 点坐标得出OG ,利用正弦定理求出外接圆的半径,根据均值不等式求出半径的最值,即可得出圆面积的最值.【详解】(1)因为双曲线的渐近线关于坐标轴及原点对称,又顶点在x 轴上,可设双曲线的方程为22221x y a b-=(0a >,0b >),从而渐近线方程为:b y x a =±,由题条件知:b a =因为双曲线的左顶点为()A ,所以a =1b =,所以双曲线的方程为:2213x y -=.(2)如图,①(),0D t ,设直线BC 的方程为:my x t =-,将x my t =+代入方程:22330x y --=,得()2223230m y mty t -++-=,当230m -≠且()22Δ1230t m =+->时,设()11,B x y ,()22,C x y ,则12223mt y y m +=--,212233t y y m -=-.设直线AG 的倾斜角为α,不妨设π02α<<,则π2AGH α∠=-,由于O ,A ,G ,H 四点共圆知:HOD AGH ∠=∠,所以直线OH 的倾斜角为π2α-,πsin πsin 2tan tan 1π2cos cos 2AG OH k k αααααα⎛⎫- ⎪⎛⎫⎝⎭⋅=⋅-=⨯= ⎪⎛⎫⎝⎭- ⎪⎝⎭.直线AC的方程为:y x =,令x t =,则y =H t ⎛ ⎝,所以OH k=AGABk k==1=((1212t y y t x x ⇒=,又11x my t =+,22xmy t =+代入上式得:((1212t y yt my t my t =++,((()(22121212t y y t m y y m t y y t ⎡⎤⇒=+++⎢⎥⎣⎦,(((2222222332333t t mtt t m m t t m m m ⎛⎤---⇒⋅=⋅+⋅++ ⎥---⎝⎦,化简得:2430t +-=,解得:t =(舍)或t =故点D 的坐标为⎫⎪⎪⎭.②直线AG 的方程为(tan y x α=⋅,由①知:t =所以G α⎫⎪⎪⎭.直线OH 方程;1tan y x α=,所以H ,若G ,H 在x 轴上方时,G 在H 的上方,即tan 0α>α>若G ,H 在x 轴下方时,即t an 0α<α<所以tan α>tan α<又直线AG 与渐近线不平行,所以tan α≠所以0πα<<,tan α>tan α<tan α≠因为OG ==设圆P 的半径为R ,面积为S ,则2sin OG R α==所以()()()2222222125tan 125tan sin cos 3164sin 64sin R αααααα+⋅++=⨯=⨯()()22222125tan 1tan 33125tan 2664tan 64tan ααααα++⎛⎫=⨯=++ ⎪⎝⎭327266416⎛⎫≥= ⎪ ⎪⎝⎭,当且仅当22125tan tan αα=即tan α=tan α>tan α<tan α≠所以22716R >且274R ≠,从而27π16S >且7π4S ≠.【点睛】关键点点睛:本题的关键点在于利用直线的倾斜角与圆的内接四边形的角的关系,得出πsin πsin 2tan tan 1π2cos cos 2AG OHk k αααααα⎛⎫- ⎪⎛⎫⎝⎭⋅=⋅-=⨯= ⎪⎛⎫⎝⎭- ⎪⎝⎭这一关键数量关系,再转化为直线与双曲线相交,利用根与系数的关系化简求参数的常规问题.10.(2024·江苏南京·二模)已知抛物线2:2(0)C y px p =>与双曲线2222:1x y E a b-=(0a >,0b >)有公共的焦点F ,且4p b =.过F 的直线1与抛物线C 交于A ,B 两点,与E 的两条近线交于P ,Q 两点(均位于y 轴右侧).(1)求E 的渐近线方程;(2)若实数λ满足1111||||||||OP OQ AF BF λ⎛⎫+=- ⎪⎝⎭,求λ的取值范围.【答案】(1)y x =(2)10,2⎡⎫⎪⎢⎣⎭【分析】(1)由两曲线有公共的焦点F ,且4p b =,得2c b =,a ,可求渐近线方程;(2)通过设直线方程,联立方程组,借助韦达定理,表示出11||||OP OQ +和11||||AF BF -,由1111OP OQ AF BF λ⎛⎫+=- ⎪⎪⎝⎭求λ的取值范围.【详解】(1)抛物线2:2(0)C y px p =>与双曲线2222:1x y E a b-=(0a >,0b >)有公共的焦点F ,设双曲线E 的焦距为2c ,则有2pc =,又4p b =,则2c b =.由222+=a b c,得a ,所以E的渐近线的方程为y =(2)设:l x my c =+,()()1122,,,P x y Q x y ,1与E 的两条近线交于P ,Q 两点均位于y 轴右侧,有23m <,由x my cy x =+⎧⎪⎨=⎪⎩,解得1y =2y =,11112OP OQ y +=+设()()3344,,,A x y B x y , 由22x my cy px=+⎧⎨=⎩,消去x 得2220y pmx p --=,则有234342,y y pm y y p +==-,1AF2p =由1111OP OQ AF BF λ⎛⎫+=- ⎪⎪⎝⎭,2pc =,有2p λ==由23m <⎡∈⎢⎣,所以10,2λ⎡⎫∈⎪⎢⎣⎭.【点睛】方法点睛:解答直线与圆锥曲线的题目时,时常把两个曲线的方程联立,消去x (或y )建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系,涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形,强化有关直线与圆锥曲线联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.11.(2024·重庆·三模)已知()2,0F ,曲线C 上任意一点到点F 的距离是到直线12x =的距离的两倍.(1)求曲线C 的方程;(2)已知曲线C 的左顶点为A ,直线l 过点F 且与曲线C 在第一、四象限分别交于M ,N 两点,直线AM 、AN 分别与直线12x =交于P ,H 两点,Q 为PH 的中点.(i )证明:QF MN ⊥;(ii )记PMQ ,HNQ ,MNQ 的面积分别为1S ,2S ,3S ,则123S S S +是否为定值?若是,求出这个定值;若不是,请说明理由.【答案】(1)2213y x -=(2)(i )证明见解析;(ii )是,12【分析】(1)设曲线C 上任意一点坐标为(),x y ,利用坐标可得曲线C 的方程;(2)(i)设直线MN :2x my =+,()11,M x y ,()22,N x y ,联立方程组可得1221231my y m +=--,122931y y m =-,求得直线AM :()1111y y x x =++,求得P ,H ,进而可得Q 的坐标,求得FQ 的坐标,直线MN 的方向向量的坐标,利用向量法可证结论.(ii) 法一:利用(i )可求得()226113mMN m +=-;QF=()()322329112213m S MN QF m+=⋅=-,进而求得()1212114S S PH x x +=⋅+-,代入运算可求得()()32212291413m S S m++=-,可求结论.法二:(利用双曲线的第二定义)由(1)知,1122MF x ⎛⎫=- ⎪⎝⎭,同理2122NF x ⎛⎫=- ⎪⎝⎭,计算可得1218S S PH MN +=⋅,又312S MN QF =⋅,12314PH S S S QF +=,进而计算可得结论成立.【详解】(1)设曲线C 上任意一点坐标为(),x y ,则由题意可知:()2222222212444441123y x y x x x y x x x ⎛⎫-+=-⇒-++=-+⇒-= ⎪⎝⎭,故曲线C 的方程为2213y x -=.(2)(i)设直线MN :2x my =+,()11,M x y ,()22,N x y ,其中m <<且11x >,21x >()22222311290330x my m y my x y =+⎧⇒-++=⎨--=⎩,故1221231my y m +=--,122931y y m =-;直线AM :()1111y y x x =++,当12x =时,()11321y y x =+,故()1131,221y P x ⎛⎫⎪ ⎪+⎝⎭,同理()2231,221y H x ⎛⎫⎪ ⎪+⎝⎭,Q 为PH 中点,故()()()()1221121212111332211411Q y x y x y y y x x x x +++⎛⎫=⋅+=⋅ ⎪++++⎝⎭;()()()()()()222212121212293693111333931m m m x x my my m y y m y y m -+-++=++=+++=-2931m =--;(*)()()()()()122112211212221836181133233131m m my x y x y my y my my y y y m m -+++=+++=++==---;故3183492Q m m y =⋅=,即13,22m Q ⎛⎫⎪⎝⎭,则33,22m FQ ⎛⎫=- ⎪⎝⎭ ,直线MN 的方向向量(),1a m =,33022m m a FQ ⋅=-+= ,故QF MN ⊥.(ii)法一:12y y -===(**)故()2226113m MN y m +=-=-;QF==又QF MN ⊥,故()()322329112213mSMN QF m+=⋅=-.()12121211111122224S S PQ x HQ x PH x x ⎛⎫⎛⎫+=⋅-+⋅-=⋅+- ⎪ ⎪⎝⎭⎝⎭;()()222121222311293133113m m m x x m y y m m +-+-+-=++==--;()()()()()()1221121212113332121211y x y x y y PH x x x x +-+=-=++++,()()()()()()12211212123339211211y my y my y y x x x x +-+-==++++,由(*)知()()12291113x x m ++=-,由(**)知12y y -=,故291329m PH -==故()()()3222122231911413413m mS S m m+++=⋅=--,则12312S S S +=.法二:(利用双曲线的第二定义)由(1)知,1122MF x ⎛⎫=- ⎪⎝⎭,同理2122NF x ⎛⎫=- ⎪⎝⎭,故()()12121111488S S PH x x PH MF NF PH MN +=+-=⋅+=⋅,又312S MN QF =⋅,故12314PH S S S QF +=,又()()12129411P H y y y y x x =++,且由(*)知229993194431P Hm y y m -==--,记直线PH 与x 轴相交于点K ,由94P Hy y =可得2PK HK FK ⋅=,即PK FK FK HK =,即PKF PFH ∽△△,故PF HF ⊥;又Q 为PH 的中点,故12QF PH =,即1231142PH S S S QF +==.【点睛】方法点睛:直线与双曲线联立问题第一步:设直线方程:有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,都可设出直线方程.。
圆锥曲线方程-抛物线(知识点、典型例题、考点、练习)

抛物线 典例剖析知识点一 抛物线概念的应用已知抛物线y 2=2x 的焦点是F ,点P 是抛物线上的动点,又有点A (3,2),求|P A |+|PF |的最小值,并求出取最小值时P 点的坐标.解将x=3代入抛物线方程 y 2=2x ,得y=〒6.6>2,∴点A 在抛物线内部.设抛物线上点P 到准线l : x=21的距离为d ,由定义知|PA|+|PF|=|PA|+d , 当PA ⊥l 时,|PA|+d 最小, 最小值为27,即|PA|+|PF|的最小值为27, 此时P 点纵坐标为2,代入y 2=2x ,得x=2, ∴点P 坐标为(2,2).知识点二 求抛物线的标准方程求适合下列条件的抛物线的标准方程:(1)过点(-3,2);(2)焦点在直线x -2y -4=0上.分析 设出抛物线的标准形式,依据条件求出p 的值.解 (1)设抛物线标准方程为y 2=-2px 或x 2=2py (p >0),则将点(-3,2)代入方程得2p =43,或2p =92,故抛物线的标准方程为y 2=-43x ,或x 2=92y .(2)①令x =0,由方程x -2y -4=0,得y =-2. ∴抛物线的焦点为F (0,-2).设抛物线方程为x 2=-2py ,则由p2=2,得2p =8.∴所求的抛物线方程为x 2=-8y .②令y =0,由x -2y -4=0,得x =4. ∴抛物线的焦点为F (4,0).设抛物线方程为y 2=2px ,由p2=4,得2p =16.∴所求抛物线方程为y 2=16x .知识点三 抛物线在实际中的应用汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线焦点处,已知灯口的直径是24 cm ,灯深10 cm ,那么灯泡与反射镜的顶点(即截得抛物线顶点)距离是多少?分析 确定抛物线方程,求出抛物线的焦点到其顶点的距离解 取反射镜的轴即抛物线的对称轴为x 轴,抛物线的顶点为坐标原点,建立直角坐标系xOy ,如图所示.因灯口直径|AB|=24.灯深|OP|=10, 所以点A 的坐标是(10,12).设抛物线的方程为y 2=2px(p>0).由点A(10,12)在抛物线上,得122=2p ×10, ∴p=7.2.抛物线的焦点F 的坐标为(3.6,0).因此灯泡与反射镜顶点的距离是3.6 cm.知识点四 抛物线几何性质的简单应用抛物线的顶点在原点,对称轴重合于椭圆9x 2+4y 2=36短轴所在的直线,抛物线焦点到顶点的距离为3,求抛物线的方程.分析 先确定抛物线方程的形式,再依条件求待定参数.解 椭圆9x 2+4y 2=36可化为x 24+y 29=1,得抛物线的对称轴为x 轴.设抛物线的方程为y 2=ax (a ≠0), 又抛物线的焦点到顶点的距离为3,则有|a4|=3,∴|a |=12,即a =±12.故所求抛物线方程为y 2=12x ,或y 2=-12x .知识点五 直线与抛物线已知过抛物线y 2=2px (p >0)的焦点的直线交抛物线于A 、B 两点,且|AB |=52p ,求AB 所在的直线方程.解 焦点F (p2,0),设A (x 1,y 1)、B (x 2,y 2),若AB ⊥Ox ,则|AB |=2p <52p ,不合题意.所以直线AB 的斜率存在,设为k ,则直线AB 的方程为y =k (x -p2),k ≠0.由⎩⎪⎨⎪⎧y =k (x -p 2),y 2=2px ,消去x ,整理得ky 2-2py -kp 2=0.韦达定理得,y 1+y 2=2pk,y 1y 2=-p 2.∴|AB |=(x 1-x 2)2+(y 1-y 2)2=(1+1k 2)·(y 1-y 2)2=1+1k2·(y 1+y 2)2-4y 1y 2=2p (1+1k 2)=52p .解得k =±2.∴AB 所在直线方程为y =2(x -p 2),或y =-2(x -p 2).知识点六 抛物线的焦点弦问题AB 是过抛物线y 2=2px (p >0)焦点F 的弦,M 是AB 的中点,l 是抛物线的准线,MN ⊥l ,N 为垂足.求证:(1)AN ⊥BN ; (2)FN ⊥AB ;(3)若MN 交抛物线于Q ,则Q 平分MN .证明 (1)作AC ⊥l ,垂足为C ,作BD ⊥l ,垂足为D ,在直角梯形ABDC 中, ∵|AF|=|AC|,|BF|=|BD|, ∴|MN|=21(|AC|+|BD|) =21(|AF|+|BF|) =21|AB|, 由平面几何知识可知△ANB 是直角三角形,即AN ⊥BN. (2)∵|AM|=|NM|, ∴∠MAN=∠MNA , ∵AC ∥MN ,∴∠CAN=∠MNA ,∴∠MAN=∠CAN.在△ACN 和△AFN 中,|AN|=|AN|,|AC|=|AF|, 且∠CAN=∠FAN ,∴△ACN ≌△AFN , ∴∠NFA=∠NCA=90°, 即FN ⊥AB.(3)在Rt △MNF 中,连结QF , 由抛物线的定义及(2)的结论得 |QN|=|QF|⇒∠QNF=∠QFN ,且∠QFN=90°-∠QFM ,∠QMF=90°-∠QNF , ∴∠QFM=∠QMF ,∴|QF|=|QM|, ∴|QN|=|QM|,即Q 平分MN.知识点七 抛物线的综合问题过抛物线y 2=2px (p >0)的焦点F 作倾斜角为θ的直线交抛物线于A 、B 两点,设△AOB 的面积为S (O 为原点).(1)用θ、p 表示S ;(2)求S 的最小值;当最小值为4时,求抛物线的方程.解 (1)设直线y =k ⎝⎛⎭⎫x -p2,代入y 2=2px , 得y 2=2p ⎝⎛⎭⎫y k +p 2,即y 2-2pk y -p 2=0,∴y 1+y 2=2pk,y 1y 2=-p 2.∴|AB |= 1+1k2·(y 1+y 2)2-4y 1y 2= k 2+1k 2·4p 2k2+4p 2=(1+1k 2)2p =(1+1tan 2θ)2p=2p sin 2θ.① 当直线AB ⊥x 轴时,①也成立.∴S =12|OF ||AF |sin θ+12|OF ||BF |sin(π-θ)=12|OF ||AB |sin θ =12·p 22p sin 2θsin θ=p 22sin θ. (2)当θ=90°时,S min =12p 2.若S min =4,则12p 2=4.∴p =2 2.∴此时抛物线的方程为y 2=42x .考题赏析1.(辽宁高考)已知点P 是抛物线y 2=2x 上的一个动点,则点P 到点(0,2)的距离与点P 到该抛物线准线的距离之和的最小值为( )A.172 B .3 C. 5 D.92解析 如图所示,由抛物线的定义知,点P 到准线x =-12的距离d 等于点P 到焦点的距离|PF |.因此点P 到点(0,2)的距离与点P 到准线的距离之和可转化为点P 到点(0,2)的距离与点P到点F 的距离之和,其最小值为点M (0,2)到点F ⎝⎛⎭⎫12,0的距离,则距离之和的最小值为4+14=172.答案 A2.(全国Ⅰ高考)已知抛物线y =ax 2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为________.解析 ∵y =ax 2-1,∴y +1=ax 2.令y +1=y ′,x =x ′,则y ′=ax ′2,∴x ′2=2×12ay ′,∴x ′2=1a y ′的焦点坐标为⎝⎛⎭⎫0,14a ,即y +1=14a , ∴y =ax 2-1的焦点坐标为⎝⎛⎭⎫0,14a -1. 又y =ax 2-1的焦点是原点,∴14a =1,∴a =14.∴y =14x 2-1.令x =0,得y =-1,令y =0,得x =±2.故y =14x 2-1与两坐标轴的三个交点为(0,-1),(2,0),(-2,0),∴围成三角形面积为S =12×4×1=2.答案 23.(全国Ⅱ高考)已知F 是抛物线C :y 2=4x 的焦点,A 、B 是抛物线C 上的两个点,线段AB 的中点为M (2,2),则△ABF 的面积等于________.解析 设A (x 1,y 1),B (x 2,y 2),则y 21=4x 1,y 22=4x 2. ∴(y 1+y 2)(y 1-y 2)=4(x 1-x 2).∵x 1≠x 2,∴y 1-y 2x 1-x 2=4y 1+y 2=1.∴直线AB 的方程为y -2=x -2,即y =x . 将其代入y 2=4x ,得A (0,0)、B (4,4).∴|AB |=4 2.又F (1,0)到y =x 的距离为22,∴S △ABF =12×22×42=2.答案 21.抛物线y 2=ax (a ≠0)的焦点到其准线的距离是( ) A.|a |4 B.|a |2C .|a |D .-a2答案 B解析 因为y 2=ax ,所以p =|a |2,即该抛物线的焦点到其准线的距离为|a |2,故选B.2.抛物线y 2=2px (p >0)上一点M 到焦点的距离是a (a >p2),则点M 的横坐标是( )A .a +p 2B .a -p2C .a +pD .a -p 答案 B解析 由抛物线的定义知:点M 到焦点的距离a 等于点M 到抛物线的准线x =-p2的距离,所以点M 的横坐标即点M 到y 轴的距离为a -p2.3.已知抛物线的方程为标准方程,焦点在x 轴上,其上点P (-3,m )到焦点F 的距离为5,则抛物线方程为( )A .y 2=8xB .y 2=-8xC .y 2=4xD .y 2=-4x 答案 B解析 点P (-3,m )在抛物线上,焦点在x 轴上,所以抛物线的标准方程可设为y 2=-2px (p >0).由抛物线定义知|PF |=3+p2=5.所以p =4,所以抛物线的标准方程是y 2=-8x .应选B.4.抛物线y 2=ax 的焦点与双曲线x 23-y 2=1的左焦点重合,则这条抛物线的方程是( )A .y 2=4xB .y 2=-4xC .y 2=-42xD .y 2=-8x 答案 D解析 因为x 23-y 2=1的左焦点为(-2,0),所以抛物线开口向左,所以a <0,且p =|a |2=4,所以a =-8,所以抛物线方程为y 2=-8x ,故选D.5.已知F 为抛物线C :y 2=4x 的焦点,过F 且斜率为1的直线交抛物线C 于A 、B 两点.设|F A |>|FB |,则|F A |与|FB |的比值等于________.答案 3+2 2解析 ∵y 2=4x 的焦点坐标为 F (1,0),准线方程为x =-1,∴过F 且斜率为1的直线方程为y = x - 1.将其代入y 2= 4x 得 x 2 - 6x + 1=0.∴x 1, 2 =62± = 3〒22.∵|FA|>|FB|,∴x A =3+22,x B =3-22.又|FA|= x +1,|FB|= x B +1,∴|FA||FB|== 3+22. 答案 -36. 过抛物线y 2 = 4x 的焦点的直线交抛物线于A 、B 两点,O 为坐标原点,则· 的值是________.. 解析 当直线过焦点且垂直于x 轴时,直线方程为x =1,代入y 2=4x ,y 1,2=±2.A 、B 点的坐标分别为(1,2),(1,-2).∴·OB →=1-4=-3.当直线过焦点不垂直x 轴时,则直线的方程可设为y =k (x -1),设A ,B 坐标分别为(x 1,y 1)(x 2,y 2).则y 21·y 22=16x 1x 2.由⎩⎪⎨⎪⎧y 2=4x ,y =k (x -1),得k 2x 2-(2k +4)x +k 2=0, ·OB →=x 1x 2+y 1y 2=1-4=-3. 7.已知圆A :(x +2)2+y 2=1与定直线l :x =1,若动圆C 与圆A 相外切,且与直线l 相切,求动圆圆心C 的轨迹方程.解 设圆心C 到直线l 的距离为d ,则由题意知|CA |=d +1从而可知圆心C 到点(-2,0)的距离和到定直线x =2的距离相等.所以动圆圆心C 的轨迹是抛物线,其焦点为(-2,0),准线为x =2,故设动圆圆心C 的轨迹方程为y 2=-2px (p >0),由p2=2,得p =4.因此动圆圆心C 的轨迹方程为y 2=-8x .8.已知点M (-2,4)及焦点为F 的抛物线y =18x 2,在此抛物线上求一点P 使|PM |+|PF |的值最小.分析 先根据已知条件画出图形,由定义知,抛物线上的点P 到焦点F 的距离等于P 到准线l 的距离d ,所以求|PM |+|PF |的最小值问题可转化为求|PM |+d 的最小值问题,让点P 在抛物线上运动,容易发现当点P 运动到过点M 且与x 轴垂直的直线与抛物线的交点处时,|PM |+d 最小.解 如图,设MN ⊥x 轴,与准线交于N ,与抛物线交于点P ,在抛物线上任取一点P ′,连P ′M ,P ′F ,作P ′N 垂直于准线,垂足为N ′.由抛物线的定义,|PN|=|PF|,|P ′N ′|=|P ′F||P ′M|+|P ′N ′|=|P ′M|+|P ′F| |PN|+|PM|=|PM|+|PF|∵|P ′M|+|P ′N ′|≥|PN|+|PM| ∴|P ′M|+|P ′F|≥|PM|+|PF|这就是说,当P ′与P 重合时,|PM|+|PF|的值最小解方程组22,1,8x y x =-⎧⎪⎨=⎪⎩得P(-2,12). 9.已知抛物线y 2=2x ,过点Q (2,1)作一条直线交抛物线于A 、B 两点,试求弦AB 中点的轨迹方程.解 设弦AB 的中点M (x ,y ),A (x 1,y 1),B (x 2,y 2),则有y 21=2x 1,y 22=2x 2, ∴y 1-y 2x 1-x 2=2y 1+y 2,又y 1+y 2=2y ,∴y 1-y 2x 1-x 2=1y,即k AB =1y .又k MQ =y -1x -2,由题意知k MQ =k AB .∴y -1x -2=1y,整理, 得y 2-x -y +2=0.所以,弦AB 中点的轨迹方程为y 2-x -y +2=0.10.抛物线的顶点在原点,以x 轴为对称轴,经过焦点且倾斜角为135°的直线,被抛物线所截得的弦长为8,试求抛物线方程.解 如右图所示,依题意设抛物线方程为y 2=2px(p>0),则直线方程为y=-x+12p. 设直线交抛物线于A(x 1,y 1), B(x 2,y 2),则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD| =x 1+2P + x 2 + 2P , 即x 1+x 2 +p=8.①又A (x 1,y 1)、B (x 2,y 2)是抛物线和直线的交点.由⎩⎪⎨⎪⎧y =-x +12p ,y 2=2px ,消去y 得x 2-3px +p 24=0,∴x 1+x 2=3p ,将其代入①得p =2. ∴所求抛物线方程为y 2=4x .当抛物线方程设为y 2=-2px (p >0)时,同理可求得抛物线方程为y 2=-4x . 故抛物线的方程为y 2=4x 或y 2=-4x .讲练学案部分2.4.1 抛物线及其标准方程.对点讲练知识点一 求抛物线的标准方程分别求出满足下列条件的抛物线的标准方程.(1)过点(3,-4).(2)焦点在直线x +3y +15=0上. 解 (1)∵点(3,-4)在第四象限,∴抛物线的标准方程为y 2=2px (p >0)或x 2=-2p 1y (p 1>0),把点(3,-4)的坐标分别代入得(-4)2=2p ×3,32=-2p 1×(-4)即2p =163,2p 1=94∴所求抛物线的方程为y 2=163x 或x 2=-94y .(2)令x =0得y =-5;令y =0得x =-15 ∴抛物线的焦点为(0,-5)或(-15,0)∴所求抛物线的标准方程为y 2=-60x 或x 2=-20y .【反思感悟】 求抛物线方程应首先确定焦点的位置,进而确定方程的形式,然后利用已知条件求p 的值.求满足下列条件的抛物线的方程.(1)以坐标轴为对称轴,且过点A (2,3);(2)以坐标轴为对称轴,焦点到准线的距离为52.解 (1)由题意,方程可设为y 2=mx 或x 2=ny , 将点A (2,3)的坐标代入,得32=m ·2或22=n ·3,∴m =92或n =43.∴所求的抛物线方程为y 2=92x 或x 2=43y .(2)由焦点到准线的距离为52,可知p =52.∴所求抛物线方程为y 2=5x 或y 2=-5x 或x 2=5y 或x 2=-5y .知识点二 抛物线定义的应用已知抛物线的顶点在原点,对称轴是x 轴,抛物线上的点M (-3,m )到焦点的距离等于5,求抛物线的方程和m 的值.解 设抛物线的方程为y 2=-2px (p >0),则准线方程为x =p2.∵点M (-3,m )是抛物线上的点,根据抛物线定义,M 点到焦点的距离等于M 点到准线的距离∴|-3|+p2=5 ∴p =4.∴抛物线方程为y 2=-8x .又点M (-3,m )在抛物线上故m 2=-8×(-3) ∴m =±2 6.【反思感悟】 涉及抛物线上一点与焦点的距离问题要注意用定义转化为该点到准线的距离,可简化计算.若动圆与圆(x -2)2+y 2=1相外切,又与直线x +1=0相切,则动圆圆心的轨迹是( )A .椭圆B .双曲线C .双曲线的一支D .抛物线答案 D解析 设动圆的圆心为M ,半径为r ,动圆与圆(x -2)2+y 2=1相外切,则M 到定点(2,0)的距离为r +1,动圆与直线x =-1相切,则点M 到定直线x =-1的距离为r ,所以M 到定点(2,0)和到定直线x =-2的距离相等,由抛物线定义知,答案选D.知识点三 抛物线知识在实际中的应用喷灌的喷头装在直立管柱OA 的顶点A 处,喷出水流的最高点B 高5 m ,且与OA 所在的直线相距4 m ,水流落在以O 为圆心,半径为9 m 的圆上,则管柱OA 的长是多少?解 如图所示,建立直角坐标系,设水流所形成的抛物线的方程为x 2= -2py(p>0),点C(5, -5)在抛物线上,所以25= -2p ·(-5),2p=5,所以抛物线的方程为x 2= -5y ,点A(-4,y 0)在抛物线上,所以16= -5y 0,y 0 = -165,所以OA 的长为5 - 165=1.8 (m).∴管柱OA 的长是1.8 m.【反思感悟】 根据题意,建立直角坐标系,用待定系数法求出抛物线方程,再利用抛物线方程解决实际问题.抛物线型拱桥顶距离水面2米,水面宽4米,当水下降1米后,水面宽________米.答案 2 6解析 可设抛物线方程为x 2=-2py ,则点(-2,-2)在抛物线上,则有:4=4p . ∴p =1,抛物线方程为x 2=-2y ,当y =-3时,x =±6. ∴水面宽为2 6. 课堂小结:1.四个标准方程的区分:焦点在一次项字母对应的坐标轴上,开口方向由一次项系数的符号确定.当系数为正时,开口方向为坐标轴的正方向;系数为负时,开口方向为坐标轴的负方向.2.焦点在y 轴上的抛物线的标准方程x 2=2py 通常又可以写成y=ax 2,这与以前学习的二次函数的解析式是完全一致的,但需要注意的是,由方程y=ax 2来求其焦点和准线时,必须先化成标准形式.3.经过抛物线的焦点的弦称为抛物线的焦点弦,它有以下特性:设焦点弦AB 的端点坐标分别为A (x 1 , y 1),B(x 2,y 2),则y 1y 2= - p 2, x 1x 2 = 24p ,|AB|= x 1 + x 2 + p.课时作业一、选择题1.已知抛物线的顶点在原点,对称轴为x 轴,焦点在曲线x 24-y 22=1上,则抛物线方程为( )A .y 2=8xB .y 2=4xC .y 2=2xD .y 2=±8x 答案 D解析 由题意知抛物线的焦点为双曲线x 24-y 22=1的顶点,即(-2,0)、(2,0),所以抛物线的方程为y 2=8x 或y 2=-8x .2.抛物线y =mx 2(m <0)的焦点坐标是( )A .(0,m 4)B .(0,14m )C .(0,-m 4)D .(0,-14m)答案 B解析 由于抛物线方程可化为x 2=1my (m <0),所以抛物线的焦点在y 轴的负半轴上,且2p =-1m ,所以p 2=-14m ,所以抛物线的焦点坐标是(0,14m),答案选B.3.过点M (2,4)作与抛物线y 2=8x 只有一个公共点的直线l 有( ) A .0条 B .1条 C .2条 D .3条 答案 C解析 容易发现点M (2,4)在抛物线y 2=8x 上,这样l 过M 点且与x 轴平行时,l 与抛物线有一个公共点,或者l 在M 点上与抛物线相切,故选C.4.已知P 1(x 1,y 1),P 2(x 2,y 2)是抛物线y 2=2px (p >0)上不同的两点,则y 1·y 2=-p 2是直线P 1P 2通过抛物线焦点的( )A .充分不必要条件B .充分必要条件C .必要不充分条件D .既不充分也不必要条件 答案 B解析 设直线P 1P 2的斜率为k ,在x 轴上的截距为x 0,则P 1P 2的方程为y =k (x -x 0), x =1ky +x 0(k =0时只有一个交点不合题意), 所以y 2=2p ⎝⎛⎭⎫1k y +x 0,即y 2-2pky -2px 0=0. 当直线P 1P 2过焦点时,x 0=p2,则y 1y 2=-p 2.当y 1y 2=-p 2时,即-2px 0=-p 2,则x 0=p2,直线过焦点.当斜率不存在时也可验证是充要条件.5.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,如果x 1+x 2=6,那么|AB |等于( )A .10B .8C .6D .4 答案 B解析 方法一 由已知得抛物线焦点为(1,0),过焦点的直线设为y =k (x -1)(由x 1+x 2=6知,此直线不平行于y 轴,因而k 存在).由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x ,消去y 得k 2x 2-2(k 2+2)x +k 2=0. 由⎩⎪⎨⎪⎧x 1+x 2=2(k 2+2)k 2=6,x 1·x 2=1得k =±1.所以|AB |2=(1+k 2)(x 1-x 2)2=2(x 1-x 2)2=64,故|AB |=8.方法二 由焦半径公式|AB |=|AF |+|BF |=x 1+p 2+x 2+p2=8.二、填空题6.抛物线2y 2+5x =0的焦点坐标为____________,准线方程为______________.答案 ⎝⎛⎭⎫-58,0 x =58解析 化抛物线2y 2+5x =0为标准方程y 2=-52x,2p =52,p 2=58,所以焦点坐标为(-58,0),准线方程为x =58.7.设点M ⎝⎛⎭⎫3,103与抛物线y 2=2x 上的点P 之间的距离为d 1,P 到抛物线准线l 的距离为d 2,则当d 1+d 2取最小值时,P 点坐标为____________.答案 (2,2)解析 当P 点是M 与焦点F ⎝⎛⎭⎫12,0连线与抛物线交点时,d 1+d 2最小,MF 的方程为y =43x -23,与抛物线y 2=2x 联立得P (2,2). 三、解答题8.过点Q (4,1)作抛物线y 2=8x 的弦AB ,若弦恰被Q 平分,求AB 所在直线方程. 解 设A (x 1,y 1),B (x 2,y 2),因点Q (4,1)为A ,B 的中点则有⎩⎪⎨⎪⎧x 1+x 2=8y 1+y 2=2将A 、B 两点坐标代入y 2=8x .则有⎩⎪⎨⎪⎧y 21=8x 1 ①y 22=8x 2 ②①-②得:(y 1-y 2)(y 1+y 2)=8(x 1-x 2),由y 1+y 2=2,则有y 1-y 2x 1-x 2=4,∴k AB =4.∴所求直线方程为y -1=4(x -4),即4x -y -15=0.9.一抛物线拱桥跨度为52米,拱顶离水面6.5米,一竹排上有一宽4米、高6米的矩形大木箱,问能否安全通过?解建立坐标系如图,设抛物线方程为 x 2= -2py ,则点(26, -6.5)在抛物线上, ∴262= -2p ·(-6.5),∴p=52,抛物线的方程为x 2= -104y ,当y=-0.5时,x=〒213,则有413>4, 所以木箱能安全通过.10.已知过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点. 求证:(1)x 1x 2为定值;(2)1|F A |+1|FB |为定值. 证明 (1)抛物线y 2=2px 的焦点为F ⎝⎛⎭⎫p 2,0,当AB 不垂直于x 轴时,设直线AB 的方程为y =k ⎝⎛⎭⎫x -p2 (k ≠0). 由⎩⎪⎨⎪⎧y =k ⎝⎛⎭⎫x -p 2y 2=2px消去y , 得k 2x 2-p (k 2+2)x +k 2p 24=0.由根与系数的关系得x 1x 2=p 24(定值).当AB ⊥x 轴时,x 1=x 2=p2,x 1x 2=p24也成立.(2)由抛物线的定义知,|F A |=x 1+p 2,|FB |=x 2+p2.又由(1)得x 1x 2=p24,所以1|F A |+1|FB |=1x 1+p 2+1x 2+p2=x 1+x 2+pp 2(x 1+x 2)+x 1x 2+p 24 =x 1+x 2+p p 2(x 1+x 2)+p 22=x 1+x 2+p p 2(x 1+x 2+p )=2p(定值). 2.4.2 抛物线的简单几何性质.对点讲练知识点一 由性质求方程已知抛物线的顶点为坐标原点,对称轴为x 轴,且与圆x 2+y 2=4相交的公共弦长等于23,求这条抛物线的方程.解 设所求抛物线方程为y 2=2px (p >0)或y 2=-2px (p >0),设交点A (x 1,y 1),B (x 2,y 2),(y 1>0,y 2<0),则|y 1|+|y 2|=23,即y 1-y 2=23,由对称性知,y 2=-y 1,代入上式得y 1=3,把y 1=3代入x 2+y 2=4得x =±1.所以点(1,3)在抛物线y 2=2px 上,点(-1,3)在抛物线y 2=-2px 上,所以3=2p 或3=-2p ×(-1).所以p =32,所以所求抛物线方程为y 2=3x 或y 2=-3x .【反思感悟】 (1)由已知的几何条件求抛物线方程,常用待定系数法.(2)由于抛物线是轴对称图形,所以与对称轴垂直的弦一定被对称轴平分.已知抛物线的焦点在x 轴上,直线y =2x +1被抛物线截得的线段长为15,求此抛物线的标准方程.解 ∵抛物线的焦点在x 轴上,∴设它的标准方程为y 2=2px由方程组⎩⎪⎨⎪⎧y 2=2pxy =2x +1得4x 2+(4-2p )x +1=0.∴|x 1-x 2|=(4-2p )2-164=p 2-4p2.∴1+22|x 1-x 2|=52p 2-4p .∴52p 2-4p =15.∴p =6或p =-2. ∴抛物线的方程为y 2=12x 或y 2=-4x .知识点二 与抛物线有关的证明问题过抛物线焦点F 的直线交抛物线于A ,B 两点,通过点A 和抛物线顶点的直线交抛物线的准线于点D ,求证:直线DB 平行于抛物线的对称轴.证明如图所示,以抛物线的对称轴为x 轴,它的顶点为原点,建立直角坐标系. 设抛物线的方程为y 2=2px ,①点A 的坐标为⎝⎛⎭⎫y 202p ,y 0,则直线OA 的方程为 y =2py 0x (y 0≠0),②抛物线的准线方程是x =-p2.③联立②③,可得点D 的纵坐标为y =-p 2y 0④因为点F 的坐标是⎝⎛⎭⎫p 2,0,当AB ⊥x 轴时,|y 0|=p 此时,|OA |=|OD |,∴DB ∥x 轴当AB 与x 轴不垂直时,即y 20≠p 2时,直线AF 的方程为y =2py 0y 20-p 2⎝⎛⎭⎫x -p 2,⑤ 联立①⑤,可得点B 的纵坐标为y =-p 2y 0.⑥由④⑥可知,DB ∥x 轴.【反思感悟】 因抛物线方程的独特形式,较之椭圆与双曲线,它上面的点便于用一个变量表示出来,如y 2=2px 上任一点,可表示为⎝ ⎛⎭⎪⎫y 22p ,y ,注意恰当运用.设抛物线y 2=2px (p >0)的焦点为F ,Q 是抛物线上除顶点外的任意一点,直线QO 交准线于P 点,过Q 且平行于抛物线对称轴的直线交准线于R 点,求证:PF ⊥RF .证明如图所示,设点Q ⎝⎛⎭⎫y 202p ,y 0,则R.(-2p,y 0 ) 直线OQ 的方程为y=02y p x , 当x=-2p 时,解得y=-02y p,∴P =2,20p p y ⎛⎫-- ⎪⎝⎭,又F (2p ,0),∴RF →=⎝⎛⎭⎫p ,p 2y 0,RF →=(p ,-y 0) ∴RF →·RF →=0,∴PF ⊥RF .知识点三 直线与抛物线的交点问题已知抛物线的方程为y 2=4x ,直线l 过定点P (-2,1),斜率为k .k 为何值时,直线l 与抛物线y 2=4x :只有一个公共点;有两个公共点;没有公共点?解 由题意,设直线l 的方程为y -1=k (x +2).由方程组⎩⎪⎨⎪⎧y -1=k (x +2)y 2=4x ,可得:ky 2-4y +4(2k +1)=0.① (1)当k =0时,由方程①得y =1.把y =1代入y 2=4x ,得x =14.这时,直线l 与抛物线只有一个公共点⎝⎛⎭⎫14,1. (2)当k ≠0时,方程①的判别式为 Δ=-16(2k 2+k -1). 1°由Δ=0,即2k 2+k -1=0,解得k =-1,或k =12.于是,当k =-1,或k =12时,方程①只有一个解,从而方程组(*)只有一个解.这时,直线l 与抛物线只有一个公共点.2°由Δ>0,即2k 2+k -1<0,解得-1<k <12.于是,当-1<k <12,且k ≠0时,方程①有两个解,从而方程组有两个解.这时,直线l与抛物线有两个公共点.3°由Δ<0,即2k 2+k -1>0,解得k <-1,或k >12.于是,当k <-1,或k >12时,方程①没有实数解,从而方程组(*)没有解.这时,直线l与抛物线没有公共点.综上,我们可得当k =-1,或k =12,或k =0时,直线l 与抛物线只有一个公共点;当-1<k <12,且k ≠0时,直线l 与抛物线有两个公共点;当k <-1,或k >12时,直线l 与抛物线没有公共点.【反思感悟】 当直线与抛物线的对称轴平行或重合时,抛物线和直线相交,只有一个交点.解决直线与抛物线位置关系问题时,不要忽视这一点,否则容易漏解.直线l :y =kx +1,抛物线C :y 2=4x ,当k 为何值时,l 与C 分别相切、相交、相离?解 将l 和C 的方程联立⎩⎪⎨⎪⎧y =kx +1, ①y 2=4x , ②①式代入②式,并整理,得 k 2x 2+(2k -4)x +1=0.当k ≠0时,是一元二次方程, ∴Δ=(2k -4)2-4k 2=16(1-k ).(1)当Δ=0时,即k =1时,l 与C 相切. (2)当Δ>0时,即k <1时,l 与C 相交. (3)当Δ<0时,即k >1时,l 与C 相离.当k =0时,直线l :y =1与曲线C :y 2=4x 相交.综上所述,当k =0或k <1时,l 与C 相交,当k =1时,l 与C 相切,当k >1时,l 与C 相离.课堂小结:1.在已知抛物线的顶点在坐标原点,对称轴为x 轴,求抛物线的标准方程时,为避免讨论张口的方向可设抛物线的方程为y 2=2ax (a ≠0).此时,不论a>0或a<0,焦点坐标都是(2a,0),准线方程都为x=-2a . 2.抛物线y 2= 2px (p>0)上任一点的坐标可用一个量y 1表示为21(1),2y y p;x 2 = 2py (p>0)上任一点坐标可设为(x 1 , 212x p).3.直线与抛物线的位置关系设直线l :y=kx+m ,抛物线:y 2=2px(p>0),将直线方程与抛物线方程联立整理成关于x 的方程:ax 2+bx+c=0,(1)若a ≠0,当Δ>0时,直线与抛物线相交,有两个交点; 当Δ=0时,直线与抛物线相切,有一个交点; 当Δ<0时,直线与抛物线相离,无公共点.(2)若a=0,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合,因此直线与抛物线有一个交点是直线与抛物线相切的必要不充分条件.一、选择题1.P (x 0,y 0)是抛物线y 2=2px (p ≠0)上任一点,则P 到焦点的距离是( )A .|x 0-p 2|B .|x 0+p2|C .|x 0-p |D .|x 0+p | 答案 B解析 当p >0时,由抛物线定义得点P (x 0,y 0)到焦点的距离为x 0+p2,当p <0时由抛物线定义知P (x 0,y 0)到焦点的距离为-p 2-x 0,综上得所求距离为|x 0+p2|,故选B.2.过抛物线y 2=4x 的焦点作直线l 交抛物线于A 、B 两点,若线段AB 中点的横坐标为4,则|AB |等于( )A .10B .8C .6D .4 答案 A解析 设A 、B 两点的横坐标分别为x A 、x B ,则有x A +x B =8,|AB |=|AF |+|BF |=x A +p 2+x B +p2=8+p =8+2=10.3.抛物线y 2=2px 与直线ax +y -4=0的一个交点是(1,2),则抛物线的焦点到该直线的距离为( )A.32 3B.25 5C.710 5D.172 答案 B解析 由已知得抛物线方程为y 2=4x ,直线方程为2x +y -4=0,抛物线y 2=4x 的焦点坐标是F (1,0),到直线2x +y -4=0的距离d =|2+0-4|22+1=255.4.若抛物线y 2=2px (p >0)上三个点的纵坐标的平方成等差数列,那么这三个点到抛物线焦点的距离的关系是( )A .成等差数列B .既成等差数列又成等比数列C .成等比数列D .既不成等比数列也不成等差数列 答案 A解析 设三点为P 1(x 1,y 1),P 2(x 2,y 2),P 3(x 3,y 3),则y 21=2px 1,y 22=2px 2,y 23=2px 3,因为2y 22=y 21+y 23, 所以x 1+x 3=2x 2,即|P 1F |-p 2+|P 3F |-p2=2⎝⎛⎭⎫|P 2F |-p 2, 所以|P 1F |+|P 3F |=2|P 2F |. 二、填空题5.抛物线的顶点在原点,准线垂直于x 轴,且焦点到顶点的距离为4,则其方程为______________________.答案 y 2=16x 或y 2=-16x解析 焦点到顶点的距离即p2=4,p =8.6.抛物线y =x 2上的点到直线2x -y -4=0的距离最短的点的坐标是____________. 答案 (1,1)解析 设点A (x ,y )是符合题设条件的点,则由点到直线的距离公式,得d =55|2x -y -4|=55|2x -x 2-4| =55|-(x -1)2-3|≥355. 当且仅当x =1时,d 取得最小值,故所求点为(1,1).7.设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是____________.答案 [-1,1]解析 Q 点坐标为(-2,0),直线l 的斜率不存在时,不满足题意,所以可设直线l 的斜率为k ,方程为y =k (x +2).当k =0时满足.当k ≠0时,x =1ky -2,代入y 2=8x ,得y 2-8k y +16=0.Δ=64k2-64≥0,k 2≤1,即-1≤k ≤1(k ≠0).综上,-1≤k ≤1.三、解答题8.过点(-3,2)的直线与抛物线y 2=4x 只有一个公共点,求此直线方程. 解 显然,直线存在斜率k , 设其方程为y -2=k (x +3), 由⎩⎪⎨⎪⎧y -2=k (x +3)y 2=4x 消去x ,整理得ky 2-4y +8+12k =0①(1)当k =0时,方程①化为-4y +8=0,即y =2, 此时过(-3,2)的直线方程为y =2,满足条件. (2)当k ≠0时,方程①应有两个相等实根. 由⎩⎪⎨⎪⎧ k ≠0Δ=0即⎩⎪⎨⎪⎧k ≠016-4k (8+12k )=0,得k =13或k =-1.∴直线方程为y -2=13(x +3)或y -2=-(x +3),即x -3y +9=0或x +y +1=0.故所求直线有三条,其方程分别为: y =2,x -3y +9=0或x +y +1=0.9.A ,B 是抛物线y 2=2px (p >0)上两点,满足OA ⊥OB ,其中O 为抛物线顶点.求证: (1)A ,B 两点的纵坐标乘积为定值; (2)直线AB 恒过一定点. 证明(1)设A(x 1,y 1),B(x 2,y 2),x 1≠0,x 2≠0,则y 12=2px 1, y 22=2px 2. ∵OA ⊥OB ,∴x 1x 2 + y 1y 2=0.∴y 12y 22、= 4p 2 x 1x 2 = 24p -y 1y 2.∴y 1y 2 =24p -为定值, x 1x 2=-y 1y 2=4p 2也为定值.∴A 、B 两点的纵坐标乘积为定值.(2)若AB ⊥x 轴,则易知直线AB 方程为x = 2p , 过点(2p,0);若AB 与x 轴不垂直,则x 1≠x 2,y 1+y 2≠0.由y 12-y 22=2p(x 1-x 2),得1212122y y px x y y -++=. ∴直线AB 的方程是y= 122py y + (x -x 1)+y 1,即y = 211121222px px y y y y y ++-+。
【高中数学】圆锥曲线之抛物线

1. 抛物线标准方程的求解步骤.2. 抛物线的几何问题.l : ( F 不在 l 上)的距离之比为常数 (0<c <a )的点的轨迹是椭圆. 2ax c=c a OxyFH Ml 焦点:定点 F 准线:直线 l离心率: (0<e <1)ce a=线 l : ( F 不在 l 上)的距离之比为常数 (0<a <c )的点的轨迹是双曲线. 2ax c=c a Oxy FH M l焦点:定点 F 准线:直线 l离心率: (e <1)ce a =焦点:定点 F 准线:直线 l 离心率:1e 不在 l 上)的距离之比为 1 的点的轨迹是抛物线.FHMl不在 l 上)的距离之比为 1 的点的轨迹是抛物线. OxyFHMl22y =x p (p 0)>标准方程:焦点: 02(,)F p准线: 2x p=-焦点在x 正半轴参数 p 的意义:焦点到准线的距离OxyFl220()y px p =->标准方程:焦点: 02(,)pF -准线: 2px =焦点在x 负半轴Oxy F l220()x py p =>标准方程:焦点: 02(,)pF 准线: 2py =-焦点在y 正半轴O xyFl220()x py p =->标准方程:焦点: 02(,)pF -准线: 2py =焦点在y 正半轴220()y px p =>焦点在x 正半轴:220()y px p =->焦点在x 负半轴:220()x py p =>焦点在y 正半轴:220()x py p =->焦点在y 负半轴:对称轴看一次项,符号决定开口方法.抛物线的顶点为(0 , 0)抛物线的离心率 e = 1例1 (1) 已知抛物线的标准方程为,求抛物线的焦点坐标和准线方程.28y x 解:参数 p =4抛物线的焦点坐标:准线方程:(2,0)焦点在x 轴的正半轴x =-2例1 (2) 已知抛物线的焦点为F (0,-2),求它的标准方程.28x y=-解:参数 p =4抛物线的标准方程:焦点在y 轴的负半轴练习 已知抛物线的方程为,求抛物线的焦点坐标和准线方程.2y ax =解:参数 p =抛物线的焦点坐标:准线方程:焦点在y 轴的正半轴抛物线的方程可化为 21x ya=12a104a (,)14x a=-练习 正三角形的一个顶点在原点,另两个顶点A 、B 在抛物线 y 2=2x 上,求这个正三角形的边长.OxyBA431. 定义法:根据抛物线的定义,确定p 的值. 再结合焦点的位置,求出抛物线的标准方程. 注意由于焦点位置的不同,标准方程有四种不同形式.及准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=4,则|该抛物线的方程是|BB 1|=a |BC |=2a 解:设|BF |=aOxy F A 1A l BB 1C|AA 1|=|AF |=411BB CBAA CA=2434a a a =+43a =根据相似定理,有OxyF A 1A l BB 1C|BF |=3a=4F 1|F 1F |=|AA 1|/2=2p = 2224y px x==及准线于点A 、B 、C ,若|BC |=2|BF |,且|AF |=4,则|该抛物线的方程是求抛物线标准方程2. 待定系数法:(1)根据抛物线焦点的位置,写出相应的抛物线标准方程,然后根据条件确定参数p 的值,从而写出抛物线的标准方程.(2)当焦点的位置不能确定时,我们需要分x轴和y轴两种情况讨论,方程分别设为y2=mx(m≠0) 和x2=my(m≠0) .当m>0,表示焦点在正半轴;反之,焦点在负半轴.例3 若抛物线的焦点为直线 3x -4y -12=0 与坐标轴的交点,求抛物线的标准方程所以抛物线的方程为 y 2=16x解:直线 3x -4y -12=0 与坐标轴的交点为(4 , 0)、(0 ,-3)则42p (1) 当焦点为(4 , 0)时,设方程为 y 2=2px (p >0)即 p =8例3 若抛物线的焦点为直线 3x -4y -12=0 与坐标轴的交点,求抛物线的标准方程所以抛物线的方程为 x 2=-12y则32p (2) 当焦点为(0 ,-3)时,设方程为 x 2=-2py (p >0)即 p =12所以所求抛物线的方程为 y 2=16x 或 x 2=-12y抛物线的几何问题1. 抛物线定义的集合语言:P = { M | |MF |=|MH | } .O xyFH Ml例4 设抛物线上的一点P 到 y 轴上的距离是4,则点P 到该抛物线焦点的距离是 .28y x =OxyFHPl 抛物线准线方程:2x =-点P 到准线的距离:PH =6点P 到焦点的距离:PF =66练习 已知F 是抛物线的焦点,A 、B 是该抛物线上的两点,且|AF |+|BF |=3,则线段AB 的中点到 y 轴的距离为 .2y x =O xyF A 1A l抛物线准线方程:14x =-点C 到y 轴的距离:B54B 1C 1C|AA 1|+|BB 1|=3|CC 1|=3/2|AF |+|BF |=3315244-=2. 抛物线的焦半径O xyFH Ml 220()y px p >OxyFl H M2. 抛物线的焦半径220y px p ()=->3. 抛物线的焦点弦|AB |= |AA 1|+|BB 1|=x 1+x 2+p220()y px p >O xyF A 1Al B B 1A (x 1 , y 1),B (x 2 , y 2)|AB |=8练习 斜率为1的直线 l 经过抛物线 y 2=4x 的焦点F ,且与抛物线相交于A 、B 两点,求线段AB 的长.OxyBAF抛物线的几何问题4. 抛物线的弦长220()y px p =>A (x 1 , y 1),B (x 2 , y 2)OxyF AlB221||1||=+-AB k x x ()例5 抛物线 y 2=2px (p >0)的焦点为F ,已知A 、B 是该抛物线上的两个动点,且满足∠AFB =120°. 过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N ,则 的最大值为MN AB ||||A. 2B.233C. 1D.33OxyFA lBMN Q P则|AQ |=a ,|BP |=b解:设|AF |=a ,|AF |=b 22AQ BP a bM N ||||||++==2222222120AB a b ab a b ab a b ab ||cos ()=+-=++=+-24a b ab ()+≤2234AB a b ||()∴≥+222222124333a b a b MN a b AB a b ab ()()||()||()++∴=≤=++-33M N AB ||||∴≤例5 抛物线 y 2=2px (p >0)的焦点为F ,已知A 、B 是该抛物线上的两个动点,且满足∠AFB =120°. 过弦AB 的中点M 作抛物线准线的垂线MN ,垂足为N ,则 的最大值为MN AB ||||A. 2B.233C. 1D.33练习 已知若抛物线 y 2=4x 的焦点为F ,过点F 且斜率为1的直线交抛物线与A 、B 两点,动点P 在曲线 y 2=-4x (y ≥0)上,则△PAB 的面积最小值为 .12PABS AB h ||=⋅∆h 为点P 到直线AB 的距离求△PAB 的面积最小值,即求h 的最小值Oxy FABP h设点P 坐标为(x 0 , y 0),则有 y 02=-4x 0直线AB 的方程为 y =x -1,即x -y -1=0 所以点P 到直线AB 的距离2000022000114224124242y y x y h y y y ||||||()-----==+++==00y ≥ 2021422y h ()+∴=≥Oxy FABP h将直线AB 的方程为 y =x -1代入抛物线方程 y 2=4x 得8A B AB x x p ||=++=2610x x -+=O xy FABPh 设点A 、B 的横坐标分别为x A 、x B ,则有111822222PABS AB h ||=⋅=⋅⋅=∆所以2y x=A. 1B. 2C. 4D. 82y x=12p =14x =-准线方程:001544AF x x ||=+=01x =练习(2014年全国II 文) 已知抛物线C :的焦点为F ,过点F 且倾斜角为30°的直线交C 于A 、B 点,则|AB | = ( )23y x = A.303B. 6C. 12D. 731343AB y x :()=-22190216x x -+=代入C 得2131222A B AB x x p ||=++=+=练习(2016年全国II 文) 设F是抛物线C:y2=4x 的焦点,曲线 (k>0)与C交于点P,PF⊥x轴,则k= ( )A. 12 B.1 C.32 D.2 kyxP(1 , 2)k =1×2=2程为更多高中数学资料,请到百度文库下载.。
圆锥曲线抛物线的基本知识点

圆锥曲线抛物线的基本知识点一、什么是抛物线?抛物线是一种特殊的圆锥曲线,它是由一个固定点(焦点)和一个固定直线(准线)确定的所有点到焦点距离等于该点到准线距离的轨迹。
二、抛物线的基本性质1. 抛物线的对称轴是准线,焦点在对称轴上;2. 抛物线上任意一点与其对称轴的距离相等;3. 焦点到抛物线上任意一点的距离与该点到准线的距离相等;4. 抛物线在对称轴上有最小值,即顶点;5. 抛物线开口方向由焦点和准线位置决定。
三、抛物线方程1. 标准式:y = ax^2 (a>0)其中 a 为常数,表示开口方向和开口大小。
2. 顶点式:y - k = a(x - h)^2其中 (h, k) 为顶点坐标。
3. 参数式:x = at^2, y = 2at其中 t 为参数。
四、抛物线应用1. 物理学中,抛物运动就是指在重力作用下,以一定初速度沿着一个确定角度投掷出去后,运动轨迹为抛物线的运动方式。
2. 工程学中,抛物线常用于设计拱形桥、天桥、高架桥等建筑结构。
3. 数学中,抛物线是圆锥曲线中最简单的一种,也是研究圆锥曲线的基础。
五、抛物线相关概念1. 焦距:焦点到顶点的距离。
2. 焦直线:过焦点且与准线垂直的直线。
3. 焦半径:从焦点到抛物线上任意一点的距离。
4. 垂直平分线:过顶点且与对称轴垂直的直线。
六、抛物线相关定理1. 抛物定理:从焦点到抛物线上任意一点的距离等于该点到准线距离的一半。
2. 切角定理:从焦点引一条切线,该切线与准线之间的夹角等于该切点处法向量与准线方向向量之间夹角(即反射角等于入射角)。
3. 两个相交抛物面交于一条直母线。
圆锥曲线之抛物线

抛物线的知识点、题型1.抛物线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程):开口向右时22(0)y px p =>,开口向左时22(0)y px p =->,开口向上时22(0)x py p =>,开口向下时22(0)x py p =->。
2. 抛物线焦点位置的判断(首先化成标准方程,然后再判断):焦点在一次项的坐标轴上,一次项的符号决定开口方向。
特别提醒:在求解抛物线问题时,首先要判断开口方向;3. 抛物线几何性质:(以22(0)y px p =>为例):①范围:0,x y R ≥∈; ②焦点:一个焦点(,0)2p ,其中p 的几何意义是:焦点到准线的距离; ③对称性:一条对称轴0y =,没有对称中心,只有一个顶点(0,0);④准线:一条准线2p x =-; ⑤离心率:c e a =,抛物线⇔1e =。
例题(1)设R a a ∈≠,0,则抛物线24ax y =的焦点坐标为________(答:)161,0(a); 4、焦半径(圆锥曲线上的点P 到焦点F 的距离)的计算方法:利用圆锥曲线的第二定义,转化到相应准线的距离,即焦半径r ed =,其中d 表示P 到与F 所对应的准线的距离。
(2)已知抛物线方程为x y 82=,若抛物线上一点到y 轴的距离等于5,则它到抛物线的焦点的距离等于____;(3)若该抛物线上的点M 到焦点的距离是4,则点M 的坐标为_____(答:7,(2,4)±); (5)抛物线x y 22=上的两点A 、B 到焦点的距离和是5,则线段AB 的中点到y 轴的距离为______(答:2);5、抛物线中与焦点弦有关的一些几何图形的性质:(1)以过焦点的弦为直径的圆和准线相切;(2)设AB 为焦点弦, M 为准线与x 轴的交点,则∠AMF =∠BMF ;(3)设AB 为焦点弦,A 、B 在准线上的射影分别为A 1,B 1,若P 为A 1B 1的中点,则PA ⊥PB ;(4)若AO 的延长线交准线于C ,则BC 平行于x 轴,反之,若过B 点平行于x 轴的直线交准线于C 点,则A ,O ,C 三点共线。
高三文科数学圆锥曲线之抛物线

圆锥曲线之抛物线图形xyO FlxyO Fl方程)0(22>=p px y )0(22>-=p px y )0(22>=p py x )0(22>-=p py x焦点 )0,2(p )0,2(p -)2,0(p)2,0(p -准线 2p x -= 2p x =2p y -=2p y =抛物线的几何性质 (1)范围因为p >0,由方程()022>=p px y 可知,这条抛物线上的点M 的坐标(x ,y )满足不等式x ≥0,所以这条抛物线在y 轴的右侧;当x 的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸。
(2)对称性以-y 代y ,方程()022>=p px y 不变,所以这条抛物线关于x 轴对称,我们把抛物线的对称轴叫做抛物线的轴。
(3)顶点抛物线和它的轴的交点叫做抛物线的顶点.在方程()022>=p px y 中,当y =0时,x =0,因此抛物线()022>=p px y 的顶点就是坐标原点。
(4)离心率抛物线上的点M 与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e 表示。
由抛物线的定义可知,e =1。
抛物线中的常用结论①过抛物线y 2=2px 的焦点F 的弦AB 长的最小值为2p②设A(x 1,y), 1B(x 2,y 2)是抛物线y 2=2px 上的两点, 则AB 过F 的充要条件是y 1y 2=-p 2③设A , B 是抛物线y 2=2px 上的两点,O 为原点, 则OA ⊥OB 的充要条件是直线AB 恒过定点(2p ,0)(4).圆锥曲线(椭圆、双曲线、抛物线统称圆锥曲线)的统一定义与一定点的距离和一条定直线的距离的比等于常数的点的轨迹叫做圆锥曲线,定点叫做焦点,定直线叫做准线、常数叫做离心率,用e 表示,当0<e <1时,是椭圆,当e >1时,是双曲线,当e =1时,是抛物线.1.【2012高考新课标文10】等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B 两点,43AB =;则C 的实轴长为( )()A 2 ()B 22 ()C 4 ()D 82.【2012高考四川文9】已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点0(2,)M y 。
圆锥曲线知识点归纳汇总 - 抛物线
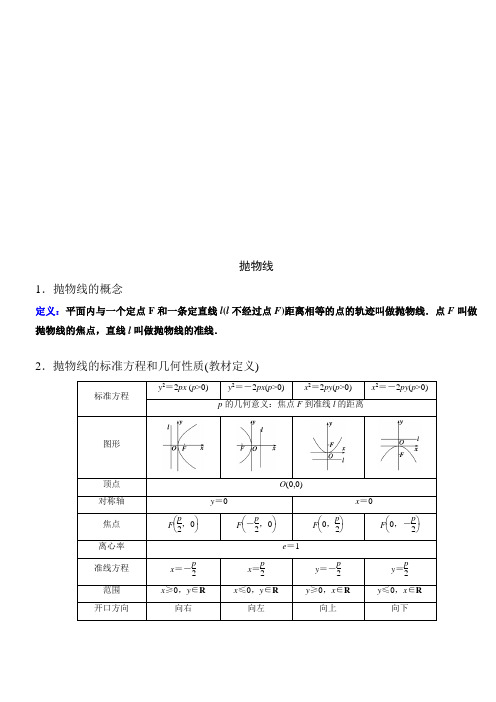
抛物线1.抛物线的概念定义:平面内与一个定点F 和一条定直线l (l 不经过点F )距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线.2.抛物线的标准方程和几何性质(教材定义)标准方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y =0x =0焦点 F ⎝⎛⎭⎫p 2,0F ⎝⎛⎭⎫-p2,0 F ⎝⎛⎭⎫0,p 2 F ⎝⎛⎭⎫0,-p2 离心率 e =1准线方程 x =-p 2x =p 2 y =-p2y =p 2 范围 x ≥0,y ∈Rx ≤0,y ∈Ry ≥0,x ∈Ry ≤0,x ∈R开口方向向右向左向上向下学习奥数的优点1、激发学生对数学学习的兴趣,更容易让学生体验成功,树立自信。
2、训练学生良好的数学思维习惯和思维品质。
要使经过奥数训练的学生,思维更敏捷,考虑问题比别人更深层次。
3、锻炼学生优良的意志品质。
可以培养持之以恒的耐心和克服困难的信心, 以及战胜难题的勇气。
可以养成坚韧不拔的毅力4、获得扎实的数学基本功,发挥创新精神和创造力的最大空间。
3.抛物线的补充的性质及二级结论以开口向右为例:y 2=2px (p >0)1)通径:(过焦点的所有弦长中通径最短为p MN 2=) 2)准线:2px l -=:准线 3)焦半径公式:如图二θp x p AF A cos -=+=12,θpx p BF B cos +=+=12 推导:A x pAP AF +==2,AFcos θRF FT RF RT AP AF +=+=== 所以:AFcos θp AF +=即θpAF cos -=1,同理可证BF4)过焦点弦长公式:如图二θsin px x p AB B A 22=++= 推导:B A B A x x p x px p BF AF AB ++=+++=+=22θsin p cos θp cos θp BF AF AB 2211=++-=+= 5)被焦点截的线段倒数之和=p24==通径 如图二所示:pBF AF 241111==+通径 推导:由焦半径公式可知θp AF cos -=1,θpBF cos +=1所以:通径421111==++-=+p p θp θBF AF cos cos 6)一般弦长公式:直线l :y =kx +m 与抛物线C 交于A (x 1,y 1)B (x 2,y 2)则弦长AB 的计算公式为()212212212411x x x x k x x k AB -++=-+=或者()21221221241111y y y y k y y k AB -++=-+=7)sin θp 2S 2OAB=∆(如图二,直线l 过F 交抛物线与A 、B 两点) 8)42p x x B A =,2p y y B A -=(如图二,直线l 过F 交抛物线与A 、B 两点)【知识拓展】1.抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点F ⎝⎛⎭⎫p 2,0的距离|PF |=x 0+p2,也称为抛物线的焦半径. 2.y 2=ax 的焦点坐标为⎝⎛⎭⎫a 4,0,准线方程为x =-a4. (1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”、“整体代入”等解法.提醒:涉及弦的中点、斜率时一般用“点差法”求解.3.抛物线的离心率e =1,体现了抛物线上的点到焦点的距离等于到准线的距离.因此,涉及抛物线的焦半径、焦点弦问题,可以优先考虑利用抛物线的定义转化为点到准线的距离,这样就可以使问题简化. 抛物线上的点到焦点的距离根据定义转化为到准线的距离,即|PF |=|x |+p 2或|PF |=|y |+p2.。
高考圆锥曲线复习之抛物线

高中数学圆锥曲线专题复习(3)-----抛物线十分重要的定义平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。
其中定点叫抛物线的焦点,定直线叫抛物线的准线。
并且,该定点不在定直线上!!定义的运用要么找定点和定直线,要么就是找等量关系(到定点=到定直线)!!!1.点P 为抛物线y 2=8x 一动点,点M(4,2),则MP+PF 的最小值为__________.62.已知动点M 的坐标满足方程,则动点M 的轨迹是( )CA. 椭圆B. 双曲线C. 抛物线D. 以上都不对3.F 为抛物线y 2=x 的焦点,A 、B 为抛物线上两点,且线段AB 过点F ,AF+BF=3,则线段AB 中点到Y 轴的距离为( )BA 34B 54C 1D 74 *4. 已知抛物线的顶点在原点,焦点在y 轴上,抛物线上一点到焦点距离为5,求m 的值。
M y 2=2px(p>0) 准线方程:y=-p 2 离心率e=1 抛物线上一点A (x 1,y 1)到焦点的距离等于其到准线的距离: 即:AF=AM (其中AM =x 1+p 2) AB 为该抛物线的一条焦点弦 A (x 1,y 1) B (x 2,y 2) 弦长l=x 1+x 2,+p x 1+x 2,≥2√x 1x 2, 当x 1=x 2,时,弦长取得最小值,为2p.A B N还记得怎么求方程吗?1)因为抛物线有四种标准方程,所以多解性要充分考虑。
需要分析p 的取值和开口方向。
2)求抛物线方程,就是要求出P 的值,运用待定系数法及几何条件求抛物线的标准方程。
3)特别注意在设标准方程时,若焦点位置不确定,要分类讨论.1.已知抛物线过点(1,1),则该抛物线的标准方程是______.y 2=x 或x 2=y;2.设抛物线y 2=mx (m ≠0)的准线与直线x =1的距离为3,求抛物线的方程.y 2=8x y 2=-16x .3.在抛物线y 2=2px (p >0)上,横坐标为4的点到焦点的距离为5,则p 的值为( )C A.12 B .1 C .2 D .44.已知抛物线C:x 2=2my (m>0)的焦点为F ,直线y=x -2与x 轴的交点Q 到F 的距离为√172,则抛物线的方程为____________.x 2=2y*5.不管a 取何值,直线(a -1)x -y+2a+1=0恒过定点P ,则过点P 的标准方程是_______________.乱七八糟的几何性质1.范围:例如 y 2=2px(p>0) 存在x ≥02.对称性:例如 y 2=2px(p>0)关于x 轴对称。
圆锥曲线抛物线的基本知识点

圆锥曲线抛物线的基本知识点一、什么是圆锥曲线抛物线?抛物线是一种特殊的圆锥曲线,它由一个平面与一个平行于该平面的直线相交而形成。
抛物线具有独特的形状,呈现出对称性和特定的数学性质。
二、抛物线的定义与特点1.定义:抛物线是平面上到一个定点距离与到一条定直线距离相等的点的轨迹。
2.特点:–抛物线具有对称性,它关于焦点和准线对称。
–抛物线的焦点是定点,准线是定直线。
–抛物线的离心率为1,是所有圆锥曲线中离心率等于1的一种情况。
–抛物线具有无穷远点,它是一条无限延伸的曲线。
三、抛物线方程的一般形式抛物线的方程通常可以表达为一般二次方程的形式:y=ax2+bx+c,其中a、b、c为常数,且a≠0。
四、抛物线的焦点与准线1.焦点:抛物线的焦点是定义抛物线的重要元素之一,与抛物线的离心率密切相关。
焦点的坐标可通过方程求解得到。
2.准线:抛物线的准线与焦点共同决定了抛物线的形状,准线的坐标也可通过方程求解得到。
五、抛物线的性质1.对称性:抛物线关于焦点对称,对称轴为准线。
这个性质使得抛物线在很多实际应用中具有重要意义。
2.焦距公式:定义抛物线焦点到准线的距离为焦距,通过焦距公式可以计算焦点到准线的距离。
3.切线方程:抛物线上任一点处的切线方程可以通过求导得到,切线斜率即为函数的导数值。
4.弧长与曲率:抛物线上任意两点之间的弧长可以通过积分计算得到,曲率表示曲线的弯曲程度。
六、抛物线的应用抛物线在现实生活和科学研究中具有广泛的应用,以下是一些例子: 1. 物理学中的抛物线轨迹:在无空气阻力的情况下,自由落体运动的轨迹为抛物线。
2. 抛物面反射:抛物面反射是一种利用抛物面的反射特性设计的照明系统,例如汽车大灯、探照灯等。
3. 投射问题:抛体在给定初始速度和角度下的运动轨迹就是抛物线,如炮弹飞行轨迹、游泳、跳水等。
七、抛物线与其他圆锥曲线的关系抛物线与其他圆锥曲线(椭圆、双曲线)具有一些相似和不同的地方: 1. 相似之处:抛物线、椭圆和双曲线都是圆锥曲线,它们的定义都可以归纳为距离比例关系。
圆锥曲线之抛物线知识点讲解(含解析)

抛物线的概念与几何性质一、知识梳理1.抛物线的定义(1)平面内与一个定点F 和一条定直线l (F ∉l )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线. (2)其数学表达式:{M ||MF |=d }(d 为点M 到准线l 的距离). 2.抛物线的标准方程与几何性质3.通径:过焦点且垂直于对称轴的弦长等于2p ,通径是过焦点最短的弦.4.焦半径:抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点F ⎝ ⎛⎭⎪⎫p 2,0的距离|PF |=x 0+p2,也称为抛物线的焦半径.二、例题精讲 + 随堂训练1.判断下列结论正误(在括号内打“√”或“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线.( )(2)方程y =ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线,且其焦点坐标是⎝ ⎛⎭⎪⎫a 4,0,准线方程是x =-a 4.( )(3)抛物线既是中心对称图形,又是轴对称图形.( )(4)过抛物线的焦点与抛物线对称轴垂直的直线被抛物线截得的线段叫做抛物线的通径,那么抛物线x 2=-2ay (a >0)的通径长为2a .( )解析 (1)当定点在定直线上时,轨迹为过定点F 与定直线l 垂直的一条直线,而非抛物线.(2)方程y =ax 2(a ≠0)可化为x 2=1a y ,是焦点在y 轴上的抛物线,且其焦点坐标是⎝ ⎛⎭⎪⎫0,14a ,准线方程是y =-14a .(3)抛物线是只有一条对称轴的轴对称图形. 答案 (1)× (2)× (3)× (4)√2.顶点在原点,且过点P (-2,3)的抛物线的标准方程是________________. 解析 设抛物线的标准方程是y 2=kx 或x 2=my ,代入点P (-2,3),解得k =-92,m =43,所以y 2=-92x 或x 2=43y .答案 y 2=-92x 或x 2=43y3. 抛物线y 2=8x 上到其焦点F 距离为5的点的个数为________.解析 设P (x 1,y 1),则|PF |=x 1+2=5,得x 1=3,y 1=±2 6.故满足条件的点的个数为2. 答案 24.(2019·黄冈联考)已知方程y 2=4x 表示抛物线,且该抛物线的焦点到直线x =m 的距离为4,则m 的值为( ) A.5B.-3或5C.-2或6D.6解析 抛物线y 2=4x 的焦点为F (1,0),它与直线x =m 的距离为d =|m -1|=4,∴m=-3或5.答案B5.(2019·北京海淀区检测)设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是()A.4B.6C.8D.12解析如图所示,抛物线的准线l的方程为x=-2,F是抛物线的焦点,过点P 作P A⊥y轴,垂足是A,延长P A交直线l于点B,则|AB|=2.由于点P到y轴的距离为4,则点P到准线l的距离|PB|=4+2=6,所以点P到焦点的距离|PF|=|PB|=6.故选B.答案B6.(2019·宁波调研)已知抛物线方程为y2=8x,若过点Q(-2,0)的直线l与抛物线有公共点,则直线l的斜率的取值范围是________.解析设直线l的方程为y=k(x+2),代入抛物线方程,消去y整理得k2x2+(4k2-8)x+4k2=0,当k=0时,显然满足题意;当k≠0时,Δ=(4k2-8)2-4k2·4k2=64(1-k2)≥0,解得-1≤k<0或0<k≤1,因此k的取值范围是[-1,1].答案[-1,1]考点一抛物线的定义及应用【例1】(1)(2019·厦门外国语模拟)已知抛物线x2=2y的焦点为F,其上有两点A(x1,y1),B(x2,y2)满足|AF|-|BF|=2,则y1+x21-y2-x22=()A.4B.6C.8D.10(2)若抛物线y2=4x的准线为l,P是抛物线上任意一点,则P到准线l的距离与P到直线3x+4y+7=0的距离之和的最小值是()A.2B.135 C.145 D.3解析 (1)由抛物线定义知|AF |=y 1+12,|BF |=y 2+12,∴|AF |-|BF |=y 1-y 2=2,又知x 21=2y 1,x 22=2y 2,∴x 21-x 22=2(y 1-y 2)=4,∴y 1+x 21-y 2-x 22=(y 1-y 2)+(x 21-x 22)=2+4=6.(2)由抛物线定义可知点P 到准线l 的距离等于点P 到焦点F 的距离,由抛物线y 2=4x 及直线方程3x +4y +7=0可得直线与抛物线相离,∴点P 到准线l 的距离与点P 到直线3x +4y +7=0的距离之和的最小值为点F (1,0)到直线3x +4y +7=0的距离,即|3+7|32+42=2. 答案 (1)B (2)A规律方法 应用抛物线定义的两个关键点(1)由抛物线定义,把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线上一点P (x 0,y 0)到焦点F 的距离|PF |=|x 0|+p2或|PF |=|y 0|+p 2.【训练1】 (1)动圆过点(1,0),且与直线x =-1相切,则动圆的圆心的轨迹方程为__________.(2)(2017·全国Ⅱ卷)已知F 是抛物线C :y 2=8x 的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则|FN |=________.解析 (1)设动圆的圆心坐标为(x ,y ),则圆心到点(1,0)的距离与到直线x =-1的距离相等,根据抛物线的定义易知动圆的圆心的轨迹方程为y 2=4x .(2)如图,不妨设点M 位于第一象限内,抛物线C 的准线交x 轴于点A ,过点M 作准线的垂线,垂足为点B ,交y 轴于点P ,∴PM ∥OF .由题意知,F (2,0),|FO |=|AO |=2. ∵点M 为FN 的中点,PM ∥OF ,∴|MP |=12|FO |=1. 又|BP |=|AO |=2, ∴|MB |=|MP |+|BP |=3.由抛物线的定义知|MF |=|MB |=3,故|FN |=2|MF |=6. 答案 (1)y 2=4x (2)6考点二 抛物线的标准方程及其性质【例2】 (1)(2018·晋城模拟)抛物线C :y 2=4x 的焦点为F ,其准线l 与x 轴交于点A ,点M 在抛物线C 上,当|MA ||MF |=2时,△AMF 的面积为( ) A.1B. 2C.2D.22(2)已知圆C 1:x 2+(y -2)2=4,抛物线C 2:y 2=2px (p >0),C 1与C 2相交于A ,B 两点,且|AB |=855,则抛物线C 2的方程为( )A.y 2=85xB.y 2=165xC.y 2=325xD.y 2=645x 解析 (1)过M 作MP 垂直于准线,垂足为P , 则|MA ||MF |=2=|MA ||MP |=1cos ∠AMP ,则cos ∠AMP =22,又0°<∠MAP <180°, 则∠AMP =45°,此时△AMP 是等腰直角三角形, 设M (m ,4m ),由|MP |=|MA |,得|m +1|=4m , 解得m =1,M (1,2),所以△AMF 的面积为12×2×2=2. (2)由题意,知直线AB 必过原点, 则设AB 的方程为y =kx (易知k >0), 圆心C 1(0,2)到直线AB 的距离d =|-2|k 2+1=22-⎝ ⎛⎭⎪⎫4552=255,解得k =2,由⎩⎨⎧y =2x ,x 2+(y -2)2=4得⎩⎨⎧x =0,y =0或⎩⎪⎨⎪⎧x =85,y =165,把⎝ ⎛⎭⎪⎫85,165代入抛物线方程, 得⎝ ⎛⎭⎪⎫1652=2p ·85,解得p =165, 所以抛物线C 2的方程为y 2=325x . 答案 (1)C (2)C规律方法 1.求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置、开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数p ,只需一个条件就可以确定抛物线的标准方程.2.在解决与抛物线的性质有关的问题时,要注意利用几何图形的形象、直观的特点来解题,特别是涉及焦点、顶点、准线的问题更是如此.【训练2】 (1)如图,过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于点A ,B ,交其准线l 于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线的方程为________.(2)(2019·济宁调研)已知点A (3,0),过抛物线y 2=4x 上一点P 的直线与直线x =-1垂直相交于点B ,若|PB |=|P A |,则P 的横坐标为( ) A.1B.32C.2D.52解析 (1)设A ,B 在准线上的射影分别为A 1,B 1, 由于|BC |=2|BF |=2|BB 1|,则直线的斜率为3, 故|AC |=2|AA 1|=6,从而|BF |=1,|AB |=4,故p |AA 1|=|CF ||AC |=12,即p =32,从而抛物线的方程为y 2=3x .(2)由抛物线定义知:|PB |=|PF |,又|PB |=|P A |,所以|P A |=|PF |,所以x P =x A +x F2=2(△PF A 为等腰三角形). 答案 (1)y 2=3x (2)C考点三 直线与抛物线的综合问题【例3】 (2019·武汉调研)已知抛物线C :x 2=2py (p >0)和定点M (0,1),设过点M 的动直线交抛物线C 于A ,B 两点,抛物线C 在A ,B 处的切线交点为N . (1)若N 在以AB 为直径的圆上,求p 的值; (2)若△ABN 面积的最小值为4,求抛物线C 的方程. 解 (1)可设AB :y =kx +1,A (x 1,y 1),B (x 2,y 2), 将AB 的方程代入抛物线C ,得x 2-2pkx -2p =0,显然方程有两不等实根, 则x 1+x 2=2pk ,x 1x 2=-2p .① 又x 2=2py 得y ′=xp ,则A ,B 处的切线斜率乘积为x 1x 2p 2=-2p =-1, 则有p =2.(2)设切线AN 为y =x 1p x +b ,又切点A 在抛物线y =x 22p 上,∴y 1=x 212p ,∴b =x 212p -x 21p =-x 212p ,切线AN 的方程为y AN =x 1p x -x 212p ,同理切线BN 的方程为y BN =x 2p x -x 222p . 又∵N 在y AN 和y BN 上,∴⎩⎪⎨⎪⎧y =x 1p x -x 212p ,y =x 2p x -x 222p,解得N ⎝ ⎛⎭⎪⎫x 1+x 22,x 1x 22p .∴N (pk ,-1). |AB |=1+k 2|x 2-x 1|=1+k 24p 2k 2+8p , 点N 到直线AB 的距离d =|kx N +1-y N |1+k 2=|pk 2+2|1+k 2,S △ABN =12·|AB |·d =p (pk 2+2)3≥22p , ∴22p =4,∴p =2, 故抛物线C 的方程为x 2=4y .规律方法 1.有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点,可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则必须用一般弦长公式.2.涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”、“整体代入”等解法.提醒:涉及弦的中点、斜率时一般用“点差法”求解.【训练3】 (2017·全国Ⅰ卷)已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A ,B 两点,直线l 2与C 交于D ,E 两点,则|AB |+|DE |的最小值为( ) A.16B.14C.12D.10解析 抛物线C :y 2=4x 的焦点为F (1,0),由题意可知l 1,l 2的斜率存在且不为0.不妨设直线l 1的斜率为k ,则l 2直线的斜率为-1k ,故l 1:y =k (x -1),l 2:y =-1k (x -1).由⎩⎨⎧y 2=4x ,y =k (x -1),消去y 得k 2x 2-(2k 2+4)x +k 2=0. 设A (x 1,y 1),B (x 2,y 2),∴x 1+x 2=2k 2+4k 2=2+4k 2, 由抛物线定义可知,|AB |=x 1+x 2+2=4+4k 2. 同理得|DE |=4+4k 2,∴|AB |+|DE |=8+4k 2+4k 2≥8+216=16. 当且仅当1k 2=k 2,即k =±1时取等号. 故|AB |+|DE |的最小值为16. 答案 A[思维升华]1.抛物线定义的实质可归结为“一动三定”:一个动点M ,一个定点F (抛物线的焦点),一条定直线l (抛物线的准线),一个定值1(抛物线的离心率).2.抛物线的焦点弦:设过抛物线y 2=2px (p >0)的焦点的直线与抛物线交于A (x 1,y 1),B (x 2,y 2),则:(1)y 1y 2=-p 2,x 1x 2=p 24;(2)若直线AB 的倾斜角为θ,则|AB |=2psin 2θ;|AB |=x 1+x 2+p ; (3)若F 为抛物线焦点,则有1|AF |+1|BF |=2p . [易错防范]1.认真区分四种形式的标准方程(1)区分y =ax 2(a ≠0)与y 2=2px (p >0),前者不是抛物线的标准方程.(2)求标准方程要先确定形式,必要时要进行分类讨论,标准方程有时可设为y 2=mx 或x 2=my (m ≠0).2.直线与抛物线结合的问题,不要忘记验证判别式.数学抽象——活用抛物线焦点弦的四个结论1.数学抽象素养水平表现为能够在关联的情境中抽象出一般的数学概念和规则,能够将已知数学命题推广到更一般情形.本课时中研究直线方程时常用到直线系方程就是其具体表现之一.2.设AB 是过抛物线y 2=2px (p >0)焦点F 的弦, 若A (x 1,y 1),B (x 2,y 2),则 (1)x 1·x 2=p 24. (2)y 1·y 2=-p 2.(3)|AB |=x 1+x 2+p =2psin 2α(α是直线AB 的倾斜角). (4)1|AF |+1|BF |=2p 为定值(F 是抛物线的焦点).【例1】 过抛物线y 2=4x 的焦点F 的直线l 与抛物线交于A ,B 两点,若|AF |=2|BF |,则|AB |等于( ) A.4B.92C.5D.6[一般解法]易知直线l 的斜率存在,设为k ,则其方程为y =k (x -1). 由⎩⎨⎧y =k (x -1),y 2=4x得k 2x 2-(2k 2+4)x +k 2=0,得x A ·x B =1,①因为|AF |=2|BF |,由抛物线的定义得x A +1=2(x B +1), 即x A =2x B +1,②由①②解得x A =2,x B =12, 所以|AB |=|AF |+|BF |=x A +x B +p =92.[应用结论]法一 由对称性不妨设点A 在x 轴的上方,如图设A ,B 在准线上的射影分别为D ,C ,作BE ⊥AD 于E ,设|BF |=m ,直线l 的倾斜角为θ, 则|AB |=3m ,由抛物线的定义知 |AD |=|AF |=2m ,|BC |=|BF |=m ,所以cos θ=|AE ||AB |=13,所以tan θ=2 2.则sin 2θ=8cos 2θ,∴sin 2θ=89.又y 2=4x ,知2p =4,故利用弦长公式|AB |=2p sin 2θ=92.法二 因为|AF |=2|BF |,1|AF |+1|BF |=12|BF |+1|BF |=32|BF |=2p =1, 解得|BF |=32,|AF |=3,故|AB |=|AF |+|BF |=92. 答案 B【例2】 设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为( ) A.334B.938C.6332D.94[一般解法]由已知得焦点坐标为F ⎝ ⎛⎭⎪⎫34,0,因此直线AB 的方程为y =33⎝ ⎛⎭⎪⎫x -34,即4x -43y -3=0.与抛物线方程联立,化简得4y 2-123y -9=0, 故|y A -y B |=(y A +y B )2-4y A y B =6.因此S△OAB =12|OF||y A-y B|=12×34×6=94.[应用结论]由2p=3,及|AB|=2p sin2α得|AB|=2psin2α=3sin230°=12.原点到直线AB的距离d=|OF|·sin 30°=3 8,故S△AOB =12|AB|·d=12×12×38=94.答案D【例3】(2019·益阳、湘潭调研)如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A,B,交其准线l于点C,若F是AC的中点,且|AF|=4,则线段AB的长为()A.5B.6C.163 D.203[一般解法]如图,设l与x轴交于点M,过点A作AD⊥l交l于点D,由抛物线的定义知,|AD|=|AF|=4,由F是AC的中点,知|AD|=2|MF|=2p,所以2p=4,解得p=2,所以抛物线的方程为y2=4x.设A(x1,y1),B(x2,y2),则|AF|=x1+p2=x1+1=4,所以x1=3,可得y1=23,所以A(3,23),又F(1,0),所以直线AF的斜率k=233-1=3,所以直线AF 的方程为y=3(x-1),代入抛物线方程y2=4x得3x2-10x+3=0,所以x1+x2=103,|AB |=x 1+x 2+p =163.故选C.[应用结论]法一 设A (x 1,y 1),B (x 2,y 2),则|AF |=x 1+p 2=x 1+1=4,所以x 1=3,又x 1x 2=p 24=1,所以x 2=13,所以|AB |=x 1+x 2+p =3+13+2=163.法二 因为1|AF |+1|BF |=2p ,|AF |=4,所以|BF |=43,所以|AB |=|AF |+|BF |=4+43=163.答案 C三、课后练习1.抛物线y 2=8x 的焦点为F ,设A ,B 是抛物线上的两个动点,|AF |+|BF |=233|AB |,则∠AFB 的最大值为( )A.π3B.3π4C.5π6D.2π3解析 设|AF |=m ,|BF |=n ,∵|AF |+|BF |=233|AB |,∴233|AB |≥2mn ,∴mn ≤13|AB |2,在△AFB 中,由余弦定理得cos ∠AFB =m 2+n 2-|AB |22mn =(m +n )2-2mn -|AB |22mn =13|AB |2-2mn 2mn ≥-12,∴∠AFB 的最大值为2π3. 答案 D2.(2019·武汉模拟)过点P (2,-1)作抛物线x 2=4y 的两条切线,切点分别为A ,B ,P A ,PB 分别交x 轴于E ,F 两点,O 为坐标原点,则△PEF 与△OAB 的面积之比为( )A.32B.33C.12D.34解析 设A (x 1,y 1),B (x 2,y 2),则点A ,B 处的切线方程为x 1x =2(y +y 1),x 2x =2(y +y 2),所以E ⎝ ⎛⎭⎪⎫2y 1x 1,0,F ⎝ ⎛⎭⎪⎫2y 2x 2,0,即E ⎝ ⎛⎭⎪⎫x 12,0,F ⎝ ⎛⎭⎪⎫x 22,0,因为这两条切线都过点P (2,-1),则⎩⎨⎧2x 1=2(-1+y 1),2x 2=2(-1+y 2),所以l AB :x =-1+y ,即l AB 过定点(0,1),则S △PEF S OAB=12×1×⎪⎪⎪⎪⎪⎪x 12-x 2212×1×|x 1-x 2|=12. 答案 C3.已知抛物线方程为y 2=-4x ,直线l 的方程为2x +y -4=0,在抛物线上有一动点A ,点A 到y 轴的距离为m ,到直线l 的距离为n ,则m +n 的最小值为________.解析 如图,过A 作AH ⊥l ,AN 垂直于抛物线的准线,则|AH |+|AN |=m +n +1,连接AF ,则|AF |+|AH |=m +n +1,由平面几何知识,知当A ,F ,H 三点共线时,|AF |+|AH |=m +n +1取得最小值,最小值为F 到直线l 的距离,即65=655,即m +n 的最小值为655-1.答案655-14.(2019·泉州一模)在平面直角坐标系xOy 中,抛物线C :x 2=2py (p >0)的焦点为F ,点A 在C 上,若|AO |=|AF |=32.(1)求抛物线C 的方程;(2)设直线l 与C 交于P ,Q ,若线段PQ 的中点的纵坐标为1,求△OPQ 的面积的最大值.解 (1)因为点A 在C 上,|AO |=|AF |=32,所以点A 的纵坐标为p 4,所以p 4+p 2=32,所以p =2,所以C 的方程为x 2=4y .(2)由题意知直线l 的斜率存在,设直线l 的方程为y =kx +b (b ≥0),代入抛物线方程,可得x 2-4kx-4b =0.设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=4k ,x 1x 2=-4b ,所以y 1+y 2=4k 2+2b , 因为线段PQ 的中点的纵坐标为1,所以2k 2+b =1,即2k 2=1-b ≥0,所以0<b ≤1,S △OPQ =12b |x 1-x 2|=12b (x 1+x 2)2-4x 1x 2=12b 16k 2+16b =b 2+2b =2·b 3+b 2(0<b ≤1),设y =b 3+b 2,y ′=3b 2+2b >0,函数单调递增,所以b =1时,△OPQ 的面积最大,最大值为2.5.已知点A (0,2),抛物线C :y 2=2px (p >0)的焦点为F ,射线F A 与抛物线C 相交于点M ,与其准线相交于点N ,若|FM ||MN |=55,则p 的值等于( ) A.14 B.2 C.4 D.8解析 过点M 作抛物线的准线的垂线,垂足为点M ′,则易得|MM ′|=|MF |,所以cos ∠NMM ′=|MM ′||MN |=|MF ||MN |=55,则k AM =-tan ∠NMM ′=-1-cos 2∠NMM ′cos 2∠NMM ′=-2,则直线AM 的方程为y -2=-2x ,令y =0得抛物线的焦点坐标F (1,0),则p =2×1=2,故选B.答案 B。
高中数学-圆锥曲线-抛物线

高中数学- 圆锥曲线【方法点拨】解析几何是高中数学的重要内容之一,也是衔接初等数学和高等数学的纽带。
而圆锥曲线是解析几何的重要内容,因而成为高考考查的重点。
研究圆锥曲线,无外乎抓住其方程和曲线两大特征。
它的方程形式具有代数的特性,而它的图像具有典型的几何特性,因此,它是代数与几何的完美结合。
高中阶段所学习和研究的圆锥曲线主要包括三类:椭圆、双曲线和抛物线。
圆锥曲线问题的基本特点是解题思路比较简单清晰,解题方法的规律性比较强,但是运算过程往往比较复杂,对学生运算能力,恒等变形能力,数形结合能力及综合运用各种数学知识和方法的能力要求较高。
1. 一要重视定义,这是学好圆锥曲线最重要的思想方法,二要数形结合,既熟练掌握方程组理论,又关注图形的几何性质.2.着力抓好运算关,提高运算与变形的能力,解析几何问题一般涉及的变量多,计算量大,解决问题的思路分析出来以后,往往因为运算不过关导致半途而废,因此要寻求合理的运算方案,探究简化运算的基本途径与方法,并在克服困难的过程中,增强解决复杂问题的信心,提高运算能力.3.突出主体内容,要紧紧围绕解析几何的两大任务来学习:一是根据已知条件求曲线方程,其中待定系数法是重要方法,二是通过方程研究圆锥曲线的性质,往往通过数形结合来体现,应引起重视.4.重视对数学思想如方程思想、函数思想、数形结合思想的归纳提炼,达到优化解题思维、简化解题过程 第1课 椭圆A 【考点导读】1. 掌握椭圆的第一定义和几何图形,掌握椭圆的标准方程,会求椭圆的标准方程,掌握椭圆简单的几何性质;2. 了解运用曲线方程研究曲线几何性质的思想方法;能运用椭圆的标准方程和几何性质处理一些简单的实际问题. 【基础练习】1.已知△ABC 的顶点B 、C 在椭圆2213x y +=上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是 2.椭圆1422=+y x 的离心率为233.已知椭圆中心在原点,一个焦点为F (-23,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是221164x y += 4. 已知椭圆19822=++y k x 的离心率21=e ,则k 的值为544k k ==-或 【范例导析】例1.(1)求经过点35(,)22-,且229445x y +=与椭圆有共同焦点的椭圆方程。
6.专题---圆锥曲线之抛物线

专题------抛物线一、抛物线的定义定义:平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做抛物线(定点F不在定直线l上)。
定点F叫做抛物线的焦点,定直线l叫做抛物线的准线。
例1.动点P到直线40x+=的距离减去它到(2,0)M的距离之差等于2,求点P的轨迹方程。
2.已知点1(,0),4F-直线1:4l x=,点B是直线l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M所在曲线是A.圆B.椭圆C.双曲线D.抛物线二、抛物线的几何性质抛物线的这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下表:(2)抛物线的几何性质的特点:有一个顶点,一个焦点,一条准线,一条对称轴,无对称中心,没有渐近线;(3)p的几何意义:焦点到准线的距离。
例3.抛物线20(0)mx ny m n+=⋅≠的焦点坐标是,准线方程是,通径长;练4.抛物线22(0)y ax a =≠的焦点坐标是________,准线方程是_______;通径长 ;例5.抛物线的顶点在原点,焦点在y 轴上,其上的点0(,4)P x -到焦点的距离为6,则抛物线方程为A.28x y =B.24x y =-C.24x y =D.28x y =-练6.抛物线24y x =上一点M 到焦点的距离为1,则点M 的纵坐标是A.78 B.1516 C.34D.0练7.已知抛物线22(0)y px p =>上有一点0(4,)M y ,它到焦点F 的距离为5,则OMF ∆的面积(O 为原点)为A .1B .2C .2D .22例8.方程02=+ny mx 与)0>>n 的曲线在同一坐标系中的示意图应是练9.在同一坐标系中,方程)0(12222>>=+b a y a x 与)0(02>>=+b a by ax 的曲线大致是提高1.若点P 在抛物线2y x =上,点Q 在圆22(3)1x y -+=上,则PQ 的最小值等于 1B.12)2 C.2 D.12)22.设F 为抛物线24y x =的焦点,A B C ,,为该抛物线上三点,若0FA FB FC ++=,则F A F B F C ++=A.9B.6C.4D.3例10.过抛物线x y 42=的焦点作一直线与抛物线相交于B A ,两点,它们到直线2-=x 的距离之和等于6,则这样的直线A.有且仅有一条B.有且仅有两条C.有无穷多条D.不存在练11.过抛物线24y x =的焦点作直线交抛物线于点1122(,),(,)A x y B x y ,若7AB =,则AB 的中点M 到抛物线准线的距离为A.52B.72 C .2 D .3练12.抛物线2:4C y x =上一点Q 到点(4,1)B 与到焦点F 的距离和最小,则点Q 的坐标为 ;例13.过抛物线22(0)y px p =>的焦点F 作倾斜角为45︒的直线交抛物线于,A B 两点,若线段8AB =,则p =_____;练14.顶点在原点,焦点在x 轴上的抛物线被直线21y x =+截得的弦长为15,求抛物线的方程。
最新高三数学专题复习资料抛物线

第七节 抛 物 线考纲下载1.掌握抛物线的定义、几何图形、标准方程及简单性质(范围、对称性、顶点、离心率等).2.了解圆锥曲线的简单应用.了解抛物线的实际背景,了解抛物线在刻画现实世界和解决实际问题中的作用.3.理解数形结合思想.1.抛物线的定义满足以下三个条件的点的轨迹是抛物线: (1)在平面内;(2)动点到定点F 的距离与到定直线l 的距离相等; (3)定点不在定直线上. 2.抛物线的标准方程和几何性质 标准 方程y 2=2px (p >0)y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0) 对称轴 y =0 x =0 焦点 F ⎝ ⎛⎭⎪⎫p 2,0 F ⎝ ⎛⎭⎪⎫-p 2,0 F ⎝⎛⎭⎪⎫0,p 2 F ⎝⎛⎭⎪⎫0,-p 2 离心率 e =1 准线 方程 x =-p 2x =p 2y =-p 2y =p 2范围x ≥0, x ≤0, y ≥0, y ≤0,y∈R y∈R x∈R x∈R 开口方向向右向左向上向下焦半径(其中P(x0,y0))|PF|=x+p2|PF|=-x0+p2|PF|=y+p2|PF|=-y0+p21.当定点F在定直线l上时,动点的轨迹是什么图形?提示:当定点F在定直线l上时,动点的轨迹是过定点F且与直线l垂直的直线.2.抛物线y2=2px(p>0)上任意一点M(x0,y0)到焦点F的距离与点M的横坐标x0有何关系?若抛物线方程为x2=2py(p>0),结果如何?提示:由抛物线定义得|MF|=x0+p2;若抛物线方程为x2=2py(p>0),则|MF|=y0+p 2 .1.设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是( ) A.y2=-8x B.y2=-4xC.y2=8x D.y2=4x解析:选C 由抛物线准线方程为x=-2知p=4,且开口向右,故抛物线方程为y2=8x.2.(A.安徽高考)抛物线y=14x2的准线方程是( )A.y=-1 B.y=-2 C.x=-1 D.x=-2解析:选A 抛物线y=14x2的标准方程为x2=4y,所以其准线方程为y=-1.3.抛物线y =2x 2的焦点坐标为( ) A.⎝ ⎛⎭⎪⎫12,0 B .(1,0) C.⎝ ⎛⎭⎪⎫0,18 D.⎝⎛⎭⎪⎫0,14解析:选C 将抛物线y =2x 2化成标准方程为x 2=12y ,所以2p =12,p 2=18,而抛物线x 2=12y 的焦点在y 轴的非负半轴上,所以焦点坐标为⎝⎛⎭⎪⎫0,18.4.抛物线的焦点为椭圆x 29+y 24=1的左焦点,顶点为椭圆中心,则抛物线方程为________.解析:由c 2=9-4=5,得F (-5,0), 则抛物线方程为y 2=-45x . 答案:y 2=-45x5.设抛物线y 2=2px (p >0)的焦点为F ,点A (0,2).若线段FA 的中点B 在抛物线上,则B 到该抛物线准线的距离为________.解析:F ⎝ ⎛⎭⎪⎫p 2,0,则B ⎝ ⎛⎭⎪⎫p 4,1, ∴2p ×p4=1,解得p = 2.∴B ⎝ ⎛⎭⎪⎫24,1,因此B 到该抛物线的准线的距离为24+22=324.答案:324[例1] 设P 是抛物线y 2=4x 上的一个动点.(1)求点P 到点A (-1,1)的距离与点P 到直线x =-1的距离之和的最小值; (2)若B (3,2),求|PB |+|PF |的最小值.[自主解答](1)如图,易知抛物线的焦点为F(1,0),准线是x=-1.由抛物线的定义知:点P到直线x=-1的距离等于点P到焦点F的距离.于是,问题转化为:在曲线上求一点P,使点P到点A(-1,1)的距离与点P到F(1,0)的距离之和最小.显然,连接AF交曲线于点P,则所求的最小值为|AF|,即为 5.(2)如图,过点B作BQ垂直准线于Q,交抛物线于点P1,则|P1Q|=|P1F|.则有|PB|+|PF|≥|P1B|+|P1Q|=|BQ|=4.即|PB|+|PF|的最小值为4.互动探究若将本例(2)中的点B坐标改为(3,4),求|PB|+|PF|的最小值.解:由题意可知点(3,4)在抛物线的外部.∵|PB|+|PF|的最小值即为B,F两点间的距离.∴|PB|+|PF|≥|BF|=42+22=16+4=2 5.即|PB|+|PF|的最小值为2 5.方法规律抛物线定义中的“转化”法利用抛物线的定义解决此类问题,应灵活地进行抛物线上的点到焦点的距离与到准线距离的等价转化.“看到准线想到焦点,看到焦点想到准线”,这是解决抛物线焦点弦有关问题的有效途径.1.(A.绍兴模拟)已知动圆过定点F ⎝ ⎛⎭⎪⎫p 2,0,且与直线x =-p 2相切,其中p >0,则动圆圆心的轨迹E 的方程为____________.解析:依题意得,圆心到定点F ⎝ ⎛⎭⎪⎫p 2,0的距离与到直线x =-p 2的距离相等,再依抛物线的定义知,动圆圆心的轨迹E 为抛物线,其方程为y 2=2px .答案:y 2=2px2.过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,若|AF |=3,则|BF |=________.解析:因为抛物线y 2=4x 的焦点F (1,0). 显然,当AB 垂直于x 轴时,|AF |≠3, 所以AB 的斜率k 存在,设AB 的方程为y =k (x -1),与抛物线y 2=4x 联立, 消去y 得k 2x 2-2k 2x -4x +k 2=0, 即k 2x 2-(2k 2+4)x +k 2=0, 设A (x 1,y 1),B (x 2,y 2). 由根与系数的关系得x 1+x 2=2k 2+4k2=2+4k2.又|AF |=3=x 1+p2=x 1+1,所以x 1=2,代入k 2x 2-2k 2x -4x +k 2=0,得k 2=8, 所以x 1+x 2=52,x 2=12,故|BF |=x 2+1=12+1=32.答案:32[例2] (1)抛物线y2=4x的焦点到双曲线x2-y23=1的渐近线的距离是( )A.12B.32C.1 D. 3(2)抛物线x2=2py(p>0)的焦点为F,其准线与双曲线x23-y23=1相交于A,B两点,若△ABF为等边三角形,则p=________.[自主解答] (1)由抛物线y2=4x,有2p=4,p=2.其焦点坐标为(1,0),双曲线x2-y23=1的渐近线方程为y=±3x.不妨取其中一条3x-y=0.由点到直线的距离公式有d=|3×1-0|3+1=32.(2)在等边三角形ABF中,AB边上的高为p,AB2=33p,所以B⎝⎛⎭⎪⎫33p,-p2.又因为点B在双曲线上,故p233-p243=1,解得p=6.[答案] (1)B (2)61.已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y0).若点M 到该抛物线焦点的距离为3,则|OM |=( )A .2 2B .2 3C .4D .2 5解析:选B 依题意,设抛物线方程是y 2=2px (p >0),则有2+p2=3,得p=2,故抛物线方程是y 2=4x ,点M 的坐标是(2,±22),|OM |=22+8=2 3.2.已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2.若抛物线C 2:x 2=2py (p >0)的焦点到双曲线C 1的渐近线的距离为2,则抛物线C 2的方程为( )A .x 2=833y B .x 2=1633y C .x 2=8y D .x 2=16y解析:选D 双曲线的渐近线方程为y =±b a x ,由于ca =a 2+b 2a 2= 1+⎝ ⎛⎭⎪⎫b a 2=2,所以b a =3,所以双曲线的渐近线方程为y =±3x .抛物线的焦点坐标为⎝⎛⎭⎪⎫0,p 2,所以p22=2,则p =8,所以抛物线方程为x 2=16y .1.直线与抛物线的位置关系,是高考命题的热点,多以解答题的形式出现,试题难度较大,多为中、高档题.2.直线与抛物线的位置关系有以下几个命题角度: (1)已知抛物线方程及其他条件,求直线方程; (2)证明直线过定点;(3)求线段长度或线段之积(和)的最值; (4)求定值. [例3](A.浙江高考)已知 △ABP 的三个顶点在抛物线C :x 2=4y 上,F 为抛物线C 的焦点,点M 为AB 的中点,.(1)若|PF | =3,求点M 的坐标; (2)求△ABP 面积的最大值.[自主解答] (1)由题意知焦点F (0,1),准线方程为y =-1.设P (x 0,y 0),由抛物线定义知|PF |=y 0+1,得到y 0=2,所以P (22,2)或P (-22,2).由,分别得M ⎝ ⎛⎭⎪⎫-223,23或M ⎝ ⎛⎭⎪⎫223,23.(2)设直线AB 的方程为y =kx +m ,点A (x 1,y 1),B (x 2,y 2),P (x 0,y 0). 由⎩⎨⎧y =kx +m ,x 2=4y得x 2-4kx -4m =0.于是Δ=16k 2+16m >0,x 1+x 2=4k ,x 1x 2=-4m , 所以AB 中点M 的坐标为(2k,2k 2+m ). 由,得(-x 0,1-y 0)=3(2k,2k 2+m -1),所以⎩⎨⎧x 0=-6k ,y 0=4-6k 2-3m .由x 20=4y 0得k 2=-15m +415. 由Δ>0,k 2≥0,得-13<m ≤43.又因为|AB |=41+k 2k 2+m , 点F (0,1)到直线AB 的距离为d =|m -1|1+k2. 所以S △ABP =4S △ABF =8|m -1|k 2+m =16153m 2-5m 2+m +1.记f (m )=3m 3-5m 2+m +1⎝ ⎛⎭⎪⎫-13<m ≤43.令f ′(m )=9m 2-10m +1=0,解得m 1=19,m 2=1.可得f (m )在⎝ ⎛⎭⎪⎫-13,19上是增函数,在⎝ ⎛⎭⎪⎫19,1上是减函数,在⎝ ⎛⎭⎪⎫1,43上是增函数.又f ⎝ ⎛⎭⎪⎫19=256243>f ⎝ ⎛⎭⎪⎫43.所以,当m =19时,f (m )取到最大值256243,此时k =±5515.所以,△ABP 面积的最大值为2565135.直线与抛物线的位置关系的常见类型及解题策略(1)求直线方程.先寻找确定直线的两个条件,若缺少一个可设出此量,利用题设条件寻找关于该量的方程,解方程即可.(2)证明直线过定点.可依题设条件寻找该直线的方程,可依据方程中的参数及其他条件确定该直线过那个定点.(3)求线段长度和线段之积(和)的最值.可依据直线与抛物线相交,依据弦长公式,求出弦长或弦长关于某个量的函数,然后利用基本不等式或利用函数的知识,求函数的最值;也可利用抛物线的定义转化为两点间的距离或点到直线的距离.(4)求定值.可借助于已知条件,将直线与抛物线联立,寻找待定式子的表达式,化简即可得到.(A.宁波模拟)已知过点A (-4,0)的动直线l 与抛物线G :x 2=2py (p >0)相交于B ,C 两点.当直线l 的斜率是12时,.(1)求抛物线G 的方程;(2)设线段BC 的中垂线在y 轴上的截距为b ,求b 的取值范围. 解:(1)设B (x 1,y 1),C (x 2,y 2),当直线l 的斜率是12时,l 的方程为y =12(x +4),即x =2y -4, 联立⎩⎨⎧x 2=2py ,x =2y -4,消去x ,得2y 2-(8+p )y +8=0,y 1+y 2=8+p2,y 1y 2=4, 由已知,∴y 2=4y 1,由韦达定理及p >0可得y 1=1,y 2=4,p =2, ∴抛物线G 的方程为x 2=4y .(2)由题意知直线l 的斜率存在,且不为0, 设l :y =k (x +4),BC 中点坐标为(x 0,y 0), 由⎩⎨⎧x 2=4y ,y =k x +4,得x 2-4kx -16k =0,由Δ>0得k <-4或k >0, ∴x 0=x B +x C2=2k ,y 0=k (x 0+4)=2k 2+4k ,BC 中垂线方程为y -2k 2-4k =-1k (x -2k ),∴b =2(k +1)2,∴b >2. 故b 的取值范围为(2,+∞).——————————————[课堂归纳——通法领悟]———————————————4个结论——直线与抛物线相交的四个结论已知抛物线y 2=2px (p >0),过其焦点的直线交抛物线于A ,B 两点,设A (x 1,y1),B(x2,y2),则有以下结论:(1)|AB|=x1+x2+p或|AB|=2psin2α(α为AB所在直线的倾斜角);(2)x1x2=p2 4;(3)y1y2=-p2;(4)过抛物线焦点且与对称轴垂直的弦称为抛物线的通径,抛物线的通径长为2p.3个注意点——抛物线问题的三个注意点(1)求抛物线的标准方程时一般要用待定系数法求p的值,但首先要判断抛物线是否为标准方程,若是标准方程,则要由焦点位置(或开口方向)判断是哪一种标准方程.(2)注意应用抛物线定义中距离相等的转化来解决问题.(3)直线与抛物线有一个交点,并不表明直线与抛物线相切,因为当直线与对称轴平行(或重合)时,直线与抛物线也只有一个交点.前沿热点(十二)与抛物线有关的交汇问题1.抛物线是一种重要的圆锥曲线,在高考中,经常以抛物线为载体与直线、圆综合考查,主要考查抛物线的方程及几何性质,直线与抛物线的综合应用,点到直线的距离等.2.直线与抛物线的综合问题,经常是将直线方程与抛物线方程联立,消去x(或y),利用方程的根与系数的关系求解,但一定要注意直线与抛物线相交的条件.[典例] (B.湖南高考)过抛物线E:x2=2py(p>0)的焦点F作斜率分别为k1,k2的两条不同直线l1,l2,且k1+k2=2,l1与E相交于点A,B,l2与E相交于点C,D,以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在直线记为l.(1)若k1>0,k2>0,证明:<2p2;(2)若点M 到直线l 的距离的最小值为755,求抛物线E 的方程. [解题指导] (1)直线l 1的方程与抛物线方程联立,得出根与系数的关系,再由向量的坐标形式得出的表达式,再证明不等式;(2)先求出点M到直线l 的距离的表达式,再求最值,结合已知条件即可求p ,从而得出抛物线方程.[解] (1)证明:由题意,抛物线E 的焦点为F ⎝ ⎛⎭⎪⎫0,p 2,直线l 1的方程为y=k 1x +p2.由⎩⎨⎧y =k 1x +p 2,x 2=2py ,得x 2-2pk 1x -p 2=0.设A ,B 两点的坐标分别为(x 1,y 1),(x 2,y 2), 则x 1,x 2是上述方程的两个实数根.从而x 1+x 2=2pk 1,y 1+y 2=k 1(x 1+x 2)+p =2pk 21+p .所以点M 的坐标为⎝⎛⎭⎪⎫pk 1,pk 21+p 2,=(pk 1,pk 21).同理可得点N 的坐标为⎝ ⎛⎭⎪⎫pk 2,pk 22+p 2,=(pk 2,pk 22).于是=p 2(k 1k 2+k 21k 22).由题设,k 1+k 2=2,k 1>0,k 2>0,k 1≠k 2, 所以0<k 1k 2<⎝⎛⎭⎪⎫k 1+k 222=1. 故<p 2(1+12)=2p 2.(2)由抛物线的定义得|FA |=y 1+p 2,|FB |=y 2+p2,所以|AB |=y 1+y 2+p =2pk 21+2p ,从而圆M 的半径r 1=pk 21+p .故圆M 的方程为(x -pk 1)2+⎝ ⎛⎭⎪⎫y -pk 21-p 22=(pk 21+p )2, 化简得x 2+y 2-2pk 1x -p (2k 21+1)y -34p 2=0.同理可得圆N 的方程为x 2+y 2-2pk 2x -p (2k 22+1)y -34p 2=0.于是圆M ,圆N 的公共弦所在直线l 的方程为(k 2-k 1)x +(k 22-k 21)y =0.又k 2-k 1≠0,k 1+k 2=2,则l 的方程为x +2y =0. 因为p >0,所以点M 到直线l 的距离 d =|2pk 21+pk 1+p |5=p |2k 21+k 1+1|5=p ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫k 1+142+785.故当k 1=-14时,d 取最小值7p85.由题设,7p 85=755,解得p =8.故所求的抛物线E 的方程为x 2=16y . [名师点评] 解答本题的关键有以下两点:(1)充分利用k 1>0,k 2>0,k 1≠k 2时,k 1·k 2<⎝⎛⎭⎪⎫k 1+k 222; (2)注意2k 21+k 1+1>0,即d =|2k 21+k 1+1|5=2k 21+k 1+15.(A.湖州模拟)已知抛物线C :y 2=2px 的焦点为F ,抛物线C 与直线l 1:y =-x 的一个交点的横坐标为8.(1)求抛物线C 的方程;(2)不过原点的直线l 2与l 1垂直,且与抛物线交于不同的两点A ,B ,若线段AB 的中点为P ,且|OP |=|PB |,求△FAB 的面积.解:(1)由题意知交点坐标为(8,-8),∴82=2p ×8, ∴2p =8,所以抛物线方程为y 2=8x . (2)∵l 1:y =-x ,又直线l 2与l 1垂直,所以可设l 2:x =y +m ,A (x 1,y 1),B (x 2,y 2),且直线l 2与x 轴交点为M . 由⎩⎨⎧y 2=8x ,x =y +m得y 2-8y -8m =0,Δ=64+32m >0, ∴m >-2.由韦达定理,y 1+y 2=8,y 1y 2=-8m , ∴x 1x 2=y 1y 2264=m 2.由题意可知OA ⊥OB ,即x 1x 2+y 1y 2=m 2-8m =0, ∴m =8或m =0(舍), ∴l 2:x =y +8,M (8,0),故S △FAB =S △FMB +S △FMA =12·|FM |·|y 1-y 2|=3y 1+y 22-4y 1y 2=24 5.[全盘巩固]1.抛物线x 2=(2a -1)y 的准线方程是y =1,则实数a =( ) A.52 B.32 C .-12 D .-32解析:选D 把抛物线方程化为x 2=-2⎝ ⎛⎭⎪⎫12-a y ,则p =12-a ,故抛物线的准线方程是y =p 2=12-a 2,则12-a2=1,解得a =-32.2.(A.辽宁高考) 已知点A(-2,3) 在抛物线C:y2=2px的准线上,记C 的焦点为F,则直线AF的斜率为( )A.-43B.-1C.-34D.-12解析:选C 因为点A在抛物线的准线上,所以-p2=-2,所以该抛物线的焦点F(2,0),所以k AF=3-0-2-2=-34,选C.3.(B.江西高考)已知点A(2,0),抛物线C:x2=4y的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|∶|MN|=( ) A.2∶ 5 B.1∶2C.1∶ 5 D.1∶3解析:选C FA:y=-12x+1,与x2=4y联立,得xM=5-1,FA:y=-12x+1,与y=-1联立,得N(4,-1),由三角形相似知|FM||MN|=xM4-x M=15.4.设F为抛物线y2=4x的焦点,A,B,C为该抛物线上三点,若则 ( )A.9 B.6 C.4 D.3解析:选B 设A(x1,y1),B(x2,y2),C(x3,y3),又(x1-1)+(x2-1)+(x3-1)=0,即x1+x2+x3=3,=x1+x2+x3+32p=6.5.已知点M(1,0),直线l:x=-1,点B是l上的动点,过点B垂直于y轴的直线与线段BM的垂直平分线交于点P,则点P的轨迹是( ) A.抛物线 B.椭圆C.双曲线的一支 D.直线解析:选A 由点P在BM的垂直平分线上,故|PB|=|PM|.又PB⊥l,因而点P到直线l的距离等于点P到点M的距离,所以点P的轨迹是抛物线.6.(A.台州模拟)O为坐标原点,F为抛物线C:y2=42x的焦点,P为C上一点,若|PF|=42,则△POF的面积为( )A.2 B.2 2C.2 3 D.4解析:选C 设P(x0,y0),根据抛物线定义得|PF|=x0+2,所以x0=32,代入抛物线方程求得y2=24,解得|y|=26,所以△POF的面积等于12·|OF|·|y|=12×2×26=2 3.7.(B.北京高考)若抛物线y2=2px的焦点坐标为(1,0),则p=________,准线方程为________.解析:∵抛物线y2=2px的焦点坐标为(1,0),∴p2=1,解得p=2,∴准线方程为x=-1.答案:2 x=-18.(A.丽水模拟)设Q为圆C:x2+y2+6x+8y+21=0上任意一点,抛物线y2=8x的准线为l.若抛物线上任意一点P到直线l的距离为m,则m+|PQ|的最小值为________.解析:如图由抛物线定义可得,点P 到准线的距离等于其到焦点F 的距离,故问题转化为点P 到焦点的距离与到圆上点的距离之和的最小值,由圆的知识可知当且仅当点P 为圆心C 和焦点F 的连线与抛物线的交点,Q 取CF 的连线与圆的交点时,距离之和取得最小值,即m +|PQ |≥|CF |-r =-3-22+-4-02-2=41-2.答案:41-2.9.抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是________. 解析:如图,设与直线4x +3y -8=0平行且与抛物线y =-x 2相切的直线为4x +3y +b =0,切线方程与抛物线方程联立得⎩⎨⎧y =-x 2,4x +3y +b =0,消去y 整理得3x 2-4x -b =0,则Δ=16+12b =0,解得b =-43,所以切线方程为4x +3y -43=0,抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是这两条平行线间的距离d =⎪⎪⎪⎪⎪⎪8-435=43.答案:4310.已知以向量v =⎝ ⎛⎭⎪⎫1,12为方向向量的直线l 过点⎝ ⎛⎭⎪⎫0,54,抛物线C :y 2=2px (p >0)的顶点关于直线l 的对称点在该抛物线的准线上.(1)求抛物线C 的方程;(2)设A ,B 是抛物线C 上两个动点,过A 作平行于x 轴的直线m ,直线OB 与直线m 交于点N ,若+p 2=0(O 为原点,A ,B 异于原点),试求点N 的轨迹方程.解:(1)由题意可得直线l的方程为y=12x+54,①过原点垂直于l的直线方程为y=-2x.②解①②得x=-1 2 .∵抛物线的顶点关于直线l的对称点在该抛物线的准线上,∴-p2=-12×2,p=2.∴抛物线C的方程为y2=4x.(2)设A(x1,y1),B(x2,y2),N(x0,y0),由题意知y0=y1. 由+p2=0,得x1x2+y1y2+4=0,又y21=4x1,y22=4x2,解得y1y2=-8,③直线ON:y=y2x2x,即y=4y2x.④由③④及y0=y1得点N的轨迹方程为x=-2(y≠0).11.已知定点A(1,0)和直线x=-1上的两个动点E,F,且(其中O为坐标原点).(1)求动点P的轨迹C的方程;(2)过点B(0,2)的直线l与(1)中的轨迹C相交于两个不同的点M,N,若,求直线l的斜率的取值范围.解:(1)设P(x,y),E(-1,y E),F(-1,y F),∵=(-2,y E)·(-2,y F)=y E·y F+4=0,∴y E·y F=-4,①∴y-y E=0且x(-y F)-y=0,∴y E =y ,y F =-y x, 代入①得y 2=4x (x ≠0),∴动点P 的轨迹C 的方程为y 2=4x (x ≠0). (2)设l :y -2=kx (易知k 存在,且k ≠0), 联立⎩⎨⎧y =kx +2,y 2=4x ,消去x ,得ky 2-4y +8=0,Δ=42-32k >0,即k <12.令M (x 1,y 1),N (x 2,y 2),则y 1+y 2=4k ,y 1·y 2=8k,=(x 1-1,y 1)·(x 2-1,y 2)=x 1x 2-(x 1+x 2)+1+y 1y 2 =y 21·y 2216-y 21+y 224+1+y 1y 2=⎝ ⎛⎭⎪⎫y 1y 242-y 1+y 224+32y 1y 2+1 =12k+1<0,∴-12<k <0,故实数k 的取值范围为(-12,0).12.(A.杭州模拟)在平面直角坐标系xOy 中,设点F ⎝ ⎛⎭⎪⎫12,0,直线l :x =-12,点P 在直线l 上移动,R 是线段PF 与y 轴的交点,RQ ⊥FP ,PQ ⊥l . (1)求动点Q 的轨迹C 的方程;(2)设圆M 过A (1,0),且圆心M 在曲线C 上,TS 是圆M 在y 轴上截得的弦,当M 运动时,弦长|TS |是否为定值?请说明理由.解:(1)依题意知,点R是线段FP的中点,且RQ⊥FP,∴RQ是线段FP的垂直平分线.∵|PQ|是点Q到直线l的距离.点Q在线段FP的垂直平分线上,∴|PQ|=|QF|.故动点Q的轨迹是以F为焦点,l为准线的抛物线,其方程为y2=2x(x>0).(2)弦长|TS|为定值.理由如下:取曲线C上点M(x0,y0),M到y轴的距离为d=|x0|=x0,圆的半径r=|MA|=x0-12+y20,则|TS|=2r2-d2=2y20-2x0+1,因为点M在曲线C上,所以x0=y2 02,所以|TS|=2y20-y20+1=2,是定值.[冲击名校]已知直线y=-2上有一个动点Q,过点Q作直线l1垂直于x轴,动点P在l1上,且满足OP⊥OQ(O为坐标原点),记点P的轨迹为C.(1)求曲线C的方程;(2)若直线l2是曲线C的一条切线,当点(0,2)到直线l2的距离最短时,求直线l2的方程.解:(1)设点P的坐标为(x,y),则点Q的坐标为(x,-2).∵OP⊥OQ,∴当x=0时,P,O,Q三点共线,不符合题意,故x≠0.当x ≠0时,得k OP ·k OQ =-1,即y x ·-2x =-1,化简得x 2=2y ,∴曲线C 的方程为x 2=2y (x ≠0).(2)∵直线l 2与曲线C 相切,∴直线l 2的斜率存在.设直线l 2的方程为y =kx +b ,由⎩⎨⎧ y =kx +b ,x 2=2y ,得x 2-2kx -2b =0.∵直线l 2与曲线C 相切,∴Δ=4k 2+8b =0,即b =-k 22.点(0,2)到直线l 2的距离d =|-2+b |k 2+1=12·k 2+4k 2+1=12⎝ ⎛⎭⎪⎫k 2+1+3k 2+1≥12×2k 2+1·3k 2+1 = 3.当且仅当k 2+1=3k 2+1,即k =±2时,等号成立.此时b =-1.∴直线l 2的方程为2x -y -1=0或2x +y +1=0.[高频滚动]1.已知点F 1(-2,0),F 2(2,0),动点P 满足|PF 2|-|PF 1|=2,当点P的纵坐标是12时,点P 到坐标原点的距离是( ) A.62 B.32C. 3 D .2 解析:选A 由已知可得c =2,a =1,∴b =1.∴双曲线方程为x 2-y 2=1(x ≤-1).将y =12代入,可得点P 的横坐标为x =-52. ∴点P 到原点的距离为 ⎝ ⎛⎭⎪⎫-522+⎝ ⎛⎭⎪⎫122=62. 2.已知双曲线x 26-y 23=1的左,右焦点分别为F 1,F 2,点M 在双曲线上且MF 1⊥x 轴,则F 1到直线F 2M 的距离为________.解析:由题意知F 1(-3,0),设M (-3,y 0),代入双曲线方程求得|y 0|=62,即|MF 1|=62.又|F 1F 2|=6,利用直角三角形性质及数形结合得F 1到直线F 2M 的距离为d =|MF 1|·|F 1F 2||MF 1|2+|F 1F 2|2=62×664+36=65.。
高中数学圆锥曲线复习(三)——抛物线

圆锥曲线复习(三)------抛物线焦点弦 过px y 22=()0>p 的焦点弦AB A(1x ,1y )B(2x ,2y )(1),sin 2221αp p x x AB =++=(2)221p y y -=,4221p x x =, (3)以AB 为直径的圆与准线相切(4)抛物线的通径:通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为2p ,通径是过焦点最短的弦. 三、直线与抛物线的位置关系(1)将直线方程与抛物线方程联立消去y (或消去x )得:20ax bx c ++=或20ay by c ++=(1)0a =或⇔>∆0相交;(2)⇔=∆0相切;(3)⇔<∆0相离 直线与抛物线只有一个公共点:相交或相切。
此时相交 该直线与对称轴平行。
(2)设直线可设()00,y y k x x y kx b -=-=+和()000,x x y y m y y x my a --=-=+抛物线px y 22=上的点可标为()00,y x 或⎪⎪⎭⎫ ⎝⎛02,2y p y 或()pt pt 2,22()R t ∈ 四、例题讲解题型一、抛物线的标准方程例1、(1)抛物线24ax y =的焦点坐标是_____________.(2)焦点在直线042=--yx 上的抛物线的标准方程是_______________.其对应的准线方程是_________________.(3) 以抛物线()022>=p py x 的一条焦点弦为直径的圆是08622=--+y x y x ,则=p _______________(4)到y 轴的距离比到点()0,2的距离小2的动点的轨迹方程是_____________解:(1)焦点F ⎪⎭⎫⎝⎛a 161,(2)因为焦点在坐标轴上,所以焦点为()0,4或()2,0-,故抛物线的标准方程为xy 162=或y x 82-=,对应的准线方程是2,4=-=y x 。
高中数学第二章圆锥曲线与方程抛物线的术语解释素材11

抛物线- 术语解释
准线、焦点:抛物线是平面内到一定点和到一条不过此点的定直线的距离相等的点的轨迹。
这一定点叫做抛物线的焦点,定直线叫做抛物线的准线。
轴:抛物线是轴对称图形,它的对称轴简称轴。
顶点:抛物线与它的轴的交点叫做抛物线的顶点.
弦:抛物线的弦是连接抛物线上任意两点的线段。
焦弦:抛物线的焦弦是经过抛物线焦点的弦。
正焦弦:抛物线的正焦弦是垂直于轴的焦弦。
直径:抛物线的直径是抛物线一组平行弦中点的轨迹。
这条直径也叫这组平行弦的共轭直径。
主要直径:抛物线的主要直径是抛物线的轴。
抛物线即把物体抛掷出去,落在远处地面,这物体在空中经过的曲线.。
圆锥曲线方程抛物线

抛物线1.定义:平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫抛物线。
点F 叫做抛物线的焦点,直线l 叫做抛物线的准线。
2.标准方程坐标系:使坐标轴经过点F 且垂直于直线l 于K ,并使原点与线段KF 的中点重合。
设|KF|=p (p>0),则抛物线的标准方程及焦点坐标、准线方程如下表: 3.几何性质以抛物线y 2=2px (p>0)为例。
(1)范围。
x ≥0,|y|随x 增大而增大,但无渐近线。
(2)对称性。
关于x 轴对称。
(对称轴与准线垂直) (3)顶点。
对称轴与抛物线的交点。
(4)离心率。
同椭圆、双曲线离心率定义。
e=1(注e 与抛物线开口大小无关,开口大小由p 值确定,画特征草图时,先画出通径(2p )过焦点且与对称轴垂直的弦)。
4.几个重要的解析结果:(1)平行抛物线对称轴的直线和抛物线只有一个交点。
(2)焦点弦两端点的纵坐标乘积为常数即y 1y 2=-p 2(p>0)(4)焦点弦长公式:|AB|=x 1+x 2+p (x 1、x 2分别为A 、B 的横坐标)或||sin ()AB pAB p =222θθ为的倾斜角,由此知,通径长为焦点弦长的最小值: 1、 抛物线28y x =的焦点到准线的距离是()A .1B .2C .4D .82、 设抛物线28y x =上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是()A .4B .6C .8D .123、 设抛物线y 2=8x 的焦点为F ,准线为l ,P 为抛物线上一点,PA ⊥l ,A 为垂足.如果直线AF 的斜率为么|PF|=()A ..8C ..164、 已知抛物线22(0)y px p =>的准线与圆22670x y x +--=相切,则p 的值为()A .12B .1C .2D .4 5、 已知抛物线22(0)y px p =>,过其焦点且斜率为1的直线交抛物线与A 、B 两点,若线段AB 的中点的纵坐标为2,则该抛物线的准线方程为()A .1x =B .1x =-C .2x =D .2x =- 6、 已知抛物线x y C =2:与直线1:+=kx y l ,“0≠k”是“直线l 与抛物线C 有两个不同交点”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件7.以抛物线24=y x 的焦点为圆心,且过坐标原点的圆的方程为( )A.2220++=x y xB.220++=x y x C.220+-=y x χ D.2220+-=x y x8已知抛物线22(0)y px p =>的焦点为F ,点111(,)P x y 、222(,)P x y 、333(,)P x y 在抛物线上,且2132x x x =+,则有()A.123FP FP FP +=B.222123FPFP FP += C.2132FP FP FP =+ D.2213FPFP FP =⋅ 9..设抛物线2y =2x 的焦点为F ,过点M (3,0)的直线与抛物线相交于A ,B 两点,与抛物线的准线相交于C ,BF =2,则∆BCF 与∆ACF 的成面积之比BCFACFS S ∆∆=(A )45 (B )23(C )47(D )1210.设斜率为2的直线l 过抛物线)0(2≠=a ax y 的焦点F ,且和y 轴交于点A ,若OAF ∆(O 为坐标原点)的面积为4,则抛物线方程为(A )42±=y (B )x y 82±= (C )x y 42=(D )x y 82=11在平面直角坐标系xOy 中,已知抛物线关于x 轴对称,顶点在原点O ,且过点P (2,4),则该抛物线的方程是. 12若直线a x -y +1=0经过抛物线x y 42=的焦点,则a=.13.抛物线x y =2的准线方程是14.过抛物线)0(22>=p px y 的焦点F 作倾斜角为450的直线交抛物线于A 、B 两点,线段AB 的长为8,则=p .15.过点A (1,0)作倾斜角为4π的直线,与抛物线22y x =交于M N 、两点,则MN =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学专题复习——圆锥曲线(抛物线)【知识网络】1.掌握抛物线的定义、标准方程和抛物线的简单几何性质. 2.了解抛物线简单应用. 3.进一步体会数形结合思想. 【典型例题】[例1](1)设R a a ∈≠,0,则抛物线24ax y =的焦点坐标为( )A、 (a,0) B、 (0,a) C、 (0,a161) D、 随a 的符号而定 (2)顶点在原点,准线为y=2的抛物线方程为(D)A .y 2=8xB .y 2=-8xC .x 2=8yD .x 2=-8y (3)已知:P为抛物线y=241x 上的任意一点,F为抛物线的焦点,点A坐标为(1,1),则|PF |+|PA |的最小值为 ( ) A .1617B .2C .12+D .12-(4)已知抛物线y 2=4x 过点P (4,0)的直线与抛物线相交于A (x 1,y 1),B(x 2,y 2)两点,则y 12+y 22的最小值是 . (5)已知抛物线C 1:y=2x 2与抛物线C 2关于直线y=-x 对称,则C 2的准线方程是 .[例2] 抛物线的焦点F 在x 轴上,直线y =-3与抛物线相交于点A,5=AF ,求抛物线的标准方程.[例3]如图,抛物线px y 22=的弦21P P 交x 轴于点Q ,过1P 、2P 分别作x 轴的垂线,垂足为M 、N ,求证:OQ 是OM 和ON 的比例中项.[例4] 如图,M (a ,0)(a >0)是抛物线y 2=4x 对称轴上一点,过M 作抛物线的弦AMB ,交抛物线与A ,B .(1)若a =2,求弦AB 中点的轨迹方程;(2)过M 作抛物线的另一条割线CMD (如图),与抛物线交于CD ,若AD 与y 轴交与点E ,连ME ,BC ,求证:ME ∥BC .【课内练习】1.以抛物线)0(22>=p px y 的焦半径PF 为直径的圆与y 轴位置关系为( )A、 相交 B、 相离 C、 相切 D、 不确定 2.抛物线方程为7x +8y 2=0,则焦点坐标为( ) A .(716 ,0) B .(-732 ,0) C .(0,- 732 ) D .(0,- 716 )3.抛物线y=-x 2上的点到直线4x +3y -8=0距离的最小值是 ( ) A .43 B .75 C .85 D .34.设O 为坐标原点,F 为抛物线y 2=4x 的焦点,A 为抛物线上一点,若OA → ·AF →=-4,则A 点坐标为 ( )A .(2,±2 2 )B .(1,±2)C .(1,2)D .(2,2 2 )5.抛物线y 2=-2px(p >0)上一点横坐标为-9,它到焦点的距离为10,这点的坐标为 . 6.过抛物线x y =2的焦点F 的直线m 的倾斜角m ,4πθ≥交抛物线于A 、B 两点,且A 点在x 轴上方,则|FA|的取值范围是 .7.一动圆M和直线:4l x =-相切,并且经过点(4,0)F ,则圆心M的轨迹方程是 . 8.直线l 过抛物线)0(22>=p px y 的焦点且与x 轴垂直,若l 被抛物线截得的线段长为6,求p 的值.9.已知直线l :y= 3 x +4被抛物线x 2=2p y(p >0)截得的弦长为4 3 .(1)求抛物线的方程;(2)在该抛物线上位于直线l 下方的部分中,求一点M ,使M 到l 的距离最远.10.已知抛物线y 2=4ax(a >0)的焦点为A ,以B (a+4,0)为圆心,|AB|长为半径画圆,在x 轴上方交抛物线于M 、N 不同的两点,若P 为MN 的中点.(1)求a 的取值范围; (2)求|AM|+|AN|的值;(3)问是否存在这样的a 值,使|AM|、|AP|、|AN|成等差数列?抛物线 A 组1.顶点为原点,抛物线对称轴为y 轴,且过点(-4,5),则抛物线的准线方程为( ) A .y=-45 B .y=45 C .x=-45 D .x=452.已知点P 是抛物线22y x =上的动点,点P 在y 轴上的射影是M ,点A 的坐标是7(,4)2A ,则||||PA PM +的最小值是( ) A .112 B .4 C .92D .53.过点(-1,0)作抛物线y=x 2+x +1的切线,则其中一条切线为 ( )A .2x +y +2=0B .3x -y +3=0C .x +y +1=0D .x -y +1=04.抛物线型拱桥的顶点距水面2m 时,水面宽8m ,若水面升1m ,此时水面宽为 . 5.过抛物线y 2=4x 焦点的直线交抛物线于A ,B 两点,已知|AB|=10,O 为坐标原点,则△OAB 的重心的坐标为 .6.求以原点为顶点,坐标轴为对称轴,且过点P(2,-4)的抛物线的方程.7.已知抛物线C 的顶点在原点,焦点F 在x 轴正半轴上,设A ,B 是抛物线C 上的两个动点(AB 不垂直于x 轴),且|AF|+|BF|=8,线段AB 的垂直平分线恒经过定点Q (6,0),求此抛物线方程.8.已知抛物线x y 22=及定点),0,1(),1,1(-B A M 是抛物线上的点,设直线BM AM ,与抛物线的另一交点分别为21,M M .求证:当点M 在抛物线上变动时(只要21,M M 存在且1M 与2M 是不同两点),直线21M M 恒过一定点,并求出定点的坐标B 组1.抛物线24y x =上的一点M 到焦点的距离为1,则点M 的纵坐标是( )A .1716 B .1516 C .78D .0 2.已知两点M (-2,0),N (2,0),点P 为坐标平面内的动点,满足|MN → |·|MP → |+MN → ·NP →=0,则动点P (x,y )的轨迹方程是 ( ) A .y 2=8x B .y 2=-8x C .y 2=4x D .y 2=-4x3.已知P 是抛物线y=2x 2+1上的动点,定点A (0,―1),点M 分PA →所成的比为2,则点M 的轨迹方程是( ) A 、y=6x 2―31 B 、x=6y 2-31 C 、y=3x 2+31D 、y=―3x 2―1 4.有一个正三角形的两个顶点在抛物线y 2=2 3 x 上,另一个顶点在原点,则这个三角形的边长是 .5.对正整数n ,设抛物线x n y )12(22+=,过)0,2(n P 任作直线l 交抛物线于n n B A ,两点,则数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⋅)1(2n n n 的前n 项和公式是 .6.焦点在x 轴上的抛物线被直线y=2x +1截得的弦长为15 ,求抛物线的标准方程.7.定长为3的线段AB 的两个端点在抛物线y 2=x 上移动,AB 的中点为M ,求点M 到y 轴的最短距离,并求出点M 的坐标.8.在直角坐标系中,已知点⎪⎭⎫⎝⎛0,2p F (p>0), 设点F 关于原点的对称点为B ,以线段FA 为直径的圆与y 轴相切. (1) 点A 的轨迹C 的方程;(2) PQ 为过F 点且平行于y 轴的曲线C 的弦,试判断PB 与QB 与曲线C 的位置关系. 21M M 是曲线C 的平行于y 轴的任意一条弦,若直线FM1与BM2的交点为M ,试证明点M在曲线C 上.抛物线【典型例题】例1 (1)C .提示:注意抛物线的开口方向. (2)D .提示:逆用准线方程公式.(3)B .提示:用抛物线定义结合三角形的性质.(4)32.提示:设出过点P 的直线方程与抛物线方程联列,用韦达定理及配方法. (5)x=18 .提示:在抛物线方程中,先用-x 换y ,同时用-y 换x .得到对称抛物线的标准方程.例2. 设所求焦点在x 轴上的抛物线的标准方程为:)0(22≠=p px y ,)3,(-m A 则由抛物线的定义得25p m AF +==,又pm 2)3(2=- 所以9,1±=±=p p故所要求抛物线的方程为:x y x y 18,222±=±=例3、设点1P 、2P 的坐标分别为),(11y x 、),(22y x ,则直线21P P 的方程为121121x x x x y y y y --=-- ①由于点Q是直线21P P 和x 轴的交点,令y =0得点Q的横坐标为 212112y y y x y x x --=.点1P 和2P 分别在x 轴的上方和下方,不妨设点1P 在x 轴的上方,点2P 在x 轴的下方,则112px y =,222px y -=.代入①,得2121122222px px px x px x x ++==21x x ,所以ON OM OQ =2即证得OQ 是OM 和ON 的比例中项. 例4、(1)当AB 斜率存在时,由a=2,设其方程为 y=k (x -2),弦AB 中点为(x 0,y 0)由24(2)y x y k x ⎧=⎨=-⎩得 22224(1)40k x k x k -++=△=16(k 2+1)2-16k 4=32k 2+16>0212022120122222212(22)22x x k x k k y y y kx k kx k k ⎧++===+⎪⎪⎨+⎪==-+-=⎪⎩消去k 得y 02=2x 0-4(x 0>2)当AB 斜率不存在时,其方程为x=2,与抛物线相交,中点为(2,0),满足y 02=2x 0-4. 综上所述,弦AB 中点的轨迹方程y 2=2x -4.(2)证明:设A (t 12,-2t ),B (t 22, 2t 2),C (t 32,-2t 3),D(t 42,-2t 4),其中t 1,t 2,t 3,t 4均为正数, 用两点式求得AB 的方程为 y(t 2-t 1)+2t 1t 2=2xCD 的方程为y (t 4-t 3)+2t 3t 4=2xAB ,CD 都经过点M ,故t 1t 2= t 3t 4=a ,AD 的方程为y(t 4-t 1)+2t 1t 4=2x AD 与y 轴交点为E (0,14142t t t t -) k ME =14412()t t a t t -而k BC =23222323222t t t t t t +=--=142a a t t -=14412()t t a t t - ∴k ME =k BC ,ME ∥BC .【课内练习】1.C .提示:利用抛物线的定义.2.B .提示:先将方程化成标准形式.3.A .提示:设出与已知直线平行且与抛物线相切的直线方程,用△法求出直线方程,再求两平行线间的距离.4.B .提示:依据对称性排除C ,D ,再用坐标法排除A . 5.(-9,±6).提示:利用抛物线的定义先求出p . 6.]221,41(+.提示:联想抛物线定义. 7.y 2=16x .提示:运用抛物线定义. 8.p=3.提示:运用通径的性质.9.(1)抛物线的方程为x 2= 23 y ;(2)所求点M的坐标为(3,12 )10.(1) 设M (x 1,y 1 ),N (x 2,y 2),P (x 0,y 0 ) 则[ x —(a +4)]2 + y 2 = 16 ( y≥0)用y 2 = 4ax (a>0) 代入得x 2 + 2 (a —4)x + 8a + a 2 = 0 由4△= ( a —4)2 — (8a + a 2) > 0得:0 < a < 1 (2) ∵A 为焦点 ∴ |AM| + |AN| = (x 1 + a ) + (x 2 + a) = x 1 + x 2 + 2a = 8—2a + 2a = 8.(3) 若存在a 使使|AM|、|AP|、|AN|成等差数列即 2|AP| = |AM| + |AN| = 8 ∴ |AP| = 4则 (x 0—a )2 + y 02 = 16,x 0 =221x x + = 4—a ,y 0 =21(y 1 + y 2) ( 4—2a )2 + a [ 8—∴ a = 1 与 0 < a < 1 矛盾 故a 不存在.抛物线 A 组1.A .提示:用待定系数法先求出抛物线的方程. 2.C .提示:联想抛物线定义.3.D .提示:设出过定点的直线方程与抛物线方程联列,用△法求解. 4.4 2 .提示:建立坐标系,写抛物线方程. 5.83 .提示:由|AB|=10,求出A ,B 两点横坐标之和.6.由于Q(2,-4)在第四象限且坐标轴是对称轴,可设抛物线方程为)0(22>=p px y 或)0(22>=p py x 将Q点的坐标代入,得4=p 或21=p 所以所要求的抛物线的方程为x y 82=或y x -=27.设抛物线方程为y 2=2px(p >0),其准线为x=-2p . 设A (x 1,y 1),B(x 2,y 2),由|AF|+|BF|=8得:x 1+x 2=8-p . ∵Q 在AB 的中垂线上,∴QA=QB即(x 1-6)2+y 12=(x 2-6)2+y 22,又y 12=2px 1, y 22=2px 2, ∴(x 1-x 2)(x 1+x 2-12+2p)=0.∵AB 与x 轴不垂直,∴x 1≠x 2,x 1+x 2-12+2p=0. ∴p=4,即抛物线的方程为y 2=8x .8.设),2(020y y M ,),2(1211y y M ,),2(2222y y M ,因为1,,M M A 三点共线,所以12122200202101--=--y y y y y y ,即21120001--=+y y y y ,即2)1)((20001-=-+y y y y ,求出12001--=y y y 同理可求出022y y =, 又因为设直线21M M 过定点),(y x U ,则点21,,M M U 共线,所以222211222121y x y y y y y y --=--,即2112121y x y y y y --=+,即211212))((y x y y y y -=-+,即02)(2121=++-x y y y y y , 所以由)3(02)()2(2)1(12212102001 =++-=--=⎪⎩⎪⎨⎧x y y y y y y y y y y消去21,y y 得042)1(2)2(020=-+-+-y y x y y x上式对任意0y 恒成立,所以得到⎪⎩⎪⎨⎧===212y x y x 所以所求的直线21M M 恒过定点)2,1(.B 组1.B .提示:用抛物线的定义. 2.B .提示:坐标代入. 3.B .提示:用坐标转移法.4.12.提示:有两个顶点关于x 轴对称,进而得到直线的倾斜角是6π和56π.5.)1(+-n n .提示:求出数列的通项公式.6.y 2=12x 或y 2=-4x .提示:设抛物线方程后,用韦达定理及弦长公式.7.M(545,4).提示:数形结合得到当且仅当AB 过焦点时M 到y 轴距离最小.设出此时的直线方程,用弦长公式解得直线AB 的斜率,并得到AB 的坐标.8.(1)解:设A (x,y ),则22p x 2y )2px (22+=+-,化简得:y 2=2px(2)由对称性知,PB 和QB 与曲线C 的位置关系是一致的,由题设,不妨P (p ,2p)而1)2p (2p 0p k PB =---=∴直线PB 的方程为y=x+2p ,代入y 2=2px ,消去y 得到关于x 的一元二次方程 x 2+px+4p 2=0,∆=0 ∴直线PB 和QB 均与抛物线相切.(3)由题意设)t ,p 2t (M 21,)t ,p2t (M 22-,则直线FM1:)2px (2p p 2tty 2--=;直线BM2:)2p x (2p p 2tty 2++-=联立方程组解得M 点坐标为23t2p (,)t p 2-,经检验,)2(2)(2322tp p t p =- ,∴点M 在曲线C 上.。
