构造全等三角形的六种常用方法
构造全等三角形的四种技巧

构造全等三角形的四种技巧在几何学中,全等三角形是一个非常重要的概念。
全等三角形是指两个或两个以上的三角形,它们的形状和大小完全相同。
理解并能够构造全等三角形,对于解决各种几何问题有着至关重要的作用。
以下是构造全等三角形的四种技巧:利用公理:全等三角形的公理是:如果两个三角形的三边对应相等,那么这两个三角形全等。
这个公理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后根据这些边长画出两个三角形。
这两个三角形的形状和大小将会完全相同。
利用角平分线:角平分线定理指出,一个角的平分线将对应的边分为两段,这两段与角的两边形成的两个小三角形是全等的。
通过这个定理,你可以通过一个角的平分线,构造出一个全等三角形。
利用中垂线:中垂线定理指出,一条中垂线将一个线段分为两段,这两段与线段的两端形成的两个小三角形是全等的。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后通过中垂线将这些边分为两段。
这样,你就可以得到两个全等的三角形。
利用平行线:平行线定理指出,如果两条平行线被第三条直线所截,那么截得的对应线段成比例。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后在两条平行线上画出对应的线段。
由于这些线段成比例,因此它们形成的两个小三角形是相似的。
如果这些相似三角形的对应边长度相等,那么它们就是全等的。
以上就是构造全等三角形的四种技巧。
理解和掌握这些技巧,对于解决各种几何问题有着重要的作用。
已知两个三角形全等,则它们对应边上的高也________;对应角平分线也________;对应边上的中线也________。
两个直角三角形全等,除了用定义外,还可以用以下________判定。
已知三角形ABC全等三角形DEF,且AB=18cm,BC=20cm,CA=15cm,则DE=________cm,DF=________cm,EF=________cm.做衣服需要依据身体部位的大小来选择布料,而教学则需要依据学生原有的知识基础来选择教学方法。
构造全等三角形的方法技巧

方法1 角形
利用“角平分线”构造全等三ห้องสมุดไป่ตู้
【方法归纳】 因角平分线本身已经具备 全等的三个条件中的两个(角相等和公共 边相等),故在处理角平分线问题时,常 作以下辅助线构造全等三角形: (1)在角的两边截取两条相等的线段; (2)过角平分线上一点作角两边的垂线.
思1.如图,AB∥CD,BE平分 ∠ABC,CE平分∠BCD,点E在AD 上,求证:BC=AB+CD. 考
2.如图,已知∠AOB=90°,OM是 ∠AOB的平分线,三角尺的直角顶点 P在射线OM上滑动,两直角边分别与 OA,OB交于点C,D,求证:PC= PD.
方法2 利用“截长补短法”构造全等 三角形
【方法归纳】 截长补短法的具体做法 :在某一条线段上截取一条线段与特定 线段相等,或将某条线段延长,使之与 特定线段相等,再利用三角形全等的有 关性质加以说明.这种方法适用于证明 线段的和、差、倍、分等类的题目.
3.如图,在△ABC中,AD平分 ∠BAC,∠C=2∠B,试判断AB, AC,CD三者之间的数量关系,并 说明理由.(想一想,你会几种方法)
方法3 利用“倍长中线法”构造全 等三角形
【方法归纳】 将中点处的线段延长 一倍,然后利用SAS证三角形全等.
6.已知:如图,AD,AE分别是 △ABC和△ABD的中线,且BA= BD.求证:AE=AC.
构造全等三角形的技巧大全【难】——八年级数学上册同步精华

第8讲 构造全等三角形的技巧【难】【补形法】 1、【★★】如图,在四边形ABCD 中,BD 平分∠ABC ,∠BAD+∠C=180°,求证:AD=CD 。
2、【★★仿上题】如图,在四边形ABCD 中,BC >BA ,AD=CD ,BD 平分∠ABC ,求证:∠A+∠C=180°.【难点突破】有角平分线时的辅助线1——作边的垂线,可得两组全等三角形3、【★★】已知:如图,在△ABC 中.∠BCA=90°,AC=BC ,AE 平分∠BAC ,BE ⊥AE .求证:BE=21AD .【难点突破】有角平分线时的辅助线2——作角平分线的垂线,可得两组全等三角形4、【★★】如图,∠AOB=90°,OM 平分∠AOB ,将直角三角板的顶点P 在射线OM 上移动,两直角边分别与OA 、OB 相交于点C 、D ,问PC 与PD 相等吗?试说明理由.【难点突破】有两个内角互补的四边形——当图中∠P+∠O=180时,∠D=∠ACP 。
为什么?5、【★★★】如图,四边形ABCD 中,AB=AD ,AC=5,∠DAB= ∠DCB=90°,则四边形ABCD 的面积为____。
【难点突破】求不规则图形面积的重要方法——图形拼接。
6、【仿上题,★★★】如图,在四边形ABCD中,AB=AD ,∠BAD=∠BCD =90°,若AC=6,则四边形ABCD 的面积为________.【难点突破】和上题完全一样,换个方向就不认识了! 7、【★★★】如图,在直角梯形ABCD 中,AD//BC ,∠C =90°,AD =5,BC =9,以A 为中心将腰AB 顺时针旋转90°至AE ,连接DE ,求△ADE 的面积【难点突破】旋转——对应边相等。
(AE=AB )8、【★★★】如图,在△ABC 中,∠ACB=90°,AB=2,点D 是线段AC 上的点,点E 是线段CB 延长线上的点,且BE=AD ,连接DE 交AB 于点F ,过点D 作DG ⊥AB ,垂足为G ,则线段FG 的长为_________.【难点突破】给你相等的线段就是要构造全等三角形。
构造全等三角形的六种常用方法课件

构造方法简介
01
02
03
04
尺规作图法
利用尺规作图工具,通过已知 条件构造全等三角形。
翻折法
将已知三角形沿某条直线翻折, 得到与原三角形全等的三角形。
平移法
将已知三角形沿某方向平移一 定距离,得到与原三角形全等
的三角形。
旋转法
将已知三角形绕某点旋转一定 角度,得到与原三角形全等的
三角形。
02 方法一:SSS全 等法
感谢观看
拓展延伸:其他构造方法及应用场景
构造中位线
利用三角形中位线性质构 造全等三角形,常用于证 明线段相等或倍长中线等 问题。
构造角平分线
利用角平分线性质构造全 等三角形,常用于证明角 相等或线段成比例等问题。
构造垂直平分线
利用垂直平分线性质构造 全等三角形,常用于证明 线段相等或点共圆等问题。
THANKS
判定条件
两个三角形中,两个角及这两个角的夹边分别相等,则这两个三角形全等。
构造步骤这两个角的夹边相等,最后根据ASA判定条件证明两个三角形全等。
示例
在△ABC和△ADE中,∠BAC=∠DAE,∠B=∠D,AB=AD。根据ASA全等法,可以判定△ABC≌△ADE。
应用场景分析
1 2 3
解决角度和边长问题 当题目中给出两个角和它们的夹边相等时,可以 利用ASA全等法证明两个三角形全等,从而解决 与角度和边长相关的问题。
构造全等三角形 在几何证明题中,有时需要构造全等三角形以证 明某些线段或角度相等。ASA全等法是构造全等 三角形的常用方法之一。
辅助线策略 当遇到复杂的几何问题时,可以通过作辅助线构 造全等三角形,将问题转化为已知的全等三角形 问题,从而简化解题过程。
三角形全等添加辅助线的5种常用方法

三角形全等添加辅助线的5种常用方法
三角形全等的证明及相关问题,是初中几何部分的基础,也是重点和难点,不管是在中考还是平时的考试中,都是高频出现。
全等三角形的基础知识点就那么几条,很容易掌握,但是一般考试中的题目,不可能直接给出几组条件让我们直接写出证明过程,很多时候都要经过分析思考,添加辅助线,才能得到全等三角形。
下面就简单介绍一下构造全等三角形的五种常用方法。
一、等腰三角形三线合一法
当我们遇到等腰三角形(等边三角形)相关题目时,用三线合一性质,很容易找出思路。
它的原理就是利用三角形全等变换中的对折重叠。
我们来看一个例题:
二、倍长中线法
遇到一个中点的时候,通常会延长经过该中点的线段。
倍长中线指延长中线至一点,使所延长部分与该中线相等,并连接该点与这一条边的一个顶点,得到两个三角形全等。
如图所示,点D为△ABC边BC的中点.延长AD至点E,使得DE=AD,并连接BE,则△ADC≌△EDB(SAS)。
我们来看一个例题:
三、遇角平分线作双垂线法
在题中遇见角平分线,做双垂直,必出全等三角形。
可以从角平分线上的点向两边作垂线,也可以过角平分线上的点作角平分线的垂线与角的两边相交。
在很多综合几何题当中,关于角平分线的辅助线添加方法最常用的就是这个。
看看在具体题目中怎么操作吧!
四、作平行线法
在几何题的证明中,作平行线的方法也非常实用,一般来讲,在等腰、等边这类特殊的三解形中,作平行线绝对是首要考虑。
五、截长补短法
题目中出现线段之间的和、差、倍、分时,考虑截长补短法;截长补短的目的是把几条线段之间的数量关系转换为两条线段间的等量关系。
全等三角形的构造技巧(2020版)

全等三角形的构造技巧一、利用角平分线,构造全等三角形【方法剖析】因为角平分线本身已经具备全等的三个条件中的两个(角相等和公共边相等),故在处理角平分线问题时,常作以下辅助线构造全等三角形:(1)在角的两边截取两条相等的线段;(2)过角平分线上一点作角两边的垂线;(3)延长角平分线的垂线.(一)在角两边截取相等线段例1.如图,AB ∥CD ,BE 平分∠ABC ,CE 平分∠BCD ,点E 在AD 上,求证:BC =AB +CD.证明:在BC 上截取BF =AB ,连接EF.∵∠ABC 、∠BCD 的平分线交AD 于点E ,∴∠ABE =∠FBE ,∠BCE =∠DCE ,在△ABE 和△FBE 中,⎩⎪⎨⎪⎧AB =FB ,∠ABE =∠FBE ,BE =BE ,∴△ABE ≌△FBE.∴∠BAE =∠BFE.∵AB ∥CD ,∴∠BAE +∠CDE =180°.∴∠BFE +∠CDE =180°.∵∠BFE +∠CFE =180°,∴∠CFE =∠CDE.在△FCE 和△DCE 中,⎩⎪⎨⎪⎧∠CFE =∠CDE ,∠FCE =∠DCE ,CE =CE ,∴△FCE ≌△DCE.∴CF =CD.∴BC =BF +CF =AB +CD.练习:1.如图,BC >AB,BD 平分∠ABC 且AD=DC,求证: ∠A+∠C=1800. 分析:在边BC 上截取AB=BE,连接DE,则△BAD ≌△BED,这样,AD 转移到了DE 的位置,∠A 与∠C 就建立了联系。
也可看成 △BAD 翻折到了△BED 的位置。
(二)利用角平分线的性质,过角平分线上一点作角两边的垂线例1.如图,∠AOB =90°,将三角尺的直角顶点落在∠AOB 的平分线上的任意一点P ,使三角尺的两条直角边与∠AOB 的两边分别相交于点E 、F ,试证PE =PF.图1 图2分析:如图1,因为OC 是角平分线,所以本题可以过P 点作PM ⊥OA 于M ,PN ⊥OB 于N ,不难发现只要证明△PME ≌△PNF ,即可得到PE =PF ,根据∠PME =∠PNF =90°、PM =PN(角平 B A M N E F O P BA E F O P G AB C E DA B C E F D 分线性质)、∠MPE =∠NPF 这三个条件,利用ASA 可以证明△PME ≌△PNF 。
构造全等三角形的常用方法
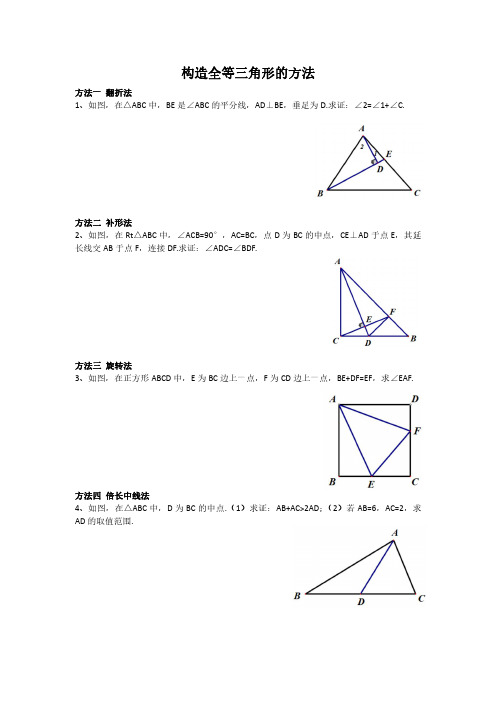
构造全等三角形的方法
方法一翻折法
1、如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.
方法二补形法
2、如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
方法三旋转法
3、如图,在正方形ABCD中,E为BC边上一点,F为CD边上一点,BE+DF=EF,求∠EAF.
方法四倍长中线法
4、如图,在△ABC中,D为BC的中点.(1)求证:AB+AC>2AD;(2)若AB=6,AC=2,求AD的取值范围.
方法五截长补短法
5、如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD 上的点,且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系并证明.
方法六作垂线法
6、如图,∠AOB=90°,OM平分∠AOB,直角三角板的顶点P在射线OM上移动,两直角边分别与OA,OB相交于点C、D,问PC与PD相等吗?试说明理由.
方法七作平行线法
7、如图,△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC 交AC于点Q.求证:AB+BP=BQ+AQ.。
初中数学——构造全等三角形的五种常用方法

所以∠1=∠2. ∠1=∠2,
在△ACD 和△CBG 中,AC=CB, ∠ACD=∠CBG=90°,
所以△ACD≌△CBG(ASA). 所以∠ADC=∠G,CD=BG. 因为点 D 为 BC 的中点,所以 CD=BD.所以 BD=BG. 因为∠DBG=90°,∠DBF=45°,
所以∠GBF=∠DBG-∠DBF=90°-45°=45°.
解:如图,过点B作BG⊥BC交CF的延长线于点G. 因为∠ACB=90°,所以∠2+∠ACF=90°. 因为CE⊥AD, 所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°. 因为CE⊥AD,所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
在△AEH 和△AEF 中,AE=AE, EH=EF,
所以△AEH≌△AEF(SSS).
所以∠EAH=∠EAF.
所以∠EAF=12∠HAF=45°.
返回
方 法 4 倍长中线法
4.如图,在△ABC中,D为BC的中点.若AB=5, AC=3,求AD长度的取值范围. 解:如图,延长AD至点E,使DE= AD,连接BE. 因为D为BC的中点,所以CD=BD.
第四章 三角形
构造全等三角形的五种常用方法
方 法 1 翻折法
1.如图,在△ABC中,BE是∠ABC的平分线, AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
解:如图,延长AD交BC于点F(相当于将AB边向下翻 折,与BC边重合,A点落在F点处,折痕为BE). 因为BE平分∠ABC, 所以∠ABE=∠CBE. 因为BD⊥AD, 所以∠ADB=∠FDB=90°.
所以∠D=∠ABH=90°. AB=AD,
在△ABH 和△ADF 中,∠ABH=∠D=90°, BH=DF,
全等三角形判定条件(六种)

全等三角形判定条件(六种)
①边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等。
②角边角公理(ASA)有两角和它们的夹边对应相等的两个三角形全等。
③推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等。
④边边边公理(SSS)有三边对应相等的两个三角形全等。
⑤斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角
三角形全等。
出现两等边三角形、两等腰直角三角形通常用SAS证全等;等腰直角
三角形常见辅助线添法--连结直角顶点和斜边中点;两直角三角形证全等
常用方法:SAS,AAS,HL;出现等腰直角三角形或正方形可能用到K型全等。
人教版八年级数学上小专题(三) 构造全等三角形的方法技巧

初中数学试卷小专题(三) 构造全等三角形的方法技巧方法一:利用补形构造全等三角形1.已知:如图,在△ABC 中,∠BCA=90°,AC=BC ,AE 平分∠BAC ,BE ⊥AE ,求证:BE=21AD.方法二:利用“截长补短”法构造全等三角形2.如图,在△ABC 中,AD 平分∠BAC,∠C=2∠B,试判断AB ,AC ,CD 三者之间的数量关系,并说明理由.(想一想,你会几种方法)3.如图,在△ABC 中,∠A=60°,BD ,CE 分别平分∠ABC 和∠ACB,BD ,CE 交于点O,试判断BE,CD,BC 的数量关系,并加以证明.4.如图,AD ∥BC,DC ⊥AD,AE 平分∠BAD,E 是DC 的中点.问:AD,BC,AB 之间有何关系?并说明理由.5.(德州中考)问题背景:如图1:在四边形ABCD 中,AB=AD ,∠BAD=120°,∠B=∠ADC=90°.E ,F 分别是BC ,CD 上的点.且∠EAF=60°.探究图中线段BE ,EF ,FD 之间的数量关系.(1)小王同学探究此问题的方法是,延长FD 到点G.使DG=BE.连接AG ,先证明△ABE ≌△ADG ,再证明△AEF ≌△AGF ,可得出结论,他的结论应是;(2)如图2,若在四边形ABCD 中,AB=AD ,∠B+∠D=180°.E ,F 分别是BC ,CD 上的点,且∠EAF=21∠BAD ,上述结论是否仍然成立,并说明理由.方法三:利用“倍长中线法”构造全等三角形6.已知,△ABC 中,AB=4 cm,BC=6 cm,BD 是AC 边上的中线,求BD 的取值范围.7.已知:如图,AD,AE 分别是△ABC 和△ABD 的中线,且BA=BD.求证:AE=21AC.8.如图,AB=AE,AB ⊥AE ,AD=AC ,AD ⊥AC,点M 为BC 的中点,求证:DE=2AM.参考答案1.图略,延长AC 、BE 交于点F ,∵∠ACB=90°,BE ⊥AE,∴∠CAD+∠CDA=90°,∠EDB+∠EBD=90°.∵∠CDA=∠EDB,∴∠CAD=∠EBD ,即∠CAD=∠CBF.在△ADC 和△BFC 中,∠CAD=∠CBF,AC=BC,∠ACD=∠BCF,∴△ADC ≌△BFC.∴AD=BF.在△AEF 和△AEB 中,∠FAE=∠BAE,AE=AE,∠AEF=∠AEB,∴△AEF ≌△AEB.∴BE=EF,即BE=21BF.∴BE=21AD. 2.AB=AC+CD.理由如下:方法1:在AB 上截取AE=AC,连接DE.易证△AED ≌△ACD(SAS),∴ED=CD,∠AED=∠C.∵∠AED=∠B+∠EDB,∴∠C=∠AED=∠B+∠EDB.又∵∠C=2∠B,∴∠B=∠EDB.∴BE=DE.∴AB=AE+BE=AC+DE=AC+CD.方法2:延长AC 到点F,使CF=CD,连接DF.∵CF=CD,∴∠CDF=∠F.∵∠ACB=∠CDF+∠F ,∴∠ACB=2∠F.又∵∠ACB=2∠B,∴∠B=∠F.∴△ABD ≌△AFD(AAS).∴AB=AF.∴AB=AF=AC+CF=AC+CD.3.证明:在BC 上截取BF=BE,连接OF.∵BD 平分∠ABC,∴∠EBO=∠FBO.∴△EBO ≌△FBO.∴∠EOB=∠FOB.∵∠A=60°,BD ,CE 分别平分∠ABC 和∠ACB,∴∠BOC=180°-∠OBC-∠OCB=180°-21∠ABC-21∠ACB=180°-21(180°-∠A)=120°.∴∠EOB=∠DOC=60°.∴∠BOF=60°,∠FOC=∠DOC=60°.∵CE 平分∠DCB,∴∠DCO=∠FCO.∴△DCO ≌△FCO.∴CD=CF.∴BC=BF+CF=BE+CD.4.AB=AD+BC.理由:作EF ⊥AB 于F,连接BE.∵AE 平分∠BAD,DC ⊥AD,EF ⊥AB,∴EF=DE.∵DE=CE,∴EC=EF.∴Rt △BFE ≌Rt △BCE(HL).∴BF=BC.同理可证:AF=AD.∴AD+BC=AF+BF=AB,即AB=AD+BC.5.(1)EF=BE+DF(2)EF=BE+DF 仍然成立.证明:图略,延长FD 到G ,使DG=BE ,连接AG ,∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG.在△ABE 和△ADG 中,DG=BE,∠B=∠ADG,AB=AD,∴△ABE ≌△ADG(SAS).∴AE=AG ,∠BAE=∠DAG.∵∠EAF=21∠BAD ,∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF.∴∠EAF=∠GAF.在△AEF 和△GAF 中,AE=AG,∠EAF=∠GAF,AF=AF,∴△AEF ≌△GAF(SAS).∴EF=FG.∵FG=DG+DF=BE+DF ,∴EF=BE+DF.6.图略,延长BD 至E,使DE=BD.连接CE.∵BD 是AC 边上的中线,∴AD=CD.∵∠BDA=∠CDE,∴△BDA ≌△EDC(SAS).∴CE=AB.在△CBE 中,BC-CE<BE<BC+CE,∴2 cm<2BD<10 cm.∴1 cm<BD<5 cm.7.证明:延长AE 至F,使EF=AE ,连接DF.∵AE 是△ABD 的中线,∴BE=DE.∵∠AEB=∠FED,∴△ABE ≌△FDE.∴∠B=∠BDF,AB=DF.∵BA=BD,∴∠BAD=∠BDA,BD=DF.∵∠ADF=∠BDA+∠BDF ,∠ADC=∠BAD+∠B ,∴∠ADF=∠ADC.∵AD 是△ABC 的中线,∴BD=CD.∴DF=CD.∴△ADF ≌△ADC(SAS).∴AC=AF=2AE,即AE=21AC. 8.延长AM 至N ,使MN=AM ,连接BN ,易证△AMC ≌△NMB(SAS),∴AC=BN,∠C=∠NBM ,∠ABN=∠ABC+∠C=180°-∠BAC=∠EAD.再证△ABN ≌△EAD(SAS).∴DE=NA.又AM=MN ,∴DE=2AM.。
构造全等三角形的四种技巧

THANKS
感谢您的观看
构造方法二:两角和一边成比例
构造步骤
首先确定两个角和一条包含的边,然后通过作图或拼接的方式构造出两个三角形,使得这两个三角形满足ASA全 等条件,同时保证两角和一边成比例。
示例
假设已知三角形ABC和三角形DEF,其中$\angle A = \angle D$,$\angle B = \angle E$,$AB/DE = BC/EF$ ,可以通过作图或拼接的方式构造出两个三角形,使得它们满足ASA全等条件,同时保证两角和一边成比例。
构造全等三角形的四 种技巧
汇报人:
202X-12-21
目录
CONTENTS
• 构造SSS全等三角形 • 构造SAS全等三角形 • 构造ASA全等三角形 • 构造AAS全等三角形
01
构造SSS全等三角 形
定义与性质
定义
如果两个三角形的三边分别相等 ,则这两个三角形全等。
性质
SSS全等三角形具有全等三角形的 所有性质,如对应角相等、对应 边相等、面积相等等。
பைடு நூலகம்4
构造AAS全等三角 形
定义与性质
定义
两个三角形中,如果两个角和其中一个角的 对边分别相等,则这两个三角形全等。
性质
AAS全等三角形的性质包括对应角相等、对 应边相等、面积相等等。
构造方法一:两角和一对边相等
描述
在两个三角形中,如果两个角和一个边分别 相等,则可以通过AAS全等条件证明两个三 角形全等。
构造方法一:三边相等
步骤
首先确定两个三角形的三边长度,然 后通过测量或计算确保三边长度分别 相等。
说明
这种方法需要先确定三边的长度,因 此适用于已知三边长度的情况。
小专题(三) 构造全等三角形的常用方法

AB=FB, ∠ABE=∠FBE, BE=BE,
∴△ABE≌△FBE(SAS). ∴∠A=∠BFE.
∵AB∥CD, ∴∠A+∠D=180°. ∴∠BFE+∠D=180°. ∵∠BFE+∠CFE=180°, ∴∠CFE=∠D. 在△FCE和△DCE中,
方法2 利用“截长补短法”构造全等三角形
截长补短法的具体做法:在某一条线段上截取一条线 段与特定线段相等,或将某条线段延长,使之与特定线段 相等,再利用三角形全等的有关性质加以说明.这种方法 适用于证明线段的和、差、倍、分等题目.
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点 E在AD上,求证:BC=AB+CD.
∠CFE=∠D, ∠FCE=∠DCE, CE=CE,
∴△FCE≌△DCE(AAS). ∴CF=CD. ∴BC=BF+CF=AB+CD.
3.(德州中考)问题背景: 如图1,在四边形ABCD中,AB=AD,∠BAD=120°, ∠B=∠ADC=90°.点E,F分别是BC,CD上的点,且 ∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系. (1)小王同学探究此问题的方法是:延长FD到点G,使 DG=BE,连接AG.先证明△ABE≌△ADG,再证明 △AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF;
(2) 如图 2,若在四边形 ABCD 中,AB=AD, ∠B+∠D=180°.E,F 分别是 BC,CD 上的点,
且∠EAF=12∠BAD,上述结论是否仍然成立?并说明理由. 解:EF=BE+DF仍然成立. 理由:延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°, ∴∠B=∠ADG. 在△ABE和△ADG中,
三角形全等添加辅助线的5种常用方法

三角形全等添加辅助线的5种常用方法三角形全等的证明及相关问题,是初中几何部分的基础,也是重点和难点,不管是在中考还是平时的考试中,都是咼频出现。
全等三角形的基础知识点就那么几条,很容易掌握,但是一般考试中的题目, 不可能直接给出几组条件让我们直接写出证明过程,很多时候都要经过分析思考,添加辅助线,才能得到全等三角形。
下面就简单介绍一下构造全等三角形的五种常用方法。
一、等腰三角形三线合一法当我们遇到等腰三角形(等边三角形)相关题目时,用三线合一性质,很容易找出思路。
它的原理就是利用三角形全等变换中的对折重叠。
我们来看一个例题:证明:延长BA, CE交于点Xl、倍长中线法遇到一个中点的时候,通常会延长经过该中点的线段。
倍长中线指延长中线至一点,使所延长部分与该中线相等,并连接该点与这一条边的一个顶点,得到两个三角形全等。
如图所示,点D为△ABC边BC的中点•延长AD至点E,使得DE = AD,并连接BE,贝UAADC 也zEDB (SAS)我们来看一个例题:三、遇角平分线作双垂线法在题中遇见角平分线,做双垂直,必出全等三角形。
可以从角平分线上的点向两边作垂线,也可以过角平分线上的点作角平分线的垂线与角的两边相交。
在很多综合几何题当中,关于角平分线的辅助线添加方法最常用的就是这个。
看看在具体题目中怎么操作吧!例 3;已知,如SLAC 平分ZBAD, CD=CB, AB>AD, 求证畫ZB+ZADC=18O0・AC证明:作CE丄AB于E,CF丄AD于F. TAC 平分 ZBADr ACE=CF.在 RtACBE 和RtACDF 中,%心RtACBE^RtACDF (HL),二ZB二ZCDF,VZCDF+ZADC=180° , A ZB+ZATC=180°四、作平行线法在几何题的证明中,作平行线的方法也非常实用,一般来讲,在等腰、等边这类特殊的三解形中,作平行线绝对是首要考虑。
例4如ffl, A ABC中,是朋上一点,F是AC延长线上一点,连EF交BC于D,若EB=CF.求证當DE=DF.五、截长补短法题目中出现线段之间的和、差、倍、分时,考虑截长补短法;截长补短的目的是把几条线段之间的数量关系转换为两条线段间的等量关系例6;如图甲.AD/BC.点E 在线段AB 上.ZADE 二ZCDE, ZDCE=ZECB,求证:CRAMBU证明:在CD 上截取CF-BC.如图乙(T - < Ji在厶 FCE^ABCE 中 - netCE CLAAFCE^ABCE(SAS), .\Z2=Z1- 又VAD/7BC,AZADC+ZBCD^180° , :.ZXE+ZCDE=90<>, /- Z2+Z3=90* , •\ ZUZ4=90° . :. Z3=Z14 LH 3)1加十 z5 = Z4A AFDE^AADli (ASA) , ADF-DAr 又 VCD=DF+CF, <\CD=AD+BC O D D{。
三角形全等证明方法

三角形全等证明方法在几何学中,全等是指两个或多个几何体的大小、形状以及内部结构完全相同。
对于三角形而言,如果两个三角形的对应边长相等,对应的角度也相等,则它们是全等三角形。
在证明两个三角形全等时,有多种方法可以使用,本文将详细介绍其中的几种方法,并给出说明和举例。
【1. SSS (Side-Side-Side) 全等法】SSS全等法则是指如果两个三角形的三边分别相等,则它们是全等的。
这个证明方法简单直接,可以通过以下步骤来证明:Step 1: 确定两个三角形的三边分别相等;Step 2: 可以使用尺规作图工具在纸上绘制出两个三角形;Step 3: 通过测量确定两个三角形的三边分别相等;Step 4: 通过观察可以得出结论,即两个三角形是全等的。
例如,我们要证明△ABC ≡ △DEF。
我们已知AB = DE,BC = EF,AC = DF。
根据SSS全等法则,根据给定的条件可以得出结论,即△ABC ≡ △DEF。
【2. SAS (Side-Angle-Side) 全等法】SAS全等法则是指如果两个三角形的两个边和夹角分别相等,则它们是全等的。
这个证明方法也是常用的,可以通过以下步骤来证明:Step 1: 确定两个三角形的两个边和夹角分别相等;Step 2: 可以使用尺规作图工具在纸上绘制出两个三角形;Step 3: 通过测量确定两个三角形的两个边和夹角分别相等;Step 4: 通过观察可以得出结论,即两个三角形是全等的。
例如,我们要证明△ABC ≡ △DEF。
我们已知∠BAC = ∠EDF,AB = DE,AC = DF。
根据SAS 全等法则,根据给定的条件可以得出结论,即△ABC ≡ △DEF。
【3. ASA (Angle-Side-Angle) 全等法】ASA全等法则是指如果两个三角形的两个角和夹边分别相等,则它们是全等的。
这个证明方法也非常常用,可以通过以下步骤来证明:Step 1: 确定两个三角形的两个角和夹边分别相等;Step 2: 可以使用尺规作图工具在纸上绘制出两个三角形;Step 3: 通过测量确定两个三角形的两个角和夹边分别相等;Step 4: 通过观察可以得出结论,即两个三角形是全等的。
证三角形全等的五种方法

证三角形全等的五种方法一、第一种方法是“边边边(SSS)”。
如果两个三角形的三边长度相应相等,那么我们就可以说这两个三角形全等。
比如,对于三角形ABC和三角形DEF,如果AB=DE,BC=EF以及AC=DF,那么三角形ABC与三角形DEF全等。
这种全等的方式十分明确,只要各边对应长度一致,不论角度如何都可以判定为全等。
二、第二种方法是“边角边(SAS)”。
若两个三角形有两边和它们之间的夹角对应相等,那么这两个三角形就可以被证明为全等。
比如,对于三角形ABC和三角形DEF,如果AB=DE,而且它们之间的夹角∠BAC=∠EDF,另外AC=DF,我们就可以断定三角形ABC和三角形DEF全等。
三、第三种方法是“角边角(ASA)”。
如果两个三角形的两个角和它们之间的边对应相等,那么他们就是全等的。
例如,对于三角形ABC和三角形DEF,如果∠BAC=∠EDF,且他们之间的边AC=DF,以及∠BCA=∠FDE,那么我们就可以认为三角形ABC全等于三角形DEF。
四、第四种方法是“角角边(AAS)”。
若两个三角形有两个角和任一边对应相等,那么它们就是全等的。
例如,对于三角形ABC和三角形DEF,如果∠BAC=∠EDF,∠BCA=∠FDE,并且边BC=EF,那么三角形ABC就全等于三角形DEF。
五、第五种方法是“右角三角形的斜边与一直角边(HL)”。
对于两个右角三角形,如果它们的斜边和一条直角边对应相等,那么我们就可以证明这两个三角形是全等的。
例如,对于三角形ABC和三角形DEF,如果∠BAC和∠EDF都是90°,且AC=DF(斜边),AB=DE(一条直角边),则三角形ABC和三角形DEF全等。
构造全等三角形的常用方法

证法一(截长法):如图①,在AB上截取AN=AC,连接PN.
在△APN和△APC中, A∠N1==A∠C2,, AP=AP, ∴△APN≌△APC(SAS).∴PN=PC.
在△BPN中,PB-PN<BN,∴PB-PC<AB-AN.
∴AB-AC>PB-PC.
证法二(补短法):如图②,延长AC至点M,使AM=AB,
∵AD是△ABC的中线,∴BD=CD.
在△ADC和△MDB中, B∠DB=DMCD=,∠CDA, DM=DA, ∴△ADC≌△MDB(SAS).∴∠M=∠MAC,BM=AC.
∵∠EAF=∠EFA,∠AFE=∠BFM,∴∠M=∠BFM.
∴BM=BF.∴AC=BF.
4.如图,在△ABC中,AB>AC,∠1=∠2,P为AD上任意 一点.求证:AB-AC>PB-PC.
解:PC=PD.理由如下: 如图,过点P分别作PE⊥OA,PF⊥OB,垂足分别为E,F. ∵OM平分∠AOB,∴PE=PF. ∵∠AOB=90°,∠PEO=∠PFO=90°. ∴∠EPF=90°. ∴∠EPC+∠CPF=90°. ∵∠CPD=90°,∴∠CPF+∠FPD=90°. ∴∠EPC=∠FPD.
∵∠ABC=80°,∴∠ABC=∠ADP.
∵AP平分∠BAC,∴∠BAP=∠CAP.
在△ABP和△ADP中, ∠ABP=∠ADP, ∠BAP=∠DAP, AP=AP, ∴△ABP≌△ADP(AAS).∴AB=AD,BP=PD.
∴AB+BP=AD+PD=AD+CD=AC.②
由①②可得AB+BP=BQ+AQ.
在△BDF和△BGF中, BD=BG, ∠DBF=∠GBF, BF=BF, ∴△BDF≌△BGF(SAS).
∴∠BDF=∠G.
