常见构造全等三角形的七种常用方法
构造全等三角形的四种技巧

构造全等三角形的四种技巧在几何学中,全等三角形是一个非常重要的概念。
全等三角形是指两个或两个以上的三角形,它们的形状和大小完全相同。
理解并能够构造全等三角形,对于解决各种几何问题有着至关重要的作用。
以下是构造全等三角形的四种技巧:利用公理:全等三角形的公理是:如果两个三角形的三边对应相等,那么这两个三角形全等。
这个公理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后根据这些边长画出两个三角形。
这两个三角形的形状和大小将会完全相同。
利用角平分线:角平分线定理指出,一个角的平分线将对应的边分为两段,这两段与角的两边形成的两个小三角形是全等的。
通过这个定理,你可以通过一个角的平分线,构造出一个全等三角形。
利用中垂线:中垂线定理指出,一条中垂线将一个线段分为两段,这两段与线段的两端形成的两个小三角形是全等的。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后通过中垂线将这些边分为两段。
这样,你就可以得到两个全等的三角形。
利用平行线:平行线定理指出,如果两条平行线被第三条直线所截,那么截得的对应线段成比例。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后在两条平行线上画出对应的线段。
由于这些线段成比例,因此它们形成的两个小三角形是相似的。
如果这些相似三角形的对应边长度相等,那么它们就是全等的。
以上就是构造全等三角形的四种技巧。
理解和掌握这些技巧,对于解决各种几何问题有着重要的作用。
已知两个三角形全等,则它们对应边上的高也________;对应角平分线也________;对应边上的中线也________。
两个直角三角形全等,除了用定义外,还可以用以下________判定。
已知三角形ABC全等三角形DEF,且AB=18cm,BC=20cm,CA=15cm,则DE=________cm,DF=________cm,EF=________cm.做衣服需要依据身体部位的大小来选择布料,而教学则需要依据学生原有的知识基础来选择教学方法。
构造全等三角形的方法技巧

方法1 角形
利用“角平分线”构造全等三ห้องสมุดไป่ตู้
【方法归纳】 因角平分线本身已经具备 全等的三个条件中的两个(角相等和公共 边相等),故在处理角平分线问题时,常 作以下辅助线构造全等三角形: (1)在角的两边截取两条相等的线段; (2)过角平分线上一点作角两边的垂线.
思1.如图,AB∥CD,BE平分 ∠ABC,CE平分∠BCD,点E在AD 上,求证:BC=AB+CD. 考
2.如图,已知∠AOB=90°,OM是 ∠AOB的平分线,三角尺的直角顶点 P在射线OM上滑动,两直角边分别与 OA,OB交于点C,D,求证:PC= PD.
方法2 利用“截长补短法”构造全等 三角形
【方法归纳】 截长补短法的具体做法 :在某一条线段上截取一条线段与特定 线段相等,或将某条线段延长,使之与 特定线段相等,再利用三角形全等的有 关性质加以说明.这种方法适用于证明 线段的和、差、倍、分等类的题目.
3.如图,在△ABC中,AD平分 ∠BAC,∠C=2∠B,试判断AB, AC,CD三者之间的数量关系,并 说明理由.(想一想,你会几种方法)
方法3 利用“倍长中线法”构造全 等三角形
【方法归纳】 将中点处的线段延长 一倍,然后利用SAS证三角形全等.
6.已知:如图,AD,AE分别是 △ABC和△ABD的中线,且BA= BD.求证:AE=AC.
构造全等三角形的六种常用方法课件

构造方法简介
01
02
03
04
尺规作图法
利用尺规作图工具,通过已知 条件构造全等三角形。
翻折法
将已知三角形沿某条直线翻折, 得到与原三角形全等的三角形。
平移法
将已知三角形沿某方向平移一 定距离,得到与原三角形全等
的三角形。
旋转法
将已知三角形绕某点旋转一定 角度,得到与原三角形全等的
三角形。
02 方法一:SSS全 等法
感谢观看
拓展延伸:其他构造方法及应用场景
构造中位线
利用三角形中位线性质构 造全等三角形,常用于证 明线段相等或倍长中线等 问题。
构造角平分线
利用角平分线性质构造全 等三角形,常用于证明角 相等或线段成比例等问题。
构造垂直平分线
利用垂直平分线性质构造 全等三角形,常用于证明 线段相等或点共圆等问题。
THANKS
判定条件
两个三角形中,两个角及这两个角的夹边分别相等,则这两个三角形全等。
构造步骤这两个角的夹边相等,最后根据ASA判定条件证明两个三角形全等。
示例
在△ABC和△ADE中,∠BAC=∠DAE,∠B=∠D,AB=AD。根据ASA全等法,可以判定△ABC≌△ADE。
应用场景分析
1 2 3
解决角度和边长问题 当题目中给出两个角和它们的夹边相等时,可以 利用ASA全等法证明两个三角形全等,从而解决 与角度和边长相关的问题。
构造全等三角形 在几何证明题中,有时需要构造全等三角形以证 明某些线段或角度相等。ASA全等法是构造全等 三角形的常用方法之一。
辅助线策略 当遇到复杂的几何问题时,可以通过作辅助线构 造全等三角形,将问题转化为已知的全等三角形 问题,从而简化解题过程。
2020最新名校课堂小专题4:构造全等三角形的常用方法

小专题4:构造全等三角形的常用方法方法1 利用“角平分线”构造全等三角形模型构建已知点P是MON⊥于⊥于点A,可以过点P作PB ON ∠平分线上一点,若PA OM点B,则PB PA=.1.感知:如图,AD平分18090,,,易知:.∠∠+∠=︒∠=︒=BAC B C B DB DC探究:如图,AD平分18090∠∠+∠=︒∠<︒,,,求证:BAC ABD ACD ABD=.DB DC模型构建若AOP BOP=,∠=∠,且点A是射线OM上任意一点,可以在ON上截取OB OA 连接PB,构造OPB OPA≌.∆∆2.如图,//∠,点E在AD上,求证:AB CD,BE平分ABC∠,CE平分BCD=+.BC AB CD方法2 利用截长补短法构造全等三角形方法指导截长补短法的具体做法:在某一条线段上截取一条线段与特定线段相等,或将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明,这种方法适用于证明线段的和差、倍、分等题目.3.问题背景:如图,在四边形ABCD中,12090AB AD BAD B ADC=∠=︒∠=∠=︒,,.点E,F分别是BC,CD上的点,且60EAF︒∠=.探究图中线段BE,EF,FD之间的数量关系.(1)小王同学探究此问题的方法是:延长FD到点G,使DG BE=,连接AG.先证明ABE ADG∆∆≌,再证明AEF AGF∆∆≌,可得出结论,他的结论应是______; (2)如图,若在四边形ABCD中,180AB AD B D=∠+∠=︒,.E,F分别是BC,CD上的点,且12EAF BAD∠=∠,上述结论是否仍然成立?并说明理由.方法3 利用“倍长中线法”构造全等三角形方法指导将中线延长一倍,然后利用“SAS”判定三角形全等.4.如图,AB AE AB AE AD AC AD AC=⊥=⊥,,,,点M为BC的中点,求证:2DE AM=.方法4 利用“三垂直”构造全等三角形模型构建如图,若AB AC AB AC,,则可过斜边的两端点B,C向过A点的直线作垂线=⊥构造ABD CAE≌.在平面直角坐标系中,过顶点A的直线常为x轴或y轴.∆∆5.已知在△ABC中,90,,将△ABC放在平面直角坐标系中,如BAC AB AC∠=︒=图所示.(1)如图,若A(1,0),B(0,3),求C点坐标;(2)如图,若A(1,3),B(10-,),求C点坐标;(3)如图3,若B(40,),求A点坐标.-,),C(01-参考答案1.证明:过点D 作DE AB ⊥于点E ,DF AC ⊥交AC 的延长线于点F . AD 平分90BAC DE AB DF AC DE DF F DEB ∠⊥⊥∴=∠=∠=︒,,,,. 180180EBD ACD ACD FCD EBD FCD ∠+∠=︒∠+∠=︒∴∠=∠,,.在△DFC 和△DEB 中,,,,F DEB FCD EBD DF DE ∠=∠⎧⎪∠=∠⎨⎪=⎩DFC DEB ∴∆∆≌(AAS ).DC DB ∴=.2.证明:在BC 上截取BF AB =,连接EF . BE 平分ABC ∠,CE BCD ∠平分,ABE FBE FCE DCE ∴∠=∠∠=∠,.在△ABE 和△FBE 中,,,,AB FB ABE FBE BE BE =⎧⎪∠=∠⎨⎪=⎩ABE FBE ∴∆∆≌(SAS ),A BFE ∴∠=∠.//180.180AB CD A D BFE D ∴∠+∠=︒∴∠+∠=︒,. 180BFE CFE CFE D ∠+∠=︒∴∠=∠,.在△FCE 和△DCE 中,,,,CFE D FCE DCE CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩FCE DCE ∴∆∆≌(AAS )..CF CD BC BF CF AB CD ∴=∴=+=+.3.解:(1)EF BE FD =+(2)EF BE FD =+仍然成立.理由:延长FD 到G ,使DG BE =,连接AG ,180180B ADC ADC ADG B ADG ∠+∠=︒∠+∠=︒∴∠=∠,,.在△ABE 和△ADG 中,,,,BE DG B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩ABE ADG ∴∆∆≌(SAS ).AE AG BAE DAG ∴=∠=∠,.12EAF BAD ∠=∠, GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠.在△AEF 和△AGF 中,,,,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩AEF AGF ∴∆∆≌(SAS ).EF FG ∴=.FG DG DF BE DF EF BE DF =+=+∴=+,.4.证明:延长AM 至N ,使MN AM =,连接BN .点M 为BC 的中点,BM CM ∴=.在△AMC 和△NMB 中,,,,AM NM CMA BMN CM BM =⎧⎪∠=∠⎨⎪=⎩AMC NMB ∴∆∆≌(SAS ).AC BN AD C NBM ∴==∠=∠,.180ABN ABC NBM ABC C BAC EAD ∴∠=∠+∠=∠+∠=︒-∠=∠.在△ABN 和△EAD 中,,,,AB EA ABN EAD BN AD =⎧⎪∠=∠⎨⎪=⎩ABN EAD ∴∆∆≌(SAS ).2DE NA AM ∴==.5.解:(1)过点C 作CD x ⊥轴,垂足为D .则90CAD ACD ∠+∠=︒. 9090.BAC BAO CAD BAO ACD ∠=︒∴∠+∠=︒∴∠=∠,.在△ABO 和△CAD 中,,,,AOB CDA BAO ACD AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO CAD ∴∆∆≌(AAS ).BO AD OA CD ∴==,.A (1,0),B (0,3)1 3.31OA OB AD CD ∴====,,,. 4.OD OA AD ∴=+=∴C (4,1).(2)过点A 作AD x ⊥轴,垂足为D ,过点C 作CE AD ⊥,垂足为E .同(1)可证ACE BAD AE BD CE AD ∆∆∴==≌,,.A (1,3),B (10-,),2 3.3 1.BD AD CE DE AD AE ∴==∴==-=∴,,C (4,1).(3)过点A AD x AE y ⊥⊥作轴,轴,垂足分别为D ,E .同(1)可证BAD CAE ∆∆≌,CE BD AE AD OE ∴===,. B (40-,),C (01-,),4 1.OB OC ∴==, 3.AE OB BD OB CE OB OC OE AE ∴=-=-=-+=-()333(,)222AE A ∴=⋅∴-。
构造全等三角形的常用方法
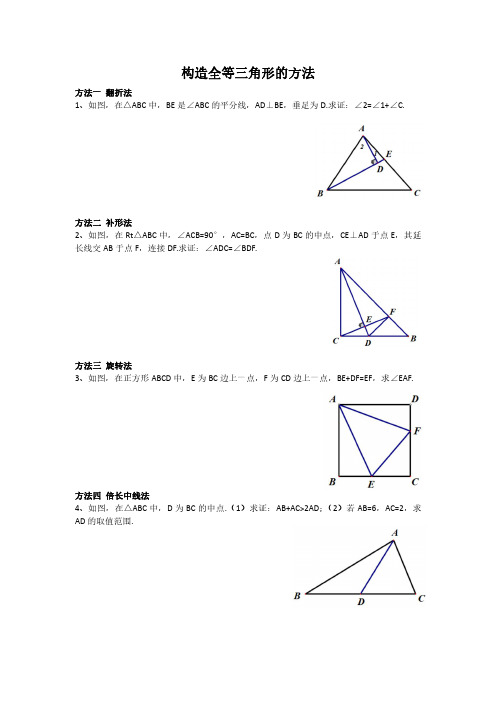
构造全等三角形的方法
方法一翻折法
1、如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.
方法二补形法
2、如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
方法三旋转法
3、如图,在正方形ABCD中,E为BC边上一点,F为CD边上一点,BE+DF=EF,求∠EAF.
方法四倍长中线法
4、如图,在△ABC中,D为BC的中点.(1)求证:AB+AC>2AD;(2)若AB=6,AC=2,求AD的取值范围.
方法五截长补短法
5、如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD 上的点,且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系并证明.
方法六作垂线法
6、如图,∠AOB=90°,OM平分∠AOB,直角三角板的顶点P在射线OM上移动,两直角边分别与OA,OB相交于点C、D,问PC与PD相等吗?试说明理由.
方法七作平行线法
7、如图,△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC 交AC于点Q.求证:AB+BP=BQ+AQ.。
初中数学三角形全等常用几何模型及构造方法大全初二

初二数学三角形全等常用几何模型及构造方法大全掌握它轻松搞定全等题!全等是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握~全等变换类型:(一)平移全等:平行等线段(平行四边形)(二)对称全等模型:角平分线或垂直或半角1:角平分线模型;2:对称半角模型;(三)旋转全等模型:相邻等线段绕公共顶点旋转1.旋转半角模型2.自旋转模型3.共旋转模型4.中点旋转如图,在△ABC的边上取两点D、E,且BD=CE,求证:AB+AC>AD+AE分析:将△ACE平移使EC与BD重合。
B\D,上方交点,左右两个三角形,两边和大于第三边!1:角平分线模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
2:对称半角模型说明:上图依次是45°、30°、 45+ °、对称(翻折)15°+30°直角三角形对称(翻折) 30+60+90直角三角形对称(翻折)翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
1.半角:有一个角含1/2角及相邻线段2.自旋转:有一对相邻等线段,需要构造旋转全等3.共旋转:有两对相邻等线段,直接寻找旋转全等(共顶点)4.中点旋转:倍长中点相关线段转换成旋转全等问题(专题七)1、旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
2、自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称3、共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
(接上------共旋转模型)模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形混用。
构造全等三角形的方法专题

知识体系利用三角形全等是证明线段或角相等的重要方法之一,但有时不能直接应用,就需要根据条件,通过作辅助线的方法构造全等三角形。
构造全等三角形的方法主要有:中线倍长,截长补短,翻折,作平行线或垂线。
(1)遇到与中点有关的条件时,通常将过中点的线段延长一倍,构造 字形全等三角形。
(2)证一条线段等于另外两条线段和或差时,通常在较长的线段上截取一条线段等于较短的线段中的某一条,(此谓之“截长”),或将两条较短的线段转化到一条线段上,(此谓之“补短”)注意:不管是截长还是补短,都要证明截取或补上的线段所在的三角形与另一个对应三角形全等。
(3)遇角平分线时,通常用翻折构造全等或向角两边作垂线构造全等。
例题选讲例1如图,在△ABC 中,AD 是∠BAC 的平分线,M 是BC 的中点,过M 作MF ∥AD 交BA 的延长线于F ,交AC 于P ,求证:CP =BF =21(AB +AC )例2如图,△ABC 中,D 为BC 的中点,M 为AB 上一动点,N 为AC 上一动点,且∠MDN =90°.(1)求证:BM +CN >MN ;FP MD C B A A M N C B D(2)若M在AB的延长线上,N在CA的延长线上,其它条件不变,(1)中的结论是否仍然成立,若成立,请证明,若不成立,说明理由;(3)若点M在BA的延长线上,点N在AC的延长线上,其它条件不变,(1)中的结论是否仍然成立,若成立,请证明,若不成立,说明理由。
例3如图,在四边形ABCD中,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°变形1,如图,在四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,求证:AD=DC变形2,如图,在四边形ABCD中,DE⊥BC于E,BD平分∠ABC,若BE=12(AB+AC),求证:∠A+∠C=180°ACBDMBACNADC BADCBADCB E变形3,如图,在四边形ABCD 中,DE ⊥BC 于E ,BD 平分∠ABC ,若∠A +∠C =180°,求证:BE =12(AB +BC )例4已知AM ∥BN ,AC 平分∠MAB ,BC 平分∠NBA① 过C 作直线DE ,分别交AM 、BN 于点D 、E ,求证:AB =AD +BE ;② 将直线绕C 转动,使DE 与AM 交于点D ,与NB 的延长线交于点E ,则AB 、AD 、BE 三条线段是否存在确定的数量关系?例5已知如图,在正方形ABCD 中AB =AD ,∠B =∠D =90°.(1)如果BE +DF =EF ,求证:①∠EAF =45°;②FA 平分∠DFE .(2)如果∠EAF =45°,求证: BE +DF =EF .A B C DE M N A B C D E M N A B CD E F A D CBEA CB F D(3)如果点F 在DC 的延长线上,点E 在CB 的延长线上,满足(1)的条件,则(1)中结论是否仍然成立? 巩固练习1.已知: 如图, AD 为△ABC 的中线, 且∠1 = ∠2, ∠3 = ∠4. 求证: BE +CF >EF说明:有角平分线时常在角两边截相等的线段, 构造全等三角形.2.已知,如图,△ABC (AB ≠AC )中,D 、E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC ,求证:AE 平分∠BAC 。
初中数学——构造全等三角形的五种常用方法

所以∠1=∠2. ∠1=∠2,
在△ACD 和△CBG 中,AC=CB, ∠ACD=∠CBG=90°,
所以△ACD≌△CBG(ASA). 所以∠ADC=∠G,CD=BG. 因为点 D 为 BC 的中点,所以 CD=BD.所以 BD=BG. 因为∠DBG=90°,∠DBF=45°,
所以∠GBF=∠DBG-∠DBF=90°-45°=45°.
解:如图,过点B作BG⊥BC交CF的延长线于点G. 因为∠ACB=90°,所以∠2+∠ACF=90°. 因为CE⊥AD, 所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°. 因为CE⊥AD,所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
在△AEH 和△AEF 中,AE=AE, EH=EF,
所以△AEH≌△AEF(SSS).
所以∠EAH=∠EAF.
所以∠EAF=12∠HAF=45°.
返回
方 法 4 倍长中线法
4.如图,在△ABC中,D为BC的中点.若AB=5, AC=3,求AD长度的取值范围. 解:如图,延长AD至点E,使DE= AD,连接BE. 因为D为BC的中点,所以CD=BD.
第四章 三角形
构造全等三角形的五种常用方法
方 法 1 翻折法
1.如图,在△ABC中,BE是∠ABC的平分线, AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
解:如图,延长AD交BC于点F(相当于将AB边向下翻 折,与BC边重合,A点落在F点处,折痕为BE). 因为BE平分∠ABC, 所以∠ABE=∠CBE. 因为BD⊥AD, 所以∠ADB=∠FDB=90°.
所以∠D=∠ABH=90°. AB=AD,
在△ABH 和△ADF 中,∠ABH=∠D=90°, BH=DF,
构造三角形全等的几种方法
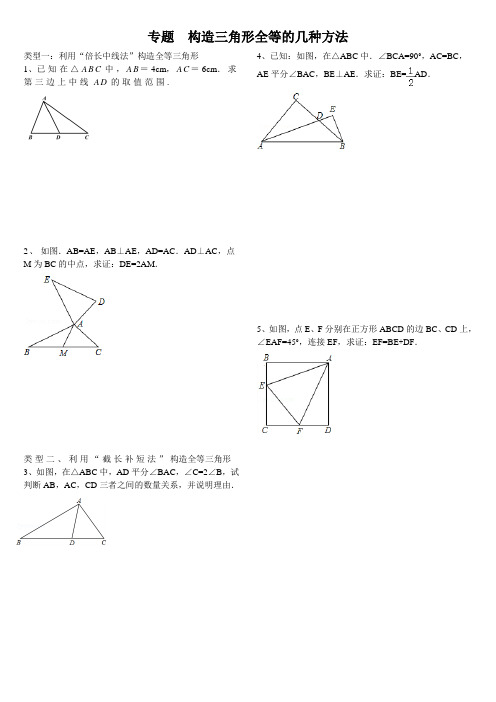
专题构造三角形全等的几种方法
类型一:利用“倍长中线法”构造全等三角形
1、已知在△A B C中,A B=4cm,A C=6cm.求第三边上中线A D的取值范围.
2、如图.AB=AE,AB⊥AE,AD=AC.AD⊥AC,点M为BC的中点,求证:DE=2AM.
类型二、利用“截长补短法”构造全等三角形3、如图,在△ABC中,AD平分∠BAC,∠C=2∠B,试判断AB,AC,CD三者之间的数量关系,并说明理由.4、已知:如图,在△ABC中.∠BCA=90°,AC=BC,AE平分∠BAC,BE⊥AE.求证:BE=AD.
5、如图,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,求证:EF=BE+DF.
类型三:利用角平分构造全等三角形
6、如图,AD是△ABC中∠BAC的平分线,P是AD上的任意一点,且AB>AC,求证:AB﹣AC>PB﹣PC.
7、如图,△AOB中,OA=OB,∠AOB=90゜,BD平分∠ABO交OA于D,AE⊥BD于E.
求证:BD=2AE.
类型四:通过作平行线构造全等三角形
8、如图,△ABC中,AB=AC,在AB上取一点E,在AC的延长线上取一点F,使CF=BE,连接EF,交BC于点D.求证:DE=DF.
9、△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC 交BC于P,BQ平分∠ABC交AC于Q,求证:
AB+BP=BQ+AQ.。
小专题(三) 构造全等三角形的常用方法

AB=FB, ∠ABE=∠FBE, BE=BE,
∴△ABE≌△FBE(SAS). ∴∠A=∠BFE.
∵AB∥CD, ∴∠A+∠D=180°. ∴∠BFE+∠D=180°. ∵∠BFE+∠CFE=180°, ∴∠CFE=∠D. 在△FCE和△DCE中,
方法2 利用“截长补短法”构造全等三角形
截长补短法的具体做法:在某一条线段上截取一条线 段与特定线段相等,或将某条线段延长,使之与特定线段 相等,再利用三角形全等的有关性质加以说明.这种方法 适用于证明线段的和、差、倍、分等题目.
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点 E在AD上,求证:BC=AB+CD.
∠CFE=∠D, ∠FCE=∠DCE, CE=CE,
∴△FCE≌△DCE(AAS). ∴CF=CD. ∴BC=BF+CF=AB+CD.
3.(德州中考)问题背景: 如图1,在四边形ABCD中,AB=AD,∠BAD=120°, ∠B=∠ADC=90°.点E,F分别是BC,CD上的点,且 ∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系. (1)小王同学探究此问题的方法是:延长FD到点G,使 DG=BE,连接AG.先证明△ABE≌△ADG,再证明 △AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF;
(2) 如图 2,若在四边形 ABCD 中,AB=AD, ∠B+∠D=180°.E,F 分别是 BC,CD 上的点,
且∠EAF=12∠BAD,上述结论是否仍然成立?并说明理由. 解:EF=BE+DF仍然成立. 理由:延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°, ∴∠B=∠ADG. 在△ABE和△ADG中,
初中数学三角形全等常用几何模型及构造方法大全

初二数学三角形全等常用几何模型及构造方法大全掌握它轻松搞定全等题!全等是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握~全等变换类型:(一)平移全等:平行等线段(平行四边形)(二)对称全等模型:角平分线或垂直或半角1:角平分线模型;2:对称半角模型;(三)旋转全等模型:相邻等线段绕公共顶点旋转1.旋转半角模型2.自旋转模型3.共旋转模型4.中点旋转如图,在△ABC的边上取两点D、E,且BD=CE,求证:AB+AC>AD+AE分析:将△ACE平移使EC与BD重合。
B\D,上方交点,左右两个三角形,两边和大于第三边!1:角平分线模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
2:对称半角模型说明:上图依次是45°、30°、 45+ 22.5°、对称(翻折)15°+30°直角三角形对称(翻折) 30+60+90直角三角形对称(翻折)翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
1.半角:有一个角含1/2角及相邻线段2.自旋转:有一对相邻等线段,需要构造旋转全等3.共旋转:有两对相邻等线段,直接寻找旋转全等(共顶点)4.中点旋转:倍长中点相关线段转换成旋转全等问题(专题七)1、旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
2、自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称3、共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
(接上------共旋转模型)模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形混用。
初中数学三角形全等常用几何模型及构造方法大全初二

初中数学三角形全等常用几何模型及构造方法大全初二文件编码(008-TTIG-UTITD-GKBTT-PUUTI-WYTUI-8256)初二数学三角形全等常用几何模型及构造方法大全掌握它轻松搞定全等题!全等是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握~全等变换类型:(一)平移全等:平行等线段(平行四边形)(二)对称全等模型:角平分线或垂直或半角1:角平分线模型;2:对称半角模型;(三)旋转全等模型:相邻等线段绕公共顶点旋转1.旋转半角模型2.自旋转模型3.共旋转模型4.中点旋转如图,在△ABC的边上取两点D、E,且BD=CE,求证:AB+AC>AD+AE分析:将△ACE平移使EC与BD重合。
B\D,上方交点,左右两个三角形,两边和大于第三边!1:角平分线模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
2:对称半角模型说明:上图依次是45°、30°、 45+ °、对称(翻折)15°+30°直角三角形对称(翻折) 30+60+90直角三角形对称(翻折)翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
1.半角:有一个角含1/2角及相邻线段2.自旋转:有一对相邻等线段,需要构造旋转全等3.共旋转:有两对相邻等线段,直接寻找旋转全等(共顶点)4.中点旋转:倍长中点相关线段转换成旋转全等问题(专题七)1、旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
2、自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称3、共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
构造全等三角形的方法(优选.)

最新文件---------------- 仅供参考--------------------已改成-----------word文本 --------------------- 方便更改赠人玫瑰,手留余香。
全等三角形的构造方法全等三角形是初中数学中的重要内容之一,是今后学习其他内容的基础。
判断三角形全等公理有SAS、ASA、AAS、SSS和HL,如果能够直接证明三角形的全等的,直接根据相应的公理就可以证明,但是如果给出的条件不全,就需要根据已知的条件结合相应的公理来进行分析,先推导出所缺的条件然后再证明。
一些较难的一些证明问题要构造合适的全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了。
构造方法有:1.截长补短法。
2.平行线法(或平移法):若题设中含有中点可以试过中点作平行线或中位线,对Rt△,有时可作出斜边的中线。
3.旋转法:对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形。
4.倍长中线法:题中条件若有中线,可延长一倍,以构造全等三角形,从而将分散条件集中在一个三角形内。
5.翻折法:若题设中含有垂线、角的平分线等条件的,可以试用轴对称性质,沿轴翻转图形来构造全等三角形。
下面举例说明几种常见的构造方法,供同学们参考.1.截长补短法(通常用来证明线段和差相等)“截长法”即把结论中最大的线段根据已知条件分成两段,使其中一段与较短线段相等,然后证明余下的线段与另一条线段相等的方法.“补短法”为把两条线段中的一条接长成为一条长线段,然后证明接成的线段与较长的线段相等,或是把一条较短的线段加长,使它等于较长的一段,然后证明加长的那部分与另一较短的线段相等.例1.如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD.例2 已知:如图,AB=AC,E为AB上一点,F是AC延长线上一点,且BE=CF,EF交BC于点D.求证:DE=DF.(2)已知:如图,AB=AC,E为AB上一点,F是AC延长线上一点,且,EF交BC于点D,且D为EF的中点.求证:BE=CF.例3(北京市数学竞赛试题,天津市数学竞赛试题)如图所示,ABC是边长为1的NMAAMN正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.1.如图已知:正方形ABCD 中,∠BAC 的平分线交BC 于E ,求证:AB+BE=AC .2.(06年北京中考题)已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.DOEC BA4321FDOE CB A3.已知:如图,ABCD是正方形,∠FAD=∠FAE. 求证:BE+DF=AE.如图,四边形ABPC中,,,,求证:.FEDCBA2.平行线法(或平移法)若题设中含有中点可以试过中点作平行线或中位线,对Rt△,有时可作出斜边的中线.例△ABC中,∠BAC=60°,∠C=440°AP平分∠BAC交BC于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ.说明:⑴本题也可以在AB截取AD=AQ,连OD,构造全等三角形,即“截长补短法".⑵本题利用“平行法”解法也较多,举例如下:①如图(2),过O作OD∥BC交AC于D,则△ADO≌△ABO来解决.②如图(3),过O作DE∥BC交AB于D,交AC于E,则△ADO≌△AQO,△ABO≌△AEO来解决.③如图(4),过P作PD∥BQ交AB的延长线于D,则△APD≌△APC 来解决.④如图(5),过P作PD∥BQ交AC于D,则△ABP≌△ADP来解决.(本题作平行线的方法还很多,感兴趣的同学自己研究)3.旋转法对题目中出现有一个公共端点的相等线段时,可试用旋转方法构造全等三角形例.已知:如图(6),P为△ABC内一点,且PA=3,PB=4,PC=5,求∠APB的度数.分析:直接求∠APB的度数,不易求,由PA=3,PB=4,PC=5,联想到构造直角三角形.4.倍长中线法题中条件若有中线,可延长一倍,以构造全等三角形,从而将分散条件集中在一个三角形内。
北师大版七年级数学下册 第四章 证明(构造)全等三角形常用方法与技巧(含答案)

第四章证明(构造)全等三角形常用方法与技巧一、截长补短法1.如图,在正方形ABCD中,E是AB上一点,点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?解:成立.理由如下:如图,延长AD至F,使DF=BE,连接CF.在正方形ABCD中,BC=DC,∠B=∠CDA=90°,所以∠CDF=∠B=90°.又因为BE=DF,所以△CBE≌△CDF(SAS).所以CE=CF,∠BCE=∠DCF.所以∠BCE+∠ECD=∠DCF+∠ECD.所以∠ECF=∠BCD=90°.因为∠GCE=45°,所以∠GCF=∠GCE=45°.又因为CE=CF,GC=GC,所以△ECG≌△FCG(SAS).所以GE=GF.所以GE=DF+GD=BE+GD.2.如图,在△ABC 中,BE 是∠ABC 的平分线,AD ⊥BE ,垂足为D.试说明:∠2=∠1+∠C.解:如图,过点B 作BG ⊥BC 交CF 的延长线于点G.因为∠ACB =90°,所以∠2+∠ACF =90°.因为CE ⊥AD ,所以∠AEC =90°.所以∠1+∠ACF =180°-∠AEC =180°-90°=90°.因为CE ⊥AD ,所以∠AEC =90°.所以∠1+∠ACF =180°-∠AEC =180°-90°=90°.在△ABD 和△F BD 中,⎩⎪⎨⎪⎧∠ABD =∠FBD ,BD =BD ,∠ADB =∠FDB =90°,所以△ABD ≌△FBD (ASA).所以∠2=∠DFB .又因为∠DFB =180°-∠AFC ,∠1+∠C =180°-∠AFC ,所以∠DFB =∠1+∠C .所以∠2=∠1+∠C .3.如图,在直角三角形ABC 中,∠ACB =90°,AC =BC ,∠ABC =45°,点D 为BC 的中点,CE ⊥AD 于点E ,其延长线交AB 于点F ,连接DF.试说明:∠ADC =∠BDF.解:如图,过点B 作BG ⊥BC 交CF 的延长线于点G.因为∠ACB =90°,所以∠2+∠ACF =90°.因为CE ⊥AD ,所以∠AEC =90°.所以∠1+∠ACF =180°-∠AEC =180°-90°=90°.因为CE ⊥AD ,所以∠AEC =90°.所以∠1+∠ACF =180°-∠AEC =180°-90°=90°.所以∠1=∠2.在△ACD 和△CBG 中,⎩⎪⎨⎪⎧∠1=∠2,AC =CB ,∠ACD =∠CBG =90°,所以△ACD ≌△CBG (ASA).所以∠ADC =∠G ,CD =BG .因为点D 为BC 的中点,所以CD =BD .所以BD =BG .所以∠GBF =∠DBG -∠DBF =90°-45°=45°.所以∠DBF =∠GBF .在△BDF 和△BGF 中,⎩⎪⎨⎪⎧BD =BG ,∠DBF =∠GBF ,BF =BF ,所以△BDF ≌△BGF (SAS).所以∠BDF =∠G .所以∠ADC =∠BDF .四、旋转法4. 如图,在正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE +DF =EF ,求∠EAF 的度数.解:如图,延长CB 到点H ,使得BH =DF ,连接AH.所以∠D =∠ABH =90°.在△ABH 和△ADF 中,⎩⎪⎨⎪⎧AB =AD ,∠ABH =∠D =90°,BH =DF ,所以△ABH ≌△ADF (SAS).所以AH =AF ,∠BAH =∠DAF .所以∠BAH +∠BAF =∠DAF +∠BAF .所以∠HAF =∠BAD =90°.因为BE +DF =EF ,所以BE +BH =EF ,即EH =EF .在△AEH 和△AEF 中,⎩⎪⎨⎪⎧AH =AF ,AE =AE ,EH =EF ,所以△AEH ≌△AEF (SSS).所以∠EAH =∠EAF .所以∠EAF=12∠HAF =45°.五、倍长中线法5. 如图,在△ABC 中,D 为BC 的中点.若AB =5,AC =3,求AD 长度的取值范围.解:如图,延长AD 至点E ,使DE =AD ,连接BE.因为D 为BC 的中点,所以CD =BD.又因为AD =ED ,∠ADC =∠EDB ,所以△ADC ≌△EDB(SAS).所以AC =EB.因为AB -EB<AE<AB +EB ,又因为AB =5,AC =3,所以2<2AD<8. 所以1<AD<4.综合练习1.如图,在△ABC 中,D 是AB 上一点,DF 交AC 于点E ,AE =EC ,DE =EF ,则下列结论中:①∠ADE =∠EFC ;②∠ADE +∠ECF +∠FEC =180°;③∠B +∠BCF =180°;④S △ABC =S 四边形DBCF ,正确的结论有( )A .4个B .3个C .2个D .1个2.如图,D ,E ,F 分别为AB ,AC ,BC 上的点,且DE ∥BC ,△ABC 沿线段DE 折叠,使点A 落在点F 处.若∠B=50°,则∠BDF =________.3.如图,已知边长为1的正方形ABCD ,AC ,BD 交于点O ,过点O 任作一条直线分别交AD ,BC 于点E ,F ,则阴影部分的面积是________.4.如图,AD ,AE 分别是△ABC 的角平分线、高线,且∠B =50°,∠C =70°,则∠EAD =________.5.如图,已知四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于点E ,且AE =1(AB +AD ),若∠D =115°,则∠B =________.6.如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A旋转,BD⊥l于D,CE⊥l于E.(1)试说明:DE=BD+CE.(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.7.在△ABC中,AB=AC,D是直线BC上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.设∠BAC=α,∠DCE=β.(1)如图①,点D在线段BC上移动时,角α与β之间的数量关系是____________,请说明理由;(2)如图②,点D在线段BC的延长线上移动时,角α与β之间的数量关系是____________,请说明理由;(3)当点D在线段BC的反向延长线上移动时,请在图③中画出完整图形并猜想角α与β之间的数量关系是________________.参考答案1.A2.80° 3.144.10° 点拨:由AD 平分∠BAC ,可得∠DAC =12∠BAC =12×(180°-50°-70°)=30°.由AE ⊥BC ,可得∠EAC =90°-∠C =20°,所以∠EAD =30°-20°=10°.5.65° 点拨:过C 作CF ⊥AD ,交AD 的延长线于F .因为AC 平分∠BAD ,所以∠CAF =∠CAE .因为CF ⊥AF ,CE ⊥AB ,所以∠AFC =∠AEC =90°.在△CAF 和△CAE 中,⎩⎪⎨⎪⎧∠CAF =∠CAE ,∠AFC =∠AEC ,AC =AC ,所以△CAF ≌△CAE (AAS ).所以FC =EC ,AF =AE .因为AE =12(AB +AD ), 所以AF =12(AE +EB +AD ), 即AF =BE +AD .所以DF =BE .在△FDC 和△EBC 中,⎩⎪⎨⎪⎧CF =CE ,∠CFD =∠CEB ,DF =BE ,所以△FDC ≌△EBC (SAS ).所以∠FDC =∠EBC .又因为∠ADC =115°,所以∠FDC =180°-115°=65°.所以∠B =65°.6.解:(1)因为BD ⊥l ,CE ⊥l ,所以∠ADB =∠AEC =90°.又因为∠BAC=90°,所以∠BAD+∠CAE=90°.所以∠DBA=∠CAE.因为AB=AC,∠ADB=∠CEA=90°,所以△ABD≌△CAE(AAS).所以AD=CE,BD=AE.则AD+AE=BD+CE,即DE=BD+CE.(2)(1)中结论不成立.DE=BD-CE.同(1)说明△ABD≌△CAE,所以BD=AE,AD=CE.又因为AE-AD=DE,所以DE=BD-CE.7.解:(1)α+β=180°理由:因为∠DAE=∠BAC,所以∠DAE-∠CAD=∠BAC-∠CAD,即∠BAD=∠CAE.又因为AB=AC,AD=AE,所以△ABD≌△ACE(SAS).所以∠ABC=∠ACE.在△ABC中,∠BAC+∠ABC+∠ACB=180°,∠ABC=∠ACE,所以∠BAC+∠ACB+∠ACE=180°.因为∠ACB+∠ACE=∠DCE=β,所以α+β=180°.(2)α=β理由:因为∠DAE=∠BAC,所以∠BAD=∠CAE.又因为AB=AC,AD=AE,所以△ABD≌△ACE(SAS).所以∠ABC=∠ACE.因为∠ABC+∠BAC+∠ACB=180°,∠ACB+∠ACD=180°,所以α=β.(3)α=β.画图略.。
构造全等三角形种常用方法

构造全等三角形种常用方法在证明两个三角形全等时,选择三角形全等得五种方法(“SSS ”,“SA S”,“ASA ”,“AAS ”,“HL ”)中,至少有一组相等得边,因此在应用时要养成先找边得习惯。
如果选择找到了一组对应边,再找第二组条件,若找到一组对应边则再找这两边得夹角用“SAS ”或再找第三组对应边用“SSS ”;若找到一组角则需找另一组角(可能用“ASA ”或“AAS ”)或夹这个角得另一组对应边用“SAS”;若就就是判定两个直角三角形全等则优先考虑“HL ”。
上述可归纳为:搞清了全等三角形得证题思路后,还要注意一些较难得一些证明问题,只要构造合适得全等三角形,把条件相对集中起来,再进行等量代换,就可以化难为易了、下面举例说明几种常见得构造方法,供同学们参考、1、截长补短法例1、如图(1)已知:正方形ABCD 中,∠BAC 得平分线交B C于E ,求证:A B+BE=AC 、 解法(一)(补短法或补全法)延长AB 至F使AF=AC ,由已知△AEF ≌△AEC,∴∠F =∠ACE=45º, ∴BF =B E,∴AB+BE =A B+BF=AF=AC 、 解法(二)(截长法或分割法)在A C上截取AG=AB,由已知 △ AB E≌△AGE,∴EG=B E, ∠A GE=∠ABE,∵∠ACE =45º, ∴CG =EG, ∴AB +BE =AG+CG=AC、 2、平行线法(或平移法)若题设中含有中点可以试过中点作平行线或中位线,对Rt △,有时可作出斜边得中线、例2、△ABC 中,∠BAC=60°,∠C =40°A P平分∠BAC 交B C于P,B Q平分∠ABC 交A C于Q, 求证:A B+B P=BQ+A Q、证明:如图(1),过O 作O D∥BC 交AB 于D,∴∠ADO =∠ABC=180°-60°-40°=80°,又∵∠AQ O=∠C +∠QBC=80°,∴∠ADO=∠AQO ,又∵∠DA O=∠QAO ,OA=AO, ∴△ADO ≌△AQO,∴OD=O Q,AD=AQ ,又∵OD ∥BP,∴∠PBO=∠DOB ,又∵∠PBO=∠D BO,∴∠DBO=∠D OB,∴BD=O D,∴AB +BP=AD+DB+B P=A Q+OQ+B O=AQ+BQ 、说明:⑴本题也可以在AB 截取AD=AQ ,连OD,构造全等三角形,即“截长补短法”、⑵本题利用“平行法”解法也较多,举例如下: ① 如图(2),过O 作OD ∥BC 交AC 于D, 则△ADO ≌△ABO 来解决、 ② 如图(3),过O 作D E∥BC 交AB 于D,交AC 于E,则△ADO≌△AQ O,△A BO ≌△AE O来解决、 ③ 如图(4),过P作P D∥B Q交A B得延长线于D,则△A PD ≌△APC 来解决、 ④ 如图(5),过P 作PD ∥BQ 交A C于D, 则△AB P≌△ADP 来解决、 (本题作平行线得方法还很多,感兴趣A B C P Q D OO A B C P Q D图(2) A B C PQ D E 图(3) O A B C P Q图(4)DOA BCP Q 图(5)D OD得同学自己研究)、 3、旋转法对题目中出现有一个公共端点得相等线段时,可试用旋转方法构造全等三角形。
模型构建:全等三角形中的常见七种解题模型全攻略(解析版)

专题11模型构建专题:全等三角形中的常见七种解题模型【考点导航】目录【典型例题】 (1)【模型一平移型模型】 (1)【模型二轴对称型模型】 (8)【模型三四边形中构造全等三角形解题】 (12)【模型四一线三等角模型】 (19)【模型五三垂直模型】 (25)【模型六旋转型模型】 (30)【模型七倍长中线模型】 (39)【典型例题】【模型一平移型模型】例题:(2023秋·江苏淮安·八年级淮安市浦东实验中学校考开学考试)如图,点E ,C 在线段BF 上,AB DE ∥,AB DE =,BE CF =.(1)求证:ABC DEF ≌;(2)若40B ∠=︒,70D ∠=︒,求ACF ∠的度数.【答案】(1)见解析(2)110︒【分析】(1)首先根据,AB DE ∥可得B DEF ∠=∠,再根据BE CF =,可得出BC EF =,即可判定ABC DEF ≌△△;(2)首先根据(1)中两三角形全等,可得70A D ∠=∠=︒,在ABC 中根据外角的性质即可求出ACF ∠.【详解】(1)证明: AB DE ∥,B DEF∴∠=∠BE CF = ,BE EC CF EC ∴+=+,即BC EF =,∴在ABC 和DEF 中,AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩,∴ABC DEF ≌△△.(2) ABC DEF ≌△△,40B ∠=︒,70D ∠=︒,70A D ∴∠=∠=︒,ACF ∠ 是ABC 的外角,110ACF A B ∴∠=∠+∠=︒.【点睛】此题主要考查平行线的性质,三角形全等的判定和性质,熟练运用性质定理,即可解题.【变式训练】1.(2023秋·浙江·八年级专题练习)如图,在ACD 和CEB 中,点A 、B 、C 在一条直线上,D E AD EC AD EC ∠=∠=,∥,.求证:ACD CBE ≌.【答案】见解析【分析】根据平行线的性质得出A ECB ∠=∠,再根据全等三角形的判定定理ASA 证明ACD CBE ≌.【详解】AD EC ∥ ,A ECB ∴∠=∠,在ACD 和CEB 中,A ECB AD ECDE ∠=∠⎧⎪=⎨⎪∠=∠⎩,(ASA)ACD CBE ∴△≌△.【点睛】本题考查了全等三角形的判定定理和平行线的性质,能熟记全等三角形的判定定理是解此题的关键.2.(2023秋·浙江·八年级专题练习)如图,已知ABC DEF ≌△△,点B ,E ,C ,F 在同一条直线上.(1)若140BED ∠=︒,75D ∠=︒,求ACB ∠的度数;(2)若2BE =,3EC =,求BF 的长.【答案】(1)65︒(2)7【分析】(1)由三角形外角性质,得65F BED D ∠=∠-∠=︒,由三角形全等知65ACB F ∠=∠=︒;(2)由条件可推出5BC BE EC =+=,由三角形全等知5BC EF ==,故7BF BE EF =+=.【详解】(1)解:∵140BED ∠=︒,75D ∠=︒,∴65F BED D ∠=∠-∠=︒.∵ABC DEF ≌△△,∴65ACB F ∠=∠=︒;(2)解:∵2BE =,3EC =,∴5BC BE EC =+=∵ABC DEF ≌△△,∴5BC EF ==,∴257BF BE EF =+=+=.故答案为:7.'='时的情形,求此时△ADE(1)如图2,善思小组的同学画出了BA BD(2)如图3,点F是BC的中点,在△ADE平移过程中,连接E F''交射线'=始终成立!请你证明这一结论;现OE OF拓展延伸:(3)请从A,B两题中任选一题作答,我选择______题.A.在△ADE平移的过程中,直接写出以F,A',D¢为顶点的三角形成为直角三角形时,ABC 是等边三角形,6AB =3AD CD ∴==,BD AC ⊥,将△ADE 从图1的位置开始,沿射线∴A D ''3AD ==,A B BD '=' ,BD AC ⊥,13ADE 是等边三角形,3AD =60DAE ∴∠=︒,3AE =,将△ADE 从图1的位置开始,沿射线60D A E DAE ∴∠=∠'=''︒,A E 'ABC 是等边三角形,6AB =190CD F ∴='∠︒,60C ∠=︒ ,30D FC ∴='∠︒,1322CD CF ∴='=,33322DD CD CD ''∴=-=-=;同理可得32A C '=,39622AA AC A C ''∴=-=-=;△ADE 平移的距离是92;综上所述,以F ,A ',D ¢为顶点的三角形成为直角三角形时,△当A '与C 重合时,如图:A D E ''' 是等边三角形,60E A D A D E E '''''∴∠=∠''=∠=︒,3A F A D '''== ,30A FD A D F ''''∴∠=∠=︒,90FD E A D F A D E ∴∠=∠'''''''+∠=︒,即以F ,D ¢,E '为顶点的三角形成为直角三角形,此时336DD CD A D =+='+'=',△ADE 平移的距离是6;当90D E F ∠=''︒时,如图:60A E D E A D ∠=︒'=∠''''' ,30A E O D E F A E D ∴∠=∠'''''''-∠=︒,30A OE D A E A E O '''''∴∠=∠'-∠='︒,A E O A OE ∴∠='∠''',3A O A E '''∴==,由()2知A OE '' ≌COF ,3CO A O '∴==,333312DD CD CO A O A D '''∴=+++=+++=',△ADE 平移的距离是12;综上所述,以F ,D ¢,E '为顶点的三角形成为直角三角形时,△ADE 平移的距离是6或12.【点睛】本题考查几何变换综合应用,涉及等边三角形的性质及应用,全等三角形的判定与性质,平移变换等知识,解题的关键是分类讨论思想的应用.【模型二轴对称型模型】例题:(2023秋·内蒙古呼伦贝尔·八年级校考期中)如图,AB AD =,BC DC =,求证:B D ∠=∠.【答案】见解析【分析】根据SSS 证明ABC ADC △≌△,得出B D ∠=∠即可.【详解】证明:∵在ABC 和ADC △中AB AD AC AC BC DC =⎧⎪=⎨⎪=⎩,∴()SSS ABC ADC ≌△△,∴B D ∠=∠.【点睛】本题主要考查了三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定方法,证明ABC ADC △≌△.【变式训练】1.(2023春·四川成都·七年级成都嘉祥外国语学校校考期中)如图,在ABC 中,AB AC =,D 是BC 的中点,EAB FAC ∠=∠,且AE AF =,求证:EDB FDC ∠=∠.【答案】见解析【分析】由等腰三角形的性质得AD BC ⊥,BAD CAD ∠=∠,再证(SAS)AED AFD △≌△,得ADE ADF ∠=∠,即可得出结论.【详解】解:证明:连接AD ,AB AC = ,D 是BC 的中点,AD BC ∴⊥,BAD CAD ∠=∠,90ADB ADC ∴∠=∠=︒,EAB FAC ∠=∠ ,EAB BAD FAC CAD ∴∠+∠=∠+∠,即DAE DAF ∠=∠,在AED △与AFD △中,AE AF DAE DAF AD AD =⎧⎪∠=∠⎨⎪=⎩,(SAS)AED AFD ∴△≌△,ADE ADF ∴∠=∠,ADB ADE ADC ADF ∴∠-∠=∠-∠,即EDB FDC ∠=∠.【点睛】本题考查了全等三角形的判定与性质以及等腰三角形的性质等知识,熟练掌握等腰三角形的性质,证明三角形全等是解题的关键.2.(2023秋·河南南阳·八年级统考期末)如图,点E 、F 是线段AB 上的两个点,CE 与DF 交于点M .已知AF BE =,AC BD =,A B ∠=∠.(1)求证:C D ∠=∠;(2)若60FME ∠=︒.求证:MFE 是等边三角形.【答案】(1)证明见解析(2)证明见解析【分析】(1)证明ACE BDF ≌△△即可.(2)根据ACE BDF ≌△△得到ME MF =,根据有一个角是60︒的等腰三角形是等边三角形证明.【详解】(1)证明:∵AF BE =,∴AF FE BE FE +=+,∴AE BF =,∵AE BF A B AC BD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ACE BDF ≌,∴C D ∠=∠.(2)∵()SAS ACE BDF ≌,∴DFE CEF ∠=∠,∴FM EM =,∵60FME ∠=︒,∴MFE 是等边三角形.【点睛】本题考查了三角形全等的判断和性质,等边三角形的判定,熟练掌握三角形全等的判断和性质,等边三角形的判定是解题的关键.3.(2023春·湖南益阳·八年级校考期中)两组邻边分别相等的四边形我们称它为筝形.如图,在筝形ABCD中,AB AD =,BC DC =,AC 、BD 相交于点O ,求证:(1)ABC ADC △≌△;(2)AC BD ⊥.【答案】(1)见解析;(2)见解析.【分析】(1)分别利用SSS 证ABC ADC ≌即可;(2)由ABC ADC ≌得ACB ACD ∠∠=,利用等腰三角形的性质即可得AC BD ⊥.【详解】(1)证明:在ABC 和ADC 中,AB AD BC DC AC AC =⎧⎪=⎨⎪=⎩,∴ABC ADC ≌(SSS ).(2)证明:由(1)得ABC ADC ≌,∴ACB ACD ∠∠=,∵BC CD =,∴AC BD ⊥.【点睛】此题考查全等三角形的判定与性质以及等腰三角形的性质,解题关键在于掌握全等三角形的判定定理.【模型三四边形中构造全等三角形解题】例题:(2023春·江苏淮安·七年级校考阶段练习)已知:如图,AC BC =,AD BD =,E 、F 分别是AC 和BC 的中点.求证:DE DF =.【答案】证明见解析.【分析】由三边对应相等的两个三角形是全等三角形可证ADC BDC ≌ ,再根据全等三角形的性质可由两边对应相等以及它们的夹角相等的两个三角形全等可证CDE CDF ≌ ,即可得出结论.【详解】证明:连接CD在ADC △与BDC 中,AC BC CD CD AD BD =⎧⎪=⎨⎪=⎩()SSS ADC BDC ∴≌ ,ACD BCD ∴∠=∠,【变式训练】1.(2023春·广西玉林·八年级统考期末)如图,在四边形ABCD 中,AB AD =,CB CD =,我们把这种两组邻边分别相等的四边形叫做筝形.根据学习平行四边形性质的经验,小文对筝形的性质进行了探究.(1)小文通过观察、实验、猜想、证明得到筝形角的性质是“筝形有一组对角相等”.请你帮他将证明过程补充完整.已知:如图,在筝形ABCD 中,AB AD =,CB CD =.求证:___________.证明:___________(2)小文连接筝形的两条对角线,探究得到筝形对角线的性质是___________.(写出一条即可)【答案】(1)B D ∠=∠,见解析(2)AC BD ⊥(或AC 垂直平分线段BD )【分析】(1)B D ∠=∠,连接AC ,证明ABC ADC △△≌,即可得结论;(2)根据全等三角形的性质即可得筝形的两条对角线互相垂直.【详解】(1)解:证明:连接AC ,在ACB △和ACD 中,AB AD AC AC BC DC =⎧⎪=⎨⎪=⎩,()SSS ABC ADC ∴≌ ,B D ∴∠=∠;(2)证明:如图,连接BD ,交AC 于点O ,由(1)知ABC ADC △△≌,BAO DAO ∴∠=∠,在ABO 与ADO △中,AO AO BAO DAO AB AD =⎧⎪∠=∠⎨⎪=⎩()SAS ABO ADO ∴≅ BO DO ∴=,AOB AOD ∠=∠,180AOB AOD ︒∠+∠= ,90AOB AOD ∴∠=∠=︒,∴AC BD ⊥,∴两条对角线互相垂直.【点睛】本题考查了三角形全等的判定与性质,熟记三角形全等的判定方法是解题的关键.2.如图,在四边形ABCD 中,CB AB ⊥于点B ,CD AD ⊥于点D ,点E ,F 分别在AB ,AD上,AE AF =,CE CF =.(1)若8AE =,6CD =,求四边形AECF 的面积;(2)猜想∠DAB ,∠ECF ,∠DFC 三者之间的数量关系,并证明你的猜想.【答案】(1)48(2)∠DAB +∠ECF =2∠DFC ,证明见解析【解析】【分析】(1)连接AC ,证明△ACE ≌△ACF ,则S △ACE =S △ACF ,根据三角形面积公式求得S △ACF 与S △ACE ,根据S 四边形AECF=S △ACF +S △ACE 求解即可;(2)由△ACE ≌△ACF 可得∠FCA =∠ECA ,∠FAC =∠EAC ,∠AFC =∠AEC ,根据垂直关系,以及三角形的外角性质可得∠DFC +∠BEC =∠FCA +∠FAC +∠ECA +∠EAC =∠DAB +∠ECF .可得∠DAB +∠ECF =2∠DFC(1)解:连接AC ,如图,在△ACE 和△ACF 中AE AF CE CF AC AC =⎧⎪=⎨⎪=⎩3.在四边形ABDC中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.(1)试说明:DE=DF:(2)在图中,若G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明所归纳结论.(3)若题中条件“∠CAB=60°,∠CDB=120°改为∠CAB=α,∠CDB=180°﹣α,G在AB上,∠EDG满足什么条件时,(2)中结论仍然成立?【答案】(1)见解析;猜想CE 、EG 、BG 之间的数量关系为:证明:在ABD ∆和ACD ∆中,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩,【模型四一线三等角模型】例题:(2023春·广西南宁·七年级南宁市天桃实验学校校考期末)(1)问题发现:如图1,射线AE 在MAN ∠的内部,点B 、C 分别在MAN ∠的边AM 、AN 上,且AB AC =,若90BAC BFE CDE ∠=∠=∠=︒,求证: ≌ABF CAD ;(2)类比探究:如图2,AB AC =,且BAC BFE CDE ∠=∠=∠.(1)中的结论是否仍然成立,请说明理由;(3)拓展延伸:如图3,在ABC 中,AB AC =,AB BC >.点E 在BC 边上,2CE BE =,点D 、F 在线段AE 上,BAC BFE CDE ∠=∠=∠.若ABC 的面积为15,2DE AD =,求BEF △与CDE 的面积之比.【答案】(1)证明见详解;(2)成立,证明见详解;(3)1:4【变式训练】1.已知CD 是经过BCA ∠顶点C 的一条直线,CA CB =.E 、F 分别是直线CD 上两点,且BEC CFA α∠=∠=∠.(1)若直线CD 经过BCA ∠的内部,且E 、F 在射线CD 上,请解决下面问题:①如图1,若90BCA ∠=︒,90α∠=︒,求证:BE CF =;②如图2,若180BCA α∠+∠=︒,探索三条线段EF BE AF ,,的数量关系,并证明你的结论;(2)如图3,若直线CD 经过BCA ∠的外部,BCA α∠=∠,题(1)②中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确的结论再给予证明.【答案】(1)①见解析;②EF BE AF =-,见解析(2)不成立,EF BE AF =+,见解析【分析】(1)①利用垂直及互余的关系得到ACF CBE ∠=∠,证明BCE ≌CAF V 即可;②利用三等角模型及互补证明ACF CBE ∠=∠,得到BCE ≌CAF V 即可;(2)利用互补的性质得到EBC ACF ∠=∠,证明BCE ≌CAF V 即可.【详解】(1)①证明:∵90EE CD AF CD ACB ⊥⊥∠=︒,,,∴90BEC AFC ∠=∠=︒,∴9090BCE ACF CBE BCE ∠+∠=︒∠+∠=︒,,在BCE 和CAF V 中,EBC FCA BEC CFA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BCE ≌CAF V ()AAS ,∴BE CF =;②解:EF BE AF =-.证明:∵180BEC CFA ACB αα∠=∠=∠∠+∠=︒,,∴180180CBE BCE ACF ACB BCE BCE αα∠=︒-∠-∠∠=∠-∠=︒-∠-∠,,∴ACF CBE ∠=∠,在BCE 和CAF V 中,EBC FCA BEC CFA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BCE ≌CAF V ()AAS ,∴BE CF CE AF ==,,∴EF CF CE BE AF =-=-;(2)解:EF BE AF =+.理由:∵BEC CFA BCA αα∠=∠=∠∠=∠,,又∵180180EBC BCE BEC BCE ACF ACB ∠=∠=∠=︒∠+∠+∠=︒,,∴EBC BCE BCE ACF ∠+∠=∠+∠,∴EBC ACF ∠=∠,在BCE 和CAF V 中,EBC FCA BEC CFA BC CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BCE ≌CAF V ()AAS ,∴AF CE BE CF ==,,∴EF BE AF =+.【点睛】本题主要考查三角形全等的判定及性质,能够熟练运用三等角模型快速证明三角形全等是解题关键.2.(2023春·上海·七年级专题练习)在直线m 上依次取互不重合的三个点,,D A E ,在直线m 上方有AB AC =,且满足BDA AEC BAC α∠=∠=∠=.(1)如图1,当90α=︒时,猜想线段,,DE BD CE 之间的数量关系是____________;(2)如图2,当0180α<<︒时,问题(1)中结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;(3)应用:如图3,在ABC 中,BAC ∠是钝角,AB AC =,,BAD CAE BDA AEC BAC ∠<∠∠=∠=∠,直线m 与CB 的延长线交于点F ,若3BC FB =,ABC 的面积是12,求FBD 与ACE △的面积之和.【答案】(1)DE =BD +CE(2)DE =BD +CE 仍然成立,理由见解析(3)△FBD 与△ACE 的面积之和为4【分析】(1)由∠BDA =∠BAC =∠AEC =90°得到∠BAD +∠EAC =∠BAD +∠DBA =90°,进而得到∠DBA =∠EAC ,然后结合AB =AC 得证△DBA ≌△EAC ,最后得到DE =BD +CE ;(2)由∠BDA =∠BAC =∠AEC =α得到∠BAD +∠EAC =∠BAD +∠DBA =180°﹣α,进而得到∠DBA =∠EAC ,然后结合AB =AC 得证△DBA ≌△EAC ,最后得到DE =BD +CE ;(3)由∠BAD >∠CAE ,∠BDA =∠AEC =∠BAC ,得出∠CAE =∠ABD ,由AAS 证得△ADB ≌△CAE ,得出S △ABD =S △CEA ,再由不同底等高的两个三角形的面积之比等于底的比,得出S △ABF 即可得出结果.【详解】(1)解:DE =BD +CE ,理由如下,∵∠BDA =∠BAC =∠AEC =90°,∴∠BAD +∠EAC =∠BAD +∠DBA =90°,∴∠DBA =∠EAC ,∵AB =AC ,【模型五三垂直模型】例题:(2023春·辽宁本溪·七年级统考期末)已知90ACB ∠=︒,AC BC =,AD NM ⊥,BE NM ⊥,垂足分别为点D ,E .(1)如图①,求证:AD BE DE=+(2)如图②,(1)中的结论还成立吗?如果不成立,请写出线段AD BE DE ,,之间的数量关系,并说明理由.【答案】(1)见解析(2)(1)中的结论不成立.结论:DE AD BE =+,理由见解析【分析】(1)证明()AAS ADC CEB ≌△△,推出CD BE =,AD CE =,再利用线段间的代换即得结论;(2)证明()AAS ADC CEB ≌△△,推出CD BE =,AD CE =,利用线段间的代换即可得到结论,进而作出判断.【详解】(1)证明:∵AD NM ⊥,BE NM ⊥,∴90ADC CEB ∠=∠=︒,∴90CAD ACD ∠+∠=︒∵90ACB ∠=︒,∴90BCE ACD ∠+∠=︒,∴CAD BCE ∠=∠,在ADC △和CEB 中ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AAS ADC CEB ≌△△,∴CD BE =,AD CE =,∴CE CD DE BE DE =+=+,∴AD BE DE =+;(2)(1)中的结论不成立.结论:DE AD BE =+;理由如下:∵AD NM ⊥,BE NM ⊥,∴90ADC CEB ∠=∠=︒∵90ACB ∠=︒,∴90BCE ACD ∠+∠=︒,∴CAD BCE∠=∠在ADC △和CEB 中ADC CEB CAD BCE AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AAS ADC CEB ≌△△,∴CD BE =,AD CE =,∵DE CD CE =+,∴DE AD BE =+.【点睛】本题考查了全等三角形的判定和性质,属于常考题型,证明三角形全等是解题的关键.【变式训练】1.(2023春·甘肃酒泉·八年级校联考期末)在ABC 中,90ACB ∠= ,AC BC =,直线MN 经过点C ,且AD MN ⊥于D ,BE MN ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①ADC CEB △≌△;②DE AD BE =+;(2)当直线MN 绕点C 旋转到图2的位置时,求证:DE AD BE =-;【答案】(1)①见解析,②见解析(2)见解析【分析】(1)①由已知推出90ADC BEC ∠=∠= ,90DAC ACD ∠+∠=o 推出DAC BCE =∠∠,根据角角边即可推出.②由①得到,AD CE CD BE ==,即可求出答案.(2)与(1)类似证出ADC CEB △≌△,得到,AD CE CD BE ==代入已知即可知道答案.【详解】(1)①证明:AD DE ⊥ ,BE DE ⊥,90ADC BEC ∴∠=∠= ,90ACB ∠= ,90ACD BCE ∴∠+∠= ,90DAC ACD ∠+∠=o ,DAC BCE ∴∠=∠,在ADC △和CEB 中,CDA BEC DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS ADC CEB ∴△≌△.②证明:由(1)知:ADC CEB △≌△,AD CE ∴=,CD BE =,DC CE DE += ,AD BE DE ∴+=.(2)证明:BE EC ⊥ ,AD CE ⊥,90ADC BEC ∴∠=∠= ,90EBC ECB∴∠+∠=o,90ACB∠=,90ECB ACE∴∠+∠= ,ACD EBC∴∠=∠,在ADC△和CEB中,ACD CBEADC BECAC BC∠=∠⎧⎪∠=∠⎨⎪=⎩,()AASADC CEB∴△≌△,AD CE∴=,CD BE=,DE EC CD AD BE∴=-=-.【点睛】本题考查了全等三角形的性质和判定,等根据已知条件证出符合全等的条件是解题的关键.2.如图,已知:在ABC中,90ACB∠=︒,AC BC=,直线MN经过点C,AD MN⊥,BE MN⊥.(1)当直线MN绕点C旋转到图(1)的位置时,求证:ADC CEB≅;(2)当直线MN绕点C旋转到图(2)的位置时,求证:DE AD BE=-;(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系:____________.【答案】(1)见解析;(2)见解析;(3)DE=BE-AD【分析】(1)由已知推出∠ADC=∠BEC=90°,因为∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,推出∠DAC=∠BCE,根据AAS即可得到答案;(2)结论:DE=AD-BE.与(1)证法类似可证出∠ACD=∠EBC,能推出△ADC≌△CEB,得到AD=CE,CD=BE,即可得到答案.(3)结论:DE=BE-AD.证明方法类似.【详解】解:(1)证明:如图1,∵AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠BEC =90°,∵∠ACB =90°,∴∠ACD +∠BCE =90°,∠DAC +∠ACD =90°,∴∠DAC =∠BCE ,在△ADC 和△CEB 中,CDA BEC DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS );(2)如图2,∵BE ⊥EC ,AD ⊥CE ,∴∠ADC =∠BEC =90°,∴∠EBC +∠ECB =90°,∵∠ACB =90°,∴∠ECB +∠ACE =90°,∴∠ACD =∠EBC ,在△ADC 和△CEB 中,ACD CBE ADC BEC AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴AD =CE ,CD =BE ,∴DE =EC -CD =AD -BE .(3)DE =BE -AD ;如图3,∵∠ACB =90°,∴∠ACD +∠BCE =90°∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,∴∠ACD +∠DAC =90°,∴∠DAC =∠ECB ,在△ACD 和△CBE 中,ADC CEB DAC ECB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (AAS ),∴AD =CE ,CD =BE ,∴DE =CD -CE =BE -AD .【点睛】本题主要考查了余角的性质,全等三角形的性质和判定等知识点,能根据已知证明△ACD ≌△CBE 是解此题的关键,题型较好,综合性比较强.【模型六旋转型模型】例题:在Rt △ABC 中,∠ACB =90°,CA =CB ,点D 是直线时针旋转90°,得到线段CE ,连接EB .(1)操作发现如图1,当点D 在线段AB 上时,请你直接写出AB 与(2)①如图2中,结论:BE=AB+BD.理由:∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,∵CA=CB,CD=CE,∴△ACD≌△BCE(SAS),∴AD=BE,∵AD=AB+BD,AD=BE,∴BE=AB+BD.②如图3中,结论:BD=AB+BE.理由:∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,∵CA=CB,CD=CE,∴△ACD≌△BCE(SAS)∴AD=BE,∵BD=AB+AD,AD=BE,∴BD=AB+BE.(3)如图2中,∵AB=5,BD=7,∴BE=AD=5+7=12,【变式训练】(1)当两个三角板如图(1)所示的位置摆放时,D、B,C在同一直线上,【类比探究】(2)当三角板ABC保持不动时,将三角板DBE绕点B顺时针旋转到如图的数量关系和位置关系,并说明理由.【拓展延伸】【详解】(1)∵ABC 和DBE 是两个都含有45︒角的大小不同的直角三角板,∴90DBE ABC ∠=∠=︒,AB BC =,BD BE =,∴()SAS DBA EBC ≅ ,∴AD CE =;(2)AD CE =,AD CE ⊥,理由如下:∵90DBE ABC ∠=∠=︒,∴90DBA BCE DBC ∠=∠=︒-∠,∵AB BC =,BD BE =,∴()SAS DBA EBC ≅ ,∴AD CE =,ADB CEB ∠=∠,延长AD 与CE 交于点O ,∵90BDE BED ∠+∠=︒,∴90BDE BEC CED ∠+∠+∠=︒,∴90BDE ADB CED ∠+∠+∠=︒,∴90ODE OED ∠+∠=︒,∴90O ∠=︒,∴AD CE ⊥;(3)过A 作AC AM ⊥交CD 延长线于M ,过A 作AN CD ⊥交CD 于N ,∵45ACD ∠=︒,∴45ACD M ∠=∠=︒,∴AC AM =,∵90,BAD AB AD∠=︒=∴90BAC DAM DAC ∠=∠=︒-∠【答案】(1),BC AD BC AD =⊥;(2)45︒;(3)见解析,45︒;(4)存在,2BM AM OM=+【分析】(1)由条件根据三角形全等判定定理SAS 得BOC AOD ≌△△,可证;(3)类比上面思路,通过构建三角形全等BON AOM ≌△△推出ON OM =,进而易得45COM ∠=︒,(4)根据(3)的结论,推导出NOM △是等腰直角三角形,然后根据等腰直角三角形的性质,化简即可得到答案.【详解】(1)由题意得,AO BO =,OC OD =,90AOB COD ∠=∠=︒,()SAS BOC AOD ∴≌△△,BC AD ∴=,CBO DAO ∠=∠,在Rt AOD 中,90DOA ADO ∠+∠=︒,90CBO ADO ∴∠+∠=︒,90BMD ∴∠=︒,即BC AD ⊥,故答案为:,BC AD BC AD =⊥.(2)45OCD ODC ∠=∠=︒ ,CD BO ∥,45COB OCD ∴∠=∠=︒,又90AOB ∠=︒,45AOC AOB BOC ∴∠=∠-∠=︒,即45α=︒,故答案为:45︒.(3)如图,过O 点作NO OM ⊥,交MB 于N 点,由(1)易知()SAS BOC AOD ≌,CBO DAO ∴∠=∠,BON NOA NOA AOM ∠+∠=∠+∠ ,BON AOM ∴∠=∠,又AO BO =,易得()ASA BON AOM ≌△△,【模型七倍长中线模型】例题:(2023春·全国·七年级专题练习)[阅读理解]课外兴趣小组活动时,老师提出了如下问题:如图1,在ABC ∆中,若8AB =,6AC =,求BC 边上的中线AD 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:如图2,延长AD 到点E ,使DE AD =,连结BE ,请根据小明的方法思考:(1)由已知和作图能得到ADC EDB ≌△△,其理由是什么?(2)AD 的取值范围是什么?[感悟]解题时,条件中出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和结论转化到一个三角形中.[问题解决](3)如图3,AD 是ABC ∆的中线,BE 交AC 于点F ,且AE EF =,试说明AC BF =.【答案】(1)见解析(2)17AD <<(3)见解析【分析】(1)根据AD DE =,ADC BDE ∠=∠,BD DC =推出ADC ∆和EDB ∆全等即可;(2)根据全等得出6BE AC ==,2AE AD =,由三角形三边关系定理得出86286AD -<<+,求出即可;(3)延长AD 到M ,使AD DM =,连接BM ,根据SAS 证ADC MDB ∆∆≌,推出BM AC =,CAD M ∠=∠,根据AE EF =,推出CAD AFE BFD ∠=∠=∠,求出BFD M ∠=∠,根据等腰三角形的性质求出即可.【详解】(1) 在ADC ∆和EDB ∆中AD DE ADC BDE BD CD =⎧⎪∠=∠⎨⎪=⎩,()ADC EDB SAS ∴∆∆≌,∴全等的理由是:SAS ;(2) 由(1)知:ADC EDB ∆∆≌,6BE AC ∴==,2AE AD =, 在ABE ∆中,8AB =,由三角形三边关系定理得:86286AD -<<+,17AD ∴<<;(3)证明:延长AD 到M ,使AD DM =,连接BM ,AD 是ABC ∆中线,CD BD ∴=,在ADC ∆和MDB △中DC DB ADC MDB DA DM =⎧⎪∠=∠⎨⎪=⎩ΔΔ()ADC MDB SAS ∴≌,BM AC ∴=,CAD M ∠=∠,AE EF = ,CAD AFE ∴∠=∠,AFE BFD ∠=∠ ,BFD CAD M ∴∠=∠=∠,BF BM AC ∴==,即AC BF =.【点睛】本题属于三角形综合题,考查了三角形的中线,三角形的三边关系定理,等腰三角形性质和判定,全等三角形的性质和判定等知识点,掌握中线倍长模型,添加辅助线是关键.【变式训练】如图①,在ABC 中,若5AB =,3AC =,求BC 边上的中线延长AD 到点E 使DE AD =,再连接BE ,这样就把AB ,AC 关系可判断线段AE 的取值范围是;则中线AD 的取值范围是(2)问题解决:如图②,在ABC 中,D 是BC 边的中点,DE DF ⊥于点D ,【答案】(1)28,14AE AD <<<<;(2)EF EB CF >+,见解析;(3)BE DF EF+=【分析】(1)延长AD 到点E 使DE AD =,再连接BE ,证明(SAS)ADC EDB ≌△△,可得AC BE =,再由三角形三角关系可得28AE <<,14AD <<;(2)延长FD 至G ,使FD DG =,连接BG ,证明(SAS)CFD GBD ≌,可得BG FC =,连接EG ,可知EFG 是等腰三角形,则FE EG =,在EBG 中,EG EB BG >+,即EF EB CF >+;(3)延长AB 至H 使BH DF =,连接CH ,证明(SAS)CBH CDF ≌,可推导出80CEH ∠=︒,再证明(SAS)FCE HCE ≌,则EH EF =,能推导出BE DF EF +=.【详解】解:(1)延长AD 到点E 使DE AD =,再连接BE ,CD BD = ,ADC BDE ∠=∠,AD DE =,(SAS)ADC EDB ∴△≌△,AC BE ∴=,在ABE 中,AB BE AE AB BE -<<+,28AE ∴<<,2AE AD = ,14AD ∴<<,故答案为:28AE <<,14AD <<;(2)延长FD 至G ,使FD DG =,连接BG ,CD BD = ,CDF BDG ∠=∠,FD DG =,(SAS)CFD GBD ∴ ≌,BG FC ∴=,连接EG ,ED FD ⊥ ,FD DG =,EFG ∴△是等腰三角形,FE EG ∴=,在EBG 中,EG EB BG >+,即EF EB CF >+;(3)延长AB 至H 使BH DF =,连接CH ,180ABC D ∠+∠=︒ ,180ABC CBH ∠+∠=︒,D CBH ∴∠=∠,CD CB = ,BH DF =,(SAS)CBH CDF ∴ ≌,CH CF ∴=,BCH DCF ∠=∠,160BCD ∠=︒ ,80ECF ∠=︒,80DCF ECB ∴∠+∠=︒,80CEH ∴∠=︒,FC CH = ,EC EC =,(SAS)FCE HCE ∴ ≌,EH EF ∴=,BE BH EH += ,BE DF EF ∴+=.【点睛】本题考查全等三角形的综合应用,熟练掌握三角形全等的判定及性质,三角形中线的定义,三角形三边关系是解题的关键.2.(2023春·江苏泰州·七年级统考期末)【发现问题】(1)数学活动课上,王老师提出了如下问题:如图1,在ABC 中,6AB =,4AC =,求BC 边上的中线AD 的取值范围.【探究方法】第一小组经过合作交流,得到了如下的解决方法:①延长AD 到E ,使得DE AD =;②连接BE ,通过三角形全等把AB 、AC 、2AD 转化在ABE ③利用三角形的三边关系可得AE 的取值范围为AB BE AE -<______.方法总结:解题时,条件中若出现“中点”、“中线”字样,可以考虑倍长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.【问题解决】(2)如图2,AD 是ABC 的中线,AE 是ADC △的中线,且中:直接写出所有正确选项的序号是______.①CAE DAE∠=∠②2AB AE =③DAE DAB ∠=∠④【问题拓展】(2)由“SAS ”可证AEC HED △≌△,可得AC DH =,ACD HDC ∠=∠,由“SAS ”可证ADB ADH ≌,可得AB AH =,BAD DAE ∠=∠,即可求解;(3)由“SAS ”可证AEO CEH △≌△,可得AO CH =,A HCO ∠=∠,由“SAS ”可证BOD HCO △≌△,可得BD OH =,可得结论;(4)由全等三角形的性质可得AEO CEH S S =△△,BOD HCO S S =△△,D COE ∠=∠,由三角形的面积公式可求解.【详解】解:(1)如图1中,延长AD 至点E ,使ED AD =.在ADC △和EDB △中,DA DE ADC EDB DC DB =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADC EDB ∴△≌△,4AC BE ∴==,=6AB ,6464AE ∴-<<+,2210AD ∴<<<,15AD ∴<<,故答案为:15AD <<;(2)如图2,延长AE 至H ,使EH AE =,连接DH ,AE 是中线,DE EC ∴=,又AEC DEH ∠=∠ ,AE EH =,(SAS)AEC HED ∴△≌△,AC DH ∴=,ACD HDC ∠=∠,ADB ADC ACD ∠=∠+∠ ,ADH ADC CDH ∠=∠+∠,∴∠=∠,ADB ADH为中线,AD∴=,BD CD,=AC CD∴===,BD DC AC DH又AD AD=,∴△≌△,ADB ADH(SAS)∴=,BAD DAEAB AH∠=∠,∴=,AB AE2故答案为:②③;=,连接CH,(3)证明:如图3,延长OE至H,使EH OE是AC的中点,E∴=,AE CE又OE EH=,AEO CEH∠=∠,∴△≌△,(SAS)AEO CEH∠=∠,∴=,A HCOAO CH∴∥,AO CH∴∠+∠=︒,180AOC HCO与COD∠AOB∠互补,∴∠+∠=︒,AOC BOD180∴∠=∠,BOD OCH=,又CH OA OB,OC OD==∴△≌△,BOD HCO(SAS)∴=,BD OH。
