2018年人教新课标小升初数学总复习第五章图形与几何综
小升初几何问题总复习

小升初几何问题总复习一、小升初考试热点及命题方向圆和立体几何近两年虽然不是考试热点,但在小升初考试中也会时常露面。
因为立体图形考察学生的空间想象能力,可以反映学生的本身潜能;而另一方面,初中很多知识点都是建立在空间问题上,所以可以说学校考察立体也是为初中选拔知识链接性好的学生。
二、2015年考点预测2015年的小升初考试如果考察圆与立体几何,不会难度太大,只需掌握我们本讲中所介绍的几类基本题型,就可成功在握。
考试热点将会出现在诸如水位问题和三维视图问题等题型。
三、典型例题解析1 与圆和扇形有关的题型【例1】(★★)如下图,等腰直角三角形ABC的腰为10厘米;以A为圆心,EF为圆弧,组成扇形AEF;阴影部分甲与乙的面积相等。
求扇形所在的圆面积。
【解】:等腰三角形的角为45度,则扇形所在圆的面积为扇形面积的8倍。
而扇形面积为等腰三角形面积:S=1/2×10×10=50。
则:圆的面积为400。
【例2】(★★★)草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见左下图)。
问:这只羊能够活动的范围有多大?【解】:(此题十分经典)如右上图所示,羊活动的范围可以分为A,B,C三部分,所以羊活动的范围是【例3】(★★)在右图中,两个四分之一圆弧的半径分别是2和4,求两个阴影部分的面积差。
【解】:我们只要看清楚阴影部分如何构成则不难求解。
左边的阴影是大扇形减去小扇形,再扣除一个长方形中的不规则白色部分,而右边的阴影是长方形扣除这块不规则白色部分,那么它们的差应为大扇形减去小扇形,再减去长方形。
则为:π/4×4×4-π/4×2×2-4×2=3×3.14-8=1.42。
【例4】(★★★)如图,ABCD 是正方形,且FA=AD=DE=1,求阴影部分的面积。
(取π=3)【解】:先看总的面积为1/4的圆,加上一个正方形,加上一个等腰直角三角形,然后扣除一个等腰直角三角形,一个1/4圆,一个45度的扇形。
小升初数学复习图形与几何完美

返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
ቤተ መጻሕፍቲ ባይዱ
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
返回目录
新人教版数学六年级下册总复习《图形与几何》课件(知识点全面)

这些计算公式是怎样推导出来的?它们之间有什么联系?
长方形和正方形是用面积单 位量出来的。
平行四边形转化成长方形。
两个完全相同的三角形或梯形 都可以拼成平行四边形。
利用割补、转化的方 法来推导图形的面积 公式。
长方形的面积是研究其它图形面积的基础。
9.三角形三边的关系
4cm
7cm
13cm
三角形其中两条线段的和大于第三条线段时,这样的三条 线段才能组成一个三角形。
30cm
上升的水的体积就是马铃薯的体积。
在方格纸上分别画出从不同方向看到左边立体图形 的形状图。
正面
左面
上面
连一连。
一个蓄水池(如下图),长10米,宽4米,深2米。 (1)蓄水池占地面积有多大?
10×4 = 40(平方米) 答:占地面积是40平方米。 (2)在蓄水池的底面和四周抹上水泥,抹水泥的面积有多大? 10×4 +(4×2+2×10)×2= 96(平方米)
三角形
锐角三角形 直角三角形
等腰三角形
(三个角都是 (有一个角是直角) 不等边三角形 (两条边相等)
锐角) 钝角三角形
(三条边都 等边三角形 不相等) (三条边都相等)
(有一个角是钝角)
1.平面图形的分类
四边形的分类
平行四边形 长方形
正方形
四边形 梯形
等腰梯形 直角梯形
2.直线、射线和线段
名称
相同点
比例尺 1∶20000
2.辨认方向
在平面图中确定方位,通常是上北、下南、左西、右东。
北
西北
东北
西
东
西南
南
东南
3.根据方向和距离,确定物体位置的一般步骤。
小升初专题复习几何图形

小升初专题复习——几何图形一、三视图及展开图例题1:用同样大小的正方体摆成的物体,从正面看到,从上面看到,从右面看到〔 〕A .B .C .D .变式练习:如图,它是用6个棱长为1分米的正方体拼成的. ①它的外表积是 . ②它的体积是 .二、三角形的底边及面积关系例题1:如图.A 、B 是长方形长和宽的中点,阴影局部的面积是长方形面积的 %.例题2:如图,三角形ABC 面积为27平方厘米,AE=CE ,BF=BC ,求三角形BEF 的面积.变式练习1:如图,直角梯形ADCB 中,三角形BEC 、四边形CEAF 和三角形CFD 的面积一样大.BC=16、AD=20、AB=12,求三角形AEF 的面积.教师姓名 学科 数学 上课时间 讲义序号 (同一学生)学生姓名年级六年级组长签字日期课题名称 几何图形变式练习2:如图,梯形ABCD中共有〔〕对面积相等的三角形A. 22 B. 3 C. 4 D. 5变式练习3:在如图中,平行四边形的面积是20平方厘米,图中甲、丙两个三角形的面积比是,阴影局部的面积是平方厘米.三、多边形内角和例题1:把表填完整多边形…边数 3 4 5 6 …内角和180°180°×2 180°×3 180°×5 …变式练习:探索〔1〕完成表格中未填局部.〔2〕根据表中规律,八边形的内角和是度.〔3〕假设图形的边数为a,内角和为s,请你用一个含有字母的关系式表示图形边数及内角和的关系..图形边数 3 4 5内角和180 180×2 180×3四、长度比拟例题1:面积相等的情况下,长方形、正方形和圆相比,〔〕的周长最短.A.长方形B.正方形C.圆例题2:如图,A是一个圆,B是由三个半圆围成的图形,那么它们周长的大小关系是C A C B.变式练习1:下面三个图形中,哪两个图形的周长相等?〔〕A.图形①和②B.图形②和③C.图形①和③变式练习2:在图形中甲的周长〔〕乙的周长.A.大于B.小于C.等于拓展提升:某高层公寓大火时,小王逃生的时候看了下疏散通道如下图,那么最快逃离到楼梯〔图中阴影〕的通道共有〔〕条.A. 3 B. 9 C. 6 D. 12五、组合图形计数例题1:如图中直角的个数为〔〕个.A. 4 B. 8 C. 10 D. 12例题2:如图,共有〔〕条线段.A. 4 B. 8 C. 10 D. 12例题3:数一数,在右图中共有〔〕个三角形.A.10 B. 11 C. 12 D. 13 E.14A.4 B. 8 C. 10 D. 12变式练习2:如图中直角有〔〕个.A. 1 B. 2 C. 3 D. 4变式练习3:这里共有〔〕条线段.A.三条B.四条C.五条D.六条变式练习4:如下图的7×7的方格内,有许多边长为整数的正方形,其中在有的正方形中黑方格及白方格的个数占一半〔同样多〕.像这样的正方形有〔〕个.A.26 B. 36 C. 46 D. 56E.66变式练习5:图中共有〔〕个长方形.A. 30 B. 28 C. 26 D. 24变式练习6:如图,三角形一共有个.拓展提升1:如图是半个正方形,它被分成一个一个小的等腰三角形,图中,正方形有10 个,三角形有47 个.拓展提升2:如图中,三角形的个数有多少?六、图形的拆拼〔切拼〕例题1:一个圆的周长是15.7分米,把这个圆等分成假设干个小扇形,拼成一个近似的长方形,这个近似的长方形的长是分米,宽是分米.例题2:爸爸给女儿买了一个圆柱形的大生日蛋糕,女儿把蛋糕竖直方向切成22块分给22个小朋友,切成的大小不一定相等.那么至少需切的刀数为?变式练习1:在一块边长为4厘米的正方形的铁皮上,剪出直径为2厘米的小圆片,最多可剪〔〕片.A. 3 B. 4 C. 5 D. 6变式练习2:用一条直线将一个正方形分成两个完全一样的两局部,有几种分法〔〕A. 1种B. 2种C. 3种D. 4种变式练习3:在一块长10分米、宽5分米的长方形铁板上,最多能截取11 个直径是2分米的圆形铁板.拓展提升:请将下面等边三角形按要求分割成假设干个形状和大小都一样的三角形〔1〕分成2个〔2〕分成3个〔3〕分成4个〔4〕分成6个七、立体图形的外表积例题1:把14个棱长为1的正方体,在地面上堆叠成如下图的立体,然后将露出的外表局部染成红色.那么红色局部的面积为〔〕A. 21 B. 24 C. 33 D. 37例题2:如图,在棱长为3的正方体中由上到下,由左到右,由前到后,有三个底面积是1的正方形高为3的长方体的洞,那么所得物体的外表积为.变式练习2:把假设干个边长2厘米的正方体重叠起来堆成如下图的立体图形,这个立体图形的外表积是平方厘米.变式练习3:如图是一个长3厘米、宽及高都是2厘米的长方体.将它挖掉一个棱长1厘米的小正方体,它的外表积〔〕A.比原来大B.比原来小C.不变拓展提升〔难〕:在一个棱长为8的立方体上切去一个三棱柱〔如图〕,那么外表积减少.八、立体图形的体积例题1:如图的体积是.〔单位:厘米〕例题2:一支没有用过的圆柱形铅笔,长18厘米,体积是9立方厘米,使用一段时间后变成了如图的样子,这时铅笔的体积是多少立方厘米?变式练习1:有一棱长为5cm的正方体机器零件,现在它的上下面挖去了一个直径为2cm的圆孔,求剩下机器零件的外表积和体积?九、等积变形例题1:如下图,把底面直径8厘米的圆柱切成假设干等分,拼成一个近似的长方体.这个长方体的外表积比原来增加80平方厘米,那么长方体的体积是立方厘米.例题2:一个酸奶瓶〔如图〕,它的瓶身呈圆柱形〔不包括瓶颈〕,容积是32.4立方厘米.当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余局部高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?变式练习1:一个圆锥形沙堆,底面积是3.6平方米,高1.2米.把这堆沙装在长2米、宽1.5米的沙坑里,可以装多高?变式练习2:有一种饮料瓶的容积是50立方厘米,瓶身呈圆柱形〔不包括瓶颈〕.现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余局部的高度为5厘米.瓶内现有饮料立方厘米.变式练习3:水平桌面上放着高度都为10厘米的两个圆柱形容器A和B,在它们高度的一半处有一连通管相连〔连通管的容积忽略不计〕,容器A、B底面直径分别为10厘米和16厘米.关闭连通管,10秒钟可注满容器B,如果翻开连通管,水管向B容器注水6秒钟后,容器A中水的高度是多少呢?〔π取3.14〕变式练习4:A和B都是高度为12厘米的圆柱形容器,底面半径分别是1厘米和2厘米,一水龙头单独向A 注水,一分钟可注满.现将两容器在它们的高度的一半出用一根细管连通〔连通管的容积忽略不计〕,仍用该水龙头向A注水,求〔1〕2分钟容器A中的水有多高?〔2〕3分钟时容器A中的水有多高.十、数阵图中找规律的问题例题1:把自然数依次排成以下数阵:1,2,4,7,11,…3,5,8,12,…6,9,13,…10,14,…15,……现规定横为行,纵为列.求〔1〕第10行第5列排的是哪一个数?〔2〕第5行第10列排的是哪一个数?〔3〕2004排在第几行第几列?变式练习1:淘气用小棒搭房子,他搭3间用了13根小棒,像这样搭15间房子要用〔〕根小棒.A. 60 B. 61 C. 65 D. 75。
图形与几何 人教新课标教育课件

角的定义
(边 )
(顶点 )
(边 )
从一点引出两条射线所组成的图形叫做角。
旧知回顾
角的度量
用量角器量角的步骤 第一:量角器的中心与角的顶点重合。
第二:0°刻度线与角的一条边重合。 第三:角的另一条边所对应的量角器上
的刻度,就是这个角的度数。
旧知回顾
角的分类
平角 周角
1平角=180° 1周角=360°
9 总复习
第 3 课时 图形与几何
旧知回顾
角的定义
线段、直线、射线
角的度量
空间与 角 角的分类 图形
平行与垂直
角的画法
平行四边形
平行四边 形和梯形
梯形
旧 知 回 顾 线段、直线、射线
名称 形状 端点 延伸
图示
线段 直的 2 不能 A
B
射线 直的 1 一端
直线 直的 0 两端 A l B
旧知回顾
•《
《
我
是
算
命
先
生
》
读
后
感
》
同学们ByeBye!
–
凡 事 都 是 多棱 镜 , 不同 的 角 度 会看 到 不 同 的结 果 。 若 能把 一 些 事 看淡 了 , 就会 有 个 好 心境 , 若 把 很多 事 看 开 了, 就 会 有 个好 心 情 。让 聚 散 离 合 犹 如月 缺 月 圆 那样 寻 常 ,
凡 事 都是 多 棱 镜 ,不 同 的 角 度会
1周角=2平角=4直角
锐角 < 直角 < 钝角 < 平角 < 周角
旧知回顾
1.下面的角各是哪一种角?
( 钝角 )
( 锐角 ) ( 直角 )
旧知回顾
小升初数学:所有图形与几何的知识合集

图形的认识、测量量的计量一、长度单位是用来测量物体的长度的。
常用的长度单位有:千米、米、分米、厘米、毫米。
三、面积单位是用来测量物体的表面或平面图形的大小的。
常用面积单位:平方千米、公顷、平方米、平方分米、平方厘米。
四、测量和计算土地面积,通常用公顷作单位。
边长100米的正方形土地,面积是1公顷。
五、测量和计算大面积的土地,通常用平方千米作单位。
边长1000米的正方形土地,面积是1平方千米。
七、体积单位是用来测量物体所占空间的大小的。
常用的体积单位有:立方米、立方分米(升)、立方厘米(毫升)。
平面图形【认识、周长、面积】一、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
线段、射线都是直线上的一部分。
线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
二、从一点引出两条射线,就组成了一个角。
角的大小与两边叉开的大小有关,与边的长短无关。
角的大小的计量单位是(°)。
三、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180 度的角是钝角;等于180度的角是平角;等于360度的角是周角。
四、相交成直角的两条直线互相垂直;在同一平面不相交的两条直线互相平行。
五、三角形是由三条线段围成的图形。
围成三角形的每条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
六、三角形按角分,可以分为锐角三角形、直角三角形和钝角三角形。
按边分,可以分为等边三角形、等腰三角形和任意三角形。
七、三角形的内角和等于180度。
八、在一个三角形中,任意两边之和大于第三边。
九、在一个三角形中,最多只有一个直角或最多只有一个钝角。
十、四边形是由四条边围成的图形。
常见的特殊四边形有:平行四边形、长方形、正方形、梯形。
十一、圆是一种曲线图形。
圆上的任意一点到圆心的距离都相等,这个距离就是圆的半径的长。
通过圆心并且两端都在圆的线段叫做圆的直径。
2021小升初数学总复习 第五章 图形与几何 第三课时

举一反三
3. 下列图形中,对称轴最多的是( B )。
A. 长方形
B. 正方形
C. 平行四边形
4. 把下列各种图形按对称轴的数量从少到多的顺序排列。
长方形、圆、等边三角形、正方形、等腰梯形
_等__腰__梯__形__<_长__方__形__<_等__边__三__角__形__<_正__方__形__<_圆___________
1. 下面的汉字中是轴对称图形的是( A )。
A. 中
B. 下
C. 手
2. 下图中轴对称图形有( AD )。通过旋转图形(
图形( E )。
C )得到
题型二 【例2】下列图形中,对称轴只有两条的图形是( C )
A. 圆
B. 等边三角形
C. 矩形
D. 等腰梯形
精析:根据轴对称图形的概念,分别判断出四个图形的对称 轴的条数:A. 圆有无数条对称轴;B. 等边三角形有3条对称 轴;C. 矩形有2条对称轴;D. 等腰梯形有1条对称轴。故选C 。
第五章 图形与几何
图形的运动与位置
1. 图形的运动
知识要点梳理
2. 图形与位置
3. 观察物体
典例精析及训练
题型一 【例1】下列交通标志图案是轴对称图形的是( B )
精析:根据轴对称图形的概念对各选项分析判断后利用排除 法求解,A、C、D不是轴对称图形, 只有B是轴对称图形, 故选B。
举一反三
举一反三 10. 王东在班级的位置用数对表示是(7,4),那么王东坐在教室
的第( 4 )行,第( 7 )列。 11. 照样子写出下图中各字母的位置。
A( 2 , 1 ),B( 1 , 2 ) , C( 2 , 5 ) ,D( 3 , 3 ), E( 5 , 3 ) ,F( 4 , 2 ) , G( 6 , 0 )
人教版数学小升初衔接练习+解析(图形与几何—图形的运动)

人教版数学小升初衔接练习+解析(图形与几何—图形的运动)试卷满分:100分考试时间:100分钟一.选择题(共5小题.每小题2分)1.快速旋转小棒.下面()小旗转动一周会形成如图的图形.A.B.C.2.将一个周长为12厘米的正方形变换成一个面积是36平方厘米的正方形.是按()的比例放大的.A.1:3 B.2:1 C.3:1 D.4:1 3.下面的图形是按一定比例缩小的.则x=().A.10 B.8 C.7.5 D.74.下列说法正确的是()A.把一个三角形按1:2的比缩小后.它每个角的度数.每条边的长度都缩小为原来的一半B.平行四边形的各边长度确定后.它的周长和面积就确定了C.三角形各边长度确定后.它的周长和面积就确定了D.ab﹣8=12 (a、b都不为0).则a和b成反比例5.下列图形中.不是轴对称图形的是()A. B.C.二.填空题(共8小题.每小题2分)6.在平面图形中.属于轴对称图形的有(至少写2个);一个长方体的长、宽、高分别为9厘米、6厘米和5厘米.这个长方体的棱长总和是厘米.7.正方形有条对称轴.圆有条对称轴.8.小李去北京动物园游玩.回家后把一张照片(如图所示)在电脑上按一定的比例放大.放大后的照片长是14.4cm.放大后的宽是cm.9.折叠一张长方形纸ABCD.如图.折叠时.C点和A点重合.产生折痕为EF.量得AE长22厘米.如果长方形的宽是20厘米.折叠后图形的面积比原来长方形面积少了平方厘米.10.如果三角形ABC按一定的比缩小成三角形DEC.那么BC长cm.11.右边是一个零件的设计图.每个小格都是边长为1cm的正方形.这个零件的体积是cm³.如果把设计图按2:1放大.那么这个零件的体积就是cm³.12.如图.有一张长方形纸片ABCD.AB=10cm.AD=6cm.将纸片折叠.使AD边落在AB边上.折痕为AE.再将三角形AED以DE为折痕向右折叠.AE与BC交于点F.则三角形CEF的面积为cm2.13.如图.把一张长方形纸折叠后.∠1=50°.∠2=.三.判断题(共5小题.每小题2分)14.放大后的长方形与原长方形对应线段的比是2:1.放大后的长方形面积与原长方形的面积比也是2:1. ()15.边长3米的正方形按2:1的比放大后.它的周长与原来的周长的比是2:1.()16.旋转不改变图形的大小和形状.只改变图形的位置.()17.线段、长方形、正方形、等腰梯形、圆都是轴对称图形.()18.婷婷中午12点睡觉.下午闹钟2点准时响起.则时针在这段时间旋转了60°.()四.操作题(共5小题.每小题5分)19.在方格中画出如图的图形.(1)平行四边形向左平移8格后的图形;(2)梯形绕点O逆时针旋转90°后的图形;(3)三角形按3:1放大后的图形.20.(1)将图中三角形向右平移3格后的图形画出来.(2)将图中三角形的各边按2:1扩大后的图形画出来. 21.观察方格图.完成下面的任务.(1)画出下面对称图形的另一半.(2)与点B对称的点C的位置是(. ).(3)以BC为底边.画一个与三角形ABC面积相等、形状不同的三角形BCD.(4)画一个与三角形ABC面积相等的梯形EFGH.22.按要求画图.(1)画出将图形A先向下平移3格.再向右平移4格后的图形;(2)画出将图形A绕点O顺时针旋转90°后的图形;(3)以虚线MN为对称轴.画出图形B的轴对称图形.23.图中的每小格表示边长1厘米的正方形.(1)将图中长方形绕D点顺时针旋转90°.画出旋转后的图形.(2)将长方形按2:1放大.画出放大后的图形.并使A点的位置在(10.5).放大后的长方形面积与原长方形面积的比是:.(3)在放大后的长方形内画一个最大的半圆.这个半圆的面积是平方厘米.(4)图中的A点在D点的偏方向.五.解答题(共8小题.每小题5分)24.按要求画图.(1)先画出图①的对称轴.再把图①绕点B逆时针旋转90度. (2)把图②各边按2:1的比放大后画在图②的东面.(3)点D的位置用数对表示是(. ).以点D为圆心画一个半径是3厘米的圆.(每小格的边长表示1厘米)25.按要求完成下面各题.每个小方格边长是1cm.(1)图中的平行四边形沿高分成了两部分.把其中阴影部分的三角形向平移cm.平行四边形就变成了长方形. (2)把三角形ABC绕点C顺时针旋转90.画出旋转后的图形.旋转后与原三角形B点相对应的点的位置用数对表示是.(3)画出图M中图形的另一半.使它成为一个轴对称图形. (4)在合适的位置画出(3)题中对称图形按1:2缩小后的图形.26.下面小方格边长表示1厘米.请按要求完成下面各题.(1)把图中的三角形绕点C逆时针旋转90°.画出旋转后的图形;旋转后.A点对应的位置用数对表示是.(2)按2:1的比将原三角形放大.画出放大后的图形.放大后的三角形面积与原来面积的比是.27.在方格子里按要求完成以下各题.(1)将平行四边形ABCD先向上平移4格后.再向右平移5格.画出平移后的图形.用数对表示出经过两次平移后点A对应点的位置是(. ).(2)将平行四边形ABCD绕A点顺时针旋转90°.画出旋转后的图形.28.画一画.(1)小旗子绕O点逆时针旋转90°后的图形.(2)小旗子按2:1扩大后的图形.29.按要求填空并在方格纸上画出图形.(每个小正方形表示1平方厘米)(1)图①中.O点的位置用数对表示是(. ).把图①绕O点逆时针旋转90°.把图①按2:1的比放大.(2)图②中.以B点为观测点.C点在B点的偏方向上.图②中.过点A作BC边上的高.(3)图③中.已经涂了4个方格.请你再涂一个方格.使得5个方格组成的图形是轴对称图形.并画出它的对称轴.30.如图.在3×3的正方形网格中.已有两个小正方形被涂黑.再将图中其余小正方形涂黑一个.使整个图案构成一个轴对称图形.31.(1)把圆平移到圆心是(6.8)的位置上.(2)把长方形绕A点顺时针旋转90°.(3)画出轴对称图形的另一半.答案解析一.选择题(共5小题.每小题2分)1.解:如图:快速旋转小棒.上面小旗转动一周会形成如图的图形.故选:B.2.解:12÷4=3(厘米)即周长是12厘米的正方形边长是3厘米;因为36=6×6所以面积是36平方厘米的正方形边长是6厘米;6:3=2:1答:是按2:1的比例放大的.故选:B.3.解:根据题意.5:4=x:64x=30x=30÷4x=7.5故选:C.4.解:由分析可得.选项A、B、C都是错误的.只有选项D正确. 故选:D.5.解:根据轴对称图形的意义可知:选项A不是轴对称图形.选项B、C都是轴对称图形;故选:A.二.填空题(共8小题.每小题2分)6.解:(9+6+5)×4=20×4=80(厘米)属于轴对称图形的有长方形、正方形;一个长方体的长、宽、高分别为9厘米、6厘米和5厘米.这个长方体的棱长总和是80厘米.故答案为:长方形、正方形;80.7.解:两组对边中点连线所在的直线以及两条对角线所在的直线就是其对称轴.如下图:正方形有四条对称轴;圆的直径所在的直线都是圆的对称轴.圆有无数条直径.就用无数条对称轴.故答案为:4.无数.8.解:14.4÷6=2.44×2.4=9.6(cm)答:放大后的宽是9.6cm.故答案为:9.6.9.解:20×22÷2=440÷2=220(平方厘米)答:折叠后图形的面积比原来长方形面积少了220平方厘米. 故答案为:220.10.解:设BC的长为x厘米.9:6=x:86x=9×8x=x=12答:BC长12厘米.故答案为:12.11.解:3.14×2×2×6×=12.56×2=25.12(立方厘米)2×2=4(厘米).高是6×2=12(厘米)3.14×4×4×12×=3.14×16×4=3.14×64=200.96(立方厘米)答:这个零件的体积是25.12cm³.如果把设计图按2:1放大.那么这个零件的体积就是200.96cm³.故答案为:25.12.200.96.12.解:4×4÷2=8(cm2);故答案为:8.13.解:由图可知∠1+∠2+∠3=180°.所以∠2+∠3=180°﹣∠1=180°﹣50°=130°.又因为∠2=∠3.130°÷2=65°所以∠2=65°故答案为:65°.三.判断题(共5小题.每小题2分)14.解:2×2=4答:放大后的长方形与原长方形对应线段的比是2:1.放大后的长方形面积与原长方形的面积比也是4:1.故答案为:×.15.解:根据正方形的周长公式:C=4a.可知正方形的周长比等于边长比.所以放大后的周长比等于边长比.原题说法正确.故答案为:√.16.解:旋转后图形的形状、大小不变.只是位置发生变化.所以原说法正确;故答案为:√.17.解:根据轴对称图形的意义可知:线段、长方形、正方形、等腰梯形、圆都是轴对称图形.说法正确;故答案为:√.18.解:婷婷中午12点睡觉.下午闹钟2点准时响起.则时针在这段时间旋转了60°.说法正确;故答案为:√.四.操作题(共5小题.每小题5分)19.解:如图:20.解:画图如下:21.解:(1)作图如下:(2)与点B对称的点C的位置用数对表示是(7.2).(3)以BC为底边.画一个与三角形ABC面积相等、形状不同的三角形BCD(画法不唯一).作图如下:(4)画一个与三角形ABC面积相等的梯形EFGH(画法不唯一). 作图如下:故答案为:7.2.22.解:①把图形A先向下平移3格(蓝色部分).再向右平移4格(红色部分).②把图形A绕O点顺时针方向旋转90°.画出旋转后的图形(黄色部分).③以虚线MN为对称轴.画出图形B的轴对称图形.(蓝色部分). 如图:23.(1)将图中长方形绕D点顺时针旋转90°.画出旋转后的图形(图中红色部分):(2)将长方形按2:1放大.画出放大后的图形.并使A点的位置在(10.5)(图中绿色部分).放大后的长方形面积与原长方形面积的比是4:1.(3)在放大后的长方形内画一个最大的半圆(图中蓝色部分).这个半圆的面积是:3.14×32÷2=28.26÷2=14.13(平方厘米)(4)图中的A点在D点的西偏北方向.故答案为:4.1;14.13;西.北.五.解答题(共8小题.每小题5分)24.解:(1)先画出图①的对称轴(下图红色虚线).再把图①绕点B逆时针旋转90度(下图).(2)把图②各边按2:1的比放大后画在图②的东面(下图). (3)点D的位置用数对表示是(14.7).以点D为圆心画一个半径是3厘米的圆(下图).故答案为:14.7.25.解:(1)图中的平行四边形沿高分成了两部分.把其中阴影部分的三角形向右平移6cm.平行四边形就变成了长方形(下图). (2)把三角形ABC绕点C顺时针旋转90.画出旋转后的图形.旋转后与原三角形B点相对应的点的位置用数对表示是(17.6). (3)画出图M中图形的另一半.使它成为一个轴对称图形(下图).(4)在合适的位置画出(3)题中对称图形按1:2缩小后的图形(下图).故答案为:右.6;(17.6).26.解:(1)(2)如图:(1)旋转后.A在第三列第四行.所以数对为(3.4);(2)放大后.底和高都扩大为原来的2倍.根据S=ah.面积扩大为原来的2×2=4倍.面积比为:4:1.故答案为:(3.4);4:1.27.解:(1)将平行四边形ABCD先向上平移4格后.再向右平移5格.画出平移后的图形(下图).用数对表示出经过两次平移后点A对应点的位置是(9.7).(2)将平行四边形ABCD绕A点顺时针旋转90°.画出旋转后的图形(下图).故答案为:9.7.28.解:作图如下:29.解:(1)O点的位置是第4列.第6行.作图如下:(2)图②中.以B点为观测点.C点在B点的西偏南45°方向上.如上图;(3)如上图(画法不唯一).30.解:如图所示:31.解:(1)由数对与位置找到平移后的圆心点是(6.8).以半径为2格长画圆即可得到平移后的位置;(2)根据图形旋转的方法.将与点A连接的两条边顺时针旋转90°.再作这两条边的平行线即可得出旋转后的图形;(3)根据轴对称图形的特征.对称点到对称轴的距离相等.找出三个对称点.然后连接即可.作图如下:.。
2018年小升初数学总复习课件-第五章图形与几何综合训练人教新课标 (共18张PPT)

•
20、每一个成就和长进,都蕴含着曾经受过的寂寞、洒过的汗水、流过的眼泪。许多时候不是看到希望才去坚持,而是坚持了才能看到希望。
•
1、机遇对于有准备的头脑有特别的亲和力。
•
2、不求与人相比,但求超越自己,要哭就哭出激动的泪水,要笑就笑出成长的性格!
•
3、在你内心深处,还有无穷的潜力,有一天当你回首看时,你就会知道这绝对是真的。
2.
(1)这种微波炉所占的空间是多少立方分米? 300×500×420=63000000(立方毫米) 63000000立方毫米=63立方分米 答:所占空间是63立方分米。
(2)这种微波炉的容积是多少升?
210×350×330=24255000(立方毫米) 24255000立方毫米=24.255升 答:这种微波炉的容积是24.255升。
•
10、你的假装努力,欺骗的只有你自己,永远不要用战术上的勤奋,来掩饰战略上的懒惰。
•
11、时间只是过客,自己才是主人,人生的路无需苛求,只要你迈步,路就在你的脚下延伸,只要你扬帆,便会有八面来风,启程了,人的生命才真正开始。
•
12、不管做什么都不要急于回报,因为播种和收获不在同一个季节,中间隔着的一段时间,我们叫它为坚持。洗牌,但是玩牌的是我们自己!
•
13、你不能左右天气,但可以改变心情。你不能改变容貌,但可以掌握自己。你不能预见明天,但可以珍惜今天。
•
14、我们总是对陌生人太客气,而对亲密的人太苛刻。
•
15、人之所以痛苦,在于追求错误的东西。
•
16、知道自己要干什么,夜深人静,问问自己,将来的打算,并朝着那个方向去实现。而不是无所事事和做一些无谓的事。
五、计算题。 1. 计算下面图形的表面积和体积。(单位:cm)
小学数学-有答案-小升初数学专项复习:几何的初步知识

小升初数学专项复习:几何的初步知识一、例题:1. 通过放大10倍的放大镜来看一个60∘的角,这个角是多少度?2. 王小明家把一块长15米,宽12米5分米的长方形草场围上篱笆,求篱笆有多长?3. 有一块正方形实验田,周长24米,它的面积是多少平方米?4. 用10.28厘米的铁丝围成一个半圆形,半圆形的面积是多少平方厘米?5. 一个长方形和一个三角形等底等高,已知三角形的面积是30平方厘米,长方形的面积是多少?6. 一块梯形棉田,上底长85米,下底长160米,高70米;在这块棉田里共收籽棉1845千克,每平方米产籽棉多少千克?二、填空题在同一平面内不相交的两条直线叫________.12个正方形可以摆成________种不同形式的长方形。
在等腰三角形中,如果顶角为124∘,底角各是________,这个三角形是________角三角形。
把两个边长都是2厘米的正方形拼成一个长方形,这个长方形的周长是________,面积是________.一个平行四边形,底是24厘米,高2分米,面积是________.一个等边三角形,周长是12.6厘米,它的边长是________厘米。
周长是28厘米的长方形,长是10厘米,面积是________.一个梯形的面积是10平方分米,高是4分米,上底是2.2分米,下底是________分米。
一个圆,周长是6.28分米,它的面积是________.圆心角是1∘的扇形的面积是________.三、判断小明画了一条25厘米长的直线。
________.(判断对错)等边三角形和等腰三角形都是锐角三角形。
________.两个面积相等的三角形一定能拼成平行四边形。
________(判断对错)平行四边形和长方形的周长相等,它们的面积也相等。
________.(判断对错)半径是2厘米的圆,它的周长和面积相等。
________.(判断对错)半圆的周长是和它相等半径的圆周长的一半。
________.(判断对错)平行四边形不是对称图形,没有对称轴。
小升初数学图形与几何知识点分类复习《常见的立体图形》一大题量附答案
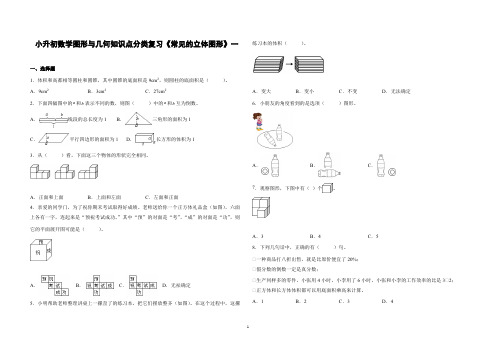
从正面看是 ,从左面看是 。
故答案为:A
【点睛】
本题考查了观察物体,能从三视图中将几何体还原是解题的关键。
12.D
【分析】
两面涂色的小正方体在大正方体的每条棱上除去两端的两个,正方体有12条棱,两面涂色的正方体的个数为:12×(4-2)个,计算出结果,即可解答。
【详解】
12×(4-2)
=12×2
46.一节通风管长1米,宽和高都是0.1米,做5节这样的通风管至少需要( )平方米铁皮。
47.把一个表面涂色的正方体每条棱都平均分成4份,切成同样大小的小正方体,3面涂色的小正方体有( )个,2面涂色的有( )个。
48.观察立体图形,下面的三幅图分别是从上面、左面和正面中的哪个方向看到的?填一填。
( ) ( ) ( )
根据分析可知,长方体酸奶盒体积:
4×5×10
=20×10
=200(立方厘米)
200立方厘米=200毫升
净含量<200毫升
故答案选:B
【点睛】
本这题考查长方体体积公式的应用,以及单位名数的互换,关键明确净含量要小于这个包装的体积。
11.A
【分析】
根据从正面和左面看到的图形,对比各选项中的几何体,直接选出正确选项即可。
49.数一数。
( )个, ( )个, ( )个, ( )个。
50.如图,把一个圆柱切成若干等份,拼成一个近似的长方体,圆柱的侧面积是( ) 。
四、作图题
51.在下图中画出长为3厘米,宽为2厘米,高为1厘米的长方体无盖纸盒的展开图(表格中每个小方格的边长为1厘米)。
五、解答题
52.一种常见的玩具陀螺是由圆柱和圆锥两部分组成的,圆柱的底面直径是4厘米,高是3厘米,圆锥的高是1.5厘米。
六年级小升初数学总复习【图形与几何】专题训练(解析卷)

六年级小升初数学总复习【图形与几何】专题训练(解析卷)六年级小升初数学总复【图形与几何】专题训练【解析卷】直线型面积】1.在图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC长8厘米。
已知阴影部分的总面积比三角形EFG的面积大10厘米2,求平行四边形ABCD的面积。
解答:因为阴影部分比三角形EFG的面积大10厘米2,都加上梯形FGCB后,根据差不变性质,所得的两个新图形的面积差不变,即平行四边形ABCD比直角三角形ECB的面积大10厘米2,所以平行四边形ABCD的面积等于10×8÷2+10=50(厘米2)。
2.图中,CA=AB=4厘米,三角形ABE比三角形CDE的面积大2厘米,求CD的长。
解答:连结CB。
三角形DCB的面积为4×4÷2-2=6(厘米2),CD=6÷4×2=3(厘米)。
3.有红、黄、绿三块同样大小的正方形纸片,放在一个正方形盒的底部,它们之间互相叠合。
已知露在外面的部分中,红色面积是20,黄色面积是14。
绿色面积是10,求正方形盒子底部的面积。
解答:把黄色正方形纸片向左移动并靠紧盒子的左边。
由于三个正方形纸片面积相等,所以原题图可以转化成下页右上图。
此时露出的黄、绿两部分的面积相等,都等于(14+10)÷2=12.因为绿:红=A∶黄,以是绿×黄=红×A,A=绿×XXX÷红12×12÷20=7.2.正方形盒子底部的面积是红+黄+绿+A=20+12+12+7.2=51.2.三角形的等积变换】:4.如左下图是两个相同的直角三角形叠在一起组成的,求阴影部分的面积。
单位:分米)谜底:32.5平方分米。
拓展:如图所示,已知正方形ABCD和正方形EFGC,且正方形EFGC的边长为6厘米,请问图中阴影部分面积是多少?答案:18平方厘米。
5.如图所示,在平行四边形ABCD中,DE=EF=FC,BG=GD.已知三角形GEF的面积是4平方厘米,求平行四边形的面积。
【人教版】小升初数学总复习知识点归纳总结

【人教版】小升初数学总复习知识点归纳总结常用的数量关系式1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1、正方形(C:周长 S:面积 a:边长)周长=边长×4 C=4a面积=边长×边长S=a×a2、正方体(V:体积 a:棱长)表面积=棱长×棱长×6 S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3、长方形( C:周长 S:面积 a:边长)周长=(长+宽)×2 C=2(a+b)面积=长×宽 S=ab4、长方体(V:体积 s:面积 a:长 b: 宽 h:高)(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高 V=abh5、三角形(s:面积 a:底 h:高)面积=底×高÷2 s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形(s:面积 a:底 h:高)面积=底×高 s=ah7、梯形(s:面积 a:上底 b:下底 h:高)面积=(上底+下底)×高÷2 s=(a+b)× h÷28、圆形(S:面积 C:周长л d=直径 r=半径)(1)周长=直径×л=2×л×半径 C=лd=2лr(2)面积=半径×半径×л9、圆柱体(v:体积 h:高 s:底面积 r:底面半径 c:底面周长)(1)侧面积=底面周长×高=ch(2лr或лd) (2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体(v:体积 h:高 s:底面积 r:底面半径)体积=底面积×高÷311、总数÷总份数=平均数15、相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间16、浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量17、利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)常用单位换算长度单位换算1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米面积单位换算1平方千米=100公顷1公顷=10000平方米1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米体(容)积单位换算1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000 千克1千克=1000克1千克=1公斤人民币单位换算1元=10角1角=10分1元=100分时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒分数的基本性质分数的基本性质:分数的分子和分母都乘以或者除以相同的数(零除外),分数的大小不变。
最新小学数学毕业总复习——第五章图形与几何第一课时图形的认识

④ 同一个圆里有无数条直径,所有的直径都相等。 ⑤ 同一个圆里,直径等于半径长度的两倍,即d=2r,或 2 d 。
r ⑥ 圆心决定圆的位置,半径决定圆的大小。直径是圆中最长的 线段。 ⑦ 圆有无数条对称轴。 (2) 圆的画法:把圆规的两脚分开,定好两脚间的距离(即半径); 把有针尖的一只脚固定在一点(即圆心)上;把装有铅笔尖的一只 脚旋转一周,就画出一个圆。
返回目录
4. 扇形
(1) 扇形的定义:一条弧和经过这条弧两端的
两条半径所围成的图形叫做扇形。
(2) 圆上AB两点之间的部分叫做弧,读作“弧
AB”,记作“AB”。
(3) 顶点在圆心的角叫做圆心角。
(4) 在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
以半圆为弧的扇形的圆心角是180度,以1/4圆为弧的扇形的圆心
返回目录
8. 下面有两条平行线,请你照着图中的样子再画3条垂线段,并 量一量它们的长度。 我发现 两条平行线之间的距离处处相等 。
画图略
返回目录
题型三
【例3】已知∠1=75°,求∠2,∠3和∠4的度数。
精析:利用平角是180°以及图中各
×
角之间的关系可以求得∠2=180°-
∠1=180°-75°=105°,又根据
返回目录
二、平面图形 1. 三角形 (1) 三角形的定义:由3条线段围成的图形(每相邻两条线段 的端点相连)叫做三角形。 (2) 三角形有三条边、三个顶点、三个角。 (3) 从三角形的一个顶点到它的对边作一条垂线,顶点和垂 足之间的线段叫做三角形的高,这条对边叫做三角形的底。三 角形有3条高。
返回目录
据之前所学,我们知道,在同一平面内,两直线的位置关系
是相交或平行。本题中,三条直线在同一平面内,因为a与b
人教版小升初六年级数学下册图形与几何、综合与实践易错题练习

六年级数学下册人教版小升初图形与几何易错题强化练习1.下图1平行四边形的面积是31.2平方厘米,A是底边的中点,如果将它沿虚线折叠后,得到下图2,那么下图2中阴影部分的面积是多少平方厘米?2.计算下图中阴影部分的面积。
(单位:厘米)3.一个密封玻璃缸,存水的空间长6分米、宽3分米,高4分米,现在缸里水深3分米。
如果缸竖起来(如图),缸里水深多少分米?4.求如图椭圆形操场的周长。
5.计算下面图形的表面积。
6.计算下面立体图形的体积。
7.如图一个大正方形里的阴影部分是两个小正方形,已知阴影部分的周长是36 dm,大正方形的面积是多少平方分米?6.已知下图中圆的半径是3cm,求阴影部分三角形的面积?7.如图:四边形ABCD是一个梯形,图中给出了三角形BOC的面积是18平方厘米,三角形ODC面积是6平方厘米,求梯形的面积.10.下图中圆的周长和长方形的周长相等,已知圆的面积是50.24平方厘米,求图中阴影部分的周长和面积各是多少?11.高都是2米,底面半径分别是1.5米、2米和2.5米的三个圆柱组成的几何体如图,求这个物体的表面积?12.在半径为10厘米,圆心角为90°的扇形中,分别以两条半径的中点E和F为圆心,以扇形半径之半为半径,画两个半圆交于D。
求图中阴影部分的面积(如下图)13.已知右图中两个正方形的边长分别是3厘米和6厘米,求阴影部分的面积。
14.下图的中的正方形的边长是2厘米,以圆弧为分界线的Ⅰ、Ⅱ两部的面积的差是多少平方厘米?15.如下图,已知直角三角形的面积是12平方厘米,求阴影部分的面积。
16.如下图,O为圆心CO垂直于AB,三角形ABC的面积是45平方厘米,以C为圆心,CA为半径画弧将圆分成两部分,求阴影部分的面积。
17.如下图,半圆的直径是10厘米,阴影部分甲比乙的面积少1.25平方厘米,求三角形△ABC的边OA的长。
18.下图,四边形ABCD是正方形,三角形ABF的面积比正方形ABCD 的面积大12厘米,线段BC的长为8厘米。
【小升初数学专项练习】《五、综合与实践4.作旋转一定角度后的图形》(附答案)

小升初数学专项练习一线名师严选内容,逐一攻克☆基本概念、基本原理、基础技能一网打尽☆点拨策略思路,侧重策略指导,拓宽眼界思路☆4.作旋转一定角度后的图形【小升初考点归纳】1.旋转作图步骤:(1)明确题目要求:弄清旋转中心、旋转方向和旋转角;(2)分析所作图形:找出构成图形的关键点;(3)找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;(4)作出新图形:顺次连接作出的各点.(5)写出结论:说明作出的图形.2.中心对称作图步骤:(1)连接原图形上的所有特殊点和对称中心;(2)再将以上连线延长找对称点,使得特殊点与对称中心的距离和对称点与对称中心的距离相等;(3)将对称点按原图形的形状顺次连接起来,即可得出关于对称中心对称的图形.【经典例题】一.选择正确的答案,把序号填在括弧中(共1小题)1.(2016•长沙模拟)下面图形中,以某一边为轴旋转一周,可以得到圆锥的是()A.B.C.D.【解析】解:直角三角形沿一条直角边旋转一周得到的几何体是一个圆锥.故选:A.二.操作题(共14小题)2.(2019春•南京月考)(1)将先向下平移5格,再向右平移13格.(2)将平行四边形沿A点顺时针方向旋转90°.【解析】解:(1)将先向下平移5格(下图红色部分),再向右平移13格(下图绿色部分):(2)将平行四边形沿A点顺时针方向旋转90°(下图蓝色部分):3.(2019春•枣阳市校级月考)(1)将图形A绕点O点顺时针旋转90°得到的图形B.(2)将图形B向右平移4格得到图形C.【解析】解:(1)将图形A绕点O点顺时针旋转90°得到的图形B(下图):(2)将图形B向右平移4格得到图形C(下图):4.(2018•泉州)(1)按要求画图.①将图中的三角形①绕O点顺时针旋转90°,画出旋转后的图形②.②将图中的三角形①平移,使平移后的三角形顶点O的位置在(9,5),画出平移后的图形③.【解析】解:根据分析可得,5.(2018春•新罗区期末)画一画:(1)把图形绕点O逆时针旋转90°.(2)把旋转后的图形向下平移两格.【解析】解:6.(2018•漳平市校级模拟)做一做,画一画(1)画出图形A的另一半,使它成为一个以直线a为对称轴的对称图形.(2)画出把图形B向右平移6格后得到的图形.(3)画出把图形C绕O点顺时针旋转90°后得到的图形.(4)用数对表示O点的位置是(8,6).【解析】解:(1)画出图形A的另一半,使它成为一个以直线a为对称轴的对称图形.(2)画出把图形B向右平移6格后得到的图形.(3)画出把图形C绕O点顺时针旋转90°后得到的图形.(4)用数对表示O点的位置是(8,6).故答案为:8,6.7.(2018春•隆化县校级期末)画出三角形AOB绕O点逆时针旋转180o后的图形.【解析】解:画出三角形AOB绕O点逆时针旋转180°后的图形(图中红色部分):8.(2018春•卢龙县期中)画出三角形AOB绕点O逆时针旋转90度的图形.【解析】解:画出三角形AOB绕点O逆时针旋转90度的图形(图中红色部分):9.(2018秋•廉江市期中)画出三角形AOB绕B点顺时针旋转90度后的图形.【解析】解:作图如下:10.(2018•兴仁县)按要求画一画.(1)画出图形A向右平移5格后得到的图形B.(2)画出图形B绕点O逆时针旋转90°后得到的图形C.【解析】解:(1)画出图形A向右平移5格后得到的图形B(下图):(2)画出图形B绕点O逆时针旋转90°后得到的图形C(下图):11.(2017春•海南区期末)画出三角形AOB绕O点顺时针旋转90度后的图形.【解析】解:根据题干分析画图如下:12.(2016春•洛阳月考)将长方形绕A点顺时针旋转90°.【解析】解:将长方形绕A点顺时针旋转90°(图中红色部分):13.(2016春•新郑市校级月考)画出下面的图象中的三角形沿着A点顺时针旋转90度后的图形.【解析】解:三角形沿着A点顺时针旋转90度后的图形(红色部分):14.(2016秋•永州期中)把如图的小三角旗绕点A沿顺时针方向旋转90度.再向右平移4格.分别画出旋转和平移后的图形.【解析】解:画图如下:15.(2016春•南海区期末)画出面积是3平方厘米的三角形AOB并绕O点逆时针旋转180o 后的图形.【解析】解:根据题干分析可得:三.解析题(共7小题)16.(2019春•东海县月考)按要求画一画.①将长方形绕A点逆时针旋转90°.②将小旗围绕B点逆时针旋转90°.【解析】解:作图如下:17.(2019春•古浪县校级期末)先将△ABC绕点C点顺时针旋转90°得到△A′B′C,再将△A′B′C′向下平移4格.【解析】解:先将△ABC绕点C点顺时针旋转90°得到△A′B′C,再将△A′B′C′向下平移4格.18.(2018春•抚宁区期末)画出绕点“O”顺时针旋转90度后的图形.【解析】解:作图如下:19.(2017秋•保定期末)画出三角形逆时针旋转90度后的图形.【解析】解:作图如下:20.(2018春•桃城区校级期末)(1)小鱼图从右下方移至左上方,先向上平移3格,又向左平移5格.(2)把梯形绕A点顺时针方向旋转90°,画出旋转后的图形.【解析】解:(1)根据题干分析可得:小鱼图从右下方移至左上方,先向上平移3格,再向左平移5格;(2)根据分析画图如下:故答案为:上、3、左、5.21.(2017春•绍兴期末)画出三角形AOB绕O点顺时针旋转90°后的图形.【解析】解:画出三角形AOB绕O点顺时针旋转90°后的图形:22.(2017春•绍兴期末)画出三角形AOB绕O点顺时针旋转90°后的图形.【解析】解:画出三角形AOB绕O点顺时针旋转90°后的图形:。
