矩形、菱形
矩形、菱形、正方形、梯形

正方形是矩形和菱形的混合体,既具有平行四边形的一般性质,又具有矩形和菱形的独特性质。它本是大家早就熟悉的几何图形,因此在研究前面矩形和菱形的经验的基础上,对正方形特征性质的研究同学们也不难得出。这里值得注意的是,要重视研究平行四边形、矩形、菱形和正方形各种图形之间的联系,并结合实际操作加深理解。
A.平行四边形 B.矩形 C. 直角梯形 D.等腰梯形
答案:1C ;2C
矩形、菱形、正方形、梯形
一、几种特殊的平行四边形
关于矩形,我们要从平行四边形的内角的变化上认识其特殊性——一个内角是直角的平行四边形。进一步研究其特有的性质——对角线相等、内角都为直角、是轴对称图形。这里还要特别注意的是平行四边形的特征,矩形也都具有。当然,识别矩形的方法也要从其特殊平行四边形的特殊性上去研究。
对角线将菱形分成的四个直角三角形,它们的面积和等于菱形的面积,由此很容易推出上面的公式。)
二、梯形
梯形也是大家早已熟悉的几何图形,所以教材直接介绍梯形、等腰梯形、直角梯形的定义,这里要特别注意“只有”两个字的重要性,也就是说“一组对边平行,而另一组对边不平行的四边形是梯形”。大家要认识等腰梯形的轴对称性,并由此推理得到等腰梯形的特征:“等腰梯形同一底上的两个内角相等”及“等腰梯形的对角线相等”通过将等腰梯形分割成平行四边形和等腰三角形来推理证明∠B=∠C的方法,应引起足够的重视,因为这是解决有关梯形问题的常用方法。通过特殊的三角形和平行四边形可以将梯形的边和角进行转移,从而达到解决问题的目的。
矩形正方形菱形平行四边形的关系

矩形正方形菱形平行四边形的关系矩形、正方形、菱形和平行四边形都是几何学中常见的图形,它们之间存在着一定的关系。
本文将介绍这四种图形之间的关系,并分别阐述它们的特点和性质。
一、矩形矩形是一种具有特殊性质的四边形,它的四个内角都是直角(即90度)。
此外,矩形的对角线相等且垂直相交,对边平行且相等。
矩形的特点使得它在日常生活和工程设计中得到广泛应用。
例如,书桌、建筑物的窗户、墙壁等都常见到矩形的形状。
二、正方形正方形是矩形的特殊形式,它的四个边长相等且内角都是直角。
由于正方形具有对边平行且相等的性质,因此它也是平行四边形。
正方形的特点使得它在几何学中具有重要的地位,在城市规划、图案设计等领域中也被广泛应用。
三、菱形菱形是一种具有特殊性质的四边形,它的对边平行且相等。
此外,菱形的对角线相等且垂直相交,内角不是直角。
菱形的特点使得它在几何学中具有独特的地位,例如,菱形的形状常常被用于设计钻石、纹身等。
四、平行四边形平行四边形是一种具有特殊性质的四边形,它的对边平行且相等。
平行四边形的特点使得它在几何学中也是一个重要的图形。
平行四边形的对角线不相等,内角之和为360度。
平行四边形的形状常常出现在建筑物的立面、道路的标线等。
矩形、正方形、菱形和平行四边形之间的关系可以总结如下:1. 矩形是一种特殊的平行四边形,它的对边平行且相等。
2. 正方形是一种特殊的矩形和平行四边形,它的四个边长相等且内角都是直角。
3. 菱形是一种特殊的平行四边形,它的对边平行且相等,但内角不是直角。
4. 平行四边形是一种具有对边平行且相等的特性的四边形,它包括了矩形和菱形。
矩形、正方形、菱形和平行四边形之间存在着紧密的关系。
它们都是具有特殊性质的四边形,但在某些方面又有所不同。
矩形和正方形具有直角和对边相等的特点,而菱形则具有对边平行且相等的特点,平行四边形则是包含了矩形和菱形的更广义的概念。
这些图形在数学和几何学中具有重要的地位,在日常生活和工程设计中也得到了广泛的应用。
专题16 矩形和菱形(知识点串讲)-解析版

专题16 矩形和菱形(知识点串讲)【知识点考点--思维导图】©知识点一:矩形的性质矩形的定义:有一个角是直角的平行四边形叫做矩形。
矩形的性质:1)矩形具有平行四边形的所有性质;2)矩形的四个角都是直角;几何描述:∵四边形ABCD是矩形∴∠BAD=∠ADC=∠BCD=∠ABC=90°3)对角线相等;几何描述:∵四边形ABCD是矩形∴AC=BD推论:1、在直角三角形中斜边的中线,等于斜边的一半。
2、直角三角形中,30度角所对应的直角边等于斜边的一半。
4)矩形既是中心对称图形,也是轴对称图形。
矩形的对称中心是矩形对角线的交点;矩形有两条对称轴,矩形的对称轴是过矩形对边中点的直线;矩形的对称轴过矩形的对称中心。
◎考点1:矩形性质的理解L 例1.(2020·贵阳市清镇养正学校九年级月考)如图,在矩形ABCD 中,DE 平分ADC ∠交BC 于点E ,EF AD ⊥交AD 于点F ,若3EF =,5AE =,则AD 等于( )A .5B .6C .7D .8【答案】C【分析】 利用勾股定理求出AF ,根据矩形的四个角是直角可得∠ADC =∠C =90°,然后求出四边形CDFE 是矩形,再根据角平分线的定义可得∠ADE =∠CDE ,再根据平行线的性质可得∠ADE =∠CED ,然后可得∠CDE =∠CED ,根据等角对等边的性质可得CD =CE ,根据邻边相等的矩形是正方形得到矩形CDFE 是正方形,根据正方形的四条边都相等求出DF ,根据AD =AF +DF 即可得解.【详解】解:∠EF AD ⊥,3EF =,5AE =,∠4AF ===,在矩形ABCD 中,∠ADC =∠C =90°,∠EF AD ⊥,∠∠DFE =90°,∠四边形CDFE 是矩形,∠DE 平分∠ADC ,∠∠ADE =∠CDE ,∠∠ADE=∠CED,∠∠CDE=∠CED,∠CD=CE,∠矩形CDFE是正方形,∠EF=3,∠DF=EF=3,∠AD=AF+DF=4+3=7.故选C.【点睛】本题考查了矩形的性质,勾股定理,角平分线的定义,平行线的性质,正方形的判定与性质.熟记各性质是解题的关键.练习1.(2020·沙坪坝区·重庆南开中学八年级月考)下列说法正确的是()A.矩形的对角线互相垂直且平分B.矩形的邻边一定相等C.对角线相等的四边形是矩形D.有三个角为直角的四边形为矩形【答案】D【分析】根据矩形的性质可知:A、B两个选项错误;根据对角线互相平分且相等的四边形是矩形这个判定知,C选项错误;三个角为直角,则第四个也为直角,根据有四个角是直角的四边形是矩形判定得,故D选项正确.A:矩形的对角线的性质是:矩形的对角线互相平分且相等,故此说法错误;B:矩形的邻边不一定相等,但对边一定相等,故此说法错误;C:对角线互相平分且相等的四边形是矩形,由此判定知,此说法错误;D:当有三个角是直角时,根据四边形内角和定理,第四个角也是直角,从而判定是矩形,此说法正确.故选:D【点睛】本题考查了矩形的判定和性质,必须准确而熟练地掌握矩形的判定和性质.练习2.(2020·吴江经济开发区实验初级中学八年级月考)一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的矩形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与矩形的一个顶点重合,其它两个顶点在矩形的边上,则剪下的等腰三角形的面积为()A.50或40或30B.50或40C.50D.50或30或20【答案】A【分析】本题中由于等腰三角形的位置不确定,因此要分三种情况进行讨论求解,①如图(1),②如图(2),③如图(3),分别求得三角形的面积.【详解】解:如图四边形ABCD是矩形,AD=18cm,AB=16cm;本题可分三种情况:①如图(1):∠AEF中,AE=AF=10cm;S ∠AEF =12•AE•AF =50cm 2;②如图(2):∠AGH 中,AG =GH =10cm ;在Rt∠BGH 中,BG =AB−AG =16−10=6cm ;根据勾股定理有:BH =8cm ;∠S ∠AGH =12AG•BH =12×8×10=40cm 2; ③如图(3):∠AMN 中,AM =MN =10cm ;在Rt∠DMN 中,MD =AD−AM =18−10=8cm ;根据勾股定理有DN =6cm ;∠S ∠AMN =12AM•DN =12×10×6=30cm 2. 故等腰三角形的面积为:50或40或30.故选:A .【点睛】本题主要考查了等腰三角形的性质、矩形的性质、勾股定理等知识,解题的关键在于能够进行正确的分类讨论.练习3.(2021·四川绵阳市·八年级期末)如图,在长方形ABCD 中,AF BD ⊥,垂足为E ,AF 交BC 于点F ,连接DF ,且DF 平分BDC ∠.下列结论中:①ABD CDB ≅;②ADE BDF S S =△△;③90ABD CDF ∠+∠=︒;④AD DF =.其中正确的个数有( )A .4个B .3个C .2个D .1个【答案】C【分析】 由长方形的性质可得:,,90,AB CD AD BC BAD BCD ==∠=∠=︒从而可判断①;由面积公式可得,ADF BDC S S =再利用角平分线的性质证明,Rt DFE Rt DFC ≌再利用面积差可判断②;由90ABD DBC ∠+∠=︒,结合90ABD CDF ∠+∠=︒,证明,DBC CDF ∠=∠ 再证明30,DBC EDF CDF ∠=∠=∠=︒ 可得AF 是BD 的垂直平分线,可得,AB AD = 则四边形ABCD 为正方形,与已知互相矛盾,可判断③;由,AF BD ⊥ 结合AD DF =,可证明BD 是AF 的垂直平分线,可得,BA BF = 从而可证明45ABE ADB ∠=∠=︒,可得,AB AD = 则四边形ABCD 为正方形,与已知互相矛盾,可判断④.【详解】 解: 长方形ABCD ,,,90,AB CD AD BC BAD BCD ∴==∠=∠=︒(),ABD CDB SAS ∴≌ 故①符合题意; 11,,22ADF BDC SAD CD S BC CD == ,ADF BDC SS ∴=,,ADE ADF DEF BDF BCD DCF S S S S S S =-=-DF 平分BDC ∠,,90,AF BD BCD ⊥∠=︒,FE FC ∴=,DF DF =(),Rt DFE Rt DFC HL ∴≌,DEF DCF SS ∴= ,ADE BDFS S ∴= 故②符合题意; 长方形ABCD ,90ABD DBC ∴∠+∠=︒,若90ABD CDF ∠+∠=︒,,DBC CDF ∴∠=∠,Rt DFE Rt DFC ≌,EDF CDF ∴∠=∠ ,DE DC =30,DBC EDF CDF ∴∠=∠=∠=︒2,BD DC ∴=E ∴是BD 的中点,AF ∴是BD 的垂直平分线,,AB AD ∴=则四边形ABCD为正方形,与已知互相矛盾,故③不符合题意;AF BD⊥,=,若AD DFAE EF∴=,∴是AF的垂直平分线,BD∴=BA BF,∠=°,ABC90∴∠=∠=︒,45BAF BFAABE ADB∴∠=∠=︒,45∴=,AB AD则四边形ABCD为正方形,与已知互相矛盾,故④不符合题意;故选:.C【点睛】本题考查全等三角形的判定与性质,矩形的性质,正方形的判定,角平分线的性质,垂直平分线的定义与判定,等腰三角形的判定与性质,含30的直角三角形的性质,掌握以上知识是解题的关键.◎考点2:利用性质求角度例1.(2021·浙江)如图,矩形ABCD中,对角线AC,BD交于点O,DE⊥AC于E,且⊥ADE:⊥EDC=3:2,则⊥COD的度数为()A.54°B.60°C.65°D.72°【答案】D【分析】设∠ADE=3α,∠EDC=2α,根据题意列出方程求出α的值,然后根据三角形的内角和定理即可求出答案.【详解】解:设∠ADE=3α,∠EDC=2α,∠3α+2α=90°,∠α=18°,∠∠CDE=2α=36°,∠DE∠AC,∠∠DCE=90°﹣36°=54°,∠OD=OC,∠∠DCE=∠ODC=54°,∠∠COD=180°﹣2×54°=72°,故选:D.【点睛】本题考查矩形的性质,三角形内角和定理,解题的关键是熟练运用矩形的性质,属于基础题型.练习1.(2021·浙江九年级专题练习)如图,E、F分别是矩形ABCD边上的两点,设⊥ADE =α,⊥EDF=β,⊥FDC=γ,若⊥AED=α+β,下列结论正确的是()A.α=βB.α=γC.α+β+2γ=90°D.2α+γ=90°【答案】B【分析】由矩形的性质得出∠A=∠ADC=90°,则α+β+γ=90°,由直角三角形的性质得出∠AED+α=90°,证出2α+β=90°,推出α+β+γ=2α+β,即可得出结果.【详解】解:∠四边形ABCD是矩形,∠∠A=∠ADC=90°,∠∠ADE=α,∠EDF=β,∠FDC=γ,∠α+β+γ=90°,∠∠AED+α=90°,∠AED=α+β,∠2α+β=90°,∠α+β+γ=2α+β,∠α=γ,故选:B.【点睛】本题考查了矩形的性质、直角三角形的性质等知识,熟练掌握矩形的性质是解题的关键.练习2.(2020·石家庄市第四十一中学八年级期中)如图,延长矩形ABCD的边BC至点E,使CE=BD,连结AE,如果⊥ADB=40°,则⊥E的度数是()A.10°B.20°C.30°D.40°【答案】B【分析】如图连接AC.只要证明CE=CA,推出∠E=∠CAE,进而即可解决问题.【详解】解:连接AC,交BD于点O,∠四边形ABCD是矩形,∠AC=BD,∠EC=BD,∠AC=CE,∠∠E=∠CAE,∠OB=OC,∠∠ACB=∠DBC ,又∠AD∠BC ,∠∠DBC=∠ADB ,∠∠ACB =∠ADB =40°,∠∠ACB =∠E +∠CAE ,∠∠E =∠CAE =20°,故选B .【点睛】本题考查矩形的性质、等腰三角形的判定和性质,三角形的外角的性质等知识,解题的关键是学会添加常用辅助线,构造等腰三角形解决问题.练习3.(2020·福建省泉州实验中学八年级月考)如图,在矩形ABCD 中,对角线AC 、BD 相交于点O ,若DF AC ⊥,:3:2ADF FDC ∠∠=,则BDF ∠=( )A .18°B .36°C .27°D .54°【答案】A【分析】 由矩形ABCD 的性质结合:3:2ADF FDC ∠∠=,求解ADF ∠,结合DF AC ⊥,求解DAC ∠,再利用矩形的性质可得:OA OD =,求解ADO ∠,再利用角的和差可得答案.【详解】 解:矩形ABCD ,90,ADC ADF CDF ∴∠=︒=∠+∠:3:2ADF FDC ∠∠=,390545ADF ∴∠=⨯︒=︒, ,DF AC ⊥9036DAC ADF ∴∠=︒-∠=︒,矩形ABCD ,,OA OD ∴=36OAD ODA ∴∠=∠=︒,543618.BDF ADF ADO ∴∠=∠-∠=︒-︒=︒故选:A .【点睛】本题考查的是矩形的性质,等腰三角形的性质,直角三角形两锐角互余,掌握以上知识是解题的关键.◎考点3:利用性质与判定求线段长例1.(2021·沙坪坝区·重庆南开中学八年级开学考试)如图,矩形ABCD 中,对角线AC 、BD 相交于点O ,过点O 作OE ⊥BD 交AD 于点E ,已知AB =2,54DOE S =,则AE 的长为( )A.1.5B.2C.2.5D 【答案】A【分析】首先连接BE,由题意可得OE为对角线BD的垂直平分线,可得BE=DE,S∠BOE=S∠DOE=54,由三角形的面积则可求得DE的长,得出BE的长,然后由勾股定理求得答案.【详解】解:连接BE,如图所示:由题意可得,OE为对角线BD的垂直平分线,∠BE=DE,S∠BOE=S∠DOE=54,∠S∠BDE=2S∠BOE=52,∠12DE•AB=52,又∠AB=2,∠DE=52,∠BE=52,在Rt∠ABE中,由勾股定理得:AE,故选:A.【点睛】此题考查了矩形的性质、勾股定理以及三角形的面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.练习1.(2021·浙江)矩形ABCD中,AB=6,BC=8,则点A到BD的距离是()A.4B.4.6C.4.8D.5【答案】C【分析】先根据矩形的性质和勾股定理求出BD=10,再根据∠ABD的面积即可得出答案.【详解】解:设点A到BD的距离为h,在矩形ABCD中,∠AB=6,BC=AD=8,∠由勾股定理可知:BD,S矩形ABCD= AD•AB=48,S∠ABD= 12S矩形ABCD=24,∠12h•BD=24,∠h=4.8,故选:C.【点睛】本题考查矩形的性质,解题的关键是熟练运用勾股定理以及矩形的性质,本题属于基础题型.练习2.(2021·四川绵阳市·八年级期末)如图,四边形ABCD 中,90A B ∠=∠=︒,60C ∠=°,2CD AD =,4AB =,点P 是AB 上一动点,则PC PD +的最小值是( )A .4B .6C .8D .10【答案】C【分析】作D 点关于AB 的对称点D ',连接CD '交AB 于P ,根据两点之间线段最短可知此时PC +PD 最小;再作D 'E ∠BC 于E ,则EB =D 'A =AD ,先根据等边对等角得出∠DCD '=∠DD 'C ,然后根据平行线的性质得出∠D 'CE =∠DD 'C ,从而求得∠D 'CE =∠DCD ',得出∠D 'CE =30°,根据30°角的直角三角形的性质求得D 'C =2D 'E =2AB ,即可求得PC +PD 的最小值.【详解】作D 点关于AB 的对称点D ',连接CD '交AB 于P ,P 即为所求,此时PC +PD =PC +PD '=CD ',根据两点之间线段最短可知此时PC +PD 最小.作D 'E ∠BC 于E ,则EB =D 'A =AD .∠CD =2AD ,∠DD '=CD ,∠∠DCD '=∠DD 'C .∠∠DAB =∠ABC =90°,∠四边形ABED '是矩形,∠DD '∠EC ,D 'E =AB =4,∠∠D 'CE =∠DD 'C ,∠∠D 'CE =∠DCD '.∠∠DCB =60°,∠∠D 'CE =30°,∠在Rt∠D 'CE 中,D 'C =2D 'E =2×4=8,∠PC +PD 的最小值为8.故选:C .【点睛】本题考查了轴对称﹣最短路线问题,轴对称的性质,矩形的判定和性质,等腰三角形的性质,平行线的性质,含30°角的直角三角形的性质等,确定出P 点是解答本题的关键.练习3.(2021·全国八年级专题练习)矩形ABCD 与ECFG 如图放置,点B ,C ,F 共线,点C ,E ,D 共线,连接AG ,取AG 的中点H ,连接EH .若4AB CF ==,2BC CE ==,则EH =( )AB .2CD 【答案】A【分析】 延长GE 交AB 于点R ,连接AE ,设AG 交DE 于点M ,过点E 作EN∠AG 于N ,先计算出RG=6,∠ARG=90︒,AR=2,根据勾股定理求出AG =,利用1122AEG S EG AR AG EN =⋅⋅=⋅⋅,求出EN =,即可利用勾股定理求出NG 、EH . 【详解】如图,延长GE 交AB 于点R ,连接AE ,设AG 交DE 于点M ,过点E 作EN∠AG 于N , ∠矩形ABCD 与ECFG 如图放置,点B ,C ,F 共线,点C ,E ,D 共线,∠RG=BF=BC+CF=2+4=6,∠ARG=90︒,AR=AR -CE=4-2=2,∠AG ===,∠H 是AG 中点,,∠1122AEG S EG AR AG EN =⋅⋅=⋅⋅,∠24⨯=,∠EN =,在Rt∠ENG 中,NG ==,∠5NH NG HG =-=,∠EH =,故选:A .【点睛】此题考查矩形的性质,勾股定理,线段中点的性质,三角形面积法求线段长度,熟记矩形的性质及熟练运用勾股定理是解题的关键.◎考点4:利用性质与判定求面积例1.(2021·全国八年级专题练习)如图,点P 是矩形ABCD 的对角线上一点,过点P 作//EF BC ,分别交,AB CD 于,E F ,连接,PB PD ,若1,3AE PF ==,则图中阴影部分的面积为( )A .3B .6C .9D .12 【答案】A【分析】先根据矩形的性质证得DFP PBE S S =,然后求解即可.【详解】解:作PM∠AD 于M ,交BC 于N ,∠四边形AEPM 、四边形DFPM 、四边形CFPN 和四边形BEPN 都是矩形,∠ADC ABC S S =△△,AMP AEP SS =,PBE PBN S S =,PFD PDM S S =,PFC PCN S S =, ∠S 矩形DFPM =S 矩形BEPN ,∠PM=AE=1,PF=NC=3, ∠131322DFP PBE S S ==⨯⨯=△△, ∠S 阴=33+=322, 故选:A .【点睛】本题主要考查矩形的性质、三角形的面积等知识,证得DFP PBE S S =是解答本题的关键. 练习1.(2020·河南洛阳市·七年级期中)如图,周长为34的矩形ABCD 被分成7个全等的矩形,则矩形ABCD的面积为()A.280B.140C.70D.196【答案】C【解析】解:设小长方形的长、宽分别为x、y,依题意得:,解得:,则矩形ABCD的面积为7×2×5=70.故选C.【点评】考查了二元一次方程组的应用,此题是一个信息题目,首先会根据图示找到所需要的数量关系,然后利用这些关系列出方程组解决问题.练习2.(2020·石阡县教育局教研室八年级期末)矩形的对角线长为20,两邻边之比为3:4,则矩形的面积为()A.56B.192C.20D.以上答案都不对【答案】B【分析】首先设矩形的两邻边长分别为:3x ,4x ,可得(3x )2+(4x )2=202,继而求得矩形的两邻边长,则可求得答案.【详解】解:∠矩形的两邻边之比为3:4,∠设矩形的两邻边长分别为:3x ,4x ,∠对角线长为20,∠(3x )2+(4x )2=202,解得:x=4,∠矩形的两邻边长分别为:12,16;∠矩形的面积为:12×16=192.故选B .练习3.(2019·浙江丽水市·九年级学业考试)在矩形ABCD 中,,BC=2,以A 为圆心,AD 为半径画弧交线段BC 于E ,连接DE ,则阴影部分的面积为( )A .2πB .22π- C .πD .2π- 【答案】A【详解】解:连接AE ,根据矩形的性质,可AE=AD=BC=2.在Rt∠ABE 中,根据勾股定理可得=然后由∠ABE 是等腰直角三角形,求得∠DAE=45°,因此可求得S 阴影=S 扇形DAE ﹣S ∠DAE =2452360π⨯﹣12=2π. 故选A .【点睛】本题考查了矩形的性质、等腰直角三角形的判定与性质、勾股定理、扇形面积公式等知识;熟练掌握矩形的性质,证明三角形是等腰直角三角形是解决问题的关键.◎考点5:利用矩形性质证明例1.(2021·广东佛山市·平洲二中九年级月考)如图,BD 是矩形ABCD 的一条对角线.(1)作BD 的垂直平分线EF ,分别交AD ,BC 于点E 、F .垂足为点O (要求用尺规作图,保留作图痕迹,不要求写作法);(2)求证:BE BF =.【答案】(1)作图见解析;(2)证明见解析.【分析】(1)分别以B 、D 为圆心,以大于BD 一半的长为半径上下画弧,上下各有一个交点,这两点的连线即为所求;(2)先通过矩形的性质得到有关条件证明DEO BFO ∆∆≌,得到 OE =OF ,再利用垂直平分线的判定得到BD 是EF 的垂直平分线,再利用垂直平分线的性质即可求解.【详解】(1)解:如图所示:EF 即为所求;(2)证明:连接BE ,四边形ABCD 为矩形,//AD BC ∴,ADB CBD ∴∠=∠. EF 垂直平分线段BD ,BO DO ∴=,90DOE BOF ==︒∠∠.在DEO ∆和BFO ∆中,ADB CBD DO BO DOE BOF ∠=∠⎧⎪=⎨⎪∠=∠⎩,(ASA)DEO BFO ∴△≌△,OE OF ∴=,又BD EF ⊥,∴BD 垂直平分EF ,BE BF ∴=.【点睛】本题综合考查了如何作线段的垂直平分线、矩形的性质、线段的垂直平分线的性质和判定、三角形全等的性质和判定等内容,要求学生熟记作图步骤,灵活运用线段垂直平分线的性质和判定进行线段关系的转化,考查了学生分析推理的能力.练习1.(2020·海南鑫源高级中学八年级期末)如图,矩形ABCD 中,O 是AC 与BD 的交点,过点O 的直线EF 与AB 、CD 的延长线分别交于点E 、F .(1)求证:BOE DOF ∆≅∆;(2)以A 、E 、C 、F 为顶点的四边形是平行四边形?试证明你的结论.【答案】(1)见解析;(2)见解析.【分析】(1)由矩形的性质:OB =OD ,AE ∠CF 证得BEO DFO ∠=∠,根据AAS 可证明∠BOE ∠∠DOF ; (2)根据BOE DOF ∆≅∆得BE =DF ,根据四边形ABCD 是矩形得AB =CD ,AE //CF ,从而进一步可证明四边形AECF 是平行四边形.【详解】解:(1)证明:∠四边形ABCD 是矩形∠OB OD =,//AE CF∠BEO DFO ∠=∠又BOE DOF ∠=∠∠BOE DOF ∆≅∆;(2)证明 :∠BOE DOF ∆≅∆,∠BE =DF∠四边形ABCD 是矩形,∠AB CD =,//AE CF∠AE AB BE =+,CF CD DF =+∠AE CF =∠四边形AECF 是平行四边形【点睛】本题考查了矩形的性质、全等三角形的判定和性质和平行四边形的判定.解答此题的关键是熟知矩形、全等三角形的判定与性质定理和平行四边形判定.练习2.(2020·赣州市赣县区第四中学八年级期中)如图,矩形ABCD 中,点E ,F 分别在AB ,CD 边上,连接CE 、AF ,⊥DCE =⊥BAF .试判断四边形AECF 的形状并加以证明.【答案】四边形AECF 是平行四边形,证明见解析.【分析】根据矩形的性质得出//DC AB ,可得出∠DFA =∠BAF ,进而得出∠DCE =∠DFA ,证得//FA CE ,再根据平行四边形的判定得出即可.【详解】解:四边形AECF 是平行四边形.∠四边形ABCD 是矩形,∠//DC AB ,∠∠DFA =∠BAF ,又∠∠DCE =∠BAF ,∠∠DCE =∠DFA∠//FA CE ,∠四边形AECF 是平行四边形.【点睛】本题考查了矩形的性质,平行线的判定以及平行四边形的判定,能灵活运用定理进行推理是解此题的关键.练习3.(2021·湖南师大附中博才实验中学九年级期末)如图,在矩形ABCD 中,点M 、N 分别在边AD 、BC 上,且连结BM 、DN .(1)若M ,N 分别为AD ,BC 的中点,求证:ABM ⊥CDN ;(2)当四边形BMDN 是菱形,AD =2AB ,AM =3时,求菱形的边长.【答案】(1)见解析;(2)5【分析】(1)根据矩形的性质和M ,N 分别为AD ,BC 的中点,可以得到∠ABM 和∠CDN 全等的条件,从而可以证明结论成立;(2)根据菱形的性质和勾股定理,可以求得菱形的边长.【详解】证明:(1)∠四边形ABCD 是矩形∠AD=BC ,AB=CD ,∠A=∠C=90°∠M ,N 分别为AD ,BC 的中点∠AM=CN在∠ABM 和∠CDN 中,AB CD A C AM CN ⎧⎪∠∠⎨⎪⎩=== ∠∠ABM ∠∠CDN (SAS )(2)设AB =x ,则AD =2x∠四边形ABCD 是矩形∠∠A=90°∠四边形BMDN 是菱形,AM =3∠BM =DM =2x -3∠AM 2+AB 2=BM 2∠32+x 2=(2x -3)2解得:x 1=0(舍去),x 2=4即AB =4∠BM 5=即菱形的边长是5.【点睛】本题考查菱形的性质、矩形的性质、全等三角形的判定与性质,解答本题的关键是明确题意,利用数形结合的思想解答.◎考点6:求矩形在平面直角坐标系中的坐标例1.(2021·全国八年级专题练习)如图,在平面直角坐标系中,四边形OABC 是矩形,点O 是坐标原点,点A 、C 的坐标分别是()6,0,()0,3,点B 在第一象限,则点B 的坐标是( )A .()3,6B .()6,3C .()6,6D .()3,3【答案】B【分析】 根据矩形的性质得出点B 的坐标即可.【详解】解:∠四边形OABC 是矩形,∠OC=AB ,CB=OA ,∠点A ,C 的坐标分别是(6,0),(0,3),∠AB=3,OA=6,∠点B 坐标为(6,3),故选:B .【点睛】此题考查矩形的性质,关键是根据矩形的性质得出点B 的坐标.练习1.(2020·山西晋中市·八年级期中)一个长方形的三个顶点在平面直角坐标系中的坐标分别为(1,1)--,(1,2)-,(3,1)-,那么第四个顶点的坐标为( )A .(3,2)B .(2,3)C .(3,3)D .(2,2)【答案】A根据长方形对边平行且相等,利用横坐标与纵坐标和已知点的横坐标或纵坐标相同即可求出第四点坐标.【详解】在平面直角坐标系中的坐标分别为(-1,-1),(-1,2),两点的横坐标相同,这两点连线平行y轴,第四点与(3,-1)连线也平行y轴,则第四点的横坐标为3,由于在平面直角坐标系中的坐标分别为(-1,-1),(3,-1)纵坐标相同,此两点连线平行x轴,为此(-1,2),与第四点两线平行x轴,则第四点的纵坐标为2,所以第四点的坐标为(3,2),故选择:A.【点睛】本题考查长方形的第四点坐标问题,掌握长方形的性质,会利用平行x轴或y轴,两点的横坐标或纵坐标相等来解决问题是关键.练习2.(2021·全国)如图,矩形OABC的顶点A在x轴上,点B的坐标为(1,2).固定边OA,向左“推”矩形OABC,使点B落在y轴的点B'的位置,则点C的对应点C'的坐标为()A.(﹣1B.1)C.(﹣1,2)D.(2,﹣1)【答案】A【分析】根据矩形的性质和勾股定理求出OB'的长,得到点C'的坐标.解:∠四边形OABC 是矩形,点B 的坐标为(1,2),∠OA =1,AB =2,由题意得:AB '=AB =2,四边形OAB 'C '是平行四边形,∠OB '==1B C OA ''==,∠点C 的对应点C '的坐标为(-.故选:A .【点睛】本题考查点坐标的求解和矩形的性质,解题的关键是掌握矩形的性质求出线段长从而得到点坐标.练习3.(2021·上海九年级专题练习)如图,在平面直角坐标系中,点P 的坐标为(4,4),点E F 、分别在x y 、轴的正半轴上,PE PF ⊥,则四边形OEPF 的面积为( )A .20B .16C .12D .8【答案】B【分析】 过点P 作PM OE ⊥,PN OF ⊥,证明△△OME PNF ≅,再根据面积计算即可;【详解】如图所示,过点P 作PM OE ⊥,PN OF ⊥,∠点P 的坐标为(4,4),∠PM=PN ,∠PE PF ⊥,∠MPE EPN FPN EPN ∠+∠=∠+∠,∠∠=∠MPE NPF ,又∠PME PNF ∠=∠,∠()△△OME PNF ASA ≅,∠四边形四边形△正方形4416OEPF ONPE PME ONPM S S S S =+==⨯=.故答案选B .【点睛】 本题主要考查了四边形与坐标系结合,全等三角形的应用,准确判断计算是解题的关键.◎考点7:矩形与折叠问题例1.(2020·海南鑫源高级中学八年级期末)如图,在矩形ABCD 中,点E 在边CD 上,将该矩形沿AE 折叠,恰好使的D 落在边BC 上的点F 处,如果⊥BAF =60°,则⊥DAE 的大小为( )A .10°B .15 °C .20 °D .25°【答案】B【分析】 由题意可知90BAD ∠=︒,12FAE DAE DAF ∠=∠=∠.再由DAF BAD BAF ∠=∠-∠,即可求出DAE ∠的大小.【详解】∠四边形ABCD 为矩形,∠90BAD ∠=︒, ∠FAE 是由DAE △沿AE 折叠而来,且F 点恰好落在BC 上, ∠12FAE DAE DAF ∠=∠=∠, ∠906030DAF BAD BAF ∠=∠-∠=︒-︒=︒, ∠130152DAE ∠=⨯︒=︒. 故选:B .【点睛】本题考查矩形的折叠问题,根据折叠的性质推出12FAE DAE DAF ∠=∠=∠是解答本题的关键.练习1.(2020·浙江杭州市·八年级期中)在矩形纸片ABCD 中,6,10AB AD ==.如图所示,折叠纸片,使点A 落在BC 边上的A '处,折痕为PQ ,当点A '在BC 边上移动时,折痕的端点P 、Q 也随之移动,若限定点P 、Q 分别在线段AB 、AD 边上移动,则点A '在BC 边上可移动的最大距离为( )A .3B .4C .5D .6【答案】B【分析】 根据翻折的性质,①当P 与B 重合时,可得BA′与AP 的关系,根据线段的和差,可得A′C ,②当Q 与D 重合时,根据勾股定理,可得A′C ,根据线段的和差,可得答案.【详解】解:①当P 与B 重合时,BA′=BA =6,CA′=BC−BA′=10−6=4,②当Q 与D 重合时,由勾股定理,得CA′8,CA′最大是8,CA′最小是4,点A′在BC 边上可移动的最大距离为8−4=4,故选:B .【点睛】本题考查了翻折变换,利用了翻折的性质,勾股定理,分类讨论是解题关键.练习2.(2021·广东汕尾市·九年级期末)如图,将矩形纸片ABCD 折叠,使点A 与点C 重合,折痕为EF .若8AB =,4BC =,那么线段EF 的长为( )A .4B .6C .D .【答案】C【分析】 连接EC ,设AC 与EF 交于点O .根据题意易得线段EF 和线段AC 互相垂直平分,即得出结论AE EC =,12OE OF EF ==,12OA OC AC ==.利用勾股定理可求出AC 的长,即得出OA 的长.设AE EC x ==,则8BE x =-,在Rt BEC △中利用勾股定理即可列出关于x 的方程,求出x ,即求出AE 长.再在Rt AOE 中,利用勾股定理即可求出OE 长,最后即得出 EF 长.【详解】连接EC ,设AC 与EF 交于点O .根据题意可知线段EF 和线段AC 互相垂直平分.∠AE EC =,12OE OF EF ==,12OA OC AC ==.在Rt ABC 中,AC =∠12OA AC == 设AE EC x ==,则8BE x =-,在Rt BEC △中,222BE BC EC +=,即2224)8(x x -+=,解得:5x =,∠5AE =,在Rt AOE 中,222OA OE AE +=,即2225OE +=,∠OE =.∠2EF OE ==故选:C .【点睛】本题考查图形的翻折变换.利用线段垂直平分线的性质,矩形的性质以及勾股定理找出边的等量关系是解答本题的关键.练习3.(2020·贵州毕节市·九年级期末)如图,将矩形纸片ABCD 沿其对角线AC 折叠,使点B 落到点B '的位置,AB '与CD 交于点E ,若7AB =,3AD =,则图中阴影部分的周长为( )A .10B .13C .17D .20【答案】D【分析】首先由四边形ABCD 为矩形及折叠的特性,得到B ′C =BC =AD ,∠B ′=∠B =∠D =90°,∠B ′EC =∠DEA ,得到∠AED ∠∠CEB ′,得出EA =EC ,再由阴影部分的周长为AD +DE +EA +EB ′+B ′C +EC ,即矩形的周长解答即可.【详解】解:∠四边形ABCD 为矩形,∠B ′C =BC =AD ,∠B ′=∠B =∠D =90°,∠∠B ′EC =∠DEA ,在∠AED 和∠CEB ′中,DEA BE C D B AD B C ∠=∠'⎧⎪∠=∠'⎨⎪='⎩, ∠∠AED ∠∠CEB ′(AAS );∠EA =EC ,∠阴影部分的周长为AD +DE +EA +EB ′+B ′C +EC=AD +DE +EC +EA +EB ′+B ′C=AD +DC +AB ′+B ′C=3+7+7+3=20,故选:D .【点睛】本题主要考查了图形的折叠问题,全等三角形的判定和性质,及矩形的性质.熟记翻折前后两个图形能够重合找出相等的角是解题的关键.◎考点8:直角三角形斜边上的中线问题例1.(2020·浙江杭州市·八年级期中)如图,公路,AC BC 互相垂直,公路AB 的中点M与点C 被湖隔开,若测得 1.2km AC =, 1.6km BC =,则M ,C 两点间的距离为( )A .2.0kmB .1.2kmC .1.0kmD .0.5km【答案】C【分析】 首先根据勾股定理求得AB 的长度,然后利用直角三角形斜边上的中线等于斜边一半的性质即可求解.【详解】解:如图,在直角∠ABC 中,∠ACB =90°,AC =1.2km ,BC =1.6km ,由勾股定理得到:AB (km ). ∠点M 是AB 的中点,∠MC =12AB =1km . 故选:C .【点睛】本题主要考查了勾股定理的应用,直角三角形斜边上的中线的性质,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.练习1.(2020·鞍山市第五十一中学九年级月考)如图,在Rt⊥ABC中,⊥ACB=90°,将⊥ABC 绕顶点C逆时针旋转得到⊥A'B'C,M是BC的中点,N是A'B'的中点,连接MN,若BC=4,⊥ABC=60°,则线段MN的最大值为()A.4B.8C.D.6【答案】D【分析】连接CN,根据直角三角形斜边中线的性质求出CN=12A′B′=4,利用三角形的三边关系即可得出结果.【详解】连接CN,如图所示:在Rt∠ABC中,∠ACB=90°,BC=4,∠B=60°,∠∠A=30°,∠AB=A′B′=2BC=8,∠NB ′=NA ′,∠CN =12A ′B ′=4, ∠CM =BM =2,∠MN ≤CN +CM =6,∠MN 的最大值为6,故选:D .【点睛】本题考查旋转的性质、含30°角直角三角形的性质、直角三角形斜边中线的性质、三角形的三边关系等知识;解题的关键是灵活运用三角形的三边关系.练习2.(2020·渝中区·重庆巴蜀中学九年级二模)已知Rt ACB △中,点D 为斜边AB 的中点,连接CD ,将DCB 沿直线DC 翻折,使点B 落在点E 的位置,连接DE 、CE 、AE ,DE 交AC 于点F , 若12BC =,16AC =,则AE 的值为( ).A .2825B .285C .145D .11225【答案】B【分析】过点D 作DM∠BC ,DN∠AE ,垂足为M 、N ,连接BE 交CD 于点G ,由折叠得CD 是BE 的中垂线,借助三角形的面积公式,可以求出BG ,进而求出BE ,由等腰三角形的性质,可得DN是三角形的中位线,得到DN等于BE的一半,求出DN,在根据勾股定理,求出AN,进而求出AE.【详解】解:过点D作DM∠BC,DN∠AE,垂足为M、N,连接BE交CD于点G,∠Rt∠ACB中,20==,∠点D为斜边AB的中点,∠CD=AD=BD=12AB=10,在∠DBC中,DC=DB,DM∠BC,∠MB=MC=12BC=6,8==,由折叠得,CD垂直平分BE,∠BDC=∠EDC,在∠ADE中,DA=DE,DN∠AE,∠AN=NE=12 AE,∠DN是∠ABE的中位线,∠DN∠BE,DN=12 BE,在∠DBC中,由三角形的面积公式得:12BC•DM=12DC•BG,即:12×8=10×BG,∠BG=485=DN,在Rt∠ADN中,145==,∠AE=2AN=285,故选:B.【点睛】考查直角三角形的性质、等腰三角形的性质、三角形的中位线以及勾股定理等知识,综合应用知识较强,理解和掌握这些知识是解决问题的前提和关键.练习3.(2021·四川省内江市第六中学九年级开学考试)如图,M是⊥ABC的边BC的中点,AN是⊥ABC的外角平分线,BN⊥AN于点N,且AB=4,MN=2.8,则AC的长是()A.1.2B.1.4C.1.6D.1.8【答案】C【分析】延长CA得射线CD,取AB的中点E,连接NE、ME,可证N、E、M三点共线,即MN与AB 的交点即为AB的中点E,从而易得ME,由AC=2ME即可求解.【详解】解:延长CA得射线CD,取AB的中点E,连接NE、ME,如图,∠M为BC的中点,∠ME//AC,ME12=AC∠BN∠AN,∠ANB∆是直角三角形,∠AE=NE12=AB=2又∠AN是∠ABC的外角平分线,∠EAN ENA NAD∠=∠=∠∠NEB ENA EAN EAN NAD DAE∠=∠+∠=∠+∠=∠∠NE//AC∠N、E、M三点共线,即MN与AB的交点即为AB的中点E,∠NE=2,MN=2.8∠ME=0.8∠AC=2 ME=20.8⨯=1.6故选:C.【点睛】本题主要考查了直角三角形的性质,中位线的性质,解题的关键是准确作出辅助线,得出M、N、AB的中点三点共线.©知识点二:矩形的判定矩形的判定:1) 有一个角是直角的平行四边形是矩形;2)对角线相等的平行四边形是矩形;3)有三个角是直角的四边形是矩形。
中考专题复习——矩形菱形正方形

中考专题复习第二十一讲矩形菱形正方形【基础知识回顾】一、矩形:1、定义:有一个角是角的平行四边形叫做矩形2、矩形的性质:⑴矩形的四个角都⑵矩形的对角线3、矩形的判定:⑴用定义判定⑵有三个角是直角的是矩形⑶对角线相等的是矩形【名师提醒:1、矩形是对称图形,对称中心是,矩形又是对称图形,对称轴有条2、矩形被它的对角线分成四个全等的三角形和两对全等的三角形3、矩形中常见题目是对角线相交成600或1200角时,利用直角三角形、等边三角形等图形的性质解决问题】二、菱形:1、定义:有一组邻边的平行四边形叫做菱形2、菱形的性质:⑴菱形的四条边都⑵菱形的对角线且每条对角线3、菱形的判定:⑴用定义判定⑵对角线互相垂直的是菱形⑶四条边都相等的是菱形【名师提醒:1、菱形既是对称图形,也是对称图形,它有条对称轴,分别是2、菱形被对角线分成四个全等的三角形和两对全等的三角形3、菱形的面积可以用平行四边形面积公式计算,也可以用两对角线积的来计算4、菱形常见题目是内角为1200或600时,利用等边三角形或直角三角形的相关知识解决的题目】三、正方形:1、定义:有一组邻边相等的是正方形,或有一个角是直角的是正方形2、性质:⑴正方形四个角都都是角,⑵正方形四边条都⑶正方形两对角线、且每条对角线平分一组内角3、判定:⑴先证是矩形,再证⑵先证是菱形,再证【名师提醒:1、菱形、正方形具有平行四边形的所有性质,正方形具有以上特殊四边形的所有性质。
这四者之间的关系可表示为:2、正方形也既是对称图形,又是对称图形,有条对称轴3、几种特殊四边形的性质和判定都是从、、三个方面来看的,要注意它们的区别和联系】【重点考点例析】考点一:与矩形有关的折叠问题例1 (2016•泸州)如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=105cm,且tan∠EFC=34,那么该矩形的周长为()A.72cm B.36cm C.20cmD.16cm对应训练1.(2016•湖州)如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则ADAB的值为()A.12B.33C.23D.22考点二:和菱形有关的对角线、周长、面积的计算问题例2 (2016•泉州)如图,菱形ABCD的周长为85,对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO= ,菱形ABCD的面积S= .对应训练2.(2016•凉山州)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14B.15C.1 D.17考点三:和正方形有关的证明题例3 (2016•湘潭)在数学活动课中,小辉将边长为2和3的两个正方形放置在直线l 上,如图1,他连结AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.思路分析:(1)根据正方形的性质可得AO=CO ,OD=OF ,∠AOC=∠DOF=90°,然后求出∠AOD=∠COF ,再利用“边角边”证明△AOD 和△COF 全等,根据全等三角形对应边相等即可得证;(2)与(1)同理求出CF=AD ,连接DF 交OE 于G ,根据正方形的对角线互相垂直平分可得DF ⊥OE ,DG=OG=12OE ,再求出AG ,然后利用勾股定理列式计算即可求出AD . 解:(1)AD=CF .理由如下:在正方形ABCO 和正方形ODEF 中,AO=CO ,OD=OF ,∠AOC=∠DOF=90°, ∴∠AOC+∠COD=∠DOF+∠COD ,即∠AOD=∠COF ,在△AOD 和△COF 中,AO CO AOD COF OD OF =⎧⎪∠=∠⎨⎪=⎩,∴△AOD ≌△COF (SAS ), ∴AD=CF ;(2)与(1)同理求出CF=AD ,如图,连接DF 交OE 于G ,则DF ⊥OE ,DG=OG=12OE ,∵正方形ODEF 的边长为2,∴OE=2×2=2,∴DG=OG=12OE=12×2=1, ∴AG=AO+OG=3+1=4,在Rt △ADG 中,AD=22224117AG DG +=+=,∴CF=AD=17.点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,(1)熟练掌握正方形的四条边都相等,四个角都是直角,对角线相等且互相垂直平分是解题的关键,(2)作辅助线构造出直角三角形是解题的关键.对应训练3.(2016•三明)如图①,在正方形ABCD 中,P 是对角线AC 上的一点,点E 在BC 的延长线上,且PE=PB .(1)求证:△BCP≌△DCP;(2)求证:∠DPE=∠ABC;(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.3.(1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,∵在△BCP和△DCP中,BC DCBCP DCPPC PC=⎧⎪∠=∠⎨⎪=⎩,∴△BCP≌△DCP(SAS);(2)证明:由(1)知,△BCP≌△DCP,∴∠CBP=∠CDP,∵PE=PB,∴∠CBP=∠E,∴∠DPE=∠DCE,∵∠1=∠2(对顶角相等),∴180°-∠1-∠CDP=180°-∠2-∠E,即∠DPE=∠DCE,∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC;(3)解:与(2)同理可得:∠DPE=∠ABC,∵∠ABC=58°,∴∠DPE=58°.故答案为:58.考点四:四边形综合性题目例4 (2016•资阳)在一个边长为a(单位:cm)的正方形ABCD中,点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.(1)如图1,当点M与点C重合,求证:DF=MN;(2)如图2,假设点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以2cm/s速度沿AC向点C运动,运动时间为t(t>0);①判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.②连结FM、FN,△MNF能否为等腰三角形?若能,请写出a,t之间的关系;若不能,请说明理由.思路分析:(1)证明△ADF≌△DNC,即可得到DF=MN;易证△MND ∽△DFA,∴ND DMAF AD=,即ND a tat aa t-=-,得ND=t.∴ND=CM=t,AN=DM=a-t.若△MNF为等腰三角形,则可能有三种情形:(I)若FN=MN,则由AN=DM知△FAN≌△NDM,∴AF=DM,即ata t-=t,得t=0,不合题意.∴此种情形不存在;(II)若FN=FM,由MN⊥DF知,HN=HM,∴DN=DM=MC,∴t=12a,此时点F与点B重合;(III)若FM=MN,显然此时点F在BC边上,如下图所示:易得△MFC≌△NMD,∴FC=DM=a-t;又由△NDM∽△DCF,∴DN DCDM FC=,即t aa t FC=-,∴FC=()a a tt-.∴()a a tt-=a-t,∴t=a,此时点F与点C重合.综上所述,当t=a或t=12a时,△MNF能够成为等腰三角形.点评:本题是运动型几何综合题,考查了相似三角形、全等三角形、正方形、等腰三角形、命题证明等知识点.解题要点是:(1)明确动点的运动过程;(2)明确运动过程中,各组成线段、三角形之间的关系;(3)运用分类讨论的数学思想,避免漏解.对应训练4.(2016•营口)如图1,△ABC为等腰直角三角形,∠ACB=90°,F是AC边上的一个动点(点F与A、C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.(1)①猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;②将图1中的正方形CDEF,绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、图3的情形.图2中BF交AC于点H,交AD于点O,请你判断①中得到的结论是否仍然成立,并选取图2证明你的判断.(2)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90°,正方形CDEF改为矩形CDEF,如图4,且AC=4,BC=3,CD=43,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值.4.解:(1)①BF=AD ,BF ⊥AD ;②BF=AD ,BF ⊥AD 仍然成立,证明:∵△ABC 是等腰直角三角形,∠ACB=90°,∴AC=BC ,∵四边形CDEF 是正方形,∴CD=CF ,∠FCD=90°,∴∠ACB+∠ACF=∠FCD+∠ACF ,即∠BCF=∠ACD ,在△BCF 和△ACD 中BC ACBCF ACD CF CD=⎧⎪∠=∠⎨⎪=⎩,∴△BCF ≌△ACD (SAS ),∴BF=AD ,∠CBF=∠CAD ,又∵∠BHC=∠AHO ,∠CBH+∠BHC=90°,∴∠CAD+∠AHO=90°,∴∠AOH=90°,∴BF ⊥AD ;(2)证明:连接DF ,∵四边形CDEF 是矩形,∴∠FCD=90°,又∵∠ACB=90°,∴∠ACB=∠FCD∴∠ACB+∠ACF=∠FCD+∠ACF ,即∠BCF=∠ACD ,∵AC=4,BC=3,CD=43,CF=1,∴34BC CF AC CD ==,∴△BCF ∽△ACD ,∴∠CBF=∠CAD ,又∵∠BHC=∠AHO ,∠CBH+∠BHC=90°∴∠CAD+∠AHO=90°,∴∠AOH=90°,∴BF⊥AD,∴∠BOD=∠AOB=90°,∴BD2=OB2+OD2,AF2=OA2+OF2,AB2=OA2+OB2,DF2=OF2+OD2,∴BD2+AF2=OB2+OD2+OA2+OF2=AB2+DF2,∵在Rt△ABC中,∠ACB=90°,AC=4,BC=3,∴AB2=AC2+BC2=32+42=25,∵在Rt△FCD中,∠FCD=90°,CD=43,CF=1,∴DF2=CD2+CF2=(43)2+12=259,∴BD2+AF2=AB2+DF2=25+259=2509.【聚焦山东中考】1.(2016•威海)如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是()A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF2.(2016•枣庄)如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为()A.3-1B.3-5C.5+1D.5-13.(2016•临沂)如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是.4.(2016•烟台)如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连结AF,CF,则图中阴影部分面积为.5.(2016•济南)如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+3.其中正确的序号是(把你认为正确的都填上).6.(2016•济宁)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.6.(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,ABE DAFAB ADBAE D∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABE≌△DAF(ASA),∴AF=BE;(2)解:MP与NQ相等.理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则与(1)的情况完全相同.7.(2016•青岛)已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM ≌△DCM ;(2)判断四边形MENF 是什么特殊四边形,并证明你的结论;(3)当AD :AB= 时,四边形MENF 是正方形(只写结论,不需证明)8.(2016•淄博)矩形纸片ABCD 中,AB=5,AD=4.(1)如图1,四边形MNEF 是在矩形纸片ABCD 中裁剪出的一个正方形.你能否在该矩形中裁剪出一个面积最大的正方形,最大面积是多少?说明理由;(2)请用矩形纸片ABCD 剪拼成一个面积最大的正方形.要求:在图2的矩形ABCD 中画出裁剪线,并在网格中画出用裁剪出的纸片拼成的正方形示意图(使正方形的顶点都在网格的格点上).8.解:(1)正方形的最大面积是16.设AM =x (0≤x ≤4),则MD =4-x .∵四边形MNEF 是正方形,∴MN =MF ,∠AMN +∠FMD =90°.∵∠AMN +∠ANM =90°,∴∠ANM =∠FMD .∵在△ANM 和△DMF 中A D ANM FMD MN FM ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ANM ≌△DMF (AAS ).∴DM =AN .∴S 正方形MNEF =MN 2=AM 2+AN 2,=x2+(4-x)2,=2(x-2)2+8∵函数S正方形MNEF=2(x-2)2+8的开口向上,对称轴是x=2,在对称轴的左侧S随x的增大而减小,在对称轴的右侧S随x的增大而增大,∵0≤x≤4,∴当x=0或x=4时,正方形MNEF的面积最大.最大值是16.(2)先将矩形纸片ABCD分割成4个全等的直角三角形和两个矩形如图1,然后拼成如图2的正方形.9.(2016•济南)(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写做法,保留作图痕迹);(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.9.解:(1)完成图形,如图所示:证明:∵△ABD和△ACE都是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,∵在△CAD和△EAB中,【备考真题过关】一、选择题1.(2016•铜仁地区)下列命题中,真命题是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直平分的四边形是正方形2.(2016•宜宾)矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分D.两组对角分别相等3.(2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是()A.25B.20C.15D.104.(2016•重庆)如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.2cm D.1cm 5.(2016•南充)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B.24C.123D.1636.(2016•巴中)如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD 的周长是()A.24B.16C.43D.237(2016•茂名)如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AC 的长是()A.2B.4C.2 3D.438.(2016•成都)如图,将矩形ABCD沿对角线BD折叠,使点C和点C′重合,若AB=2,则C′D的长为()A.1B.2C.3D.4 9.(2016•包头)如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是()A.S1>S2B.S1=S2C.S1<S2D.3S1=2S210.(2016•扬州)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC 于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°11.(2016•绵阳)如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A.2825cm B.2120cm C.2815cm D.2521cm12.(2016•雅安)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有()个.A.2B.3C.4D.5二、填空题13.(2016•宿迁)如图,一个平行四边形的活动框架,对角线是两根橡皮筋.若改变框架的形状,则∠α也随之变化,两条对角线长度也在发生改变.当∠α为------度时,两条对角线长度相等.14.(2016•淮安)若菱形的两条对角线分别为2和3,则此菱形的面积是.15.(2013•无锡)如图,菱形ABCD中,对角线AC交BD于O,AB=8,E是CD的中点,则OE的长等于.16.(2016•黔西南州)如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF⊥CD于F,∠B=60°,则菱形的面积为.17.(2016•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=35,BE=4,则tan ∠DBE的值是.18.(2016•南充)如图,正方形ABCD的边长为2,过点A作AE⊥AC,AE=1,连接BE,则tanE= .19.(2016•苏州)如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若1CGGB k=,则ADAB=用含k的代数式表示).20.(2016•哈尔滨)如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为.21.(2016•北京)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为.22.(2016•南京)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF= cm.23.(2016•舟山)如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程为.24.(2016•桂林)如图,已知线段AB=10,AC=BD=2,点P是CD 上一动点,分别以AP 、PB 为边向上、向下作正方形APEF 和PHKB ,设正方形对角线的交点分别为O 1、O 2,当点P 从点C 运动到点D 时,线段O 1O 2中点G 的运动路径的长是 .25.(2016•荆州)如图,将矩形ABCD 沿对角线AC 剪开,再把△ACD 沿CA 方向平移得到△A 1C 1D 1,连结AD 1、BC 1.若∠ACB=30°,AB=1,CC 1=x ,△ACD 与△A 1C 1D 1重叠部分的面积为s ,则下列结论:①△A 1AD 1≌△CC 1B ;②当x=1时,四边形ABC 1D 1是菱形;③当x=2时,△BDD 1为等边三角形;④s=38(x -2)2 (0<x <2); 其中正确的是 (填序号).三、解答题26.(2016•南通)如图,AB=AC ,AD=AE ,DE=BC ,且∠BAD=∠CAE .求证:四边形BCDE 是矩形.26.证明:∵∠BAD=∠CAE ,∴∠BAD -∠BAC=∠CAE -∠BAC ,∴∠BAE=∠CAD ,∵在△BAE 和△CAD 中AE AD BAE CAD AB AC =⎧⎪∠=∠⎨⎪=⎩∴△BAE ≌△CAD (SAS ), ∴∠BEA=∠CDA ,BE=CD ,∵DE=BC ,∴四边形BCDE 是平行四边形,∵AE=AD ,∴∠AED=∠ADE ,∵∠BEA=∠CDA ,∴∠BED=∠CDE ,∵四边形BCDE 是平行四边形,∴BE ∥CD ,∴∠CDE+∠BED=180°,∴∠BED=∠CDE=90°,∴四边形BCDE 是矩形.27.(2016•广州)如图,四边形ABCD 是菱形,对角线AC 与BD相交于O ,AB=5,AO=4,求BD 的长.27.解:∵四边形ABCD 是菱形,对角线AC 与BD 相交于O ,∴AC ⊥BD ,DO=BO ,∵AB=5,AO=4,∴BO=2254-=3,∴BD=2BO=2×3=6.28.(2013•厦门)如图所示,在正方形ABCD 中,点G 是边BC 上任意一点,DE ⊥AG ,垂足为E ,延长DE 交AB 于点F .在线段AG 上取点H ,使得AG=DE+HG ,连接BH .求证:∠ABH=∠CDE .28.证明:如图,在正方形ABCD 中,AB=AD ,∠ABG=∠DAF=90°,∵DE ⊥AG ,∴∠2+∠EAD=90°,又∵∠1+∠EAD=90°,∴∠1=∠2,在△ABG 和△DAF 中, 1 290AB AD ABG DAF =⎧⎪=⎨⎪∠=∠=︒⎩,∴△ABG ≌△DAF (ASA ),∴AF=BG ,AG=DF ,∠AFD=∠BGA ,∵AG=DE+HG ,AG=DE+EF ,∴EF=HG ,在△AEF 和△BHG 中,AF BG AFD BGA EF HG =⎧⎪∠=∠⎨⎪=⎩,∴△AEF ≌△BHG (SAS ),∴∠1=∠3,∴∠2=∠3,∵∠2+∠CDE=∠ADC=90°,∠3+∠ABH=∠ABC=90°,∴∠ABH=∠CDE .29.(2013•黔东南州)如图,在正方形ABCD 中,点M 是对角线BD 上的一点,过点M 作ME ∥CD 交BC 于点E ,作MF ∥BC 交CD 于点F .求证:AM=EF .29.证明:过M 点作MQ ⊥AD ,垂足为Q ,作MP 垂足AB ,垂足为P ,∵四边形ABCD 是正方形,∴四边形MFDQ 和四边形PBEM 是正方形,四边形APMQ 是矩形,∴AP=QM=DF=MF ,PM=PB=ME ,∵在△APM 和△FME 中,AP MF APM FME PM ME =⎧⎪∠=∠⎨⎪=⎩, ∴△APM ≌△FME (SAS ), ∴AM=EF .30.(2016•铁岭)如图,△ABC 中,AB=AC ,AD 是△ABC 的角平分线,点O 为AB 的中点,连接DO 并延长到点E ,使OE=OD ,连接AE ,BE .(1)求证:四边形AEBD 是矩形;(2)当△ABC 满足什么条件时,矩形AEBD 是正方形,并说明理由.30.(1)证明:∵点O 为AB 的中点,连接DO 并延长到点E ,使OE=OD ,∴四边形AEBD 是平行四边形,∵AB=AC ,AD 是△ABC 的角平分线,∴AD ⊥BC ,∴∠ADB=90°,∴平行四边形AEBD 是矩形;(2)当∠BAC=90°时,理由:∵∠BAC=90°,AB=AC ,AD 是△ABC 的角平分线,∴AD=BD=CD ,∵由(1)得四边形AEBD 是矩形,∴矩形AEBD 是正方形.31.(2016•南宁)如图,在菱形ABCD 中,AC 为对角线,点E 、F 分别是边BC 、AD 的中点.(1)求证:△ABE ≌△CDF ;(2)若∠B=60°,AB=4,求线段AE 的长.31.解:(1)∵四边形ABCD 是菱形,∴AB=BC=AD=CD ,∠B=∠D ,∵点E 、F 分别是边BC 、AD 的中点,∴BE=DF ,在△ABE 和△CDF 中,∵AB CD B D BE DF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABE ≌△CDF (SAS );(2)∵∠B=60°,∴△ABC 是等边三角形,∵点E 是边BC 的中点,∴AE ⊥BC ,在Rt △AEB 中,∠B=60°,AB=4,sin60°=4AE AE AB =, 解得AE=23.32.(2016•贵阳)已知:如图,在菱形ABCD 中,F 是BC 上任意一点,连接AF 交对角线BD 于点E ,连接EC .(1)求证:AE=EC ;(2)当∠ABC=60°,∠CEF=60°时,点F 在线段BC 上的什么位置?说明理由.32.(1)证明:如图,连接AC ,∵BD 也是菱形ABCD 的对角线,∴BD 垂直平分AC ,∴AE=EC ;(2)解:点F 是线段BC 的中点.理由如下:在菱形ABCD 中,AB=BC ,又∵∠ABC=60°,∴△ABC 是等边三角形,∴∠BAC=60°,∵AE=EC ,∠CEF=60°,∴∠EAC=12∠BAC=30°, ∴AF 是△ABC 的角平分线,∵AF 交BC 于F ,∴AF 是△ABC 的BC 边上的中线,∴点F 是线段BC 的中点.33.(2016•曲靖)如图,点E 在正方形ABCD 的边AB 上,连接DE ,过点C 作CF ⊥DE 于F ,过点A 作AG ∥CF 交DE 于点G .(1)求证:△DCF ≌△ADG .(2)若点E 是AB 的中点,设∠DCF=α,求sinα的值.33.(1)证明:在正方形ABCD 中,AD=DC ,∠ADC=90°,∵CF ⊥DE ,∴∠CFD=∠CFG=90°,35.(2016•绥化)已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF(1)如图1,当点D在线段BC上时.求证CF+CD=BC;(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD 三条线段之间的关系;(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;①请直接写出CF,BC,CD三条线段之间的关系;②若正方形ADEF的边长为22,对角线AE,DF相交于点O,连接OC.求OC的长度.35.证明:(1)∵∠BAC=90°,∠ABC=45°,线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.(1)如图 ,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)如图 ,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;(3)在(2)的条件下,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由.36.解:(1)∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠PBA=90°∵在△PBA和△FBC中,AB BCPBA ABCBP BF=⎧⎪∠=∠⎨⎪=⎩,∴△PBA≌△FBC(SAS),∴PA=FC,∠PAB=∠FCB.∵PA=PE,∴PE=FC.∵∠PAB+∠APB=90°,∴∠FCB+∠APB=90°.∵∠EPA=90°,∴∠APB+∠EPA+∠FPC=180°,即∠EPC+∠PCF=180°,∴EP∥FC,∴四边形EPCF是平行四边形;(2)结论:四边形EPCF是平行四边形,∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠CBF=90°∵在△PBA和△FBC中,AB BCPBA ABCBP BF=⎧⎪∠=∠⎨⎪=⎩,∴△PBA≌△FBC(SAS),∴PA=FC,∠PAB=∠FCB.∵PA=PE,。
菱形矩形正方形的判定

问题:
判断矩形、菱形、正方形有 什么作用?
Байду номын сангаас
1、一组对边相等的四边形是平行四边形. 2、有两个角是直角的四边形是矩形.
3、有一个角是直角的菱形是正方形.
4、有一个角是60º 的平行四边形是菱形.
5、有两边相等的矩形是菱形.
6、有一组邻边相等的四边形是菱形. 7、两条对角线相等的四边形是矩形. 8、两条对角线相等的平行四边形是正方形. 9、有三个角相等的四边形是正方形.
的四边形是矩形. 的四边形是矩形.
菱形的判定 一、平行四边形 1、 2、 菱形 的平行四边形是菱形. 的平行四边形是菱形.
二、四边形
1、 2、
菱形
的四边形是菱形. 的四边形是菱形.
正方形的判定
一、矩形 二、菱形
三、平行四边形 四、四边形
正方形 正方形
正方形 正方形
特殊四边形的判定应注意层次
判断
特殊四边形的判定
正方形
矩形
菱形
平行四边形
四边形
一般到特殊的演变
矩形
有一个角 是直角
有一组 邻边相等
平行四边形
有一个角是直角 且有一组邻边相等 正方形
有一组 邻边相等
菱形
有一个 角是直角
矩形的判定 一、平行四边形 1、 2、 矩形 的平行四边形是矩形. 的平行四边形是矩形.
二、四边形
1、 2、
矩形
判断
10、一条对角线平分另一条对角线的四边形是 平行四边形.
11、两条对角线互相垂直的四边形是菱形.
12、一组对边平行、一组对角相等的四边形是 平行四边形. 13、有两条边相等的平行四边形是菱形. 14、一组对角的两边分别垂直的四边形是 平行四边形. 15、一组邻边相等、另一组邻边也相等的四边形 是菱形.
四边形的分类与判定方法

四边形的分类与判定方法四边形是几何学中一种常见的图形,它由四条边和四个角组成。
在不同的边长和角度的组合下,四边形可以被划分为多个不同的类型。
本文将介绍四边形的分类以及判定方法,以帮助读者更好地理解和应用几何学知识。
一、四边形的分类四边形的分类主要根据其边长和角度来进行划分,常见的四边形类型包括正方形、矩形、菱形、平行四边形、梯形和不规则四边形。
1. 正方形正方形是一种特殊的矩形,它的四条边相等且四个角均为直角。
可以通过边长或对角线长相等来判定一个四边形是否为正方形。
2. 矩形矩形也是一种边长相等的四边形,但它的四个角并不一定都为直角。
判定一个四边形是否是矩形的方法是检查它的对角线是否相等。
3. 菱形菱形是一种具有边长相等但角度不一定相等的四边形。
一个四边形若两对相邻边相等,则可以被判定为菱形。
4. 平行四边形平行四边形具有两对相对平行的边,它的对边长度相等。
要判断一个四边形是否为平行四边形,可以检查它的对边是否平行。
5. 梯形梯形是只有一对对边平行的四边形,其余两条边不平行。
通过检查四边形的边是否满足其中两条边平行的条件,即可判定它是否为梯形。
6. 不规则四边形不规则四边形是指不属于上述任何一种特殊类型的四边形。
它的边和角都没有特殊的限制条件,因此可以被视为一般性的四边形。
二、四边形的判定方法判定一个四边形的类型有多种方法,下面将介绍针对常见四边形类型的判定方法。
1. 正方形的判定方法(描述正方形判定方法)2. 矩形的判定方法(描述矩形判定方法)3. 菱形的判定方法(描述菱形判定方法)4. 平行四边形的判定方法(描述平行四边形判定方法)5. 梯形的判定方法(描述梯形判定方法)6. 不规则四边形的判定方法(描述不规则四边形判定方法)三、四边形的应用四边形在几何学中具有广泛的应用。
它们的性质和特点可以用于解决各种几何问题,例如计算面积、判断形状等。
1. 面积计算根据不同类型的四边形,可以通过不同的公式计算其面积。
矩形、菱形性质与判定

一、什么是矩形?有一个角是直角的平行四边形叫做矩形.如图平行四边形ABCD ,∠A=90°,四边形ABCD 为矩形 .CABD二、什么是菱形?有一组邻边相等的平行四边形叫做菱形.如图平行四边形ABCD ,AD=AB ,四边形ABCD 为菱形. AC1.矩形的性质矩形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质: ① 边的性质:对边平行且相等. ② 角的性质:四个角都是直角. ③ 对角线性质:对角线互相平分且相等.④ 对称性:矩形是中心对称图形,也是轴对称图形.直角三角形斜边上的中线等于斜边的一半. 直角三角形中,30 角所对的边等于斜边的一半.点评:这两条直角三角形的性质在教材上是应用矩形的对角线推得,用三角形知识也可推得.矩形、菱形的性质与判定知识回顾知识讲解2.矩形的判定判定①:有一个角是直角的平行四边形是矩形.判定②:对角线相等的平行四边形是矩形.判定③:有三个角是直角的四边形是矩形.3.菱形的性质菱形是特殊的平行四边形,它具有平行四边形的所有性质,•还具有自己独特的性质:①边的性质:对边平行且四边相等.②角的性质:邻角互补,对角相等.③对角线性质:对角线互相垂直平分且每条对角线平分一组对角.④对称性:菱形是中心对称图形,也是轴对称图形.菱形的面积等于底乘以高,等于对角线乘积的一半.点评:其实只要四边形的对角线互相垂直,其面积就等于对角线乘积的一半.4.菱形的判定判定①:一组邻边相等的平行四边形是菱形.判定②:对角线互相垂直的平行四边形是菱形.判定③:四边相等的四边形是菱形.5.三角形的中位线中位线:连结三角形两边的中点所得的线段叫做三角形的中位线.也可以过三角形一边的中点作平行于三角形另外一边交于第三边所得的线段也是中位线.以上是中位线的两种作法,第一种可以直接用中位线的性质,第二种需要说明理由为什么是中位线,再用中位线的性质.中点中点平行中点模块一 矩形的概念与性质【例1】 矩形的定义:__________________的平行四边形叫做矩形.【例2】 矩形的性质:矩形是一个特殊的平行四边形,它除了具有四边形和平行四边形所有的性质,还有:矩形的四个角______;矩形的对角线______;矩形是轴对称图形,它的对称轴是____________.【例3】 矩形的判定:一个角是直角的______是矩形;对角线______的平行四边形是矩形;有______个角是直角的四边形是矩形.【巩固】矩形ABCD 中,点H 为AD 的中点,P 为BC 上任意一点,PE HC ⊥交HC 于点E ,PF BH⊥交BH 于点F ,当AB BC ,满足条件 时,四边形PEHF 是矩形【例4】 如图,矩形ABCD 沿AE 折叠,使D 点落在BC 边上的F 点处,如果60BAF ∠=︒,则DAE ∠=FED CBA【例5】 矩形ABCD 中,对角线AC 、BD 相交于O ,∠AOB =60°,AC =12cm ,则BC =______cm ,周长为 .【例6】 如图,在矩形ABCD 中,点E 是BC 上一点,AE AD =,DF AE ⊥,垂足为F .线段DF 与图中的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明。
矩形菱形正方形

我思,我进步
1
四边形之间的关系
四边形之间有何关系? 特殊的平行四边形之间呢 还记得它们与平行四边形的关系吗? ? 能用一张图来表示它们之间的关系吗?
矩形 平行四边形 正方形 菱形 四边形
等腰梯形
梯形 直角梯形
驶向胜利 的彼岸
类型一 矩形的性质与判定
(1)如图, 已知矩形 ABCD 沿对角线 BD 折叠, 记点 C 的对应点为 C′, 若∠ADC′ =20° ,则∠BDC 的度数为________.
解:(1)四边形 EFGH 为平行四边形,连结 AC. 1 ∵E、F 分别是 AB、BC 的中点,EF∥AC,EF= AC. 2 1 同理 HG∥AC,HG= AC. 2 ∴EF∥HG,EF=HG. ∴四边形 EFGH 是平行四边形 (2)四边形 ABCD 的对角线垂直且相等.
一、选择题 1.菱形的周长为 8 cm,高为 1 cm,则菱形两邻角度数比为( A.3∶1 B.4∶1 C.5∶1 D.6∶1
第 2 讲 矩形 菱形 正方形
①矩形;②菱形;③正方形.
知识点一 矩形的定义、性质和判定
1.定义:有一个角是直角的平行四边形是矩形. 2.性质:(1)矩形的四个角都是直角;(2)矩形的对角线互相平分且相等;(3)矩形既是轴 对称图形,又是中心对称图形,它有两个对称轴;它的对称中心是对角线的交点. 3.判定:(1)有一个角是直角的平行四边形是矩形;(2)有三个角是直角的四边形是矩形; (3)对角线相等的平行四边形是矩形.
2 010 解析:机器人每走 8 米为一循环, 余数为 2,则最终停在 C 点. 8
答案:C
11.如图,将矩形纸片 ABCD 折叠,使点 D 与点 B 重合,点 C 落在 C′处,折痕为 EF, 若∠ABE=20° ,那么∠EFC′的度数为________度.
特殊的平行四边形是哪两个

特殊的平行四边形
特殊的平行四边形有菱形和矩形。
菱形:特殊的平行四边形之一。
有一组邻边相等的平行四边形。
菱形的性质:
(1)在一个平面内,有一组邻边相等的平行四边形是菱形;
(2)菱形的四条边都相等;
(3)菱形的对角线互相垂直平分且平分每一组对角;
(4)菱形是轴对称图形,对称轴有2条,即两条对角线所在直线;(5)菱形是中心对称图形;菱形的中点四边形总是矩形。
矩形:有一个角是直角的平行四边形。
矩形的判定定理:
(1)判定定义:有一个角是直角的平行四边形是是矩形。
(2)判定定理1:有三个角是直角的四边形是矩形。
(3)判定定理2:对角线相等的平行四边形是矩形。
矩形的性质:
(1)具有平行四边形的一切性质。
(2)矩形的四个角都是直角。
(3)矩形的对角线相等。
(4)矩形既是轴对称图形又是中心对称图形。
矩形的面积:矩形的面积=长×宽特殊的平行四边形。
矩形、菱形、正方形---菱形的判定

§20.3.矩形、菱形、正方形----菱形的判定复习巩固1、矩形的判定定理: 从角考虑:___________________________的平行四边形是矩形。
从对角线考虑:____________________________的平行四边形是矩形。
从角考虑:____________________________的四边形是矩形。
2.矩形的性质:3.菱形的性质:4、菱形的判定方法1: 定义:有一组邻边__________的平行四边形是菱形. 几何表示:∵四边形ABCD 是平行四边形,AB=CD∴四边形ABCD 是菱形。
5、菱形的判定方法2: ________________平行四边形是菱形. 应用判定方法2时,要注意其性质包括两个条件:(1)是平行四边形;(2)两条对角线互相垂直.已知:平行四边形ABCD ,对角线AC⊥BD ,求证:四边形ABCD 是菱形证明:在ABCD 中,OB=OD∵AC ⊥BD∴∠AOB____∠AOD在△AOB 与△AOD 中,∴四边形ABCD 是菱形思考:对角线互相垂直的四边形是菱形吗?为什么?____________________________________ 画一个菱形,使它的边长为6cm 。
(草稿)通过菱形的作图,可以得到从一般四边形直接判定菱形的方法:6.菱形的判定方法3:___________的四边形是菱形.已知:四边形ABCD 中,AB=BC=CD=DA 求证:四边形ABCD 是菱形。
证明:已知:如图ABCD 的垂直平分线与边AD 、BC 分别交12(2011云南保山)如图,在平行四边形ABCD 中,点P 是对角线AC 上一点,PE ⊥AB ,PF ⊥AD ,垂足分别为E 、F ,且PE=PF ,平行四边形ABCD 是菱形吗?为什么?13.如图所示,在梯形ABCD 中,AD ∥BC ,AB=AD ,∠BAD 的平分线AE 交BC 于点E ,连接DE . (1)求证:四边形ABED 是菱形;(2)若∠ABC=60°,CE=2BE ,试判断△CDE 的形状,并说明理由.15.已知:如图,在梯形ABCD 中,AB ∥CD ,BC =CD ,AD ⊥BD ,E 为AB 中点,求证:四边形BCDE 是菱形.16. 如图,在□ABCD 中,E ,F 分别为边AB ,CD 的中点,连结DE ,BF ,BD . (1)求证:△ADE ≌△CBF .(2)若AD ⊥BD ,则四边形BFDE 是什么特殊四边形?请证明你的结论.17.(2011新疆乌鲁木齐)如图,在平行四边形ABCD 中,∠DAB =60°,AB =2AD ,点 E 、F 分别是CD 的中点,过点A 作AG ∥BD ,交CB 的延长线于点G .(1)求证:四边形DEBF 是菱形;(2)请判断四边形AGBD 是什么特殊四边形?并加以证明.18.如图,四边形ABCD 中,AB ∥CD ,AC 平分∠BAD ,CE ∥AD 交AB 于E .(1)求证:四边形AECD 是菱形;(2)若点E 是AB 的中点,试判断△ABC 的形状,并说明理由.19.如图,在四边形ABCD 中,AB =CD ,M ,N ,P ,Q 分别是AD ,BC ,BD ,AC 的中点.求证:MN 与PQ 互相垂直平分。
矩形和菱形

y
A
D
O (B) C
x
例 21.菱形 ABCD的边长为 2, ABC 45 ,则点 D 的坐标为_______.
【基础达标】 1.菱形的周长是 8 cm,则菱形的一边长是______. 2.菱形的一个内角为 120°,平分这个内角的对角线长为 11 厘米,菱形的周长为______. 3.菱形的对角线的一半的长分别为 8 cm 和 11 cm,则菱形的面积是_______. 4.菱形的面积为 24 cm2,一对角线长为 6 cm,则另一对角线长为______,边长为______.
安
教学内 容
一、知识梳理
1.菱形、矩形的有关概念 矩形:有一个角是直角的平行四边形叫做矩形. 菱形:有一组邻边相等的平行四边形叫做菱形. 2.菱形、矩形的性质
图形
形状
边
菱形
对边平行,四 条边都相等
角 对角相等
性质 对角线
两对角线互相垂直平 分,每一条对角线平
分一组对角
对称性
中心对称轴对 称
矩形
对边平行且 相等
。
安
对角相等
对角线互相平分且相 中心对称轴对
等
称
温馨提醒: (1)矩 形 、 菱 形 具 有 平 行 四 边 形 的 一 切 性 质 ; (2)依据矩形的性质,得出直角三角形具有的性质斜边上的中线等于斜边的一半; (3)矩形、菱形既是轴对称图形又是中心对称图形; 3.菱形、矩形的判定 矩形的判定方法:①有一个角是直角的平行四边形是矩形.
A
D
O
E
B
C
23.已知,如图,矩形 ABCD 中,AC=10,ABCD 的面积是 25 3 ,求 CAB 的度数。
专题六 矩形、菱形与正方形

专题六 矩形 、菱形和正方形【要点整合】 1、矩形(1)定义: . (2)它具有平行四边形的所有性质,还具有特殊的性质: ①角: ②对角线: 结合图6-1矩形的性质可表示为: ∵四边形ABCD 是矩形∴由此得到:直角三角形斜边的中线等于 .用符号语言可表示:∵ ∠ABC=90°,AO=CO ∴ (3)矩形判定方法:① 的平行四边形是矩形。
② 的平行四边形是矩形。
③ 的四边形是矩形。
(4)面积关系:S 矩形ABCD = S △ABC = S △AOB = S △AOD 2、菱形(1)定义: . (2)特殊性质:①边: ②对角线: 结合图6-2菱形性质用符号语言可表示为: ∵ ∴ABDC图6-1O你能用符号语言表示吗?试试看B AD C图6-2O(3)菱形判定方法:① 的平行四边形是菱形。
② 的平行四边形是菱形。
③ 的四边形是菱形。
(4)面积计算:S 菱形ABCD =S 菱形ABCD = S △ABC = S △AOB = S △AOD3、正方形(1)定义: . (2)特殊性质:①边: ②角: ③对角线 结合图6-3正方形性质用符号语言可表示为: ∵ ∴ (3)判定方法.① 的矩形是正方形。
② 的矩形是正方形。
③ 的菱形是正方形。
④ 的菱形是正方形。
4、面积计算:S 正方形ABCD = = S □ABCD = S △ABD = S △ABC = S △AOB【自主探究】1、如图6-4,如图,在矩形ABCD 中,若AC=2AB ,则∠AOB 的大小是( ) A .30°B .45°C .60°D .90°尝试用符号语言表示菱形的判定定理.图6-3BADCO尝试用符号语言表示正方形的判定定理.6-4 6-5 6-6 2、如图6-5,要使平行四边形ABCD 成为矩形,需添加的条件是( ). A .AB=BC B .AC ⊥BD C .∠ABC=90° D .∠1=∠23、如图6-6,菱形ABCD 的两条对角线相交于O ,若AC=6,BD=4,则菱形ABCD 的周长是 .4、如图,在□ABCD 中,对角线AC 与BD 相交于点O ,过点O 作EF ⊥AC 交BC 于点E ,交AD 于点F ,连接AE 、CF .则四边形AECF 是 .5、在矩形ABCD 中,点E 是BC 上一点,AE=AD ,DF ⊥AE ,垂足为F ; 求证:DF=DC .6、在正方形ABCD 中,点G 是BC 上任意一点,连接AG ,过B ,D 两点分别作BE ⊥AG ,DF ⊥AG ,垂足分别为E ,F 两点,求证:△ADF ≌△BAE .家长签字:年 月 日6-76-8ABDCG FE【例题精析】例1、如图,在Rt △ABC 中,∠A=90°,AB=3,AC=4,P 为边BC 上一动点,PE ⊥AB 于E ,PF ⊥AC 于F ,则EF 的最小值为( ) A .2B .2.2C .2.4D .2.5分析根据已知得出四边形AEPF 是矩形,连接对角线AP ,得出EF=AP ,要使EF 最小,只要AP 最小即可,根据垂线段最短得出即可. 解:连接AP ,∵∠A=90°,PE ⊥AB ,PF ⊥AC , ∴∠A=∠AEP=∠AFP=90°, ∴四边形AFPE 是 ∴EF= ,要使EF 最小,只要 最小即可, 过A 作AP ⊥BC 于P ,此时AP 最小,在Rt △BAC 中,∠A=90°,AC=4,AB=3,由勾股定理得:AB=5, 由三角形面积公式得: 21AB ·AC=21 BC ·AP ,即21×3×4=21×5×AP ∴AP= ,即EF= ,故选.考点:矩形的判定与性质;垂线段最短;勾股定理.例2如图,菱形ABCD 中,AB=4,∠B=60°,AE ⊥BC ,AF ⊥CD ,垂足分别为E ,F ,连接EF ,则△AEF 的面积是 .分析:首先利用菱形的性质及等边三角形的判定可得判断出△AEF 是等边三角形,再根据勾股定理计算出AE=EF 的值,再过A 作AM ⊥EF ,再进一步利用勾股定理计算出AM 的值,即可算出三角形的面积. 解题思路6-9 6-106-11考点:菱形的性质;等边三角形的判定与性质.例3、如图6-12中①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.6-12(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE 1、AB之间的数量关系,并说明理由;(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB 之间的数量关系.(不需要证明)考点:正方形的性质;全等三角形的判定与性质.:解:【拓展探究】已知:如图,在正方形ABCD 外取一点E ,连接AE 、BE 、DE .过点A 作AE 的垂线交DE 于点P .若AE=AP=1,PB=5.下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为2;③EB ⊥ED ;④S △APD+S △APB=21+6; ⑤S 正方形ABCD=4+6.其中正确结论的序号是 解题思路【当堂测练】1、如图6-14,如图,矩形纸片ABCD 中,AB=6cm ,BC=8cm ,现将其沿AE 对折,使得点B 落在边AD 上的点B 1处,折痕与边BC 交于点E ,则CE 的长为( ) A .6cm B .4cm C .2cm D .1cm6-14 6-15 6-16 2、如图6-15,如图所示,在矩形ABCD 中,AB=2,BC=2,对角线AC 、BD 相交于点O ,过点O 作OE 垂直AC 交AD 于点E ,则AE 的长是 3、如图6-16,在菱形ABCD 中,对角线AC 与BD 交于点O ,OE ⊥AB ,垂足为E ,若∠ADC=130°,则∠AOE的大小为 .4、如图6-17所示,已知菱形ABCD 的对角线AC ,BD 的长分别为12cm ,16cm ,AE ⊥BC 于点E ,则AE 的长是6-136-17 6-18 6-195、如图6-18所示,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODC交OC于点E,若AB=2,则线段OE的长为.6、如图6-19,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PF⊥BD 于F,PE⊥AC于E,则PE+PF的值为.7、如下图所示,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为8、如图6-20,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证:AM=EF.家长寄语:年月日6-20。
矩形,菱形

O
2
2
1
2
OA OB
A
B
1 2
ABC 90
AOB 120
1 2 AOB 180 BC
1 2
AC
1 30
即AC 2BC
在上题中,若已知
AC=2BC,你能求出
∠AOB的度数吗?
D
C
能证明吗?
O
A
B
例2:已知在矩。形ABCD中,AE平分∠DAB, ∠ACB=30 ,求∠BEO的度数。
矩形、菱形
平行四边形
矩形
矩形的四个角都 是 直角 。
矩形的对角线 相等。
12
菱形
菱形的四条边都相等 。
菱形的对角线互 相 垂直 ,且每一 条对角线平分一组对角。
矩形:
1.定义:有一个内角是直角的平行四边形叫做矩形。
2.性质:1)矩形的对边平行;
2)矩形的对边相等;
A
D
O
3)矩形的四个角都是直角;
思考:如果已知矩形
ABCD的两条对角线
交于点O,且 ∠AOB=120。,你能看
出AC与BC的关系吗?
D
C
O
能证明吗?
A
B
例1:已知矩形ABCD的两条对角线交于点 O,且∠AOB=120。,求证AC=2BC
证明:四边形ABCD是矩形 D
C
ABC 90, AC BD
OA 1 AC,OB 1 BD
1.矩形的一边长为3cm,对角线长5cm,则另一边长为 4cm ,面 积为 12cm2 。
2.在菱形ABCD中,已知AB=2,则菱形的周长为 8 ,
若A 35 ,则 D 145◦ 。
3.菱形的周长为20cm,一条对角线长为8cm,另一条对角线长 为 6cm 。
矩形、菱形正方形----菱形的定义与性质

20.3矩形、菱形、正方形----菱形的定义与性质 学习准备1、复习平行四边形定义: 叫平行四边形。
2.矩形定义:有一个角为 的 叫矩形。
34、矩形是特殊的平行四边形,因此矩形具有 的所有性质。
矩形特有的性质:① ②5、平行四边形是 对称图形。
矩形是 对称图形,又是 对称图形 6.定义: 的平行四边形叫菱形。
7、菱形是特殊的平行四边形,除了具有平行四边形的性质外,还特殊在:(1)菱形的 都相等。
(2)菱形的两条对角线 , 并且 。
请证明菱形对角线特殊性质 如图已知:求证:8、菱形 对称图形,菱形有 对称轴。
【知识延展】:(1)、由菱形性质:BD 平分∠ ∠ ,AC 平分∠ ∠ ,所以对角线交点是菱形四个内角角平分线的交点,由角平分线性质 ∴菱形形对角线的交点O 到各 距离相等(2)、由菱形性质:对角线 ,由图可知,在菱形中有个直角三角形,由菱形性质: ,由图可知,有 个等腰三角形,它们分别是8.如图:菱形ABCD 中,E 是AB 的中点,且DE ⊥AB ,AB=a .求: (1)∠ABC 的度数;(2)对角线AC 的长;(3)菱形ABCD 的面积.9. 在菱形ABCD 中,∠A 与∠B 的度数比为1:2,周长是48cm . 求:(1)两条对角线的长度;(2)菱形的面积.10.从菱形钝角的顶点向对边作垂线,且垂线平分对边,求菱形各角的度数. 如图所示,在边长为2的菱形ABCD 中,∠DAB=60°,点E 为AB 中点,点F 是AC 上一动点,则EF+BF 的最小值为 (提示:根据轴对称的性质)11.如图,O 为菱形ABCD 对角线的交点,DE ∥AC ,CE ∥BD . (1)试判断四边形OCED 的形状,并说明理由; (2)若AC=6,BD=8,求线段OE 的长.12.在菱形ABCD 中,对角线AC 与BD 相交于点O ,AB=5,AC=6.过D 点作DE ∥AC 交BC 的延长线于点E . (1)点P 为线段BC 上的点,连接PO 并延长交AD 于点Q .求证:BP=DQ . (2)求△BDE 的周长.B【达标检测】1、在菱形ABCD 中 ,AB=5cm ,则此菱形的周长为( )。
几何公式定理:矩形,菱形、正方形

几何公式定理:矩形,菱形、正方形
几何公式定理:矩形
1、矩形性质定理1矩形的四个角都是直角
2、矩形性质定理2矩形的对角线相等
3、矩形判定定理1有三个角是直角的四边形是矩形
4、矩形判定定理2对角线相等的平行四边形是矩形
几何公式定理:菱形
5、菱形性质定理1菱形的四条边都相等
6、菱形性质定理2菱形的对角线互相垂直,并且每一条对角线平分一组对角
7、菱形面积=对角线乘积的一半,即S=(ab)2
8、菱形判定定理1四边都相等的四边形是菱形
9、菱形判定定理2对角线互相垂直的平行四边形是菱形
几何公式定理:正方形
1、正方形性质定理1正方形的四个角都是直角,四条边都相等
2、正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
3、定理1关于中心对称的两个图形是全等的
4、定理2关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分
5、逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称。
矩形、菱形、正方形的定义、性质及判定定理-知识梳理总结
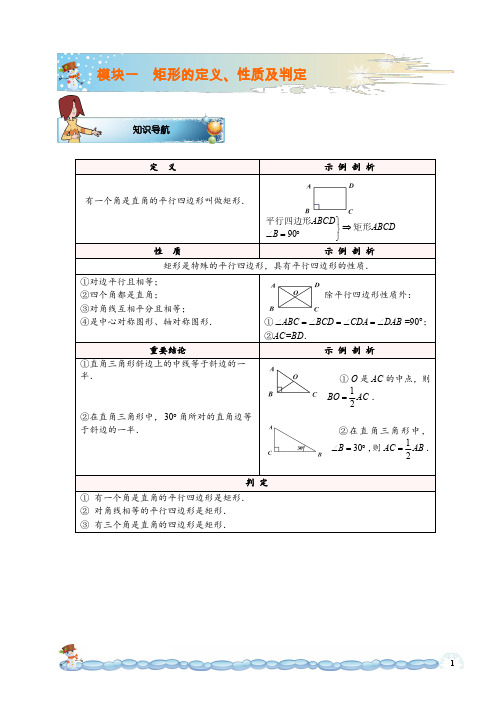
模块一矩形的定义、性质及判定知识导航定义示例剖析有一个角是直角的平行四边形叫做矩形.90ABCD ABCDB ⎫⇒⎬∠=︒⎭平行四边形矩形性质示例剖析矩形是特殊的平行四边形,具有平行四边形的性质.①对边平行且相等;②四个角都是直角;③对角线互相平分且相等;④是中心对称图形、轴对称图形.除平行四边形性质外:①ABC BCD CDA DAB ∠=∠=∠=∠=90°;②AC=BD .重要结论示例剖析①直角三角形斜边上的中线等于斜边的一半.②在直角三角形中,30︒角所对的直角边等于斜边的一半.①O 是AC 的中点,则12BO AC =.②在直角三角形中,30B ∠=︒,则12AC AB =.判定①有一个角是直角的平行四边形是矩形.②对角线相等的平行四边形是矩形.③有三个角是直角的四边形是矩形.模块二菱形的定义、性质及判定知识导航定义示例剖析有一组邻边相等的平行四边形叫做菱形.ABCD ABCDAB BC ⎫⇒⎬=⎭平行四边形菱形性质示例剖析菱形是特殊的平行四边形,具有平行四边形的性质.①对边平行且四边都相等;②邻角互补,对角相等;③对角线互相垂直平分且每条对角线平分一组对角;④是中心对称图形、轴对称图形.除拥有平行四边形性质外:①AB=BC=CD =AD ;②AC ⊥BD 且AC 、BD 分别为DAB ∠、ABC ∠的角平分线.①菱形的面积等于底乘以高,等于对角线乘积的一半.②推广:对角线互相垂直的四边形,其面积就等于对角线乘积的一半.(注:不能直接使用)①12ABCD S AC BD =⋅菱形②12ABCD S AC BD =⋅四边形判定1一组邻边相等的平行四边形是菱形.②对角线互相垂直的平行四边形是菱形.③四边相等的四边形是菱形.模块三正方形的定义、性质及判定知识导航定义示例剖析有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.90ABCD AB BC ABCDB ⎫⎪=⇒⎬⎪∠=︒⎭平行四边形正方形性质示例剖析正方形是特殊的平行四边形,具有平行四边形的性质.①对边平行且四边都相等;②四个角都是直角;③两条对角线互相垂直平分且相等,每条对角线平分一组对角;④是中心对称图形、轴对称图形.除平行四边形性质外:①AB=BC=CD =AD ;②ABC BCD CDA DAB ∠=∠=∠=∠=90°;③AC=BD ,AC ⊥BD ,AC 、BD 分别为DAB ∠、ABC ∠的角平分线.正方形轴对称性质(用时需证明).正方形ABCD 中,P 为对角线BD 上任一点.结论:①AP =CP②△ADP ≌△CDP ③△ABP ≌△CBP判定①有一组邻边相等的矩形是正方形.②有一个角是直角的菱形是正方形.。
讲义矩形和菱形

讲义矩形和菱形-CAL-FENGHAI.-(YICAI)-Company One1龙文教育学科教师辅导讲义【答案】3:2例1. 如图,菱形ABCD 中,AC 和BD 交于点O ,OE ⊥AB 于E ,OF ⊥BC 于F ,OG ⊥CD 于G ,OH ⊥AD 于H ,试说明四边形EFGH 为矩形。
分析:四边形EFGH 与已知条件有关的主要是对角线,如果能够证明对角线EG 和HF 相等且互相平分,那么就能够判定四边形EFGH 是矩形,根据菱形的对角线平分每一组对角,知AC 是∠DAB 和∠DCB 的角平分线,DE 是∠ADC 和∠ABC 的角平分线,因为OE ⊥AB ,OF ⊥BC ,OG ⊥CD ,OH ⊥AD ,根据角平分线的性质很容易得出OE =OF =OG =OH 解:∵四边形ABCD 是菱形 ∴AC 、BD 平分对角∴O 点在∠DAB 、∠BCD 、∠CDA 、∠ABC 的角平分线上 又∵OE ⊥AB ,OF ⊥BC ,OG ⊥CD ,OH ⊥AD ∴OE =OF =OG =OH又∵AB ︒=∠120AOD 4cm BD CE ⊥1:3:=∠∠ECB DCE ACE ∠(2011甘肃兰州,20,4分)如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去。
已知第一个矩形的面积为1,则第n 个矩形的面积为 。
【答案】114n -6. (2011四川绵阳17,4)如图,将长8cm ,宽4cm 的矩形纸片ABCD 折叠,使点A 与C 重合,则折痕EF 的长为_____cm.【答案】257.如图,矩形ABCD 中,CE 平分15,=∠∠ACE BCD °,求BOE DOC ∠∠,的度数。
8、如图,矩形纸片ABCD 中,3cm 4cm AB BC ==,,现将A C 、重合使纸片折叠压平,设折痕为E F 、,则重叠部分AEF △的面积为多少…… A BO C D D A OB C E D A CB H GF EA E BFODCA FDCBED 'BEDF 是菱形FEDCBA【巩固】 已知:如图,平行四边形ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别相交于E 、F .求证:四边形AFCE 是菱形.ODEFC AB【例3】 ☆如图,E 是菱形ABCD 的边AD 的中点,EF AC ⊥于H ,交CB 的延长线于F ,交AB 于P ,证明:AB 与EF 互相平分AB CDEF P PF EDC B A【巩固】 ☆如图,M 是矩形ABCD 内的任意一点,将MAB ∆沿AD 方向平移,使AB 与DC 重合,点M 移动到点'M 的位置⑴画出平移后的三角形; ⑵连结'MD MC MM ,,,试说明四边形'MDM C 的对角线互相垂直,且长度分别等于AB AD ,的长;⑶当M 在矩形内的什么位置时,在上述变换下,四边形'MDM C 是菱形为什么M'MDC BA【巩固】(湖南湘西24,10分)如图,已知矩形ABCD 的两条对角线相交于O,∠ACB=30°,AB=2. (1)求AC 的长.(2)求∠AOB 的度数.(3)以OB 、OC 为邻边作菱形OBEC,求菱形OBEC 的面积.【综合题】已知等腰ABC △中,AB AC =,AD 平分BAC ∠交BC 于D 点,在线段AD 上任取一点P (A 点除外),过P 点作EF AB ∥,分别交AC 、BC 于E 、F 点,作PM AC ∥,交AB 于M 点,连结ME .⑴求证四边形AEPM 为菱形⑵当P 点在何处时,菱形AEPM 的面积为四边形EFBM 面积的一半MPFABCDE考点三:矩形和菱形的综合应用例(2011山东德州16,4分)长为1,宽为a 的矩形纸片(121<<a ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n 此操作后,剩下的矩形为 正方形,则操作终止.当n =3时,a 的值为_____________.练习1:(2011江苏南京,21,7分)如图,将□ABCD 的边DC 延长到点E ,使CE=DC ,连接AE ,交BC 于点F .⑴求证:△ABF ≌△ECF⑵若∠AFC=2∠D ,连接AC 、BE .求证:四边形ABEC 是矩形.练习2(2011湖南衡阳,26,10分)如图,在矩形ABCD 中,AD =4,AB =m (m >4),点P 是AB 边上的任意一点(不与A 、B 重合),连结PD ,过点P 作PQ ⊥PD ,交直线BC 于点Q .(1)当m =10时,是否存在点P 使得点Q 与点C 重合若存在,求出此时AP 的长;若不存在,说明理由;(2)连结AC ,若PQ ∥AC ,求线段BQ 的长(用含m 的代数式表示)(3)若△PQD 为等腰三角形,求以P 、Q 、C 、D 为顶点的四边形的面积S 与m 之间的函数关系式,并写出m 的取值范围.ABCD EF(第21题) 第一次操作第二次操作∴∠AOM=60°∴△AOM为等边三角形∴MA=MO=ME′,∠'AE M=∠'E AM又∵∠'AE M+∠'E AM=∠AMO即2∠'AE M=60°∴∠'AE M=30°∴∠'AE M+∠AOE′=30°+60°=90°∴△AOE′为直角三角形.2011湖南衡阳,26,10分【解】(1) 假设当m=10时,存在点P使得点Q与点C重合(如下图),∵PQ⊥PD∴∠DPC=90°,∴∠APD+∠BPC=90°,又∠ADP+∠APD=90°,∴∠BPC=∠ADP,又∠B=∠A=90°,∴△PBC∽△DAP,∴PB BCDA AP=,∴1044APAP-=,∴2AP=或8,∴存在点P使得点Q与点C重合,出此时AP的长2 或8.(2) 如下图,∵PQ∥AC,∴∠BPQ=∠BAC,∵∠BPQ=∠ADP,∴∠BAC=∠ADP,又∠B=∠DAP=90°,∴△ABC∽△DAP,∴AB BCDA AP=,即44mAP=,∴16APm=.∵PQ∥AC,∴∠BPQ=∠BAC,∵∠B=∠B,∴△PBQ∽△ABC,PB BQAB BC=,即164m BQmm-=,∴2164BQm=-.(3)由已知PQ⊥PD,所以只有当DP=PQ时,△PQD为等腰三角形(如图),∴∠BPQ=∠ADP,又∠B=∠A=90°,∴△PBQ≌△DAP,∴PB=DA=4,AP=BQ=4m-,∴以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式为:S四边形PQCD= S矩形ABCD-S△DAP-。
4.4矩形、菱形

C
菱形
菱形
有一组邻边相等的平行四边形.
菱形性质定理
定理1
菱形的四条边相等.
定理2
菱形的对角线互相垂直,并且每一条对角线 B 平分一组对角.
A C
D
AB=BC=CD=DA AC⊥BD
菱形判定定理
定理1 四条边都相等的四边形是菱形. 定理2 对角线互相垂直的平行四边形是
菱形.
A O B C
D
已知: □ABCD中,对角线AC⊥BD. 求证: □ABCD是菱形.
菱形判定定理
证明
∵ 四边形ABCD是平行四边形, A ∴ OB=OD.
O B C
D
又 AC⊥BD,垂足为O, ∴ AB=AD. ∴ □菱形.
D
B
C
已知:在□ABCD中,AC=DB. 求证: □ABCD是矩形.
矩形判定定理
证明
∵ AC=DB,BC=CB,AB=DC, ∴ △ABC ≌ △DCB. A ∴ ∠ABC = ∠DCB. 又 AB∥DC, B ∴ ∠ABC + ∠DCB=180. ∴ ∠ABC =90. ∴ □ABCD是矩形.
D
4.5
矩形、菱形
矩形 菱形
矩形
矩形
有一个角是直角的平行四边形.
矩形性质定理
定理1 矩形的四个角都是直角. 定理2 矩形的对角线相等.
A D
∠A = ∠ B =∠ C =∠ D=90
B C
AC=BD
推论 直角三角形斜边上的中线等于斜边的一半
矩形判定定理
定理1
定理2
A
由三个角是直角的四边形是矩形. 对角线相等的平行四边形是矩形.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矩形、菱形
一.知识点:
1.矩形的性质、判定方法;
2.直角三角形中线性质;
3.菱形的性质、判定方法。
二.运用:
1.如图,顺次连接四边形ABCD 各边的中点,若得到的四边形EFGH 为矩形,则四边形ABCD
一定满足( )
A.AB=CD
B.AC=BD
C.AC ⊥BD
D.AD//BC
2.如图,矩形ABCD 的对角线AC,BD 相交于点O,CE//BD,DE//AC,若AC=4,则四边形CODE 的
周长( )
A.4
B.6
C.8
D.10
3.如图,点P 是边长为1的菱形ABCD 对角线AC 上一动点,点M,N 分别为AB,BC 边上的中点,
则MP+NP 的最小值是( ) A.2 B.1 C.2 D.2
1 4.如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O,过点O 作EF ⊥AC 交点E,交AD
于点F,连接AE,CF.则四边形AECF 是( )
A.梯形
B.矩形
C.菱形
D.正方形
5.如图,过四边形ABCD 的各顶点作对角线BD 和AC 的平行线围成四边形EFGH,若四边形EFGH
是菱形,则原四边形ABCD 一定是( )
A.矩形
B.平行四边形
C.菱形
D.对角线相等的四边形
第1题 第2题 第3题 第4题 第5题
6.如图,M 是矩形ABCD 的边AD 的中点,P 为BC 上一点,PE ⊥MC,PF ⊥MB,当AB,BC 满足条件 时,四边形PEMF 为矩形。
7.如图,在Rt △ABC 中∠ACB=90°,D,E,F 分别是AB,BC,CA 的中点,若CD=5㎝,则EF=
8.如图,矩形ABCD 中,AB=3,BC=5,过对角线交点O 作OE ⊥AC 交AD 于E,则AE=
9.如图,分别以直角△ABC 的斜边AB,直角边AC 为边向△ABC 外作等边△ABD 和等边△ACE,F
为AB 的中点,DE 与AB 交于点G,EF 与AC 交于点H,∠ACB=90°,∠BAC=30°.给出如下
结论:①EF ⊥AC;②四边形ADFE 为菱形;③AD=4AG;④FH=4
1BD,其中正确的结论 为 。
(请将所有正确的序号都填上)。
第6题 第7题 第8题 第9题
10.已知平行四边形ABCD 的对角线交于点O,分别添加下列条件:①∠ABC=90°;
②AD ⊥BD ;③AC=BD ;④OA=OD.使平行四边形ABCD 是矩形的条件的序号是
11.在矩形ABCD 中,对角线AC,BD 相交于点O,若∠AOB=60°,AC=10,则AB= .
12.如图,在矩形ABCD 中,P 为边AD 上一动点,PE ⊥AC 于E,PF ⊥BD 于F.
求证:PE+PF 为定值。
13.如图,在矩形ABCD 中,E 为边AD 上一点,EF ⊥CE 交AB 于F,若DE=2,
矩形的周长为16,且CE=EF,求AE 的长?
14.如图,在矩形ABCD 中AC 、BD 相交于O,AE 平分∠BAD 交BC 于E.若∠CAE=15°, 求∠BOE 的度数。
15.如图,BD,CE 为△ABC 的高,G,F 分别为BC,DE 的中点,求证:FG ⊥DE.
16.已知,如图所示的平行四边形ABCD 中,对角线AC,BD 交于点O,EF ⊥AC,点O 是垂足, EF 分别交AB,CD 于点E,F,且BE=OE=2
1AE.求证:平行四边形ABCD 是矩形。
17.如图,平行四边形ABCD 中,AC,BD 交于点O,E 为平行四边形ABCD 外一点,
且∠AEC=∠BED=90°,求证:平行四边形ABCD 是矩形。
18.如图,在矩形ABCD中,EF//BC,GH//AB,且矩形AEOH,矩形HOFD,矩形OGCF的面积
分别为9,4,7,则△HBF的面积是。
19.在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F,求证:DF=DC.
20.如图,D是△ABC的边AB上一点,CN//AB,DN交AC于点M,MA=MC.
(1)求证:CD=AN;
(2)若∠AMD=2∠MCD,求证:四边形ADCN是矩形。
21.如图,在四边形ABCD中,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点。
(1)猜一猜,MN与BD的位置关系,并证明你的结论;
(2)如果∠BCD=45°,BD=2,求MN的长。
22.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC
交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证:OE=OF;
(2)若BC=23,求AB的长。
23.如图,△ABC 中,点O 是边AC 上一个动点,过O 作直线MN//BC,设MN 交∠ACB 的平分线 于点E,交∠ACB 的外角平分线于点E.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC 的长;
(3)当点O 在边AC 上运动到什么位置时,四边形AECF 是矩形?并说明理由。
24.已知:如图,在菱形ABCD 中,F 是BC 上任意一点,连接AF 交对角线BD 于点E,连接EC.
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F 在线段BC 上的什么位置?说明理由。
25.将一块直角三角板的直角顶点绕着矩形ABCD 的对角线交点O 旋转,图中M 、N 分别为直角 三角板的直角边与矩形ABCD 的边CD 、BC 的交点。
⑴在图1中三角板的一直角边与OD 重合时,有结论:2
22CD CN BN +=;在图3中三
角板的一直角边与OC 重合时,有结论:222CD BN CN +=请选一个证明。
⑵探究图2中BN 、CN 、CM 、DM 这四条线段之间的关系,写出结论并证明。
⑶将矩形ABCD 改为边长为1的正方形,直角三角板的直角顶点绕着点O 旋转到图4,两 直角边与AB 、BC 分别交于M 、N,直接写出BN 、CN 、CM 、DM 这四条线段之间的关系。
图1 图2 图3 图4
折叠问题:
1.如图,把矩形ABCD 沿EF 对折后使两部分重合,若∠1=50°,则∠AEF=( ).
A.110°
B.115°
C.120°
D.130°
2.如图,矩形ABCD 的长AD=8㎝,宽AB=6㎝,将其折叠,使点D 与点B 重合,那么折叠后 DF 的长和折痕EF 的长分别为 。
3.如图,将矩形纸片沿对角线BD 折叠,使点C 落在平面上的点C '处,C B '交AD 于点E, 若∠EBD=20°,则∠DE C '的度数为 。
4.如图,已知长方形ABCD ,AB=3㎝,AD=4㎝,过对角线BD 的中点O 作BD 的垂线EF, 分别交AD,BC 于点E,F 。
则AE 的长为 。
第1题 第2题 第3题 第4题
5.如图,把矩形纸片ABCD 沿EF 折叠,使点B 落在边AD 上的点B '处,点A 落在点A '处。
(1)求证:BF E B =';
(2)设AE=a ,AB=b ,BF=c ,试猜想c b a ,,之间的一种关系,并给予证明。
