天津大学物理化学课件第四章 多组分系统热力学概要
合集下载
天津大学物理化学第五版-第四章-多组分系统热力学
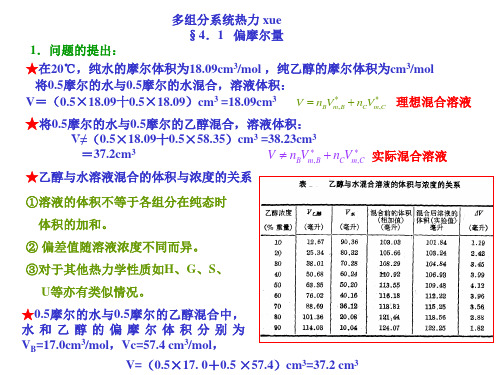
G ( ) T , nB V B p
B ( ) T , x VB p
B ( ) T Vm ,B p
结论:几种纯液体在恒温恒压下,混合成理想液态混合物时,混合前 后系统的体积不变。
( 2)
mix H 0
结论:几种纯液体在恒温恒压了混合成理想液态混合物时,混合前 后系统的焓不变,因而混合(焓)热等于零。
4.偏摩尔量与摩尔量的差别 [1]若B,C形成理想混合物 V*m,B和V*m,C为两纯液体的摩尔体积
Vm~xc作图得一条直线(见图中虚线) 截距:V*m,B 斜率:V*m,C-V*m,B
[2]若B,C形成了真实混合物 Vm~xc作图得一条曲线(见图中实线) 过d作Vm~xc曲线的切线,此切线在纵坐标轴上的 截距为该组成下两组分的偏摩尔体积VB,Vc
>0 非自发过程
化学势判据
★
3、化学势判据及应用举例 在恒温恒压下,若系统中存在有多相(α,β…),多组分(B,C …) 则:
dG dG dG
dn dn B B B B dn B B
B B B
<0 自发过程 =0 平衡状态
由享利定律可知,当溶质、溶剂和温度都一定时,亨利常数就为定值, 气体的分压越大,则该气体在溶液中的溶解度也就越大。所以增加气体的 压力有利于吸收操作。 由下表可知,随温度的升高,k值增大,因而当CO2分压相同时,随 着温度的升高,CO2的溶解度xCO2将下降。反之降低温度,则xCO2的溶解 度将增大,所以低温有利于吸收操作。
3.拉乌尔定律和亨利定律的微观解释 ※拉乌尔定律的微观解释 溶液中加入溶质 B ,单位液面上 A 分子数占液面总分子数的分数从纯 溶剂时的1下降至溶液的xA,致使单位液面上溶剂 A的蒸发速率按比例下降, 溶液中溶剂A的饱和蒸气压也相应地按比例下降。 pA=p*AxA ※亨利定律的微观解释 在溶解平衡时,气相中B在单位表面上的凝结速率与蒸发速率相等,故 气相中B的平衡分压力正比于溶液中B的摩尔分数。
天津大学物理化学课件第四章 多组分系统热力学概要

证:在 P 点 V总=xBVB + xCVC
Q VB*
P
VC*
Q xB xC 1 Vt VB (VC VB ) xC
B
xC Q=VB , R=VC
C
P点的切线方程:( y = b + m x )
R-Q V总=Q+ xC , 相应地 1
15
4. 偏摩尔量与摩尔量的差别
由截距法及图可看出其差别
若系统是开放的或组成发生变化时则不再适用。对于
组成可变的多组分系统,必须建立相应的热力学方程。 这一问题是由Gibbs(美 1839-1903)解决的。
23
吉布斯(美,1839-1903): 1874年发表:《以热力学 的原理决定化学平衡》; 1876、1877年发表:《关 于物质的多项平衡》 (文章长 达300多页,有700多个公式) ; 1891年吉布斯的文章被 奥斯瓦尔德译成德文《热力 学的研究》; 1899年被译成法文《化 学体系的平衡》。
(需代入实际气体状态方程,形式复杂)
为使实际气体的 B 表达式也具有较简单的形式,
pB 和逸度因子B 的概念 Lewis引入了逸度 %
32
1. 逸度与逸度因子
实际气体
$ B B RT ln(% pB / p$ )
* * p
p RT dp RT ln pO p
27
* = + RT ln ( p / p)
:p = 100 kPa 时的化学势,又称为标准化学势
对于理想气体混合物,其中的 B 组分,有:
pB GB G RT ln $ p
17
§4.2 化学势
定义:混合物(或溶液)中组分B的偏摩尔 吉布斯函数GB又称为B的化学势
Q VB*
P
VC*
Q xB xC 1 Vt VB (VC VB ) xC
B
xC Q=VB , R=VC
C
P点的切线方程:( y = b + m x )
R-Q V总=Q+ xC , 相应地 1
15
4. 偏摩尔量与摩尔量的差别
由截距法及图可看出其差别
若系统是开放的或组成发生变化时则不再适用。对于
组成可变的多组分系统,必须建立相应的热力学方程。 这一问题是由Gibbs(美 1839-1903)解决的。
23
吉布斯(美,1839-1903): 1874年发表:《以热力学 的原理决定化学平衡》; 1876、1877年发表:《关 于物质的多项平衡》 (文章长 达300多页,有700多个公式) ; 1891年吉布斯的文章被 奥斯瓦尔德译成德文《热力 学的研究》; 1899年被译成法文《化 学体系的平衡》。
(需代入实际气体状态方程,形式复杂)
为使实际气体的 B 表达式也具有较简单的形式,
pB 和逸度因子B 的概念 Lewis引入了逸度 %
32
1. 逸度与逸度因子
实际气体
$ B B RT ln(% pB / p$ )
* * p
p RT dp RT ln pO p
27
* = + RT ln ( p / p)
:p = 100 kPa 时的化学势,又称为标准化学势
对于理想气体混合物,其中的 B 组分,有:
pB GB G RT ln $ p
17
§4.2 化学势
定义:混合物(或溶液)中组分B的偏摩尔 吉布斯函数GB又称为B的化学势
天津大学版物理化学课件第四章

即稀溶液中溶剂蒸气压下降值Δp与纯溶剂蒸气压之 比等于溶质的摩尔分数,而与溶质种类无关。 表4.4.1以甘露蜜醇的水溶液为例,列出了不同浓度下溶剂 蒸气压下降的实验值与拉乌尔定律的计算值。可以看出, 在所测的浓度范围内两者是很一致的。
表4.4.1 甘露蜜醇水溶液的蒸气压下降值(20℃)
溶质的摩尔分 数 103xB 1.769 蒸气压下降值△p/Pa 实验值 计算值 相对百分误差 %
dG -SdT Vdp B dnB
B
这四个方程时适用于均匀系统的更为普遍的热力学基本 方程,不仅适用于变组成的封闭系统,也适用于开放系 统。在封闭系统内的任一均匀部分(纯物质、混合物或 溶液)中组分B、C等的物质的量发生变化,是由于系统 内部发生了相变化或化学变化引起的。
如果将U、H、A表示成如下函数关系:
4.分配定律:
实验证明:在一定的温度、压力下,当溶质在共存的两互 不相溶液体间成平衡时,若形成的溶液的浓度不大,则 溶质在两液相中的质量浓度比为一常数。这就是能斯特 分配定律。比例系数称为分配系数,符号为K。
K bB ( ) / b( )
(4.6.18)
K是比例系数,称为分配系数。 这一经验定律可以由溶质在α、β两相间达到平衡时化学势 相等得出。
质量摩尔浓 度 b/(mol· -1) kg
0.0984
4.093
4.146
+1.3
0.2962
0.4938 0.6934 0.8913
5.307
8.817 12.34 15.80
12.29
20.48 28.83 37.23
12.41
20.60 28.83 36.95
+1.0
+0.6 0.0 -0.7
物化第4章多组分体系热力学

80%
相平衡的计算方法
相平衡的计算方法包括等温蒸发 法、等温蒸发结露法和等温升华 法等。
化学平衡
化学平衡的定义
化学平衡是指在一定温度和压 力下,可逆反应达到的动态平 衡状态,此时正逆反应速率相 等,各组分浓度不再发生变化 。
化学平衡的条件
化学平衡的条件是各组分浓度 不变,且正逆反应速率相等。 在等温、等压条件下,化学平 衡常数Kc=Kp/Kw。
相平衡和化学平衡的区别在于它们的 关注点不同。相平衡主要关注各相之 间的分界面性质和相组成,而化学平 衡主要关注可逆反应的正逆反应速率 和各组分浓度的变化。
相平衡和化学平衡的 相互影响
在多组分体系中,相平衡和化学平衡 之间存在相互影响。例如,在液态混 合物中,各组分的化学势差异会导致 物质传递和扩散现象的发生,从而影 响相平衡状态;同时,化学反应的进 行也会影响各相的组成和性质,从而 影响相平衡状态。因此,在多组分体 系的研究中,需要综合考虑相平衡和 化学平衡的影响。
化学平衡的计算方法
化学平衡的计算方法包括平衡 常数法、物料守恒法和电荷守 恒法等。
相平衡和化学平衡的关系
相平衡和化学平衡的 联系
相平衡和化学平衡都是热力学平衡态 的表现形式,它们之间存在密切的联 系。在多组分体系中,化学平衡通常 存在于相平衡状态中,而相平衡也是 化学平衡的表现形式之一。
相平衡和化学平衡的 区别
04
02
03
04
热容
表示物质吸收或放出热量的能 力,与温度和物质种类有关。
熵
表示系统无序度的量,与系统 内分子运动状态和排列有关。
焓
表示物质内能和压力势能的量 ,与物质的化学组成和温度有 关。
自由能
表示系统在恒温恒压下的自由 程度,与系统内部能量和熵有 关。
物理化学课件:第四章 多组分系统

指液态溶液。 液体与液体以任意比例相互混合成均相即形成
混合物,气体、液体或固体溶于液体溶剂中即形成 溶液。
溶质有电解质和非电解质之分,本章主要讨 论非电介质所形成的溶液。
按规律性来划分 混合物:理想混合物、真实混合物。
溶液:理想稀溶液、真实溶液。
理想混合物在全部浓度范围内,理想稀溶液在 适当小的范围内,均有简单的规律性。
组成表示 ① 质量摩尔浓度(molality) bB:
bB
def
nB mA
溶质物质的量,单位 mol 溶剂的质量,单位 kg
bB 的单位:mol kg 1 。
② 物质的量浓度(molarity) cB:
cB
def
nB V
cB 的单位:mol m 3 。如果文献中用 molarity,则指单位 为 mol dm 3 。
B
dnB
=0
B
dnB
BdnB 0
B
该平衡条件与化学反应达到平衡的方式无关。
23
§4.3 气体组分的化学势
标准态:温度 T,标准压力 p 100 kPa ,理想气体。
该状态下的化学势称为标准化学势,以符合μBΘ(g)表示。 对于纯气体则省略下标B。 1.纯理想气体的化学势
使某纯理想气体B在温度T下由标准压力pΘ变至某一压力p,
Bl
Bg
RT
ln
pB* p
RT lnxB
* Bl
Bg
RT
ln
pB* p
40
因此
Bl
B* l RT lnxB
由纯液体 B 标准态的定义可知,
p
* Bl
Bl
p Vm*,B l dp
最后得到理想液态混合物中 B 组分化学势表达式:
混合物,气体、液体或固体溶于液体溶剂中即形成 溶液。
溶质有电解质和非电解质之分,本章主要讨 论非电介质所形成的溶液。
按规律性来划分 混合物:理想混合物、真实混合物。
溶液:理想稀溶液、真实溶液。
理想混合物在全部浓度范围内,理想稀溶液在 适当小的范围内,均有简单的规律性。
组成表示 ① 质量摩尔浓度(molality) bB:
bB
def
nB mA
溶质物质的量,单位 mol 溶剂的质量,单位 kg
bB 的单位:mol kg 1 。
② 物质的量浓度(molarity) cB:
cB
def
nB V
cB 的单位:mol m 3 。如果文献中用 molarity,则指单位 为 mol dm 3 。
B
dnB
=0
B
dnB
BdnB 0
B
该平衡条件与化学反应达到平衡的方式无关。
23
§4.3 气体组分的化学势
标准态:温度 T,标准压力 p 100 kPa ,理想气体。
该状态下的化学势称为标准化学势,以符合μBΘ(g)表示。 对于纯气体则省略下标B。 1.纯理想气体的化学势
使某纯理想气体B在温度T下由标准压力pΘ变至某一压力p,
Bl
Bg
RT
ln
pB* p
RT lnxB
* Bl
Bg
RT
ln
pB* p
40
因此
Bl
B* l RT lnxB
由纯液体 B 标准态的定义可知,
p
* Bl
Bl
p Vm*,B l dp
最后得到理想液态混合物中 B 组分化学势表达式:
最新物理化学课件(天大第五版)04-01溶液热力学

第四章 多组分系统 热力学
Chapter 4 the Thermodynamics of Multicomponent System
1
系统按照所含组分数和相数可划分为:
单组分均相系统 多组分均相系统
单组分多相系统 多组分多相系统
多组分均相系统 :由两种或两种以上物质以分子状态 相互混合而成的均匀系统
与该组分在混合物中摩尔分数的乘积。
30
p 0 VB
RT p
dp
定义:
~pB
pB
exp
p 0
VB RT
1 p
dp
对于纯气体
~p*
p exp
p 0
Vm* RT
1 p
dp
对于理想气体积分项为0
~pB pB
22
逸度因子
B
def
~p B pB
对于理想气体 ~pB pB
1
(1)线的差异
~p
Pa
(2)标准态
23
2.逸度因子的计算及普遍化逸度因子图
11
5.吉布斯–杜亥姆方程(Gibbs-Duhem)
X nB X B
B
dX (nBdX B X BdnB )
B
dX
X T
p,nC
dT
X p
T ,nC
dp
B
X B dn B
恒温恒压: dX XBdnB
B
nBdX B 0
B
xBdX B 0
B
二元系统: xAdX A xBdXB 0
p
G G1 G2 G3 RT ln p
p 0
Vm*
RT p
dp
* ( g)
RT
Chapter 4 the Thermodynamics of Multicomponent System
1
系统按照所含组分数和相数可划分为:
单组分均相系统 多组分均相系统
单组分多相系统 多组分多相系统
多组分均相系统 :由两种或两种以上物质以分子状态 相互混合而成的均匀系统
与该组分在混合物中摩尔分数的乘积。
30
p 0 VB
RT p
dp
定义:
~pB
pB
exp
p 0
VB RT
1 p
dp
对于纯气体
~p*
p exp
p 0
Vm* RT
1 p
dp
对于理想气体积分项为0
~pB pB
22
逸度因子
B
def
~p B pB
对于理想气体 ~pB pB
1
(1)线的差异
~p
Pa
(2)标准态
23
2.逸度因子的计算及普遍化逸度因子图
11
5.吉布斯–杜亥姆方程(Gibbs-Duhem)
X nB X B
B
dX (nBdX B X BdnB )
B
dX
X T
p,nC
dT
X p
T ,nC
dp
B
X B dn B
恒温恒压: dX XBdnB
B
nBdX B 0
B
xBdX B 0
B
二元系统: xAdX A xBdXB 0
p
G G1 G2 G3 RT ln p
p 0
Vm*
RT p
dp
* ( g)
RT
大学物理化学经典课件4-3-多组分体系热力学

教学目的
本课程旨在帮助学生掌握多组分体系热力学的基本概念、原理和 方法,培养学生运用热力学原理分析复杂体系的能力,为后续的 科研和工程实践打下基础。
多组分体系热力学概述
定义与特点
多组分体系是指由两种或两种以上不同物质组成的体系。多 组分体系热力学主要研究这类体系的热力学性质及其变化规 律,包括相平衡、化学平衡、能量转换等内容。
溶液的理论来处理真实溶液的问题。
活度系数
活度系数是描述真实溶液与理想溶液差异程度的物理量,它与溶液中的离子强度、溶剂 化作用等因素有关。活度系数的引入使得我们可以更准确地描述真实溶液的性质和行为。
03
多组分体系的相平衡
相律与相图
相律
描述多组分体系相平衡的基本规律, 即体系自由度、组分数和相数之间的 关系。
理论联系实际
将所学理论知识与实际问题相结合,通过分析和 解决具体问题来加深对理论知识的理解。
多做习题
通过大量的习题练习,可以巩固所学知识,提高 分析问题和解决问题的能力。
领域前沿与展望
新理论和新方法
随着科学研究的不断深入,多组分体系热力学领域不断涌现出新的理论和方法 ,如非平衡态热力学、微观热力学等,为相关领域的发展提供了新的思路。
电镀
利用电解原理在某些金属表面镀 上一薄层其他金属或合金的过程, 多组分体系热力学对于控制镀层 质量和厚度具有重要意义。
电解
通过电流作用使物质发生化学变 化的过程,多组分体系热力学研 究有助于降低能耗和提高产率。
高分子溶液中的应用
高分子合成
通过控制反应条件,合成具有特定结构和性能的高分子化合物,多 组分体系热力学研究有助于优化合成路线和提高产率。
相图
用图形表示多组分体系在不同条件下 的相平衡关系,包括温度、压力、组 成等。
本课程旨在帮助学生掌握多组分体系热力学的基本概念、原理和 方法,培养学生运用热力学原理分析复杂体系的能力,为后续的 科研和工程实践打下基础。
多组分体系热力学概述
定义与特点
多组分体系是指由两种或两种以上不同物质组成的体系。多 组分体系热力学主要研究这类体系的热力学性质及其变化规 律,包括相平衡、化学平衡、能量转换等内容。
溶液的理论来处理真实溶液的问题。
活度系数
活度系数是描述真实溶液与理想溶液差异程度的物理量,它与溶液中的离子强度、溶剂 化作用等因素有关。活度系数的引入使得我们可以更准确地描述真实溶液的性质和行为。
03
多组分体系的相平衡
相律与相图
相律
描述多组分体系相平衡的基本规律, 即体系自由度、组分数和相数之间的 关系。
理论联系实际
将所学理论知识与实际问题相结合,通过分析和 解决具体问题来加深对理论知识的理解。
多做习题
通过大量的习题练习,可以巩固所学知识,提高 分析问题和解决问题的能力。
领域前沿与展望
新理论和新方法
随着科学研究的不断深入,多组分体系热力学领域不断涌现出新的理论和方法 ,如非平衡态热力学、微观热力学等,为相关领域的发展提供了新的思路。
电镀
利用电解原理在某些金属表面镀 上一薄层其他金属或合金的过程, 多组分体系热力学对于控制镀层 质量和厚度具有重要意义。
电解
通过电流作用使物质发生化学变 化的过程,多组分体系热力学研 究有助于降低能耗和提高产率。
高分子溶液中的应用
高分子合成
通过控制反应条件,合成具有特定结构和性能的高分子化合物,多 组分体系热力学研究有助于优化合成路线和提高产率。
相图
用图形表示多组分体系在不同条件下 的相平衡关系,包括温度、压力、组 成等。
第四章 多组分系统热力学【课件】物理化学课件(天津大学第五版)

B
dT 0, dp 0
dX X B dnB nB dX B
B
B
2020/8/7
除以n
nBdX B 0
B
xBdX B 0
B
吉布斯-杜亥姆方程
吉布斯—杜亥姆方程说明:在恒温, 恒压下, 偏 摩尔量之间是具有一定联系的。某一偏摩尔量的变 化可从其它偏摩尔量的变化中求得。
2020/8/7
只有两种组分
VC V nBVB / nC
解析法:
2020/8/7
V= f (nB)
V ( nB )T ,P,nc f '(nB )
V
V ( nB )T ,P,nc
nB
4. 偏摩尔量与摩尔量的差别
摩尔量:纯组分的 偏摩尔量:混合物
Xm
X n
X
XB
( nB
)T
, p,nC
若体系仅有一种组分(即纯物质),则根据摩尔量 的定义,XB就是摩尔量。
H2O(A)的偏摩尔体积。
解 :
V
V
VB ( nB )T , p,nc ( m )T , p,nc
23.189
3
2.197
1
m2
2 0.178 m
2
2020/8/7
以m = 0.25 molkg-1和m = 0.50 molkg-1代入,分别得到在两种浓 度时NaBr的偏摩尔体积
VB,1=
24.748
X B def
X ( nB )T , p,nc
XB称为物质B的某种广度性质X的偏摩尔量
2020/8/7
使用偏摩尔量时应注意: 1.偏摩尔量的含义是:在恒温、恒压、保持B物质以外的所有组分的物质的量不 变的条件下,改变dnB 所引起广度性质X的变化值,或在恒温、恒压条件下,在 大量的定组成体系中加入单位物质的量的B物质所引起广度性质X的变化值。
dT 0, dp 0
dX X B dnB nB dX B
B
B
2020/8/7
除以n
nBdX B 0
B
xBdX B 0
B
吉布斯-杜亥姆方程
吉布斯—杜亥姆方程说明:在恒温, 恒压下, 偏 摩尔量之间是具有一定联系的。某一偏摩尔量的变 化可从其它偏摩尔量的变化中求得。
2020/8/7
只有两种组分
VC V nBVB / nC
解析法:
2020/8/7
V= f (nB)
V ( nB )T ,P,nc f '(nB )
V
V ( nB )T ,P,nc
nB
4. 偏摩尔量与摩尔量的差别
摩尔量:纯组分的 偏摩尔量:混合物
Xm
X n
X
XB
( nB
)T
, p,nC
若体系仅有一种组分(即纯物质),则根据摩尔量 的定义,XB就是摩尔量。
H2O(A)的偏摩尔体积。
解 :
V
V
VB ( nB )T , p,nc ( m )T , p,nc
23.189
3
2.197
1
m2
2 0.178 m
2
2020/8/7
以m = 0.25 molkg-1和m = 0.50 molkg-1代入,分别得到在两种浓 度时NaBr的偏摩尔体积
VB,1=
24.748
X B def
X ( nB )T , p,nc
XB称为物质B的某种广度性质X的偏摩尔量
2020/8/7
使用偏摩尔量时应注意: 1.偏摩尔量的含义是:在恒温、恒压、保持B物质以外的所有组分的物质的量不 变的条件下,改变dnB 所引起广度性质X的变化值,或在恒温、恒压条件下,在 大量的定组成体系中加入单位物质的量的B物质所引起广度性质X的变化值。
第四章 多组分系统热力学 物理化学课件.ppt

其它形式:
③适用条件:稀溶液中的挥发性溶质
亨利定律: 稀溶液中的挥发性溶质 pB(溶质)~ xB
拉乌尔定律:稀溶液中的溶剂
pA(溶剂)~ xA
亨利定律是化工单元操作“吸收”的依据,利用溶剂对混合气体中 各种气体的溶解度的差异进行吸收分离。把溶解度大的气体吸收下来, 达到从混合气体中回收或除去某种气体的目的。
几种纯液体在恒温恒压下,混合成理想液态混合物时,混合前后系 统的体积不变。
(2) mixH 0
几种纯液体在恒温恒压下,混合成理想液态混合物时,混合前后 系统的焓不变,因而混合(焓)热等于零。
恒压、恒温下液体的混合过程是一个自发过程 。
B
dnB
B
恒温恒压下非体积功等于零的条件下: dG
<0 自发过程 =0 平衡状态
>0 非自发过程
化学势判据
§4.3 气体组分的化学势
1.纯理想气体的化学势
纯理想气体:μ =GB =Gm
▲标准状态下的化学势:
B
(
g
)
▲任意压力下的化学势:μ *
T
2.理想气体混合物中任一组分的化学势
小结
★化学势判据 (恒温恒压)
B
dnB
B
★气体的化学势 ●理想气体
纯 混合物
纯 ●真实气体
混合物
<0 自发过程 =0 平衡状态 >0 非自发过程
★拉乌尔定律 适用条件:理想液态混合物 或理想稀溶液中的溶剂 pA(溶剂)~ xA ★亨利定律 适用条件:稀溶液中的挥发性溶质 pB(溶质)~ xB
③对于其他热力学性质如H、G、S、
U等亦有类似情况。
《多组分系统热力学》课件

02
03
气候变化
多组分系统热力学可用于研究温室气 体在大气中的分布和变化,为气候变 化研究提供数据支持。
在生物学中的应用
生物代谢过程
多组分系统热力学可用于研 究生物体内的代谢过程,分 析代谢产物的生成和能量转
换效率。
生物分子相互作用
利用多组分系统热力学模型 ,可以研究生物分子之间的 相互作用和结合机制,为药 物设计和生物工程提供理论
依据。
生物系统稳定性
通过多组分系统热力学模型 ,可以分析生物系统的稳定 性和动态变化,为生物保护 和生态平衡提供理论支持。
THANK YOU
感谢聆听
相变过程
相变的概念
物质在一定条件下,从一种相转变为另一种相的过程 。
相变的热力学条件
相变过程总是向着熵增加的方向进行,同时满足热力 学第一定律和第二定律。
相变过程的分类
根据相变过程中物质状态的变化,可以分为凝聚态物 质相变和气态物质相变等。
化学反应过程
化学反应的概念
化学反应是指分子破裂成原子,原子 重新排列组合生成新分子的过程。
化学势具有加和性,即对于多组分 系统中的某一组分,其化学势等于 其他组分的化学势之和。
相平衡和化学平衡
相平衡是指多组分系统中各相之间的平衡状态,是 热力学的基本概念之一。
化学平衡是指多组分系统中化学反应达到平衡状态 时的状态,是热力学的基本概念之一。
相平衡和化学平衡是相互关联的,可以通过化学势 来判断是否达到相平衡或化学平衡状态。
04
多组分系统的热力学过程
热力学过程
热力学第一定律
能量守恒定律,即在一个封闭系统中,能量不能被 创造或消灭,只能从一种形式转化为另一种形式。
天津大学物理化学课程资料第四章多组分系统热力学

,
p,nC
dnB
18
在组成不变时:
G T
p,nB
S
,
G p
T ,nB
V
代入上式有:
dG SdT Vdp BdnB
B
结合 dU = d (G-pV +T S) dH = d (G +T S) , dA = d (G-pV)
19
dU TdS pdV BdnB dH TdS Vdp BdnB dA SdT pdV BdnB
dp
X
nB
T , p,nC
dnB
下标 nB表示:各组分的摩尔数都没改变; 下标 nc 表示:除B组外,其它各组分的摩尔数都未变
7
定义:
XB
X nB
T ,P ,nC
XB 偏摩尔量
意义: 在恒T、p及其它组分都不变时,加入极微量dnB的B 组分后,引起系统 X 性质的改变 dX。
或: 在恒T、p下,于足够大量的某一定组成的溶液中加入 1 mol B组分,而溶液浓度可视为不变时,1 mol B组 分对此种溶液中 X 性质的贡献。
第四章 多组分系统热力学
1
多组分系统
气态混合物
混合物 液态混合物
溶液
固态混合物
(第六章)
固态溶液
液态溶液 非电解质溶液
电解质溶液 (第七章)
混合物:各组分标准态相同; 溶液:溶质、溶剂标准态不同
研究方法:理想 实际
2
组成表示法:
1. 物质B的摩尔分数:
xB xB xB
B
xB 1
B
2. 物质B的质量分数:
wB mB
mB
B
wB 1
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 多组分系统热力学
1
气态混合物 混合物 多组分系统 液态混合物
固态混合物
(第六章) 固态溶液
溶液
液态溶液
非电解质溶液
电解质溶液 (第七章)
混合物:各组分标准态相同;
溶液:溶质、溶剂标准态不同
研究方法:理想 实际
2
组成表示法:
1. 物质B的摩尔分数:
xB xB
x
B
B
x
26
§4.3 气体组分的化学势
1. 理想气体的化学势
纯理想气体的化学势* 即为其摩尔吉布斯函数Gm*
恒T 下,将1mol 理想气体从 p 变到 p :
B(g, p ) B(g, p)
p
*
p pO
由公式: dG = -S dT + V dP 有:Δ ΔG O Vdp
$ B
因
B GB
$ B
pB B RT ln $ p
28
2. 真实气体的化学势
真实纯气体的* 纯真实气体的标准态:T,p 的理想气体 (理气) T,p T,p (真实)
G
*
G1 G2
G3
(理气) T,p T,p0 (真实)
V VB n B T , p ,nC VC V nBVB / nC
V
V n B T , p ,nc
nB
也可将V~ nB关系拟合为数学式,然后求导得到VB
14
2) 截距法
二元溶液,作Vm~xC 图
Vm R
截距 Q=VB , R=VC
x1dX 1 x2dX 2
即:恒温恒压下,当混合物的组成发生微小变化时, 如果一组分的偏摩尔量增加,则另一组分的偏摩尔量将 减少,且变化的比例与两组分的摩尔分数成反比。
13
3. 偏摩尔量的测定法举例 1) 作图法
T、p 恒定,二组分(B,C)溶液,
nC 一定下,加入B,测总体积 作V~nB 图
p
p * $ $ * * (g, p) (g, p ) RT ln $ Vm Vm, 理 dp p 0
30
p * RT * $ $ 或: (g, p) (g, p ) RTln $ Vm dp p p 0
B
因 XB 与组成有关, 在组成不变下(即XB为常数)积分上式,可得:
X nB X B
B
在恒T、p下,将上式微分:
dX
nB dX B
B
X B dnB
B
与前式比较可有:
nB dX B 0
B
12
将上式除以
n nB ,可得:
B
xBdX B 0
B
上两式均称为吉布斯-杜亥姆方程 对于二组分系统,有:
B
21
dG B dnB 0
B
自发 平衡
例: 一定T, p 下, 物质B以, 两种相态存在, 有:
dG dn dn
如有dn物质自发从 转移到, 则dn>0, dn<0, 而dG<0,
如两相平衡, dG=0, 则:
17
§4.2 化学势
定义:混合物(或溶液)中组分B的偏摩尔 吉布斯函数GB又称为B的化学势
G B GB n B T , p ,nC
1. 基本式 多组分系统:G = G (T, p, nB, nC, nD,…)
G G G dG dp dnB dT T p ,nB p T ,nB nB T , p,nC
H n B
S SB n B G GB n B
A AB n B
注意:1) 必须在恒T、p的条件下; 2) 只有广度性质有偏摩尔量。 (但偏摩尔量本身为强度量)
11
恒T、p下,有: dX X BdnB
(需代入实际气体状态方程,形式复杂)
为使实际气体的 B 表达式也具有较简单的形式,
pB 和逸度因子B 的概念 Lewis引入了逸度 %
32
1. 逸度与逸度因子
实际气体
$ B B RT ln(% pB / p$ )
18
在组成不变时:
G G T S , p V p , nB T , nB
代入上式有:
dG SdT Vdp BdnB
B
结合 dU = d (G-pV +T S) d H = d ( G +T S ) , dA = d (G-pV)
3) 混合真实气体
31Βιβλιοθήκη § 4.4 逸度与逸度因子
pB 理想气体 B RT ln $ p p pB RT $ 实际气体 B B +RT ln $ VB dp p p 0
$ B
要求 实际气体的 B VB ~ p的关系
19
dU TdS pdV BdnB dH TdS Vdp BdnB dA SdT pdV BdnB
同时可看出:
B
U n B A n B H n B S ,V ,nC G n B T ,V ,nC S , p ,nC T , p ,nC
物质量:
nA nB nA nB
* nAVm,A * nBVm,B
— 不变 — 变化
体积:
V
不同浓度时,偏差不同
5
这说明
同是1mol物质:
在混合物中对体积贡献不同于单独存在时对体积贡献
偏摩尔体积 不同于 摩尔体积
VB
称为偏摩尔量
V
* m, B
VB 混合物中1 mol B物质在该组成时对体积的贡献
24
多相、多组分系统恒T、p时有
α α dG B dnB 0 α B
相率,Clapeyron方程
化学反应等温方程
化学反应
精馏,结晶
萃取 膜分离 吸附
25
吸附势,吸附热 渗透压
分配定律
麦克斯韦尔曾说过:“如果热力学只是 在解释蒸汽机的功能,固然可以满足工业家 所需要的,但是若蒸气工业过去了,热力学 就过去了”。是Gibbs将热力学引入了化学, 使热力学在化学中焕发了强有力的生命力, 同时使化学成为一门有理论指导的科学。
* * p
p RT dp RT ln pO p
27
* = + RT ln ( p / p)
:p = 100 kPa 时的化学势,又称为标准化学势
对于理想气体混合物,其中的 B 组分,有:
pB GB G RT ln $ p
即: 在恒T, p下,物质总是从化学势高的一相向化学势低 的一相转移,两相化学势相等时达到平衡。
22
关于化学势
十九世纪五、六十年代,热力学基本规律已经明
确起来,但一些热力学概念还较模糊,数学处理很麻
烦,不能用来解决稍微复杂一点的问题———如化学 反应的方向问题。 基本热力学方程是热力学理论框架的中心,然而 第三章中的基本方程只适用于组成不变的封闭系统。
下标 nB表示:各组分的摩尔数都没改变; 下标 nc 表示:除B组外,其它各组分的摩尔数都未变
7
定义:
X XB n B T , P ,nC
XB 偏摩尔量
意义: 在恒T、p及其它组分都不变时,加入极微量dnB的B
组分后,引起系统 X 性质的改变 dX。 或: 在恒T、p下,于足够大量的某一定组成的溶液中加入
真实气体混合物中B组分,相应地有:
p
pB RT B ( g )= +RT ln $ VB dp p p 0
$ B
p
上式适用于:
注意:p为总压
1)纯理想气体及其混合物,(VB – RT/p) 积分项为0; 2)纯真实气体,VB 变为Vm* ;
1) 偏摩尔量 摩尔量
Vm
R
P
Q VB*
VC*
2) 偏摩尔量随组成而变
B
xC
C
16
5. 偏摩尔量之间的关系
纯组分系统热力学函数之间的关系也适用于 偏摩尔函数, 如:
H B U B pVB , AB U B TSB
GB H B TSB AB pVB GB VB p T ,nB GB , SB T p ,nB
G 其中只有 n B
为偏摩尔量 T , p ,nC
20
2. 化学势判据
T , p 恒定时:(W =0) dG 0
自发 平衡
多相、多组分时:
dG dG dG L
B dnB μB dnB L
B B
B dnB
证:在 P 点 V总=xBVB + xCVC
Q VB*
P
VC*
Q xB xC 1 Vt VB (VC VB ) xC
B
xC Q=VB , R=VC
C
P点的切线方程:( y = b + m x )
R-Q V总=Q+ xC , 相应地 1
15
4. 偏摩尔量与摩尔量的差别
由截距法及图可看出其差别
V nAVA nBVB
V nBVB
1
气态混合物 混合物 多组分系统 液态混合物
固态混合物
(第六章) 固态溶液
溶液
液态溶液
非电解质溶液
电解质溶液 (第七章)
混合物:各组分标准态相同;
溶液:溶质、溶剂标准态不同
研究方法:理想 实际
2
组成表示法:
1. 物质B的摩尔分数:
xB xB
x
B
B
x
26
§4.3 气体组分的化学势
1. 理想气体的化学势
纯理想气体的化学势* 即为其摩尔吉布斯函数Gm*
恒T 下,将1mol 理想气体从 p 变到 p :
B(g, p ) B(g, p)
p
*
p pO
由公式: dG = -S dT + V dP 有:Δ ΔG O Vdp
$ B
因
B GB
$ B
pB B RT ln $ p
28
2. 真实气体的化学势
真实纯气体的* 纯真实气体的标准态:T,p 的理想气体 (理气) T,p T,p (真实)
G
*
G1 G2
G3
(理气) T,p T,p0 (真实)
V VB n B T , p ,nC VC V nBVB / nC
V
V n B T , p ,nc
nB
也可将V~ nB关系拟合为数学式,然后求导得到VB
14
2) 截距法
二元溶液,作Vm~xC 图
Vm R
截距 Q=VB , R=VC
x1dX 1 x2dX 2
即:恒温恒压下,当混合物的组成发生微小变化时, 如果一组分的偏摩尔量增加,则另一组分的偏摩尔量将 减少,且变化的比例与两组分的摩尔分数成反比。
13
3. 偏摩尔量的测定法举例 1) 作图法
T、p 恒定,二组分(B,C)溶液,
nC 一定下,加入B,测总体积 作V~nB 图
p
p * $ $ * * (g, p) (g, p ) RT ln $ Vm Vm, 理 dp p 0
30
p * RT * $ $ 或: (g, p) (g, p ) RTln $ Vm dp p p 0
B
因 XB 与组成有关, 在组成不变下(即XB为常数)积分上式,可得:
X nB X B
B
在恒T、p下,将上式微分:
dX
nB dX B
B
X B dnB
B
与前式比较可有:
nB dX B 0
B
12
将上式除以
n nB ,可得:
B
xBdX B 0
B
上两式均称为吉布斯-杜亥姆方程 对于二组分系统,有:
B
21
dG B dnB 0
B
自发 平衡
例: 一定T, p 下, 物质B以, 两种相态存在, 有:
dG dn dn
如有dn物质自发从 转移到, 则dn>0, dn<0, 而dG<0,
如两相平衡, dG=0, 则:
17
§4.2 化学势
定义:混合物(或溶液)中组分B的偏摩尔 吉布斯函数GB又称为B的化学势
G B GB n B T , p ,nC
1. 基本式 多组分系统:G = G (T, p, nB, nC, nD,…)
G G G dG dp dnB dT T p ,nB p T ,nB nB T , p,nC
H n B
S SB n B G GB n B
A AB n B
注意:1) 必须在恒T、p的条件下; 2) 只有广度性质有偏摩尔量。 (但偏摩尔量本身为强度量)
11
恒T、p下,有: dX X BdnB
(需代入实际气体状态方程,形式复杂)
为使实际气体的 B 表达式也具有较简单的形式,
pB 和逸度因子B 的概念 Lewis引入了逸度 %
32
1. 逸度与逸度因子
实际气体
$ B B RT ln(% pB / p$ )
18
在组成不变时:
G G T S , p V p , nB T , nB
代入上式有:
dG SdT Vdp BdnB
B
结合 dU = d (G-pV +T S) d H = d ( G +T S ) , dA = d (G-pV)
3) 混合真实气体
31Βιβλιοθήκη § 4.4 逸度与逸度因子
pB 理想气体 B RT ln $ p p pB RT $ 实际气体 B B +RT ln $ VB dp p p 0
$ B
要求 实际气体的 B VB ~ p的关系
19
dU TdS pdV BdnB dH TdS Vdp BdnB dA SdT pdV BdnB
同时可看出:
B
U n B A n B H n B S ,V ,nC G n B T ,V ,nC S , p ,nC T , p ,nC
物质量:
nA nB nA nB
* nAVm,A * nBVm,B
— 不变 — 变化
体积:
V
不同浓度时,偏差不同
5
这说明
同是1mol物质:
在混合物中对体积贡献不同于单独存在时对体积贡献
偏摩尔体积 不同于 摩尔体积
VB
称为偏摩尔量
V
* m, B
VB 混合物中1 mol B物质在该组成时对体积的贡献
24
多相、多组分系统恒T、p时有
α α dG B dnB 0 α B
相率,Clapeyron方程
化学反应等温方程
化学反应
精馏,结晶
萃取 膜分离 吸附
25
吸附势,吸附热 渗透压
分配定律
麦克斯韦尔曾说过:“如果热力学只是 在解释蒸汽机的功能,固然可以满足工业家 所需要的,但是若蒸气工业过去了,热力学 就过去了”。是Gibbs将热力学引入了化学, 使热力学在化学中焕发了强有力的生命力, 同时使化学成为一门有理论指导的科学。
* * p
p RT dp RT ln pO p
27
* = + RT ln ( p / p)
:p = 100 kPa 时的化学势,又称为标准化学势
对于理想气体混合物,其中的 B 组分,有:
pB GB G RT ln $ p
即: 在恒T, p下,物质总是从化学势高的一相向化学势低 的一相转移,两相化学势相等时达到平衡。
22
关于化学势
十九世纪五、六十年代,热力学基本规律已经明
确起来,但一些热力学概念还较模糊,数学处理很麻
烦,不能用来解决稍微复杂一点的问题———如化学 反应的方向问题。 基本热力学方程是热力学理论框架的中心,然而 第三章中的基本方程只适用于组成不变的封闭系统。
下标 nB表示:各组分的摩尔数都没改变; 下标 nc 表示:除B组外,其它各组分的摩尔数都未变
7
定义:
X XB n B T , P ,nC
XB 偏摩尔量
意义: 在恒T、p及其它组分都不变时,加入极微量dnB的B
组分后,引起系统 X 性质的改变 dX。 或: 在恒T、p下,于足够大量的某一定组成的溶液中加入
真实气体混合物中B组分,相应地有:
p
pB RT B ( g )= +RT ln $ VB dp p p 0
$ B
p
上式适用于:
注意:p为总压
1)纯理想气体及其混合物,(VB – RT/p) 积分项为0; 2)纯真实气体,VB 变为Vm* ;
1) 偏摩尔量 摩尔量
Vm
R
P
Q VB*
VC*
2) 偏摩尔量随组成而变
B
xC
C
16
5. 偏摩尔量之间的关系
纯组分系统热力学函数之间的关系也适用于 偏摩尔函数, 如:
H B U B pVB , AB U B TSB
GB H B TSB AB pVB GB VB p T ,nB GB , SB T p ,nB
G 其中只有 n B
为偏摩尔量 T , p ,nC
20
2. 化学势判据
T , p 恒定时:(W =0) dG 0
自发 平衡
多相、多组分时:
dG dG dG L
B dnB μB dnB L
B B
B dnB
证:在 P 点 V总=xBVB + xCVC
Q VB*
P
VC*
Q xB xC 1 Vt VB (VC VB ) xC
B
xC Q=VB , R=VC
C
P点的切线方程:( y = b + m x )
R-Q V总=Q+ xC , 相应地 1
15
4. 偏摩尔量与摩尔量的差别
由截距法及图可看出其差别
V nAVA nBVB
V nBVB
