特殊平行四边形折叠问题
专题02特殊平行四边形中的折叠问题教师版

专题02 特殊平行四边形中的折叠问题【典型例题】1.(2020·河北定州初三二模)如图,正方形ABCD 中,AB =6,G 是BC 的中点.将△ABG 沿AG 对折至△AFG ,延长GF 交DC 于点E ,则DE 的长是 ( )A .1B .1.5C .2D .2.5【解析】连接AE ,∵AB =AD =AF ,∠D =∠AFE =90°,由折叠的性质得:Rt △ABG ≌Rt △AFG ,在△AFE 和△ADE 中,∵AE =AE ,AD =AF ,∠D =∠AFE ,∴Rt △AFE ≌Rt △ADE ,∴EF =DE ,设DE =FE =x ,则CG =3,EC =6−x .在直角△ECG 中,根据勾股定理,得:(6−x )2+9=(x +3)2,解得x =2.则DE =2. 2.(2019·全国初三单元测试)如图,在菱形ABCD 中,AE ⊥BC 于E ,将△ABE 沿AE 所在直线翻折得△AEF ,若AB =2,∠B =45°,则△AEF 与菱形ABCD 重叠部分(阴影部分)的面积为( ).A .2B .C .D .【解析】∵在边长为2的菱形ABCD 中,∠B =45°,AE 为BC 边上的高,∴AE ,由折叠的性质可知,△ABF 为等腰直角三角形,∴S △ABF =12AB •AF =2,S △ABE =1,∴CF =BF -BC =-2,∵AB ∥CD ,∴∠GCF =∠B =45°,又由折叠的性质知,∠F =∠B =45°,∴CG =GF =2∴S △CGF =12GC •GF =3-,∴重叠部分的面积为:2-1-(3-)=2,故选D . 3.(2020·全国)如图,把矩形纸片ABCD 沿EF 折叠后,使得点D 与点B 重合,点C 落在点C ′的位置上.(1)折叠后,DC 的对应线段是 ,CF 的对应线段是 ;(2)若∠1=50°,求∠2、∠3的度数;(3)若AB =8,DE =10,求CF 的长度.【答案】(1)由折叠的性质可得:折叠后,DC 的对应线段是BC ′,CF 的对应线段是C ′F ;故答案为:BC ′,C ′F . (2)由折叠的性质可得:∠2=∠BEF ,∵AD ∥BC ,∴∠1=∠2=50°.∴∠2=∠BEF =50°,∴∠3=180°﹣50°﹣50°=80°; 故答案为:50°,80°(3)∵AB =8,DE =10,∴BE =10,∴AE 6,∴AD =BC =6+10=16,∵∠1=∠BEF =50°,∴BF =BE =10, ∴CF =BC ﹣BF =16﹣10=6.故答案为:6【专题训练】一、选择题1.(2020·海南临高)如图,在矩形纸片ABCD 中,AB =3,点E 在边BC 上,将△ABE 沿直线AE 折叠,点B 恰好落在对角线AC 上的点F 处,若∠EAC =∠ECA ,则AC 的长是( )A .B .6C .4D .5【解析】∵将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,∴AF=AB,∠AFE=∠B=90°,∴EF⊥AC,∵∠EAC=∠ECA,∴AE=CE,∴AF=CF,∴AC=2AB=6,选B.2.(2020·全国)如图,将一张长方形纸片ABCD按图中方式折叠,若AE=3,AB=4,BE=5,则重叠部分的面积为( )A.6B.8C.10D.12【解析】解:∵长方形纸片ABCD按图中那样折叠,∴∠1=∠2,而∠1=∠3,∴∠2=∠3,∴ED=EB=5,∵矩形ABCD中,∠A=90°∴重叠部分△BDE的面积=12DE×AB=12×5×4=10.故选:C..3.(2020·全国)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为()A.3B.4C.6D.8【解析】解:将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,由折叠特性可得,CD=BC′=AB,∠FC′B=∠EAB=90°,∠EBC′=∠ABC=90°,∵∠ABE+∠EBF=∠C′BF+∠EBF=90°∴∠ABE=∠C′BF在△BAE和△BC′F中,∴△BAE≌△BC′F(ASA),∵△ABE的周长=AB+AE+EB=AB+AE+ED=AB+AD=1+2=3,△ABE和△BC′F的周长=2△ABE的周长=2×3=6.故选C.4.(2020·新疆昌吉初三一模)如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN,则线段CN的长是()A.3cm B.4cm C.5cm D.6cm【解析】设CN=xcm,则DN=(8﹣x)cm,由折叠的性质知EN=DN=(8﹣x)cm,而EC=12BC=4cm,在Rt△ECN中,由勾股定理可知EN2=EC2+CN2,即(8﹣x)2=16+x2,整理得16x=48,所以x=3.故选:A.5.(2019·河北遵化初三一模)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为()A.78°B.75°C.60°D.45°【解析】试题分析:连接BD,∵四边形ABCD为菱形,∠A=60°,∴△ABD为等边三角形,∠ADC=120°,∠C=60°.∵P为AB的中点,∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°.∴∠PDC=90°.∴由折叠的性质得到∠CDE=∠PDE=45°.在△DEC中,.故选B.6.(2020·全国)如图,已知四边形ABCD 是边长为6的菱形,且∠BAD =120°,点E ,F 分别在AB ,BC 边上,将菱形沿EF 折叠,点B 正好落在AD 边的点G 处.若EG ⊥AC ,则FG 的长为( )A .3B .6C .D .【解析】如图,设AC 与EG 交于点O ,FG 交AC 于点H .∵ 四边形ABCD 是菱形,∠BAD =120°,∴60B D ∠=∠=︒, ∴ABC ACD 、是等边三角形.∴60CAD B ∠=∠=︒.∵EG AC ⊥,∴90GOH ∠=︒.∵60EGF B ∠=∠=︒,∴30OHG ∠=︒,∴18090AGH CAD OHG ∠=︒-∠-∠=︒,∴FG AD ⊥,∴FG 是菱形ABCD 的高,即为等边三角形ABC 的高,∴ =C .7.(2020·兴仁市真武山街道办事处黔龙学校)如图,把一个矩形纸片ABCD 沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置,若∠EFB =65°,则∠AED ′为( )。
平行四边形折叠问题

平行四边形折叠问题
平行四边形折叠问题是一个几何问题,它涉及到将一个平行四边形沿着其边界线进行折叠,使得一些特定的条件得到满足。
具体来说,给定一个平行四边形,我们可以将它的两个相对边折叠在一起,形成一个三角形或者一个平行四边形。
问题的目标通常是找到能够实现特定条件的折叠方式。
有一些常见的平行四边形折叠问题,例如:
1. 平行四边形的对角线折叠问题:给定一个平行四边形,我们需要找到一种折叠方式,使得对角线之间的夹角保持不变。
2. 平行四边形的三角形折叠问题:给定一个平行四边形,我们需要找到一种折叠方式,使得折叠后形成的是一个三角形。
3. 平行四边形的正方形折叠问题:给定一个平行四边形,我们需要找到一种折叠方式,使得折叠后形成的是一个正方形。
对于这些问题,一般可以通过几何知识和数学推理来解决。
可以使用平行四边形的性质、角度关系、对称性等来推导出正确的折叠方式。
专题07 特殊的平行四边形中折叠问题(解析版)八年级数学下册期末综合复习专题提优训练(人教版)

2020-2021学年八年级数学下册期末综合复习专题提优训练(人教版)专题07 特殊的平行四边形中折叠问题【典型例题】1.如图所示,长方形纸片ABCD 的长AD =8cm ,宽AB =4cm ,将其折叠,使点D 与点B 重合. (1)求证:BE =BF ;(2)求折叠后DE 的长;(2)求以折痕EF 为边的正方形面积.【答案】(1)证明见解析;(2)5cm ;(3)20cm 2.【详解】(1)在长方形ABCD 中,AD //BC ,DEF EFB ∴∠=∠,DEF BEF ∠=∠,EFB BEF ∴∠=∠,∴ BE =BF ,设DE =x cm ,则BE =x cm ,AE =()8x cm -,在Rt ABE △中,由勾股定理()22248x x +-=, ∴5x =,即DE 的长为5cm .(2)过E 作EH BF ⊥于点H ,则EH =AB =4,BH =AE =3,∴ HF =BF -BH =5-3=2,∴2222420EF =+=,∴ 以EF 为边长的正方形的面积为220cm .【专题训练】一、选择题1.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为4,120B ∠=︒,则EF 的值是( )A B .2 C .D .4【答案】B【分析】 根据菱形的性质证明∴ABD 是等边三角形,求得BD =4,再证明EF 是∴ABD 的中位线即可得到结论.【详解】解:连接AC ,BD∴四边形ABCD 是菱形,∴AC BD ⊥,BD 平分∴ABC ,4AB BC CD DA ==== ∴∴111206022ABD ABC ︒=∠=⨯=︒ ∴AB AD =∴∴ABD 是等边三角形,∴ 4.BD =由折叠的性质得:EF AO ⊥,EF 平分AO ,又∴BD AC ⊥,∴//EF BD∴EF 为∴ABD 的中位线, ∴122EF BD == 故选:B .【点睛】本题考查了折叠性质,菱形性质,主要考查学生综合运用定理进行推理和计算的能力.2.如图,把正方形纸片ABCD 沿对边中点所在的直线对折后展开,折痕为MN ,再过点C 折叠纸片,使点C 落在MN 上的点F 处,折痕为BE .若AB 的长为1,则FM 的长为( )A .1B .2C .2D .12【答案】B【分析】根据翻折得到1FB BC ==,12BM =,在Rt BFM 中,可利用勾股定理求出FM 的值. 【详解】 解:四边形ABCD 是正方形, 1AB BC ∴==,由折叠的性质可知,1FB BC ==,1122BM AB ==, 在Rt BFM 中,由勾股定理得:2FM ===. 故选:B .【点睛】本题考查翻折、正方形的性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键. 3.将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF .若AB =3,则BC 的长为( )A .1B .2CD 【答案】D【分析】 根据菱形及矩形的性质可得到∴BAC 的度数,从而根据直角三角形的性质求得BC 的长.【详解】解:∴四边形AECF 为菱形,∴∴FCO =∴ECO ,EC =AE ,由折叠的性质可知,∴ECO =∴BCE ,又∴FCO +∴ECO +∴BCE =90°,∴∴FCO =∴ECO =∴BCE =30°,在Rt ∴EBC 中,EC =2EB ,又∴EC =AE ,AB =AE +EB =3,∴EB=1,EC=2,∴Rt∴BCE中,BC ,故选:D.【点睛】本题主要考查了菱形的性质以及矩形的性质,解决问题的关键是根据折叠以及菱形的性质发现特殊角,根据30°的直角三角形中各边之间的关系求得BC的长.4.如图,在正方形ABCD中,AB=6,点E,F分别在边AB,CD上,∴EFC=120°.若将四边形EBCF沿EF 折叠,点B恰好落在AD边上,则AE的长度为()A.2B C D.1【答案】A【分析】依据正方形的性质以及折叠的性质,即可得到∴AEB'=60°,再根据含30°角的直角三角形的性质,即可得到AE的长.【详解】解:∴四边形ABCD是正方形,∴AB∴CD,∴A=90°,∴∴BEF=180°-∴EFC=60°,∴将四边形EBCF沿EF折叠,点B恰好落在AD边上,∴∴BEF=∴FEB'=60°,BE=B'E,∴∴AEB'=180°-∴BEF-∴FEB'=60°,∴∴AB'E=30°,∴B'E=2AE,设AE=x,则B'E=2x=BE,∴AB=6,∴x+2x=6,解得x=2.故选:A.【点睛】本题考查了正方形的性质,折叠的性质,含30°角的直角三角形的性质等知识点,能综合性运用性质进行推理是解此题的关键.5.如图,菱形ABCD中,∴ABC=60°,AB=4,E是边AD上一动点,将∴CDE沿CE折叠,得到∴CFE,则∴BCF 面积的最大值是()A.8B.C.16D.【答案】A【分析】由三角形底边BC是定长,所以当∴BCF的高最大时,∴BCF的面积最大,即当FC∴BC时,三角形有最大面积.【详解】解:在菱形ABCD中,BC=CD=AB=4又∴将∴CDE沿CE折叠,得到∴CFE,∴FC=CD=4由此,∴BCF的底边BC是定长,所以当∴BCF的高最大时,∴BCF的面积最大,即当FC∴BC时,三角形有最大面积∴∴BCF面积的最大值是11448 22BC FC=⨯⨯=故选:A.【点睛】本题考查菱形的性质和折叠的性质,掌握三角形面积的计算方法和菱形的性质正确推理计算是解题关键. 6.如图,有一张矩形纸条ABCD ,AB =5cm ,BC =2cm ,点M ,N 分别在边AB ,CD 上,CN =1cm .现将四边形BCNM 沿MN 折叠,使点B ,C 分别落在点B ′,C ′上.在点M 从点A 运动到点B 的过程中,若边MB '与边CD 交于点E ,则点E 相应运动的路径长为( )cm .A 32B .52CD .32【答案】A【分析】探究点E 的运动轨迹,寻找特殊位置解决问题即可.【详解】解:如图1中,∴四边形ABCD 是矩形,∴AB ∴CD ,∴∴1=∴3,由翻折的性质可知:∴1=∴2,BM =MB ′,∴∴2=∴3,∴MB ′=NB ′,∴NB '==cm ),∴BM NB '==(cm ).如图2中,当点M 与A 重合时,同理可得:AE =EN ,设AE =EN =x cm ,在Rt ∴ADE 中,则有2222(4)=+-x x ,解得x =52, ∴53422DE =-=(cm ), 如图3中,当点M 运动到MB ′∴AB 时,DE ′的值最大,DE ′=5-1-2=2(cm ),如图4中,当点M 运动到点B ′落在CD 时,DB ′(即DE ″)51(4=-=(cm ),∴点E 的运动轨迹E →E ′→E ″,运动路径3322(4)22EE E B '''=+=-+-=(cm ). 故选:A .【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考填空题中的压轴题.二、填空题7.如图a 是长方形纸带,∴DEF =22°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∴CFE 的度数是________°.【答案】114°【分析】根据两直线平行,内错角相等可得∴EFB=∴DEF,再根据翻折的性质,图c中∴EFB处重叠3层,然后根据∴CFE=180°-3∴EFB代入数据行计算即可得解【详解】∴∴DEF =22°长方形ABCD的对边AD//BC∴∴EFB=∴DEF=22°由折叠,∴EFB处折叠了3层∴∴CFE=180° -3∴EFB=180°—3 × 22°=114°故答案为:114°【点睛】本题考查折叠问题,熟知折叠中蕴含着全等,有相等的角与边进行分析是关键.8.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC 边上的点F处,则CE=_____.【答案】4 3【分析】由折叠求出BF和CF,再设CF=x,在∴CEF中用勾股定理列方程即可得答案.【详解】解:∴矩形ABCD沿AE折叠,AB=3,AD=5,∴AF=AD=5,∴B=∴C=90°,DE=EF,∴BF4,∴CF=BC﹣BF=1,设CE=x,则EF=DE=3﹣x,在Rt∴CEF中,CE2+CF2=EF2,∴x2+12=(3﹣x)2,解得x=43,∴CE=43.故答案为:43.【点睛】本题考查矩形性质及勾股定理应用等知识,解题的关键是在Rt∴CEF中用勾股定理列方程.9.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若32NEC FMN∠=︒∠=,_____︒.【答案】119【分析】根据正方形的性质得到∴A=∴C=∴D=90°,根据折叠的性质得到∴F=∴A=90°,∴FEN=∴C=90°,∴DNM=∴ENM,根据平角的定义得到∴ENM=12(180°-∴ENC)=12(180°-58°)=61°,根据四边形的内角和即可得到结论.【详解】解:∴四边形ABCD是正方形,∴∴A=∴C=∴D=90°,∴将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,∴∴F=∴A=90°,∴FEN=∴D=90°,∴DNM=∴ENM,∴∴NEC=32°,∴∴ENC=58°,∴∴ENM=12(180°-∴ENC)=12(180°-58°)=61°,∴∴FMN =360°-90°-90°-61°=119°,故答案为:119.【点睛】本题考查了角的计算,翻折变换的问题,折叠问题其实质是轴对称,对应线段相等,对应角相等,找到相等的角是解决本题的关键.10.对角线长分别为6和8的菱形ABCD 如图所示,点O 为对角线的交点,过点O 折叠菱形,使B ,B '两点重合,MN 是折痕.若1B M '=,则CN 的长为_______.【答案】4【分析】连接AC 、BD ,如图,利用菱形的性质得132OC AC ==,142OD BD ==,90COD ∠=︒,再利用勾股定理计算出5CD =,接着证明OBM ODN ∆≅∆得到DN BM =,然后根据折叠的性质得1BM BM'==,从而有1DN =,于是计算CD DN -即可.【详解】解:连接AC 、BD ,如图,点O 为菱形ABCD 的对角线的交点,132OC AC ∴==,142OD BD ==,90COD ∠=︒, 在Rt COD ∆中,5CD ==,//AB CD ,MBO NDO ∴∠=∠,在OBM ∆和ODN ∆中MBO NDO OB ODBOM DON ∠=∠⎧⎪=⎨⎪∠=∠⎩, OBM ODN ∴∆≅∆,DN BM ∴=,过点O 折叠菱形,使B ,B ′两点重合,MN 是折痕,1BM BM'∴==, 1DN ∴=,514CN CD DN ∴=-=-=,故答案为:4.【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了菱形的性质.11.如图,矩形ABCD 中,6,8AB BC ==,点E 是BC 边上一点,连接AE ,把ABE △沿AE 折叠,使点B 落在点F 处,当CEF △为直角三角形时,CF 的长为________.【答案】4或【分析】当CEF △为直角三角形时,有两种情况:①当点F 落在矩形内部时,如答图1所示.连接AC ,先利用勾股定理计算出10AC =,根据折叠的性质得90AFE B ∠=∠=︒,而当CEF △为直角三角形时,只能得到90EFC ∠=︒,所以点A 、F 、C 共线,即B 沿AE 折叠,使点B 落在对角线AC 上的点F 处,则,6EB EF AB AF ===,可计算出CF ; ②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形,根据勾股定理计算出CF .【详解】解:当CEF △为直角三角形时,有两种情况:①当点F 落在矩形内部时,如答图1所示.连接AC ,在Rt ABC 中,6,8AB BC ==,∴10AC =,∴B 沿AE 折叠,使点B 落在点F 处,∴90AFE B ∠=∠=︒,当CEF △为直角三角形时,只能得到90EFC ∠=︒,∴点A 、F 、C 共线,即B 沿AE 折叠,使点B 落在对角线AC 上的点F 处,∴,6EB EF AB AF ===,∴1064CF =-=;②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形,∴6,862BE AB CE ===-=,∴CF =综上所述,CF 的长为4或.故答案为:4或.【点睛】本题考查折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.解题的关键是要注意本题有两种情况,需要分类讨论,避免漏解.12.如图,在正方形ABCD 中,12AB =,点E 在边CD 上,3CD DE =.将ADE 沿AE 对折至AFE △,延长EF 交边BC 于点G ,连接AG ,CF .有下列结论:①ABG AFG ≅;②BG GC =;③//AG CF ;④6FGC S =△.其中正确的结论是__________.(填序号)【答案】①②③【分析】由正方形的性质和折叠的性质得出AB =AF ,∴AFG =90°,由HL 证明Rt ∴ABG ∴Rt ∴AFG ,得出①正确;设BG =FG =x ,则CG =12-x .由勾股定理得出方程,解方程求出BG ,得出GC ,即可得出②正确;由全等三角形的性质和三角形内角和定理得出∴AGB =∴AGF =∴GFC =∴GCF ,得出AG ∴CF ,即可得出③正确;通过计算三角形的面积得出④错误;即可得出结果.【详解】解:①正确.理由如下:四边形ABCD 是正方形,12AB BC CD AD ∴====,90B GCE D ∠=∠=∠=︒,由折叠的性质得:AF AD =,90AFE D ∠=∠=︒,90AFG ∴∠=︒,AB AF =,在Rt ABG △和Rt AFG △中,AG AG AB AF=⎧⎨=⎩, Rt Rt (HL)ABG AFG ∴≅△△;②正确.理由如下: 由题意得:143EF DE CD ===,设BG FG x ==,则12CG x =-. 在直角ECG 中,根据勾股定理,得222(12)8(4)x x -+=+,解得:6x =,6BG ∴=,1266GC ∴=-=,BG GC ∴=;③正确.理由如下:CG BG =,BG GF =,CG GF ∴=,FGC ∴△是等腰三角形,GFC GCF ∠=∠.又∴Rt Rt ABG AFG ≅△△,AGB AGF ∴∠=∠,218022+==︒-=+==∠∠∠∠∠∠∠∠AGB AGF AGB FGC GFC GCF GFC GCF ,AGB AGF GFC GCF ∴∠=∠=∠=∠,//AG CF ∴;④错误;理由如下:11682422GCE S GC CE =⋅=⨯⨯=△, 6GF =,4EF =,GFC 和FCE △等高,:3:2GFC FCE S S ∴=△△,37224655GFC S ∴=⨯=≠△. 故④不正确.∴正确的个数有①②③.故答案为:①②③.【点睛】本题考查的是翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算等知识;本题综合性强,有一定的难度.三、解答题13.如图,矩形纸片 ABCD 的长 AD =10cm ,宽 AB =5cm ,将其折叠,使点 D 与点 B 重合,那么折叠后AE 的长是多少?【答案】154cm【分析】设DE =x ,根据折叠的性质可得BE =x ,表示出AE =10−x ,然后在Rt ∴ABE 中,利用勾股定理列式计算即可得解.【详解】解:设 DE =xcm ,则BE =xcm ,∴AE =(10﹣x )cm ,∴在 Rt ∴ABE 中,AB 2+AE 2=BE 2,∴52+(10﹣x )2=x 2,∴解得:x =254, ∴AE =10﹣254=154cm 答:折叠后AE 的长是154cm . 【点睛】本题考查了矩形的性质,折叠的性质,勾股定理的应用,根据勾股定理列出方程是解题的关键. 14.如图,在菱形ABCD 中,120ABC ∠=︒,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B D ,重合),折痕为EF ,若26DG BG ==,,求AF 的长.【答案】AF 的长为267. 【分析】 作FH BD ⊥于点H ,通过菱形的性质和折叠的性质证明ABD △为等边三角形,设AF x =,则FG x =,8DF x =-,在Rt DFH 中,利用特殊角表示出DH ,FH ,最后在Rt FHG 中利用勾股定理即可求解.【详解】如图,作FH BD ⊥于点H .由折叠的性质可知,FG FA =.由题意,得8BD DG BG =+=.∴ 四边形ABCD 是菱形. ∴1602AD AB ABD CBD ABC =∠=∠=∠=︒,, ∴ABD △为等边三角形,∴8AD BD ==.设AF x =,则FG x =,8DF x =-,在Rt DFH 中,∴60FDH ∠=︒,∴()118422DH x x =-=-,)822FH x x =-=, ∴1222HG DH x =-=-. 在Rt FHG 中,222FG FH GH =+,即222122x x x ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪⎝⎭⎝⎭, 解得267x =, ∴AF 的长为267. 【点睛】本题主要考查菱形的性质,含30°的直角三角形的性质,折叠的性质,勾股定理,掌握菱形的性质,勾股定理及方程的思想是解题的关键.15.如图,正方形纸片ABCD 的边长为6,点E 、F 分别在边BC 、CD 上,将AB 、AD 分别沿AE 、AF 折叠,点B 、D 恰好都在点G 处,已知2BE =,求FC 的长.【答案】3【分析】因为正方形ABCD 的边长为6,由图形折叠可得=2BE EG =,624EC =-=,6DF FG x ==-, 再利用勾股定理进行计算即可.【详解】解:设FC x =,由图形折叠可得=2BE EG =,624EC =-=,6DF FG x ==-,在直角ECF ∆中,∴222EF EC CF =+,∴222(426)x x +-=+,解得3x =,∴3=FC .【点睛】此题考查了折叠问题,解题的关键是找准不变的线段,利用勾股定理求解线段.16.如图,AC 为矩形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF 折叠,使点D 落在AC 上的点N 处.(1)求证:四边形AECF 是平行四边形;(2)若AB =6,AC =10,求四边形AECF 的面积.【答案】(1)证明见解析;(2)30.【解析】试题分析:(1)首先由矩形的性质和折叠的性质证得AB =CD ,AD ∴BC ,∴ANF =90°,∴CME =90°,易得AN =CM ,可得∴ANF∴∴CME(ASA),由平行四边形的判定定理可得结论;(2)由AB=6,AC=10,可得BC=8,设CE=x,则EM=8-x,CM=10-6=4,在Rt∴CEM中,利用勾股定理可解得x,由平行四边形的面积公式可得结果.试题解析:(1)证明:∴折叠,∴AM=AB,CN=CD,∴FNC=∴D=90°,∴AME=∴B=90°,∴∴ANF=90°,∴CME=90°,∴四边形ABCD为矩形,∴AB=CD,AD∴BC,∴AM=CN,∴AM﹣MN=CN﹣MN,即AN=CM,在∴ANF和∴CME中,{FAN EMC AN CMANF CME∠=∠=∠=∠,∴∴ANF∴∴CME(ASA),∴AF=CE,又∴AF∴CE,∴四边形AECF是平行四边形;(2)解:∴AB=6,AC=10,∴BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt∴CEM中,(8﹣x)2+42=x2,解得:x=5,∴四边形AECF的面积的面积为:EC•AB=5×6=30.17.如图1.将矩形ABCD沿DE折叠使点A落在A'处,然后将矩形展平,沿EF折叠使点A落在折痕DE 上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处,如图2.(1)求证:EG=CH;(2)已知AF∴CDE的面积.【答案】(1)见解析;(2)∴CDE的面积=4+【分析】(1)由折叠的性质及矩形的性质可得AD AE BC ==,AE EG =,BC CH =,可得结论;(2)由折叠的性质可知45ADE ∠=︒,90FGE A ∠=∠=︒,AF =,那么DG =,利用勾股定理求出2DF =,于是可得2AD AF DF =+=;再利用AAS 证明AEF BCE △≌△,得到AF BE =,于是22AB AE BE =+=+=,即可求解.【详解】(1)证明:四边形ABCD 是矩形, AD BC ∴=,将矩形ABCD 沿DE 折叠使点A 落在A '处,AD A D '∴=,AE A E '=,45ADE A DE '∠=∠=︒,45ADE AED ∴∠=∠=︒,AD AE ∴=,AE BC ∴=,由折叠的性质可得AE EG =,BC CH =,EG CH ∴=;(2)45ADE ∠=︒,90FGE A ∠=∠=︒,AFDG ∴=2DF =,2AD AF DF ∴=+;由折叠知AEF GEF ∠=∠,BEC HEC ∠=∠,90GEF HEC ∴∠+∠=︒,90AEF BEC ∠+∠=︒,90∠+∠=︒AEF AFE ,BEC AFE ∴∠=∠,在AEF 与BCE 中,90AFE BEC A B AE BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ()AEF BCE AAS ∴△≌△,AF BE∴=,22AB AE BE CD ∴=+=+==,CDE ∴的面积11(2(24 22CD AD=⨯⨯=⨯+⨯=+【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了全等三角形的判定与性质,矩形的性质,勾股定理等知识.18.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF 折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)当∴BAE为多少度时,四边形AECF是菱形?请说明理由.【答案】(1)证明见解析(2)当∴BAE=30°时,四边形AECF是菱形【分析】(1)首先证明∴ABE∴∴CDF,则DF=BE,然后可得到AF=EC,依据一组对边平行且相等四边形是平行四边形可证明AECF是平行四边形;(2)由折叠性质得到∴BAE=∴CAE=30°,求得∴ACE=90°-30°=60°,即∴CAE=∴ACE,得到EA=EC,于是得到结论.【详解】(1)∴四边形ABCD为矩形,∴AB=CD,AD∴BC,∴B=∴D=90°,∴BAC=∴DCA.由翻折的性质可知:∴EAB=12∴BAC,∴DCF=12∴DCA.∴∴EAB=∴DCF.在∴ABE和∴CDF中B DAB CDEAB DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴∴ABE∴∴CDF(ASA),∴DF=BE.∴AF=EC.又∴AF∴EC,∴四边形AECF是平行四边形;(2)当∴BAE=30°时,四边形AECF是菱形,理由:由折叠可知,∴BAE=∴CAE=30°,∴∴B=90°,∴∴ACE=90°-30°=60°,即∴CAE=∴ACE,∴EA=EC,∴四边形AECF是平行四边形,∴四边形AECF是菱形.【点睛】本题主要考查了菱形的判定,全等三角形的判定和性质,折叠的性质、矩形的性质、平行四边形的判定定理和勾股定理等,综合运用各定理是解答此题的关键.19.探究:如图①点E、F分别在正方形ABCD的边BC、CD上,连结AE、AF、EF,将∴ABE、∴ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与∴AEF完全重合的三角形.若BE=2,DF=3,求AB的长;拓展:如图②点E、F分别在四边形BACD的边BC、CD上,且∴B=∴D=90°.连结AE、AF、EF将∴ABE、∴ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与∴AEF完全重合的三角形.若∴EAF=30°,AB=4,则∴ECF的周长是.【答案】探究:AB=6;拓展:.3【分析】探究:设:正方形的边长为a,则EC=a-2,CF=a-3,则由勾股定理得:EF2=EC2+CF2,即可求解;拓展:证明∴ABC∴∴ADC,∴BAE+∴DAF=∴EAF=30°,则∴BAD=60°,∴BAC=∴DAC=12(∴BAD)=30°,CD=BC=ABtan∴BAC,即可求解.【详解】探究:设:正方形的边长为a,则EC=a﹣2,CF=a﹣3,则EF=BE+DF=5,则EF2=EC2+CF2,即:25=(a﹣2)2+(a﹣3)2,解得:a=6或﹣1(舍去﹣1),故AB=6;拓展:由题意得:AB=CD=4,连接AC,∴AB=CD,AC=AC,∴∴ABC∴∴ADC,∴BC=CD,∴BAC=∴DAC,∴点E、F分别在四边形BACD的边BC、CD上,故:∴BAE+∴DAF=∴EAF=30°,则∴BAD=60°,∴∴BAC=∴DAC=12(∴BAD)=30°,CD=BC=ABtan∴BAC=4∴ECF的周长=EF+EC+FC=AE+FD+EC+FC=AC+CD=2CD,故答案为:3. 【点睛】 本题考查的是翻折变换(折叠问题),涉及到正方形的性质、三角形全等等,其中(2)证明∴ABC ∴∴ADC ,是本题解题的关键.20.(1)如图1,将矩形ABCD 折叠,使AB 落在对角线AC 上,折痕为AE ,点B 落在点1B 处,若66DAC ∠=︒,则BAE ∠= º;(2)小丽手中有一张矩形纸片,9AB =,4=AD .她准备按如下两种方式进行折叠:①如图2,点F 在这张矩形纸片的边CD 上,将纸片折叠,使点D 落在边AB 上的点1D 处,折痕为FG ,若5DF =,求AG 的长;②如图3,点H 在这张矩形纸片的边AB 上,将纸片折叠,使HA 落在射线HC 上,折痕为HK ,点A ,D 分别落在1A ,2D 处,若73DK =,求1AC 的长. 【答案】(1)12;(2)①AG =32;②13A C = 【分析】 (1)由折叠的性质可得∴BAE =∴CAE =12°;(2)①过点F 作FH ∴AB 于H ,可证四边形DFHA 是矩形,可得AD =FH =4,由勾股定理可求D 1H =3,由勾股定理可求AG 的长;②首先证明CK =CH ,利用勾股定理求出BH ,可得AH ,再利用翻折不变性,可知AH =A 1H ,由此即可解决问题.【详解】解:(1)∴∴DAC =66°,∴∴CAB =24°∴将矩形ABCD 折叠,使AB 落在对角线AC 上,∴∴BAE=∴CAE=12°故答案为:12;(2)如图2,过点F作FH∴AB于H,∴∴D=∴A=90°,FH∴AB∴四边形DFHA是矩形∴AD=FH=4,∴将纸片ABCD折叠∴DF=D1F=5,DG=D1G,∴D 1H2225163FH,∴AD1=2∴AG2+D1A2=D1G2,∴AG2+4=(4−AG)2,∴AG=32;②∴DK=73,CD=9,∴CK=9−73=203,∴四边形ABCD是矩形,∴DC∴AB,∴∴CKH=∴AHK,由翻折不变性可知,∴AHK=∴CHK,∴∴CKH=∴CHK,∴CK=CH=203,∴CB=AD=4,∴B=90°,∴在Rt∴CDF中,BH22400161693BC,∴AH=AB−BH=11 3,由翻折不变性可知,AH=A1H=11 3,∴A1C=CH−A1H=3.【点睛】本题考查四边形综合题、矩形的性质、翻折变换、勾股定理,解题的关键是灵活运用所学知识解决问题,学会利用翻折不变性解决问题,属于中考压轴题.。
九年级数学 第一章 特殊平行四边形专题课堂(二)特殊平行四边形中的折叠问题

证明:由折叠可知△MOP≌△MNP,∴OM=MN,∠OMP=∠NMP =21 ∠OMN=30°=∠B,∠MOP=∠MNP=90°,∴∠BOP=∠MOP =90°.∵OP=OP,∴△MOP≌△BOP(AAS).∴MO=BO=21 BM.∴MN =21 BM
FG=AF= 2 ,∴DG=FG= 2 ,DF= DG2+FG2 =2,∴AD=AF+DF = 2 +2.由折叠可知∠AEF=∠GEF,∠BEC=∠HEC,∴∠AEF+∠BEC =90°,∵∠AEF+∠AFE=90°,∴∠BEC=∠AFE,在△AEF 与△BCE
∠AFE=∠BEC, 中,∠A=∠B=90°, ∴△AEF≌△BCE(AAS),∴BE=AF= 2 ,∴AB
则 AC 的长是( B )
A.3 3 B.6 C.4 D.5
第7题图
8.如图,将边长为 6 cm 的正方形纸片 ABCD 折叠,使点 D 落在 AB 边中点 E 处,点 C 落在点 Q 处,折痕为 FH,则线段 AF 的长是___94____cm.
第8题图
9.如图,正方形纸片ABCD的边长AB=12,E是DC上一点,CE=5,折叠 正方形纸片使点B和点E重合,折痕为FG,则FG的长为____1_3_.
折痕BE,BF,则∠EBF的大小为( C)
A.15° B.30° C.45° D.60°
第2题图
3.如图,在菱形ABCD中,∠A=120°,E是AD上的点,沿BE折叠△ABE,
点A恰好落在BD上的点F处,连接CF,那么∠BFC的度数是( ) C
A.60° B.70° C.75° D.80°
第3题图
6.如图,将矩形 ABCD 沿 EF 折叠,使顶点 C 恰好落在 AB 边的中
点 C′上.若 AB=6,BC=9,则 BF 的长为( A )
湘教版2019年度八年级数学下册第2章专题训练二特殊平行四边形中的折叠问题练习含答案

专题训练(二) 特殊平行四边形中的折叠问题►类型之一把一个顶点折叠到一条边上1.2017·天水如图2-ZT-1,在矩形ABCD中,∠DAC=65°,E是CD上一点,BE交AC于点F,将△BCE 沿BE折叠,点C恰好落在AB边上的点C′处,则∠AFC′=________°.图2-ZT-12.如图2-ZT-2,将矩形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为9,△ECF的周长为3,则矩形ABCD的周长为________.图2-ZT-23.如图2-ZT-3,在矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC 上的点F处.若AE=5,BF=3,求CD的长.图2-ZT-34.某校八年级(3)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20 cm,宽AB=16 cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处.请你根据①②步骤计算EC的长.5.如图2-ZT-4,已知矩形纸片ABCD,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G,F,AE与FG交于点O.求证:A,G,E,F四点构成的四边形是菱形.图2-ZT-4►类型之二把一条边折叠到对角线上6.如图2-ZT-5,在矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )图2-ZT-5A.3 B.4 C.5 D.67.准备一张矩形纸片ABCD,按如图2-ZT-6所示操作:将△ABE沿BE翻折,使点A落在对角线BD上的点M处,将△CDF沿DF翻折,使点C落在对角线BD上的点N处.(1)求证:四边形BFDE是平行四边形;(2)若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.图2-ZT-6►类型之三把一个顶点折叠到另一个顶点上8.如图2-ZT-7,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若AB =1,BC=2,则△ABE和△BC′F的周长之和为( )图2-ZT-7A.3 B.4 C.6 D.89.把一张矩形纸片ABCD按图2-ZT-8的所示方式折叠,使顶点B和点D重合,折痕为EF.若AB=3 cm,BC=5 cm,则重叠部分△DEF的面积为________cm2.图2-ZT-810.如图2-ZT-9,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,求折痕EF的长.图2-ZT-9►类型之四沿一条直线折叠11.如图2-ZT-10,已知正方形ABCD的对角线长为2 2,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为( )图2-ZT-10A.8 2 B.4 2 C.8 D.612.如图2-ZT-11,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在的直线折叠得到△EB′F,连接B′D,则B′D的最小值是( )图2-ZT-11A.2 10-2 B.6C.2 13-2 D.413.2017·宁夏如图2-ZT-12,将平行四边形ABCD沿对角线BD折叠,使点A落在点A′处.若∠1=∠2=50°,则∠A′的度数为________.图2-ZT-1214.2017·西宁如图2-ZT-13,将平行四边形ABCD沿EF对折,使点A落在点C处.若∠A=60°,AD =4,AB=6,则AE的长为________.图2-ZT-1315.如图2-ZT-14,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使点B落在点P处,折痕为EC,连接AP并延长交CD于点F,连接BP.(1)求证:四边形AECF为平行四边形;(2)若△AEP是等边三角形,求证:△APB≌△EPC;(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.图2-ZT-14详解详析1.[答案] 40 2.[答案] 12[解析] 由折叠的性质知,AF =AB ,EF =BE.所以矩形的周长等于△AFD 和△CFE 的周长的和.故矩形ABCD 的周长为12.3.解:根据折叠的性质,得EF =AE =5.根据矩形的性质,得∠B =90°.在Rt △BEF 中,∠B =90°,EF =5,BF =3,根据勾股定理,得BE =EF 2-BF 2=52-32=4,∴CD =AB =AE +BE =5+4=9.4.解:设EC =x cm ,则EF =DE =(16-x) cm.由题意得AF =AD =20 cm.在Rt △ABF 中,BF =AF 2-AB 2=12 cm ,FC =BC -BF =20-12=8(cm).在Rt △EFC 中,EF 2=FC 2+EC 2,即(16-x)2=82+x 2, 解得x =6,∴EC 的长为6 cm.5.证明:连接AF.由折叠的性质,得AG =EG ,∠AGF =∠EGF. ∵DC ∥AB ,∴∠EFG =∠AGF , ∴∠EFG =∠EGF , ∴EF =EG. 又∵AG =EG , ∴EF =AG ,∴四边形AGEF 是平行四边形. 又∵AG =EG ,∴平行四边形AGEF 是菱形,即A ,G ,E ,F 四点构成的四边形是菱形. 6.D7.解:(1)证明:∵四边形ABCD 是矩形, ∴AB ∥CD ,∴∠ABD =∠CDB.又由折叠的性质,知∠ABE =∠EBD ,∠CDF = ∠FDB ,∴∠EBD =∠FDB , ∴EB ∥DF. 又∵ED ∥BF ,∴四边形BFDE 是平行四边形. (2)∵四边形BFDE 是菱形,∴BE =ED =BF ,∠EBD =∠FBD =∠ABE. ∵四边形ABCD 是矩形, ∴AD =BC ,∠ABC =90°, ∴∠ABE =30°.∵∠A =90°,AB =2,∴AE =2 33,BF =BE =2AE =4 33,∴菱形BFDE 的面积为4 33×2=8 33.8.C9.[答案] 5110[解析] 设ED =x cm ,则根据折叠和矩形的性质,得A′E=AE =(5-x) cm ,A ′D =AB =3 cm. 根据勾股定理,得ED 2=A′E 2+A′D 2,即x 2=(5-x)2+32,解得x =175,∴S △DEF =12×175×3=5110(cm 2).10.解:设BE =x ,则CE =BC -BE =16-x.∵沿EF 翻折后点C 与点A 重合, ∴AE =CE =16-x.在Rt △ABE 中,AB 2+BE 2=AE 2,即82+x 2=(16-x)2, 解得x =6,∴AE =16-6=10.由翻折的性质,得∠AEF =∠CEF. ∵矩形ABCD 的对边AD ∥BC , ∴∠AFE =∠CEF , ∴∠AEF =∠AFE , ∴AE =AF =10.过点E 作EH ⊥AD 于点H ,则四边形ABEH 是矩形, ∴EH =AB =8,AH =BE =6, ∴FH =AF -AH =10-6=4.在Rt △EFH 中,EF =EH 2+FH 2=82+42=4 5. 11.C 12.A13.[答案] 105°[解析] 在平行四边形ABCD 中,AD ∥BC ,得∠DBC =∠ADB.又由折叠,得∠A =∠A′,∠BDA ′=∠BDA ,所以∠DBC =∠BDA′.根据三角形的一个外角等于和它不相邻的两个内角和,以及∠1=50°,可得∠DBC =25°,则∠ABC =∠2+∠DBC =75°.因为AD ∥BC ,所以∠A +∠ABC =180°,所以∠A =105°,∴∠A ′=105°.14.[答案] 194[解析] 作CH ⊥AB 于点H ,则BH =2,CH =2 3,则AH =8.在Rt △ACH 中,设AE =CE =a ,则EH =8-a ,由CH 2+EH 2=CE 2,得(8-a)2+(2 3)2=a 2,解得a =194,即AE =194.15.解:(1)证明:在矩形ABCD 中,AB ∥DC.∵E 为AB 的中点, ∴AE =BE.又由翻折,知EC ⊥BP ,EP =EB =AE , ∴∠EAP =∠EPA ,∠EPB =∠EBP.在△ABP 中,∠EAP +∠EPA +∠EPB +∠EBP =180°, ∴∠EPA +∠EPB =∠APB =90°, ∴EC ∥AF ,∴四边形AECF 为平行四边形. (2)证明:∵△AEP 是等边三角形,∴AP =EP =AE ,∠PAB =∠AEP =∠APE =60°, ∴∠PEC =∠BEC =60°, ∴∠PAB =∠PEC =60°.由(1)与题可知APB =∠EPC =90°, ∴△APB ≌△EPC.(3)∵AB =6,BC =4,E 是AB 边的中点, ∴AE =BE =12AB =3.在Rt △BEC 中,EC =BE 2+BC 2=5, ∵四边形AECF 为平行四边形, ∴AF =EC =5.如图,设CE 与BP 交于点H.∵BE ·BC =EC·BH, ∴BH =125,∴PH =BH =125,∴BP =245.在Rt △BPA 中,AP =BA 2-BP 2=185,∴PF =75.过点C 作CG ⊥AF 交AF 的延长线于点G , ∴CG =PH =125,∴△CPF 的面积S =12PF·CG=12×75×125=4225.。
中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案

中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一 单选题1.如图 在矩形纸片ABCD 中 将BCD △沿BD 折叠 C 点落在C '处 则图中共有全等三角形( )A .2对B .3对C .4对D .5对2.如图 对折矩形纸片ABCD 使AB 与DC 重合得到折痕EF 将纸片展平 再一次折叠 使点D 落到EF 上点G 处 并使折痕经过点A 展平纸片后DAG ∠的大小为( )A .40︒B .60︒C .55︒D .75︒3.如图 在矩形ABCD 中 5AB = 8BC = 点E 和F 是边BC 上的两点 连结AE DF 、 将ABE 和CDF 沿AE DF 、折叠后 点B 和点C 重合于点M 则EF 的长是( )A .2.5B .3C .1.5D .44.如图 在矩形纸片ABCD 中 已知8AD = 折叠纸片使AB 边与对角线AC 重合 点B 落在点F 处 折痕为AE 且3EF = 则ABE 的面积为( )A .10B .9C .8D .75.如图 在矩形OABC 中 9OA = 15AB = E 是BC 上一点 沿AE 折叠 使点B 恰好落在x 轴的点D 处.E 点坐标是( )A .()5,15B .()3,15C .()15,2D .()15,4 6.如图 在矩形ABCD 中 点E 是边CD 的中点 将ADE 沿AE 折叠后得到AFE △ 且点F 在矩形ABCD 的内部 将AF 延长后交边BC 于点G 且45CG GB = 则AB AD 的值为( )A .43B .56C .1D .77.如图 把矩形纸片ABCD 沿对角线BD 折叠 设重叠部分为EBD △ 则下列结论不一定成立的是( )A .AB CD = B .BAE DCE ≌△△C .EB ED = D .30ABE ∠=︒ 8.如图 在一张菱形纸片ABCD 中 2AB = 30B ∠=︒ 点E 在BC 边上(不与B C 重合)将ABE 沿直线AE 折叠得到AFE △ 连接BF EF DF 有以下四个结论:AE EF =① 105BFD ∠=︒② ③当AE BC ⊥时 FD AC = ④当FE 平分AFB ∠时 则23FD = 其中正确的结论个数是( )A .1B .2C .3D .4二 填空题9.如图 正方形纸片ABCD 的边长为12 E 是边CD 上一点 连接AE 折叠该纸片 使点A 落在AE 上的点G 并使折痕经过点B 得到折痕BF 点F 在AD 上.若5DE = 则GE 的长为 .10.将一张长方形纸片ABCD 按如图所示方式折叠 AE AF 为折痕 点B D 折叠后的对应点分别为B' 'D 若''4B AD ∠=︒ 则EAF ∠的度数为 .11.如图 在长方形ABCD 中 3AD = 2AB = 点F 是AB 上一点 1AF = 点E 是BC 上一动点 连接EF 将BEF △沿EF 折叠 记点B 的对应点为点B ' 连接DB ' 则FB DB '+'的最小值是 .12.如图 在矩形ABCD 中 5AB = 8AD = 边AD 上有一动点P 连结BP 把ABP沿BP 折叠当点A 的对应点A '刚好落在BC 的垂直平分线上时 点A '到AD 的距离为 .13.如图所示 在完全重合放置的两张矩形纸片ABCD 中 8AB = 16BC = 将上面的矩形纸片折叠 使点C 与点A 重合 折痕为EF 点D 的对应点为点G 连接DG 则图中阴影部分的面积为 .三 解答题14.如图 正方形纸片ABCD 的边长12AB = E 是DC 上一点 5CE = 折叠正方形纸片 使点B 和点E 重合 折痕为FG 试求FG 的长.15.如图 把一张长方形纸片ABCD 折叠起来 使其对角顶点A 与C 重合 D 与G 重合 若长方形的长BC 为8 宽AB 为4(1)求DE 的长(2)求阴影部分的面积.16.如图1 将矩形纸片()ABCD AD AB >折叠 使点C 刚好落在线段AD 上 且折痕分别与边BC AD 相交 设折叠后点C D 的对应点分别为点G H 折痕分别与边BC AD 相交于点E F .(1)求证:四边形CEGF 是菱形(2)如图2 若3AB = 9BC = 当点G 与点A 重合时 求折痕EF 的长.17.如图 在四边形纸片ABCD 中 AD BC ∥ AD CD > 将纸片沿过点D 的直线折叠 使点C 落在AD 上的点C '处 折痕DE 交BC 于点E 连接C E '.(1)请确定四边形CDC E '的形状 并说明理由(2)若30BCD ∠=︒ 2CE = 过点C '作C F BC '⊥于F 连接CC '交DE 于点M 连接FM : ①四边形CDC E '的面积为①2FM = .18.已知矩形ABCD 中 4AB = 6AD = 点P 是边AD 的中点.(1)如图1 连接BP 并延长 与CD 的延长线交干点F 问:线段CF 上是否存在点Q 使得PFQ △是以PF 为腰的等腰三角形 若存在 请直接写出DQ 的长 若不存在 请说明理由.(2)①如图2 把矩形ABCD 沿直线MN 折叠 使点B 落在点D 上 直线MN 与AD BD BC 、、的交点分别为M H N 求折痕MN 的长.①如图3:在①的条件下 以点A 为原点 分别以矩形ABCD 的两条边AD AB 、所在的直线为x 轴和y 轴建立平面直角坐标系 若点R 在x 轴上 在平面内是否存在点S 使以R M N S 为顶点的四边形是菱形?若存在 请求出点S 的坐标 若不存在 请说明理由.(3)如图4:若点E 为CD 边上的一个动点 连结PE 以PE 为边向下方作等边PEG △ 连结AG 则AG 的最小值是______.(请直接写出答案)参考答案:1.C2.B3.B4.B5.D6.A7.D8.B9.491310.43︒111012.213.72514.解:如图 过点F 作FM BC ⊥ 垂足为M 连接BE .①四边形ABCD 为正方形①AB BC CD AD === 90A ABC C D ∠=∠=∠=∠=︒①90A ABC BMF ===︒∠∠∠①四边形ABMF 为矩形①12MF AB BC ===①将正方形纸片ABCD 折叠 使点B 落在边CD 上的点E 折痕为FG ①90C FMG ∠=∠=︒ BE FG ⊥①90BNG C ∠=∠=︒①90MGF CBE BEC CBE ∠+∠=∠+∠=︒ ①MGF CEB ∠=∠在FMG 和BCE 中 MGF CEB FMG C FM BC ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS FMG BCE ≌①MG CE =.又①5CE =①5MG =.在Rt MFG 中 根据勾股定理得13FG == 即FG 的长是13.15.(1)设DE EG x == 则8AE x =- 在Rt AEG △中 222AG EG AE +=所以()22168x x +=-解得:3x =即3DE =(2)过点G 作GM AD ⊥于M 则1122AG GE AE GM ⨯=⨯4AG AB == 5AE = 3GE = 所以1143522GM ⨯⨯=⨯⨯所以125GM = 所以11825CED S GM DE =⨯=△. 16.解:(1)证明:①四边形ABCD 是矩形 ①AD ①BC①①GFE =①FEC①图形翻折后点G 与点C 重合 EF 为折线 ①①GEF =①FEC FG =FC EG =EC ①①GFE =①FEG①GF =GE①GE =EC =CF =FG①四边形CEGF 为菱形(2)当G 与A 重合时 由折叠的性质得AE =CE ①①B =90° AB =3 BC =9 BE =9-CE ①Rt ①ABE 中 AE 2=AB 2+BE 2即CE 2=32+(9-CE )2解得 CE =5.AC 222239310AB BC ++=由(1)知四边形CEGF 为菱形 ①12CEGF S EF AC CE AB =⨯=⨯菱形 ①10310EF == 17.(1)解:四边形CDC E '是菱形 理由如下: 根据折叠的性质可得:CD C D C DE CDE '∠=∠ CE C E '= ①AD BC ∥①C DE CED '∠=∠①CDE CED ∠=∠①CD CE =①CD C D C E CE ''===①四边形CDC E '为菱形(2)①①四边形CDC E '是菱形 ①2C E CE '== C E CD '∥ CM C M '= ①30C EF DCB '∠=∠=︒ ①C F BE '⊥ ①112C F C E ''== EF F '=①四边形CDC E '的面积212CE C F '=⨯=⨯= 故答案为:2①①EF = 2CE =①2CF =①(2222218C C C F CF ''=+=+=+①C F BC CM C M ''⊥=, ①12FM C C '=①22124FM C C '==故答案为:2 18.(1)解:存在 理由如下: 四边形ABCD 是矩形 90A ADC ∴∠=∠=︒ AB CD = 90FDP ∴∠=︒点P 是边AD 的中点 AP DP ∴=又APB DPF ∠=∠ ()ASA ABP DFP ∴△≌△ PF PB ∴= AB DF = 4,6AB AD ==4DF AB ∴== 132AP PD AD === 90A ∠=︒在Rt ABP 中:2222345PB AB AP +=+=5PF ∴=PFQ △为等腰三角形 以PF 为腰的等腰三角形分为两种情形: ①当PF PQ =时 此时点Q 与点C 重合 故4DQ DC == ①当FP FQ =时 如图:5PF = 5FQ = FD =4541DQ FQ FD =-=-=综合①① DQ 的长为:4或1(2)解:①如图:连接BM DN根据题意可知:MN 垂直平分BD ,MN BD BH DH ∴⊥= ,NB ND MB MD == 四边形ABCD 是矩形AD BN ∴MDH HBN ∴∠=∠ 又MHD NHB ∠=∠MHD NHB ∴△≌△MH HN ∴= MD NB =∴四边形MBND 是菱形设AM b = 则6MD MB b ==-在Rt AMB △中222BM AM AB =+即:222(6)4b b -=+ 解得:53b = 5513,6333AM BM ∴==-= 在Rt △ABD 中BD 12BH BD ∴=MH BD ⊥∴在Rt MHB △中MH ==2MN MH ∴== ①建立平面直角坐标系如图:由①知:53AM = 133BN MD MB ===4AB = MN = ①5130433M N ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,,, R M N S 为顶点的四边形是菱形 点R 在x 轴上当MR 为对角线时 MR NS ⊥,M R 都在x 轴上 ∴,N S 关于x 轴对称 1343S ⎛⎫∴ ⎪⎝⎭, 当MN 为对角线时 MN RS ⊥ 由(2)知 四边形MBND 是菱形 则S 与点B 重合 ∴此时(0,4)S -当MS 为对角线时 则MR SN ∥ MR SN =MN = 13(,4)3N -①1343S ⎛⎫- ⎪ ⎪⎝⎭综上可知 存在点S 使得以R M N S 为顶点的四边形是菱形 点S 坐标为:134134⎫--⎪⎪⎝⎭ 134134⎫+-⎪⎪⎝⎭ 13,43⎛⎫⎪⎝⎭ (0,4)- (3)解:如图:分别以PD PC 为边向下方作等边,PDF PCH △△ 过点F 作FI AD ⊥垂足为I 连接AF HF P 为AD 中点 ∴132AP PD AD ===PDF △为等边三角形1322PI PD ∴== 60DPF ∠=︒ PD PF =PA PF = 60DPF ∠=︒30PAF PFA ∴∠=∠=︒120APF ∴∠=︒92AI AP PI ∴=+=点E 为CD 边上的一个动点 以PE 为边向下方作等边PEG △ 当点E 与点D 重合时 点G 与点F 重合 当点E 与点C 重合时 点G 与点H 重合 ∴点G 在线段FH 上运动 当AG HF ⊥时 AG 最小 PEG △为等边三角形60EPG ∴∠=︒ PE PG =60 FPG FPE FPE EPD∴∠+∠=∠+∠=︒FPG DPE∴∠=∠∴FPG DPE△≌△PDE PFG∴∠=∠90PDE∠=︒∴90PFG∠=︒PF FH∴⊥当AG HF⊥时AG PF120,30APF PAF∠=︒∠=︒18012060PAG∴∠=︒-︒=︒603030 FAG PAG PAF∠=∠-∠=︒-︒=︒IAF GAF∴∠=∠FI AD⊥90AIF∴=︒在AFI和AFI中AIF AGFAF AFFAG FAI∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASAAFI AFI≌AG AI∴=∴当AG HF⊥时92AG AI==故答案为:92.。
北师大版九年级数学上学期题型全攻略专题01 特殊平行四边形中的折叠问题全梳理(解析版)

专题01特殊平行四边形中的折叠问题全梳理目录【方法归纳】 (1)【考法一、三角形翻折问题】 (1)【考法二、四边形翻折问题】 (16)【课后练习】 (28)【方法归纳】1.折叠的基本性质:翻折前后对应的边与角相等;2.对于翻折都不确定的情况,注意分类讨论,避免漏掉解;3.方程思想:灵活设未知数,通过勾股定理建立方程,解出答案4.综合性:把折叠性质与四边形性质相结合,建立边角之间的关系。
【考法一、矩形翻折问题】例.如图,在矩形OABC 中8AB =,4BC =,点D 为对角线OB 中点,点E 在OC 所在的直线上运动,连结DE ,把ODE 沿DE 翻折,点O 的对应点为点F ,连结BF .(1)当点F 在OC 下方时(如图1),求证:DE BF ∥.(2)当点F 落在矩形的对称轴上时,求EF 的长.(3)是否存在点E ,使得以D ,E ,F ,B 为顶点的四边形是平行四边形?若存在,求OE 的长;若不存在,请说明理由.当四边形△中,在Rt ABO222=+=OB AB AO8BC OC⊥∴∥,且D为OBDM BC中位线,DM∴为OCBOE EF BD DO ∴==,,25OE OD ∴==;如图,当四边形DEBF 为平行四边形时,DF OD BE ∴=,25BE ∴=,在Rt BEC △中,EC =826OE ∴=-=;DF OD BD DF == ,25BE OD ∴==,在Rt BCE 中,2CE BE =-在矩形ABCD 中,8AB =,6AD =,现将纸片折叠,点D 的对应点记为点P ,折痕为EF (点E 、F 是折痕与矩形的边的交点),再将纸片还原.【初步思考】(1)若点P落在矩形ABCD的边AB上(如图①)当点P与点A重合时,DEF∠=_____︒,当点E与点A重合时,DEF∠=______︒;【深入探究】(2)若点P落在矩形ABCD的内部(如图②),且点E、F分别在AD、DC边上,AP的最小值是______;【拓展延伸】(3)若点F与点C重合,点E在AD上,射线BA与射线FP交于点M(如图③)在各种不同的折叠位置中,是否存在某一情况,使得线段AM与线段DE的长度相等?若存在,请求出线段AE的长度;若不存在,请说明理由.【答案】(1)90;45(2)2(3)存在某一情况,使得线段AM与线段DE的长度相等,线段AE的长度为65或4211【分析】(1)当点P与点A重合时,画出图形可得结论;当点E与点A重合时,则EF平分DAB∠,即可得出答案;(2)当F与C重合,点P在对角线AC上时,AP有最小值,根据折叠的性质求8CD PC==,由勾股定理求10AC=,即可得出结果;(3)分两种情况根据全等三角形的判定和性质以及勾股定理解答即可.【详解】解:(1)四边形ABCD是矩形,90DAB D∴∠=∠=︒,当点P与点A重合时,EF是AD的中垂线,90DEF∴∠=︒,当点E与点A重合时,如图,则EF平分DAB∠,==,则AF=设DF PF x当A,P,F在一直线上时,当x最大为8时,AP最小值为四边形ABCD是矩形,A ADC B∴∠=∠=∠=90∠由折叠的性质得:EPM ,AM DE=∴=,AM EP四边形ABCD是矩形,∴∠=∠=∠=︒,DAM ADC B90∠=∠由折叠的性质得:EPC ADC ∴∠=∠=︒,GAM GPE90变式2.【问题情境】折纸操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘,下面是折纸过程.【动手操作】步骤1:对折矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,展平纸片;步骤2:点M 为边AD 上任意一点(与点A ,D 不重合),ABM 沿BM 折叠得到A BM '△,折痕BM 交EF 于点N .【问题探究】(1)如图1,当点A 的对称点A '落在EF 上时,连接AN .求证:四边形ANA M '为菱形;(2)已知2BC AB =,继续对折矩形纸片ABCD ,使AB 与DC 重合,折痕GH 与EF 交于点O .将ABM 沿BM 折叠,连接MO ,若点A 的对称点A '恰好落在线段MO 上,此时2AM =.①尺规作图:请在图2中用直尺和圆规,作点A 的对称点A '(保留作图痕迹,不写作法);②求AB 的长度;【拓展迁移】如图3,在矩形纸片ABCD 的边AB 上取一点P ,折叠纸片,使P ,B 两点重合,展平纸片,得到折痕EF ;点B '为EF 上任意一点(与点E ,F 不重合),折叠纸片使B ,B '两点重合,得到折痕l 及点P 的对应点P ',折痕l 交EF 于点K ,展平纸片,连接BP ',KP '.(3)猜想P B K ∠'与BC P '∠的数量关系,并证明.【答案】(1)见解析;(2)①见解析;②6AB =;(3)3P BC BP K ''∠∠=,理由见解析【分析】(1)根据折叠可得出NA NA '=,MA MA '=,AMB A MB '∠=∠,,证明AD EF ∥,利用平行线的性质得出AMB MNA '∠=∠,则A MB MNA ''∠=∠,利用等角对等边得出MA NA ''=,即可得证;(2)①以M 为圆心,MA 为半径画弧交MO 于A '即可;②利用折叠的性质,矩形的判定与性质可得出2BH AB A B AG OG '====,证明()HL OA B OHB ' ≌,得出OA OH OG '==,在Rt MGO △中,根据勾股定理,可求出OG ,进而求出AB ;(3)连接PK ,BK ,延长BK 交P B ''于点M ,可证明EB B MBB ''≌ ,得出BE B M '=,90FEB BMB '∠=∠=︒,由折叠可得BK PK P K B K ''===,利用等边对等角和三线合一的性质可得出P BK BP K ''∠=∠,KBB KB B ''∠=∠,MB MP ''=,利用线段垂直平分线的性质BP BB ''=,利用三线合一性质可得出P BK KBB ''∠=∠,则P BK BP K KBB KB B ''''∠=∠=∠=∠,由(1)中BC EF ∥,可得出B BC KB B ''∠=∠,即可得证.【详解】(1)证明:连接AA ',∵ABM 沿BM 折叠,得到A BM '△,∴BM 垂直平分AA ',∴NA NA '=,MA MA '=,AMB A MB '∠=∠,由折叠可知:AEF BEF ∠=∠,∵180AEF BEF ∠+∠=︒,∴90BEF ∠=︒,∵四边形ABCD 为矩形,∴90DAB ∠=︒,∴90BEF DAB ∠=∠=︒,∴AD EF ∥,∴AMB MNA '∠=∠,∴A MB MNA ''∠=∠,∴MA NA ''=,∴MA NA NA MA ''===,∴四边形ANA M '为菱形;点A'即为所求,解:连接BO,由折叠可知:AB A B'=,MA 由(1)得90∠=∠=︒GHB HGA∵l为折痕,∴P B B PBB'''∠=∠,BP B P''=,l ∴KP KP'=,=,KB KB'∴KBB KB B''∠=∠,∵B B BB''=,∴BE B M '=,90FEB BMB '∠=∠=︒,由折叠可知:KP KB =,EP EB =,90FEB ∠=︒,∴KP KB '=,KP KB ''=∴P BK BP K ''∠=∠,MB MP ''=∴BP BB ''=,∴P BK BP K KBB KB B ''''∠=∠=∠=∠,由(1)可知BC EF ∥,∴B BC KB B ''∠=∠,∴3P BC BP K ''∠=∠.【点睛】本题考查了矩形与折叠,等腰三角形的判定与性质,全等三角形的判定与性质,线段垂直平分线的性质等知识,明确题意,灵活运用所学知识解决问题是解题的关键.变式3.如图1,在矩形ABCD 中,点E 是边AB 上的一点,连接DE .(1)若DE 平分ADC ∠,点G 是CD 上的一点,连接EC ,EG ,且EC EG =.过点C 作CQ EG⊥于Q ,CQ 延长线交ED 于H ,过点H 作HP CD ⊥于P ,如图.①填空:AED △的形状是______三角形;②求证:PHC BEC△△≌(2)将图1的矩形ABCD 画在纸上,若DE 平分ADC ∠,沿过点E 的直线折叠,点C 恰好落在AD 上的点C '处,点B 落在点B '处,得到折痕EF ,B C ''交AB 于点M ,如图.求证:MC ME '=.(3)如图,延长DE 交CB 的延长线于点K 使得AB BK =,此时恰好BE BC =,连接AC 交DK 于点J ,连接BJ .请证明:KJ AJ BJ >+.【答案】(1)①等腰直角;②见解析(2)见解析(3)见解析【分析】(1)①根据矩形的性质和角平分线的性质可得45AED ADE ∠=∠=︒,进而得出结果;②可证得BCE PCH ∠=∠,EC HC =,90HPC B ︒∠=∠=,进而得出结论;(2)连接C E ',可证得Rt Rt EC A C EB ''' ≌,可得C EA EC B '''∠=∠,根据等角对等边即可得出结论;(3)在线段EK 上取点I ,使得KI AJ =,连接BI ,可证KBE ABC ≌△△,得BKE BAC ∠=∠,在证KBI ABJ ≌△△,得KBI ABJ ∠=∠,90IBJ KBA ︒∠=∠=,得出IJ BJ >,进一步得出结论.【详解】(1)① 四边形ABCD 是矩形,∴90A ADC ∠=∠=︒,DE 平分ADC ∠,∴1452ADE ADC ∠=∠=︒,∴9045AED ADE ∠=︒-∠=︒,∴AED ADE ∠=∠,∴AE DE =,∴AED △等腰直角三角形,故答案为:等腰直角②证明:如图,过点E 作EW CD ⊥于W .EC EG = ,EGC ECG ∴∠=∠,CH EG ⊥ ,90HCP EGC ∴∠+∠=︒,90BCE ECG ∠︒∠+= ,BCE PCH ∴∠=∠,45EDW DEW ∠︒∠== ,45EHC EDW PCH PCH ∴∠=∠︒+∠=+∠,DEC DEW CEW ∠=∠+∠,EW BC ∥,BCE CEW PCH ∴∠=∠=∠,DEC EHC ∴∠=∠,EC HC ∴=,90HPC B ∠=∠=︒PHC BEC ∴△△≌.(2)证明:如图,连接C E ',由(1)知,AED △为等腰直角三角形,AD AE ∴=,四边形ABCD 是矩形,AD BC ∴=,90EAC B '∠=∠=︒,由折叠知,B C BC ''=,B B '∠=∠,AE B C ''∴=,EAC B ''∠=∠,又EC C E ''=,在Rt EC A '△和Rt C EB ''△中,EC C E ''=,AE B C ''=,∴Rt Rt EC A C EB ''' ≌,C EA EC B '''∴∠=∠,MC ME '∴=.(3)如图,在线段EK 上取点I ,使得KI AJ =,连接BI ,在AJB 与KIB △中,BK AB =,ABC ABK ∠=∠,BE BC =,KBE ABC ∴△△≌,BKE BAC ∴∠=∠.KI AJ = ,BK AB =,BKE BAC ∠=∠,KBI ABJ ∴△△≌,KBI ABJ ∴∠=∠,90IBJ IBA ABJ IBA KBI KBA ∴∠=∠+∠=∠+∠=∠=︒,IBJ ∴△为直角三角形,IJ BJ ∴>,KJ AJ BJ ∴>+.【点睛】本题是四边形综合题,考查了等腰直角三角形的判定和性质,矩形的性质,全等三角形的判定和性质,轴对称的性质,准确添加常用辅助线,构造特殊三角形和证明全等三角形是解本题的关键。
小专题(九) 特殊平行四边形中的折叠与最值问题

第5题图
5.如图,在矩形纸片 中, , ,点 为 边上的动点(点 不与点 , 重合).将纸片沿 折叠,则 的最小值为___.
8
第6题图
6.如图,正方形纸片 的边长为4, , , 分别是边 , , 上的一点,将纸片沿 折叠,使点 恰好落在 边的中点 处,点 的对应点为点 ,则折痕 的长为_____.
解:作点 关于直线 的对称点 (易知点 在 上),连接 ,交 于点 ,连接 ,则 , .
.此时点 即为所求的使 最小的点.∵正方形 的边长为4, , 为 的中点, , . .
过点 作 于点 ,则 .∵四边形 是正方形, .∴四边形 是矩形. , . .∴在 中, . 的最小值为 .
第3题图
3.如图,在矩形纸片 中, ,将 向内翻折,点 落在 上,记为 ,折痕为 .若将 沿 向内翻折,点 恰好落在 上,记为 ,则下列结论不正确的是( )
D
A. B. C. D.
第4题图
4.(2022·雅安)如图,把一张矩形纸片沿对角线折叠.若 , ,那么阴影部分的面积为_ __.B来自A. B. C. D.
第2题图
2.(2021·遵义)如图,将矩形纸片 的两个直角进行折叠,使 , 恰好落在对角线 上, , 分别是 , 的对应点,折痕分别为 , .若 , ,则线段 的长是( )
D
A. B. C. D.
【例2】(2022·河南改编)(教材P64“数学活动”变式)如图,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平;再次折叠纸片,使点 落在
上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你猜想 的度数是多少,并证明你的结论.
解:猜想: .证明:连接 .∵直线 是 的垂直平分线,点 在 上,
北师大版数学九年级上册:第一章 特殊平行四边形——特殊平行四边形的折叠问题(含答案)
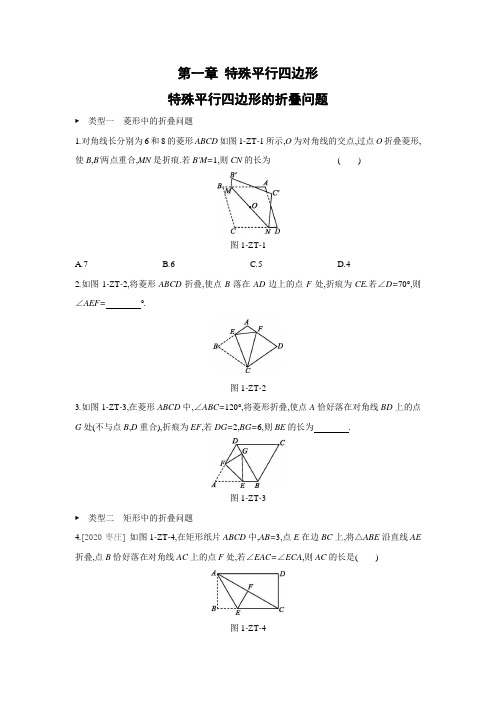
第一章特殊平行四边形特殊平行四边形的折叠问题▶类型一菱形中的折叠问题1.对角线长分别为6和8的菱形ABCD如图1-ZT-1所示,O为对角线的交点,过点O折叠菱形,使B,B'两点重合,MN是折痕.若B'M=1,则CN的长为()图1-ZT-1A.7B.6C.5D.42.如图1-ZT-2,将菱形ABCD折叠,使点B落在AD边上的点F处,折痕为CE.若∠D=70°,则∠AEF=°.图1-ZT-23.如图1-ZT-3,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与点B,D重合),折痕为EF,若DG=2,BG=6,则BE的长为.图1-ZT-3▶类型二矩形中的折叠问题4.[2020·枣庄]如图1-ZT-4,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE 折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是()图1-ZT-4A.3√3B.4C.5D.65.[2020·青岛]如图1-ZT-5,将矩形ABCD折叠,使点C和点A重合,折痕为EF,EF与AC交于点O.若AE=5,BF=3,则AO的长为()图1-ZT-5A.√5B.32√5C.2√5D.4√56.[2020·衢州]如图1-ZT-6,把一张矩形纸片ABCD按所示方法进行两次折叠,得到等腰直角三角形BEF,若BC=1,则AB的长度为()图1-ZT-6A.√2B.√2+12C.√5+12D.437.如图1-ZT-7,在矩形ABCD中,AB=6,BC=8,E为AD的中点,F为AB上一点,将△AEF沿EF 折叠后,点A恰好落到CF上的点G处,求折痕EF的长.图1-ZT-7▶类型三正方形中的折叠问题8.[2020·广东]如图1-ZT-8,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上的点B'处,则BE的长度为()图1-ZT-8A.1B.√2C.√3D.29.如图1-ZT-9,在平面直角坐标系中,正方形OABC的顶点A的坐标为(0,2),E是线段BC上一点,且∠AEB=67.5°,沿AE折叠正方形后点B落在点F处,那么点F的坐标为.图1-ZT-9参考答案1.D [解析] 连接AC ,BD ,如图.∵O 为菱形ABCD 对角线的交点,∴OC=12AC=3,OB=OD=12BD=4,∠COD=90°.在Rt △COD 中,CD=√32+42=5. ∵AB ∥CD ,∴∠MBO=∠NDO. 又∵∠BOM=∠DON ,OB=OD , ∴△OBM ≌△ODN ,∴DN=BM.∵过点O 折叠菱形ABCD ,使B ,B'两点重合,MN 是折痕, ∴BM=B'M=1,∴DN=1, ∴CN=CD-DN=5-1=4.故选D .2.30 [解析] ∵四边形ABCD 是菱形,∠D=70°, ∴∠B=70°,∠A=110°.∵将菱形ABCD 折叠,使点B 落在AD 边上的点F 处, ∴∠B=∠EFC=70°,CF=BC=CD , 则∠CFD=∠D=70°, ∴∠AFE=180°-70°-70°=40°,∴∠AEF=180°-∠A-∠AFE=30°.故答案为30. 3.2.8[解析] 如图,过点E 作EH ⊥BD 于点H.由折叠的性质可知EG=EA. 由题意得BD=DG+BG=8. ∵四边形ABCD 是菱形,∴AD=AB ,∠ABD=∠CBD=12∠ABC=60°,∴△ABD 为等边三角形,∠BEH=30°, ∴AB=BD=8.设BE=x ,则EG=AE=8-x.在Rt △EHB 中,BH=12x ,EH=√BE 2-BH 2=√32x.在Rt △EHG 中,EG 2=EH 2+GH 2, 即(8-x )2=(√32x )2+(6-12x )2,解得x=2.8,即BE=2.8. 故答案为2.8.4.D [解析] ∵将△ABE 沿直线AE 折叠,点B 恰好落在对角线AC 上的点F 处, ∴AF=AB ,∠AFE=∠B=90°,∴EF ⊥AC , ∵∠EAC=∠ECA ,∴AE=CE ,∴AF=CF , ∴AC=2AB=6. 故选D .5.C [解析] ∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠EFC=∠AEF . 由折叠得∠EFC=∠AFE ,∴∠AFE=∠AEF ,∴AE=AF=5. 由折叠得FC=AF ,OA=OC ,∴BC=3+5=8. 在Rt △ABF 中,AB=√AF 2-BF 2=√52-32=4. 在Rt △ABC 中,AC=√AB 2+BC 2=√42+82=4√5, ∴OA=OC=2√5.故选C .6.A [解析] 由折叠补全图形如图所示.∵四边形ABCD 是矩形,∴∠ADC=∠A=90°,AD=BC=1,CD=AB. 由第一次折叠得∠ADE=12∠ADC=45°, ∴∠AED=∠ADE=45°, ∴AE=AD=1.在Rt △ADE 中,根据勾股定理,得DE=√2AD=√2. 由第二次折叠知CD=DE=√2, ∴AB=√2. 故选A .7.解:∵四边形ABCD 是矩形,∴AB=CD=6,BC=AD=8,∠A=∠D=90°.如图,连接CE.∵E 为AD 的中点, ∴AE=DE=4.由折叠可得AE=GE ,∠EGF=∠A=90°, ∴DE=GE.又∵∠D=90°,∴∠EGC=∠D=90°. 又∵CE=CE.∴Rt △CDE ≌Rt △CGE (HL), ∴CD=CG=6.设AF=x ,则GF=x ,BF=6-x ,则CF=6+x. 在Rt △BCF 中,BF 2+BC 2=CF 2, 即(6-x )2+82=(6+x )2,解得x=83,∴AF=83.在Rt △AEF 中,EF=√AE 2+AF 2=√42+(83) 2=43√13. 8.D [解析] ∵四边形ABCD 是正方形, ∴AB ∥CD ,∠A=90°, ∴∠EFD=∠BEF=60°.∵将四边形EBCF 沿EF 折叠,点B 恰好落在AD 边上, ∴∠BEF=∠FEB'=60°,BE=B'E , ∴∠AEB'=180°-∠BEF-∠FEB'=60°, ∴∠AB'E=30°,∴B'E=2AE. 设BE=x ,则B'E=x ,AE=3-x ,∴2(3-x)=x,解得x=2.故选D.9.(-√2,2-√2)[解析] 如图,过点F作FD⊥CO于点D,FG⊥AO于点G.∵∠AEB=67.5°,沿AE折叠后点B落在点F处,∴∠BAE=∠EAF=22.5°,AF=AB=2,∴∠F AG=45°,∴FG=AG=√2,∴GO=2-√2,∴点F的坐标为(-√2,2-√2).故答案为(-√2,2-√2).。
特殊平行四边形折叠问题

特殊平行四边形折叠问题1. 引言哎呀,今天咱们聊聊一个看起来挺抽象的话题——特殊平行四边形折叠问题。
乍一听,有点像数学课上那些让人抓耳挠腮的难题,对吧?但别担心,咱们不打算像学霸那样死抠公式,而是轻松聊聊其中的乐趣和奇妙之处。
生活就像一块折纸,咱们要学会把它折得既美观又实用!2. 特殊平行四边形的魅力2.1 什么是特殊平行四边形?特殊平行四边形,其实就是那种边平行、角度相等的家伙。
想象一下,一个长方形或是正方形,这些都是特殊平行四边形的好朋友。
简单来说,它们的结构稳定得像一座大厦,让人一眼看去就觉得安心。
就像人们总说的,“万事开头难”,这类形状的基础知识可一点都不难。
2.2 折叠的乐趣说到折叠,咱们先来个小互动:谁小时候没折过纸飞机呢?想想当时那种心情,跟朋友们比赛谁的飞机飞得更远。
其实,折叠不仅仅是孩子们的游戏,也是数学里的一个重要概念。
把平行四边形折叠起来,可以生成一些意想不到的形状和图案。
就像是生活中的惊喜,没准一不小心就折出了个小怪兽!。
3. 折叠背后的奥秘3.1 数学与生活的交汇有人可能会问,折叠这些形状有什么用呢?其实,折叠不仅能帮助我们理解空间关系,还能启发我们的创造力。
在日常生活中,很多东西都得经过折叠,比如纸袋、便携式桌子,还有那些时尚的折叠伞。
就像“巧妙应对”,灵活的折叠设计能让我们的生活变得更加便捷。
3.2 折叠的艺术当然,折叠的过程可不仅仅是把纸一折了之,更多的是一种艺术。
想想那些精致的折纸作品,简直美得让人目不转睛。
那些作品往往需要精准的计算和独特的创意,才能把简单的平行四边形变成一只活灵活现的纸鹤。
正所谓“心灵手巧”,只要你愿意动手,总能从平凡中找到不平凡。
4. 结尾好啦,经过这一番聊天下来,咱们发现特殊平行四边形折叠问题不仅是个数学难题,更是一种生活哲学。
它告诉我们,灵活应对,活学活用,才能在这个复杂的世界里找到自己的位置。
生活就像一块大折纸,有时候你得先把它折起来,才能看到不一样的风景。
平行四边形的折叠问题

特殊平行四边形中的折叠问题1 、矩形中的折叠例1 如图,在矩形ABCD 中,AB =6,BC =8.将矩形ABCD 沿CE 折叠后,使点D 恰好落在对角线AC 上的点F 处.求EF 的长.例2 如图,把矩形纸片ABCD 沿EF 折叠,使点B 落在边AD 上的点B ′处,点A 落在点A ′处.(1)试说明B ′E =BF ;(2)设AE =a ,AB =b ,BF =c ,试猜想a 、b 、c 之间有何等量关系,并给予说理.2、 菱形中的折叠例3 如图,在菱形ABCD 中,∠ABC =120°,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B 、D 重合),折痕为EF ,若BC =4,BG =3,则GE 的长为 .3、 正方形中的折叠例4如图,在正方形ABCD 中,E 为边BC 上一点,将∠ABE 沿AE 折叠至∠ABE 处,BE 与AC 交于点F ,若∠EFC =69°,则∠CAE 的大小为( )A .10°B .12°C .14°D .15°例5 如图,正方形ABCD 的边长为9,将正方形折叠,使顶点D 落在BC 边上的点E 处,折痕为GH .若BE :EC =2:1,则线段CH 的长是( )A .3B .4C .5D .6AB CDFA ′B ′EFB A CD E G O E B CA D P EN M CD BA F G E C DB A F E DCA BEFGB A HB'CDAB EGFECDBAE B CA D 跟踪练习:1.如图,将矩形纸片ABCD 沿EF 折叠后,点D 、C 分别落在点D 1、C 1的位置,ED 1的延长线交BC 于点G ,若∠EFG =64°,则∠EGB 等于( ) A .128° B .130° C .132° D .136°(1题图) (2题图) (3题图) (4题图)2.如上图,矩形ABCD 中,AB =8,BC =6,P 为AD 上一点,将∠ABP 沿BP 翻折至∠EBP ,PE 与CD 相交于点O ,BE 与CD 相交于点G ,且OE =OD ,则AP 的长为_________.3.如图,菱形纸片ABCD 中,∠A =60°,折叠菱形纸片ABCD ,使点C 落在DP (P 为AB 的中点)所在的直线上,得到经过点D 的折痕DE ,若菱形边长为1,则点E 到CD 的距离为 .4. 如图,已知E 是正方形ABCD 的边AB 上一点,点A 关于DE 的对称点为F ,若正方形ABCD 的边长为1,且∠BFC =90°,则AE 的长是__________;综合练习:1.如图,在矩形ABCD 中,AB =5,AD =3,点E 为BC 上一点,把∠CDE 沿DE 翻折,点C 恰好落在AB 边上的F 处,则CE 的长是( )A .1B .43C .32D .53(1题图) (2题图) (3题图) (4题图)2.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为4,∠B =120°,则EF 的值是( ) A .√3 B .2 C .2√3 D .43.如图,在矩形ABCD 中,E 是AD 的中点,∠ABE 沿直线BE 折叠后得到∠GBE ,延长BG 交CD 于点F ,若AB =6,BC =46,则FD 的长为( ) A .2 B .4 C .6 D .234.如图,矩形ABCD 中,AD >AB ,将矩形ABCD 折叠,使点C 与点A 重合,折痕为MN ,连接CN ,若∠CDN 的面积与∠CMN 的面积比为1∠4,则MN ∠BM 的值是( ) A .4 B .5 C .25 D .265.在四边形ABCD 中,∠ABC =∠C =90°,DC =DA ,∠D =60°,AB =2,将四边形ABCD 折叠,使点D 和点B 重合,折痕为EF ,则EF 的长为( ) A .2B .3215C .72110D .4215(5题图) (6题图) (7题图) (8题图)6.如图,四边形ABCD 为矩形纸片,把紙片ABCD 折叠,使点B 恰好落在CD 边的中点E 处,折痕为AF .若CD =10,AF 的值为_________.7.如图,矩形ABCD 中,AB =6,BC =8,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B ′处,当∠CB ′E =90°时,BE 的长为__________; 8.如图,已知矩形ABCD 的边AB =6,BC =8.将矩形的一部分沿EF 折叠,使D 点与B 点重合,C 点的对应点为G .则EF 的长是_________.将∠BEF 绕着点B 顺时针旋转角度α (0°<α<180°),得到∠BE 1F 1,直线E 1F 1分别与射线EF 、射线ED 交于点M 、N .当EN =MN 时,FM 的长是__________; 9.如图,在正方形ABCD 中,AB =6,M 是AD 边上的一点,AM :MD =1:2.将∠BMA 沿BM 对折至∠BMN ,连接DN ,则DN 的长是________.10.如图,矩形ABCD 中,AB =4,BC =2.E 是AB 的中点,直线l 平行于直线CE ,且直线l 与直线EC 之间的距离为2,点F 在矩形ABCD 边上,将矩形ABCD 沿直线EF 折叠,使点A 恰好落在直线l 上,则DF 的长为__________.。
特殊平行四边形的折叠问题

特殊平行四边形的折叠问题一,基础热身例1,如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=3cm,AB=8 cm,则图中阴影部分面积为 __________cm2.例2,如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F处,已知CE=3,AB=8,则BF= _________例3,如图(上题),将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知DE=5,AB=8,则BF=_______ 例4,如图(上题),将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF= ________例5,如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在ABC边上F点处,已知CE=4cm,AB=9cm,则矩形ABCD的面积为_________m2.例6,如图(上题),将矩形ABCD沿直线AE折叠,使点D+落在BC边上的点F处,若已知∠BAF=60°,则∠DAE度数是()A, 15° B,30° C, 45° D,60°二,菱形中的折叠问题例7,如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连结A′C,则A′C长度的最小值________,例8,如图,在菱形纸片ABCD 中,∠A=60°将纸片折叠,点A,D 分别落在A ′,D ′处,且 A ′D ′经过点B ,EF 为折痕.当D ′F⊥CD时,=___________三,矩形中的折叠问题例9,如图,在矩形纸片ABCD 中,AB=8cm ,把矩形纸片沿直线AC 折叠,点B 落在点E 处,AE 交DC 于点F ,若AF =则AD 的长为_______。
例10,如图,已知矩形纸片ABCD ,点E 是AB 的终点,点G 是BC 上的一点,∠BEG >60°.现沿直线EG 将折叠,使B 落在纸片上的H 处,连接AH ,则与∠BEG 相等的角的个数为_______。
平行四边形中的折叠问题含答案

平行四边形中的折叠问题一、新课导入(一)学习目标熟练掌握平行四边形的性质与判定,并能运用相关性质、判定解决平行四边形中的折叠问题.(二)预习导入1.如图,将▱ABCD沿对角线BD折叠,点A落在点A′处,若∠A=55°,∠ABD=45°,则∠A′BC的大小为().A.30°B.35°C.40°D.45°2.如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C'处,折痕为EF,若AB=1,BC=2,则△ABE和△BC'F的周长之和是________.二、典型问题知识点一:在折叠中求角度和边长例1如图,矩形ABCD中,点M,N分别在AD、BC边上.将矩形ABCD沿MN翻折,点C恰好落在AD边上的点F处.若MD=1,∠MNC=60°,则∠EFM的度数为_______,AB的长为________.分析:由折叠变换可得EF=CD,MD=EM=1,∠MNC=∠FNM=60°,∠C=∠EFN=90°,由平行线的性质可得∠FMN=∠MNC=60°,即可求得∠EFM的度数,由直角三角形的性质可求得EF的长,即为AB的长.知识点二:在折叠中判定平行四边形例2如图,已知矩形ABCD,将纸片折叠,使顶点A与C重合,折痕EF分别于DC,AB 交于E,F.求证:E,A,F,C四点构成的四边形为菱形.分析:连接AE,AC,AC交EF于O,由折叠的性质得,AO=CO,EF⊥AC,根据全等三角形的性质得到AF=CE,则即可得解.三、阶梯训练A组:基础练习1.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点A'处.若∠1=∠2=50°,则∠A'为_________.2.把矩形ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=4cm,BC=8cm,则DF的长度是________cm.3.如图,▱ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,则FC的长为_________.4.如图,将菱形纸片ABCD折叠,使点B落在AD边的点F处,折痕为CE,若∠D=80°,则∠ECF的度数是__________.5.在▱ABCD中,点E为AB边的中点,连接CE,将△BCE沿着CE翻折,点B落在点G 处,连接AG并延长,交CD于F.求证:四边形AECF是平行四边形.6.准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M 点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.(1)求证:四边形BFDE是平行四边形;(2)若四边形BFDE是菱形,BE=2,求菱形BFDE的面积.B组:拓展练习7.如图,已知正方形纸片ABCD,M,N分别是AD,BC的中点,把BC边向上翻折,使点C恰好落在MN上的P点处,BQ为折痕,则∠PBQ的度数为_________.8.如图,菱形纸片ABCD中,∠A=60°,点P是AB边的中点,折叠纸片,使点C落在直线DP上的C处,折痕为经过点D的线段DE.则∠DEC的度数为_________.9.如图,正方形ABCD的边长AB=12,翻折AD到GN分别交CD于点M,交BC于点N,BN=5,连接AN.(1)求△AEN的面积;(2)试判断EF与AN的关系,并说明理由.平行四边形中的折叠问题答案预习导入1.B.2.6.例130°,3.例2连接AE,AC交EF于O.由折叠的性质得,AO=CO,EF⊥AC,∴AE=CE,AF=CF.∵AB∥CD,∴∠ECO=∠OAF.在△AOF与△COE中,∠ 쫠⩊=∠ ,쫠 = ,∠쫠 ⩊=∠ ,∴△AOF≌△COE.∴AF=CE.∴AE=AF=CE=CF.∴E,A,F,C四点构成的四边形为菱形.1.105°.2.5.3.7.4.40°.5.证明:∵四边形ABCD是平行四边形,∴AE∥FC.∵点E是AB边的中点,∴AE=BE.∵将△BCE沿着CE翻折,点B落在点G处,∴BE=GE,∠CEB=∠CEG.∴AE=GE.∴∠FAE=∠AGE.∵∠BEG=∠FAE+∠AGE,∴∠FAE=12∠BEG.又∵∠CEB=∠CEG=12∠BEG,∴∠FAE=∠CEB.∴AF∥EC.∴四边形AECF是平行四边形.6.(1)证明:∵四边形ABCD是矩形,∴∠A=∠C=90°,AB=CD,AB∥CD.∴∠ABD=∠CDB.由翻折变换的性质可知,∠ABE=∠EBD,∠CDF=∠FDB,∴∠EBD=∠FDB.∴EB∥DF.∵ED∥BF,∴四边形BFDE为平行四边形.(2)∵四边形BFDE为菱形,∴∠EBD=∠FBD.∵∠EBD=∠ABE,∴∠EBD=∠FBD=∠ABE.∵四边形ABCD是矩形,∴∠ABC=90°.∴∠EBD=∠FBD=∠ABE=30°.∴AB=3.∴菱形BFDE的面积S=DE×AB=23.7.30°.8.75°.9.(1)∵四边形ABCD是正方形,∴∠B=90°.由折叠的性质,得NE=AE.设NE=AE=x,则BE=AB-AE=12-x.在Rt△ABN中,由勾股定理,得52+(12-x)2=x2,解得x=16924.∴AE=16924.∴△AEN的面积=12AE×BN=84548.(2)EF⊥AN,EF=AN,理由如下:作FH⊥AB于H,如图所示.则FH=AD=AB,∠EFH+∠FEH=90°.由折叠的性质,得EF⊥AN,∴∠NAB+∠FEH=90°.∴∠EFH=∠NAB.在△EFH和△NAB中,∠ ⩊h=∠ 쫠 ,⩊h=쫠 ,∠⩊h =∠ =90°,∴△EFH≌△NAB.∴EF=AN.。
解决特殊平行四边形中折叠问题的4种方法

解决特别平行四边形中折叠问题的4种方法►方法一用方程思想解决特别平行四边形中的折叠问题1、如图1-ZT-1,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上、若AB=6,BC=9,则BF的长为()图1-ZT-1A、4 B、3 2C、4、5D、52、把一张矩形纸片(矩形ABCD)按如图1-ZT-2所示的方式折叠,使顶点B和点D重合,折痕为EF、若AB=3 cm,BC=5cm,则重叠部分△DEF的面积是________cm2、:学*科*网Z*X*X*K]图1-ZT—23。
如图1-ZT—3,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且点D落在对角线D′处、若AB=3,AD=4,则ED的长为()图1—ZT-3A、\f(3,2)B、3C。
1D。
\f(4,3)[来源:1]4。
如图1-ZT-4,折叠矩形ABCD的一边AD,使点D落在BC边上的点F处,已知折痕AE=5 5 cm,且EC∶FC=BF∶AB=3∶4、那么矩形ABCD的周长为________cm、图1—ZT-45、如图1-ZT—5,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG、(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求CEDE的值。
图1-ZT-5►方法二用数形结合思想解决特别平行四边形中的折叠问题6。
如图1—ZT—6,在矩形ABCD中,AB=4,BC=6,E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为()图1-ZT-6A、95B。
\f(12,5)C、\f(16,5)D、\f(18,5)7。
如图1—ZT-7,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处、若点D的坐标为(10,8),则点E的坐标为________、图1-ZT-78、如图1-ZT-8,在矩形ABCD中,AB=6 cm,E,F分别是边BC,AD上一点,将矩形ABCD沿EF折叠,使点C,D分别落在点C′,D′处、若C′E⊥AD,则EF的长为________cm。
特殊平行四边形折叠问题

折叠问题1.如图所示,把一个长方形纸片沿EF 折叠后,点D ,C 分别落在D ′,C ′的位置.若∠EFB =65°,则∠AED ′为 度.2.如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C ′处,折痕为EF ,若∠ABE =20°,那么∠EFC ′的度数为 度.3.如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为 度.4.如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,︒>∠60BEG ,现沿直线EG 将纸片折叠,使点B 落在约片上的点H 处,连接AH ,则与BEG ∠相等的角有 个。
A.4B. 3C.2D.1EDBC′FCD ′A5.如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则AM 的长是6.如图,在梯形ABCD 中,AD ∥BC ,AD =2,AB =3,BC =6,沿AE •翻折梯形ABCD ,使点B 落在AD 的延长线上,记为B ′,连结B ′E 交CD 于F ,则DE:FC=A. 13B. 14C. 15D. 167.如图,在梯形ABCD 中,∠DCB =90°,AB ∥CD ,AB =25,BC =24. 将该梯形折叠,点A 恰好与点D 重合,BE 为折痕,那么AD 的长度为_______.8.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是 .9.如图2是一张矩形纸片ABCD ,AD =10cm ,若将纸片沿DE 折叠,使DC 落在DA 上,点C 的对应点为点F ,若BE =6cm ,则CD 的长是A B CDMNA 'B ' F E DB A C①② 3 4 1010.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长 是11.如图,矩形纸片ABCD 中,AB =4,AD =3,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,则A'G 的长是 。
2024年北师大版九年级上册数学第一章特殊平行四边形专项突破2特殊平行四边形的折叠问题

7. 如图,将矩形 ABCD 对折,使边 AB 与 DC , BC 与 AD 分
别重合,展开后得到四边形 EFGH . 若 AB =2, BC =4,
则四边形 EFGH 的面积为(
A. 2
B. 4
C. 5
D. 6
1
2
3
4
5
B
6
)
7
8
9
10
11
8. 如图,正方形 ABCD 的边长为3, E 为 BC 边上一点, BE
∴四边形 AGEF 的面积= S正方形 ABCD - S△ ADF - S△ ECF -
S△ GBE =32- ×3× - ×2× - ×1× =9-1-
- =5.
1
2
3
4
5
6
7
8
9
10
11
9. [教材P28复习题T15变式]如图,将矩形 ABCD 沿对角线
设 CF = a ,则 DF = CD - CF =3- a .
由折叠的性质可知 AG = EG , AF = EF .
在△ ECF 和△ ADF 中,
∵ AF2= AD2+ DF2, EF2= CE2+ CF2,
1
2
3
4
5
6
7
8
9
10
11
∴ AD2+ DF2= CE2+ CF2,即32+(3- a )2=22+ a2,
则 DE 长为(
A
)
A. 5
B. 3
C. 5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
折叠问题
1.如图所示,把一个长方形纸片沿EF 折叠后,点D ,C 分别落在D ′,C ′的位置.若∠EFB =65°,则∠AED
′为
度.
2.如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C ′处,折痕为EF ,若∠ABE =20°,那么∠EFC ′的度数为 度.
3.如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为 度.
4.如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,︒
>∠60BEG ,现沿直线EG 将纸片折叠,使点B 落在约片上的点H 处,连接AH ,则与BEG ∠相等的角有 个。
A.4
B. 3
C.2
D.1
E
D
B
C′
F
C
D ′
A
5.如图,四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则AM
的长是
6.如图,在梯形ABCD 中,AD ∥BC ,AD =2,AB =3,BC =6,沿AE•翻折梯形ABCD ,使点B 落在AD 的延长线上,记为B ′,连结B ′E 交CD 于F ,则DE:FC=
A. 13
B. 14
C. 15
D. 1
6
7.如图,在梯形ABCD 中,∠DCB =90°,AB ∥CD ,AB =25,BC =24. 将该梯形折叠,点A 恰好与点D 重合,BE 为折痕,那么AD 的长度为_______.
8.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是 . 9.如图2是一张矩形纸片ABCD ,AD =10cm ,若将纸片沿DE 折叠,使DC 落在DA 上,点C 的对应点为点F ,若BE =6cm ,则CD 的长是
A B C
D
M
N
A '
B ' F E D
B A C
①
② 3 4
10.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB
=3,折叠后,点
C 落在A
D 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长 是
11.如图,矩形纸片ABCD 中,AB =4,AD =3,折叠纸片使AD 边与对角线BD 重合,折痕为DG ,则A'G 的长是 。
12. AB = 3 cm ,BC = 5 cm ,则重叠部分△DEF 的面积是 cm 2
.
13.如图,在矩形ABCD 中,AB=12cm ,BC=6cm ,点E 、F 分别在AB 、CD 上,将矩形ABCD 沿EF 折叠,使点A 、D 分别落在矩形ABCD 外部的点A’,D’处,则整个阴影部分图形的周长..是
14.矩形纸片ABCD 中,AB =4,BD =3,将纸片折叠,使点B 落在边CD 上的B ’处,折痕为AE .在折痕AE 上存在一点P 到边CD 的距离与到点B 的距离相等,则此相等距离为________.
C
B ’ D
P
15.如图矩形纸片ABCD ,AB =5cm ,BC =10cm ,CD 上有一点E ,ED =2cm ,AD 上有一点P ,PD =3cm ,过P 作PF ⊥AD 交BC 于F ,将纸片折叠,使P 点与E 点重合,折痕与PF 交于Q 点,则PQ 的长是____________cm.
16.在正方形ABCD 中,正方形的边长为2,对角线AC 、BD 交于点O ,折叠正方形纸片ABCD ,使AD 落在BD 上,点A 恰与BD 上的点F 重合,展开后,折痕DE 分别交AB 、AC 于点E 、G ,
连接GF 。
则ΔEFD 的面积为。
17.小明尝试着将矩形纸片ABCD (如图①,AD >CD )沿过A 点的直线折叠,使得B 点落在AD 边上的点F 处,折痕为AE (如图②);再沿过D 点的直线折叠,使得C 点落在DA 边上的点N 处,E 点落在AE 边上的点M 处,折痕为DG (如图③).如果第二次折叠后,M 点正好在∠NDG 的平分线上,那么矩形ABCD 长与宽的比值为 .
18取一张矩形纸片按照图1、图2中的方法对折,并沿图3中过矩形顶点的斜线(虚线)剪开,那剪下的①这部分展开,平铺在桌面上,若平铺的这个图形是正六边形,则这张矩形纸片的宽和长之比为 .
19.长为1,宽为a 的矩形纸片(
12
1
<<a ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n 此操作后,剩下的矩形为正方形,则操作终止.当n =3时,a 的____________.
A
B B B D ①
② C D G M ③
20.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH 的值,并说明理由.
21.如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P,连接EP.
(1)如图②,若M为AD边的中点,
①,△AEM的周长=_____cm;
②求证:EP=AE+DP;
(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.
22、在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,OC=3.
(1)求对角线OB所在直线的解析式
(2)如图,将△OAB沿对角线OB翻折得打△OBN,ON与AB交于点M;
①判断△OBM是什么三角形,并说明理由
②试求直线MN的解析式。
23.如图,在平面直角坐标系中,四边形是正方形,A点坐标为(0,a),E是线段BC上一点,且∠AEB=60°,沿AE折叠后B点落在点F处,那么点F的坐标是。
24.如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,
在CD上取一点N,将纸片沿MN折叠,使MB与D N交于点K,得到△MNK.
(1)若∠1=70°,求∠MNK的度数.
(2)△MNK的面积能否小于1
2
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
A
F D C E
B D '
(备用图)
25.将平行四边形纸片ABCD 按如图方式折叠,使点C 与A 重合,点D 落到D '处,折痕为EF .
(1)求证:ABE AD F '△≌△;
(2)连结CF ,判断四边形AECF 是什么特殊四边形?说明你的结论.
26.如图,在直角梯形纸片ABCD 中,AB DC ∥,90A ∠=,CD AD >,将纸片沿过点D 的直线折叠,使点A 落在边CD 上的点E 处,折痕为DF .连接EF 并展开纸片. (1)求证:四边形ADEF 是正方形;
(2)取线段AF 的中点G ,连接EG ,如果BG CD =,试说明四边形GBCE 是等腰梯形.
27.如图所示,在等腰梯形ABCD 中,AD//BC ,∠DBC=45°,翻折梯形ABCD ,使点B 重合于点D ,折痕分别交边AB,BC 于点F ,E,若AD=2,BC=8.求: (1) DE 的长;
(2) ∠CDE 的正切值。
28.如图,在矩形纸片ABCD 中,AB =3BC =6,沿EF 折叠后,点C 落在AB 边上的点P 处,点D 落在点Q 处,AD 与PQ 相交于点H ,∠BPE =30°. (1)求BE 、QF 的长. (2)求四边形PEFH 的面积.
E
C
B
D
A G F
29.把一张矩形ABCD纸片按如图方式折叠,使点A与点E重合,点C与点F重合(E、F两点均在BD上),折痕分别为BH、DG。
(1)求证:△BHE≌△DGF;
(2)若AB=6cm,BC=8cm,求线段FG的长。
