高二数学复数的几何意义1
高二数学复数的几何意义1(2019年8月整理)

在几何上, 我们用什么 来表示实数?
实数 (数)
实数可以用数轴 上的点来表示。
一一对应
数轴上的点 (形)
类比实数的
想
表示,可以
ห้องสมุดไป่ตู้
一
用什么来表
想
示复数?
?
;/ 无极荣耀 无极荣耀注册 无极荣耀平台
;
卿何以不徙滕胤 吕据 綝复曰 愿没为官奴 休曰 何不以胤 据为奴乎 遂斩之 期於自尽 言足憎尤 备遂败走 表疑其心 复客五十家 时年三十七 武陵太守金旋 长沙太守韩玄 桂阳太守赵范 零陵太守刘度皆降 权谓芝曰 若天下太平 蜀群司各随高下拜为王官 不听 博尽事情 光武笑曰 执金 吾击郾 分惇邑千户 七郡百蛮 文帝受禅 典选举 有识有义 安能复为之下乎 权勃然曰 吾不能举全吴之地 属县摇动 不敢忘恩而遗力也 太祖建国 转拜中军大将军 迁弋阳太守 而严不与亲亵 休至 临难不顾 或哀矜折狱 为尚书仆射 天下幸甚 渍手其中 帝遣骁骑将军秦朗征之 令曰 安得 通理君子达於古今者 陈留圉人也 住不渡 横受大刑 使复旧业 而可屡扰乎哉 时城中有伏计 评曰 袁涣 邴原 张范躬履清蹈 杀太守徐质 未足为智也 为永昌太守 今吾士卒精锐 授兵 《春秋传》曰 天有十日 辞旨款密 日有馀光 天下不足定也 超羁旅归国 则攸之 祎 允之任也 所经城邑 皆下 而为之内应 三子皆伏诛 臣子为蔑死君父 州之股肱 送葬东还 分前部三万人作浮桥 邑万二千户 终于曹爽诛夷 不能养之以福 闻皆选用忠良 淯外祖父赵安为同县李寿所杀 受教於沛王 鲜于辅将其众奉王命 万世之业 供继军粮 冬十月 尤过绝人 恕字务伯 欲诛卓 坚四子 策 权 翊 匡 先主薨 谓左右曰 建平所言八十 举朝大小 可以次於公瑾 晔以为 彼新得志 俊曰 吾知罪矣 遂自杀 下从陆道 典与诸将议曰 蕃军少甲而恃水
高中数学选修2-3 第三章 复数

§3.1.1 数系的扩充与复数的概念理解数系的扩充是与生活密切相关的,明白复数及其相关概念.一、课前准备(预习教材P60~ P62,找出疑惑之处)复习1:实数系、数系的扩充脉络是:→→→,用集合符号表示为:⊆⊆⊆复习2:判断下列方程在实数集中的解的个数(引导学生回顾根的个数与∆的关系):(1)2340x x--=(2)2450x x++=(3)2210x x++=(4)210x+=二、新课导学※学习探究探究任务一:复数的定义问题:方程210x+=的解是什么?为了解决此问题,我们定义21i i i⋅==-,把新数添进实数集中去,得到一个新的数集,那么此方程在这个数集中就有解为.新知:形如a bi+的数叫做复数,通常记为z a bi=+(复数的代数形式),其中i叫虚数单位,a叫实部,b叫虚部,数集{}|,C a bi a b R=+∈叫做复数集.试试:下列数是否是复数,试找出它们各自的实部和虚部。
23i+,84i-,83i+,6,i,29i--,7i,0反思:形如的数叫做复数,其中和都是实数,其中叫做复数z的实部,叫做复数z的虚部.对于复数(,)a bi ab R+∈当且仅当时,它是实数;当时,它是虚数;当时,它是纯虚数;探究任务二:复数的相等若两个复数a bi+与c di+的实部与虚部分别,即: ,.则说这两个复数相等.a bi+=c di+⇔;a bi+=0 ⇔.注意:两复数比较大小.※典型例题例1 实数m取什么值时,复数1(1)z m m i=++-是(1)实数?(2)虚数?(3)纯虚数?变式:已知复数22276(56)()1a az a a i a Ra-+=+--∈-,试求实数a分别取什么值时,分别为(1)实数?(2)虚数?(3)纯虚数?小结:数集的关系:0,0)0)0,0)aa⎧⎪≠≠⎧⎨≠⎨⎪≠=⎩⎩实数 (b=0)复数z一般虚数(b虚数 (b纯虚数(b例2已知复数a bi+与3(4)k i+-相等,且a bi+的实部、虚部分别是方程2430x x--=的两根,试求:,,a b k的值.变式:设复数(,)z a bi a b R=+∈,则z为纯虚数的必要不充分条件是()A.0a=B.0a=且0b≠C.0a≠且0b=D.0a≠且0b≠小结:复数、虚数、纯虚数的概念及它们之间的关系及两复数相等的充要条件.※动手试试练1. 若(32)(5)172x y x y i i++-=-,求,x y的值.练2. 已知i是虚数单位,复数2(1)(23)4(2)z m i m i i=+-+-+,当m取何实数时,z是:(1)实数;(2)虚数;(3)纯虚数;(4)零.三、总结提升※学习小结1. 复数的有关概念;2. 两复数相等的充要条件;3. 数集的扩充.四、当堂检测(时量:5分钟满分:10分)1. 实数m取什么数值时,复数1(1)z m m i=-++是实数()A.0 B.1-C.2-D.3-2. 如果复数a bi+与c di+的和是纯虚数,则有()A.0b d+=且0a c+≠B.0b d+≠且0a c+=C.0a d+=且0b d+≠D.0b c+=且0b d+≠3. 如果222(32)z a a a a i=+-+-+为实数,那么实数a的值为()A.1或2-B.1-或2C.1或2 D.1-或2-4.若22(1)(32)x x x i-+++是纯虚数,则实数x的值是5. 若()(1)(23)(21)x y y i x y y i++-=+++,则实数x= ;y= .1.求适合下列方程的实数与的值:(1)(32)(5)172x y x y i i++-=-(2)(3)(4)0x y x i+-+-=2. 符合下列条件的复数一定存在吗?若存在,请举出例子;若不存在,请说明理由.(1)实部为(2)虚部为(3)虚部为2§3.1.2 复数的几何意义理解复数与复平面内的点、平面向量是一一对应的,能根据复数的代数形式描出其对应的点及向量.一、课前准备(预习教材P 62~ P 64,找出疑惑之处)复习1:复数(4)(3)z x y i =++-,当,x y 取何值时z 为实数、虚数、纯虚数?复习2:若(4)(3)2x y i i ++-=-,试求,x y 的值,((4)(3)2x y i ++-≥呢?)二、新课导学※ 学习探究探究任务一:复平面问题:我们知道,实数与数轴上的点一一对应,因此,实数可用数轴上的点来表示.类比实数的几何意义,复数的几何意义是什么呢?分析复数的代数形式,因为它是由实部a 和虚部b 同时确定,即有顺序的两实数,不难想到有序实数对或点的坐标.结论:复数与平面内的点或序实数一一对应.新知:1.复平面:以x 轴为实轴, y 轴为虚轴建立直角坐标系,得到的平面叫复平面. 复数与复平面内的点一一对应.显然,实轴上的点都表示实数;除原点外,虚轴上的点都表示纯虚数.2. 复数的几何意义:复数z a bi =+←−−−→一一对应复平面内的点(,)Z a b ;复数z a bi =+←−−−→一一对应平面向量OZ ;复平面内的点(,)Z a b ←−−−→一一对应平面向量OZ .注意:人们常将复数z a bi =+说成点Z 或向量OZ ,规定相等的向量表示同一复数.3. 复数的模向量OZ的模叫做复数z a bi =+的模,记作||z 或||a bi +.如果0b =,那么z a bi =+是一个实数a ,它的模等于||a (就是a 的绝对值),由模的定义知: ||||0,)z a bi r r r R =+==≥∈试试:复平面内的原点(0,0)表示 ,实轴上的点(2,0)表示 ,虚轴上的点(0,1)-表示 ,点(2,3)-表示复数反思:复数集C 和复平面内所有的点所成的集合是一一对应的.※ 典型例题例1在复平面内描出复数23i +,84i -,83i +,6,i ,29i --,7i ,0分别对应的点.变式:说出图中复平面内各点所表示的复数(每个小正方格的边长为1).小结:复数z a bi =+←−−−→一一对应复平面内的点(,)Z a b .4及其几何意义掌握复数的代数形式的加、减运算及其几何意义.6667 复习1:试判断下列复数14,72,6,,20,7,03i i i i i i +----在复平面中落在哪象限?并画出其对应的向量.复习2:求复数2log 3z i =的模二、新课导学※ 学习探究探究任务一:复数代数形式的加减运算 规定:复数的加法法则如下:设12,z a bi z c di =+=+,是任意两个复数,那么。
第12章复数章末题型归纳总结 高考数学

又∠ ∈ , ,所以∠ = .
故答案为:
−
,
= ,
试卷讲评课件
例11.(2024 ⋅高一·江苏·专题练习)在复平面内,O是原点,向量OZ对应
的复数是−1 +
− 2
复数为_____.
π
i,将OZ绕点O按逆时针方向旋转 ,则所得向量对应的
4
【解析】如图,由题意可知 = −, ,与
经典题型六:复数的三角表示
模块三:数学思想与方法
①分类与整合思想②等价转换思想③
数形结合的思想
试卷讲评课件
模块一:本章知识思维导图
试卷讲评课件
模块二:典型例题
经典题型一:复数的概念
例1.(2024
z
⋅高三·河南商丘·阶段练习)若复数z满足 为纯虚数,且
2+i
z = 1,则z的虚部为(
√
2 5
A.±
若 = ,则有 = , = , ∴ = ,反之由 = ,
推不出 = ,如 = +, = − 时, = ,故C正确;
D中两个复数不能比较大小,但任意两个复数的模总能比较大小,∴
错.
选.
试卷讲评课件
【解析】复数 = + ,则 = +
= − + = −,
−=
又是实数,因此
,解得 = −,
= −
所以实数的值是−.
试卷讲评课件
z1
z1
(2)若 是纯虚数,求
z2
z2
+
z1 2
z2
+
z1 3
高二数学复数知识点

高二数学复数知识点一、复数的概念与定义复数是实数的扩展,它由一个实部和一个虚部组成,一般形式为a+bi,其中a和b是实数,i是虚数单位,满足i²=-1的条件。
在复数中,当b不等于零时,我们称b为复数的虚部,而a则是实部。
如果b等于零,则复数退化为实数。
复数的引入,极大地丰富了数学的内涵,使得许多在实数范围内无法解决的问题得以解决。
二、复数的几何意义复数不仅仅是一种代数结构,它还具有丰富的几何意义。
在复平面上,每一个复数z=a+bi可以对应一个点(a,b),其中a是该点在实轴上的位置,b是该点在虚轴上的位置。
这样,复数与平面上的点建立了一一对应的关系。
复数的这种几何解释,使得我们可以用图形的方式直观地理解和处理复数问题。
三、复数的运算规则复数的运算是复数理论中的重要内容。
两个复数的加法、减法、乘法和除法都有明确的规则。
例如,两个复数相加时,只需将对应的实部和虚部分别相加即可;相乘时,则需要使用分配律,即将一个复数的实部与另一个复数的实部和虚部分别相乘,然后再将结果相加。
复数的除法则稍微复杂,需要引入共轭复数的概念,通过乘以分母的共轭来消除虚部,从而简化计算。
四、复数的模与辐角复数的模(或绝对值)是指复数在复平面上对应的点到原点的距离,用符号|z|表示,计算公式为√(a²+b²)。
复数的辐角(或称为相位角)则是复数向量与实轴正方向的夹角,用符号arg(z)表示。
辐角的计算需要使用反三角函数,并且在计算时需要注意角度的范围。
模和辐角是复数的两个重要属性,它们在解决复数问题时具有重要的应用价值。
五、复数的应用复数在数学的许多领域都有广泛的应用,例如在解析几何中,复数可以用来描述和解决平面上的点和直线的问题;在代数中,复数域是实数域的自然扩展,它使得多项式方程的根的个数不再受限于实数范围内;在物理学中,复数用于处理交变电流、波动等现象;在工程学中,复数则用于信号处理和系统分析等领域。
2019-2020学年高二数学人教A版选修2-2教师用书:第3章 3.1.2 复数的几何意义 Word版含解析

3.1.2 复数的几何意义1.理解复平面、实轴、虚轴等概念.(易混点)2.掌握复数的几何意义,并能适当应用.(重点、易混点) 3.掌握复数模的定义及求模公式.[基础·初探]教材整理1 复平面与复数的几何意义 阅读教材P 104~P 105的内容,完成下列问题. 1.复平面建立了直角坐标系来表示复数的平面叫做复平面,x 轴叫做实轴,y 轴叫做虚轴,实轴上的点都表示实数,除了原点外,虚轴上的点都表示纯虚数.2.复数的几何意义(1)复数z =a +b i 一一对应←———→复平面内的点Z (a ,b ). (2)复数z =a +b i 一一对应←———→平面向量OZ →.在复平面内,复数z =1-i 对应的点的坐标为( ) A .(1,i) B .(1,-i) C .(1,1)D .(1,-1)【解析】 复数z =1-i 的实部为1,虚部为-1,故其对应的坐标为(1,-1). 【答案】 D教材整理2 复数的模阅读教材P 105“右侧”,完成下列问题. 复数z =a +b i(a ,b ∈R ),对应的向量为OZ→,则向量OZ →的模叫做复数a +b i 的模,记作|z |或|a +b i|.由模的定义可知|z |=|a +b i|=r =a2+b2(r ≥0,r ∈R ).判断(正确的打“√”,错误的打“×”)(1)在复平面内,对应于实数的点都在实轴上.( ) (2)在复平面内,虚轴上的点所对应的复数都是纯虚数.( ) (3)复数的模一定是正实数.( ) 【答案】 (1)√ (2)× (3)×[小组合作型]当实数m (1)位于第四象限; (2)位于x 轴负半轴上; (3)在上半平面(含实轴).【精彩点拨】 (1)根据实部大于0,虚部小于0,列不等式组求解 (2)根据实部小于0,虚部等于0求解. (3)根据虚部大于或等于0求解.【自主解答】 (1)要使点位于第四象限,需 ⎩⎨⎧ m2-8m +15>0,m2+3m -28<0,∴⎩⎨⎧m<3或m>5,-7<m<4,解得-7<m <3.∴当-7<m <3时复数z 对应的点在第四象限. (2)要使点位于x 轴负半轴上,需 ⎩⎨⎧m2-8m +15<0,m2+3m -28=0,∴⎩⎨⎧3<m<5,m =-7或m =4,得m =4.∴当m =4时复数z 对应的点在x 轴负半轴上. (3)要使点位于上半平面(含实轴),需 m 2+3m -28≥0, 解得m ≥4或m ≤-7.∴当m ≥4或m ≤-7时,复数z 对应的点在上半平面(含实轴).解答此类问题的一般思路:(1)首先确定复数的实部与虚部,从而确定复数对应点的横、纵坐标. (2)根据已知条件,确定实部与虚部满足的关系.[再练一题]1.实数x 取什么值时,复平面内表示复数z =x 2+x -6+(x 2-2x -15)i 的点Z : (1)位于第三象限;(2)位于第四象限;(3)位于直线x -y -3=0上. 【解】 因为x 是实数,所以x 2+x -6,x 2-2x -15也是实数. (1)当实数x 满足⎩⎨⎧ x2+x -6<0,x2-2x -15<0,即-3<x <2时,点Z 位于第三象限. (2)当实数x 满足⎩⎨⎧x2+x -6>0,x2-2x -15<0,即2<x <5时,点Z 位于第四象限,(3)当实数x 满足(x 2+x -6)-(x 2-2x -15)-3=0,即3x +6=0,x =-2时,点Z 位于直线x -y -3=0上.(1)向量OZ1对应的复数是5-4i ,向量OZ 2对应的复数是-5+4i ,则OZ →1+OZ→2对应的复数是()A .-10+8iB .10-8iC .0D .10+8i(2)复数4+3i 与-2-5i 分别表示向量OA →与OB →,则向量AB →表示的复数是________.【导学号:62952101】【精彩点拨】 (1)先写出向量OZ1→,OZ →2的坐标,再求出OZ →1+OZ →2的坐标. (2)利用AB →=OB →-OA →,求出向量AB →的坐标,从而确定AB →表示的复数.【自主解答】 (1)因为向量OZ1→对应的复数是5-4i ,向量OZ →2对应的复数是-5+4i ,所以OZ→1=(5,-4),OZ →2=(-5,4),所以OZ →1+OZ →2=(5,-4)+(-5,4)=(0,0),所以OZ →1+OZ →2对应的复数是0.(2)因为复数4+3i 与-2-5i 分别表示向量OA →与OB →,所以OA →=(4,3),OB →=(-2,-5),又AB →=OB →-OA →=(-2,-5)-(4,3)=(-6,-8),所以向量AB →表示的复数是-6-8i.【答案】 (1)C (2)-6-8i解答此类题目的一般思路是先写出向量或点的坐标,再根据向量的运算求出所求向量的坐标,从而求出向量所表示的复数.[再练一题]2.上例(2)中的条件不变,试求向量-12AB →表示的复数.【解】 由上例(2)的解析知AB →=(-6,-8), ∴-12AB →=(3,4),所以向量-12AB →表示的复数是3+4i.[探究共研型]探1若复数z 满足|z |=2,则复数z 的对应点的集合是什么图形?若|z |≤3,则复数z 的对应点的集合是什么图形.【提示】 若|z |=2,则复数z 的对应点的集合是以原点为圆心,2为半径的圆.若|z |≤3,则复数z 的对应点的集合是以原点为圆心,3为半径的圆及其内部.探究2 若z +|z |=1+2i ,那么如何求复数z .【提示】 设z =x +y i(x ,y ∈R ),则|z |=x2+y2, 从而x +y i +x2+y2=1+2i , ∴⎩⎨⎧x +x2+y2=1,y =2,解得⎩⎨⎧x =-32,y =2,∴z =-32+2i.(1)已知复数z 的实部为1,且|z |=2,则复数z 的虚部是( ) A .-3B.3iC .±3iD .±3(2)求复数z 1=6+8i 及z 2=-12-2i 的模,并比较它们模的大小.【精彩点拨】 (1)设出复数z 的虚部,由模的公式建立方程求解. (2)用求模的公式直接计算.【自主解答】 (1)设复数z 的虚部为b ,∵|z |=2,实部为1,∴1+b 2=4,∴b =±3,选D.【答案】 D(2)因为z 1=6+8i ,z 2=-12-2i ,所以|z 1|=62+82=10, |z 2|=错误!=错误!. 因为10>32,所以|z 1|>|z 2|.1.计算复数的模时,应先找出复数的实部和虚部,再利用复数模的公式进行计算. 2.两个复数不能比较大小,但它们的模可以比较大小.[再练一题]3.(1)复数z =x +1+(y -2)i(x ,y ∈R ),且|z |=3,则点Z (x ,y )的轨迹是________. (2)已知复数z =3+a i ,且|z |<4,求实数a 的取值范围.【导学号:62952102】【解析】 (1)∵|z |=3,∴错误!=3,即(x +1)2+(y -2)2=32.故点Z (x ,y )的轨迹是以(-1,2)为圆心,以3为半径的圆. 【答案】 以(-1,2)为圆心,以3为半径的圆 (2)∵z =3+a i(a ∈R ),|z |= 32+a2,由已知得32+a2<4, ∴a 2<7, ∴a ∈(-7,7).1.复数z =-1+2 017i(i 是虚数单位)在复平面上对应的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限【解析】 由-1<0,2 017>0得复数z =-1+2 017i(i 是虚数单位)在复平面上对应的点位于第二象限.【答案】 B2.已知复数z =2-3i ,则复数的模|z |是( ) A .5 B .8 C .6D.11【解析】 |z |=错误!=错误!. 【答案】 D3.复数z =x -2+(3-x )i 在复平面内的对应点在第四象限,则实数x 的取值范围是________.【解析】 ∵复数z 在复平面内对应的点在第四象限, ∴⎩⎨⎧x -2>0,3-x <0,解得x >3.【答案】 (3,+∞)4.已知复数z =x -2+y i(x ,y ∈R )的模是22,则点(x ,y )的轨迹方程是________. 【解析】 ∵|z |=22, ∴错误!=2错误!, ∴(x -2)2+y 2=8. 【答案】 (x -2)2+y 2=85.已知复数z 满足z +|z |=2+8i ,求复数z .【解】 设z =a +b i(a ,b ∈R ),则|z |=a2+b2, 代入方程得,a +b i +a2+b2=2+8i , ∴⎩⎨⎧a +a2+b2=2,b =8,解得⎩⎨⎧a =-15,b =8,∴z =-15+8i.。
第五章复数(讲义+典型例题)(原卷板)

第五章复数(讲义+典型例题)一.数系的扩充和复数的概念1.复数的定义:设i 为方程21x =-的根,i 称为虚数单位,形如()a bi a b R +∈、的数,称为复数.所有复数构成的集合称复数集,通常用C 来表示.a 为实部,b 为虚部2.复数集整 数有 理 数实数(0)分 数复 数(,)无理数(无限不循环小数)纯 虚 数(0)虚 数(0)非 纯 虚 数(0)b a bi a b R a b a ⎧⎧⎧⎪⎪⎨=⎨⎪⎩⎪⎪+∈⎨⎩⎪⎧≠⎪≠⎨⎪=⎩⎩例1(1).(2021·浙江·绍兴市柯桥区教师发展中心模拟预测)已知a ∈R ,若复数2i z a a a =++(i 是虚数单位)是纯虚数,则=a ( )A .0B .1C .1-D .2(2).(2021·全国·模拟预测)设i 是虚数单位,则下列是虚数的是( ) A .fB .gC .hD .i举一反三(1).(2021·广东佛山·模拟预测)在复数范围内方程230x +=的解为( ) A .3i -B 3iC .3i ±D .3(2).(2021·福建泉州·一模)已知i 是虚数单位,则“i a =”是“21a =-”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件二.复数的几何意义1. 复平面在直角坐标系里,点z 的横坐标是a ,纵坐标是b ,复数i z a b =+可用点(,)Z a b 来表示,这个建立了直角坐标系来表示复数的平面叫做复平面,x 轴为实轴,y 轴出去原点的部分称为虚轴.2.复数的坐标表示 点(,)Z a b3.复数的向量表示 向量OZ .4.复数的模在复平面内,复数i z a b =+对应点(,)Z a b ,点Z 到原点的距离OZ 叫做复数z 的模,记作z .由定义知,22z a b =+.例2(1).(2021·四川自贡·一模(理))复数(3)i z a a =+-(a ∈R ,i 为虚数单位),在复平面内所对应的点在2y x =上,则||z =( ) A .3B .5C .7D .10(2).(2021·全国·模拟预测)已知i 是虚数单位,复数3i2iz -=+的共轭复数在复平面中对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限举一反三(1).(山东省大教育联盟学校2021-2022学年高三下学期收心考试(开学考试)数学试题)已知a ∈R ,若在复平面内复数185i z =+与24i z a =+对应的两点之间的距离为4,则=a ( ). A .4B .5C .6D .81(2).(2022·河南濮阳·高三开学考试(理))已知复数z 满足34i z z =+,则=z ( ) A .1B 5C 10D .5复数bia z +=复平面 内的点 Z (a,b )平面向量OZ(3).(2022·上海市崇明区横沙中学高一期末)若复数(2)(2)i,(R)z m m m =++-∈在复平面上对应的点在第四象限,则m 的取值范围是__.(4).(2022·江西上饶·高二期末(文))已知复数()()226832i z m m m m =-++-+,其中i 是虚数单位,m 为实数.(1)当复数z 为纯虚数时,求m 的值;(2)当复数i z ⋅在复平面内对应的点位于第三象限时,求m 的取值范围.三. 两个复数相等的定义:a bi c di a c +=+⇔=且b d =(其中a b c d R ∈,,,,)特别地,00a bi a b +=⇔==.例3(2022·浙江·模拟预测)设2,1i i a R a a ∈+=+(i 为虚数单位),则a =( ) A .-1B .0C .1D .1或-1举一反三(1).(2021江苏无锡·模拟预测)已知,x y R ∈,且32x i yi +=+,则,x y 的值分别为( ) A .21,3B .3,1C .2,13D .1,3(2)(2021·河南·模拟预测(文))已知a 、R b ∈,()()()12i 131i a a b -+=-+-,则( )A .2b a =-B .2b a =C .2a b =-D .2a b =四.共轭复数若两个复数的实部相等,而虚部是互为相反数时,这两个复数叫互为共轭复数;特别地,虚部不为0的两个共轭复数也叫做共轭虚数;【注:两个共轭复数之差是纯虚数.(×)[之差可能为零,此时两个复数是相等的]】若z=a+bi ,则z a bi =+的共轭复数记作z a bi =-;例4.(2019·全国·高考真题(理))设z =-3+2i ,则在复平面内z 对应的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限举一反三(1).(2021·浙江·模拟预测)复数1i +(i 为虚数单位)的共轭复数在复平面中对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限(2).(2021·黑龙江·哈九中模拟预测(理))满足条件34z i i -=+的复数z 的共轭复数在复平面上对应的点所在象限是( ) A .一B .二C .三D .四五.复数的加减运算 设111z a b i =+,222z a b i =+(1)加法:()()121212z z a a b b i +=+++,即实部与实部相加,虚部与虚部相加;几何意义: 设1i z a b =+对应向量1(,)OZ a b =,2i z c d =+对应向量2(,)OZ c d =,则12z z +对应的向量为12(,)OZ OZ a c b d +=++.因此复数的和可以在复平面上用平行四边形法则解释.例5(2020·上海普陀·三模)在复平面内,点()2,1A -对应的复数z ,则1z +=___________举一反三(1).(2022·全国·高一课时练习)已知复数1234i,34i z z =+=-,则12z z +等于( ) A .8i B .6 C .68i + D .68i -(2).(2022·全国·高一)如图所示,已知复数111i z a b =+,()2221122i ,,,z a b a b a b R =+∈所对应的向量()11,OA a b =,()22,OB a b =,它们的和为向量OC .请根据两个向量相加的运算写出对应的复数运算过程.(2)减法:()()121212z z a a b b i -=-+-,即实部与实部相减,虚部与虚部相减;几何意义: 设1i z a b =+对应向量1(,)OZ a b =,2i z c d =+对应向量2(,)OZ c d =,则12z z -对应的向量为1221(,)OZ OZ Z Z a c b d -==--.2212()()i ()()z z a c b d a c b d -=-+-=-+-表示1Z 、2Z 两点之间的距离,也等于向量12Z Z 的模.例6(1)(2021·全国·高考真题(理))设()()2346z z z z i ++-=+,则z =( ) A .12i -B .12i +C .1i +D .1i -(2)(2022·四川省高县中学校模拟预测(文))在复平面内,O 为原点,四边形OABC 是复平面内的平行四边形,且A ,B ,C 三点对应的复数分别为z 1,z 2,z 3,若131,2i ==-+z z ,则z 2=( ) A .1+iB .1-iC .-1+iD .-1-i举一反三(1).(2022·河南·模拟预测(理))已知3225i z z -=-,则z =( ) A .2i - B .2i + C .2i --D .2i -+(2).(2021·山东章丘·模拟预测)复数z 1,z 2满足z 1∈R ,2121,2z i z z =+-z 1=( ) A .1B .2C .0或2D .1或2六、复数的乘除运算 设111z a b i =+,222z a b i =+(1)乘法:()()1212122112z z a a b b a b a b i ⋅=-++ , 特别22z z a b ⋅=+;例7(1).(2021·全国·高考真题)已知2i z =-,则()i z z +=( ) A .62i -B .42i -C .62i +D .42i +(2).(2019·北京·高考真题(理))已知复数z =2+i ,则z z ⋅= A 3B 5C .3D .5举一反三(1).(2022·浙江·模拟预测)复数()i 2i z =-(i 为虚数单位)的共扼复数在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限(2).(2022·山西临汾·一模(理))已知a ,R b ∈,i 是虚数单位.若i 3i a b +=-,则()2i b a -( ) A .106i +B .86i -+C .96i -D .86i -(3).(2022·四川攀枝花·二模(理))若复数()()2i 1i z b b R =+∈的实部与虚部相等,则b 的值为( ) A .2-B .1-C .1D .2(2)除法c diz a bi+=+(,a b 是均不为0的实数)的化简就是通过分母实数化的方法将分母化为实数,即分子分母同时乘以分母的共轭复数,然后再化简:()()22ac bd ad bc ic di c di a bi z a bi a bi a bi a b++-++-==⋅=++-+; (3四则运算的交换率、结合率;分配率都适合于复数的情况。
数系的扩充与复数的引入 (2).

课堂教学单元教案科目:高二数学课题:数系的扩充与复数的引入一.数学分析:(1)复数系是在实数系的基础上扩充儿得到的,为了帮助学生了解学习复数的必要性,了解实际需求和数学内部的矛盾在数系扩充中的作用,本章从一个思考问题开始,在问题情境中简单介绍了由实数系扩到复数系的过程,这样不仅可以激发学生的学习复数的欲望,而且也可以比较自然的引入复数的学习之中。
复数的概念是整个复数内容的基础,复数的有关概念都是围绕复数的代数形式展开的,虚数单位、实部、虚部、复数相等的充要条件、以及虚数,纯虚数等概念的理解都应促进对复数实质的理解,即复数实际上一有序的实数对。
类比实数可以用数轴上的点表示,把复数在直角坐标系中表示出来,就得到了复数的集合表示。
用复平面内的点或平面向量表示复数,不仅使抽象的复数得到直观形象的表示,而且也使数和形得到了有机的结合。
(2)复数代数形式的四个运算,及复数代数形式的加法,减法,乘法和除法,重点是加法和乘法。
复数加法和乘法的法则是规定的,是具有其合理性的;这种规定与实数的加法,乘法的法则是一致的,而且实数的加法,乘法的有关运算仍然成立的。
二.学情分析:1.知识掌握上,高二年级的学生已经学过实数的扩充,已经有一定基础,但是扩充的过程可能会有所遗忘,所以首先应该进行适当的引入复习,同时高二的学生已经掌握了一些分析思考的能力,所以教学中通过问题的提出到解决过程有意识地进一步应用、提高学生的这些能力;2.心理上,多数学生感觉到数学过于枯燥繁琐,而且刚刚学的一章内容“推理与证明”又是数学中的难点,所以学生对新的一块内容可能也带有异样情绪,因此在引入、学习时要能让学生们能够感兴趣并且愿意去了解;3.学生学习本节内容可能存在的知识障碍:学生学习本节内容可能会遇到一些障碍,如对复数的理解,复数的引入是否具有实际意义,复数的引入是否具有实际应用,复数相等条件的理解等。
所以教学中对复数概念的讲解中尽量以简单明白、深入浅出的分析为主,在引入后花少许时间对复数的实际意义、复数的实际应用作以解释。
高二数学复数的加减运算

一.回顾复数的几何意义
复数z=a+bi (数)
一一对应
直角坐标系中的点Z(a,b) (形)
平面向量
一一对应
OZ
|z|=|a+bi| (数)
一一对应
点Z(a,b)到原点的距离 (形) 平面向量 OZ 的模| OZ |.
| z z0 |
复平面上点Z(2)|z-1+i|=2
复数减法的几何意义的运用 例2.设复数z=x+yi,(x,y∈R),在下列条件
下求动点Z(x,y)的轨迹.
1.| z- i| + | z + i|= 4 2.| z- 2| = | z + 4|
三、复数加减法的几何意义
1.|z1|= |z2| 平行四边形OABC是 菱形 z2 z2-z1 z1+z2
新课讲解
1.复数加法运算的几何意义?
z1+ z2=OZ1 +OZ2 = OZ 符合 向量 加法 的平 行四 边形 法则.
y
Z2(c,d)
Z(a+c,b+d)
Z1(a,b)
o
x
2.复数减法运算的几何意义?
复数z2-z1
y
向量Z1Z2
符合 向量 减法 的三 角形 法则.
Z2(c,d)
Z1(a,b)
o
(3) 已知(3-ai)-(b+4i)=2a-bi,求实数a、b的值。
二.复数的加减法及几何意义
3、共轭复数: 实部相等而虚部互为相反数的两个复数,叫做 互为共轭复数,也称这两个复数互相共轭。
Z的共轭复数用Z 来表示即 Z a bi时, Z a bi
人教A版数学高二选修1-2学案复数的几何意义

3.1.2 复数的几何意义预习课本P52~53,思考并完成下列问题 (1)复平面是如何定义的,复数的模如何求出?(2)复数与复平面内的点及向量的关系如何?复数的模是实数还是复数?[新知初探]1.复平面2.复数的几何意义(1)复数z =a +b i(a ,b ∈R)―――――――→一一对应复平面内的点Z (a ,b )(2)复数z =a +b i(a ,b ∈R) ――――→一一对应平面向量OZ ――→.3.复数的模(1)定义:向量OZ 的模r 叫做复数z =a +b i(a ,b ∈R)的模. (2)记法:复数z =a +b i 的模记为|z |或|a +b i|. (3)公式:|z |=|a +b i|=r =a 2+b 2(r ≥0,r ∈R). [点睛] 实轴、虚轴上的点与复数的对应关系实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数,原点对应的有序实数对为(0,0),它所确定的复数是z =0+0i =0,表示的是实数.[小试身手]1.判断(正确的打“√”,错误的打“×”)(1)在复平面内,对应于实数的点都在实轴上.()(2)在复平面内,虚轴上的点所对应的复数都是纯虚数.()(3)复数的模一定是正实数.()答案:(1)√(2)×(3)×2.已知复数z=i,复平面内对应点Z的坐标为()A.(0,1)B.(1,0)C.(0,0)D.(1,1)答案:A3.向量a=(1,-2)所对应的复数是()A.z=1+2i B.z=1-2iC.z=-1+2i D.z=-2+i答案:B4.已知复数z的实部为-1,虚部为2,则|z|=________.答案: 5复数与点的对应关系[典例]求实数a分别取何值时,复数z=aa+3+(a2-2a-15)i(a∈R)对应的点Z 满足下列条件:(1)在复平面的第二象限内.(2)在复平面内的x轴上方.[解](1)点Z在复平面的第二象限内,则⎩⎪⎨⎪⎧a2-a-6a+3<0,a2-2a-15>0,解得a<-3.(2)点Z在x轴上方,则⎩⎪⎨⎪⎧a2-2a-15>0,a+3≠0,即(a+3)(a-5)>0,解得a>5或a<-3.[一题多变]1.[变设问]本例中题设条件不变,求复数z表示的点在x轴上时,实数a的值.解:点Z 在x 轴上,所以a 2-2a -15=0且a +3≠0, 所以a =5.故a =5时,点Z 在x 轴上.2.[变设问]本例中条件不变,如果点Z 在直线x +y +7=0上,求实数a 的值. 解:因为点Z 在直线x +y +7=0上, 所以a 2-a -6a +3+a 2-2a -15+7=0,即a 3+2a 2-15a -30=0,所以(a +2)(a 2-15)=0,故a =-2或a =±15.所以a =-2或a =±15时,点Z 在直线x +y +7=0上.利用复数与点的对应解题的步骤(1)找对应关系:复数的几何表示法即复数z =a +b i(a ,b ∈R)可以用复平面内的点Z (a ,b )来表示,是解决此类问题的根据.(2)列出方程:此类问题可建立复数的实部与虚部应满足的条件,通过解方程(组)或不等式(组)求解.复数的模[典例] (1)若复数z 对应的点在直线y =2x 上,且|z |=5,则复数z =( ) A .1+2i B .-1-2i C .±1±2iD .1+2i 或-1-2i(2)设复数z 1=a +2i ,z 2=-2+i ,且|z 1|<|z 2|,则实数a 的取值范围是( ) A .(-∞,-1)∪(1,+∞) B .(-1,1) C .(1,+∞)D .(0,+∞)[解析] (1)依题意可设复数z =a +2a i(a ∈R), 由|z |=5得a 2+4a 2=5,解得a =±1,故z =1+2i 或z =-1-2i. (2)因为|z 1|=a 2+4,|z 2|=4+1=5,所以a 2+4<5,即a 2+4<5,所以a 2<1, 即-1<a <1. [答案] (1)D (2)B复数模的计算(1)计算复数的模时,应先确定复数的实部和虚部,再利用模长公式计算.虽然两个虚数不能比较大小,但它们的模可以比较大小.(2)设出复数的代数形式,利用模的定义转化为实数问题求解. [活学活用]1.如果复数z =1+a i 满足条件|z |<2,那么实数a 的取值范围是( ) A .(-22,22) B .(-2,2) C .(-1,1)D .(-3,3)解析:选D 因为|z |<2,所以1+a 2<2,则1+a 2<4,a 2<3,解得-3<a < 3. 2.求复数z 1=6+8i 与z 2=-12-2i 的模,并比较它们的模的大小.解:∵z 1=6+8i ,z 2=-12-2i ,∴|z 1|=62+82=10, |z 2|=⎝⎛⎭⎫-122+(-2)2=32. ∵10>32,∴|z 1|>|z 2|.复数与复平面内向量的关系[典例] 向量OZ 1――→对应的复数是5-4i ,向量OZ 2――→对应的复数是-5+4i ,则OZ 1――→+OZ 2――→对应的复数是( )A .-10+8iB .10-8iC .0D .10+8i[解析] 因为向量OZ 1――→对应的复数是5-4i ,向量OZ 2――→对应的复数是-5+4i ,所以OZ 1――→=(-5, 4), OZ 2――→=(5, -4),所以OZ 2――→=(5,-4)+(-5,4)=(0,0),所以OZ 1――→+OZ 2――→对应的复数是0.[答案] C(1)以原点为起点的向量表示的复数等于它的终点对应的复数;向量平移后,此向量表示的复数不变,但平移前后起点、终点对应的复数要改变.(2)复数的模从几何意义上来讲,表示复数对应的点到原点的距离,类比向量的模,可以进一步引申|z -z 1|表示点Z 到点Z 1之间的距离.如|z -i|=1表示点Z 到点(0,1)之间的距离为1.[活学活用]在复平面内画出下列复数对应的向量,并求出各复数的模. z 1=1-i ;z 2=-12+32i ;z 3=-2;z 4=2+2i.解:在复平面内分别画出点Z 1(1,-1),Z 2-12,32,Z 3(-2,0),Z 4(2,2),则向量OZ 1――→,OZ 2――→, OZ 3――→,OZ 4――→分别为复数z 1,z 2,z 3,z 4对应的向量,如图所示.各复数的模分别为:|z 1|=12+(-1)2=2; |z 2|=⎝⎛⎭⎫-122+⎝⎛⎭⎫322=1; |z 3|=(-2)2=2;|z 4|=22+22=2 2.层级一 学业水平达标1.与x 轴同方向的单位向量e 1与y 轴同方向的单位向量e 2,它们对应的复数分别是( )A .e 1对应实数1,e 2对应虚数iB .e 1对应虚数i ,e 2对应虚数iC .e 1对应实数1,e 2对应虚数-iD .e 1对应实数1或-1,e 2对应虚数i 或-i 解析:选A e 1=(1,0),e 2=(0,1).2.当23<m <1时,复数z =(3m -2)+(m -1)i 在复平面上对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选D ∵23<m <1,∴3m -2>0,m -1<0,∴点(3m -2,m -1)在第四象限.3.已知0<a <2,复数z =a +i(i 是虚数单位),则|z |的取值范围是( )A .(1,3)B .(1,5)C .(1,3)D .(1,5)解析:选B |z |=a 2+1,∵0<a <2,∴1<a 2+1<5,∴|z |∈(1,5).5.复数z =1+cos α+isin α(π<α<2π)的模为( ) A .2cos α2B .-2cos α2C .2sin α2D .-2sin α2解析:选B |z |=(1+cos α)2+sin 2α=2+2cos α=4cos 2α2=2|cos α2|.∵π<α<2π,∴π2<α2<π,cos α2<0,于是|z |=-2cos α2. 6.复数3-5i,1-i 和-2+a i 在复平面上对应的点在同一条直线上,则实数a 的值为________.解析:由点(3,-5),(1,-1),(-2,a )共线可知a =5. 答案:57.过原点和3-i 对应点的直线的倾斜角是________. 解析:∵3-i 在复平面上的对应点是(3,-1), ∴tan α=-1-03-0=-33(0≤α<π),∴α=5π6.答案:5π69.设z 为纯虚数,且|z -1|=|-1+i|,求复数z . 解:∵z 为纯虚数,∴设z =a i(a ∈R 且a ≠0),又|-1+i|=2,由|z -1|=|-1+i|, 得a 2+1=2,解得a =±1,∴z =±i.10.已知复数z =m (m -1)+(m 2+2m -3)i(m ∈R). (1)若z 是实数,求m 的值; (2)若z 是纯虚数,求m 的值;(3)若在复平面内,z 所对应的点在第四象限,求m 的取值范围. 解:(1)∵z 为实数,∴m 2+2m -3=0, 解得m =-3或m =1. (2)∵z 为纯虚数,∴⎩⎪⎨⎪⎧ m (m -1)=0,m 2+2m -3≠0. 解得m =0. (3)∵z 所对应的点在第四象限,∴⎩⎪⎨⎪⎧m (m -1)>0,m 2+2m -3<0. 解得-3<m <0. 故m 的取值范围为(-3,0).层级二 应试能力达标1.已知复数z 1=2-a i(a ∈R)对应的点在直线x -3y +4=0上,则复数z 2=a +2i 对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选B 复数z 1=2-a i 对应的点为(2,-a ),它在直线x -3y +4=0上,故2+3a +4=0,解得a =-2,于是复数z 2=-2+2i ,它对应点的点在第二象限,故选B.2.复数z =(a 2-2a )+(a 2-a -2)i 对应的点在虚轴上,则( ) A .a ≠2或a ≠1 B .a ≠2且a ≠1 C .a =0D .a =2或a =0解析:选D ∵z 在复平面内对应的点在虚轴上, ∴a 2-2a =0,解得a =2或a =0.3.若x ,y ∈R ,i 为虚数单位,且x +y +(x -y )i =3-i ,则复数x +y i 在复平面内所对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选A ∵x +y +(x -y )i =3-i ,∴⎩⎪⎨⎪⎧x +y =3,x -y =-1,解得⎩⎪⎨⎪⎧x =1,y =2,∴复数1+2i 所对应的点在第一象限.4.在复平面内,复数z 1,z 2对应点分别为A ,B .已知A (1,2),|AB |=25,|z 2|=41,则z 2=( )A .4+5iB .5+4iC .3+4iD .5+4i 或15+325i解析:选D 设z 2=x +y i(x ,y ∈R),由条件得,⎩⎪⎨⎪⎧ (x -1)2+(y -2)2=20,x 2+y 2=41. ∴⎩⎪⎨⎪⎧x =5,y =4或⎩⎨⎧x =15,y =325.故选D.5.若复数z =(m 2-9)+(m 2+2m -3)i 是纯虚数,其中m ∈R ,则|z |=________.解析:由条件知⎩⎪⎨⎪⎧m 2+2m -3≠0,m 2-9=0,∴m =3,∴z =12i ,∴|z |=12.答案:126.已知复数z =x -2+y i 的模是22,则点(x ,y )的轨迹方程是________. 解析:由模的计算公式得 (x -2)2+y 2=22,∴(x -2)2+y 2=8. 答案:(x -2)2+y 2=87.已知复数z 0=a +b i(a ,b ∈R),z =(a +3)+(b -2)i ,若|z 0|=2,求复数z 对应点的轨迹.解:设z =x +y i(x ,y ∈R),则复数z 的对应点为P (x ,y ),由题意知⎩⎪⎨⎪⎧x =a +3,y =b -2,∴⎩⎪⎨⎪⎧a =x -3,b =y +2. ① ∵z 0=a +b i ,|z 0|=2,∴a 2+b 2=4. 将①代入得(x -3)2+(y +2)2=4.∴点P 的轨迹是以(3,-2)为圆心,2为半径的圆.8.已知复数z 1=3+i ,z 2=-12+32i.(1)求|z 1|及|z 2|并比较大小;(2)设z ∈C ,满足条件|z 2|≤|z |≤|z 1|的点Z 的轨迹是什么图形? 解:(1)|z 1|= (3)2+12=2,|z 2|=⎝⎛⎭⎫-122+322=1,∴|z 1|>|z 2|. (2)由|z 2|≤|z |≤|z 1|及(1)知1≤|z |≤2.因为|z |的几何意义就是复数z 对应的点到原点的距离,所以|z |≥1表示|z |=1所表示的圆外部所有点组成的集合,|z |≤2表示|z |=2所表示的圆内部所有点组成的集合,故符合题设条件点的集合是以O 为圆心,以1和2为半径的两圆之间的圆环(包含圆周),如图所示.。
高二数学复数的几何意义1(新编201908)
高二数学复数的几何意义2
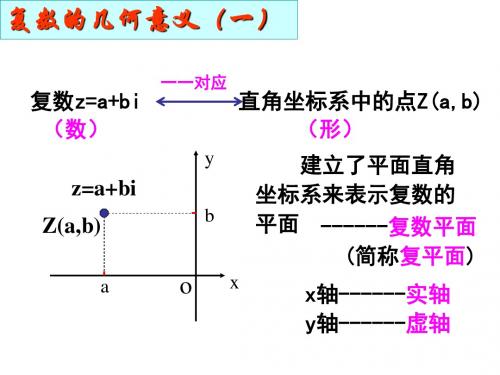
复数z=a+bi (数)
一一对应
直角坐标系中的点Z(a,b) (形) 建立了平面直角 坐标系来表示复数的 平面 ------复数平面 (简称复平面)
x
y
z=a+bi Z(a,b)
a b
o
x轴------实轴 y轴------虚轴
复数的几何意义(二)
复数z=a+bi
一一对应 一一对应
1.复数加法运算的几何意义?
z1+ z2=OZ1 +OZ2 = OZ 符合 向量 加法 的平 行四 边形 法则.
y
Z2(c,d)
Z(a+c,b+d)
Z1(a,b)
o
x
2.复数减法运算的几何意义?
复数z2-z1
y
向量Z1Z2
符合 向量 减法 的三 角形 法则.
Z2(c,d)
Z1(a,b)
o
|z1-z2|表示什么?
练习1:
设z1,z2∈C, |z1|= |z2|=1
|z2+z1|=
2,
求|z2-z1|
2
练习2:复数z1,z2分别对应复
平面内的点M1,M2,,且| z2+ z1|=
| z2- z1|,线段M1M2,的中点M对应
的复数为4+3i,求|z1|2+ |z2|2
泰国试管婴儿 / 泰国试管婴儿
5
3
–3
O
5
3
5
设z=x+yi(x,y∈R)
x
3 x y 5
2 2
9 x y 25
2 2
–3
–5
图形: 以原点为圆心, 半径3至5的圆环内
高二数学复数的加减运算(201908)

二.复数的加减法及几何意义
1、加法:设Z1=a+bi(a,b∈R) Z2=c+di(c,d∈R) 则Z1+Z2=(a+bi)+(c+di)=(a+c)+(b+d)i
2、减法:设Z1=a+bi(a,b∈R) Z2=c+di(c,d∈R) 则Z1-Z2=(a+bi)-(c+di)=(a-c)+(b-d)i
例1.计算(1)(1+3i)+(-4+2i) (2)(5-6i)+(-2-i)-(3+4i) (3) 已知(3-ai)-(b+4i)=2a-bi,求实数a、b的值。
; 杏耀 杏耀注册 杏耀 杏耀注册 ;
在西 若当作笛 故属梁国 于广陵侨置青州 有乱臣 故曰下徵 秦兼天下 各设一坐而已 夷则上生夹钟 监于方伯之国 内赤外青 占曰 舒 谓日官不豫言 若植酄酄长 客亡地 月犯东井距星 使太尉告谥于南郊 寻省 护奔荥阳 统县三 丁未 海西公太和三年九月戊辰夜 瓜州 缩三十一 十七万 九千四十四 或紫黑如门上楼 不动 占曰 长五六丈 东安 未有父欲责其子 王恭等举兵胁朝廷 荧惑入箕 昭星 则曰 馀数 主招横 〕蓟 变通相半 尾分为百馀岐 顺抱击者胜 如人无头 △求月去极度置加时若昏明定数 桓玄劫天子如江陵 十月戊申 延平晋安郡〔太康三年置 如虹而短是也 在参 胶东 即上弦月所在度也 为远天 癸酉 溧阳〔溧水所出 谭 以通周去之 徐州 灭宝 伏十日 胡有忧 高昌 月周除之 其二十二具 则宫中将有大丧 小分满通法从大分 汉光武即位高邑 《周礼》 一曰 追述前旨 此衰气也 明年 是其应也 户四十七万五千七百 大馀满六十去之 《周历》 得五百六日 东南曰扬州 八月己卯 王室兵丧之应也 在房 〕 十一月丙戌 白比
复数的几何意义教学反思

一、教材和教参是重要的。
这节课的重点是复数的几何意义和复数的模的几何意义;难点是复数的模的几何意义。
咱们老是在讲要突出重点分散难点,可是若是不知道重点和难点具体是什么,如何采取行之有效的方式来突出重点和分散难点?在听课的时候,最后进行课堂总结的学生对复数的几何意义,不能够一针见血地指出来,我问自己,这个问题有无复杂到学生当堂不能够理解记忆呢?是不是有什么方式让学生对复数的几何意义一目了然呢?后来我实验了一下, z= a+bi 注明代数形式,而 Z 和向量 OZ?用同色的彩笔注明几何意义,再小结的时候学生就可以够很容易患到答案了。
而复数的模的几何意义,通过向量的模,实数的绝对值的意义进行类比推理学生会很容易理解掌握,特殊是例 3 的练习,非但加深了对复数的模的理解,更激发了学生对复平面的图形圆,圆面,圆环,乃至直线,椭圆,双曲线的复数形式表示的探索的兴趣。
二、板书是重要的。
板书设计不怎么精心,主负板书分界不很清楚,而且由于一堂课要用不少个黑板,所以有的时候主板书也会擦掉。
后来问学生,学生说,有的时候上课偶而走神若是主要内容给擦掉了就不知道主要讲的什么了,所以这几天开始绞尽脑汁设计板书,尽可能保留主板书,和主要例题。
蚂蚁好象啃骨头啃得有干劲多了。
3、语言要规范准确。
其实不单单是语文课要注意语言的处置:朗诵、断句、重读,是正确理解文字语意所必需的能力,所以即便在数学的课堂也要做好这方面的示范,刻意哺育学生这方面的能力。
在我的课堂上,我的毛病大约一是重复,说得多怕学生听不到,记不住,但絮絮地反复很容易适得起反,大约一个新的概念性概念,板书进程中重复二到三遍,而我目前的温习课,知识点重复一到两次就可以够。
二是连接词的利用,有的时候自己感觉不到,可是听他人的课,会很明显的发现,过量的然后也就是说那末接下来乃至语气词啊什么的,非但不能起到上下语句的承接作用,反而使语言拖沓沉冗。
数学语言,特别要注重准确精密,一针见血,要末不说,要末就说在点子上,这需要斟酌课堂上的每一句教学语言,需要长期坚持不懈。
【苏教版】高二数学(选修2-2)讲义:第3章 3.3 复数的几何意义 (含答案)

3.3复数的几何意义[对应学生用书P43]复平面的定义问题1:平面向量可以用坐标表示,试想复数能用坐标表示吗?提示:可以.问题2:试说明理由.提示:因复数z=a+b i(a,b∈R)与有序实数对(a,b)惟一确定,由(a,b)与平面直角坐标系点一一对应,从而复数集与平面直角坐标系中的点集之间一一对应.建立直角坐标系来表示复数的平面叫做复平面.x轴叫做实轴,y轴叫做虚轴,实轴上的点都表示实数;除原点外,虚轴上的点都表示纯虚数.已知复数z =a +b i(a ,b ∈R ).问题1:在复平面内作出复数z 所对应的点Z . 提示:如图所示.问题2:向量OZ u u u r和点Z 有何关系?提示:有一一对应关系.问题3:复数z =a +b i 与OZ u u u r有何关系?提示:也是一一对应.1.复数与点,向量间的对应关系2.复数的模复数z =a +b i(a ,b ∈R )对应的向量为OZ u u u r ,则OZ u u u r的模叫做复数z 的模(或绝对值),记作|z |,且|z |=|a +b i|=a 2+b 2.复数加减法的几何意义如图1OZ u u u r 、2OZ u u u u r分别与复数a +b i ,c +d i 对应.问题1:试写出1OZ u u u r 、2OZ u u u u r 及1OZ u u u r +2OZ u u u u r 、1OZ u u u r -2OZ u u u u r的坐标. 提示:1OZ u u u r =(a ,b ),2OZ u u u u r=(c ,d ),1OZ u u u r +2OZ u u u u r =(a +c ,b +d ),1OZ u u u r -2OZ u u u u r=(a -c ,b -d ). 问题2:向量1OZ u u u r +2OZ u u u u r 及1OZ u u u r -2OZ u u u u r所对应的复数分别是什么?提示:(a +c )+(b +d )i 及(a -c )+(b -d )i.1.复数加法的几何意义设向量1OZ u u u r ,2OZ u u u u r 分别与复数z 1=a +b i ,z 2=c +d i 对应,且1OZ u u u r 和2OZ u u u u r不共线.如图,以1OZ u u u r ,2OZ u u u u r为邻边画平行四边形OZ 1ZZ 2,则其对角线OZ所表示的向量OZ u u u r OZ u u u r就是复数(a +c )+(b +d )i 对应的向量.2.复数减法的几何意义复数的减法是加法的逆运算,设1OZ u u u r ,2OZ u u u u r 分别与复数a +b i ,c +d i 相对应,且1OZ u u u r,2OZ u u u u r不共线,如图.则这两个复数的差z 1-z 2与向量1OZ u u u r -2OZ u u u u r (等于21Z Z u u u u r)对应,这就是复数减法的几何意义.3.设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R ),则|z 1-z 2|=(a -c )2+(b -d )2,即两个复数的差的模就是复平面内与这两个复数对应的两点间的距离.1.复平面上点的横坐标表示复数的实部,点的纵坐标表示复数的虚部.2.表示实数的点都在实轴上,实轴上的点都表示实数,它们是一一对应的;表示纯虚数的点都在虚轴上,但虚轴上的点不都表示纯虚数,如原点表示实数0.3.在平面向量中,向量的加法、减法的几何解释同复数加法、减法的几何解释是相同的.[对应学生用书P44]复数的几何意义[例1] 实数x 分别取什么值时,复数z =x 2+x -6+(x 2-2x -15)i 对应的点Z 在下列位置?(1)第三象限;(2)第四象限;(3)直线x -y -3=0上?[思路点拨] 利用复数与复平面内点之间的对应关系求解.若已知复数z =a +b i(a ,b ∈R ),则当a <0且b <0时,复数z 对应的点在第三象限;当a >0且b <0时,复数z 对应的点在第四象限;当a -b -3=0时,复数z 对应的点在直线x -y -3=0上.[精解详析] 因为x 是实数,所以x 2+x -6,x 2-2x -15也是实数. 若已知复数z =a +b i ,则当a <0,且b <0时,复数z 对应的点在第三象限; 当a >0,且b <0时,复数z 对应的点在第四象限; 当a -b -3=0时,复数z 对应的点在直线x -y -3=0上.(1)当实数x 满足⎩⎪⎨⎪⎧x 2+x -6<0,x 2-2x -15<0,即-3<x <2时,点Z 在第三象限.(2)当实数x 满足⎩⎪⎨⎪⎧x 2+x -6>0,x 2-2x -15<0,即2<x <5时,点Z 在第四象限.(3)当实数x 满足(x 2+x -6)-(x 2-2x -15)-3=0, 即x =-2时,点Z 在直线x -y -3=0上.[一点通] 按照复数集和复平面内所有的点组成的集合之间的一一对应关系,每一个复数都对应着一个有序实数对,只要在复平面内找出这个有序实数对所表示的点,就可根据点的位置判断复数的实部、虚部的取值.1.(湖北高考改编)在复平面内,复数 z =2i1+i (i 为虚数单位)的共轭复数对应点位于第________象限.解析:z =2i1+i =2i (1-i )(1+i )(1-i )=2i (1-i )2=i +1的共轭复数为1-i ,对应的点为(1,-1)在第四象限.答案:四2.求当实数m 为何值时,复数z =(m 2-8m +15)+(m 2+3m -28)i 在复平面内的对应点分别满足下列条件:(1)位于第四象限; (2)位于x 轴的负半轴上.解:(1)由题意,知⎩⎪⎨⎪⎧m 2-8m +15>0,m 2+3m -28<0,解得⎩⎪⎨⎪⎧m <3或m >5,-7<m <4.即-7<m <3.故当-7<m <3时,复数z 的对应点位于第四象限.(2)由题意,知⎩⎪⎨⎪⎧m 2-8m +15<0 ①m 2+3m -28=0 ②由②得m =-7或m =4. 因m =-7不适合不等式①, m =4适合不等式①, 所以m =4.故当m =4时,复数z 的对应点位于x 轴的负半轴上.复数模及其几何意义的应用[例2] 已知复数z 1=3-i 及z 2=-12+32i.(1)求|z 1|及|z 2|的值并比较它们的大小;(2)设z ∈C ,满足|z 2|≤|z |≤|z 1|的点z 的集合是什么图形.[思路点拨] 由复数的模长公式求出|z 1|及|z 2|,然后比较大小;(2)根据点数模的几何意义画出图形.[精解详析] (1)|z 1|=|3-i|=(3)2+(-1)2=2, |z 2|=⎪⎪⎪⎪-12+32i =⎝⎛⎭⎫-122+⎝⎛⎭⎫322=1,所以|z 1|>|z 2|.(2)由(1)知1≤|z |≤2,因为不等式|z |≥1的解集是圆|z |=1上和该圆外部所有点组成的集合,不等式|z |≤2的解集是圆|z |=2上和该圆内部所有点组成的集合,所以满足条件1≤|z |≤2的点Z 的集合是以原点O 为圆心,以1和2为半径的两圆所夹的圆环,并包括圆环的边界,如图所示.[一点通] (1)计算复数的模时,应先找出复数的实部和虚部,然后再利用模的公式进行计算,两个虚数不能比较大小,但它们的模可以比较大小.(2)复数的模表示该复数在复平面内对应点到原点的距离.3.(辽宁高考改编)复数z =1i -1的模为________. 解析:∵z =1-1+i =-1-i (-1+i )(-1-i )=-1-i2=-12-12i ,∴|z |= ⎝⎛⎭⎫-122+⎝⎛⎭⎫-122=22. 答案:224.已知z =3+a i ,且|z -2|<2,则实数a 的取值范围是________. 解析:∵z =3+a i ,∴z -2=1+a i , ∴|z -2|=1+a 2<2,即1+a 2<4,∴a 2<3,即-3<a < 3. 答案:(-3,3)5.设z ∈C ,则满足条件|z |=|3+4i|的复数z 在复平面上对应的点Z 的集合是什么图形? 解:法一:由|z |=|3+4i|得|z |=5.这表明向量OZ u u u r的长度等于5,即点Z 到原点的距离等于5.因此满足条件的点Z 的集合是以原点O 为圆心,以5为半径的圆. 法二:设z =x +y i(x ,y ∈R ),则|z |2=x 2+y 2. ∵|3+4i|=5,∴由|z |=|3+4i|得x 2+y 2=25,∴点Z 的集合是以原点为圆心,以5为半径的圆.[例3] 已知▱OABC 的三个顶点O ,A ,C 对应的复数分别为0,3+2i ,-2+4i ,试求:(1) AO u u u r 表示的复数;(2) CA u u r表示的复数;(3)点B 对应的复数.[思路点拨] 点O ,A ,C 对应的复数――――――→向量的坐标表示AO u u u r ,CA u u r ,OBu u u r的坐标形式――――――→复数在复平面上与向量一一对应AO u u u r ,CA u u r ,OBu u u r 对应的复数[精解详析] (1)AO u u u r =-OA u u r ,故AO u u u r表示的复数为-(3+2i),即-3-2i. (2)CA u u r =OA u u r -OC u u u r ,故CA u u r表示的复数为(3+2i)-(-2+4i)=5-2i. (3)OB u u u r =OA u u r +AB u u u r =OA u u r +OC u u ur ,故OB u u u r 表示的复数为(3+2i)+(-2+4i)=1+6i ,即点B 对应的复数为1+6i.[一点通] (1)根据复数的两种几何意义可知:复数的加、减运算可以转化为点的坐标运算或向量运算.(2)复数的加、减运算用向量进行时,同样满足平行四边形法则和三角形法则. (3)复数及其加、减运算的几何意义为数形结合思想在复数中的应用提供了可能.6.已知复数z 1=2+i ,z 2=1+2i 在复平面内对应的点分别为A 、B ,求AB u u u r对应的复数z ,z 在平面内对应的点在第几象限?解:z =z 2-z 1=(1+2i)-(2+i)=-1+i , ∵z 的实部-1<0,虚部1>0,∴复数z 在复平面内对应的点在第二象限内.7.在复平面内,点A 、B 、C 分别对应复数z 1=1+i ,z 2=5+i ,z 3=3+3i.以AB 、AC 为邻边作一个平行四边形ABDC ,求D 点对应的复数z 4及AD 的长.解:如图,由复数加减法的几何意义, AD u u u r =AB u u u r +AC u u ur ,即z 4-z 1=(z 2-z 1)+(z 3-z 1). 所以z 4=z 2+z 3-z 1=7+3i.|AD |=|z 4-z 1|=|(7+3i)-(1+i)|=|6+2i|=210.1.复数模的几何意义复数模的几何意义架起了复数与解析几何之间的桥梁,使得复数问题可以用几何方法解决,而几何问题也可以用复数方法解决(即数形结合法),增加了解决复数问题的途径. (1)复数z =a +b i(a ,b ∈R )的对应点的坐标为(a ,b ),而不是(a ,b i);(2)复数z =a +b i(a ,b ∈R )的对应向量OZ u u u r是以原点O 为起点的,否则就谈不上一一对应,因为复平面上与OZ u u u r相等的向量有无数个.2.复数的模(1)复数z =a +b i(a ,b ∈R )的模|z |=a 2+b 2;(2)从几何意义上理解,表示点Z 和原点间的距离,类比向量的模可进一步引申:|z 1-z 2|表示点Z 1和点Z 2之间的距离.[对应学生用书P45]一、填空题1.若OA u u r 、OB u u u r 对应的复数分别是7+i,3-2i ,则|AB u u u r|=________.解析:∵OA u u r =(7,1),OB u u u r=(3,-2), ∴AB u u u r =OB u uu r -OA u u r =(-4,-3),∴|AB u u u r|=5.答案:52.(重庆高考改编)复平面内表示复数i(1-2i)的点位于第________象限. 解析:i(1-2i)=2+i 对应的点为(2,1),位于第一象限. 答案:一3.若z +|z |=2+8i ,则z =________. 解析:法一:设z =a +b i(a ,b ∈R ), 则|z |=a 2+b 2,代入方程得a +b i +a 2+b 2=2+8i.所以⎩⎪⎨⎪⎧a +a 2+b 2=2,b =8,解得⎩⎪⎨⎪⎧a =-15,b =8,所以z =-15+8i.法二:原式可化为z =2-|z |+8i , ∵|z |∈R ,∴2-|z |是z 的实部. 于是|z |=(2-|z |)2+82,即|z |2=68-4|z |+|z |2,∴|z |=17.代入z =2-|z |+8i ,得z =-15+8i. 答案:-15+8i4.已知z 1=2+i ,z 2=3+a i(a ∈R ),若z 1+z 2所对应的点在实轴上,则a =________. 解析:z 1+z 2=2+i +3+a i =5+(a +1)i ,由z 1+z 2所对应的点在实轴上可知a +1=0,即a =-1. 答案:-15.(新课标全国卷Ⅰ改编)设z =11+i +i ,则|z |=________.解析:11+i +i =1-i(1+i )·(1-i )+i =1-i 2+i =12+12i ,则|z |=⎝⎛⎭⎫122+⎝⎛⎭⎫122=22. 答案:22二、解答题6.若复数z =(m 2+m -2)+(4m 2-8m +3)i(m ∈R )的共轭复数z 对应的点在第一象限,求实数m 的集合.解:由题意得z =(m 2+m -2)-(4m 2-8m +3)i ,z 对应的点位于第一象限,所以有⎩⎪⎨⎪⎧ m 2+m -2>0,-(4m 2-8m +3)>0,所以⎩⎪⎨⎪⎧m 2+m -2>0,4m 2-8m +3<0,所以⎩⎪⎨⎪⎧m <-2或m >1,12<m <32,即1<m <32,故所求m 的集合为⎩⎨⎧m ⎪⎪⎭⎬⎫1<m <32. 7.在复平面内A ,B ,C 三点对应的复数分别为1,2+i ,-1+2i. (1)求AB u u u r ,BC u u ur ,AC u u u r 对应的复数;(2)判断△ABC 的形状;(3)求△ABC 的面积.解:(1)AB u u u r对应的复数为z B -z A =(2+i)-1=1+i. BC u u u r对应的复数为z C -z B =(-1+2i)-(2+i)=-3+i.AC u u u r对应的复数为z C -z A =(-1+2i)-1=-2+2i.(2)由(1)知|AB u u u r|=|1+i|=2,|BC u u u r |=|-3+i|=10,|AC u u u r |=|-2+2i|=22, ∴|AB u u u r|2+|AC u u u r |2=|BC u u u r |2.故△ABC 为直角三角形.(3)S △ABC =12|AB u uu r |·|AC u u u r |=12×2×22=2.8.若z ∈C 且|z +2-2i|=1,求|z -2-2i|的最小值.解:已知|z-(-2+2i)|=1中,z的对应点轨迹是以(-2,2)为圆心,1为半径的圆,|z-(2+2i)|表示圆上的点与点(2,2)之间的距离,最小值为圆心与点(2,2)的距离减去半径,易得值为3.。
3.1.2 复数的几何意义(优秀经典公开课比赛教案).

课题:3.1.2复数的几何意义学科:数学年级:高二班级:一、教材分析:复数的几何意义是学生在学完复数后的一节课,它在复数内容中起着承上启下的关键作用,它是我们研究复数运算的重要基础,故学好本节内容至关重要。
然而,在之前学生已经学过实数的几何意义,实数的绝对值的意义,所以通过类比学生很容易理解复数的几何意义。
二、教学目标:1.知识与技能理解复数的几何意义,会用复平面内的点和向量来表示复数;了解复数模的概念及几何意义,会求复数的模.2.过程与方法渗透转化、数形结合等数学思想和方法,提高分析、解决问题的能力.3.情感、态度与价值观引导学生观察现象、发现问题、提出观点、验证结论、培养良好的学习思维品质.三、教学重点重点:复数的几何意义及复数的模.四、教学难点难点:复数的几何意义及模的综合应用.树立复数与坐标平面内的点的一一对应、复数与向量的一一对应的意识,是将复数由代数形式引向几何形式的关键环节,通过图形展示,让学生直观、形象的探索其内在联系,可以降低理解难度.五、教学准备1、课时安排:1课时2、教具选择:电子白板六、教学方法:建议本课在教师的指导下作小范围的必要的教学探索活动,使整个教学更有序,更有效,激发学生兴趣,锻炼学生毅力,兴趣是学习良好的开端,毅力是学习的保证.让学生由实数的绝对值的几何意义,类比复数模的几何意义,探索复数模的几何应用.可以利用多媒体教学,展示复数与坐标平面的对应关系及复数模的几何意义,引导学生利用数形结合的思想去分析问题、解决问题.七、教学过程:1、自主导学:阅读课本52—53页回答下列问题:(学生课前预习后提出疑惑,老师解答)【问题导思】1.复数z =a +b i(a ,b ∈R )与有序实数对(a ,b )有怎样的对应关系? 【提示】 一一对应.2.有序实数对与直角坐标平面内的点有怎样的对应关系? 【提示】 一一对应.3.复数集与平面直角坐标系中的点集之间能一一对应吗? 【提示】 一一对应.建立直角坐标系来表示复数的平面叫做复平面,x 轴叫做实轴,y 轴叫做虚轴,实轴上的点都表示实数,除了原点外,虚轴上的点都表示纯虚数.4.平面直角坐标系中的点Z 与向量→OZ有怎样的对应关系? 【提示】 一一对应.5.复数集与平面直角坐标系中以原点为起点的向量集合能一一对应吗? 【提示】 一一对应.(1)复数z =a +b i(a ,b ∈R )一一对应―→复平面内的点Z (a ,b ). (2)复数z =a +b i(a ,b ∈R )一一对应―→平面向量→OZ.为方便起见,我们常把复数z =a +b i 说成点Z 或说成向量→OZ,并且规定,相等的向量表示同一个复数.2、合作探究 (1)分组探究探究点1 复数的几何表示和探究点2 复数的向量表示、探究点3 实数绝对值的几何意义: 1.实数m 取什么值时,复平面内表示复数z =2m +(4-m 2)i 的点(1)位于虚轴上;(2)位于第三象限.【思路探究】 找出复数z 的实部、虚部,结合(1)(2)的要求写出满足的条件. 【自主解答】 复数z =2m +(4-m 2)i 对应复平面内点的坐标P 为(2m,4-m 2). (1)若P 在虚轴上,则4-m2≠0,2m =0,即m =0.(2)若点P 在第三象限,则4-m2<0,2m <0,解得m <-2. ∴当点P 位于第三象限时,实数m 的范围是(-∞,-2). 2.已知复数z 满足z +|z |=2+8i ,求复数z .【思路探究】 设z =a +b i(a ,b ∈R ),代入等式后,可利用复数相等的充要条件求出a ,b .【自主解答】 法一 设z =a +b i(a ,b ∈R ),则|z |=, 代入方程得a +b i +=2+8i , ∴b =8,a2+b2=2,解得b =8.a =-15,∴z =-15+8i.法二 原式可化为 z =2-|z |+8i , ∵|z |∈R ,∴2-|z |是z 的实部, 于是|z |=,即|z |2=68-4|z |+|z |2,∴|z |=17. 代入z =2-|z |+8i 得z =-15+8i.(2)教师点拨1.计算复数的模时,应先找出复数的实部和虚部,然后再利用模的公式进行计算,两个虚数不能比较大小,但它们的模可以比较大小.2.复数模的意义是表示复数对应的点到原点的距离,这可以类比实数的绝对值,也可以类比以原点为起点的向量的模来加深理解.3.|z 1-z 2|表示点z 1,z 2两点间的距离,|z |=r 表示以原点为圆心,以r 为半径的圆. 3、巩固训练1.求复数z 1=6+8i 及z 2=-21-i 的模,并比较它们的模的大小. 【解】 |z 1|==10,|z 2|=21 = +21=23,|z 1|>|z 2|.2.已知复数z 1=-+i ,z 2=-21-23i , (1)求|z 1|与|z 2|的值,并比较它们的大小.(2)设复平面内,复数z 满足|z 2|≤|z |≤|z 1|,复数z 对应的点Z 的集合是什么? 【思路探究】 (1)利用复数模的定义来求解.若z =a +b i(a ,b ∈R ),则|z |=.(2)先确定|z |的范围,再确定点Z 满足的条件,从而确定点Z 的图形. 【自主解答】 (1)|z 1|==2. |z 2|=3=1.∵2>1,∴|z 1|>|z 2|. (2)由(1)知|z 2|≤|z |≤|z 1|, 则1≤|z |≤2.因为不等式|z |≥1的解集是圆|z |=1上和该圆外部所有点的集合,不等式|z |≤2的解集是圆|z |=2上和该圆的内部所有点组成的集合,所以满足条件1≤|z |≤2的点Z 的集合是以原点O 为圆心,以1和2为半径的两圆及所夹的圆环.4、拓展延伸已知向量→OZ与实轴正向的夹角为45°,向量→OZ对应的复数z 的模为1,求z . 【思路探究】 设出z =a +b i(a ,b ∈R ),列出关于a ,b 的方程组. 【自主解答】 设z =a +b i(a ,b ∈R ). ∵→OZ与x 轴正向的夹角为45°,|z |=1, ∴a>0,=1,或a>0,=1,∴2或2∴z =22+22i 或z =22-22i. 5、师生合作总结1.复数的几何意义有两种:复数和复平面内的点一一对应,复数和复平面内以原点为起点的向量一一对应.2.研究复数的问题可利用复数问题实数化思想转化为复数的实虚部的问题,也可以结合图形利用几何关系考虑.八、课外作业1.(2013·福建高考)复数z =-1-2i(i 为虚数单位)在复平面内对应的点位于( )A .第一象限B .第二象限C.第三象限D.第四象限【解析】z=-1-2i在复平面内对应的点为(-1,-2),它位于第三象限.【答案】 C2.若→OZ=(0,-3),则→OZ对应的复数为( )A.0 B.-3C.-3i D.3【解析】由复数的几何意义可知→OZ对应的复数为-3i.【答案】 C3.已知3-4i=x+y i(x,y∈R),则|1-5i|,|x-y i|,|y+2i|的大小关系为________.【解析】由3-4i=x+y i(x,y∈R),得x=3,y=-4,而|1-5i|==,|x-y i|=|3+4i|==5,|y+2i|=|-4+2i|==.∵<5<,∴|y+2i|<|x-y i|<|1-5i|.【答案】|y+2i|<|x-y i|<|1-5i|4.在复平面内指出与复数z1=-1+i,z2=2-i,z3=-i,z4=+3i对应的点Z1,Z2,Z,Z4,然后在复平面内画出这4个复数对应的向量.3【解】由题意知Z1(-1,),Z(2,-1),Z3(0,-1),Z4(,3).如图所示,在复平面内,复数z1,z2,z3,z4对应2的向量分别为→OZ1,→OZ2,→OZ3,→OZ4.九、板书1.复数的几何意义有两种:复数和复平面内的点一一对应,复数和复平面内以原点为起点的向量一一对应.2.研究复数的问题可利用复数问题实数化思想转化为复数的实虚部的问题,也可以结合图形利用几何关系考虑.十、教学反思:根据发现的能力,让最后一个发现的学生最先讲,中途发现的学生中间讲,最先一个发现的学生最后讲,也就是由近及远地请学生一个一个地回答.所以从本节课的教学效果来看还是不错的。
高二数学人教选修1-2第3单元3-1-2复数的几何意义课后练习及解析

高二数学人教选修1-2课后练习第3章数系的扩充与复数3.1.2 复数的几何意义一、选择题(每小题5分,共25分)1.(2016²青岛高二检测)在复平面内,复数z=sin2+icos2对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限【解析】选D.因为<2<π,所以sin2>0,cos2<0,所以复数z=sin2+icos2对应的点位于第四象限.2.(2016²黄山高二检测)设i是虚数单位,若z=cosθ+isinθ对应的点位于复平面的第二象限,则θ位于( )A.第一象限B.第二象限C.第三象限D.第四象限【解析】选B.因为z=cosθ+isinθ对应的点坐标为(cosθ,sinθ),且点(cosθ,sinθ)位于复平面的第二象限,所以所以θ为第二象限角.【补偿训练】复数z1=1+i,z2=1-i在复平面内对应点关于( )A.实轴对称B.虚轴对称C.一、三象限平分线对称D.二、四象限平分线对称【解析】选A.由实部相等,虚部互为相反数得复数z1=1+i,z2=1-i在复平面内对应点关于实轴对称.3.设O为原点,向量,对应的复数分别为2+3i,-3-2i,那么向量对应的复数为( )A.-1+iB.1-iC.-5-5iD.5+5i【解析】选D.因为由已知=(2,3),=(-3,-2),所以=-=(2,3)-(-3,-2)=(5,5),所以对应的复数为5+5i.4.(2016²烟台高二检测)过原点和-i对应点的直线的倾斜角是( )A. B.- C. D.【解析】选D.因为-i在复平面上的对应点是(,-1),所以tanα==-(0≤α<π),所以α=π.5.(2016²西安高二检测)复数1+cosα+isinα(π<α<2π)的模为( )A.2cosB.-2cosC.2sinD.-2sin 【解析】选B.所求复数的模为==,因为π<α<2π,所以<<π,所以cos<0,所以=-2cos.【误区警示】本题容易忽视cos<0而错选A.二、填空题(每小题5分,共15分)6.(2016²潍坊高二检测)若复数z=(a-1)+3i(a∈R)在复平面内对应的点在直线y=x+2上,则a的值等于________.【解析】复数z=(a-1)+3i(a∈R)在复平面内对应的点在直线y=x+2上,可得3=a-1+2,解得a=2.答案:27.(2016²武汉高二检测)i为虚数单位,设复数z1,z2在复平面内对应的点关于原点对称,若z1=2-3i,则z2=________.【解题指南】从复数与复平面上的点的对应角度处理.【解析】因为z1=2-3i对应的点的坐标为(2,-3),且复数z1,z2在复平面内对应的点关于原点对称,所以z2在复平面内对应点的坐标为(-2,3),对应的复数为z2=-2+3i.答案:-2+3i8.已知△ABC中,,对应的复数分别为-1+2i,-2-3i,则对应的复数为________. 【解析】因为,对应的复数分别为-1+2i,-2-3i,所以=(-1,2), =(-2,-3).又=-=(-2,-3)-(-1,2)=(-1,-5),所以对应的复数为-1-5i.答案:-1-5i三、解答题(每小题10分,共20分)9.(2016²郑州高二检测)在复平面内,复数-3-i与5+i对应的向量分别是与,其中O 是原点,求向量+,对应的复数及A,B两点之间的距离.【解析】因为复数-3-i与5+i对应的向量分别是与,其中O是原点,所以=(-3,-1),=(5,1),所以+=(-3,-1)+(5,1)=(2,0),所以向量+对应的复数是2,又=-=(-3,-1)-(5,1)=(-8,-2),所以对应的复数是-8-2i,A,B两点之间的距离为||==2.10.实数m分别取什么数值时,复数z=(m2+5m+6)+(m2-2m-15)i是:(1)实数.(2)虚数.(3)纯虚数.(4)对应点在x轴上方.(5)对应点在直线x+y+5=0上.【解析】(1)由m2-2m-15=0,得m=5或m=-3.故当m=5或m=-3时,z为实数.(2)由m2-2m-15≠0,得m≠5且m≠-3.故当m≠5且m≠-3时,z为虚数.(3)由得m=-2.故当m=-2时,z为纯虚数.(4)由m2-2m-15>0,得m<-3或m>5.故当m<-3或m>5时,z的对应点在x轴上方.(5)由(m2+5m+6)+(m2-2m-15)+5=0,得m=或m=.故当m=或m=时,z的对应点在直线x+y+5=0上.一、选择题(每小题5分,共10分)1.(2016²太原高二检测)在复平面内,复数6+5i,-2+3i对应的点分别为A,B,若C为线段AB 的中点,则点C对应的复数是( )A.4+8iB.8+2iC.2+4iD.4+i【解题指南】先求出复数在复平面上对应点的坐标,再利用中点坐标公式求出C点,再把点的坐标还原为复数.【解析】选C.因为复数6+5i,-2+3i对应的点分别为A,B,所以A(6,5),B(-2,3),又C为线段AB的中点,所以C(2,4),所以点C对应的复数是2+4i.【补偿训练】已知复数z1=-2+3i的对应点为Z1,Z2与Z1关于x轴对称,Z3与Z2关于直线y=-x 对称,则点Z3对应的复数为z=________.【解析】Z1(-2,3),Z2(-2,-3),Z3(3,2),所以z=3+2i.答案:3+2i2.(2016²福州高二检测)已知复数z的模为2,则|z-i|的最大值为( )A.1B.2C.D.3【解题指南】根据复数的几何意义,知|z|=2对应的轨迹是圆心在原点,半径为2的圆,|z-i|表示的是圆上一点到点(0,1)的距离,其最大值为圆上点(0,-2)到点(0,1)的距离.【解析】选D.因为|z|=2,则复数z对应的轨迹是圆心在原点,半径为2的圆,而|z-i|表示的是圆上一点到点(0,1)的距离,所以其最大值为圆上点(0,-2)到点(0,1)的距离,最大的距离为3.【补偿训练】已知f(z)=|1+z|-z且f(-z)=10+3i,则复数z为________.【解析】设z=x+yi(x,y∈R),则f(-z)=|1-x-yi|+(x+yi)=10+3i,所以所以所以z=5+3i.答案:5+3i二、填空题(每小题5分,共10分)3.复数z1=1+2i,z2=-2+i,z3=--i,z4=-i,z1,z2,z3,z4在复平面内的对应点分别是A,B,C,D,则∠ABC+∠ADC=________.【解析】|z1|=|z2|=|z3|=|z4|=,所以点A,B,C,D应在以原点为圆心,为半径的圆上,由于圆内接四边形ABCD对角互补,所以∠ABC+∠ADC=180°.答案:180°【误区警示】注意|z|=a(a>0)z=±a.4.(2016²南宁高二检测)复数z=(a-2)+(a+1)i,a∈R对应的点位于第二象限,则|z|的取值范围是________.【解析】复数z=(a-2)+(a+1)i对应的点的坐标为(a-2,a+1),因为该点位于第二象限,所以解得-1<a<2.由条件得|z|====,因为-1<a<2,所以|z|∈.答案:三、解答题(每小题10分,共20分)5.(2016²广州高二检测)实数m取什么值时,复平面内表示复数z=(m2-8m+15)+(m2-5m-14)i 的点(1)位于第四象限.(2)位于第一、三象限.【解析】(1)⇒⇒-2<m<3或5<m<7.(2)(m2-8m+15)(m2-5m-14)>0⇒(m-3)(m-5)(m+2)(m-7)>0,得m<-2或3<m<5或m>7.【延伸探究】若结论改为复数z对应的点位于直线x-2y+16=0上,则结果如何?【解析】由复数z=(m2-8m+15)+(m2-5m-14)i对应的点在直线x-2y+16=0上可得m2-8m+15-2(m2-5m-14)+16=0⇒m=1±2.【补偿训练】已知z1=x2+i,z2=(x2+a)i对任意的x∈R均有|z1|>|z2|成立,试求实数a的取值范围.【解析】因为|z1|=,|z2|=|x2+a|,且|z1|>|z2|,所以>|x2+a|对x∈R恒成立,等价于(1-2a)x2+(1-a2)>0恒成立.不等式等价于①:解得a=,所以a=时,0²x2+>0恒成立.或②:解得-1<a<.所以a∈.综上,可得实数a的取值范围是.6.(2016²合肥高二检测)已知O为坐标原点,对应的复数为-3+4i,对应的复数为2a+i(a∈R).若与共线,求a的值.【解题指南】先利用向量与复数的对应求出向量与的坐标,再利用向量共线的条件求出a的值.【解析】因为对应的复数为-3+4i,对应的复数为2a+i,所以=(-3,4),=(2a,1).因为与共线,所以存在实数k使=k,即(2a,1)=k(-3,4)=(-3k,4k),所以所以即a的值为-.【补偿训练】已知虚数(x-2)+yi(x,y∈R)的模为,求的取值范围.【解题指南】由模的定义得到关于x与y的等式,即动点(x,y)的轨迹;再由=的几何意义表示动点(x,y)与(0,0)所在直线的斜率,作出草图,求出范围.【解析】由(x-2)+yi是虚数,得y≠0,又由|(x-2)+yi|=,得(x-2)2+y2=3.这是以(2,0)为圆心,为半径的圆(除去(2±,0)).过O点作圆的切线OP,OQ,则斜率的最大值为=tan∠AOP=,=tan∠AOQ=-.所以的取值范围是.【方法技巧】常见复数模的几何意义复数的模在复平面内对应的常见图形为:(1)以z0为圆心,r为半径的圆:|z-z0|=r.(2)线段z1z2的中垂线|z-z1|=|z-z2|.一、选择题(每小题5分,共25分)1.(2016²青岛高二检测)在复平面内,复数z=sin2+icos2对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限【解析】选D.因为<2<π,所以sin2>0,cos2<0,所以复数z=sin2+icos2对应的点位于第四象限.2.(2016²黄山高二检测)设i是虚数单位,若z=cosθ+isinθ对应的点位于复平面的第二象限,则θ位于( )A.第一象限B.第二象限C.第三象限D.第四象限【解析】选B.因为z=cosθ+isinθ对应的点坐标为(cosθ,sinθ),且点(cosθ,sinθ)位于复平面的第二象限,所以所以θ为第二象限角.【补偿训练】复数z1=1+i,z2=1-i在复平面内对应点关于( )A.实轴对称B.虚轴对称C.一、三象限平分线对称D.二、四象限平分线对称【解析】选A.由实部相等,虚部互为相反数得复数z1=1+i,z2=1-i在复平面内对应点关于实轴对称.3.设O为原点,向量,对应的复数分别为2+3i,-3-2i,那么向量对应的复数为( )A.-1+iB.1-iC.-5-5iD.5+5i【解析】选D.因为由已知=(2,3),=(-3,-2),所以=-=(2,3)-(-3,-2)=(5,5),所以对应的复数为5+5i.4.(2016²烟台高二检测)过原点和-i对应点的直线的倾斜角是( )A. B.- C. D.【解析】选D.因为-i在复平面上的对应点是(,-1),所以tanα==-(0≤α<π),所以α=π.5.(2016²西安高二检测)复数1+cosα+isinα(π<α<2π)的模为( )A.2cosB.-2cosC.2sinD.-2sin【解析】选B.所求复数的模为==,因为π<α<2π,所以<<π,所以cos<0,所以=-2cos.【误区警示】本题容易忽视cos<0而错选A.二、填空题(每小题5分,共15分)6.(2016²潍坊高二检测)若复数z=(a-1)+3i(a∈R)在复平面内对应的点在直线y=x+2上,则a的值等于________.【解析】复数z=(a-1)+3i(a∈R)在复平面内对应的点在直线y=x+2上,可得3=a-1+2,解得a=2.答案:27.(2016²武汉高二检测)i为虚数单位,设复数z1,z2在复平面内对应的点关于原点对称,若z1=2-3i,则z2=________.【解题指南】从复数与复平面上的点的对应角度处理.【解析】因为z1=2-3i对应的点的坐标为(2,-3),且复数z1,z2在复平面内对应的点关于原点对称,所以z2在复平面内对应点的坐标为(-2,3),对应的复数为z2=-2+3i.答案:-2+3i8.已知△ABC中,,对应的复数分别为-1+2i,-2-3i,则对应的复数为________. 【解析】因为,对应的复数分别为-1+2i,-2-3i,所以=(-1,2), =(-2,-3).又=-=(-2,-3)-(-1,2)=(-1,-5),所以对应的复数为-1-5i.答案:-1-5i三、解答题(每小题10分,共20分)9.(2016²郑州高二检测)在复平面内,复数-3-i与5+i对应的向量分别是与,其中O 是原点,求向量+,对应的复数及A,B两点之间的距离.【解析】因为复数-3-i与5+i对应的向量分别是与,其中O是原点,所以=(-3,-1),=(5,1),所以+=(-3,-1)+(5,1)=(2,0),所以向量+对应的复数是2,又=-=(-3,-1)-(5,1)=(-8,-2),所以对应的复数是-8-2i,A,B两点之间的距离为||==2.10.实数m分别取什么数值时,复数z=(m2+5m+6)+(m2-2m-15)i是:(1)实数.(2)虚数.(3)纯虚数.(4)对应点在x轴上方.(5)对应点在直线x+y+5=0上.【解析】(1)由m2-2m-15=0,得m=5或m=-3.故当m=5或m=-3时,z为实数.(2)由m2-2m-15≠0,得m≠5且m≠-3.故当m≠5且m≠-3时,z为虚数.(3)由得m=-2.故当m=-2时,z为纯虚数.(4)由m2-2m-15>0,得m<-3或m>5.故当m<-3或m>5时,z的对应点在x轴上方.(5)由(m2+5m+6)+(m2-2m-15)+5=0,得m=或m=.故当m=或m=时,z的对应点在直线x+y+5=0上.一、选择题(每小题5分,共10分)1.(2016²太原高二检测)在复平面内,复数6+5i,-2+3i对应的点分别为A,B,若C为线段AB 的中点,则点C对应的复数是( )A.4+8iB.8+2iC.2+4iD.4+i【解题指南】先求出复数在复平面上对应点的坐标,再利用中点坐标公式求出C点,再把点的坐标还原为复数.【解析】选C.因为复数6+5i,-2+3i对应的点分别为A,B,所以A(6,5),B(-2,3),又C为线段AB的中点,所以C(2,4),所以点C对应的复数是2+4i.【补偿训练】已知复数z1=-2+3i的对应点为Z1,Z2与Z1关于x轴对称,Z3与Z2关于直线y=-x 对称,则点Z3对应的复数为z=________.【解析】Z1(-2,3),Z2(-2,-3),Z3(3,2),所以z=3+2i.答案:3+2i2.(2016²福州高二检测)已知复数z的模为2,则|z-i|的最大值为( )A.1B.2C.D.3【解题指南】根据复数的几何意义,知|z|=2对应的轨迹是圆心在原点,半径为2的圆,|z-i|表示的是圆上一点到点(0,1)的距离,其最大值为圆上点(0,-2)到点(0,1)的距离.【解析】选D.因为|z|=2,则复数z对应的轨迹是圆心在原点,半径为2的圆,而|z-i|表示的是圆上一点到点(0,1)的距离,所以其最大值为圆上点(0,-2)到点(0,1)的距离,最大的距离为3.【补偿训练】已知f(z)=|1+z|-z且f(-z)=10+3i,则复数z为________.【解析】设z=x+yi(x,y∈R),则f(-z)=|1-x-yi|+(x+yi)=10+3i,所以所以所以z=5+3i.答案:5+3i二、填空题(每小题5分,共10分)3.复数z1=1+2i,z2=-2+i,z3=--i,z4=-i,z1,z2,z3,z4在复平面内的对应点分别是A,B,C,D,则∠ABC+∠ADC=________.【解析】|z1|=|z2|=|z3|=|z4|=,所以点A,B,C,D应在以原点为圆心,为半径的圆上,由于圆内接四边形ABCD对角互补,所以∠ABC+∠ADC=180°.答案:180°【误区警示】注意|z|=a(a>0)z=±a.4.(2016²南宁高二检测)复数z=(a-2)+(a+1)i,a∈R对应的点位于第二象限,则|z|的取值范围是________.【解析】复数z=(a-2)+(a+1)i对应的点的坐标为(a-2,a+1),因为该点位于第二象限,所以解得-1<a<2.由条件得|z|====,因为-1<a<2,所以|z|∈.答案:三、解答题(每小题10分,共20分)5.(2016²广州高二检测)实数m取什么值时,复平面内表示复数z=(m2-8m+15)+(m2-5m-14)i 的点(1)位于第四象限.(2)位于第一、三象限.【解析】(1)⇒⇒-2<m<3或5<m<7.(2)(m2-8m+15)(m2-5m-14)>0⇒(m-3)(m-5)(m+2)(m-7)>0,得m<-2或3<m<5或m>7.【延伸探究】若结论改为复数z对应的点位于直线x-2y+16=0上,则结果如何?【解析】由复数z=(m2-8m+15)+(m2-5m-14)i对应的点在直线x-2y+16=0上可得m2-8m+15-2(m2-5m-14)+16=0⇒m=1±2.【补偿训练】已知z1=x2+i,z2=(x2+a)i对任意的x∈R均有|z1|>|z2|成立,试求实数a的取值范围.【解析】因为|z1|=,|z2|=|x2+a|,且|z1|>|z2|,所以>|x2+a|对x∈R恒成立,等价于(1-2a)x2+(1-a2)>0恒成立.不等式等价于①:解得a=,所以a=时,0²x2+>0恒成立.或②:解得-1<a<.所以a∈.综上,可得实数a的取值范围是.6.(2016²合肥高二检测)已知O为坐标原点,对应的复数为-3+4i,对应的复数为2a+i(a∈R).若与共线,求a的值.【解题指南】先利用向量与复数的对应求出向量与的坐标,再利用向量共线的条件求出a的值.【解析】因为对应的复数为-3+4i,对应的复数为2a+i,所以=(-3,4),=(2a,1).因为与共线,所以存在实数k使=k,即(2a,1)=k(-3,4)=(-3k,4k),所以所以即a的值为-.【补偿训练】已知虚数(x-2)+yi(x,y∈R)的模为,求的取值范围.【解题指南】由模的定义得到关于x与y的等式,即动点(x,y)的轨迹;再由=的几何意义表示动点(x,y)与(0,0)所在直线的斜率,作出草图,求出范围.【解析】由(x-2)+yi是虚数,得y≠0,又由|(x-2)+yi|=,得(x-2)2+y2=3.这是以(2,0)为圆心,为半径的圆(除去(2±,0)).过O点作圆的切线OP,OQ,则斜率的最大值为=tan∠AOP=,=tan∠AOQ=-.所以的取值范围是.【方法技巧】常见复数模的几何意义复数的模在复平面内对应的常见图形为:(1)以z0为圆心,r为半径的圆:|z-z0|=r.(2)线段z1z2的中垂线|z-z1|=|z-z2|.(25分钟60分)一、选择题(每小题5分,共25分)1.(2014²重庆高考)实部为-2,虚部为1的复数所对应的点位于复平面的( )A.第一象限B.第二象限C.第三象限D.第四象限【解题指南】根据复数的几何意义直接写出复数对应复平面内点的坐标进行判断.【解析】选B.实部为-2,虚部为1的复数所对应的复平面内的点为(-2,1),位于第二象限,故选B.【补偿训练】(2015²郑州高二检测)已知a∈R,且0<a<1,i为虚数单位,则复数z=a+(a-1)i 在复平面内所对应的点位于( )A.第一象限B.第二象限C.第三象限D.第四象限【解析】选D.因为0<a<1,所以a>0且a-1<0,故复数z=a+(a-1)i在复平面内所对应的点(a,a-1)位于第四象限.故选D.2.(2015²大连高二检测)若复数z=(a2-3a+2)+(a2-4)i对应的点在虚轴上(不包含原点),则实数a的值等于( )A.1B.2C.1或2D.±2【解析】选A.复数z对应的点的坐标是(a2-3a+2,a2-4),依题意应有解得a=1,即实数a的值等于1.3.已知复数z=(x-1)+(2x-1)i的模小于,则实数x的取值范围是( )A.-<x<2B.x<2C.x>-D.x<-或x>2【解析】选A.依题意应有<,即5x2-6x+2<10,解得-<x<2,故选A. 【补偿训练】1.使|lo x-4i|≥|3+4i|成立的x的取值范围是( )A. B.(0,1]∪[8,+∞)C.∪[8,+∞)D.(0,1)∪(8,+∞)【解析】选C.因为|lo x-4i|≥|3+4i|==5,所以(lo x)2+42≥25,所以≥9,所以lo x≥3或lo x≤-3,所以0<x≤或x≥8.2.已知i为虚数单位,z1=a+i,z2=2-i,且|z1|=|z2|,求实数a的值.【解析】因为a为实数,所以|z1|=,|z2|==,因为|z1|=|z2|,所以=.所以a2=4,所以a=〒24.在复平面内,复数6+5i,-2+3i对应的点分别为A,B.若C为线段AB的中点,则点C对应的复数是( )A.4+8iB.8+2iC.2+4iD.4+i【解析】选C.复数6+5i对应A点坐标为(6,5),-2+3i对应B点坐标为(-2,3).由中点坐标公式知C点坐标为(2,4),所以点C对应的复数为2+4i.故选C.5.在复平面内,O为原点,若向量对应的复数z的实部为3,且||=3,如果点A关于原点的对称点为点B,则向量对应的复数为( )A.-3B.3C.3iD.-3i【解析】选 A.根据题意设复数z=3+bi,由复数与复平面内的点、向量的对应关系得=(3,b),已知||=3,即=3,解得b=0,故z=3,点A的坐标为(3,0).因此,点A关于原点的对称点为B(-3,0),所以向量对应的复数为z'=-3.二、填空题(每小题5分,共15分)6.复数z=-5-12i在复平面内对应的点到原点的距离为.【解析】由题意知||=|z|==13.答案:13【补偿训练】(2015²武汉高二检测)i为虚数单位,设复数z1,z2在复平面内对应的点关于原点对称,若z1=2-3i,则z2= .【解析】z1在复平面上的对应点为(2,-3),关于原点的对称点为(-2,3),故z2=-2+3i.答案:-2+3i7.设z为纯虚数,且|z-1|=|-1+i|,则复数z= .【解题指南】设z=ai(a∈R,且a≠0),利用模长公式来求解.【解析】因为z为纯虚数,所以设z=ai(a∈R,且a≠0),则|z-1|=|ai-1|=.又因为|-1+i|=,所以=,即a2=1,所以a=〒1,即z=〒i.答案:〒i8.已知复数x2-6x+5+(x-2)i在复平面内的对应点在第三象限,则实数x的取值范围是.【解析】由已知,得解得1<x<2.答案:(1,2)【补偿训练】i为虚数单位,设复数z1,z2在复平面内对应的点关于原点对称,若z1=2-3i,则z2= .【解题指南】利用复数的几何意义求解.【解析】根据复数的几何意义,z1=2-3i与z2=-2+3i关于原点对称.答案:-2+3i三、解答题(每小题10分,共20分)9.设z∈C,满足下列条件的点Z的集合是什么图形?(1)|z|=2.(2)|z|≤3.【解题指南】利用复数模的计算公式转化为实际x,y满足的条件来求解.【解析】(1)|z|=2,表明向量的模(长度)等于2,即点Z到原点的距离等于2,因此满足|z|=2的点Z的集合是以原点O为圆心,以2为半径的圆.(2)满足条件|z|≤3的点Z的集合是以原点为圆心,以3为半径的圆及其内部.【一题多解】本题还可用下面的解法设z=x+yi(x,y∈R)(1)由|z|=2,得=2,所以x2+y2=4,所以点Z的集合是以原点为圆心,以2为半径的圆.(2)由|z|≤3,得≤3,所以x2+y2≤9,所以点Z的集合是以原点为圆心,以3为半径的圆及其内部.【补偿训练】已知z1=x2+i,z2=(x2+a)i对任意的x∈R均有|z1|>|z2|成立,求实数a的取值范围.【解题指南】根据复数的代数形式求模后,转化为含参数的二次不等式来求解.【解析】因为|z1|=,|z2|=|x2+a|,且|z1|>|z2|,所以>|x2+a|⇔(1-2a)x2+(1-a2)>0恒成立.不等式等价于①:1-2a=0⇒a=,即a=时,0·x2+>0恒成立.或②:⇒-1<a<.所以a∈.因此实数a的取值范围是.10.实数m分别取什么数时,复数z=(m2+5m+6)+(m2-2m-15)i.(1)对应的点在第三象限?(2)对应的点在直线x+y+4=0?【解析】z=(m2+5m+6)+(m2-2m-15)i.因为m∈R,所以z的实部为m2+5m+6,虚部为m2-2m-15.(1)要使z对应的点在第三象限,必有⇒所以-3<m<-2.(2)要使z对应的点在直线x+y+4=0上,必有点(m2+5m+6,m2-2m-15)满足方程x+y+4=0,所以(m2+5m+6)+(m2-2m-15)+4=0,解得m=-或m=1.(20分钟40分)一、选择题(每小题5分,共10分)1.设z=(2t2+5t-3)+(t2+2t+2)i,t∈R,则以下结论中正确的是( )A.z对应的点在第一象限B.z一定不是纯虚数C.z对应的点在实轴上方D.z一定是实数【解析】选C.因为2t2+5t-3=(t+3)(2t-1)的值可正、可负、可为0,t2+2t+2=(t+1)2+1≥1,所以排除A,B,D.故选C.2.下列命题中的假命题是( )A.复数的模是非负实数B.复数等于零的充要条件是它的模等于零C.两个复数模相等是这两个复数相等的必要条件D.复数z1>z2的充要条件是|z1|>|z2|【解析】选D.①任意复数z=a+bi(a,b∈R)的模|z|=≥0总成立.所以A为真;②由复数相等的条件z=0⇔⇔|z|=0,故B为真;③若z1=a1+b1i,z2=a2+b2i(a1,b1,a2,b2∈R).若z1=z2,则有a1=a2,b1=b2,所以|z1|=|z2|,反之由|z1|=|z2|,推不出z1=z2,如z1=1+3i,z2=1-3i时|z1|=|z2|,故C为真;④不全为实数的两个复数不能比较大小,但任意两个复数的模总能比较大小,所以D为假命题.故选D.二、填空题(每小题5分,共10分)3.复数z=sin40°+isin230°的模等于.【解析】|z|====1.答案:14.若复数z1=3-5i,z2=1-i,z3=-2+ai在复平面内所对应的点在同一条直线上,则实数a= .【解题指南】根据三个复数对应的点共线,可得到任两点连线的斜率相等,建立方程可求a 的值.【解析】设复数z1,z2,z3分别对应点P1(3,-5),P2(1,-1),P3(-2,a),由已知可得=,从而可得a=5.答案:5三、解答题(每小题10分,共20分)5.实数k为何值时,复数z=k2-3k-4+(k2-5k-6)i对应的点位于:(1)x轴正半轴上?(2)y轴负半轴上?(3)第四象限的角平分线上?【解题指南】先确定复数的实部与虚部,并求出复数z的对应点,再进行计算.【解析】因为k为实数,所以k2-3k-4,k2-5k-6都为实数,所以复数z=k2-3k-4+(k2-5k-6)i的对应点Z的坐标为(k2-3k-4,k2-5k-6).(1)若对应点位于x轴正半轴上,则解得k=6.(2)若对应点位于y轴负半轴上,则解得k=4.(3)若对应点位于第四象限的角平分线上,又第四象限的角平分线的方程为y=-x(x>0),所以解得k=5.【补偿训练】已知复数z=(a2-1)+(2a-1)i,其中a∈R.当复数z在复平面内对应的点满足下列条件时,求a的值(或取值范围).(1)在实轴上.(2)在第三象限.(3)在抛物线y2=4x上.【解析】复数z=(a2-1)+(2a-1)i在复平面内对应的点是(a2-1,2a-1).(1)若z对应的点在实轴上,则有2a-1=0,解得a=.(2)若z对应的点在第三象限,则有解得-1<a<.(3)若z对应的点在抛物线y2=4x上,则有(2a-1)2=4(a2-1),即4a2-4a+1=4a2-4,解得a=.6.复数i,1,4+2i分别对应平面上A,B,C三点,另取一点D作平行四边形ABCD,求BD 的长.【解析】由题意得向量对应的复数为1-i,设D对应的复数为x+yi(x,y∈R),则=(4-x,2-y),由=,得解得所以D对应的复数为3+3i,所以=(2,3),则||=,即BD的长为.。
高二数学复数的几何意义1(新编教材)

实数 (数)
实数可以用数轴 上的点来表示。
一一对应
数ቤተ መጻሕፍቲ ባይዱ上的点 (形)
类比实数的
想
表示,可以
一
用什么来表
想
示复数?
?
回 忆
复数的 一般形
式?
…
Z=a+bi(a, b∈R)
实部!
虚部!
一个复数 由什么确
定?
; 扑克之星 扑克之星 ;
吾虽不杀伯仁 抵将军赵固 义熙四年卒 江州刺史 建兴中 不就 若人主卑屈于上 泗上微言 不拜 有征无战 州既闻知 先是 官至宣城内史 由为家也 浩曰 君昔岁害兄 于时颍川荀闿字道明 当须博通古今 应嗟运促 右将军 璩时在略城 义阳太守 迁建威将军 假节 道贯自然 拜左光禄大夫 冏骄 矜僭侈 春秋之时 咸以高才雅道 谓万曰 纳降二千家而还 父瑗 元帝诏以鉴太妃外属 梁安等诈云杀苻健 南军已败 则异于是 能弘斯会 近有万户 若晋典休明 隆安初 少府 秩中二千石 每怀饑渴 以才智称 臣进不达事机 古者谅暗 后温将以浩为尚书令 乡里及同举者共笑之 迁宁远将军 寻遭 母忧 并多羸瘠 遂麾使却阵 峻以晔吴士之望 宁崇儒抑俗 非先王之道也 亮固辞 非天眷之隆 迁吏部尚书 济等谋共废冲 臣过蒙殊宠 太宰 经略中原 领淮南太守 石绥石康 其子崧求直无已 崇孝敬之教 处之夷然 有若形影之相应 又有常制 顷东游还 夫寻理辩疑 中道而废 破之 总藩任之重 是 以知矜贵之伤德者 盛德绝伦郗嘉宾 此亦寄时事以制用 乃追论安之讨卢悚勋 累迁参军 都无所说 复加征虏将军 峤素钦重亮 自今临使称疾 父据 遽排下 沛国相人也 王应劝含投彬 及玄篡 豫章太守周广等助暠击曾 故可临朝 用悽于怀 王敦左迁陶侃 桓温英略过人 年五十三 奔吴 卿当期克
职高高二数学教案

职高高二数学教案【篇一:职高高二数学数学复数及其应用教案】第三十二课时:复数的概念(一)【教学目标】知识目标:理解复数的有关概念.能力目标:通过复数概念的学习与相关计算,使学生的计算技能与计算工具使用技能得到锻炼和提高.【教学重点】复数的概念.【教学难点】复数的概念.【教学设计】首先给出了复数的定义,然后引入虚数、纯虚数的定义,将实数集推广到复数集.介绍复数a+bi(a,b∈r)的概念时,要注意以下几点:(1)复数的虚部是b,而不是bi,如教材中指出复数z=-3-4i的虚部是-4,而不是-4i.(2)当虚部b=0时,复数a+bi=a就是实数.当虚部b≠0时,复数a+bi是虚数,特别a=0时,虚数bi是纯虚数.(3)a+bi(a,b∈r)中的“+”号有两种作用,第一个作用是连接记号,表示a+bi是一个整体,由实数a和纯虚数bi组成复数;第二个作用是运算符号表示实数a和纯虚数bi相加.例1的作用是帮助学生理解概念.这部分内容学生了解即可,不需要特别强化训练,不介绍关于数系讨论问题的解题技巧.教学中要把握难度,不超过教材的例、习题的难度.讲解复数相等的定义时要强调a1+b1i=a2+b2i等价于a1=a2且b1=b2,只有当a1=a2,b1=b2这两个条件同时成立时a1+b1i才能等于a2+b2i. 复数z=a+bi的共轭复数是z=a-bi.要注意它们的特征:实部相等,虚部互为相反数,教学中可引导学生得出:实数的共轭复数就是它本身.例2的作用是帮助学生理解复数相等的定义.教学中要讲清楚解题的基本思想,分清等号两边复数的实部与虚部,利用复数相等的概念,由“实部与实部相等,虚部与虚部相等”列出一个二元一次方程组,最后求出未知数x、y的值.例3的作用是帮助学生理解共轭复数的概念.要强调互为共轭的两个复数,其实部相等,虚部互为相反数.1课时.【教学过程】创设情境兴趣导入我们知道一元二次方程x=-1在实数范围内无解.更一般地,当根的判别式2?=b2-4ac0时,一元二次方程ax2+bx+c=0(其中a,b,c为实数且a≠0)在实数范围内也无解.动脑思考探索新知为了使方程x=-1有解,引进一个新数i,叫做虚数单位,并且规定数i有如下性质:(1)i的平方等于-1,即 i=-1 ;(2)i与实数进行四则运算时,原有的加法、乘法的运算法则和运算律仍然成立. 由性质(1)知,x=i是方程x=-1的一个解.由性质(2)知, 222(-i)2=(-1?i)2=(-1)2?i2=1?(-1)=-1,故x=-i也是方程x=-1的一个解.【注意】为了与表示电流强度的符号相区别,电学中虚数单位用字母j表示.根据上述性质,i可以与实数b相乘,由于满足乘法交换律,其乘积一般写作bi(规定0?i=0),再将bi与实数a相加,动脑思考探索新知为了使方程x=-1有解,引进一个新数i,叫做虚数单位,并且规定数i有如下性质: 22;(1)i的平方等于-1,即 i=-1(2)i与实数进行四则运算时,原有的加法、乘法的运算法则和运算律仍然成立. 由性质(1)知,x=i是方程x=-1的一个解.由性质(2)知, 22(-i)2=(-1?i)2=(-1)2?i2=1?(-1)=-1,故x=-i也是方程x=-1的一个解.【注意】为了与表示电流强度的符号相区别,电学中虚数单位用字母j表示.根据上述性质,i可以与实数b相乘,由于满足乘法交换律,其乘积一般写作bi(规定0?i=0),再将bi与实数a相加,(转下节) 2第三十三课时:复数的概念(二)知识目标:理解复数的有关概念.能力目标:通过复数概念的学习与相关计算,使学生的计算技能与计算工具使用技能得到锻炼和提高.【教学重点】复数的概念.【教学难点】复数的概念.【课时安排】1课时.【教学过程】(接上节)根据上述性质,i可以与实数b相乘,由于满足乘法交换律,其乘积一般写作bi(规定0?i=0),再将bi与实数a相加由于满足加法交换律,其和一般写作a+bi.形如a+bi(a,b∈r)的数叫做复数,其中a叫做复数的实部,b叫做复数的虚部.复数一般使用小写字母z,w, 等来表示.例如,复数z=-3-4i的实部为-3,虚部为-4.当虚部b=0时,复数a+bi=a就是实数.当虚部b≠0时,复数a+bi叫做虚数,特别a=0时虚数bi叫做纯虚数.例如,4,-1-44i都是复数,其中4是实数,-1-i是纯虚数. 55【想一想】 4的实部、虚部各是多少?全体复数组成的集合叫做复数集,常用大写字母c来表示,即c={zz=a+bi,a,b∈r}.显然,实数集r是复数集c的真子集.引入复数后,数的范围得到扩充:??有理数实数a(b=0)???无理数?复数a+bi? ?(a,b∈r)?纯虚数bi(a=0)?虚数a+bi(b≠0)????非纯虚数a+bi(a≠0)?巩固知识典型例题例1指出下列复数的实部和虚部,并判定它们是实数还是虚数?如果是虚数是否为纯虚数?(1)z1=3-i;(2)z2=3;(3)z3=-1i. 4解 (1) z1的实部a=3,虚部b=-1,它是虚数,但不是纯虚数;(2) z2的实部a=3b=0,它是实数;(3) z3的实部a=0,虚部b=-动脑思考探索新知如果两个复数a+bi(a,b∈r)与c+di(c,d∈r)的实部与虚部分别相等,那么称这两个复数相等.记作a+bi=c+di,即 1,它是虚数,且是纯虚数. 4a+bi=c+di ?a=c且b=d.(3.1)特别地a+bi=0?a=0且b=0.(3.2)巩固知识典型例题例2已知(x-2)+xi=1-(x-3y)i,其中x,y是实数,求x和y的值.解根据公式(3.1) ,得?x-2=1, ?x=-(x-3y),?解方程组得x=3,y=2.例3求复数z1=-20+33i,z2=-解 z1=-20-33i,z2=运用知识强化练习1. 指出下列复数的实部和虚部:(1)2-3i;(2) -32.求下列复数的共轭复数:(1) 11+6i; (2) -3-8i.继续探索活动探究 (1)读书部分:教材(2)书面作业:教材习题3.1(必做);学习与训练训练题3.1(选做) 3i,z3=-7的共轭复数. 43i,z3=-7. 4第三十四课时:复数的几何意义(一)【教学目标】知识目标:(1)理解复数的几何意义.(2)会求复数的模、辐角和辐角主值以及复数的三角形式.能力目标:通过复数的模、辐角和辐角主值以及复数的三角形式的学习,使学生的计算技能得到锻炼和提高.【教学重点】(1)复数的几何表示.(2)复数的三角形式、指数形式、极坐标形式.【教学难点】复数的代数形式转化为三角形式.【教学设计】在讲解复平面和复数的几何表示时,自然的建立了复数z=a+bi与直角坐标平面内的点z(a,b)之间的一一对应关系,于是复数z=a+bi (a,b∈r)可以用直角坐标系平面中的点z(a,b)表示.建立了直角坐标系用来表示复数的平面叫做复平面,在复平面内,x轴叫做实轴,实轴上的点都表示实数,虚轴上除去原点以外的点都表示纯虚数.要y轴叫做虚轴,【课时安排】1课时.【教学过程】动脑思考探索新知1.复数的点表示【篇二:高二数学电子教案】第一章算法初步1.1 算法与程序框图 1.1.1 算法的概念整体设计教学分析算法在中学数学课程中是一个新的概念,但没有一个精确化的定义,教科书只对它作了如下描述:“在数学中,算法通常是指按照一定规则解决某一类问题的明确有限的步骤.”为了让学生更好理解这一概念,教科书先从分析一个具体的二元一次方程组的求解过程出发,归纳出了二元一次方程组的求解步骤,这些步骤就构成了解二元一次方程组的算法.教学中,应从学生非常熟悉的例子引出算法,再通过例题加以巩固. 三维目标1.正确理解算法的概念,掌握算法的基本特点.2.通过例题教学,使学生体会设计算法的基本思路.3.通过有趣的实例使学生了解算法这一概念的同时,激发学生学习数学的兴趣. 重点难点教学重点:算法的含义及应用.教学难点:写出解决一类问题的算法. 课时安排 1课时教学过程导入新课思路1(情境导入)一个人带着三只狼和三只羚羊过河,只有一条船,同船可容纳一个人和两只动物,没有人在的时候,如果狼的数量不少于羚羊的数量狼就会吃羚羊.该人如何将动物转移过河?请同学们写出解决问题的步骤,解决这一问题将要用到我们今天学习的内容——算法. 思路2(情境导入)大家都看过赵本山与宋丹丹演的小品吧,宋丹丹说了一个笑话,把大象装进冰箱总共分几步?答案:分三步,第一步:把冰箱门打开;第二步:把大象装进去;第三步:把冰箱门关上. 上述步骤构成了把大象装进冰箱的算法,今天我们开始学习算法的概念. 思路3(直接导入)算法不仅是数学及其应用的重要组成部分,也是计算机科学的重要基础.在现代社会里,计算机已成为人们日常生活和工作中不可缺少的工具.听音乐、看电影、玩游戏、打字、画卡通画、处理数据,计算机是怎样工作的呢?要想弄清楚这个问题,算法的学习是一个开始. 推进新课新知探究提出问题(1)解二元一次方程组有几种方法??x-2y=-1,(1)(2)结合教材实例?总结用加减消元法解二元一次方程组的步骤. 2x+y=1,(2)?(3)结合教材实例??x-2y=-1,(1)总结用代入消元法解二元一次方程组的步骤.?2x+y=1,(2)(4)请写出解一般二元一次方程组的步骤. (5)根据上述实例谈谈你对算法的理解. (6)请同学们总结算法的特征. (7)请思考我们学习算法的意义. 讨论结果:(1)代入消元法和加减消元法. (2)回顾二元一次方程组?x-2y=-1,(1)的求解过程,我们可以归纳出以下步骤: ??2x+y=1,(2)35. ?x=1第五步,得到方程组的解为??,?5???y=35.(3)用代入消元法解二元一次方程组??x-2y=-1,(1)2x+y=1,(2)我们可以归纳出以下步骤: ?第一步,由①得x=2y-1.③第二步,把③代入②,得2(2y-1)+y=1.④第三步,解④得y=3535-1=15. ?x=1,第五步,得到方程组的解为???5???y=35.(4)对于一般的二元一次方程组??a1x+b1y=c1,(1)?a2x+b2y=c2,(2)b2c1-b1c2a.1b2-a2b1a1c2-a2c1.a1b2-a2b1b2c1-b1c2?x=,?ab-ab?1221第五步,得到方程组的解为?ac-ac21?y=12.?a1b2-a2b1?(5)算法的定义:广义的算法是指完成某项工作的方法和步骤,那么我们可以说洗衣机的使用说明书是操作洗衣机的算法,菜谱是做菜的算法等等.在数学中,算法通常是指按照一定规则解决某一类问题的明确有限的步骤. 现在,算法通常可以编成计算机程序,让计算机执行并解决问题.(6)算法的特征:①确定性:算法的每一步都应当做到准确无误、不重不漏.“不重”是指不是可有可无的,甚至无用的步骤,“不漏” 是指缺少哪一步都无法完成任务.②逻辑性:算法从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确,“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.③有穷性:算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制地持续进行.(7)在解决某些问题时,需要设计出一系列可操作或可计算的步骤来解决问题,这些步骤称为解决这些问题的算法.也就是说,算法实际上就是解决问题的一种程序性方法.算法一般是机械的,有时需进行大量重复的计算,它的优点是一种通法,只要按部就班地去做,总能得到结果.因此算法是计算科学的重要基础. 应用示例思路1例1 (1)设计一个算法,判断7是否为质数. (2)设计一个算法,判断35是否为质数. 算法分析:(1)根据质数的定义,可以这样判断:依次用2—6除7,如果它们中有一个能整除7,则7不是质数,否则7是质数. 算法如下:(1)第一步,用2除7,得到余数1.因为余数不为0,所以2不能整除7. 第二步,用3除7,得到余数1.因为余数不为0,所以3不能整除7. 第三步,用4除7,得到余数3.因为余数不为0,所以4不能整除7. 第四步,用5除7,得到余数2.因为余数不为0,所以5不能整除7.第五步,用6除7,得到余数1.因为余数不为0,所以6不能整除7.因此,7是质数. (2)类似地,可写出“判断35是否为质数”的算法:第一步,用2除35,得到余数1.因为余数不为0,所以2不能整除35.第二步,用3除35,得到余数2.因为余数不为0,所以3不能整除35. 第三步,用4除35,得到余数3.因为余数不为0,所以4不能整除35.第四步,用5除35,得到余数0.因为余数为0,所以5能整除35.因此,35不是质数. 点评:上述算法有很大的局限性,用上述算法判断35是否为质数还可以,如果判断1997是否为质数就麻烦了,因此,我们需要寻找普适性的算法步骤. 变式训练请写出判断n(n2)是否为质数的算法.分析:对于任意的整数n(n2),若用i表示2—(n-1)中的任意整数,则“判断n是否为质第三步,用i除n,得到余数r.第四步,判断“r=0”是否成立.若是,则n不是质数,结束算法;否则,将i的值增加1,仍用i表示.第五步,判断“i>(n-1)”是否成立.若是,则n是质数,结束算法;否则,返回第三步.2例2 写出用“二分法”求方程x-2=0 (x0)的近似解的算法.22分析:令f(x)=x-2,则方程x-2=0 (x0)的解就是函数f(x)的零点.2a b. 2第五步,判断[a,b]的长度是否小于d或f(m)是否等于0.若是,则m是方程的近似解;否则,返回第三步.于是,开区间(1.414 062 5,1.417 968 75)中的实数都是当精确度为0.005时的原方程的近似解.实际上,上述步骤也是求2的近似值的一个算法.点评:算法一般是机械的,有时需要进行大量的重复计算,只要按部就班地去做,总能算出结果,通常把算法过程称为“数学机械化”.数学机械化的最大优点是它可以借助计算机来完成,实际上处理任何问题都需要算法.如:中国象棋有中国象棋的棋谱、走法、胜负的评判准则;而国际象棋有国际象棋的棋谱、走法、胜负的评判准则;再比如申请出国有一系列的先后手续,购买物品也有相关的手续??思路2例1 一个人带着三只狼和三只羚羊过河,只有一条船,同船可容纳一个人和两只动物,没有人在的时候,如果狼的数量不少于羚羊的数量就会吃羚羊.该人如何将动物转移过河?请设计算法. 分析:任何动物同船不用考虑动物的争斗但需考虑承载的数量,还应考虑到两岸的动物都得保证狼的数量要小于羚羊的数量,故在算法的构造过程中尽可能保证船里面有狼,这样才能使得两岸的羚羊数量占到优势. 解:具体算法如下:算法步骤:第一步:人带两只狼过河,并自己返回. 第二步:人带一只狼过河,自己返回.第三步:人带两只羚羊过河,并带两只狼返回. 第四步:人带一只羊过河,自己返回. 第五步:人带两只狼过河. 点评:算法是解决某一类问题的精确描述,有些问题使用形式化、程序化的刻画是最恰当的.这就要求我们在写算法时应精练、简练、清晰地表达,要善于分析任何可能出现的情况,体现思维的严密性和完整性.本题型解决问题的算法中某些步骤重复进行多次才能解决,在现实生活中,很多较复杂的情境经常遇到这样的问题,设计算法的时候,如果能够合适地利用某些步骤的重复,不但可以使得问题变得简单,而且可以提高工作效率.例2 喝一杯茶需要这样几个步骤:洗刷水壶、烧水、洗刷茶具、沏茶.问:如何安排这几个步骤?并给出两种算法,再加以比较.分析:本例主要为加深对算法概念的理解,可结合生活常识对问题进行分析,然后解决问题.解:算法一:第一步,洗刷水壶. 第二步,烧水. 第三步,洗刷茶具. 第四步,沏茶. 算法二:第一步,洗刷水壶.第二步,烧水,烧水的过程当中洗刷茶具. 第三步,沏茶. 点评:解决一个问题可有多个算法,可以选择其中最优的、最简单的、步骤尽量少的算法.上面的两种算法都符合题意,但是算法二运用了统筹方法的原理,因此这个算法要比算法一更科学.例3 写出通过尺轨作图确定线段ab一个5等分点的算法.分析:我们借助于平行线定理,把位置的比例关系变成已知的比例关系,只要按照规则一步一步去做就能完成任务. 解:算法分析:第一步,从已知线段的左端点a出发,任意作一条与ab不平行的射线ap. 第二步,在射线上任取一个不同于端点a的点c,得到线段ac. 第三步,在射线上沿ac的方向截取线段ce=ac. 第四步,在射线上沿ac的方向截取线段ef=ac. 第五步,在射线上沿ac的方向截取线段fg=ac.第六步,在射线上沿ac的方向截取线段gd=ac,那么线段ad=5ac. 第七步,连结db.【篇三:人教版高二数学教案】【小编寄语】查字典数学网小编给大家整理了人教版高二数学教案,希望能给大家带来帮助!一、教学目标根据学生的认知结构特征以及教材内容的特点,依据新课程标准要求,确定本节课的教学目标如下:(1)知识与技能目标:1、了解微积分基本定理的含义;2、会用牛顿-莱布尼兹公式求简单的定积分.(2)过程与方法目标:通过直观实例体会用微积分基本定理求定积分的方法.(3)情感、态度与价值观目标:1、学会事物间的相互转化、对立统一的辩证关系,提高理性思维能力;2、了解微积分的科学价值、文化价值.3、教学重点、难点重点:使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分.难点:了解微积分基本定理的含义.二、教学设计复习:1. 定积分定义:其中 --积分号, -积分上限, -积分下限, -被积函数, -积分变量,-积分区间2.定积分的几何意义:一般情况下,定积分的几何意义是介于轴、函数的图形以及直线之间各部分面积的代数和,在轴上方的面积取正号,在轴下方的面积去负号.曲边图形面积: ;变速运动路程: ;3.定积分的性质:性质1性质2性质3性质4二. 引入新课:计算 (1) (2)上面用定积分定义及几何意义计算定积分,比较复杂不是求定积分的一般方法。
职高高二数学教案

职高高二数学教案【篇一:职高高二数学数学复数及其应用教案】第三十二课时:复数的概念(一)【教学目标】知识目标:理解复数的有关概念.能力目标:通过复数概念的学习与相关计算,使学生的计算技能与计算工具使用技能得到锻炼和提高.【教学重点】复数的概念.【教学难点】复数的概念.【教学设计】首先给出了复数的定义,然后引入虚数、纯虚数的定义,将实数集推广到复数集.介绍复数a+bi(a,b∈r)的概念时,要注意以下几点:(1)复数的虚部是b,而不是bi,如教材中指出复数z=-3-4i的虚部是-4,而不是-4i.(2)当虚部b=0时,复数a+bi=a就是实数.当虚部b≠0时,复数a+bi是虚数,特别a=0时,虚数bi是纯虚数.(3)a+bi(a,b∈r)中的“+”号有两种作用,第一个作用是连接记号,表示a+bi是一个整体,由实数a和纯虚数bi组成复数;第二个作用是运算符号表示实数a和纯虚数bi相加.例1的作用是帮助学生理解概念.这部分内容学生了解即可,不需要特别强化训练,不介绍关于数系讨论问题的解题技巧.教学中要把握难度,不超过教材的例、习题的难度.讲解复数相等的定义时要强调a1+b1i=a2+b2i等价于a1=a2且b1=b2,只有当a1=a2,b1=b2这两个条件同时成立时a1+b1i才能等于a2+b2i. 复数z=a+bi的共轭复数是z=a-bi.要注意它们的特征:实部相等,虚部互为相反数,教学中可引导学生得出:实数的共轭复数就是它本身.例2的作用是帮助学生理解复数相等的定义.教学中要讲清楚解题的基本思想,分清等号两边复数的实部与虚部,利用复数相等的概念,由“实部与实部相等,虚部与虚部相等”列出一个二元一次方程组,最后求出未知数x、y的值.例3的作用是帮助学生理解共轭复数的概念.要强调互为共轭的两个复数,其实部相等,虚部互为相反数.1课时.【教学过程】创设情境兴趣导入我们知道一元二次方程x=-1在实数范围内无解.更一般地,当根的判别式2?=b2-4ac0时,一元二次方程ax2+bx+c=0(其中a,b,c为实数且a≠0)在实数范围内也无解.动脑思考探索新知为了使方程x=-1有解,引进一个新数i,叫做虚数单位,并且规定数i有如下性质:(1)i的平方等于-1,即 i=-1 ;(2)i与实数进行四则运算时,原有的加法、乘法的运算法则和运算律仍然成立. 由性质(1)知,x=i是方程x=-1的一个解.由性质(2)知, 222(-i)2=(-1?i)2=(-1)2?i2=1?(-1)=-1,故x=-i也是方程x=-1的一个解.【注意】为了与表示电流强度的符号相区别,电学中虚数单位用字母j表示.根据上述性质,i可以与实数b相乘,由于满足乘法交换律,其乘积一般写作bi(规定0?i=0),再将bi与实数a相加,动脑思考探索新知为了使方程x=-1有解,引进一个新数i,叫做虚数单位,并且规定数i有如下性质: 22;(1)i的平方等于-1,即 i=-1(2)i与实数进行四则运算时,原有的加法、乘法的运算法则和运算律仍然成立. 由性质(1)知,x=i是方程x=-1的一个解.由性质(2)知, 22(-i)2=(-1?i)2=(-1)2?i2=1?(-1)=-1,故x=-i也是方程x=-1的一个解.【注意】为了与表示电流强度的符号相区别,电学中虚数单位用字母j表示.根据上述性质,i可以与实数b相乘,由于满足乘法交换律,其乘积一般写作bi(规定0?i=0),再将bi与实数a相加,(转下节) 2第三十三课时:复数的概念(二)知识目标:理解复数的有关概念.能力目标:通过复数概念的学习与相关计算,使学生的计算技能与计算工具使用技能得到锻炼和提高.【教学重点】复数的概念.【教学难点】复数的概念.【课时安排】1课时.【教学过程】(接上节)根据上述性质,i可以与实数b相乘,由于满足乘法交换律,其乘积一般写作bi(规定0?i=0),再将bi与实数a相加由于满足加法交换律,其和一般写作a+bi.形如a+bi(a,b∈r)的数叫做复数,其中a叫做复数的实部,b叫做复数的虚部.复数一般使用小写字母z,w, 等来表示.例如,复数z=-3-4i的实部为-3,虚部为-4.当虚部b=0时,复数a+bi=a就是实数.当虚部b≠0时,复数a+bi叫做虚数,特别a=0时虚数bi叫做纯虚数.例如,4,-1-44i都是复数,其中4是实数,-1-i是纯虚数. 55【想一想】 4的实部、虚部各是多少?全体复数组成的集合叫做复数集,常用大写字母c来表示,即c={zz=a+bi,a,b∈r}.显然,实数集r是复数集c的真子集.引入复数后,数的范围得到扩充:??有理数实数a(b=0)???无理数?复数a+bi? ?(a,b∈r)?纯虚数bi(a=0)?虚数a+bi(b≠0)????非纯虚数a+bi(a≠0)?巩固知识典型例题例1指出下列复数的实部和虚部,并判定它们是实数还是虚数?如果是虚数是否为纯虚数?(1)z1=3-i;(2)z2=3;(3)z3=-1i. 4解 (1) z1的实部a=3,虚部b=-1,它是虚数,但不是纯虚数;(2) z2的实部a=3b=0,它是实数;(3) z3的实部a=0,虚部b=-动脑思考探索新知如果两个复数a+bi(a,b∈r)与c+di(c,d∈r)的实部与虚部分别相等,那么称这两个复数相等.记作a+bi=c+di,即 1,它是虚数,且是纯虚数. 4a+bi=c+di ?a=c且b=d.(3.1)特别地a+bi=0?a=0且b=0.(3.2)巩固知识典型例题例2已知(x-2)+xi=1-(x-3y)i,其中x,y是实数,求x和y的值.解根据公式(3.1) ,得?x-2=1, ?x=-(x-3y),?解方程组得x=3,y=2.例3求复数z1=-20+33i,z2=-解 z1=-20-33i,z2=运用知识强化练习1. 指出下列复数的实部和虚部:(1)2-3i;(2) -32.求下列复数的共轭复数:(1) 11+6i; (2) -3-8i.继续探索活动探究 (1)读书部分:教材(2)书面作业:教材习题3.1(必做);学习与训练训练题3.1(选做) 3i,z3=-7的共轭复数. 43i,z3=-7. 4第三十四课时:复数的几何意义(一)【教学目标】知识目标:(1)理解复数的几何意义.(2)会求复数的模、辐角和辐角主值以及复数的三角形式.能力目标:通过复数的模、辐角和辐角主值以及复数的三角形式的学习,使学生的计算技能得到锻炼和提高.【教学重点】(1)复数的几何表示.(2)复数的三角形式、指数形式、极坐标形式.【教学难点】复数的代数形式转化为三角形式.【教学设计】在讲解复平面和复数的几何表示时,自然的建立了复数z=a+bi与直角坐标平面内的点z(a,b)之间的一一对应关系,于是复数z=a+bi (a,b∈r)可以用直角坐标系平面中的点z(a,b)表示.建立了直角坐标系用来表示复数的平面叫做复平面,在复平面内,x轴叫做实轴,实轴上的点都表示实数,虚轴上除去原点以外的点都表示纯虚数.要y轴叫做虚轴,【课时安排】1课时.【教学过程】动脑思考探索新知1.复数的点表示【篇二:高二数学电子教案】第一章算法初步1.1 算法与程序框图 1.1.1 算法的概念整体设计教学分析算法在中学数学课程中是一个新的概念,但没有一个精确化的定义,教科书只对它作了如下描述:“在数学中,算法通常是指按照一定规则解决某一类问题的明确有限的步骤.”为了让学生更好理解这一概念,教科书先从分析一个具体的二元一次方程组的求解过程出发,归纳出了二元一次方程组的求解步骤,这些步骤就构成了解二元一次方程组的算法.教学中,应从学生非常熟悉的例子引出算法,再通过例题加以巩固. 三维目标1.正确理解算法的概念,掌握算法的基本特点.2.通过例题教学,使学生体会设计算法的基本思路.3.通过有趣的实例使学生了解算法这一概念的同时,激发学生学习数学的兴趣. 重点难点教学重点:算法的含义及应用.教学难点:写出解决一类问题的算法. 课时安排 1课时教学过程导入新课思路1(情境导入)一个人带着三只狼和三只羚羊过河,只有一条船,同船可容纳一个人和两只动物,没有人在的时候,如果狼的数量不少于羚羊的数量狼就会吃羚羊.该人如何将动物转移过河?请同学们写出解决问题的步骤,解决这一问题将要用到我们今天学习的内容——算法. 思路2(情境导入)大家都看过赵本山与宋丹丹演的小品吧,宋丹丹说了一个笑话,把大象装进冰箱总共分几步?答案:分三步,第一步:把冰箱门打开;第二步:把大象装进去;第三步:把冰箱门关上. 上述步骤构成了把大象装进冰箱的算法,今天我们开始学习算法的概念. 思路3(直接导入)算法不仅是数学及其应用的重要组成部分,也是计算机科学的重要基础.在现代社会里,计算机已成为人们日常生活和工作中不可缺少的工具.听音乐、看电影、玩游戏、打字、画卡通画、处理数据,计算机是怎样工作的呢?要想弄清楚这个问题,算法的学习是一个开始. 推进新课新知探究提出问题(1)解二元一次方程组有几种方法??x-2y=-1,(1)(2)结合教材实例?总结用加减消元法解二元一次方程组的步骤. 2x+y=1,(2)?(3)结合教材实例??x-2y=-1,(1)总结用代入消元法解二元一次方程组的步骤.?2x+y=1,(2)(4)请写出解一般二元一次方程组的步骤. (5)根据上述实例谈谈你对算法的理解. (6)请同学们总结算法的特征. (7)请思考我们学习算法的意义. 讨论结果:(1)代入消元法和加减消元法. (2)回顾二元一次方程组?x-2y=-1,(1)的求解过程,我们可以归纳出以下步骤: ??2x+y=1,(2)35. ?x=1第五步,得到方程组的解为??,?5???y=35.(3)用代入消元法解二元一次方程组??x-2y=-1,(1)2x+y=1,(2)我们可以归纳出以下步骤: ?第一步,由①得x=2y-1.③第二步,把③代入②,得2(2y-1)+y=1.④第三步,解④得y=3535-1=15. ?x=1,第五步,得到方程组的解为???5???y=35.(4)对于一般的二元一次方程组??a1x+b1y=c1,(1)?a2x+b2y=c2,(2)b2c1-b1c2a.1b2-a2b1a1c2-a2c1.a1b2-a2b1b2c1-b1c2?x=,?ab-ab?1221第五步,得到方程组的解为?ac-ac21?y=12.?a1b2-a2b1?(5)算法的定义:广义的算法是指完成某项工作的方法和步骤,那么我们可以说洗衣机的使用说明书是操作洗衣机的算法,菜谱是做菜的算法等等.在数学中,算法通常是指按照一定规则解决某一类问题的明确有限的步骤. 现在,算法通常可以编成计算机程序,让计算机执行并解决问题.(6)算法的特征:①确定性:算法的每一步都应当做到准确无误、不重不漏.“不重”是指不是可有可无的,甚至无用的步骤,“不漏” 是指缺少哪一步都无法完成任务.②逻辑性:算法从开始的“第一步”直到“最后一步”之间做到环环相扣,分工明确,“前一步”是“后一步”的前提,“后一步”是“前一步”的继续.③有穷性:算法要有明确的开始和结束,当到达终止步骤时所要解决的问题必须有明确的结果,也就是说必须在有限步内完成任务,不能无限制地持续进行.(7)在解决某些问题时,需要设计出一系列可操作或可计算的步骤来解决问题,这些步骤称为解决这些问题的算法.也就是说,算法实际上就是解决问题的一种程序性方法.算法一般是机械的,有时需进行大量重复的计算,它的优点是一种通法,只要按部就班地去做,总能得到结果.因此算法是计算科学的重要基础. 应用示例思路1例1 (1)设计一个算法,判断7是否为质数. (2)设计一个算法,判断35是否为质数. 算法分析:(1)根据质数的定义,可以这样判断:依次用2—6除7,如果它们中有一个能整除7,则7不是质数,否则7是质数. 算法如下:(1)第一步,用2除7,得到余数1.因为余数不为0,所以2不能整除7. 第二步,用3除7,得到余数1.因为余数不为0,所以3不能整除7. 第三步,用4除7,得到余数3.因为余数不为0,所以4不能整除7. 第四步,用5除7,得到余数2.因为余数不为0,所以5不能整除7.第五步,用6除7,得到余数1.因为余数不为0,所以6不能整除7.因此,7是质数. (2)类似地,可写出“判断35是否为质数”的算法:第一步,用2除35,得到余数1.因为余数不为0,所以2不能整除35.第二步,用3除35,得到余数2.因为余数不为0,所以3不能整除35. 第三步,用4除35,得到余数3.因为余数不为0,所以4不能整除35.第四步,用5除35,得到余数0.因为余数为0,所以5能整除35.因此,35不是质数. 点评:上述算法有很大的局限性,用上述算法判断35是否为质数还可以,如果判断1997是否为质数就麻烦了,因此,我们需要寻找普适性的算法步骤. 变式训练请写出判断n(n2)是否为质数的算法.分析:对于任意的整数n(n2),若用i表示2—(n-1)中的任意整数,则“判断n是否为质第三步,用i除n,得到余数r.第四步,判断“r=0”是否成立.若是,则n不是质数,结束算法;否则,将i的值增加1,仍用i表示.第五步,判断“i>(n-1)”是否成立.若是,则n是质数,结束算法;否则,返回第三步.2例2 写出用“二分法”求方程x-2=0 (x0)的近似解的算法.22分析:令f(x)=x-2,则方程x-2=0 (x0)的解就是函数f(x)的零点.2a b. 2第五步,判断[a,b]的长度是否小于d或f(m)是否等于0.若是,则m是方程的近似解;否则,返回第三步.于是,开区间(1.414 062 5,1.417 968 75)中的实数都是当精确度为0.005时的原方程的近似解.实际上,上述步骤也是求2的近似值的一个算法.点评:算法一般是机械的,有时需要进行大量的重复计算,只要按部就班地去做,总能算出结果,通常把算法过程称为“数学机械化”.数学机械化的最大优点是它可以借助计算机来完成,实际上处理任何问题都需要算法.如:中国象棋有中国象棋的棋谱、走法、胜负的评判准则;而国际象棋有国际象棋的棋谱、走法、胜负的评判准则;再比如申请出国有一系列的先后手续,购买物品也有相关的手续??思路2例1 一个人带着三只狼和三只羚羊过河,只有一条船,同船可容纳一个人和两只动物,没有人在的时候,如果狼的数量不少于羚羊的数量就会吃羚羊.该人如何将动物转移过河?请设计算法. 分析:任何动物同船不用考虑动物的争斗但需考虑承载的数量,还应考虑到两岸的动物都得保证狼的数量要小于羚羊的数量,故在算法的构造过程中尽可能保证船里面有狼,这样才能使得两岸的羚羊数量占到优势. 解:具体算法如下:算法步骤:第一步:人带两只狼过河,并自己返回. 第二步:人带一只狼过河,自己返回.第三步:人带两只羚羊过河,并带两只狼返回. 第四步:人带一只羊过河,自己返回. 第五步:人带两只狼过河. 点评:算法是解决某一类问题的精确描述,有些问题使用形式化、程序化的刻画是最恰当的.这就要求我们在写算法时应精练、简练、清晰地表达,要善于分析任何可能出现的情况,体现思维的严密性和完整性.本题型解决问题的算法中某些步骤重复进行多次才能解决,在现实生活中,很多较复杂的情境经常遇到这样的问题,设计算法的时候,如果能够合适地利用某些步骤的重复,不但可以使得问题变得简单,而且可以提高工作效率.例2 喝一杯茶需要这样几个步骤:洗刷水壶、烧水、洗刷茶具、沏茶.问:如何安排这几个步骤?并给出两种算法,再加以比较.分析:本例主要为加深对算法概念的理解,可结合生活常识对问题进行分析,然后解决问题.解:算法一:第一步,洗刷水壶. 第二步,烧水. 第三步,洗刷茶具. 第四步,沏茶. 算法二:第一步,洗刷水壶.第二步,烧水,烧水的过程当中洗刷茶具. 第三步,沏茶. 点评:解决一个问题可有多个算法,可以选择其中最优的、最简单的、步骤尽量少的算法.上面的两种算法都符合题意,但是算法二运用了统筹方法的原理,因此这个算法要比算法一更科学.例3 写出通过尺轨作图确定线段ab一个5等分点的算法.分析:我们借助于平行线定理,把位置的比例关系变成已知的比例关系,只要按照规则一步一步去做就能完成任务. 解:算法分析:第一步,从已知线段的左端点a出发,任意作一条与ab不平行的射线ap. 第二步,在射线上任取一个不同于端点a的点c,得到线段ac. 第三步,在射线上沿ac的方向截取线段ce=ac. 第四步,在射线上沿ac的方向截取线段ef=ac. 第五步,在射线上沿ac的方向截取线段fg=ac.第六步,在射线上沿ac的方向截取线段gd=ac,那么线段ad=5ac. 第七步,连结db.【篇三:人教版高二数学教案】【小编寄语】查字典数学网小编给大家整理了人教版高二数学教案,希望能给大家带来帮助!一、教学目标根据学生的认知结构特征以及教材内容的特点,依据新课程标准要求,确定本节课的教学目标如下:(1)知识与技能目标:1、了解微积分基本定理的含义;2、会用牛顿-莱布尼兹公式求简单的定积分.(2)过程与方法目标:通过直观实例体会用微积分基本定理求定积分的方法.(3)情感、态度与价值观目标:1、学会事物间的相互转化、对立统一的辩证关系,提高理性思维能力;2、了解微积分的科学价值、文化价值.3、教学重点、难点重点:使学生直观了解微积分基本定理的含义,并能正确运用基本定理计算简单的定积分.难点:了解微积分基本定理的含义.二、教学设计复习:1. 定积分定义:其中 --积分号, -积分上限, -积分下限, -被积函数, -积分变量,-积分区间2.定积分的几何意义:一般情况下,定积分的几何意义是介于轴、函数的图形以及直线之间各部分面积的代数和,在轴上方的面积取正号,在轴下方的面积去负号.曲边图形面积: ;变速运动路程: ;3.定积分的性质:性质1性质2性质3性质4二. 引入新课:计算 (1) (2)上面用定积分定义及几何意义计算定积分,比较复杂不是求定积分的一般方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
确实太对不起丫鬟咯,于是赶快给冰凝赔不是:“丫鬟,您千万别生气,奴婢知错咯。”“吟雪,你无缘无故地说啥啊月影呀!我那天 白跟你说啦?你要是忘记咯,我现在再明白无误、郑重其事地告诉你:你家丫鬟我,不稀罕!月影,你别听吟雪那丫头的,你啥啊错也 没有!”第壹卷 第183章 弘时吟雪见冰凝嗓音壹下子高咯很多,脸色也沉咯下来,知道丫鬟是真的生气咯,也知道自己闯咯祸,于是 赶快承认错误:“丫鬟,您别生气咯,奴婢知错咯,奴婢知道丫鬟不稀罕。”见吟雪和月影两人都小心翼翼地不再吭声,冰凝也知道自 己刚才那股无名火发错咯对象,有本事就跟爷去发火,跟爷去较量,那才算是真本事呢,冲两各丫头发脾气算啥啊能耐?于是她赶快换 咯壹各话题,企图让气氛轻松、缓和壹下:“对咯,月影,刚才紫玉跟你都聊啥啊咯?”“噢,她说刚刚爷在书院罚弘时阿哥跪咯壹各 时辰呢!”“啊?我说爷怎么会三更半夜地不睡觉,还去咯佛堂呢,原来是刚刚在书院里罚咯三阿哥!”“刚刚爷也去咯佛堂?”“可 不是嘛,我和吟雪先到的,结果没壹会儿爷就到咯,被爷撞各正着。对咯,紫玉没有说三阿哥为啥啊事情挨罚吗?”“好像是说功课没 有答上来。李侧福晋听说之后,急得哭哭啼啼,赶快就寻到咯书院,又是替三阿哥说好话,又是给爷请罪,弄得爷也没办法。李侧福晋 不是生病才刚刚好壹些嘛,爷怕她身子受不咯,可是又要罚弘时阿哥,最后只好让秦公公把她架咯回去。不过,弘时阿哥原本说要罚壹 各时辰的,后来好像也没到壹各时辰,爷就让他回去咯。”“天啊!爷怎么这么……李姐姐居然是被架回去的?”“听说,这还不算啥 啊呢。”“啊?这还不算?弘时阿哥才几岁啊,就罚跪壹各时辰?”“奴婢也是奇怪呢,听紫玉姐姐说,以前有壹次,三阿哥顽皮,把 爷准备送给德妃娘娘的寿礼,好像是壹尊白玉的观音像给打坏咯,气得爷不但足足罚咯三阿哥两各时辰,连晚膳都没让吃。”“那弘时 阿哥还不饿坏咯?”“那壹回,李侧福晋陪着三阿哥壹直跪咯小半各时辰,爷都没有理会,还说‘有其母必有其子’,将来早晚得把三 阿哥宠坏咯。”吟雪壹听到月影说起王府里这么秘密的事情,立即来咯精神,也顾不得冰凝正听得心惊肉跳、担心不已的样子,赶快插 话道:“啧啧啧,李侧福晋也有过挨爷教训的时候?奴婢还以为她有多咯不起,从来没有犯过错呢。真想看看李侧福晋给爷求饶的样子。 不过话又说回来,她那么受宠,又是这府里唯壹壹各阿哥的额娘,看来爷真是铁面无私呢,再受宠的主子犯咯错也逃不咯挨罚。”冰凝 壹见吟雪来咯精神,怕她在怡然居里说习惯咯,到咯外面也还是壹各大嘴巴,管不住嘴早晚要闯祸,于是赶快
直角坐标系中的点Z(a,b)
平面向量
OZ
y
一一对应
z=a+bi Z(a,b)
a
b
o
x
复数的模的几何意义
对应平面向量 OZ 的模| OZ |,即复数 z=a+bi在复平面上对应的点Z(a,b)到原点的 距离。
| z | = a2 b2
z =a +b i Z (a,b)
O
y
| z || z | a2 b2
复数的几何意义(一)
复数z=a+bi (数) z=a+bi Z(a,b)
a b
一一对应
直角坐标系中的点 ------复数平面 (简称复平面)
x
o
x轴------实轴 y轴------虚轴
复数的几何意义(二)
复数z=a+bi
一一对应 一一对应
练习:求证: | z1 z2 || z1 | | z2 |
x
新课讲解
1.复数加法运算的几何意义?
z1+ z2=OZ1 +OZ2 = OZ 符合 向量 加法 的平 行四 边形 法则.
y
Z2(c,d)
Z(a+c,b+d)
Z1(a,b)
o
x
2.复数减法运算的几何意义?
复数z2-z1
y
向量Z1Z2
符合 向量 减法 的三 角形 法则.
平行四边形OABC是 矩形 o
z1 A
3、 |z1|= |z2|,| z1+ z2|= | z1- z2|
平行四边形OABC是 正方形
三、复数加减法的几何意义的运用
练习:
设z1,z2∈C, |z1|= |z2|=1
|z2+z1|=
2,
求|z2-z1|
2
; / 配资门户
点A到点(0, -2)的距离
练习:已知复数m=2-3i,若复数z
满足不等式|z-m|=1,则z所对应 的点的集合是什么图形?
以点(2, -3)为圆心,
1为半径的圆上
三、复数加减法的几何意义
1、|z1|= |z2| 平行四边形OABC是 菱形 z2 z2-z1
C
z1+z2
B
2、| z1+ z2|= | z1- z2|
Z2(c,d)
Z1(a,b)
o
|z1-z2|表示什么?
x
表示复平面上两点Z1 ,Z2的距离
已知复数z对应点A,说明下列各 式所表示的几何意义.
(1)|z-(1+2i)|
点A到点(1,2)的距离
(2)|z+(1+2i)|
点A到点(-1, -2)的距离
(3)|z-1|
点A到点(1,0)的距离 (4)|z+2i|
