定积分在特殊图形面积问题中的应用
定积分求平面图形面积在生活上的应用

定积分求平面图形面积在生活上的应用
定积分是一种重要的数学方法,可以求出曲线或平面图形的面积,它可以用来预测及解决许多实际问题。
其实,定积分在我们的生活中也起着广泛的作用,即通过定积分可以求得许多日常中的实际图形图形的面积,再进而用于实际应用。
首先,定积分可以用来求解拟空间图形的体积,如正方体、圆柱体等。
在家装工程、楼宇建筑等工程中,我们往往希望通过计算室内分段图形物体的体积,来确定施工量、进行报价。
因此,定积分可以方便地计算出各自图形的面积,求得一个准确的体积,有利于家装施工工作。
其次,定积分还可以延伸到土木建筑学方面,主要应用在把土堤劈开形成群堤劈口时,需要用定积分来计算滩坝的面积。
在给江河加固筑坝中,也会用定积分帮助计算出河道及整体筑堤的面积,以便进行设计分析标志,精确洪水启动洪水的等级,把握工程参数,使工程质量更有保障。
而且,还可以控制工程造价,提高工程施工质量。
最后,定积分也广泛用于测量地理空间,如绘制剖分图形等。
目前,在社会经济发展过程中,各种自然资源、土地开发成为重要话题,资源管理成为一个完善的管理体系。
地块剖分时,根据图形形状和边缘位置,即以定积分来求出这些图形的面积,从而能很好地管理相应的资源和土地使用。
通过以上叙述,可以很清晰地看出定积分在我们的生活中起着非常重要的作用。
它有助于计算出各种图形的面积,从而可以在家庭清淤、室内装修工程、水利筑坝工程及地块剖分等领域派上用场,它不仅可以提高工程品质,也能控制造价,极大的方便了实际工程的日常管理和分析等。
定积分法求面积探究毕业论文

定积分法求面积的探究教学系:_____________专业:_________________年级:______________________姓名:_____________________学号:__________导师及职称:定积分是数学中十分重要的工具,其中求图形的面积正是它的运用之一,它的思想就是切割求和,在不同的坐标系下可采用特定的方法求解面积。
本文介绍了几种运用定积分来求面积的方法,其中列举了特殊的例题以及重要的问题解决方法。
如果实际问题中的所求量与某一区间有关且在该区间上具有可加性,我们就可以用函数的定积分来表示这个所求的量,因此我们就可以运用定积分来解决一些实际问题。
同时利用定积分求不规则平面图形的面积,是定积分在几何中的重要应用之一。
如何灵活地运用定积分的定义及有关公式,巧妙地将求不规则图形的面积问题等价转化为求定积分的数值问题就是一大关键,本文结合实例,介绍几种常用的转化方法与求解策略。
从而充分的体现数形结合的数学思想方法。
关键词:定积分;封闭图形;曲面域;对称性Research of square in defi nite in tegralABSTRACTA definite integral is very important mathematical tools, for which the graphics area is one of its applicati on, its thought is to cut and, un der differe nt coordi nate systems can use specific method to find the area. This paper introduces several methods of using the integral area to seek the. Which lists the specific examples and an important method to solve the problem. If practical problems for quantity with a certain interval and in the interval is additive, we can use the definite integral of a function to represent the desired amount. Therefore, we can use the defi nite in tegral to solve some practical problems.At the same time, the use of definite integrals for the irregular plane graphics area, is one of the important applications of integral in geometry. How to flexibly use definite integral is defi ned and the related formulae and skillfully will seek irregular graphic area equivale nt transformation to calculate the numerical integral is one of key, the paper with examples, in troduces several common ly used tran sformati on method and soluti on strategy. I n order to fully reflect the comb in ati on of the mathematical thought and method.Keywords: defi nite in tegral; closed graph; surface area; symmetry目录一、引言 (5)二、相关概念 (5)1.1 定积分的定义 (5)1.2定积分的常用计算方法 (5)1.2.1直接利用公式及性质计算 (5)1.2.2利用定积分的区间可加性计算 (2)三、定积分在面积问题中的应用 (2)3.1直角坐标系下求面积 (2)3.1.1 平面面积 (2)3.1.2 曲面面积 (5)3.2 极坐标 (6)3.3求旋转曲面的面积 (7)四、常见方法 (10)4.1 巧选积分变量 (10)4.2巧用对称性 (11)4.3巧用分割计算 (11)五、结束语 (12)参考文献 (13)致谢 (13)、引言积分在自然科学、工程技术、经济管理中有着广泛的应用,比如利用积分求平面图 形的面积、变力做功等都是微积分中定积分的应用问题, 在数学分析中占据了重要地位。
定积分在几何和物理中的应用

定积分在几何和物理中的应用定积分是高等数学中非常重要的一个概念,它可以用于计算曲线、曲面的面积或体积,还可以应用到物理学、工程学中。
在本文中,我们将着重探讨定积分在几何和物理中的应用。
一、计算面积我们首先来看一个简单的例子,如果我们想要计算一个曲线所围成的面积,我们需要怎么做呢?假设曲线为y=f(x),我们可以将这条曲线分成若干个无限小的小矩形,每个小矩形的宽度为Δx,高度为函数值f(x),则该小矩形的面积为f(x)Δx。
我们将所有小矩形的面积相加,得到所求的曲线面积S:S=∫a^b f(x) dx其中a和b分别是曲线的起点和终点。
这里的∫符号代表积分符号,具体的计算方法不在本文中详细说明。
二、计算体积在物理学中,我们经常需要计算物体的体积,定积分也可以帮助我们实现这一目的。
比如我们需要计算一个旋转曲线所围成的立体体积,我们可以依然使用之前的方法将其分解成无限小的小圆柱体积,每个小圆柱的体积可以表示为:V=π[f(x)]^2dx我们将所有小圆柱的体积相加,得到所求的立体体积V:V=∫a^b π[f(x)]^2dx三、计算重心和质心在物理学中,重心和质心是非常重要的概念。
对于一个平面图形或者一个立体体形,它的重心和质心分别表示为:重心:(∫xdS)/(∫dS)质心:(∫xdm)/(∫dm)这里的dS和dm分别表示面元和质量元,x则表示距离中心的距离。
我们可以通过对图形进行分割并使用定积分来计算重心和质心。
四、积分在物理学中的应用定积分在物理学中的应用非常广泛,比如我们可以使用它来计算弹性势能、动能、功、功率等物理量。
举一个简单的例子,假设质量为m的物体从高度为h处自由落下,当它下落到高度为y 时,它的速度为v,我们可以使用动能和势能的转化关系求出v,设重力加速度为g,则它下落过程中失去的重力势能为mgh-mgy,同时增加的动能为(1/2)mv^2,因此:mgh-mgy=(1/2)mv^2v=sqrt(2g(h-y))我们可以使用定积分来求解物体在过程中的运动状态,以及计算其他物理量的值。
试论定积分在物理及其他领域的应用

试论定积分在物理及其他领域的应用1. 引言1.1 定积分的基本概念定积分是微积分的一个重要概念,它在数学中有着广泛的应用。
定积分的基本概念可以简单地理解为一个函数在一定区间内的累积效果。
在几何学中,定积分可以用来计算曲线下面积,图形的面积和体积等问题。
在数学上,定积分可以看作是不定积分的反运算,通过定积分我们可以求解函数的定积分值。
在实际应用中,定积分被广泛运用于物理、工程、经济等领域。
它的应用使得复杂问题的计算变得简单清晰。
通过定积分,我们可以计算出物体的质量、力的大小、功的大小等物理量。
在力学中,定积分可以用来描述物体的运动规律,计算出物体的位置、速度和加速度等。
在电磁学中,定积分常常用来计算电场强度、磁场强度等问题。
在热力学中,定积分可以用来计算热量、熵等热力学量。
在工程学中,定积分可以帮助工程师计算出工程设计中的各种参数。
在经济学中,定积分在求解供求关系、成本、收益等问题上起着重要作用。
定积分在各个领域中都有着重要的应用价值。
它的基本概念对于理解定积分的应用具有重要意义。
通过深入研究定积分的基本概念,可以更好地理解其在不同领域中的具体应用。
1.2 定积分在物理领域的重要性定积分在物理领域的重要性体现在多个方面,首先在力学中,定积分可以用来描述物体的质量、速度、加速度、力和能量等物理量随时间的变化,从而帮助解决力学中的各种问题。
在电磁学中,定积分可以用来描述电流、电荷、电场、磁场等物理量在空间中的分布和变化规律,从而帮助解决电磁学中的各种问题。
在热力学中,定积分可以用来描述热量、温度、熵等热力学量在空间中的分布和变化规律,从而帮助解决热力学中的各种问题。
在工程学和经济学中,定积分也有着重要的应用,可以用来描述工程和经济系统中的各种物理量的变化规律,从而帮助解决工程和经济学中的各种问题。
定积分在物理领域中的重要性不可忽视,它为我们理解和应用物理定律提供了重要的数学工具和方法。
2. 正文2.1 定积分在力学中的应用在力学中,定积分是一个非常重要的数学工具,它可以用来描述物体在运动过程中的各种性质和运动规律。
定积分在几何学上的应用

一、平面图形的面积
1. 直角坐标情形
y y f (x)
设曲线
与直线
及 x 轴所围曲 边梯形面积为 A , 则
o
a
x
x
dbx
x
dA f (x) dx
b
A a f (x) dx
y y f1(x) y f2 (x)
右图所示图形面积为
b
A a f1(x) f2 (x) dx
A 40 y d x
利用椭圆的参数方程
x y
a cos t b sin t
(0 t 2 )
y b
o xxdxa x
应用定积分换元法得
4
ab
12
2
ab
4ab 2 sin 2 t dt 0
当 a = b 时得圆面积公式
一、平面图形的面积
2. 极坐标情形
求由曲线
及
围成的曲边扇形的面积 .
在区间
2
(1
1 y 2 ) 2d y 1 (2 y)2 d y 0
内容小结
1. 平面图形的面积 直角坐标方程
边界方程 极坐标方程
2. 已知平行截面面面积函数的立体体积
旋转体的体积 绕x轴: 绕y轴:
上任取小区间
则对应该小区间上曲边扇形面积的近似值为
dA 1 ( ) 2 d
2
所求曲边扇形的面积为
r ( ) d
A 1 2 ( ) d 2
x
一、平面图形的面积
例 计算阿基米德螺线 到 2 所围图形面积 .
解:
A 2 1 (a )2 d
02
a2 2
13
3
定积分求曲边图形面积精析

定积分求曲边图形面积精析曾玲莉 熊明军定积分是课标教材的新增内容,在数学方面主要包括平面图形的面积及微积分基本定理,而利用定积分求含曲边的平面图形面积问题在平面几何中是难以用常规方法加以解决的。
定积分知识的引入,为此类问题的解决提供了强有力的方法工具,也充分体现了新内容引进的必要性。
一、利用定积分求平面曲边图形面积的步骤及理论基本步骤:①画图形→②求交点→③写积分→④算面积。
基本理论:①如果函数()x f 和()x g 在],[b a 上可积,并且满足()()],[,b a x x g x f ∈∀≥, 那么介于直线b x a x ==,和曲线()()x g y x f y ==,之间的图形面积可以表示为定积分:()()dx x g x f S ba ⎰-=][图形面积. ②如果函数()y ϕ和()y φ在],[b a 上可积,并且满足()()],[,b a y y y ∈∀≥φϕ, 那么介于直线b y a y ==,和曲线()()y x y x φϕ==,之间的图形面积可以表示为定积分:()()dy y y S ba ⎰-=][φϕ图形面积. *注意:在基本步骤中,第③步怎样写出图形面积对应的定积分表达式是重点也是难点,由于定积分值不一定为正,但平面曲边图形的面积总是正值,因此,在这里要注意准确把握基本理论,就是根据所画图形查找是否有一条曲线(直线)在另一条曲线(直线)之上,x 做积分变量不行就换y 做积分变量。
即:①对于x 做积分变量时,()()],[,b a x x g x f ∈∀≥;②对于y 做积分变量时,()()],[,b a y y y ∈∀≥φϕ。
二、定积分求平面曲边图形面积的典例精析例1:求曲线x y sin =与x 轴在区间]2,0[π上所围成阴影部分的面积。
x解析:①画图形:如上图已知;②求交点:()()()0,2,0,,0,0ππ;③写积分:以x 作为积分变量,在],0[π上,0sin ≥x ,直线0=y 与曲线x y sin =所围成的曲边图形面积:()dx x dx x S ⎰⎰=-=ππ00sin 0sin 图形面积;在]2,[ππ上,x sin 0≥,同理可得图形面积为()()dx x dx x dx x S ⎰⎰⎰-=-=-=ππππππ222sin sin sin 0图形面积。
利用定积分求平面图形面积的一些讨论

利用定积分求平面图形面积的一些讨论定积分是数学中的一个重要概念,它能够求得平面图形的面积。
在实际生活中,我们常常需要计算各种形状的物体的面积,因此定积分的应用非常广泛。
首先,我们需要了解定积分的定义和原理。
在数学中,定积分是对函数在一定区间内的积分进行求和,并将其视为一个数值。
通过定积分,我们可以得到函数在区间内的平均值和总和。
这意味着,如果我们将函数视为图形,定积分可以帮助我们计算出这个图形的面积。
接下来,我们来看几个实际的例子。
假设我们想计算一个矩形的面积。
我们可以通过将矩形分成无数个小矩形,在每个小矩形中取一个样本点,然后将所有小矩形的面积相加,得到整个矩形的面积。
这个方法就是通过定积分来计算面积的。
再例如,我们想计算一个曲线下面的面积。
我们可以将曲线分成无数个小矩形,在每个小矩形中取一个样本点,并将所有小矩形的面积相加。
这个方法就是通过定积分来计算曲线下面的面积的。
在实际计算中,我们常常需要将图形分成无数个小块,然后在每个小块中计算出一个样本点,最后将所有小块的面积相加。
这个方法是通过近似来得到定积分的,称为黎曼和。
随着小块的数量越来越多,近似值会越来越接近准确值。
因此,对于一些形状复杂的图形,我们可以通过将其分成无数个小块,并采用近似方法来计算其面积。
定积分的应用还包括计算物体的体积、质心、弧长、表面积等等。
因此,掌握定积分的应用是非常重要的。
在实际工作和生活中,我们常常需要计算各种形状的物体的面积和体积,这时候掌握定积分的方法就能大大提高我们的工作效率。
总之,定积分的应用非常广泛,可以帮助我们计算各种形状的物体的面积、体积、质心、弧长等等。
通过学习并掌握定积分的方法,我们可以在实际工作和生活中更加高效地完成各种计算。
同时,我们也能够更深入地理解数学中的定积分这一重要概念。
1.7定积分的几何应用

2
2
围成图形的面积.
解:作出y2=x,y=x2的图象如图所示:
解方程组 x 0 x 1 y x 或 2 y 0 y 1 y x
y
y
y xx
2
B
2
即两曲线的交点为(0,0),(1,1)
S = S曲 边 梯 形 OABC - S曲 边 梯 形 OABD
B(1,- 1). ∴围成图形 (阴影部分 )面积为
S=
-2
1
(- x2- x+ 2)dx 9 = . 2
1 3 1 2 = (- x - x + 2x) 3 2
9 答案: (1) 2
例 2 计算由曲线 y 围成的图形的面积.
2x
,直线 y
x 4 以及
y 2x
x 轴所
解:
两曲线的交点
2
|0 8
8
X型求解法
40 3
x 1 2 y
2
16 2 8
1 2
3
2
[( 4 y )
y ]d y
4
(4 y
44
1 2 1
2
y
2
2
1 6
x 4 y
y ) |0
1 6
3
4
4
40 3
Y型求解法
练习 1(例 2 变式题) : 计算由曲线 y 2 x 和直线 y x 4 所围成的图形的面积
2π 4 A. B. 5 3 3 π C. D. 2 2 解析:选 B.由图象可知二次函数的表达式为 f(x)= 1- x2,∴ S= 1 3 1 1 4 1 2 = (1- )-(- 1+ )= . -1 (1- x )dx= (x-3x ) 3 3 3
定积分在几何中的应用
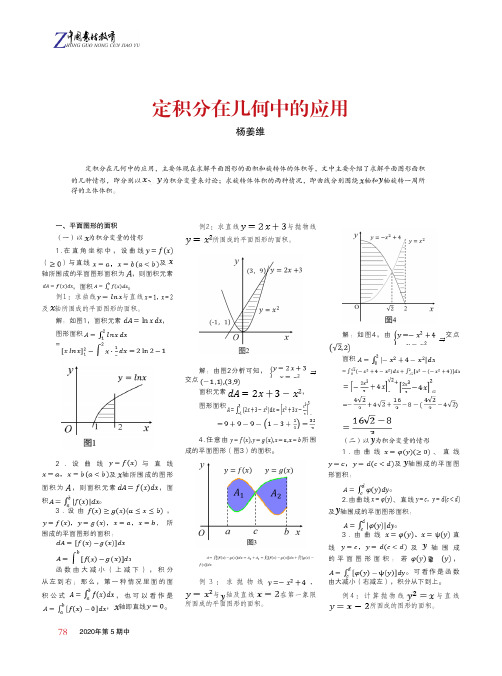
782020年第 5 期中定积分在几何中的应用杨姜维一、平面图形的面积(一)以为积分变量的情形1.在直角坐标中,设曲线()与直线及轴所围成的平面图形面积为,则面积元素,面积。
例1:求曲线与直线及轴所围成的平面图形的面积。
解:如图1,面积元素,图形面积=2.设曲线与直线及轴所围成的图形面积为,则面积元素,面积。
3.设由,所围成的平面图形的面积:函数由大减小(上减下),积分从左到右;那么,第一种情况里面的面积公式,也可以看作是,轴即直线。
例2:求直线与抛物线所围成的平面图形的面积。
解:由图2分析可知,交点面积元素,图形面积4.任意由所围成的平面图形(图3)的面积。
例3:求抛物线,与轴及直线在第一象限所围成的平面图形的面积。
解:如图4,由交点面积+(二)以为积分变量的情形1.由曲线、直线及轴围成的平面图形面积:。
2.由曲线、直线及轴围成的平面图形面积:。
3.由曲线直线及轴围成的平面图形面积:若,。
可看作是函数由大减小(右减左),积分从下到上。
例4:计算抛物线与直线所围成的图形的面积。
定积分在几何中的应用,主要体现在求解平面图形的面积和旋转体的体积等,文中主要介绍了求解平面图形面积的几种情形,即分别以为积分变量来讨论;求旋转体体积的两种情况,即曲线分别围绕轴和轴旋转一周所得的立体体积。
JIAO HAI TAN HANG/教海探航解:如图5,由交点为方便计算,选取为积分变量,则有4.任意由曲线直线及轴围成的平面图形面积:。
二、旋转体的体积一个平面图形围绕其所在平面上的一条直线旋转一周而成的立体即为旋转体,常见的旋转体有圆柱体、圆锥、圆台、球体等,这些都有对应的体积公式,面对日常生活中所用到的水杯、花瓶等立体物件,求解体积时可考虑以下情况:(一)曲线绕轴旋转的情形由连续曲线与直线及轴所围成的曲边梯形绕轴旋转一周而成的立体,选为积分变量,该旋转体的体积元素,体积为。
(二)曲线绕轴旋转的情形由曲线、直线及轴围成的平面图形绕轴旋转一周所得的立体,选为积分变量,该旋转体的体积元素,体积为。
定积分法求面积探究毕业论文

定积分法求面积的探究教学系:专业:年级:姓名:学号:导师及职称:摘要定积分是数学中十分重要的工具,其中求图形的面积正是它的运用之一,它的思想就是切割求和,在不同的坐标系下可采用特定的方法求解面积。
本文介绍了几种运用定积分来求面积的方法,其中列举了特殊的例题以及重要的问题解决方法。
如果实际问题中的所求量与某一区间有关且在该区间上具有可加性,我们就可以用函数的定积分来表示这个所求的量,因此我们就可以运用定积分来解决一些实际问题。
同时利用定积分求不规则平面图形的面积,是定积分在几何中的重要应用之一。
如何灵活地运用定积分的定义及有关公式,巧妙地将求不规则图形的面积问题等价转化为求定积分的数值问题就是一大关键,本文结合实例,介绍几种常用的转化方法与求解策略。
从而充分的体现数形结合的数学思想方法。
关键词:定积分;封闭图形;曲面域;对称性Research of square in definite integralABSTRACTA definite integral is very important mathematical tools, for which the graphics area is one of its application, its thought is to cut and, under different coordinate systems can use specific method to find the area. This paper introduces several methods of using the integral area to seek the. Which lists the specific examples and an important method to solve the problem. If practical problems for quantity with a certain interval and in the interval is additive, we can use the definite integral of a function to represent the desired amount. Therefore, we can use the definite integral to solve some practical problems.At the same time, the use of definite integrals for the irregular plane graphics area, is one of the important applications of integral in geometry. How to flexibly use definite integral is defined and the related formulae and skillfully will seek irregular graphic area equivalent transformation to calculate the numerical integral is one of key, the paper with examples, introduces several commonly used transformation method and solution strategy. In order to fully reflect the combination of the mathematical thought and method.Keywords: definite integral; closed graph; surface area; symmetry目录一、引言 (5)二、相关概念 (5)1.1 定积分的定义 (5)1.2 定积分的常用计算方法 (5)1.2.1 直接利用公式及性质计算 (5)1.2.2 利用定积分的区间可加性计算 (6)三、定积分在面积问题中的应用 (6)3.1 直角坐标系下求面积 (6)3.1.1 平面面积 (6)3.1.2 曲面面积 (9)3.2 极坐标 (10)3.3 求旋转曲面的面积 (11)四、常见方法 (10)4.1 巧选积分变量 (14)4.2 巧用对称性 (15)4.3 巧用分割计算 (15)五、结束语 (16)参考文献 (17)致 (13)一、引言积分在自然科学、工程技术、经济管理中有着广泛的应用,比如利用积分求平面图形的面积、变力做功等都是微积分中定积分的应用问题,在数学分析中占据了重要地位。
定积分的应用: 平面图形面积讲解

y y f (x)
y
y f2(x)
o a x x xb x 曲边梯形的面积
A
b
a
f
(
x)dx
y f1( x)
oa
xx b x
曲边梯形的面积
A
b
a[
f2(x)
f1( x)]dx
例 1 计算由两条抛物线y2 x 和y x2 所围成的
图形的面积.
解: 设抛物线上切点为
则该点处的切线方程为
B
M
它与 x , y 轴的交点分别为
A
所指面积
得[ 0 , 1] 上的唯一驻点 且为最小点 . 故所求切线为
B M
A
如果曲边梯形的曲边为参数方程
x y
(t) (t)
曲边梯形的面积 A t2 (t)(t)dt. t1
(其中t1和t2 对应曲线起点与终点的参数值)
3 2
2 sin
1 sin 2
4
0
ห้องสมุดไป่ตู้
3 2
a2 .
三、小结
求在直角坐标系下、参数方程形式 下、极坐标系下平面图形的面积.
(注意恰当的选择积分变量有助于简化 积分运算)
直角坐标方 边界方程 参 程数方程
极坐标方程
b
A a f1(x) f2 (x) dx
思考题
设曲线 y f ( x)过原点及点(2,3) ,且 f ( x)
2
4ab 2 sin2 tdt ab. 0
二、极坐标系情形
设由曲线r ( )及射线 、 围成一曲边扇 形,求其面积.这里, ( )
定积分求平面图形的面积

解: 由
得交点
为简便计算, 选取 y 作积分变量,
则有
计算抛物线
与直线
的面积 .
所围图形
例2
训练
1.求曲线 与x 轴所围成的图形面积。 2.求曲线 与直线 x=-1,x =1及x轴所围成的图形面积. 3.求曲线 与 所围成的图形面积。 4.求曲线 与直线y=x,x=2所围成的图形面积。
演讲结速,谢谢观赏
Thank you.
PPT常用编辑图使用方法
1.取消组合
2.填充颜色
3.调图标元素
商务 图标元素
商务 图标元素
商务 图标元素
商务 图标元素
商务 图标元素
商务 图标元素
商务 图标元素
Excellent handout training template
定积分求平面图形的面积
定积分的应用-----求平面图形面积
引入
1.复习定积分的定义及其几何意义 2.如何用定积分求平面图形的面积
一、微元法
设曲线
与直线
及 x 轴所围曲
则
边梯形面积为 A ,
其中 为面积元素,
y
x
a
b
o
若曲线 与 及x=a,x=b 所围成的图形为如图:
面积A,
设曲线
与直线
及 x 轴所围曲
则
边梯形面积为 A ,
计算两条抛物线
在第一象限
所围图形的面积 .
解: 由
得交点
例1
分析,归纳解题步骤: 1.画草图,求出曲线的交点坐标. 2.将曲边形面积转化为曲边梯形面积. 3.根据图形特点选择适当的积分变量 4.确定被积函数和积分区间,计算定积分,求出面积。
【教学随笔】定积分求特殊图形的面积
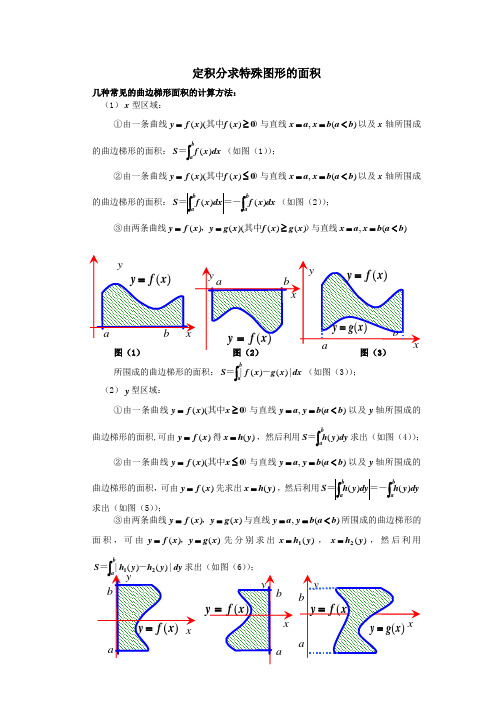
定积分求特殊图形的面积几种常见的曲边梯形面积的计算方法: (1)x 型区域:①由一条曲线)其中0≥=)()((x f x f y 与直线)(,b a b x a x <==以及x 轴所围成的曲边梯形的面积:⎰badx x f S )(=(如图(1));②由一条曲线)其中0≤=)()((x f x f y 与直线)(,b a b x a x <==以及x 轴所围成的曲边梯形的面积:⎰⎰babadx x f dx x f S )()(=-=(如图(2));③由两条曲线)其中,)()()(()(x g x f x g y x f y ≥==与直线)(,b a b x a x <==所围成的曲边梯形的面积:⎰badx x g x f S |)()(|-=(如图(3));(2)y 型区域:①由一条曲线)其中0≥=x x f y )((与直线)(,b a b y a y <==以及y 轴所围成的曲边梯形的面积,可由)(x f y =得)(y h x =,然后利用⎰bady y h S )(=求出(如图(4));②由一条曲线)其中0≤=x x f y )((与直线)(,b a b y a y <==以及y 轴所围成的曲边梯形的面积,可由)(x f y =先求出)(y h x =,然后利用⎰⎰babadyy h dy y h S )()(=-=求出(如图(5));③由两条曲线)()(x g y x f y ==,与直线)(,b a b y a y <==所围成的曲边梯形的面积,可由)()(x g y x f y ==,先分别求出)(y h x 1=,)(y h x 2=,然后利用bdy y h y h S |)()(|-=求出(如图(6));图(4) 图(5) 图(6)例1.计算由两条抛物线2y x =和2y x =所围成的图形的面积.【分析】两条抛物线所围成的图形的面积,可以由以两条曲线所对应的曲边梯形的面积的差得到。
定积分在特殊图形面积问题中的应用

积分在特殊图形面积问题中的应用就是用来计算曲面面积的。
它可以用来计算椭圆形、圆形、三角形、多边形等特殊图形的面积。
例如,若要计算一个椭圆的面积,可以使用椭圆积分公式:
S = πab
其中a为椭圆的长轴,b为椭圆的短轴。
另外,若要计算圆形的面积,可以使用圆形积分公式:
S = πr2
其中r为圆的半径。
此外,若要计算三角形的面积,可以使用三角形积分公式:
S = 1/2absinC
其中a为三角形的第一边的长度,b为三角形的第二边的长度,C为三角形的夹角。
最后,若要计算多边形的面积,可以使用多边形积分公式:
S = 1/2∑i=1n(xi-1yi+xiyn+1)
其中x1,y1,x2,y2...xn,yn为多边形的每一个顶点的坐标。
定积分求平面图形面积在实际生活中的应用案例

定积分求平面图形面积在实际生活中的
应用案例
面积的应用案例
面积的应用案例在我们的日常生活中是随处可见的,最常见的例子之一就是制作房屋,也就是建筑学中所说的建筑物的平面布局图。
建筑物的平面布局图是建筑设计的一个重要组成部分,在平面布局图中,通过把不同房间以图形的形式表示出来,将特定房间以不同形式圈出来,通过计算图形的面积,可以大致了解建筑中每一个房间的大小,而且通过计算建筑物的总面积,可以比较容易了解建筑物的大小。
另外,人们在种植面积大小也是一个重要因素,用于决定可以种植的农作物数量是多少,在实际中,用了计算一块土地的面积来决定可以种植的农作物数量是很重要的,特别是在把田拆分出来种植小麦,小麦是面类粮食的主要来源,所以拆分的田地的面积是一个很有意义的参考因素,有助于农民们更好的估计可以收获多少,从而提高种植小麦的效益。
平面图形的面积还有一个历史悠久的应用,即地图解绘,即设计出特定地区的地图,地图解绘也是一种非常严谨的科学,需要准确测量出特定地区的面积,再结合空间关系进行综合分析,比如地质勘查和土地利用图
等,这些都需要准确解绘出平面图形的面积进行分析,最后得出比较准确
的数据。
当然,许多日常物品也是由平面图形组成的,比如妆桌,牙刷,笔等,而这些物品的制作都需要精确测量出平面图形的面积,这样才能保证精确
制作出非常好用的物品。
可见,积分求平面图形面积已经渗透到了我们的日常生活,是影响我
们实际生活的一个非常重要的技术和工具,它的应用覆盖的范围很广,由
于它潜移默化的作用,使我们的日常生活变得更加舒适便捷。
因此,我们
可以以此来彰显积分求平面图形面积在实际生活中的应用价值。
定积分在几何上的应用(面积)

r()
d
面积元素 dA1[()2]d
2
曲边扇形的面积为:
o
x
A 1[()2]d. 2
圆 扇 形 的 面 A积1r为 2
2
例 6求 双 纽 线 2 a 2c2 o所 s围 平 面 图 形
的 面 积 .
解 由对称性知总面积=4倍第
一象限部分面积
yx
A4A1
A404
1a2co2sd
2
a2.
A1 2a2co2s
ax
x bx
x+dx
b
b
Aa f(x)d xaydx
例 1计 算 由 两 条 抛 物 线 y2x和 yx 2所 围 成 的
图 形 的 面 积 .
解 两曲线的交点 (0,0) (1,1) 选 x为积分变量 x[0,1]
x y2 y x2
面积微元 dA ( xx2)dx
1
A0(
xx2)dx 32
1根据问题的具体情况选取一个变量例如分成n个小区间取其中任一小区间并记为与dx的乘积就把dx称为量f的微元且记作df上曲线下曲线xdxdx面积微元dx可直接由公式得到xdx求面积的一般步骤
第五章 定积分及其应用
§6 定积分在几何上的应用
§5.6 定积分在几何上的应用
若能把某个量表示 成定积分,我们就可以 计算了.
n
小窄曲边梯形的面积为Ai ,则AAi .
i1
( 2 ) 计 算 A i 的 近 似 值 A if(i) x i i xi
n
(3) 求和,得A的近似值 A f(i)xi.
(4) 求极限,得A的精确值 i1
n
Al i0m i1f(i)xi abf(x)dx
用定积分求面积的两个重要公式
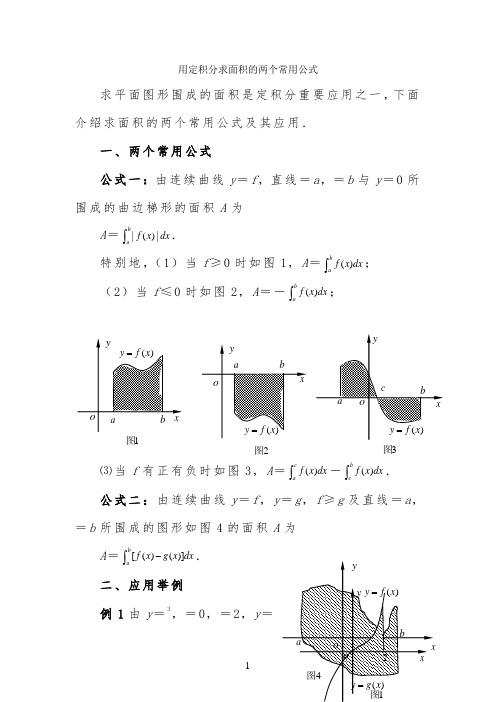
用定积分求面积的两个常用公式求平面图形围成的面积是定积分重要应用之一,下面介绍求面积的两个常用公式及其应用.一、两个常用公式公式一:由连续曲线y =f ,直线=a ,=b 与y =0所围成的曲边梯形的面积A 为A =|()|ba f x dx ⎰.特别地,(1)当f ≥0时如图1,A =()ba f x dx ⎰;(2)当f ≤0时如图2,A =-()baf x dx ⎰;⑶当f 有正有负时如图3,A =()caf x dx ⎰-()bcf x dx ⎰.公式二:由连续曲线y =f ,y =g ,f ≥g 及直线=a ,=b 所围成的图形如图4的面积A 为A =[()()]ba f x g x dx -⎰.二、应用举例例1由y =3,=0,=2,y =1图2图3图0围成的图形面积.分析:先画出图象,利用公式1转化为定积分问题即可解决.解:(1)如图1,由公式1,得S =230x dx ⎰=42440111|204444x =⨯-⨯=.评注:注意定积分与利用定积分计算曲线围成图形的面积区别.定积分是一种积分和的极限,可为正,也可为负或零,而平面图形的面积在一般意义上总为正.一般情况下,借助定积分分别求出每一部分曲边梯形的面积,然后将它们加在一起.例2(1)由曲线y =2,y 2=所围成图形的面积. (2)由y =142-1,y =12,y =34x 在第一象限所围成图形的面积.分析:先画图象找出范围,利用公式2,用积分表示,再求积分.解:(1)如图2,所求面积为阴影部分. 解方程组22y xy x⎧=⎪⎨=⎪⎩,得交点0,0,1,1,由公式2,得S =120)x dx ⎰=331202211()|33333x x -=-=.(2)如图3,解方程组211412y x y x ⎧=-⎪⎪⎨⎪=⎪⎩和211434y x y x ⎧=-⎪⎪⎨⎪=⎪⎩,得=0,=1+的舍去,=4.由公式2,得图形面积S=1031()42x dx -⎰+42111[(1)]42x x dx --⎰216-=.3图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
% ’ # .’! 得直线% ’ #.’ 解析 ! 解方程组 #! ! %’ 槡
,
! # ! " ! # ! 因此它们所围 # 有且只有两个交点 " # # ! # .’ 成 的图形在直线# ’#及# ’!之间 ! 可以不画图 ! 也 ! +上 两 曲 线 的 上 $ 不考虑在区间 * 下 位 置 关 系! 而 # ! 直接将两函数式相减并取绝对值 ! 然后积分 !
’
! & ! ! ! ! 令# )# 由 题意 ! 则% ’ % ’& . !# ! % )#! /
!
$
#
# $’
#
(
’
’
’ # ! %
槡
! & ! ! 故该椭圆在 第 一 象 限 内 的 # # # # /# ! & . !# " /
点评 ! 实际上 ! 图"中阴影部分的面积除了可 以用 ( 补 )的方法 " 求和 #来计算之外 ! 还可以用 ( 割)
!
!
出直线 % ’ # .’! 曲线 % ’ 槡 # ! " ! 草图 # 则它们 与 # 轴 所 围 成 的 图 形为图 " 中的阴影部分 ! 故所求面积 A ’
( ’ #
! # 7 #$ 5槡
% !
图" !槡 ! " # . # " ! %
% !
5
!! *槡 # + ! # ." #.’ # ’ 槡# 7 ’ %
! # ! #
的 方法 " 求差 # 来计算 ! 即A ’ ’ !槡 ! # %
% !
( #
! # 7 #. H’H’ ! 5槡
"
(
.(’
#
’ #( 和( 补) 都是解决几何问 !割) %
题的重要手段 !
! ! 与% ’ ! 例 !! 计算曲线 % ’ ! #.# # #所 .’
围成的图形的面积 A!
面积 A " ’
/
#
5槡
! & ! ! & #! . !# 7 /
" 下转第 " #页#
责 编 ! 顾 ! 俊 ! 邮 箱 !! " " $ % & ’ % % ’!’ ( )* + , #
) ! # # $ 年第 ! 期 ’ ! !! !
!!!!!! ! 高二 · 语数外
!!!!!!!!!!!!!!!!!! 拾
方
法
点
拨 !!!!!!!!!!!!!!!!!!!!!!!! !!
高二 · 语数外
理 科
定积分在特殊图形面积问题中的应用
" 岳修艳 !! 求曲边平面图形的面积在平面几何中是很难解 决的问题 ! 而定积分则为这类问题提供了很好的解 决方法 ! 我 们知 道 ! 定 积分 的 几 何 意 义 便是 曲 边 梯 形 " 或曲边三角 形 #的 面 积 ! 因 此! 一 方 面! 我们可以通 过计算曲 边 梯 形 " 或 曲 边 三 角 形 #的 面 积 来 求 定 积 ! 分! 但这要进行 ( 分 割$ 以 直 代 曲$ 作 和$ 逼 近) 十分 麻烦 ! 在实 际 中 很 少 应 用 ’ 另 一 方 面! 我们可以通过 计算定积分来 求 曲 边 梯 形 " 或 曲 边 三 角 形 #的 面 积 ! 而这只要求 被 积 函 数的 原函 数 ! 再将 积 分上 $ 下限代 入计算 ! 十分方便 ! 某些曲边图形的面 积 可 以 表 示 成 几 个 曲 边 梯 形 " 或曲边三角形 #的 和 或 差 ! 因此也可以用定积分来 计算 ! 本文 撷取 几例 ! 以说 明 定 积 分 在 求特 殊 图 形 的 面积时的应用 ! $ 曲线% ’ 槡 例 %! 计算直线% ’ #.’ # 以及 ! # 轴所围成的图形的面积A!
解析 ! 由
,
# .# ! % ’! 解 ! # #! .’ % ’!
!
得# ’#或# ’! ! 如 图!所示 ! 可得所求面积A ’
#.# # # .’ ## #’ ! 7 ! ." 5 55" 图! # .% # 57 # ’5% # .# 5 ’ ’! 55&
! ! ! ! ! % # ! ! 与% ’! 点评 ! 注意 ! 非封闭曲线% ’! #.# #
"
& . #7 # 呢0 / 5槡
! #
可进行三角换元 ! ! # ’/ . / + : " # 由题意 ! 可设 # .: # ! ! $ + , : % ’&
,
# # " &" 7 + , : 7 / . / + : , : / + , : : ’ & . 5& 5+ / & " / & # / + ! 7 & + : 7 :’ : :’ :. ’/ ! !" 5, 5 "..
" !以 0 ) 的 中 点 1 为 原 点$
0 ) 所在的直线为#轴 $ 0 ) 的垂直
平分线为% 轴 $ 建立如右图所示的 坐标系 $ 点 + 的轨迹方程为" ".
! ! ! ! ! ! " # " # # /# # # $"$/ "./ "./ $" $! % ’ #! !
该轨迹是半径为 当/ - " 时 $
(!5’65+ ("5! 5+
$可 得 再 用 定 义# 又 5+ (! 5 (" 5’ ! /" . 5+
@.! " % !" %$ ’ ! !$ $ 4# !"
" $ ! B 真则##/ #"$ B 假则/ )"& L 真则##/ # "或 $ 假则 " $ ! /) $ L ./ . ! ! ! ! 由题意 $ 所以/ / B 与L 一 真 一 假 $ $ ! $ 4# "$ ! #频率分布表如下 ! " & !" "
槡
&
! !
! & ! ! & . !# 的 原 函 数 很 难 /
曲线 ! 更是一次伟大的 ( 借用 ) ! 总之 ! 通 过 以 上 几 例 我 们 可 以 看 出! 求多条曲 " 直 #线围成的平面图形的面积可以分为以下几步 % " #在直角坐标系中画出曲 " 直# 线的大致图像 ’ " " #确定平面图形的范围 ! 即通过解方程组求出 ! 曲" 直 #线交点的横坐标 ! 定出积分上 $ 下限 ’ " #确定被积 函 数 ! 要 注 意 分 清 曲 线 的 上$ 下位 % ’ 置关系 " 或直接加上绝对值符号 # " #写出平面图形面积的定积分表达式 ’ ’ " #运用微积分基本定理计算定积分 ! 求出平面 $ 图形的面积 ! 巩 固 练 习
/ $ 6 / ! ! ("5’ (!5’ ! 5+ 5+ 6." 6."
# "$6 /" 又由 5+ 即! ("5 (!5*5("(!5$ $ 5+ * 6."
! 整理得6 ! -$ 6." . #! .!
$ " 8 *" ! #
$ 解得6 / " 又6 ) "$ !$" ! " 槡 ! 求轨迹方程的几种常用方法 &$# 的规律可知最后一个 !! " 由#$"! ! ! 的定义域又是 " 那么当 而=" # 是正整数 ! ## # $ 4# # 如# ’" 对 应 的 函 数 值 =" " : $ # 不是正整数 ! ! $时! 无法表示 ! 矛盾 ! 总之 ! 当函数是无限 项 的 和 时 ! 不能采用求导的 方法研究其性质 ! 实际上 ! 通常 " 根 据 单 调 性 的 定 义 #采 用 作 差 比 较的方法研究数列的单调性 ! 本题的正确的解法为 %
分!组 . # " !! $$ " $! $ . # " $! $$ " (! $ . # " (! $$ ! "! $ . # ! "! $$ ! ’! $ . # ! ’! $$ ! 5! $ . # ! 5! $$ % #! $ . # % #! $$ % %! $ 合计 频!数 频!率 & " & " ( ! ! ! # " # ( " # # # & #! #! " & " ( #! ! ! #! ! # #! " # #! # ( #! "
" 上接第 ’ )页# 我们发现 ! 函数 % ’ 求得 ! 那么如何求
/
!
" " " #’ % 则 =" @$" $ $1$ $ ! @$! @$% ! @
而要应 用 求 导 法 的 方 法 判 断 数 列 的 单 调 性 ! 必 " #定 义 域 可 连 续 化 ’ " #对 应 的 须具备两个 条 件 % " ! 函数可求导 ! 同学们在用求导的 方 法 求 数 列 的 单 调 性 时 应 慎 重对待 ! $ ( ’ 数方程 ! 就是一种 ( 融入 ) 借用 ) 又如 % 用方程表示
5
" .
! ".# 7 # ’ !!! ! 槡
