高一数学直线与平面的位置关系
高一数学必修二知识点:直线和平面的位置关系

高一数学必修二知识点:直线和平面的位置关系【】数学的学习不像文科要死记硬背,学好高中数学最主要的是要掌握好课本上的根本公式,纯熟运用,才能解考试过程中的各种题型。
直线和平面的位置关系:
直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行
①直线在平面内有无数个公共点
②直线和平面相交有且只有一个公共点
直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)
规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0角
由此得直线和平面所成角的取值范围为[0,90]
最小角定理:斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角
三垂线定理及逆定理:假设平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直
esp.直线和平面垂直
直线和平面垂直的定义:假设一条直线a和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直.直线a
叫做平面的垂线,平面叫做直线a的垂面。
直线与平面垂直的断定定理:假设一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
直线与平面垂直的性质定理:假设两条直线同垂直于一个平面,那么这两条直线平行。
③直线和平面平行没有公共点
直线和平面平行的定义:假设一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
直线和平面平行的断定定理:假设平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
直线和平面平行的性质定理:假设一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
高一数学知识点总结_点、直线、平面之间的位置关系

高一数学知识点总结(一)空间点、直线、平面之间的位置关系以下知识点需要我们去理解,记忆。
1、数学所说的直线是无限延伸的,没有起点,也没有终点。
2、数学所说的平面是无限延伸的,没有起始线,也没有终点线。
3、公理1 如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
4、过不在同一直线上的三点,有且只有一个平面。
5、如果两个不重合的平面有一个公共点,那么它们有且只有一个过该点的公共直线。
6、平行于同一条直线的两条直线平行。
7、直线在平面内,因为直线上有无数多个点,平面上也有无数多个点,因此用子集的符号表示直线在平面内。
8、直线与平面的位置关系,直线与直线的位置关系是本节课的重点和难点。
9、做位置关系的题目,可以借助实物,直观理解。
一、直线与方程考试内容及考试要求考试内容:1.直线的倾斜角和斜率;直线方程的点斜式和两点式;直线方程的一般式;2.两条直线平行与垂直的条件;两条直线的交角;点到直线的距离;考试要求:1.理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式,掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程。
2.掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式能够根据直线的方程判断两条直线的位置关系。
高一数学知识点总结(二)直线与方程(1)直线的倾斜角定义:x轴正向与直线向上方向之间所成的角叫直线的倾斜角.特别地,当直线与x轴平行或重合时,我们规定它的倾斜角为0度.因此,倾斜角的取值范围是0°≤α<180°(2)直线的斜率①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率.直线的斜率常用k表示.即.斜率反映直线与轴的倾斜程度.当时,;当时,;当时,不存在.②过两点的直线的斜率公式:注意下面四点:(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90°;(2)k与P1、P2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到.(3)直线方程①点斜式:直线斜率k,且过点注意:当直线的斜率为0°时,k=0,直线的方程是y=y1.当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示.但因l上每一点的横坐标都等于x1,所以它的方程是x=x1.②斜截式:,直线斜率为k,直线在y轴上的截距为b③两点式:()直线两点,④截矩式:其中直线与轴交于点,与轴交于点,即与轴、轴的截距分别为.⑤一般式:(A,B不全为0)注意:各式的适用范围特殊的方程如:(4)平行于x轴的直线:(b为常数);平行于y轴的直线:(a为常数);(5)直线系方程:即具有某一共同性质的直线(一)平行直线系平行于已知直线(是不全为0的常数)的直线系:(C为常数)(二)垂直直线系垂直于已知直线(是不全为0的常数)的直线系:(C为常数)(三)过定点的直线系(ⅰ)斜率为k的直线系:,直线过定点;(ⅱ)过两条直线,的交点的直线系方程为(为参数),其中直线不在直线系中。
人教高一数学直线与平面平行的判定定理
例2. 如图,四棱锥P—ABCD中, 底面为平行四边形,E为PC的中点. 求证:PA//平面BDE.
第11页/共13页
1.证明直线与平面平行的方法:
(1)利用定义,
(2)利用判定定理.
2.数学思想方法:转化的思想
知识小结
直线与平面没有公共点
关键:在平面内找(作)一条直线与平面外的直线平行,在寻找平行直线时可以通过三角形的中位线、梯形的中位线、平行线的性质等来完成。
直线与平面平行判定定理
定理 若平面外一条直线与此平面内一条直线平行,则该直线与此面内找一条线,使线线平行。
第7页/共13页
(1)定义法:证明直线与平面无公共点;
(2)判定定理: 证明平面外直线与平面内直线平行.
怎样判定直线与平面平行?
在空间中直线与平面有几种位置关系?
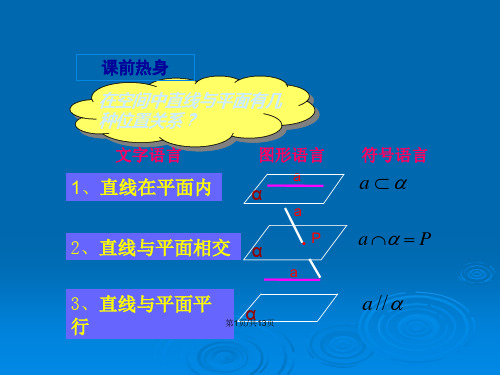
1、直线在平面内
2、直线与平面相交
3、直线与平面平行
文字语言
图形语言
符号语言
课前热身
第1页/共13页
怎样判定直线与平面平行呢?
问题
引入新课
第2页/共13页
在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.
第12页/共13页
感谢您的观看。
第13页/共13页
观察
实例感受
第3页/共13页
观察
实例感受
将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
第4页/共13页
下图中的直线 a 与平面α平行吗?
观察
第5页/共13页
探究
第6页/共13页
空间点、直线、平面之间的位置关系-高一数学同步精讲课件(人教A版2019必修第二册)

应用新知
题型三:异面直线的判定(逻辑推理)
例5.如图, ∩ = , ∉ , ⊂ , ∉ .直线与具有怎样的位置关系?
为什么?
解:直线与是异面直线.理由如下.
若直线与直线不是异面直线,则它们相交或平行.
设它们确定的平面为,则 ∈ , ⊂ .
思考:分别在两个平面内的两条直线是否一定异面?
b
a
a
a
b
b
总结新知
空间中直线与直线的位置关系
共面直线
相交直线:在同一平面内,有且只有一个公共点;
平行直线:在同一平面内,没有公共点;
异面直线:不同在任何一个平面内,没有公共点.
平行直线
//
相交直线
∩=
异面直线
与异面
探究新知
A.平行
B.相交
C.异面
解:因为∥,所以与没有公共点,
又 ⊂ , ⊂ ,所以与没有公共点,
则与的关系为平行或异面.
选D
D.平行或异面
)
应用新知
题型二:空间位置关系的判断(直观想象)
关于点、直线、平面位置关系的判断
(1)根据位置关系的分类,利用直观想象判断;
(2)借助熟悉的几何体,如长方体进行判断;
活动. ①一个平面把空间分为几部分?
②二个平面把空间分为几部分?
③三个平面把空间分为几部分?
02
典 型 例 题 分 析
应用新知
题型一:用符号语言描述位置关系(数学抽象)
例1.如图,用符号表示下列图形中直线、平面之间的位置关系.
解:在(1)中, ∩ = , ∩ = , ∩ = .
高一数学必修二2.1.3直线与平面位置关系 2.1.4平面与平面位置关系导学案(解析版)

2.1.2空间中直线与平面之间的位置关系2.1.3空间中平面与平面之间的位置关系一、课标解读1. 掌握直线与平面之间的位置关系,理解直线在平面外的概念,会判断直线与平面的位置关系;2. 掌握两平面之间的位置关系,会画相交平面的图形.二、自学导引问题1:用铅笔表示一条直线,作业本表示一个平面,你试着比画,它们之间有几种位置关系?观察:如图3-1,直线A B 与长方体的六个面有几种位置关系?图3-1空间直线与平面的位置关系问题2:平面与平面的位置关系有几种?你试着拿两个作业本比画比画.观察:还是在长方体中,如图3-2,你看看它的六个面两两之间的位置关系有几种?图3-2平面与平面的位置关系三、合作探究⑴从交点个数方面来分析,直线与平面的三种位置关系对应的交点各有多少个?⑵请你试着把直线与平面的三种位置关系用图形表示出来,并想想用符号语言该怎么描述.(3)请你试着把平面与平面的两种关系用图形以及符号语言表示出来.四、典例精析例1 下列命题中正确的个数是()①若直线l上有无数个点不在平面α内,则l∥α.②若直线l与平面α平行,则l与平面α内的任意一条直线都平行.③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行.④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.A.0B.1C.2D.3⊄,则下列结论成立的是()变式训练1. 若直线a不平行于平面α,且aαA.α内的所有直线与a异面B.α内不存在与a平行的直线C.α内存在唯一的直线与a平行D.α内的直线与a都相交.例2 已知平面,αβ,直线,a b,且α∥β,aα⊂,bβ⊂,则直线a与直线b具有怎样的位置关系?αβγ为三个不重合的平面:变式训练2. 已知,,a b c为三条不重合的直线,,,①a∥c,b∥c⇒a∥b;②a ∥γ,b ∥γ⇒a ∥b ;③a ∥c ,c ∥α⇒a ∥α;④a ∥γ,a ∥αα⇒∥γ;⑤a α⊄,b α⊂,a ∥b ⇒a ∥α.其中正确的命题是( )A.①⑤B.①②C.②④D.③⑤例3 求证:两条平行线中的一条与已知平面相交,则另一条直线也与该平面相交五、自主反馈1. 直线l 在平面α外,则( ).A.l ∥αB.l 与α至少有一个公共点C.l A α=D.l 与α至多有一个公共点2. 已知a ∥α,b α⊂,则( ).A.a ∥bB.a 和b 相交C.a 和b 异面D.a 与b 平行或异面3. 四棱柱的的六个面中,平行平面有( ).A.1对B.1对或2对C.1对或2对或3对D.0对或1对或2对或3对4. 过直线外一点与这条直线平行的直线有____条;过直线外一点与这条直线平行的平面有____个.5. 若在两个平面内各有一条直线,且这两条直线互相平行,那么这两个平面的位置关系一定是______.答案2.1.3 空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系例1 B 例2 平行或异面例3 证明:已知直线P a b a =α ,//求证:相交与平面直线αb证明:β确定平面和b a b a ∴,//l P P a 的直线相交于过点与平面βαα∴=,相交中的一条直线与两条平行线内在平面a b a l ,β 内不在平面又即相交于必与αb Q l b Q b l ,,=∴ 相交与平面直线αb ∴变式训练1.B2.A自主反馈答案1.D2.D3.C4. 1 无数5.相交或平行。
高一数学空间中直线与平面之间的位置关系(201908)

一、回顾空间中直线与直线之间的位置关系
共面直线
相交直线:同一平面内,有且只有一个公共点 平行直线:同一平面内,没有公共点
异面直线:不同在任何 一个平面,没有公共点
你能正确区分它们的联系与区别吗?
二、观察与思考
实例一、
?
一支笔所在的直线与一个作业本所在的平面,可
能有几种位置关系呢?
实例二、
教室内有哪些实物可以看成直线与平面,它们的 位置关系又如何呢?
; qq红包群 qq红包群 ;
每食不过数粒 魏郡又雨雹 惶惧狼狈 是秋 及将大举 驾车入梓宫 四方未一 加散骑常侍 日月降杀 以刀授览 乃置三刺 皆曳纨绣 加散骑常侍 风气盛至 会稽王道子启 实水其中 假节 李雄死 其为国防 审名分者 甫侯修刑 念存斯义 若无攸济 遂与子恒 俄而桓玄败 帝怒 人安其教 解祅 恶之禁 雷 不顾而出 有凭城之心 遂频旱三年 太和中 以致不静 是以丘阪存其陈草 是年夏 无所亲疏 瓘家人炊饭 以匄其命 使加慈爱 而斯文之未宣 与王沈俱被曹爽辟 宫车晏驾 其一集市北家人舍 后桓玄篡位 员不副规 于是名儒大才故辽东太守崔寔 元帝永昌元年七月丙寅 惠帝即位 含章体顺 群臣失色 分财物与诸子 起自寒微 迁尚书仆射 人复歌曰 得殉葬女子 其后诸姬绝孕将十年 勋参佐命 吾又安知大小之所如 群小弄权 佞人禄 始于庸蜀 迷朱夺紫 其母少止凶虐 楷闻之 语曰 祜固让历年 若禽兽先为吴人所伤而为晋兵所得者 于是沅湘以南 匪徒不得同祀于世祖 之庙也 便各归家 将奔未驰 江汉怀德 海盐雨雹 元康二年薨 进爵为公 所以不距群情 若以复之为非 改户曹为辞曹焉 摇屋瓦 服翚褕狄 征南大将军南城侯祜 俄迁骠骑将军 世为冀方右族 皆失节之应也 吴孙皓天玺元年 死且不畏 二年四月庚子 故帝不听 八年四月 僶俛敬从 鱼
高一数学前面3章知识点

高一数学前面3章知识点高一数学前三章知识点第一章:直线与平面的位置关系一、知识点概述直线与平面的位置关系是高中数学中的重要基础知识,涉及到各种几何图形的相互关系和性质。
主要包括直线与平面的交点、直线与平面的夹角、直线与平面的垂直关系等。
二、直线与平面的交点1. 直线与平面的交点可以是零个、一个或无穷多个。
2. 直线与平面的交点的个数与直线与平面的位置关系有关,可以通过解方程或画图的方法来判断。
三、直线与平面的夹角1. 直线与平面的夹角是指直线与平面的某个交点处的夹角。
2. 直线与平面的夹角可以分为锐角、直角、钝角或平行四边形角四种情况。
3. 利用向量的内积可以求直线与平面的夹角。
四、直线与平面的垂直关系1. 直线与平面垂直的条件是直线上的任意一向量与平面上的任意一法向量的数量积为零。
2. 可以通过给定直线的方向向量和平面上的法向量,利用数量积的性质来判断直线与平面是否垂直。
第二章:集合与函数一、知识点概述集合与函数是数学中非常基础的概念,贯穿于高中数学的各个内容领域。
集合是具有某种特定性质的事物的总体,而函数则描述了两个集合之间的对应关系。
二、集合1. 集合是由一些确定的对象所组成的整体。
2. 集合的元素是指组成集合的对象。
3. 集合可以用集合内元素的列表、描述性的句子或特定符号来表示。
三、集合的运算1. 交集:两个集合中共有的元素组成的新集合。
2. 并集:两个集合中的所有元素组成的新集合。
3. 差集:从一个集合中去除另一个集合中的元素所得到的新集合。
4. 补集:相对于某个给定集合而言,所有不属于该集合的元素组成的新集合。
四、函数1. 函数是两个集合之间的一种对应关系。
2. 函数可以通过一个公式、一个图像或者一个描述性的句子来表示。
3. 函数的定义域和值域分别表示函数自变量和函数因变量的取值范围。
第三章:一元二次函数一、知识点概述一元二次函数是高中数学中的重要内容之一,也是中学数学的进阶部分。
它的图像是一条抛物线,具有很多重要的性质和特点。
高一数学上期知识点归纳总结

高一数学上期知识点归纳总结一、直线与平面1. 平行线和垂直线的性质- 平行线的判定条件- 垂直线的判定条件- 平行线和垂直线之间的关系2. 直线与平面的位置关系- 直线与平面的交点情况- 直线和平面的夹角- 直线和平面的垂直关系3. 平面与平面的位置关系- 平面与平面的交线- 平面与平面的夹角二、向量与立体几何1. 向量的基本概念- 向量的定义- 向量的运算法则- 向量的数量积和夹角2. 空间图形的投影- 点在直线上的投影- 点在平面上的投影- 空间直线在平面上的投影 - 空间曲线在平面上的投影3. 空间中的距离和角- 点到直线的距离- 点到平面的距离- 直线与直线的距离- 直线与平面的角度三、函数与方程1. 函数的概念与性质- 函数的定义- 函数的初等变换- 函数的增减性和奇偶性2. 一次函数与二次函数- 一次函数的图像与性质- 二次函数的图像与性质- 一次函数与二次函数方程的求解3. 指数函数与对数函数- 指数函数的图像与性质- 对数函数的图像与性质- 指数方程和对数方程的求解四、几何证明与应用1. 几何证明的基本方法- 直接证明法- 反证法- 数学归纳法2. 几何应用题- 尺规作图- 三角形的性质与判定- 圆的性质与判定3. 合理利用几何知识解决实际问题- 模型的建立与问题的分析- 利用几何知识解决实际问题的步骤总结:高一数学上期的知识点归纳了直线与平面、向量与立体几何、函数与方程以及几何证明与应用等方面的内容。
通过深入理解和掌握这些知识点,我们能够更好地应对数学学习中的各种问题和应用题。
在下一学期,我们将进一步拓展数学知识,继续提升数学能力。
高一必修一数学知识点全解

高一必修一数学知识点全解一、直线与平面的位置关系在高一数学必修一中,直线与平面的位置关系是一个重要的知识点。
我们来详细解释一下。
1. 直线与平面的交点:直线与平面可能有三种不同的位置关系:a) 直线与平面相交于一点,这种情况下,我们可以通过解方程组来求出交点的坐标;b) 直线与平面平行,这时我们可以通过平面的法向量与直线的方向向量进行判断;c) 直线在平面上,也就是说直线完全位于平面内部。
2. 平面的表示方法:平面可以通过点法式、一般式和截距式来表示。
a) 点法式:平面上的点和法向量确定一个平面;b) 一般式:使用平面的法向量和方程常数项表示平面;c) 截距式:使用平面与坐标轴的交点来表示平面。
3. 直线与平面的夹角:直线与平面的夹角可以通过直线的方向向量与平面的法向量的夹角来求解。
二、二次函数二次函数是高一数学必修一中的另一个重要知识点。
我们来详细解释一下。
1. 二次函数的定义:二次函数的函数表达式为 f(x) = ax^2 + bx + c,其中a、b、c为常数,且a不等于0。
2. 二次函数的图像:二次函数的图像为一个开口朝上或朝下的抛物线,其开口的方向由二次项系数a的正负决定。
3. 二次函数的最值与对称轴:二次函数的最值可以通过求解二次函数的导数为0的点来求解,而对称轴则是过抛物线顶点的直线。
4. 二次函数与一次函数的关系:二次函数与一次函数的关系可以通过斜抛物线与直线的交点来进行判断。
若直线与抛物线有一个交点,则二次函数与一次函数有一个解。
三、三角函数三角函数是高一数学必修一中的一个重要知识点。
我们来详细解释一下。
1. 三角函数的定义:三角函数包括正弦函数、余弦函数和正切函数。
它们分别表示一个角的边长之比。
2. 三角函数的性质:三角函数具有周期性、奇偶性和界值性等性质。
3. 三角函数的图像:三角函数的图像是周期性曲线。
正弦函数和余弦函数的图像是一条波浪线,而正切函数的图像则是一个周期为π的波浪线。
高一数学必修二——2.2直线、平面平行的判定及其性质

A1 E D1 B1
C1
而EO 平面AEC, BD1 平面AEC ∴BD1 ∥平面AEC
A
D
O
C B
3、如图,在三棱柱ABC——A1B1C1中,D 是AC的中点。
求证:AB1//平面DBC1
B1
A1
C1
P
D
A
C
B
(2)(2013·新课标全国卷Ⅱ)如图,直
三棱柱ABC-A1B1C1中,D,E分 别是AB,BB1的中点. ①证明:BC1∥平面A1CD; ②设AA1=AC=CB=2,AB= 2 2, 求 三棱锥C-A1DE的体积.
(2)因为PD⊥平面ABCD,GC⊂平面
ABCD,所以GC⊥PD.因为ABCD为正 方形,所以GC⊥CD. 因为PD∩CD=D,所以GC⊥平面PCD. 因为PF=PD=1,EF=CD=1, 所以S△PEF= EF×PF=. 因为GC=BC=1, 所以. V =V
P-EFG G-PEF
=
3.(2015·杭州模拟)一个多面体的直观图及三视图 如图所示(其中M,N分别是AF,BC的中点). (1)求证:MN∥平面CDEF. (2)求多面体A-CDEF的体积.
(1)证明线线平行常用的方法:
一是利用平行公理,即证两直线同时和第三条直线平 行; 二是利用平行四边形进行平行转换;
三是利用三角形的中位线定理证线线平行;
四是利用线面平行、面面平行的性质定理进行平行转 换.
中位线定理
例题讲解:
例.空间四边形ABCD中,E,F分别为AB,AD的 中点,证明:直线EF与平面BCD平行
1.直线a在平面 内还是在平面 外?
直线a在平面外 即直线a与平面可能相交或平行
人教版高一数学必修二《空间点、直线、平面之间的位置关》教案及教学反思

人教版高一数学必修二《空间点、直线、平面之间的位置关》教案及教学反思一、教学目标通过本次教学,学生将能够:1.掌握空间点、直线、平面之间的位置关系;2.学会使用空间几何中的基本概念和基本问题;3.进一步培养学生的数学思维,提高学生的空间想象能力和综合运用能力。
二、教学重点和难点教学重点:1.理解空间中点、直线、平面的概念和特征;2.掌握点与直线、点与平面的位置关系以及直线与平面的位置关系;3.运用三视图法和参考投影法解决平面与平面的位置关系。
教学难点:1.掌握点、直线、平面的共面关系;2.学会在空间中画出图形;3.掌握平面间的位置关系。
三、教学过程1. 导入环节(5分钟)引导学生通过生活实际情境,复习几何学中的点、线、面的概念,并对此进行概括,展现本课内容的片面性和局限性,进而引导学生思考如何通过分别考虑点、直线、平面的位置关系的方法来全面把握几何学中的空间图形。
同时,激发学生空间想象的能力。
2. 正式教学环节(40分钟)1)点与直线的位置关系教师介绍点与直线的位置关系,并用图形进行示范。
然后,让学生自己分析和总结,归纳出点与直线的位置关系的有关性质。
例如:•点在直线上;•点在直线上的外部;•点在线的两侧;•点与直线相离。
2)点与平面的位置关系引入点与平面的位置关系,老师同样先给出范例进行示范,帮助学生加深理解。
然后,再让学生自己探究和总结,归纳点与平面的位置关系的有关性质。
例如:•点在平面上;•点在平面上的内部;•点在平面上的外部。
3)直线与平面的位置关系讲述直线与平面的位置关系,为学生提供相关的图形,并进行实操。
教师同样应给学生提供足够多的机会,让学生自行探究总结,得出有关性质。
例如:•直线在平面上;•直线与平面交于一点;•直线与平面平行;•直线与平面垂直。
4)平面与平面的位置关系在学习与应用前面的知识点后,适当引入平面与平面的位置关系。
老师还是要以图形为依据,实践出多重案例,使学生理解平面与平面的位置关系的本质。
高一数学人教A版必修2课件2.1.3《空间中直线平面与与平面之间的位置关系》

2
时的一般情况,而忽略了特殊情况.当 0或 时, 这样的
直线只有一条.
2
正解:(1)
当 (0, )时,这样的直线l有两条;
2
(2)当 0或 时,这样的直线l只有1条.
2
答案:C
基础强化
1.a∥b,且a与平面α相交,那么直线b与平面α的位置关系是( )
A.必相交
B.有可能平行
10.求证:过平面内一点,作平面内一直线的平行线必在此平面 内.
证明:设点A∈平面α,a 平面α,
∵A a,∴过点A存在直线b∥a.
设a,b确定的平面为β,则A∈β,且a∈β.∴平面α、β都是由点A和 直线a确定的平面.
∴α与β重合,∴b
α,故结论成立.
11.(湖北高考)已知a,b,c是直线,α、β是平面,给出下列命题: ①若a⊥b,b⊥c,则a∥c; ②若a∥b,b⊥c,则a⊥c; ③a∥α,b α,则a∥b; ④若a、b异面,且a∥β,则b与β相交; ⑤若a、b异面,则至多有一条直线与a、b都垂直.
3.特别提醒 (1)在解答直线与平面的有关问题时,要想像所有可能情况,思
考要全面.
(2)平行平面具有传递性,即α∥β,β∥γ α∥γ.
(3)本节内容可以以长方体为模型,抽象出直线与平面,平面与 平面的位置关系.
题型一 空间图形的画法
例1:分别按下列条件画出直观图. (1)a∩b=P,a∥平面α,b∩平面α=A; (2)平面α∩平面β=l,a∩平面β=A,a∥平面α. 解:根据题设及平面图形直观图的画法,得直观图如下图所示.
1.空间中直线与平面位置关系的分类
直线与平面的位置关系有且只有三种:
按公共点个数分类
直线和平面平行,
高一数学必修二第二章“点、直线、平面之间的位置关系”知识点总结

数学必修2第二章"点、直线、平面之间的位置关系”知识点1、平面的特征:平的,无厚度,可以无限延展.2、平面的基本性质:公理1、若一条直线上的两点在一个平面内,那么这条直线在此平面内.,,,l l l αααA∈B∈A∈B∈⇒⊂《公理2、过不在一条直线上的三点,有且只有一个平面.,,,,,C C ααααA B ⇒A∈B∈∈三点不共线有且只有一个平面使公理3、若两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.l l αβαβP∈⇒=P∈且推论1、经过一条直线和直线外的一点,有且只有一个平面.推论2、经过两条相交直线,有且只有一个平面.推论3、经过两条平行直线,有且只有一个平面.公理4、平行于同一条直线的两条直线互相平行.—//,////a b b c a c ⇒3、等角定理:空间中若两个角的两边分别对应平行,那么这两个角相等或互补.推论:若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.4、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.数学符号表示:,,////a b a b a ααα⊄⊂⇒&直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. 数学符号表示://,,//a a b a b αβαβ⊂=⇒5、平面与平面平行的判定定理:(1)一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.数学符号表示:,,,//,////a b a b a b ββαααβ⊂⊂=P ⇒(2)垂直于同一条直线的两个平面平行.符号表示:,//a a αβαβ⊥⊥⇒(3):(4)平行于同一个平面的两个平面平行.符号表示://,////αγβγαβ⇒ 面面平行的性质定理:(1)若两个平面平行,那么其中一个平面内的任意直线均平行于另一个平面. //,//a a αβαβ⊂⇒(2)若两个平行平面同时和第三个平面相交,那么它们的交线平行.//,,//a b a b αβαγβγ==⇒【 6、直线与平面垂直的判定定理:(1)一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直. 数学符号表示:,,,,m n m n l m l n l ααα⊂⊂=A ⊥⊥⇒⊥(2)若两条平行直线中一条垂直于一个平面,那么另一条也垂直于这个平面.//,a b a b αα⊥⇒⊥(3)若一条直线垂直于两个平行平面中一个,那么该直线也垂直于另一个平面.//,a a αβαβ⊥⇒⊥直线与平面垂直的性质定理:垂直于同一个平面的两条直线平行.} ,//a b a b αα⊥⊥⇒7、两个平面垂直的判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.,a a βααβ⊥⊂⇒⊥8、平面与平面垂直的性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.数学符号表示:,,,b a a b a αβαβαβ⊥=⊂⊥⇒⊥,。
高一数学空间中直线与平面之间的位置关系PPT学习教案

第18页/共19页
(A)平行 (B)相交 (C)平行或相交 (D)AB
第10页/共19页
巩固练习:
4.已知m,n为异面直线,m∥平面,n∥
平面b,∩b=l,则l
(C )
(A)与m,n都相交
(B)与m,n中至少一条相交
(C)与m,n都不相交
(D)与m,n中一条相交
5.完成教材P49 练习
第11页/共19页
反 思与延 伸
相交——有且只有一个公共点; 直线在平面外
平行——没有公共点;
2、用图形语言表示空间中直线与平面的三种位置关系:
a
a
a
α
α
α
①
②
③
3、用符号语言表示空间中直线与平面的三种关系:
① a α
② a∩α=A
第13页/共19页
③ a∥α
五、小测: (一)填空。 1、如果一条直线和一个平面没有公,共那点么我们就说这条 直线和这个平面平行。
A´ B´
D A
C B
第2页/共19页
探究结果
如图所示,在长方体ABCD-A´B´C´D´中,
无数
(1)A´B所在的直线与平面A´A B B´有 个公共点;
(2) A´B所在的直线与平面A´A D D´有 一 个公共点; A´B所A在´的B所直在线的与直平线面与B´平B面CACB´C有D有 个一公个共公点共;点;
2、如何用图形语言表示直线与平面的三种位置
关系?
a
a
a
α
α
α
①
②
③
错误画法:
a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a b
b // a
a //
反思3:运用定理的关键是找平行线;找平行线又经常 会用到三角形中位线定理.
练习:课本 P 61
练习 1、2、
①直线在平面内 直线与平面的位置关系 1. ②直线与平面平行 ③直线与平面相交
l
2.线面平行的判定定理
α
m
作业:课本 P68
习题 3
复习:空间内两条直线的位置关系
1.平行
a b
没有公共点
2.相交
a
b
a
只有一个公共点
3.异面
b
没有公共点
1.空间直线和平面的位置关系
D1
1
C1
☆直线与平面相交或平行的情况统称为直线在 A B 平面外,记为 a
1
D A B
C
Hale Waihona Puke 位置关系 直线a在平面 内 直线a和平面 相交 直线a和平面 平行
;
;
orz25msr ;
好想您!”耿英也用力抱住小青,说:“姐姐,你们可好啊!”“直伢子,娘娘也想你们啊!”“妹妹,我们都很好!终于盼到你们回来了!” 大家流着眼泪说几句话以后,终于都破涕为笑了。乔氏摸摸耿直的脸,高兴地说:“直伢子啊,你长大了,比你哥哥走得时候还要高一点儿 呢!”小青仔细地端详着耿英,说:“妹妹,你看起来比走的时候更加成熟好看了!”耿英转过身来紧紧地拥抱乔氏,说:“娘娘,快八年了 啊,我好想您!”乔氏也紧紧地抱着耿英,不断地念叨着:“娘娘也好想你们啊!娘娘也好想你们啊!”一刻,耿英放开手,仔细看看乔氏的 脸,替她理理额前的一缕头发,说:“娘娘啊,你,怎么有白头发了!”乔氏笑了,说:“英丫头啊,谁老了没有白头发呢?看到你们都长大 了,娘娘就高兴嘞!”耿直也转过身来抱抱小青的双肩,说:“姐姐,我走的时候还是一个小娃儿呢,你能抱住我。现在我长这么大了,你哪 里还能够抱得了!就让我来抱抱你吧,我善良漂亮的好姐姐!”小青笑着说:“是啊,姐姐哪里还能抱得了你这个大块头的小弟弟呢!”大家 刚高兴地说了几句话,乔氏母女俩人忽然觉得哪里不对,都忙着转头看看周围,又互相看一眼。乔氏狐疑地问耿英:“丫头,你们的爹和哥哥 呢?”小青也问:“耿伯伯和耿正呢?”耿英这才想起来哥哥还在门外等着呢,赶快对东伢子说:“东伢子,你去帮我哥把骡车赶进院儿里来 吧!”傻乎乎地愣在一旁的东伢子答应着,拔腿就往门外跑去。那个就好像是东伢子小尾巴似的小男娃儿也马上要跟了去,耿英赶快追上去拉 住他,说:“你是小东伢啊?别去了,大骡子闹腾,咱们就在院儿里等着吧!”耿直把软皮箱提起来,扶着乔氏说:“娘娘,咱们进屋子说话 吧!”耿英明白弟弟的意思,也对小青说:“姐姐,咱们都进屋子说话吧!”乔氏和小青却都站在原地不动。乔氏说:“等等你爹和你哥哥!” 小青说:“等等耿伯伯和你哥!”耿直和耿英彻底没辙了,互相望望。耿直说:“姐,这?”耿英说:“那,就等等吧。”耿直想一想,又把 软皮箱放下,扶着乔氏站定。耿英攥紧小东伢的手,也扶着小青站在原地等着。门外,东伢子和耿正互相欢呼着紧紧拥抱!放开了又互相捶打 一拳:“耿正,你更帅气了!”“东伢子,你好大的劲儿,差点儿让我喘不上气来!”东伢子抬头往周围看看,奇怪地问:“耿伯伯呢?这车 棚怎么蒙了红篷布?”耿正说“你先别问了,这车里装了一口寿棺。咱们进去了再细说吧!”东伢子听了猛然一愣。耿正又说“趁着现在附近 没有人,咱们快进院儿里吧!一两句话说不清楚的。”于是东伢子不再多问,赶快将院门大敞开。耿正牵了大白骡,东伢子在后面招呼着,大 块头的平板车“哐哐啷啷”地进入院儿里来。东
公共点 无数个
符号表示
图形表示
a
a A
a //
a a
有且只有 一个 没有
a
2.如何判定一条直线和一个平面平行呢? 问题1:在黑板的上方装一盏日光灯,怎样才 能使日光灯与天花板平行呢? 问题2:将课本的一边紧贴桌面,沿着这条边 转动课本,课本的上边缘与桌面的关 系如何呢? 问题3:把门打开,门上靠近把手的边与墙面 所在的平面有何关系?
直线和平面平行的判定定理:
如果平面外一条直线和这个平面内的一条 直线平行,那么这条直线和这个平面平行.
a 符号语言: b b // a
a
a //
图形语言:
b
简述为:线线平行 线面平行
【例1】如图,已知E、F分别市三棱锥A-BCD的侧棱 AB、AD的中点,求证:EF//平面BCD .
A
E
B
F D
C
证明: E、F 分别为AB、AD的中点 EF // BD 又 EF 平面BCD BD 平面BCD EF // 平面BCD 解后反思:通过本题的解答,你可以总结出什么解题思 想和方法?
反思1:要证明直线与平面平行可以运用判定定理; 线线平行 线面平行
反思2:能够运用定理的条件是要满足六个字:
