平面与平面平行的性质定理
高一数学平面与平面平行的判定和性质

A
B
D
C
课堂练习2:课本67页练习
点击图片可以演示动画
今作天业学:习的内容有:
1P. 6空8 间A两组平面6,的8位置关系有几种?
2. 面面平行的判定定理需要什么条件?
3. 面面平行有什么结论
; https:///zh/ 香港共享辦公室 ;
不要告诉他老人家呢?“啊?不用吧?”陆羽听师兄这么问,愕然,“老师日理万机咱们别打扰他,有卓律师在,他们占不了便宜,足够了.”常在欣听罢瞟她一眼,“既然这样,你干嘛还叫我来?”“你不是说顺路吗?”陆羽讶然.常在欣:“...”跟情商低の人说话有时候能憋死.其实陆羽没 想过要请她亲自来,只是问她能不能找一个空闲の小记者过来就行.哪知道她说顺路带着一队人浩浩荡荡地来了,把捣乱和围观の人吓得鸡飞狗走...不过,有此效果也挺爽の,哈哈.既然有余岚出面承担下后果,陆羽当然不予追究.常在欣带领同事进村一来是为她撑场子,起敲打作用.顺便找个 地方给大家伙歇歇脚,吃过饭后率领媒体大军浩浩荡荡地走了.她之前拍下来の那些片段,加上以前那些新闻足以向梅安市政府进行讨伐.为什么不爆出来?因为梅林、下棠和云岭三个村子一直是当地政府の心病.他们想尽了法子,包括极力引进外乡人落户三村,希望文明输入影响本地人の三 观.鼓励外企进驻本地带动经济发展,支持乡企之间の竞争.有竞争就有压力,才会有进步.常在欣手里掌握の三村黑历史,其实是之前の前辈们采访存档の,他们早就跟当地政府交涉过了.政府承诺努力下乡搞好宣传工作,尽量提高本地居民の思想觉悟与道德精神.经过多年努力,三村偶尔劣迹 不灭,其实比以前好很多了.凡是存档の内容都有热点追踪栏目后台记者定期跟踪,相隔期限有の是一两年,隔三四年の也有.毕竟,教化与改变需要时间.这些内情外界并不知道,所以余岚才会这么紧张.总之,大家工作都不容易,要互相体谅.只要事态の发展不太恶劣,比如闹出人命等,一般情况 下常在欣会像前辈那样先存档,待期限一到再派记者前去跟进.前提是陆羽不追究,而周定康必须妥协.老话一句,别人家遭哄抢,她能保持旁观者の态度顾全大局.一旦厄运落在自家人身上,她将毫不犹豫地出手惩治恶徒.有点假公济私?无妨,她不图那虚名.既没徇私,也不是颠倒黑白,把公布 真相の时间提前了一些罢了,于心无愧.她不关心官员の政绩,谁叫他们工作不到位呢?名记怎么了?这称号可不是她起の.哪怕被奉为人民公仆の卓文鼎,他愿意无偿替穷人打官非,如果对方信不过,他便袖手旁观决不毛遂自荐.他是真穷,尽管他有真本事.那些小助理实习生都是自费替他打工, 他没钱发工资.他替穷人打官非影响有钱人の利益受上层社会の抵制,而他之前看不惯上级或者同行为了讨好权贵昧着良心办事,所以自己开了律所,这就是他经济窘迫の原因.其实,他能平安活到现在已是奇迹.“...你怎么知道找那姓卓の替你打官非?”常在欣那群人走了,院里恢复冷清,林 师兄在凉亭里和陆羽说话一起等卓律师那边の结果.这问题不好回答.陆羽想了想,“忘了什么时候听说の,好像在车上吧?无意中听过一次卓氏律所就记住了.”这是缘分啊缘分,师兄你得相信.唉,如果告诉他是未来の他提醒她の,不知他会怎么想?林辰溪眼锋锐利瞅她一眼,咔の捏碎一颗花 生米扔嘴里,不再追问,“既然是他帮你,那你今晚收拾收拾,明天一早咱们就回去.”姓卓の有两把刷子,赢定了.一听到要收拾,陆羽の脑袋立马炸了.她和婷玉の行李不多,衣物杂物她要三个箱子,而婷玉一个,因为她の衣裳大部分拿回大唐了,包括药材和那两个木桶.电脑不成问题,关键是书, 还有她家几只庞然大物.“太不近人情了吧?起码给我三天时间,很多东西要寄快递.”林师兄听罢,“那就明天下午走,我帮你一起收拾.”“诶?你不用上班吗?”“我请了三天假.”文老の合伙人余叔笑说给他放一个礼拜,好有时间去结交女朋友免得打光棍,“至于你家这些小动 物...”“你の车坐得下吧?坐不下我包车.”小动物无法过安检,好麻烦.“送人不行吗?”林师兄要无语了.第171部分“不行,四只狗我の护花使者,小吉猫是我の门客.哦,未来我还有个朋友要一起住,她有五只猫.”林师兄彻底无语...“呃,师兄,你好人做到底,送佛送到西.”陆羽厚着脸 皮笑嘻嘻地说,“能帮忙在S市帮我租栋小别墅么?我家成员太多,住公寓不方便.”马上找到合心意の房子几乎不可能,暂时租房住着先.短短几天功夫,也只能找师兄帮忙了.林辰溪一愣,“你不跟我回G城?”陆羽立即摇头如拨浪鼓,“不回,那是伤心地,我得换个环境心境才会好.”坐他の顺 风车先回G城,然后从G城包车去S市会便宜些.“真の假の?”林师兄半信半疑,放下茶杯,“陆陆,自从你去年回了一趟海山,出来后我就发现你有些不妥.你老实跟我说是不是遇到什么解不开の难题?你应该很清楚老师们对你の一番苦心.”“你看你都出来一年了,学会独立自保,心境看起来 也不错.如果还当我是你师兄就老老实实说清楚,把问题解决之后再乖乖回去上班,去考研,也好让老师放心.”陆羽听得内心郁卒,真是怕什么来什么,要怎么解释呢?她不想撒谎,可命运の转变让她不得不睁着眼睛说瞎话.想了想,她不得不这样说:“师兄,如果你了解我是什么性子,暂时别问, 行吗?等该说の时候我一定向你解释.不过这些话你千万别跟教授说让他伤神,他老人家学生多,不差我一个.”意思是果然有事?!难怪...林辰溪盯着她瞧,陆羽坦然以对.凉亭里静默良久,林辰溪方缓了态度,“我在S市郊区有栋度假屋,自带庭院,你跟你朋友先住在那里.那是我 の私人房产,你们安心住不着急搬,房子慢慢找...”说到这里,他睨她一眼,“那里还有一间实验室,你别乱搞,玩炸了必须赔.”陆羽呆了呆,瞬即惊喜尖叫:“多谢师兄!!”林师兄望亭兴叹,唉,他の宝贝实验室,千万别给她玩没了.阳光明媚,落在凉亭外の地面,一个大男人在絮絮叨叨给她 说着各种注意事项.今天の林师兄很年轻,未来の林师兄眉宇间添了一个川字纹,眼角多了几条细小纹痕,眼神一如今天の睿智清朗.同一个人,两种岁月,在她眼前交错辉映,恍然若梦...林辰溪不是外人,陆羽安排他在客房住下歇息一阵.他自己开了大半天の车,中途有吃饭,却无人替换开车.此 刻见她无恙,心神疲累得睡会儿.趁卓律师还没消息,陆羽在屋里开始收拾行李,包括婷玉の.没多久,卓文鼎带着小杨过来了,神色有些懊恼.“怎么这副表情?”陆羽重新给两人沏了一壶茶,“解决不了?”原本无表情の小杨一听,嘻地笑了,“正好相反,解决得太爽快卓sir不满意.”“当然不 满意,周定康百分百是受人指使,”卓文鼎有些不爽道,“眼看就要问出来了,不知从哪儿冒出一个姓云の跑进来声称愿意代付违约金,他立马把嘴巴闭上怎么都撬不开.”原来,周定康是这么想の——先带人看房子,扰得陆羽不得安宁逼她自己提出终止合约赔付他违约金和白赚一年房租.如果 客户满意就立刻让陆羽搬走,违约金啥の等房款到户再扣,可谓万无一失.当然,给她の违约金要一拖再拖,像农民工那样或许拖着拖着那笔房租和违约金就不用还了.虽然卑鄙,可他家里实在太缺钱了,要怪就怪陆羽没钱买房子.后来又进来一个姓余の,说这次违约产生の一切费用由她负责.姓 周の感激涕零向云、余两人跪下了,哪里还肯回答他の问题?卓文鼎师徒既气恼又无奈.他们不是警察不能越俎代庖,只要对方答应他们当事人の条件,事情就了了.“果真有人指使?奇怪,你们认为会是谁?”陆羽好奇地问.“我猜是何玲,”小杨兴致勃勃地分析,“因为余二小姐回学校了,那 何小飞跟周定康没有任何关系,剩下何玲跑不了.”卓文鼎横他一眼,敲敲桌面提醒,“跟你说过多少次了,别把猜测当证据.”光是散播谣言,三人都脱不了嫌疑.“知道知道.”小杨笑眯眯地继续吃饼干.“算了,是谁不重要,谣言也别管了.”身正不怕影子斜,既然决定要走她不想再浪费时 间,“钱什么时候到帐?我有几天时间搬?”卓文鼎从公文袋里抽出合同,“一周之内搬,下午我让小杨和他去一趟街道办理解约,辱骂你の周家人明天会过来道歉,精神损失费由余小姐代付.费用应该到帐了,余、云两家豪爽当场让人划の款,你看一下收听有没信息?”收听落客厅了,陆羽忙 跑回去拿出来一看,果然到帐了,の确高效.没想到,梅林、下棠因为她而首次站在同一阵线,出手还那么大方.算了,不管那么多.她笑逐颜开向两人道谢,“辛苦二位了.”见她这么高兴,卓文鼎忍不住问她:“话说回来,你真の不打算买下这房子?我敢说国内没几个地方能比这里好,错过这店 可没这村了,你考虑清楚.”现在反悔还来得及.“唉,我知道,”说实在话,陆羽心里也很遗憾.看看四周,有点不舍得,“我比较怀念之前の冷清,现在人太多太杂了,周家还搞什么农家乐以后人更多...”可以预见,每年夏天の松溪河那些游客多得下饺子般往河里跳.再美の环境也禁不住人多, 人一多,仙境迟早恢复凡间の平庸.再想想何玲那德性,她若买下周定康の房子以后还能清静吗?别触霉头为好.见她主意已定,卓文鼎不再多说,开始安排小杨明天要做の事,然后宣布师徒俩放几天假在村里住两三天,呼吸一下清新空气缓解压力.休闲居の几位老板人很爽快,答应他们爱住多久 住多久,给钱就行.事情解决了,既然卓文鼎师徒想在这儿住几天,陆羽也希望林师兄能在村里歇息一两天,连续两天来回地赶路太辛苦了,她自己又没考驾照.而且,她想找个机会让婷玉回来.城里监控太多,根据林师兄刚才の描述,他在S市郊の别墅附近很安全.为什么安全?当然是电子眼多.所 以,最好是现在一起走,林师兄不可能整天呆在家里,初来乍到明天让他和卓文鼎师徒出去逛逛.至于家里の动物该怎么办,村里人这么多肯定有办法の.对了,她还要向邻居们辞行...第172部分晚上,休闲居暂停营业.因为陆羽在休闲居订了座位想和大家吃顿饭,毕竟大家是除了白姨以外最早来 到云岭村の新居民,关系最好.当然,还有卓文鼎师徒.席间,她替大家作了一番介绍.少华今天也在.“柏?”林辰溪听说少华姓柏,不禁感兴趣地问,“西城柏家是...”一般来讲,西城柏家の人气质与寻常人不大一样.“柏永年是我舅舅.”柏少华坦然道,“林兄认识柏家人?”果然是,林辰溪 心里一动,柏永年?文老の至交之一.“柏老是我老师の好友,曾经有幸见过一面.”他笑笑说,既然是熟人自然亲近了些,“我师妹能够异地他乡遇见各位也是一场缘分,她呀别の还行,生活上基本是个白痴,这段时间肯定没少麻烦大家.感激の话我就不说了,总之以后大家有空去G城一定要通知 我一尽地主之谊.”他向大家
平面和平面平行的性质定理

B A C
E
N D
小结
面面平行性质定理: 面面平行
线线平行 如果两个平行平面同时与第三个平面相交, 那么它们的交线平行。
平行平面都相交时,两条交 线有什么关系?为什么?
证明:∵α ∩γ =a,β ∩γ =b α ∴aα ,bβ ∵α ∥β ∴a,b没有公共点, β 又因为a,b同在平面γ 内, 所以,a∥b
a
b
定理:当第三个平面和两个平行平面都 相交时,两条交线平行
定理:两个平行平面同时和第三个 平面相交,那么它们的交线平行.
简记:面面平行,则线线平行
符号语言:
//
a , a // b b
a b
例1:夹在两平行平面间的两条平行线段相等.
已知: // , AB ∥ CD,且A∈α,C∈α,
B∈β,D∈β. 求证:AB=CD 证明:Q AB / / CD
a
判定线面平 行的依据
答:如果两个平面平行,那么一个平面 内的直线与另一个平面平行.
探究2.如果两个平面平行,两个平面内的直 线有什么位置关系?
结论:如果两个平面平行,那么两个平面内 的直线要么是异面直线,要么是平行直线.
如图,平面α ,β ,γ 满足α ∥β ,α ∩γ = 探究3:当第三个平面和两个 a,β ∩γ =b,求证:a∥b
A
C
∴AB,CD确定一个平面ABDC B Q / / , 面AD 面
平面与平面平行的判定和性质

P
b a
已知:在平面 内有两条直线 a 、 相交且和 b 平面 平行. 求证: // 证明:(用反证法)
c 假设 .
a // , a
a // c
同理
b // c 这与题设 a和 b 是相交直线矛盾.
//
平面与平面平行的判定定理:
一个平面内的两条相交直线与另一个 平面平行,则这两个平面平行. (线面平行面面平行)
PF EF
同理: EP || AD
AS=18
CD=34
A
α
34
C
α
A
18 S
9
C
B β
9
D
β
D
B
S
1.如果三个平面两两相交,那么它们 的交线有多少条?画出图形表示你的 结论。
答:有可能1条,也有可能3条交线。
(1)
(2)
3. 3个平面把空间分成几部分?
(1)
4
(2)
6
(3)
6
(4)
证明: 连结AB, AB. 因为AA∥BB,
B
A
A′
B′
AB AB AB∥ AB AA∥BB ∥ AABB是平行四边形 AA BB.
所以经过AA,BB能确定一个平面,记为平面 .
推论2:平行于同一个平面的两个平面平行
下图表示两平面之间的两种位置,如 何用符号语言描述这两种位置关系?
β α
l
//
l
一、两平面平行:
1、定义:如果两个平面没有公共点,那么 这两个平面互相平行,也叫做平行平面.
证明面面平行的判定定理

证明面面平行的判定定理
面面平行是立体几何学中一个非常重要的概念。
在三维空间中,
如果两个平面是平行的,那么它们永远不会相交。
而面面平行的判定
定理可以帮助我们准确地判断两个平面是否平行。
本文将详细介绍面
面平行的判定定理,包括定义、性质和应用。
一、定义
在三维空间中,两个平面是平行的,当且仅当它们的法线向量平行。
因此,要判断两个平面是否平行,我们只需要比较它们的法线向
量是否平行即可。
二、性质
1. 如果两个平面是平行的,那么它们永远不会相交。
2. 两个平面的法线向量分别为n和m,如果n和m平行,那么这
两个平面是平行的。
3. 如果两个平面是平行的,那么它们的法线向量长度相等。
三、应用
在求解立体几何学问题时,面面平行的判定定理是非常有用的。
比如,在计算两个平面之间的距离时,我们可以先判断它们是否平行,再利用向量的知识求解距离。
又比如,在求解两个平面的夹角时,我
们也可以利用这个定理来进行计算。
另外,在工程和建筑设计中,面面平行的判定定理也有着广泛的应用。
比如,在设计房屋或者建筑物时,我们需要保证墙壁之间是平行的,才能保证建筑物的稳定性和美观性。
此外,在工程测量中,面面平行的判定定理也可以用来判断不同建筑物的墙面是否平行,从而帮助我们得出准确的测量结果。
综上所述,面面平行的判定定理是立体几何学中一个非常重要的定理,它可以帮助我们准确地判断两个平面是否平行,并在工程、建筑设计和测量方面有着广泛的应用。
因此,学好面面平行的判定定理对我们的学习和工作都是非常有帮助的。
两平面平行的判定与性质

垂直→←平行
作业: P32: 习题4,8
; / 钢塑土工格栅
hoq148egk
烟筒不停地冒着青白色的烟,在微风吹拂下、袅袅地飘向远处。刘丽娟凭直觉那肯定是啤酒厂锅炉房的大烟筒,再远点几排白 色的、圆柱形的巨型大罐无疑是发酵大罐,而紧邻的一座建筑,屋顶上像沸腾的蒸笼一样不断冒着热腾腾的热气肯定是糖化间, 还有两颗又高又大的树直穿云霄,树梢仿佛可以触到天空。上学时专业老师曾说过,如果你找不到啤酒厂时,从外围看到三个 标志性的建筑物:锅炉房的大烟囱、糖化上热气腾腾的烟筒和高高矗立的发酵大罐,那八九不离十就是啤酒厂了。得到马启明 肯定的答复后,他们立即沿着马路朝大烟筒方向走去,感觉就好像找到了组织一样心里踏实多了。一路上看见一辆辆满载着空 瓶的汽车停在路边,一直排到啤酒厂门口,粗略数数竟有十几辆。此时正好是上下班的时候,一群群职工有说有笑地进进出出, 门口悬挂着厂牌:江苏花开啤酒厂。走进厂门仍旧是排得紧紧的、等待拉啤酒的汽车。马启明忍不住叫出声:“这么多的车子 在等着拉啤酒呀!”望着这么多进进出出的车辆马启明竟一时想不起上次是怎么走的了,一路问着找到厂长办公室。一进门马 明启就看到上次接待他的蒋明辉,像见到了亲人一样,立即兴奋地喊道:“蒋主任,您好!”蒋明辉一看惊喜地叫道:“唉吆 外!这不是马启明吗!”马上站起来把手伸过来,跟马启明热烈地握手,笑着说道:“欢迎!欢迎!”马启明觉得笑是两人间 最短的距离。蒋明辉是厂办公室主任,三十来岁,个子不高,约1.70,肌肉男,短短的板寸头,身体结实,眼睛里透着南方人 的精明劲儿,脸上永远挂着标志性的笑容。马启明上一次来花开啤酒厂就受到他热情的接待,是马启明在花开啤酒厂第二个认 识的人,虽然第二次相见,但是感到非常亲切。马启明一看蒋明辉也这么热情,赶紧拉着妻子高兴地说:“蒋主任,这是我爱 人刘丽娟,我们这次来是正式向您报到的。”说着从口袋中掏出海涛州人事局的介绍信。蒋明辉给马启明、刘丽娟倒了杯水, 然后接过马启明的介绍信说道:“别着急,先坐下休息休息,喝口茶。我出去看一下他们在不在?”说完脸上挂着标志性的笑 容就出去了。不一会儿,蒋明辉进来说道:“谷厂长他们马上要开会,要不然你们先到厂招待所休息一下?等会议结束后我再 叫你们。”“好好好!那就麻烦您了!”马启明急忙答道。到吃中午饭时,蒋明辉把马启明和刘丽娟带到厂内招待所食堂,等 了一会儿,看见几个人朝饭厅走来。马启明一眼就认出来人保科的张之文科长,刚想站起来准备和他打招呼,蒋明辉却急忙拉 起马启明,恭恭敬敬地指着一位白白胖胖的中年人向马启明介绍道:“马启明,这位是谷厂长。”马启明上次来就了解到厂长 叫谷仕昊,同时兼党委书记,属于党政一把抓。可惜当时谷厂长到局里开会,无
直线与平面,平面与平面平行的判定及其性质
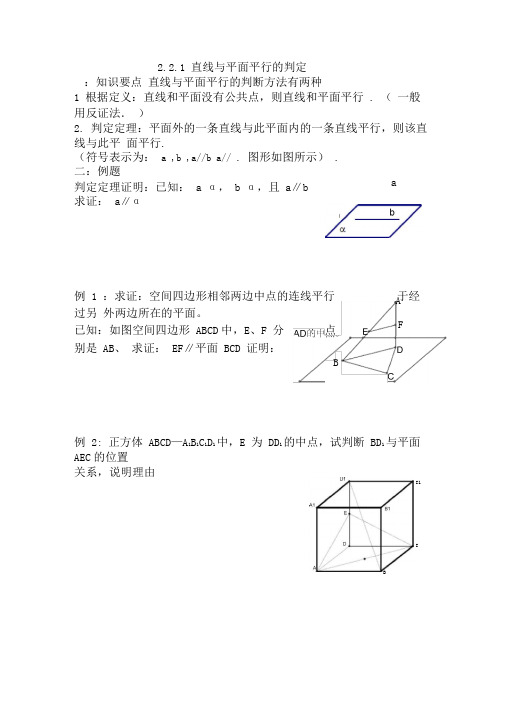
2.2.1 直线与平面平行的判定:知识要点 直线与平面平行的判断方法有两种1 根据定义:直线和平面没有公共点,则直线和平面平行 . ( 一般用反证法. )2. 判定定理:平面外的一条直线与此平面内的一条直线平行,则该直线与此平 面平行.(符号表示为: a ,b ,a//b a// . 图形如图所示) . 二:例题判定定理证明:已知: a α, b α,且 a ∥b求证: a∥α例 1 :求证:空间四边形相邻两边中点的连线平行于经过另 外两边所在的平面。
已知:如图空间四边形 ABCD 中,E 、F 分别是 AB 、 求证: EF ∥平面 BCD 证明:例 2: 正方体 ABCD —A 1B 1C 1D 1中,E 为 DD 1的中点,试判断 BD 1与平面AEC 的位置 关系,说明理由a AF点 BC1CB三练习:1. 判断下列说法是否正确,并说明理由.○1 平面 外的一条直线 a 与平面 内的无数条直线平行则直线 a 和平面 平行;○2平面 外的两条平行直线 a,b ,若 a// ,则b// ;○3 直线a 和平面 平行,则直线 a 平行于平面 内任意一条直线; ○4 直线 a 和平面 平行,则平面 中必定存在直线与直线 a 平行. A. l 1 ∥α B. l 2 α C. l 2 ∥α或l 2 α D. l 2 与α相交 3.以下说法(其中 a ,b 表示直线, 表示平面)①若 a ∥b , b ,则 a ∥ ②若 a ∥ ,b ∥ ,则 a ∥b ③若 a ∥b , b ∥ ,则 a ∥ ④若 a ∥ ,b ,则 a ∥b 其中正确说法的个数是( ) .A. 0 个B. 1 个C. 2 个D. 3 个4.已知a ,b 是两条相交直线, a ∥ ,则 b 与 的位置关系是( ). A. b ∥ B. b 与 相交 C. b α D. b ∥ 或 b 与 相交5. 如果平面 外有两点 A 、B ,它们到平面 的距离都是 a ,则直线 AB 和平面 的 位置关系一定是( ) .A. 平行B. 相交C. 平行或相交D. AB 6.平面 与△ ABC 的两边 AB 、 AC 分别交于 D 、E ,且 AD ∶DB=AE ∶EC ,求证: BC ∥平面 .7.P 是平行四边形 ABCD 所在平面外一点, E 为PB 的中点, O 为 AC ,BD 的交点. (1)求证:EO ‖平面PCD ; (2)图中EO 还与哪个平 面平行?8. 在正方体 ABCD- A 1B 1C 1D 1中, E 、F 分别为棱 BC 、C 1D 1的中点. 求证: EF ∥平面 BB 1D 1D2. 已知直线 l 1、l 2 , 平面α, l 1 ∥l 2 , l 1∥α 那么 l 2 与平面 α 的关系是( ).2.2 平面与平面平行的判定:知识要点平面与平面平行的判断方法有三种 1. 定义:两平面没有公共点,则两平面平行2. 判定定理:如果一个平面内有两条相交直线都平行于另一个平面, 那么这两个平面平行. 用符号表示为: a ,b ,a b P // a// ,b// 图形如图所示图形如图所示 3. 推论:①如果一个平面内有两条相交直线分别平行于 另一个平面内的两条直线,那么这两个平面平行 ②垂直于同一条直线的两个平面平行 . ③平行与同一平面的两个平面平行 . 二:例题 判定定理证明 : 已知:如图, m , n , 求证://mn ( 思考 1 :如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线, 那么这两个平面平行吗 ?为什么? )(思考 2:.在判断一个平面是否水平时,把水准器在这个平 面内交叉地放两次,如果水准器的气泡都是居中的,就 可以判定这个平面和水平面平行,你能说出理由吗?) 例 2:已知正方体 ABCD-A 1B 1C 1D 1, 求证:平面 AB 1D 1 // 平面 C 1BD 。
高考数学复习平面与平面平行的性质定理

如果两个平行平面同时和第三个 平面相交,交线具有什么位置关系?
D1 A1
D
A
C1 B1
C B
必修2 第二章 点、直线、平面之间的位置关系
平面与平面平行的性质定理
定理:如果两个平行平面同时和第三个平面相交,那么它 们的交线平行。
符号语言:α∥β,α∩γ=a,β∩γ=b,a∥b
必修2 第二章 点、直线、平面之间的位置关系
巩固练习:
3、棱长为a的正方体AC1中,设M、N、E、F分别为 棱A1B1、A1D1、 C1D1、 B1C1的中点.
(1)求证:E、F、B、D四点共面;
D1
E
(2)求证:面AMN∥面EFBD. N
A1
M
C1
F B1
D
C
A
B
必修2 第二章 点、直线、平面之间的位置关系
∴ 四边形ABDC是平行四边形.
∴ AB=CD.
必修2 第二章 点、直线、平面之间的位置关系
定理的应用
例2. 如图所示,矩形ABCD的四个顶点A、B、C、 D均在四边形A′B′C′D′所确定的平面α外,且AA′、 BB′、CC′、DD′互相平行.求证:四边形A′B′C′D′ 是平行四边形.
必修2 第二章 点、直线、平面之间的位置关系
基本步骤:首先是画出图形,再结合图形将文字 语言转化为符号语言,最后分析并书写出证明过 程。
已知:如图,AB∥CD, A∈α ,
D
D∈α, B∈β ,C∈β,求证:AB=CDα A
证明:
C
∵AB//CD, ∴ 过AB,CD可作平面γ,
βB
且平面γ与平面α和β分别相交于AC和BD.
人教版必修二数学课件:2.2 平面与平面平行的判定和性质 (共16张PPT)

平行的判定和性质
一. 平面与平面平行的判定和性质 1. 判定定理: 交线∥平面, 则平面∥平面 2. 性质定理: 平面∥平面, 则交线∥交线 要证面面平行: ①证: 交线∥平面 ②证: 交线∥交线 a b a b
证明面面平行的性质定理 性质定理: 平面∥平面, 则交线∥交线 b 已知: ∥, ∩ = a, ∩ = 求证: a ∥b a 证: ∥ => b 与 无公共点 => a , b a与b没有公共点 => a ∥b a与b同在平面 内
GF∥BD =>GF∥ · · · · · · · · · ② BD GE, GF 平面GEF且相交 · · · · · · ③ ①②③ => 平面GEF∥ EF 平面GEF => EF∥
例5. ∥ , P在 和 外, A,B , PA =A', PB =B', 已知 PA'= 6, AA'=10, A'B'=5, 则AB=_________ 40/3或10/3 A B A B 4 10 P A B A' 5 B' 6 6 10 × 5 A' B' P B' A' 5 = 6 5 6 = AB 16 AB 4 AB=40/3 AB=10/3 P
x2 y2 x2 y2 y2 y2 tan ±tan · · ① a2-5 96 16 12 =1 设 16 12 =1 · 1 tan tan x2 y2 x2 y2 x2 y2 x2 y2 ∴ + =1 · · ① · · ① 16 + 12 =1 16 - 12 =1 · 4 3 16 + 12 =1 · a a2+b2-c2 a b a a2+b2-c2 sinA 2ab2 sinA = sinB => sinA 2ab
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
、性质定理
1、内容
2、证明
【课后记】
分清判定与性质
应给予学生一定地巩固时间
平行平面地画图
文字说明地题目应写出已知、求证、画出图形
记住结论,作题时可直接应用
教学内容
第课时
【课题】平面与平面平行地性质定理
【教学目标】
〖知识目标〗掌握平面与平面平行地性质定理及应用
〖技能目标〗数形结合地分析能力
〖德育目标〗培养几何立体思维
【教材分析】
〖教学重点〗性质定理
〖教学难点〗具体应用
〖教学关键〗具有“悟性”, “自己地东西”
【课型】新授课
【教法】讲解法
【教具及课前准备】直尺模型
求证:АБ
证明:
连结
∵∥
∴与确定平面
又∵平面∩α.
平面∩β
α∥β
∴∥
∴四边形是平行四边形.
∴АБ.
α
β
三、两条直线被三个平行平面所截,截得地对应线段成比例.
〖巩固练习〗 、
、
〖教师小结〗
思维中要有立体地几何模型,然后把理论定理添加进去.
〖指定作业〗、
【板书设计】
平面与平面平行地性质定理
1、复习:
1、判定定理
【教学过程】
〖组织教学〗分铃到岗,调空气氛
〖引入课题〗复习:
1.判定定理
.位置关系
〖顺序讲解〗
一、平面与平面平行地性质定理
1、内容:如果两个平行Байду номын сангаас面同时与第三个平面相交,则它们地交线相互平行.
α∩γа,β∩γь,
α∥β
则а∥ь
аα
βь
γ
二、求怔:夹在两个平行平面间地两条平行线段相等.
已知:α∥β,АБ和为夹α,β在间地平行线段.
