高中数学-平面与平面平行的性质
高中数学必杀1-4线面平行与面面平行的判定及性质
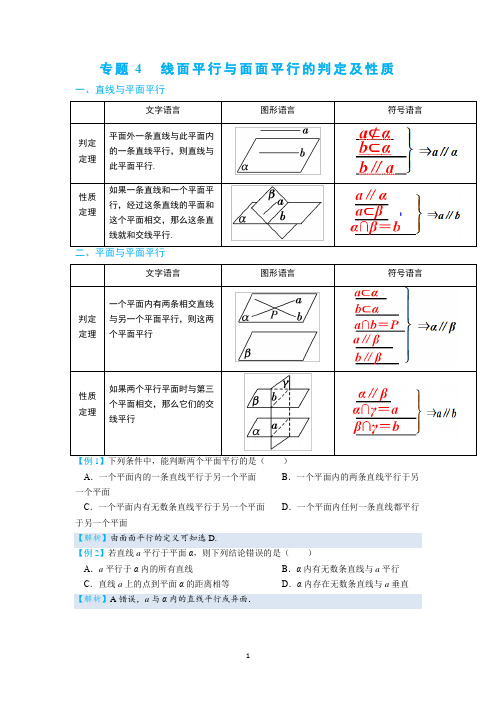
专题4 线面平行与面面平行的判定及性质一、直线与平面平行下列条件中,能判断两个平面平行的是()A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面【解析】由面面平行的定义可知选D.【例2】若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直【解析】A错误,a与α内的直线平行或异面.【例3】已知不重合的直线a ,b 和平面α,①若a ∥α,b ⊂α,则a ∥b ;②若a ∥α,b ∥α,则a ∥b ;③若a ∥b ,b ⊂α,则a ∥α;④若a ∥b ,a ∥α,则b ∥α或b ⊂α,上面命题中正确的是________(填序号).【解析】 ①中a 与b 可能异面;②中a 与b 可能相交、平行或异面;③中a 可能在平面α内,④正确.【例4】已知α、β是平面,m 、n 是直线,给出下列命题:①若m ⊥α,m ⊂β,则α⊥β.②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β.③如果m ⊂α,α⊄n ,m 、n 是异面直线,那么n 与α相交.④若α∩β=m ,n ∥m ,且α⊄n ,β⊄n ,则n ∥α且n ∥β其中正确命题的个数是( )A .1B .2C .3D .4【解析】对于①,由定理“如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直”得知,①正确;对于②,注意到直线m ,n 可能是两条平行直线,此时平面α,β可能是相交平面,因此②不正确;对于③,满足条件的直线n 可能平行于平面α,因此③不正确;对于④,由定理“如果平面外一条直线平行于平面内一条直线,那么这条直线平行于这个平面”得知,④正确.综上所述,其中正确的命题是①④,故选B.【例5】已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题: ①n m n m //⇒⎩⎨⎧⊥⊥αα;①αα//n n m m ⇒⎩⎨⎧⊥⊥;①n m n m ⊥⇒⎩⎨⎧⊥αα//其中真命题的个数为( ) A .0 B .1 C .2 D .3【解析】若⎩⎨⎧⊥⊥ααn m ,则m ①n ,即命题①正确;若⎩⎨⎧⊥⊥n m m α,则n ①α或n ①α,即命题①不正确;若⎩⎨⎧⊥αα//n m ,则m ①n ,即命题①正确;综上可得,真命题共有2个.故选C .【例6】已知m 、n 、l 1、l 2表示直线,α、β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则以下条件中,能推出α∥β的是( ) A .m ∥β且l 1∥α B .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2【解析】由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.【例7】在下列条件中,可判断平面α与β平行的是( ) A .α、β都平行于直线l B .α内存在不共线的三点到β的距离相等C .l 、m 是α内两条直线,且l ①β,m ①βD .l 、m 是两条异面直线,且l ①α,m ①α,l ①β,m ①β【解析】排除法,A 中α、β可以是相交平面;B 中三点可面平面两侧;C 中两直线可以不相交.故选D ,也可直接证明.【例8】经过平面外的两点作该平面的平行平面可以作( )A .0个B .1个C .0个或1个D .1个或2个【解析】这两点可以是在平面同侧或两侧.故选C .达标训练11.(2019•延安一模)已知m ,n 表示两条不同的直线,α表示平面.下列说法正确的是( )A .若//m α,//n α,则//m nB .若m α⊥,n α⊥,则//m nC .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥ 2.(2019•湖北期中)平面α与平面β平行的条件可以是( )A .α内有无数多条直线都与β平行B .直线a α⊂,b β⊂,且//a β,//b αC .直线//a α,//a β,且直线a 不在α内,也不在β内D .一个平面α内两条不平行的直线都平行于另一个平面β3.(2019•深圳二模)己知正方体1111ABCD A B C D -,P 为棱1CC 的动点,Q 为棱1AA 的中点,设直线m 为平面BDP 与平面11B D P 的交线,以下关系中正确的是( ) A .1//m D Q B .//m 平面11B D QC .1m B Q ⊥D .m ⊥平面11ABB A4.(2019•聊城二模)在长方体1111ABCD A B C D -中,F ,F ,G ,H 分别为棱11A B ,1BB ,1CC ,11C D 的中点,则下列结论中正确的是( )A .1//AD 平面EFGHB .1//BD GHC .//BD EFD .平面//EFGH 平面11A BCD5.(2019•汕头月考)如图,在正方体1111ABCD A B C D -中,M ,N 分别是1BC ,1CD 的中点,则下列判断错误的是( ) A .1MN CC ⊥B .MN ⊥平面11ACC AC .//MN 平面ABCDD .11//MN A B6.(2019•大连一模)已知m ,n 为两条不重合直线,α,β为两个不重合平面,下列条件中,可以作为//αβ的充分条件的是( ) A .//m n ,m α⊂,n β⊂ B .//m n ,m α⊥,n β⊥ C .m n ⊥,//m α,//n βD .m n ⊥,m α⊥,n β⊥7.(2019•汕头一模)在正方体1111ABCD A B C D -中,点O 是四边形ABCD 的中心,关于直线1A O ,下列说法正确的是( )A .11//AO D C B .1AO BC ⊥C .1//A O 平面11B CDD .1A O ⊥平面11AB D8.(2019•青云月考)如图,四棱锥P ABCD -中,M ,N 分别为AC ,PC 上的点,且//MN 平面PAD ,则( ) A .//MN PD B .//MN PAC .//MN ADD .以上均有可能9.(2019•上饶一模)设m ,n 表示不同的直线,α,β表示不同的平面,且m ,n α⊂.则“//αβ”是“//m β且//n β”的( ) A .充分但不必要条件 B .必要但不充分条件C .充要条件D .既不充分又不必要条件10.(2018•沧州一模)如图,在下列四个正方体中,P ,R ,Q ,M ,N ,G ,H 为所在棱的中点,则在这四个正方体中,阴影平面与PRQ 所在平面平行的是( )A .B .C .D .11.(2017•洛南期末)已知平面//α平面β,直线m α⊂,直线n β⊂,下列结论中不正确的是( ) A .//m βB .//n αC .//m nD .m 与n 不相交12.(2018•杭州期中)如图,四棱锥P ABCD -的底面ABCD 是平行四边形,M 、N 分别为线段PC 、PB 上一点,若:3:1PM MC =,且//AN 平面BDM ,则:PN NB =( )A .4:1B .3:1C .3:2D .2:113.(2018•厦门二模)如图,在正方体1111ABCD A B C D -中,M ,N ,P 分别是11C D ,BC ,11A D 的中点,则下列命题正确的是( )A .//MN APB .1//MN BDC .//MN 平面11BBD DD .//MN 平面BDP14.(2018•辛集期中)在四棱锥P ABCD -中,底面ABCD 为菱形,60BAD ∠=︒,Q 为AD 的中点,点M 在线段PC 上,PM tPC =,//PA 平面MQB ,则实数t 的值为( ) A .15B .14 C .13D .1215.(2018•四川模拟)如图是某几何体的平面展开图,其中四边形ABCD 为正方形,E ,F 分别为PA ,PD 的中点.在此几何体中,以下结论一定成立的是( ) A .直线//BE PFB .直线//EF 平面PBCC .平面BCE ⊥平面PAD D .直线PB 与DC 所成角为60︒16.(2017•万州期末)平面α与ABC ∆的两边AB ,AC 分别交于点D ,E ,且::AD DB AE EC =,如图,则BC 与α的位置关系是( )A .异面B .相交C .平行或相交D .平行17.(2018•桃城模拟)如图,各棱长均为1的正三棱柱111ABC A B C -,M ,N 分别为线段1A B ,1B C 上的动点,且//MN 平面11ACC A ,则这样的MN 有( )A .1条B .2条C .3条D .无数条18.(2018•雁江月考)已知P 为ABC ∆所在平面外一点,平面//α平面ABC ,且α交线段PA ,PB ,PC 于点A ',B ',C ',若:2:3PA AA ''=,则:A B C ABC S S '''=△△( )A .2:3B .2:5C .4:9D .4:2519.(2018•香坊四模)对于不重合的两个平面α和β,给定下列条件: ①存在直线l ,使得l α⊥,且l β⊥; ①存在平面γ,使得αγ⊥且βγ⊥; ①α内有不共线的三点到β的距离相等;①存在异面直线l ,m ,使得//l α,//l β,//m α,//m β. 其中,可以判定α与β平行的条件有( ) A .1个B .2个C .3个D .4个20.(2018•西城期末)在直三棱柱111ABC A B C -中,D 为1AA 中点,点P 在侧面11BCC B 上运动,当点P 满足条件 时,1//A P 平面BCD (答案不唯一,填一个满足题意的条件即可达标训练21.(2017•新课标①)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )A .B .C .D .2.(2011•浙江)若直线l 不平行于平面α,且l α⊂/,则( ) A .α内存在直线与l 异面 B .α内存在与l 平行的直线C .α内存在唯一的直线与l 平行D .α内的直线与l 都相交 3.(2010•浙江)设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是( ) A .若l m ⊥,m α⊂,则l α⊥ B .若l α⊥,//l m ,则m α⊥C .若//l α,m α⊂,则//l mD .若//l α,//m α,则//l m 4.(2010•江西)如图,M 是正方体1111ABCD A B C D -的棱1DD 的中点,给出下列命题 ①过M 点有且只有一条直线与直线AB 、11B C 都相交; ①过M 点有且只有一条直线与直线AB 、11B C 都垂直; ①过M 点有且只有一个平面与直线AB 、11B C 都相交; ①过M 点有且只有一个平面与直线AB 、11B C 都平行. 其中真命题是( ) A .①①①B .①①①C .①①①D .①①①5.(2008•湖南)已知直线m 、n 和平面α、β满足m n ⊥,m α⊥,αβ⊥,则( ) A .n β⊥ B .//n β,或n β⊂ C .n α⊥D .//n α,或n α⊂6.(2007•北京)平面//α平面β的一个充分条件是( ) A .存在一条直线a ,//a α,//a β B .存在一条直线a ,a α⊂,//a βC .存在两条平行直线a ,b ,a α⊂,b β⊂,//a β,//b αD .存在两条异面直线a ,b ,a α⊂,b β⊂,//a β,//b α7.(2011•福建)如图,正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在CD 上,若//EF 平面1AB C ,则线段EF 的长度等于 .。
高中数学-直线与平面平行、平面与平面平行的性质

【证明】证法一:如图所示,分别取AA1,A1B1 的中点M,N,连接MN,NQ,MP.
∵P,Q分别是面AA1 D1D,面A1B1C1D1的中点,
∴MP∥AD, MP=
NQ=
1 2
A1D1.
1 2
AD,NQ∥A1D1,
∴MP∥NQ且MP=NQ.
∴四边形PQNM为平行四边形.
∴PQ∥MN.
∵MN AA1B1B,
∵CQ∥
∴CQ∥MN.
∵EF是△ABC的中位线,∴M是PC的中点,
则N是PQ的中点,即PQ被平面EFGH平分.
【点评】P,C,Q三点所确定的辅助平面是解决本题的 核心.有了面PCQ,就有了连接CD与面EFGH的桥梁, 线面平行的性质才能得以应用.
返回
如图2-3-4所示,已知ABCD是平行四边形,点P是平面 ABCD外一点,M是PC的中点,在DM上取一点G,过G 和AP作平面交平面BDM于GH.求证:AP∥GH.
.
∴AC∥MN∥AC,且AC= 13AC.
∴AC∥平面ABC.
同理,A′B′∥平面ABC.
又∵AC∩A′B′=A′,
∴平面A′B′C′∥平面ABC.
1
1
(2)同理A′B′= AB3 , B=C BC3 ,
∴△A′B′C′∽△ABC.
∴S△A′B′C′
S△ABC =1:9.
返回
1.如何理解线面平行的性质定理?
表示平面的平行四边形的外面,并且使它与平行四边形的一 边或平行四边形内的一条线段平行.
返回
2.如何理解两个平面平行的性质定理?
平面平行的性质是根据面面平行、线面平行、线线平行的 定义直接给出的;判定直线与直线平行,进而判定直线与 平面平行和平面与平面平行,或者反过来由后者判定前者, 是立体几何最基本又最常见的一类问题.证明线面平行往往 转化为证明面面平行.
人教A版高中数学必修二课件第五讲直线与平面、平面与平面平行的性质.pptx

思考:教室内的日光灯管所在的直线与地 面平行,如何在地面上作一条直线与灯管 所在的直线平行?
Aa B
思考:教室内的日光灯管所在的直线与地 面平行,如何在地面上作一条直线与灯管 所在的直线平行?
Aa B
思考:教室内的日光灯管所在的直线与地 面平行,如何在地面上作一条直线与灯管 所在的直线平行?
∴a与b无公共点. 又∵ a , b ,
解决问题
已知:直线a∥平面, a , b.
求证:a∥b.
a
b
证明: b, b , 又a //
∴a与b无公共点. 又∵ a , b , 即a与b共面.
解决问题
已知:直线a∥平面, a , b.
BC 面BC' 面BC' 面A'C' B'C'
BC//B'C'
EF//B'C'
BC//EF
D'
A'
P E
D
F B'
C' C
EF、BE、CF共面. A
B
则EF、BE、CF为应画的线.
直线与平面平行的性质定理的运用: 例1 如图所示的一块木料中, 棱BC平行于面A'C'.
⑴要经过面内的一点P和棱BC将木料锯开,应怎
a
b
讲授新课
直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线 的任一个平面与此平面的交线和该直线平行.
符号语言:
a
b
讲授新课
直线与平面平行的性质定理
专题2:平面与平面平行的判定与性质基础知识与典型例题2020-21学年高中数学平行和垂直证明常见题型

专题2:平面与平面平行的判定与性质平面与平面的位置关系:平行——没有公共点:符号α∥β相交——有一条公共直线: 符号α∩β=a1.平面与平面平行的判定(1)定义:两个平面没有公共点,称这两个平面平行;(2)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
简记为:线面平行,则面面平行.符号:,,a ba b Aa bαααβββ⊂⊂⎫⎪=⇒⎬⎪⎭1.如图所示,四棱锥P ABCD-中,底面ABCD为平行四边形,E、F分别为PD、PA的中点,AC、BD交于点O.(1)求证:平面//PBC平面EFO;2.如图,正方体1111ABCD A B C D-中,E,F,P,Q分别是BC,11C D,1AD,BD的中点.(1)求证:平面PQB //平面11CB D ;3.如图,在棱长为2的正方体1111ABCD A B C D 中,E ,F 分别为11A D ,11B C 的中点.(1)求证:平面1//AB E 平面1BD F ;4.如图所示,在三棱柱ABC -A 1B 1C 1中,E ,F ,G ,H 分别是AB ,AC ,A 1B 1,A 1C 1的中点,求证:(1)平面EF A 1∥平面BCHG .(2)5.如图,三棱锥P ABC -中,,,PC AC BC 两两垂直,1BC PC ==,2AC =,,,E F G 分别是,,AB AC AP 的中点.(1)证明:平面//GEF 面PCB ;6.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,点M ,N ,Q 分别在PA ,BD ,PD 上(不与端点重合),且:::PM MA BN ND PQ QD ==.求证:平面//MNQ 平面PBC .7.如图所示,在正三棱柱ABC-A 1B 1C 1中,E ,F ,G 是侧面对角线上的点,且BE=CF=AG ,平面与平面平行的性质定理:如果两个平行的平面同时与第三个平面相交,那么它们的交线平行。
高中数学知识点总结(第八章 立体几何 第四节 直线、平面平行的判定与性质)

第四节 直线、平面平行的判定与性质一、基础知识1.直线与平面平行的判定定理和性质定理文字语言图形语言符号语言 判定定理平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行(线线平行⇒线面平行)∵l ∥a ,a ⊂α, l ⊄α,∴l ∥α性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)∵l ∥α,l ⊂β,α∩β=b ,∴l ∥b⎣⎢⎡⎦⎥⎤❶应用判定定理时,要注意“内”“外”“平行”三个条件必须都具备,缺一不可. 2.平面与平面平行的判定定理和性质定理文字语言 图形语言符号语言 判定定理一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)∵a ∥β, b ∥β, a ∩b =P ,a ⊂α, b ⊂α, ∴α∥β 性质定理如果两个平行平面同时和第三个平面相交,那么它们的交线平行∵α∥β,α∩γ=a ,β∩γ=b ,∴a ∥b⎣⎢⎢⎡⎦⎥⎥⎤❷如果一个平面内的两条相交直线分别平行于另一个平面的两条直线,那么这两个平面互相平行.符号表示:a ⊂α,b ⊂α,a ∩b =O ,a ′⊂β,b ′⊂β,a ∥a ′,b ∥b ′⇒α∥β.二、常用结论平面与平面平行的三个性质(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.(2)夹在两个平行平面间的平行线段长度相等.(3)两条直线被三个平行平面所截,截得的对应线段成比例.考点一直线与平面平行的判定与性质考法(一)直线与平面平行的判定[典例]如图,在直三棱柱ABCA1B1C1中,点M,N分别为线段A1B,AC1的中点.求证:MN∥平面BB1C1C.[证明]如图,连接A1C.在直三棱柱ABCA1B1C1中,侧面AA1C1C为平行四边形.又因为N为线段AC1的中点,所以A1C与AC1相交于点N,即A1C经过点N,且N为线段A1C的中点.因为M为线段A1B的中点,所以MN∥BC.又因为MN⊄平面BB1C1C,BC⊂平面BB1C1C,所以MN∥平面BB1C1C.考法(二)线面平行性质定理的应用[典例](2018·豫东名校联考)如图,在四棱柱ABCDA1B1C1D1中,E为线段AD上的任意一点(不包括A,D两点),平面CEC1与平面BB1D交于FG.求证:FG∥平面AA1B1B.[证明]在四棱柱ABCDA1B1C1D1中,BB1∥CC1,BB1⊂平面BB1D,CC1⊄平面BB1D,所以CC1∥平面BB1D.又CC1⊂平面CEC1,平面CEC1与平面BB1D交于FG,所以CC1∥FG.因为BB1∥CC1,所以BB1∥FG.因为BB1⊂平面AA1B1B,FG⊄平面AA1B1B,所以FG∥平面AA1B1B.[题组训练]1.(2018·浙江高考)已知平面α,直线m ,n 满足m ⊄α,n ⊂α,则“m ∥n ”是“m ∥α”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件解析:选A ∵若m ⊄α,n ⊂α,且m ∥n ,由线面平行的判定定理知m ∥α,但若m ⊄α,n ⊂α,且m ∥α,则m 与n 有可能异面,∴“m ∥n ”是“m ∥α”的充分不必要条件.2.如图,在四棱锥P ABCD 中,AB ∥CD ,AB =2,CD =3,M 为PC 上一点,且PM =2MC .求证:BM ∥平面P AD .证明:法一:如图,过点M 作MN ∥CD 交PD 于点N ,连接AN . ∵PM =2MC ,∴MN =23CD .又AB =23CD ,且AB ∥CD ,∴AB 綊MN ,∴四边形ABMN 为平行四边形, ∴BM ∥AN .又BM ⊄平面P AD ,AN ⊂平面P AD , ∴BM ∥平面P AD .法二:如图,过点M 作MN ∥PD 交CD 于点N ,连接BN . ∵PM =2MC ,∴DN =2NC , 又AB ∥CD ,AB =23CD ,∴AB 綊DN ,∴四边形ABND 为平行四边形, ∴BN ∥AD .∵BN ⊂平面MBN ,MN ⊂平面MBN ,BN ∩MN =N , AD ⊂平面P AD ,PD ⊂平面P AD ,AD ∩PD =D , ∴平面MBN ∥平面P AD .∵BM ⊂平面MBN ,∴BM ∥平面P AD .3.如图所示,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和P A作平面P AHG交平面BMD于GH.求证:P A∥GH.证明:如图所示,连接AC交BD于点O,连接MO,∵四边形ABCD是平行四边形,∴O是AC的中点,又M是PC的中点,∴P A∥MO.又MO⊂平面BMD,P A⊄平面BMD,∴P A∥平面BMD.∵平面P AHG∩平面BMD=GH,P A⊂平面P AHG,∴P A∥GH.考点二平面与平面平行的判定与性质[典例]如图,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EF A1∥平面BCHG.[证明](1)∵GH是△A1B1C1的中位线,∴GH∥B1C1.又∵B1C1∥BC,∴GH∥BC,∴B,C,H,G四点共面.(2)∵E,F分别为AB,AC的中点,∴EF∥BC,∵EF⊄平面BCHG,BC⊂平面BCHG,∴EF∥平面BCHG.∵A1G綊EB,∴四边形A1EBG是平行四边形,∴A1E∥GB.∵A1E⊄平面BCHG,GB⊂平面BCHG,∴A1E∥平面BCHG.∵A1E∩EF=E,∴平面EF A1∥平面BCHG.[变透练清]1.变结论在本例条件下,若D1,D分别为B1C1,BC的中点,求证:平面A1BD1∥平面AC1D.证明:如图所示,连接A1C,AC1,设交点为M,∵四边形A1ACC1是平行四边形,∴M是A1C的中点,连接MD,∵D为BC的中点,∴A1B∥DM.∵DM⊄平面A1BD1,A1B⊂平面A1BD1,∴DM∥平面A1BD1.又由三棱柱的性质知D1C1綊BD,∴四边形BDC1D1为平行四边形,∴DC1∥BD1.又DC1⊄平面A1BD1,BD1⊂平面A1BD1,∴DC1∥平面A1BD1,又∵DC1∩DM=D,DC1⊂平面AC1D,DM⊂平面AC1D,∴平面A1BD1∥平面AC1D.2.如图,四边形ABCD与四边形ADEF为平行四边形,M,N,G分别是AB,AD,EF 的中点,求证:(1)BE∥平面DMF;(2)平面BDE∥平面MNG.证明:(1)如图,连接AE,设DF与GN的交点为O,则AE必过DF与GN的交点O.连接MO,则MO为△ABE的中位线,所以BE∥MO.又BE⊄平面DMF,MO⊂平面DMF,所以BE∥平面DMF.(2)因为N ,G 分别为平行四边形ADEF 的边AD ,EF 的中点, 所以DE ∥GN .又DE ⊄平面MNG ,GN ⊂平面MNG , 所以DE ∥平面MNG . 又M 为AB 中点,所以MN 为△ABD 的中位线, 所以BD ∥MN .又BD ⊄平面MNG ,MN ⊂平面MNG , 所以BD ∥平面MNG .又DE ⊂平面BDE ,BD ⊂平面BDE ,DE ∩BD =D , 所以平面BDE ∥平面MNG .[课时跟踪检测]A 级1.已知直线a 与直线b 平行,直线a 与平面α平行,则直线b 与α的关系为( ) A .平行 B .相交C .直线b 在平面α内D .平行或直线b 在平面α内解析:选D 依题意,直线a 必与平面α内的某直线平行,又a ∥b ,因此直线b 与平面α的位置关系是平行或直线b 在平面α内.2.若平面α∥平面β,直线a ∥平面α,点B ∈β,则在平面β内且过B 点的所有直线中( )A .不一定存在与a 平行的直线B .只有两条与a 平行的直线C .存在无数条与a 平行的直线D .存在唯一与a 平行的直线解析:选A 当直线a 在平面β内且过B 点时,不存在与a 平行的直线,故选A. 3.在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE ∶EB =CF ∶FB =1∶2,则对角线AC 和平面DEF 的位置关系是( )A .平行B .相交C .在平面内D .不能确定解析:选A 如图,由AE EB =CFFB 得AC ∥EF .又因为EF ⊂平面DEF ,AC ⊄平面DEF , 所以AC ∥平面DEF .4.(2019·重庆六校联考)设a ,b 是两条不同的直线,α,β是两个不同的平面,则α∥β的一个充分条件是( )A .存在一条直线a ,a ∥α,a ∥βB .存在一条直线a ,a ⊂α,a ∥βC .存在两条平行直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥αD .存在两条异面直线a ,b ,a ⊂α,b ⊂β,a ∥β,b ∥α解析:选D 对于选项A ,若存在一条直线a ,a ∥α,a ∥β,则α∥β或α与β相交,若α∥β,则存在一条直线a ,使得a ∥α,a ∥β,所以选项A 的内容是α∥β的一个必要条件;同理,选项B 、C 的内容也是α∥β的一个必要条件而不是充分条件;对于选项D ,可以通过平移把两条异面直线平移到一个平面中,成为相交直线,则有α∥β,所以选项D 的内容是α∥β的一个充分条件.故选D.5.如图,透明塑料制成的长方体容器ABCD A 1B 1C 1D 1内灌进一些水,固定容器底面一边BC 于地面上,再将容器倾斜,随着倾斜度的不同,有下面四个命题:①没有水的部分始终呈棱柱形;②水面EFGH 所在四边形的面积为定值; ③棱A 1D 1始终与水面所在平面平行; ④当容器倾斜如图所示时,BE ·BF 是定值. 其中正确命题的个数是( ) A .1 B .2 C .3D .4解析:选C 由题图,显然①是正确的,②是错误的; 对于③,∵A 1D 1∥BC ,BC ∥FG ,∴A 1D 1∥FG 且A 1D 1⊄平面EFGH ,FG ⊂平面EFGH , ∴A 1D 1∥平面EFGH (水面). ∴③是正确的;对于④,∵水是定量的(定体积V ), ∴S △BEF ·BC =V ,即12BE ·BF ·BC =V .∴BE ·BF =2VBC(定值),即④是正确的,故选C.6.如图,平面α∥平面β,△P AB 所在的平面与α,β分别交于CD ,AB ,若PC =2,CA =3,CD =1,则AB =________.解析:∵平面α∥平面β,∴CD ∥AB , 则PC P A =CD AB ,∴AB =P A ×CD PC =5×12=52.答案:527.设α,β,γ是三个平面,a ,b 是两条不同直线,有下列三个条件: ①a ∥γ,b ⊂β;②a ∥γ,b ∥β;③b ∥β,a ⊂γ.如果命题“α∩β=a ,b ⊂γ,且________,则a ∥b ”为真命题,则可以在横线处填入的条件是________(填序号).解析:由面面平行的性质定理可知,①正确;当b ∥β,a ⊂γ时,a 和b 在同一平面内,且没有公共点,所以平行,③正确.故应填入的条件为①或③.答案:①或③8.在三棱锥P ABC 中,PB =6,AC =3,G 为△P AC 的重心,过点G 作三棱锥的一个截面,使截面平行于PB 和AC ,则截面的周长为________.解析:如图,过点G 作EF ∥AC ,分别交P A ,PC 于点E ,F ,过点E 作EN ∥PB 交AB 于点N ,过点F 作FM ∥PB 交BC 于点M ,连接MN ,则四边形EFMN 是平行四边形(平面EFMN 为所求截面),且EF =MN =23AC =2,FM =EN =13PB =2,所以截面的周长为2×4=8.10.(2019·南昌摸底调研)如图,在四棱锥P ABCD 中,∠ABC = ∠ACD =90°,∠BAC =∠CAD =60°,P A ⊥平面ABCD ,P A =2,AB =1.设M ,N 分别为PD ,AD 的中点.(1)求证:平面CMN ∥平面P AB ; (2)求三棱锥P ABM 的体积.解:(1)证明:∵M ,N 分别为PD ,AD 的中点, ∴MN ∥P A ,又MN ⊄平面P AB ,P A ⊂平面P AB , ∴MN ∥平面P AB .在Rt △ACD 中,∠CAD =60°,CN =AN , ∴∠ACN =60°.又∠BAC =60°,∴CN ∥AB . ∵CN ⊄平面P AB ,AB ⊂平面P AB , ∴CN ∥平面P AB . 又CN ∩MN =N , ∴平面CMN ∥平面P AB .(2)由(1)知,平面CMN ∥平面P AB ,∴点M 到平面P AB 的距离等于点C 到平面P AB 的距离.∵AB =1,∠ABC =90°,∠BAC =60°,∴BC =3,∴三棱锥P ABM 的体积V =V M P AB =V C P AB =V P ABC =13×12×1×3×2=33.B 级1.如图,四棱锥P ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB =AD =AC =3,P A =BC =4,M 为线段AD 上一点,AM =2MD ,N 为PC 的中点.(1)求证:MN ∥平面P AB ; (2)求四面体N BCM 的体积. 解:(1)证明:由已知得AM =23AD =2.取BP 的中点T ,连接AT ,TN , 由N 为PC 的中点知TN ∥BC , TN =12BC =2.又AD ∥BC ,故TN 綊AM ,四边形AMNT 为平行四边形,于是MN ∥AT . 因为AT ⊂平面P AB ,MN ⊄平面P AB , 所以MN ∥平面P AB .(2)因为P A ⊥平面ABCD ,N 为PC 的中点,所以N 到平面ABCD 的距离为12P A .取BC 的中点E ,连接AE .由AB =AC =3,得AE ⊥BC ,AE =AB 2-BE 2= 5. 由AM ∥BC 得M 到BC 的距离为5, 故S △BCM =12×4×5=2 5.所以四面体N BCM 的体积V N BCM =13×S △BCM ×P A 2=453.2.如图所示,几何体E ABCD 是四棱锥,△ABD 为正三角形,CB =CD ,EC ⊥BD . (1)求证:BE =DE ;(2)若∠BCD =120°,M 为线段AE 的中点,求证:DM ∥平面BEC . 证明:(1)如图所示,取BD 的中点O ,连接OC ,OE . ∵CB =CD ,∴CO ⊥BD . 又∵EC ⊥BD ,EC ∩CO =C ,∴BD⊥平面OEC,∴BD⊥EO.又∵O为BD中点.∴OE为BD的中垂线,∴BE=DE.(2)取BA的中点N,连接DN,MN.∵M为AE的中点,∴MN∥BE.∵△ABD为等边三角形,N为AB的中点,∴DN⊥AB.∵∠DCB=120°,DC=BC,∴∠OBC=30°,∴∠CBN=90°,即BC⊥AB,∴DN∥BC.∵DN∩MN=N,BC∩BE=B,∴平面MND∥平面BEC.又∵DM⊂平面MND,∴DM∥平面BEC.。
8.5.3 平面与平面平行课件ppt

又AB1∥C1D,∴PM∥C1D.
又PM⊄平面C1BD,C1D⊂平面C1BD,
∴PM∥平面C1BD.
同理MN∥平面C1BD.
又PM∩MN=M,
∴平面PMN∥平面C1BD.
探究二
面面平行性质定理的应用
例2如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线
PB,PD分别与α,β相交于点A,B和C,D.
D.平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行
或相交
答案 CD
解析 如图①,在平面α内作α,β交线的无数条平行线,可知A,B错误;
对C,由题意可知AB∥β,BC∥β,AB∩BC=B,由面面平行的判定定理可知
α∥β,C正确;
对D,参考选项C的解析,假设α内有一个点位于点A处,而其余点均位于直线
所以PQ∥平面CBE.
(方法二)如图②,连接AC,则Q∈AC,且Q是AC的中点.
因为P是AE的中点,所以PQ∥EC.
因为PQ⊄平面CBE,EC⊂平面CBE,
所以PQ∥平面CBE.
方法点睛 (1)线线、线面、面面间的平行关系的判定和性质,常常是通过
线线关系、线面关系、面面关系的相互转化来表达的,因此在证明有关问
4
3
15
∴ = ,∴5 = ,∴CD= 4 ,
15 27
∴PD=PC+CD=3+ 4 = 4 .
反思感悟 证明线线平行的方法
(1)定义法:在同一个平面内没有公共点的两条直线平行.
(2)平行线的传递性:平行于同一条直线的两条直线平行.
∥
(3)线面平行的性质定理: ⊂
⇒a∥b,应用时题目条件中需有线面平行.
高中数学课件:直线、平面平行的判定与性质

(2)连接FH,OH, ∵F,H分别是PC,CD的中点,∴FH∥PD. ∵PD⊂平面PAD,FH⊄平面PAD,∴FH∥平面PAD. 又∵O是AC的中点,H是CD的中点,∴OH∥AD, 又∵AD⊂平面PAD,OH⊄平面PAD, ∴OH∥平面PAD. 又FH∩OH=H,∴平面OHF∥平面PAD. 又∵GH⊂平面OHF,∴GH∥平面PAD.
的角为 60°,转化为三角形的一个角有关的问题 还缺少所需要用的三角形,可连接 AD,取 AD 的中 差什么 点 M,连接 ME,MF,得三角形 MEF,利用平行 找什么 关系可找到 ME 与 MF 所成的角,然后利用余弦定 理求解即可
[解题方略] 证明面面平行的常用方法
(1)面面平行的定义,即证两个平面没有公共点(不常用); (2)面面平行的判定定理:如果一个平面内有两条相交直线 都平行于另一个平面,那么这两个平面平行(主要方法); (3)利用垂直于同一条直线的两个平面平行(客观题常用); (4)如果两个平面同时平行于第三个平面,那么这两个平面 平行(客观题常用); (5)利用“线线平行”“线面平行”“面面平行”的相互转 化进行证明.
所以四边形BDC1D1为平行四边形, 所以BD1∥C1D. BD1⊄平面AC1D,C1D⊂平面AC1D, 所以BD1∥平面AC1D, 又因为A1B∩BD1=B, 所以平面A1BD1∥平面AC1D.
2.如图,四棱锥P-ABCD中,AD∥BC,AB=BC
=
1 2
AD,E,F,H分别为线段AD,PC,CD的
考法(二) 直线与平面平行性质定理的应用 [例2] 如图所示,四边形ABCD是平行四 边形,点P是平面ABCD外一点,M是PC的中 点,在DM上取一点G,过G和AP作平面交平面 BDM于GH. 求证:AP∥GH.
高中数学课件两个平面平行的判定与性质ppt课件.优秀文档PPT

定义
如果两个平面有公共点,它们就相交于一条过该公共点的直线,就称这两个平面相交.
提问:能否加上某些条件,从而由“线线平行”推出“面面平行”。
形式:讲述、提问、讨论
返回
过程分析 ——设计思路
问题: (1)若两条直线平行,则分别经过这两条直线的
(2)平面 BC CB内的直 BC 和 线 BC有什么关系?为
(3)若AA12,直A线 A和平A面 B所 C 成 NhomakorabeaC
3
的角6是 0,则两个平A行 B和 C平面A 2
B
ABC的距离是多少?
4C
1
A
B
课时小结
a
1.两个平面平行的性质
(1)一个结论 / /,a a/ /
面面平行
线面平行
(2)性质定理a/,/ba//b
②一条直线和两个平行平面相交,则此直线和两个平
面成等角;
③一条直线和两个平面成等角,则此两个平面平行;
④夹在两个平行平面间的两条线段长相等,那么这两
条线段平行.
A1 B2 C3 D4
巩固与拓展
3且.一不个为平零面,则上这不两同个的平三面点到另一个平面的距离( B相等)
A. 平行
B. 相交
C. 平行或重合
9.5.2两个平面平行的判定和性质
珲春一中 崔星
复习与引入
1.两个平面的位置关系
两个平面的位置关系只有两种 (1)两个平面平行——没有公共点 (2)两个平面相交——有一条公共直线.
l
符号表示 //
l
2.两个平面平行的判定
(1)判定定理:如果一
个平面内有两条相交直线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
γ
a
b
α
βБайду номын сангаас
举例
例1 求证: 夹在两个平行平面间的
平行线段相等.(证明略)
A
D
B
C
例2如图, // , AB // CD,且A,C ,
B,D.
求证:AB CD.
AC
证 明 :因 为AB // CD, B D 所 以 过AB,CD可 作 平 面, 且 平 面与 平 面和分 别 相 交 于AC和BD. 因 为 // , 所 以BD // AC . 因 此 , 四 边 形ABCD是 平 行 四 边 形. 所 以, AB CD
小结
1. 复习平面与平面平行的概念 及判定 2. 学习并掌握平面与平面平行 的性质
作业
课本第61页练习 习题2.2 A组7题,8题
平面与平面 平行的性质
引入
1、什么叫两平面平行?
2、两平面平行的判定定理? 一个平面内的两条相交直线与另一个平面 平行,则这两个平面平行.
3、推论: 如果一个平面内的两条相交直线分别
平行于另一个平面内的两条直线,那么这 两个平面平行.
平面与平面平行的性质
若 // ,且 a,则与 的位置关系如何?
(A)1种 (B) 2种 (√C)3种 (D)4种
举例
例2 如图,设AB、CD为夹在两个平行
平面 之间的线段,且直线AB、CD为异面直
线,M、P 分别为AB、CD 的中点,
求证:直线MP // 平面 .
A
C
NP
M
D
B
证 明: 连 接BC, 设 其 中 点 为N, 连 接MN,NP,MP 在BCD中 ,NP//BD, NP//平 面 在BCA中 ,NM//AC, NM// 平 面 平 面 // 平 面 NM // 平 面 NM与NP相 交 于 点N 平 面PNM // 平 面 直 线MP // 平 面
设 b,则直线a、b的位置 关系如何?为什么?
平面与平面平行性质
性质定理 如果两个平行平面同时和 第三个平面相交, 那么它们 的交线平 行.
αa
β
b
γ
练习 (1)设 // ,A,过点A作直线
l // ,则l与的位置关系如何?为什 么?
αA l
β
(2) 若平面α、β都与平面γ相交,且交 线平行,则α∥β吗?
归纳
两个平面平行的其它性质
性质:夹在两个平行平面间的平行 线段相等.
性质:经过平面外一点有且只有一 个平面和已知平面平行.
练习
1. 经过平面外两点可作该平面的平行平 面的个数为( )
(A) 0 (B) 1 (√C) 0或1 (D) 1或2
2. 平面M∥平面N,直线a M,直线b N, 下面四种情形: (1)a ∥ b (2)a ⊥ b (3)a与b异面 (4)a与b相交 其中可能出现的情形有 ( )
