第五节曲线的凹凸性拐点与渐近线培训资料
合集下载
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线、函数作图

定义
设有曲线段 y = f ( x ) , x ∈ ( a , b ) ,
若函数 f 在 (a , b) 上为凸函数(凹函数) 即对于其上任 上为凸函数(凹函数) ,即 , 上方(或 何两点 A, B , 弦 AB 总位于所夹曲线弧 AB 的 上方 或 向下凸(或向上凸)。 下方 ),则称曲线段 y = f ( x ) 在 (a , b) 内向下凸 或向上凸 。 ,
y
y = f ( x)
A
o a x1
D B
C
x
x2 b x
y
A
D y = f ( x) B
C
x2 b x
5
向下凸
o a x1 x 向上凸
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图 函数的凹凸与曲线的凸向、
定理 6
内可导, 设函数 f 在区间 I 内可导,且导函数 f ′( x )
的拐点, (3)若 ( x0 , f ( x0 )) 是曲线 y = f ( x ) 的拐点, 且 f ′′( x ) 连续, 反之未必。 在 点 x0 连续,则 f ′′( x0 ) = 0 ,反之未必。
例如: 例如: f ( x ) = x 4 , f ′′( x ) = 12 x 2 ,有 f ′′(0) = 0 ,但 (0,0)不是拐点。 不是拐点。
14
2.8.3-5 函数的凹凸与曲线的凸向、拐点和渐近线及函数作图 函数的凹凸与曲线的凸向、
3、斜渐近线 、
f ( x) lim 若 = a, x→∞ x ( 或 x → +∞ )
( 或 x → −∞ )
x→∞ ( 或 x → +∞ ) ( 或 x → −∞ )
lim [ f ( x ) − ax ] = b ,
曲线的渐近线

2若在a, b内,f x 0,则f x在a, b上的图形是凸的。
证明 对于(1),设 x1, x2 a, b, 且 x1 x2 ,
记 x0
x1 x2 , 2
并记
x2 x0 x0 x1 h,
则 x2 x0 h, x1 x0 h,
lim
x x0
x3
x2
x1
x
3 0
x
2 0
x0
1
所以该曲线既无水平渐近线,
也无铅直渐近线。
5 f 1 32 , f 1 16 ,
3 27 3 27 f (1) 0 得到函数图形上三个点:
1 , 32 3 27
x
x
x
则y C是 函 数y f ( x)的 一 条 水 平 渐 近 线
(2)、垂直渐近线
若 lim f ( x) (或 lim f ( x) ;lim f ( x) )
xx0 0
x x0
xx0 0
则x x0是函数y f ( x)的一条铅直渐近线。
第五节 曲线的凹凸和函数作图
C
B
D A
a
b
弧ACB与弧ADB的凹向不同。
1
1.凹凸性的定义
f x1 f x2
2
f x1
f
x1
2
x2
f
x2
f
x1
2
x2
f x1 f x2
f x1 2 f x2
例1. 画出y x 3 x 2 x 1的图形.
曲线的凹凸性与拐点及图象

注意:若 f ( x0 ) 不存在,点 ( x0 , f ( x0 )) 也可能
是连续曲线 y f ( x)的拐点.
练习:讨论曲线 y (x 1)3 x5 的凹凸性与拐点.
解 函数的定义域为 (,) .
由于
y
x
8 3
5
x3
,
y
8 3
5
x3
5 3
2
x3
,
y
40 9
x
2 3
10 9
1
x3
10 9
4x
3
练习: 作函数 (x)
1
x2
e2
的图形.
2
解 D : (,), W : 0 ( x) 1 0.4.
2
偶函数,图形关于y轴对称.
( x)
x
x2
e 2,
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
2
令 ( x) 0, 得驻点 x 0,
令 ( x) 0, 得特殊点 x 1, x 1.
例3 作函数 f ( x) x3 x2 x 1 的图形.
解 D : (,), 无奇偶性及周期性.
f ( x) (3x 1)( x 1), f ( x) 2(3x 1). 令 f ( x) 0, 得驻点 x 1 , x 1.
3 令 f ( x) 0, 得特殊点 x 1 .
x (,3) 3 (3,2) 2 (2,0) 0 (0,)
f ( x)
0 不存在
f (x)
0
f (x)
拐点
(3, 26) 9
极值点
3
间 断 点
补充点 : (1 3,0), (1 3,0);
是连续曲线 y f ( x)的拐点.
练习:讨论曲线 y (x 1)3 x5 的凹凸性与拐点.
解 函数的定义域为 (,) .
由于
y
x
8 3
5
x3
,
y
8 3
5
x3
5 3
2
x3
,
y
40 9
x
2 3
10 9
1
x3
10 9
4x
3
练习: 作函数 (x)
1
x2
e2
的图形.
2
解 D : (,), W : 0 ( x) 1 0.4.
2
偶函数,图形关于y轴对称.
( x)
x
x2
e 2,
(
x)
(
x
1)(
x
1)
e
x2 2
.
2
2
令 ( x) 0, 得驻点 x 0,
令 ( x) 0, 得特殊点 x 1, x 1.
例3 作函数 f ( x) x3 x2 x 1 的图形.
解 D : (,), 无奇偶性及周期性.
f ( x) (3x 1)( x 1), f ( x) 2(3x 1). 令 f ( x) 0, 得驻点 x 1 , x 1.
3 令 f ( x) 0, 得特殊点 x 1 .
x (,3) 3 (3,2) 2 (2,0) 0 (0,)
f ( x)
0 不存在
f (x)
0
f (x)
拐点
(3, 26) 9
极值点
3
间 断 点
补充点 : (1 3,0), (1 3,0);
高等数学--45曲线凸性、拐点与渐近线-精品文档
)存在且连续 , 证: f (x) 二阶可导 , f(x
则 f ( x ) [ f ( x ) ] 在 x 两边变 , 0
f ( x ) 在 x 取得极值 , 由可导函数取极值的条件. 0
又 ( x ,f ( x ) ) 是拐点 , 0 0
(x f . 0) 0
在 ( 0 , ) 内 , y 0 ,曲线在 [ 0 , ) 上是凸的 .
3 点 ( 0 , 0 ) 是曲线 y x 的拐点 .
9
信息学院
考研题欣赏 (2019年3,4)设
罗捍东
f( x )xx ( 1 ) ,则
(A)x=0是f(x)的极值点,但(0,0)不是曲线y=f(x)的拐点。 (B)x=0不是f(x)的极值点,但(0,0)是曲线y=f(x)的拐点。 (C)x=0是f(x)的极值点,且(0,0)是曲线y=f(x)的拐点。
3
信息学院
2 3 y x , y 6 x , 解:
罗捍东
3 例1:判断曲线 yx 的凹凸性 .
当 x0 时,y 0 ,
曲线 在 ( , 0 ] 为凸的;
0 y , 当 x0 时, 曲线 在 [ 0 , ) 为凹的;
(0,0)是曲线由凸变凹的分界 点 . 注意到, 点
信息学院
4.5.1 曲线凸性与拐点
罗捍东
C
B
A
o
x
yf( x )
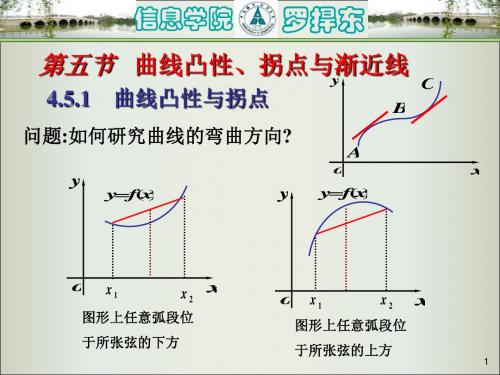
第五节 曲线凸性、拐点与渐近线 y
问题:如何研究曲线的弯曲方向?
y
yf( x )
y
o
x1
x2 x
图形上任意弧段位 于所张弦的下方
o x1
x2
x
3-5 凹凸性 拐点.渐近线

0
0
f ( x ) 递增
y 0
f ( x ) 递减
y 0
机动
目录
上页
下页
返回
结束
例1. 判断曲线
解: 函数的定义域为
的凹凸性.
1 y , x 1 y 2 x
所以在函数的定义域 由定理1知 曲线
1 内,y 2 0 x
是凸的.
机动
目录
上页
下页
2 x 2 3x b lim [ f ( x) x] lim 2 x x x 2 x 3
y x 2 为曲线的斜渐近线 . 无水平渐近线 .
机动 目录 上页 下页 返回 结束
y 0是曲线的水平渐近线
1 x lim +ln(1+e ) = x 0 x
x 0是曲线的垂直渐近线
机动
目录
上页
下页
返回
结束
1 例3 求曲线y=f(x)= +ln(1+e x )的渐近线 x f ( x) 1 ln(1+e x ) lim 2 + 考虑斜渐近线. lim x x x x x
第五节
第三章
曲线的凹凸性,拐点与渐近线
一、曲线的凹凸性 二、曲线的拐点 三、渐近线
机动
目录
上页
下页
返回
结束
1、曲线凹凸性的概念
定义 . 设函数 在区间 I 上连续 ,
(1) 若恒有
图形是凹的; (2) 若恒有
B
则称
则称
A 图形是凸的 .
yy
oo
x1 x x1 x x1x1 2 2x2x2 x x 2 2
§4.5 曲线的凹向、拐点与渐近线

15/25
2.1、 2.1、渐近线的定义 若曲线y=f(x)上的动点 沿曲线无限远离坐标原 上的动点P沿曲线无限远离坐标原 若曲线 上的动点 点时,该点P与某条定直线 的距离趋于零, 与某条定直线L的距离趋于零 点时,该点 与某条定直线 的距离趋于零,则称该 定直线L为曲线 为曲线y=f(x)的一条渐近线. 的一条渐近线. 定直线 为曲线 的一条渐近线 2.2、 2.2、分类 ⑴水平渐近线 (平 于 轴 渐 线 行 x 的 近 ) 如 果 lim f (x) = b或lim f (x) = b (b为 数 常 )
x = 0是不可导点, y′, y′′均不存在 .
但在( −∞ ,0)内, y′′ > 0, 曲线在 ( −∞ ,0 ]上是凹的 ;
y
y =3 x
在(0,+∞ )内, y′′ < 0,
曲线在[0,+∞ )上是凸的.
o
x
∴ 点(0,0)是曲线 y = 3 x的拐点.
微积分四 微积分四⑤
10/25
xe 的凹向区间及拐点. 例5.求曲线 y = 的凹向区间及拐点.
y
y = f (x)
y
C
B
A
x
y = f (x)
o
y
o
x1
x2 x
o
x1
x2
x
曲线向上弯曲的弧段 位于其上任一点处切 上凹. 线的上方, 称为上凹 线的上方 称为上凹
微积分四 微积分四⑤
曲线向下弯曲的弧段 位于其上任一点处切 线的下方,称为下凹. 称为下凹 线的下方 称为下凹
4/25
1.2、 1.2、曲线凹向的定义 定义4.3 若在某个区间内 曲线弧位于其上任一 若在某个区间内, ⑴定义 点的切线上方, 则称曲线在该区间内是上 点的切线上方 则称曲线在该区间内是上凹的; 若 曲线弧位于其上任一点的切线下方, 曲线弧位于其上任一点的切线下方 则称曲线在该 区间内是下 区间内是下凹的. 简称凹 也称下凸 下凸; 简称凸 也称上凸 上凸. 注: 上凹简称凹, 也称下凸 下凹简称凸, 也称上凸 y = f (x) ⑵图形分析 B y y y= f (x) B =
凹凸性、渐近线、作图资料

[解] 定义域:(,), 是偶函数.
因 为 lim e x2 0, 所 以 直 线y 0 x
是 水 平 渐 近 线.
y 2xex2
y 2ex2 (2x2 1)
令 y 0 驻点:x 0
令 y 0 x 1
10/15/2019
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x
(,
1 )
5
y '' -
y凸
1
5
0
8 25
拐点
(1 , ) 5
+
凹
在 x 1 两侧 y ''符号发生改变,则(1 , 8 )是拐点.
5
5 25
1
例3.求曲线 y x3 的拐点.
1
解:函数 y x3 的定义域为 (, )
函数的凹凸性、渐近线 与作图
一、函数的凹凸性 二、曲线的渐近线 三、函数作图
10/15/2019
1
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
f (x2 )
则称f (x)在该区间上的图形是凸的.
10/15/2019
4
凹曲线的一阶导数变化规律:
若 f (x)是凹函数,则 f (x)单调增加;
10/15/2019
5
凸曲线的一阶导数变化规律:
若 f (x)是凸函数,则 f (x)单调减少.
10/15/2019
6
因 为 lim e x2 0, 所 以 直 线y 0 x
是 水 平 渐 近 线.
y 2xex2
y 2ex2 (2x2 1)
令 y 0 驻点:x 0
令 y 0 x 1
10/15/2019
令 y '' 0, 得 x 1 , 没有二阶导数不存在的点 列表如下:5
x
(,
1 )
5
y '' -
y凸
1
5
0
8 25
拐点
(1 , ) 5
+
凹
在 x 1 两侧 y ''符号发生改变,则(1 , 8 )是拐点.
5
5 25
1
例3.求曲线 y x3 的拐点.
1
解:函数 y x3 的定义域为 (, )
函数的凹凸性、渐近线 与作图
一、函数的凹凸性 二、曲线的渐近线 三、函数作图
10/15/2019
1
一、函数的凹凸性
若在某区间内,曲线上每一点的切线都位 于该曲线的下方,则称曲线在该区间内是凹的; 若曲线上每一点的切线都位于该曲线的上方,
则称曲线在该区间内是凸的.
(a)中曲线上任意两点的割线在曲线的上方
f (x2 )
则称f (x)在该区间上的图形是凸的.
10/15/2019
4
凹曲线的一阶导数变化规律:
若 f (x)是凹函数,则 f (x)单调增加;
10/15/2019
5
凸曲线的一阶导数变化规律:
若 f (x)是凸函数,则 f (x)单调减少.
10/15/2019
6
高等数学-曲线的凹凸性及拐点

曲线的凹凸性和拐点的判别
例3 求曲线 =
解
3
的凹凸区间和拐点.
定义域为(−∞, +∞).
′
=
1
3
3 2
,
″
=−
2
39Leabharlann 2. = 0时, ′ ,′′都不存在.
+
凹
0
凸
由表可知,曲线的凹区间为(−∞, 0) ,凸区间为(0, + ∞),
曲线的拐点为 (0,0).
9
″ () = 12 2 − 30 + 12 = 6(2 − 1)( − 2),
令 ″ ()
= 0,得1 =
+
凹
1
,2
2
0
= 2.
凸
0
+
凹
1
由表可知,曲线的凹区间为(−∞, )和(2, +∞),凸区间为
2
1
1 7
( , 2),曲线的拐点为( , )和(2, −5).
2
2 16
8
02
微分中值定理及导数的应用
第6讲
曲线的凹凸性及拐点
本节内容
01 曲线的凹凸性和拐点的定义
02 曲线的凹凸性和拐点的判别
2
01 曲线的凹凸性和拐点的定义
定义3.2
设函数 = ()在开区间(, )内可导,在该
区间内如果曲线位于其任何一点切线的上方,
那么称此曲线在区间(, )内是凹的,区间
区间(, )内具有二阶导数.
(1)在(, )内,若 ″ () > 0,那么曲线 = ()在
[, ]上是凹的.
(2)在(, )内,若 ″ () < 0,那么曲线 = ()在
曲线的凹凸性和拐点、函数图像的描绘

高等数学
曲线的凹凸性和拐点、函数图 像的描绘
一、曲线的凹凸性与拐点 1.曲线凹凸性的定义及其判定
首先观察图3-9所示的两条曲线。
图3-9
如图3-9所示,有一类曲线向上弯曲,它在任何点处的切 线总位于曲线的下方;另一类曲线向下弯曲,它在任何点处的 切线总位于曲线的上方,由此我们给出关于曲线凹凸的定义:
x x0
则称直线 x x0 为曲线 y f (x)的垂直渐近线。
其一般步骤如下:
2.函数图像的描绘
(1)确定函数 y f (x) 的定义域、间断点及函数所具有的某些特 性(如奇偶性、周期性等); (2)求出函数的一阶导数 f (x) 和二阶导数 f (x),解方程
f (x)=0,f (x) 0 在定义域内的全部实根及 f (x) 和 f (x)不存在的 点,应用这些根和点,将函数的定义域划分为若干个子区间; (3)列表讨论 f (x)和 f (x) 在(2)中所得各子区间内的符号,由 此确定函数的单调性、极值、曲线的凹凸性和拐点; (4)如有渐近线,求出渐近线,并确定其他变化趋势; (5)求辅助点,如曲线与坐标轴的交点等; (6)在直角坐标系中,根据上面讨论,描点作图。
例2 求曲线 y x4 2x3 1 的凹凸点区间和拐点。 解 函数 y x4 2x3 1 的定义域为( , )
y 4x3 6x2 y 12x2 12x 12x(x 1) , 令 y 0,得 x 0 和 x 1。 列表讨论如下:
x y
曲线
( ,0) +
0 0 拐点 (0,1)
如果将定理中的区间改为其他区间,结论仍然成立。
例1 判定曲线 y x3 的凹凸性。 解 函数的定义域为 ( , ) ,y 3x2,y 6x
(当 x 0 时,y 0 ,故曲线在 ( ,0] 内是凸的;当 x 0 时,y 0,股曲线在 [0 , ) 内是凹的;当x 0时,y 0。 点(0,0)是曲线 y x3由凸变凹的分界点(图3-11)
曲线的凹凸性和拐点、函数图 像的描绘
一、曲线的凹凸性与拐点 1.曲线凹凸性的定义及其判定
首先观察图3-9所示的两条曲线。
图3-9
如图3-9所示,有一类曲线向上弯曲,它在任何点处的切 线总位于曲线的下方;另一类曲线向下弯曲,它在任何点处的 切线总位于曲线的上方,由此我们给出关于曲线凹凸的定义:
x x0
则称直线 x x0 为曲线 y f (x)的垂直渐近线。
其一般步骤如下:
2.函数图像的描绘
(1)确定函数 y f (x) 的定义域、间断点及函数所具有的某些特 性(如奇偶性、周期性等); (2)求出函数的一阶导数 f (x) 和二阶导数 f (x),解方程
f (x)=0,f (x) 0 在定义域内的全部实根及 f (x) 和 f (x)不存在的 点,应用这些根和点,将函数的定义域划分为若干个子区间; (3)列表讨论 f (x)和 f (x) 在(2)中所得各子区间内的符号,由 此确定函数的单调性、极值、曲线的凹凸性和拐点; (4)如有渐近线,求出渐近线,并确定其他变化趋势; (5)求辅助点,如曲线与坐标轴的交点等; (6)在直角坐标系中,根据上面讨论,描点作图。
例2 求曲线 y x4 2x3 1 的凹凸点区间和拐点。 解 函数 y x4 2x3 1 的定义域为( , )
y 4x3 6x2 y 12x2 12x 12x(x 1) , 令 y 0,得 x 0 和 x 1。 列表讨论如下:
x y
曲线
( ,0) +
0 0 拐点 (0,1)
如果将定理中的区间改为其他区间,结论仍然成立。
例1 判定曲线 y x3 的凹凸性。 解 函数的定义域为 ( , ) ,y 3x2,y 6x
(当 x 0 时,y 0 ,故曲线在 ( ,0] 内是凸的;当 x 0 时,y 0,股曲线在 [0 , ) 内是凹的;当x 0时,y 0。 点(0,0)是曲线 y x3由凸变凹的分界点(图3-11)
曲线的凹凸性、拐点与渐近线

x1 x2 f ( x 1 ) f ( x2 ) f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凸的(凸弧)。 x x y y f( )
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在; x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在, x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1:设 f ( x )在区间 I 上连续,如果对于 I 上任意两点 x1 , x2, x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧);
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断,且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
如果恒有
1
2
f ( x1 ) f ( x2 ) f ( x1 ) 2 x x2 f( 1 ) 2 x1 x2 2
f ( x2 )
2013-9-12 9
§2.4.2 曲线的凹凸性、拐点与渐近线
注 如果 f ( x) (1)lim 不存在; x x f ( x) (2)lim a , 但 lim[ f ( x ) ax ]不存在, x x x 则可以判断y f ( x )不存在斜渐近线。
2013-9-12
§2.4.2 曲线的凹凸性、拐点与渐近线
1.函数的凹凸性与拐点 定义1:设 f ( x )在区间 I 上连续,如果对于 I 上任意两点 x1 , x2, x1 x2 f ( x 1 ) f ( x2 ) 恒有 f( ) , 2 2 则称 f ( x )在 I 上的图形是(向上)凹的(凹弧);
2013-9-12
13
§2.4.2 曲线的凹凸性、拐点与渐近线
x2 例8 求曲线 f ( x ) 的渐近线。 x 1
2013-9-12
14x x 来自则直线 y C 是曲线 y f ( x )的水平渐近线。
(2)垂直渐近线 若曲线 y f ( x )在点 x0处间断,且 lim f ( x ) 或 lim f ( x ) ,
x x0 x x0
则直线 x x0是曲线 y f ( x )的垂直渐近线。 f ( x) (3)斜渐近线 若 lim a , lim[ f ( x ) ax ] b, x x x 则直线y ax b是曲线 y f ( x )的斜渐近线。
3.5函数的凹凸性、曲线的拐点及渐近线

o
x
图形上弧段总是位于任
意切线的上方……凹弧
y
y f (x)
方,则称曲线弧AB是向上凹的或
称凹弧(向上凸的,或称凸弧), o
x
记为“∪”(“∩”)。
图形上弧段总是位于任 意切线的下方……凸弧
分析:
y
y f (x) B
y f (x)
y
B
A A
oa
bx
f ( x) 递增 y 0
oa
bx
f ( x) 递减 y 0
例8
描绘函数
y
4
x 1
x2
2的图形
解:1)定义域为 ,0 0,
2)
y
4x
x3
2
,
由y 0,得x 2
y
8x 3,
x4
由y 0得x
3;
3)列表确定函数及曲线的特性
3)列表确定函数及曲线的特性
x ,3 3 3,2 2 2,0
y
0
y
0
y f x
拐点 3, 26
9
极小值 3
1
有垂直渐近线
x =-1,x =1
3.曲线的斜渐近线
若 lim f x a, lim f x ax b ,则直线
x x
x
y = ax +b 是曲线 y = f (x)的斜渐近线.
例7
求曲线
y
x3 x2 2x 3
的斜渐近线.
x3
解:因为 lim f x lim x2 2x 3 1, 所以a 1
改变弯曲方向的点——拐点;
凹凸性的判定.
2.应用
拐点的求法.
1.水平渐近线
二、曲线的渐近线
曲线的凹凸与拐点概述课件

几何意义
对于凹函数,其图像在任何一点处切线的斜率都大于0;对于凸函数,其图像在任何一点 处切线的斜率都小于0。
应用
在经济学、生物学、工程学等领域中,凹函数和凸函数都有广泛的应用。例如,在经济学 中,凹函数可以描述成本、收益等经济变量的变化规律;在生物学中,凸函数可以描述种 群数量、资源分配等生物变量的变化规律。
凸
对于给定曲线y = f(x),如果在区间(a,b)内,对于任意 x1<x2<x3,都有f(x2) > f(x1) + (x2 - x1) * (x3 - x2) / (x3 x1),则称f(x)在区间(a,b)内是凸函数。
拐点的定义
• 拐点:对于给定曲线y = f(x),如果存在点x0,使得f'(x0) = 0,且在x0的左侧和右侧,f'(x)的符号相反,则称x0为拐点。
二次函数
在极值点处有拐点,因为极值点 处函数的单调性发生改变。
三角函数
在正弦函数和余弦函数的周期性 变化过程中,每一个周期内都有
两个拐点。
拐点的应用
经济预测
利用拐点预测经济周期的转换点。
科学计算
在求解函数的极值点和最值点时,拐点是一个重 要的参考指标。
工程设计
在机械工程中,拐点被用来确定机构的临界状态 和设计参数。
04 曲线凹凸与拐点的实际意义
CHAPTER
经济中的应用
股价走势分析
通过分析股票价格的拐点,可以 判断股票价格的未来趋势,为投 资者提供参考。
经济学模型
拐点在经济学模型中可以用于描 述经济变量的转折点或变化趋势 的转折点。
自然科学中的应用
生态学
拐点可以描述生态系统中的转折点, 如气候变化对生物多样性的影响等。
对于凹函数,其图像在任何一点处切线的斜率都大于0;对于凸函数,其图像在任何一点 处切线的斜率都小于0。
应用
在经济学、生物学、工程学等领域中,凹函数和凸函数都有广泛的应用。例如,在经济学 中,凹函数可以描述成本、收益等经济变量的变化规律;在生物学中,凸函数可以描述种 群数量、资源分配等生物变量的变化规律。
凸
对于给定曲线y = f(x),如果在区间(a,b)内,对于任意 x1<x2<x3,都有f(x2) > f(x1) + (x2 - x1) * (x3 - x2) / (x3 x1),则称f(x)在区间(a,b)内是凸函数。
拐点的定义
• 拐点:对于给定曲线y = f(x),如果存在点x0,使得f'(x0) = 0,且在x0的左侧和右侧,f'(x)的符号相反,则称x0为拐点。
二次函数
在极值点处有拐点,因为极值点 处函数的单调性发生改变。
三角函数
在正弦函数和余弦函数的周期性 变化过程中,每一个周期内都有
两个拐点。
拐点的应用
经济预测
利用拐点预测经济周期的转换点。
科学计算
在求解函数的极值点和最值点时,拐点是一个重 要的参考指标。
工程设计
在机械工程中,拐点被用来确定机构的临界状态 和设计参数。
04 曲线凹凸与拐点的实际意义
CHAPTER
经济中的应用
股价走势分析
通过分析股票价格的拐点,可以 判断股票价格的未来趋势,为投 资者提供参考。
经济学模型
拐点在经济学模型中可以用于描 述经济变量的转折点或变化趋势 的转折点。
自然科学中的应用
生态学
拐点可以描述生态系统中的转折点, 如气候变化对生物多样性的影响等。
微积分4.4曲线的凹凸性、拐点与渐近线

点和阶导数不存在的点; (3) 用(2)中求出的点将函数定义域分成若干个部分区间,
在各个部分区间内讨论二阶导数的符号, 确定曲线是否存在 拐点, 若在拐点, 求出拐点.
例2 判断曲线 y(x1)3 x5 的凸性, 并求其拐点. 解 定 义 域 为 (- ,)
15
而 y 8x5 3 5x2 3, y 10 4 x 1
x -
x
其 中 a 和 b 为 常 数 ,且 a 0 ,则称直线 y = ax + b为曲线
y =ƒ(x) 的斜渐近线. (如图)
y
αM˘•
•
Q
y=ƒ(x)
•
L:y=ax+b
o »α
x
22
分析: 如果曲线 y =ƒ(x)有斜渐近线 y = ax + b, 则由定义知,
必有
lim[f(x)ax]b 或lim [f(x)ax]b
f (x0) 0 或 f ( x0 )不存在.
但是, 若f (x0) 0或 f ( x0 )不存在时, 曲线 y f (x)
上的点 (x0, f (x0))不一定是拐点, 还必须用下面的定理判断.
13
定理4.4.3 (拐点存在的充分条件) 设函数 y = ƒ(x)在 x0 的某邻域内二阶可导 (f(x0)可 以 不 存 在 ),且f(x0)0 或 f(x0)不 存 在 ,
从而, 当 f ( x ) 存在时, 则可用二阶导数的符号来判别
曲线的凹凸性.
6
定理4.4.1 设函数 y = ƒ(x)在 I 内有二阶导数, 则
(1 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凹 的 ;
(2 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凸 的 .
在各个部分区间内讨论二阶导数的符号, 确定曲线是否存在 拐点, 若在拐点, 求出拐点.
例2 判断曲线 y(x1)3 x5 的凸性, 并求其拐点. 解 定 义 域 为 (- ,)
15
而 y 8x5 3 5x2 3, y 10 4 x 1
x -
x
其 中 a 和 b 为 常 数 ,且 a 0 ,则称直线 y = ax + b为曲线
y =ƒ(x) 的斜渐近线. (如图)
y
αM˘•
•
Q
y=ƒ(x)
•
L:y=ax+b
o »α
x
22
分析: 如果曲线 y =ƒ(x)有斜渐近线 y = ax + b, 则由定义知,
必有
lim[f(x)ax]b 或lim [f(x)ax]b
f (x0) 0 或 f ( x0 )不存在.
但是, 若f (x0) 0或 f ( x0 )不存在时, 曲线 y f (x)
上的点 (x0, f (x0))不一定是拐点, 还必须用下面的定理判断.
13
定理4.4.3 (拐点存在的充分条件) 设函数 y = ƒ(x)在 x0 的某邻域内二阶可导 (f(x0)可 以 不 存 在 ),且f(x0)0 或 f(x0)不 存 在 ,
从而, 当 f ( x ) 存在时, 则可用二阶导数的符号来判别
曲线的凹凸性.
6
定理4.4.1 设函数 y = ƒ(x)在 I 内有二阶导数, 则
(1 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凹 的 ;
(2 ) x (a ,b ),均 有 f(x ) 0 , yf(x )在 (a ,b )上 是 凸 的 .
第五节曲线的凹凸性拐点与渐近线

例3 讨论曲线 f (x) x4 2x3 1 拐点.
解 f ( x)的定义域为(,)
f ( x) 4x3 6x2
f ( x) 12x( x 1)
令 f ( x) 0 得 x 0, x 1
x
f ( x) f (x)
( ,0) 0 (0,1)
0
拐点(0,1)
1 (1, )
0
拐点(1,0)
x0
x0
故有垂直渐近线 x 0.
练习 求曲线
y
(1
1 1
x)e x
的渐近线.
解
(3)
lim
f (x)
lim(1
1
1
)e
1 x
e0
x x
x
x
1 1
lim [ f ( x) ex ] lim[(1 x)e x ex]
x
x
1 1
1 1
1 1
lim[e x x(e x e)] e l i m x(e x e)
例4 讨论曲线 f ( x) ( x 1)3 x5 的凹凸性与拐点 解 f ( x)的定义域为(,)
f
( x)
8
5
x3
5
2
x3
33
令
f
(
x)
0
得
x
1 4
f ( x) 10 4x 1 9 3x
另 f (0) 不存在
x ( ,0) 0
1 (0, )
4
1 4
( 1 , ) 4
f (x)ຫໍສະໝຸດ 不存在 利用凹凸性证明不等式
例2
试证明0
x
时,有
sinx 2
x
.
曲线的凹凸性与拐点教案12

(2)如果在(a,b)内f″(x)<0,那么曲线在[a,b]上的图形是凸的。
该定理对于其他类型区间也成立。
一、曲线凹凸性定义及其判定法
定义1
设f(x)在区间I上连续,如果对I上任意两点x1,x2,恒有
那么称f(x)在I上的图象是(向上)凹的;如果恒有
那么称f(x)在I上的图象是(向上)凸的。
例2判断曲线y=x4-2x3+3的凹凸性。
教学
难点
曲线的凹凸性与拐点、简单函数图象的描绘
教学
方法
讲授法、讨论法、案例教学法
教学
准备
教师:教案
学生:预习相关知识
教学过程设计
教学内容
教师活动
学生活动
第五节曲线的凹凸性与拐点
定理
设函数f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数。
(1)如果在(a,b)内f″(x)>0,那么曲线在[a,b]上的图形是凹的;
课程名称
高等数学
年级
专业
授课教师
授课时间
学时
授课
题目
曲线的凹凸性与拐点
教学
目标
知识目标:
掌握曲线的凹凸性与拐点、简单函数图象的描绘,培养学生联系的、辩证统一的思想;培养学生解决实际问题的能力。
技能目标:
会利用高等数学的知识解决问题
素质目标:
学会用高数的思维考虑问题
教学
重点
曲线的凹凸性与拐点、简单函数图象的描绘
解y′=4x3-6x2
y″=12x2-12x=12x(x-1)
当x<0或x>1时,y″>0;当0<x<1时,y″<0。
所以曲线在区间(-∞,0)和(1,+∞)内是凹的,而在区间(0,1)内是凸的。
该定理对于其他类型区间也成立。
一、曲线凹凸性定义及其判定法
定义1
设f(x)在区间I上连续,如果对I上任意两点x1,x2,恒有
那么称f(x)在I上的图象是(向上)凹的;如果恒有
那么称f(x)在I上的图象是(向上)凸的。
例2判断曲线y=x4-2x3+3的凹凸性。
教学
难点
曲线的凹凸性与拐点、简单函数图象的描绘
教学
方法
讲授法、讨论法、案例教学法
教学
准备
教师:教案
学生:预习相关知识
教学过程设计
教学内容
教师活动
学生活动
第五节曲线的凹凸性与拐点
定理
设函数f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数。
(1)如果在(a,b)内f″(x)>0,那么曲线在[a,b]上的图形是凹的;
课程名称
高等数学
年级
专业
授课教师
授课时间
学时
授课
题目
曲线的凹凸性与拐点
教学
目标
知识目标:
掌握曲线的凹凸性与拐点、简单函数图象的描绘,培养学生联系的、辩证统一的思想;培养学生解决实际问题的能力。
技能目标:
会利用高等数学的知识解决问题
素质目标:
学会用高数的思维考虑问题
教学
重点
曲线的凹凸性与拐点、简单函数图象的描绘
解y′=4x3-6x2
y″=12x2-12x=12x(x-1)
当x<0或x>1时,y″>0;当0<x<1时,y″<0。
所以曲线在区间(-∞,0)和(1,+∞)内是凹的,而在区间(0,1)内是凸的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)式与(2)式相加得
[f( x 2 ) f( x 1 )x ] 2 ( x 1 ) 0
故 f(x2)f(x1) 从而 f (x) 单调增加.
定理4.11 设函数 f ( x)在区间(a,b)内有 二阶导数, 那么 ①如果x(a,b)时, 恒有 f(x)0,
则曲线 f ( x) 在区间(a,b) 内是凹曲线; ②如果x(a,b)时, 恒有 f(x)0,
例2
试证明
0x时,有
sin
x 2
x
.
(99年考题)
证明 f(x)sinx x 2
又 f(0)0 f()0
f(x)12cos2x1
f(x)1sinx 0 42
所以曲线是凸的
故 0x 时
f(x)sinx x 0
2 即 sin x x .
2
二.曲线的拐点 定义 曲线凹与凸的分界点称为曲线的拐点. 拐点定理 如果P(x0, f(x0))为曲线 f ( x) 的拐点,
设函数 y y(x) 由方程 ylnyxy0确定,
试判断曲线 y y(x) 在点 ( 1 , 1 ) 附近的凹凸性.
解 ylny2y10 y 1
ln y 2
1 y
y
(ln
y y 2)2
1 y(ln y 2)3
0
y y(x) 在点 ( 1 , 1 ) 附近是凸的.
利用凹凸性证明不等式
y f(x)
c是 f ( x)的间断点
P
xc是铅垂渐近线
第五节 曲线的凹凸性、拐点与渐近线
y
oa
b
x
一.曲线的凹凸性 定义1 直观定义.
注 (1)凹 凸
(2)凹也称上凹、下凸 凸也称上凸、下凹.
y
y
oa
bx o a
bx
定义2 如果在某个区间内, 曲线位于其上 任一点切线的上方, 则称该曲线在 这个区间内是凹曲线; 如果在某个区间内, 曲线位于其上 任一点切线的下方, 则称该曲线在 这个区间内是凸曲线;
则必有 f(x0)0或 f (x0) 不存在.
f(x)0 f (x)不存在
注 (1)一般来说圈中的点为 有限多个.
(2)拐点是曲线上的点,表 示拐点要用两个坐标.
例3 讨论曲线 f(x)x42x31拐点.
解 f ( x)的定义域为(,)
f(x)4x36x2
f(x)1x 2 (x1 )
令 f(x)0得 x0,x1
定义3 如果对某区间内任意两点x1, x2 有
f(x1x2)f(x1)f(x2),
2
2
则称曲线为凹曲线;
如果对某区间内任意两点x1, x2 有
f(x1x2)f(x1)f(x2),
2
2
则称曲线为凸曲线.
定理4.10 如果函数 f ( x)在区间 (a,b)内可导,
则曲线 f ( x)在区间(a,b) 内凹(凸)
则曲线 f ( x) 在区间(a,b) 内是凸曲线.
例1 讨论曲线 f(x)x42x31的凹凸性.
解 f ( x)的定义域为(,)
f(x)4x36x2
f(x)1x 2 (x1 )
令 f(x)0得 x0,x1
x
f (x) f (x)
( ,0)
(0,1)
(1, )
补充:07年考研真题10分
x
f (x) f)
(0,1) 1 0
(1, )
拐点(1,0)
例4 讨论曲线 f(x)(x1)3 x5 的凹凸性与拐点 解 f ( x)的定义域为(,)
f(x)8x53 5x32 33
令 f(x)0得 x
1 4
f(x) 10 4x1 9 3x
另 f (0)不存在
x ( ,0) 0
1 (0, )
4
1 4
( 1 , ) 4
f(x) 不存在
0
13
f (x)
(0,0)
( ,
)
4 163 16
三.曲线的渐近线 定义 如果曲线上的动点 P沿着曲线无限
地远离原点时,点 P与某一固定直线 的距离趋于零,则称该直线为曲线的 渐近线.
1.水平渐近线
渐近线 2.垂直渐近线或铅垂渐近线 3.斜渐近线
1.水平渐近线
y b是水平渐近线
y y f(x)
lim [f(x)b]0 x
P
b
或 lim [f(x)b]0 x
limf(x)b x
o xx
或 limf(x)b
x
例5
求曲线 y
1 x
的水平渐近线.
解 因 lim 1 0 水平渐近线为 y 0.
x x
2.垂直渐近线或铅垂渐近线
y
f ( x 1 ) f ( x 2 ) f ( x 2 )x 1 ( x 2 )
从而
f ( x 2 ) f ( x 1 ) f ( x 1 ) x 2 ( x 1 ) ( 1 )
f ( x 1 ) f ( x 2 ) f ( x 2 ) x 1 ( x 2 ) ( 2 )
[f() f(x 0 )x ] ( x 0 ) 0
• ••
a x0
•x
• b
所以 f(x ) f(x 0 ) f(x 0 )x ( x 0 )
故曲线为凹曲线.
(条件:曲线 f ( x), 结论: f (x) )
设 x1 x2是 (a,b) 内任意两点 曲线上过x1 处的切线: y f(x 1 ) f(x 1 )x ( x 1 )
只需证 f(x ) f(x 0 ) f(x 0 )x ( x 0 )(x x0)
设 f (x) 单调增加, 对 x(a,b)
f(x ) [f(x 0 ) f(x 0 )x ( x 0 )]
[ f ( x ) f ( x 0 ) ] f ( x 0 )x (x 0 )
f()x (x 0 ) f( x 0 )x (x 0 )
曲线上过x 2 处的切线: y f(x 2 ) f(x 2 )x ( x 2 )
因曲线
f
(
x
)
,
故
f( x ) f( x 1 ) f( x 1 )x (x 1 )
f( x ) f( x 2 ) f( x 2 )x (x 2 )
从而
f ( x 2 ) f ( x 1 ) f ( x 1 )x 2 ( x 1 )
导函数 f (x) 在区间 (a,b) 内单调增加(减少).
证 (条件: f (x) ,结论:曲线 f ( x) )
曲线: y f(x) 曲线上任一点 x 0 处的切线: y f(x 0 ) f(x 0 )x ( x 0 )即 y f(x 0 ) f(x 0 )x ( x 0 ) 只需证 f(x ) f(x 0 ) f(x 0 )x ( x 0 )(x x0)
