8-2正态总体均值的假设检验
正态总体均值的假设检验

2 用 分布
检验
下,若能求得检验统计量的 极限分布,依据它去决定临界值C.
例 1 (用例中数据,但未知)
n=10, =0.05, 0=10 t10-1(/2)=t9(0.025)=2.2622
X 10.05,S2 0.05, S 0.224 X 10 0.05 , 即未落入拒绝域为 S 10 2.262 0.160 S 10 2.262
抽取 样本
检验 假设
拒绝还是不能 拒绝H0
P(T W)=
类错误的概率, W为拒绝域
对差异进行定量的分析, 确定其性质(是随机误差 显著性 水平
还是系统误差. 为给出两 者界限,找一检验统计量T, 在H0成立下其分布已知.)
-----犯第一
一般说来,按照检验所用的统计量的分布, 分为 U 检验 用正态分布
以上检验法叫U检验法.
X ~tn 1 S/ n
0
于是当原假设 H0:μ =μ X 0 ~tn 1 S/ n
成立时,有:
X 0 P tn 1 2 S / n S 即P X 0 tn 1 n 2 S 拒绝域为 X 0 tn 1 n 2 以上检验法叫t检验法.
第八章 第二节
正态总体均值的假设检验
一、单个正态总体N(,2)均值的检验
(I) H0:μ = μ
0
H1:μ ≠ μ
0
设X1,X2, ,Xn为来自总体N(,2)的样本. 求:对以上假设的显著性水平=的假设检验. 方差2已知的情况
根据第一节例1,当原假设 H0:μ =μ , 有:
概率论与数理统计 8-2

H 0 : µ ≤ µ 0 = 225, H 1 : µ > 225,
取 α = 0.05, n = 16, x = 241.5, s = 98.725 0.6685 t0.05 (15) = 1.7531 > t = s/ n
故接受 H 0 , 认为元件的平均寿命不 大于 225小时.
n = 15,
x = 10.48, α = 0.05, s = 0.237,
x − µ 0 10.48 − 10.5 t = = t分布表 = 0.327, s/ n 0.237 / 15 查表得 tα / 2 ( n − 1) = t 0.025 (14) = 2.1448 > t = 0.327, 故接受 H 0 , 认为金属棒的平均长度 无显著变化 .
n2 = 10,
y = 79.43, s2 = 2.225,
2
且s
2 w
(10 −1)s + (10 −1)s = = 2.775, 10 + 10 − 2
2 1 2 2
查表可知 t0.05 (18) = 1.7341,
查表8.1知其拒绝域为 查表 知其拒绝域为 t ≤ − tα ( n1 + n2 − 2). x− y = −4.295, 因为 t = 1 1 sw + 10 10
某切割机在正常工作时, 例1 某切割机在正常工作时 切割每段金属棒的 平均长度为10.5cm, 标准差是 标准差是0.15cm, 今从一批产 平均长度为 品中随机的抽取15段进行测量 其结果如下: 段进行测量, 品中随机的抽取 段进行测量 其结果如下 10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2
根据第六章 第六章§ 定理四 定理四知 当H 0为真时, 根据第六章§2定理四知,
总体均数的假设检验

$number {01}
目 录
• 引言 • 假设检验的基本原理 • 总体均数的假设检验方法 • 实例分析 • 总结与展望
01 引言
目的和背景
确定样本数据是否与假设的总体均数 存在显著差异,从而对总体均数进行 假设检验。
在科学实验、统计学、医学研究等领 域广泛应用,用于评估样本数据是否 支持或拒绝关于总体均数的假设。
配对样本均数假设检验实例
总结词
配对样本均数假设检验用于比较同一组研究对象在不同条件下的均数是否存在统计学显 著性差异。
详细描述
例如,为了比较同一组患者在接受两种不同治疗措施前后的改善程度,研究者收集了患 者的基线数据和接受不同治疗措施后的数据,并计算出各自治疗组的平均改善程度。然 后,研究者使用配对样本均数假设检验来比较同一组患者在不同治疗措施下的平均改善
概念简介
假设检验是一种统计推断方法,通过 检验样本数据是否符合某个假设,从 而对总体参数进行推断。
它基于概率论原理,通过计算样本数 据与假设的总体参数之间的差异,评 估这种差异是否具有统计学上的显著 性。
02
假设检验的基本原理
假设检验的步骤
建立假设
根据研究目的,提出一个关于总 体参数的假设,通常包括零假设 和备择假设。
收集样本数据
从总体中随机抽取一定数量的样 本,并记录样本数据。
确定检验水准
选择合适的检验水准,如α和β, 以平衡第一类和第二类错误的概 率。
计算统计量
根据样本数据计算适当的统计量, 如t值、Z值或χ^2值。
假设检验的类型
1 2
3
单样本均数检验
比较一个样本均数与已知总体均数或正常值范围。
两样本均数比较
总体均值的假设检验

总体均值的假设检验一、正态总体均值的检验设n X X X ,,, 21为总体),(2σμN 的一个容量为n 的样本. 1.方差2σ已知,μ的检验——u 检验法. 当202σσ=已知时,假设检验问题:0100μμμμ≠=:;:H H . 选择检验统计量nX U /00σμ-=,当0H 成立时,)1,0(~N U .给定显著性水平α,由标准正态分布分位点的定义, 有αα=>}|{|2/u U P ,故拒绝域}{}{}|{|2/2/2/αααu U u U u U W >-<=>= ,这种利用服从正态分布的检验统计量的检验方法称为u 检验法.有时我们只关心总体的均值是否增大(或减小).比如,经过工艺改革后,产品的质量(如材料的强度)比以前是否提高,此时我们要研究的是新工艺下总体的均值μ是小于等于原来的均值0μ,还是大于0μ,即检验假设 0100μμμμ>≤:;:H H . 可以证明,在显著性水平α下,上述假设检验问题和检验假设0100μμμμ>=:;:H H 有相同的拒绝域,因此,遇到形如00μμ≤:H 的检验问题,可归结为后一个假设检验问题讨论. 类似地,形如0100μμμμ<≥:;:H H 的检验问题, 可归结为检验假设 0100μμμμ<=:;:H H .这都是单边检验问题.给定显著性水平α,求得的临界值点是上α分位点或上α-1分位点.例1 某厂生产的某种钢索的断裂强度X 服从),(2σμN ,其中40=σ(kg/cm 2),现从这批钢索中抽取容量为9的样本,测得断裂强度的平均值x 较以往正常生产的μ大20(kg/cm 2),设总体方差不变,问在1.00=α下,能否认为这批钢索质量有显著提高?解 依题意,检验假设0100μμμμ>≤:;:H H , 由于40=σ已知,选择检验统计量nX U /0σμ-=因为0H 中的μ全部都比1H 中的μ要小,从直观上看,当0H 成立时,X 的取值x 不应比μ大很多,若偏差0μ-x 过大,则拒绝0H 而接受1H .因为 0100μμμμ>=:;:H H 的拒绝域为}{αu U W >=, 故在显著性水平1.00=α下原假设的拒绝域为}{}{0nu X u U W σμαα+>=>=.本题中,9=n ,40=σ,200=-μx ,33.201.0=u , 计算U 的值33.25.1/0<=-=nx u σμ因此在显著性水平1.00=α下不能拒绝0H ,即认为这批钢索质量没有显著提高.2.方差2σ未知,μ的检验——t 检验法. 检验假设0100μμμμ≠=:;:H H .因为2σ未知,而样本方差2S 是总体方差2σ的无偏估计量,用S 代替σ. 选择检验统计量 nS X T /0μ-=,当0H 成立时,)1(~-n t T .给定显著性水平α,由t 分布分位点的定义, 有αα=->)}1(|{|2/n t T P ,故拒绝域)}1({)}1({)}1(|{|2/2/2/->--<=->=n t T n t T n t T W ααα , 这种利用服从t 分布的检验统计量的检验方法称为t 检验法.例2 某切割机工作正常时,切割每段金属棒的平均长度为10.5cm .今在某段时间随机地抽取15段进行测量,其结果如下(cm):10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2 10.9 10.6 10.8 10.5 10.7 10.2 10.7问此段时间该机工作是否正常(5.00=α)?假设金属棒长度服从正态分布.解 依题意,检验假设0100.510μμμμ≠==:;:H H , 由于2σ未知,故选择检验统计量nS X T /0μ-=.在0H 下,)1(~-n t T ,15=n .给定显著性水平5.00=α,查t 分布表, 得临界值1448.2)14()1(025.02/==-t n t α,故拒绝域)}1(|{|2/->=n t T W α.由已知条件可得48.102.15715111=⨯==∑=n i i x n x056.0784.0141)(11122=⨯=--=∑=n i ix x n s 故2366.0=s .计算统计量的值3274.015/2366.05.1048.10/0-=-=-=ns x t μ因为)1(||2/-<n t t α,所以接受0H ,认为切割机工作正常.例3 设木材的小头直径),(~2σμN X ,12≥μcm 为合格,今抽出12根测得小头直径的样本均值为2.11=x cm ,样本方差为44.12=s cm 2,问该批木材是否合格(5.00=α)?解 依题意,检验假设010012μμμμ<=≥:;:H H ,选择检验统计量nS X T /0μ-=.在假设0100μμμμ<=:;:H H 下,)1(~-n t T ,12=n .给定显著性水平5.00=α,查t 分布表,得临界值7959.1)11()1(05.0==-t n t α,故拒绝域)}1({--<=n t T W α,也是假设010012μμμμ<=≥:;:H H 的拒绝域. 由于2.11=x ,44.12=s ,计算统计量的值3094.212/44.1122.11/0-=-=-=ns x t μ因为)1(--<n t t α,故拒绝0H ,认为该批木材是不合格的. 二、正态总体方差的检验——2χ检验法设n X X X ,,, 21为来自总体),(2σμN 的一个样本,检验假设 20212020σσσσ≠=:;:H H .1.均值μ已知. 因为)1,0(~N X i σμ-,n i ,,2,1 =,则选取检验统计量∑∑==-=⎪⎪⎭⎫ ⎝⎛-=ni ini i XX 12201202)(1μσσμχ.当0H 成立时,)(~22n χχ,给定显著性水平α,由2χ分布表分位点的定义,有αχχχχαα=><-))}(())({(22/222/12n n P ,故得拒绝域)}({)}({22/222/12n n W ααχχχχ><=- .2.均值μ未知.因为X 是总体均值μ的无偏估计量,用X 代替μ.选择检验统计量202122)1(σσχS n XX ni i -=⎪⎪⎭⎫ ⎝⎛-=∑=. 当0H 成立时,)1(~22-n χχ,给定显著性水平α,由2χ分布表分位点的定义,有αχχχχαα=->-<-))}1(())1({(22/222/12n n P故得拒绝域)}1({)}1({22/222/12->-<=-n n W ααχχχχ .类似地,在μ已知和μ未知时,可以求出检验假设20212020σσσσ>≤:;:H H 和20212020σσσσ<≥:;:H H的拒绝域.例如,在μ未知时,检验假设2020σσ≤:H 的拒绝域为)}1({22->=n W αχχ.上述检验所用的检验统计量均服从2χ分布,称这种检验方法为2χ检验法例4 某无线电厂生产的一种高频管,其中一指标服从正态分布),(2σμN ,今从一批产品中抽取8只管子,测得指标数据:68 43 70 65 55 56 60 72(1) 总体均值60=μ时,检验228=σ(取5.00=α); (2) 总体均值μ未知时,检验228=σ(取5.00=α). 解 本题是在显著性水平5.00=α下,检验假设2021220208σσσσ≠==:;:H H ,这里8=n .(1) 60=μ已知时临界值35.517)8()(2025.022/==χχαn ,80.12)8()(2975.022/1==-χχαn ,而检验统计量的值359.10663641)(811222=⨯=-=∑=ni i x μχ, 由于)()(22/222/1n n ααχχχ<<-,故接受0H .(2) μ未知时临界值13.016)7()1(2025.022/==-χχαn ,90.61)7()1(2975.022/1==--χχαn ,而125.614898111=⨯==∑=n i i x n x ,875.652)()1(122=-=-∑=ni i x x s n ,检验统计量的值2012.1075.86526412=⨯=χ, 由于)1()1(22/222/1-<<--n n ααχχχ,故接受0H .§8.3 两个正态总体参数的假设检验设121n X X X ,,, 为总体),(~112σμN X 的一个样本,221n Y Y Y ,,, 为总体),(~222σμN Y 的一个样本.∑==1111n i i X n X 和∑==2121n i iYn Y 分别是两个样本的样本均值,∑=--=112121)(11n i i X X n S 和∑=--=212222)(11n i i Y Y n S 是相应的两个样本方差.设这两个样本相互独立..一、两个正态总体均值的检验考虑检验假设 211210μμμμ≠=:;:H H . 1.方差21σ与22σ已知——u 检验法. 选取 22212121)()(n n Y X U σσμμ+---=.当0H 成立时,检验统计量)1,0(~222121N n n YX U σσ+-=.给定显著性水平α,由标准正态分布表分位点的定义,有αα=>}|{|2/u U P ,故拒绝域}{}{}|{|2/2/2/αααu U u U u U W >-<=>= .例1 设从甲乙两场所生产的钢丝总体X ,Y 中各取50束作拉力强度试验,得1208=x ,1282=y ,已知801=σ,942=σ,请问两厂钢丝的抗拉强度是否有显著差别(5.00=α)?解 本题是在显著性水平5.00=α下, 检验假设211210μμμμ≠=:;:H H , 这里5021==n n .选取检验统计量222121n n YX U σσ+-=.给定显著性水平05.0=α,查标准正态分布表,得临界值96.1025.02/==u u α,故拒绝域}|{|2/αu U W >=.由于1208=x ,1282=y ,801=σ,942=σ, 计算检验统计量的值2392.450/)(2221-=+-=σσy x u .由于2/||αu u >,故拒绝0H ,认为两厂钢丝的抗拉强度有显著差别. 2.方差21σ与22σ未知,但2221σσ=——t 检验法.选取 212111)()(n n S Y X T w+---=μμ.这里2)1()1(21222211-+-+-=n n S n S n S w .当0H 成立时,检验统计量)2(~112121-++-=n n t n n S Y X T w.给定显著性水平α,由t 分布表分位点的定义, 有αα=-+>)}2(|{|212/n n t T P ,故拒绝域)}2({)}2({212/212/-+>-+-<=n n t T n n t T W αα .例2 某烟厂生产两种香烟,独立地随机抽取样本容量相同的烟叶标本测其尼古丁含量的毫克数,分别测得:甲种香烟:25 28 23 26 29 22 乙种香烟:28 23 30 25 21 27假定尼古丁含量都服从正态分布且具有公共方差,在显著性水平5.00=α下,判断两种香烟的尼古丁含量有无显著差异?解 检验假设211210μμμμ≠=:;:H H ,这里621==n n ..525=x ,67.625=y ,7386.21=s ,3267.32=s ,0469.3=w s . 选取检验统计量2111n n S Y X T w+-=.给定显著性水平5.00=α,查t 分布表,得临界值2281.2)10()2(025.0212/==-+t n n t α,故拒绝域)}2(|{|212/-+>=n n t T W α.计算统计量的值0949.00469.33)667.255.25(1121-=⨯-=+-=n n s y x t w.由于)2(||212/-+<n n t t α,故接受0H ,认为两种香烟的尼古丁含量无显著差异. 二、两个正态总体方差的检验——F 检验法 考虑检验假设 2221122210σσσσ≠=:;:H H . 1.均值1μ与2μ已知.因为)(~)(11212121211n Xn i iχμσχ∑=-=,)(~)(12212222222n Yn i iχμσχ∑=-=,选取221222211211222121/)(1/)(1//21σμσμχχ∑∑==--==n i i n i i Y n X n n n F . 当0H 成立时,检验统计量),(~)(1)(1211222121121n n F Y n X n F n i i n i i ∑∑==--=μμ.给定显著性水平α,由F 分布分位点的定义,有ααα=><-))},(()),({(212/212/1n n F F n n F F P , 故得拒绝域)},({)},({212/212/1n n F F n n F F W αα><=- . 2.均值1μ与2μ未知.因为)1(~)1()(112212111221211--=-=∑=n S n X X n i i χσσχ,)1(~)1()(122222221222222--=-=∑=n S n Y Yn i iχσσχ,选取22222121222121//)1/()1/(σσχχS S n n F =--=.当0H 成立时,检验统计量)1,1(~212221--=n n F S S F .给定显著性水平α,由F 分布分位点的定义,有ααα=-->--<-))}1,1(())1,1({(212/212/1n n F F n n F F P , 故得拒绝域)}1,1({)}1,1({212/212/1-->--<=-n n F F n n F F W αα .例3某烟厂生产两种香烟,独立地随机抽取样本容量相同的烟叶标本测其尼古丁含量的毫克数,分别测得:甲种香烟:25 28 23 26 29 22 乙种香烟:28 23 30 25 21 27假定尼古丁含量都服从正态分布且具有公共方差,在显著性水平5.00=α下,判断两种香烟的尼古丁含量的方差是否相等? 解 考虑检验假设2221122210σσσσ≠=:;:H H . 由于两个正态总体的均值都未知,选取检验统计量)1,1(~212221--=n n F S S F .给定显著性水平α,查F 分布表,得两个临界值:15.7)5,5()1,1(025.0212/==--F n n F α1399.015.71)5,5(1)5,5()1,1(025.0975.0212/1====---F F n n F α,故得拒绝域}15.7{}1399.0{><=F F W . 计算统计量的值6777.03267.37386.2222221===s s F .由于15.71399.0<<F , 故接受0H ,认为两种香烟的尼古丁含量的方差也无显著差异.§8.4 非正态总体参数的大样本检验本节讨论一般总体参数的检验.设总体X 的均值为μ,方差为2σ, n X X X ,,, 21为总体X 的一个样本.由中心极限定理可知,当样本容量n 足够大时,nX U /σμ-=近似地服从标准正态分布.因此,我们可以用正态分布去近似.如果对均值μ进行检验,方差2σ未知时,可以用样本方差2S 代替2σ;如果对方差2σ进行检验,均值μ未知时,可以用样本均值X 代替μ.下面举两个例子.例1 设某段高速公路上汽车限速为104.6km/h ,现检验85辆汽车的样本,测出的平均车速为106.7km/h ,已知总体标准差为.413=σ km/h ,但不知总体是否服从正态分布.在显著性水平50.0=α下,试检验高速公路上的汽车是否比限制速度104.6km/h 显著地快?解 依题意,检验假设0100.6104μμμμ>=≤:;:H H , 由于.413=σ已知,n =85足够大, 选择检验统计量nX U /0σμ-=近似地服从)10(,N .其拒绝域}{αu U W >=,其中65.105.0==u u α. 计算U 的值449.4185/4.136.1047.106=-=u ,由于αu u <,因此接受0H ,没有理由认为高速公路上的汽车比限制速度104.6km/h 显著地快.例2 为比较甲乙两种小麦植株的高度(单位:cm),分别抽得甲、乙小麦各100穗,在相同条件下进行高度测定,算得甲乙小麦样本均值和样本方差分别为28=x ,8.3521=s ,26=y ,3.3222=s ,问这两种小麦的株高有无显著差异(50.0=α)?解 依题意,检验假设 211210μμμμ≠=:;:H H , 选取 22212121)()(n n Y X U σσμμ+---=,这里两个方差用样本方差代替.当0H 成立时, 检验统计量 222121n Sn S Y X U +-=近似地服从)1,0(N .给定显著性水平05.0=α,查附表3,得临界值96.1025.02/==u u α, 得拒绝域}|{|2/αu U W >=.计算U 的值4236.21003.328.352628=+-=u ,由于αu u >,因此拒绝0H ,认为这两种小麦的株高有显著差异.当总体服从(0-1)分布),1(p b 时,由于只有一个参数p ,总体均值p 和方差)1(p p -均只与p 有关,这时对参数p 进行假设检验时,检验统计量可以直接用样本和参数p 表示出来.例3 某厂有一批产品须经检验后方可出厂.按规定二级品率不得超过10%,从中随机抽取100件产品进行检查,发现有二级品14件,问这批产品是否可以出厂(50.0=α)?解 这里n =100,14.0=x .检验假设01001.0p p H p p H >=≤:;:, 选取检验统计量 np p p X U )1(000--=,U 近似地服从)1,0(N .由显著性水平50.0=α,可以得到拒绝域}{αu U W >=,其中65.105.0==u u α,计算U 的值333.31100.90.10.104.10=⨯-=u ,由于αu u <,因此接受0H ,认为这批产品二级品率没有超过10%,可以出厂.§8.5 分布的拟合检验前几节的检验都是参数的检验.实际问题中,有时需要对分布作出假设,进行检验.本节只介绍一种分布的检验方法——皮尔逊2χ检验法,它只适合于大样本的情形,一般要求样本容量50≥n .设总体X 的分布函数为)(x F ,)(0x F 为一个已知的分布函数,n X X X ,,, 21为总体X 的一个样本,我们来检验关于总体分布的假设)()()()(0100x F x F H x F x F H ≠=:;:.一、基本原理2χ检验法的基本思想是:将随机试验的所有可能结果的全体分成k 个两两互不相容的事件k A A A ,,, 21,在n 次试验中,将i A 发生的次数i f 叫做i A 发生的频数,如果0H 为真,则由大数定律,在n 次试验中(n 足够大),i A (k i ,,, 21=)出现的实际频率nf i与理论频率)(i i A P p =(可由分布函数)(0x F 算出)不应相差很大.基于这种想法,皮尔逊构造了统计量∑=-=ki i i i np np f 122)(χ或∑=-=ki i i i p n p n f 122ˆ)ˆ(χ, 其中i p ˆ是由)(ˆ0x F 计算出来的理论频率,)(ˆ0x F 是)(0x F 中未知参数估计出后的分布函数,并证明了如下定理:定理1 若n 足够大,当0H 成立时,统计量2χ总是近似地服从自由度为1--r k 的2χ分布,其中r 是已知的分布函数)(0x F 中未知参数的个数.直观上看,2χ值表示实际观测结果与理论期望结果的相对差异的总和,当它的取值大于临界值时,应拒绝0H . 二、检验步骤如果)(0x F 为不带有未知参数的已知分布,皮尔逊2χ检验法的具体步骤如下:(1) 将总体X 的值域划分成k 个不交的区间i A (k i ,,, 21=),使得每个区间包含的理论频数满足5≥i np ,否则将区间适当调整; (2) 在0H 成立时,计算各理论频率即概率i p 的值:)()()(100--==i i i i y F y F A P p ,k i ,,, 21=.这里1-i y 与i y 为区间i A 的端点,即](1i i i y y A ,-=;(3) 数出i A 中含有样本值的个数,即i A 的频数i f ,并计算统计量∑=-=ki i iinp np f 122)(χ 的值2χ;(4) 由2χ分布,对于给定的显著性水平α,找出临界值)1(2-k αχ; (5) 判断:若)1(22->k αχχ,则拒绝0H ,否则可接受0H . 如果总体X 是离散型的,则假设0H 相当于假设总体X 的概率分布00}{i i p x X P H ==:, ,,21=i .如果总体X 是连续型的,则假设0H 相当于)()(00x f x f H =:,这里)(x f 为总体的概率密度.例1 至1984年底,市开办有奖储蓄以来,13期兑奖中诸数码的频数汇总如表8.1:表8.1试检验器械或操作方法是否有问题(50.0=α).解 设抽取的数码为X ,它可能的取值为0~9,如果检验器械或操作方法没有问题,则0~9出现是等可能的,即检验假设 1010=i p H :,9210,,,, =i ,这里}{i X P p i ==. 依题意知k =10,令}{i A i =,9210,,,, =i ,n =350,则理论频数35=i np .57.61935688)(9022==-=∑=i ii i np np f χ给定显著性水平5.00=α,查2χ分布表,得临界值9.16)9()1(205.02==-χχαk .由于19.675>16.9,故拒绝0H ,即认为器械或操作方法有问题.如果)(0x F 为带有未知参数的已知分布,未知参数为r θθθ,,, 21,这时用这r 个未知参数的极大似然估计量r θθθˆˆˆ21,,, 来代替)(0x F 中的参数r θθθ,,, 21,得到分布函数)(ˆ0x F ,然后建立统计量∑=-=ki ii i p n p n f 122ˆ)ˆ(χ,这里i p ˆ是由)(ˆ0x F 计算出来的理论频率,再用以上检验步骤进行检验,但此时检验统计量2χ近似服从)1(2--r k χ分布(这里k >r +1).例2 某高校对100名新生的身高(厘米)做了检查,把测得的100个数据按由大到小的顺序排列,相同的数合并得表8.2:表8.2试问,在显著性水平5.00=α下是否可以认为学生身高X 服从正态分布? 解 这里n =100,我们来检验假设222)(021)(σμσπ--=x ex f H :,+∞<<∞-x ,这里)(x f 为正态分布),(2σμN 的概率密度,设其分布函数为)(x F ,μ与0>σ为未知参数.先求μ与2σ的极大似然估计值μˆ,2ˆσ: 33.1661ˆ1==∑=n i i x n μ, 06.28)ˆ(1ˆ212=-=∑=μσn i i x n . 设服从正态分布)ˆ,ˆ(2σμN 的随机变量为Y ,分布函数为)(ˆy F .按照分组要求,每个小区间的理论频数i pn ˆ不应小于5,因此我们将数据分成了7个组,使得每组的实际频数不小于5,各计算结果如下表8.3所示.表8.3中第3列i pˆ的计算如下: )(ˆ)(ˆ}{ˆ11---=≤<=i i i i i y F y F y Y y P p ,7210,,,, =i , 例如,}06.2833.1665.164ˆˆ06.2833.1665.161{}5.1645.161{ˆ3-≤-<-=≤<=σμY P Y P p1837.0)911.0()345.0(=-Φ--Φ=.给定显著性水平5.00=α,查2χ分布表,得临界值488.9)4()127()1(205.0205.02==--=--χχχαr k .由于1.8843<9.488,故接受0H ,即认为学生身高服从正态分布.。
正态分布均值的假设检验

VS
详细描述
在单样本均值假设检验中,我们首先需要 确定一个期望的均值,然后计算样本的均 值。通过比较这两个值,我们可以判断样 本均值是否显著地偏离了期望的均值。常 用的统计量包括z分数和t分数,用于评估 样本均值与已知期望值之间的差异是否具 有统计学上的显著性。
双样本均值的假设检验
总结词
双样本均值的假设检验是检验两个独立样本的均值是否存在显著差异。
详细描述
在双样本均值假设检验中,我们需要比较两个独立样本的均值。通过计算两组样本的均值,并比较这两个值,我 们可以判断两个样本的均值是否存在显著差异。常用的统计量包括t检验和z分数,用于评估两个样本均值之间的 差异是否具有统计学上的显著性。
配对样本均值的假设检验
总结词
配对样本均值的假设检验是检验两个相关样本的均值是否存在显著差异。
Part
0(H0)
样本数据来自的总体均值等于某一固 定值。
备择假设(H1)
样本数据来自的总体均值不等于该固 定值。
选择合适的检验统计量
• 常用的检验统计量有t统计量、Z统计量等,根据具体情况选择合适的统计量。
确定显著性水平
• 显著性水平(α):在假设检验中,原假设为真但被拒绝 的概率,通常取值在0.01至0.05之间。
正态分布在统计学中的重要性
基础性
正态分布是统计学中最重要的概 率分布之一,许多统计方法和理 论都基于正态分布。
广泛应用性
正态分布在自然和社会科学领域 都有广泛的应用,如生物学、医 学、经济学、心理学等。
理论依据
正态分布在统计学中提供了理论 依据,许多统计推断和决策方法 都基于正态分布的性质和假设。
1 2
判断假设是否成立
通过假设检验,可以判断一个假设是否成立,从 而为进一步的研究或决策提供依据。
概率论与数理统计02-82.2 两个正态总体均值的检验_70

第八章假设检验第二节正态总体均值的假设检验2. 两个正态总体在寿命问题中提出了两个正态总体均值是否相等的假设012:H μμ=112:H μμ≠这种情形经常发生在当研究对象的外界条件发生了改变时,判断研究对象是否受到了这种影响.检验统计量如何构造呢?例3对用两种不同热处理方法加工的金属材料做抗拉强度试验,得到的试验数据如下:方法Ⅰ:31,34,29,26,32,35,38,34,30,29,32,31方法Ⅱ:26,24,28,29,30,29,32,26,31,29,32,28设两种热处理加工的金属材料的抗拉强度都服从正态分布,且方差相等.比较两种方法所得金属材料的平均抗拉强度有无显著差异().05.0=α).,(),,(2221σμσμN N 解:记两总体的正态分布为.:,:211210μμμμ≠=H H 本题是要检验假设关键问题在于找到拒绝域12k μμ->X Y k->121212()()~(2),11w X Y t n n S n n μμ---+-+222112212(1)(1)2w n S n S S n n -+-=+-其中12221212()()~(0,1)X Y N n n μμσσ---+).,(),,(2221σμσμN N 解:记两总体的正态分布为.:,:211210μμμμ≠=H H 本题是要检验假设1212~(2)11w X Y T t n n S n n -=+-+检验统计量为21212||(2)11w x y t t n n S n n α-=≥+-+拒绝域为,1221==n n ,75.31=x .67.28=y ,25.112)1(211=-s n ,64.66)1(222=-s n .85.2=w s .647.26185.2|67.2875.31|11||||21=-=+-=n n s y x t w 计算统计值074.2)22()2(025.0212==-+t n n t α查t 分布表,得/212||(2)t t n n α>+-统计判决:由于故拒绝H 0.即认为两种热处理方法加工的金属材料的平均抗拉强度有显著差异.解:休息一下吧。
第二节 正态总体均值的假设检验8-2

14
三、基于成对数据的检验(t 检验):
设X和Y是两个正态总体, 均值分别为 1 和 2 , X 和 Y不是相互独立的。取成对样本 : (X1 , Y1) , (X2 , Y2) , … , ( Xn , Yn )。 要检验: H0 : 1 = 2 , H1 : 1 ≠ 2 . 可以把这个问题转化成单个总体的假设检验 , 令Z = X - Y , 它服从 N ( , 2) , 这里 (= 1- 2) , 2 均未知。 Zi = Xi – Yi (i=1 , 2 , … , n)是来自该正态总体的样本。 显然 , 检验 H0 : 1= 2 , H1 : 1 ≠ 2 等价于检验 H0 : =0 , H1: ≠0,
11
例 2. 在平炉上进行一项试验以确定改变操作方法的建 议是否会增加钢的得率, 试验是在同一只平炉上进行 的. 每炼一炉钢时除操作方法外, 其它条件都尽可能 做到相同. 先用标准方法炼一炉, 然后用建议的方法 炼一炉, 以后交替进行, 各炼了10炉, 其得率分别为: 标准方法: 78.1 72.4 76.2 74.3 77.4 78.4 新方法: 79.1 76.0 81.0 75.5 76.7 77.3 80.0 77.3 79.1
16
解: 分别作各对数据的差 zi = xi - yi ,如上表 ,
并假设 z1 , z2 , … , z9 来自正态总体N ( , 2 ) ,
这里 , 2 均属未知 。若两台仪器的性能一样, 则各对数据的差异可看作是随机误差, 而随机误差可以认为服从正态分布, 其均值为零, 因此本题归结为检验假设: H0: =0 , H1: ≠ 0. 由前面的结论知,可取 T =
问是否有理由认为元件的平均寿命大于225小时?
解 : 按题意需检验 H 0 : 0 = 225 , H 1 : > 225 . X- 取 a = 0 .05,统计量: t = 。 S n 当 H 0 成立时,由 X - 0 S n X- S n ,
正态总体均值的假设检验

假设检验
正态总体均值的假设检验
1.1 单个正态总体均值的假设检验
3.大样本单个正态总体均值的检验
设总体为 X ,它的分布是任意的,方差 2 未知, X1 ,X2 , ,Xn 为 来自总体 X 的样本,H0 : 0( 0 已知).当样本容量 n 很大( n 30 )
时,无论总体是否服从正态分布,统计量 t X 0 都近似服从正态分 S/ n
解 依题意,建立假设 由于 2 未知,故选取统计量
H0 : 0 72,H1 : 72 . t X 0 , S/ n
已知 0.05 ,故此检验问题的拒绝域为
W t | | t |
x 0
s/ n
t
/
2
(n
1)
.
又知 n 26,x 74.2,s 6.2,查表得 t /2 (25) t0.025 (25) 2.06 ,则有 | t | x 0 74.2 72 1.81 2.06 , s/ n 6.2/ 26
解 依题意,建立假设 由于 2 未知,取检验统计量
H0 : 0.8,H1 : 0.8 .
t X 0 ~ t(n 1) , S/ n
已知 0.05 ,故此检验问题的拒绝域为
W t | t x 0 s/ n
t (n 1) .
又知 n 16 ,x 0.92,s 0.32 ,查表得 t0.05 (16 1) t0.05 (15) 1.75,则有 t x 0 0.92 0.8 1.50 1.75 , s/ n 0.32/ 16
假设检验 H0 : 0 ,H1 : 0 的拒绝域为 W {t | t t (n 1)}.
(7-8) (7-9)
假设检验
正态总体均值的假设检验
1.1 单个正态总体均值的假设检验
两个正态总体均值的检验.

S
2 w
(n1
1)S1*2 (n2 1)S2*2 n1 n2 2
.
当H0为真时, 根据第六章§3定理2知,
T ~ t(n1 n2 2).
第八章 假设检验
§8.3 两个正态总体参数的假设检验
对给定的 , 由t分布的分位表可查得 t/ 2(n1 n2 2).
X Y
使得P{ Sw
1 1 t / 2 (n1 n2 2)}
,
2均为
2
未
知.
需要检验假设:
H0
:
2 1
22,
H1 :12 22 ,
第八章 假设检验
§8.3 两个正态总体参数的假设检验
当 H0 为真时,
E
(
S1*
2
)
2 1
2 2
E(S2*2 ),
当 H1 为真时,
E(
S1*2
)
2 1
22
E(S2*2 ),
当 H1 为真时,
观
察
值S1*
S
* 2
2 2
有 偏
大
或
偏
小
的
趋
势
故拒绝域的形式为 s1*2 s2* 2
k1或
s1* 2 s2* 2
k2,
此处 k1和k2 的值由下式确定:
第八章 假设检验
P
S1* S2*
2 2
k1
S1*2 S2*2
k2
§8.3
两个正态总体参数的假设检验
为了计算方便, 习惯上取
P
S1* S2*
2 2
k1
,
2
P
P{| ( X Y ) /
故拒绝域为
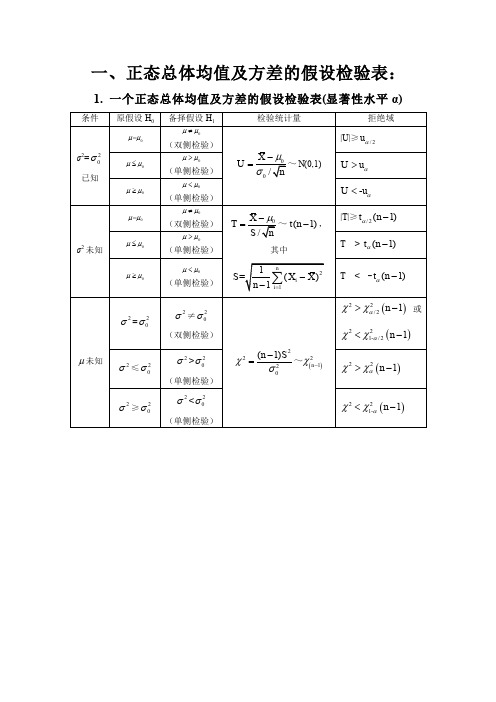
正态分布总体的区间估计与假设检验汇总表
(单侧检验)
2
(n
1)S 2
2 0
~2n1
2
2 /2
n
1
或
2
2 1- / 2
n 1
2 2 n 1
2
≥
2 0
2
<
2 0
(单侧检验)
2
2 1-
n
1
2. 两个正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 备择假设 H1
检验统计量
拒绝域
12
,
2 2
已知
1 =2 1 2 1 2
1 2
1 2
(单侧检验)
SW
(n1 1)S12 (n2 1)S22 n1 n2 2
T < - t (n1 n2 2)
1,2
未知
2 1
=
2 2
2 1
≤
2 2
2 1
≠
2 2
(双侧检验)
2 1
>
2 2
(单侧检验)
F
S12 S22
~
F ( n1 - 1, n2 - 1)
F ≥ F /2 n1 1, n2 1
已知
0 / n
X
0 n
u
/2,
X
0 n
u
/2
2 未知 T X 0 ~ t(n 1) S/ n
X
S n 1
t / 2
n
1 ,
X
S n
1
t
/
2
n
1
方差 2
未知
2
(n 1)S 2
2 0
~2n1
(n 2 /
1)S 2
8.2正态总体均值的假设检验

t t ( n1 n2 2).
x y 因为 t 4.295, 1 1 sw 10 10
t0.05 (18) 1.7341,
所以拒绝 H 0 ,
即认为建议的新操作方法较原来的方法为优.
例5 有甲、乙两台机床加工相同的产品, 从这两台机床加工 的产品中随机地抽取若干件, 测得产品直径(单位:mm)为 机床甲: 20.5, 19.8, 19.7, 20.4, 20.1, 20.0, 19.0, 19.9
X 0 P Z / n
拒绝域为 Z Z
或 H0: 0;H1:0
X 0 P Z / n
拒绝域为 Z Z
2、方差未知 问题:总体 X~N(,2),2未知 假设 H0:=0;H1:≠0 构造T统计量 T X 0 ~ t (n 1)
t检验 双边检验
X 0 由 P t 2 (n 1) S n 确定拒绝域 T t 2 (n 1) x 0 如果统计量的观测值 T t 2 (n 1) S n
则拒绝原假设;否则接受原假设
S
n
例2 化工厂用自动包装机包装化肥,每包重量服从正态 分布,额定重量为100公斤。某日开工后,为了确定包 装机这天的工作是否正常,随机抽取9袋化肥,称得平 均重量为99.978,均方差为1.212,能否认为这天的包 装机工作正常?(=0.1) 解 由题意可知:化肥重量X~N(,2),0=100 方差未知,要求对均值进行检验,采用T检验法。
得 k t / 2 (n1 n2 2).
故拒绝域为
( x y) t t / 2 ( n1 n2 2). 1 1 sw n1 n2
§8.2 正态总体参数的假设检验

已
知
202 2>02 2 i1
2 0
202 2<02
H0的拒绝域 2 2 2 (n)
或 2
2 1
2 (n)
2 2(n)
2 12(n)
2 检验
2 2 2(n1)
未
知
2=02 202
2
(n
1)S2
02
202 2>02
或2
2 1
2(n1)
22(n1)
202 2<02
212(n1)
例2.1 用热敏电阻测温仪间接测量地热,
检验法 条件 H0 H1 检验统计量
Z检 验
已
知
=0 0
0 >0
Z
X
0
0 <0
n
T检 验
未
知
=0
0 0
0 >0
<0
T
X 0
Sn
H0的拒绝域 |Z|z/2
Zz Z–z |T|t/2(n–1) Tt(n–1) T–t(n–1)
检验法 条件 H0 H1 检验统计量
2 检验
2=02 202
n
(Xi )2
故t 11.2811.26 0.46592.4469 1.13587
所以接受原假设, 认为用热敏电阻测温仪间接测量温度无系 统偏差。
例2.2 某厂生产的某种型号的电池, 其
寿命长期以来服从方差2=5000(小时2)的
正态分布。现有一批这种电池, 从它的生 产情况来看, 寿命的波动性有所改变。现 随机取26只电池, 测出其样本方差 s2=9200(小时2), 试根据这一数据能否推 断这批电池的寿命的波动性较以往的有
《概率论与数理统计教学课件》8第八章—正态总体均值和方差的假设检验

真)
P1 2
(
x y
11
k)
k t (n1 n2 2)
sw
n1 n2
2
概率统计
在显著性水平 下, H0 的拒绝域:
x y
sw
11
t (n1 n2 2)
2
n1 n2
注:
当
2 1
2 2
2
未知时
检验假设
或
H0 : 1 -2 (或1 2 ), H0 : 1 2 (或1 2 ),
2
概率统计
所以拒绝H 0 ,可认为这两种轮胎的耐磨性有显著差异。
注: ▲ 用两种不同的方法得到了两种不同的结论,那么
究竟应该采取哪一个结论比较合理呢?
显然,应该采取第二种方法得出的结论是合理的
因为数据配对的方法是针对同一架飞机的,它是 排除了因飞机之间的试验条件的不同而对数据产 生的干扰,所以它是直接反映了这两种轮胎的耐 磨性的显著差异的情况,因此,应采取第二种方 法得出的结论,即可认为这两种轮胎的耐磨性有 显著差异。
概率统计
按单个正态总体中当 2 未知时,关于 的假设检验
的计算公式,可得 H0 的拒绝域为:
C { t t t (n 1)}
2
经计算 d 320 , s2 89425 ,
t
d s
320 2.83 89425
n
8
t (n 1) t0.05 (7) 2.365
2
2
因为: t 2.83 t0.05 (7) 2.365
为已知常数,显著水平为
概率统计
Q 检验统计量
(X Y)
~ N (0,1)
2 1
2 2
n1 n2
第8章 平均数的假设检验

重点
• 根据样本平均数的抽样分布,可以对总体 平均数进行差异显著性检验,需考虑总体 方差是否已知,总体是否服从正态分布, 是大样本还是小样本等问题。
• 根据两个独立样本平均数之差的抽样分布, 可以检验两个总体的平均数有无显著差异, 需考虑两总体的方差是否已知,两总体是 否服从正态分布,方差是否齐性,是大样 本还是小样本等问题。
• 显著性水平和可靠性程度(置信水平)之间 的关系是:两者之和为1。
双侧检验与单侧检验
• 双侧检验(two-tailed test,twosided test):将α等分为左右两个部分,
左右两边各设置一个拒绝域,中间是接受域。 每个拒绝域相应的概率为α/2. 零假设为无显著 差异的情况;
• 单侧检验(one-tailed test):要么将与α
– 备择假设(alternative hypothesis,或称 研究假设、对立假设),用H1表示。
假设检验是从零假设出发,视其被拒绝的概 率,从而得出决断。
假设检验的步骤
• 2.确定适当的检验统计量并计算其值
• 确定检验统计量时,要根据抽样分布做出 选择。不同类型的问题涉及到的抽样分布 不同,要选择不同的检验统计量。
假设检验的基本思想
设(X1,X2,…,Xn)
是抽自正态分布总体 X~N(μ, σ2)的一个容 量为n的简单随机样 本,则其样本均值也 是一个正态分布随机 变量,且有
E(X) X
D(
X
)
2 X
2
n
X ~ N(, 2 )
n
Z X ~ N (0,12 ) / n
假设检验
正态总体参数的假设检验

正态总体参数的假设检验 正态总体中有两个参数:正态均值与正态⽅差。
有关这两个参数的假设检验问题经常出现,现逐⼀叙述如下。
(⼀) 正态均值的假设检验 ( 已知情形) 建⽴⼀个检验法则,关键在于前三步l,2,3。
5.判断(同前) 注:这个检验法称为u检验。
(⼆) 正态均值的假设检验 ( 未知情形) 在未知场合,可⽤样本标准差s去替代总体标准差,这样⼀来,u统计量变为t统计量,具体操作如下: 1.关于正态均值常⽤的三对假设为 5.判断 (同前) 注:这个检验法称为t检验。
(三)正态⽅差的假设检验 检验正态⽅差有关命题成⽴与否,⾸先想到要⽤样本⽅差。
在基础上依据抽样分布特点可构造统计量作为检验之⽤。
具体操作如下: 1.关于正态⽅差常⽤的三对假设为 5.判断(同前) 注:这个检验法称为检验。
注:关于正态标准差的假设与上述三对假设等价,不另作讨论。
(四) ⼩结与例⼦ 上述三组有关正态总体参数的假设检验可综合在表1.5-1上,以供⽐较和查阅。
续表 [例1.5-2] 某电⼯器材⼚⽣产⼀种云母带,其厚度在正常⽣产下服从N(0.13,0.0152)。
某⽇在⽣产的产品中抽查了10次,发现平均厚度为0.136,如果标准差不变,试问⽣产是否正常?(取 =0.05)来源:考试通 解:①⽴假设:②由于已知,故选⽤u检验。
③~④根据显著性⽔平 =0.05及备择假设可确定拒绝域为{ >1.96}。
⑤由样本观测值,求得检验统计量: 由于u未落在拒绝域中,所以不能拒绝原假设,可以认为该天⽣产正常。
[例1.5-3] 根据某地环境保护法规定,倾⼊河流的废⽔中⼀种有毒化学物质的平均含量不得超过3ppm。
已知废⽔中该有毒化学物质的含量X服从正态分布。
该地区环保组织对沿河的⼀个⼯⼚进⾏检查,测定每⽇倾⼊河流的废⽔中该物质的含量,15天的记录如下(单位:ppm)3.2,3.2,3.3,2.9,3.5,3.4,2.5,4.3,2.9,3.6,3.2,3.0,2.7,3.5,2.9 试在⽔平上判断该⼚是否符合环保规定? 解:①如果符合环保规定,那么应该不超过3ppm,不符合的话应该⼤于3ppm。
82两个正态总体均值差和方差的假设检验2-精选文档

二.基于成对数据的检验
2.单边假设检验 未知方差2,H0: 0 ,H1: > 0 (1) 提出原假设H0: 0 ,H1: > 0.
(2) 选择统计量
X T S n
(4) 选择检验水平 ,查正态分布表,得临界值z/2, 即
K由下式确定:
P { ( X Y ) ( ) K } 1 2
: ,H : . 0 1 2 (1) 提出原假设 H 1 1 1 SW n1 n 2
2 2 ( n 1 ) S ( n 1 ) S 1 1 2 2 其中 S W n n 2 1 2
§8.2 两个正态总体均值差 和 方差的假设检验(2) 一.两个正态总体均值是否相等的 检验 二.未知两个正态总体方差的 检验
一.两个正态总体均值差的检验
2 2 两个正态总体 N ( , ), N ( , ) 1 1 2 2
X X 是来自于第一个 样总 本体 ;的 1, X 2,..., n 1
(≥50) 检验对象H0:μ1=μ2 X Y U 选择统计量: 2 2
S1 S2 n1 n2
~ N0,1
2 2 S S 2 于是 K 1+ Z , 否定域约为 X Y K 2 n n 1 2
(3)t检验
2 2 2 未知(称方差齐性) 1 2
检验对象H0:μ1=μ2 选择统计量:
21 . 5 18 . 0 t 2 . 245 . 30 . 02 7078 1 1 7 5 4 由于t 2 .245 2 .3646 W,因此 , 。即 t
接受原假设 H 0 即认为两矿煤的含灰率无显 著差异。
但是由于 2.245 与临界值 2.3646比较接近,
单个正态总体参数的假设检验

576.2 576 x 576 0.079 其中 | U | 8 / 10 8/ n
查表 z / 2 z0.025 1.96 0.079 故未落在拒绝域之内,故接受H0 ,即可以认为 576.
综合⑴与⑵,该生跳远成绩水平与鉴定成绩无显著差异.
X -0 取统计量 t ~ t (n 1) S/ n
x -0 拒绝域为 | t | t / 2 (n 1) s/ n 计算 | t | 2.6
| t | 2.6 t0.025 (35) 2.0301
故落在拒绝域之内,拒绝H0 ,接受H1 即不能认为全体考生的平均成绩为70分。 ⑵ μ的置信水平为0.95的置信区间为
2 2 2 双边假设检验 H 0 : 2 0 , H1 : 0
拒绝域为
(n 1) s 2
2 0
12 / 2 (n 1) 或 f y
2 2
(n 1) s 2
2 0
2 / 2 ( n 1)
2 12 / 2 (n 1) / 2 ( n 1)
观测5台压缩机的冷却用水的升高温的平均值为 x 5.34,
样本方差为 s 2 0.631. ⑴ 在显著水平α=0.05下是否可以
认为冷却用水升高温度的平均值不多于5°?(2)求σ2的
置信水平为0.95的置信区间。
解: ⑴ 先提出假设 H 0 : 0 5, H1 : 0
H1 : 0 ,拒绝域为
| x -0 | | u | z / 2 / n
2. σ2未知,检验μ (t 检验法)
n 1 2 可用样本方差 S 2 ( X X ) 代替σ2 k n 1 k 1
两个正态总体均值差和方差的假设检验

方差齐性检验是检验 两个正态总体方差是 否相等的统计方法。
常用的方差齐性检验 方法有:Levene检验、 Bartlett检验和Welch 检验。
Levene检验基于方差 分析,通过比较不同 组间的方差来判断方 差是否齐性。
Bartlett检验基于 Kruskal-Wallis秩和 检验,通过比较不同 组间的中位数和四分 位距来判断方差是否 齐性。
独立样本的均值检验
1
独立样本的均值检验是用来比较两个独立正态总 体的均值是否存在显著差异的统计方法。
2
常用的独立样本均值检验方法包括t检验和z检验, 其中t检验适用于小样本和大样本,而z检验适用 于大样本。
3
在进行独立样本均值检验时,需要满足独立性、 正态性和方差齐性的假设,以确保检验结果的准 确性和可靠性。
根据研究目的和数据类型,选择合适的统计量 来描述样本数据。
确定临界值
根据统计量的分布和显著性水平,确定临界值。
计算样本统计量
根据样本数据计算所选统计量的值。
做出决策
将样本统计量的值与临界值进行比较,做出接受 或拒绝原假设的决策。
解读结果
根据决策结果解读研究问题,给出结论和建议。
Part
02
两个正态总体均值的假设检验
Part
05
结论与展望
假设检验的优缺点
理论基础坚实
假设检验基于概率论和统计学原理,具有坚实的理论基础。
操作简便
假设检验提供了清晰的步骤和标准,方便研究者进行操作。
假设检验的优缺点
• 实用性强:假设检验广泛应用于各个领域,为科学研究和实践提供了有效的工具。
假设检验的优缺点
01
对数据要求较高
假设检验对数据的分布、样本量 等有一定的要求,不符合条件的 样本可能导致检验结果不准确。
8-2正态分布均值的假设检验

)
的情况
利用t检验法检验具有相同方差的两正态总 体均值差的假设.
设 X1, X2 ,, Xn 为来自正态总体N (1, 2 ) 的样本, Y1,Y2 ,,Yn 为来自正态总体N (2 , 2 )的
样本, 且设两样本独立. 注意两总体的方差相等.
又设 X ,Y 分别是总体的样本均值, S12 , S22是样本
因为 2 未知, 不能利用 X 0 来确定拒绝域. / n
因为 S 2 是 2 的无偏估计, 故用 S 来取代 , 即采用t X 0 来作为检验统计量.
S/ n
当观察值
t
x 0
s/ n
过分大时就拒绝H0,
拒绝域的形式为 t x 0 k . s/ n
根据第六章§2定理三知,
定理三
当H0为真时,
79.1, 81.0, 77.3, 79.1, 80.0, 78.1, 79.1, 77.3, 80.2, 82.1; 设这两个样本相互独立, 且分别来自正态总
体 N (1, 2 )和 N (2, 2 ), 1, 2, 2均为未知, 问建议的新操作方法能否提高得率? (取 0.05)
解 需要检验假设 H0 : 1 2 0, H1 : 1 2 0.
即甲、乙两台机床加工的产品直径无显著差异.
三、基于成对数据的检验( t 检验 )
从直观上看, 合理的检验法则是:
若观察值 x 与 0 的差 x 0 过分大, 即 x 0 k ,
则我们拒绝 H0 接受 H1 .
拒绝域的形式 x 0 k , ( k 待定). 由标准正态分布的分布函数 (•) 的单调性可知,
P{拒绝 H0 | H0 为真 } P0 ( x 0 k)
P 0
要检验假设 H0 : 10.5, H1 : 10.5,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 H0 : 40, H1 : 40
n 25, 2, x 41.25, 0 40
在 0.05 下, z0.05 1.645 接受域为 (, 1.645)
若H0真,由样本观察值计算
z
x
/
0
n
41.25 40 2 / 25
3.125
左边检验 H0 : 0, H1 : 0 接受域为 (t (n 1), )
x1, x2
, xn计算
z x 0 / n
由 z (z /2 , z /2 ) 或 (z / 2 , z / 2 ) 决定是否接受H0.
(2) 右边检验 H0 : 0, H1 : 0 ;
给定显著性水平 , 查表得 z
接受域为 z z , 即 (, z )
若H0真,由样本观察值
x1, x2
1
(0 k) / n
0
(0 /
n
k) 0
0
(0 / n
k
)
/
k
n
,
因此要控制 P{拒绝 H0 | H0 为真} ,
只需令
/
k
n
,
即 k ( /
n)z ,
检验问题 H0 : 0, H1 : 0 的拒绝域为
x 0 ( /
n)z ,
即
x
/
0
n
/ n
因为 S 2 是 2 的无偏估计, 故用 S 来取代 , 即采用t X 0 来作为检验统计量.
S/ n
当观察值
t
x 0
s/ n
过分大时就拒绝H0,
方法(称为 t 检验法):
定理三
当H0为真时,
X 0 ~ t(n 1),
S/ n
查表得
t (n 1) 2
P{拒绝
H0
当
H0
为真
}
P
X S
, xn计算
z x 0 / n
由 z (, z ) 或 (, z ) 决定是否接受H0.
(3) 左边检验 H0 : 0, H1 : 0 .
给定显著性水平 , 查表得 z
拒绝域为 z z , 即 (z ,)
若H0真,由样本观察值
x1, x2
,
xn计算
z
x
/
0
n
由 z (z , ) 或 (z , ) 决定是否接受H0.
/ n 0.15 / 15
故接受 H0, 认为该机工作正常.
例2 某工厂生产的固体燃料推进器的燃烧率服
从正态分布 N (, 2 ), 40cm / s, 2cm / s. 现
用新方法生产了一批推进器, 随机取 n 25只, 测 得燃烧率的样本均值为x 41.25cm / s. 设在新方 法下总体均方差仍为2cm / s,问用新方法生产的 推进器的燃烧率是否较以往生产的推进器的燃
~
N (0,1)
在显著性水平 0.05, 查表得 z0.025 1.96, 即
P(1.96 Z 1.96) 0.95 , 接受域为(-1.96, 1.96)
n 15, x 10.48, 0.05, 因此 z x 0 10.48 10.5 0.516 (1.96,1.96)
z
.
比较正态总体N ( , 2 )在方差 2已知时, 对均值
的两种检验问题
H0 : 0, H1 : 0 和 H0 : 0, H1 : 0 ,
尽管原假设H0的形式不同, 实际意义也不同,但对
于相同的显著性水平 , 它们的拒绝域相同.
第二类形式的检验问题可归结为第一类形式讨论.
例1 某切割机在正常工作时, 切割每段金属棒的 平均长度为10.5cm, 标准差是0.15cm, 今从一批产 品中随机的抽取15段进行测量, 其结果如下: 10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2
若观察值 x 与 0 的差 x 0 过分大, 即 x 0 k ,
则我们拒绝 H0 接受 H1 .
拒绝域的形式 x 0 k , ( k 待定). 由标准正态分布的分布函数 (•) 的单调性可知,
P{拒绝 H0 | H0 为真 } P0 ( x 0 k)
P 0
x
/
0
n
0 k /
n
第二节 正态总体均值的假设检验
一、单个总体均值 的检验
二、两个总体均值差的检验 三、基于成对数据的检验 四、小结
一、单个总体 N(, 2) 均值 的检验
1. 2 为已知, 关于的检验( Z 检验)
(1) 假设检验 H0 : 0, H1 : 0 ; (2) 假设检验 H0 : 0, H1 : 0 ;
/
0
n
t (n 1) ,
2
拒绝域为 (,t (n 1)][t (n 1),]
2
2
即接受域为 (t (n 1), t (n 1))
2
2
由样本观察值
x1, x2
, xn计算tBiblioteka x s/0
n
决定是否接受H0.
同理,对于单边检验有:. 右边检验 H0 : 0, H1 : 0 接受域为 (, t (n 1))
(3) 假设检验 H0 : 0, H1 : 0 .
方法:
作统计量 Z X
n 则 Z~N ( 0, 1 )
(1) 假设检验 H0 : 0, H1 : 0 ;
给定显著性水平 , 查表得 z / 2
接受域为 | z | z / 2 , 即 (z /2 , z /2 )
若H0真,由样本观察值
(, 1.645)
故在显著性水平 0.05 下拒绝 H0 .
即认为这批推进器的燃烧率较以往有显著提高.
2. 2为未知, 关于 的检验( t 检验)
设总体 X ~ N(, 2 ), 其中, 2 未知, 显著性水平为 .
(1) 假设检验 H0 : 0, H1 : 0 ;
因为 2 未知, X 0 不能作为检验统计量
一个有用的结论
当显著性水平均为 时,
检验问题 H0 : 0 , H1 : 0和检验问题 H0 : 0 , H1 : 0 有相同的接受域(拒绝域).
证明 在检验问题 H0 : 0 , H1 : 0 中, 因为 H0 中的 都比 H1 中的 小,
从直观上看, 合理的检验法则是:
10.9 10.6 10.8 10.5 10.7 10.2 10.7 假定切割的长度服从正态分布, 且标准差没有变
化, 试问该机工作是否正常? ( 0.05)
解 因为 X ~ N(, 2 ), 0.15, 要检验假设
H0 : 10.5, H1 : 10.5,
若
H0 真,则 Z
x
0
/n
