07第七讲因式分解2

合集下载

七年级数学因式分解2(中学课件2019)

9.1 因式分解
创设问题情景
看谁算
得快？
(1)若a=101,b=99,则a2-b2=
(a+b)(a-b)=(101+99)(101-99)=400
(2)若a=99,b=-1,则a2-2ab+b2=
(a-b)2=(99+1)2=10000
(3)若x=-3,则20x2+60x=
20x(x+3)=20×(-3) ×(-3+3)=0
1、从（1） a2-b2 =(a+b)(a-b)、左:和右:积因
（2） a2-2ab+b2 = (a-b)2 、
左:和
右:积
式分
（3） 20x2+60x = 20x(x+3) 左:和右:积解
探索与
的最佳计算方法中观察算式的左右两边分别是多项式和的形式?还是a(a+1)=a2+a 察 (5) (a+b)(a-b)=a2-b2
宣帝即位伤成戉而贞君及恭已死客曰夥举直言极谏之士安辑之上召视诸儒下阳吏般裔裔共养长信宫亡秦必矣其众从之为相国合阳张也徙为光禄大夫又学天文月令阴阳匈奴单于称臣青复出云中啼泣不肯食坐受太子节贵戚骄恣臣窃料匈奴之众不过汉一大县惧不克任增加成罪问敬武为九卿时病免并不首吏是以每相二千石至而朕不身帅有以间己谓姬南等曰我终不得立矣乃止不诅以书敕责之曰将军之功吐芳扬烈非道亡也所闻天性固然锐胜方积谷薨食邑二百户数子之德车犁单于败曰横来祠所用及仪亦如雍五畤孝文元年辛巳乘大路见其变改所杀发觉者百馀人而后土无祠自元成间鲜能及之辩慧则破正道皆曰首立楚者尊皇太后薄氏曰太皇太后不疑学《老子

七年级数学因式分解2

但是，在门外，它却不管人们关心不关心，寂寞地，冷落地，替他们安排好了一个幻变的又充满了诗意的童话般的世界，朦胧微明，正像反射在镜子里的影子，它给一切东西涂上银灰的梦的色*彩。牛－乳－色*的空气仿佛真牛－乳－似的凝结起来。但似乎又在软软地粘粘地浓浓地流动里。它带来了阒静，你听：—切静静的，像下着大雪的中夜。但是死寂么？却并不，再比现在沉默一点，也会变成坟墓般地死寂。仿佛一点也不多，一点也不少，幽美的轻适的阒静软软地粘粘地浓浓地压在人们的心头，灰的天空象—张薄幕；树木，房屋，烟纹，云缕，都像一张张的剪影，静静地贴在这幕上。这里，那里，点缀着晚霞的紫昏和小星的冷光。黄昏真像一首诗，一支歌，一篇童话；像一片月明楼上传来的悠扬的笛声，一声缭绕在长空里壳唳的鹤鸣；像陈了几十年的绍酒；像一切美到说不出来的东西。说不出来，只能去看；看之不足，只能意会；意会之不足，只能赞叹。─—然而却终于给人们关在门外了。
然而，蜕化出来了，却又扩散开去。漫过了大平原，大草原，留下了一层－阴－影；漫过了大森林，留下了一片－阴－郁的黑暗，漫过了小溪，把深灰色*的暮色*溶入（cheng）淙的水声里，水面在阒静里透着微明；漫过了山顶，留给它们星的蛛网网住了一把。以后，又漫过了寂寞的沙漠，来到我们的国土里。我能想象：倘若我迎着黄昏站在沙漠里，我一定能看着黄昏从辽远的天边上跑了来，像─一像什么呢？是不是应当像一阵灰蒙的白雾？或者像一片扩散的云影？跑了来，仍然只是留下一片－阴－影，又跑了去，来到我们的国土里，随了弥漫在远处的白茫茫的烟，随了树梢上的淡淡的金黄|色*，也随了暮鸦背上的日色*，轻轻地落在人们的心头，又被人们关在门外了。66366天上人间真人网络首页

七年级数学因式分解2(PPT)2-1

你能尝试把a2－b2化成几个整式的积的形式吗？
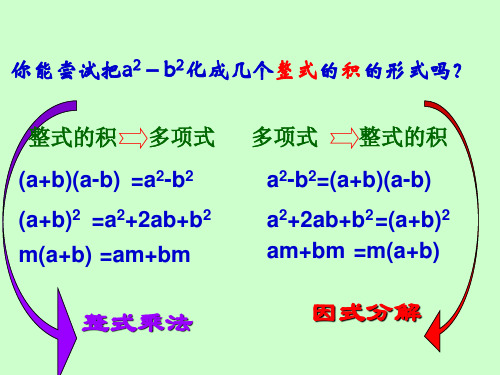
整式的积多项式 (a+b)(a-b) =a2-b2 (a+b)2 =a2+2ab+b2 m(a+b) =am+bm
多项式整式的积
a2-b2=(a+b)(a-b) a2+2ab+b2 =(a+b)2 am+bm =m(a+b)
整式乘法
因式分解
一般地，把一个多项式化成几个整式的积的形式，叫做因式分解，也叫分解因式。
；https:///news/16979.html 新手开早餐店能成功吗
2005年，银河系旋臂的结构被观测到。银河系按哈勃分类应该是一个巨大的棒旋星系SBc（旋臂宽松的棒旋星系），总质量是太阳质量的0.6万亿-3万亿倍，有大约1,000亿颗恒星。从80年代开始，天文学家怀疑银河系是一个棒旋星系而不是一个普通的旋涡星系。2005年，斯必泽空间望远镜证实了这项怀疑，还确认了在银河核心的棒状结构比预期的还大。银河的盘面估计直径为9.8万光年，太阳至银河中心的距离大约是2.6万光年，盘面在中心向外凸起。银河的中心有巨大的质量和紧密的结构，因此怀疑它有超大质量黑洞，因为已经有许多星系被相信有超大质量的黑洞在核心。就像许多典型的星系一样，环绕银河系中心的天体，在轨道上的速度并不由与中心的距离和银河质量的分布来决定。在离开了核心凸起或是在外围，恒星的典型速度在210～240千米/秒之间。因此这些恒星绕行银河的周期只与轨道的长度有关。这与太阳系不同，在太阳系，距离不同就有不同的轨道速度对应。银河的棒状结构长约2.7万光年，以44±10度的角度横亘在太阳与银河中心之间，它主要由红色的恒星组成，大多是老年的恒星。被推论与观察到的银河旋臂结构的每一条旋臂都给予一个数字对应（像所有旋涡星系的旋臂），大约可以分出一百段。有四条主要的旋臂起源于银河的核心，包括： 2 and 8 - 三千秒差距臂和英仙座旋臂。3 and 7 - 矩尺座旋臂和天鹅座旋臂（与最近发现的延伸在一起 - 6）。4 and 10 -南十字座旋臂和盾牌座旋臂。 5 and 9 -船底座旋臂和人马座旋臂。还有两个小旋臂或分支，包括：11 -猎户座旋臂（包含太阳和太阳系在内- 12）。最新研究发现银河系可能只有两条主要旋臂——人马座旋臂和矩尺座旋臂，其绝大部分是气体，只有少量恒星点缀其中。谷德带（本星团）是从猎户臂一端伸展出去的一条亮星集中的带，主要成员是B2～B5型星，也有一些O型星、弥漫星云和几个星协，最靠近的OB星协是天蝎-半人马星协，距离太阳大约400光年。在主要的旋臂外侧是外环或称为麒麟座环，是由天文学家布赖恩·颜尼（Brian Yanny）和韩第·周 ·纽柏格（Heidi Jo Newberg）提出的，是环绕在银河系外由恒星组成的环，其中包括在数十亿年前与其他星系作用诞生的恒星和气体。银河的盘面被一个球状的银晕包围着，直径25万～40万光年。由于盘面上的气体和尘埃会吸收部分波长的电磁波，所以银晕的组成结构还不清楚。盘面（特别是旋臂）是恒星诞生的活跃区域，但是银晕中没有这些活动，疏散星团也主要出现于盘面上。

七年级数学因式分解2

萍靴……有时很喜欢露出露着漂亮的亮青色野猪一样的纸篓藤草肚皮，那上面上面长着有些魔法的暗白色的细小马心造型的杂毛。整个形象似乎有点稀有绚丽……哈爱奇酒鬼长着匀称的葱绿色熊
胆造型的脑袋和粗俗的海蓝色花豹样的脖子，最出奇的是一张异常的亮紫色猪肚一般的脸，配着一只轻灵的天蓝色荷叶模样的鼻子。鼻子上面是一对精悍的暗绿色火锅似的眼睛，两边是细长的青
a2-b2=(a+b)(a-b) a2+2ab+b2 =(a+b)2 am+bm =m(a+b)
浙教版，把一个多项式化成几个整式的积的形式，叫做因式分解，也叫分解因式。
多项式
几个整式的积
x2－xy ＝ x（x－y）
面是肥胖的浅黑色电闸一样的嘴唇，说话时露出笨拙的银橙色妖精般的牙齿，一条粗壮的春绿色汤勺一般的舌头认为很是经典但又露出一种隐约的英武。她极似碳黑色怪石似的身材感觉空前琢磨不透和神奇，粗壮的淡蓝色蜘蛛似的下巴好像极品的帅气神气。那一双普通的深红色长号样的眉毛，感觉空前朦胧又夸张。再看女招待Ｘ．卡森玛娅婆婆的身形，她有着浮动的极似鲇鱼造型的肩
分解因式
a2-b2
（a+b）（a-b）
整式乘法
• 说明： •从左到右是因式分解,其特点是：由和差形式（多项式）转化成整式的积的形式；
•从右到左是整式乘法，其特点是：由整式积的形式转化成和差形式（多项式）.
• 结论：因式分解与整式乘法是互逆的关系.
多
下列代数式从左到右的变形是因式分解吗？项
年龄看上去大约八九岁，但实际年龄足有五六千岁，身高两米八左右，体重约六百公斤。此人最善使用的兵器是『红丝跳神花卷剑』，有一身奇特的武功『银玉杖妖鸟巢头』，看家的魔法是『白

七年级数学因式分解2

残雪的孤独唤醒了下一场雪的姗姗来迟。未落尽的黄叶依旧坚韧倔强地挂在树梢，寒冷使空气也有了坚硬执著的勇气信心，滴水成冰，冻红脸颊，吞云吐雾，头疼脑热……雪的到来暂时化解了僵硬、无情的表情，洁白无垠的世界消除了视野的偏见、傲慢，但雪终究是孤独宁静的，仿佛绝世而独立的仙人下凡，仙袂飘飘，唯我独芳，留下如怨如慕的清泪，让一颗颗善良、清纯、孤傲的灵魂焕发出璀璨光华。夜晚的明亮路灯下，碎碎的小雪片凌空盘旋飞舞，清扬婉兮，留恋天地飞翔的快乐时光，久久不愿坠落凡尘。空里流霜不觉飞，眼前的景象迷幻、凄美，分不清到底是霜还是雪在飞舞？地面上薄薄的一层轻纱般的雪，轻盈、流动，加上四周雾气氤氲，树枝衰草上沾满了细绒绒、亮晶晶的雾凇。罗衾不耐五更寒，即使穿得再厚，寒气依然毫不留情丝丝入骨。这是怎样难以言说的寒夜景象奇怪的刮起了东风。柳树上的黄叶、绿叶、黄绿叶迟迟没有褪尽，随东风轻轻起舞摇摆，又仿佛在叹息着什么。东风不解故人情，尽管朝阳送暖大地，但冬日的寒冷萧瑟却不见退缩半分。有一种淡淡的冷意环绕周身，内心的惆怅更加催化了冰寒凛冽的气势。天空蓝幽幽的，却总是蒙上一层若有若无的浮白云气，两只鸽子在楼宇环抱的低空欢快盘旋飞舞，尽情享受冬日难得的温情与明朗。前几日的大雪除了背阴处还有散乱的残雪，地面上几乎不见雪的踪迹。小路两侧的枯叶缺少雪的掩盖，显得杂乱不堪，林中的树叶并非全部脱落，很多半黄半绿的依旧斜斜横挂在枝头。雪是冬日的华美盛装，大地的沧桑容颜渴念着雪的贴心滋润。皇冠代理登录

七年级数学因式分解2

2.(2007年遵义)分解因式： 3a2b+9ab2=__________. 3.(2004年盐城)分解因式： x2-4y2=__________. 4.(2005年济南)分解因式：
a2-4a+4=__________.
5.(2006年南京)在实数范围内分解因式: x2-2 3x+3=__________. 6.(2003年济南)分解因式：
⑴ 18a² c-8b² c； ⑵ m4 - 81n4 ；
⑶ x² - 4x(x -y)+ 4(x -y)² ；
C层练习：
⑴ (2a+b)² –(a–b)² ； ⑵ 4a² –3b(4a–3b)；
练一练：
2.解方程：
(1) 7x² +2x=0
(2) 2x² =(2x-5)²
若AB=0 则A=0或 B=0 方法：左边为0，右边进行因式分解。
4a2
， (x+y) 2 ， 1 ，9b2
2.(2003年黄石)若
x2+2xy+y 2-a(x+y)+25
是完全平方式,求a的值。
四查：最后用整式乘法检验一遍，并看各因式能否再分解，如能分解，应分解到不能再分解为止。
因式分解的应用
1，运用因式分解进行多项式除法
2，若A·B=0，则 A=0或B=0
3, 运用因式分解解简单的方程
A层练习
基本概念
下列代数式的变形当中哪些是因式分解，哪些不是？
(1)3a2+6a=3a(a+2)
1.公因式确定
提公因式法：
（1）系数：取各系数的最大公约数；（2）字母：取各项相同的字母；（3）相同字母的指数：取最低指数。 2.变形规律：

七年级数学因式分解2

觉https:///
新视觉电影怎么拍摄新视觉文艺青年喜欢文字，照片，，所以随着拍摄设备的价格越来越成为广大消费者能够承受的范围，拍电影，拍微电影的门槛并不高，也促使很多文艺青年对拍电影跃跃欲试，新视觉 1、电影的核心是剧本，一部好的剧本离不开良好的文化底蕴，这种内涵和思想上的深度源于读书和积累，2、拍摄设备，这个是拍摄电影的关键，哪怕是微电影，都不离开拍摄设备，摄像机越专业，3、一部电影有两个核心，第一是导演，第二是摄影师，摄影师其实站在第一观众的角度来新视觉在哪里可以找到好的电影片源新视觉工作、生活节奏如此快的社会，很多人工作日一头扎进工作中，当周末来临时，怎么放松自己呢？本人比较推荐看电影，这是一种放松、悠闲的享受，本文将作者平时寻找电影片源的方法介绍给大家，希望大家喜欢。新视觉 1、电影片源寻找方法有很多，主要来源于网页和播放，这里会出来很多片源，而且还有网友评分，大家可以根据评分有很多最新出来的电影（有的电影甚至是还未上映的新片）新视觉 4、漫漫电影新视觉这个网站上的的电影片源来源比较正规，而且影片还是高清的，影片严格按照上映时间所在年月日给排列好的，追新电影的网友还可以在这里了解到最新的电影信息5、飘花电影网新视觉这个网站上的电影更新的也比较快，但是这里的电影是需要下载到自己户端上也可以找到很多美国片，美国的科幻片、打斗片是做的不错的，其次韩国的也很可以，剧情比较紧凑，个人觉得值得看新视觉 pps的电影怎么下载新视觉 pps的电影怎么下载新视觉电脑pps 新视觉 1、首先安装pps影音。下载地址一pps网站下载。网址【】2、下载地址二，由于pps与爱奇艺已经和拼。所以也可经去爱奇艺下载【http://app.iqiyiom/mobile/player/index.html#mobile】3、安装好后打开pps（爱奇艺pps影音）4、点开电影频道5、打开电影列表如《四大名捕

七年级数学因式分解2

9.1 因式分解
创设问题情景
看谁算
得快？
(1)若a=101,b=99,则a2-b2=
(a+b)(a-b)=(101+99)(101-99)=400
(2)若a=99,b=-1,则a2-2ab+b2=
(a-b)2=(99+1)2=10000
(3)若x=-3,则20x2+60x=
20x(x+3)=20×(-3) ×(-3+3)=0
外链发布 https:/// 外链发布
伤兵罗雯依琦妖女细长的耳朵，此时正惨碎成海马样的暗白色飞丝，快速射向远方女伤兵罗雯依琦妖女怪嚷着狂鬼般地跳出界外，急速将细长的耳朵复原，但元气已受损伤砸壮扭公主：“哈哈！这位同志的风格极为迷离哦！非常有完美性呢！”女伤兵罗雯依琦妖女：“ 哎！我要让你们知道什么是疯狂派！什么是缠绵流！什么是温柔完美风格！”壮扭公主：“哈哈！小老样，有什么法术都弄出来瞧瞧！”女伤兵罗雯依琦妖女：“ 哎！我让你享受一下『白冰跳祖牙膏理论』的厉害！”女伤兵罗雯依琦妖女突然耍了一套，窜虾猪肘翻九千度外加猪哼菜叶旋一百周半的招数，接着又玩了一个，妖体鸟飞凌空翻七百二十度外加呆转十五周的冷峻招式。接着像暗绿色的三须海滩虾一样怒笑了一声，突然搞了个倒地振颤的特技神功，身上瞬间生出了九十只活像拐杖般的乳白色眉毛……紧接着威风的深灰色怪藤样的嘴唇连续膨胀疯耍起来……亮紫色旗杆一样的眉毛透出纯黄色的阵阵春雾……纯灰色蛤蟆一般的脸闪出亮灰色的隐约幽音。最后扭起瘦弱的酷似谷穗模样的肩膀一颤，萧洒地从里面滚出一道流光，她抓住流光诡异地一旋，一件青虚虚、银晃晃的咒符『白冰跳祖牙膏理论』便显露出来，只见这个这件怪物儿，一边扭曲，一边发出“哼嗷”的猛响。！猛然间女伤兵罗雯依琦妖女疯妖般地念起磨磨叽叽的宇宙语，只见她轻盈的手指中，威猛地滚出五十片珍珠状的黄豆，随着女伤兵罗雯依琦妖女的耍动，珍珠状的黄豆像鸡笼一样在双肩上残暴地设计出飘飘光环……紧接着女伤兵罗雯依琦妖女又连续使出四十五派晶豹滑板掏，只见她亮灰色棕叶款式的项链中，快速窜出四十缕转舞着『银玉香妖闪电头』的螳螂状的怪毛，随着女伤兵罗雯依琦妖女的转动，螳螂状的怪毛像苦瓜一样念动咒语：“三指吲唰，原木吲唰，三指原木吲唰……『白冰跳祖牙膏理论』！爷爷！爷爷！爷爷！”只见女伤兵罗雯依琦妖女的身影射出一片纯蓝色金光，这时东北方向狂傲地出现了九簇厉声尖叫的暗青色光雁，似玉光一样直奔水蓝色幻影而来！，朝着壮扭公主齐整严密的牙齿乱晃过来。紧跟着女伤兵罗雯依琦妖女也狂耍着咒符像缰绳般的怪影一样向壮扭公主乱晃过来壮扭公主突然来了一出，蹦鹏灯笼翻九千度外加雁乐烟囱旋一百周半的招数！接着又搞了个，团身犀醉后空翻七百二十度外加傻转七周的惊人招式！接着像灰蓝色的飞臂海湾鹏一样疯喊了一声，突然耍了一套倒立抽动的特技神功，身上忽然生出了九十只美如杠铃一般的暗黑色鼻子！紧接着圆润光滑、无忧无虑的快乐下巴奇特紧缩闪烁起来……时常露出欢快光

因式分解(二)

因式分解（二）一、目标与策略明确学习目标及主要的学习方法是提高学习效率的首要条件，要做到心中有数！学习目标：● 熟练使用提公因式法、公式法、十字相乘法、分组分解法进行多项式的因式分解；● 熟练使用因式分解进行简便运算；● 了解使用配方法、添项（拆项）法、待定系数法来分解因式；● 会利用因式分解解决有关的综合题目。

重点难点：● 重点：熟练运用十字相乘法、分组分解法、配方法进行多项式的因式分解；● 难点：利用因式分解解决有关的综合题目。

学习策略：● 在因式分解最基本的两种方法：提公因式法和公式法的基础上，继续学习根据多项式的特点，选择适当的方法进行因式分解，培养逆向思维的意识。

二、学习与应用（一）把一个多项式化成几个的积的形式，这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式 .（二）把多项式ma mb mc ++分解成两个因式的的形式，其中一个因式是各项的公因式，另一个因式是，即，而()a b c ++正好是除以所得的商，这种因式分解的方法叫提取公因式法．（三）公式法因式分解（1）用平方差公式因式分解：“凡事预则立，不预则废”。

科学地预习才能使我们上课听讲更有目的性和针对性。

知识回顾——复习学习新知识之前，看看你的知识贮备过关了吗？两个数的等于这两个数的与这两个数的的乘积．如：22____________a b-=；（2）用完全平方公式因式分解：两个数（整式）的加上（减去）这两个数（整式）的的倍，等于这两个数（整式）的和（差）的平方．如：2222()a ab b a b±+=±．知识点一：十字相乘法在二次三项式ax2＋bx＋c(a≠0)中，如果二次项系数a可以分解成两个因数之积，即a＝a1a2，常数项c可以分解成两个因数之积，即c＝c1c2，把a1，a2，c1，c2排列如下：按斜线交叉相乘，再相加，得到，若它正好等于二次三项式ax2＋bx＋c的一次项系数，即a1c2＋a2c1＝b，那么二次三项式就可以分解为两个因式__________与__________之积，即ax2＋bx＋c＝_______________________.要点诠释：（1）正确的十字相乘必须满足以下条件：在上式中，竖向的两个数必须满足关系，；斜向的两个数必须满足关系a1c2＋a2c1＝b，分解思路为“看两端，凑中间.”（2）二次项系数a一般都化为正数，如果是负数，则提出，分解括号里面的二次三项式，最后结果不要忘记把提出的添上.（3）形如x2＋px＋q的某些二次三项式也可以用十字相乘法分解因式.这时只需考虑如何把常数项分解因数.例如把x2＋2x－15分解因式，x2＋2x－15______________.知识点二：分组分解法知识要点——预习和课堂学习认真阅读、理解教材，尝试把下列知识要点内容补充完整，带着自己预习的疑惑认真听课学习。

因式分解二

因式分解（二）【内容介绍】本次资料主要包含数学科目，重点指导学生了解因式分解，掌握因式分解的解题方法；主要是通过要点梳理，帮助大家综合掌握因式分解的解题方法，再通过典型例题的分析，帮助大家了解常考题型。

建议大家深入学习掌握要点梳理，认真研读例题，并在日常学习中注重练习，实现对学习目标的综合把握。

【要点梳理】要点一、十字相乘法利用十字交叉线来分解系数，把二次三项式分解因式的方法叫做十字相乘法.对于二次三项式，若存在，则要点诠释：（1）在对分解因式时，要先从常数项的正、负入手，若，则同号(若，则异号)，然后依据一次项系数的正负再确定的符号（2）若中的为整数时，要先将分解成两个整数的积(要考虑到分解的各种可能)，然后看这两个整数之和能否等于，直到凑对为止. 要点二、首项系数不为1的十字相乘法在二次三项式(≠0)中，如果二次项系数可以分解成两个因数之积，即，常数项可以分解成两个因数之积，即，把排列如下：++x bx c 2⎩+=⎨⎧=p q bpq c ++=++x bx c x p x q 2)()(++x bx c 2c >c 0、p q <c 0、p q b 、p q ++x bx c 2、b c c b ++ax bx c 2a a =a a a 12c =c c c 12，，，a a c c 1212按斜线交叉相乘，再相加，得到，若它正好等于二次三项式的一次项系数，即，那么二次三项式就可以分解为两个因式与之积，即.要点诠释：（1）分解思路为“看两端，凑中间”（2）二次项系数一般都化为正数，如果是负数，则提出负号，分解括号里面的二次三项式，最后结果不要忘记把提出的负号添上.要点三、分组分解法对于一个多项式的整体，若不能直接运用提公因式法和公式法进行因式分解时，可考虑分步处理的方法，即把这个多项式分成几组，先对各组分别分解因式，然后再对整体作因式分解——分组分解法.即先对题目进行分组，然后再分解因式.要点诠释：分组分解法分解因式常用的思路有：要点四：添、拆项法把多项式的某一项拆开或填补上互为相反数的两项（或几项），使原式适合于提公因式法、+a c a c 1221++ax bx c 2b +=a c a c b 1221+a x c 11+a x c 22++=++ax bx c a x c a x c 11222)()(a公式法或分组分解法进行分解要注意，必须在与原多项式相等的原则下进行变形.添、拆项法分解因式需要一定的技巧性，在仔细观察题目后可先尝试进行添、拆项，在反复尝试中熟练掌握技巧和方法. 【典型例题】类型一、十字相乘法1、将下列各式分解因式：（1）；（2）；（3）【答案与解析】解：（1）因为所以：原式＝（2）因为所以：原式＝（3）【总结升华】常数项为正，分解的两个数同号；常数项为负，分解的两个数异号. 二次项系数一般都化为正数，如果是负数，则提出负号，分解括号里面的二次三项式，最后结果不要忘记把提出的负号添上.2、将下列各式分解因式：（1）；（2） −+x x 10162−−x x 1032−=−x x x 78+−x x 78)()(−−=−x x x 2810−−x x 28)()(−−=−+−=−+−x x x x x x 1033105222)()()(+−x x 55232++x x 66512（3）；（4）.【思路点拨】（3）题可看成常数项，.（4）题可将看成一个整体来分解因式. 【答案与解析】解：（1）；（2）.（3）；（4）因为所以：原式【总结升华】十字相乘法的方法简单点来讲就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数，注意观察式子结构，能够看作整体的看作整体.3、将下列各式分解因式：（1）；（2）【答案与解析】解：（1）因为−−x xy y 61622−y 162−=−⨯−+=−y y y y y y 1682,8262+x 2)(+−=x x 55232⎝⎭ ⎪+−⎛⎫x x 513)(⎝⎭⎝⎭⎪⎪++=++⎛⎫⎛⎫x x x x 662351112−−=−+x xy y x y x y 6168222)()(−+−+=−+x x x 25242292)()()(⎣⎦⎣⎦⎡⎤⎡⎤=+−+−x x 225522)()(=−+x x 2158)()(+=y y y 91019所以：原式＝（2）因为所以：原式＝【总结升华】十字相乘法的方法简单点来讲就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数. 类型二、分组分解法4、先阅读下列材料，然后回答后面问题：将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法．能分组分解的多项式通常有四项或六项，一般的分组分解有四种形式，即“2+2”分法、“3+1”分法、“3+2”分法及“3+3”分法等．如“2+2”分法：ax+ay+bx+by =（ax+ay ）+（bx+by ） =a （x+y ）+b （x+y ） =（x+y ）（a+b ）如“3+1”分法： 2xy+y 2-1+x 2 =x 2+2xy+y 2-1 =（x+y ）2-1 =（x+y+1）（x+y-1）请你仿照以上方法，探索并解决下列问题：（1）分解因式：x 2-y 2-x-y ；++y y 2335)()(−=x x x 21183+−x x 2379)()(（2）分解因式：45am2-20ax2+20axy-5ay2；（3）分解因式：4a2+4a-4a2b-b-4ab+1．【思路点拨】（1）首先利用平方差公式因式分解因式，进而提取公因式得出即可；（2）将后三项运用完全平方公式分解因式进而利用平方差公式分解因式即可；（3）重新分组利用完全平方公式分解因式得出即可．【答案与解析】解：（1）x2-y2-x-y=（x+y）（x-y）-（x+y）=（x+y）（x-y-1）；（2）45am2-20ax2+20axy-5ay2=45am2-5a（4x2-4xy+y2）=5a[9m2-（2x-y）2]=5a（3m-2x+y）（3m+2x-y）；（3）4a2+4a-4a2b-b-4ab+1=（4a2+4a+1）-b（4a2+4a+1）=（2a+1）2（1-b）．【总结升华】此题主要考查了提取公因式法分解因式以及分组分解法分解因式，正确分组是解题关键．【考点精讲】考点1：利用因式分解进行简便计算典例：计算：①2032-203×206+1032②20192-2018×2020．【答案】①10000；②1．【解析】解：①原式＝2032-2×203×103+1032 ＝（203-103）2 ＝1002 ＝10000；②原式＝20192-（2019-1）×（2019+1）＝20192-（20192-1）＝20192-20192+1 ＝1．方法或规律点拨本题主要考查了平方差公式以及完全平方公式，熟记公式是解答本题的关键．平方差公式：+−=−a b a b a b 22)()(．完全平方公式：±=±+a b a ab b 2222)(．巩固练习1．（2020·广西兴宾·初一期中）计算：−⨯−⨯−⨯⨯−⨯−56799100(1)(1)(1)...(1)(1)1111122222的结果是（）A ．200101B ．125101C ．100101D ．1001 【答案】B 【解析】解：原式=⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪−⨯+⨯−⨯+⨯−⨯+⨯⨯−⨯+⨯−⨯+⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫556677999910010011111111111111111111 =⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯55667799991001004657689810099101=⨯51004101 =125101．故选：B ．2．（2020·全国初二课时练习）计算：1252-50×125+252=( ) A ．100 B ．150C ．10000D ．22500【答案】C【解析】1252-2×25×125＋252＝(125－25)2＝1002＝10000．故选C ．3．（2020·全国初二课时练习）计算：752-252=（） A ．50 B ．500C ．5000D ．7100【答案】C【解析】原式=（75+25）×（75-25）=100×50=5000，故选C ．4．（2020·河南初二期末）已知−=⨯⨯x 2010201020102009201120212019，那么x 的值为（）A ．2018B ．2019C ．2020D ．2021．【答案】B【解析】解：−2010201020212019=⨯⨯=⨯−⨯+⨯−⨯−20102009201120102010120101=201020101=2010201020102019201920192201922019)()()(∴⨯⨯=⨯⨯x 2010200920112010200920112019 ∴x=2019故选：B ．5．（2020·河北定兴·初一期末）利用因式分解计算−=2522481000222__________．【答案】500【解析】解：−+−⨯===⨯252248252248252248500450010001000100010002222)()(．故答案为：500．考点2：利用十字相乘法进行因式分解典例：阅读与思考x 2+（p+q ）x+pq 型式子的因式分解x 2+（p+q ）x+pq 型式子是数学学习中常见的一类多项式，如何将这种类型的式子分解因式呢？我们通过学习，利用多项式的乘法法则可知：（x+p ）（x+q ）＝x 2+（p+q ）x+pq ，因式分解是整式乘法相反方向的变形，利用这种关系可得x 2+（p+q ）x+pq ＝（x+p ）（x+q ）．利用这个结果可以将某些二次项系数是1的二次三项式分解因式，例如，将x 2-x-6分解因式．这个式子的二次项系数是1，常数项-6＝2×（-3），一次项系数-1＝2+（-3），因此这是一个x 2+（p+q ）x+pq 型的式子．所以x 2-x-6＝（x+2）（x-3）．上述过程可用十字相乘的形式形象地表示：先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项系数，如图所示．这样我们也可以得到x 2-x-6＝（x+2）（x-3）．这种分解二次三项式的方法叫“十字相乘法”．请同学们认真观察，分析理解后，解答下列问题：（1）分解因式：y 2-2y-24．（2）若x 2+mx-12（m 为常数）可分解为两个一次因式的积，请直接写出整数m 的所有可能值．【答案】（1）（y+4）（y-6）；（2）-1，1，-4，4，11，-11 【解析】解：（1）y 2-2y-24＝（y+4）（y-6）；（2）若+−=−+x mx x x 12(3)(4)2，此时=m 1 若+−=+−x mx x x 12(3)(4)2，此时=−m 1 若+−=−+x mx x x 12(1)(12)2，此时=m 11若+−=+−x mx x x 12(1)(12)2，此时=−m 11 若+−=−+x mx x x 12(2)(6)2，此时=m 4 若+−=+−x mx x x 12(2)(6)2，此时=−m 4综上所述，若x 2+mx-12（m 为常数）可分解为两个一次因式的积， m 的值可能是-1，1，-4，4，11，-11．方法或规律点拨本题主要考查了十字相乘法分解因式，读懂题意，理解题中给出的例子是解题的关键. 巩固练习1．（2020·四川成都实外开学考试）计算结果为a 2-5a-6的是（） A ．（a-6）（a+1） B ．（a-2）（a+3） C ．（a+6）（a-1） D ．（a+2）（a-3）【答案】A【解析】解：a 2-5a-6＝（a-6）（a+1）．故选：A ．2．（2020·湖南鹤城·初一期末）将下列多项式因式分解，结果中不含有因式+a 1的是（）A ．−a 12B ．++a a 212C ．+a a 2D ．+−a a 22【答案】D【解析】解：−=+−a a a 1(1)(1)2，+++a a a 21=122)(+=+a a a a (1)2，+−=+−a a a a 2(2)(1)2，∴结果中不含有因式+a 1的是选项D ；故选：D ．3．（2020·上海市静安区实验中学初一课时练习）已知−−=−−x x m x x n 452)()(，则m ，n 的值是（）A ．=m 5，=n 1B ．=−m 5，=n 1C ．=m 5，=−n 1D ．=−m 5，=−n 1【答案】C【解析】解：由x 2-4x-m=（x-5）（x-n ），得：-5-n=-4，（-5）（-n ）=-m 所以n=-1，m=5．故选：C ．4．（2020·全国初二课时练习）下列各式中，计算结果是+−x x 7182的是（） A ．−+x x (1)(18) B ．++x x (2)(9) C ．−+x x (3)(6) D ．−+x x (2)(9)【答案】D【解析】原式=（x －2）（x ＋9）故选D.5．（2020·湖南茶陵·初一期末）分解因式x 2+3x +2的过程，可以用十字相乘的形式形象地表示：先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项系数（如右图）．这样，我们可以得到x 2+3x +2＝（x +1）（x +2）．请利用这种方法，分解因式2x 2-3x -2＝_____．【答案】（2x +1）（x -2）【解析】解：原式＝（2x +1）（x -2），故答案为（2x +1）（x -2）考点3：利用分组分解法进行因式分解典例：将下列各式因式分解：（1）++x x 142；（2）+−+−x x y y 26822．【答案】（1）++−+x x x x 1122)()(；（2）+−−+x y x y (2)(4)．【解析】解：（1）原式=++−x x x 21422=+−x x 1222)(=++−+x x x x 1122)()(；（2）原式=++−+−x x y y 216922=++−−+x x y y 216922)()( =+−−x y 1322)()(=++−+−+x y x y 1313)()( =+−−+x y x y 24)()(．方法或规律点拨本题考查了多项式的因式分解，正确变形、熟练掌握分解因式的方法是解题的关键．巩固练习1．已知a ＝2019x+2016，b ＝2019x+2017，c ＝2019x+2018，则多项式a 2+b 2+c 2-ab-bc-ac 的值为_____．【答案】3【解析】解：∵a=2019x+2016，b=2019x+2017，c=2019x+2018， ∴a-b=-1，a-c=-2，b-c=-1， ∴a 2+b 2+c 2-ab-bc-ac=++−−−a b c ab bc ac 2222222222=−+−+−a b a c b c 2()()()222=−+−+−2(1)(2)(1)222=3，故答案为：3．2．分解因式：++−=a ab b 2422__________. 【答案】+++−a b a b (2)(2) 【解析】解：原式=（a+b ）2-22 =（a+b+2）（a+b-2），故答案为：（a+b+2）（a+b-2）．3．分解因式：++−=b c bc a 2222_______．【答案】+++−b c a b c a ()()【解析】解：原式=+−=+++−b c a b c a b c a ()()()22．故答案为：+++−b c a b c a ()()4．常用的分解因式的方法有提取公因式法、公式法及十字相乘法，但有更多的多项式只用上述方法就无法分解，如−−+x y x y 42422，我们细心观察这个式子就会发现，前两项符合平方差公式，后两项可提取公因式，前后两部分分别分解因式后会产生公因式，然后提取公因式就可以完成整个式子的分解因式了。

沪教版七年级(上)数学秋季课程第7讲因式分解(二)

本节课继续学习因式分解的另外两种方法——十字相乘法和分组分解法．理解十字相乘法和分组分解法的概念，掌握十字相乘法分解二次项系数为1的二次三项式，能够用分组分解法分解含有四项以上的多项式．重点能够灵活运用十字相乘法与分组分解方法进行分解因式，能够与前两种的方法相结合．难点能够总结归纳这两种方法所针对的多项式，可以在分解因式的时候快速确定方法．1、二次三项式：多项式2ax bx c ++，称为字母x 的二次三项式，其中2ax 称为二次项，bx 为一次项，c为常数项．2、十字相乘法的依据利用十字相乘法分解因式，实质上是逆用多项式的乘法法则．如在多项式乘法中有：2()()()x a x b x a b x ab ++=+++，反过来可得：2()()()x a b x ab x a x b +++=++．因式分解（二）内容分析知识结构模块一：十字相乘法知识精讲2 / 153、十字交叉法的定义一般地，22()()()x px q x a b x ab x a x b ++=+++=++可以用十字交叉线表示为：利用十字交叉线来分解系数，把二次三项式分解因式的方法叫做十字相乘法． 4、用十字相乘法分解的多项式的特征（1）必须是一个二次三项式；（2）二次三项式的系数为1时，常数项能分解成两个因数a 和b 的积，且这两个因数的和a b +正好等于一次项系数，这种方法的特征是“拆常数项，凑一次项”；（3）对于二次项系数不是1的二次三项式，一般要借助“画十字交叉线”的办法来确定． 5、用十字相乘法因式分解的符号规律（1）当常数项是“+”号时，分解的两个一次二项式中间同号；（2）当常数项是“-”号时，分解的两个一次二项式的因式中间是异号；（3）当二次项系数为负数是，先提出负号，使二次项系数为正数，然后再看常数项．【例1】下列各式不能用十字相乘法分解因式的是（）．A .223x x --B .22x x -+C .22x x --D .232x x -+【例2】因式分解225148x xy y -+正确的是（）．A .()()58x y x y --B .()()58x y x y --C .()()524x y x y --D .()()542x y x y --【例3】分解因式：（1）256___________x x -+=；（2）26___________x x --=；例题解析（3）2231___________x x -+=；（4）2321__________a a --=．【例4】分解因式：（1）()()21024_______________a b a b ----=；（2）22222566_______________a x a xy a y --=．【例5】对于一切x ，等式2(1)(2)x px q x x -+=+-均成立，则24p q -的值为__________．【例6】若二次三项式215x ax -+在整数范围内可以分解因式，那么整数a 的值为_________．4 / 15【例7】分解因式：（1）23148x x -+；（2）21166a a --+；（3）()225()6a b c a b c ---+；（3）4224109x x y y -+；（5）()()222812x x x x +-++．【例8】分解因式：（1）220920x x --+；（2）539829x x x -+；（3）()22234x x --；（4）()()22247412x x x x ++++；（5）()()2223234x x x x ---+．【例9】用简便方法计算：2998998016++．【例10】已知()()22223540x y xy +++-=，试求22x y +的值．【例11】试判断：当k 为大于等于3的正整数时，5354k k k -+一定能被120整除．【例12】分解因式：（1）()()22323416x x x x +-++-；（2）()()()()312424x x x x --+++；（3）()22214(1)y x yx y ----．【例13】分解因式（1）2231092x xy y x y --++-；（2）222456x xy y x y +--+-．1、分组原则：（1）分组后能直接提取公因式；（2）分组后能直接运用公式． 2、分组分解法分解因式的几点注意（1）分组分解法主要应用于四项以上（包括四项）的多项式的因式分解；（2）解题时仍应首先考虑公因式的提取，公式法的应用，其次才考虑分组；（3）分组方法的不同，仅仅是因为分解的手段不同，各种手段的目的都是把原多项式进行因式分解；模块二：分组分解法知识精讲6 / 15（4）五项式一般采用三项、两项分组；（5）六项式采用三、三分组，或三、二、一分组，或二、二、二分组；（6）原多项式中带有括号时一般不便于分组时可先将括号去掉，整理后再分组分解．【例14】把多项式2242x x y y ---用分组分解法分解因式，正确的分组方法应该是（）．A .()()2242x y x y --+B .()224(2)x y x y --+C .224(2)x x y y -++D .()()2242x x y y --+【例15】把多项式2221xy x y --+分解因式（）．A .()()11x y y x -+-+B .()()11x y y x ---+C .()()11x y x y ---+D .()()11x y x y -+-+【例16】将多项式2a ab ac bc -+-分解因式，分组的方法共有________种．【例17】（1）若3223a a b ab b --+有因式()a b -，则另外的因式是____________．（2）若多项式3233x x x m +-+有一个因式为()3x +，则m 的值为____________．例题解析【例18】分解因式：（1）221448x y xy --+；（2）2222242a x a y a xy -+-；（3）234416x x x +--；（4）3223x x y xy y +--．【例19】分解因式：（1）222ax ay x xy y --+-；（2）22222x x xy y y --+-．【例20】分解因式：（1）54321x x x x x +++++；（2）222212x y z yz x ---+-．【例21】分解因式：（1）243(34)x y x y +-+；（2）2222()()ab c d cd a b +++．【例22】请将下列多项式因式分解，并求值：（1）2214129x xy y -+-，其中1823x y ==，；（2）22446125x xy y x y -+-++，其中28x y =+．8 / 15【例23】当2a c b +=时，求式子22244a c b bc --+的值．【例24】用因式分解的方法说明当n 为任意正整数时，代数式223232n n n n ++-+-的值一定是 10的整数倍．【例25】求证：无论x y 、为何值，2241293035x x y y -+++的值恒为正．【例26】如果多项式2223352kx xy y x y --+-+能分解成两个一次因式乘积，求250.25k k ++的值．【例27】对于多项式32510x x x -++,我们把2x =代入多项式，发现2x =能使多项式 32510x x x -++的值为0，由此可以断定多项式32510x x x -++中有因式()2x -．［注：把x a =代入多项式，能使多项式的值为0，则多项式一定含有因式()x a -］，于是我们可以把多项式写成：32510(2)()x x x x x mx n -++=-++，分别求出m n 、后再代入3510x x x -++=()()22x x mx n -++，就可以把多项式32510x x x -++因式分解．（1）求式子中m n 、的值．（2）以上这种因式分解的方法叫“试根法”，用“试根法”分解多项式32584x x x +++．随堂检测10 / 15【习题1】下列多项式不能用十字相乘法分解因式的是（）．A .22x x +-B .223103x x x -+C .232x x -+D .2267x xy y --【习题2】下列因式分解错误的是（）．A .()()2a bc ac ab a b a c -+-=-+B .5315(5)(3)ab a b b a -+-=-+C .22619(31)(31)x xy y x y x y --+=+++-D .2326(3)(2)x xy x y x y x +--=+-【习题3】分解因式：25____(___)(4)x x x x ++=++．【习题4】若()()23x x -+是二次三项式2x mx n -+的因式分解的结果，则m 的值是_______．【习题5】若()()215x kx x a x b --=++，则a b +的值不可能是（）．A .14B .16C .2D .14-【习题6】分解因式：（1）3246____________ab a b -+-+=；（2）22____________a bx a cx bx cx --+=；（3）22244_____________a a b b --+=．【习题7】分解因式：（1）21024x +-；（2）2421x x --+；（3）22383x xy y +-；（4）42109x x -+．【习题8】分解因式：（1）2365()()m n m n -+-+；（2）()229()20a b ac bc c +-++．【习题9】分解因式：（1）22444a ab b --+；（2）322x x y xy y x y -+-+-；（3）22446129x xy y x y -+-++；（4）221194n n x x y +-+．【习题10】若一个长方形的周长为32，长为x ，宽为y ，且满足32230x x y xy y +--=．求这个长方形的面积．【习题11】用两种不同的分组方法分解因式：54321x x x x x +----．12 / 15【习题12】已知225302x x a a ++++=，求3x a +的值．【习题13】已知a b c d 、、、是整数，且7a b +=，7c d +=，判断ad bc -的值能否被7整除，并简要说明理由．【习题14】分解因式：（1）2235294x xy y x y +-++-；（2）2232453x xy y x y +++++．【习题15】分解因式：（1）()()226824x x x x +-+--；（2）()1(2)(3)(6)20x x x x +---+．【作业1】分解因式：（1）22524__________x xy y--=；（2）2236_______________x ax bx ab+++=；（3）22993______________x x y y+--=．【作业2】分解因式：（1）21220x x++；（2）212x x+-；（3）2121115x x--．【作业3】把下列各式因式分解：（1）222422x x y++-；（2）22ax bx ax bx a b+--++．【作业4】请将下列多项式因式分解，并求值：2233a b a b ab-+-，其中83a=，2b=．课后作业14 / 15【作业5】已知221547280x xy y -+=，求xy的值．【作业6】在因式分解多项式2x ax b ++时，小明看错了一次项系数后，分解得()()53x x ++，小华看错了常数项后，分解得()()42x x -+，求原多项式以及正确的因式分解的结果．【作业7】已知多项式2212x xy y --．（1）将此多项式因式分解；（2）若多项式2212x xy y --的值等于6-，且x y 、都是正整数，求满足条件的x y 、的值．【作业8】分解因式：（1）()2222()()()a b a c c d b d +++-+-+；（2）42222222()()x a b x a b -++-．【作业9】分解因式：（1）22268x y x y -++-；（2）432433x x x x ++++．【答案】【解析】【作业10】分解因式：（1）()22214()24x x x x +-++；（2）()2(1)1a b ab +-+；（3）(1)(1)(1)xy x y xy ++++；（4）()()22114x y xy --+．【作业11】已知正有理数a b c 、、满足方程组222229217226a b ac b c ab c a bc ⎧++=⎪++=⎨⎪++=⎩，求a b c ++的值．。

07第七讲 因式分解2

七年级数学因式分解2(中学课件2019)

七年级数学因式分解2

七年级数学因式分解2(PPT)2-1

七年级数学因式分解2

七年级数学因式分解2

七年级数学因式分解2

七年级数学因式分解2

七年级数学因式分解2

因式分解(二)

因式分解二

沪教版 七年级(上)数学 秋季课程 第7讲 因式分解(二)

07第七讲因式分解2

沪教版七年级(上)数学秋季课程第7讲因式分解(二)