气体动力学基础2 (13)

合集下载

气体动力学基础答案

气体动力学基础答案1. 什么是气体动力学？气体动力学是研究气体在力的作用下及热力学条件下的运动规律和性质的学科。

它主要研究气体的物理性质、状态方程以及气体的运动、扩散和传热等过程。

2. 描述气体的状态有哪些基本参数？气体的状态可以由以下几个基本参数来描述：•压力（P）：指气体分子对容器壁的撞击给容器壁单位面积上的力，通常以帕斯卡（Pascal）表示。

•体积（V）：指气体所占据的空间大小，通常以立方米（m³）表示。

•温度（T）：指气体的热度，通常以开尔文（Kelvin）表示。

•物质量（n）：指气体中的物质量，通常以摩尔（mol）表示。

这些参数可以通过状态方程来描述气体的状态，常见的状态方程有理想气体状态方程（PV=nRT）和范德瓦尔斯状态方程。

3. 什么是理想气体状态方程？理想气体状态方程是描述理想气体状态的数学公式，由理想气体定律得到。

理想气体状态方程可以表示为PV=nRT，其中P表示气体的压力，V表示气体的体积，n表示气体的物质量（摩尔数），R表示气体常量，T表示气体的温度（开尔文）。

理想气体状态方程可以用于描述气体的状态和变化，例如计算气体的压力、体积和温度的关系以及计算气体的摩尔数等。

4. 理想气体状态方程适用的条件有哪些？理想气体状态方程适用于以下条件下的气体：•气体分子之间不存在相互作用力；•气体分子之间的体积可以忽略；•气体分子之间的碰撞是完全弹性碰撞；•气体分子之间的相互作用不会受到温度的影响。

在实际情况下，很多气体都可以近似看作是理想气体，特别是在低密度、高温度的条件下。

但在高密度、低温度的情况下，气体分子之间的相互作用力会变得更加显著，此时理想气体状态方程将不再适用，需使用修正的状态方程进行计算。

5. 范德瓦尔斯状态方程是什么？范德瓦尔斯状态方程是对理想气体状态方程的修正，考虑了气体分子之间的相互作用力和气体分子的体积。

范德瓦尔斯状态方程可以表示为： \[ (P + \frac{an2}{V2})(V - nb) = nRT \] 其中P表示气体的压力，V表示气体的体积，n表示气体的物质量（摩尔数），R表示气体常量，T表示气体的温度（开尔文），a和b是范德瓦尔斯常量。

空气动力学基础空气动力学课件PPT

（2）层流附面层和紊流附面层
前段附面层内层流附面层。后段附面层紊流附面层。附面层由层流状态转变为紊流状态叫转捩转捩段转换段是很窄的区域，可近似看成一点，称为“转捩
点”。
转捩原因
流动距离越长，附面层内的分层流动越不稳机体表面对附面层施加扰动
在紊流附面层的底层，机体表面气流的阻滞作用要比层流附面层大得多。
1. 气流在机体表面的流动状态
（1）附面层（2）层流附面层和紊流附面层（3）附面层的分离
（1）附面层
附面层
沿机体表面法向方向，流速由零逐渐增加到外界气流流速的薄薄的一层空气层；机体表面到附面层边界(流速增大到外界气流流速99% 处)的距离为附面层的厚度（δ）
附面层的厚度越来越厚
(2) 减小压差阻力的措施
①尽量减小飞机机体的迎风面积。 ②暴露在空气中的机体各部件外形应采用流线型。 ③飞行时，除了起气动作用的部件外，其他机体部件的铀钱
应尽量与气流方向平行。
4. 干扰阻力
（1）干扰阻力的产生
流过机体各部件的气流在部件结合处互相干扰而产生的阻力干扰阻力与各部件组合时的相对位置有关，也和部件结合部
a平板翼型 b弯板翼型 c超临界翼型 d哥廷根398 e低亚音速翼型
f
g对称翼型，常用于尾翼 h i超音速菱形翼型
j超音速双弧形翼型
2.机翼平面形状和参数
机翼平面形状
机翼平面形状是飞机处于水平状态时，机翼在水平面上的投影形状
（a）矩形；（b）梯形；（c）椭圆形；
（d）后掠翼；（e）（f）和（g）为三角
在机翼的前缘有一点(A) ，气流速度减小到零，正压达到最大值，此点你为驻点。
机翼上表面有一点(B) ，气流速度最大，负压达到最大值，称为最低压力点。

流体力学第十二章气体动力学基础.ppt

s d
由理想气体状态方程故
p RT

p

kRT
s
第6页
（12.6）
退出返回
第十二章
气体动力学基础第一节压力波的传播，音速
流体力学
中国科学文化出版社
退出
第十二章气体动力学基础
第一节压力波的传播，音速第二节运动点扰源产生的扰动场，马赫数与马
赫角第三节一元稳定等熵流动的基本方程第四节理想气体一元稳定等熵流动的基本特性第五节气流参数与流道截面积的关系第六节渐缩喷管和拉伐尔喷管
退出返回
第十二章
气体动力学基础第一节压力波的传播，音速
为压缩声波，反之，就称为膨胀声波。如果活塞左右作微小的往复振动，那么就有压缩声波和膨胀声波间隔地以音速a 向右传播，声波到达处的流体
跟着作微小的左右往复振动。
由于微弱扰动传播过程中介质压力、密度和温度变化很小，因此可假定这
个过程是等熵过程，即
第5页
退出返回
第十二章
气体动力学基础第一节压力波的传播，音速
第3页
退出返回
第十二章
气体动力学基础第一节压力波的传播，音速
而扰动未波及处，流体仍是静止的，压力和密度仍为 p、。如果原来管内的流体不是静止的，而是以均匀速度 w 向右流动，那么加一微弱扰动后的情形就如图12.2（b）所示。这时微弱扰动在流速为 w 的流体中以相对速度a 传播，且传播的绝对速度与流体运动的速度 w 有关。在顺流方向，微弱扰动的绝对传播速度为 a w；在逆流方向，微弱扰动的绝对传播速度为 a w。显然在上述两种情况下，管内流体的运动都是不稳定的。为了方便分析，设想将坐标系固连在以速度 a 或 w a 前进的压力分界面上，这样相对该坐标来说，流动就是稳定的，如图12.2（c）所示。站在相对坐标上的观察者看到流体稳定地从右向左流动，穿过压力分界面时，速度由 a 降至 a dw ，而压力由 p 升高到p dp ，密度由增加为 d 。

《气体动力学》课件-绪论

声速
166x Galileo Galilei 认识声速和光速差别
1500 Leonardo Da Vinci, 发现声音以波的形式传播
1640 Marin Mersenne 首次测量声音在空气中的传播速度
1660 Robert Boyle 发现声音传播必须有介质
1687 Newton 推导声速关系式；Maxwell 推导声速关系式
1910 瑞利和泰勒
激波的不可逆性
1933 泰勒和马科尔
圆锥激波的数Biblioteka 解气体动力学基础_113
1.3 气体动力学发展简史
第三阶段：气体热力学发展阶段（20世纪30年代中50年代末）
1935年召开“航空中的高速流动问题”学术大会，表明流体力学先驱者对高速问题的关注和重视。之后，由于以喷气飞机、涡轮喷气发动机、火箭发动机等为背景的工程问题发展的需求，将空气动力学与热力学相结合，这个时期为气体热力学的发展阶段，其特点是在完全气体假设下的气体动力学理论和实验逐渐成熟
气体动力学基础_1
11
1.3 气体动力学发展简史
第一阶段：气体动力学基础阶段
1869 1987
1881
1883 1887 1899 1905 1902
朗金/兰金(英) 雨贡钮/许贡纽(法)
描述大波幅强扰动波－激波的兰金(英)－许贡纽 (法)理论
贝特洛Berthelot(法) 马兰德Mallard
实验发现管中火焰传播速度高达1－3.5 km/s （超音速3-10倍）的超音速燃烧现象，爆轰波＝激波＋燃烧波
气动是在经典流体力学的基础上，结合热力学和化学动力学发展起来（气动热力学），可分为
亚音速流动，跨音速流动，超音速流动高超音速流动

气体动力学基础

气体动力学基础气体动力学是研究气体运动规律以及与其他物体之间相互作用的学科。

它的研究对象包括气体的压力、体积、温度和分子速度等特性，以及这些特性之间的相互关系。

本文将介绍气体动力学的基础概念、理论模型和重要定律。

一、气体分子模型气体分子模型是气体动力学研究的基础，它假设气体是由大量极小的分子组成的。

这些分子之间几乎没有相互作用力，它们以高速不规则运动，并且具有各向同性的特性。

二、理想气体状态方程理想气体状态方程是描述气体状态的基本定律之一。

根据理想气体状态方程，气体的压力（P）、体积（V）和温度（T）之间存在着下列关系：P * V = n * R * T其中，n代表气体的摩尔数，R代表气体常数。

这个方程表明，在一定温度和摩尔数的条件下，气体的压力和体积成反比，而与气体的物理性质（例如分子大小和形状）无关。

三、气体的压强气体分子在容器壁上会产生压力，这种压力被称为气体的压强。

根据气体分子的运动特性，我们可以得到气体的压强与分子速度和撞击频率之间的关系。

通常情况下，气体的压强与气体分子的速度平方成正比。

四、气体的温度气体的温度是指气体分子的平均动能。

根据气体分子模型，气体分子的速度与其温度之间呈正相关关系。

在绝对温标上，温度与气体分子的平均动能之间存在着线性关系。

五、气体的体积气体的体积是气体占据的空间大小。

根据观察和实验结果，气体的体积与其分子数量和分子碰撞的频率有关。

当温度不变时，气体的体积与其压强成反比。

六、亚音速和超音速流动亚音速流动是指气体在流动过程中，流速小于音速的情况。

这种流动模式下，气体能够传递信息，且压力和温度分布相对均匀。

超音速流动则是指气体的流速大于音速。

在超音速流动中，气体的压力和温度存在明显的不均匀分布。

七、伯努利定理根据伯努利定理，沿着气体流动的方向，气体的总能量保持不变。

这意味着当气体流速增大时，气体的压强会降低，从而产生较低的静压力。

八、霍金定理霍金定理是描述亚音速气体流动的基本原理。

气体动力学的基础理想气体和真实气体的特性

气体动力学的基础理想气体和真实气体的特性气体动力学是研究气体在不同条件下的运动和相互作用的学科。

在气体动力学中，我们通常将气体分为两种类型：理想气体和真实气体。

理想气体是指具有一些理想特性的气体模型，而真实气体则更接近于实际气体的行为。

本文将介绍理想气体和真实气体的基本特性和区别。

一、理想气体的特性理想气体是一种理论模型，用于描述气体在一定条件下的行为。

它具有以下几个基本特性：1. 分子无体积：理想气体假设分子的体积可以忽略不计，因此分子之间不存在相互作用。

2. 分子无吸引力和斥力：理想气体假设分子之间没有相互引力或斥力，它们只在碰撞瞬间产生弹性碰撞。

3. 分子运动无规律：理想气体假设分子运动是无规律的，碰撞时的速度和方向是随机的。

4. 温度与能量成正比：理想气体的温度是由分子的平均动能决定的，温度越高，分子的平均动能越大。

5. 状态方程：理想气体的状态可以由状态方程表示，最常用的是理想气体状态方程PV=nRT（P为气体压强，V为体积，n为物质的摩尔数，R为气体常数，T为气体的绝对温度）。

二、真实气体的特性真实气体与理想气体相比，更接近于实际气体的行为。

尽管真实气体的行为更复杂，但我们仍可以总结出一些共同的特性和区别：1. 分子有体积：真实气体中的分子具有一定的体积，相比于容器的体积来说可以忽略不计，但在高压和低温条件下，分子间的体积效应将变得显著。

2. 分子间有相互作用：真实气体分子之间存在吸引力和斥力，这种相互作用会影响气体的压强、体积和温度。

3. 分子运动有规律：真实气体分子的运动是有规律的，符合动量守恒和能量守恒定律。

4. 温度与能量关系复杂：真实气体的温度与分子的平均动能之间的关系并不像理想气体那样简单，因为分子间的相互作用会导致分子的动能分布不均匀。

5. 状态方程复杂：真实气体的状态方程并非像理想气体状态方程那样简洁，不同的气体有不同的状态方程，例如范德华方程等。

总结：理想气体和真实气体是描述气体行为的两种模型。

气体动力学基础

ห้องสมุดไป่ตู้
连续介质分子间隙
§1.2 流体的粘性
虚拟演示粘性演示 PLAY
定义：在流动的流体中，定义：在流动的流体中，如果各流体层的流速不相等，不相等，那么在相邻的两流体层之间的接触面就会形成一对等值而反向的内摩擦力（上，就会形成一对等值而反向的内摩擦力（或粘性阻力）来阻碍两气体层作相对运动。粘性阻力）来阻碍两气体层作相对运动。即流体质点具有抵抗其质点作相对运动的性质，体质点具有抵抗其质点作相对运动的性质，就称为流体的粘性。称为流体的粘性。
例2 续
于是作用在轴表面的阻力矩为 M= τAr= V/ δ πdl d/2 消耗的功率 N=Mω=V/δ πdld/2 2πn/60 ω δ π π =0.72 3.77/(0.2 10-3) π 0.36 1 0.36/2 2π π π 200/60 =57.9(kw)
第二阶段（第二阶段（可压缩流体动力学的发展阶段）的发展阶段）
1908年普朗特和迈耶提出了激波和膨胀年普朗特和迈耶提出了激波和膨胀波理论 1910年瑞利和泰勒研究得出了激波的不年瑞利和泰勒研究得出了激波的不可逆性；可逆性； 1933年泰勒和马科尔提出了圆锥激波的年泰勒和马科尔提出了圆锥激波的数值解
粘性举例
譬如看看河中的流水，譬如看看河中的流水，观察水面上漂浮的树叶等物的速度差别可以发现靠岸处的水流就比河中心的水流慢这是典型的粘性影响. 些。这是典型的粘性影响摩擦盘也是粘性力在起作用。摩擦盘也是粘性力在起作用。
粘性产生的物理原因
分子不规则运动的动量交换分子间的吸引力
y
v≈v ∞ v ∞
=(F/A) (h/V)=0.004 N s/ m2
【例2】转轴直径d=0.36m，轴承长度l=1m，轴与轴承之间的缝转轴直径d=0.36m，轴承长度l=1m， d=0.36m l=1m 隙宽度δ=0.2mm其中充满 =0.72Pas的油，其中充满 s的油隙宽度δ=0.2mm其中充满=0.72Pas的油，若轴的转速 n=200r/min，求克服油的粘性阻力所消耗的功率。 n=200r/min，求克服油的粘性阻力所消耗的功率。【解】由驱动力矩=阻力力矩得到由驱动力矩阻力力矩得到 τ1(2πr1l)r1= τ2 (2πr2l)r2 π π 再由 τ=dV/dy (dV/dy)1=(dV/dy)2 (r2/r1)2 则得因为缝隙很小，近似认为r 因为缝隙很小，近似认为 1=r2，速度成线性分布即速度梯度为 dV/dy=V/ δ 其中，粘附于轴表面的油的运动速度V等于轴表面的周向速度等于轴表面的周向速度，其中，粘附于轴表面的油的运动速度等于轴表面的周向速度，即 V= πdn/60= π 0.36 200/60=3.77m/s

空气动力学公式范文

空气动力学公式范文空气动力学公式指的是描述物体在空气中受力和运动的数学公式。

在工程和物理学领域中，空气动力学公式被广泛应用于空气动力学研究、航空航天工程设计、汽车设计以及建筑设计等方面。

下面是一篇超过1200字的空气动力学公式范文，介绍了一些常见的空气动力学公式及其应用。

一、气体动力学理论基础在空气动力学研究中，气体动力学理论是非常重要的基础。

根据气体动力学理论，气体中的压力（P）、密度（ρ）和温度（T）之间存在一定的关系。

根据理想气体状态方程，可以得到如下公式：1.理想气体状态方程P=ρRT其中，P为气体的压力，ρ为气体的密度，R为气体的气体常数（通常为287 J/(kg·K)），T为气体的绝对温度。

2.理想气体压力与温度之间的关系P∝T根据理想气体状态方程，可以得出气体的压力与温度成正比。

二、飞行器气动力学公式在航空航天工程中，空气动力学公式用于描述飞行器受力和运动过程。

以下是一些常见的飞行器气动力学公式及其应用。

1.飞行器升力与气动系数之间的关系L = 0.5C_liftρV^2S其中，L为飞行器的升力，C_lift为升力系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积。

2.飞行器阻力与气动系数之间的关系D = 0.5C_dragρV^2S其中，D为飞行器的阻力，C_drag为阻力系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积。

3.飞行器侧向力与气动系数之间的关系Y = 0.5C_sideρV^2S其中，Y为飞行器的侧向力，C_side为侧向力系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积。

4.飞行器俯仰力矩与气动系数之间的关系M_pitch = 0.5C_pitchρV^2SC_bar其中，M_pitch为飞行器的俯仰力矩，C_pitch为俯仰力矩系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积，C_bar为平均气动弦长。

三、车辆空气动力学公式在汽车设计中，空气动力学公式用于描述汽车在行驶过程中受到的空气阻力。

气体动力学基础试题与答案

一、解释下列各对名词并说明它们之间的区别与联系 1．轨线和流线2．马赫数M 和速度系数λ 5．膨胀波和激波二、回答下列问题1．膨胀波在自由表面上反射为什么波为什么4．收敛喷管的三种流动状态分别是什么各有何特点三、（１2分）已知压气机入口处的空气温度Ｔ１＝２８０Ｋ，压力Ｐ１=１.０bar ，在经过压气机进行可逆绝热压缩以后，使其压力升高了２５倍，即增压比Ｐ２／Ｐ１＝２５，试求压气机出口处温度和比容，压气机所需要的容积功。

设比热容为常数，且比热比k=。

四、空气沿如图1所示的扩散管道流动，在截面1-1处空气的压强5110033.1⨯=p N/m 2,温度ο151=t C,速度2721=V 米/秒，截面1-1的面积1A =10厘米2，在截面2-2处空气速度降低到2V =米/秒。

设空气在扩散管中的流动为绝能等熵流动，试求：（1）进、出口气流的马赫数1M 和2M ；（2）进、出口气流总温及总压；（3）气流作用于管道内壁的力。

六、(15分)在超声速风洞的前室中空气的滞止温度为T *=288K,在喷管出口处空气的速度V 1=530米/秒，当流过试验段中的模型时产生正激波（如图1所示），求激波后空气的速度。

图 1 第四题示意图图2 第五题示意图一、解释下列各对名词并说明它们之间的区别与联系（共２０分，每题４分）1．轨线和流线答：轨线是流体质点运动的轨迹；流线是一条空间曲线，该曲线上任一点的切线与流体在同一点的速度方向一致。

区别：轨线的是同一质点不同时刻的位置所连成的曲线；流线是同一时刻不同质点运动速度矢量所连成的曲线。

联系：在定常流动中轨迹线和流线重合。

2．马赫数M和速度系数λ答：马赫数M是气体运动速度与当地声速的比值；速度系数λ是气体运动速度与临界声速的比值。

区别：速度相同时气体的马赫数与静温有关，最大值为无限大，而速度系数于总温有关，其最大值为有限值。

联系：已知马赫数可以计算速度系数，反之亦然。

3．膨胀波和激波答：膨胀波是超声速绕外钝角偏转或加速时所产生的压力扰动波；激波是超音速气流流动方向向内偏转所产生强压缩波。

气体动力学课后习题答案

气体动力学课后习题答案气体动力学课后习题答案气体动力学是研究气体在不同条件下的行为和性质的学科。

它涉及到许多基本概念和公式，需要通过大量的练习来加深理解和掌握。

下面是一些常见的气体动力学习题及其答案，希望对大家的学习有所帮助。

1. 一个气体体积为3L，温度为300K，压强为2 atm，求气体的物质的量。

答案：根据理想气体状态方程PV=nRT，其中P为压强，V为体积，n为物质的量，R为气体常数，T为温度。

将已知条件代入方程，得到n = PV/RT = (2 atm × 3L) / (0.0821 atm·L/mol·K × 300K) ≈ 0.296 mol。

2. 一定体积的气体在常温下压强为1 atm，将其加热至温度翻倍时，求新的压强。

答案：根据查理定律，当气体的温度和物质的量不变时，气体的压强与温度成正比。

即P1/T1 = P2/T2。

已知P1 = 1 atm，T1为常温，T2为常温翻倍后的温度。

代入已知条件，得到P2 = P1 × T2/T1 = 1 atm × 2/1 = 2 atm。

3. 一个气体在压强为2 atm、温度为300K的条件下体积为3L，将其压缩至体积减少一半，求新的温度。

答案：根据波义耳定律，当气体的压强和物质的量不变时，气体的体积与温度成反比。

即V1/T1 = V2/T2。

已知V1 = 3L，T1 = 300K，V2 = V1/2。

代入已知条件，得到T2 = T1 × V1/V2 = 300K × 3L/(3L/2) = 600K。

4. 一个容器中有1 mol的气体，在常温下体积为10L，将其压缩至体积减少一半，求新的物质的量。

答案：根据阿伏伽德罗定律，当气体的压强和温度不变时，气体的物质的量与体积成正比。

即n1/V1 = n2/V2。

已知n1 = 1 mol，V1 = 10L，V2 = V1/2。

《气体动力学》课件-膨胀波与激波

及波AB、BC、A’B、B’C 的波角
气体动力学基础_1
29
3.5 弱波的反射与相交
膨胀波在自由边界的反射
自由边界：运动介质和其它介质之间的切向交界面
边界特性：接触面两边的压强相等
C’
A’
⑤
p2 p3 pa p4 pa p5 p6 pa
Ma1
②
max
()
2
k k
1 1
1
Ma=1 O
k 1.4, max 13027
气体动力学基础_1
20
13027
3.3 弱波的普朗特-迈耶流动解
Prandtl-Meyer 流动——超声速气流流过外凸壁
右伸波： (Ma) C2
(Ma) 1 (Ma1 ) C2
➢ 对于任意两个马赫数Ma1和Ma2 的膨胀过程，有
➢ 超声速气流每经过一步微弱的膨胀，气流的流动方向、马赫数和压强等诸气流参数都将产生微小的变化
➢ 把原来的连续膨胀分得愈细，数目愈多，计算出来的结果就
气体愈动准力学确基础_1
27
3.5 弱波的反射与相交
膨胀波在直固壁上的反射
B
①
i
②
Ma1
Ma2
1 2
③
Ma3
3
A
C
➢ 膨胀波在固壁上反射为膨胀波，一般反射角 γ 并不等于入射角i
7
3.1 弱扰动的传播规律
4. 气流运动——超声速
➢马赫角 μ 的大小，反映了受扰
4c
动区域的大小
V>c
3c 2c c
sin1 1
Ma
O
O1
O2
O3
O4
Vn Vt
V

气体动力学的基本原理

气体动力学的基本原理气体动力学是研究气体在运动中的物理性质和行为的学科，其基本原理涉及气体的压力、体积、温度以及分子运动等方面。

本文将介绍气体动力学的基本原理，包括理想气体状态方程、分子速度分布和碰撞等相关内容。

一、理想气体状态方程理想气体状态方程是描述气体状态的基本关系式，表达为PV = nRT，其中P表示气体的压力，V表示气体的体积，n表示气体的摩尔数量，R表示气体常量，T表示气体的温度。

根据理想气体状态方程，可以推导出布尔定律、盖-吕萨克定律以及查理定律等气体性质和规律。

二、分子速度分布气体分子在运动中具有不同的速度分布，其分子速度与温度有关。

根据麦克斯韦分布定律（麦分布），分子速度分布可以用麦克斯韦-玻尔兹曼速度分布函数来描述。

该函数表示各个速度分量的分布概率密度，可以用于计算气体中分子的平均速度、最概然速度和均方根速度等重要参数。

三、碰撞气体分子之间的碰撞是气体动力学中重要的研究内容。

分子之间的碰撞导致气体分子的运动方向和速度发生变化，从而实现了气体的传导、散射和扩散等现象。

碰撞模型可通过玻尔兹曼方程进行描述，该方程反映了气体分子数密度随时间和空间变化的关系，是研究气体动力学的重要工具。

四、气体扩散气体扩散是气体动力学的重要研究内容之一，涉及气体分子的运动和传播过程。

根据菲克定律，气体在压力差驱动下会自然地由高压区向低压区扩散。

扩散速率与温度、压力以及气体分子的大小和形状等因素有关，可通过斯托克斯-爱因斯坦方程进行定量计算。

总结：本文介绍了气体动力学的基本原理，包括理想气体状态方程、分子速度分布和碰撞以及气体扩散等方面。

这些原理为我们理解和解释气体的运动和行为提供了基础，也为相关领域的应用提供了理论支持。

理解气体动力学的基本原理对于工程技术和科学研究都具有重要意义。

气体动力学基础(2)

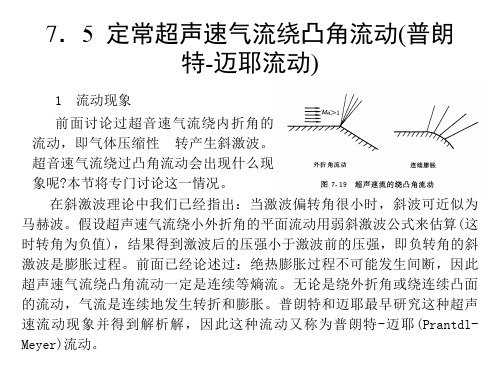
1
*u*A* A**a* A* p00 2 1 2( 1)
(7.66)′
堵塞流量是给定滞止参数下，变截面管流中气体等熵流动可能达到的最
大流量。就是说，当滞止参数给定后，管道出口压强降低时，通过管道的
气体流量不断增加；当流量达到堵塞流量后，再降低出口压强，通过管道
的流量不会再增加。根据变截面气体的等熵流动原理，这时在管道的最小截面上，气体流速达到当地声速，而这一速度是气流在最小截面上的最大速度，无论怎样减小出口压强，都不会使最小截面上的速度增大。
2 普朗特-迈耶(P-M)流动关系式
我们来分析连续转折的超声速气流运动。均匀气流在某一直线上开始发生膨胀转折，而后超声速气流绕凸角的平面流动，它通过一系列连续转折的马赫波完成等熵膨胀，因此连续转折的马赫波又称马赫线或膨胀波。根据上述分析我们首先导出超声速气流通过一道马赫线微弱膨胀的 P-M关系式。
亚声速定常等熵流在收缩通道中将加速，但始终保持亚声速；超声速定常等熵流在收缩通道中将减速，但始终保持超声速。如图7．24所示。
(2)扩张通道流动亚声速定常等熵流在扩张通道中将减速，并保持亚声速；超声速定常等熵流在扩张通道中将加速，且始终保持超声速。如图7．25所示。
(3)收缩扩张管流收缩扩张通道中气体等熵流动情况较简单收缩或扩张通道中流动复杂。
主流速度远远大于横向速度，准一维假定是很好的近似。从几何边界条件
来说：如果通道截面的变化率很小，就能满足一维近似的要求。具体来说
，准一维近似要求： L A 1 ，其中L是通道的特征长度。 A x
如果外界没有热量输入，气体流动过程也没有化学反应、蒸发等内部
生成热，气体的粘度又很小，气体流动可以认为是理想绝热的。下面我们

气体动力学

气体动力学是流体力学的一个分支。

在连续介质的假设下，研究了与热力学现象有关的气体运动规律及其与相对运动物体的相互作用。

气体在低速时是不可压缩的流动，其热力学状态的变化可以忽略不计；但是，在高速流动时（例如，马赫数大于0.3），气体的压缩效果不容忽视，其热力学状态也发生明显变化。

气体运动应同时满足流体力学和热力学定律。

气体动力学[1] [2]由流体力学和热力学的紧密结合形成。

书籍目录第一章基础知识第二章是流体运动的基本方程第三章一维稳态流基本方程第四章停滞参数与空气动力功能第五章膨胀波和冲击波1个气体动力学空气动力学始于射弹运动和蒸汽轮机的研究。

随着航空航天业的蓬勃发展，出现了许多新的分支机构。

高温气体动力学高温气体动力学。

研究了高温气体的流动规律及其伴随的理化变化，能量传递和转化规律。

例如，在喷气发动机的燃烧室中，重返航天器表面的冲击层和高超音速尾流，气体温度极高，气体的比热不再恒定，并且完美的气体状态方程（p =ρRT，P，ρ，T为气体的压力，密度和温度，R为气体常数）不再适用。

另外，气体分子中各种能级的激发（平移，旋转和振动等）处于不平衡状态，导致流动不平衡。

在非常高的温度下，气流伴随着离解和电离过程以及物体表面的烧蚀。

因此，对高温气体动力学的研究应将气体动力学与热力学，统计物理学，分子物理学，化学动力学和电磁学相结合，并使用物理，化学和气体动力学等实验技术，光谱，激光，电子学等测量方法机械师和测试设备，例如冲击管和电弧加热器。

高温气体动力学的研究对航空航天工业，激光和等离子体技术的发展具有重要意义。

稀有气体动力学稀有气体的动力学。

研究了努氏数Kn（见流体力学相似性准则）不小于1的稀有气体的运动规律。

对于在高空飞行的航天器来说，Kn 值不小，并且气体分子的离散结构显示出其影响，因此经典连续谱模型不再适用。

在研究5微米以下的气溶胶颗粒在地面上的运动时，我们还应考虑稀有气体效应。

为了研究稀有气体动力学，需要玻尔兹曼气体分子运动方程和气体分子与固体表面相互作用的理论，以及低密度风洞，冲击风洞和分子束装置等实验设备。

空气动力学复习资料

空气动力学复习一、基本概念1 粘性施加于流体的应力和由此产生的变形速率以一定的关系联系起来的流体的一种宏观属性，表现为流体的内摩擦。

以气体为例，气体分子的速度是由平均速度和热运动速度两部分叠加而成，前者是气体团的宏观速度，后者决定气体的温度。

若相邻两部分气体团以不同的宏观速度运动，由于它们之间有许多分子相互交换，从而带来动量的交换，使气体团的速度有平均化的趋势，这便是气体粘性的由来。

2 压缩性流体的压缩性是流体质点在一定压力差或温度差的条件下，其体积或密度可以改变的性质。

其物理意义是：单位体积流体的体积对压强的变化率。

气体流速变化时，会引起气体的压强和密度发生变化。

在低速气流中，由于气流速度变化而引起的气体密度的相对变化量很小，可以把气体看作不可压缩流体来处理；高速气流压缩性的影响不能忽略，必须按可压流体来处理。

一般0.3Ma作为气体是否可压的分界点。

3 理想气体忽略气体分子的自身体积，将分子看成是有质量的几何点；假设分子间没有相互吸引和排斥，即不计分子势能，分子之间及分子与器壁之间发生的碰撞是完全弹性的，不造成动能损失。

这种气体称为理想气体。

严格遵从气体状态方程的气体，叫做理想气体(Ideal gas.有些书上，指严格符合气体三大定律的气体。

）从微观角度来看是指：气体分子本身的体积和气体分子间的作用力都可以忽略不计，不计分子势能的气体称为是理想气体。

4 焓热力学中表征物质系统能量的一个重要状态参量，焓的物理意义是体系中热学能（内能）再附加上PV（压能）这部分能量的一种能量。

5理想流体不可压缩、不计粘性（粘度为零）的流体。

欧拉在忽略粘性的假定下，建立了描述理想流体运动的基本方程。

理想流体和理想气体是两个不同的概念，前者指流体没有粘性，后者指气体状态参量满足气体状态方程的气体。

6 音速音速是介质中弱扰动的传播速度，其大小因媒质的性质和状态而异。

在流动的气体中，相对于气流而言，微弱扰动的传播速度也是声速。

气体动力学基础试题与答案

设比热容为常数，且比热比k=。

四、空气沿如图1所示的扩散管道流动，在截面1-1处空气的压强5110033.1⨯=p N/m 2,温度 151=t C,速度2721=V 米/秒，截面1-1的面积1A =10厘米2，在截面2-2处空气速度降低到2V =米/秒。

设空气在扩散管中的流动为绝能等熵流动，试求：（1）进、出口气流的马赫数1M 和2M ；（2）进、出口气流总温及总压；（3）气流作用于管道内壁的力。

区别：轨线的是同一质点不同时刻的位置所连成的曲线；流线是同一时刻不同质点运动速度矢量所连成的曲线。

联系：在定常流动中轨迹线和流线重合。

2．马赫数M和速度系数λ答：马赫数M是气体运动速度与当地声速的比值；速度系数λ是气体运动速度与临界声速的比值。

区别：速度相同时气体的马赫数与静温有关，最大值为无限大，而速度系数于总温有关，其最大值为有限值。

联系：已知马赫数可以计算速度系数，反之亦然。

3．膨胀波和激波答：膨胀波是超声速绕外钝角偏转或加速时所产生的压力扰动波；激波是超音速气流流动方向向内偏转所产生强压缩波。

(仅供参考)气体动力学基础王新月1-6章答案

y
y
t=0 时 x/y=1
② dx x 积分得x (1 t)C dt 1 t
t=0 时，x=1 带入得 C=3
dy y积分得y e(tC) dt
t=0 时，y=1 带入得 C=0
x 1t
迹线方程
y ex1(t 0时的迹线)
y et
3.5 解： dx dy y 2 2 y 2tx 0 1 y t
by
3 AE
（二）作用点计算 yD1 yC
JC yC AAE
h1C sin
12 yC AAE
0.7695 m
hD1 yD1 sin 0.666m
by
2 EB
3 2
hDBE
hCEB
J C sin a yC2 AEB
1
12 yC2 AEB
yC2
h1 h2 / 2 (h h / 2) * sin a
2 3
4/
3 2.309
AEB
LEB
b
h2 b sin a
4/
3 2.309
板 BE 的几何中心 y 的坐标为 yC2
by
3 BE
y
' D
2
yC' 2
JC2 yC 2 ABE
yEC 2
JC2 yEC 2 LBE
h2 / 2 sin a
12 yEC 2 LBE
距点 E：
h2 1.1547 sin a 1.1547 0.16667 1.32137
当 t=1;x=0;y=0 时 y 2 2y 2x 0
3.6 解：Vx x2 y ；Vy 4 y; Vz 3z 2
由式
3.10
得到
a
(2x3