2017年秋季新版浙教版七年级数学上学期6.9、直线的相交同步练习

合集下载

浙教版初中数学七年级上册《6.9 直线的相交》同步练习卷

浙教新版七年级上学期《6.9 直线的相交》同步练习卷一．填空题（共20小题）1．在同一平面内，两条相交直线公共点的个数是；两条平行直线的公共点的个数是；两条直线重合，公共点有个．2．观察如图图形，并阅读图形下面的相关文字．像这样的十条直线相交最多的交点个数有．3．如图所示，直线AB、CD相交于O，∠BOC＝135°，则直线AB与直线CD 的夹角是°．4．当光线从空气中射入水中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射，如图，AB与CD相交于水平面点F，一束光线沿CD射入水面，在点F处发生折射，沿FE射入水内．如果∠1＝50°，∠2＝36°，则光的传播方向改变了度．5．如图，已知直线AB、CD交于点E，EF⊥CD，∠AEF＝50°，那么∠BED＝°．6．如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1＝30°，则∠2＝．7．如图，把水渠中的水引到水池C，先过C点向渠岸AB画垂线，垂足为D，再沿垂线CD开沟才能使沟最短，其依据是．8．如图，点P在直线l外，PB⊥l于B，A为l上任意一点，则P A与PB的大小关系是P A PB．9．在△ABC中∠B＝90°，BC＝5，AB＝12，AC＝13，则点B到斜边AC的距离是．10．如图，BC⊥AC，BC＝8，AC＝6，AB＝10，则点C到线段AB的距离是．11．平面内有10条直线两两相交，交点个数最多有m个，最少有n个，则m+n 的值为．12．平面内有n条直线，任意两条直线都相交，则最多有个交点．13．已知，直线AB和直线CD交于点O，∠BOD是它的邻补角的3倍，则直线AB与直线CD的夹角是度．14．如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE 表示正东方向，已知射线OB的方向是南偏东60°，射线OC在∠NOE内，且∠NOC与∠BOS互余，射线OA平分∠BON，图中与∠COA互余的角是．15．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠CON＝2∠COM，则∠BOD的度数为．16．如图，已知AO⊥BC于O，∠AOD＝30°，那么∠DOC＝°．17．如图，体育课上老师测量跳远成绩是这样操作的：用一块直角三角板的一边附在踏跳板上，另一边与拉直的皮尺重合，并且使皮尺经过被测试同学的落点，这样做的理由是．18．如图，点A，B，C，D，E在直线l上，点P在直线l外，PC⊥l于点C，在线段P A，PB，PC，PD，PE中，最短的一条线段是，理由是19．如图，CD⊥AB，点E、F在AB上，且CE＝10cm，CD＝8cm，CF＝12cm，则点C到AB的距离是．20．如图，点B到直线DC的距离是指线段的长度．二．解答题（共15小题）21．在同一平面内有四条直线（1）这四条直线的交点个数可能有哪些？（2）请你画出两种交点个数是4的图形．22．如图，直线AB，CD相交于点O，OF平分∠AOC，∠COE＝90°，∠DOF ＝160°．（1）求∠COF的度数；（2）求∠BOE的度数．23．如图，直线AB，CD相交于点O，OE⊥CD于点0，OD平分∠BOF，∠BOE ＝50°，求∠AOC，∠AOF，∠EOF的度数．24．如图，在直线MN的异侧有A、B两点，按要求画图取点，并注明画图取点的依据．（1）在直线MN上取一点C，使线段AC最短．依据是．（2）在直线MN上取一点D，使线段AD+BD最短．依据是．25．如图，点A表示小雨家，点B表示小樱家，点C表示小丽家，她们三家恰好组成一个直角三角形，其中AC⊥BC，AC＝900米，BC＝1200米，AB＝1500米．（1）试说出小雨家到街道BC的距离以及小樱家到街道AC的距离．（2）画出表示小丽家到街道AB距离的线段．26．观察下列图形，阅读下面的相关文字并回答以下问题：两条直线相交三条直线相交四条直线相交只有一个交点最多的3个交点最多有6个交；猜想：①5条直线相交最多有几个交点？②6条直线相交最多有几个交点？③n条直线相交最多有n个交点？27．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？28．如图，直线AB，CD相交于点O，OA平分∠EOC．若∠EOC＝68°，求∠BOD的度数．29．如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC＝80°，求∠BOD的度数；（2）若∠EOC＝∠EOD，求∠BOD的度数．30．如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD＝38°，求∠AOC和∠COB的大小．31．如图，AOB为一直线，∠AOD：∠DOB＝3：1，OD平分∠COB．请判断AB与OC的位置关系．32．已知：点P是直线MN外一点，点A、B、C是直线MN上三点，分别连接P A、PB、PC．（1）通过测量的方法，比较P A、PB、PC的大小，直接用“＞”连接；（2）在直线MN上能否找到一点D，使PD的长度最短？如果有，请在图中作出线段PD，并说明它的理论依据；如果没有，请说明理由．33．如图，点P，点Q分别代表两个村庄，直线l代表两个村庄中间的一条公路．根据居民出行的需要，计划在公路l上的某处设置一个公交站．（1）若考虑到村庄P居住的老年人较多，计划建一个离村庄P最近的车站，请在公路l上画出车站的位置（用点M表示），依据是；（2）若考虑到修路的费用问题，希望车站的位置到村庄P和村庄Q的距离之和最小，请在公路l上画出车站的位置（用点N表示），依据是．34．如图，点M，N分别在直线AB，CD上．（1）请在图中作出表示M，N两点间的距离的线段a，和表示点N到直线AB的距离的线段b；（2）请比较（1）中线段a，b的大小，并说明理由．35．如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；（1）过点P画OA的垂线，垂足为H；（2）线段PH的长度是点P到的距离，是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是（用“＜”号连接）浙教新版七年级上学期《6.9 直线的相交》同步练习卷参考答案与试题解析一．填空题（共20小题）1．在同一平面内，两条相交直线公共点的个数是1个；两条平行直线的公共点的个数是0个；两条直线重合，公共点有无数个．【分析】先画出两条直线平行、相交及重合的图示，再由其交点情况进行解答．【解答】解：如图所示：由（1）可知同一平面内，两条相交直线公共点的个数是1个；由（2）可知两条平行直线的公共点的个数是0个；由（3）可知两条直线重合，公共点有无数个．故答案为：一个、0个、无数．【点评】本题考查的是两条直线的位置关系，即相交、平行、重合．2．观察如图图形，并阅读图形下面的相关文字．像这样的十条直线相交最多的交点个数有45．【分析】根据直线两两相交且不交于同一点，可得答案．【解答】解：十条直线相交最多的交点个数有＝45，故答案为：45．【点评】本题考查了相交线，n每条直线都与其它直线有一个交点，可有（n﹣1）个交点，n条直线用n（n﹣1）个交点，每个交点都重复了一次，n条直线最多有个交点．3．如图所示，直线AB、CD相交于O，∠BOC＝135°，则直线AB与直线CD 的夹角是45°．【分析】先根据邻补角的定义求出∠AOC，再根据直线的夹角为锐角解答．【解答】解：∵∠BOC＝135°，∴∠AOC＝180°﹣∠BOC＝180°﹣135°＝45°，∴直线AB与直线CD的夹角是45°．故答案为：45．【点评】本题考查了邻补角的定义，要注意直线的夹角是锐角．4．当光线从空气中射入水中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射，如图，AB与CD相交于水平面点F，一束光线沿CD射入水面，在点F处发生折射，沿FE射入水内．如果∠1＝50°，∠2＝36°，则光的传播方向改变了14度．【分析】根据对顶角相等得出∠DFB＝∠1，进而解答即可．【解答】解：∵∠1＝50°，∴∠DFB＝∠1＝50°，∵∠2＝36°，∴∠DFE＝50°﹣36°＝14°，故答案为：14【点评】此题考查对顶角问题，关键是根据对顶角相等得出∠DFB＝∠1．5．如图，已知直线AB、CD交于点E，EF⊥CD，∠AEF＝50°，那么∠BED＝40°．【分析】根据垂直的定义可得∠CEF＝90°，然后求出∠AEC，再根据对顶角相等解答．【解答】解：∵EF⊥CD，∴∠CEF＝90°，∴∠AEC＝∠CEF﹣∠AEF＝90°﹣50°＝40°，∴∠BED＝∠AEC＝40°．故答案为：40．【点评】本题考查了垂线的定义，对顶角相等的性质，是基础题，准确识图是解题的关键．6．如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1＝30°，则∠2＝60°．【分析】根据对顶角相等求出∠EOD，继而得出∠2．【解答】解：∵∠EOD与∠1互为对顶角，∴∠EOD＝∠1＝30°，又∵AB⊥CD，∴∠AOD＝∠BOD＝90°，∴∠2＝90°﹣∠EOD＝60°．故答案为：60°．【点评】本题考查了垂线的定义，用到的知识点为：对顶角相等，垂线产生直角．7．如图，把水渠中的水引到水池C，先过C点向渠岸AB画垂线，垂足为D，再沿垂线CD开沟才能使沟最短，其依据是垂线段最短．【分析】过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．据此作答．【解答】解：其依据是：连接直线外一点与直线上各点的所有线段中，垂线段最短．故答案为：垂线段最短．【点评】本题考查了垂线的性质在实际生活中的运用，关键是掌握垂线段的性质：垂线段最短．8．如图，点P在直线l外，PB⊥l于B，A为l上任意一点，则P A与PB的大小关系是P A≥PB．【分析】由垂线段的定义可知，线段PB为垂线段，再根据垂线段的性质判断．【解答】解：∵PB⊥l于B，∴线段PB为点P到直线l的垂线段．根据从直线外一点到这条直线上各点所连的线段中，垂线段最短．可知P A≥PB．故答案为：≥．【点评】此题主要考查了从直线外一点到这条直线上各点所连的线段中，垂线段最短的性质．9．在△ABC中∠B＝90°，BC＝5，AB＝12，AC＝13，则点B到斜边AC的距离是．【分析】设AC边上的高为h，再根据三角形的面积公式即可得出结论．【解答】解：设AC边上的高为h，∵在Rt△ABC中，∠B＝90°，AB＝5，BC＝12，AC＝13，∴AB•BC＝AC•h，∴h＝＝＝．故答案为：．【点评】本题考查的是三角形的面积，熟知三角形的面积公式是解答此题的关键．10．如图，BC⊥AC，BC＝8，AC＝6，AB＝10，则点C到线段AB的距离是 4.8．【分析】设点C到线段AB的距离是x，然后根据△ABC的面积列方程求解即可．【解答】解：设点C到线段AB的距离是x，∵BC⊥AC，＝AB•x＝AC•BC，∴S△ABC即×10•x＝×6×8，解得x＝4.8，即点C到线段AB的距离是4.8．故答案为：4.8．【点评】本题考查了点到直线的距离，解题的关键在于利用三角形的面积列出方程．11．平面内有10条直线两两相交，交点个数最多有m个，最少有n个，则m+n 的值为46．【分析】由题意可得10条直线相交于一点时交点最少，任意两直线相交都产生一个交点时交点最多，由此可得出m，n的值，从而得出答案．【解答】解：根据题意可得：10条直线相交于一点时交点最少，此时交点为1个，即n＝1；任意两直线相交都产生一个交点时，交点最多，∴此时交点为：10×（10﹣1）÷2＝45，即m＝45；则m+n＝45+1＝46．故答案为：46．【点评】本题考查直线的交点问题，注意掌握直线相交于一点时交点最少，任意n条直线两两相交时交点最多为n（n﹣1）个．12．平面内有n条直线，任意两条直线都相交，则最多有个交点．【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数，找出规律即可解答．【解答】解：2条直线相交最多有1个交点；3条直线相交最多有1+2个交点；4条直线相交最多有1+2+3个交点；5条直线相交最多有1+2+3+4个交点；6条直线相交最多有1+2+3+4+5个交点；…n条直线相交最多有1+2+3+4+5+…+（n﹣1）＝个交点．故答案为：．【点评】本题考查的是多条直线相交的交点问题，解答此题的关键是根据2条、3条、4条、5条、6条直线相交时最多的交点个数发现规律．13．已知，直线AB和直线CD交于点O，∠BOD是它的邻补角的3倍，则直线AB与直线CD的夹角是45度．【分析】设∠BOD＝x°，则它的补角为3x°，根据邻补角互补可得x+3x＝180，再解方程即可．【解答】解：设∠BOD＝x°，则它的补角为3x°，x+3x＝180，x＝45，故答案为：45°．【点评】此题主要考查了邻补角，关键是掌握邻补角互补．14．如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向，已知射线OB的方向是南偏东60°，射线OC在∠NOE内，且∠NOC与∠BOS互余，射线OA平分∠BON，图中与∠COA互余的角是∠BOC、∠NOA、∠AOB、∠COE．【分析】根据方位角的定义及角平分线的定义、余角的概念分别求出∠BOS、∠NOC、∠NOA、∠AOB的度数可得答案．【解答】解：∵∠BOS＝60°、∠NOC与∠BOS互余，∴∠NOC＝30°，∠BON＝120°，又∵OA平分∠BON，∴∠NOA＝∠AOB＝60°，则∠AOC＝∠NOA﹣∠NOC＝30°，∵∠NOE＝90°、∠NOC＝30°，∴∠COE＝60°，综上，∠COA互余的角有∠BOS、∠NOA、∠AOB、∠COE，故答案为：∠BOS、∠NOA、∠AOB、∠COE．【点评】本题主要考查方位角、余角和补角，解题的关键是掌握方位角的定义及角平分线的定义、余角的概念．15．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠CON＝2∠COM，则∠BOD的度数为60°．【分析】根据垂直得出∠NOM＝90°，根据角平分线定义得出∠AOM＝∠COM，再利用∠CON＝2∠COM，即可得出答案．【解答】解：∵ON⊥OM，∴∠NOM＝90°，∵∠CON＝2∠COM，∴设∠COM＝x，则∠CON＝2x，故x+2x＝90°，解得：x＝30°，∵射线OM平分∠AOC，∴∠AOM＝∠COM＝30°，∴∠AOC＝∠BOD＝2∠COM＝60°，故答案为：60°．【点评】本题考查了垂直定义，角平分线定义等知识点，能求出∠COM的度数是解此题的关键．16．如图，已知AO⊥BC于O，∠AOD＝30°，那么∠DOC＝60°．【分析】根据垂直的定义得到∠AOC＝90°，结合图形找到相关角间的和差关系进行解答即可．【解答】解：如图，∵AO⊥BC，∴∠AOC＝90°，又∠AOD＝30°，∴∠DOC＝90°﹣∠AOD＝60°．故答案是：60．【点评】本题考查了垂直的定义，如果两个角的和等于90°，两个角互为余角．17．如图，体育课上老师测量跳远成绩是这样操作的：用一块直角三角板的一边附在踏跳板上，另一边与拉直的皮尺重合，并且使皮尺经过被测试同学的落点，这样做的理由是垂线段最短．【分析】根据垂线段的性质，可得答案．【解答】解：用一块直角三角板的一边附在踏跳板上，另一边与拉直的皮尺重合，并且使皮尺经过被测试同学的落点，这样做的理由是垂线段最短，故答案为：垂线段最短．【点评】本题考查了垂线段，利用垂线段的性质是解题关键．18．如图，点A，B，C，D，E在直线l上，点P在直线l外，PC⊥l于点C，在线段P A，PB，PC，PD，PE中，最短的一条线段是PC，理由是垂线段最短【分析】点到直线的距离是指该点到直线的垂线段的长，根据定义即可选出答案．【解答】解：根据点到直线的距离的定义得出线段PC的长是点P到直线l的距离，从直线外一点到这条直线所作的垂线段最短．故答案是：PC；垂线段最短．【点评】本题考查了对点到直线的距离的应用，注意：点到直线的距离是指该点到直线的垂线段的长．19．如图，CD⊥AB，点E、F在AB上，且CE＝10cm，CD＝8cm，CF＝12cm，则点C到AB的距离是8cm．【分析】根据点到直线的距离是垂线段的长度，可得答案．【解答】解：∵CD⊥AB，点E、F在AB上，CD＝8cm，∴点C到AB的距离是CD＝8cm，故答案为：8cm．【点评】本题考查了点到直线的距离，利用点到直线的距离是垂线段的长度是解题关键．20．如图，点B到直线DC的距离是指线段BC的长度．【分析】直接利用直线外一点到直线的垂线段的长度，叫做点到直线的距离，进而得出答案．【解答】解：点B到直线DC的距离是指线段BC的长度．故答案为：BC．【点评】此题主要考查了点到直线的距离，正确把握相关定义是解题关键．二．解答题（共15小题）21．在同一平面内有四条直线（1）这四条直线的交点个数可能有哪些？（2）请你画出两种交点个数是4的图形．【分析】（1）根据两直线的位置即确定；（2）四条直线两两相交有6个交点，交点的个数是4，即6个中的三个重合．【解答】解：（1）这四条直线的交点个数可能是：0，1，4，5，6；（2）作图如下：【点评】本题考查了相交线的应用，主要考查学生的画图能力和理解能力．22．如图，直线AB，CD相交于点O，OF平分∠AOC，∠COE＝90°，∠DOF ＝160°．（1）求∠COF的度数；（2）求∠BOE的度数．【分析】（1）根据∠COF＝∠DOC﹣∠DOF求出即可；（2）先根据角平分线定义求出∠AOC，根据对顶角求出∠BOD，求出∠DOE，即可求出答案．【解答】解：（1）∵∠DOC＝180°，∠DOF＝160°，∴∠COF＝∠DOC﹣∠DOF＝20°；（2）∵∠COF＝20°，OF平分∠AOC，∴∠AOC＝2∠COF＝40°，∴∠DOB＝∠AOC＝40°，∵∠COE＝90°，∴∠DOE＝180°﹣90°＝90°，∴∠BOE＝∠BOD+∠DOE＝40°+90°＝130°．【点评】本题考查了对顶角、邻补角、角平分线定义等知识点，能求出各个角的度数是解此题的关键．23．如图，直线AB，CD相交于点O，OE⊥CD于点0，OD平分∠BOF，∠BOE ＝50°，求∠AOC，∠AOF，∠EOF的度数．【分析】根据题意即可推出∠EOD＝90°，∠BOD＝40°，既而得，∠AOC＝40°，∠BOF＝80°，得：∠EOF＝130°，∠AOF＝100°．【解答】解：∵OE⊥CD于点O，∴∠EOD＝90°（垂直的定义）∵∠BOE＝50°，∴∠BOD＝90°﹣50°＝40°，∴∠AOC＝∠BOD＝40°（对顶角相等）．∵OD平分∠BOF，∴∠BOF＝2∠BOD＝80°（角平分线的定义），∴∠AOF＝180°﹣80°＝100°，（平角的定义）∴∠EOF＝∠EOB+∠BOF＝130°．答：∠AOC＝40°，∠AOF＝100°，∠EOF＝130°．【点评】本题主要考查垂线的定义、角平分线的定义、对顶角的性质、邻补角的性质，关键在于熟练运用各性质定理，推出相关角的度数．24．如图，在直线MN的异侧有A、B两点，按要求画图取点，并注明画图取点的依据．（1）在直线MN上取一点C，使线段AC最短．依据是垂线段最短．（2）在直线MN上取一点D，使线段AD+BD最短．依据是两点之间线段最短．【分析】（1）过A作AC⊥MN，AC最短；（2）连接AB交MN于D，这时线段AD+BD最短．【解答】解：（1）过A作AC⊥MN，根据：垂线段最短．（2）连接AB交MN于D，根据是：两点之间线段最短．【点评】此题主要考查了垂线段的性质和线段的性质，关键是掌握垂线段最短；两点之间线段最短．25．如图，点A表示小雨家，点B表示小樱家，点C表示小丽家，她们三家恰好组成一个直角三角形，其中AC⊥BC，AC＝900米，BC＝1200米，AB＝1500米．（1）试说出小雨家到街道BC的距离以及小樱家到街道AC的距离．（2）画出表示小丽家到街道AB距离的线段．【分析】（1）利用点到直线的距离定义分别得出答案；（2）过点C作CD⊥AB进而得出答案．【解答】解：（1）∵AC＝900米，BC＝1200米，AB＝1500米，∴AC⊥BC，∴小雨家到街道BC的距离为：900m，小樱家到街道AC的距离为：1200m；（2）如图所示：CD即为小丽家到街道AB距离．【点评】此题主要考查了点到直线的距离定义，正确把握定义是解题关键．26．观察下列图形，阅读下面的相关文字并回答以下问题：两条直线相交三条直线相交四条直线相交只有一个交点最多的3个交点最多有6个交；猜想：①5条直线相交最多有几个交点？②6条直线相交最多有几个交点？③n条直线相交最多有n个交点？【分析】先观察图形，找出交点的个数与直线的条数之间的关系，然后进行计算即可．【解答】解：①5条直线相交最多有＝10个交点；②6条直线相交最多有＝15个交点；③n条直线相交最多有个交点．【点评】此题考查了相交线，关键是观察图形，找出规律，用到的知识点是同一平面内内n条直线相交最多有个交点．27．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？【分析】延长∠AOB的一边，然后根据邻补角的和等于180°即可求解．【解答】解：如图，延长AO，先测量出∠BOC的度数，然后根据∠AOB与∠BOC是邻补角即可求解，∠AOB＝180°﹣∠BOC．【点评】本题考查了相交线的性质，主要利用了邻补角的和等于180°的性质．28．如图，直线AB，CD相交于点O，OA平分∠EOC．若∠EOC＝68°，求∠BOD的度数．【分析】根据角平分线定义得到∠AOC＝∠EOC＝×68°＝34°，然后根据对顶角相等得到∠BOD＝∠AOC＝34°．【解答】解：∵OA平分∠EOC，∴∠AOC＝∠EOC＝×68°＝34°，∴∠BOD＝∠AOC＝34°．【点评】本题考查了角的计算：1直角＝90°；1平角＝180°．也考查了角平分线的定义和对顶角的性质．解决本题的关键是熟记对顶角相等．29．如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC＝80°，求∠BOD的度数；（2）若∠EOC＝∠EOD，求∠BOD的度数．【分析】（1）根据角平分线定义得到∠AOC＝∠EOC＝×80°＝40°，然后根据对顶角相等得到∠BOD＝∠AOC＝40°；（2）先设∠EOC＝x，∠EOD＝x，根据平角的定义得x+x＝180°，解得x＝90°，则∠EOC＝x＝90°，然后与（1）的计算方法一样．【解答】解：（1）∵OA平分∠EOC，∴∠AOC＝∠EOC＝×80°＝40°，∴∠BOD＝∠AOC＝40°；（2）设∠EOC＝x，∠EOD＝x，根据题意得x+x＝180°，解得x＝90°，∴∠EOC＝x＝90°，∴∠AOC＝∠EOC＝×90°＝45°，∴∠BOD＝∠AOC＝45°．【点评】考查了角的计算：1直角＝90°；1平角＝180°．也考查了角平分线的定义和对顶角的性质．30．如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD＝38°，求∠AOC和∠COB的大小．【分析】由OE⊥AB，可得出∠EOB＝90°，结合∠EOD＝38°可求出∠DOB 的度数，根据对顶角相等即可求出∠AOC的度数，再由∠COB与∠AOC互补可求出∠COB的大小．【解答】解：∵OE⊥AB，∴∠EOB＝90°，又∠EOD＝38°，∴∠DOB＝90°﹣38°＝52°，∵∠AOC＝∠DOB，∴∠AOC＝52°．∵∠COB与∠AOC互补，∴∠COB＝180°﹣52°＝128°．【点评】本题考查了垂线、对顶角以及邻补角，牢记“对顶角相等、邻补角互补”是解题的关键．31．如图，AOB为一直线，∠AOD：∠DOB＝3：1，OD平分∠COB．请判断AB与OC的位置关系．【分析】由已知条件和观察图形可知∠AOD与∠DOB互补，利用∠AOD：∠DOB ＝3：1及角平分线的定义这些关系，得出∠AOC＝90°，可证垂直．【解答】解：AB⊥OC．∵∠AOD：∠DOB＝3：1∴∠AOD＝3∠DOB∵∠AOB＝180°∴∠AOD+∠DOB＝180°即3∠DOB+∠DOB＝180°∴∠DOB＝45°又∵OD平分∠COB，有∠COD＝∠DOB＝45°，∴∠BOC＝∠DOB+∠COD＝45°+45°＝90°．由∠BOC＝90°，可知AB⊥OC．【点评】利用垂直的定义除了由垂直得直角外，还能由直角判定垂直，判断两直线的夹角是否为90°是判断两直线是否垂直的基本方法．32．已知：点P是直线MN外一点，点A、B、C是直线MN上三点，分别连接P A、PB、PC．（1）通过测量的方法，比较P A、PB、PC的大小，直接用“＞”连接；（2）在直线MN上能否找到一点D，使PD的长度最短？如果有，请在图中作出线段PD，并说明它的理论依据；如果没有，请说明理由．【分析】（1）根据测量可直接得出结论；（2）过点P作PD⊥MN，根据点到直线距离的定义可得出结论．【解答】解：（1）通过测量可知，P A＞PB＞PC；（2）过点P作PD⊥MN，则PD最短（垂线段最短）．【点评】本题考查的是垂线段最短，熟知从直线外一点到这条直线所作的垂线段最短是解答此题的关键．33．如图，点P，点Q分别代表两个村庄，直线l代表两个村庄中间的一条公路．根据居民出行的需要，计划在公路l上的某处设置一个公交站．（1）若考虑到村庄P居住的老年人较多，计划建一个离村庄P最近的车站，请在公路l上画出车站的位置（用点M表示），依据是直线外一点与直线上各点连接的所有线段中垂线段最短；（2）若考虑到修路的费用问题，希望车站的位置到村庄P和村庄Q的距离之和最小，请在公路l上画出车站的位置（用点N表示），依据是两点之间线段最短．【分析】（1）直接利用点到直线的距离的定义得出答案；（2）利用线段的性质得出答案．【解答】解：（1）如图，点M即为所示．依据是直线外一点与直线上各点连接的所有线段中垂线段最短（2）如图，点N即为所示．依据是两点之间线段最短；故答案为：直线外一点与直线上各点连接的所有线段中垂线段最短；两点之间线段最短．【点评】此题主要考查了应用设计与作图，正确理解线段的性质是解题关键．34．如图，点M，N分别在直线AB，CD上．（1）请在图中作出表示M，N两点间的距离的线段a，和表示点N到直线AB 的距离的线段b；（2）请比较（1）中线段a，b的大小，并说明理由．【分析】（1）根据线段的意义，点到直线的距离，可得答案；（2）根据垂线段的性质，可得答案．【解答】解：（1）连接MN，过N作NE⊥AB，如图，（2）由垂线段最短，得MN＞NE，即a＞b，理由是垂线段最短．【点评】本题考查了点到直线的距离，利用垂线段的性质是解题关键35．如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；（1）过点P画OA的垂线，垂足为H；（2）线段PH的长度是点P到OA的距离，线段CP的长度是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是PH＜PC＜OC（用“＜”号连接）【分析】（1）过点P画OA的垂线，即过点P画∠PHO＝90°即可，（2）利用点到直线的距离可以判断线段PH的长度是点P到OA的距离，PC是点C到直线OB的距离，线段PC、PH、OC这三条线段大小关系是PH＜PC ＜OC．【解答】解：（1）如图：（2）线段PH的长度是点P到直线OA的距离，线段CP的长度是点C到直线OB的距离，根据垂线段最短可得：PH＜PC＜OC，故答案为：OA，线段CP，PH＜PC＜OC．【点评】本题主要考查了基本作图﹣﹣﹣﹣作已知直线的垂线，另外还需利用点到直线的距离才可解决问题．。

浙教版数学七年级上册6.9《直线的相交一》习题2

《直线的相交一》习题一、选择题1.下列语句中，是对顶角的语句为( )A .两条直线相交所成的角B .有公共顶点且方向相反的两个角C .两条直线相交所成的角，且有一个公共顶点，而没有公共边D .有公共顶点并且相等的两个角2.图中，∠∠12、是对顶角的为( )1 2A B C D121122 3.三条直线相交于一点，所成的对顶角的对数是( )A .3B .4C .5D .64.点到直线的距离是指这点到这条直线的( )A .垂线段B .垂线的长C .长度D .垂线段的长度5.如图，三条直线l l l 123，，相交于点O ，则∠+∠+∠=123( )A .90︒B .120︒C .180︒D .360︒1 O 32 l 1l 2l 3二、填空题6.两个互为邻补角的角平分线___________；两个对顶角的角平分线形成___________.7.直线AB 与CD 互相垂直，垂足为O ，P 是直线CD 上一点，则P 到AB 的距离是__________.8.如图1，直线AB 、CD 、EF 都经过O 点，并且已知∠=︒∠=︒AOC COE 3546，，则∠=EOB __________，∠=BOC _________，∠=DOF ________，∠=FOA ______.A FC O DE B图19.如图，直线AB 、CD 、EF 相交于O ，且AB CD ⊥，∠=︒127，则∠=2_______，∠=FOB __________.CEA 2 OB 1FD10.已知：如图，AO BO ⊥∠=∠，12.求证：CO DO ⊥.BCD2 31O A。

浙教版初中数学6.9 直线的相交 2017-2018学年习题(含答案)

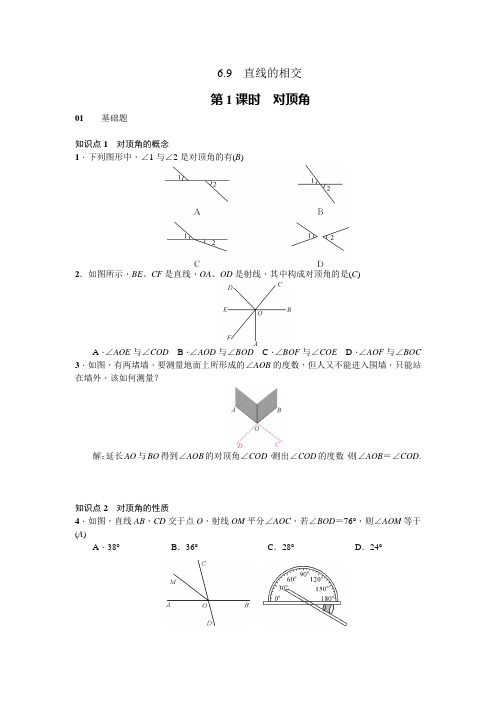
6.9直线的相交第1课时对顶角01基础题知识点1对顶角的概念1．下列图形中，∠1与∠2是对顶角的有(B)2．如图所示，BE、CF是直线，OA、OD是射线，其中构成对顶角的是(C)A．∠AOE与∠COD B．∠AOD与∠BOD C．∠BOF与∠COE D．∠AOF与∠BOC 3．如图，有两堵墙，要测量地面上所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，该如何测量？解：延长AO与BO得到∠AOB的对顶角∠COD，测出∠COD的度数，则∠AOB＝∠COD.知识点2对顶角的性质4．如图，直线AB，CD交于点O，射线OM平分∠AOC，若∠BOD＝76°，则∠AOM等于(A)A．38°B．36°C．28°D．24°第4题图第5题图5．(吉林中考)图中是对顶角量角器，用它测量角的原理是对顶角相等． 6．如图，直线a ，b 相交，∠2＝3∠1，则∠3＝45°．第6题图第7题图 7．如图，三条直线l 1，l 2，l 3相交于一点，则∠1＋∠2＋∠3＝180°． 8．如图，直线AB ，CD ，EF 相交于点O ，且∠AOD ＝90°，∠1＝40°，求∠2的度数．解：∵直线AB ，CD ，EF 相交于点O ，且∠AOD ＝90°， ∴∠BOD ＝90°. ∵∠1＝40°，∴∠DOF ＝40°. ∴∠2＝90°－40°＝50°.9．如图，直线AB 、CD 相交于点O ，OE 把∠BOD 分成两部分．(1)直接写出图中∠AOC 的对顶角为∠BOD ； (2)若∠AOC ＝70°，且∠BOE ∶∠EOD ＝2∶3，求∠DOE 的度数．解：∵∠AOC 的对顶角为∠BOD ， ∴∠BOD ＝∠AOC ＝70°.又∵∠BOE ∶∠EOD ＝2∶3， ∴∠DOE ＝35∠DOB ＝35×70°＝42°.02中档题10．平面内三条直线的交点个数可能有(D)A．1个或3个B．2个或3个C．1个或2个或3个D．0个或1个或2个或3个11．如图，直线AB，CD相交于点O，OA平分∠EOC，∠EOC∶∠EOD＝2∶3，则∠BOD ＝(B)A．30°B．36°C．45°D．72°第11题图第13题图12．一个角的补角是这个角的对顶角的4倍，则这个角的度数为36°．13．如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE.∠BOF＝30°，则∠AOC ＝80°．14．已知点O是直线AB上一点，OC，OD是两条射线，且∠AOC＝∠BOD，则∠AOC与∠BOD是对顶角吗？为什么？解：∠AOC与∠BOD不一定是对顶角．如图1所示，当射线OC，OD位于直线AB的同侧时，不是对顶角；如图2所示，当射线OC，OD位于直线AB的异侧时，是对顶角．15．如图，已知直线AB和CD相交于点O，∠COF与∠EOF互余，OF平分∠AOE，∠COF ＝28°，求∠BOD的度数．解：∵∠COF与∠EOF互余，∴∠COF＋∠EOF＝90°.∴∠EOF＝90°－∠COF＝90°－28°＝62°.∵OF平分∠AOE，∴∠AOF＝∠EOF＝62°.∴∠AOC＝∠AOF－∠COF＝62°－28°＝34°.∴∠BOD＝∠AOC＝34°.16．如图，直线AB，CD，EF相交于点O，∠AOE＝30°，∠BOC＝2∠AOC，求∠DOF的度数．解：设∠AOC＝x°，则∠BOC＝2x°.由邻补角的定义，可得2x＋x＝180.解得x＝60.所以∠AOC＝60°.所以∠EOC＝∠AOC－∠AOE＝60°－30°＝30°.所以∠DOF＝∠EOC＝30°.03综合题17．观察下列图形，寻找对顶角(不含平角)．(1)两条直线相交于一点，如图1，共有2对对顶角；(2)三条直线相交于一点，如图2，共有6对对顶角；(3)四条直线相交于一点，如图3，共有12对对顶角；(4)根据填空结果探究：当n条直线相交于一点时，所构成的对顶角的对数与直线条数之间的关系；(5)根据探究结果，求2 017条直线相交于一点时，所构成的对顶角的对数．解：(4)(n－1)·n.(5)2 016×2 017＝4 066 272.第2课时垂线01基础题知识点1垂线的相关概念及计算1．如图，直线AB、CD相交于点O，下列条件中，不能说明AB⊥CD的是(C)A．∠AOD＝90°B．∠AOC＝∠BOCC．∠BOC＋∠BOD＝180°D．∠AOC＋∠BOD＝180°2．如图，已知点O在直线AB上，CO⊥DO于点O，若∠1＝145°，则∠3的度数为(C) A．35°B．45°C．55°D．65°第2题图第3题图3．如图，直线AB，CD相交于点O，EO⊥AB，垂足为O.若∠EOD＝20°，则∠COB的度数为110°．4．如图，直线AB、EF相交于点D，CD⊥AB，DF平分∠BDC，求∠EDC.解：∵CD⊥AB，∴∠ADC＝∠CDB＝90°.∵DF平分∠BDC，∴∠CDF＝∠BDF＝∠ADE＝45°.∴∠EDC＝∠ADC＋∠ADE＝90°＋45°＝135°.5．(诸暨期末)如图，直线AE与CD相交于点B，且BF⊥AE，∠DBE＝50°.(1)请直接写出与∠DBE互余的角；(2)求∠CBF的度数．解：(1)∠DBF.(2)∵BF⊥AE，∴∠FBE＝∠ABF＝90°.∵∠DBE＝50°，∵∠ABC＝∠DBE＝50°，∴∠CBF＝180°－∠ABC＝140°.知识点2垂线的画法6．(1)如图1，用三角板过点A画直线l的垂线；(2)如图2，过点B作直线AC的垂线BD，垂足为D.解：如图所示．知识点3垂线的基本事实7．如图，已知ON⊥l，OM⊥l，则OM与ON重合，其理由是(B)A．两点确定一条直线B．过一点有且只有一条直线垂直于已知直线C．垂线段最短D．过一点只能作一条垂线知识点4垂线段最短8．如图，△ABC中，∠C＝90°，AC＝3 cm，点P是边BC上的动点，则AP长不可能是(A)A．2.5 cm B．3 cm C．4 cm D．5 cm 9．如图所示，要把水渠中的水引到水池中，水池在C处，在渠岸AB的何处开挖才能使水沟最短？解：过点C作CD⊥AB，垂足为D，根据垂线段最短，可知在D处开挖可以使水沟CD 最短．知识点5点到直线的距离10．(西湖区期末)如图，A是直线l外一点，点B、C、E、D在直线l上，且AD⊥l，D为垂足，如果AC＝8 cm，AD＝6 cm，AE＝7 cm，AB＝13 cm，那么点A到直线l的距离是(D)A．13 cm B．8 cm C．7 cm D．6 cm02中档题11．如图，OA⊥OC，OB⊥OD，∠AOB＝25°，则∠COD的度数是(A)A．25°B．35°C．45°D．55°第11题图第13题图12．若A，B，C是直线l上的三点，P是直线l外一点，且P A＝5 cm，PB＝4 cm，PC＝3 cm，则点P到直线l的距离(C)A．等于3 cm B．大于3 cm而小于4 cm C．不大于3 cm D．小于3 cm 13．如图，CD⊥AB，垂足为C，∠1＝130°，则∠2＝40度．14．(滨江区期末)如图，点C是∠AOB的边OB上的一点，按下列要求画图并回答问题：(1)过C点画OB的垂线，交OA于点D；(2)过C点画OA的垂线，垂足为E；(3)比较线段CE，OD，CD的大小(请直接写出结论)；(4)请写出第(3)小题图中与∠AOB互余的角(不增添其他字母)．解：(1)、(2)如图所示．(3)CE＜CD＜OD.(4)与∠AOB互余的角是∠OCE和∠ODC.15．如图，已知直线AB和CD相交于点O，射线OE⊥AB于点O，射线OF⊥CD于点O，且∠BOF＝25°，求∠AOC和∠EOD的度数．解：∵OF⊥CD，∴∠DOF＝90°.又∵∠BOF＝25°，∴∠BOD＝90°＋25°＝115°.∴∠AOC＝∠BOD＝115°.∵OE⊥AB，∴∠BOE＝90°.又∵∠BOF＝25°，∴∠EOF＝65°.∴∠EOD＝∠DOF－∠EOF＝25°.16．如图，直线AB、CD相交于点O，∠AOC与∠AOD的度数比为4∶5，OE⊥AB，OF 平分∠DOB，求∠EOF的度数．解：设∠AOC＝4x，则∠AOD＝5x.∵∠AOC＋∠AOD＝180°，∴4x＋5x＝180°.解得x＝20°.∴∠AOC＝4x＝80°.∴∠BOD＝80°.∵OE⊥AB，∴∠BOE＝90°.∴∠DOE＝∠BOE－∠BOD＝10°.又∵OF 平分∠DOB ， ∴∠DOF ＝12∠BOD ＝40°.∴∠EOF ＝∠EOD ＋∠DOF ＝10°＋40°＝50°.03 综合题17．如图，点O 是直线AB 、CD 的交点，OE ⊥AB ，OF ⊥CD ，OM 是∠BOF 的平分线．(1)填空：①由OM 是∠BOF 的平分线，可得∠FOM ＝∠BOM ； ②若∠AOC ＝34°，则∠BOD ＝34度；③根据同角的余角相等，可得∠EOF ＝∠AOC ；(2)若∠AOC ＝α，求∠COM .(用含α的代数式表示，并写出过程)解：∵∠AOC ＝α， ∴∠BOD ＝∠AOC ＝α. ∵OF ⊥CD ，∴∠BOF ＝90°－∠BOD ＝90°－α. ∵OM 是∠BOF 的平分线， ∴∠MOF ＝12∠BOF ＝45°－12α.∵OF ⊥CD ，∴∠COM ＝90°＋∠MOF ＝90°＋45°－12α＝135°－12α.。

2017浙教版数学七年级上册69《直线的相交》同步练习1

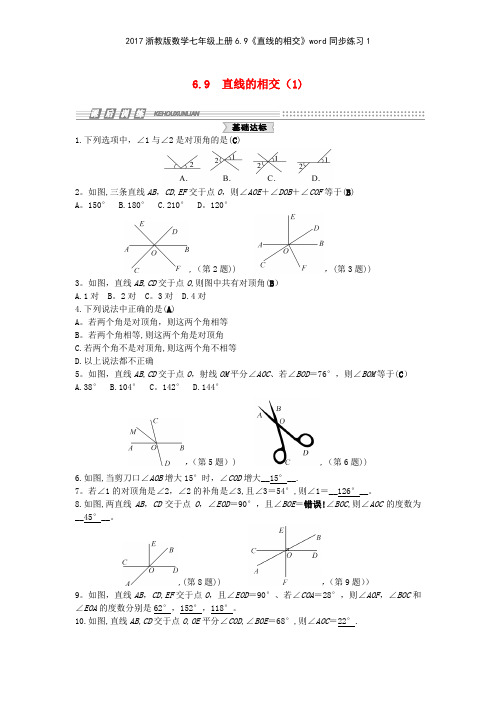
6.9 直线的相交（1)1.下列选项中，∠1与∠2是对顶角的是(C)2。

如图,三条直线AB，CD,EF交于点O，则∠AOE＋∠DOB＋∠COF等于(B)A。

150° B.180° C.210° D。

120°,（第2题)) ，(第3题))3。

如图，直线AB,CD交于点O,则图中共有对顶角(B）A.1对 B。

2对 C。

3对 D.4对4.下列说法中正确的是(A)A。

若两个角是对顶角，则这两个角相等B。

若两个角相等,则这两个角是对顶角C.若两个角不是对顶角,则这两个角不相等D.以上说法都不正确5。

如图，直线AB,CD交于点O，射线OM平分∠AOC、若∠BOD＝76°，则∠BOM等于(C）A.38° B.104° C。

142° D.144°，（第5题）) ,（第6题))6.如图,当剪刀口∠AOB增大15°时，∠COD增大__15°__.7。

若∠1的对顶角是∠2，∠2的补角是∠3,且∠3＝54°,则∠1＝__126°__。

8.如图,两直线AB，CD交于点O，∠EOD＝90°，且∠BOE＝错误!∠BOC,则∠AOC的度数为__45°__。

,(第8题)) ，（第9题））9。

如图，直线AB，CD,EF交于点O，且∠EOD＝90°、若∠COA＝28°，则∠AOF，∠BOC和∠EOA的度数分别是62°，152°，118°。

10.如图,直线AB,CD交于点O,OE平分∠COD,∠BOE＝68°,则∠AOC＝22°.，(第10题)），(第11题)）11.如图，直线AB ,CD 交于点O ,OE 平分∠AOD ，OF 平分∠BOD 、已知∠AOF ＝160°，那么∠COE ＝__110°__.12.如图,直线AB ,CD 交于点O ，OE 平分∠BOD ,且∠AOC ＝∠AOD －80°，求∠AOE 的度数.（第12题）【解】 ∵∠AOD ＝180°－∠AOC （平角的定义），∠AOC ＝∠AOD －80°(已知）,∴∠AOC ＝180°－∠AOC －80°、∴∠AOC ＝50°,∠AOD ＝130°、∴∠BOD ＝∠AOC ＝50°(对顶角相等）.∵OE 平分∠BOD (已知）,∴∠DOE ＝错误!∠BOD ＝25°(角平分线的意义)。

七年级数学上册 6.9 直线的相交同步练习(新版)浙教版

七年级数学上册 6.9 直线的相交同步练习（新版）浙教版【提高训练】1.如果两条直线只有一个，则这两条直线相交，该公共点叫做这两条直线的 .2.若直线AB，CD相交于点0，则∠AOC是的对顶角.3.对顶角的性质是： .4.两条直线相交于一点，共有对对顶角.5.如图，直线AB，CD相交于点0，∠AOD=150°，则∠BOC= °.【课题讲练】典型例题1 说出图中的对顶角.巩固练习1 如图，AB，CD，EF三条直线两两相交，找出图中的对顶角.典型例题2 如图，直线AB，CD相交于点0，OE平分∠AOC，若∠AOD=50°，求∠BOE的度数.巩固练习2 如图所示，直线AB，CD，EF相交于点0∠AOF=4∠BOF，∠EOC=54°，求∠AOD的度数.【跟踪提醒】一、选择题1.下列图形中，∠l与∠2是对顶角的是 ( )2.以下四种说法：①对顶角相等；②相等的角是对顶角；③不是对顶角的两个角不相等；④不相等的两个角不是对顶角，其中正确的是 ( )A.1个B.2个C.3个D.4个3. ∠a的对顶角是∠b，∠b的补角是l35°，则∠a的度数是 ( )A.45°B.135°C.45°或l35°D.90。

二、填空题4.如图，图中共有对对顶角.5.如图，直线AB，CD相交于点0，∠AOD+∠BOC=290°，则么AOC等于度.6.如图，直线AB⊥CD于0，直线EF过点0，且∠AOE=40°，则∠DOF= 度.7.如图，是用对顶角的量角器测量圆锥形零件的锥角的示意图，此零件的锥角等于度.三、解答题8.如图，直线AB，CD相交于点0，OE平分∠B OD，∠AOD=2∠AOC，求∠BOE和∠COE的度数.9.已知直线AB，CD，EF相交于点0，∠l：∠3=3：1，∠2=20°，(1)图中的对顶角有哪几对?(2)求∠DOE的度数.10.如图，小明想测地面上两堵墙所形成的∠AOB的度数，但他不能进入围墙内，请问该如何测量?测量的依据是什么?参考答案：【课前热身】1.公共点交点2.∠BOD3.对顶角相等4.25.150 【课堂讲练】典型例题l ∠BOM 和∠AO N ，∠AOM 和∠BO N ，∠MO'D 和∠C0’A，∠MO'C 和∠D0’A.巩固练习l ∠AMC 和∠DMB，∠AMD 和∠CMB，∠END 和∠CNF ，∠C NE 和∠D NF ，∠BOE 和∠AOF ，∠AOE 和∠B0F.典型例题 2 ∠BOC 和∠AOD 是对顶角，∴∠BOC=∠A OD=50° ∵∠AOD 和∠AOC 互补，∴∠AOC=130°， ∵OE 平分∠AOC，∴∠COE=21∠AOC=65°，∴∠BOE=∠BOC+∠COE=115°. 巩固练习2 90°. 【跟踪演练】1.B2.B3.A4.25.356.507.308.∠BOE=30°，∠COE=150°.9.(1)略；(2)140°. l0.延长A0到C ，延长B0到D ，测量∠COD 的度数即为∠AOB 的度数，依据对顶角相等。

浙教版数学七年级上册6.9《直线的相交》同步练习2

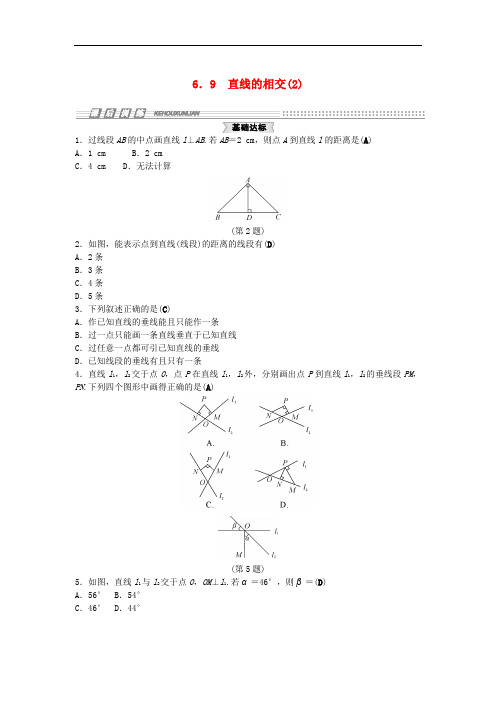
6．9 直线的相交(2)1．过线段AB的中点画直线l⊥AB.若AB＝2 cm，则点A到直线l的距离是(A)A．1 cm B．2 cmC．4 cm D．无法计算(第2题)2．如图，能表示点到直线(线段)的距离的线段有(D)A．2条B．3条C．4条D．5条3．下列叙述正确的是(C)A．作已知直线的垂线能且只能作一条B．过一点只能画一条直线垂直于已知直线C．过任意一点都可引已知直线的垂线D．已知线段的垂线有且只有一条4．直线l1，l2交于点O，点P在直线l1，l2外，分别画出点P到直线l1，l2的垂线段PM，PN.下列四个图形中画得正确的是(A)(第5题)5．如图，直线l1与l2交于点O，OM⊥l1.若α＝46°，则β＝(D)A．56° B．54°C．46° D．44°(第6题)6．如图，ON⊥l，OM⊥l，则直线OM与ON重合的理由是(C)A．过两点只有一条直线B．经过一点只有一条直线垂直于已知直线C．在同一平面内，过一点只能作一条垂直于已知直线的直线D．垂线段最短7．P为直线m外一点，A，B，C为直线m上三点，PA＝4 cm，PB＝5 cm，PC＝2 cm，则点P 到直线m的距离为(D)A．4 cm B．2 cmC．小于2 cm D．不大于2 cm8．如图①②分别是铅球和立定跳远场地的示意图，点E，B为相应的落地点，则铅球和立定跳远的成绩分别对应的是线段(D)(第8题)A．OE和AB的长 B．DE和AB的长C．OE和BC的长 D．EF和BC的长9．如图，当∠1与∠2满足条件__∠1＋∠2＝90°__时，OA⊥OB.,(第9题)) ,(第10题))10．如图，OC⊥AE，OB⊥OD，则图中互余的角有__4__对．11．如图，OD⊥AB，垂足为O，∠DOC∶∠AOC＝2∶1，则∠BOC＝__150°__．,(第11题)) ,(第12题))12．如图，根据图形填空：(1)直线AD与直线CD交于点__D__；(2)__BE__⊥AD，垂足为__E__；AC⊥__CD__，垂足为__C__；(3)点B到直线AD的距离是线段__BE__的__长度__，点D到直线AB的距离是线段__DC__的__长度__；(4)若AB ＝2 cm ，BC ＝1.5 cm ，则点A 到直线CD 的距离为__3.5__cm.(第13题)13．如图，AB ，CD 交于点E ，EF ⊥CD .若EB 平分∠DEF ，求∠AEF 的度数．【解】 ∵EF ⊥CD ， ∴∠DEF ＝90°. 又∵EB 平分∠DEF ， ∴∠BEF ＝12∠DEF ＝45°.又∵∠AEF ＋∠BEF ＝180°， ∴∠AEF ＝180°－45°＝135°.14．如图，∠BAC ＝90°，AD ⊥BC ，则下列结论中，正确的有(C )①点B 到AC 的垂线段是线段AB ②线段AC 是点C 到AB 的垂线段 ③线段AD 是点D 到BC 的垂线段 ④线段BD 是点B 到AD 的垂线段A ．1个B ．2个C ．3个D ．4个【解】正确的结论是①②④.,(第14题)) ,(第15题))15．如图，在△ABC 中，∠C ＝90°，BC ＝3，AC ＝4，AB ＝5，则点C 到AB 的距离为(A ) A ．2.4 B ．3 C ．4 D ．无法确定【解】设点C 到AB 的距离为h ，则3×42＝5h 2，解得h ＝2.4，故选A.(第16题)16．如图，直线AB ，CD 交于点O ，OM ⊥AB . (1)若∠1＝∠2，求∠NOD 的度数；(2)若∠1＝14∠BOC ，求∠AOC 和∠MOD 的度数．【解】 (1)∵OM ⊥AB ，∠1＝∠2， ∴∠1＋∠AOC ＝∠2＋∠AOC ＝90°，即∠CON ＝90°.又∵∠CON ＋∠NOD ＝180°， ∴∠NOD ＝90°.(2)∵OM ⊥AB ，∠1＝14∠BOC ，∴∠BOC ＝120°，∠1＝30°. 又∵∠AOC ＋∠BOC ＝180°， ∴∠AOC ＝60°. 又∵∠AOC ＝∠BOD ，∴∠MOD ＝∠MOB ＋∠BOD ＝∠MOB ＋∠AOC ＝150°.。

七年级数学上册(浙教版)练习：6.9直线的相交1.docx

6．9 直线的相交(1)1．下列选项中，∠1与∠2是对顶角的是(C )2．如图，三条直线AB ，CD ，EF 交于点O ，则∠AOE ＋∠DOB ＋∠COF 等于(B )A ．150° B．180° C．210° D．120°,(第2题)) ,(第3题))3．如图，直线AB ，CD 交于点O ，则图中共有对顶角(B )A ．1对B ．2对C ．3对D ．4对4．下列说法中正确的是(A )A ．若两个角是对顶角，则这两个角相等B ．若两个角相等，则这两个角是对顶角C ．若两个角不是对顶角，则这两个角不相等D ．以上说法都不正确5．如图，直线AB ，CD 交于点O ，射线OM 平分∠AOC .若∠BOD ＝76°，则∠BOM 等于(C )A ．38° B．104° C．142° D．144°,(第5题)) ,(第6题))6．如图，当剪刀口∠AOB 增大15°时，∠COD 增大__15°__．7．若∠1的对顶角是∠2，∠2的补角是∠3，且∠3＝54°，则∠1＝__126°__．8．如图，两直线AB ，CD 交于点O ，∠EOD ＝90°，且∠BOE ＝13∠BOC ，则∠AOC 的度数为__45°__．,(第8题)) ,(第9题))9．如图，直线AB ，CD ，EF 交于点O ，且∠EOD ＝90°.若∠COA ＝28°，则∠AOF ，∠BOC 和∠EOA 的度数分别是62°，152°，118°．10．如图，直线AB ，CD 交于点O ，OE 平分∠COD ，∠BOE ＝68°，则∠AOC ＝22°．,(第10题)) ,(第11题))11．如图，直线AB ，CD 交于点O ，OE 平分∠AOD ，OF 平分∠BOD .已知∠AOF ＝160°，那么∠COE ＝__110°__．12．如图，直线AB ，CD 交于点O ，OE 平分∠BOD ，且∠AOC ＝∠AOD －80°，求∠AOE 的度数．(第12题)【解】 ∵∠AOD ＝180°－∠AOC (平角的定义)，∠AOC ＝∠AOD －80°(已知)，∴∠AOC ＝180°－∠AOC －80°.∴∠AOC ＝50°，∠AOD ＝130°.∴∠BOD ＝∠AOC ＝50°(对顶角相等)．∵OE 平分∠BOD (已知)，∴∠DOE ＝12∠BOD ＝25°(角平分线的意义)． ∴∠AOE ＝∠AOD ＋∠DOE ＝130°＋25°＝155°.(第13题)13．如图，直线AB ，CD 交于点O ，OE 平分∠BOD .(1)若∠AOC ＝70°，∠DOF ＝90°，求∠EOF 的度数；(2)若OF 平分∠COE ，∠BOF ＝15°，求∠AOC 的度数．【解】 (1)∵OE 平分∠BOD ，∠BOD ＝∠AOC ＝70°，∴∠DOE ＝12∠BOD ＝35°. ∴∠EOF ＝∠DOF －∠DOE ＝90°－35°＝55°.(2)设∠AOC ＝x ，则∠BOD ＝x .∵OE 平分∠BOD ，∴∠DOE ＝∠EOB ＝12∠BOD ＝x 2. ∴∠COE ＝180°－∠DOE ＝180°－x 2. ∵∠EOF ＝∠EOB ＋∠BOF ，∴∠EOF ＝x 2＋15°. ∵OF 平分∠COE ，∴∠COE ＝2∠EOF . ∴180°－x 2＝2⎝ ⎛⎭⎪⎫x 2＋15°，解得x ＝100°，即∠AOC ＝100°.14．如图，直线AB ，CD 交于点M ，MN 是∠BMC 的平分线，∠AMN ＝136°，求∠AMD 的度数．(第14题)【解】 ∵∠AMN＝136°，∴∠BMN ＝44°.又∵MN 是∠BMC 的平分线，∴∠AMD ＝∠BMC ＝2∠BMN ＝88°.15．如图，已知直线AB 与CD 交于点O ，OE 平分∠BOD ，OF 平分∠AOB .(1)若∠BOE ＝40°，求∠AOF 与∠COF 的度数；(2)若∠BOE ＝x (x ＜45°)，请用含x 的代数式表示∠COF 的度数．(第15题)【解】 (1)∵OE 平分∠BOD ，∴∠BOE ＝12∠BOD . ∵∠BOE ＝40°，∴∠BOD ＝80°，∴∠BOC ＝100°.∵OF 平分∠AOB ，∴∠AOF ＝∠BOF ＝90°，∴∠COF ＝100°－90°＝10°.(2)∠COF ＝180°－2x －90°＝90°－2x .初中数学试卷桑水出品。

浙教版数学七年级上册6.9直线的相交.docx

6.9直线的相交一．选择题（共8小题）1．同一平面内，三条不同直线的交点个数可能是（）个．A．1或3 B．0、1或3 C．0、1或2 D．0、1、2或32．下列各组角中，∠1与∠2是对顶角的为（）A． B．C． D．3．如图，直线AB与直线CD相交于点O，MO⊥AB，垂足为O，已知∠AOD=136°，则∠COM的度数为（）A．36° B．44° C．46° D．54°4．如图，把水渠中的水引到水池C，先过C点向渠岸AB画垂线，垂足为D，再沿垂线CD开沟才能使沟最短，其依据是（）A．垂线最短B．过一点确定一条直线与已知直线垂直C．垂线段最短D．以上说法都不对5．已知△ABC中，BC=6，AC=3，CP⊥AB，垂足为P，则CP的长可能是（）A．2 B．4 C．5 D．76．如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有（）A．2条B．3条C．4条D．5条7．已知∠α的两边分别与∠β的两边垂直，且∠α=20°，则∠β的度数为（）A．20° B．160°C．20°或160°D．70°8．如图，点A在直线l1上，点B，C分别在直线l2上，AB⊥l2，AC⊥l1，AB=4，BC=3，则下列说法正确的是（）A．点B到直线 l1的距离等于4 B．点C到直线l1的距离等于5C．直线l1，l2的距离等于4 D．点B到直线AC的距离等于3二．填空题（共4小题）9．如图，直线AB、CD相交于点O，∠1=50°，则∠2= 度．10．已知，如图，直线AB与CD相交于点O，OE平分∠AOC，若∠EOC=25°，则∠BOD的度数为．11．如图，直线AB与CD相交于E点，EF⊥AB，垂足为E，∠1=130°，则∠2= 度．12．如图，直线a，b相交，∠2=3∠1，则∠3= °．三．解答题（共3小题）13．如图，直线AB，CD相交于O，射线OM平分∠AOC，若∠BOD=80°，求∠BOM的度数．14．如图，直线AB与CD相交于点O，OD恰为∠BOE的角平分线．（1）请直接写出和∠AOD能成为互为补角的角；（把符合条件的角都填出来）（2）若∠AOD=142°，求∠AOE的度数．15．如图，直线AB与CD相交于点O，∠AOM=90°．（1）如图1，若OC平分∠AOM，求∠AOD的度数；（2）如图2，若∠BOC=4∠NOB，且OM平分∠NOC，求∠MON的度数．\初中数学试卷。

初中数学浙教版七年级上册6.9直线的相交同步练习

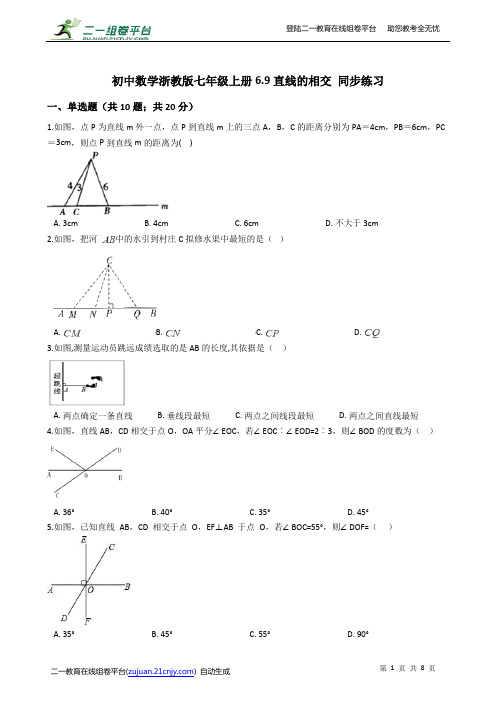
初中数学浙教版七年级上册6.9直线的相交同步练习一、单选题（共10题；共20分）1.如图，点P为直线m外一点，点P到直线m上的三点A，B，C的距离分别为PA＝4cm，PB＝6cm，PC ＝3cm，则点P到直线m的距离为( )A. 3cmB. 4cmC. 6cmD. 不大于3cm2.如图，把河中的水引到村庄C拟修水渠中最短的是（）A. B. C. D.3.如图,测量运动员跳远成绩选取的是AB的长度,其依据是（）A. 两点确定一条直线B. 垂线段最短C. 两点之间线段最短D. 两点之间直线最短4.如图，直线AB，CD相交于点O，OA平分∠EOC，若∠EOC︰∠EOD=2︰3，则∠BOD的度数为（）A. 36°B. 40°C. 35°D. 45°5.如图，已知直线AB，CD 相交于点O，EF⊥AB 于点O，若∠BOC=55°，则∠DOF=（）A. 35°B. 45°C. 55°D. 90°6.如图，在平面内作已知直线m的垂线，可作垂线的条数有（）A. 0条B. 1条C. 2条D. 无数条7.下列各图中，过直线外的点画直线的垂线，三角尺操作正确的是（）A. B.C. D.8.下列说法中不正确的是( )A. 在同一平面内，经过一点能画一条且只能画一条直线与已知直线垂直B. 从直线外一点到这条直线的垂线段叫做点到直线的距离C. 一条直线的垂线可以画无数条D. 连接直线外一点与直线上各点的所有线段中，垂线段最短9.三条共点直线都与第四条直线相交，一共有（）对对顶角.A. 12B. 24C. 7D. 1110.下列语句中，正确的是（）A. 相等的角一定是对顶角B. 互为补角的两个角不相等C. 有一个公共顶点，两边互为反向延长线的两个角是对顶角D. 交于一点的三条直线形成3对对顶角二、填空题（共5题；共6分）11.经过一点________一条直线垂直于已知直线．12.如图，AC⊥BC, 且BC=6，AC=8，AB=10，则点A到BC的距离是________点B到点A的距离是________．13.如图所示，其中共有________对对顶角．14.如图，CD⊥AB，垂足是点D，AC＝7，BC＝5，CD＝4，点E是线段AB上的一个动点（包括端点），连接CE，那么CE长的范围是________．15.如图，直线AB，CD相交于点O，若∠AOC=20°，则∠BOD的大小为________（度）．三、解答题（共3题；共20分）16.画一条线段的垂线，就是画它所在直线的垂线．如图，请你过点P画出线段的垂线，垂足分别为点．17.如图，∠1=28°，AB⊥CD，垂足为O，EF经过点O.求∠2、∠3的度数.18.如图，直线与相交于点O，平分，．（1）若，求的度数；（2）在的内部作射线，探究与之间有怎样的关系？并说明理由．答案解析部分一、单选题1.【答案】D【解析】【解答】解：∵点P到直线m上的三点A，B，C的距离分别为PA＝4cm，PB＝6cm，PC＝3cm，∴点P到直线m的距离为不大于3cm.故答案为：D.【分析】根据垂线段最短，可得点P到直线m的距离的取值范围。

七年级数学上册6.9直线的相交同步练习(新版)浙教版【含解析】

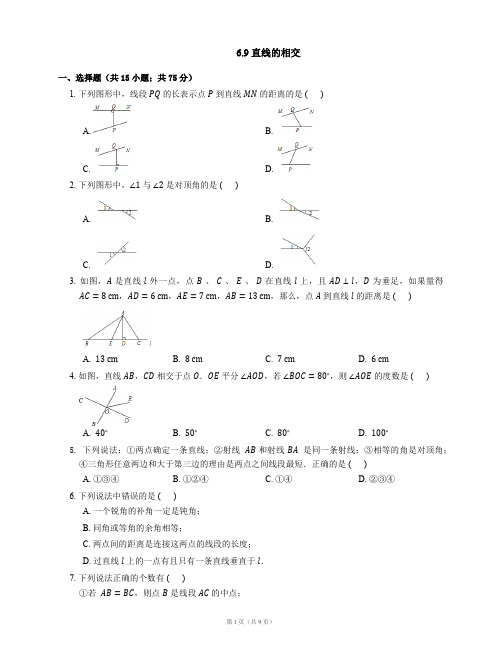
6.9 直线的相交一、选择题（共15小题；共75分）1. 下列图形中，线段PQ的长表示点P到直线MN的距离的是 ( )A. B.C. D.2. 下列图形中，∠1与∠2是对顶角的是 ( )A. B.C. D.3. 如图，A是直线l外一点，点B、C、E、D在直线l上，且AD⊥l，D为垂足，如果量得AC=8 cm，AD=6 cm，AE=7 cm，AB=13 cm，那么，点A到直线l的距离是 ( )A. 13 cmB. 8 cmC. 7 cmD. 6 cm4. 如图，直线AB，CD相交于点O．OE平分∠AOD，若∠BOC=80∘，则∠AOE的度数是 ( )A. 40∘B. 50∘C. 80∘D. 100∘5. 下列说法：①两点确定一条直线；②射线AB和射线BA是同一条射线；③相等的角是对顶角；④三角形任意两边和大于第三边的理由是两点之间线段最短．正确的是 ( )A. ①③④B. ①②④C. ①④D. ②③④6. 下列说法中错误的是 ( )A. 一个锐角的补角一定是钝角；B. 同角或等角的余角相等；C. 两点间的距离是连接这两点的线段的长度；D. 过直线l上的一点有且只有一条直线垂直于l．7. 下列说法正确的个数有 ( )①若AB=BC，则点B是线段AC的中点；②从直线外一点到这条直线的垂线段，叫做点到直线的距离；③若AB=MA+MB，AB<NA+NB，则点M在线段AB上，点N在线段AB外；④在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线．A. 0B. 1C. 2D. 38. 挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走．如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，⋯，则第6次应拿走 ( )A. ②号棒B. ⑦号棒C. ⑧号棒D. ⑩号棒9. 如图，直线AB，CD，EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD=28∘，则∠AOG为 ( )A. 56∘B. 59∘C. 60∘D. 62∘10. 已知如图，直线AB、CD相交于点O，∠AOC=70∘，OE把∠BOD分成两部分，且∠BOE:∠EOD=2:3，则∠AOE= ( )A. 162∘B. 152∘C. 142∘D. 132∘11. 如图所示，已知AB⊥BD，BC⊥CD，AD=6 cm，BC=4 cm，则线段BD的范围是 ( )A. 大于4 cmB. 小于4 cmC. 大于4 cm且小于6 cmD. 小于6 cm或大于4 cm12. 用3根火柴棒最多能拼出 ( )A. 4个直角B. 8个直角C. 12个直角D. 16个直角13. 三条直线两两相交于同一点时，对顶角有m对，交于不同三点时，对顶角有n对，则m与n的关系 ( )A. m=nB. m>nC. m<nD. m+n=1014. 观察下列图形，并阅读图形下面的相关文字：两条直线相交，三条直线相交，四条直线相交，⋯⋯最多有1个交点；最多有3个交点；最多有6个交点⋯⋯像这样，十条直线相交，最多交点的个数是 ( )．A. 40个B. 45个C. 50个D. 55个15. 如图，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15∘30’，则下列结论中不正确的是 ( )．A. ∠2=45∘B. ∠1=∠3C. ∠AOD与∠1互为补角D. ∠1的余角等于75∘30ʹ二、填空题（共15小题；共75分）16. A是直线l外的一点，A到l的距离为10 cm，P是l上任意一点，则PA的最小值是cm．17. 如图所示，直线a、b相交于点O，∠1=50∘，则∠2=度．18. 如图，直线AB，CD相交于点O．若∠BOD=40∘，OA平分∠COE，则∠AOE=．∠B，那么∠B=．19. 若∠A与∠B互为邻补角，且∠A=1320. 如图，直线AB和CD相交于点O，OE平分∠DOB，∠AOC=40∘，则∠DOE=度．21. 如图所示，点P是∠AOB的边OB上的一点．①过点P作OB的垂线，交OA于点C．②过点P作OA的垂线，垂足为H．③线段PH的长度是点P到的距离，线段的长度是点C到直线OB的距离．④因为直线外一点与直线上各点所连的所有线中，垂线段最短，所以PC，PH，OC这三条线段的大小关系是（用“ <”连接）．22. 在同一平面内，三条直线两两相交，最多有3个交点，那么4条直线两两相交，最多有个交点，8条直线两两相交，最多有个交点．23. 下列说法正确的是．（写出正确的序号）① 三条直线两两相交有三个交点；② 两条直线相交不可能有两个交点；③在同一平面内的三条直线的交点个数可能为0，1，2，3；n(n−1)个交点；④同一平面内的n条直线两两相交，其中无三线共点，则可得12⑤ 同一平面内的n条直线经过同一点可得2n(n−1)个角（平角除外）．24. O为平面上一点，过O在这个平面上引2005条不同的直线l1，l2，l3，⋯，l2005，则可形成对以O为顶点的对顶角．25. 如图，AB与CD相交于点O，若∠DOE=90∘，∠BOE=52∘，则∠AOC=．26. 如图，AB、CD、EF相交于O点，EF⊥AB，OG为∠COF的平分线，OH为∠DOG的平分线．若∠AOC:∠COG=4:7，则∠DOH=度.27. 如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD=35∘，则∠COB= .28. 如图，直线AB，CD相交于点O，已知∠AOC=70∘，OE把∠BOD分成两部分，且∠BOE:∠EOD=3:2．则∠EOD=．29. 已知OA⊥OB，∠AOC：∠AOB=2：3，则∠BOC=．30. 如图所示，两条直线相交，有对对顶角，三条直线相交于同一点，有对顶角；四条直线相交于同一点，有对对顶角，⋯，n条直线相交于同一点有对对顶角．三、解答题（共5小题；共65分）31. 如图，建筑工人经常要测量两堵围墙所成的∠AOB，但人不能进入围墙，聪明的你帮助工人师傅想想办法吧．要求：画出两种不同测量方案示意图，直接给出求∠AOB的表达式．32. 如图：点C是∠AOB的边OB上的一点，按下列要求画图并回答问题．Ⅰ过C点画OB的垂线，交OA于点D；Ⅱ过C点画OA的垂线，垂足为E；Ⅲ比较线段CE，OD，CD的大小（请直接写出结论）；Ⅳ请写出第（3）小题图中与∠AOB互余的角（不增添其它字母）．33. 如图，直线AB，CD相交于点O，OE⊥CD，OF平分∠BOD，若∠AOE=26∘，求∠COF的度数．34. 根据下列条件画图如图示点A、B、C分别代表三个村庄Ⅰ画射线ACⅡ画线段ABⅢ若线段AB是连接A村和B村的一条公路，现C村庄也要修一条公路与A、B两村庄之间的公路连通，为了减少修路开支，C村庄应该如何修路?请在同一图上用三角板画出示意图，并说明画图理由．35. 两条直线相交，四个交角中的一个锐角或一个直角称为这两条直线的“夹角”（如图）．如果在平面上画L条直线，要求它们两两相交，并且“夹角”只能是15∘，30∘，45∘，60∘，75∘，90∘之一，问：ⅠL的最大值是多少?Ⅱ当L取最大值时，问所有的“夹角”的和是多少?答案第一部分1. A2. C3. D4. A5. C6. D7. C8. D9. B 10. B11. C 12. C 13. A 14. B 15. D第二部分16. 1017. 5018. 40∘19. 135∘20. 2021. ①②如图所示．③ OA，PC．④ PH<PC<OC．22. 6；2823. ② ③ ④ ⑤24. 401802025. 38∘26. 72.5∘27. 125∘28. 28∘．29. 150∘或30∘30. 两；六；十二；n(n−1)第三部分31. 方案1图：∠AOB=∠DOC．方案2图：∠AOB=180∘−∠BOC．32. （1）如图：（2）如图：（3）CE<CD<OD．（4）∵CE⊥OA，∴∠AOB+∠OCE=90∘．∵CD⊥OB，∴∠AOB+∠ODC=90∘．∴与∠AOB互余的角是∠OCE与∠ODC．33. ∵OE⊥CD，∴∠EOD=90∘．∵∠AOE=26∘，∴∠DOB=180∘−∠AOE−∠EOD=64∘．∵OF平分∠BOD，∠DOB=32∘．∴∠DOF=12∴∠COF=180∘−∠DOF=148∘．34. （1）（2）（3）如图所示，过点C作CD⊥AB，垂足为D．理由：连接直线外一点与直线上各点的所有线段中，垂线段最短．35. （1）固定平面上一条直线，其它直线与此条固定直线的交角自这条固定直线起逆时针计算，只能是15∘，30∘，45∘，60∘，75∘，90∘，105∘，120∘，135∘，150∘，165∘十一种角度之一，所以，平面上最多有12条直线．否则，必有两条直线平行．（2）如图，将所有直线做平行移动，使它们交于同一个点，这样的平行移动显然不改变两条直线的“夹角”．无妨设其中一条直线水平，从水平直线开始，逆时针将12条直线分别记为第一条、第二条、⋯和第十二条直线．（1）如图：第二条至第十二条直线与第一条直线的“夹角”和是：15+30+45+60+75+90+75+60+45+30+15=540（度）；（2）第三条至第十二条直线与第二条直线相交的“夹角”和是：15+30+45+60+75+90+75+60+45+30=(540−15)（度）；（3）第四条至第十二条直线与第三条直线相交的“夹角”和是：15+30+45+60+75+90+75+60+45=(540−15−30)（度）；⋯；（10）第十一条和第十二条直线与第十条直线相交的“夹角”和是(30+15)（度），（11）第十二条直线与第十一条直线相交的“夹角”和是15（度）；将（2）和（11）、（3）和（10）、（4）和（9）、（5）和（8）、（6）和（7）配对，得到所有的“夹角”之和是6×540=3240（度）．。

新版浙教版数学七上同步练习：6.9直线的相交第1课时对顶角同步练习

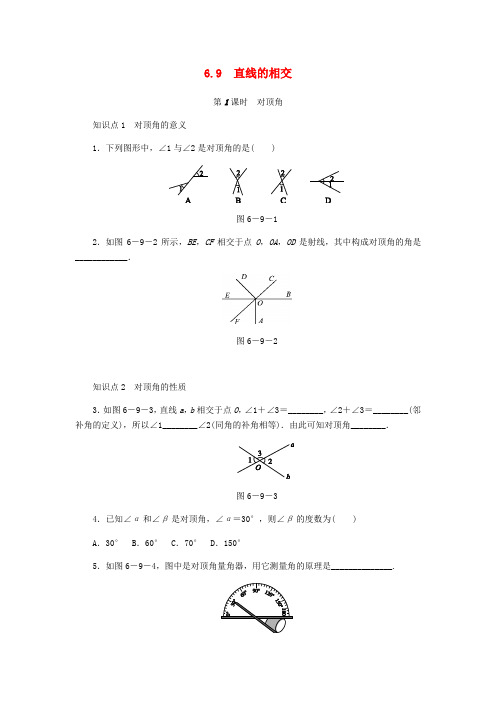
6.9 直线的相交第1课时对顶角知识点1 对顶角的意义1．下列图形中，∠1与∠2是对顶角的是( )图6－9－12．如图6－9－2所示，BE，CF相交于点O，OA，OD是射线，其中构成对顶角的角是____________．图6－9－2知识点2 对顶角的性质3．如图6－9－3，直线a，b相交于点O，∠1＋∠3＝________，∠2＋∠3＝________(邻补角的定义)，所以∠1________∠2(同角的补角相等)．由此可知对顶角________．图6－9－34．已知∠α和∠β是对顶角，∠α＝30°，则∠β的度数为( )A．30° B．60° C．70° D．150°5．如图6－9－4，图中是对顶角量角器，用它测量角的原理是______________.图6－9－46．如图6－9－5，直线AB，CD，EF交于一点O.图6－9－5(1)∠EOB的对顶角是________；(2)________是∠AOE的对顶角；(3)若∠AOC＝76°，则∠BOD的度数为________．7．如图6－9－6所示，直线AB与CD相交于点O，若∠AOC＋∠BOD＝90°，则∠BOC＝________°.图6－9－68．如图6－9－7所示，∠1＝120°，∠2＋∠3＝180°，则∠4＝________°.图6－9－79. 如图6－9－8，直线AB，CD相交于点O，∠1＝40°，求∠2，∠3，∠4的度数．图6－9－810．如图6－9－9所示，直线AB，CD相交于点O，OE平分∠AOC，∠EOC＝35°，求∠BOD 的度数．图6－9－911．如图6－9－10，直线AB，CD，EF相交于点O，∠AOD＝150°，∠EOD＝80°，求∠AOF 的度数．图6－9－1012．如图6－9－11，直线AB，CD相交于点O，OE平分∠AOC，OF平分∠DOB，则点E，O，F在同一直线上，请说明理由．(补全解答过程)图6－9－11解：∵直线AB，CD相交于点O，∴∠AOC＝________(对顶角相等)．∵OE平分∠AOC，OF平分∠DOB，∴∠AOE＝______∠AOC，∠BOF＝______∠DOB，∴∠AOE＝________．∵∠AOF＋∠BOF＝∠AOB＝180°，∴∠AOF＋∠AOE＝∠EOF＝180°，∴点E，O，F在同一直线上．13．如图6－9－12，直线AB与CD相交于点O，∠BOE＝∠COF＝90°，且∠BOF＝32°，求∠AOC与∠EOD的度数．图6－9－1214．已知：如图6－9－13所示，直线AB，CD，EF相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE的度数．图6－9－1315．观察图6－9－14，回答下列各题．(1)图①中，共有________对对顶角，可以看作________＝________×________；(2)图②中，共有________对对顶角，可以看作________＝________×________；(3)图③中，共有________对对顶角，可以看作________＝________×________；(4)通过(1)～(3)各题中直线条数与对顶角对数之间的关系，若有n(n≥2)条直线相交于一点，则可形成几对对顶角？图6－9－141．C 2.∠EOF和∠BOC，∠COE和∠BOF3．180°180°＝相等4．A 5.对顶角相等6．(1)∠AOF(2)∠BOF(3)76°7．135 8.609．解：∵∠1＝40°，∠1＝∠2，∴∠2＝40°. ∵∠1＝40°，∠1＋∠3＝180°，∴∠3＝140°. 又∵∠3＝∠4，∴∠4＝140°.10. 解：∵OE平分∠AOC，∠EOC＝35°，∴∠AOC＝2∠EOC＝35°×2＝70°.由对顶角相等可知：∠BOD＝∠AOC＝70°. 11．解：∵∠AOD＝150°，∠AOD＋∠BOD＝180°，∴∠BOD＝30°.又∵∠EOD＝80°，∴∠EOB＝80°－30°＝50°，∴∠AOF＝∠EOB＝50°.12．∠DOB 1212∠BOF13．解：∵∠COF＝90°，∠BOF＝32°，∴∠COB＝90°－32°＝58°＝∠AOD.∵∠BOE＝90°，∴∠EOA＝180°－90°＝90°，∠EOC＝90°－∠COB＝32°，∴∠AOC＝∠EOA＋∠EOC＝122°，∠EOD＝∠EOA＋∠AOD＝148°.14．解：∵∠1＋∠2＋∠3＝180°，且∠1∶∠3＝3∶1，∠2＝30°，∴∠1＝112.5°，∠3＝37.5°，∴∠BOE＝∠1＝112.5°.15．解：(1)共有2对对顶角，可以看作2＝2×1.(2)单个角是对顶角的有3对，两个角组成复合角的对顶角有3对，共有6对，可以看作6＝3×2.(3)单个角是对顶角的有4对，两个角组成复合角的对顶角有4对，三个角组成复合角的对顶角有4对，共有12对，可以看作12＝4×3.(4)n(n≥2)条直线相交于一点，可形成n(n－1)对对顶角．。

新版浙教版数学七上同步练习：6.9直线的相交第1课时分层训练

6.9 直线的相交(第1课时)1．如果两条直线____________，就说这两条直线相交，该公共点叫做这两条直线的____________．2．顶点____________，角的两边____________所组成的角叫对顶角．3．对顶角____________．A组基础训练1．以下四种说法：①对顶角相等；②相等的角是对顶角；③不是对顶角的两个角不相等；④不相等的两个角不是对顶角．其中正确的是( )A．1个 B．2个C．3个 D．4个2．∠1的对顶角是∠2，∠2与∠3互补，若∠3＝45°，则∠1的度数为( )A．45° B．135°C．45°或135° D．90°3．平面内三条直线两两相交构成的对顶角共有( )A．3对 B．6对C．12对 D．不能确定4．(宁波中考)如图，直线AB与直线CD相交于点O，E是∠AOD内一点，已知∠AOE＝90°，∠BOD＝45°，则∠COE的度数是( )第4题图A．125° B．135°C．145° D．155°5．(1)如图1，用图中这种测量工具，可以量出图中零件上AB与CD两条轮廓线的延长线所成的角．其中的道理是____________．图1图2第5题图(2)如图2，当剪刀口∠AOB增大15°时，∠COD增大____________．6．如图，三条直线交于同一点，若∠1＋∠2＝80°，则∠3＝____________.第6题图7．如图，已知直线AB，BC，CA两两相交于A，B，C三点，已知∠1与∠3互补，若∠2＝51°，则∠4＝____________.第7题图8．如图，直线EF分别交∠AOB的两边于C，D两点，写出图中所有的对顶角．第8题图9．如图，直线AB与CD相交于点O，∠AOD＋∠BOC＝260°，求∠AO C的度数．第9题图10．如图，直线AB，CD交于点O，OE平分∠AOD.(1)若∠AOC＝46°，求∠DOE的度数；(2)若∠AOC＝x，求∠COE的度数．第10题图11．如图，直线AB，CD相交于点O，∠AOE比∠DOE大30°，∠BOD比∠DOE小30°，求∠AOE和∠A OC的度数．第11题图12．如图所示，直线AB，CD相交于点O，OE平分∠AOD，∠FOC＝90°，∠1＝40°，求∠2和∠3的度数．第12题图B组自主提高13．同一平面内的三条直线的交点个数为____________．14．如图，已知直线AB与CD交于点O，OE平分∠BOD，OF平分∠AOB.(1)若∠BOE＝40°，求∠AOF与∠COF的度数；(2)若∠BOE＝x(x＜45°)，请用含x的代数式表示∠COF的度数．第14题图C组综合运用15．观察下图，回答下列问题．第15题图(1)图1中共有____________对对顶角；(2)图2中共有____________对对顶角；(3)图3中共有____________对对顶角；(4)当n(n≥2，且n为整数)条直线相交于一点时，会形成____________对对顶角．参考答案6．9 直线的相交(第1课时)【课堂笔记】1．只有一个公共点交点 2.相同互为反向延长线 3.相等【分层训练】 1．B 2.B 3.B 4.B 5．(1)对顶角相等 (2)15° 6．100° 7.51°8．∠ECO 与∠ACD，∠ACE 与∠OCD，∠CDO 与∠BDF，∠CDB 与∠ODF. 9．∠AOC＝50°10．(1)∵∠AOC＋∠AOD＝180°，∠AOC ＝46°，∴∠AOD ＝180°－46°＝134°.∵OE 平分∠AOD，∴∠DOE ＝12∠AOD ＝67°.(2)∠COE＝∠AOC＋∠AOE＝x ＋12(180°－x)＝90°＋12x.11．∠AOE＝90°，∠AOC ＝30°.12．∠3＝180°－∠COF－∠1＝50°，∴∠AOD ＝180°－∠3＝130°.∵OE 平分∠AOD，∴∠2＝12∠AOD ＝65°.13．0个或1个或2个或3个14．(1)∵OE 平分∠BOD，∴∠BOE ＝12∠BOD.∵∠BOE ＝40°，∴∠BOD ＝80°，∴∠BOC＝100°.∵OF 平分∠AOB，∴∠AOF ＝∠BOF＝90°，∴∠COF ＝100°－90°＝10°. (2)∠COF ＝180°－2x －90°＝90°－2x.15．(1)2 (2)6 (3)12 (4)n(n －1)。