第三章 X射线的强度
合集下载
3X射线衍射强度

= 3:4:8:11:12:16
……
结构因数只与原子的种类及其在单胞中的位置有关,而 不受单胞的形状和大小的影响。例如对体心点阵,不论 是立方晶系、正方晶系还是斜方晶系,其消光规律是相 同的,因此系统消光规律具有广泛的适用性。
18
三种点阵晶体衍射线的分布状况
图中m = H2 + K2 + L2,产生衍射的 干涉面指数平方和之比分别为: 简单点阵 1:2:3:4:5:6:8:9 ……
1
1
1
2
2
2
3
3
3
= 1:2:3:4:5:6:8:9
……
2. 体心点阵
体心点阵的单胞中有两种位置的原子,即坐标为 (0,0,0) 的顶角原子和坐标为(1/2, 1/2, 1/2)的体心原子,原子散
射因数均为 f。其结构因数为:
2 2
FHKL f 1 cos ( H K L)
1/(sin cos) (即1/sin2 )成正比。
衍射的积分强度
26
第三节 洛伦兹-偏振因数
3.3.1 衍射的积分强度
3.3.2 参加衍射的晶粒分数 3.3.3 单位弧长的衍射强度 3.3.4 洛伦兹-偏振因数
27
3.3.2 参加衍射的晶粒分数
多晶样品中,各晶粒的取向在空间等几率分布。各晶 粒中所有同族 (HKL)晶面的面间距相同,产生衍射的布 拉格角相等。
第三节 洛伦兹-偏振因数
3.3.1 衍射的积分强度
3.3.2 参加衍射的晶粒分数 3.3.3 单位弧长的衍射强度 3.3.4 洛伦兹-偏振因数
30
3.3.3 单位弧长的衍射强度
第三章 X射线衍射强度

温度因子
e
2 M
IT I
式中:IT — 原子热振动影响时的强度 I — 理相状态的强度 热振动的方向无规则性,使得非衍射方 向散射强度↑,增加衍射花样背底。
5 吸收因子 A(θ )
试样对x-ray的吸收造成衍射强度的衰减。
无吸收A(θ
)=1,吸收越多,其值越小。 圆柱状试样的A(θ )是试样 l 和半径r的 函数,可通过查表求得。 1 板状试样的A(θ )与θ 无关, A( ) 2
角顶 Cs (0,0,0) FHKL = f Cs + f Cl e H + k + L = 偶数 F = f Cs+ f Cl 强度高 (110)(200)(211)… H + k + L= 奇数 F = f Cs – f Cl 强度低 (100)(111)(210)…
1 1 1 体心 Cl( 2 , 2 , 2 ) iπ(H+K+L)
2 多重性因子 P
表示多晶体中同族晶面{HKL}的等同晶面
数。
P值越大,晶面获得衍射的几率越大,对应
的衍射线越强。
d同
θ同 衍射线重叠在同一衍射线环上。
P数值随晶系及晶面指数而变化。
例:
立方晶系(a
= b = c α=β=γ=90°)
P100= 6 四方晶系(a = b≠c α=β=γ=90°) P100= 4 P001= 2
系统消光
衍射线I=0,衍射线消失,称为系统消光。
(原子在晶胞中的位置不同引起某些方向 衍射线的消失--点阵消光)。
尽管满足衍射条件,因F
= 0使衍射线消失
的现象。
对于体心点阵,可以产生衍射的晶面为
第三章 X射线衍射强度.

式中:Io—入射x-ray强度 m、e — 电子的质量与电荷 c— 光速 λ— 入射x-ray波长 R— 衍射仪半径 cm V— 试样被x-ray照射体积,cm3 Vo— 晶胞体积 cm3 F— 结构因子 P— 多重性因子 e-2M — 温度因子
( ) — 角因子 A(θ) — 吸收因子
同一衍射花样中,e、m、c为固定物理常数, Io、λ、R、V、Vo对同一物相的各衍射线均相 等,衍射线的相对积分强度可用 5个强度因子的乘积来表示:
而(100),(111),(210),(221)等均无散射
4. 面心晶胞:四种位置的原子坐标分别是(0 0 0)和 (½ ½ 0),( ½ 0 ½ ),(0 ½ ½)。
F fe2 i0 fe2 ih/ 2k / 2 fe fe 2 ik / 2l / 2 2 il / 2h/ 2 f 1 eihk eikl eilh
当h, k, l为全奇或全偶,(h + k),(k+l) 和
(h+l) 必为偶数,故F = 4f,F 2 = 16f 2
当h, k, l中有两个奇数或两个偶数时,则在(h+k),(k+l) 和 (h+l)中必有两项为奇数,一项为偶数,故F = 0, F2 = 0 所以(111),(200),(220),(311)有反射,而 (100),(110) ,(112),(221)等无反射。
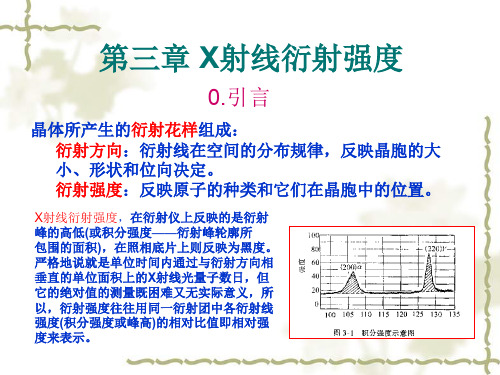
衍射线强度的测量采用衍 射仪法,得到I~θ曲线。
每个衍射峰下面的 面积(积分面积)称 为积分强度或累积强度。
x射线衍射线束的强度
波长λ强度Io的x-ray,照射到 晶胞体积Vo的多晶试样上,被 照射晶体的体积V,与入射线 夹角为2θ方向上产生(HKL) 晶面的衍射,距试样R处记录 到的衍射线其单位长度上积分 强度为:
第3章 X射线的衍射强度

1 1 1 2 i h k l F f 1 e 4 4 4
2) 当hkl全为奇数时,Ff=Fa。h+k+l=2n+1,其中n为任 意整数,则有
1 e
i
2
h k l
1 cos
2
h k l i sin
I=A2
实际上,晶体要产生x射线衍射,x射线的波长应当 与晶体中原子间距在同一数量级。
与入射x射线平行的方向上(XX’): 相位差为0,所以Aa=ZAe 除了XX’方向:各电子的散射波之 间存在一定的相位差。 如在YY’方向上a、b两个电子产 生的散射波的波程差为CB-AD,
会产生干涉作用。 由于原子半径的尺度比x射线的波长的尺度要小,所以各电子的
四、一个晶胞对x射线的衍射
1、复杂点阵的衍射分析
简单点阵只由一种原子组成,每个晶胞只有一个原子,它 分布在晶胞的顶角上,单位晶胞的散射强度相当于一个原 子的散射强度。 复杂点阵晶胞中含有n个相同或不同种类的原子,它们除 占据单胞的顶角外,还可能出现在体心、面心或其他位置。 复杂点阵的衍射特点 (1)任何复杂点阵都是由完全相同且平行的几个简单点阵 镶嵌而成的; (2)整个复杂点阵的衍射可以看做是由各个简单点阵及基 点原子在相同方向的衍射合成结果; (3)复杂点阵的可能衍射方向不可能多余其中任何一个简 单点阵的衍射方向,只能减少或相等。
假定一个晶胞中有n个原子, 它们的坐标分别为u1v1w1、u2v2w2……unvnwn; 每个原子的原子散射因子分别为f1、f2、f3…… fn ;它们的散射波的振幅为 Aef1、Aef2、Aef3……Ae fn 各原子散射波与入射波的位相差分别为φ1、φ2、φ3、……φn。 那么,这n 个原子的散射波互相叠加合成的整个晶胞的散射波的振幅Ab为
2) 当hkl全为奇数时,Ff=Fa。h+k+l=2n+1,其中n为任 意整数,则有
1 e
i
2
h k l
1 cos
2
h k l i sin
I=A2
实际上,晶体要产生x射线衍射,x射线的波长应当 与晶体中原子间距在同一数量级。
与入射x射线平行的方向上(XX’): 相位差为0,所以Aa=ZAe 除了XX’方向:各电子的散射波之 间存在一定的相位差。 如在YY’方向上a、b两个电子产 生的散射波的波程差为CB-AD,
会产生干涉作用。 由于原子半径的尺度比x射线的波长的尺度要小,所以各电子的
四、一个晶胞对x射线的衍射
1、复杂点阵的衍射分析
简单点阵只由一种原子组成,每个晶胞只有一个原子,它 分布在晶胞的顶角上,单位晶胞的散射强度相当于一个原 子的散射强度。 复杂点阵晶胞中含有n个相同或不同种类的原子,它们除 占据单胞的顶角外,还可能出现在体心、面心或其他位置。 复杂点阵的衍射特点 (1)任何复杂点阵都是由完全相同且平行的几个简单点阵 镶嵌而成的; (2)整个复杂点阵的衍射可以看做是由各个简单点阵及基 点原子在相同方向的衍射合成结果; (3)复杂点阵的可能衍射方向不可能多余其中任何一个简 单点阵的衍射方向,只能减少或相等。
假定一个晶胞中有n个原子, 它们的坐标分别为u1v1w1、u2v2w2……unvnwn; 每个原子的原子散射因子分别为f1、f2、f3…… fn ;它们的散射波的振幅为 Aef1、Aef2、Aef3……Ae fn 各原子散射波与入射波的位相差分别为φ1、φ2、φ3、……φn。 那么,这n 个原子的散射波互相叠加合成的整个晶胞的散射波的振幅Ab为
第三章 X射线衍射强度

由此可见,图3-2(a)中的(001) 晶面会参于衍射,而(b)中(001)面却 不产生衍射,也就是说原子位置改变,衍 射强度改变。
二 . 结构因素的概念
1. 系统消光——因原子在晶体中的位置不同或 原子种类不同,衍射线相互干涉,造成在某些 方向上衍射线强度减弱甚至消失的现象称之系 统消光。
2. 结构因数——定量地表征原子排布以及原子种 类对衍射强度影响规律的参数。即晶体结构对 衍射强度影响规律的参数。
晶体的衍射强度与参加衍射晶粒数目成正比.
∵ 参加衍射的晶粒分数=(cosθΔθ)/2 ∴ 这一数目与衍射角有关,即I ∝ cosθ。
也将这一项称为第二几何因子。
⑶单位弧长的衍射强度(第三几何因子,即 衍射线位置对强度测量的影响)
意义:描述了衍射线所处位置不同对衍射强度的影 响,即2θ↓衍射线圆弧半径↓,单位弧长上的强度↑。
2.三种衍射几何对衍射强度的影响规律
⑴.晶粒大小的影响(第一几何因子)
由于实际晶体的不完整性、入射线也不可能是绝对 单色的,且不会绝对平行而是具有一定的发散角。因此, 衍射线的强度尽管在满足布拉格方程的方向上最大,但 偏离一定的布拉格角时也不会为零,故衍射曲线呈山峰 状,具有一定的宽度,而不是严格的直线。
2
当2θ=90。时
1 cos2 2
2对x射线的散射
1. 原子核对X-ray的散射
由于散射波强度与引起散射的粒子 质量成反比,原子核质量是电子质量的1840 倍,因此原子核引起的散射强度极弱,可忽 略不计。
2 . 原子中Z个电子对X-ray的散射
⑴ . 首先假设原子中的电子集于一点,即所有 电子散射波之间无位相差,则原子序数为Z的原 子对X-ray散射波振幅Aa为电子散射波振幅Ae的 Z倍,即 :
第3章X射线的强度详解

Z个电子散射的叠加。 (1)若不存在电子电子散射位相差:
其中Ae为一个电子散射 的振幅
7
(1)实际上,存在位相差,引入原子散射
因子:
即Aa=f Ae 。 其中f与有关、与λ有关。
散射强度:
(f总是小于Z)
8
原子散射因子
9
一个单胞对X射线的散射
1. 讨论对象及主要结论:
这里引入了FHKL ――结构因子
19
3.2 单胞对X射线的散射
体心点阵
FHKL2=fa2[cos2π(0)+cos2π(H/2+K/2+L/2)]2+ fa2[sin2π(0)+sin2π(H/2+K/2+L/2)]2
分析 = fa2[1+cosπ(H+K+L)]2
当H+K+L为偶数时, FHKL=2fa
当H+K+L为奇数时, FHKL=0
17
3.2 单胞对X射线的散射
底心点阵 分析:
当H+K为偶数时,即H,K全为奇数或全为 偶数: FHKL2=fa2(1+1)2=4fa2
当H+K为奇数时,即H、K中有一个奇数 和一个偶数: FHKL2=fa2(1-1)2=0
结论 在底心点阵中,FHKL不受L的影响,只有当H、 K全为奇数或全为偶数时才能产生衍射
25
四种基本点阵的消光规律
布拉菲点 阵
出现的反射
消失的反射
简单点阵
全部
无
底心点阵 体心点阵 面心点阵
H、K全为奇数或全为偶数 H+K+L为偶数
H、K、L全为奇数或全为偶数
H、K奇偶混 杂
其中Ae为一个电子散射 的振幅
7
(1)实际上,存在位相差,引入原子散射
因子:
即Aa=f Ae 。 其中f与有关、与λ有关。
散射强度:
(f总是小于Z)
8
原子散射因子
9
一个单胞对X射线的散射
1. 讨论对象及主要结论:
这里引入了FHKL ――结构因子
19
3.2 单胞对X射线的散射
体心点阵
FHKL2=fa2[cos2π(0)+cos2π(H/2+K/2+L/2)]2+ fa2[sin2π(0)+sin2π(H/2+K/2+L/2)]2
分析 = fa2[1+cosπ(H+K+L)]2
当H+K+L为偶数时, FHKL=2fa
当H+K+L为奇数时, FHKL=0
17
3.2 单胞对X射线的散射
底心点阵 分析:
当H+K为偶数时,即H,K全为奇数或全为 偶数: FHKL2=fa2(1+1)2=4fa2
当H+K为奇数时,即H、K中有一个奇数 和一个偶数: FHKL2=fa2(1-1)2=0
结论 在底心点阵中,FHKL不受L的影响,只有当H、 K全为奇数或全为偶数时才能产生衍射
25
四种基本点阵的消光规律
布拉菲点 阵
出现的反射
消失的反射
简单点阵
全部
无
底心点阵 体心点阵 面心点阵
H、K全为奇数或全为偶数 H+K+L为偶数
H、K、L全为奇数或全为偶数
H、K奇偶混 杂
X射线的衍射强度

有序固溶体分析
(1)完全无序 每个晶胞中含有四个平均原子(0.75 Cu+0.25Au)属面心立 方点阵。坐标000 1/2 1/2 0 1/2 0 1/2 0 1/2 1/2
FHKL=f平均[1+eπi(H+K)+eπi(H+L)+eπi(K+L)] 当H、K、L全为奇数或全为偶数时 FHKL=4 f平均=fAu+3fCu 当H、K、L为奇偶混杂时,FHKL=0消光
一个原子对X射线的散射
原子散射因子曲线 对于不同类型的原子,其原子散射因子 f 是可变的,它与sinθ和λ有关。随 sinθ/λ的值的增大而变小。 Sinθ=0时,f=Z. 原子序数越小,非相干散射越强。(核外电子所占比例增大)
一个晶胞对X射线的散射
预备知识: X射线的波前电场强度随时间的变化可以用周期函数表示:
实际上,原子中的电子是按照电子云状态分布在原子空 间的不同位置上,故各个电子散射波之间是存在位相差的, 这一位相差使得合成波的强度减弱。
一个原子对X射线的散射
X射线受到一个原子的散射
一个原子对X射线的散射
经过修正: 一个电子对X射线散射后空间某点强度可用Ie表示,那么一个 原子对X射线散射后该点的强度Ia:
fe 2 2 2
= f [1+ eπi(h+k+l) ]
F = 2 f (h+k+l)为偶数 F2 = 4f 2
F = 0 (h+k+l)为奇数
体心点阵中,只有当H+K + L为 偶数时才能产生衍射
体心立方
面心立方晶胞的结构因子
每个晶胞中有4个同类原子,分别位于000、1/2 1/2
第三章 X射线强度

2、系统消光与消光规律
1) 系统消光 分析一下晶胞中原子的位置和种类是如何影响x
射线的衍射,并通过结构因子的公式讨论其规律性。 比较同种和不同种底心晶胞和体心晶胞(001)面
的衍射情况。
二、结构因子 1) 系统消光
把因原子位置和种类不同而引起的某些 方向上衍射线消失的现象叫系统消光。
可见布拉格方程只是x射线衍射的必要条 件而不是充分条件。也就是说,晶体中产生 衍射必需满足布拉格方程,但满足布拉格方 程的方向上,不一定产生衍射线。
如何确定x射线衍射强度?
分析的思路: *一个电子对x射线的衍射强度 *一个原子对x射线的衍射强度 *一个晶胞(多个原子)对x射线的衍射强度 *多晶体样品对x射线的的衍射强度
二、结构因子
(一) 电子对x射线的衍射 相干散射
电子在x射线电场的作用下产生强迫振动,向四周幅射x射线散射波: *振动频率(波长)与原x射线相同 *各个方向的x射线频率相同
b、当相邻层的光程差为1/2λ 时,相邻层的反射相消干涉。
无衍射线产生。
c、当相邻层的光程 差为1/8λ时,第0层与 第4层的反射线产生相 消干涉 。第1层与5层 的反射相消干涉……第 3层与第7层反射相消干 涉,最后所有的反射线 全部抵消,不产生衍射 线。
d、当晶体有m+1 层时,如相邻 层的光程差为λ/m,必然存在第 m/2层,它与第0层的光程差为λ/2。 于是,第0层反射与第m/2层反射相 消干涉,第1层与第m/2+1层相 消……第m/2-1层与第m层相消干涉。 最终晶体上半部的反射与晶体下半 部的反射全部相消,衍射强度为0。
n个向量合成的 新向量就可很容易 地写成各个向量的 和 e=acosφ+iasinφ
进行向量合成 的运算时,指数函 数形式比三角函数 形式更为简单,因 此更为常用。
第三章 X射线的强度

b、两偶一奇
2
结构消光 结构消光
F 0
2
例题4:具有底心阵胞的点阵,由同名原子组成,m=2 ;
u、v、w=(0、0、0);(1/2、1/2、0)
2 m
F
2
f
m
exp[2πi(um H v m K wm L)]
2
1 1 f1 exp[2i (0H 0K 0L)]+f 2 exp[2i ( H K 0L)] 2 2
2 f 2 1+exp(i L) exp[ i (H 2K)] 3 讨论: ① 当H+2K=3n(n为任意整数)和L为奇数时:
2
F 0
② 当H、K、L为其它组合时:
2
F 0
2
例题6:由异名原子组成晶体结构,计算NaCl 的结构因数,NaCl晶体 结构中,每个晶胞中有4个钠原子和4个氯原子,原子散射因数分别为 fNa 和 fCl : 钠原子的坐标为:
位相和振幅不同的正弦波的合成
两个波长相同而位相和 振幅不同,其波函数可用下
式表示:
E1 A1 sin( 2πν t 1 )
E2 A2 sin( 2 t 2 )
若求两个波的合成,可
用复数方法进行解析运算。
波的向量合成
波的解析表达式:
A cos Ai sin ix 又:e cos x i sin x
j 1 m i j
令:
Ab m i j F f je Ae j 1
结构因子
衍射波的位相与衍射面和原子的位置有关
2 ( Hu Kv Lw)
FHKL f j e
j 1 m 2 i ( Hu j Kv j Lw j )
2
结构消光 结构消光
F 0
2
例题4:具有底心阵胞的点阵,由同名原子组成,m=2 ;
u、v、w=(0、0、0);(1/2、1/2、0)
2 m
F
2
f
m
exp[2πi(um H v m K wm L)]
2
1 1 f1 exp[2i (0H 0K 0L)]+f 2 exp[2i ( H K 0L)] 2 2
2 f 2 1+exp(i L) exp[ i (H 2K)] 3 讨论: ① 当H+2K=3n(n为任意整数)和L为奇数时:
2
F 0
② 当H、K、L为其它组合时:
2
F 0
2
例题6:由异名原子组成晶体结构,计算NaCl 的结构因数,NaCl晶体 结构中,每个晶胞中有4个钠原子和4个氯原子,原子散射因数分别为 fNa 和 fCl : 钠原子的坐标为:
位相和振幅不同的正弦波的合成
两个波长相同而位相和 振幅不同,其波函数可用下
式表示:
E1 A1 sin( 2πν t 1 )
E2 A2 sin( 2 t 2 )
若求两个波的合成,可
用复数方法进行解析运算。
波的向量合成
波的解析表达式:
A cos Ai sin ix 又:e cos x i sin x
j 1 m i j
令:
Ab m i j F f je Ae j 1
结构因子
衍射波的位相与衍射面和原子的位置有关
2 ( Hu Kv Lw)
FHKL f j e
j 1 m 2 i ( Hu j Kv j Lw j )
第三章X射线衍射强度gqf详解

Modern Analytical Instruments and Technology for Materials 7
X射线衍射强度理论包括运动学理论和动力学理论,前者 只考虑入射X射线的一次散射,后者考虑入射X射线的多 次散射。
X射线衍射强度涉及因素较多,问题比较复杂。一般从基 元散射,即一个电子对X射线的(相干)散射强度开始, 逐步进行处理。
(原子散射因子)
晶胞内 各原子 散射波
合成
一个晶胞对X射 线的散射强度 (结构因子)
引入吸收因 子、温度因 子、多重性
因子
(粉末)多 晶体衍射
(积分)强 度
温度对强度 的影响
吸收对强度 的影响
等同晶面数 对强度的影
响
小晶体 内各晶 胞散射 波合成
单位弧长衍 射强度
参加衍射的晶 粒(小晶体)
数目
一个小晶体对X射线 的散射强度与衍射
(积分)强度 (干涉函数)
X射线衍射强度问题的处理过程
Modern Analytical Instruments and Technology for Materials 9
3.2 一个电子对X射线的散射 P15
电子在入射X射线电场矢量作用下会产生受迫振动。获得变 加速运动的电子,作为新的波源向四周辐射与入射X射线频 率相同并具有确定周相关系的电磁波。
Chapter 3
X射线衍射强度
The Diffracted Intensity of X-Ray
Modern Analytical Instruments and Technology for Materials
本章主要内容
了解影响衍射强度的各种因素,多重 因子,角因子,吸收因子,温度因子 和结构因子。
X射线衍射强度理论包括运动学理论和动力学理论,前者 只考虑入射X射线的一次散射,后者考虑入射X射线的多 次散射。
X射线衍射强度涉及因素较多,问题比较复杂。一般从基 元散射,即一个电子对X射线的(相干)散射强度开始, 逐步进行处理。
(原子散射因子)
晶胞内 各原子 散射波
合成
一个晶胞对X射 线的散射强度 (结构因子)
引入吸收因 子、温度因 子、多重性
因子
(粉末)多 晶体衍射
(积分)强 度
温度对强度 的影响
吸收对强度 的影响
等同晶面数 对强度的影
响
小晶体 内各晶 胞散射 波合成
单位弧长衍 射强度
参加衍射的晶 粒(小晶体)
数目
一个小晶体对X射线 的散射强度与衍射
(积分)强度 (干涉函数)
X射线衍射强度问题的处理过程
Modern Analytical Instruments and Technology for Materials 9
3.2 一个电子对X射线的散射 P15
电子在入射X射线电场矢量作用下会产生受迫振动。获得变 加速运动的电子,作为新的波源向四周辐射与入射X射线频 率相同并具有确定周相关系的电磁波。
Chapter 3
X射线衍射强度
The Diffracted Intensity of X-Ray
Modern Analytical Instruments and Technology for Materials
本章主要内容
了解影响衍射强度的各种因素,多重 因子,角因子,吸收因子,温度因子 和结构因子。
第三章 X射线散射强度

归纳:在衍射图上出现非零衍射的位置取决于晶胞 参数;衍射强度取决于晶格类型。
晶格类型
消光条件
简单晶胞
体心I 面心F 底心C
无消光现象
h+k+l=奇数 h、k、l奇偶混杂 h+k=奇数
注意:衍射条件与消光条件正好相反。
晶格类型
衍射条件
简单晶胞
体心I 面心F 底心C
无条件
h+k+l=偶数 h、k、l全奇或全偶 h+k=偶数
aazae为表达原子散射能力的大小定义eaaaf??振幅一个电子相干散射波的振幅一个原子相干散射波的振幅一个电子相干散射波的振幅一个原子相干散射波的三晶胞对x射线的散射结构因子bhklaaf????一个电子的散射波振幅振幅一个晶胞相干散射波的1结构因子的定义及计算式ea个电子的散射波振幅晶胞对x光的散射为晶胞内每个原子散射的加和
e:电子电荷 m:质量 c:光速
R I0 O 2
P
二、原子对X射线的散射,原子散射因子(f)
若原子序数为 Z ,核外有 Z 个电子,将 其视为点电荷,其电量为-Z· e 原子散射:电子 原子核
因原子核质量与电子相比大很多倍,振幅很小, 产生的相干散射线强度相比可忽略。 故可看作电子散射波的叠加;
F fe2 i 0 fe2 i h / 2 k / 2 fe2 i k / 2l / 2 fe2 i l / 2 h / 2 f 1 ei h k ei k l ei l h
当h, k, l为全奇或全偶,(h + k),(k+l) 和 (h+l) 必为偶数,故F = 4f,F 2 = 16f 2 当h, k, l中有两个奇数或两个偶数时,则在(h+k),(k+l) 和 (h+l)中必有两项为奇数,一项为偶数,故F = 0, F2 = 0 所以(111),(200),(220),(311)有反射,而 (100),(110) ,(112),(221)等无反射。
第三章 X射线的强度
位相差:
j
2
j
2rj
S
S0
2 (hu kv lw)
结构振幅的计算
结构振幅为:
n
FHKL
f jei j
j 1
2 (hu j kvj lwj )
其中:uj、vj、wj是j原子的阵点坐标; (hkl)是发生衍射的晶面指数
可将复数展开成三角函数形式 ei cos i sin
面心点阵
结论
在面心立方中,只有当H、K、L全为奇数或全 为偶数时才能产生衍射。如Al的衍射数据:
1)当H、K、L全为奇数或全为偶数时
2)当H、K、L为奇数混杂时(2个奇数1个偶数或2个偶 数1个奇数)
即面心立方点阵只有指数为全奇或全偶的晶面才能 产生衍射,例如(111)、(200)、(220) (311)、(222)、(400)…。能够出现的衍射线, 其指数平方和之比是:3:4:8:11;12:16…=1; 1.33:2.67:3.67:4:5.33…
(2
),3'1'
3'1'
(2
)
2hx
a
当原子B的位置系用分数座标u x 标明时,则该周相差即成为 a
3'1' 2hu
这种推理可推广到三维空间中,原子的坐标 (xyz),其分数坐标(x/a,y/b,z/c),相应等 于(uvw),对于原子B和位于原点A散射波的周相 差,对于(hkl)反射来说,其周相差为
3.4 面心点阵对X射线的散射
面心点阵每个晶胞中有4 个同类原子
000, ½ ½ 0, ½ 0 ½, 0 ½½
第3章X射线衍射强度

结构因子只与原子的种类和原子在晶
胞中的位置有关,而不受晶胞的形状 和大小的影响。
结构消光
衍射强度: I Fhkl
2
满足布拉格方程条件2dsinθ=λ但结 构因子F=0导致衍射线强度I为零的 现象称之为结构消光。
小结
一个电子对X-ray的散射情况 偏振因子
一个原子对X-ray的散射情况 原子散射因子f 一个单胞对X-ray的散射情况 结构因子
e e
h l 2i ( ) 2 2
e
k l 2i ( ) 2 2
]
h k l 2i ( ) 2 2 2
e
k 2i ( ) 2
e
h 2i ( ) 2
]
讨论:
(1)h、k、l全为偶数时, F=4fNa+4fCl |F|2=(4fNa+4fCl)2
(2)h、k、l全为奇数时, F=4fNa-4fCl |F|2=(4fNa-4fCl)2 (3)h、k、l奇偶混杂时 F=0 NaCl属于面心布拉菲点阵,可衍射的 指数是111、200、220· · · · · · 、
当h, k, l为全奇或全偶,(h + k), (k+l) 和 (h+l) 必为偶数,故F = 4f, F 2 = 16f 2 当h, k, l中有两个奇数或两个偶数时,则在(h+k),(k+l) 和(h+l)中必有两项为奇数,一项为偶数,故F = 0, F2 = 0
所以(111),(200),(220),(311)时F≠0,这些 晶面衍射线存在,而(100),(110) ,(112),(221) 等F=0,出现消光,衍射线不存在
3.3 结构因子
【材料课件】03X射线衍射强度

其中:Xj、Yj、Zj是j原子的阵点坐标; H K L是发生衍射的晶面。
所以有:
2
2
n
FHKL f j cos2 HX j KYj LZ j
j1
2
n
f j sin 2 HX j KYj LX j
6/1/2019
j1
各晶面族的多重因子列表.
6/1/2019
HNU-ZLP
32
各晶面族的多重因子列表
指数
晶系
H00 0K0 00L HHH HH0 HK0 0KL H0L HHL HKL
立方
菱方、六方
正方 斜方 单斜 三斜
6/1/2019
P
6
8 12
24
24 48
62
6
12
24
42
48
8
16
2
4
8
2
42
4
2
2
2
HNU-ZLP
它分为:点阵消光 结构消光。
四种基本点阵的消光规律 (图表)
6/1/2019
HNU-ZLP
22
四种基本点阵的消光规律
布拉菲点 阵
出现的反射
消失的反射
简单点阵
全部
无
底心点阵 体心点阵
H、K全为奇数或全为偶数 H+K+L为偶数
H、K奇偶混 杂
H+K+L为奇 数
面心点阵 H、K、L全为奇数或全为偶数
H、K、L奇 偶混杂
因原子在晶体中位置不同或原子种类不同 而引起的某些方向上衍射线消失的现象, 称为系统消光。
根据系统消光结果以及通过测定X射线强 度的变化可以推断出原子在晶体中的位置。
X射线衍射强度

6
衍射强度-原子种类,原子位置
电子
晶体
思路:
晶胞
原子
一个原子 核
In电子
I原子核
I原子
I晶胞
I晶体
I多晶
7
二、电子对X射线的衍射
晶体的X射线衍射作用是由电子的相干 散射引起的.
当一束X射线碰到一个电子时,该电子在X射 线电场的作用下产生强迫振动,向四周幅射振动频 率(波长)与原X射线频率相同的X射线。这就是相 干散射。电子就成为一个新的X射线源。
46
四种基本点阵的消光规律
布拉菲点 阵
出现的反射 全部
消失的反射 无
简单点阵
H、K奇偶混 底心点阵 H、K全为奇数或全为偶数 杂 H+K+L为奇 体心点阵 H+K+L为偶数 数 H、K、L奇 面心点阵 H、K、L全为奇数或全为偶数 偶混杂
47
结构消光
由两种以上等同点构成的点阵结构来说,一方面 要遵循点阵消光规律,另一方面,因为有附加原 子的存在,还有附加的消光,称为结构消光
(3)体心点阵
每个晶胞中有2个同类原子,其坐标为 000和1/2 1/2 1/2 ,其原子散射因子相同
41
– 分析
• 当H+K+L为偶数时, • 当H+K+L为奇数时,
结论: 在体心点阵中,只有当H+K+L为偶数时 才能产生衍射
42
(4)面心点阵
– 每个晶胞中有4个同类原子
43
分析
• 当H、K、L全为奇数或偶数时,则(H+K)、 (H+K)、(K+L)均为偶数,这时:
这些消光规律,存在于金刚石结构、密堆六方等 结构中
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四种基本点阵的消光规律
布拉菲点阵 简单点阵 底心点阵 体心点阵 面心点阵 出现的反射
全部
消失的反射
无
H、K全为奇数或全为 偶数 (H+K为偶数)
H+K+L为偶数 H、K、L全为奇数或全 为偶数
H、K奇偶混杂(H+K 为奇数)
H+K+L为奇数 H、K、L奇偶混杂
第三节 洛仑兹因数
在多晶衍射分析中,通常要考虑衍射圆环上单位弧长 的累积强度或积分强度。 洛仑兹因数可说明衍射的几何条件对衍射强度的影响, 它考虑了以下三个衍射几何而得出的: (1)衍射的积分强度—晶粒大小 (2)参加衍射的晶粒分数 (3)单位弧长的衍射强度
R
2θ
距离式样为R的衍射圆环上,单位弧长的积分强度:
I HKL 环单位 I环 2Rsin2
第三节 洛仑兹因数
第三节 洛仑兹因数
(1+cos 2) / (sin cos)
相对强度
1 为洛仑兹因数 2 sin cos 1 cos2 2 为角因数 2 sin cos
单位晶胞对X射线的散射与结构因素
3.一个单胞对X射线的散射
底心点阵 每个晶胞中有2个同类原子,其坐标分别为000和 1/2 1/2 0,原子散射因子相同,都为fa。
(1)当H+K为偶数时,即H,K全为奇数或全 为偶数:
(2)当H+K为奇数时,即H、K中有一个奇数和一个 偶数:
在底心点阵中,FHKL不受L的影响,只有当H、K全为 奇数或全为偶数时才能产生衍射。
洛仑兹因数
(1)衍射的积分强度—晶粒大小
洛仑兹因数
(1)衍射的积分强度—晶粒大小
洛仑兹因数
(1)衍射的积分强度—晶粒大小
洛仑兹因数
(1)衍射的积分强度—晶粒大小
洛仑兹因数
(1)衍射的积分强度—晶粒大小
洛仑兹因数
(1)衍射的积分强度—晶粒大小
洛仑兹因数
(1)衍射的积分强度—晶粒大小
洛仑兹因数
几何条件(晶粒大小、 温度对强度 吸收对强度 等同晶面数对 参与衍射的晶粒大小、 一个晶胞对X射 的影响 的影响 强度的影响 单位弧长的衍射强度) 线的散射强度 (结构因子) (温度因子) (吸收因数) (多重性因子) (角因子)
eቤተ መጻሕፍቲ ባይዱ
2 M
A(θ)
P
( )
FHKL
2
(粉末)多晶体衍射(积分)强度
50 40 30 20 10
角因数
定性地说,衍射峰 的峰高随角度增加 而降低。
2
2
0
20 40 60 80 100 120 140
角因数与角关系
第四节 影响衍射强度的其他因数
(1)多重性因数
在多晶体衍射中同一晶面族{HKL}各等同晶面的面间距相等,根据布拉格方程 这些晶面的衍射角2 都相同,因此,等同晶面族的反射强度都重叠在一个衍射 圆环上。把同族晶面{HKL}的等同晶面数P称为衍射强度的多重因子。各晶系中 的各晶面族的多重因子列于表中。
T愈高,x愈小,即原子热振动愈剧烈,衍射强度减弱愈显著。 当T一定, θ愈大,e-2M愈小。
第四节影响衍射强度的其他因数
(3)温度因数
e
-2M
0.9
当T一定, θ愈 大,e-2M愈小。
0.8 0.7 0.6 0.5 0.0 0.2 0.4 0.6 0.8 1.0
sin/
铁在200C时的温度因数
则该晶胞的散射振幅为这n种原子叠加:
Ab Ae f j e
j 1 n i j
引入结构参数 :
FHKL
n Ab i f j e j Ae j 1
可知晶胞中(H K L)晶面的衍射强度:
I a FHKL
2
Ie
单位晶胞对X射线的散射与结构因素
关于结构因子:
因为:
作业
1. 用单色X射线照射圆柱多晶试样,其衍射在 空间形成什么图案?为摄取德拜图像,应当采 用什么样的底片去记录? 2.洛伦兹因子的三个几何因子反映什么对衍 射强度的影响。 3. 总结简单点阵、体心点阵和面心点阵衍射 线的系统消光规律。
其中:Ie —— 一个电子散射的X射线的强度 I0 ——入射X射线的强度 re ——是个常数,称经典电子半径,等于2.817938×10-15m R ——电场中任一点P到发生散射电子的距离 2θ ——散射线方向与入射X射线方向的夹角 e为电子电荷 m为电子质量,ε0为真空 介电常数,c为光速
单位晶胞对X射线的散射与结构因素
实际应用中考虑的是衍射线的相对强度,即同一实验条件下同一物相中 各衍射线之间的强度比(通常是与最强衍射线的比值)。对同一实验条件 下同一物相中各衍射线来说 相同,故:
相对强度:
多晶衍射的积分强度
一个电子对X射 线的散射强度 (偏振因子)
原子内各 电子散射 波的合成
一个原子对X射线 的散射强度 (原子散射因子)
指数 晶系 立方 菱方、六方 正方 斜方 单斜 三斜 6 4 2 2 2 4 2 H00 0K0 6 2 2 00L HHH 8 HH0 P 12 6 4 8 4 2 24 12 8 24 48 24 16 8 4 2 HK0 0KL H0L HHL HKL
影响衍射强度的其他因数
(2)吸收因数
影响衍射强度的其他因数
1. 一个电子对X射线的散射
分析汤姆逊公式可以看出电子对X射线散射的特点:
re 2 1 (cos 2 ) 2 Ie Io ( ) R 2
1、散射X射线的强度很弱。 假定R=1cm,2θ=0处 Ie/I0=7.94×10-23 2、散射X射线的强度与电子到观测点之间的距离的平方成反比。 3、不同方向上,即2θ不同时,散射强度不同。 平行入射X射线方向(2θ=0 或180°)散射线强度最大。垂直入射X 射线方向(2θ=90或270°)时,散射的强度最弱。为平行方向的1/2。 其余方向则散射线的强度在二者之间。
多晶衍射的积分强度公式:
I HKL
e2 V 2 2 I0 PHKL FHKL ( ) A(θ)e 2 M 32R mc V0 2
3
2
式中:I0入射X射线的强度;λ 为入射X射线的波长: R 为试样到观测点之间的距离;V 为被照射晶体的体积; Vc 为单位晶胞体积;P 为多重性因子; F 为结构因子;A(θ ) 为吸收因子 -2M φ (θ ) 为角因子;e- 为温度因子
第三章 X射线衍射强度
第一节 多晶体衍射图相的形成 第二节 单位晶胞对X射线的散射与结构因素 1.一个电子对X射线的散射 2.原子对X射线的散射 3.单胞对X射线的散射 4.晶体对X射线的散射 第三节 洛仑兹因素 多晶体的HKL面的衍射强度 第四节 影响衍射强度的其他因素
第一节 多晶体的衍射图相的形成
(1)衍射的积分强度—晶粒大小
这是洛仑兹因子中反映晶粒大小对衍射强度影响的第一几何因子。
洛仑兹因数
(2)参加衍射的晶粒分数
参与衍射的晶粒数目与cosθ呈正比,而粉末样品的衍射强 度与参与衍射的晶粒数呈正比,所以I∝cosθ
洛仑兹因数
(3)单位弧长的衍射强度
衍射圆锥
入射X射线
衍射环的半径:Rsin2θ 衍射环的周长:2πRsin2θ
(2)吸收因数
影响衍射强度的其他因数
(2)吸收因数
第四节 影响衍射强度的其他因数
(3)温度因数
第四节 影响衍射强度的其他因数
(3)温度因数
IT和I分别是TK和0K时的衍射X射线强度。 IT/I=e-2M 由固体物理理论可导出:
式中 h——普朗克常数;ma——原子的质量;k——玻耳兹曼常数; Θ——以热力学温度表示的特征温度平均值; χ一特征温度与试样的热力学温度之比, 即χ=Θ/T; φ(χ)——德拜函数;θ——半衍射角;λ——入射X射线波长。
I HKL PHKL FHKL ( ) A(θ)e 2 M
2
第三章 X射线衍射强度
知识要点
1.产生衍射的必要条件和充分条件。 2.通过衍射图谱如何判断晶粒大小。 3. 洛伦兹因子的三个几何因子反映什么对衍 射强度的影响。 4.多晶衍射的积分强度的影响因素。
第三章 X射线衍射强度
在面心立方中,只有当H、K、L全为奇数或全为偶数时 才能产生衍射。
3.一个单胞对X射线的散射
消光规律与晶体点阵 结构因子中不包含点阵常数。因此,结构因子只与 原子品种和晶胞的位置有关,而不受晶胞形状和大 小的影响 例如:只要是体心晶胞,则体心立方、正方体心、 斜方体心,系统消光规律是相同的
单位晶胞对X射线的散射与结构因素
3.一个单胞对X射线的散射
体心点阵 每个晶胞中有2个同类原子,其坐标为000和1/2 1/2 1/2 ,其原子散射因子相同:
(1)当H+K+L为偶数时,
(2)当H+K+L为奇数时,
在体心点阵中,只有当H+K+L为偶数时才能产生衍射。
3.一个单胞对X射线的散射
单位晶胞对X射线的散射与结构因素
2. 一个原子对X射线的散射
一个电子对X射线散射后空间某点强度可用Ie表 示,那么一个原子对X射线散射后该点的强度:
Ia f Ie
2
这里引入了f――原子散射因子
单位晶胞对X射线的散射与结构因素
推导过程:
一个原子包含Z个电子,那么可看成Z个电子散射的叠加。 (1)若不存在电子电子散射位相差:
产生衍射的充分条件: 满足布拉格方程且FHKL≠0。 由于FHKL=0而使衍射线消失的现象称为系统消光
单位晶胞对X射线的散射与结构因素
3.一个单胞对X射线的散射
