常微分习题5_2答案
常微分方程计算题及答案

计 算 题(每题10分)1、求解微分方程2'22x y xy xe -+=。
2、试用逐次逼近法求方程2y x dxdy+=通过点(0,0)的第三次近似解. 3、求解方程'2x y y y e -''+-=的通解4、求方程组dx dt ydydtx y ==+⎧⎨⎪⎩⎪2的通解5、求解微分方程'24y xy x +=6、试用逐次逼近法求方程2y x dxdy-=通过点(1,0)的第二次近似解。
7、求解方程''+-=-y y y e x '22的通解8、求方程组dxdt x ydydtx y =+=+⎧⎨⎪⎩⎪234的通解9、求解微分方程xy y x '-2=24 10、试用逐次逼近法求方程2y x dxdy-=通过(0,0)的第三次近似解. 11、求解方程''+-=-y y y e x '24的通解12、求方程组dxdtx y dydtx y =+=+⎧⎨⎪⎩⎪2332的通解13、求解微分方程x y y e x (')-=14、试用逐次逼近法求方程22x y dxdy+=通过点(0,0)的第三次逼近解. 15、求解方程''+-=--y y y e x '22的通解16、求解方程x e y y y -=-+''32 的通解17、求方程组⎪⎩⎪⎨⎧-+=-+=yx dt dydtdx x y dt dy dt dx243452的通解 18、解微分方程22(1)(1)0x y dx y x dy -+-= 19、试用逐次逼近法求方程2dyx y dx=-满足初始条件(0)0y =的近似解:0123(),(),(),()x x x x ϕϕϕϕ.20、利用逐次逼近法,求方程22dyy x dx=-适合初值条件(0)1y =的近似解:012(),(),()x x x ϕϕϕ。
常微分方程标准答案-一二章

习题1.24. 给定一阶微分方程2dyx dx=, (1). 求出它的通解; (2). 求通过点()1,4的特解; (3). 求出与直线23y x =+相切的解; (4). 求出满足条件102ydx =⎰的解;(5). 绘出(2),(3),(4)中的解得图形。
解:(1). 通解显然为2,y x c c =+∈;(2). 把1,4x y ==代入2y x c =+得3c =,故通过点()1,4的特解为23y x =+;(3). 因为所求直线与直线23y x =+相切,所以223y x cy x ⎧=+⎨=+⎩只有唯一解,即223x c x +=+只有唯一实根,从而4c =,故与直线23y x =+相切的解是24y x =+;(4). 把2y x c =+代入12ydx =⎰即得5c =,故满足条件12ydx =⎰的解是253y x =+;(5). 图形如下:-1.5-1-0.500.51 1.512345675. 求下列两个微分方程的公共解:242422,2y y x x y x x x y y ''=+-=++--解:由2424222y x x x x x y y +-=++--可得()()222210y x xy -++=所以2y x =或212y x =--,2y x =代入原微分方程满足,而212y x =--代入原微分方程不满足,故所求公共解是代入原微分方程不满足。
6. 求微分方程20y xy y ''+-=的直线积分曲线。
解:设所求直线积分曲线是y kx b =+,则将其代入原微分方程可得2200010k b k xk kx b k b k b k k -=⎧+--=⇒⇒====⎨-=⎩或所以所求直线积分曲线是0y =或1y x =+。
8. 试建立分别具有下列性质的曲线所满足的微分方程:(2). 曲线上任一点的切线介于两坐标轴之间的部分等于定长l ; (5). 曲线上任一点的切线的纵截距等于切点横坐标的平方。
常微分方程(第三版) 王高雄等编 高等教育出版社 课后习题答案

1常微分方程习题答案2.11.xy dx dy2=,并求满足初始条件:x=0,y=1的特解.解:对原式进行变量分离得。
故它的特解为代入得把即两边同时积分得:e e xx y c y x x c y c y xdx dy y22,11,0,ln ,212=====+==,0)1(.22=++dy x dx y 并求满足初始条件:x=0,y=1的特解.解:对原式进行变量分离得:。
故特解是时,代入式子得。
当时显然也是原方程的解当即时,两边同时积分得;当xy c y x y x c y c y x y dy dx x y++=====++=+=+≠=+-1ln 11,11,001ln 1,11ln 0,11123.yxy dx dy x y 321++=解:原式可化为:x x y xxyxyx yyxyc c c c x dx x dy y yx ydxdy2222222232232)1(1)1)(1(),0(ln 1ln 21ln 1ln 2111,0111=++=++≠++-=++=+≠+∙+=+)故原方程的解为(即两边积分得故分离变量得显然.0;0;ln ,ln ,ln ln 0110000)1()1(4===-==-+=-++=-=+≠===-++x y c y x xy c y x xy c y y x x dy y y dx x x xy x y xdy y ydx x 故原方程的解为即两边积分时,变量分离是方程的解,当或解:由:10ln 1ln ln 1ln 1,0ln 0)ln (ln :931:8.cos ln sin ln 07ln sgn arcsin ln sgn arcsin 1sgn 11,)1(,,,6ln )1ln(21111,11,,,0)()(:53322222222222c dxdy dx dy xycy ud uudx x x y u dx xydy x y ydx dy y x x c dy yy yydxdy c x y tgxdx ctgydy ctgxdy tgydx cx x xycx x u dxx x du xdxdudxdux u dx dy ux y u x y y dx dy xc x arctgu dx x du u u u dx du x u dxdu xu dx dy ux y u x y x y x y dx dy dx x y dy x y ee ee ee eexy uu xy x uu xyxyyx xx+===+=+-===-∙-=--+-=-=+-===-=+∙=+∙=∙=--=+===-+=+-=++=++-++=++===+-==-++-+--两边积分解:变量分离:。
常微分方程课后习题答案.doc

习题2.1 1.dxdy =2xy,并满足初始条件:x=0,y=1的特解。
解:ydy =2xdx 两边积分有:ln|y|=x 2+cy=e 2x +e c =cex 2另外y=0也是原方程的解,c=0时,y=0原方程的通解为y= cex 2,x=0 y=1时 c=1 特解为y= e 2x .2. y 2dx+(x+1)dy=0 并求满足初始条件:x=0,y=1的特解。
解:y 2dx=-(x+1)dy2ydy dy=-11+x dx两边积分: -y1=-ln|x+1|+ln|c| y=|)1(|ln 1+x c另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e 特解:y=|)1(|ln 1+x c3.dxdy =yx xy y321++解:原方程为:dx dy =yy 21+31xx +yy 21+dy=31xx +dx两边积分:x(1+x 2)(1+y 2)=cx 24. (1+x)ydx+(1-y)xdy=0 解:原方程为:yy -1dy=-xx 1+dx两边积分:ln|xy|+x-y=c另外 x=0,y=0也是原方程的解。
5.(y+x )dy+(x-y)dx=0 解:原方程为:dxdy =-yx y x +-令xy =u 则dx dy =u+x dxdu 代入有:-112++uu du=x1dxln(u 2+1)x=c-2arctgu 即 ln(y 2+x 2)=c-2arctg 2xy .6. xdxdy -y+22y x -=0解:原方程为:dx dy =xy +x x ||-2)(1xy -则令xy =u dxdy =u+ xdxdu211u- du=sgnx x1dxarcsinxy =sgnx ln|x|+c7. tgydx-ctgxdy=0 解:原方程为:tgydy =ctgxdx两边积分:ln|siny|=-ln|cosx|-ln|c| siny=xc cos 1=xc cos 另外y=0也是原方程的解,而c=0时,y=0.所以原方程的通解为sinycosx=c. 8dxdy +yexy 32+=0解:原方程为:dxdy =yey2e x 32 ex3-3e2y-=c.9.x(lnx-lny)dy-ydx=0 解:原方程为:dx dy =xy lnx y令xy =u ,则dxdy =u+ xdxduu+ xdxdu =ulnuln(lnu-1)=-ln|cx| 1+lnxy =cy.10.dxdy =e y x -解:原方程为:dxdy =e x e y -e y =ce x11dxdy =(x+y)2解:令x+y=u,则dxdy =dxdu -1dxdu -1=u 2211u+du=dxarctgu=x+c arctg(x+y)=x+c12.dxdy =2)(1y x +解:令x+y=u,则dxdy =dxdu -1dxdu -1=21uu-arctgu=x+c y-arctg(x+y)=c. 13.dxdy =1212+-+-y x y x解: 原方程为:(x-2y+1)dy=(2x-y+1)dx xdy+ydx-(2y-1)dy-(2x+1)dx=0 dxy-d(y 2-y)-dx 2+x=c xy-y 2+y-x 2-x=c14: dxdy =25--+-y x y x解:原方程为:(x-y-2)dy=(x-y+5)dx xdy+ydx-(y+2)dy-(x+5)dx=0 dxy-d(21y 2+2y)-d(21x 2+5x)=0y 2+4y+x 2+10x-2xy=c. 15:dxdy =(x+1) 2+(4y+1) 2+8xy 1+解:原方程为:dx dy=(x+4y )2+3 令x+4y=u 则dxdy=41dxdu -4141dx du -41=u 2+3dxdu =4 u 2+13u=23tg(6x+c)-1tg(6x+c)=32(x+4y+1).16:证明方程y x dxdy =f(xy),经变换xy=u 可化为变量分离方程,并由此求下列方程:1) y(1+x 2y 2)dx=xdy2) y x dxdy =2222x -2 y x 2y+证明: 令xy=u,则x dxdy +y=dxdu则dxdy =x 1dxdu -2xu ,有:u x dxdu =f(u)+1)1)((1+u f u du=x1dx所以原方程可化为变量分离方程。
常微分方程第5章答案

习题1.给定方程组x = x x= (*)a)试验证u(t)= ,v(t)= 分别是方程组(*)的满足初始条件u(0)= , v(0)= 的解.b)试验证w(t)=c u(t)+c v(t)是方程组(*)的满足初始条件w(0)= 的解,其中是任意常数.解:a) u(0)= =u (t)= = u(t)又 v(0)= =v (t)= = = v(t)因此 u(t),v(t)分别是给定初值问题的解.b) w(0)= u(0)+ u(0)= + =w (t)= u (t)+ v (t)= +=== w(t)因此 w(t)是给定方程初值问题的解.2. 将下面的初值问题化为与之等价的一阶方程组的初值问题:a) x +2x +7tx=e ,x(1)=7, x (1)=-2b) x +x=te ,x(0)=1, x (0)=-1,x (0)=2,x (0)=0c)x(0)=1, x (0)=0,y(0)=0,y (0)=1解:a)令 x =x, x = x , 得即又 x =x(1)=7 x (1)= x (1)=-2于是把原初值问题化成了与之等价的一阶方程的初值问题:x = x(1)=其中 x= .b) 令=x ===则得:且 (0)=x(0)=1, = (0)=-1, (0)= (0)=2,(0)= (0)=0于是把原初值问题化成了与之等价的一阶方程的初值问题:= x(0)= , 其中 x= .c) 令w =x, w =,w =y,w =y ,则原初值问题可化为:且即 ww(0)= 其中 w=3. 试用逐步逼近法求方程组= x x=满足初始条件x(0)=的第三次近似解.解:0241201 杨素玲习题02412—02 02412—031.试验证 =是方程组x = x,x= ,在任何不包含原点的区间a 上的基解矩阵。
解:令的第一列为 (t)= ,这时 (t)= = (t)故 (t)是一个解。
同样如果以 (t)表示第二列,我们有 (t)= = (t)这样 (t)也是一个解。
常微分课后答案第五章

常微分课后答案第五章第五章 线性微分方程组§5.1 存在唯一性定理习题5.11.给定方程组x x ⎥⎦⎤⎢⎣⎡-='0110,⎪⎪⎭⎫ ⎝⎛=21x x x . (*))a 试验证⎪⎪⎭⎫ ⎝⎛-=t t t u sin cos )(,⎪⎪⎭⎫ ⎝⎛=t t t v cos sin )(分别是方程组(*)的满足初始条件⎪⎪⎭⎫ ⎝⎛=01)0(u ,⎪⎪⎭⎫⎝⎛=10)0(v 的解;)b 试验证)()()(21t v c t u c t w +=是方程组(*)的满足初始条件⎪⎪⎭⎫⎝⎛=21)(c c t w 的解,其中21,c c 是任意常数.证明)a ⎪⎪⎭⎫ ⎝⎛=01)0(u ,⎪⎪⎭⎫ ⎝⎛=10)0(v 显然.)(0110sin cos 0110cos sin )(t u t t t t t u ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--=',)(0110cos sin 0110sin cos )(t v t t t t t v ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=',所以⎪⎪⎭⎫ ⎝⎛-=t t t u sin cos )(,⎪⎪⎭⎫⎝⎛=t t t v cos sin )(分别是方程组(*)的满足初始条件⎪⎪⎭⎫ ⎝⎛=01)0(u ,⎪⎪⎭⎫ ⎝⎛=10)0(v 的解.)b ⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=2121211001)0()0()0(c c c c v c u c w ,又)(0110)(0110)()()(2121t v c t u c t v c t u c t w ⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛-='+'=')(0110))()((011021t w t v c t u c ⎪⎪⎭⎫⎝⎛-=+⎪⎪⎭⎫ ⎝⎛-=,所以)()()(21t v c t u c t w +=是方程组(*)的满足初始条件⎪⎪⎭⎫⎝⎛=21)(c c t w 的解,其中21,c c 是任意常数.2.将下面的初值问题化为与之等价的一阶方程组的初值问题:)a t e tx x x -=+'+''72,7)1(=x ,2)1(-='x ;)b tte x x =+)4(,1)0(=x ,1)0(-='x ,2)0(=''x ,0)0(='''x ;)c ⎩⎨⎧=-'+-''=+-'+''tx y y y e y x y x t cos 15132,675,1)0(=x ,0)0(='x ,0)0(=y ,1)0(='y .(提示:令y w y w x w x w '=='==4321,,,)解 )a 设x x x x '==21,,则21x x x ='=',te tx xx x -+--=''='12272,即与该初值问题等价的一阶方程组的初值问题为⎪⎩⎪⎨⎧-==+--='='-.2)1(,7)1(,27,2121221x x e x tx x x x t)b 设x x x x x x x x'''=''='==4321,,,,则21x x x ='=',32x x x =''=',43x x x ='''=',tte xx +-='14,则得等价的一阶方程组的初值问题为⎪⎪⎩⎪⎪⎨⎧+-='='='='tte x x x x x x x x 14433221,,,,⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0211)0()0()0()0()0(4321x x x x x .)c 令y w y w x w x w'=='==4321,,,,有⎪⎪⎩⎪⎪⎨⎧+-+='='+--='='tw w w w w w e w w w w w w t cos 13215,,567,431443431221 ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1001)0()0()0()0()0(4321w w w w w ,为与原初值问题等价的一阶方程组的初值问题. 3.试用逐步逼近法求方程组xx ⎪⎪⎭⎫⎝⎛-='0110,⎪⎪⎭⎫⎝⎛=21x x x满足初始条件⎪⎪⎭⎫ ⎝⎛=10)0(x 的第三次近似解.解 ⎪⎪⎭⎫⎝⎛=10)(0t ϕ,⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎰110011010)(01t ds t tϕ, ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫⎝⎛=⎰2210211011010)(t t ds s t tϕ,第三次近似解为 ⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛=⎰2213610221*********)(t t t ds s s t t ϕ.§5.2 线性微分方程组的一般理论习题5.21.试验证⎥⎦⎤⎢⎣⎡=Φ12)(2t t t t是方程组x t tx ⎥⎥⎦⎤⎢⎢⎣⎡-='22102,⎥⎦⎤⎢⎣⎡=21x x x在任何不包含原点的区间b t a ≤≤上的基解矩阵. 证明 设⎪⎪⎭⎫⎝⎛=t t t 2)(21ϕ,⎪⎪⎭⎫ ⎝⎛=1)(2t t ϕ,则由于)(22102221022)(12221t t t t t t t t t ϕϕ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=',)(22101221001)(2222t t t t t t t ϕϕ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛=',所以)(,)(21t t ϕϕ都是方程组的解,因而[])()()(21t t t ϕϕ=Φ是所给方程组的解矩阵.又由于在任何不包含原点的区间],[b a 上,0)(det 2≠-=Φt t (],[b a t ∈),故)(t Φ是所给方程组的基解矩阵. 2.考虑方程组xt A x )(=', (5.15)其中)(t A 是区间b t a ≤≤上的连续n n ⨯矩阵,它的元素为)(t a ij,n j i ,,2,1, =.)a 如果)(,,)(,)(21t x t x t x n是(5.15)的任意n 个解,那么它们的Wronsky 行列式)](,,)(,)([21t x t x t x W n满足下面的一阶线性微分方程Wt a t a t a W nn )]()()([2211+++=' .(提示:利用行列式的微分公式,求出W '的表达式);)b 解上面的一阶线性微分方程,证明下面的公式:⎰=+++tt nn dss a s a s a e t W t W 02211)]()()([0)()( ,],[,0b a t t∈.证明 )a)()()()()()()()()()()()()()()()()()()(212222111211212222111211t x t x t x t x t x t x t x t x t x t x t x t x t x t x t x t x t x t x t W nn n nn n nn n n n n '''++'''='+=∑∑∑===)()()()()()()()()()()()(212222111121111t x t x t x t x t x t x t x t at x t at x t ann n n n nk kn knk k knk k k∑∑∑===+nk kn nknk k nknk k nkn n t x t at x t at x t at x t x t x t x t x t x 112112222111211)()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()()(21222211121121222211121111t x t x t x t x t x t x t x t x t x t a t x t x t x t x t x t x t x t x t x t a nn n n n n nn nn n n n n++=)()]()([11t W t a t a nn ++= ,所以)(t W 是一阶线性微分方程Wt a t a t a W nn )]()()([2211+++=' 的解.)b 由)a 知,Wt a t a t aW nn )]()()([2211+++=' ,分离变量后两边积分求解得⎰=+++tt nn dss a s a s a cet W 02211)]()()([)( ,t t =时就得到)(0t W c =,所以⎰=+++tt nn dss a s a s a et W t W 02211)]()()([0)()( ,],[,0b a t t ∈.3.设)(t A 为区间],[b a 上的连续n n ⨯实矩阵,)(t Φ为方程x t A x )(='的基解矩阵,而)(t x ϕ=为其一解.试证:)a 对于方程yt Ay T)(-='的任一解)(t ψ必有=)()(t t Tϕψ常数;)b )(t ψ为方程yt Ay T)(-='的基解矩阵的充要条件是存在非奇异的常数矩阵C ,使Ct t T=Φψ)()(.证明)a 由于)(t ϕ是方程x t A x )(='的解,故有)()()(t t A t ϕϕ=',)(t ψ为方程yt A y T )(-='的解,故)()()(t t A t T ψψ-='.所以[][])()()()]([)()()()()()(t t t t t t t t t t TTTTTϕψϕψϕψϕψϕψ'+'='+'=')()()()()]()([t t A t t t t A TT T ϕψϕψ+-=)()()()()()(=+-=t t A t t t A t T T ϕψϕψ,所以=)()(t t Tϕψ常数.)b “⇒” )(t Φ是方程x t A x )(='的基解矩阵,因此)()()(t t A t Φ=Φ',)(t ψ是方程yt Ay T)(-='的基解矩阵,故)()()(t t A t T ψ-=ψ',且0)(det ≠Φt 和0)(det ≠t ψ.所以[][])()()()]([)()()()()()(t t t t t t t t t t TTTTTΦ'ψ+Φψ'=Φ'ψ+Φ'ψ='Φψ)()()()()]()([t t A t t t t A TTTΦψ+Φψ-=)()()()()()(=Φψ+Φψ-=t t A t t t A t T T , 故)()(t t TΦψ是常数矩阵,设Ct t T=Φψ)()(,则)(det )(det )(det )(det )]()(det[det ≠Φ⋅ψ=Φ⋅ψ=Φψ=t t t t t t C T T ,因此存在非奇异常数矩阵C ,使Ct t T=Φψ)()(.“⇐”若存在非奇异常数矩阵C ,使Ct t T=Φψ)()(,则有)(det )(det )(det )(det )]()(det[det 0t t t t t t C T T Φ⋅ψ=Φ⋅ψ=Φψ=≠,所以0)(det ≠ψt ,即)(t ψ是非奇异矩阵或说)(t ψ的各列是线性无关的.又[])()()()()]([)()()(])([)()(0t t A t t t t t t t t t T T T t T Φψ+Φψ'=Φ'ψ+Φ'ψ='Φψ=,并注意到)(det ≠Φt ,有)()()]([t A t t T T ψ-=ψ',即)()()(t t A t T ψ-=ψ'.从而)(t ψ是方程yt Ay T)(-='的基解矩阵.4.设)(t Φ为方程Ax x ='(A 为n n ⨯常数矩阵)的标准基解矩阵(即E =Φ)0(),证明)()()(001t t t t -Φ=ΦΦ-,其中0t 为某一值.证明 由于A 为n n ⨯常数矩阵,故A 在),(∞+-∞有定义、连续,从而它的解也在),(∞+-∞连续可导.由)(t Φ为方程Ax x ='的基解矩阵,故),(∞+-∞∈∀t ,有0)(det ≠Φt ,并且有)()(t A t Φ=Φ',从而对某个0t ,有)(det 0≠-Φt t ,且)()()()(])([00000t t A t t t t t t t t -Φ=-Φ'='-⋅-Φ'='-Φ,即)(0t t -Φ亦为方程Ax x ='的基解矩阵.由推论2*,存在一个非奇异常数矩阵G ,使得在区间),(∞+-∞上,G t t t )()(0Φ=-Φ.又因为Gt t tE )()()0(000Φ=-Φ=Φ=,所以)(01t G -Φ=.因此)()()(001t t t t -Φ=ΦΦ-,其中0t 为某一值.5.设)(,)(t f t A 分别为在区间],[b a 上连续的n n ⨯矩阵和n 维列向量.证明方程组)()(t f x t A x +='存在且最多存在1+n 个线性无关解. 证明 设方程组xt A x )(='的基解矩阵为)](,,)(,)([)(21t t t t n ϕϕϕ =Φ,而)(~t ϕ是方程组)()(t f x t A x +='的一个特解,则其通解为)(~)(t c t x ϕ+Φ=,其中c 是任意的常数列向量.若)(t f 不恒为0,则)(~t ϕ必与)(,,)(,)(21t t t n ϕϕϕ 线性无关,从而)(~t ϕ,)(~)(1t t ϕϕ+,)(~)(2t t ϕϕ+,)(~)(,2t t ϕϕ+ 线性无关,即方程组)()(t f x t A x +='存在1+n 个线性无关解.又假若)(t x 是方程组)()(t f x t A x +='的任意一个解,则一定有确定的常数列向量c ,使得)(~)()(t c t t x ϕ+Φ=,将其加入)(~t ϕ,)(~)(1t t ϕϕ+,)(~)(2t t ϕϕ+,)(~)(,2t t ϕϕ+ 这一组向量就线性相关,故方程组)()(t f x t A x +='的任何2+n 个解必线性相关.从而方程组)()(t f x t A x +='存在且最多存在1+n 个线性无关解.6.试证非齐线性微分方程组的叠加原理:设)(,)(21t x t x 分别是方程组)()(1t f x t A x +=',)()(2t fx t A x +='的解,则)()(21t x t x +是方程组)()()(21t f t f x t A x ++='的解. 证明 因为)(,)(21t x t x 分别是方程组)()(1t f x t A x +=',)()(2t fx t A x +='的解,故)()()()(111t f t x t A t x +=',)()()()(222t f t x t A t x +=',所以有)]()()([)]()()([)()(])()([22112121t f t x t A t f t x t A t x t x t x t x +++='+'='+)()()]()()[(2121t f t f t x t x t A +++=,所以)()(21t x t x +是方程组)()()(21t f t f x t A x ++='的解. 7.考虑方程组)(t f Ax x +=',其中⎪⎪⎭⎫⎝⎛=2012A ,⎪⎪⎭⎫ ⎝⎛=21x x x ,⎪⎪⎭⎫⎝⎛=t t t f cos sin )(. )a 试验证⎪⎪⎭⎫ ⎝⎛=Φt t te te e t 2220)(是Ax x ='的基解矩阵;)b 试求)(t f Ax x +='的满足初始条件⎪⎪⎭⎫⎝⎛-=11)0(ϕ的解)(t ϕ.证明)a 00)(det 4222≠==Φtt t te ete e t ,),(∞+-∞∈∀t 成立.而)(0201220)12(2)(222222t A e te e e e t e t t t tt t tΦ=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+=Φ',所以)(t Φ是Ax x ='的基解矩阵.)b ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-=Φ--10101)(222241s e e se e es s s s s s,这样,由定理8,方程组满足初始条件⎪⎪⎭⎫ ⎝⎛=00)0(ψ的解就是⎰⎰⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=ΦΦ=--t s t t ttds s s s e e te e ds s f s t t 0222201cos sin 1010)()()()(ψ⎰⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛=-t s t t tds s s s s e e te e 02222cos cos sin 0⎪⎪⎪⎪⎭⎫ ⎝⎛+-++++--⎪⎪⎭⎫ ⎝⎛=--52)cos 2(sin 51252)cos 2sin 14sin 5cos 10(251022222t t e t t t t t t e e te e t tt tt⎪⎪⎪⎪⎭⎫ ⎝⎛-+--+=)cos 2sin 2(51)cos sin 75(252222t t e t t e te t tt ,对应的齐线性方程组满足初始条件⎪⎪⎭⎫⎝⎛-=11)0(h ϕ的解就是⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=ΦΦ=--t t t t th h e t e E e te e t t 2212221)1(110)0()0()()(ϕϕ,所以,所求方程组)(t f Ax x +='的满足初始条件⎪⎪⎭⎫⎝⎛-=11)0(ϕ的解为⎪⎪⎪⎪⎭⎫⎝⎛-+-+--=+=)cos 2(sin 5153)cos sin 7(252)1527(251)()()(22t t e t t t e t t t t t h ψϕϕ.8.试求)(t f Ax x +=',其中⎪⎪⎭⎫ ⎝⎛=2012A ,⎪⎪⎭⎫ ⎝⎛=21x x x ,⎪⎪⎭⎫⎝⎛=t t t f cos sin )( 满足初始条件⎪⎪⎭⎫⎝⎛-=11)0(ϕ的解)(t ϕ.解 由上题知⎪⎪⎭⎫⎝⎛--=t t h e t e t 22)1()(ϕ,且这里⎰⎰⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=ΦΦ=--t s s t t ttds e s e e te e ds s f s t t 0222220101010)()()()(ψ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛=⎰t t t t t t t t tte e t t t e te e ds s e te e 222222202222121010,所以,所求方程组)(t f Ax x +='的满足初始条件⎪⎪⎭⎫⎝⎛-=11)0(ϕ的解为⎪⎪⎪⎭⎫ ⎝⎛-+-=+=t t h e t e t t t t t 222)1()211()()()(ψϕϕ.9.试求下列方程的通解:)a t x x sec =+'',22ππ<<-t ; )b te x x 28=-'''; )c te x x x =+'-''96.解 )a 易知对应的齐线性方程0=+''x x 的基本解组为t t x cos )(1=,t t x sin )(2=,用公式(5.31)来求方程的一个解.这时1cos sin sin cos )](,)([21=-=tt t t t x t x W ,取0=t,有 ⎰⎰-=-=t t t sdss t s t ds s f s x s x W s x t x s x t x t 0212112sec )sin cos cos (sin )()](,)([)()()()()(0ϕtt t t sds t ds t tt cos ln cos sin tan cos sin 0+=-=⎰⎰所以方程的通解为tt t t t c t c x cos ln cos sin sin cos 21+++=. )b 由于特征方程083=-λ的根是21=λ,i313,2±-=λ,故对应的齐线性方程的基本解组为te t x 21)(=,te t x t 3cos )(2-=,tet x t3sin )(3-=.原方程的一个特解由公式(5.29)有(取0=t),∑⎰==313213210)()](,)(,)([)](,)(,)([)()(k tt k k dss f s x s x s x W s x s x s x W t x t ϕ,其中)](,)(,)([)(321t x t x t x W t W =)3sin 3cos 3(2)3sin 33(cos 24)3sin 3cos 3()3sin 33(cos 23sin 3cos 222t t e t t e e t t e t t e e te te e t t tt t tt t t +----+-=------312=,)](,)(,)([)(3211t x t x t x W t W =)3sin 3cos 3(2)3sin 33(cos 21)3sin 3cos 3()3sin 33(cos 03sin 3cos 0t t e t t e t t e t t e te te t t t t t t +----+-=------te 23-=,)](,)(,)([)(3212t x t x t x W t W =)3cos 33sin 3()3sin 3cos 3(214)3sin 3cos 3(023sin 0222t t e t t e e t t e e te e t t tt tt t -=+--=---,)](,)(,)([)(3213t x t x t x W t W =)3sin 33cos 3(1)3sin 33(cos 240)3sin 33(cos 203cos 222t t e t t e e t t e e te e t t tt tt t +-=--+-=---.所以⎰⎰-+⋅=--ts s tts stdse s s e t e ds e eet 020222312)3cos 33sin 3(3cos 3123)(ϕ⎰+-+-ts s tdse s s e t e 02312)3sin 33cos 3(3sin)3cos 33(sin 324124112122t t e e te t t t ++-=-,故通解tt tte t c t c e ec t x 23221121)3sin 3cos ()(+++=-.)c 特征方程0962=+-λλ,得到特征根32,1=λ,故对应的齐线性方程的基本解组为te t x 31)(=,tte t x 32)(=,tttt tee t ete e t W 63333)31(3)(=+=.取0=t,由(5.31),得特解⎰⎰⋅-=-=t sss t st tt dse e se e e te ds sf s W s x t x s x t x t 06333321120)()()()()()()(ϕtt t ts t e te e ds e s t e 33023412141)(++=-=⎰-,所以得到通解tt e et c ct x 41)()(321++=.10.给定方程)(78t f x x x =+'+'',其中)(t f 在+∞<≤t 0上连续,试利用常数变易公式,证明:)a 若)(t f 在+∞<≤t 0上有界,则上面方程的每一个解在+∞<≤t 0上有界;)b 若当∞→t 时,0)(→t f ,则上面方程的每一个解)(t ϕ,满足0)(→t ϕ(当∞→t 时). 证明 对应的特征方程0782=++λλ有特征根7,1--,故对应的齐线性方程的基本解组te t x -=)(1,tet x 72)(-=,ttt t tee e e e t W 87767)(------=--=.由公式(5.31)得原方程的一个特解(0=t)为⎰⎰-------=-=t s st st tt dss f e e e e e ds s f s W s x t x s x t x t 08772112)(6)()()()()()()(~0ϕ⎰⎰---=t s t t s t dss f e e ds s f e e 0770)(61)(61,所以方程的任一解可写为⎰⎰-----++=t st t s t ttdss f e e ds s f e e ec e c t 0770721)(61)(61)(ϕ.)a 由于)(t f 在+∞<≤t 0上有界,故0>∃M ,),0[∞+∈∀t ,有M t f ≤)(.又由于10≤<-te ,107≤<-te,从而当),0[∞+∈t 时,⎰⎰⋅+⋅++≤--ts t ts t ds e M e ds e M e c c t 0770216161)(ϕ=)1(42)1(67721-+-++--tt t t e e M e e M c c)1(42)1(6721t t e M e M c c ---+-++=M c c 21421++<,即方程的每一个解在+∞<≤t 0上有界.)b 当∞→t 时,0)(→t f ,故由⎰⎰-----++=ts t ts t t t ds s f e e ds s f e e e c e c t 0770721)(61)(61)(ϕ知,若⎰t sdss f e)(有界,则)(0)(610∞→→⎰-t ds s f e e t st ,若⎰t sdss f e)(无界,由于)(s f 在),0[∞+连续,故⎰t s dss f e 0)(为无穷大量,因此0)(lim 616)(lim 6)(lim )(61lim 00====∞→∞→∞→-∞→⎰⎰t f et f e e ds s f e ds s f e e t t t t t tst t s t t ,即总有)(0)(610∞→→⎰-t ds s f e e t st .同理)(0)(61077∞→→⎰-t ds s f e e t st .从而对方程的每一个解)(t ϕ,有)(0)(∞→→t t ϕ.11.给定方程组x t A x )(=',这里)(t A 是区间],[b a 上的连续n n ⨯矩阵.设)(t Φ是它的一个基解矩阵,n 维向量函数),(x t F 在∞<≤≤x b t a ,上连续,],[0b a t∈.试证明初值问题:⎩⎨⎧=+='ηϕ)(,),()(0t x t F x t A x(*)的唯一解)(t ϕ是积分方程组⎰--ΦΦ+ΦΦ=tt dss x s F s t t t t x 0))(,()()()()()(101η (**)的连续解.反之,(**)的连续解也是初值问题(*)的解. 证明)(t ϕ是初值问题(*)的解,故))(,()()()(t t F t t A t ϕϕϕ+=',这说明),(x t F 是t 的向量函数,于是由公式(5.27)得⎰--ΦΦ+ΦΦ=t t ds s s F s t t t t 0))(,()()()()()(101ϕηϕ,即)(t ϕ是积分方程组(**)的连续解.反之,设)(t ϕ是积分方程组(**)的连续解,则有⎰--ΦΦ+ΦΦ=t t ds s s F s t t t t 0))(,()()()()()(101ϕηϕ,两端对t 求导,就有))(,()()())(,()()()()()(11010t t F t t ds s s F s t t t t t t ϕϕηϕ---ΦΦ+ΦΦ'+ΦΦ'='⎰))(,(]))(,()()()[(0101t t F ds s s F s t t tt ϕϕη+Φ+ΦΦ'=⎰-- ))(,(]))(,()()()[()(0101t t F ds s s F s t t t A t t ϕϕη+Φ+ΦΦ=⎰-- ))(,(]))(,()()()()()[(0101t t F ds s s F s t t t t A t t ϕϕη+ΦΦ+ΦΦ=⎰--))(,()()(t t F t t A ϕϕ+=,即)(t ϕ也是初值问题(*)的解.§5.3 常系数线性微分方程组习题5.31.假设A 是n n ⨯矩阵,试证:)a 对任意的常数21,c c 都有A c A c A c A c 2121exp exp )exp(⋅=+;)b 对任意整数k ,都有kAA kexp )(exp =.(当k是负整数时,规定kk A A --=])[(exp )(exp 1.证明 )a 因为))(())((1222121A c A c A c c A c A c ==,所以矩阵Ac 1与A c 2可交换,故Ac A c A c A c 2121exp exp )exp(⋅=+.)b ①先证明N k ∈∀,有kAA kexp )(exp =,这只须对k 施以数学归纳法. 当1=k 时,)1exp(exp )(exp 1A A A ⋅==成立,设当k 时,kAA k exp )(exp =,则当1+k 时,有Ak A kA A A A k k )1exp(exp exp exp )(exp )(exp 1+===+,故对一切自然数k ,kAA kexp )(exp =.②)0exp(0exp )(exp 0A E A ===.③若k 是负整数,则N k ∈-,注意到)exp()(exp 1A A -=-,并由以上证明应用于矩阵A -,就有kAA k A A A k k k exp )](exp[)][exp(])[(exp )(exp 1=--=-==---,由①②③,对一切整数k ,均有kAA kexp )(exp =.2.试证:如果)(t ϕ是Ax x ='满足初始条件ηϕ=)(0t 的解,那么ηϕ)]([exp )(0t t A t -=.证明 由于 ηηϕ⋅⋅-='-='A t t A t t A t )]([exp ])([exp )(0,)(})]({[exp 0t A t t A A ϕη=-=,又ηηηϕ==⋅=E A t )]0[exp()(0,故ηϕ)]([exp )(0t t A t -=是方程组Axx ='满足初始条件ηϕ=)(0t 的解.由解的唯一性,命题得证.3.试计算下列矩阵的特征值及对应的特征向量.)a ⎪⎪⎭⎫ ⎝⎛3421; )b ⎪⎪⎪⎭⎫⎝⎛---244354332;)c ⎪⎪⎪⎭⎫⎝⎛-102111121;)d ⎪⎪⎪⎭⎫ ⎝⎛---6116100010.解 )a 特征方程0543421)det(2=--=----=-λλλλλA E ,特征值11-=λ,52=λ,对应于特征值11-=λ的特征向量⎪⎪⎭⎫ ⎝⎛=21u u u 必须满足方程组0)(1=+-u E A λ,得到0≠∀α,⎪⎪⎭⎫ ⎝⎛-=11αu 是对应于特征值11-=λ的特征向量.类似地可求得对应于特征值52=λ的特征向量为⎪⎪⎭⎫ ⎝⎛=21βv ,其中0≠β的任意常数.)b 特征方程0)2)(1)(2(244354332)det(=++-=---+---=-λλλλλλλA E ,特征值21-=λ,12-=λ,23=λ.对应于特征值21-=λ的特征向量u 必须满足方程组0)(1=+-u E A λ,得到≠∀α,⎪⎪⎪⎭⎫ ⎝⎛=110αu 是对应于特征值21-=λ的特征向量.类似地,可以求出对应于特征值12-=λ以及23=λ的特征向量分别为⎪⎪⎪⎭⎫ ⎝⎛=011βv (0≠β的任意常数)和⎪⎪⎪⎭⎫ ⎝⎛=111γw (0≠γ的任意常数).)c 特征方程0)1)(3(12111121)det(2=+-=---+----=-λλλλλλA E ,特征值12,1-=λ,33=λ.对应于特征值12,1-=λ的特征向量⎪⎪⎪⎭⎫ ⎝⎛=321u u u u 必须满足方程组0)(1=+-u E A λ,得0≠∀α,⎪⎪⎪⎭⎫ ⎝⎛--=212αu 是对应于特征值12,1-=λ的特征向量.类似地,可以求出对应于特征值33=λ的特征向量为⎪⎪⎪⎭⎫ ⎝⎛=212βv (0≠β的任意常数).)d 特征方程0)3)(2)(1(61161001)det(=+++=+--=-λλλλλλλA E ,特征值11-=λ,22-=λ,33-=λ.由0)(1=+-u E A λ,推出0≠∀α,⎪⎪⎪⎭⎫ ⎝⎛-=111αu 是对应于特征值11-=λ的特征向量.同样可求得对应于特征值22-=λ和33-=λ的特征向量分别为⎪⎪⎪⎭⎫⎝⎛-=421βv (0≠β的任意常数)和⎪⎪⎪⎭⎫ ⎝⎛-=931γw (0≠γ的任意常数).4.试求方程组Ax x ='的一个基解矩阵,并计算Atexp ,其中A 为:)a ⎪⎪⎭⎫⎝⎛--2112;)b ⎪⎪⎭⎫⎝⎛3421;)c ⎪⎪⎪⎭⎫⎝⎛---244354332;)d ⎪⎪⎪⎭⎫⎝⎛--115118301.解)a 特征方程032112)det(2=-=--+=-λλλλA E ,得32,1±=λ是特征值.对应的特征向量分别为⎪⎪⎭⎫⎝⎛-=3211αu ,⎪⎪⎭⎫ ⎝⎛+=3212βu ,0,0≠≠βα为任意常数.所以方程组Axx ='的一个基解矩阵为⎪⎪⎭⎫ ⎝⎛+-=Φ--t ttt e e ee t 3333)32()32()(.133331323211)32()32()0()(exp ----⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛+-=ΦΦ=t ttt e e ee t At⎪⎪⎭⎫⎝⎛--+----+=----t ttttt tt e eee e ee e 33333333)32()32()32()32(63.)b 由第3题)a 立即得到方程组Ax x ='的一个基解矩阵为⎪⎪⎭⎫⎝⎛-=Φ--t tt te e e e t 552)(. 155121112)0()(exp ----⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=ΦΦ=t tt t e e e e t At⎪⎪⎭⎫ ⎝⎛+--+=----t t t t t t tt e e e e e e e e 55552)(2231.)c 由第3题)b 立即得到方程组Ax x ='的一个基解矩阵为⎪⎪⎪⎭⎫ ⎝⎛=Φ----t t t t tt t e e e e ee e t 222220)(.12222211011111100)0()(exp ------⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=ΦΦ=t t tt tt t e e e e ee e t At⎪⎪⎪⎭⎫⎝⎛----+---=--------t tt t t tt tt t t tt t t t te e e e e e e e e e e e e e e e e 2222222222222. )d 特征方程)34)(3(11511831)det(2=--+=+------=-λλλλλλλA E ,特征值为31-=λ,723,2±=λ.对应的特征向量分别为⎪⎪⎪⎭⎫ ⎝⎛-=4731αu ,⎪⎪⎪⎭⎫ ⎝⎛++-=7174532βu ,⎪⎪⎪⎭⎫⎝⎛+-+-=7174533γu ,γβα,,均为不等于零的任意常数.故方程组Ax x ='的一个基解矩阵为⎪⎪⎪⎪⎭⎫⎝⎛-++---=Φ-+--+--+-t tt tt tttt e e e ee e e e e t )72()72(3)72()72(3)72()72(3)17()17(4)574()574(7333)(.由)0()(exp 1-ΦΦ=t At 立即可得[])()()(exp 321t t t At ψψψ=,其中列向量函数⎪⎪⎪⎪⎭⎫⎝⎛-+++--+++--+++=-+--+--+-t t t t t t t t t e e e ee e e e e t )72()72(3)72()72(3)72()72(31)7514(2)7514(256)71349()49713(98)737(3)737(342841)(ψ, ⎪⎪⎪⎪⎭⎫⎝⎛++-+-++-+-+-+-+=-+--+--+-t t t tt t t t t e e e e e e e e e t )72()72(3)72()72(3)72()72(31)714(2)714(256)753175()753175(98)757(3)757(3422521)(ψ,⎪⎪⎪⎪⎭⎫⎝⎛-++++--+++-+-=-+--+--+-t t t tt t t t t e e e e e e e e e t )72()72(3)72()72(3)72()72(31)7137()7137(112)98761()98761(196)714(3)714(3841261)(ψ.(该题计算量太大,作为该法的习题不是太好!)5.试求方程组Ax x ='的一个基解矩阵,并求满足初始条件ηϕ=)0(的解)(t ϕ:)a ⎪⎪⎭⎫⎝⎛=3421A ,⎪⎪⎭⎫⎝⎛=33η;)b ⎪⎪⎪⎭⎫⎝⎛--=115118301A ,⎪⎪⎪⎭⎫⎝⎛--=720η;)c ⎪⎪⎪⎭⎫ ⎝⎛-=102111121A ,⎪⎪⎪⎭⎫ ⎝⎛=001η.解 )a 由上题)b 知⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=--1112231exp 55t tt te e e e At ,所以所求解为⎪⎪⎭⎫⎝⎛+-+==--t t t t e e e e At t 5542)(exp )(ηϕ.)b 由上题)d 知)0()(exp 1-ΦΦ=t At ,其中⎪⎪⎪⎪⎭⎫⎝⎛-++---=Φ-+--+--+-t tt tt tttte e e ee e e e e t )72()72(3)72()72(3)72()72(3)17()17(4)574()574(7333)(.所以所求解为⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛++---+--⋅Φ==720)714(2775)773(3)714(2775)773(33214422521)()(exp )(t At t ηϕ ⎪⎪⎪⎪⎭⎫⎝⎛-++--+--+-++-+=-+--+--+-t t t tt t t t t e e e e e e ee e )72()72(3)72()72(3)72()72(3)7317(3)78977(728)7160289(3)7374511(1274)7435(9)9172(35461261.)c 由第3题)c 知,矩阵A 的特征值为12,1-=λ,33=λ.对应于特征值33=λ的特征向量⎪⎪⎪⎭⎫ ⎝⎛=212αv (0≠α的任意常数).又由648324648)(32121=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=-u u u u A E λ,得到⎪⎪⎪⎭⎫⎝⎛+-=)24(3331γβγβu (γβ,是任意常数),由⎪⎪⎪⎭⎫⎝⎛+-+⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=)24(3331212001γβγβαη解出41,21,41-===γβα.依公式(5.52),得满足初始条件ηϕ=)0(的解为⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫⎝⎛+++⎪⎪⎪⎭⎫ ⎝⎛=+++=--212120212124121241)]([)(33t tt t tt t e e u E A t E e Ev e t t t t t ϕ⎪⎪⎪⎭⎫⎝⎛--+=---)(2)(241333t t tt t t e e e e e e6.试求方程组)(t f Ax x +='的解)(t ϕ:)a ⎪⎪⎭⎫⎝⎛-=11)0(ϕ,⎪⎪⎭⎫ ⎝⎛=3421A ,⎪⎪⎭⎫⎝⎛=1)(t e t f ;)b ⎪⎪⎪⎭⎫ ⎝⎛=000)0(ϕ,⎪⎪⎪⎭⎫ ⎝⎛---=6116100010A ,⎪⎪⎪⎭⎫⎝⎛=-t e t f 00)(;)c ⎪⎪⎭⎫⎝⎛=21)0(ηηϕ,⎪⎪⎭⎫⎝⎛--=1234A ,⎪⎪⎭⎫⎝⎛-=t t t f cos 2sin )(.解 )a 由第4题)b 知,⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=--1112231exp 55t tt te e e e At ,由公式(5.61)得⎰-+=t ds s f A s t At t 0)(])exp[()(exp )(ηϕ⎰⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=--------t s s t s t s t s t t t t tds e e e e e e e e e 0)(5)()(5)(5511112231111112231⎪⎪⎪⎪⎭⎫ ⎝⎛+++-++-=--53109235420934355t t t t tt e e e e e e .)b 由第3题)d 知A 的特征值11-=λ,22-=λ,33-=λ,对应的特征向量分别为⎪⎪⎪⎭⎫⎝⎛-=111αu ,⎪⎪⎪⎭⎫ ⎝⎛-=421βv ,⎪⎪⎪⎭⎫ ⎝⎛-=931γw ,其中γβα,,均是不为零的任意常数.Ax x ='的一个基解矩阵为⎪⎪⎪⎭⎫⎝⎛---==Φ---------t tt tt tt t ttt te e e e e ee e e w e v e u et 3232329432][)(321λλλ.⎪⎪⎪⎭⎫⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛---=Φ--13228615621941321111)0(11,而)0()(exp 1-ΦΦ=t At .由公式(5.61)得⎰-+=t ds s f A s t At t 0)(])exp[()(exp )(ηϕ⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛---=---------000132286156943221323232t tt tt t t t te e ee e e e e e⎰⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛---+-------------------t s s t s t s t s t s t s t s t s t s t dse e e e e e e e e e 0)(3)(2)()(3)(2)()(3)(2)(00132286156943221⎪⎪⎪⎭⎫⎝⎛-+-+---+-=⎪⎪⎪⎭⎫ ⎝⎛+--+-+-=------------------⎰t t t tt t t t t t t s t s t t s t s t t s t s t e e e t e e e t e e e t ds e e e e e e e e e 3232320322322322916)72(38)25(4)32(419834221.)c A的特征方程0)2)(1(1234)det(=--=+--=-λλλλλA E ,求解得特征值11=λ,22=λ,对应的特征向量分别是⎪⎪⎭⎫ ⎝⎛=11αu ,⎪⎪⎭⎫ ⎝⎛=23βv ,其中βα,是不为零的任意常数.所以方程组Axx ='的一个基解矩阵为⎪⎪⎭⎫⎝⎛==Φt tt t tte e e e v eu e t 2223][)(21λλ,从而,⎪⎪⎭⎫⎝⎛--Φ=ΦΦ=-1132)()0()(exp 1t t At .由公式(5.61)得⎰-+=t ds s f A s t At t 0)(])exp[()(exp )(ηϕ⎰⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-----t s t s t s t s t t t t tds s s e ee e e e e e 0)(2)()(2)(2122cos 2sin 113223113223ηη⎪⎪⎭⎫⎝⎛+-+-+-+-+⎪⎪⎭⎫ ⎝⎛-+--+-=t t e e t t e e e e e e t t t t t t t t cos 2sin 224cos sin 234)(2)23()(3)23(222211222112ηηηηηηηη⎪⎪⎭⎫⎝⎛+--+--+--+--=t t e e t t e e t t t t cos 2sin 2)(2)423(cos sin 2)(3)423(2211222112ηηηηηηηη.7.假设m 不是矩阵A 的特征值,试证非齐线性方程组mtce Ax x +='有一解形如mte t ρϕ=)(,其中ρ,c 是常数向量.证明 设方程组有形如mte t ρϕ=)(的解,代入方程得m tm t m t ce e A e m +=ρρ,由此得cA m +=ρρ,即cA mE =-ρ)(.因为m 不是矩阵A 的特征值,故0)det(≠-A mE ,即矩阵A mE -可逆,得到c A mE 1)(--=ρ唯一确定.所以方程组有一解m tm t e ce A mE t ρϕ=-=-1)()(8.给定方程组⎩⎨⎧=+'+-'=-'++'-''.02,023221122111x x x x x x x x x)a 试证上面方程组等价于方程组Au u =',其中⎪⎪⎪⎭⎫⎝⎛'=⎪⎪⎪⎭⎫ ⎝⎛=211321x x x u u u u ,⎪⎪⎪⎭⎫ ⎝⎛---=112244010A ;)b 试求)a 中的方程组的基解矩阵;)c 试求原方程组满足初始条件0)0(1=x ,1)0(1='x ,)0(2=x 的解.解 )a 设11x u=,12x u'=,23x u=,则原方程组化为⎪⎩⎪⎨⎧--='=''-+-=''='='=',2,23,32123331212211u u u x u u u u u x u u x u或⎪⎩⎪⎨⎧--='++-='='32133212212,244,uu u u u u u u u u ,即u u ⎪⎪⎪⎭⎫ ⎝⎛---='112244010或Au u ='.反之,设11u x =,21u x =',32u x=,则方程组Au u ='化为⎩⎨⎧-'-='+'+-=''.211221112,244x x x x x x x x即⎩⎨⎧=+'+-'=-'++'-''.02,023221122111x x x x x x x x x)b 由0)2)(1(11224401)det(=--=+----=-λλλλλλλA E ,得矩阵A的特征值01=λ,12=λ,23=λ.对应的特征向量分别为⎪⎪⎪⎭⎫⎝⎛=201αu ,⎪⎪⎪⎭⎫ ⎝⎛=122βv ,⎪⎪⎪⎭⎫ ⎝⎛=021γw ,其中γβα,,均为不等于零的任意常数.由此得Au u ='的一个基解矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==Φ0222021][)(22321t t tt t t t t e e e e e w e v e u e t λλλ.)c 求与之等价的方程组Au u =',满足初始条件η=⎪⎪⎪⎭⎫⎝⎛=010)0(u 的解ηη)0()()(exp )(1-ΦΦ==t At t u⎪⎪⎪⎭⎫ ⎝⎛-+-+-=⎪⎪⎪⎭⎫⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-t tt t t t t t t t e e e e e e e e e e 226434121010012220121022202122122,所以,原方程组满足初始条件0)0(1=x ,1)0(1='x ,0)0(2=x 的解为⎪⎪⎭⎫⎝⎛-+-=t t t e e e t 2234121)(2ϕ.9.试用Laplace 变换法解第5题和第6题. 解 5.)a 方程组两边取Laplace 变换,有)()(s AX s sX =-η,即η=-)()(s X A sE ,由具体数值代入得方程组⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛----33)()(342121s X s X s s ,根据Gramer 法则得 5211)(1-++=s s s X ,5411)(2-++-=s s s X,所以tte et -+=512)(ϕ,tte et --=524)(ϕ,故初值问题5.)a 的解为⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛=--t t t t e e e e t t t 552142)()()(ϕϕϕ.5.)b 对方程组两边施行Laplace 变换,并化简有η=-)()(s X A sE ,用具体数值代入得方程组⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛+------720)()()(115118301321s X s X s X s s s ,根据Gramer 法则得)72(427291)72(4272913313)34)(3(1521)(21--+-+---+=--++-=s s s s s s s s X ,)72(1267376511)72(12673765113991)34)(3(14372)(222--+++--++-=--+-+-=s s s s s s s s s X ,)72(12678977)72(126789773952)34)(3(5127)(223----+-+-+-=--+-+-=s s s s s s s s s X ,所以ttt e e e t )72()72(31427291427291313)(-+-+---=ϕ,ttt ee e t )72()72(3212673765111267376511991)(-+-++-+-=ϕ,ttt ee e t )72()72(331267897712678977952)(-+---+--=ϕ,故初值问题5.)b 的解为⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--+--++-+-+---=⎪⎪⎪⎭⎫ ⎝⎛=-+--+--+-t t t t t t t t t e e e e e e ee e t t t t )72()72(3)72()72(3)72()72(3321126789771267897795212673765111267376511991427291427291313)()()()(ϕϕϕϕ.5.)c 对方程组两边施行Laplace 变换,并化简有η=-)()(s X A sE ,用具体数值代入得方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛---+----001)()()(102111121321s X s X s X s s s ,根据Gramer 法则得31211121)(1-++=s s s X ,31411141)(2--+=s s s X,31211121)(1-++-=s s s X , 所以)(21)(31t te e t -+=ϕ,)(41)(32t te e t ---=ϕ,)(21)(33t te e t --=ϕ,故初值问题5.)a 的解为。
常微分方程-习题作业-第一章第二节作业及详细解答

1习题 1.22.放射性物质镭的裂变速度与存余量成正比k.设已知在某时刻t0容器中镭的质量是R0g.要求确定镭在任意时刻t的质量R(t).解:不难看出R(t)满足初值问题dRdt=−kR,R(t0)=R0.由此得dRR =−kdt,两边积分得通解R(t)=Ce−kt,其中C为任意常数.代入初值条件R(t0)=R0求出C=R0e kt0,因此R(t)=R0e−k(t−t0).4.把例1.3和例1.4的微分方程化成规范的一阶方程组形式.解:对例1.3的微分方程,令y=dxdt,则可将其化成规范的一阶方程组:dx dt =y,dydt=−kmx−µmy.对例1.4的微分方程,令x1=θ,x2=dθdt,则可将其化成规范的一阶方程组:dx1 dt =x2,dx2dt=−gsin x1.5.作出下列方程的方向场,并描出经过指定点的积分曲线:(1)dxdt=|x|,(0,0),(0,−1).(2)dxdt =t2+x2,(0,0),(0,−1/2),(√2,0).图0-1:第5(1)题图0-2:第5(2)题解:利用如下的Maple命令可作出相应方程的方向场和积分曲线,见图0-1,0-2: with(DEtools):phaseportrait(D(x)(t)=abs(x(t)),x(t),t=-3..3,[[x(0)=0],[x(0)=-1]],x=-3..3,color=black,linecolor=black);phaseportrait(D(x)(t)=t^2+x^2,x(t),t=-2..2,[[x(0)=0],[x(0)=-1/2],[x(sqrt(2))=0]],x=-2..2,color=black,linecolor=black);。
大学一年级上学期-微积分课后练习及答案-5-2-一阶微分方程

u2 + 1 Y
y+2
法 2:若将Y 视为 X 的函数,则再令 u = Y ,则方程 (*) 变形为 u + X du = 2( u )2 ,
X
dX 1 + u
即X
du dX
=
−
u(1 + u2 (1 + u)2
)
,这是一个可分离变量方程,
分离变量
⎡ ⎢⎣
1 u
+
1
2 +u
2
⎥⎦⎤du
=
− dX X
令 u = x ,即 x = uy ,故 dx = udy + ydu ,代入方程(*)得 (1 − u2 )dy + 2uydu = 0 y
这 是 一 个 可 分 离 变 量 的 微 分 方 程 , 分 离 变 量 得 2udu = dy , 两 端 积 分 得 u2 − 1 y
ln(u2 − 1) = ln y + ln C ,即 ln(u2 − 1) = ln Cy ,得 u2 − 1 = Cy ,所以 u2 − 1 = Cy ,因
1
解:注意到方程中各项关于 x 、 y 都是 2 次幂的,故这是一个齐次方程. 方程变形为
(1 − 3 x 2 )dy + 2 x dx = 0
(*)
y2
y
(注:在不考虑初始条件时,我们一般均采用方程两端同除 x 2 对方程进行变形,这里初始
条件给出 x = 0 处的值,而此时 y ≠ 0 ,故采用方程两端同除 y 2 对方程进行变形)
(3) y′ = 2( y + 2 )2 x+ y−1
第 5 章 常微分方程 第 2 节 一阶微分方程 2/12
常微分方程第5章答案

又因为=-A (t) (t),所以=- (t) A(t)
[ (t) (t)] =- (t) (t)A(t)+ (t) A(t) (t)=0,
所以对于方程y =-A (t)y的任一解y= (t)必有(t) (t)=常数
b)“”假设为方程y =-A (t)y的基解矩阵,则
又v(0)= =
v (t)= = = v(t)
因此u(t),v(t)分别是给定初值问题的解.
b) w(0)= u(0)+ u(0)= + =
w (t)= u (t)+ v (t)
= +
=
=
= w(t)
因此w(t)是给定方程初值问题的解.
2.将下面的初值问题化为与之等价的一阶方程组的初值问题:
a) x +2x +7tx=e ,x(1)=7, x (1)=-2
习题5.1
1.给定方程组
x = x x=(*)
a)试验证u(t)= ,v(t)=分别是方程组(*)的满足初始条件u(0)= , v(0)=的解.
b)试验证w(t)=c u(t)+c v(t)是方程组(*)的满足初始条件w(0)=的解,其中是任意常数.
解:a) u(0)= =
u (t)= = u(t)
6、试证非齐线性微分方程组的叠加原理:
的解,则是方程组
的解。
证明:(1)(2)
分别将代入(1)和(2)
则
则
令
即证
7.考虑方程组,其中
a)试验证是的基解矩阵;
b)试求的满足初始条件的解。
证明:a)首先验证它是基解矩阵
常微分课后答案解析第二章

第一章 绪论§ 微分方程:某些物理过程的数学模型§ 基本概念习题1.指出下面微分方程的阶数,并回答方程是否线性的:(1)y x dxdy-=24; (2)012222=+⎪⎭⎫ ⎝⎛-xy dx dy dx y d ; (3)0322=-+⎪⎭⎫ ⎝⎛y dx dy x dx dy ; (4)x xy dx dy dx y d xsin 3522=+-; (5)02cos =++x y dxdy; (6)x e dx y d y=+⎪⎪⎭⎫ ⎝⎛22sin . 解 (1)一阶线性微分方程;(2)二阶非线性微分方程; (3)一阶非线性微分方程; (4)二阶线性微分方程; (5)一阶非线性微分方程; (6)二阶非线性微分方程.2.试验证下面函数均为方程0222=+y dxy d ω的解,这里0>ω是常数. (1)x y ωcos =;(2)11(cos C x C y ω=是任意常数); (3)x y ωsin =;(4)22(sin C x C y ω=是任意常数);(5)2121,(sin cos C C x C x C y ωω+=是任意常数); (6)B A B x A y ,()sin(+=ω是任意常数).解 (1)y x dx y d x dxdy2222cos ,sin ωωωωω-=-=-=,所以0222=+y dxy d ω,故x y ωcos =为方程的解.(2)y x C y x C y 2211cos ,sin ωωωωω-=-=''-=',所以0222=+y dxyd ω,故x C y ωcos 1=为方程的解.(3)y x dx y d x dxdy2222sin ,cos ωωωωω-=-==,所以0222=+y dxy d ω,故x y ωsin =为方程的解.(4)y x C y x C y 2222sin ,cos ωωωωω-=-=''=',所以0222=+y dxy d ω,故x C y ωsin 2=为方程的解.(5)y x C x C y x C x C y 2222121sin cos ,cos sin ωωωωωωωωω-=--=''+-=',所以0222=+y dxyd ω,故x C x C y ωωsin cos 21+=为方程的解. (6)y B x A y B x A y 22)sin(,)cos(ωωωωω-=+-=''+=',故0222=+y dxyd ω,因此)sin(B x A y +=ω为方程的解.3.验证下列各函数是相应微分方程的解: (1)xxy sin =,x y y x cos =+'; (2)212x C y -+=,x xy y x 2)1(2=+'-(C 是任意常数); (3)xCe y =,02=+'-''y y y (C 是任意常数); (4)xe y =,x x xe ye y ey 2212-=-+'-;(5)x y sin =,0cos sin sin 222=-+-+'x x x y y y ; (6)xy 1-=,1222++='xy y x y x ; (7)12+=x y ,x y x y y 2)1(22++-=';(8))()(x f x g y =,)()()()(2x f x g y x g x f y '-'='.证明 (1)因为2sin cos xx x x y -=',所以x x xx x x x y y x cos sin sin cos =+-=+'. (2)由于21xCx y --=',故x x C x x Cx x xy y x 2)12(1)1()1(2222=-++--⋅-=+'-.(3)由于xCe y =',xCe y ='',于是022=+-=+'-''xxxCe Ce Ce y y y .(4)由x e y =',因此x x x x x x x xe e e e e e ye y ey 22212)(2-=⋅-+⋅=-+'--.(5)因为x y cos =',所以cos sin sin sin 2sin cos cos sin sin 22222=-+⋅-+=-+-+'x x x x x x x x x y y y .(6)从21x y =',得1111122222++=+⎪⎭⎫⎝⎛-⋅+⎪⎭⎫ ⎝⎛-⋅=='xy y x x x x x y x .(7)由x y 2=',得到x y x y x x x x x y 2)1(2)1)(1()1(2222222++-=+++-+=='.(8))()()()()()()()()()()()()()()(222x f x g y x g x f x f x g x f x g x g x f x f x g x f x g x f y '-'='-⎪⎪⎭⎫ ⎝⎛⋅'='-'='. 4.给定一阶微分方程x dxdy2=, (1)求出它的通解; (2)求通过点)4,1(的特解;(3)求出与直线32+=x y 相切的解; (4)求出满足条件21=⎰ydx 的解;(5)绘出(2),(3),(4)中的解的图形. 解 (1)通解 C x xdx y +==⎰22.(2)由41==x y ,得到3=C ,所以过点)4,1(的特解为32+=x y .(3)这时122=⇒=x x ,切点坐标为)5,1(,由51==x y ,得到4=C ,所以与直线32+=x y 相切的解为42+=x y .(4)由231)31()(1310210=+=+=+=⎰⎰C Cx x dx C x ydx ,得到35=C ,故满足条件21=⎰ydx 的解为352+=x y . (5)如图1-1所示.图1-15.求下列两个微分方程的公共解: (1)422x x y y -+='; (2)2422y y x x x y --++='.解 公共解必须满足2424222y y x x x x x y --++=-+,即022242=-+-x y x y ,得到2x y =或212--=x y 是微分方程422x x y y -+='和2422y y x x x y --++='的公共解.6.求微分方程02=-'+'y y x y 的直线积分曲线.解 设直线积分曲线为0=++C By Ax ,两边对x 求导得,0='+y B A ,若0=B ,则0=A ,得到0=C ,不可能.故必有0≠B ,则BAy -=',代入原方程有02=++⎪⎭⎫ ⎝⎛-+-B Cx B A B A x B A ,或0)(22=-++B A B C x B A B A ,所以, ⎪⎪⎩⎪⎪⎨⎧=-=+0,022BA B C BAB A ,得到 ⎩⎨⎧==0,0C A 或B C A -==.所求直线积分曲线为0=y 和1+=x y .7.微分方程32224xy y y x =-',证明其积分曲线关于坐标原点)0,0(成中心对称的曲线,也是此微分方程的积分曲线.证明 设0),(=y x F 是微分方程32224xy y y x =-'的积分曲线,则与其关于坐标原点)0,0(成中心对称的曲线是0),(=--y x F .由于0),(=y x F 适合微分方程32224xy y y x =-',故3222),(),(4xy y y x F y x F x y x =-⎥⎥⎦⎤⎢⎢⎣⎡-⋅,分别以y x --,代y x ,,亦有3222))(()(),(),()(4y x y y x F y x F x y x --=--⎥⎥⎦⎤⎢⎢⎣⎡-----⋅-,而由0),(=--y x F ,得到),(),(y x F y x F y y x -----=',从而0),(=--y x F 也是此微分方程的积分曲线.8.物体在空气中的冷却速度与物体和空气的温差成比例,如果物体在20分钟内由100C 冷至60C ,那么,在多久的时间内,这个物体的温度达到30C 假设空气的温度为20C .解 设物体在时刻t 的温度为)(t u u =,20=a u ,微分方程为)(a u u k dtdu--=,解得kta Ce u u -+= ,根据初始条件10000===u u t ,得800=-=a u u C ,因此kt a a e u u u u --+=)(0,根据60,201===u u t ,得到ka a e u u u u 2001)(--+=,由此202ln ln 20110=--=a a u u u u k ,所以得到t e u 202ln 8020-+=,当30=u 时,解出60=t (分钟)1=(小时). 在1小时的时间内,这个物体的温度达到30C .9.试建立分别具有下列性质的曲线所满足的微分方程: (1)曲线上任一点的切线与该点的向径夹角为α;(2)曲线上任一点的切线介于两坐标轴之间的部分等于定长l ;(3)曲线上任一点的切线与两坐标轴所围成的三角形的面积都等于常数2a ; (4)曲线上任一点的切线介于两坐标轴之间的部分被切点等分; (5)曲线上任一点的切线的纵截距等于切点横坐标的平方;(6)曲线上任一点的切线的纵截距是切点的横坐标和纵坐标的等差中项; (7)曲线上任一点的切线的斜率与切点的横坐标成正比.(提示:过点),(y x d 的横截距和纵截距分别为'-y y x 和y x y '-).解 (1)曲线上任一点为),(y x ,则xy y x yy '+-'=1tan α,即ααtan tan y x x y y -+='. (2)曲线上任一点),(y x 处的切线方程为y y x Y X y -'=-',与两坐标轴交点为),0(y x y '-和)0,(y yy x '-',两点间距离为l y x y y y y x ='-+⎪⎪⎭⎫ ⎝⎛'-'22)(,即 222)()(l y x y y y x ='-+'-. (3)由(2),有221a y x y y yy x ='-'-',或y a y y x '=-'222)(.(4)由(2),有 2y x y y '-=,或0=+'y y x . (5)由(2),2x y x y ='-. (6)同样由(2),2yx y x y +='-,或x y x y ='-2. (7)易得kx y =' (k 为常数且0>k ).。
(完整版)常微分方程试题及答案2023年修改整理

第十二章 常微分方程(A)一、是非题1.任意微分方程都有通解。
( X )2.微分方程的通解中包含了它所有的解。
( X )3.函数x x y cos 4sin 3-=是微分方程0=+''y y 的解。
( O ) 4.函数x e x y ⋅=2是微分方程02=+'-''y y y 的解。
( X )5.微分方程0ln =-'x y x 的通解是()C x y +=2ln 21 (C 为任意常数)。
( O )6.y y sin ='是一阶线性微分方程。
( X ) 7.xy y x y +='33不是一阶线性微分方程。
( O ) 8.052=+'-''y y y 的特征方程为0522=+-r r 。
( O )9.221xy y x dxdy +++=是可分离变量的微分方程。
( O )二、填空题1.在横线上填上方程的名称①()0ln 3=-⋅-xdy xdx y 是可分离变量微分方程。
②()()022=-++dy y x y dx x xy 是可分离变量微分方程。
③xy y dx dy x ln ⋅=是齐次方程。
④x x y y x sin 2+='是一阶线性微分方程。
⑤02=-'+''y y y 是二阶常系数齐次线性微分方程。
2.x x y x y cos sin =-'+'''的通解中应含 3 个独立常数。
3.x e y 2-=''的通解是21241C x C e x ++-。
4.x x y cos 2sin -=''的通解是21cos 2sin 41C x C x x +++-。
5.124322+=+'+'''x y x y x y x 是 3 阶微分方程。
6.微分方程()06='-''⋅y y y 是 2 阶微分方程。
常微分方程教程丁同仁第二版答案完整版

dy y ,所以求 B 的运动轨迹即是求此微分方程满足 y (0) = b 的解. =− 2 dx b − y2
7. (
y + x 2 )dx + (ln x − 2 y )dy = 0 x y 2 解: P ( x, y ) = + x Q ( x, y ) = ln x − 2 y, x ∂P 1 ∂Q 1 = , = , ∂y x ∂x x
所以
则
∂P ∂Q ,即 原方程为恰当方程 = ∂y ∂x
则(
y dx + ln xdy ) + x 2 dx − 2 ydy = 0 x x3 + y ln x − y 2 = C. 3
常微分方程教程(第二版)-丁同仁等编-高等教育出版社-参考答案
5. (t 2 + 1) cos udu + 2 t sin udt = 0 解: P (t , u ) = (t 2 + 1) cos u , 则
Q(t , u ) = 2t sin u
所以
∂P ∂Q = 2t cos u , = 2t cos u , ∂t ∂x
∂Q ∂P ∂P ∂Q = 2 ,所以 = 0, ≠ ∂x ∂y ∂y ∂x
即,原方程不是恰当方程.
2. ( x + 2 y ) dx + (2 x + y ) dy = 0 解: P ( x, y ) = x + 2 y,
Q ( x, y ) = 2 x − y ,
《常微分方程》习题解答5.2

王高雄版《常微分方程》习题解答5.2习题5.202412—02 02412—031.试验证()t Φ=⎥⎦⎤⎢⎣⎡122t t t是方程组x '=⎥⎥⎦⎤⎢⎢⎣⎡-t t 22102x,x=⎥⎦⎤⎢⎣⎡21x x ,在任何不包含原点的区间a b t ≤≤上的基解矩阵。
解:令()t Φ的第一列为1ϕ(t)=⎪⎪⎭⎫ ⎝⎛t t 22 ,这时'1ϕ(t)=⎪⎪⎭⎫⎝⎛22t =⎪⎪⎭⎫⎝⎛-t t 22102 1ϕ(t)故1ϕ(t)是一个解。
同样如果以2ϕ(t)表示()t Φ第二列,我们有2ϕ(t)=⎪⎪⎭⎫⎝⎛01=⎪⎪⎭⎫⎝⎛-t t221022ϕ(t)这样2ϕ(t)也是一个解。
因此()t Φ是解矩阵。
又因为det ()t Φ=-t 2故()t Φ是基解矩阵。
2.考虑方程组x '=A(t)x (5.15)其中A(t)是区间a b t ≤≤上的连续n ⨯n 矩阵,它的元素为a ij (t),i ,j=1,2,…,na) 如果x 1(t),x 2(t),…,x n (t)是(5.15)的任意n 个解,那么它们的伏朗斯基行列式W[x 1(t),x 2(t),…,x n (t)]≡W(t)满足下面的一阶线性微分方程W '=[a 11(t)+a 22(t)+…+a nn (t)]Wb) 解上面的一阶线性微分方程,证明下面公式:W(t)=W(t 0)edss a s a s a nn t t )](...)()([22110++⎰ t 0,t ∈[a,b]解:w '(t)=nn n n nn x x x x x x x x x ....... (2)1222'21'1'12'11+'...... (2)12'22'2111211nn n n n n x x x x x x x x x +…+nnnnnn x x x x x x x x x '''....... (2122221)11211 =nnn n n nn n n n n n n n x x x x x x x a x a x a x a x a x a x a x a x a (2)122221121211121221212111121121111+++++++++…+nnnn nn n n nn n n nn n n n x a x a x a x a x a x a x x x x x x ++++++............... (122111)1112222111211=nn n n n x x x x x x n x a x a x a ..........1 (2)1222211112111111+…+nnnn n nn n nn n n x a x a x a x x x x x x ....... (2)12222111211整理后原式变为(a 11+…+a nn )nnn n nnx x x x x x x x x (2)12222111211=(a 11+…+a nn )w(t) =(a 11(t)+…+a nn (t))w(t)b)由于w '(t)=[ a 11(t)+…+a nn (t)] w(t),即)()(t w t dw =[ a 11(t)+…+a nn (t)]dt 两边从t到t 积分ln )(t w -ln )(0t w =⎰++tt nn ds s a s a)](...)([11即w(t)=w(t 0)e dss a s a tt nn ])(...)([011⎰++,t ∈[a,b]3.设A(t)为区间a b t ≤≤上的连续n ⨯n 实矩阵,()t Φ为方程x '=A(t)x 的基解矩阵,而x=ϕ(t)为其一解,试证:a) 对于方程y '=-A T (t)y 的任一解y=ψ(t)必有ψT (t) ϕ(t)=常数; b)ψ(t)为方程y '=-A T (t)y 的基解矩阵的充要条件是存在非奇异的常数矩阵C ,使ψT (t) ϕ(t)=C.解a)[ ψT (t) ϕ(t)]'= ψ'T ϕ(t)+ ψT ϕ'(t)= ψT 'ϕ(t)+ ψT (t)A(t)ϕ 又因为ψ'=-A T (t) ψ(t),所以ψT '=-ψT (t) A(t) [ ψT (t) ϕ(t)]'=- ψT (t) ϕ(t)A(t)+ ψT (t) A(t) ϕ(t)=0,所以对于方程y'=-A T(t)y的任一解y=ψ(t)必有ψT(t) ϕ(t)=常数b)“⇐”假设为方程y'=-A T(t)y的基解矩阵,则[ ψT(t) ϕ(t)]'= [ψT(t)]'()tΦ+ψT(t) 'Φ(t)=[- A T(t) ψ(t)]()tΦ+ ψT(t) A T(t) )()tΦ+ ψT(t)[ A(t) ϕ(t)]=- ψT(t) A T(t) ()tΦ+ψT(t) A T(t) ()tΦ=0,故ψT(t) ϕ(t)=C“⇒”若存在非奇异常数矩阵C,detc≠0,使ψT(t) ϕ(t)=C,则[ ψT(t) ϕ(t)]'= ψ'Tϕ(t)+ ψTϕ'(t)=0,故ψ'T(t)ϕ(t)=- ψT(t) ϕ(t)A(t) ψ'T(t)=- ψT(t) A(t) 所以ψT'(t)=- ψT(t) A(t), ψ'(t)=- ψT(t) A T(t)即ψ(t)为方程y'=-A T(t)y的基解矩阵4.设()tΦ为方程x'=Ax(A为n⨯n常数矩阵)的标准基解矩阵(即Φ(0)=E),证明:()tΦ1-Φ(t0)=Φ(t- t)其中t为某一值.证明:(1)()tΦ,Φ(t- t)是基解矩阵。
常微分方程习题与答案

第十二章常微分方程(A)、是非题1.任意微分方程都有通解。
()2 •微分方程的通解中包含了它所有的解。
()3. 函数y =3si nx-4cosx是微分方程y,y=0的解。
()4. 函数y = x2・e x是微分方程y';"-2y ' y = 0的解。
()5. 微分方程xy"T nx=0的通解是y =丄(1 nx)2+C (C为任意常数)。
()26. y"=siny是一阶线性微分方程。
()7. / = x3y3 xy不是一阶线性微分方程。
()8 . /-2/ 5^0的特征方程为『-2—5=0。
()9. dy = 1 x y2 xy2是可分离变量的微分方程。
()dx、填空题1 .在横线上填上方程的名称①y _ 3 ln xdx _ xdy 二0 是__________________________ 。
②xy2 x dx y _ x2 y dy = 0 是__________________________ 。
③x-d^ = y l n 丫是。
dx x④xy := y x2 sin x 是__________________ 。
⑤y y -2y =0是________________________ 。
2 . y si nxy"-x=cosx的通解中应含____________ 个独立常数。
3. _____________________________________ y “ = e Qx的通解是。
4. ______________________________________ y = sin 2x - cos x 的通解是。
5. _______________________________ x^ 2x2y 2,x3y=x4,1是阶微分方程。
6•微分方程y y - y Q =0是________________ 阶微分方程。
i7. y-丄所满足的微分方程是。
常微分方程证明题及答案

证 明 题(每题10分)1、设函数f (t)在[,)0+∞上连续且有界,试证明方程dxdtx f t +=()的所有解均在[,)0+∞上有界.证明:设x=x(t)为方程的任一解,它满足某初始条件x(t 0)=x 0,t 0∈[0+∞)由一阶线性方程的求解公式有y x y ef s e ds x x s x x x()()()()=+---⎰000现只证x(t)在[t 0,+∞)有界,设|f(t)|≤M ,t ∈[0+∞) 于是对t 0≤t<+∞有||||()y y e M x x ≤+--00|()|()f s e ds M s t xx -⎰≤|x 0|+Me -te ds st t⎰≤|x 0|+M[10--e t t ()]≤|x 0|+M 即证2、设函数f (x),p(x)在[,0+∞)上连续,且b x f a x p x <>=+∞→|)(|0)(lim 且(a,b ,为3、设函数f (x)在[,0+∞)上连续,且lim ()x f x b →+∞=又a >04、设函数y (x)在[,)0+∞上连续且可微,且lim['()()]x y x y x →+∞+=0试证lim ()x y x →+∞=05、若y 1(x ),y 2(x )为微分方程0)()()(21=+'+''x p x y x p y 的两个解,则它们的朗斯基行列式为w y y ke p x dx(,)()121==⎰-其中k 为由y 1(x ),y 2(x )确定的常数6、求微分方程()()'x y xyy x 22212-'-=的通解 7、解方程xdx x y dx x y dyx y++--+=()()220 8、解方程()()'x y xyy x 22212-'-= 9、解方程xdx x y dx x y dyx y ++--+=()()2210、解方程23()()0yy y y ''''-+=11、已知()f x 是连续函数。
常微分数值方法部分课后习题答案

第二章 偏微分方程的有限差分法
- 1 -
第二章 椭圆型微分方程的有限差分法
两式做差, 整理变形有
u ( xi ) − u ( xi − h) 1 1 1 = u '( xi − h) + 2 h 2 u '''( xi − h) + O ( h3 ) 2 2 h 2 3!
由此容易验证 2 3 ⎛ [u ]i − [u ]i −1 ⎞ h ⎡ d u ⎤ ⎡ du ⎤ = − p p p + O(h3 ) , 1 ⎢ ⎜ ⎟ 24 3 ⎥ ⎢ dx ⎥ 1 i− h ⎣ ⎦i − ⎠ ⎣ dx ⎦ i 2 ⎝
将上面的数值积分和数值微分公式代入(2.3)式, 得
[u ] − [u ]i −1 ⎛ [u ]i − [u ]i −1 ⎞ ⎛ [u ] − [u ]i ⎞ − p 1 ⎜ i +1 + ri i +1 + qi [u ]i h = f i h + O ( h3 ) ⎜ ⎟ ⎟ i + 2 h h ⎝ ⎠ ⎠ 2 ⎝ 省略掉误差项, 用 ui 代替 [u ]i , 则可定义差分格式为: p
2 2
h1 ⎡ ∂u ⎤ ⎡ ∂u ⎤ ⎢ p ∂y ⎥ 1 − ⎢ p ∂y ⎥ 1 ⎣ ⎦i, j + ⎣ ⎦i, j −
2
+ O(h12 ) =Байду номын сангаас
[u ]i +1, j − [u ]i , j [u ]i , j − [u ]i −1, j ⎤ 1⎡ 2 −p 1 ⎢ pi + 1 , j ⎥ + O(h1 ) i − j , h1 ⎣ 2 h1 h 1 ⎦ 2
高等教育出版常微分答案
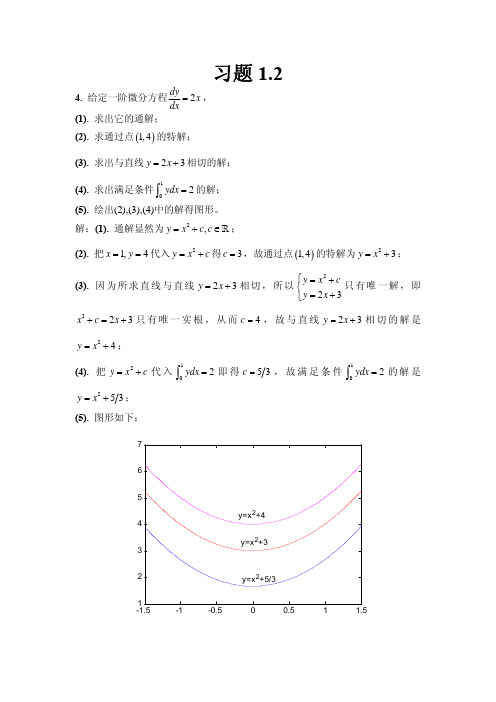
习题1.24. 给定一阶微分方程2dyx dx=, (1). 求出它的通解; (2). 求通过点()1,4的特解; (3). 求出与直线23y x =+相切的解; (4). 求出满足条件102ydx =∫的解;(5). 绘出(2),(3),(4)中的解得图形。
解:(1). 通解显然为2,y x c c =+∈ ;(2). 把1,4x y ==代入2y x c =+得3c =,故通过点()1,4的特解为23y x =+;(3). 因为所求直线与直线23y x =+相切,所以223y x cy x ⎧=+⎨=+⎩只有唯一解,即223x c x +=+只有唯一实根,从而4c =,故与直线23y x =+相切的解是24y x =+;(4). 把2y x c =+代入12ydx =∫即得5c =,故满足条件12ydx =∫的解是25y x =+; (5). 图形如下:-1.5-1-0.500.51 1.512345675. 求下列两个微分方程的公共解:242422,2y y x x y x x x y y ′′=+−=++−−解:由2424222y x x x x x y y +−=++−−可得()()222210y x xy −++=所以2y x =或212y x =−−,2y x =代入原微分方程满足,而212y x =−−代入原微分方程不满足,故所求公共解是代入原微分方程不满足。
6. 求微分方程20y xy y ′′+−=的直线积分曲线。
解:设所求直线积分曲线是y kx b =+,则将其代入原微分方程可得2200010k b k xk kx b k b k b k k −=⎧+−−=⇒⇒====⎨−=⎩或所以所求直线积分曲线是0y =或1y x =+。
8. 试建立分别具有下列性质的曲线所满足的微分方程:(2). 曲线上任一点的切线介于两坐标轴之间的部分等于定长l ; (5). 曲线上任一点的切线的纵截距等于切点横坐标的平方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答案5.2
1.解: 解曲线是:t x y t
x x sin cos 00==
相平面的轨线是: 2022x y x =+2.解: 由方程组1),,cy x y
x dy dx == 过点(1,2)x y 2=∴,由非自治系统 101−−==−−t e c x t x dt
dx t t e c y y dt
dy 2== 过点(1,2) t t t t e y t e
t x +−+−=−−+=002,1)2(0 即 1ln 2ln )2
1(00−−+−+=y t y t x 3.证明:0000yx xy cy x cy
x y x dy dx ===∴=, 当时,从出发的解与初始时刻无关。
其原因是由于右端有相同的因子,可以通过时间变换将其变化为自治系统。
0t t =),(00y x 0t
4.证明: 1) 性质4:
设有两条轨线 及有 )(),(t y y t x x ==0,)
(),(0>∃∃+=+=T t T t y y T t x x )()(),()(0000T t y t y y T t x t x x +==+==
∴ 两条轨线交于同一点 ,由性质2可知. 由解的存在唯一性定理. ))(),((00t y t x 过相平面上一点系统有且仅有一条轨线通过.
∀),(00y x )()()
()(T t y t y T t x t x +=+=∴
2) 性质5:(反证法)
若系统出发于∀非奇点的轨线在有限时间内达到某奇点, 即有一轨线过点, 而系统又),(∗∗y x ),(∗∗y x ∃一条常轨线
,,∗∗==y y x x 由解的唯一性定理, 两条轨线不可能交于同一点.
∃∗∗==y y x x , ∴ 性质5得证.
5解: 由方程可得, 该方程组有4个平衡点
⎟⎟⎠
⎞⎜⎜⎝⎛−−−−12121121122122121122
,
)0,(),0()0,0(0βααββαβαβααβαβr r r r C r B r A 解轨线的走向请参阅例5.2.3和下面的图形
restart:with(DEtools):
ODE1 :=[diff(x(t),t)=x(t)*(3-2*x(t)-y(t)),
diff(y(t),t)=y(t)*(3-x(t)-2*y(t))];
DEplot( ODE1, [x(t),y(t)],t=-100..100,
[[x(0)=0,y(0)=1],[x(0)=0,y(0)=5],
[x(0)=0.1,y(0)=0.6],[x(0)=0.6,y(0)=0.1],
[x(0)=5,y(0)=0],[x(0)=2,y(0)=1],[x(0)=0.1,y(0)=0.1],
[x(0)=5,y(0)=5], [x(0)=1.5,y(0)=5],[x(0)=0.1,y(0)=0.2],
[x(0)=0.2,y(0)=0.1],[x(0)=1,y(0)=0],[x(0)=5,y(0)=3],
[x(0)=5,y(0)=0.5],[x(0)=0.5,y(0)=5],[x(0)=3,y(0)=5]], x=0..5,y=0..5,stepsize=0.05, dirgrid=[21,21],
color=red, linecolor=blue,axes=BOXED,
title="Phase portrait of the Linear System",
arrows=SLIM);
:= ODE1⎡⎣⎢⎢⎤⎦
⎥⎥, = ∂∂t ()x t ()x t () − − 32()x t ()y t = ∂∂t ()y t ()y t () − − 3()x t 2()y t
6.对不同的参数值所得到的解轨线如下
restart:with(DEtools): mu:=0.1; a:=4;
ODE1 :=[diff(x(t),t)=y(t),
diff(y(t),t)=-x(t)-mu*y(t)*(x(t)^2-1)];
DEplot( ODE1, [x(t),y(t)],t=-100..100,
[[x(0)=0.1,y(0)=0.1],[x(0)=0,y(0)=0.8*a],
[x(0)=0,y(0)=-0.8*a],
[x(0)=-0.8*a,y(0)=0],[x(0)=0.8*a,y(0)=0]],
x=-a..a,y=-a..a,stepsize=0.05, dirgrid=[21,21], color=red, linecolor=blue,axes=BOXED,
title="Phase portrait of the Nonlinear System", arrows=SLIM);
:= μ.1
:= a 4
:= ODE1⎡⎣⎢⎢⎤⎦
⎥⎥, = ∂∂t ()x t ()y t = ∂∂t ()y t − − ()x t .1()y t () − ()x t 21
restart:with(DEtools): mu:=0.5; a:=4;
ODE1 :=[diff(x(t),t)=y(t),
diff(y(t),t)=-x(t)-mu*y(t)*(x(t)^2-1)];
DEplot( ODE1, [x(t),y(t)],t=-100..100,
[[x(0)=0.1,y(0)=0.1],[x(0)=0,y(0)=0.8*a],
[x(0)=0,y(0)=-0.8*a],
[x(0)=-0.8*a,y(0)=0],[x(0)=0.8*a,y(0)=0]],
x=-a..a,y=-a..a,stepsize=0.05, dirgrid=[21,21], color=red, linecolor=blue,axes=BOXED,
title="Phase portrait of the Nonlinear System", arrows=SLIM);
:= μ.5
:= a 4
:= ODE1⎡⎣⎢⎢⎤⎦
⎥⎥, = ∂()x t ()y t = ∂()y t − − ()x t .5()y t () − ()x t 21
> restart:with(DEtools): mu:=1; a:=4;
ODE1 :=[diff(x(t),t)=y(t),
diff(y(t),t)=-x(t)-mu*y(t)*(x(t)^2-1)];
DEplot( ODE1, [x(t),y(t)],t=-100..100,
[[x(0)=0.1,y(0)=0.1],[x(0)=0,y(0)=0.8*a],
[x(0)=0,y(0)=-0.8*a],
[x(0)=-0.8*a,y(0)=0],[x(0)=0.8*a,y(0)=0]],
x=-a..a,y=-a..a,stepsize=0.05, dirgrid=[21,21], color=red, linecolor=blue,axes=BOXED,
title="Phase portrait of the Nonlinear System", arrows=SLIM);
:= μ1
:= a 4
:= ODE1⎡⎣⎢⎢⎤⎦
⎥⎥, = ∂∂t ()x t ()y t = ∂∂t ()y t − − ()x t ()y t () − ()x t 21
> restart:with(DEtools): mu:=2; a:=4;
ODE1 :=[diff(x(t),t)=y(t),
diff(y(t),t)=-x(t)-mu*y(t)*(x(t)^2-1)];
DEplot( ODE1, [x(t),y(t)],t=-100..100,
[[x(0)=0.1,y(0)=0.1],[x(0)=0,y(0)=0.8*a],
[x(0)=0,y(0)=-0.8*a],
[x(0)=-0.8*a,y(0)=0],[x(0)=0.8*a,y(0)=0]],
x=-a..a,y=-a..a,stepsize=0.05, dirgrid=[21,21], color=red, linecolor=blue,axes=BOXED,
title="Phase portrait of the Nonlinear System", arrows=SLIM);
:= μ2
:= a 4
:= ODE1⎡⎣⎢⎢⎤⎦
⎥⎥, = ∂∂t ()x t ()y t = ∂∂t ()y t − − ()x t 2()y t () − ()x t 21。
