2016-2017北京市顺义初三二模数学试题及答案

合集下载

2016-2017学年北京市顺义区中考二模数学试卷(带解析)

2016-2017学年北京市顺义区中考二模数学试卷（带解析）满分:班级：_________ 姓名：_________ 考号：_________一、单选题（共10小题）1．实数4的算术平方根是（）A．B．C．D ．【答案】B【解析】4的算术平方根是22．2015年“十一”黄金周的第二天，北京故宫景点，接待游客超过了最大接待容量，当天接待92 800人次．将92 800用科学记数法表示应为（）A．B．C．D．【答案】C【解析】92 800=3．如图，数轴上有A，B，C，D四个点，其中表示互为相反数的点是（）A．点A与点BB．点B与点CC．点B与点DD．点A与点D【答案】D【解析】A表示的点为-2，D表示的点为2，-2和2是相反数，所以选D4．函数中，自变量的取值范围是（）A．B ．C．D．【答案】C【解析】x-3≥0，x≥35．在下列调查中，适宜采用全面调查的是（）A．了解七（1）班学生校服的尺码情况B．了解我市中学生视力情况C．检测一批电灯泡的使用寿命D．调查顺义电视台《师说》栏目的收视率【答案】A【解析】适合全面调查的必须有2点，数量不是很多不能是损耗品,所以选A6．下图是顺义区地图的一部分，小明家在怡馨家园小区，小宇家在小明家的北偏东约15°方向上，则小宇家可能住在（）A．裕龙花园三区B．双兴南区C．石园北区D．万科四季花城【答案】B【解析】以小明家为坐标原点，建立平面直角坐标系，然后就可以得到答案，选B7．四张质地、大小相同的卡片上，分别画上如下图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是轴对称图形的概率为（）A．B．C．D．1【答案】A【解析】概率及计算8．如图，四边形内接于⊙，，则的度数是（）A ．B ．C．D ．【答案】D【解析】∠A+∠C=180°，∠A=110°∴∠C=70°∵∠BOD=2∠C∴∠BOD=140° .9．如图是一个正方体的展开图，把展开图折叠成正方体后，“你”字一面相对的面上的字是（）A．梦B．我C．中D．国【答案】A【解析】做一个正方体，然后展开，写上字，就可以得到答案，选A10．已知点M为某封闭图形边界上一定点，动点P从点M出发，沿其边界逆时针运动一周，设点P走过的路程为x，线段MP的长为y，表示y与x的函数关系的图象大致如图所示，则该封闭图形可能是（）A．B．C．D．【答案】D【解析】MP是先增大，到达最大值后减小，只有圆的运动轨迹符合要求，故选D第II卷（非选择题）本试卷第二部分共有19道试题。

11.2017.6顺义区初三二模数学试题及答案

DC BA 0123-2-1-3A BCD顺义区2017届初三第二次统一练习数学试卷一、选择题（本题共30分，每小题3分）第1-10题均有四个选项，符合题意的选项只有．．一个． 1．“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京召开，“一带”指的是“丝绸之路经济带”，“一路”指的是“21世纪海上丝绸之路”. “一带一路”沿线大多是新兴经济体和发展中国家，经济总量约210 000亿美元，将“210 000亿”用科学记数法表示应为A ．42110⨯亿 B ．42.110⨯亿 C ．52.110⨯亿 D ．60.2110⨯亿 2．内角和为540︒的多边形是 A ．四边形 B ．五边形 C ．六边形D ．七边形3．如图，数轴上的A ，B ，C ，D 四点中，与表示2的点最接近的是A ．点AB ．点BC ．点CD ．点D4．能与60︒的角互余的角是A B C D5．如图，△ABC 中，∠A =60︒，BD ，CD 分别是∠ABC ，∠ACB 的平分线，则∠BDC 的度数是A ．100︒B ．110︒C ．120︒D ．130︒6．甲、乙、丙、丁四名跳高运动员最近10次训练成绩的平均数与方差如下表所示：甲乙丙丁平均数/cm 180 180 185 185 方差8.23.97.53.9根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择的是A ．甲B ．乙C ．丙D ．丁7．每年5月份的第二个周日为母亲节，今年的母亲节是5月14日，小娜在这一天送给妈妈一束鲜花，她选了3只百合，6只郁金香，9只康乃馨．若百合每只a 元，郁金香每只b 元，康乃馨每只c 元，则小娜购买这束鲜花的费用是A ．(369)a b c ++元B ．(963)a b c ++元C ．6()a b c ++元D ．(369)()a b c ++++元8．图1是一个几何体的三视图，则该几何体的展开图是 DCB A 图19．小宝的妈妈让他从袋子里挑选一颗糖果．小宝无法看到袋子里的糖果．下图是袋子里各种颜色糖果的数量，则小宝选到红色糖果的概率是A ．12 B ．14 C ．15 D ．11010．如图，木杆AB 斜靠在墙壁上，∠OAB =30︒，AB =4米．当木杆的上端A 沿墙壁NO 下滑时，木杆的底端B 也随之沿着地面上的射线OM 方向滑动．设木杆的顶端A 匀速下滑到点O 停止，则木杆的中点P 到射线OM 的距离y （米）与下滑的时间x （秒）之间的函数图象大致是二、填空题（共6道小题，每小题3分，共18分） 11．分解因式：24m n n -= ．12．若关于x 的方程240x x a -+-=没有实数根，写出一个满足条件的整数a 的值：a =______．13．小明的爸爸承包了一个鱼塘，小明想知道鱼塘的长（即A ，B 间的距离）．他通过下面的方法测量 A ，B 间的距离：先在AB 外选一点C ，然后测出AC ，BC 的中点M ，N ，并测得MN 的长为20m ，由此他就知道了A ，B 间的距离．请你回答A ，B 间的距离是．14．工人师傅测量一种圆柱体工件的直径，随机抽取10件测量，得到以下数值（单位：cm ）．8.03，8.04，7.95，7.98，7.95，7.98，8.00，7.98，7.94，8.05如果要取其中一个数据作为工件直径的估计值，则该估计值是______cm ，理由是．15．如图，在正方形ABCD 和正方形AEFG 中，顶点E 在边AD 上，连接DG 交EF 于点H ，若FH ＝1，EH ＝2，则DG 的长为．16．阅读下面材料：在数学课上，老师提出如下问题：H G FEDCB ANMCBA小丽的作法如下：老师说：“小丽的作法正确．”请回答：小丽的作图依据是________________________________________．三、解答题（本题共72分，第17-26题，每小题5分，第27、28题每小题7分，第29题8分）解答应写出文字说明，演算步骤或证明过程．17．计算：221326tan 3033-⎛⎫--︒+- ⎪⎝⎭．18．已知2220a a +-=，求代数式(32)(32)2(41)a a a a +---的值．19．如图，△ABC 中，点D 在AB 的延长线上，BE 平分∠CBD ，BE ∥AC ．求证：AB=BC ． 20．解方程：2511224x x x +-=++．21．如图，在平面直角坐标系xOy 中，反比例函数(0)ky k x=≠与一次函数4(0)y ax a =+≠的图象只有ABCDE已知：如图，△ABC ．求作：BC 边上的高线．CBA（1）以点C 为圆心，CA 为半径画弧①；（2）以点B 为圆心，BA 为半径画弧②，两弧相交于点D ；（3）连结AD ，交BC 的延长线于点E ．所以线段AE 就是所求作的BC 边上的高线．②①DECBA一个公共点A （2，2），直线(0)y mx m =≠也过点A ．（1）求k 、 a 及m 的值；（2）结合图象，写出4kmx ax x<+<时x 的取值范围．22．顺义区某中学举行春季运动会，初二年级决定从本年级300名女生中挑选64人组成花束方队，要求身高基本一致，这个工作交给年级学生会体育部小红、小冬和小芳来完成．为了达到年级的选拔要求，小红、小冬和小芳各自对本学校初二年级的女生身高进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3．表1 小红抽样调查初二年级4名女同学身高统计表（单位：cm ）序号 1 2 3 4 身高155160165172表2 小冬抽样调查初二年级15名女同学身高统计表（单位：cm ）表3 小芳抽样调查初二年级15名女同学身高统计表（单位：cm ）根据自己的调查数据，小红说应选取身高为163cm （数据的平均数）的同学参加方队，小冬说应选取身高为165cm （数据的中位数）的同学参加方队，小芳说应选取身高为160cm （数据的众数）的同学参加方队．根据以上材料回答问题：小红、小冬和小芳三人中，哪一位同学的抽样调查及得出的结论更符合年级的要求，并简要说明符合要求的理由，同时其他两位同学的抽样调查或得出结论的不足之处．23．已知：如图，四边形ABCD 中，∠ABC =∠ADC =90︒，AB =AD . （1）求证：BC= CD ；序号 123456789101112131415身高 148 149 150 152 152 160 160 165 166 167 168 169 170 171 175序号 123 4 5 6 7 8910 111213 14 15 身高 145 160 150152160154160166 167 168160 169173174175DCBA（2）若∠A =60︒，将线段BC 绕着点B 逆时针旋转60︒，得到线段BE ，连接DE ，在图中补全图形，并证明四边形BCDE 是菱形．24．评价组对某区九年级教师的试卷讲评课的学生参与度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名同学的参与情况，绘制成如图所示的扇形统计图和条形统计图（均不完整），请根据图中所给信息解答下列问题：（1）在这次评价中，一共抽查了名同学；（2）请将条形统计图补充完整；（3）如果全区有6 000名九年级学生，那么在试卷评讲课中，“独立思考”的约有多少人？（4）根据统计反映的情况，请你对该区的九年级同学提出一条对待试卷讲评课的建议．25．如图，在Rt △ABC 中，∠CA B =90︒，以AB 为直径的⊙O 交BC 于点D ，点E 是AC 的中点，连接DE ．（1）求证：DE 是⊙O 的切线；（2）点P 是BD 上一点，连接AP ，DP ，若BD :CD=4:1，求sin ∠APD 的值．BDE O26．阅读下列材料：实验数据显示，一般成人喝250毫升低度白酒后，其血液中酒精含量（毫克／百毫升）随时间的增加逐步增高达到峰值，之后血液中酒精含量随时间的增加逐渐降低．小明根据相关数据和学习函数的经验，对血液中酒精含量随时间变化的规律进行了探究，发现血液中酒精含量y 是时间x 的函数，其中y 表示血液中酒精含量（毫克／百毫升），x 表示饮酒后的时间（小时）.下表记录了6小时内11个时间点血液中酒精含量y (毫克／百毫升)随饮酒后的时间x （小时）（x >0）的变化情况：饮酒后的时间x （小时） …4121 43 145 23 2 3456 …血液中酒精含量y （毫克／百毫升） (2175)1502375 200 2375150 222532254225456225…下面是小明的探究过程，请补充完整：（1）如图，在平面直角坐标系xOy 中，描出了上表中各对对应值为坐标的点，根据描出的点，画出血液中酒精含量y 随时间x 变化的函数图象；（2）观察表中数据及图象可发现此函数图象在直线x =23两侧可以用不同的函数表达式表示，请你任选其中一部分写出表达式．（3）按国家规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克／百毫升时属于“酒后驾驶”，不能驾车上路．参照上述数学模型，假设某驾驶员晚上20∶00在家喝完250毫升低度白酒，第二天早上6∶30能否驾车去上班?请说明理由．27．如图，在平面直角坐标系xOy 中，抛物线2y x bx c =-++经过A （﹣1，0），B （3，0）两点．（1）求抛物线的表达式；（2）抛物线2y x bx c =-++在第一象限内的部分记为图象G ，如果过点P （-3，4）的直线y =mx +n （m ≠0）与图象G 有唯一公共点，请结合图象，求n 的取值范围．28．在△ABC 中，AB=AC ，D 为线段BC 上一点，DB=DA ，E 为射线AD 上一点，且AE=CD ，连接BE ．（1）如图1，若∠B=30°，AC =，请补全图形并求DE 的长；（2）如图2，若BE=2CD ，连接CE 并延长，交AB 于点F ，小明通过观察、实验提出猜想：CE=2EF ．小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：过A 作AM ∥BC 交CF 的延长线于点M ，先证出△ABE ≌△CAD ，再证出△AEM 是等腰三角形即可；想法2：过D 作DN ∥AB 交CE 于点N ，先证出△ABE ≌△CAD ，再证点N 为线段CE 的中点即可．请你参考上面的想法，帮助小明证明CE=2EF ．（一种方法即可）29．在平面直角坐标系xOy 中，已知点M （1，1），N （1，-1），经过某点且平行于OM 、ON 或MN 的直线，叫该点关于△OMN 的“关联线”．例如，如图1，点P （3，0）关于△OMN 的“关联线”是： y =x +3，y =-x +3，x =3．（1）在以下3条线中，是点（4，3）关于△OMN 的“关联线”（填出所有正确的序号； ①x =4； ②y =-x -5； ③y =x -1 ．（2）如图2，抛物线n m x y +-=2)(41经过点A （4，4），顶点B 在第一象限，且B 点有一条关于△OMN 的“关联线”是y = -x +5，求此抛物线的表达式；（3）在（2）的条件下，过点A 作AC ⊥x 轴于点C ，点E 是线段AC 上除点C 外的任意一点，连接OE ，将△OCE 沿着OE 折叠，点C 落在点C ′的位置，当点C ′在B 点关于△OMN 的平行于MN 的“关联线”上时，满足（2）中条件的抛物线沿对称轴向下平移多少距离，其顶点落在OE 上？21AB CDE顺义区2017届初三第二次统一练习数学答案及评分参考题号 1 2 3 4 5 6 7 8 9 10 答案CBBACDABCB二、填空题（本题共18分，每小题3分）11．(2)(2)n m m +-12．5(答案不唯一)；13．40m ； 14．答案不唯一，如：7.98，出现频数最多；15．310 16．到线段两个端点距离相等的点在线段的垂直平分线上．三、解答题（本题共72分，第17-26题，每小题5分，第27题、28题各7分，29题8分）17221326tan 3033-⎛⎫-︒+- ⎪⎝⎭31123699=+-………………………………………………………4分233=- ……………………………………………………………………… 5分18．解：222(32)(32)2(41)948224a a a a a a a a a +---=--+=+-…………3分当2220aa +-=时，原式=-2．………………………………………………5分19．证明：∵BE 平分∠CBD ，∴∠1=∠2．…………………………………1分 ∵BE ∥AC ，∴∠1=∠A ，∠2=∠C ．…………………3分 ∴∠A=∠C ．………………………………4分 ∴ AB=BC ．…………………………………5分20．解：去分母，得2(25)124x x +-=+ …………………………………………1分去括号，得410124x x +-=+ …………………………………………2分移项，合并同类项得25x =- ……………………………………………3分系数化为1，得52x =-………………………………………………4分经检验，52x =-是原方程的解．…………………………………………… 5分DCBAE ABCD21．解：（1）∵点A （2，2）在反比例函数ky x=的图象上， ∴4k =．………………………………………………………… 1分∵点A （2，2）在一次函数4y ax =+的图象上，∴1a =-． ………………………………………………………2分 ∵点A （2，2）在正比例函数y mx =的图象上，∴1m =． …………………………………………………………3分（2）x 的取值范围是02x <<． ……………………………………5分22．解：小芳的结论更符合年级的要求． …………………………………………1分小芳的15个数据中的众数为160cm ，说明全年级身高为160cm 的女生最多，估计约有80人，因此将挑选标准定在160cm ，便于组成身高整齐的花束方队． …………………………………………3分小红的结论是由数据平均数得出的，但调查的样本容量较少；…………4分小冬的结论是由数据中位数得出的，但不能表明165cm 身高的学生够64人． …………………………………………5分23．（1）证明：连接AC ，∵∠ABC =∠ADC =90︒，∴△ABC 和△ADC 均为直角三角形．……… 1分 ∵AB =AD ， AC=AC ，∴Rt △ABC ≌Rt △ADC ．∴BC=CD ．………………………………………………………………2分（2）解：补全图如图所示．…………………………………………………………3分由旋转得BE =BC ，∠CBE =60︒． ∴BE =CD ．∵∠BAD=60︒，∠ABC =∠ADC =90︒， ∴∠BCD =120︒． ∴∠CBE +∠BCD =180︒． ∴BE ∥CD ．∴四边形BCDE 是平行四边形．………………………………………4分又∵BE =CD ，∴□BCDE 是菱形．……………………………………………………5分24．（1）560；……………………………………………………………………1分（2）“讲解题目”的人数是：560-84-168-224=84（人）．………………2分21A B CD E O P OE D CBA12 补全统计图如图所示：…………………3分（3）在试卷评讲课中，“独立思考”的初三学生约有：6000×560168=1800（人）． …………………………………………………………4分（4）略．………………………………………………………………………5分25．（1）证明：连接OD ，AD ，∵AB 为⊙O 的直径，∴∠ADB =90°．………………………………1分 ∴∠ADC =90°．∵点E 是AC 的中点，∴12DE AC CE ==．……………………2分 ∴∠C =∠1．∵OB =OD ，∴∠B =∠2．在Rt △ABC 中， ∵∠CAB =90°， ∴∠C +∠B =90°． ∴∠1+∠2=90°． ∴∠ODE =180°-（∠1+∠2）=90°． ∴OD ⊥DE ．∴DE 是⊙O 的切线．………………………………………………3分（2）解：设BD =4x ，CD =x ，则BC =5x ．由△ABC ∽△DAC ，得AC BCCD AC=． ∴55AC CD BC x x x ===．∴55sin 55AC x B BC x ===． ∵∠APD=∠B ，∴5sin sin 5APD B ∠==． …………………………………………5分26．解：（1）画图象．…………………2分（2）y =-200x 2+400x 或xy 225=…………………………3分（3）把y =20代入反比例函数xy 225=得x =11.25． ∴喝完酒经过11.25小时为早上7：15．∴第二天早上7：15以后才可以驾驶，6：30不能驾车去上班．…………5分27．解：（1）将A 、B 两点的坐标代入抛物线的表达式中，得：10930b c b c --+=⎧⎨-++=⎩，解得23b c =⎧⎨=⎩，………………………………………2分 ∴抛物线的表达式为223y x x =-++．………………………………3分（2）设抛物线223y x x =-++与y 轴交于点C ，则点C 的坐标为（0，3）．抛物线223y x x =-++的顶点坐标为（1，4）．可求直线PB 的表达式为223y x =-+，与y 轴交于点E （0，2）．…………5分直线PD 平行于x 轴，与y 轴交于点F （0，4）．由图象可知，当过点P 的直线与y 轴交点在C 、E （含点C ，不含点E ）之间时，与图象G 有唯一公共点，另外，直线PD 与图象G 也有唯一公共点但此时m=0．∴n 的取值范围是2<n ≤3．…………………………………………7分28．（1）解：∵DA=DB ，∠ABC=30°，∴∠BAD = ∠ABC =30°． ∵AB=AC ，ABDECG FECDBA∴∠C =∠ABC =30°． ∴∠BAC =120°．∴∠CAD=90°．………………………………………………………2分 ∴AD=AC ×tan30°=1，AE=CD=2AD=2， ∴DE=AE -AD=1．……………………………………………………3分（2）证明：如图，过A 作AG ∥BC ，交BF 延长线与点G ，∵DB=DA ，AB=AC ，∴∠BAD=∠ABC ，∠ABC=∠ACB ． ∴∠BAD=∠ACB ． ∵AE=CD ，∴△ABE ≌△CAD ．……………………4分 ∴BE=AD ． ∵BE=2CD ， ∴AD=2CD=2AE ． ∴AE=DE ． ∵AG ∥BC ，∴∠G=∠DCE ，∠GAE=∠CDE ．∴△AGE ≌△DCE ．………………………………………………5分 ∴EG=CE ，AG=CD=AE ． ∴△AGE 为等腰三角形． ∴∠GAF=∠ABC=∠BAD ．∴F 为GE 的中点． ………………………………………………6分 ∴CE=EG=2EF ．……………………………………………………7分29．解：（1）①③．…………………………………………………………2分（2）∵抛物线的顶点B （m ，n ）有一条关于△OMN 的关联线是y =-x +5，∴-m +5=n ．…………………………………………………………3分又∵抛物线过点A （4，4），或 ∴214(4)4m n =-+．…………………………………………4分 ∴2,3.m n =⎧⎨=⎩或10,5.m n =⎧⎨=-⎩∵顶点B 在第一象限，∴2,3.m n =⎧⎨=⎩∴抛物线的表达式为21(2)34y x =-+．……………………5分（3）由（2）可得，B （2，3）．依题意有OC ′=OC =4，OH =2， ∴∠C ′OH=60°．∴∠C ′OP=∠COP=30°．∴PH=323tan 30233OH ︒=⨯=． ∴抛物线需要向下平移的距离 BP=BH -PH=3323-=3329-． ……………………………………8分7、我们各种习气中再没有一种象克服骄傲那麽难的了。

2017北京市中考数学二模分类25题圆和答案解析

2017年北京市中考数学分类25题圆顺义25．如图，在Rt△ABC中，∠CA B=90 ，以AB为直径的⊙O交BC于点D，点E是AC的中点，连接DE．（1）求证：DE是⊙O的切线；（2）点P是BD上一点，连接AP，DP，若BD:CD=4:1，求sin∠APD的值．EB房山25.如图，△ABC 中，AC=BC=a，AB=b．以BC为直径作⊙O交AB于点D，交AC 于点E，过点D作⊙O的切线MN，交CB的延长线于点M，交AC 于点N．(1)求证： MN⊥AC；(2) 连接BE，写出求BE长的思路．丰台26．如图，AB 为半圆的直径，O 为圆心，C 为圆弧上一点，AD 垂直于过点C 的切线，垂足为点D ，AB 的延长线交切线CD 于点E ．（1）求证：AC 平分∠DAB ；（2）若AB =4，B 为OE 的中点，CF ⊥AB ，垂足为点F ，求CF 的长.平谷25．如图，已知△ABC 内接于⊙O ，AB 是⊙O 的直径，点F 在⊙O 上，且点C 是BF 的中点，过点C 作⊙O 的切线交AB 的延长线于点D ，交AF 的延长线于点E ．（1）求证：AE ⊥DE ；（2）若∠BAF =60°，AF=4，求CE 的长．石景山25．如图，AB为⊙O的直径，弦BC，DE相交于点F，且DE⊥AB于点G，过点C 作⊙O的切线交DE的延长线于点H.（1）求证：HC HF（2）若⊙O的半径为5，点F是BC的中点，tan HCF m∠=，写出求线段BC长的思路.朝阳25．如图，△ABC中，∠A=45°，D是AC边上一点，⊙O过D、A、B三点，OD∥BC．（1）求证：直线BC是⊙O的切线；（2）OD， AB相交于点E，若AB=AC，OD=r，写出求AE长的思路．西城25．如图，AB 是⊙O 的直径，C 是⊙O 上一点，过点B 作⊙O 的切线，与AC 延长线交于点D ，连接BC ，OE ∥BC 交⊙O 于点E ，连接BE 交AC 于点H ．（1）求证：BE 平分∠ABC ；（2）连接OD ，若BH =BD =2，求OD 的长．海淀25．如图，AB 是⊙O 的直径，BC 为弦，D 为AC 的中点，AC ，BD 相交于E 点，过点A 作⊙O 的切线交BD 的延长线于P 点．（1）求证：∠PAC =2∠CBE ；（2）若PD =m ，∠CBE=α，请写出求线段CE 长的思路．东城25.如图，AB 是⊙O 的直径，点C 在AB 的延长线上，CD 与⊙O 相切于点D ，CE ⊥AD 交AD 的延长线于点E ．（1）求证：∠BDC =∠A ；（2）若CE =4，DE =2，求AD 的长．通州24.如图，AB 是⊙O 的直径，PC 切⊙O 于点C ，AB 的延长线与PC 交于点P ，PC 的延长线与AD 交于点D ，AC 平分∠DAB .（1）求证：AD ⊥PC ；（2）连接BC ，如果∠ABC ＝60°，BC ＝2，P求线段PC 的长．昌平25.如图，AB 为⊙O 的直径，点D ，E 为⊙O 上的两个点，延长AD 至C ，使∠CBD=∠BED .（1）求证：BC 是⊙O 的切线；（2）当点E 为弧AD 的中点且∠BED=30°时，⊙O 半径为2，求DF 的长度.BCA怀柔25.如图，AB 是⊙O 的直径，CD 为⊙O 的弦，过点B 作⊙O 的切线，交AD 的延长线于点E ，连接AC 并延长，过点E 作EG ⊥AC 的延长线于点G ，并且∠GCD = ∠GAB .BAEEA（1）求证：AC BD =；（2）若AB =10，sin ∠ADC =35，求AG 的长．2017年北京市中考数学二模分类25题圆答案顺义25．（1）证明：连接OD ，AD ，∵AB 为⊙O 的直径，∴∠ADB =90°．∴∠ADC =90°．∵点E 是AC 的中点，∴12DE AC CE ==． ∴∠C =∠1．∵OB =OD ，∴∠B =∠2．在Rt △ABC 中，∵∠CAB =90°，∴∠C +∠B =90°．∴∠1+∠2=90°．∴∠ODE =180°-（∠1+∠2）=90°．∴OD ⊥DE ． ∴DE 是⊙O 的切线．（2）解：设BD =4x ，CD =x ，则BC =5x ．由△ABC ∽△DAC ，得AC BCCD AC=． ∴55AC x x x ===．∴sin AC B BC ===． ∵∠APD=∠B ，∴sin sin 5APD B ∠==．房山25. (1)证明：连接 OD ，CD ．∵BC 是⊙O 的直径，321oEDC A∴∠BDC =90°，即CD ⊥AB ∵AC =BC ， ∴D 是AB 的中点又∵BC 是⊙O 的直径，即O 为 BC 的中点 ∴OD ∥AC ，∠MDO =∠MNC ∵MN 是⊙O 的切线，切点为D∴OD ⊥MN 即∠MDO =90°=∠MNC ∴MN ⊥ (2) 由BC 是⊙O 的直径，可得∠BEC =90°；由CD ⊥AB ，在 Rt △ACD 中，AD 、AC 的长可知，用勾股定理可求CD 的长；由AB ⋅CD =2S △ABC =AC ⋅BE ，可得BE 的长．丰台26．（1）证明：连接OC ，∵DE 与⊙O 切于点C ，∴OC ⊥DE .∵AD ⊥DE ，∴OC ∥AD ．∴∠2=∠3．∵OA =OC ，∴∠1=∠3．∴∠1=∠2，即AC 平分∠DAB ．（2）解：∵AB =4，B 是OE 的中点，∴OB =BE =2，OC =2．∵CF ⊥OE ，∴∠CFO = 90º，∵∠COF = ∠EOC ，∠OCE = ∠CFO ，∴△OCE ∽△OFC ，∴OEOC OCOF =，∴OF =1．∴CF =3．平谷25．（1）证明：连接OC ．∵DE 切⊙O 于C ，∴OC ⊥DE 于C ．∵点C 是BF 的中点,∴∠BAC =∠EAC ．∵OC=OA ，∴∠BAC =∠OCA ．∴∠EAC =∠OCA ．∴OC ∥AE ．∴AE ⊥DE 于E ．（2）连接BF ．∵AB 是⊙O 直径，∴∠BFA =∠AEC =∠ECO =90°． ∴四边形CEFG 是矩形．即CO ⊥BF 于G ． ∴BG=GF=CE ．∵∠BAE =60°，AF =4，∴BF =CE =石景山25．（1）证明：连接OC ，如图1．∵CH 是⊙O 的切线， ∴2190∠+∠=°． ∵DE ⊥AB ， ∴3490∠+∠=°．∵OB OC =，∴14∠=∠．∴23∠=∠．又∵53∠=∠∴25∠=∠． ∴HC HF =．（2）求解思路如下：思路一：连接OF ，如图2．① OF 过圆心且点F 是BC 的中点，由垂径定理可得2BC CF =，90OFC ∠=°； ② 由6∠与1∠互余，2∠与1∠互余可得62∠=∠，从而可知tan 6m ∠=；图1③ 在Rt OFC △中，由tan 6CF m OF∠==，可设OF x =，CF mx =，由勾股定理，得222()5x mx +=，可解得x 的值；④ 由22BC CF mx ==，可求BC 的长．思路二：连接AC ，如图3．① 由AB 是⊙O 的直径，可得ACB △是直角三角形，知6∠与4∠互余，又DE ⊥AB 可知3∠与4∠互余，得63∠=∠；② 由63∠=∠，32∠=∠，可得62∠=∠，从而可知tan 6m ∠=；③ 在Rt ACB △中，由tan 6BCm AC ∠==，可设AC x =，BC mx =，由勾股定理，得222()10x mx +=，可解得x 的值； ④ 由BC mx =，可求BC 的长．朝阳25．（1）证明：连接OB ．∵∠A =45°， ∴∠DOB =90°． ∵OD ∥BC ,∴∠DOB +∠CBO =180°. ∴∠CBO =90°．∴ 直线BC 是⊙O 的切线．（2）求解思路如下：如图,延长BO 交⊙O 于点F ，连接AF .①由AB =AC ，∠BAC =45°，可得∠ABC =67.5°，∠ABF =22.5°； ②在Rt △EOB 中，由OB =r ，可求BE 的长；③由BF 是直径,可得∠FAB =90°，在Rt △FAB 中，由BF =2r ，可求AB 的长，进而可求AE 的长.西城25（1）∵AB 是⊙O 的直径∴ ∠ACB = 90°∵OE ∥BC ∴ OE ⊥AC ∴ 弧AE =弧EC ．∴ ∠1= ∠2 ．∴BE 平分∠ABC ．H图 2 图3（2）BD 是⊙O 的切线，∴ ∠ABD = 90°．∵∠ACB = 90°，BH =BD =2，∴ ∠BDH =∠3．∴∠CBD =∠2．∴∠1= ∠2 =∠CBD ．∴∠CBD =30°．∠ADB =60°．在Rt △ABD中， ∠ADB =90°，∴AB=OB Rt △OBD 中，222OD OB BD =+，∴ OD ．海淀25．（1）证明：∵D 为AC 的中点，∴∠CBA =2∠CBE ．∵AB 是⊙O 的直径，∴∠ACB =90°，∴∠1+∠CBA =90°．∴∠1+2∠CBE =90°．∵AP 是⊙O 的切线，∴∠PAB =∠1+∠PAC =90°． ∴∠PAC =2∠CBE ．（2）思路：①连接AD ，由D 是AC 的中点，∠2=∠CBE ，由∠ACB =∠PAB =90°，得∠P =∠3=∠4，故AP =AE ； ②由AB 是⊙O 的直径，可得∠ADB =90°；由AP =AE ，得PE =2PD =2m ，∠5=12∠PAC =∠CBE =α③在Rt △PAD 中，由PD =m ，∠5=α，可求PA 的长；④在Rt △PAB 中，由PA 的长和∠2=α，可求BP 的长；由BE PB PE =-可求BE 的长； ⑤在Rt △BCE 中，由BE 的长和CBE α∠=，可求CE 的长．东城25.（1）证明：连接OD .∵CD 是⊙O 切线，∴∠ODC =90°.即∠ODB +∠BDC =90°. ∵AB 为⊙O 的直径，∴∠ADB =90°.即∠ODB +∠ADO =90°. ∴∠BDC =∠ADO .∵OA =OD ，∴∠ADO =∠A .∴∠BDC =∠A . （2）∵CE ⊥AE ，∴∠E =∠ADB =90°.∴DB ∥EC .∴∠DCE =∠BDC .∵∠BD C=∠A ，∴∠A =∠DCE .∵∠E=∠E ，∴△AEC ∽△CED .∴EC 2=DE •AE .∴16=2（2+AD ）.∴AD =6．通州24.（1）①连接OC ，OC //AD ②AD ⊥PC （2）32昌平25.（1）证明：∵AB 为⊙O 的直径∴∠ADB=90°∴∠A+∠DBA=90°∵ 弧BD =弧BD 错误！未指定书签。

2016北京中考数学各区二模28题汇编(含答案)

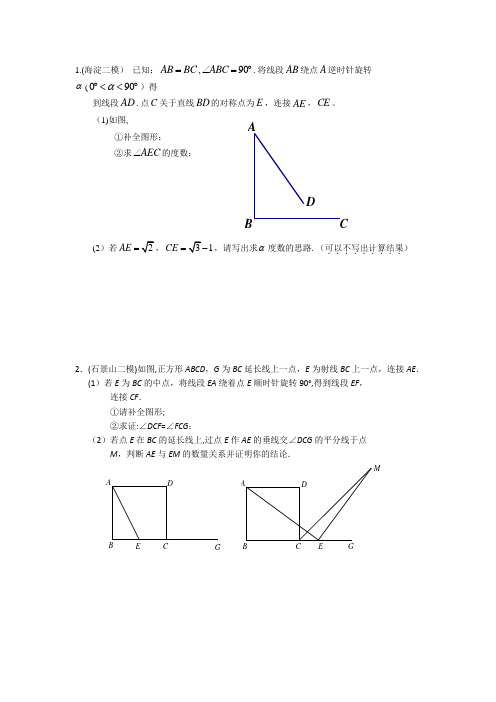
1.(海淀二模）已知：AB BC =,90ABC ∠=︒.将线段AB 绕点A 逆时针旋转α(090α︒<<︒）得到线段AD .点C 关于直线BD 的对称点为E ，连接AE ，CE 。

（1)如图, ①补全图形；②求AEC ∠的度数；(2）若AE =1CE =，请写出求α度数的思路.（可以不写出计算结果．．．．．．．．．）2．(石景山二模)如图,正方形ABCD ，G 为BC 延长线上一点，E 为射线BC 上一点，连接AE ． (1）若E 为BC 的中点，将线段EA 绕着点E 顺时针旋转90°,得到线段EF ，连接CF ． ①请补全图形; ②求证:∠DCF =∠FCG ；（2）若点E 在BC 的延长线上,过点E 作AE 的垂线交∠DCG 的平分线于点M ，判断AE 与EM 的数量关系并证明你的结论．EGD CBAMABCDGE3.（顺义二模）已知:如图，90ACD ∠=︒，MN 是过点A 的直线,AC DC =，DB MN ⊥于点B ．图2图3图1ABCDNMABCDNMNMABCD（1）在图1中，过点C 作CE CB ⊥，与直线MN 于点E ，①依题意补全图形；②求证:BCE ∆是等腰直角三角形；③图1中,线段BD 、AB 、CB 满足的数量关系是； (2）当MN 绕A 旋转到如图（2）和图（3）两个位置时，其它条件不变. 在图2中，线段BD 、AB 、CB 满足的数量关系是；在图3中，线段BD 、AB 、CB 满足的数量关系是；（3）MN 在绕点A 旋转过程中,当30BCD ∠=︒，BD =则CB = ．4.（通州二模）已知，在菱形ABCD 中,∠ADC=60°，点F 为CD 上任意一点（不与C 、D 重合）,过点F 作CD 的垂线，交BD 于点E ，连接AE 。

（1）①依愿意补全图1；②线段EF 、CF 、AE 之间的等量关系是 . （2）在图1中将ΔDEF 绕点D 逆时针旋转，当点F 、E 、C 在一条直线上(如图2）. 线段EF 、CE 、AE 之间的等量关系是。

初三数学二模题答案-顺义

顺义区2015届初三第二次统一练习数学答案一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的．二、填空题（本题共18分，每小题3分）11．4a ； 12．()221m -； 13．14.3； 14．3； 15．12，8；（第一空1分第二空2分）16． 1A （1，1），3A （4，4），11nn n A --（2,2）．（每空1分）三、解答题（本题共30分，每小题5分）17．解：2113tan30+3-⎛⎫- ⎪⎝⎭19=-+…………...4分（其中第一、三项化简各1分，第二项化简2分）8=…………………………………………………………………………………....5分18．证明：∵AB ∥CD ，∴∠C =∠ABC ．…………………………....1分又∵AB =BC ，∠A =∠1，……………………..3分 ∴△ABE ≌△BCD ，………………..……...4分 ∴BE =CD ．………………………………....5分 19．解：2(2)(32)x x x +-+224432x x x x =++--…………………………………………......2分（每项1分） 24x x =-+……………………………………………………………….……......3分∵25x x -=，∴原式24x x =-+54=-+1=-．………………………......5分20．解：()2214x x x +-=-…………………………………………………....2分22214x x x +-=-23x =-32x =-………………………………………………………………..…….....3分经检验可知32x =-是原方程的根，…………………………….…...……...4分∴原方程的根是32x =-．…………………………………………….…..……....5分1EACD21．解：（1）∵点A 的坐标是（-1，a ），在直线22y x =-+上，∴a =4，…………………………………………………………………………………........1分 ∴点A 的坐标是（-1，4），代入反比例函数my x=， ∴m =-4．…………………………………………………………………………………......2分（2）∵OP 与直线22y x =-+平行，∴OP 的解析式为2y x =-， …………………………………………………………......3分∵点P 是双曲线4y x =-上一点， ∴设点P 坐标为（x , 4x-），代入到2y x =-中， ∴4=2x x--，.......................................................................................................................4分∴x = ∴点P的坐标为-或(．………………………………..………......5分22．解：设2012年到2014年烟花爆竹销售量的年平均下降率为x ．…………….....1分依题意可列：()2200011280x -=…………………………………………………......3分解得0.2x =……………………………………………………………………………......4分答：2012年到2014年烟花爆竹销售量的年平均下降率为20%．…………………......5分四、解答题（本题共20分，每小题5分）23．画图………………………………………………………………………1分（1）证明：∵四边形ABCD 是矩形， ∴∠ADC =90º，CD =AB ， ∵EF ⊥AD ， ∴∠EHD =90º， ∴∠EHD =∠ADC ， ∴EF ∥CD ，又∵DE ∥AC ，∴四边形EFCD 是平行四边形，……………......2分又∵DE =AB ， ∴DE =CD ，∴四边形EFCD 是菱形．……………………......3分HEDC BAF（2）解：过点D作DG⊥AC于G．在Rt△ABC中，AB=3，BC=∴tan3ACB∠==，CD=3，∴∠ACB=30º，……………………………………......4分∴∠1=60º，∴在Rt△DCG中，CD=3，sin1322DG CD=⋅∠=⨯=∴平行线DE与AC…………......5分24．解：（1）5200；………………………….…......1分补图……………………………………..3分（2）0.40，0.35，0.30．………………………........4分说明恩格尔系数越小消费水平越高．.................5分25．（1）证明：∵AB=AC，AD=DC，∴∠1=∠C=∠B，..................................................1分又∵∠E=∠B，∴∠1=∠E，∵AE是⊙O的直径，∴∠ADE=90°，∴∠E+∠EAD=90°，∴∠1+∠EAD=90°，∴AC是⊙O的切线．...........................................2分（2）解：过点D作DF⊥AC于点F，∵DA=DC，AC=6，∴CF=12AC=3，..................................... ............3分∵4sin5E=，∴4sin5C=，∴在Rt△DFC中，DF=4，DC=5，∴AD=5，∵∠ADE =∠DFC=90°，∠E =∠C，∴△ADE∽△DFC，.............................................4分∴AD DFAE DC=，∴545AE=，∴AE=254，∴⊙O的直径为254．....................5分CH1GFAB CDE26．解：（1）D （3，2），'D （8，-6），..................................................................................2分（2）依题可列：21,3 6.a k a k -+=⎧⎨+=⎩则a =1，k =3，2b =4，b =2，.........................................................4分（a ，b ，k 求出一个给1分） ∵点E （2，1），∴'E （5，2）．.....................................................................................................5分五、解答题（本题共22分，第27题7分，第28题7分，第29题8分） 27．解：（1）24b ac -=()()2243m m ---........................................................1分 =244412m m m -+-+ =2816m m -+ =()24m - ∵()240m -≥，∴方程()2230x m x m +-+-=总有两个实数根．..............................................2分（2）1,2x =()242m m -±-．...............................................3分∴11x =-，23x m =-+，∴抛物线()223y x m x m =+-+-总过x 轴上的一个定点（-1,0）．................4分（3）∵抛物线()223y x m x m =+-+-与x 轴的另一个交点为B ，与y 轴交于点C ， ∴B （3-m ,0），C （0, m -3），...................................................................................5分 ∴△OBC 为等腰直角三角形， ∵△OBC 的面积小于或等于8， ∴OB ，OC 小于或等于4， 30m -≠，∴3m -≤4且3m ≠， ...........................................................................................6分又∵A ，B 不重合，∴4m ≠，∴-1≤m ≤7且3m ≠，4m ≠．................................................................................7分（1）∵边BA绕点B顺时针旋转α角得到线段BP，∴BA= BP，∵α=60°，∴△ABP是等边三角形，..................................1分∴∠BAP=60º，AP= AC，又∵∠BAC=90°，∴∠P AC=30º，∠ACP=75º，∵PD⊥AC于点D，∴∠DPC=15º．....................................................................2分（2）结论：∠DPC=75º．..................................................3分（3）画图.............................................................................4分过点A作AE⊥BP于E．∴∠AEB=90º，∵∠ABP=150°，∴∠1=30º，∠BAE=60º，又∵BA= BP，∴∠2=∠3=15º，∴∠P AE=75º，∵∠BAC=90°，∴∠4=75º，∴∠P AE=∠4，∵PD⊥AC于点D，∴∠AEP=∠ADP =90º，∴△APE≌△APD，..............................................................5分∴AE= AD，在Rt△ABE中，∠1=30º，∴12AE AB=，又∵AB=AC，∴1122AE AD AB AC ===，∴AD=CD，又∵∠ADP=∠CDP=90º，∴△ADP≌△CDP，.............................................................6分∴∠DCP=∠4=75º，∴∠DPC=15º．.......................................................................7分4123EDBAC PEBP321EAPCBD（1）∵点C （0，8）在抛物线223y x bx c =-++上， ∴8c =，................................................................................................................................1分又∵B （6，0）在抛物线2283y x bx =-++上， ∴02468b =-++， ∴83b =， ∴抛物线的表达式为228833y x x =-++．......................................................................2分（2）结论：以P ，C ，E ，'E 为顶点的四边形为菱形．..............................................3分证明：∵E 和'E 关于直线PC 对称，∴∠'E CP =∠ECP ，'EP E P =，'EC E C =，又∵PE ∥y 轴，∴∠EPC =∠'E CP =∠ECP ，∴EP =EC ，..........................................................................................................................5分 ∴''EC E C EP E P ===，∴四边形'E CEP 为菱形．................................................................................................6分（3）∵B （6，0），C （0，8）， ∴BC 的表达式为483y x =-+．设228,833P x x x ⎛⎫-++ ⎪⎝⎭，则4,83E x x ⎛⎫-+ ⎪⎝⎭， ∴PE 的长为228488333x x x ⎛⎫⎛⎫-++--+ ⎪ ⎪⎝⎭⎝⎭=2243x +x -，过点E 作EF ⊥y 轴于点F ， ∴△CFE ∽△COB ，∴35EF CE =，∴53CE EF =，即53CE x =．由PE =EC 得225433x +x x -=，解得72x =，∴点P 的坐标为755,26⎛⎫ ⎪⎝⎭．................................................8分（不需要过程，结论正确给2分）。

5.北京2016初三中考二模数学word版答案-东城

5.北京2016初三中考二模数学试题及答案word 版答案-东城初三数学参考答案及评分标准 2016.6二、填空题（本题共18分，每小题3分）三、解答题（本题共72分，第17—26题，每小题5分，第27题7分，第28题7分，第29题8分） 17．计算：0112sin 60(3π)()4-︒-+.解：原式14+ …………4分 =3 …………5分18. 解： 22422a b a b a ab-++=224(2)(2)a b a a b a a b -++ =2a ba - …………3分 023a b=≠ ， ∴设2,3.a k b k == …………4分∴ 原式=-2 . …………5分 19. 证明： △ABD 和△BCE 为等边三角形， ∴∠ABD =∠CBE =60°，BA=BD ，BC=BE. …………2分∴∠ABD+∠ABC =∠CBE+∠ABC ，即∠CBD =∠ABE. …………3分∴△CBD ≌△EBA.（SAS ） …………4分∴AE=CD. …………5分20.解：设打折前一件商品A 的价格为x 元，一件商品B 的价格为y 元. …………1分依据题意，得631083494x y x y +=⎧⎨+=⎩. …………3分解得：1016x y =⎧⎨=⎩. …………4分所以5×10+4×16-86=28（元）答：比打折前节省了28元. …………5分 21. 满足条件的所有图形如图所示：…………5分注意：画出一个给2分，二个给4分，三个给5分. 22.解：（1）∵矩形ABCD ，∴∠B =∠BAC =90°.∵EF ⊥AM ，∴∠AFE =∠B =∠BAD =90°.∴∠BAM +∠EAF =∠AEF+∠EAF =90°. ∴∠BAM =∠AEF . …………2分（2）在Rt △ABM 中，∠B =90°，AB =4，cos ∠BAM =45， ∴AM =5.∵F 为AM 中点， ∴AF =52. ∵∠BAM =∠AEF ， ∴cos ∠BAM = cos ∠AEF =45. ∴sin ∠AEF =35.在Rt △AEF 中， ∠AFE =90°，AF =52，sin ∠AEF =35， ∴AE =256. ∴DE=AC-AE =6-256=116. …………5分 23.解：（1）∵四边形ABCD 是平行四边形，点(10)(31)(33)A B C ，，，，，，∴BC =2.∴D （1,2）. ∵反比例函数my x=的图象经过点D ， ∴21m =. ∴2m =.∴2y x=. …………3分（2）233p x <<. …………5分 24.解：（1）172；133. …………2分25.（1）证明：连结BD .∵AB 是O 的直径， ∴90ADB ∠=︒.∴90DAB DBA ∠+∠=︒. ∵AB AC =，∴2ABD ABC ∠=∠，12AD AC =. ∵AF 为⊙O 的切线， ∴∠F AB =90°.∴90FAC CAB ∠+∠=︒. ∴FAC ABD ∠=∠.∴2.ABC CAF ∠=∠ …………2分⑵ 解：连接AE.∴∠AEB =∠AEC =90°.∵sin CAF ABD CAF CBD CAE ∠=∠=∠=∠=∠，∴sin sin ABD CAF ∠=∠=．∵90ABD AC ∠=︒=，∴AD 10sin ADAB ABD==∠=BC .∵90AEC AC ∠=︒=， ∴sin 2CE AC CAE =⋅∠=.∴1028BE BC CE =-=-=. …………5分26.解：（1）sin α=13， sin2α…………2分（2）∵AC = cos α，BC =sin α，∴CD =AC BCAB⨯=sin cos αα⋅.∵∠DCB =∠A ，∴在Rt △BCD 中，BD =sin 2α.∴OD =12- sin 2α. ∴tan2α=CD OD =22sin cos 2sin cos 112sin sin 2αααααα⋅⋅=--. …………5分 27.解：（1）∵21:C y x bx c =++的图象过点A （-1,2），B （4,7），∴217164.b c b c =-+⎧⎨=++⎩，∴21.b c =-⎧⎨=-⎩，∴221y x x =--. …………2分（2）∵二次函数2C 与1C 的图象关于x 轴对称，∴22:21C y x x =-++. ∴2C 的顶点为（1,2）. ∵A （-1,2），B （4,7）,∴过A 、B 两点的直线的解析式：3y x =+. 令x =1，则y =4.∴2C 的顶点不在直线AB 上. …………4分（3）414m <≤或4m =-. …………7分28.解：【探究发现】：相等. …………1分【数学思考】证明：在AC 上截取CG=CE ，连接GE. ∵∠ACB =90°,∴∠CGE =∠CEG =45°.∵AE ⊥EF ，AB ⊥BF ，∴∠AEF =∠ABF =∠ACB =90°,∴∠FEB +∠AEF =∠AEB =∠EAC +∠ACB. ∴∠FEB =∠EAC. ∵CA=CB ，∴AG=BE ，∠CBA =∠CAB =45°. ∴∠AGE =∠EBF =135°. ∴△AGE ≌△EBF .∴AE=EF . …………5分【拓展应用】ABC S △：AEF S △=1：（222n n ++） …………7分29.解：（1）图象略；是. …………2分（2）①2. …………4分②M （3,3）. …………6分…………8分。

中考试题北京市顺义区二模试卷.docx

2016年北京市顺义区中考二模数学试卷一、单选题（共10小题）1．实数4的算术平方根是（）A．B．C．D．考点：平方根、算术平方根、立方根答案：B试题解析：4的算术平方根是22．2015年“十一”黄金周的第二天，北京故宫景点，接待游客超过了最大接待容量，当天接待92 800人次．将92 800用科学记数法表示应为（）A．B．C．D．考点：科学记数法和近似数、有效数字答案：C试题解析：92 800=3．如图，数轴上有A，B，C，D四个点，其中表示互为相反数的点是（）A．点A与点B B．点B与点CC．点B与点D D．点A与点D考点：实数的相关概念答案：D试题解析：A表示的点为-2，D表示的点为2，-2和2是相反数，所以选D4．函数中，自变量的取值范围是（）A．B．C．D．考点：二次根式及其性质答案：C试题解析：x-3≥0，x≥35．在下列调查中，适宜采用全面调查的是（）A．了解七（1）班学生校服的尺码情况B．了解我市中学生视力情况C．检测一批电灯泡的使用寿命D．调查顺义电视台《师说》栏目的收视率考点：数据的收集与整理答案：A试题解析：适合全面调查的必须有2点，数量不是很多不能是损耗品,所以选A6．下图是顺义区地图的一部分，小明家在怡馨家园小区，小宇家在小明家的北偏东约15°方向上，则小宇家可能住在（）A．裕龙花园三区B．双兴南区C．石园北区D．万科四季花城考点：平面直角坐标系及点的坐标答案：B试题解析：以小明家为坐标原点，建立平面直角坐标系，然后就可以得到答案，选B7．四张质地、大小相同的卡片上，分别画上如下图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是轴对称图形的概率为（）A．B．C．D．1考点：概率及计算答案：A试题解析：概率及计算8．如图，四边形内接于⊙，，则的度数是（）A ．B．C．D．考点：圆周角定理及推论答案：D试题解析：∠A+∠C=180°，∠A=110°∴∠C=70°∵∠BOD=2∠C∴∠BOD=140° .9．如图是一个正方体的展开图，把展开图折叠成正方体后，“你”字一面相对的面上的字是（）A．梦B．我C．中D．国考点：立体图形的展开与折叠答案：A试题解析：做一个正方体，然后展开，写上字，就可以得到答案，选A10．已知点M为某封闭图形边界上一定点，动点P从点M出发，沿其边界逆时针运动一周，设点P走过的路程为x，线段MP的长为y，表示y与x的函数关系的图象大致如图所示，则该封闭图形可能是（）A．B．C．D．考点：函数的表示方法及其图像答案：D试题解析：MP是先增大，到达最大值后减小，只有圆的运动轨迹符合要求，故选D二、填空题（共6小题）11.若，则．考点：实数的相关概念答案：3试题解析：根据题意得：m-2=0，n-1=0，解得：m=2，n=1，所以m+n=312.甲、乙两地某月上旬的日平均气温如图所示，则甲、乙两地这10天日平均气温方差大小关系为S甲2 S乙2（填＞或＜）．考点：极差、方差、标准差答案：>试题解析：方差表示的数据变化情况，方差大，说明数据变化大，根据图形，发现甲地的气温变化大，所以甲地气温的数据的方差大．13.小林、小芳和小亮三人玩飞镖游戏，各投5支飞镖，规定在同一圆环内得分相同，中靶和得分情况如图，则小亮的得分是．考点：二元一次方程（组）及其解法答案：21试题解析：设内圈得分为x分，外圈得分为y分，根据题意得：解得：x=5，y=3，3x+2y=15+6=2114.如图，在中，．按以下步骤作图：①以点为圆心，小于的长为半径画弧，分别交、于点、；②分别以点、为圆心，大于的长为半径画弧，两弧相交于点；③作射线交边于点．则的度数为__________．考点：尺规作图答案：70°试题解析：根据尺规作图，AD是∠CAB的角平分线，∵∠CAB=40°，∴∠CAD=20°，∴∠CDA=70°15.某函数符合如下条件：①图象经过点（1，3）；②随的增大而减小．请写出一个符合上述条件的函数表达式．考点：一次函数解析式的确定答案：y=-x+4试题解析：设解析式为y=kx+b，把x=1，y=3代入得：3=k+b，b=3-k，因为y随x的增大而减小，所以k<0，设k=-1，b=4，y=-x+416.如图，为了使电线杆稳固的垂直于地面，两侧常用拉紧的钢丝绳索固定，由于钢丝绳的交点E在电线杆的上三分之一处，所以知道BE的高度就可以知道电线杆AB的高度了．要想得到BE的高度，需要测量出一些数据，然后通过计算得出．请你设计出要测量的对象：；请你写出计算AB高度的思路：．考点：解直角三角形答案：和线段；思路：在Rt中，由，求出试题解析：和线段；思路：在Rt中，由，求出三、计算题（共1小题）17.计算：．考点：实数运算答案：见解析试题解析：四、解答题（共11小题）18.解不等式组：，并写出它的所有整数解．考点：一次不等式（组）的解法及其解集的表示答案：见解析试题解析：解不等式，得．解不等式，得，∴原不等式组的解集为，∴原不等式组的所有整数解为、、019.已知，求代数式的值．考点：代数式及其求值答案：见解析试题解析：原式====，∵，∴，∴原式=20.某地为了打造风景带，将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成，共用时20天，已知甲工程队每天整治24m，乙工程队每天整治16m，求甲、乙两个工程队分别整治了多长的河道．考点：一次方程（组）的应用答案：见解析试题解析：设甲工程队整治了米的河道，则乙工程队整治了米的河道根据题意得：，解得：，∴。

顺义区初三二模数学试题

顺义区2017届初三第二次一致练习数学试卷一、选择题（此题共32分，每题4分）（四个选项，此中只有一个是切合题意的）1、9的算术平方根是（）A、9 B、－3 C、3 D、±32、以下书写的四个汉字，此中为轴对称图形的是3、一副扑克牌，去掉大小王，从中任抽一张，恰巧抽到的牌是 8的概率是（）11C、11A、B、D、4 5413524、把代数式ab26ab 9a分解因式，以下结果中正确的选项是（）A、a(b3)2B、a（b+3）（b－3）C、a(b4)2D、a(b3)25、函数y=kx－k与y k(k0)在同一坐标系中的图象可能是（）x6、如图，AE∥BD，∠1=120°，∠2=40°，则∠C的度数是（）A、10°B、20°C、30°D、40°7、若a2=2－a，则a的取值范围是（）A、a 2B、a0C、a2D、a8、右图中是左面正方体的睁开图的是（）二、填空（本共16分，每小4分）2 x9、函数y中，自量x的取范是x 310、甲、乙两个旅行点今年5月上旬每日招待旅客的人数如所示，甲、乙两景点日招待旅客人数的方差大小关系S甲2S乙211、若把代数式x 22k的形式，此中m,k常数，ｋ－ｍ= +5x+7化（x-m）12、正方形A1B1C1O，A2B2C2C1，A3B3C3C2，⋯按如所示的方式搁置。

A1,A2,A3，⋯和点C1,C2,C3⋯分在直y=kx+b（k＞0）和x上，已知点B1（1,1），B2（3,2），点B6的坐是＿＿＿＿＿＿，点B n的坐是＿＿＿＿＿＿三、解答1-213、算：27-（403tan303-2）214、解方程2-x11 x-33-x15、已知：x2+x－2=0，求代数式x22x(x3)(x3)(x1)的16、已知：如，在△ABC中，AC=BC，∠ACB=90°，MN是点C的一条直，AM⊥MN于M，BM⊥MN于N 求：AM=CN17、列方程或方程解用某企向四川雅安地震灾区捐助价17.6万元的甲、乙两种篷共 200，已知甲种篷每800元，乙种篷每1000元，甲、乙两种篷个多少18、如，在平面直角坐xOy系，一次函数y=－2x+2的象与ｘ订交于点Ｂ，与ｙ订交于点Ｃ，与反比率函数象订交于点Ａ，且AB=2BC，(1)求反比率函数的分析式；（2）若点P在x上，且△的面等于12，直接写出点P的坐19、已知：如图，四边形 ABCD 中，对角线AC 、BD 相较于点E ，∠ABC=∠ACD=90°，AB=BC=62，tan ∠CDE=2，求对角线 BD 的长和△ABD 的面积320、已知：如图，⊙ O 是Rt △ABC 的外接圆，∠ABC=90°，点P 是⊙O 外一点，PA 切⊙O 于点A ，且PA=PB（1）求证：PB 是⊙O 的切线；（2）已知PA=2 3，BC=2，求⊙O 的半径21、甲、乙两学校都派同样人数的学生参加综合素质测试，测试结束后，发现每名参赛学生的成绩都是70分、80分、90分、100分这四种成绩中的一种，而且甲、乙两学校的学生获取依据甲学校学生成绩的条形统计图和乙学校学生的扇形统计图，解答以下问题：100分的人数相等。

2016-2017学年九年级二模数学答案与评分标准

2016-2017学年九年级二模数学答案与评分标准一、选择题（30分）二、填空题（18分）11.7 12.1 13.91 14.6° 15.4π16．22或4-22 三、解答题（共8题，共72分）17. 15x －3＝3(x -4)15x -3=3x -12…………3分 12x=-9 …………6分 x=43-…………8分 18． OA=OB,AC=BD …………2分 △ABD ≌△BAC …………6分 AD ＝BC …………8分19.⑴50，72；…………4分 ⑵略； …………6分 ⑶400. …………8分20．设A ，B 两种产品应分别生产x,(10-x)件 (1)x+3(10-x)=14 解答x=8答：A ，B 两种产品应分别生产8,2件…………4分 (2)由题知⎩⎨⎧≤-+>-+44)10(52,14)10(3x x x x解得2≤x<8设利润为W,则W=x+3(10-x)=30-2x因为k=-2<0，所以W 的值随k 的增大而减小故当x=2时,W 有最大值26.…………8分21．（1）线段PB ，AB 之间的数量关系为：AB =3PB ．理由：连接OC ， ∠PCB =∠PAC ， △PCB ∽△PAC ， ∴，∴PC 2=PB •PA ，∵PC =2PB ，∴PA =4PB ，∴AB =3PB .…………4分（2）过点O 作OH ⊥AD 于点H ，四边形OCEH 是矩形， ∴OC =HE ，∴AE =+OC ， ∵OC ∥AE ，∴△PCO ∽△PEA ，∴，∴=，∴OC =，∴AB =5.…………8分22．(1)P(2，3) m=6…………3分 (2) 设P(t,t 6) C 2-C 1=2t+t 12-10=)3)(2(2--t t t∵t>2,∴当2<t<3时，C 2<C 1;当t=3时，C 2=C 1;当t>3时，C 2>C 1；…………7分 (3)46…………10分23.(1)略：…………3分 (20证△ADH ∽△ACE,AC AD AE AH =…………5分同理△ABG ∽△ACFACABAF AG = ∴AE AHAF AG = ∴△AGH ∽△AFE …………7分 (3)21-3…………10分24.解：（1）（3，0）；（2）点、点的位置如图所示；（3）①如图，∵特征点C为直线上一点，∴.∵抛物线的对称轴与x轴交于点D，∴对称轴.∴点D的坐标为.∵点F的坐标为（1,0），∴.∵特征直线y=ax+b交y轴于点E，∴点E的坐标为.∵点C的坐标为，∴CE∥DF.∵DE∥CF，∴四边形DECF为平行四边形.∴∴.∴特征点C的坐标为.②或。

2016北京市各区初三数学二模-第26题汇编包含答案

8 3
3
2
0
3 2
n…
求 m，n 的值；
（3）如下图，在平面直角坐标系 xOy xOy 中，描出了以上表中各对 y
对应值为坐标的点. 根据描出的点，画出该函数的图象；
5
4
（4）结合函数的图象，写出该函数的性质
3
（一条即可）：________________.
2 1
-3
-2
-1
O -1
12 345
x
-2
C
C 点横坐标为 x3．请你计算 1 1 与 1 的值，并判断
x3
x1 x2 x3
它们的数量关系．
y
B A
x1 O
x2 x
（2）在数学的世界里，有很多结论的形式是统一的，这也体现了数学的美．请你在下列两
组条件中选．择．一．组．，证明
1 x1
1 x2
与
1 x3
仍具有（1）中的数量关系．
①如图，∠APC=120º，PB 平分∠APC，直线 l 与 PA、
则 cosA A的邻边 AC
斜边
AB
3 2
.
类似的，可以在等腰三角形中建立边角之间的联系，我们定
义：等腰三角形中底边与腰的比叫做顶角的正对. 如图 2，在△ ABC 中，AB=AC，顶角 A 的
正对记作 sadA，这时，sadA= 底边 BC . 容易知道一个角的大小与这个角的正对值也是相腰 AB
26．（1）解：由题意可得 x2 1 x 3 ． 2
∵ x1 x2 ，
∴
x1
3 2
，
x
2 2
．
…………………………………………………1 分
∴ 1 1 1．

北京市顺义区2016-2017学年度上期期末九年级数学试题及答案

顺义区2016——2017学年度第一学期期末九年级教学质量检测数学试卷一、选择题（共10道小题，每小题3分，共30分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．网上购物已成为现在的主要购物方式之一，根据阿里巴巴公布的数据显示，“2016天猫双11全球狂欢节”当天总交易额超120700 000 000元，将120700 000 000用科学记数法表示应为A ．8120710⨯B ．1012.0710⨯C ．111.20710⨯D ．121.20710⨯ 2．实数a ，b ，c 在数轴上的对应点的位置如图所示，则正确的结论是A ．a b <B ．a c <C ．22a b <D ．ac b +<3．如图，每个小正方形的边长为1，那么sin B 的值是A ．12B C D4．如图，AB ∥CD ，AD ，BC 相交于点O ，点E ，F 分别是OA ，OB 的中点，若OB=4，OC=3，EF=4，则CD 的长为 A ．83B ．4C ．6D ．85．将抛物线22(1)2y x =--先向右平移2个单位，再向下平移3个单位后，得到的抛物线表达式为A ．22(3)5y x =-- B ．22(3)1y x =-+ C ．22(1)5y x =+- D ．22(1)1y x =++FEO ABCDAB C6．如果3a b -=，那么代数式2()b aa a a b-+的值是A ．3B ．-3C ．13 D ．13- 7．如图，在⊙O 中，点C 是AB 上一点，若126AOB ∠=︒，则C ∠的度数为A ．127︒B ．117︒C ．63︒D ．54︒8．下列函数中，当0x <时，y 随x 的增大而减小的是 A ．2y x = B ．2y x =- C ．1y x =D ．1y x=-9．如图，△ABC 中，∠BAC =80°，AB =4，AC =6．甲、乙、丙、丁四名同学分别在△ABC 内画出一个阴影三角形与△ABC 相似，其中画的错误的是丁丙乙甲3232A BC ABCAB CABC 80°80°A ．甲B ．乙C ．丙D ．丁10．如图，以O 为圆心，半径为1的弧交坐标轴于A ，B 两点，M 是AB 上一点（不与A ，B 重合），连接OM ，设∠MOB ＝α，则点M 的坐标为A ．(cos ,sin )ααB ．(sin ,cos )ααC ．(cos ,cos )ααD ．(sin ,sin )αα二、填空题（共6道小题，每小题3分，共18分） 11．分解因式：22344a b ab b -+= ．12．将二次函数245y x x =-+化为2()y x h k =-+的形式，则h -k = ． 13．地质勘探人员为了估算某条河的宽度，在河对岸选定一个目标点O ，再在他们所在的这一侧选点A ，B ，D ，使得AB ⊥AO ，DB ⊥AB ，然后找出DO 和AB 的交点C ，如图所示．测得AC = 12 m ，BC = 6 m ，BD = 8 m ，则这条河的宽AO 为______m ．14．如图，一把折扇在打开时最大的张角∠AOB =120°，量得OB=30cm ，则这把扇子打开到最大时的扇形的弧长为CBOAy xMOABαA BC80°（结果保留π）．15．老师给出一个二次函数，甲、乙、丙、丁四名同学各指出这个函数的一个性质．甲：函数图象不经过第三、四象限；乙：当1x <时，y 随x 的增大而减小；丙：函数有最小值；丁：当1x ≠时，0y >．已知这四位同学的描述都正确，请你写出满足上述所有性质的一个二次函数表达式． 16．阅读下面材料：在数学课上，老师提出如下问题：小亮的作法如下：老师说：“小亮的作法正确．”请回答：小亮的作图依据是________________________________________．三、解答题（共13道小题，共72分，其中第17-26题每小题5分，第27、28题每小题7分，第29题8分）17．计算：13tan 454cos30-︒-︒．18．解不等式组：3(1)5,23 2.3x x x x -≤+⎧⎪-⎨<-⎪⎩是垂19．如图，□ABCD 中，AE ⊥BC ，AF ⊥CD ，E ，F 分别足．求证：AB AEBC AF=．20．已知二次函数22y x bx c =-++的图象经过点（1，0），（2，-7），求此二次函数的表达式．21．已知：如图，△ABC 中，以AB 为直径的⊙O 分别交BC ，AC 于点D ，E ，连接DE ，若DE =DC ．求证：BD =DE ．22．已知：如图，在ABC △中，290sin 5C A ==∠°,，D 为AC 上一点，60BDC =∠°，2DC =，求AB 及AD 的长．23．已知：如图，在Rt △ABC 中，∠ACB =90︒，AC =BC =3，点D是BC 边上一点，且BD =2DC ，DE ⊥AB 于E ，连接CE .求线段AE的长及∠ECA 的正切值.24．如图，在平面直角坐标系xOy 中，已知反比例函数(0,0)ky k x x=≠>与一次函数(0)y ax b a =+≠的图象相交于点A（1，8）和B （4，m ）．（1）分别求反比例函数和一次函数的表达式；（2）过动点P （n ，0）且垂直于x 轴的直线分别与反比例函数图象和一次函数图象交于C 、D 两点，当点C 位于点D 下方时，写出n 的取值范围．25．如图，在一座高为15m 的建筑物顶端C 处，测得旗杆底部B的俯角α为60︒ ，旗杆顶部A 的仰角β 为30︒．请你计算旗杆AB 的高．ABCDEABDCDCBA15mβαFEDCBAOEDCB A26．已知y 是x 的函数，自变量x 的取值范围是全体实数，下表是y 与x 的几组对应值 x … -4 -3 -2 -1 12- 0 12 1 2 3 4 … y (5)-3-472- -3 72- -4 -3 0 5…小京根据学习函数的经验，利用上述表格所反映出的y 与x 之间的变化规律，对该函数的图象与性质进行了探究．下面是小京的探究过程，请补充完整：（1）如图，在平面直角坐标系xOy 中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；（2）根据画出的函数图象，写出：①x ＝52对应的函数值y 约为； ②该函数的一条性质：．27．已知：如图，⊙O 为ABC △的外接圆，DE 切⊙O 于点D ，且DE ∥BC ，DE =BC ．（1）请仅用无刻度的直尺，在图中画出一条弦，使这条弦将ABC △的面积分成相等的两部分（保留作图痕迹，不写作法）；（2）设（1）中所作的弦交BD 于点F ，若14BF DF =，写出求该弦把四边形BCED 分成的两部分的面积比的思路．28．数学课上，老师给出了如下问题：如图，在ABC △中，D 是边AC 上一点．（1）如图1，若∠ABD =∠C ，求证：2AB AD AC =；（2）如图2，点E 是BD 的中点，且∠DCE =∠ABD ，若AB=3，AC=4，求CD 的长．图2图1ABCDEABCD小宇观察图1，发现第（1）问可以通过证明两三角形相似得出比例式，进而化为等积式；他OABCDE猜想，第（2）问是否可以构造类似图1那样的相似三角形，小宇把这个猜想与同学们交流，通过讨论，发现可以借助点E 是BD 的中点，在形内或形外构造类似图1的相似三角形的目的，进而求解．请你参考小宇的发现、猜想及与同学们的交流内容，解答问题．29．如图，在平面直角坐标系xOy 中，若抛物线2(0)y ax bx c a =++≠与x 轴交于A 、B 两点，与y 轴交于C 点，则称ABC △为抛物线的“交轴三角形”．（1）求抛物线21y x =-的“交轴三角形”的面积；（2）写出抛物线2(0)y ax bx c a =++≠存在“交轴三角形”的条件；（3）已知：抛物线24y ax bx =++过点M （3，0）．①若此抛物线的“交轴三角形”是以y 轴为对称轴的等腰三角形，求抛物线的表达式；②若此抛物线的“交轴三角形”是不以y 轴为对称轴的等腰三角形，求“交轴三角形”的面积．顺义区2016—2017学年度第一学期期末九年级数学检测参考答案一、选择题（共10道小题，每小题3分，共30分）题号 1 2 3 4 5 6 7 8 9 10 答案CDBCABBCDA二、填空题（共6道小题，每小题3分，共18分）11．2(2)b a b -； 12．1； 13．16； 14．20π； 15．答案不唯一，如2(1)y x =-； 16．直径所对的圆周角是直角，经过半径外端且垂直于这条半径的直线是圆的切线．三、解答题（共13道小题，共72分） 17．解：原式=321233142--+⨯-⨯…………………………………… 4分 =2123323--+-2 …………………………………………………… 5分 18．解：原不等式组可化为4,3.x x ≤⎧⎨>⎩………………………………………… 4分∴不等式组的解集为34x <≤．……………………………………… 5分 19．证明：∵四边形ABCD 是平行四边形，∴∠B=∠D ，AD=BC ． …………………………………………… 1分 ∵AE ⊥BC ，AF ⊥CD ，∴∠AEB =∠AFD =90°． …………………………………………… 2分 ∴△ABE ∽△ADF ． ………………………………………………… 3分 ∴AB AEAD AF=． …………………………………………………… 4分又∵AD=BC ， ∴AB AEBC AF=． …………………………………………………… 5分 20．解：依题意，得 20,827.b c b c -++=⎧⎨-++=-⎩…………………………………… 2分解得1,3.b c =-⎧⎨=⎩………………………………………………………… 4分所以二次函数表达式为223y x x =--+． …………………………… 5分21．证明：∵四边形ABDE 为圆内接四边形，∴∠B+∠AED=180°． ……………………………………………… 1分又∵∠DEC+∠AED=180°，∴∠B=∠DEC ． …………………………………………………… 2分 ∵DE =DC ，∴∠DEC =∠C ． ∴∠B=∠C ． …………………… 3分连接AD ， ∵AB 是直径， ∴∠ADB =90°． ………………… 4分∴∠B +∠BAD =90°，∠C +∠CAD =90°．∴∠BAD =∠CAD ． ∴BD=DE ． …………………… 5分22．解：∵∠C=90°，∠BDC =60°，2DC =，∴tan BCBDC DC∠=． …………………………………………………1分∴tan 60BC DC =︒=．………………………………………… 2分∵2sin 5BC A AB ==，∴52AB BC == ……………………………………………… 3分∴AC ==== 4分∴2AD AC DC =-=． …………………………………… 5分23．解：∵∠∴AB ==，∠A ＝∠B ＝45°．………1分∵BD=2DC ， ∴BD=2，DC=1． ∵DE ⊥AB ， ∴∠BED=90°．∴cos BEB BD=． ∴cos 2BE BD B ===………………………………… 2分∴AE AB BE =-==．……………………………… 3分过点E 作EF ⊥AC 于F ．在Rt △AEF 中，AE =A ＝45°， ∴EF =AF =2，CF = AC -AF=1． ……………………………………… 4分∴在Rt △CEF 中，2tan 21EF ECA CF ∠===．……………………… 5分 24．解：（1）∵点A （1，8）和B （4，m ）在反比例函数ky x=的图象上，∴8k =，2m =．∴反比例函数表达式为8(0)y x x=>． …………………… 1分点B 的坐标为B （4，2）．……………………………………… 2分 ∵点A （1，8）和B （4，2）在一次函数y ax b =+的图象上，∴8,4 2.a b a b +=⎧⎨+=⎩ 解得2,10.a b =-⎧⎨=⎩∴一次函数表达式为210y x =-+． ………………………… 4分（2）n 的取值范围是 14n <<． ……………………………… 5分FE ABDCM O A B C D E 25．解：过点C 作CE ⊥AB 于E ．∴BE= CD=15m ． ……………………… 1分在Rt △BCE 中，tan BECEα=，∴15tan 60CE︒=． ∴53CE =． ……… 2分在Rt △ACE 中，tan AECEβ=，∴tan 3053AE︒=． ∴5AE =． ……… 4分 ∴AB =AE +BE =5+15=20．答：旗杆AB 的高为20m ． ……………………………………………… 5分 26．解：（1）画出图象如图所示． ………………………… 2分（2）①x ＝52对应的函数值y 约为 - ；………………… 3分②该函数的一条性质：(答案不唯一)如关于y 轴对称．……………………… 5分27．解：（1）如图1，弦AM 即为所求． ……………………………… 2分图1 图2（2）如图2，连接DC ，设所作的弦AM 交BC 于点G ．由作图可知BG =CG ，进而可得 △BDG 与△CDG 的面积相等．G MO AB C D F E EDCB A15mβα由14BF DF =，可知△BFG 与△DFG 的面积比为14．…………… 3分进而可得△BFG 与△BDG 的面积比为15． …………………… 4分所以△BFG 与△BDC 的面积比为110． ………………………… 5分由DE ∥BC ，DE =BC ，可得四边形BCED 是平行四边形．进而可知△BDC 的面积是□BCED 的面积的一半．所以△BFG 的面积是□BCED 的面积的120． ………………… 6分所以弦AM 把□BCED 分成的两部分的面积比为119．…………… 7分28．（1）证明：∵∠ABD =∠C ，∠A =∠A ，∴△ABD ∽△ACB ．……………………………………………… 1分 ∴AB ADAC AB=． ∴2AB AD AC =．…………………………………………… 2分（2）解：延长DC 到点F ，使CF =DC ，连接BF ，如图2．∵点E 是BD 的中点， ∴EC 是△DBF 的中位线．…………………… 3分∴EC ∥BF ．∴∠DCE =∠F ．∵∠DCE =∠ABD ，∴∠F =∠ABD ． ………… 4分又∵∠A ＝∠A ，∴△ABD ∽△AFB ．……… 5分F图2A BCDE∴AB AD AF AB=． ∴2AB AF AD =．…………………………………………… 6分设CD=CF=x ，则AD=AC - CD=4- x ，AF=AC + CF=4+ x ．∴23(4)(4)x x =+-．∴27x =．∴x =．∴CD． ……………………………………………… 7分另解：取AD 的中点F ，连接EF ，如图3．得EF 是△ABD 的中位线．…………………… 3分可得∠FED =∠DCE ． ……… 4分进而有△FED ∽△FCE ． …… 5分∴2EF FD FC =．…………… 6分设CD= x ，列方程为23(4)(4)()222x x -+=．解得x =．∴CD ． ……………………………………………… 7分29．解：（1）抛物线21y x =-与x 轴交点坐标为A （-1，0），B （1，0），与y 轴交点坐标为C （0，-1）． ………………………………………………… 1分∴12112ABC S ∆=⨯⨯=． …………………………………………… 2分（2）抛物线2(0)y ax bx c a =++≠存在“交轴三角形”的条件是240b ac ∆=->且0c ≠． ……………………………………… 4分（3）抛物线24y ax bx =++与y 轴交点坐标为P （0，4），与x 轴的一个交点坐标为M （3，0）． ……………………………………………… 5分①由题意知抛物线与x 轴的另一个交点坐标为N （-3，0）， ∴9340,9340.a b a b ++=⎧⎨-+=⎩ 解得2,90.a b ⎧=-⎪⎨⎪=⎩ E D C BA 图3F∴抛物线的表达式为2249y x =-+． ………………………… 6分 ②由题意知抛物线与x 轴的另一个交点坐标为N 1（8，0）或N 2（-2，0）或 N 3（76-，0）．当抛物线与x 轴的另一个交点坐标为N 1（8，0）或N 2（-2，0）时，“交轴三角形”的面积均为154102⨯⨯=． ………………… 7分当抛物线与x 轴的另一个交点坐标为N 3（76-，0）时， “交轴三角形”的面积为125254263⨯⨯=．………………… 8分综上，“交轴三角形”的面积为10或253．。

2016顺义二模数学答案

13. 【答案】21
爱
智
康
14. 【答案】70∘
15. 【答案】y = −x + 4 （答案不唯一）
16. 【答案】1．∠BC E 和线段BC 2．①在Rt△BC E 中，由tan ∠BC E =
BE = 2 3 AB BE BC
，求出BE = BC ⋅ tan ∠BC E ， ②由AE = ．
1பைடு நூலகம்3
21. 【答案】甲工程队整治了120 米的河道，乙工程队整治了240 米的河道．
22. 【答案】（1）证明见解析．（2）BD = 6 ．
23. 【答案】（1）k = −3 ，点B 的坐标是(1， − 4) ．（2）点P 的是坐标(3，0) 或(−11，0) ．
24. 【答案】（1）证明见解析．（2）sin ∠C AE =
√3 3
25. 【答案】（1）1．18 2．0.18 （2）直方图见解析．（3）80 ～90 （4）约有105 人．
爱
．
智
康
19. 【答案】4
26. 【答案】（1）点E 是四边形ABC D 的边AB 上的相似点．（2）画图见解析．
27. 【答案】（1）证明见解析．（2）y = x2 + 2x − 3 ．（3）b >
AB
，可求
，求得AB =
3 2
BE =
3 2
BC ⋅ tan ∠BC E
三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）
17. 【答案】2 + 2√2
18. 【答案】原不等式组的解集为−3 < x < 1 ，整数解为−2 、−1 、0 ．

4.北京2016初三中考二模数学word版答案-顺义

4.北京2016初三中考二模数学试题及答案word 版答案-顺义数学答案及评分参考一、选择题（本题共30分，每小题3分）二、填空题（本题共18分，每小题3分）11．3； 12．>； 13．21； 14．70︒； 15．4y x =-+（不唯一）； 16.BCE ∠和线段BC ；思路：①在Rt BCE ∆中，由tan BEBCE BC∠=，求出tan BE BC BCE =⋅∠， ②由13AE AB =，可求23BE AB =，求得33tan 22AB BE BC BCE ==⋅∠．三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）17．解：1112cos453-⎛⎫++-︒ ⎪⎝⎭312=+…………………………..…………………...………4分2=+ …….…………………………………………………….……….….…5分18．解：解不等式532x x -< ，得1x <. …….…………….…….……….…1分解不等式7332x x +> ，得3x >- ..……………….…….……….…2分 ∴原不等式组的解集为31x -<< . ………….…………….…4分 ∴原不等式组的所有整数解为2-、1-、0 . ……….………….….…5分 19．解：原式=2(1)(1)11(1)12x x x x x x +-+⋅+-++ ……………….…….……….…1分=1112x x x ++-+ ……………………………………….………2分 =2(1)(1)(1)(2)(1)(2)x x x x x x x +-++-+-+ ………………….……….….…3分=2212x x x x +++- ……………………………………….……….…4分∵ 230x x +-= ∴ 23x x +=∴原式=221314232x x x x +++==+-- ………………….………….….…5分 20．证明：∵AB AC =，AD 是BC 边上的中线，∴90ADC ∠=︒．………………………………………………………………………….….1分又∵E 是AC 的中点，∴AE DE =，………………………..…………………………………………………….….2分 ∴=90ADE EAD C ∠=∠-∠．………………………………………………………..…..3分 ∵BF CA ⊥延长线于点F ，∴=90CBF C ∠-∠．……………………………………………………………………….4分 ∴CBF ADE ∠=∠．……………………………………………………………………..….5分21．解：设甲工程队整治了x 米的河道，则乙工程队整治了(360)x -米的河道. …….………………………………1分根据题意得：360202416x x -+= ……………………………………….…...…3分解得：120x = ………………………………………….….….…4分 ∴360240x -=答：甲工程队整治了120米的河道，乙工程队整治了240米的河道 ….………..5分 22．（1）证明：∵AC BD ⊥，AE AC ⊥，∴AE ∥BD ，……………………………………………………………………..………….1分 ∵AB ∥DC ， ∴AB ∥DE ．∴四边形ABDE 为平行四边形．……………………………………………..…………..….2分（2）解：∵四边形ABDE 为平行四边形，∴BD AE =，E ABD ∠=∠．………………………………………………………...….3分 ∵4sin 5ABD ∠=， ∴4sin 5E ∠=．……………………………………………………………….………....….4分在RT △EAC 中，8AC =， ∴10CE =，6AE =，∴6BD =．………………………………………………………………………..…...….5分23．解：（1）把A （－4，n ）代入4y x=-中，得1n =， …………………....….1分把A （－4，1）代入y x k =-+中，得3k =- ……………….….…….2分解方程组3,4.y x y x =--⎧⎪⎨=-⎪⎩得4,1.x y =-⎧⎨=⎩ , 1,4.x y =⎧⎨=-⎩∴点B 的坐标是(1,4)- ……………………………………….…...…3分（2）点P 的是坐标(3,0)或(11,0)- ……………………………….…...…5分24．（1）证明：∵AB 为⊙O 的直径，∴90ADB ∠=︒.………………………………………………………………………..……1分又∵AD DC =，∴AB BC =.…………………………………………………………………………………2分（2）解：∵BF 切⊙O 于点B ，∴90ABF ∠=︒.…………………………………………………………………………………………………..…………3分 ∴90BAF F ∠+∠=︒.又∵90BAF ABD ∠+∠=︒， ∴ABD F ∠=∠， ∴△ABD ∽△BFD ， ∴AD BDBD DF=， ∴2BD AD DF =⋅.又∵CF DC =， ∴CF DC AD ==，设=CF DC AD k ==，则2222BD AD DF k k k =⋅=⋅=，∴BD .在RT △BCD中，BC，sin 3CBD ∠==, 又∵CBD CAE ∠=∠，……………………..………………………………………………………………….……4分∴sin 3CAE ∠=.…………………………………………………………..…………5分 25．解：（1）18，0.18；…………………………………..…………………………….……2分（2）…………………………..………3分（3）80-90；…………………………………..…………………………………………4分（4）3500.30105⨯=（人）…………………………………..………………..……5分答：约有105人． 26．解：（1）结论：点是四边形在边上的相似点.……….…1分证明：∵50A B DEC ∠=∠=∠=︒， ∴1+2=130∠∠︒，1+3=130∠∠︒，∴2=3∠∠，………………………………………………..……2分 ∴△AED ∽△BCE ，∴点是四边形在边上的相似点.…………….…3分（2）E ABCD AB E ABCD AB 321ABCDE 成绩/分9080706050010084频数或BA D CEE CD AB……………………………………………………………………5分27．解：（1）[]22224(21)42441(21)b ac m m m m m ∆=-=-+-⨯=-+=- -----1分∵不论m 为任何实数时，总有2(21)0m ∆=-≥，∴该方程总有两个实数根 . --------------------------------------------------2分（2）(21)(21)2m m x +±-==∴12x m =， 21x = ………………………………………………….… 4分不妨设点(1,0)B ，依题意则点(3,0)A - ∴ 32m =-∴ 抛物线的表达式为223y x x =+- …………….…………………5分（3）134b >……………………………………………...………………….…7分 28.（1）①……………………….…………………1分②证明：∵90ACD ∠=︒，又∵CE CB ⊥， ∴90=ECB ACD ∠=︒∠, ∴1=2∠∠.∵DB MN ⊥于点B ， ∴90ABD ∠=︒， ∴180BAC D ∠+∠=︒．E12NMABCD又∵180BAC EAC ∠+∠=︒，∴D EAC ∠=∠．……………………………………………….…..……2分 ∴△CAE ≌△CDB ，∴CE CB =．………………………………………………………..……3分BD AB =+．……………………………………………....….4分（2AB BD =-BD AB =-.……………….…………6分（31.…………………………………………………..……7分 29．解：（1）① 在点M ，N ，E ，F 中，⊙O 的关联点是M ，N ； ….………..2分② ∵过点F 作直线l 交y 于点G ，使30GFO ∠=︒，点F∴OF = 2OG =∴ 点G 的坐标是（0 ，2） ----------------------------------------------------3分设直线l 的表达式为y kx b =+，又直线l 过点点F 和点(0,2)G∴ 直线l 的表达式为23y x =-+ ----------------------------------------4分 ∵ 直线l 上的点(,)P m n 是⊙O 的关联点∴直线l 上的点(,)P m n 满足2OP ≤的所有点都是⊙O 的关联点∴当2OP =时， 224m n +=，即 22(2)4m ++= --------5分∴ 10m = ，2m =∴m 的取值范围是0m ≤ ------------------------------------------------6分（2） 2r ≥ --------------------------------------------------------------------------------8分。

中考试题北京市顺义区二模试卷

2016年北京市顺义区中考二模数学试卷一、单选题（共10小题）1．实数4的算术平方根是（）A．B．C．D．考点：平方根、算术平方根、立方根答案：B试题解析：4的算术平方根是22．2015年“十一”黄金周的第二天，北京故宫景点，接待游客超过了最大接待容量，当天接待92 800人次．将92 800用科学记数法表示应为（）A．B．C．D．考点：科学记数法和近似数、有效数字答案：C试题解析：92 800=3．如图，数轴上有A，B，C，D四个点，其中表示互为相反数的点是（）A．点A与点B B．点B与点CC．点B与点D D．点A与点D考点：实数的相关概念答案：D试题解析：A表示的点为-2，D表示的点为2，-2和2是相反数，所以选D4．函数中，自变量的取值范围是（）A ．B．C．D．考点：二次根式及其性质答案：C试题解析：x-3≥0，x≥35．在下列调查中，适宜采用全面调查的是（）A．了解七（1）班学生校服的尺码情况B．了解我市中学生视力情况C．检测一批电灯泡的使用寿命D．调查顺义电视台《师说》栏目的收视率考点：数据的收集与整理答案：A试题解析：适合全面调查的必须有2点，数量不是很多不能是损耗品,所以选A6．下图是顺义区地图的一部分，小明家在怡馨家园小区，小宇家在小明家的北偏东约15°方向上，则小宇家可能住在（）A．裕龙花园三区B．双兴南区C．石园北区D．万科四季花城考点：平面直角坐标系及点的坐标答案：B试题解析：以小明家为坐标原点，建立平面直角坐标系，然后就可以得到答案，选B7．四张质地、大小相同的卡片上，分别画上如下图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是轴对称图形的概率为（）A．B．C．D．1考点：概率及计算答案：A试题解析：概率及计算8．如图，四边形内接于⊙，，则的度数是（）A ．B．C．D．考点：圆周角定理及推论答案：D试题解析：∠A+∠C=180°，∠A=110°∴∠C=70°∵∠BOD=2∠C∴∠BOD=140° .9．如图是一个正方体的展开图，把展开图折叠成正方体后，“你”字一面相对的面上的字是（）A．梦B．我C．中D．国考点：立体图形的展开与折叠答案：A试题解析：做一个正方体，然后展开，写上字，就可以得到答案，选A10．已知点M为某封闭图形边界上一定点，动点P从点M出发，沿其边界逆时针运动一周，设点P走过的路程为x，线段MP的长为y，表示y与x的函数关系的图象大致如图所示，则该封闭图形可能是（）A．B．C．D．考点：函数的表示方法及其图像答案：D试题解析：MP是先增大，到达最大值后减小，只有圆的运动轨迹符合要求，故选D二、填空题（共6小题）11.若，则．考点：实数的相关概念答案：3试题解析：根据题意得：m-2=0，n-1=0，解得：m=2，n=1，所以m+n=312.甲、乙两地某月上旬的日平均气温如图所示，则甲、乙两地这10天日平均气温方差大小关系为S甲2S乙2（填＞或＜）．考点：极差、方差、标准差答案：>试题解析：方差表示的数据变化情况，方差大，说明数据变化大，根据图形，发现甲地的气温变化大，所以甲地气温的数据的方差大．13.小林、小芳和小亮三人玩飞镖游戏，各投5支飞镖，规定在同一圆环内得分相同，中靶和得分情况如图，则小亮的得分是．考点：二元一次方程（组）及其解法答案：21试题解析：设内圈得分为x分，外圈得分为y分，根据题意得：解得：x=5，y=3，3x+2y=15+6=2114.如图，在中，．按以下步骤作图：①以点为圆心，小于的长为半径画弧，分别交、于点、；②分别以点、为圆心，大于的长为半径画弧，两弧相交于点；③作射线交边于点．则的度数为__________．考点：尺规作图答案：70°试题解析：根据尺规作图，AD是∠CAB的角平分线，∵∠CAB=40°，∴∠CAD=20°，∴∠CDA=70°15.某函数符合如下条件：①图象经过点（1，3）；②随的增大而减小．请写出一个符合上述条件的函数表达式．考点：一次函数解析式的确定答案：y=-x+4试题解析：设解析式为y=kx+b，把x=1，y=3代入得：3=k+b，b=3-k，因为y随x的增大而减小，所以k<0，设k=-1，b=4，y=-x+416.如图，为了使电线杆稳固的垂直于地面，两侧常用拉紧的钢丝绳索固定，由于钢丝绳的交点E在电线杆的上三分之一处，所以知道BE的高度就可以知道电线杆AB的高度了．要想得到BE的高度，需要测量出一些数据，然后通过计算得出．请你设计出要测量的对象：；请你写出计算AB高度的思路：．考点：解直角三角形答案：和线段；思路：在Rt中，由，求出试题解析：和线段；思路：在Rt中，由，求出三、计算题（共1小题）17.计算：．考点：实数运算答案：见解析试题解析：四、解答题（共11小题）18.解不等式组：，并写出它的所有整数解．考点：一次不等式（组）的解法及其解集的表示答案：见解析试题解析：解不等式，得．解不等式，得，∴原不等式组的解集为，∴原不等式组的所有整数解为、、019.已知，求代数式的值．考点：代数式及其求值答案：见解析试题解析：原式====，∵，∴，∴原式=20.某地为了打造风景带，将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成，共用时20天，已知甲工程队每天整治24m，乙工程队每天整治16m，求甲、乙两个工程队分别整治了多长的河道．考点：一次方程（组）的应用答案：见解析试题解析：设甲工程队整治了米的河道，则乙工程队整治了米的河道根据题意得：，解得：，∴。

(完整word版)顺义区2016-2017学年度第一学期期末九年级数学试题(word文档良心出品)

顺义区2016－2017学年度第一学期期末九年级教学质量检测数学试卷一、选择题1、网上购物已成为现在的主要购物方式之一，根据阿里巴巴公布的数据显示，“2016天猫双11全球狂欢节”当天总交易额超120700 000 000元，将120700 000 000用科学记数法表示应为（）A 、8101207⨯B 、101007.12⨯C 、1110207.1⨯D 、1210207.1⨯2、实数a ，b ，c 在数轴上的对应点的位置如图所示，则正确的结论是（）A 、a ＜bB 、a ＜cC 、22b a ＜D 、c a +＜b3、如图，每个正方形的边长为1，那么B sin 的值是（）A 、21 B 、22 C 、23 D 、33 4、如图，CD AB //，AD 、BC 相交于点O ，点E 、F 分别是OA 、OB 的中点，若OB ＝4，OC ＝3，EF ＝4，则CD 的长为A 、38 B 、4 C 、6 D 、8 C BAO FED C B A5、将抛物线2)1(22--=x y 先向右平移2个单位，再向下平移3个单位后，得到的抛物线表达式为（）A 、5)3(22--=x yB 、1)3(22+-=x yC 、5)1(22-+=x yD 、1)1(22++=x y 6、如果3=-b a ，那么代数式ba a a ab +⋅-)(2的值是（） A 、3 B 、－3 C 、31 D 、－31 7、如图，在⊙O 中，点C 是AB 上一点，若o AOB 126=∠，则C ∠的度数为（）A 、o 127B 、o 117C 、o 63D 、o 548、下列函数中，当x ＜0时，y 随x 的增大而减小的是（）A 、x y 2=B 、2x y -=C 、x y 1=D 、x y 1-= 9、如图，△ABC 中，o ABC 80=∠，AB ＝4，AC ＝6，甲、乙、丙、丁四名同学分别在△ABC 内画出一个阴影三角形与△ABC 相似，其中画的错误的是（）80o C B A甲乙丙3丁CA 、甲B 、乙C 、丙D 、丁10、如图，以O 为圆心，半径为1的弧交坐标轴于A ，B 两点，M 是AB 上一点（不与A ，B 重合），连接OM ，设α=∠MOB ，则点M 的坐标为（） A 、（cos α，sin α） B 、（sin α，cos α） C 、（cos α，cos α） D 、（sin α，sin α）二、填空题 11、分解因式：32244b ab b a +-＝_____________。

顺义区中考二模数学试题答案.doc

2010年顺义区中考二模数学试题三、解答题：（本题共30分，每小题5分） 13．解：原式1219=-+ …………………………………………… 4分 89= ………………………………………………………… 5分14．解：5432,4.3x x x x -<+⎧⎪+⎨>-⎪⎩解不等式①，得 3x <， ………………………………………………… 1分解不等式②，得 1x >-． ……………………………………………… 2分 ∴不等式组的解集为 13x -<<． ……………………………………… 4分不等式组的整数解为 0，1，2． ………………………………………… 5分15．解：去分母，得 3(1)2(2)2(2)(x x x x x +++=++ …………………… 1分去括号，得 223324264x x x x x +++=++ ……………………… 2分移项，并整理得 1x = ………………………………………………… 3分经检验：1x =是原方程的根． ………………………………………… 4分 ∴原方程的根为1x =． ………………………………………………… 5分16．证明：∵D 、E 为AC 边的三等分点，∴13AD ED AC ==． ………… 1分 ∵EF ∥AB ，∴12∠=∠，34∠=∠． ……… 3分在△ABD 和△EFD 中，12,34,,AD ED ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ △ABD ≌△EFD ．……………………………………………………… 4分 ∴ BD =FD ．∴ 点D 是BF 的中点． ………………………………………………… 5分4321FE D CBA17．解：2(1)(3)(3)(3)(1)x x x x x -++-+--22221943x x x x x =-++-+-+ ……………………………………… 3分 2365x x =-- …………………………………………………………… 4分∵222x x -=，∴原式23(2)5651x x =--=-=． …………………………………… 5分18．解：设每套演出服的成本是x 元，根据题意，得 ………………………… 1分25100(40)x x =- ……………………………………………………… 3分解这个方程，得 32x =． …………………………………………… 4分答：每套演出服的成本是32元． …………………………………………… 5分四、解答题（本题共20分，第19题5分，第20题6分，第21题5分，第22题4分） 19．解：分别过点A 、D 作AM BC ⊥，DN BC ⊥，垂足分别为M 、N ．可得四边形AMND 是矩形．∴MN=AD=6． ……………… 1分∵AB=45B ∠=︒，∴3AM BM ==， ………… 2分∴DN=AM=3． …………………………………………………………… 3分 ∵30E ∠=︒，∴NE = …………………………………………………………… 4分 ∴BE=BM+MN+NE=369++=+ ………………………… 5分 20．解：（1）如图；………………………… 1分（2）乙x =90（分）；………………… 2分（3）甲队成绩的极差是18分，乙队成绩的极差是30分；…………… 4分（4）从平均分看，两队的平均分相同，实力大体相当；从折线的走势看，甲队比赛成绩呈上升趋势，而乙队比赛成绩呈下降趋势；从获胜场数看，甲队胜三场，乙队胜两场，甲队成绩较好；从极差看，甲队比赛成绩比乙队比赛成绩波动小，甲队成绩较稳定．综上，选派甲队参赛更能取得好成绩．…………………………………… 6分21．（1）证明：∵AB 是⊙O 的直径，∴90ACB ∠=︒． ………………………………………… 1分 ∴90CAB B ∠+∠=︒． ∵D CAB ∠=∠，NMED CBA甲、乙两球队比赛成绩折线统计图场次/场∴90D B ∠+∠=︒．∴90DAB ∠=︒． ………………………………………… 2分 ∴AD 为⊙O 的切线． ……………………………………… 3分（2）解：∵4sin 5D =，6AD =，在Rt ACD △中，24sin 5AC AD D =⋅=，185CD =．在Rt DAB △中，sin D =45AB DB =． ∴8AB =，10DB =． ……………………………………… 4分 ∵AE 平分BAC ∠，EF AB ⊥，90ACB ∠=︒， ∴CE EF =．设CE EF x ==，则18105BE x =--， ∵90EFB DAB ∠=∠=︒，B B ∠=∠， ∴BEF △∽BDA △．∴EF BE DA BD =，即18105610xx --=． ∴125x =．即CE 的长为125． ……………………………………………… 5分22．解：（1）OAB △的面积11342(12)11222=-⨯⨯⨯-⨯⨯=． …………… 1分（2）如图，平移后的三角形为'''O A B △．（画图正确给1分，累计2分）平移的距离'OO = …………………………………… 3分平移过程中OAB △所扫过的面积为四边形''OAA O 与'''O A B △的面积和，即13232(52)222⨯⨯⨯+=． …………………………………… 4分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．解：（1）旋转后的图象解析式为4y x=-(0)x >． ……………………… 1分（2）由旋转可得'A （4，-1）、'B （1，-4）． ………………………… 3分（3）依题意，可知'45B ∠=︒．若'MNB △为直角三角形，则'MNB △同时也是等腰三角形，因此，只需求使'MNB △为直角三角形的t 值．分两种情况讨论：①当'B NM ∠是直角，'B N MN =时，如图1，∵AB ′=8，B ′A ′==AM=B ′N=MN=t ，4321HGFED CBA ∴B ′M=8-t ，∵222''B N MN B M +=，∴222(8)t t t +=-． ………… 4分解得8t =-±，∴8t =-+ ……………… 5分 ②当'B MN ∠是直角，'B M MN =时，如图2，∵AB ′=8，B ′A ′==AM=B ′N=t ， ∴B ′M=MN=8-t ，∵222''B M MN B N +=， ∴222(8)(8)t t t -+-=，解得16t =±∵168+>，16-> ∴此时t 值不存在． …………… 6分（此类情况不计算，通过画图说明t 值不存在也可以）综上所述，当8t =-+'MNB △为等腰直角三角形． ……………… 7分24．（1）解：等腰梯形（或矩形，或正方形）． ……………………………… 1分（2）证法一：取AC 的中点H ，连接HE 、HF ．∵点E 为BC 的中点，∴EH 为ABC △的中位线．∴EH ∥AB ，且12EH AB =． ………………………… 2分同理 FH ∥DC ，且12FH DC =． …………………… 3分∵AB=AC ，DC=AC ， ∴AB=DC ． ∴EH=FH ．∴12∠=∠． ………………… 4分 ∵EH ∥AB ，FH ∥DC ，∴24∠=∠，13∠=∠． ∴43∠=∠．AB CD EFG12∵4180AGE ∠+∠=︒，3180GEC ∠+∠=︒，∴AGE GEC ∠=∠． ………………………………………… 5分 ∴四边形AGEC 是等邻角四边形． …………………………… 6分证法二：连接AE ．设B ∠的度数为x ， ∵AB=AC ，CD=CA ，∴C B x ∠=∠=，18019022x x︒-∠==︒-．………………… 2分 ∵F 是AD 的中点， ∴12EF DF AD ==．…… 3分 ∴21902x ∠=∠=︒-． ∴2909022x xAGE B x ∠=∠+∠=+︒-=︒+．180(90)9022x xGEC ∠=︒-︒-=︒+． …………………… 4分∴AGE GEC ∠=∠． ………………………………………… 5分∴四边形AGEC 是等邻角四边形． …………………………… 6分（3）存在等邻角四边形，为四边形AGHC ． ……………………… 7分25．解：（1）依题意，得420,1640.b c b c ++=⎧⎨++=⎩ 解得 6,8.b c =-⎧⎨=⎩∴抛物线的解析式是268y x x =-+．…………………… 2分（2）依题意，得 (0,2)C ，(8,6)D ．………………………… 3分作点(0,2)C 关于x 轴的对称点'(0,2)C -，求直线'C D 的解析式为2y x =-，直线'C D 与x 轴的交点即为P 点．因此，P 点坐标为(2,0)．………………………………………………………………………… 4分（3）左右平移抛物线268y x x =-+，因为线段A ′B ′=2和=均是定值，所以要使四边形A ′B ′DC 的周长最小，只要使A ′C +B ′D 的值最小； …………………………………………………………………… 5分因为A ′B ′=2，因此将点C 向右平移2个单位得C 1(2，2)，作点C 1关于x 轴的对称点C 2，C 2点的坐标为 (2，-2)，设直线C 2D 的解析式为y kx b =+，将点C 2 (2，-2)、D （8，6）代入解析式，得22,8 6.k b k b +=-⎧⎨+=⎩解得 4,314.3k b ⎧=⎪⎪⎨⎪=-⎪⎩∴直线C 2D 的解析式为41433y x =-． ∴直线C 2D 与x 轴的交点即为B ′点，可求B ′（72，0），因此A ′（32，0）．所以当四边形''A B DC 的周长最小时，抛物线的解析式为37()()22y x x =--，即22154y x x =-+． …… 6分 ∵A ′C +B ′D=C 210=． ………………………………… 7分 ∴四边形''A B DC的周长最小值为21012+=+． …… 8分。