2011年绵阳南山中学自主招生考试数学试卷
2011年四川省绵阳市中考既升学考试数学试题及答案(word版)

绵阳市初2011级学业考试暨高中阶段招生考试满分150分,考试时间120分钟.一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算:-1-2 =( ).A .-1B .1C .-3D .3 2.下列运算正确的是( ).A .a + a 2 = a 3B .2a + 3b = 5abC .(a 3)2 = a 9D .a 3÷a 2= a3.抛掷一个质地均匀且六个面上依次刻有1-6的点数的正方体型骰子,如图.观察向上的一面的点数,下列情况属必然事件的是( ).A .出现的点数是7B .出现的点数不会是0C .出现的点数是2D .出现的点数为奇数4.函数x y 21-=有意义的自变量x 的取值范围是( ).A .x ≤21 B .x ≠21 C .x ≥21 D .x <215.将一副常规的三角尺按如图方式放置,则图中∠AOB 的度数为( ).A .75︒B .95︒C .105︒D .120︒6.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( ).A .0根B .1根C .2根D .3根 7.下列关于矩形的说法,正确的是( ).A .对角线相等的四边形是矩形B .对角线互相平分的四边形是矩形C .矩形的对角线互相垂直且平分D .矩形的对角线相等且互相平分8.由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是( ).A .B .C .D .9购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,少人?( ).A .男村民3人,女村民12人 B .男村民5人,女村民10人 C .男村民6人,女村民9人 D .男村民7人,女村民8人 10.周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用 她们所学的知识测算南塔的高度.如图,小芳站在A 处测得她看塔顶 的仰角α 为45︒,小丽站在B 处(A 、B 与塔的轴心共线)测得她看塔 顶的仰角β 为30︒.她们又测出A 、B 两点的距离为30米.假设她们的眼睛离头顶都为10 cm ,则可计算出塔高约为(结果精确到0.01,参考数据:2≈1.414,3≈1.732)( ).A .36.21米B .37.71米C .40.98米D .42.48米11.已知等腰梯形ABCD 中,AB ∥CD ,对角线AC 、BD 相交于O ,∠ABD = 30︒,AC ⊥BC ,AB = 8 cm ,则△COD 的面积为( ). A .334cm 2 B .34cm 2 C .332cm 2 D .32cm 212.若x 1,x 2(x 1<x 2)是方程(x -a )(x -b )= 1(a <b )的两个根,则实数x 1,x 2,a ,b 的大小关系为( ).A .x 1<x 2<a <bB .x 1<a <x 2<bC .x 1<a <b <x 2D .a <x 1<b <x 2β αBA二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上.13.因式分解:a 3-a = .14.如图,AB ∥CD ,CP 交AB 于O ,AO = PO ,若∠C = 50︒,则∠A = 度.15.2011年4月第六次全国人口普查,结果显示:绵阳市常住人口为461万人,用科学记数法表示这一数据为 .16.如图,将正六边形ABCDEF 放在直角坐标系中,中心与坐标原点重合,若A 点的坐标为(-1,0),则点C 的坐标为 .17.如图,将长8 cm ,宽4 cm 的矩形纸片ABCD 折叠,使点A 与C 重合,则折痕EF 的长等于120个★. 20.鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查.通过随机抽样调查50家客户,得到如下数据:A B B A B B A C A C A B A D A A B B A A D B A B A C A C B A A D A A A B B D A A A B A C A B D A B A (1)请你补全下面的数据统计表:家装风格统计表(2(3)如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?21.右图中曲线是反比例函数xn y 7+=的图象的一支. (1)这个反比例函数图象的另一支位于哪个象限?常数n (2)若一次函数3432+-=x y 的图象与反比例函数的图象交于点A ,与x 轴交于点B ,△AOB 的面积为2,求n 的值.22.如图,在梯形ABCD 中,AB ∥CD ,∠BAD = 90︒,以AD 为直径的半圆D (1)求证:OB ⊥OC ;(2)若AD = 12,∠BCD = 60︒,⊙O 1与半⊙O 外切,并与BC 、CD 相切,求⊙O 1的面积.23.王伟准备用一段长30a 米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.(1)请用a 表示第三条边长;(2)问第一条边长可以为7米吗?请说明理由,并求出a 的取值范围; (3调查问卷对于家庭装修风格,你最喜爱的是( ).(单选) A .中式 B .欧式 C .韩式 D .其他由.24.已知抛物线y = x 2-2x + m -1与x 轴只有一个交点,且与y 轴交于A 点,如图,设它的顶点为B .(1)求m 的值;(2)过A 作x 轴的平行线,交抛物线于点C ,求证:△ABC(3)将此抛物线向下平移4个单位后,得到抛物线C ′,且与x 交于E 点,与y 轴交于F 点,如图.请在抛物线C ′上求点P ,使得△EFP 是以EF 为直角边的直角三角形.25.已知△ABC 是等腰直角三角形,∠A = 90 ,D 是腰AC 长线,垂足为E ,如图.(1)若BD 是AC 的中线,求CEBD的值; (2)若BD 是∠ABC 的角平分线,求CEBD的值;(3)结合(1)、(2),试推断CE BD 的取值范围(直接写出结论,不必证明),并探究CE BD 的值能小于34吗?若能,求出满足条件的D 点的位置;若不能,说明理由.ED C AB参考答案一、选择题: CDBA CBDA BDAC二、填空题: 13.a (a -1)(a + 1) 14.25︒ 15.4.61×10616.)23,21(-17.25 18.15 三、解答题:19.(1)原式= 4-(3-22)+233= 4-3 + 22+22=2251+. (2)原方程去分母可化为为 2x (2x + 5)-2(2x -5)=(2x -5)(2x + 5),展开,得 4x 2 + 10x -4x + 10 = 4x 2-25, 整理,得 6x =-35, 解得 635-=x . 检验:当635-=x 时,2x + 5≠0,且2x -5≠0,所以635-=x 是原分式方程的解. 20.(1(2)A 中式 50%×360︒ = 180︒, B 欧式 30%×360︒ = 108︒, C 韩式 10%×360︒ = 36︒, D 其他 10%×360︒ = 36︒.扇形统计图如右图所示. (3) ∵ 10×50% = 5,10×30% = 3,10×10% = 1,10×10% = 1,∴ 中式设计师招5人,欧式设计师招3人,韩式设计师招1人,其他类型设计师招1人. 21.(1)这个反比例函数图象的另一支位于第四象限.由 n + 7<0,解得n <-7,即常数n 的取值范围是n <-7.(2)在3432+-=x y 中令y = 0,得x = 2,即OB = 2.过A 作x 轴的垂线,垂足为C ,如图. ∵ S △AOB = 2, 即21OB · AC = 2, ∴ 21×2×AC = 2,解得AC = 2,即A把y = 2代入3432+-=x y 中,得x =-1,即A (-1,2).所以 172-+=n ,得n =-9.22.(1) ∵ AB ,BC ,CD 均与半圆O 相切,∴ ∠ABO =∠CBO ,∠DCD =∠BCO . 又 AB ∥CD ,∴ ∠ABC +∠BCD = 180︒,即 ∠ABO +∠CBO +∠BCO +∠DCO = 180︒. ∴ 2∠CBO + 2∠BCO = 180︒,于是 ∠CBO +∠BCO = 90︒,∴ ∠BOC = 180︒-(∠CBO +∠BCO )= 180︒-90︒ = 90︒,即 OB ⊥OC . (2)设CD 切⊙O 1于点M ,连接O 1M ,则O 1M ⊥CD .设⊙O 1的半径为r . ∵ ∠BCD = 60︒,且由(1)知 ∠BCO =∠O 1CM ,∴ ∠O 1CM = 30︒.在Rt △O 1CM 中,CO 1 = 2 O 1M = 2 r . 在Rt △OCD 中,OC = 2 OD = AD = 12.∵ ⊙O 1与半圆D 外切, ∴ OO 1 = 6 + r ,于是,由 OO 1 + O 1C = OC 有 6 + r + 2 r = 12, 解得 r = 2,因此⊙O 1的面积为4π.180︒ 中式 50% 其它 10% 韩式10%欧式30%36︒ 36︒ 108︒23.(1) ∵ 第二条边长为2a + 2, ∴ 第三条边长为30-a -(2a + 2)= 28-3a . (2)当a = 7时,三边长分别为7,16,7.由于 7 + 7<16,所以不能构成三角形,即第一条边长不能为7米. 由⎩⎨⎧-<-+->++aa a a a a 328)22(,328)22( 可解得 213313<<a .即a 的取值范围是213313<<a . (3)在(2)的条件下,注意到a 为整数,所以a 只能取5或6.当a = 5时,三角形的三边长分别为5,12,13. 由52 + 122 = 132知,恰好能构成直角三角形.当a = 6时,三角形的三边长分别为6,14,10. 由62 + 102 ≠142知,此时不能构成直角三角形. 综上所述,能围成满足条件的小圈,它们的三边长分别为5米,12米,13米.24.(1)∵ 抛物线y = x 2-2x + m -1与x 轴只有一个交点,∴ △=(-2)2-4×1×(m -1)= 0,解得 m = 2.(2)由(1)知抛物线的解析式为 y = x 2-2x + 1,易得顶点B (1,0),当 x = 0时,y = 1,得A (0,1).由 1 = x 2-2x + 1 解得 x = 0(舍),或 x = 2,所以C (2,1). 过C 作x 轴的垂线,垂足为D ,则 CD = 1,BD = x D -x B = 1.∴ 在Rt △CDB 中,∠CBD = 45︒,BC =2.同理,在Rt △AOB 中,AO = OB = 1,于是 ∠ABO = 45︒,AB =2.∴ ∠ABC = 180︒-∠CBD -∠ABO = 90︒,AB = BC ,因此△ABC 是等腰直角三角形.(3)由题知,抛物线C ′ 的解析式为y = x 2-2x -3,当 x = 0时,y =-3;当y = 0时,x =-1,或x = 3,∴ E (-1,0),F (0,-3),即 OE = 1,OF = 3.① 若以E 点为直角顶点,设此时满足条件的点为P 1(x 1,y 1),作P 1M ⊥x 轴于M . ∵ ∠P 1EM +∠OEF =∠EFO +∠OEF = 90︒,∴ ∠P 1EM =∠EFO ,得 Rt △EFO ∽Rt △P 1EM ,于是 311==OF OE EM M P ,即EM = 3 P 1M . ∵ EM = x 1 + 1,P 1M = y 1,∴ x 1 + 1 = 3 y 1. (*)由于P 1(x 1,y 1)在抛物线C ′ 上,有 3(x 12-2x 1-3)= x 1 + 1, 整理得 3x 12-7x 1-10 = 0,解得 x 1 =-1(舍),或3101=x . 把3101=x 代人(*)中可解得3191=y . ∴ P 1(310,313). ② 若以F 点为直角顶点,设此时满足条件的点为P 2(x 2,y 2),作P 2N ⊥与y 轴于N .同①,易知 Rt △EFO ∽Rt △FP 2N ,得 312==OF OE N P FN ,即P 2N = 3 FN .∵ P 2N = x 2,FN = 3 + y 2,∴ x 2 = 3(3 + y 2). (**)由于P 2(x 2,y 2)在抛物线C ′ 上,有 x 2 = 3(3 + x 22-2x 2-3), 整理得 3x 22-7x 2 = 0,解得 x 2 = 0(舍),或372=x . 把372=x 代人(**)中可解得9202-=y . ∴ P 2(37,920-). 综上所述,满足条件的P 点的坐标为(310,313)或(37,920-).25.解法1 设AB = AC = 1,CD = x ,则0<x <1,BC =2,AD = 1-x . 在Rt △ABD 中,BD 2= AB 2+ AD 2= 1 +(1-x )2= x 2-2x + 2. 由已知可得 Rt △ABD ∽Rt △ECD , ∴BDCDAB CE =, 即 2212+-=x x x CE ,从而 222+-=x x x CE ,∴ 22222222222-+=+-=+-+-==x x x x x x x x x x CEBDy ,0<x <1,(1)若BD 是AC 的中线,则CD = AD = x =21,得 25==CE BD y . (2)若BD 是∠ABC 的角平分线,则 ABBCAD CD =,得 121=-x x ,解得 22-=x , ∴ 2222222=--+-==CE BD y . (3)若3422=-+==x x CE BD y ,则有 3x 2-10x + 6 = 0,解得 375-=x ∈(0,1), ∴6171-=-=x x DC AD ,表明随着点D 从A 向C 移动时,BD 逐渐增大,而CE 逐渐减小,的值则随着D 从A 向C 移动而逐渐增大.解法2 设AB = AC = 1,∠ABD = α,则 BC =2,∠CBE = 45︒-α. 在Rt △ABD 中,有 αcos 1cos =∠=ABD AB BD ; 在Rt △BCE 中,有 CE = BC · sin ∠CBE =2sin (45︒-α). 因此)452sin(212cos sin cos 1cos )45sin(212︒--=-=-︒=ααααααCE BD .下略…… 解法3 (1)∵ ∠A =∠E = 90︒,∠ADB =∠CDE ,∴ △ADB ∽△EDC , ∴ CEDEAB AD =. 由于D 是中点,且AB = AC ,知AB = 2 AD ,于是 CE = 2 DE . 在Rt △ADB 中,BD =AD AD AD AD AB 542222=+=+. 在Rt △CDE 中,由 CE 2+ DE 2= CD 2,有 CE 2+41CE 2= CD 2,于是CD CE 52=. 而 AD = CD ,所以25=CE BD . (2)如图,延长CE 、BA 相交于点F .∵ BE 是∠ABC 的平分线,且BE ⊥CF ,∴ △CBE ≌△FBE ,得 CE = EF ,于是 CF = 2 CE .又 ∠ABD +∠ADB =∠CDE +∠FCA = 90︒,且 ∠ADB =∠CDE ,∴ ∠ABD =∠FCA ,进而有 △ABD ≌△ACF ,得 BD = 2 CE ,2=CEBD. (3)CE BD 的值的取值范围为CEBD≥1.下略……。
南山中学自主招生考试数学(一)及答案

2011年绵阳南山中学实验学校自主招生考试模拟试题(一)数学试题注意事项:1.本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题36分;第Ⅱ卷为非选择题114分;全卷共150分.考试时间为120分钟.2.本试卷的选择题答案用2B 铅笔涂在机读卡上,非选择题在卷Ⅱ上作答.3..4.非选择题必须在指定的区域内作答,不能超出指定区域或在非指定区域作答,否则答案无效.卷I (选择题,共36分)一.选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算3×(-2) 的结果是( )A .5B .-5C .6D .-62.如图1,在△ABC 中,D 是BC 延长线上一点,∠B = 40°,∠ACD = 120°,则∠A 等于( ) A .60° B .70°C .80°D .90°3.下列计算中,正确的是( )A .020=B . 623)(a a = C3± D .2a a a =+4.如图2,在□ABCD 中,AC 平分∠DAB ,AB = 3,则□ABCD 的周长为( ) A .6 B .9 C .12D .155.把不等式2x -< 4的解集表示在数轴上,正确的是( )6.如图3,在5×5正方形网格中,一条圆弧经过A ,B ,C 三点, 那么这条圆弧所在圆的圆心是( )A .点PB .点MC .点RD .点Q7.若220x x +=,则xy 的值为( )A .6或0B .6-或0C .5或0D .8-或0AB CD图2ABC D 40°120°图1图3A B D C8.已知y x a b b y b b a x b a ,,,,0则--=-+=<<的大小关系是 ( ) A .y x > B .x =y C .y x < D .与a 、b 的取值有关 9.如图4,已知边长为1的正方形ABCD ,E 为CD 边的中点,动点P 在正方形ABCD 边上沿A B C E →→→运动,设点P 经过的路程 为 x ,△APE 的面积为y ,则y 关于x 的函数的图象大致为( )10.如图5,两个正六边形的边长均为1,其中一个正六边形 一边恰在另一个正六边形的对角线上,则这个图形(阴影部 分)外轮廓线的周长是( )A .7B .8C .9D .1011.如图6,已知二次函数2y ax bx c =++的图像如图所示,则下列6个代数式,,,,2,ab ac a b c a b c a b ++-++ 2a b -中其值为正的式子个数为( )A .1个B .2个C .3个D .4个12.将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图7-1.在图7-2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图7-1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )卷Ⅱ(非选择题,共114分)二.填空题:本大题共6个小题,每小题4分,共24分.将答案直接填写在题中横线上.13.-的相反数是 .14.如图8,矩形ABCD 的顶点A ,B 在数轴上, CD = 6, 点A 对应的数为1-,则点B 所对应的数为.图8图7-1图7-2图515.如图9,有五张点数分别为2,3,7,8,9的扑克牌, 从中任意抽取两张,则其点数之积是偶数的概率为 .16.已知x = 1是一元二次方程02=++n mx x 的一个根,则 222n mn m ++的值为 .17.把三张大小相同的正方形卡片A ,B ,C 叠放在一 个底面为正方形的盒底上,底面未被卡片覆盖的部分用 阴影表示.若按图10-1摆放时,阴影部分的面积为S 1; 若按图10-2摆放时,阴影部分的面积为S 2,则S 1 S 2(填“>”、“<”或“=”). 18.南山中学高一年级举办数学竞赛,A 、B 、C 、D 、E 五位同学得了前五名,发奖前,老师让他们猜一猜各人的名次排列情况. A 说:B 第三名,C 第五名; B 说:E 第四名,D 第五名; C 说:A 第一名,E 第四名; D 说:C 第一名,B 第二名; E 说:A 第三名,D 第四名.老师说:每个名次都有人猜对,试判断获得第一至第五名的依次为 .三、解答题(本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤) 19.(1)(本小题满分8分)解方程:1211+=-x x . (2)(本小题满分8分)先化简再求值: 22214()2442a a a a a a a a ----÷++++,其中22430a a +-=. 20.(本小题满分12分)甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.甲校成绩统计表 图10-1 图10-2 乙校成绩扇形统计图 图11-1图9(1)在图11-1中,“7分”所在扇形的圆心角 等于 °.(2)请你将图11-2的统计图补充完整.(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.(4)如果该教育局要组织8人的代表队参加市级团体赛,为便管理,决定从这两所学校中的一所挑选参赛选手, 请你分析,应选哪所学校?21.(本小题满分12分) 如图12,在直角坐标系中,矩形OABC 的顶点O 与 坐标原点重合,顶点A ,C 分别在坐标轴上,顶点B 的坐标为(4,2).过点D (0,3)和E (6,0)的直 线分别与AB ,BC 交于点M ,N .(1)求直线DE 的解析式和点M 的坐标; (2)若反比例函数xmy =(x >0)的图象经过点M , 求该反比例函数的解析式,并通过计算判断点N 是否在该函数的图象上; (3)若反比例函数xmy =(x >0)的图象与△MNB 有公共点,请直接..写出m 的取值范围. 22.(本小题满分12分)某仪器厂计划制造A 、B 两种型号的仪器共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于制造仪器,两种型号的制造成本和售价如下表:(1)该厂对这两种型号仪器有哪几种制造方案? (2)该厂应该选用哪种方案制造可获得利润最大?(3)根据市场调查,每套B 型仪器的售价不会改变,每套A 型仪器的售价将会提高a 万元(a >0),且所制造的两种仪器可全部售出,问该厂又将如何制造才能获得最大利润?乙校成绩条形统计图图13-2AD OBC 21 MN图13-1AD BM N1 2图13-3AD O BC 21MNO 23.(本小题满分12分)在图13-1至图15-3中,直线MN 与线段AB 相交 于点O ,∠1 = ∠2 = 45°.(1)如图13-1,若AO = OB ,请写出AO 与BD 的数量关系和位置关系;(2)将图13-1中的MN 绕点O 顺时针旋转得到 图13-2,其中AO = OB . 求证:AC = BD ,AC ⊥ BD ;(3)将图13-2中的OB 拉长为AO 的k 倍得到 图13-3,求ACBD的值. 24.(本小题满分12分)如图14,在直角梯形ABCD 中,AD ∥BC ,90B ∠=︒,AD = 6,BC = 8,33=AB ,点M 是BC 的中点.点P 从点M 出发沿MB 以每秒1个单位长的速度向点B 匀速运动,到达点B 后立刻以原速度沿BM 返回;点Q 从点M 出发以每秒1个单位长的速度在射线MC 上匀速运动.在点P ,Q 的运动过程中,以PQ 为边作等边三角形EPQ ,使它与梯形ABCD 在射线BC 的同侧.点P ,Q 同时出发,当点P 返回到点M 时停止运动,点Q 也随之停止. 设点P ,Q 运动的时间是t 秒(t >0).(1)设PQ 的长为y ,在点P 从点M 向点B 运动的过程中,写出y 与t 之间的函数关系式(不必写t 的取值范围). (2)当BP = 1时,求△EPQ 与梯形ABCD 重叠部分的面积. (3)随着时间t 的变化,线段AD 会有一部分被△EPQ 覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最 大值能否持续一个时段?若能,直接..写出t 的取值范围; 若不能,请说明理由.P Q图14 (备用图)25.(本小题满分14分)如图15,抛物线2(0)y ax bx c a =++≠经过x 轴上的两点1(,0)A x 、2(,0)B x 和y 轴上的点3(0,)2C -,P 的圆心P 在y 轴上,且经过B 、C两点,若b =,AB = 求:(1)抛物线的解析式;(2)D 在抛物线上,且C 、D 两点关于抛物线的对称轴对称,问直线BD 是否经过圆心P ? 并说明理由;(3)设直线BD 交P 于另一点E ,求经过点E 和P 的切线的解析式.2011年绵阳南山中学实验学校自主招生考试模拟试题(一)数学参考答案一、选择题二、填空题13.5 14.5 15. 71016.1 17. = 18. C 、B 、A 、E 、D. 三、解答题19.(1)解:)1(21-=+x x ,3=x .经检验知,3=x 是原方程的解.………………8分(2)解:………………6分由已知得2322a a +=,代入上式的原式23=………………8分20.解:(1)144;………………3分(2)如图1;………………6分(3)甲校的平均分为8.3分,中位数为7分;………………8分 由于两校平均分相等,乙校成绩的中位数大于甲 校的中位数,所以从平均分和中位数角度上判断, 乙校的成绩较好.………………9分乙校成绩条形统计图图12222222212[](2)(2)4(2)(2)(1)2(2)442(2)442(2)41(2)12a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a--+=-⨯++--+--+=⨯+---++=⨯+--+=⨯+-=+=+原式(4)因为选8名学生参加市级口语团体赛,甲校得10分的有8人,而乙校得10分的只有5人,所以应选甲校.………………12分21.解:(1)设直线DE 的解析式为b kx y +=, ∵点D ,E 的坐标为(0,3)、(6,0),∴ ⎩⎨⎧+==.60,3b k b解得 ⎪⎩⎪⎨⎧=-=.3,21b k ∴ 321+-=x y .………………2分∵ 点M 在AB 边上,B (4,2),而四边形OABC 是矩形, ∴ 点M 的纵坐标为2.又 ∵ 点M 在直线321+-=x y 上,∴ 2 = 321+-x .∴ x = 2.∴ M (2,2).………………4分(2)∵xmy =(x >0)经过点M (2,2), ∴ 4=m .∴xy 4=.………………5分又 ∵ 点N 在BC 边上,B (4,2), ∴点N 的横坐标为4.∵ 点N 在直线321+-=x y 上,∴ 1=y .∴ N (4,1). ………………8分∵ 当4=x 时,y =4x= 1, ∴点N 在函数 xy 4=的图象上.………………9分 (3)4≤ m ≤8.………………12分22.解:(1) 设A 种型号的仪器造x 套,则B 种型号的仪器造(80-x)套, 由题意得:()20968028252090≤-+≤x x解之得:5048≤≤x ………………2分所以 x=48、49、50 三种方案:即:A 型48套,B 型32套;A 型49套,B 型31套;A 型50套,B 型30套。
四川省绵阳市2011年中考数学试题(含答案)

绵阳市初2011级学业考试暨高中阶段招生考试满分150分,考试时间120分钟.一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算:-1-2=().A .-1B .1C .-3D .32.下列运算正确的是().A .a +a 2=a 3B .2a +3b =5ab C .(a 3)2=a 9D .a 3÷a 2=a3.抛掷一个质地均匀且六个面上依次刻有1-6的点数的正方体型骰子,如图.观察向上的一面的点数,下列情况属必然事件的是().A .出现的点数是7B .出现的点数不会是0C .出现的点数是2D .出现的点数为奇数4.函数x y 21-=有意义的自变量x 的取值范围是().A .x ≤21B .x ≠21C .x ≥21D .x <215.将一副常规的三角尺按如图方式放置,则图中∠AOB 的度数为().A .75︒B .95︒C .105︒D .120︒6.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?().A .0根B .1根C .2根D .3根7.下列关于矩形的说法,正确的是().A .对角线相等的四边形是矩形B .对角线互相平分的四边形是矩形C .矩形的对角线互相垂直且平分D .矩形的对角线相等且互相平分8.由四个相同的小正方体搭建了一个积木,它的三视图如图所示,则这个积木可能是().A .B .C .D .9.灾后重建,四川从悲壮走向豪迈.灾民发扬伟大的抗震救灾精神,桂花村派男女村民共15人到山外采购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,共购回15包.请问这次采购派男女村民各多少人?().A .男村民3人,女村民12人B .男村民5人,女村民10人C .男村民6人,女村民9人D .男村民7人,女村民8人10.周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A 处测得她看塔顶的仰角α为45︒,小丽站在B 处(A 、B 与塔的轴心共线)测得她看塔顶的仰角β为30︒.她们又测出A 、B 两点的距离为30米.假设她们的眼睛离头顶都为10cm ,则可计算出塔高约为(结果精确到0.01,参考BA O 主视图左视图俯视图βαBA数据:2≈1.414,3≈1.732)().A .36.21米B .37.71米C .40.98米D .42.48米11.已知等腰梯形ABCD 中,AB ∥CD ,对角线AC 、BD 相交于O ,∠ABD =30︒,AC ⊥BC ,AB =8cm ,则△COD 的面积为().A .334cm 2B .34cm 2C .332cm 2D .32cm 212.若x 1,x 2(x 1<x 2)是方程(x -a )(x -b )=1(a <b )的两个根,则实数x 1,x 2,a ,b 的大小关系为().A .x 1<x 2<a <bB .x 1<a <x 2<bC .x 1<a <b <x 2D .a <x 1<b <x 2二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上.13.因式分解:a 3-a =.14.如图,AB ∥CD ,CP 交AB 于O ,AO =PO ,若∠C =50︒,则∠A =度.15.2011年4月第六次全国人口普查,结果显示:绵阳市常住人口为461万人,用科学记数法表示这一数据为.16.如图,将正六边形ABCDEF 放在直角坐标系中,中心与坐标原点重合,若A 点的坐标为(-1,0),则点C 的坐标为.17.如图,将长8cm ,宽4cm 的矩形纸片ABCD 折叠,使点A 与C 重合,则折痕EF 的长等于cm .18.观察下面的图形,它们是按一定规律排列的,依照此规律,第个图形共有120个★.三、解答题:本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤.19.(1)化简:183|322|21(2+---;O DB A CP50︒A BC D EFOxy D ′FEBC (A ′)DA★★★★★★★★★★★★★★★★★★★★第1个图形第2个图形第3个图形第4个图形(2)解方程:1522522=+--x x x .20.鲁班家装公司为芙蓉小区做家装设计,调查员设计了如下问卷,对家装风格进行专项调查.通过随机抽样调查50家客户,得到如下数据:A B B A B B A C A C A B A D A A B B A A D B A B A C A C B A A D A AA B B D A A A B A C A B D A B A(1)请你补全下面的数据统计表:家装风格统计表装修风格划记户数百分比A 中式正正正正正2550%B 欧式C 韩式510%D 其他正10%合计50100%(2)请用扇形统计图描述(1)表中的统计数据;(注:请标明各部分的圆心角度数)(3)如果公司准备招聘10名装修设计师,你认为各种装修风格的设计师应分别招多少人?调查问卷对于家庭装修风格,你最喜爱的是().(单选)A .中式B .欧式C .韩式D .其他21.右图中曲线是反比例函数xn y 7+=的图象的一支.(1)这个反比例函数图象的另一支位于哪个象限?常数n的取值范围是什么?(2)若一次函数3432+-=x y 的图象与反比例函数的图象交于点A ,与x 轴交于点B ,△AOB 的面积为2,求n 的值.22.如图,在梯形ABCD 中,AB ∥CD ,∠BAD =90︒,以AD 为直径的半圆D 与BC 相切.(1)求证:OB ⊥OC ;(2)若AD =12,∠BCD =60︒,⊙O 1与半⊙O 外切,并与BC 、CD 相切,求⊙O 1的面积.A B Oxy23.王伟准备用一段长30米的篱笆围成一个三角形形状的小圈,用于饲养家兔.已知第一条边长为a 米,由于受地势限制,第二条边长只能是第一条边长的2倍多2米.(1)请用a表示第三条边长;(2)问第一条边长可以为7米吗?请说明理由,并求出a的取值范围;(3)能否使得围成的小圈是直角三角形形状,且各边长均为整数?若能,说明你的围法;若不能,说明理由.24.已知抛物线y =x 2-2x +m -1与x 轴只有一个交点,且与y 轴交于A 点,如图,设它的顶点为B .(1)求m 的值;(2)过A 作x 轴的平行线,交抛物线于点C ,求证:△ABC 是等腰直角三角形;(3)将此抛物线向下平移4个单位后,得到抛物线C ′,且与x 轴的左半轴交于E 点,与y 轴交于F 点,如图.请在抛物线C ′上求点P ,使得△EFP 是以EF 为直角边的直角三角形.FE CO A B x y25.已知△ABC 是等腰直角三角形,∠A =90 ,D 是腰AC 上的一个动点,过C 作CE 垂直于BD 或BD 的延长线,垂足为E ,如图.(1)若BD 是AC 的中线,求CEBD的值;(2)若BD 是∠ABC 的角平分线,求CEBD的值;(3)结合(1)、(2),试推断CE BD 的取值范围(直接写出结论,不必证明),并探究CE BD 的值能小于34吗?若能,求出满足条件的D 点的位置;若不能,说明理由.ED C AB ED CAB参考答案一、选择题:CDBACBDABDAC二、填空题:13.a (a -1)(a +1)14.25︒15.4.61×10616.)23,21(-17.2518.15三、解答题:19.(1)原式=4-(3-22)+233=4-3+22+22=2251+.(2)原方程去分母可化为为2x (2x +5)-2(2x -5)=(2x -5)(2x +5),展开,得4x 2+10x -4x +10=4x 2-25,整理,得6x =-35,解得635-=x .检验:当635-=x 时,2x +5≠0,且2x -5≠0,所以635-=x 是原分式方程的解.20.(1)补全的统计表为:装修风格划记户数百分比A 中式正正正正正2550%B 欧式正正正1530%C 韩式正510%D 其他正510%合计50100%(2)A 中式50%×360︒=180︒,B 欧式30%×360︒=108︒,C 韩式10%×360︒=36︒,D 其他10%×360︒=36︒.扇形统计图如右图所示.(3)∵10×50%=5,10×30%=3,10×10%=1,10×10%=1,∴中式设计师招5人,欧式设计师招3人,韩式设计师招1人,其他类型设计师招1人.21.(1)这个反比例函数图象的另一支位于第四象限.由n +7<0,解得n <-7,即常数n 的取值范围是n <-7.(2)在3432+-=x y 中令y =0,得x =2,即OB =2.过A 作x 轴的垂线,垂足为C ,如图.∵S △AOB =2,即21OB ·AC =2,∴21×2×AC =2,解得AC =2,即A 点的纵坐标为2.把y =2代入3432+-=x y 中,得x =-1,即A (-1,2).所以172-+=n ,得n =-9.22.(1)∵AB ,BC ,CD 均与半圆O 相切,∴∠ABO =∠CBO ,∠DCD =∠BCO .又AB ∥CD ,∴∠ABC +∠BCD =180︒,即∠ABO +∠CBO +∠BCO +∠DCO =180︒.∴2∠CBO +2∠BCO =180︒,于是∠CBO +∠BCO =90︒,∴∠BOC =180︒-(∠CBO +∠BCO )=180︒-90︒=90︒,即OB ⊥OC .(2)设CD 切⊙O 1于点M ,连接O 1M ,则O 1M ⊥CD .设⊙O 1的半径为r .180︒中式50%其它10%韩式10%欧式30%36︒36︒108︒OA BC xy∵∠BCD =60︒,且由(1)知∠BCO =∠O 1CM ,∴∠O 1CM =30︒.在Rt △O 1CM 中,CO 1=2O 1M =2r .在Rt △OCD 中,OC =2OD =AD =12.∵⊙O 1与半圆D 外切,∴OO 1=6+r ,于是,由OO 1+O 1C =OC 有6+r +2r =12,解得r =2,因此⊙O 1的面积为4π.23.(1)∵第二条边长为2a +2,∴第三条边长为30-a -(2a +2)=28-3a .(2)当a =7时,三边长分别为7,16,7.由于7+7<16,所以不能构成三角形,即第一条边长不能为7米.由⎩⎨⎧-<-+->++aa a a a a 328)22(,328)22(可解得213313<<a .即a 的取值范围是213313<<a .(3)在(2)的条件下,注意到a 为整数,所以a 只能取5或6.当a =5时,三角形的三边长分别为5,12,13.由52+122=132知,恰好能构成直角三角形.当a =6时,三角形的三边长分别为6,14,10.由62+102≠142知,此时不能构成直角三角形.综上所述,能围成满足条件的小圈,它们的三边长分别为5米,12米,13米.24.(1)∵抛物线y =x 2-2x +m -1与x 轴只有一个交点,∴△=(-2)2-4×1×(m -1)=0,解得m =2.(2)由(1)知抛物线的解析式为y =x 2-2x +1,易得顶点B (1,0),当x =0时,y =1,得A (0,1).由1=x 2-2x +1解得x =0(舍),或x =2,所以C (2,1).过C 作x 轴的垂线,垂足为D ,则CD =1,BD =x D -x B =1.∴在Rt △CDB 中,∠CBD =45︒,BC =2.同理,在Rt △AOB 中,AO =OB =1,于是∠ABO =45︒,AB =2.∴∠ABC =180︒-∠CBD -∠ABO =90︒,AB =BC ,因此△ABC 是等腰直角三角形.(3)由题知,抛物线C ′的解析式为y =x 2-2x -3,当x =0时,y =-3;当y =0时,x =-1,或x =3,∴E (-1,0),F (0,-3),即OE =1,OF =3.①若以E 点为直角顶点,设此时满足条件的点为P 1(x 1,y 1),作P 1M ⊥x 轴于M .∵∠P 1EM +∠OEF =∠EFO +∠OEF =90︒,∴∠P 1EM =∠EFO ,得Rt △EFO ∽Rt △P 1EM ,于是311==OF OE EM M P ,即EM =3P 1M .∵EM =x 1+1,P 1M =y 1,∴x 1+1=3y 1.(*)由于P 1(x 1,y 1)在抛物线C ′上,有3(x 12-2x 1-3)=x 1+1,整理得3x 12-7x 1-10=0,解得x 1=-1(舍),或3101=x .把3101=x 代人(*)中可解得3191=y .∴P 1(310,313).②若以F 点为直角顶点,设此时满足条件的点为P 2(x 2,y 2),作P 2N ⊥与y 轴于N .同①,易知Rt △EFO ∽Rt △FP 2N ,得312==OF OE N P FN ,即P 2N =3FN .∵P 2N =x 2,FN =3+y 2,∴x 2=3(3+y 2).(**)由于P 2(x 2,y 2)在抛物线C ′上,有x 2=3(3+x 22-2x 2-3),整理得3x 22-7x 2=0,解得x 2=0(舍),或372=x .把372=x 代人(**)中可解得9202-=y .∴P 2(37,920-).综上所述,满足条件的P 点的坐标为(310,313)或(37,920-).25.解法1设AB =AC =1,CD =x ,则0<x <1,BC =2,AD =1-x .在Rt △ABD 中,BD 2=AB 2+AD 2=1+(1-x )2=x 2-2x +2.由已知可得Rt △ABD ∽Rt △ECD ,∴BD CD AB CE =,即2212+-=x x x CE,从而222+-=x x x CE ,∴22222222222-+=+-=+-+-==x x x x x x x x x x CEBDy ,0<x <1,(1)若BD 是AC 的中线,则CD =AD =x =21,得25==CE BD y .(2)若BD 是∠ABC 的角平分线,则AB BCAD CD =,得121=-x x ,解得22-=x ,∴2222222=--+-==CE BD y .(3)若3422=-+==x x CE BD y ,则有3x 2-10x +6=0,解得375-=x ∈(0,1),∴6171-=-=x x DC AD ,表明随着点D 从A 向C 移动时,BD 逐渐增大,而CE 逐渐减小,的值则随着D 从A 向C 移动而逐渐增大.解法2设AB =AC =1,∠ABD =α,则BC =2,∠CBE =45︒-α.在Rt △ABD 中,有αcos 1cos =∠=ABD AB BD ;在Rt △BCE 中,有CE =BC ·sin ∠CBE =2sin (45︒-α).因此)452sin(212cos sin cos 1cos )45sin(212︒--=-=-︒=ααααααCEBD.下略……解法3(1)∵∠A =∠E =90︒,∠ADB =∠CDE ,∴△ADB ∽△EDC ,∴CEDEAB AD =.由于D 是中点,且AB =AC ,知AB =2AD ,于是CE =2DE .在Rt △ADB 中,BD =AD AD AD AD AB 542222=+=+.11在Rt △CDE 中,由CE 2+DE 2=CD 2,有CE 2+41CE 2=CD 2,于是CD CE 52=.而AD =CD ,所以25=CE BD .(2)如图,延长CE 、BA 相交于点F .∵BE 是∠ABC 的平分线,且BE ⊥CF ,∴△CBE ≌△FBE ,得CE =EF ,于是CF =2CE .又∠ABD +∠ADB =∠CDE +∠FCA =90︒,且∠ADB =∠CDE ,∴∠ABD =∠FCA ,进而有△ABD ≌△ACF ,得BD =2CE ,2=CEBD .(3)CE BD 的值的取值范围为CE BD ≥1.下略……。
2011年南山区高一下学期期末统一考试数学试题含答案

高一数学试题 第1页(共6页)2011年南山区高一下学期期末统一考试数 学2010.07.04本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.第Ⅰ卷(选择题共50分)注意事项:1、答卷前,考生首先检查答题卡是否整洁无缺损.之后务必用黑色签字笔在答题卡指定位置填写自己的学校、班级、姓名及座位号,在右上角的信息栏填写自己的考号,并用2B 铅笔填涂相应的信息点.2、选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.不按要求填涂的,答案无效.3、非选择题必须用黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排.如需改动,先划掉原来的答案,然后再写上新的答案.不准使用铅笔和涂改液.不按以上要求作答的答案无效.4、考生必须保持答题卡的整洁,不折叠,不破损.考试结束后,将答题卡交回.5、考试可以使用计器.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的编号用铅笔涂在..............答题卡上..... 1、已知角α的终边上一点P(-3,4),则cos α的值为A 、45 B 、35 C 、45- D 、35- 2、在四边形ABCD 中,若AB (61)= ,,BC (x y)= ,,CD (23)=--,,且BC//DA,则x+2y 的值为A 、0B 、2C 、0.5D 、-23、已知3tan()5α+β=,1tan()44πβ-=,那么tan()4πα+为 A 、1318 B 、1323 C 、318 D 、7234、若向量00a (cos23cos67)= ,,00b (cos53cos37)= , ,则a b ⋅=高一数学试题 第2页(共6页)A 、32-B 、12C 、32D 、12-5、将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是6、为了得到函数πy =sin(2x )3-的图象,只需将函数y=sin2x 的图象单A 、向右平移π3 B 、向左平移π3C 、向右平移π6D 、向左平移π67、右边框图的功能是计算220111 (222)+++ 的值,那么在①②两处应填入A 、n=0或和n ≤10B 、n=1或和n ≤10C 、n=0或和n<10D 、n=1或和n<108、若f(tanx)=sin2x ,则f(-1)的值是A 、1B 、-1C 、0.5D 、09、一块各面均涂有油漆的正方体被锯成1000个同样大小的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是A 、12125 B 、325 C 、110D 、11210、定义在R 上的偶函数f(x),满足f(x+2)= f(x),且f(x)在[-3,-2]上是减函数,又α,β是锐角三角形的两个内角,则A 、f(sin α)<f(cos β)B 、f(cos α)<f(cos β)C 、f(sin α)>f(cos β)D 、f(sin α)<f(sin β) 一、选择题答案表:题 号 1 2 3 4 5 6 7 8 9 10 答 案a=b b=a A Bc=b b=aa=c C b=a a=b D a=c c=b b=a 否是 输出s结束开始第7题图 ②S=0, ①n=n=1 n1s s 2=+高一数学试题 第3页(共6页)第Ⅱ卷(非选择题共100分)二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题.......卷上... 11、已知一扇形所在圆的半径为10cm ,扇形的周长是45cm ,那么这个扇形的圆心角为 ____ 弧度.12、如图是某单位200名职工的 年龄分布情况,现要从中抽取40 名职工样本,用系统抽样法,将全 体职工随机按1~200编号,并按编号顺序0平均分为40组(1~5号, 6~10号,…,196~200号),若第五组抽出的号码为22,则第8组抽出的号码是_____,若用分层抽样方法, 则50岁以上年龄段在40名名样本中应抽取____人.13、不等式13tan x 0+≥的解集是 ________ . 14、下列结论中正确的是 ___________ .(写出所有正确结论的序号)①若a b 0⋅= ,则a 0= 或b 0=;②若|a b ||a ||b |⋅=⋅,则a //b ;③若a b 0⋅= ,则|a b ||a b |+=- ;④在△ABC 中,点M 满足MA MB MC 0++=,若存在实数λ使得 AB AC AM +=λ⋅成立,则λ=3.三、解答题:本大题共6小题,共80分,解答应写出文字说明或演算步骤.15、(本小题满分12分)设集合A={1,2,3,4,5},集合B={1,2,3},在集合A 中任取一个数为x ,在集合B 中任取一个数为y ,组成点(x ,y). (Ⅰ)写出所有的基本事件;(Ⅱ)求事件“x+y 为偶数”的概率; (Ⅲ) 求事件“xy 为奇数”的概率;50%20% 30%40岁以下50岁以上40~50岁第12题图高一数学试题 第4页(共6页)16、(本小题满分12分)已知A(5,0),B(0,5),C(cos α,sin α),α∈(0,π)点O 是坐标原点.(Ⅰ)若AC BC ⊥,求sin2α;(Ⅱ)若|OA+OC|31=,求OB 和OC 的夹角.17、(本小题满分14分)某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图. 观察图形的信息,回答下列问题:(Ⅰ)求分数在[70,80)内的频率;并补全频率分布直方图; (Ⅱ)求在[60,70),[70,80)分数段上各有多少人?(Ⅲ)用分层抽样方法在分数段[60,80)的学生中抽取一个容量为6的样本.将该样本看成一个总体,从中任取2人,求至多有一人在分数段[60,80)的概率.第17题图分数频率/组距10040 50 60 7080 0.015 0.010 0.0050.020 0.025 0.030 0.035 90高一数学试题 第5页(共6页)18、(本小题满分14分)已知点P(0,5)及圆C :x 2+y 2+4x -12y+24=0.(Ⅰ)若直线l 过点P 且被圆C 截得的线段长为43,求直线l 的方程; (Ⅱ)过点P 作圆C 的弦,求该弦的中点的轨迹方程.19、(本小题满分14分)如图是函数 f(x)=Asin(ωx+φ) (A>0,ω>0,||2πφ<)在一个周期的图象. (Ⅰ)求函数f(x)的表达式; (Ⅱ)求函数f(x)的单调区间;(Ⅲ)设0<α<π,若方程f(x)=m 有两个不同的实数根,求实数m 的取值范围和这两个根的和.20、(本小题满分14分)若向量33a (cos x sin x)22= ,,x x b (cos sin )22=- ,,且x []44ππ∈-,. (Ⅰ)求|a b |+ ;(Ⅱ)若f (x)a b =⋅,求函数f(x)关于x 的解析式和值域;(Ⅲ)设t=2f(x)+a 的值域为D ,且函数21g(t)=t t 22+-在D 上的最小值为2,求实数a 的值.(命题人:华侨城中学 王宏 审题人:区教研室 罗诚)xyO-22 11π12第19题图1高一数学试题 第6页(共6页)高一数学参考答案及评分标准2010.7.4 一、选择题:(10×5'=50') 题 号 1 2 3 4 5 6 7 8 9 10 答 案DADCBCCBAC二、填空题:(4×5'=20')11、_2. 5_; 12、_37__ ,__8_(前空2分,后空3分); 13、ππ{x |+k πx <+k πk Z}62-≤∈,; 14、②③④. 三、解答题:(80')15、(本小题满分12分)解:解:设(x ,y)表示一个基本事件,则所有基本事件包括:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3), (4,1),(4,2),(4,3),(5,1),(5,2),(5,3),共15个基本事件.……3分 (Ⅰ) 事件“x+y 为偶数” 记为A ,事件A 包括: (1,1),(1,3),(2,2), (3,1),(3,3),(4,2),(5,1),(5,3),共8个基本事件, ……5分 且是等可能的,故所求的事件A 概率为8P(A)15=; ……7分 (Ⅱ)设事件“xy 为奇数”记为B ,则事件B 包括: (1,1),(1,3),(3,1),(3,3),(5,1),(5,3)共6个基本事件, ……9分且是等可能的,故所求的事件A 概率为62155= .……11分 答:事件“x+y 为偶数”的概率为815;事件“xy 为奇数”的概率为25……12分16、(本小题满分12分)解:(Ⅰ)由A(5,0),B(0,5),C(cosα,sinα),得A C (c o s 5s i n )=α-α,, BC (cos sin 5)=αα-,, .……1分 若AC BC ⊥ ,则AC BC=0⋅,即cosα(cosα-5)+sinα(sinα-5)=0,.……3分 ∴5(si nα+cosα)=sin 2α+cos 2α=1, ……4分高一数学试题 第7页(共6页)∴25(1+sin2α)=1,∴224sin 225α=-. .……5分 (Ⅱ)OA =(50) ,,OB =(05) ,,OC (cos sin )=αα ,,∴OA+OC =(5+cos αsin α),, …… 6分22|OA+OC|(5+cos )+sin =31=αα, …… 7分∵α∈(0,π),∴1cos =2α,3sin =2α, …… 9分 即 13OC ()22= ,,|OC|=1 ,又|OB|=5 ,1353OB OC (05)()=222⋅=⋅ ,,, …… 10分设OB 和OC 的夹角为θ,则53OB OC 32cos 152|OB ||OC |⋅θ===⨯⋅,…… 11分故OB 和OC的夹角为300. …… 12分17、(本小题满分14分)解:(Ⅰ)分数在[70,80)内的频率为:高一数学试题 第8页(共6页)1-(0.010+0.015+0.015+0.025+0.005)×10=0.3,故0.3=0.0310. ……2分 如图所示: ……4分 如图所示:(求频率2分,作图2分) (Ⅱ)由题意,[60,70)分数段的人数为:0.15×60=9人; …… 6分 [70,80)分数段的人数为:0.3×60=18人; …… 8分 (Ⅲ)∵在[60,80)的学生中抽取一个容量为6的样本,∴[60,70)分数段抽取2人,分别记为m ,n ;[70,80)分数段抽取4人,分别记为a ,b ,c ,d ; …… 10分 设从样本中任取2人,则此基本事件空间包含的基本事件有:(m ,n),(m ,a),(m ,b),(m ,c),(m ,d),(n ,a),(n ,b),(n ,c), (n ,d),(a ,b),(a ,c),(a ,d),(b ,c),(b ,d),(c ,d)共15种基本事件, ……11分 若至多有1人在分数段[70,80)为事件A ,则事件A 包含的基本事件有: (m ,n),(m ,a),(m ,b),(m ,c),(m ,d), (n ,a),(n ,b),(n ,c), (n ,d),共9种基本事件, …… 12分且是等可能的,∴93P(A)155==. …… 13分 答:至多有1人在分数段[70,80)的概率为35. …… 14分18、(本小题满分14分)解:(Ⅰ)圆的方程可化为(x+2)2+(y -6)2=16,…… 1分高一数学试题 第9页(共6页)xO yC A BD P圆心C(-2,6)],半径r=4,如图所示,AB 43=,D 是AB 的中点, …… 2分 CD ⊥AB ,AD =23,AC=4,在直角△ACD 中,可得CD=2. ……3分 设所求直线的斜率为k ,则直线的方程为y -5=kx , 即kx -y+5=0. …… 4分 由点C 到直线AB 的距离公式得:22|2k 6+5|=2k +(1)---, ……5分解之得3k 4=. ……6分当3k 4=时,直线l 的方程为3x -4y+20=0; ……7分又直线l 的斜率不存在时,也满足题意,此时方程为x=0. ……8分 所以所求直线方程为3x -4y+20=0或x=0. ……9分 (Ⅱ)设过P 点的圆C 的弦的中点为D(x ,y),则CD ⊥PD ,即CD PD =0⋅, ……11分则(x+2,y -6)· (x ,y -5)=0,即(x+2)x+(y -6)(y -5)=0, ……12分 经化简得所求轨迹方程为x 2+y 2+2x -11y+30=0. ……14分 19、(本小题满分14分)解:(Ⅰ)显然A=2, ……1分 又图象过(0,1)点,∴f(0)=1,∴ 1sin 2φ=,∵π||<2φ,∴π=6φ; ……2分 由图象结合“五点法”可知,11(0)12π,对应函数y=sinx 图象的点(2π,0), ∴11ππω+=2π126⨯,ω=2. ……4分 所以所求的函数的解析式为:πf (x)=2sin(2x +)6. ……5分高一数学试题 第10页(共6页)(Ⅱ)当πππ2k π2x +2k π+ (k z)262-≤≤∈,时,函数πf (x)=2sin(2x +)6单调递增,即2ππ2k π2x 2k π+ (k z)33-≤≤∈,. ……7分 解得ππk πx k π(k z)36-≤≤+∈. ……8分故函数πf (x)=2sin(2x +)6单调递增区间为ππ[k πk π](k z)36-+∈,.……9分(Ⅲ)如图所示,在同一坐标系中画出πy =2sin(2x +)6和y=m(m ∈R) 的图象,由图可知,当-2<m<1或1<m<2时,直线y=m 与曲线有两个不同的交点,即原方程有两个不同的实数根. ……10分 ∴m 的取值范围为:-2<m<1或1<m<2; ……12分 当-2<m<1时,两根和为3π;当1<m<2时,两根和为43π. ……14分 20、(本小题满分14分)解:3x 3xa +b =(cos x +cos sin x sin )2222- ,, ……1分223x 3x |a +b |(cos x +cos )(sin x sin )2222=+-高一数学试题 第11页(共6页) 3x 3x =2+2(cos x cos sin x sin )2222⋅-⋅ ……2分 2=2(1+cos2x)=22cos x =2cosx ⨯(由x 44ππ∈-[,]知cosx>0). ……3分(Ⅱ) 3x 3x f(x)=a b =cos x cos sin x sin =cos2x 2222⋅⋅-⋅ . ……4分 由题意,2x 22ππ∈-[,],从而[]1,02cos ∈x ,即f(x)的值域为[0,1]. ……6分 (Ⅲ)由(Ⅱ)得D=[a ,a+2] ……7分 可以求出22115g(t)=t +t 2=(t +1)222--可知其对称轴为t=-1. ……8分 下面分情况讨论:①当a≤-1≤a+2时,即-3≤a≤-1时,min 5g(t)=g(1)=2--, 不成立; ……9分 ②当a+2<-1时,即a<-3时,2min 1g(t)=g(a +2)=a +3a +22. ……10分 由21a +3a +2=22,得a=-6 (a=0舍去). ……11分 ③ 当a>-1时,2min 1g(t)=g(a)=a +a 2=22-, ……12分 解得a=2 (a=-4舍去), ……13分 综上知,a=-6或a=2. ……14分。
绵阳南山中学2011年秋季高2013级期末模拟考试

绵阳南山中学2011年秋季高2013级期末模拟考试数学试题(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,考试时间:120分钟 试卷满分:150分.第Ⅰ卷(选择题 共60分)一.选择题(每题5分,共60分)1、 已知数列的通项公式为1)1(+-=n na nn ,则=3a ( ).A 43- .B 43 .C 32- .D 322、抛物线22x y -=的准线方程是( )A .21=x B .81=x C .21=y D .81=y3、对于实数a 、b 、c ,下列命题中正确的是( )A .24>⇒>+a b a 且2>bB .a b b a 11>⇒>C .b aa bb a <⇒<<0 D .22bc ac b a >⇒>4、设集合}21|{<-=x x M ,{}0)3(|>-=x x x N ,那么“M a ∈”是“N a ∈”的() A .必要不充分条件 B .充分不必要条件C .充分必要条件D .既不充分也不必要条件5、在等比数列{}n a 中,1a 和10a 是方程22510x x ++=的两个根,则47a a ⋅=( ).A 52- .B 22 .C 12- .D 126、已知三角形ABC 的周长为20,且顶点B(0,-4),C(0-4),顶点A 的轨迹方程为( ).A .)0(1203622≠=+x y x .B )0(1362022≠=+x y x.C )0(120622≠=+x y x .D )0(162022≠=+x y x7、不等式0213≤--x x 的解集是( )2011年12月A .⎭⎬⎫⎩⎨⎧≤≤231|x x B .⎭⎬⎫⎩⎨⎧<≤231|x x C .⎭⎬⎫⎩⎨⎧>≤231|x x x 或 D .⎭⎬⎫⎩⎨⎧>31|x x 8、在△AB C 中,角A 、B 、C 的对边分别为a 、b 、c ,若(a 2+c 2-b 2)·tan B =3ac ,则 角B 的值为( ).A .π6 .B .π3 .C π6或5π6 .D .π3或2π39、已知正方体ABCD A 1B 1C 1D 1,E ,F 分别是正方形A 1B 1C 1D 1和ADD 1A 1的中心,则EF 和CD 所成的角是( )A .60°B .45°C .30°D .90° 10、设变量y x ,满足⎪⎩⎪⎨⎧≤+≥≥12340y x x y x ,则132+++x y x 的取值范围是( ) A. []5,1 B. []6,2 C. []10,3 D. []11,311、两次购买同一物品,可以用两种不同的策略,第一种是不考虑物品价格的升降,每次购买这种物品的数量一定;第二种是不考虑物品价格的升降,每次购买这种物品所花的钱数一定,则购买方式比较经济是( )A .第一种B .第二种C .两种一样D .不能确定12、已知F 1、F 2是椭圆的两个焦点,满足MF 1→·MF 2→=0的点M 总在椭圆内部,则椭圆离心率的取值范围是( )A .(0,1) B.⎝⎛⎦⎤0,12 C.⎝⎛⎭⎫0,22 D.⎣⎡⎭⎫22,1 二.填空题(本大题共4个小题,每题5分,共20分)13、在等差数列{}n a 中,13a =,415a =,则其前n 项和n S = ;14、 关于x 的不等式210x ax -+>恒成立,则实数a 的取值范围是 ;15、已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A 、B 两点,|AB |= 12,P 为C 的准线上一点,则△ABP 的面积为 ;16、以下四个关于圆锥曲线的命题中: ①双曲线92522y x -=1与椭圆352x +y 2=1有相同的焦点; ②已知直线l 过抛物线22x y =的焦点,且与抛物线交于A 、B 两点,则AB 的最小值为2; ③双曲线12222=-by a x 的左焦点为1F ,顶点为1A 、2A ,P 是双曲线上任意一点,则分别以线段1PF 、21A A 为直径的两圆的位置关系为内切或外切;④椭圆2212516x y +=的左右焦点分别为12,F F ,弦AB 过1F ,若2ABF ∆的内切圆周长为π,,A B 两点的坐标分别为1122(,),(,)x y x y ,则12y y -值为53; 其中真命题的序号为___________(写出所有真命题的序号).三.解答题(本大题共6个小题,期中17题10分,其余每题12分,共70分)17、若A={}023|2≤+-x x x ,{}0)13)(1(4|2≤+-+-=a a ax x x B ,命题A x p ∈:,命题B x q ∈:。
【VIP专享】2011年绵阳南山中学实验学校自主招生各科考试模拟试题含答案

C. how much it costD. how much it costs( ) 9. —Do you mind if I sit here?—_____. It’s for Mr. Lee.A. Not at allB. Never mindC. Better notD. Of course not( ) 10. ______Oscar night, the shining stars in beautiful clothes walk on red carpets and drink champagne to celebrate their success.A. AtB. InC. OnD. For( ) 11. — Mary, you’re going to buy an apartment here, aren’t you?—Yes, but I can’t_______an expensive one.A. spendB. costC. payD. afford( ) 12. They are your skirts. Please __________.A. put it awayB. put out itC. put them awayD. put them out( ) 13.—How long have you _______ the car?— For about two weeks.A. hadB. boughtC. borrowedD. lent( ) 14. Dashan has known a lot of Chinese since he_____ to China ten years ago.A. has comeB. comeC. cameD. had come( ) 15. — What a clean and bright school, isn’t it?— Yes, It’s always clean and bright because it ________every day.A. cleanB. cleanedC. is cleanedD. was cleaned( ) 16. At least 500 million people are using QQ ________ by Ma Huateng to chat on line.A. createdB. createC. creatingD. to create( ) 17. —Do you know__________?—I’m not sure. Maybe an artist.A. what is the man with long hairB. who the man with long hair isC. what the man with long hair isD. who is the man with long hair( ) 18. Everyone ________go through the security check(安检)when entering thedrink champagne and celebrate their success!( ) 36.The meaning for the underlined word “animated” is________.A. 纪事的B. 动漫的C. 爱情的D. 暴力的( ) 37.The first Oscar was in______________.A. 1900B. 2004C. 1939D. 1929( ) 38. How often does Oscar take place?A. Once every four yearsB. Once a yearC. Twice a yearD. Once every two years( ) 39. Where was the 76th Oscar held?A. We are not toldB. In New York, USAC. In Los AngelesD. In the capital of the USA( ) 40. Which of the following statements is Not True?A. The golden statues are not very big.B. The name “Oscar” came from a librarian’s uncle named Oscar.C. People can know who has won the Oscar before the night.D. The Oscar statues are given to the persons who achieve great success inmovie making.(B)You leave the palm trees(棕榈树)in the Union Square—the heart of San Francisco—and from the shop signs and the faces around you, you will notice that in the city, live people from many nations—Australians ,Italians, Chinese and others—giving each part a special character. More Chinese live in San Francisco’s Chinatown than in any other part of the world outside China. Here, with Chinese restaurants, Chinese postboxes, and even odd(奇异的)telephone-boxes that look like pagoda(塔),it is easy to feel you are in China itself.( ) 41. This passage is most probably taken from ________.A. a Chinese textbook about the United StatesB. a novel published in San FranciscoC. a traveller’s guideD. a letter to parents( ) 42. Union Square _________.A. lies in San Francisco’s ChinatownB. has many plat trees around itC .is a shopping centre of the cityD. has some telephone-boxes which looks like pagodas( ) 43. The main idea of this paragraph is that______________.A. there are many Chinese living in ChinatownB. people living in San Francisco like ChinatownC. the area around Union Square is the centre of San FranciscoD. San Francisco is a city made up of different people with various cultures ( ) 44. The Chinese in San Francisco_______.A. are still living in Chinese wayB. do everything according to the Chinese tradition(传统)C. feel they are in China itselfD. have built Chinatown into an area with a Chinese character( ) 45. From the passage we can see that _________.A. the Chinese culture is the greatest in the worldB. people living San Francisco come from all parts of the worldC. the Chinese have turned San Francisco into a ChinatownD. in San Francisco there are more Chinese than Australians, Italians and so on(C)Why are Arabic figures(数字) used everywhere in the world? In the past, other counting figures once existed in many countries, but they all died away.The Roman figures, for example, were popular in Europe before the 13th century. However, they are hardly in use now, except on some clocks and on other rare occasions. Look at the following and you will know why it is so.The Romans used seven letters, each representing a different number, I for 1,V for 5,X for 10 ,L for 50,C for 100,D for 500,and M for 1,000.To express a small number, the Romans would use repetitions or additions, or subtractions. For instance, II means 2, XXX means 30(repetition); VII means 7(addition) while IX expresses 4(subtraction).Western Plains became a Dust Bowl. Farmers had a very hard time until they started to use modern farming methods.Now farmers plant a different crop every year. Some years they give part of their land a rest. The land stays healthy and rich. Modern farmers form rows in curving(弯曲) lines and plant trees to stop the wind. Modern crops are much larger and more dependable.Dry land farming is both a science and an art. From the air, the farms look like pieces of modern art.( ) 51.Why did farmers lose so many crops? Because _______.(1). drought turned land to dust(2). winds blew the good land(3). a dry period lasted for a long time sometimes(4).farmers used different methodsA.(1)(2)and(3)B.(3)and(4)C.(2)and(4)D. All of the above( )52.Which of the following is TRUE according to the passage?A. The fields were in long straight rows so there was no space for farmers to planttrees.B. The land became poor because farmers used too much fertilizer (化肥).C. The situation got worse because farmers didn’t understand the modern methods.D. The planting of the same crops and too much use made the land become poor. ( ) 53.What happened on the Western Plains in the 1930’s?A. Farmers lived a hard life until 1930.B. Farmers began to use modern farming methods in 1930.C. The drought made the farmland become a Dust Bowl.D. The land became healthier and richer.( ) 54.Which of the following is NOT TRUE according to the passage?A. Modern farmers give part of their land a rest so as to find places to plant trees.B. Modern farmers give land a rest from time to time and grow different crops everyyear, so the land becomes healthy and rich.C. Trees are planted so that they protect the land from the wind.第一节:单项填空(每题1分,满分20分)1-5BBBAC 6-10ABDDC 11-15DCACC 16-20ACAAD第二节:完形填空(共15小题,每小题2分,满分30分)21-25 DCABD 26-30 ACDBD31-35 DBBDC第二部分:阅读理解(共20小题,每小题2分,满分40分)36-40 BDBCC 41-45 CBDDB 46-50 ABDBD 51-55 ADCAB第二节:补全对话(共5个小题,每小题2分,满分10分)56-60 DBAEC第Ⅱ卷(非选择题,共50分)第一节:任务型阅读(共5小题,每小题2分,满分10分)61. Good education 62. programmes 63.examinations/exams64. community service 65. rich/colourful第二节.综合填空。
绵阳南山中学(实验学校)自主招生考试数学试题及答案

2C . ( -8, 4)或( 8, - 4) D. ( -2, 1)或( 2, -1) 8. 如图,在 Rt △ ABC 中,∠ C=90°, AC=6 , BC=8 ,⊙ O 为△ ABC 的内切圆,点 D是斜边 AB 的中点,则 tan ∠ ODA 的值为( )C 保密★启用前绵阳南山中学 ( 实验学校 )2015 年自主招生考试试题3 3 A.B. O23BA数 学本套试卷分试题卷和答题卷两部份 ,试题卷共 6 页,答题卷共 6 页,满分 150 分,考试时间 120 分钟 .注意事项 :C. 3D.29. 若关于 x 的一元二次方程 kx 22 x A. k1B.k 1 且 k 0 D1 0 有两个不相等的实数根,则k 的取值范围是 ( )C. k1D.k 1 且 k 01. 答卷前 ,考生务必将自己的姓名、考试号用 0.5 毫米的黑色墨水签字笔或黑色墨水钢笔填写在答题卷与机读卡对应位置上 ,并认真核对姓名与考号 ;10. 如图,△ ABC 的周长为 26,点 D , E 都在边 BC 上,∠ ABC 的平分线垂直于 AE ,垂足为 Q ,∠ACB 的平分线垂直于AD ,垂足为 P ,若 BC=10,则 PQ 的长为( )。
2. 选择题每小题选出答案后,用 2B 铅笔将机读卡上对应题目的答案标号涂黑,如需改动 ,用橡皮擦干净后 ,再选涂其它答案标号 ,答在试题卷上无效 ;A. 32 B. 5A 2 3. 非选择题 (主观题 )用 0.5 毫米的黑色墨水签字笔或黑色墨水钢笔直接答在答题卷上每题对应的位置上 ,答在试题卷上无效 .作图一律用 2B 铅笔或 0.5 毫米黑色签字笔 ;4. 考试结束后 ,请将本试题卷、答题卷与机读卡一并上交.C.3D.4PQBD E C(第 10 题)第 I 卷( 选择题, 共 36 分)11.如图,在平面直角坐标系中,点A 的坐标为( 0,3),△ OAB 沿 x 轴向右平移后得到△O ′A ′B一.选择题 (本大题共 12 个小题 ,每小题 3 分,共 36 分) 1.- 4 的倒数是( ) A . 4B .- 4C . 14D .- 14点 A 的对应点在直线 y 9A.43x 上一点,则点 B 与其对应点 B ′间的距离为()4B. 3C. 4D. 52. 下列运算正确的是() A . a 3a 32a3B . a3a3a6C . ( 2 x ) 36x 3D . a 6a2a 412.如图 12,抛物线 y ax bx+c(a 0) 过点( 1,0)和点( 0,-2),且顶点在第三象限, 设 P= a b c ,则 P 的取值范围是() .3.用科学记数法表示 0.000031 ,结果是( )A . 3.1 ×10-4B . 3.1 ×10-5C . 0.31 ×10-5D .31×10-6A . - 4< P <0B . - 4< P < -2 a 2C . - 2< P < 0D . - 1< P <04. 要使式子有意义,则 a 的取值范围为 ( )a二、填空题(每小题4 分,共 24 分)A. a2 B.a 2 C.a 2且a 0 D. a 213.分解因式: 4ax12ax 9 a =.图 1216 题图 5. 如图是由 5 个大小相同的正方体摆成的立方体图形 ,它的左视图是()14:已知 22m -6m-1=0 求 2m 1 -6m+2 =.Cm2x m 15. 已知关于x 的方程3 的解是正数,则 m 的取值范围为 :.x 1AOBAB C D16. 在平面直角坐标系中,点O 是原点,点 B ( 0, 3),17 题图6. 如图,已知直线AB ∥ CD , C 125°,点 A 在第一象限且 AB ⊥BO ,点 E 是线段 AO 的中点,点 M 在线段 AB 上.若点 B 和点 E 关于直线A 45°,那么 E 的大小为( ) OM 对称,且则点 M 的坐标是 ( ,) .A. 70°B. 80° 17.如图, AB 是半圆 O 的直径,且 AB 8 ,点 C 为半圆上的一点.将此C.90°D. 100° 7. 在平面直角坐标系中,已知点 E( -4, 2), F(- 2, -2),以原点 O 为位似中心,相似比为1 ,把△ EFO 缩小,则点 E 的对应点 E ′的坐标是()2半圆沿 BC 所在的直线折叠,若圆弧 BC 恰好过圆心 O ,则图中阴影部分的面积是(结果保留).18.射线 QN 与等边△ ABC 的两边 AB , BC 分别交于点 M ,N ,且 AC ∥ QN ,18 题A . ( -2, 1)B. ( -8, 4)AM=MB=2cm ,QM=4cm 。
四川省绵阳市绵阳中学2011年自主招生数学试题(含答案)

2011年绵中自主招生数学检测试题一、 选择题:1.335-的值在( )A .1和2之间B .2和3之间C .3和4之间D .4和5之间 2.81的平方根与()23-的差等于( )A .6B .6或-12C .-6或12D .0或-63.若24x =,3y =,0<xy ,则x y -的值为( )A .5或-5B .1或-1C .5或1D .-5或-14.在等腰ABC ∆中,AB AC =,中线BD 将这个三角形的周长分成15和18两部分,则这个三角形底边的长为( )A .9B .13C .9或13D .10或12 5.已知函数ab y x=,当0x >时,y 随x 增大而减小,则关于x 的方程230ax x b +-=的根的情况是( )A .有两个正根B .有一个正根一个负根C .有两个负根D .没有实根 6.如图,已知41ABC ∠=,一束光线从BC 上的D 点发出,经BA 反射后,反射光线EF 恰好与BC 平行,则EDC ∠=( ) A .82 B .86 C .88D .907.如图,Rt ABC ∆中,90=∠B ,16AB =,12BC =,分别以A 、C 为圆心,2AC为半径作圆,则阴影部分的周长为( ) A .48B .582π+ C .85π+D .9625π-jFDEACB8.在某些情况下,我们可用图像法解二元一次方程组,那么下图中所解的二元一次方程组是( ) A .203210x y x y +-=⎧⎨--=⎩ B .20210x y x y +-=⎧⎨--=⎩C .2103210x y x y --=⎧⎨--=⎩D .2103250x y x y --=⎧⎨+-=⎩9.已知圆锥的底面半径为cm 5,侧面积为260cm π,设圆锥的母线与高的夹角为θ,则sin θ的值为( ) A .313 B .513 C .512 D .121310.如图,在圆O 中有折线ABCO ,12BC =,7CO =,60B C ∠=∠=,则AB 的长为( )A .17B .18C .19D .2011.在两行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别刻有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退.如图,现从左上角一格翻动到右下角一格,则骰子最终朝上的点数不可能是( )A .2B .3C .4D .512.现有2011个人排队,第一个人站在点1(1,1)P ,第二个人站在点2(2,1)P ……,第k 个人站在点(,)k k kP x y ,当2k ≥时,111215551255k k k k k k x x k k y y --⎧⎛--⎫⎡⎤⎡⎤=+--⎪ ⎪⎢⎥⎢⎥⎪⎣⎦⎣⎦⎝⎭⎨--⎡⎤⎡⎤⎪=+-⎢⎥⎢⎥⎪⎣⎦⎣⎦⎩,[]a 表示非负实数a 的整数部分,例如[]0.60=,[]1.91=,照此站下去,第2011个人站的点的坐标是( )A .(5,2011)B .(2011,1)C .(2,402)D .(1,403)P(1,1)21-1-1321oxyC OBAθ二、填空题 1.已知方程组5531ax y x by +=-⎧⎨-=-⎩,张三看错了a ,得到的解是27x y =⎧⎨=⎩;而李四看错了b ,得到的解是51x y =-⎧⎨=⎩,那么原方程组的正确的解是_____________________2.关于x 的不等式(2)320a b x a b --+>的解集是43x <,则不等式0ax b +>的解集是__________________3.如图,某人工湖两侧各有一个凉亭A 、B ,现测得70AC m =,30BC m =,120ABC ∠=,则AB =________________4.有一列数1a 、2a 、3a 、……、n a ,从第二个数开始,每一个数等于1与它前面那个数的倒数的差,若1a =2,则2014a =________________ 5.一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,这个几何体最多可以由________________个这样的正方体组成.6.对于0x >,规定()1x f x x =+,例如22(2)213f ==+,1112()12312f ==+,那么1111()()()()(1)(2)(2011)2011201032f f f f f f f ++⋯+++++⋯+=_______________左视图正视图CBA三、解答题1.先化简,再求值:0445222222231102)(23⎪⎪⎭⎫ ⎝⎛++⨯-+--÷+++-y x y x y x xyx y xy x y x y x xy . 其中=4sin 452cos60x -,30y =.2.如图,四边形ABCD 是平行四边形,'A BD ∆与ABD ∆关于BD 所在的直线对称,'A B 与DC 相交于点E ,连接'AA .⑴ 请直接写出图中所有的等腰三角形(不另加字母); ⑵ 求证:'A E CE =.EA'DCBA3.如图,点C 是圆O 的直径AB 延长线上一点,点D 在圆O 上,且BC BD BO ==,E 是劣弧AD 上一点,BE 交AD 于F . ⑴ 求证:CD 是圆O 的切线;⑵ 若DEF ∆的面积为12,2cos 3BFD ∠=,求ABF ∆的面积.4.某县组织30辆汽车装运甲、乙、丙三种苹果到外地销售.要求同一辆汽车只能装同一种苹果,且30辆汽车都必须装满,这样每次总共装运150吨.根据下表提供的信息,解答以下问题:⑴ 设运甲、乙两种苹果的车辆数分别为x 、y ,求y 与x 之间的函数关系式;⑵ 若运每种苹果的车辆数都不少于6辆,那么车辆安排方案有几种?写出每种安排方案; ⑶ 若要使这次销售获利最大,应采用哪种方案?并求出利润的最大值.AFEDCB O5.如图,等腰Rt ABC ∆的直角边AB 、AC 分别与圆O 相切于点E 、D ,3AD =,5DC =,直线FG 与AC 、BC 分别交于点F 、G ,且∠CFG =60°.⑴ 求阴影部分的面积;⑵ 设点C 到直线FG 的距离为d ,当1≤d ≤4时,试判断直线FG 与圆O 的位置关系,并说明理由.6.已知函数1y x =,22y x mx n =++,1x 、2x 是方程12y y =的两个实根,点(,)P s t 在函数2y 的图像上.⑴ 若122,4x x ==,求,m n 的值;⑵ 在⑴的条件下,当0≤s ≤6时,求t 的取值范围;⑶ 当12x x 0<<<1,s 0<<1时,试确定t ,1x ,2x 三者之间的大小关系.7.如图,抛物线与坐标轴分别交于点(,0)A a ,(,0)B b ,(0,)C c ,其中9abc =,a 、b 、c 均为整数,且a <0,0b >,0c <,a b c <=,以AB 为直径作圆R ,过抛物线上一点P 作直线PD 切圆R 于D ,并与圆R 的切线AE 交于点E ,连接DR 并延长交圆R 于点Q ,连接AQ ,AD .⑴ 求抛物线所对应的函数关系式;⑵ 若四边形EARD的面积为PD⑶ 抛物线上是否存在点P ,使得四边形EARD 求出P 点的坐标;若不存在,说明理由.x参考答案一、选择题1 2 3 4 5 6 7 8 9 10 11 12 题号答B D AC 5 A C B C CD D 案。
南山中学招生考试题模拟考试
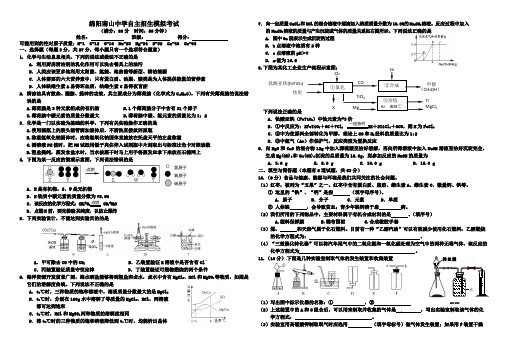
点燃TiCl4MgTiMgCl2 Cl2一定条件绵阳南山中学自主招生模拟考试(满分:80分时间:50分钟)姓名:班级:得分:可能用到的性对原子质量:H-1 C-12 O-16 Na-23 Mg-24 S-32 Ca-40 Cu-64一、选择题(每题3分,共27分,每小题只有一个选项符合题意)1. 化学与生活息息相关,下列的说法或做法不正确的是A.利用厨房清洁剂的乳化作用可以洗去餐具上的油污B.人类应该更多地利用太阳能、氢能、地热能等新型、清洁能源C.人体需要的六大营养素中,只有蛋白质、油脂、糖类是为人体提供能量的营养素D.人体缺维生素A易得坏血病,缺维生素C易得夜盲症2. 清凉油具有散热、醒脑、提神的功效,其主要成分为薄荷脑(化学式为C10H20O),下列有关薄荷脑的说法错误的是A.薄荷脑是3种元素组成的有机物B.1个薄荷脑分子中含有31个原子C.薄荷脑中碳元素的质量分数最大D.薄荷脑中碳、氢元素的质量比为1:23.化学是一门以实验为基础的科学,下列有关实验操作正确的是A.使用滴瓶上的胶头滴管滴加液体后,不清洗直接放回原瓶B.称量氢氧化钠固体时,应将氢氧化钠固体直接放在托盘天平的左盘称量C.测溶液PH值时,把PH试纸用镊子夹住伸入试剂瓶中片刻取出与标准比色卡对照读数D.粗盐提纯,蒸发食盐水时,当水被蒸干时马上用手将蒸发皿拿下来放在石棉网上4. 下图为某一反应的微观示意图,下列说法错误的是A.X是有机物,Z、W是无机物B.X物质中碳元素的质量分数为75.0%C.该反应的化学方程式:CH4+O2 CO2+H2OD.点燃X前,要先检验其纯度,以防止爆炸5.下列实验设计,不能达到实验目的的是A.甲可除去CO中的CO2 B.乙装置验证X溶液中是否含有Cl—C.丙装置验证质量守恒定律 D.丁装置验证可燃物燃烧的两个条件6. 海洋资源开发前景广阔,海水晒盐能够得到粗盐和卤水,卤水中含有MgCl2、KCl和MgSO4等物质,如图是它们的溶解度曲线。
四川省绵阳南山中学高2011级自主招生考试(DOC)

四川省绵阳南山中学高2011级自主招生考试理科综合试题说明:①本试题分物理、化学两部分,满分200分,其中物理120分,化学80分。
考试时间120分钟。
②考生解题时必须将答案写在答卷上,做在试卷上无效。
考试结束时将试卷和答卷一并交回。
物理部分第Ⅰ卷(共40分)一、选择题(每小题4分,共40分。
每小题只有一个答案符合题意,请你把选出的答案的字母代号,填在答题卷上的对应位置)1.下列数据中最接近事实的是( )A .一只鸡蛋的质量是50gB .人步行的速度是5m/sC .洗澡水的温度是70℃D .家用台灯正常工作时的电流是lA2.一颗人造地球卫星,正绕着地球做匀速圆周运动,如果在这时它受到的所有的外力突然同时消失,则这颗卫星将( )A .仍在原轨道继续做匀速圆周运动B .立即匀速落向地面C .沿直线匀速飞向太空D .停在原处3.水是人类生存不可缺少的物质,图中能正确描述水的各物理量之间关系的图象是( )4.在公园平静的湖水中,经常能看到从湖底产生的气泡向上升,则气泡在水中向上升的过程中,下列说法正确的是( )A.气泡所受的液体压强不变B.气泡所受的液体压强变小C.气泡所受的浮力变小D.气泡所受的浮力不变5.在图所示的电路中,电源电压不变,当开关S 1、S 2都闭合时,电压表V l 、V 2的示数之比为5︰3;当开关S 1闭合,S 2断开时,电压表V 1、V 2的示数之比为3︰2。
在后一种情况下,全部通电时间内,电阻R 1与R 2产生的热量之比为( )A .2︰1B .1︰3C .3︰2D .2︰36.如图所示,在水面上S 点有一发光物体,那么在S 点正下方的s ′位置的水下观察者看来,该物体的像应当位于( )A .S 点之上B .S 点之下C .S 点D .S 点右下方7.张华同学在“探究通过导体的电流与其两端电压的关系”时,将记录的实验数据通过整理作出了如右上图所示的图象,根据图象,下列说法错误的是A B C D( )A .当在导体乙的两端加上1V 的电压时,通过导体乙的电流为0.1AB .将甲、乙两导体并联后接到电压为3V 的电源上时,干路中的电流为0.9AC .通过导体甲的电流与其两端的电压成正比D .导体甲的电阻大于导体乙的电阻8.如图,一木箱放在水平地面上,当用一逐渐增大的水平向右的力F 拉木箱时,下列哪个图能正确反映摩擦力f 随拉力F 的变化关系( )9.如图所示不正确的是( )10.如图所示把凉牛奶放在热水中加热,经过一段较长时间,它们的温度随时间变化的图象如图所示,下列说法中正确的是( ) A .水和牛奶最后温度相同B .水的温度变化比牛奶大C .牛奶温度变化比水慢D .甲是牛奶温度变化图象第Ⅱ卷(共80分)二、填空题(每空2分,共28分)11.唐代诗人张继写的著名七绝诗《枫桥夜泊》中前两句是:“月落乌啼霜满天,江枫渔火对愁眠”。
2011年南山中学自主招生考试理综试题(定稿)1

机密★启用前绵阳南山中学(实验校区)2011年自主招生考试理科综合试题本试卷分试题卷和答题卷两部分。
试卷共8页,答题卷3页,满分200分。
考试时间120分钟。
可能用到的相对原子质量:H-1 C-12 N-14 O-16 Cl-35.5 Mg-24 Ca-40 Fe-56注意事项:1.答题前,考生务必将自己的姓名、考号用钢笔或黑色签字笔填写在机读卡和答题卷上,并核对相关信息是否一致。
2.选择题使用2B铅笔填涂在机读卡对应题目标号的位置上,非选择题用钢笔或黑色签字笔书写在答题卷的对应位置。
在草稿纸、试卷上答题无效。
3.考试结束后,将试题卷、机读卡和答题卷一并交回。
第Ⅰ卷(选择题,共75分)一.选择题(共21个小题,1-9小题为化学试题,每小题3分;10-21为物理试题,每小题4分。
每小题有且只有一个选项满足题意。
)1.生活中的下列做法利用了化学反应原理的是A.自制简易净水器净化自来水 B.门锁不易打开时灌入铅笔芯粉末C.用天然气做燃料煮饭 D.用活性炭除去冰箱中的异味2.阳刚同学按教材中的家庭小实验自制汽水,可是家里没有冰箱,为了使自制的汽水变得冰凉可口,他想到可以从集镇上购买一种商品来产生制冷效果,他应该购买的是A.硝酸铵 B.小苏打 C.生石灰 D.食盐3.瘦肉精是一类对人体健康危害极大的化学物质,政府已严禁在猪饲料中添加瘦肉精。
常见的瘦肉精化学式为C12H18OCl2N2,下列有关这种瘦肉精的说法中正确的是A.是一种无机化合物B.分子中碳、氢、氧三种元素的质量比为72:9:8C.相对分子量为277 gD.由C12H18O、Cl2、N2三种分子组成4.人们常在可燃建筑材料中添加阻燃剂以防止火灾。
Mg(OH)2是一种常用的阻燃剂,它在380℃时分解成水蒸气和耐高温的MgO,并吸收大量的热。
下列说法错误的是A.Mg(OH)2分解吸热能降低可燃物的着火点 B. Mg(OH)2分解吸热能降低可燃物的温度C.Mg(OH)2分解的产物能使可燃物与氧气隔绝 D. MgCO3比CaCO3易分解,也可做阻燃剂5.下列实验操作不符合...规范的是A.点燃可燃性气体之前检验气体的纯度B.蒸发滤液时用玻璃棒不断搅拌滤液C.通过口尝来确定实验中某种试剂的味道D.用酒精灯加热试管里的固体时先预热6.右图是甲、乙、丙三种物质的溶解度曲线。
四川省绵阳南山中学2011届高三九月月考——文科数学 doc

绵阳南山中学高2011级第五学期九月月考试题数 学(文史财经类)1.本试卷分选择题和非选择题两部分,共4页,满分为150分,考试用时120分钟.2.命题范围:绵阳一诊内容;命题老师:张家寿.使用时间:2010年9月25日下午3:00-5:00.3.注意事项:(1)答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和学号填写在答题卡和答卷密封线内相应的位置上,用2B 铅笔将自己的学号填涂在答题卡上.(2)选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上.(3)非选择题必须用蓝、黑色字迹的钢笔或签字笔在答卷纸上作答,答案必须写在答卷纸各题目指定区域内的相应位置上,超出指定区域的答案无效;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效. (4)考生必须保持答题卡的整洁和平整.4.参考公式:n 次独立重复试验中恰好发生k 次的概率 ()(1)k kn k n nP k C P P -=-. 第I 部分 选择题(共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|213}A x x =+>,2{|60}B x x x =+-≤,则A B = ( )A.[3,2)(1,2]-- B.(3,2](1,)--+∞C.(3,2][1,2)--D.(,3)(1,2]-∞-2.函数)1()1(2-+=x x y 在1=x 处的导数等于 ( ) A .1B .2C .3D .43.设()f x 是定义在R 上的奇函数,且当0x >时,)lg()(2x x x f -=,则(2)f -=( )A. 21lgB. 2lgC. 2lg 2D. 6lg 4.函数212()log (32)f x x x =--的值域为 ( )A. (,)-∞+∞B. [)1-+∞,C. (0,)+∞D. [)1,0-5.已知等比数列{}n a 的前三项依次为1,1,4a a a -++,则{}n a 的通项公式n a = ( ) A .34()2n⋅ B .24()3n⋅ C .134()2n -⋅ D. 124()3n -⋅6. 设3.02131)21(,3log ,2log ===c b a ,则 ( )A .a<b<cB .a<c<bC .b<c<a D. b<a<c7.若不等式(a -2)x 2+2(a -2)x -4<0对一切x ∈R 恒成立,则a 的取值范围是 ( ) A.(-∞,2] B. (-2,2]C. [-2,2]D.(-∞,-2)8. 若S n 是等差数列{a n }的前n 项和,有1038=-S S ,则11S 的值为 ( ) A. 12B. 18C. 22D. 449.若(1),4()2,4x f x x f x x +<⎧=⎨≥⎩,则()2log 3f =( )A .-23B .11C .19D . 2410.若关于x 的二次方程222320ax x a ---=的一根大于1,另一根小于1,则a 的取值范围是 ( ) A .a >0或a <-4 B .a <-4 C .a >0 D .-4<a <011.若函数()f x 满足:“对于区间(1,2)上的任意实数1212,()x x x x ≠,2121|()()|||f x f x x x -<- 恒成立”,则称()f x 为优美函数.在下列四个函数中,优美函数是 ( )A .()||f x x =B .1()f x x=C .()2x f x =D .2()f x x = 12.已知曲线:C 24x y =,直线:1l y =-.PA 、PB 为曲线C 的两切线,切点为,A B . 令甲:若P 在l 上,乙:PA PB ⊥;则甲是乙的 ( )A.充分不必要条件B.必要不充分条件C.充分且必要条件D.既不充分也不必要条件第II 部分 非选择题(共90分)二、填空题:请把答案填在答卷的相应横线上,本大题共4个小题,每小题4分,共16分. 13.不等式224122x x +-≤的解集为 . 14.某路段属于限速路段,规定通过该路段的汽车时速不得超过70/km h ,否则视为违规扣分.某天,有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图如图所示,则违规扣分的汽车大约为 辆.15. 设p :x 2-x -20>0, q :212-+x x <0,则p 是q ⌝的 条件.16.在数列}{n a 中,若都有22(2,*)1a a p n n N n n -=≥∈-(p 为常数),则称{}a n 为“等方差数列”.下列是对“等方差数列”的判断:(1)若数列{}a n 是等方差数列,则数列2{}a n 是等差数列;(第14题)(2)数列{(1)}n-是等方差数列;(3)若数列{}a n 既是等方差数列,又是等差数列,则该数列必为常数列;(4)若数列{}a n 是等方差数列,则数列{}a kn (k 为常数,*)k N ∈也是等方差数列. 则正确命题序号为 .三、解答题:解答应写出文字说明、证明过程或演算步骤,本大题共6个大题,共74分. 17.(本小题满分12分)设全集是实数集R ,A ={x|2x 2-7x +3≤0},B ={x|x 2+a<0}.(I)当4a =-时,求A∩B 和A ∪B ; (II)若(R A)∩B =B ,求实数a 的取值范围.18.(本小题满分12分)我校高一年级研究性学习小组共有9名学生,其中有3名男生和6名女生. 在研究学习过程中,要进行两次汇报活动(即开题汇报和结题汇报),每次汇报都从这9名学生中随机选1人作为代表发言. 设每人每次被选中与否均互不影响. (Ⅰ)求两次汇报活动都是由小组成员甲发言的概率; (Ⅱ)求男生发言次数不少于女生发言次数的概率.19.(本小题满分12分)某校为解决教师后顾之忧,拟在一块长AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如右图中矩形ABCD 的教师公寓,要求顶点C 在地块的对角线MN 上, B ,D 分别在边AM ,AN 上,假设AB 长度为x 米.(Ⅰ)要使矩形教师公寓ABCD 的面积不小于144平方米, AB 的长度应在什么范围?(Ⅱ)长度AB 和宽度AD 分别为多少米时矩形教师公寓 ABCD 的面积最大?最大值是多少平方米?BA DN M PC20.(本小题满分12分)已知函数1()ln1x f x x +=-. (Ⅰ)求函数的定义域,并证明1()ln 1x f x x +=-在定义域上是奇函数;(Ⅱ)对于[2,6]x ∈1()lnln 1(1)(7)x mf x x x x +=>---恒成立,求实数m 的取值范围.21.(本小题满分12分) 已知数列{a n }的前n 项和S n 满足1(1)2n n S a =-(n ∈N *). (Ⅰ)求数列{a n }的通项公式,并比较n s 与12的大小; (Ⅱ) 设函数13()log f x x =,令12()()()n n b f a f a f a =+++,求数列1{}b n的前n 项和T n .22.(本小题满分14分)已知函数32()231f x ax ax =-+,3()42a g x x =-+,a R ∈. (I )当1a =时,求函数()y f x =的单调区间;(II )若任意给定的[]00,2x ∈,在[]0,2上总存在两个不同的(1,2)i x i =,使得 0()()i f x g x =成立,求a 的取值范围.[]2011级第五学期九月月考文科数学参考答案一、选择题:ADAB CDBC DABC二、填空题:13. [3,1]-; 14.110; 15. 充分不必要; 16. (1)(2)(3)(4). 三、解答题:17.解:(I)∵A ={x|12≤x ≤3},当a =-4时,B ={x|-2<x<2},∴A∩B ={x|12≤x<2},A ∪B ={x|-2<x ≤3}.…………………6分 18.(Ⅰ)解:记“2次汇报活动都是由小组成员甲发言” 为事件A . 1分由题意,得事件A 的概率111()9981P A =?, 即2次汇报活动都是由小组成员甲发言的概率为181. ----------------4分(Ⅱ)解:由题意,每次汇报时,男生被选为代表的概率为3193=,女生被选为代表的概率为12133-=.-----6分 记“男生发言次数不少于女生发言次数”为事件B , 由题意,事件B 包括以下两个互斥事件:○1事件B 1:男生发言2次女生发言0次,其概率为 02012111()C ()(1)339P B =-=, ------------------8分 ○2事件B 2:男生发言1次女生发言1次,其概率为 11122114()C ()(1)339P B =-=, ---------------------10分 所以,男生发言次数不少于女生发言次数的概率为125()()()9P B P B P B =+=.---12分19.解析(1)依题意NDC ∆∽NAM ∆, 所以,202030,ADx NA ND AM DC -==即,x AD 3220-=……(2分)矩形ABCD 的面积为,32202x x S -=根据条件,300<<x ……4分要使教师公寓ABCD 的面积不小于144平方米,即,14432202≥-=x x S 化简得,0216302≤+-x x ,解得1812≤≤x ……5分 B A DN MPC即AB 的长度应在[12,18]内……6分(Ⅱ)150)230(32)30(32322022=+-≤-=-=x x x x x x S (平方米)……9分15301=⇒-=x x x (米)……10分 此时AD=201032=-x 米……11分答:AB=15O 米,AD=10米时,公寓ABCD 的面积最大, 最大值是150平方米----12分 20.(Ⅰ)由101x x +>-,解得1x <-或1x >,∴ 函数的定义域为(,1)(1,)-∞-+∞…2分 当(,1)(1,)x ∈-∞-+∞时,11111()ln ln ln()ln ()1111x x x x f x f x x x x x --+-++-====-=---+--∴ 1()ln1x f x x +=-在定义域上是奇函数.--------------------------------.6分 (Ⅱ)由[2,6]x ∈时,1()lnln 1(1)(7)x mf x x x x +=>---恒成立, ∴10,[2,6]1(1)(7)x m x x x x +>>∈--- ∴ 0(1)(7)m x x <<+-在[2,6]x ∈成立--9分令2()(1)(7)(3)16g x x x x =+-=--+,[2,6]x ∈,由二次函数的性质可知[2,3]x ∈时函数单调递增,[3,6]x ∈时函数单调递减,[2,6]x ∈时,min ()(6)7g x g ==……..11分 ∴07m << ….12分21.解:(Ⅰ)当2n ≥时,111111(1)(1)2222n n n n n a a a a a --=---=-+, 12n n n a a a -=-+.∴113n n a a -=,由1111(1)2S a a ==-得113a =.∴数列{}n a 是首项113a =公比为13的等比数列 ∴1111()()333n n n a -=⨯=.……4分由1(1)2n n S a =-得11[1()]23n n S =- 11()13n -< ∴111[1()]232n -< ∴12n S <.…6分(Ⅱ)13()log f x x =11121333log log log n n b a a a ∴=+++=1123log ()n a a a=12131(1)log ()1232nn n n ++++=+++=……………….8分 ∵12112()(1)1n b n n n n ==-++ ∴n T 12111n b b b =+++=111112[(1)()()]2231n n -+-++-+=21nn +.……12分 22.解:(I )2()666(1).f x x x x x '=-=-…………2分由()0,10f x x x '>><得或;由()0,01f x x '<<<得;…………4分 故函数(][)(),01,f x -∞+∞的单调递增区间是和; 单调递减区间是[0,1].…………6分 (II )/2()666(1)f x ax ax ax x =-=-①当0a =时,显然不可能; …………7分②当0a >时,x0 (0,1) 1 (1,2) 2 ()f x ' 0 — 0 +()f x1极小值1a -14a +又因为当30,()[0,2]42a a g x x >=-+时在上是减函数, 对任意33[0,2],()[,]222a x g x ∈∈-+,不合题意; …………10分③当0a <时,x0 (0,1) 1 (1,2) 2 ()f x '0 + 0 —()f x1极小值1a -14a +又因为当30,()42a a g x x <=-+时在[0,2]上是增函数,对任意 33[0,2],()[,]222a x g x ∈∈-+,由题意可得31, 1.32a a a -+<-<-解得 …………13分综上,a 的取值范围为(,1).-∞- …………14分。
四川省绵阳南山中学11-12学年高一10月月考(数学)

南山中学高2014级2011年秋季10月月考数学试题本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,共100分。
考试时间100分钟。
第Ⅰ卷(选择题,共48分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
一、填空题:本大题共12小题.每小题4分,共48分。
在每小题列出的四个选项中,选出符合题目要求的一项.1. 设全集{1,2,3,4,5}U =,{1,3,4}M =,{2,4,5}N =,则()()U U C M C N ⋂等于( )A 、{4}B 、{1,3}C 、{2,5}D 、∅2. 下列四个函数中是奇函数的是( )A 、xx x f 1)(+= B 、12)(3+--=x x x f C 、 12)(2-+=x x x f D 、12)(+=x x f 3. 函数f(x)=2-x +(x -4)0的定义域为( ) A 、{x |x >2,x ≠4} B 、[)()2,44,+∞ C 、[)2,+∞ D 、(]2,∞-4. 下列各组函数是同一函数的是( )①32)(x x f -=与x x x g 2)(-=; ②x x f =)(与2)()(x x g =; ③0)(x x f =与01)(xx g =; ④12)(2--=x x x f 与12)(2--=t t t g A 、①② B 、①③ C 、③④ D 、②④5. 集合A 可表示为}1,,{aba ,也可表示为{2a ,a +b ,0},则20112011a b +的值为( )A 、0B 、-1C 、1D 、±16. 已知函数⎩⎨⎧<-≥+=)1(5)1(12)(x x x x x f ,则)(x f 的递减区间是( )A 、),1[+∞B 、)1,(-∞C 、),0(+∞D 、]1,(-∞7. 已知函数2)1(2)(2+-+=x a x x f 在区间(]4,∞-上是减函数,则实数a 取值范围是( )A 、(]3,-∞-B 、[)+∞-,3C 、(]3,+∞-D 、[)+∞,38. 图中曲线C 1、C 2、C 3、C 4分别是指数函数y=a x ,y=b x ,y=c x ,y=d x的图像,则a 、b 、c 、d 与1之间的大小关系是( ) A 、a <b <1<c <d B 、a <b <1<d <c C 、b <a <1<c <d D 、b <a <1<d <c 9. 已知1)1(+=+x x f ,则函数)(x f 的解析式为( ) A 、2)(x x f = B 、)1(1)(2≥+=x x x f C 、)1(22)(2≥+-=x x x x f D 、)1(2)(2≥-=x x x x f 10. 函数562---=x x y 的值域为( )A 、[]2,0B 、[]4,0C 、(]4,∞-D 、[)∞+.0 11. 函数)0)(()1221()(≠-+=x x f x F x是偶函数,且)(x f 不恒等于零,则)(x f ( ) A 、是偶函数 B 、是奇函数C 、可能是奇函数也可能是偶函数D 、不是奇函数也不是偶函数 12. 已知函数)12(+x f 是偶函数,则函数)2(x f 的图象的对称轴方程是( )A 、1-=xB 、1=xC 、21-=xD 、21=x第Ⅱ卷 (非选择题,共52分)注意事项:本卷的答案均要求写在答题卷上二、填空题:本大题共4小题,每小题3分,共12分,把答案填在题中横线上13.已知集合{}{}4),(,2),(=-==+=y x y x N y x y x M ,那么集合=⋂N M .14.若21()22x -≤,则x 的取值范围是 .15.已知函数b a bx ax x f +++=3)(2是偶函数,定义域]2,1[a a -,则函数)(x f 的值域是_____. 16.若方程243x x m -+=有4个不相等的实数根,则实数m 的取值范围是 . 三、解答题:本大题共4小题,共40分。
第1周 2011年绵阳中学自主招生数学试题

第1周 自主招生小测题 姓名一.选择题:1、下列因式分解中,结果正确的是( )A.2322()x y y y x y -=-B.424(2)(2)(2)x x x x -=+-+C.211(1)x x x x x--=-- D.21(2)(1)(3)a a a --=-- 2、“已知二次函数2y ax bx c =++的图像如图所示,试判断a b c ++与0的大小.”一同学是这样回答的:“由图像可知:当1x =时0y <,所以0a b c ++<.”他这种说明问题的方式体现的数学思想方法叫做( )A.换元法B.配方法C.数形结合法D.分类讨论法 3、已知实数x 满足22114x x x x++-=,则x x 1-的值是( ) A.-2 B.1 C.-1或2 D.-2或14、若直线21y x =-与反比例函数k y x =的图像交于点(2,)P a ,则反比例函数k y x=的图像还必过点( ) A. (-1,6) B.(1,-6) C.(-2,-3) D.(2,12)5、现规定一种新的运算:“*”:*()m n m n m n -=+,那么51*22=( )A.54B.5C.3D.9 6、一副三角板,如图所示叠放在一起,则AOB COD ∠+∠=( )A.180°B.150°C.160°D.170°7、某中学对2005年、2006年、2007年该校住校人数统计时发现,2006年比2005年增加20%,2007年比2006年减少20%,那么2007年比2005年( )A.不增不减B.增加4%C.减少4%D.减少2%8、一半径为8的圆中,圆心角θ为锐角,且sin 32θ=,则角θ所对的弦长等于( ) A.8 B.10 C.82D.16 9、一支长为13cm 的金属筷子(粗细忽略不计),放入一个长、宽、高分别是4cm 、3cm 、16cm 的长方体水槽中,那么水槽至少要放进( )深的水才能完全淹没筷子。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绵阳南山中学(实验校区)2011年自主招生考试数 学 试 题 卷本试卷满分150分,考试时间120分钟。
第I 卷(选择题,共36分)一、选择题:本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的 1、)72(--等于( )A 、27 B 、72 C 、27-D 、72-2、计算=-32)2(b a ( )A 、244b aB 、368b aC 、368b a -D 、358b a3、下列属于必然事件的是( )A 、度量三角形的内角和,结果是3600B 、2011年6月19日绵阳是雨天C 、掷一枚正方体骰子,向上的点数不小于1D 、从一副扑克牌中抽取一张,其点数是54、下列图形具有稳定性的是( )A 、矩形B 、平行四边形C 、菱形D 、直角三角形5、下列四边形:①等腰梯形,②正方形,③矩形,④菱形,其中对角线一定相等的是( )A 、①②③B 、①②③④C 、①②D 、②③6、右图所示的三角形绕虚线旋转一周所得的几何体是( )DC BA7、右图是小明用八块相同的小正方体搭建的一个积木,它的俯视图是( )8、如图,一次函数b kx y +=的图象过点A 、B,则0>+b kx 的解集是( )A 、0>xB 、2>xC 、3->xD 、23<<-x9、南山中学高二某英才班40名学生为“希望小学”捐款,共捐1000元,捐款情况如下表:表中捐款20元和30元人数不小心被墨水污染,已经看不清楚,请你根据表中信息计算出捐款20元和30元的人数分别为( )A 、15人,12人B 、13人,14人C 、12人,15人D 、14人,13人10、如图,在Rt △ABC 中,∠ACB=900,CD ⊥AB 于点D ,∠ACD=3∠BCD ,点E 是AB 中点,AB=10,线段DE 的长度为( )A 、3B 、5C 、25D 、225 11、如图,点C 是线段BD 上一点,在BD 同侧作正三角形ABC 和正三角形ECD,BE 交AC 于点M,AD 交CE 于点N,连结MN,则下列关系中不.正确..的是( ) A 、BE=AD B 、DC=DN C 、CM=CND 、MN//BD12、如图,在Rt △ABC 中,∠C=900,∠A=300,点O 在斜边AB 上, 半径为2的圆O 过点B ,切AC 于点D,交BC 于点E,则图中阴影部分的周长为( )A 、π3121++B 、π3131++C 、π3231++ D 、π6122++AB CDE DCABOB第II 卷(非选择题,共114分)二、填空题:本大题共6个小题,每小题4分,共24分.13、分解因式:=-x x 43;14、如图,CD AB //,EF与AB 、CD 分别交于点E 、F ,EF EP ⊥,FP 平分EFD ∠,若 40=∠BEP ,则=∠EPF ;15、2011年4月,第六次全国人口普查结果公布,中国内地人口已达13.39亿人,用科学记数法表示这一数据应为 人;16、ABC ∆中任意一点),(00y x P 经平移后对应点为点)3,5(001-+y x P ,将ABC ∆作同样平移得到111C B A ∆,若点)3,2(-A ,则点1A 的坐标为 ;17、如图,南山中学数学研究性学习小组制作了一个脸谱,它的上半部分是半圆,眉心在圆心处,两眼在直径AB 上;下半部分是一段抛物线,下鄂恰好在顶点处. 经过测量,两眼所在的直径AB 长24cm ,下鄂点到头 顶中点长24cm .请你计算,过眉心且与直径AB 成45角的线段CD 的 长约为 cm .(参考数据:163.310,414.12≈≈,结果精确到18、如图,四边形ABCD 为矩形,4=AB ,3=AD ,把矩形ABCD 沿对角线AC 折叠,点B 落在点E 处,点P 、Q分别是AD 、EC 中点,PQ 交AE 、CD 于点M 、N ,则线段MN 的长度为 。
三、解答题:本大题7个小题,共90分.解答应写出文字说明、证明过程或演算步骤.19、(本题共2个小题,每小题8分,共16分)(1)计算:845sin )21()2011(2⨯+-+--; (2)计算:)(3)235(22222y x x y yx xy y x y xy -÷---+.A B CP20、(本题满分12分)如图,用一长为m 24的篱笆,一面利用墙(墙的最大可用长度为m 5.3)围成中间有三道篱笆(均平行于墙CD )的矩形饲养场ABCD.(1)若围成的饲养场面积为216m ,求边AB 的长;(2)能否围成面积为220m 的饲养场?若能,求出边AB 的长;若不能,请说明理由.21、(本题满分12分)南山中学今年高一某班进行了体能测试,根据成绩绘制了下列统计图1和图2:图1(1)请在原图上补全统计图1和图2(图2中,请标明各部分的圆心角的度数); (2)分别计算该班本次体能测试成绩的平均数和中位数; (3)你能得出哪些结论?(只要求写出其中两条)图240分20%22、(本题满分12分)一次函数的图象与反比例的图象交于点)1,2(--A 和),1(n B .(1)求一次函数和反比例函数的解析式;(2)设一次函数图象与x 轴、y 轴分别交于C 、D 两点,点C 关于y 轴对称点为点E,求CDE ∆和BCE ∆面积之比。
23、(本题满分12分)如图,AB 为⊙O 的直径,点C 是⊙O 上一点,AC 平分∠DAB ,AD ⊥CD ,线段AB 与DC 的延长线交于点P 。
(1)求证:CD 是⊙O 的切线;(2)若PB=BO=1,求图中阴影部分的面积(结果保留根号)。
24、(本题满分12分)已知二次函数c bx x y ++=2的图象过点A (-1,0)和点B (5,12)。
(1)求此函数的解析式及图象的对称轴;(2)在对称轴上是否存在点P ,使得PA=PB ?若存在,求出点P 的坐标;若不存在,请说明理由;(3)在二次函数的图象上求点Q ,使得△QAB 是以AB 为直角边的直角三角形。
25、(本题满分14分)已知正方形ABCE ,一等腰直角三角形的一个锐角顶点与点A 重合,将此三角形绕点A 旋转,两边分别与线段BC 、CD (或其延长线上)交于点M 、N 。
(1)当点M 、N 在边BC 、CD 上时,如图1,求证:MN DN BM =+;(2)当点M 、N 在边BC 、CD 延长线上时,如图2,线段BM 、DN 、MN 间又有何数量关系?并证明;(3)在(2)中作直线BD 分别交直线AM8=,求AQ .图1图2绵阳南山中学(实验校区)2011年自主招生考试数学试卷参考答案及评分意见说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准相应给分.2.对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不在给分.3.解答右端所注分数,表示考生正确地做到这一步就得的累加分数.一.选择题: 本大题共12个小题,每小题3分,共36分. 在每小题给出的四个选项中,只有一项是符合题目要求的1. B2.C3.C4.D5.A6.B7. D8.C9.A 10.D 11.B 12.C二.填空题:每小题4分,共24分13. )2)(2(+-x x x 14. 65 15. 910339.1⨯16. )0,3( 17. 49.22 18. 59三.解答题:本大题7个小题,共90分.解答应写出文字说明、证明过程或演算步骤.19. (本题共2个小题,每小题8分,共16分) 解:(1)原式=222241⨯++ ……………………….…………………………….6分 241++=.7= ………………..…………………………………………………8分(2)原式=)(333222y x x yyx y xy -÷-+ …………………….……………………………….2分 yy x x y x y x y x y )(3))(()(3-⋅+-+=………………………….……………………….6分.9x = ………………………………………………………………………8分20.(本题满分12分)解: (1)设x AB =,由题意得,2122424x xAD -=-=…………….....………………1分 可列方程:,16)212(=-x x ………………………………………………4分 解得2=x 或.4=x ………………………………………………………6分 又,5.30≤<x ……………………….……….………...………………7分,2=∴x 即.2=AB ………………………………………………………9分(2)由题意得,20)212(=-x x整理得01062=+-x x ,,041014)6(2<-=⨯⨯--=∆∴此方程无解.………………………………….………………………11分 ∴不能围成面积为220m 的饲养场. ………………………..……….12分21. (本题满分12分)解:(1)设高一某班总人数为x 人,.40,8%20==⋅x x∴38分的人数为10)86124(40=+++-(人) ………………………………….2分.3分图2图130分:,36440360 =⨯ 35分:,1081240360=⨯ 36分:,54640360 =⨯ 38分:,901040360=⨯ 40分:.72840360 =⨯ …………………………………5分 补全统计图2见上. …………………………..…………………………...………6分 (2)平均数为4.364040838103663512304=⨯+⨯+⨯+⨯+⨯ ………………………….7分中位数为:36 ………………………………………………………………………8分 (3)答案不唯一,可参考如下:①可估计高一年级35分人数最多,占30% ; ②可估计高一年级30分人数最少,占10% ;③从平均数和中位数看高一年级有45% 的人超过36分;④因为年级有55%的学生未达到平均成绩,故以后学生必须加强体育锻炼. …12分 22. (本题满分12分)解:(1)设反比例函数的解析式为)0(>=k xky ,即.xy k = 由题意得⎩⎨⎧⨯=-⨯-=,1,)1()2(n k k 解得⎩⎨⎧==.4,2n k∴反比例函数的解析式为.)2,1(,2B xy =………………………………………………3分 设一次函数的解析式为)0(≠+=a b ax y ,由题意得⎩⎨⎧=+-=+-,2,12b a b a 解得⎩⎨⎧==.1,1b a∴一次函数的解析式为.1+=x y ………………………………………………………6分 (2)由1+=x y 得),1,0(),0,1(D C -.222=+=∴OD OC CD由点E 是点C 关于y 轴对称点知)0,1(E ,B 点与E 点的横坐标相同,x BE ⊥∴轴.,2222=+=∴BE CE CB ……………………………………………………………9分CDE ∆ 和CBE ∆高相同,CDE ∆∴和CBE ∆面积之比为CD 与CB 的长度之比.,2:122:2:==CB CDCDE ∆∴和CBE ∆面积之比为.2:1 ……………………………………………………12分23.(本题满分12分) (1)证明:连结.OC由,OC OA =得OCA OAC ∠=∠ 又AC 平分DAB ∠,,OAC DAC ∠=∠∴于是,OCA DAC ∠=∠ (3).//AD OC ∴∴由CD AD ⊥,得CD OC ⊥CD ∴是圆O 的切线. ………………………6分(2)设AD 交圆O 于E ,连结.,CB OE在PCO Rt ∆中, 1==BO PB ,.1====∴CB PB OB OC,,60BCP P COB CBO ∠=∠=∠=∠∴ 由 602=∠=∠CBO P ,得,30 =∠P 在PAD Rt ∆中, ,233,23,33====PD AD OA PA 在PCO Rt ∆中, ,3,22===PC BO PO.23=-=∴PC PD CD …………………………………………………….9分 ∴阴影部分的面积:O CE AO E AO CD S S S S 扇形梯形--=∆43)(212CD OC AD ⋅-⋅+= 14323)123(212-⨯-⨯+= .6833π-=24. (本题满分12分)A解:(1)由题意得⎩⎨⎧=++=+-,12525,01c b c b 解得⎩⎨⎧-=-=.3,2c b∴二次函数的解析式为.322--=x x y∴对称轴方程为1212=⨯--=x x 即 ………………3分 (2)设点),1(m P ,对称轴交x 轴于点C ,作BD 垂直于对称轴,垂足为D .于是).12,1(),0,1(D C .4|,12|=-=∴BD m PD在PBD Rt ∆中, ,160244)12(222222+-=+-=+=m m m BD PD PB在PCA Rt ∆中, ,42222m PC AC PA +=+=,PB PA =∴ ,41602422+=+-∴m m m 解得.213=m ∴点P 的坐标为).213,1( …………………………………………………………….7分 (3)设点)32,(0200--x x x Q①若A ∠为直角,作x QM ⊥轴于M ,x BN ⊥轴于N ,QM BR ⊥于R .)12,(),0,5(),0,(00x R N x M ∴在BQR Rt ∆中, ,)5(]12)32[(202020222-+---=+=x x x RB QR BQ在AMQ Rt ∆中, ,)32()1(202020222--++=+=x x x QM AM AQ在ABN Rt ∆中, ,180********=+=+=BN AN AB,222QB AB AQ =+即.)5(]12)32[(180)32()1(20202002020-+---=+--++x x x x x x展开整理得,0532020=--x x 解得10-=x (舍去)或.250=x ∴点).47,25(-Q ……………………………………………………………………..9分 ②若B ∠为直角,由,222QB AB AQ +=同理可求).465,27(-Q .11综上所述,点Q 的坐标为)47,25(-或).465,27(- ……………12分 25. (本题满分14分)证明:(1)延长MB 到E ,使,DN BE =连结.AE 如右图.,,,ADN ABE DN BE AD AB ∠=∠== .ADN ABE ∆≅∆∴.,DAN BAE AN AE ∠=∠=∴ ,90 =∠+∠+∠DAN MAN BAM ,90 =∠+∠+∠∴BAE MAN BAM即 90=∠+∠MAN MAE , 由,45 =∠MAN 得.45 =∠MAE .MAE MAN ∠=∠∴ 又..,ME MN MAN MAE AM AM =∴∆≅∆∴=又,DN BM BE BM ME +=+=MN DN BM =+∴. ………………………………………………………………4分(2)在线段BC 上截取BF ,使DN BF =,连结AF ,易得.ADN ABF ∆≅∆ .,AN AF DAN BAF =∠=∠∴,90,90 =∠+∠∴=∠+∠FAD DAN FAD BAF 即.90 =∠FAN∴由,45 =∠MAN 得.45 =∠FAM .FAM MAN ∠=∠∴又..,NM FM ANM AFM AM AM =∴∆≅∆∴=即.MN BF BM =-MN DN BM =-∴. ………………………………………………………………9分(3)连结AC ,如右图.在MNC Rt ∆中, .622=-=CN MN CM由(2)知MN DN BM =-,即()(BC CN CM BC --+ 整理得,122=-+=CM CN MN BC 即,6==AC BC 在ABM Rt ∆中, .5622=+=BM AB AM,45,45 =∠+∠=∠+∠DAN MAD MAD CAM,135, =∠=∠∠=∠∴ADQ ACM DAQ CAM 又.~ADQ ACM ∆∆∴.AC AD AM AQ =∴ .10326656=⨯=⋅=∴AC AD AM AQ ……………………………………………..14分。
