高一数学单元测试题(八)
高一数学测试题(含答案)

高一数学测试题(含答案)一.选择题1..下列结论正确的是A.若,a b c d >>,则a c b d ->-B. 若,a b c d >>,则a d b c ->-C.若,a b c d >>,则ac bd >D. 若,a b c d >>,则a b d c> 2.若直线a 不平行于平面α,且a α⊄,则下列结论成立的是A. α内所有的直线与a 异面.B. α内不存在与a 平行的直线.C. α内存在唯一的直线与a 平行.D. α内的直线与a 都相交. 3.圆x 2+y 2=1和圆x 2+y 2-6y +5=0的位置关系是A .外切B .内切C .外离D .内含二.填空题 1.已知sin cos tan 2,sin cos a aa a a+=--则的值是2.已知向量b a ,的夹角为3π,3,1==b a ,则b a -的值是 3.求值:οοοο15sin 105sin 15cos 105cos -=4.设函数⎪⎩⎪⎨⎧≥-<=-2),1(log 2,2)(231x x x e x f x 则))2((f f 的值为= 5.等比数列{}n a 中,0n a >,569a a =,则313233310log log log log a a a a +++⋅⋅⋅+= 6.已知函数f (x )满足f (x )=(2),0,2,0,xf x x x +<⎧⎨⎩≥ 则(7.5)f -=( ).。
三.解答题1.已知)2,(),3,2(x b a ==,(1)当b a 2-与b a +2平行时,求x 的值; (2)当a 与b 夹角为锐角时,求x 的范围.2.已知函数2()2sin 1f x x x θ=+-,⎥⎦⎤⎢⎣⎡-∈23,21x(1)当6πθ=时,求()f x 的最大值和最小值;(2)若()f x 在⎥⎦⎤⎢⎣⎡-∈23,21x 上是单调增函数,且[0,2)θπ∈,求θ的取值范围.3.求过两直线3420x y +-=和220x y ++=的交点且与直线3240x y -+=垂直的直线方程.4. (满分12分)如图,在正方体1111ABCD A B C D -中,E 、F 、G 分别为1CC 、11B C 、1DD 的中点,O 为BF 与1B E 的交点,(1)证明:BF ⊥面11A B EG(2)求直线1A B 与平面11A B EG 所成角的正弦值.5.已知数列{}n a 中,*1121,()2nn na a a n N a +==∈+ (1)求 1234,,,a a a a ; (2)求数列{}n a 的通项公式.高一测试题答案 一.选择题1.B2.B3.A4.C5.A6.D7.C 二.填空题 1.312、73、21- 4、2 5、10 6、2 三.解答题 1.解:(1)由题意得:b a 2-=)1,22(--xb a +2=)8,4(x + 由b a 2-与b a +2平行得:0)4()1(8)22(=+⋅--⋅-x x 分34=∴x (2)由题意得:⎪⎩⎪⎨⎧>•不共线与b a b a 0(3) 即⎩⎨⎧≠->+034062x x343≠->∴x x 且 2解:(1)当6πθ=时,45)21(1)(22-+=-+=x x x x f 分∴当21-=x 时,函数)(x f 有最小值45-当23=x 时,函数)(x f 有最大值4123- (2)要使()f x 在⎥⎦⎤⎢⎣⎡-∈23,21x 上是单调增函数, 则 -sin θ≤-21即sin θ≥21 又)2,0[πθ∈Θ 解得:⎥⎦⎤⎢⎣⎡∈65,6ππθ 3.。
高一数学解三角形单元测试及答案

高一数学解三角形单元测试及答案解三角形本章测试本次测试共有12道选择题,每题5分,总分60分。
在每道题中,只有一个选项是正确的,请将正确选项填涂在答题卡上。
1.在三角形ABC中,已知a=2,b=2,B=π/6,则A=()A。
3π/4 B。
π/3 C。
4π/3 D。
π/42.在三角形ABC中,已知a²=b²+c²+bc,则角A为()A。
30° B。
45° C。
120° D。
150°3.已知三角形ABC中,A:B:C=11:4,则a:b:c的比值为()A。
1:1:3 B。
2:2:3 C。
1:1:2 D。
1:1:44.在三角形ABC中,a、b、c分别为三个内角A、B、C的对边,若a=2,b=1,B=29°,则此三角形的解为()A。
无解 B。
有一解 C。
有两解 D。
有无数解5.在三角形ABC中,∠C=90°,0<A<45°,则下列各式中,正确的是()A。
sinA>XXX>XXX<XXX<sinB6.一艘船自西向东航行,上午10时到达灯塔的南偏西75°、距塔68海里的M处,下午2时到达这座灯塔的东南方向的N 处,则这艘船航行的速度为()A。
176/22海里/时 B。
346海里/时 C。
22海里/时 D。
342/22海里/时7.已知三角形ABC的面积为S,三个内角A、B、C的对边分别为a、b、c,若4S=a²-(b-c)²,bc=4,则S=()A。
2 B。
4 C。
3 D。
15/28.已知三角形ABC的内角A、B、C所对的边分别为a、b、c,若cosC=1/4,4bcosA+acosB=3,则三角形ABC外接圆的半径为()A。
2/3 B。
2√2 C。
4 D。
69.在三角形ABC中,已知asinA/bsinB=(a²+c²-b²)/(b²+c²-a²),则三角形ABC的形状为()A。
必修第8章 立体几何初步单元测试(考试版)

…○………………内………………○………………装………………○………………订………………○………………线………………○…………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校:______________姓名:_____________班级:_______________考号:______________________绝密★启用前第八单元 立体几何初步单元测试卷高一数学(考试时间:120分钟 试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.测试范围:人教必修二2019第八单元 立体几何初步。
5.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、单项选择题:(本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.(2022·辽宁朝阳·高二开学考试)若m ,n ,l 为空间三条不同的直线,,,αβγ为空间三个不同的平面,则下列为真命题的是( ) A .若,m l n l ⊥⊥,则m n ∥ B .若,m m αβ∥∥,则αβ∥C .若,αγβγ⊥⊥,则αβ∥D .若,,m n m n αβ⊥⊥∥,则αβ∥2.(2022·河北张家口·一模)下图是战国时期的一个铜镞,其由两部分组成,前段是高为2cm 、底面边长为1cm 的正三棱锥,后段是高为0.6cm 的圆柱,圆柱底面圆与正三棱锥底面的正三角形内切,则此铜镞的体积约为( )A .30.25cmB .30.65cmC .30.15cmD .30.45cm3.(2021·陕西·西安市远东一中高一期末)如图,在正四棱柱1111ABCD A B C D -中,122AA AD ==,点E 为棱1BB 的中点,过A ,E ,1C 三点的平面截正四棱柱1111ABCD A B C D -所得的截面面积为( )A .2B .22C .23D 34.(2022·北京市第一六一中学高三阶段练习)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则该球的半径为( )A .5cmB .6cmC .7cmD .8cm5.(2021·江苏苏州·高三阶段练习)用一平面截圆柱,得到如图所示的几何体,截面椭圆的长轴两端点到底面的距离分别为3和5,圆柱的底面直径为4,则该几何体的体积为( )A .16πB .32πC .8πD .64π6.(2022·云南昭通·高三阶段练习(文))如图所示,在正方体1111-ABCD A B C D 中,点F 是棱1AA 上的一个…○………………内………………○………………装………………○………………订………………○………………线………………○……………○………………外………………○………………装………………○………………订………………○………………线………………○…………… 学校:______________姓名:_____________班级:_______________考号:______________________动点,平面1BFD 交棱1CC 于点E ,则下列命题中假命题是( )A .存在点F ,使得11A C ∥平面1BED FB .存在点F ,使得1B D ∥平面1BED FC .对于任意的点F ,四边形1BED F 均为平行四边形 D .对于任意的点F ,三棱锥11F BB D -的体积均不变7.(2022·云南师大附中高三阶段练习(理))如图,在矩形ABCD 中,2,2AB BC ==,E 为BC 中点,把ABE △和CDE △分别沿,AE DE 折起,使点B 与点C 重合于点P ,若三棱锥P ADE -的四个顶点都在球O的球面上,则球O 的表面积为( )A .3πB .4πC .5πD .9π8.(2022·河南·模拟预测(理))已知球面被平面所截得的部分叫做球冠,垂直于截面的直径被截得的一段叫做球冠的高,若球的半径是R ,球冠的高是h ,则球冠的面积为2πRh .某机械零件的结构是在一个圆台的底部嵌入一颗小球,其正视图和侧视图均如图所示,已知圆台的任意母线均与小球的表面相切,则小球突出圆台部分的球冠面积为( )A .25πB .253πC 253D .1003π 二、多项选择题:(本题共4小题,每小题5分,共20分。
第八章立体几何初步单元测试 2020-2021学年高一下学期数学人教A版(2019)必修第二册

第八章 立体几何初步考试时间120分钟,满分150分.一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线; ②有一个面是多边形,其余各面都是三角形的几何体是棱锥; ③棱台的上、下底面可以不相似,但侧棱长一定相等. 其中真命题的个数是( ) A .0 B .1 C .2D .32.以长为8 cm ,宽为6 cm 的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( ) A .64π cm 2B .36π cm 2C .64π cm 2或36π cm 2D .48π cm 23.梯形ABCD 中,AB ∥CD ,AB ⊂平面α,CD ⊄平面α,则直线CD 与平面α内的直线的位置关系只能是( )A .平行B .平行或异面C .平行或相交D .异面或相交4.空间四点A ,B ,C ,D 共面而不共线,那么这四点中( ) A .必有三点共线 B .必有三点不共线 C .至少有三点共线D .不可能有三点共线5.如图所示,正方形ABCD 中,E ,F 分别是AB ,AD 的中点,将此正方形沿EF 折成直二面角后,异面直线AF 与BE 所成角的余弦值为( )A .22 B .3 C .12D .326.E ,F ,G 分别是空间四边形ABCD 的棱BC ,CD ,DA 的中点,则此四面体中与过E ,F ,G 的截面平行的棱的条数是( )A .0B .1C .2D .37.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )A .81π4 B .16π C .9πD .27π48.如图,在直三棱柱ABC -A 1B 1C 1中,D 为A 1B 1的中点,AB =BC =BB 1=2,AC =25,则异面直线BD 与AC 所成的角为( )A .30°B .45°C .60°D .90°二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得2分,有选错的得0分)9.以下关于空间几何体特征性质的描述,错误的是( )A .以直角三角形一边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体是圆锥B .有两个面互相平行,其余各面都是四边形的几何体是棱柱C .有一个面是多边形,其余各面都是三角形的几何体是棱锥D .两底面互相平行,其余各面都是梯形,侧棱延长线交于一点的几何体是棱台 10.如图,在平行六面体ABCD -A 1B 1C 1D 1中,点M ,P ,Q 分别为棱AB ,CD ,BC 的中点,若平行六面体的各棱长均相等,则下列说法正确的是( )A .A 1M ∥D 1PB .A 1M ∥B 1QC .A 1M ∥平面DCC 1D 1 D .A 1M ∥平面D 1PQB 111.如图,在四面体ABCD 中,截面PQMN 是正方形,则在下列命题中,一定正确的为( )A .AC ⊥BDB .AC ∥截面PQMN C .AC =BDD .异面直线PM 与BD 所成的角为45°12.正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F ,G 分别为BC ,CC 1,BB 1的中点.则( )A .直线D 1D 与直线AF 垂直B .直线A 1G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为98D .点C 与点G 到平面AEF 的距离相等三、填空题(本大题共4小题,每小题5分,共20分)13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是___.14.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为____厘米.15.已知a ,b 表示直线,α,β,γ表示平面.①若α∩β=a ,b ⊂α,a ⊥b ,则α⊥β;②若a ⊂α,a 垂直于β内任意一条直线,则α⊥β;③若α⊥β,α∩β=a ,α∩γ=b ,则a ⊥b ;④若a ⊥α,b ⊥β,a ∥b ,则α∥β.上述命题中,正确命题的序号是____.16.(2020·全国Ⅰ卷理)如图,在三棱锥P -ABC 的平面展开图中,AC =1,AB =AD =3,AB ⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB = ____.四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)某高速公路收费站入口处的安全标识墩如图所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.长方体的长、宽、高分别是40 cm、40 cm、20 cm,正四棱锥P-EFGH的高为60 cm.(1)求该安全标识墩的体积;(2)求该安全标识墩的侧面积.18.(本小题满分12分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.19.(本小题满分12分)如图所示,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.(1)若CD∥平面PBO,试指出点O的位置;(2)求证:平面PAB⊥平面PCD.20.(本小题满分12分)(2020·江苏卷)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.21.(本小题满分12分)在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC 且分别交AC,SC于D,E,又SA=AB,SB=BC.(1)求证:BD⊥平面SAC;(2)求二面角E-BD-C的大小.22.(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=BC,AB =2A1A=4,以AB,BC为邻边作平行四边形ABCD,连接A1D,DC1.(1)求证:DC1∥平面A1ABB1;(2)若二面角A1-DC-A为45°.①求证:平面A1C1D⊥平面A1AD;②求直线AB1与平面A1AD所成角的正切值.第八章立体几何初步考试时间120分钟,满分150分.一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②有一个面是多边形,其余各面都是三角形的几何体是棱锥;③棱台的上、下底面可以不相似,但侧棱长一定相等.其中真命题的个数是(A)A.0B.1C.2D.3[解析]①不一定,只有当这两点的连线平行于轴时才是母线;②不一定,因为“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,如图所示;③错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱延长线交于一点,但是侧棱长不一定相等.2.以长为8 cm ,宽为6 cm 的矩形的一边为旋转轴旋转而成的圆柱的底面面积为( C ) A .64π cm 2B .36π cm 2C .64π cm 2或36π cm 2D .48π cm 2[解析] 分别以长为8 cm ,宽为6 cm 的边所在的直线为旋转轴,即可得到两种不同大小的圆柱,显然C 选项正确.3.梯形ABCD 中,AB ∥CD ,AB ⊂平面α,CD ⊄平面α,则直线CD 与平面α内的直线的位置关系只能是( B )A .平行B .平行或异面C .平行或相交D .异面或相交[解析] 由直线与平面平行的判定定理,可知CD ∥α,所以CD 与平面α内的直线没有公共点.4.空间四点A ,B ,C ,D 共面而不共线,那么这四点中( B ) A .必有三点共线 B .必有三点不共线 C .至少有三点共线D .不可能有三点共线[解析] ∵A ,B ,C ,D 共面而不共线,这四点可能有三点共线,也可能任意三点不共线,A 错.如果四点中没有三点不共线,则四点共线,矛盾,B 正确.当任意三点不共线时,也满足条件,C 错.当其中三点共线,第四个点不共线时,也满足条件,D 错.5.如图所示,正方形ABCD 中,E ,F 分别是AB ,AD 的中点,将此正方形沿EF 折成直二面角后,异面直线AF 与BE 所成角的余弦值为( C )A .22 B .3 C .12D .32[解析] 过点F 作FH ∥DC ,交BC 于H ,过点A 作AG ⊥EF ,交EF 于G ,连接GH ,AH ,则∠AFH 为异面直线AF 与BE 所成的角.设正方形ABCD 的边长为2,在△AGH 中,AH =52+24=3,在△AFH 中,AF =1,FH =2,AH =3,∴cos ∠AFH =12.6.E ,F ,G 分别是空间四边形ABCD 的棱BC ,CD ,DA 的中点,则此四面体中与过E ,F ,G 的截面平行的棱的条数是( C )A .0B .1C .2D .3[解析] 在△ACD 中,∵G ,F 分别为AD 与CD 的中点,∴GF ∥AC .而GF ⊂平面EFG ,AC ⊄平面EFG ,∴AC ∥平面EFG .同理,BD ∥平面EFG .故选C .7.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( A )A .81π4 B .16π C .9πD .27π4[解析] 如图所示,设球的半径为R ,球心为O ,正四棱锥的底面中心为O ′.∵正四棱锥P -ABCD 中AB =2,∴AO ′= 2.∵PO ′=4,∴在Rt △AOO ′中,AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×⎝⎛⎭⎫942=81π4,故选A .8.如图,在直三棱柱ABC -A 1B 1C 1中,D 为A 1B 1的中点,AB =BC =BB 1=2,AC =25,则异面直线BD 与AC 所成的角为( C )A .30°B .45°C .60°D .90°[解析] 如图,取B 1C 1的中点E ,连接BE ,DE ,则AC ∥A 1C 1∥DE ,则∠BDE 即为异面直线BD 与AC 所成的角.由条件可知BD =DE =EB =5,所以∠BDE =60°,故选C .二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,选对但不全的得2分,有选错的得0分) 9.以下关于空间几何体特征性质的描述,错误的是(ABC)A.以直角三角形一边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体是圆锥B.有两个面互相平行,其余各面都是四边形的几何体是棱柱C.有一个面是多边形,其余各面都是三角形的几何体是棱锥D.两底面互相平行,其余各面都是梯形,侧棱延长线交于一点的几何体是棱台[解析]以直角三角形的一个直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体是圆锥,可得A错误;有两个面互相平行,其余各面都是四边形的几何体可能是棱台,不一定是棱柱,故B错误;有一个面是多边形,其余各面都是有公共顶点三角形的几何体叫棱锥,故C错误;根据棱台的定义,可得D正确.故选ABC.10.如图,在平行六面体ABCD-A1B1C1D1中,点M,P,Q分别为棱AB,CD,BC的中点,若平行六面体的各棱长均相等,则下列说法正确的是(ACD)A.A1M∥D1P B.A1M∥B1QC.A1M∥平面DCC1D1D.A1M∥平面D1PQB1[解析]连接PM,因为M、P为AB、CD的中点,故PM平行且等于AD.由题意知AD 平行且等于A1D1,故PM平行且等于A1D1,所以PMA1D1为平行四边形,所以A1M∥D1P.故A正确;显然A1M与B1Q为异面直线,故B错误;由A知A1M∥D1P,由于D1P既在平面DCC1D1内,又在平面D1PQB1内,且A1M即不在平面DCC1D1内,又不在平面D1PQB1内,故C、D正确.故选ACD.11.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,一定正确的为(ABD)A .AC ⊥BDB .AC ∥截面PQMN C .AC =BDD .异面直线PM 与BD 所成的角为45°[解析] ∵QM ∥PN ,∴QM ∥平面ABD ,∴QM ∥BD ,同理可得AC ∥MN ,∵QM ∥BD ,AC ∥MN ,MN ⊥QM ,∴AC ⊥BD ,A 正确;∵AC ∥MN ,∴AC ∥截面PQMN ,B 正确;∵QM ∥BD ,AC ∥MN ,∴MN AC +QMBD =1,C 不一定正确;∵QM ∥BD ,∴异面直线PM 与BD 所成的角为∠PMQ =45°,D 正确.故选ABD .12.正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F ,G 分别为BC ,CC 1,BB 1的中点.则( BC )A .直线D 1D 与直线AF 垂直B .直线A 1G 与平面AEF 平行C .平面AEF 截正方体所得的截面面积为98 D .点C 与点G 到平面AEF 的距离相等[解析] 取DD 1中点M ,则AM 为AF 在平面AA 1D 1D 上的射影,∵AM 与DD 1不垂直,∴AF 与DD 1不垂直,故A 选项错误;∵A 1G ∥D 1F ,A 1G ⊄平面AEFD 1,∴A 1G ∥平面AEFD 1,故B 选项正确;平面AEF 截正方体所得截面为等腰梯形AEFD 1,易知梯形面积为98,故C 选项正确;假设C 与G 到平面AEF 的距离相等,即平面AEF 将CG 平分,则平面AEF 必过CG 中点,连接CG 交EF 于H ,而H 不是CG 中点,则假设不成立.故D 选项错误.故选BC .三、填空题(本大题共4小题,每小题5分,共20分)13.一个圆柱的侧面展开图是一个边长为1的正方形,则该圆柱的体积是__14π__. [解析] ∵圆柱的侧面展开图是边长为1的正方形, ∴该圆柱的高h =1,底面周长2πr =1,∴底面半径r =12π, ∴该圆柱的体积V =π×14π2×1=14π.14.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为__12__厘米.[解析] V =Sh =πr 2h =43πR 3,R =364×27=12(cm).15.已知a ,b 表示直线,α,β,γ表示平面.①若α∩β=a ,b ⊂α,a ⊥b ,则α⊥β;②若a ⊂α,a 垂直于β内任意一条直线,则α⊥β;③若α⊥β,α∩β=a ,α∩γ=b ,则a ⊥b ;④若a ⊥α,b ⊥β,a ∥b ,则α∥β.上述命题中,正确命题的序号是__②④__.[解析] 对①可举反例,如图,需b ⊥β才能推出α⊥β;对③可举反例说明,当γ不与α,β的交线垂直时,即可知a ,b 不垂直;根据面面、线面垂直的定义与判定知②④正确.16.(2020·全国Ⅰ卷理)如图,在三棱锥P -ABC 的平面展开图中,AC =1,AB =AD =3,AB ⊥AC ,AB ⊥AD ,∠CAE =30°,则cos ∠FCB = __-14__.[解析] ∵AB ⊥AC ,AB =3,AC =1,由勾股定理得BC =AB 2+AC 2=2,同理得BD =6,∴BF =BD =6,在△ACE 中,AC =1,AE =AD =3,∠CAE =30°, 由余弦定理得CE 2=AC 2+AE 2-2AC ·AE cos30°=1+3-2×1×3×32=1,∴CF =CE =1,在△BCF 中,BC =2,BF =6,CF =1, 由余弦定理得cos ∠FCB =CF 2+BC 2-BF 22CF ·BC=1+4-62×1×2=-14. 四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)某高速公路收费站入口处的安全标识墩如图所示,墩的上半部分是正四棱锥P -EFGH ,下半部分是长方体ABCD -EFGH .长方体的长、宽、高分别是40 cm 、40 cm 、20 cm ,正四棱锥P -EFGH 的高为60 cm.(1)求该安全标识墩的体积; (2)求该安全标识墩的侧面积.[解析] (1)该安全标识墩的体积V =V P -EFGH +V ABCD -EFGH =13×402×60+402×20=64 000(cm 3).(2)如图,连接EG ,HF 交于点O ,连接PO ,结合三视图可知OP =60 cm ,OG =12EG =20 2 cm ,可得PG =602+(202)2=2011(cm).于是四棱锥P -EFGH 的侧面积S 1=4×12×40×(2011)2-202=1 60010(cm 2), 四棱柱EFGH -ABCD 的侧面积S 2=4×40×20=3 200(cm 2), 故该安全标识墩的侧面积S =S 1+S 2=1 600(10+2)(cm 2).18.(本小题满分12分)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.[解析] 不会溢出杯子.理由如下:由题图可知半球的半径为4 cm ,所以V 半球=12×43πR 3=12×43π×43=1283π(cm 3),V 圆锥=13πr 2h =13π×42×12=64π(c m 3).因为V 半球<V 圆锥,所以如果冰淇淋融化了,不会溢出杯子.19.(本小题满分12分)如图所示,在四棱锥P -ABCD 中,侧面PAD ⊥底面ABCD ,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.(1)若CD∥平面PBO,试指出点O的位置;(2)求证:平面PAB⊥平面PCD.[解析](1)∵CD∥平面PBO,CD⊂平面ABCD,且平面ABCD∩平面PBO=BO,∴BO∥CD.又BC∥AD,∴四边形BCDO为平行四边形,则BC=DO,而AD=3BC,∴AD=3OD,即点O是靠近点D的线段AD的一个三等分点.(2)证明:∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,AB⊂底面ABCD,且AB⊥AD,∴AB⊥平面PAD.又PD⊂平面PAD,∴AB⊥PD.又PA⊥PD,AB∩PA=A,AB,PA⊂平面PAB,∴PD⊥平面PAB.又PD⊂平面PCD,∴平面PAB⊥平面PCD.20.(本小题满分12分)(2020·江苏卷)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.[解析](1)因为E,F分别是AC,B1C的中点,所以EF∥AB1.又EF⊄平面AB1C1,AB1⊂平面AB1C1,所以EF∥平面AB1C1.(2)因为B1C⊥平面ABC,AB⊂平面ABC,所以B1C⊥AB.又AB⊥AC,B1C⊂平面AB1C1,AC⊂平面AB1C,B1C∩AC=C,所以AB⊥平面AB1C.又因为AB⊂平面ABB1,所以平面AB1C⊥平面ABB1.21.(本小题满分12分)在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC 且分别交AC,SC于D,E,又SA=AB,SB=BC.(1)求证:BD⊥平面SAC;(2)求二面角E-BD-C的大小.[解析](1)证明:如图,∵DE⊥SC,且E为SC的中点,又SB=BC,∴BE⊥SC.又DE∩BE=E,根据直线与平面垂直的判定定理知SC⊥平面BDE,∵BD⊂平面BDE,∴SC⊥BD.又SA⊥平面ABC,BD⊂平面ABC,∴SA⊥BD.又SA∩SC=S,∴BD⊥平面SAC.(2)由(1)知∠EDC为二面角E-BD-C的平面角,又△SAC∽△DEC,∴∠EDC=∠ASC.在Rt△SAB中,∠SAB=90°,设SA=AB=1,则SB= 2.由SA⊥BC,AB⊥BC,AB∩SA=A,∴BC⊥平面SAB,SB⊂平面SAB,∴BC⊥SB.在Rt △SBC 中,SB =BC =2,∠SBC =90°,则SC =2. 在Rt △SAC 中,∠SAC =90°,SA =1,SC =2. ∴cos ∠ASC =SA SC =12,∴∠ASC =60°,即二面角E -BD -C 的大小为60°. 22.(本小题满分12分)如图,在三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC ,AC =BC ,AB =2A 1A =4,以AB ,BC 为邻边作平行四边形ABCD ,连接A 1D ,DC 1.(1)求证:DC 1∥平面A 1ABB 1; (2)若二面角A 1-DC -A 为45°. ①求证:平面A 1C 1D ⊥平面A 1AD ; ②求直线AB 1与平面A 1AD 所成角的正切值. [解析] (1)证明:连接AB 1, ∵AD ∥BC ∥B 1C 1且AD =BC =B 1C 1, ∴四边形ADC 1B 1为平行四边形, ∴AB 1∥DC 1,又∵AB 1⊂平面A 1ABB 1,DC 1⊄平面A 1ABB 1. ∴DC 1∥平面A 1ABB 1.(2)①证明:如图,取DC 的中点M ,连接A 1M ,AM .易知Rt △A 1AD ≌Rt △A 1AC , ∴A 1D =A 1C ,∴A 1M ⊥DC , 又AM ⊥DC ,∴∠A 1MA 为二面角A 1-DC -A 的平面角, ∴∠A 1MA =45°. ∴在Rt △A 1AM 中,AA 1=AM =2, ∴AD =AC =22,∴AC 2+AD 2=DC 2,∴AC ⊥AD ,又∵AC ⊥AA 1,AD ∩AA 1=A ,∴AC ⊥平面A 1AD . 又∵AC ∥A 1C 1,∴A 1C 1⊥平面A 1AD .∵A 1C 1⊂平面A 1C 1D , ∴平面A 1C 1D ⊥平面A 1AD . ②∵AB 1∥DC 1,∴DC 1与平面A 1AD 所成角等于AB 1与平面A 1AD 所成角. 由①知A 1C 1⊥平面A 1AD ,∴A 1D 为DC 1在平面A 1AD 内的射影, 故∠A 1DC 1为直线DC 1与平面A 1AD 所成角, 在Rt △A 1DC 1中,tan ∠A 1DC 1=A 1C 1A 1D =63, ∴直线AB 1与平面A 1AD 所成角的正切值为63.。
新教材人教版高一数学上册单元测试题含答案全套

新教材人教版高一数学上册单元测试题含答案全套人教版高中数学必修第一册第一章测试题集合与常用逻辑用语注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合,,则等于( )A .B .C .D .【答案】B【解析】集合,,.2.是的( )条件 A .充分不必要 B .必要不充分 C .充要 D .既不充分也不必要 【答案】B【解析】由不能推得,反之由可推得, 所以是的必要不充分条件. 3.已知集合,,若,则实数的值为( )A .B .C .D .【答案】B【解析】∵集合,,且,∴,因此. 4.下列命题中正确的是( ){}1,2,3,4,5A ={}21,B y y x x A ==-∈A B {2,4}{1,3,5}{2,4,7,9}{1,2,3,4,5,7,9}{}1,2,3,4,5A ={}{}21,1,3,5,7,9B y y x x A ==-∈={}1,3,5A B =1x >4x >1x >4x >4x >1x >1x >4x >{1,3}A =-2{2,}B a ={1,2,3,9}A B =-a 1±3±1-3{1,3}A =-2{2,}B a ={1,2,3,9}A B =-29a =3a =±A .任何一个集合必有两个以上的子集B .空集是任何集合的子集C .空集没有子集D .空集是任何集合的真子集 【答案】B【解析】空集只有一个子集,故A 错;B 正确; 空集是本身的子集,故C 错;空集不能是空集的真子集,故D 错. 5.已知集合,则中元素的个数为( )A .B .C .D .【答案】A【解析】因为集合,所以满足且,的点有,,,,,,,,共个.6.已知,则( )A .B .C .D .【答案】B 【解析】,故A 错,B 对,显然,所以C 不对,而,所以D 也不对,故本题选B .7.命题“存在实数,使”的否定是( ) A .对任意实数,都有 B .对任意实数,都有 C .不存在实数,使 D .存在实数, 【答案】B【解析】命题“存在实数,使”的否定是“对任意实数,都有”. 8.集合中的不能取的值的个数是( ) A .B .C .D .【答案】B【解析】由题意可知,且且, 故集合中的不能取的值的个数是个. 9.下列集合中,是空集的是( ) A . B .C .D .【答案】B(){}22,3,,A x y xy x y =+≤∈∈Z Z A 9854(){}22,3,,A x y xy x y =+≤∈∈Z Z 223x y +≤x ∈Z y ∈Z (1,1)--(1,0)-(1,1)-(0,1)-(0,0)(0,1)(1,1)-(1,0)(1,1)9a ={A x x =≥a A ∉a A ∈{}a A ={}a a ∉>a A ∈{}a A ≠{}a a ∈x 1x >x 1x >x 1x ≤x 1x ≤x 1x ≤x 1x >x 1x ≤{}22,4,0x x --x 2345222040224x x x x x -≠-≠⇒≠-≠⎧⎪⎨⎪⎩-2x ≠-1x ≠-{}22,4,0x x --x 3{}0|2x x +={}210,x x x +=∈R {}1|x x <(){}22,,,x y yx x y =-∈R【解析】对于A 选项,,不是空集, 对于B 选项,没有实数根,故为空集, 对于C 选项,显然不是空集,对于D 选项,集合为,故不是空集. 10.下列各组集合中表示同一集合的是( ) A ., B ., C ., D .,【答案】B【解析】对于A ,,表示点集,,表示数集,故不是同一集合; 对于B ,,,根据集合的无序性,集合表示同一集合; 对于C ,集合的元素是数,集合的元素是等式;对于D ,,集合的元素是点,, 集合的元素是点,集合不表示同一集合.11.学校先举办了一次田径运动会,某班共有名同学参赛,又举办了一次球类运动会,这个班有名同学参赛,两次运动会都参赛的有人.两次运动会中,这个班总共的参赛人数为( ) A . B . C . D . 【答案】B【解析】因为参加田径运动会的有名同学,参加球类运动会的有名同学,两次运动会都参加的有人,所以两次运动会中,这个班总共的参赛人数为.12.已知集合,.若, 则实数的取值范围为( ) A . B .C .D .【答案】D【解析】, 当为空集时,;当不为空集时,,综上所述得.第Ⅱ卷二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.集合,则集合的子集的个数为 个.2x =-210x +={(0,0)}{(3,2)}M ={3,2}N ={2,3}M ={3,2}N ={2,3}M ={2,3}N x y ==={(2,3)}M ={(5,4)}N ={(3,2)}M =M {3,2}N =N {2,3}M ={3,2}N =,M N M N {(2,3)}M =M (2,3){(5,4)}N =N (5,4),M N 8123201714238123812317+-={}|25A x x =-≤≤{}|121B x m x m =+≤≤-B A ⊆m 3m ≥23m ≤≤2m ≥3m ≤{}|121B x m x m =+≤≤-B 2112m m m -<+⇒<B 22152312m m m m ≥⎧⎪-≤⇒≤≤⎨⎪+≥-⎩3m ≤2{}1,A =A【答案】【解析】由已知,集合的子集个数为.14.命题“”是命题“”的 (“充分不必要,必要不充分,充要,既不充分也不必要”)条件. 【答案】必要不充分【解析】的解为或,所以当“”成立时,则“”未必成立; 若“”,则“”成立,故命题“”是命题“”的必要不充分条件.15.命题“,”的否定是 .【答案】,【解析】由全称量词命题的否定是存在量词命题可知,命题“,”的否定是“,”.16.设全集是实数集,,, 则图中阴影部分所表示的集合是 .【答案】【解析】由图可知,阴影部分为,∵,∴,∴.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)已知集合,且,求的取值集合. 【答案】.【解析】∵,∴或,即或.4A 224=220x x --=1x =-220x x --=1x =-2x =220x x --=1x =-1x =-220x x --=220x x --=1x =-x ∀∈R 23210x x -+>0x ∃∈R 2003210x x -+≤x ∀∈R 23210x x -+>0x ∃∈R 2003210x x -+≤U R {}22M x x x =<->或{}13N x x =<<{}12x x <≤Venn ()UN M {}22M x x x =<->或{}22UM x x -=≤≤(){}12UNM x x =<≤{}21,2,4M m m =++5M ∈m {}1,3{}251,2,4m m ∈++25m +=245m +=3m =1m =±当时,;当时,; 当时,不满足互异性, ∴的取值集合为{}1,3.18.(12分)已知集合,,若,求实数,的值.【答案】或.【解析】由已知,得①,解得或, 当时,集合不满足互异性, 当时,集合,集合,符合题意; ②,解得(舍)或,当时,集合,集合符合题意,综上所述,可得或.19.(12分)设集合,. (1)若,试判定集合与的关系; (2)若,求实数的取值集合.【答案】(1)是的真子集;(2).3m ={}1,5,13M =1m ={}1,3,5M =1m =-{}1,1,5M =m {,,2}A a b =2{2,,2}B b a =A B =a b 01a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩A B =22a a b b =⎧⎨=⎩00a b =⎧⎨=⎩01a b =⎧⎨=⎩00a b =⎧⎨=⎩{0,0,2}A =01a b =⎧⎨=⎩{0,1,2}A ={2,1,0}B =22a b b a ⎧=⎨=⎩00a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩11{,,2}42A =11{2,,}42B =01a b =⎧⎨=⎩1412a b ⎧=⎪⎪⎨⎪=⎪⎩{}28150A x x x =-+={}10B x ax =-=15a =A B B A ⊆a B A 110,,35⎧⎫⎨⎬⎩⎭【解析】(1),,∴是的真子集. (2)当时,满足,此时;当时,,集合,又,得或,解得或. 综上,实数的取值集合为.20.(12分)已知全集,集合,.求: (1),,;(2),;(3)设集合且,求的取值范围.【答案】(1)见解析;(2)见解析;(3). 【解析】(1),∵,,.(2),∴.(3)由(2)可知,∵,∴,解得.21.(12分)已知集合为全体实数集,,. (1)若,求;(2)若,求实数的取值范围. 【答案】(1);(2).【解析】(1)当时,,所以,所以.(2)①,即时,,此时满足.②当,即时,,由得,或, 所以.{3,5}A ={5}B =B A B =∅B A ⊆0a =B ≠∅0a ≠1B a ⎧⎫=⎨⎬⎩⎭B A ⊆13a =15a=13a =15a 110,,35⎧⎫⎨⎬⎩⎭{}6U x x =∈<N {}1,2,3A ={}2,4B =A B UA UB AB ()UA B {|21}C x a x a =-<≤-()UA CB ⊆a 3a ≥2A B ={0,1,2,3,4,5}U ={0,4,5}UA ={0,1,3,5}UB ={1,2,3,4}AB =(){0,5}UA B =(){0,5}UA B =()U A C B ⊆021521a a a a -<⎧⎪-≥⎨⎪->-⎩3a ≥U {}25M x x x =≤-≥或{}121N x a x a =+≤≤-3a =UMN N M ⊆a {}45Ux x x MN =<≥或{}24a a a <≥或3a ={}45|N x x =≤≤{}45UN x x x =<>或{}45Ux x x MN =<≥或211a a -<+2a <N =∅N M ⊆211a a -≥+2a ≥N ≠∅N M ⊆15a +≥212a -≤-4a ≥综上,实数的取值范围为.22.(12分)已知二次函数,非空集合.(1)当时,二次函数的最小值为,求实数的取值范围;(2)是否存在整数的值,使得“”是“二次函数的大值为”的充分条件, 如果存在,求出一个整数的值,如果不存在,请说明理由. 【答案】(1);(2)见解析.【解析】(1),当且仅当时,二次函数有最小值为,由已知时,二次函数的最小值为,则,所以. (2)二次函数,开口向上,对称轴为,作出二次函数图象如图所示,由“”是“二次函数的大值为”的充分条件, 即时,二次函数的最大值为,,即为,令,解得或,由图像可知,当或时,二次函数的最大值不等于,不符合充分条件, 则,即可取的整数值为,,,,任意一个.第一册第二章测试题一元二次函数、方程和不等式注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
第八章 立体几何初步 单元测试-2022-2023学年高一下学期数学人教A版(2019)必修第二册

2022-2023学年高一第二学期第八章《立体几何初步》单元测试(新人教A 版必修第二册)一、单项选择题(每小题5分,共40分)1、下列说法中正确的是 A .若一个平面内有3个不共线的点到另一个平面的距离相等,则这两个平面平行B .以直角三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥C .有两个面平行,其余各面都是四边形的几何体是棱柱D .过直线外一点有且仅有一条直线与该直线平行2、已知正三角形的边长为2,那么的直观图△的面积为 ABCD3、已知S 为圆锥的顶点,O为底面圆心,圆锥的体积为 ABCD4、如图:已知正四面体中E 在棱上,,G 为的重心,则异面直线与所成角为( )A. B. C. D. 5.已知直线,与平面,,,则能使成立的充分条件是 A .,B .,C .,D .,,6、如图,正方体的棱长为1,则下列四个命题错误的是 ()ABC ABC ∆A B C '''()SO =()ABCD CD 2EC DE =ABC V EG BD 30°45︒60︒90︒m n αβγαβ⊥()αγ⊥βγ⊥//m α//m β//m αm β⊥m n ⊥m αβ= n β⊂1111ABCD A B C D -()A .直线与平面所成的角等于B .点到面C .两条异面直线和所成的角为D .三棱柱7、端午佳节,人们有包粽子和吃粽子的习俗. 粽子主要分为南北两大派系,地方细分特色鲜明, 且形状各异. 裹蒸粽是广东肇庆地区最为出名的粽子, 是用当地特有的冬叶、水草包裹糯米、绿豆、猪肉、咸蛋黄等蒸制而成的金字塔形的粽子. 现将裹蒸粽看作一个正四面体, 其内部的咸蛋黄看作一个球体,那么,当咸蛋黄的体积为时,该裹蒸粽的高的最小值为A. B. C. D. 8、已知三棱锥中,,,三点在以为球心的球面上,若,,且三棱锥的半径为 A .2B.5C .13D 二、多项选择题(每小题5分,共20分,有多项符合要求,全部选对得5分,部分选对得2分,有选错得0分)9、高空走钢丝是杂技的一种,渊源于古代百戏的走索,演员手拿一根平衡杆,在一根两头拴住的钢丝上来回走动,并表演各种动作.在表演时,假定演员手中的平衡杆是笔直的,水平地面内一定存在直线与演员手中的平衡杆所在直线 A .垂直B .相交C .异面D .平行10、设,,表示不同的点,,表示不同的直线,,表示不同的平面,下列说法错误的是 A .若,,,则B .若,,,,则C .若,,,,,,则D .若,,,则11、如图,在菱形中,,,将沿折起,使到,点不落在底面内,若为线段的中点,则在翻折过程中,以下命题中正确的是 BC 11ABC D 4πC 11ABCD 1D C 1BC 4π1111AA D BB C -43π46810O ABC -A B C O 2AB BC ==120ABC ∠=︒O ABC -O ()()A B C n l αβ()l αβ= //n α//n β//n l A B l ∈A B α∉//l αA B α∈A B C β∈l αβ= C l ∈//αβl α⊂n β⊂//l n ABCD 2AB =3BAD π∠=ABD ∆BD A A 'A 'BCD M A C 'ABD ∆()A .四面体的体积的最大值为1B .存在某一位置,使得C .异面直线,所成的角为定值D .当二面角的余弦值为时,四面体12、四面体的四个顶点都在球的球面上,,,点,,分别为棱,,的中点,则下列说法正确的是 A .过点,,做四面体的截面,则该截面的面积为2B .四面体C .与的公垂线段的长为D .过作球的截面,则截面面积的最大值与最小值的比为二、填空题(每小题5分,共20分)13、将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积为 .14、在正方体中,为的中点,则直线与所成的角为 .15、某校高一级学生进行创客活动,利用3D 打印技术制作模型.如图,该模型为长方体挖去正四棱台后所得的几何体,其中,为增强其观赏性和耐用性,现对该模型表面镀上一层金属膜,每平方厘米需要金属,不考虑损耗,所需金属膜的质量为____________.A BCD '-BM CD ⊥BM A D 'A BD C '--13A BCD '-ABCD O 4AB BC CD DA ====AC BD ==EFG BC CD AD ()E F G ABCD ABCD AC BD E O 5:41111ABCD A B C D -P 11B D PB 1AD 1111ABCD A B C D -ABCD EFGH -122,6cm,4cm AB EF BF AB BC AA =====2mg mg16、如图,在长方体中,四边形是边长为4的正方形,,为棱的中点,为棱(包括端点)上的动点,则三棱锥外接球表面积的最小值是 .三 解答题(共6小题,共计70分)17、(10分)如图,在三棱锥中,平面,是直角三角形,,.,分别是棱,的中点.(1)证明:平面平面.(2)求三棱锥的体积.18.(12分)如图,在三棱锥中,,底面.1111ABCD A B C D -ABCD 13AA =E CD F 11C D A DEF -P ABC -PA ⊥ABC ABC ∆AC BC =6PA AB ==D E PB PC PAC ⊥ADE P ADE -P ABC -90ACB ∠=︒PA ⊥ABC(1)求证:平面平面;(2)若,,求与平面所成角的正弦值.19.(12分)如图,在直四棱柱中,四边形是平行四边形,是的中点,点是线段上,且.(1)证明:直线平面.(2)若,,,求点到平面的距离.20、(12分)如图,在四棱锥中,,,,分别为,的中点底面四边形是边长为2的菱形,且,交于点.(1)求证:平面;(2)二面角的平面角为,若.①求与底面所成角的大小;②求点到平面的距离.21、(12分)如图在直三棱柱中,,,,是上的一点,且,、、分别是、、的中点,与相交于.(Ⅰ)求证:平面;(Ⅱ)求证:平面平面;PAC ⊥PBC 2AC PA ==3BC =AB PBC 1111ABCD A B C D -ABCD F 1BD E 1CD 12D E CE =//AF BDE 13AA AB ==2AD =60BAD ∠=︒F BDE P ABCD -PB PD =PA PC ⊥M N PA BC ABCD 60DAB ∠=︒AC BD O //MN PCD B PC D --θ1cos 7θ=-PA ABCD N CDP 111ABC A B C -90ABC ∠=︒2BC =14CC =E 1BB 11EB =D F G 1CC 11B C 11A C EF 1B D H 1B D ⊥ABD //EFG ABD(Ⅲ)求平面与平面的距离.22、(12分)如图,在四棱锥,底面为梯形,且,,等边三角形所在的平面垂直于底面,.(1)求证:平面;(2)若直线与平面,求二面角的余弦值.参考答案1、D2、D3、B4、A5、C6、C7、A8、D 8、【解析】设的外接圆的圆心为,半径为,在中,,,由余弦定理可得,由正弦定理可得,解得,所以又三棱锥所以EGF ABD P ABCD -ABCD 12BC AD =//BC AD PCD ABCD BC PD ⊥BC ⊥PCD PB ABCD P AB D --ABC ∆1O r ABC ∆2AB BC ==120ABC ∠=︒222cos AC AB BC AB BC ABC =+-⋅⋅∠=24sin AC r ABC ===∠2r =11sin 2222ABC S AB BC ABC ∆=⋅⋅⋅∠=⨯⨯=O ABC -111133O ABC ABC V S OO OO -∆=⋅⋅==故三棱锥的高,所以球.9、AC10、BCD 11、ABD 12、ACD9、【解析】根据题意可得:对直线与平面的任何位置关系,平面内均存在直线与直线垂直,A 正确;平衡杆所在直线与水平地面的位置关系:平行或相交,根据线面关系可知:若直线与平面平行,则该直线与平面内的直线的位置关系:平行或异面,若直线与平面相交,则该直线与平面内的直线的位置关系:相交或异面,C 正确,B 、D 错误;【答案】AC11、【解析】连接交于,连接,取的中点,连接,,对于A ,当平面平面时,四面体的体积最大,点到平面的距离最大,此时在菱形中,,则,都是等边三角形,则,此时四面体的体积为,所以四面体的体积的最大值为1,故A 正确;对于B ,因为,分别为,的中点,所以,且,由题意,则,当时,,因为,O ABC -13OO =O =l l AC BD O OA 'CD N MN BN A BD '⊥BCD A BCD '-A 'BCD ABCD 2AB =3BAD π∠=ABD ∆BCD ∆OA OA OC '===A BCD '-112132⨯⨯=A BCD '-M N C 'CD BN CD ⊥//MN A D '112MN A D ='=2(0,)3A DC π∠'∈2(0,3MNC π∠∈2MNC π∠=MN CD ⊥MN BN N =所以当时,平面,又平面,所以,所以存在某一位置,使得,故B正确;对于C,因为,所以异面直线,所成的角即为或其补角,,因为不为定值,所以不为定值,即异面直线,,所成的角不为定值,故C错误;对于D,因为,,所以即为二面角的平面角,则,所以,所以四面体为正四面体,如图,补全正四面体,即四面体的D正确.【答案】ABD12、【解析】如图所示:取中点,连结、,则有:,且,同理可得,且所以,且为平行四边形,2MNCπ∠=CD⊥BMNBM⊂BMN CD BM⊥BM CD⊥//MN A D'BM A D'BMN∠2131cos22BM BMBMNBM BM+-∠==-BM cos BMN∠BM A D'OC BD⊥OA BD'⊥A OC∠'A BD C'--26163A CA OC-'∠'==2A C'=A BCD'-A BCD'-=A BCD'-AB H EH HG//HG BD12GH BD==//EF BD12EF BD== //HG EF HG EF==EFGH同理可得,且,所以平行四边形的菱形;取中点,连结、,因为,所以,同理,所以平面,所以,又因为,,所以,所以菱形的正方形,所以,故A 正确;因为,,,所以,同理可得,在中,,所以边上的高,又因为平面,为中点,所以,故B 错;因为平面,平面,所以,又因为,所以是与的公垂线,由选项可知,故C 正确;取中点,则为球心,理由如下:因为平面,,所以,同理,,所以,所以即为球心,所以,又因为,所以过所作的面积最小的截面是以为圆心,为半径的圆;面积最大的截面是过,的大圆,//HE GF HE GF ==EFGH BD Q AQ CQ AB AD =AQ BD ⊥CQ BD ⊥BD ⊥ACQ BD AC ⊥//HG BD //HE AC HG HE ⊥EFGH 2EFGH S =4AB AD ==BD =AQ BD ⊥BQ DQ ==AQ =CQ =ACQ ∆AQ CQ ==AC =AC QM ==12ACQ S AC QM ∆=⋅⋅=BD ⊥ACQ Q BD 1122233A BCD B ACQ ACQ V V S BQ --∆==⨯⨯=⨯⨯=BD ⊥ACQ QM ⊆ACQ BD QM ⊥QM AC ⊥QM AC BD B QM =QM S S O BD ⊥ACQ BQ DQ =12QS QM ==225SB SD ==12MS QM ==225SA SC ==SA SB SC SD ====S O R =OE BC ⊥E E 2BE =O E所以,故D 正确.13、 14、15、16、15、【详解】由题意,该几何体侧面4个面的面积和为,底面积,正方形面积.考虑梯形,高为,故正四棱台的侧面积为,故该模型表面积为,故所需金属膜的质量为16、【解析】如图,取的中点,过作平面的垂线,与平面交于点,过作的垂线,垂足为,则三棱锥外接球的球心在上,设,,则,设球的半径为,则,即,所以.因为,所以,则.()()22::5:4S S R BE ππ==大小2π6π282+2449π244696cm ⨯⨯=26636cm ⨯=EFGH 2339cm ⨯=ABFE =()214362⨯+=(296369141cm +++=+((2141282mg⨯+=+AE 1O 1O ABCD 1111A B C D M M 11C D N E ADF -O 1MO 1OO m =NF n =03n ……O R 222R OE OF ==22222225(3)4R m OM MN NF m n =+=++=-++286n m +=03n ......41736m (2261)59R m =+…故三棱锥外接球的表面积.17、(1)证明:因为是直角三角形,且,所以.因为平面,且平面,所以.因为平面,平面,且,所以平面.因为,分别是棱,的中点,所以,,因为平面,所以平面.因为平面,所以平面平面.(2)解:因为,所以因为平面,且,所以三棱锥的体积.连接,因为是棱的中点,所以三棱锥的体积.因为是棱的中点,所以三棱锥的体积.因为三棱锥与三棱锥是同一个三棱锥,所以的体积为.18.(1)证明:底面.,又,,又,平面,又平面,平面平面;(2)解:取的中点,连接、,,,又平面平面且交线为,平面,A DEF -224449S R ππ=…ABC ∆AC BC =AC BC ⊥PA ⊥ABC BC ⊂ABC PA BC ⊥PA ⊂PAC AC ⊂PAC PA AC A = BC ⊥PAC D E PB PC 12DE BC =//DE BC BC ⊥PAC DE ⊥PAC DE ⊂ADE PAC ⊥ADE 6AB =AC BC ==PA ⊥ABC 6PA =P ABC -1161832V =⨯⨯=CD D PB D PAC -11118922V ==⨯=E PC D PAE -211199222V V ==⨯=P ADE -D PAE -P ADE -92PA ⊥ ABC PA BC ∴⊥90ACB ∠=︒ AC BC ∴⊥PA AC A = BC ∴⊥PAC BC ⊂PBC ∴PBC ⊥PAC PC O AO BO PA AC = AO PC ∴⊥ PBC ⊥PAC PC AO ∴⊥PBC直线在平面中的射影为,为与平面所成的角,在直角中,,,.19.(1)证明:连接,记,连接.取线段的中点,连接,.因为四边形是平行四边形,所以是的中点.因为是的中点,且,所以是的中点,因为,分别是,的中点,所以.因为平面,平面,所以平面.因为,分别是,的中点,所以.因为平面,平面,所以平面.因为平面,平面,且,所以平面平面.因为平面,所以平面.(2)解:由(1)可知平面,则点到平面的距离等于点到平面的距离.因为,,,所以的面积为作,垂足为,连接,则平面.因为,所以,,则.因为,,,所以AB PBC OB ABO ∴∠AB PBC AOB ∆AB =AO =∴sin ABO ∠=AC AC BD O = OE 1D E H AH HF ABCD O AC H 1D E 12D E CE =E HC O E AC HC //OE AH OE ⊂BDE AH ⊂/BDE //AH BDE H F 1D E 1BD //HF BE BE ⊂BDE HF ⊂/BDE //HF BDE AH ⊂AHF HF ⊂AHF AH HF H = //AHF BDE AF ⊂AHF //AF BDE //AF BDE F BDE A BDE 2AD =3AB =60BAD ∠=︒ABD ∆1sin 2AD AB BAD ⋅∠=EG CD ⊥G BG EG ⊥ABCD 12D E CE =1113EG DD ==22DG GC ==DE =3AB =2AD =60BAD ∠=︒BD因为,,,所以,则.在中,由余弦定理可得.故的面积为.设点到平面的距离为,因为三棱锥的体积等于三棱锥的体积,所以,解得到平面20、(1)证明:取得中点,连接,,如图,为的中点,,为的中点且四边形为菱形,,,,四边形为平行四边形,,又平面,平面,平面;(2)解:①连接,过作于,连接,,由,是的中点,,由菱形知,又,平面,平面,平面平面,且交线为,直线在平面上的射影为,即与底面所成角为,平面,,且在平面上的射影为,,又,,是的中点,是的中点,,由知,,,为二面角的平面角,,1CG =2BC =60BCG ∠=︒BG =2BE =BDE ∆cos BED ∠==sin BED ∠=BDE ∆11sin 222BE DE BED ⋅∠=⨯=F BDE h E ABD -A BDE -11133=h =F BDE PD E ME CE M PA ∴1,//2ME AD ME AD =N BC ABCD ∴1//,2NC AD NC AD =//NC ME ∴NC ME =∴MNCE //MN EC ∴MN ⊂/PCD CE ⊂PCD //MN ∴PCD PO B BF PC ⊥F DF OF PB PD =O BD PO BD ∴⊥ABCD AC BD ⊥PO AC O = BD ∴⊥PAC BD ⊂ ABCD ∴PAC ⊥ABCD AC ∴PA ABCD AC PA ABCD PAC ∠BD ⊥ PAC BF PC ⊥BF PAC OF OF PC ∴⊥PA PC ⊥//OF PA ∴O BD F ∴PC 2PB BC ∴==BPC DPC ∆≅∆DF PC ⊥BF DF =BFD ∴∠B PC D --∴2222222162cos 277BD BF DF BF DF BFD BF BF BF =+-⋅∠=+=即,解得,,,,,即与底面所成角的大小为;②连接,过作于,由,平面,平面,平面,点到平面的距离即点到平面的距离,,,,平面,平面平面,且是交线,,平面,在中,,由等积法可得,即,即点到平面.21、(12分)(Ⅰ)证明:由直三棱柱的性质,得平面平面,又,平面,又平面,,,在和△中,,,即,又,平面.(Ⅱ)证明:由题意知,在△中,,又,,平面,不包含于平面,平面,、分别为、的中点,,又,,,不包含平面,平面,平面,平面,,平面平面.(Ⅲ)解:平面,平面平面,平面,为平行平面与之间的距离,21647BF =274BF =∴23PC FC ===∴sin 2PC PC PAC AC AO ∠====090PAC ︒∠︒ ……60PAC ∴∠=︒PA ABCD 60︒ON O OG FD ⊥G //ON CD ON ⊂/PCD CD ⊂PCD //ON ∴PCD ∴N CDP O CDP BF PC ⊥ DF PC ⊥BF DF F = PC ∴⊥BFD ∴PCD ⊥BDF DF OG FD ⊥ OG ∴⊥PCD Rt OFD ∆1,OF OD DF ===OF OD FD OG ⋅=⋅OG =N CDP ABC ⊥11BB C C AB BC ⊥AB ∴⊥11BB C C 1B D ⊂11BB C C 1AB B D ∴⊥1112BC CD DC B C ==== ∴Rt BCD ∆Rt 11DC B 1145BDC B DC ∠=∠=︒190BDB ∴∠=︒1B D BD ⊥AB BD B = 1B D ∴⊥ABD 111EB B F ==∴Rt 1EB F 145FEB ∠=︒145DBB ∠=︒//EF BD ∴BD ⊂ ABD EF ABD //EF ∴ABD G F 11A C 11B C 11//GF A B ∴11//A B AB //GF AB ∴\AB ABD ⊂ 平面GF ABD //GF ∴ABD EF ⊂ EFG GF ⊂EFG EF GF F = ∴//EFG ABD 1B D ⊥ ABD //EGF ABD 1B D ∴⊥EGF HD ∴EFG ABD.22、证明:(1)如图所示,取中点,连接,是正三角形,又平面平面,且平面平面,平面,平面,,,且,平面;如图所示,连接,,过点,作,,分别与交于点,,过点作,交于点,连接,设,,,则,由(1)得平面,即为直线与平面所成角的平面角,平面,,则,解得:,故,,解得又,所以平面,,,,解得所以点为线段的中点,故点也为线段中点,11HD B D B H ∴=-==CD O PO PCD ∆ PO CD∴⊥PCD ⊥ABCD PCD ⋂ABCD CD =PO ∴⊥ABCD BC ⊂ABCD PO BC ∴⊥BC PD ⊥ PO PD P = BC ∴⊥PCD OB BD D P DM AB ⊥PN AB ⊥AB M N M //MQ NP AP Q DQ 22AD BC ==2CD a =0a >OP =OP ⊥ABCD OBP ∴∠PB ABCD BC ⊥PCD BC CP ∴⊥OP PB OBP BP =∠===1a =BD AB ====BM AM =DM //BC AD AD ⊥PCD AD PD ⊥PA ===BN AN PN ===M AN Q AP所以,所以即为二面角的平面角,.12QM PN DQ ===DMQ ∠P AB D --222cos 2DM QM DQ DMQ DM QM +-∠===⋅。
人教版高一数学必修第二册同步单元测试卷第08章 立体几何初步(B卷提高篇)原卷版

第八章立体几何初步B(提高卷)试卷副标题考试范围:xxx;考试时间:100分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________题号一二三四总分得分第Ⅰ卷(选择题)请点击修改第I卷的文字说明评卷人得分一.选择题(共8小题)1.(2019春•辽宁期中)直角三角形的三边满足a<b<c,分别以a,b,c三边为轴将三角形旋转一周所得旋转体的体积记为V a,V b,V c,则()A.V c<V b<V a B.V a<V b<V c C.V c<V a<V b D.V b<V a<V c2.(2020•大连二模)已知三棱锥P﹣ABC,面P AB⊥面ABC,P A=PB=4,,∠ACB=90°,则三棱锥P ﹣ABC外接球的表面积()A.20πB.32πC.64πD.80π3.(2020•泰安模拟)我国古代数学名著《九章算术》中记载:“刍甍者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”今有底面为正方形的屋脊形状的多面体(如图所示),下底面是边长为2的正方形,上棱,EF ∥平面ABCD,EF与平面ABCD的距离为2,该刍甍的体积为()A.6 B.C.D.124.(2020•全国Ⅰ卷模拟)已知O为等腰直角三角形POD的直角顶点,以OP为旋转轴旋转一周得到几何体,CD 是底面圆O上的弦,△COD为等边三角形,则异面直线OC与PD所成角的余弦值为()A.B.C.D.5.(2020•合肥模拟)已知四棱锥S﹣ABCD中,四边形ABCD为等腰梯形,AD∥BC,∠BAD=120°,△SAD是等边三角形,且SA=AB=2,若点P在四棱锥S﹣ABCD的外接球面上运动,记点P到平面ABCD的距离为d,若平面SAD⊥平面ABCD,则d的最大值为()A. 1 B. 2 C. 1 D. 26.(2020•葫芦岛模拟)正方体ABCD﹣A1B1C1D1的棱长为2,在A,B,C,D,C1,D1这六个顶点中,选择两个点与A1,B1构成正三棱锥P,在剩下的四个顶点中选择两个点与A1,B1构成正三棱锥Q,M表示P与Q的公共部分,则M的体积为()A.B.C.D.17.(2020•广东二模)如图,在矩形ABCD中,已知AB=2AD=2a,E是AB的中点,将△ADE沿直线DE翻折成△A1DE,连接A1C.若当三棱锥A1﹣CDE的体积取得最大值时,三棱锥A1﹣CDE外接球的体积为π,则a=()A.2 B.C.2D.48.(2020•新疆模拟)半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形为面的多面体,体现了数学的对称美.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,如此共可截去八个三棱锥,得到一个有十四个面的半正多面体,它们的棱长都相等,其中八个为正三角形,六个为正方形,称这样的半正多面体为二十四等边体.一个二十四等边体的各个顶点都在同一个球面上,若该球的表面积为16π,则该二十四等边体的表面积为()A.B.C.D.第Ⅱ卷(非选择题)请点击修改第Ⅱ卷的文字说明评卷人得分二.多选题(共4小题)9.(2020春•宝应县期中)如图所示,P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,下列结论正确的是()A.OM∥PD B.OM∥平面PCD C.OM∥平面PDA D.OM∥平面PBA 10.(2020•山东模拟)已知α、β是两个不同的平面,m、n是两条不同的直线,下列说法中正确的是()A.若m⊥α,m∥n,n⊂β,则α⊥βB.若α∥β,m⊥α,n⊥β,则m∥nC.若α∥β,m⊂α,n⊂β,则m∥nD.若α⊥β,m⊂α,α∩β=n,m⊥n,则m⊥β11.(2020•市中区校级模拟)《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”;四个面均为直角三角形的四面体称为“鳖膈”.如图在堑堵ABC﹣A1B1C1中,AC⊥BC,且AA1=AB=2.下列说法正确的是()A.四棱锥B﹣A1ACC1为“阳马”B.四面体A1C1CB为“鳖膈”C.四棱锥B﹣A1ACC1体积最大为D.过A点分别作AE⊥A1B于点E,AF⊥A1C于点F,则EF⊥A1B12.(2020•4月份模拟)如图,正方体ABCD﹣A1B1C1D1的棱长为a,线段B1D1上有两个动点E,F,且EF a,以下结论正确的有()A.AC⊥BEB.点A到△BEF的距离为定值C.三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的D.异面直线AE,BF所成的角为定值评卷人得分三.填空题(共4小题)13.(2020•昆山市模拟)在长方体ABCD﹣A1B1C1D1中,AB=4,AD=4,AA1=3,若在长方体中挖去一个体积最大的圆柱,则此圆柱与原长方体的体积比为.14.(2020•珠海三模)在三棱锥P﹣ABC中,平面P AB⊥平面ABC,△ABC是边长为2的正三角形,△P AB是以AB为斜边的直角三角形,则该三棱锥外接球的表面积为.15.(2020•中山区校级一模)如图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后、左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体有个面,其体积为.16.(2020春•江西月考)在四棱锥P﹣ABCD中,底面ABCD为正方形,平面P AD⊥平面ABCD,且△P AD为等边三角形,若四棱锥P﹣ABCD的体积与四棱锥P﹣ABCD外接球的表面积大小之比为,则正方形ABCD 的边长为.评卷人得分四.参考解答题(共5小题)17.(2020•新课标Ⅰ)如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P为DO上一点,∠APC=90°.(1)证明:平面P AB⊥平面P AC;(2)设DO,圆锥的侧面积为π,求三棱锥P﹣ABC的体积.18.(2020春•房山区期末)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,平面P AD⊥平面ABCD,P A=PD =AD=2,AB=3.点M,N分别是AB,PC的中点.(Ⅰ)求证:MN∥平面P AD;(Ⅱ)求四棱锥P﹣ABCD的体积;(Ⅲ)在棱CD上是否存在一点T,使得直线BT⊥PC?请给出你的判断,并说明理由.19.(2020•宜昌模拟)已知菱形ABCD的边长为2,∠ABC=60°,对角线AC、BD交于点O,平面外一点P在平面ABCD内的射影为O,PB与平面ABCD所成角为30°.(1)求证:BD⊥P A;(2)点N在线段PB上,且,求的值.20.(2020春•东城区校级月考)如图,在三棱柱ABC﹣A1B1C1中,BB1⊥平面ABC,AB⊥BC,AA1=AB=BC=2.(Ⅰ)求证:BC1⊥平面A1B1C;(Ⅱ)求异面直线B1C与A1B所成角的大小;(Ⅲ)点M在线段B1C上,且,点N在线段A1B上,若MN∥平面A1ACC1,求的值.21.(2020•重庆模拟)如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.(Ⅰ)求证:平面BFC⊥平面BDC;(Ⅱ)若直线DF与平面BCDE所成角的正切值为,求点C到平面DEF的距离.。
高一数学必修第一二章测试题及答案

第一.二章三角函数单元检测试卷一、选择题:本答题共12小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是符合题目要求的;1.在平行四边形ABCD 中,BD CD AB +-等于A .DBB .ADC .ABD .AC2.若|a |=2,|b |=5,|a +b |=4,则|a -b |的值A .13B .3C .42D .73.函数sin(2)3y x π=+图像的对称轴方程可能是A .6x π=-B .12x π=-C .6x π=D .12x π=5.点Ax,y 是300°角终边上异于原点的一点,则xy值为 333333函数)32sin(π-=x y 的单调递增区间是A .⎥⎦⎤⎢⎣⎡+-125,12ππππk k Z k ∈ B .⎥⎦⎤⎢⎣⎡+-1252,122ππππk k Z k ∈ C .⎥⎦⎤⎢⎣⎡+-65,6ππππk k Z k ∈ D .⎥⎦⎤⎢⎣⎡+-652,62ππππk k Z k ∈ 7.sin -310π的值等于 A .21B .-21C .23D .-238.在△ABC 中,若)sin()sin(C B A C B A +-=-+,则△ABC 必是 A .等腰三角形B .直角三角形C .等腰或直角三角形D .等腰直角三角9.函数x x y sin sin -=的值域是A .0B .[]1,1-C .[]1,0D .[]0,2-10.函数x x y sin sin -=的值域是A .[]1,1-B .[]2,0C .[]2,2-D .[]0,2-11.函数x x y tan sin +=的奇偶性是A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数 12.比较大小,正确的是 A .5sin 3sin )5sin(<<- B .5sin 3sin )5sin(>>-C .5sin )5sin(3sin <-<D .5sin )5sin(3sin >->二、填空题每小题5分,共20分13.终边在坐标轴上的角的集合为_________.14.已知扇形的周长等于它所在圆的周长的一半,则这个扇形的圆心角是________________. 15.已知角α的终边经过点P-5,12,则sin α+2cos α的值为______.16.一个扇形的周长是6厘米,该扇形的中心角是1弧度,该扇形的面积是________________. 三、解答题:本大题共6小题,共70分;解答应写出文字说明及演算步骤.; 17.8分已知tan 3α=-,且α是第二象限的角,求αsin 和αcos ; 18.10分已知3tan =α,计算ααααsin 3cos 5cos 2sin 4+-的值;19.12分求函数)32tan(π+=x y 的定义域和单调区间. 第一章三角函数单元检测试卷参考答案一、选择题每小题5分,共60分1----6、BBDCBA7----12、CCDCAB 二、填空题每小题5分,共20分13.{α|}Z n n ∈=,2πα14.rad )2(-π 132三、解答题共70分17.1sin ,cos αα==2tan 2α=18.解、∵3tan =α∴0cos ≠α∴原式=ααααααcos 1)sin 3cos 5(cos 1)cos 2sin 4(⨯+⨯- =ααtan 352tan 4+- =335234⨯+-⨯ =7519.解:函数自变量x 应满足πππk x +≠+232,z k ∈,即ππk x 23+≠,z k ∈所以函数的定义域是⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,23ππ; 由ππk +-2<32π+x <ππk +2,z k ∈,解得ππk 235+-<x <ππk 23+,z k ∈所以,函数的单调递增区间是)23,235(ππππk k ++-,z k ∈;20.解:令t=cosx,则]1,1[t -∈所以函数解析式可化为:453y 2++-=t t =2)23(2+--t 因为]1,1[-∈t ,所以由二次函数的图像可知:当23=t 时,函数有最大值为2,此时Z k k x ∈++=k 611262,或ππππ 当t=-1时,函数有最小值为341-,此时Z k ∈+=k 2x ,ππ 21解:32π函数的最小正周期为 ,3322===∴ωπωπ即T又2-函数的最小值为 ,2=∴A 所以函数解析式可写为)3sin(2y ϕ+=x又因为函数图像过点95π,0, 所以有:0)953(sin 2=+⨯ϕπ解得35ππϕ-=k 323,ππϕπϕ-=∴≤或 所以,函数解析式为:)323sin(2y )33sin(2y ππ-=+=x x 或 22.解:Ⅰ8x π=是函数)(x f y =的图象的对称轴Ⅱ由Ⅰ知34πϕ=-,因此3sin(2)4y xπ=-由题意得3222,242k x k k Z πππππ-≤-≤+∈所以函数3sin(2)4y xπ=-的单调递增区间为Ⅲ由3sin(2)4y xπ=-可知故函数)(xfy=在区间[]0,π上的图象是。
高一(上)数学第二章函数单元测试题7-8 人教版

高一(上)数学第二章函数单元测试题7-8(时间:45分钟 满分100分)一、 选择题1.若3a=2,则log 38-2log 36用a 的代数式可表示为( )(A )a-2 (B )3a-(1+a)2 (C )5a-2 (D )3a-a 22.2log a (M-2N)=log a M+log a N,则NM的值为( ) (A )41(B )4 (C )1 (D )4或1 3.已知x 2+y 2=1,x>0,y>0,且log a (1+x)=m,logaya n xlog ,11则=-等于( ) (A )m+n (B )m-n (C )21(m+n) (D )21(m-n)4.如果方程lg2x+(lg5+lg7)lgx+lg5·lg7=0的两根是α、β,则α·β的值是( ) (A )lg5·lg7(B )lg35(C )35 (D )351 5.已知log 7[log 3(log 2x)]=0,那么x 21-等于( )(A )31(B )321 (C )221 (D )331 6.函数y=lg (112-+x)的图像关于( ) (A )x 轴对称 (B )y 轴对称 (C )原点对称 (D )直线y=x 对称 7.函数y=log 2x-123-x 的定义域是( )(A )(32,1)⋃(1,+∞) (B )(21,1)⋃(1,+∞) (C )(32,+∞) (D )(21,+∞)8.函数y=log 21(x 2-6x+17)的值域是( )(A )R (B )[8,+∞](C )(-∞,-3) (D )[3,+∞] 9.函数y=log 21(2x 2-3x+1)的递减区间为( )(A )(1,+∞) (B )(-∞,43] (C )(21,+∞) (D )(-∞,21]10.函数y=(21)2x +1+2,(x<0)的反函数为( )(A )y=-)2(1log )2(21>--x x (B ))2(1log )2(21>--x x(C )y=-)252(1log )2(21<<--x x (D )y=-)252(1log )2(21<<--x x11.若log m 9<log n 9<0,那么m,n 满足的条件是( )(A )m>n>1 (B )n>m>1 (C )0<n<m<1 (D )0<m<n<112.log a132<,则a 的取值X 围是( ) (A )(0,32)⋃(1,+∞) (B )(32,+∞)(C )(1,32) (D )(0,32)⋃(32,+∞)13.若1<x<b,a=log 2b x,c=log a x,则a,b,c 的关系是( )(A )a<b<c (B )a<c<b (C )c<b<a (D )c<a<b 14.下列函数中,在(0,2)上为增函数的是( ) (A )y=log 21(x+1) (B )y=log 212-x(C )y=log 2x 1(D )y=log 21(x 2-4x+5) 15.下列函数中,同时满足:有反函数,是奇函数,定义域和值域相同的函数是( )(A )y=2x x e e -+(B )y=lg xx+-11(C )y=-x3(D )y=x16.已知函数y=log a (2-ax)在[0,1]上是x 的减函数,则a 的取值X 围是( )(A )(0,1) (B )(1,2) (C )(0,2) (D )[2,+∞) 17.已知g(x)=log a 1+x (a>0且a ≠1)在(-1,0)上有g(x)>0,则f(x)=a1+x 是( )(A )在(-∞,0)上的增函数 (B )在(-∞,0)上的减函数 (C )在(-∞,-1)上的增函数 (D )在(-∞,-1)上的减函数18.若0<a<1,b>1,则M=a b ,N=log b a,p=b a的大小是( ) (A )M<N<P (B )N<M<P (C )P<M<N (D )P<N<M19.“等式log 3x 2=2成立”是“等式log 3x=1成立”的( ) (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件 20.已知函数f(x)=x lg ,0<a<b,且f(a)>f(b),则( )(A )ab>1 (B )ab<1 (C )ab=1 (D )(a-1)(b-1)>0 二、填空题1.若log a 2=m,log a 3=n,a 2m+n=。
湖北省某校高一(上)数学单元测试卷(有答案)

湖北省某校高一(上)数学单元测试卷一、选择题(本大题共12小题,每小题5分,共60分)1. 下列各组对象解构不成集合的有()(1)所有的长方体(2)英德市区内的所有大超市(3)所有的数学难题(4)函数y=x图象上所有的点(5)英德华侨茶场2003年生产的所有茶叶(6)2014附近的数.A.(1)(4)(5)B.(1)(2)(4)C.(1)(5)(6)D.(2)(3)(6)2. 如果M={x|x+1>0},则()A.⌀∈MB.0⊊MC.{0}∈MD.{0}⊆M3. 设全集为R,函数f(x)=√x2−1的定义域为M,则M为()A.(−∞, −1)∪(1, +∞)B.[0, 1)C.(0, 1]D.(−∞, −1]∪[1, +∞)4. 已知U={x|−1≤x≤3},A={x|−1≤x<3},B={x|x2−2x−3=0},C= {x|−1<x<3},则有()A.A⊇CB.C∪B=CC.B∩U=CD.C∪A=B5. 设集合P={立方后等于自身的数},那么集合P的真子集的个数是()A.3B.4C.7D.86. 已知集合A={y|y=−x2+3,x∈R},B={x|y=√x+3},则A∩B=()A.{(0, 3), (1, 2)}B.(−3, −3)C.[−3, 3]D.{y|y≤3}7. 与y=|x|为相等函数的是( )A.y=(√x)2B.y=√x2C.y={x,(x>0)−x,(x<0) D.y=√x 338. 如果函数f(x)=x2+2(a−1)x+2在区间(−∞, 2]上单调递减,那么实数a的取值A.a ≤−2B.a ≥−2C.a ≤−1D.a ≥19. 若偶函数f(x)在(−∞, −1]上是增函数,则下列关系式中成立的是( )A.f(−32)<f(−1)<f(2)B.f(−1)<f(−32)<f(2)C.f(2)<f(−1)<f(−32)D.f(2)<f(−32)<f(−1)10. 已知函数f(x)={x 2,x ≥0x +1,x <0,则f[f(−2)]的值为( ) A.0B.1C.2D.311. 下列各图中,可表示函数y =f(x)的图象的只可能是( )A. B.C.D.12. 图中阴影部分所表示的集合是( )A.B ∩[∁U (A ∪C)]B.(B ∪C)∩(∁U A)C.(A ∪C)∩(∁U B)D.(∁U A)∩B二、填空题(本大题共4小题,每小题5分,共20分)若函数f(x)=x 2−2x(x ∈[0, 4]),则f(x)的最小值是________.奇函数f(x)在(−∞, 0)上的解析式为f(x)=2x +1,则f(x)在(0, +∞)上的解析式为________.已知f(x)=x5+ax3+bx−8,若f(−2)=10,则f(2)=________.对于定义域为D的函数f(x),若存在x0∈D,使f(x0)=x0,则称点(x0, x0)为f(x)图象上的一个不动点.由此函数f(x)=4x的图象上不动点的坐标为________.三、解答题(本大题共6小题,共70分)求下列函数的定义域(1)y=√1−x+√x+3−1;(2)y=12−|x|+√x2−1.已知集合A={x|a−1<x<2a+1},B={x|0<x<1},(1)若A∩B=⌀,求a的取值范围;(2)若A∪B=B,求a的取值范围.(1)判断函数f(x)=x3+1x3的奇偶性;(2)判断函数f(x)=xx2−1在(−1, 1)内的单调性并用单调性的定义证明.已知集合P={x|x2+6x+9=0},Q={x|ax+1=0}满足Q⊆P,求a的一切值.已知函数f(x)={4−x2(x>0) 2(x=0)1−2x(x<0)求:(2)求f(f(3))的值;(3)当−4≤x<3时,求f(x)取值的集合.,x∈(0, +∞)取最小值时x的值,列表如下:探究函数f(x)=x+4x请观察表中y值随x值变化的特点,完成以下的问题:(1)函数(x)=x+4(x>0)在区间(0, 2)上递减;函数f(x)在区间________上递增.当xx=________ 时,y min=________.(2)证明:函数f(x)=x+4(x>0)在区间(0, 2)上递减.x参考答案与试题解析湖北省某校高一(上)数学单元测试卷一、选择题(本大题共12小题,每小题5分,共60分)1.【答案】D【考点】集合的含义与表示【解析】通过对选项判断集合中元素是否具有确定性即可判断.【解答】解:(1)所有的长方体,其中的对象是明确的,能构成集合;(2)英德市区内的所有大超市,其中的对象大超市不是明确的,不能构成集合;(3)所有的数学难题,其中的对象难题不是明确的,不能构成集合;(4)函数y=x图象上所有的点,其中的对象是明确的,能构成集合;(5)英德华侨茶场2003年生产的所有茶叶,其中的对象是明确的,能构成集合;(6)2014附近的数.其中的对象附近的数不是明确的,不能构成集合;故选:D.2.【答案】D【考点】子集与真子集【解析】由于M={x|x+1>0}={x|x>−1}.利用元素与集合、集合之间的关系可得:⌀⊊M,0∈M,{0}⊆M.【解答】解:M={x|x+1>0}={x|x>−1}.可得⌀⊊M,0∈M,{0}⊆M.因此A,B,C不正确,只有D正确.故选:D.3.【答案】D【考点】函数的定义域及其求法【解析】根据函数成立的条件即可求函数的定义域.【解答】解:要使函数有意义,则x2−1≥0,解得x≥1或x≤−1,故函数的定义域为(−∞, −1]∪[1, +∞),故选:D4.【答案】【考点】交集及其运算并集及其运算【解析】求出B中方程的解确定出B,利用集合间的包含关系,并集以及交集的定义判断即可.【解答】解:由B中方程变形得:(x−3)(x+1)=0,解得:x=3或x=−1,即B={−1, 3},∵U={x|−1≤x≤3},A={x|−1≤x<3},B={−1, 3},C={x|−1<x<3},∴C⊆A,C∪B={x|−1≤x≤3}≠C,B∩U=B,C∪A=A,故选:A.5.【答案】C【考点】子集与真子集【解析】先根据立方后等于自身的数写出集合P,再根据集合的元素数目与真子集个数的关系,而P有3个元素,计算可得答案.【解答】解:根据题意得:x3=x,则x(x2−1)=0,即x(x−1)(x+1)=0,∴P={0, 1, −1},那么集合P真子集的个数为23−1=7.故选C.6.【答案】C【考点】交集及其运算【解析】由二次函数的性质求出集合A,由偶次根号下被开方数大于等于零求出集合B,由交集的运算求出A∩B.【解答】解:由y=−x2+3≤3得,则集合A={y|y≤3}=(−∞, 3],由x+3≥0得x≥−3,则集合B=[−3, +∞),所以A∩B=[−3, 3],故选:C.7.【答案】B【考点】判断两个函数是否为同一函数【解析】先求y=|x|的定义域与值域,再分别求出所给的四个函数的定义域与值域,进行对比得出答案.解:易知函数y =|x|的定义域为R ,值域为[0, +∞).A ,函数的定义域为[0, +∞),不是同一个函数,故A 不符合题意;B ,√x 2=|x|,两者是同一个函数,故B 符合题意;C ,定义域中无实数0,定义域不同,故C 不符合题意;D 中,函数值可以取负值,值域不同,故D 不符合题意.故选B .8.【答案】C【考点】二次函数的性质【解析】求出二次函数的对称轴,根据单调区间与对称轴之间的关系建立条件,即可求出a 的取值范围.【解答】解:∵ 函数f(x)=x 2+2(a −1)x +2∴ 二次函数的对称轴为x =−2(a−1)2=1−a ,抛物线开口向上,∴ 函数在(−∞, 1−a]上单调递减,要使f(x)在区间(−∞, 2]上单调递减,则对称轴1−a ≥2,解得a ≤−1.故选:C .9.【答案】D【考点】函数单调性的性质函数奇偶性的性质【解析】题目中条件:“f(x)为偶函数,”说明:“f(−x)=f(x)”,将不在(−∝, −1)上的数值转化成区间(−∝, −1)上,再结合f(x)在(−∝, −1)上是增函数,即可进行判断.【解答】解:∵ f(x)是偶函数,∴ f(−32)=f(32),f(−1)=f(1),f(−2)=f(2), 又f(x)在(−∞, −1)上是增函数,∴ f(−2)<f(−32)<f(−1),即f(2)<f(−32)<f(−1),故选D .10.【答案】A将x=−2代入函数的表达式,求出f(−2)=−1,从而求出f(−1)的值即可.【解答】解:∵f(−2)=−2+1=−1,∴f(−1)=−1+1=0,∴f[f(−2)]=f(−1)=0,故选:A.11.【答案】D【考点】函数的图象变换【解析】根据函数的概念得:因变量(函数),随着自变量的变化而变化,且自变量取唯一值时,因变量(函数)有且只有唯一值与其相对应,结合图象特征进行判断即可.【解答】解:根据函数的定义知:自变量取唯一值时,因变量(函数)有且只有唯一值与其相对应.∴从图象上看,任意一条与x轴垂直的直线与函数图象的交点最多只能有一个交点.从而排除A,B,C,故选:D.12.【答案】D【考点】Venn图表达集合的关系及运算【解析】根据Venn图和集合的关系进行判断即可.【解答】解:由Venn图可知元素属于B但不属于A,即对于的集合为(∁U A)∩B,故选:D.二、填空题(本大题共4小题,每小题5分,共20分)【答案】−1【考点】二次函数在闭区间上的最值【解析】二次函数开口向上,对称轴x=1,函数在[0, 1]上递减,在[1, 4]递增,得到最小值为f(1).【解答】解:由已知函数的对称轴为x=1,所以f(x)=x2−2x在[0, 1]上递减,在[1, 4]递增,所以最小值为f(1)=1−2=−1;故答案为:−1.函数奇偶性的性质【解析】求f(x)在(0, +∞)上的解析式,所以设x ∈(0, +∞),便有−x ∈(−∞, 0),所以便有f(−x)=−2x +1=−f(x),从而可求得f(x),即求出f(x)在(0, +∞)上的解析式.【解答】解:设x ∈(0, +∞),−x ∈(−∞, 0);∴ f(x)=−f(−x)=−(−2x +1)=2x −1;即f(x)在(0, +∞)上的解析式为f(x)=2x −1.故答案为:f(x)=2x −1.【答案】−26【考点】函数的求值【解析】把f(x)=x 5+ax 3+bx −8,转化为令g(x)=f(x)+8=x 5+ax 3+bx 是一个奇函数,即可计算出.【解答】解:由f(x)=x 5+ax 3+bx −8,可令g(x)=f(x)+8=x 5+ax 3+bx ,可知:g(−x)=f(−x)+8=−g(x),∴ f(−2)+8=−[f(2)+8].∴ f(2)=−18−8=−26.故答案为:−26.【答案】(2, 2),(−2, −2)【考点】函数的求值【解析】根据定义解方程f(x)=4x =x ,即可.【解答】解:根据不动点的定义,由f(x)=4x =x 得x 2=4,解得x =2或x =−2,即不动点的坐标为(2, 2),(−2, −2),故答案为:(2, 2),(−2, −2)三、解答题(本大题共6小题,共70分)【答案】解:(1)由题意得:{1−x ≥0x +3≥0,解得:−3≤x ≤1, ∴ 定义域是[−3, 1];(2)由题意得:{2−|x|≠0√x 2−1≥0,解得:x ≥2且x ≠2或x ≤−1且x ≠−2, ∴ 定义域是{x|x ≥2且x ≠2或x ≤−1且x ≠−2}.函数的定义域及其求法【解析】(1)(2)结合二次根式的性质得到不等式组,从而求出函数的定义域.【解答】解:(1)由题意得:{1−x ≥0x +3≥0,解得:−3≤x ≤1, ∴ 定义域是[−3, 1];(2)由题意得:{2−|x|≠0√x 2−1≥0,解得:x ≥2且x ≠2或x ≤−1且x ≠−2, ∴ 定义域是{x|x ≥2且x ≠2或x ≤−1且x ≠−2}.【答案】解:(1)若A =⌀,即a −1≥2a +1,解得a ≤−2,此时满足A ∩B =⌀, 若A ≠⌀,若A ∩B =⌀,则{a −1<2a +1a −1≥1或{a −1<2a +12a +1≤0, 即{a >−2a ≥2或{a >−2a ≤−12, 解得a ≥2或−2<a ≤−12,综上a ≥2或a ≤−12;(2)若A ∪B =B ,则A ⊆B ,若A =⌀,即a −1≥2a +1,解得a ≤−2,此时满足A ⊆B ,若A ≠⌀,A ⊆B ,则{a −1<2a +1a −1≥02a +1≤1,即{a >−2a ≥1a ≤0,解得0≤a ≤1即a 的取值范围[0, 1].【考点】并集及其运算交集及其运算【解析】(1)根据A ∩B =⌀,建立条件关系即可求a 的取值范围;(2)若A ∪B =B ,则A ⊆B ,求a 的取值范围.【解答】解:(1)若A =⌀,即a −1≥2a +1,解得a ≤−2,此时满足A ∩B =⌀, 若A ≠⌀,若A ∩B =⌀,则{a −1<2a +1a −1≥1或{a −1<2a +12a +1≤0, 即{a >−2a ≥2或{a >−2a ≤−12, 解得a ≥2或−2<a ≤−12,1(2)若A ∪B =B ,则A ⊆B ,若A =⌀,即a −1≥2a +1,解得a ≤−2,此时满足A ⊆B ,若A ≠⌀,A ⊆B ,则{a −1<2a +1a −1≥02a +1≤1,即{a >−2a ≥1a ≤0,解得0≤a ≤1即a 的取值范围[0, 1].【答案】解:(1)函数的定义域为(−∞, 0)∪(0, +∞),则f(−x)=−x 3−1x 3=−(x 3+1x 3)=−f(x),故函数f(x)是奇函数;(2)函数f(x)=x x 2−1在(−1, 1)内的单调递减,设1>x 1>x 2>−1,则f(x 1)−f(x 2)=x 1x 12−1−x 2x 22−1=(x 2−x 1)(1+x 1x 2)(x 12−1)(x 22−1),∵ 1>x 1>x 2>−1,∴ x 2−x 1>0,且x 12<1,x 22<1,x 1x 2<1,∴ f(x 1)−f(x 2)<0,即f(x 1)<f(x 2),故函数f(x)在区间(−1, 1)上是减函数.【考点】函数奇偶性的判断函数单调性的判断与证明【解析】(1)利用函数奇偶性的定义即可判断函数f(x)=x 3+1x 3的奇偶性;(2)根据函数单调性的定义进行证明即可.【解答】解:(1)函数的定义域为(−∞, 0)∪(0, +∞),则f(−x)=−x 3−1x 3=−(x 3+1x 3)=−f(x),故函数f(x)是奇函数;(2)函数f(x)=xx 2−1在(−1, 1)内的单调递减,设1>x 1>x 2>−1,则f(x 1)−f(x 2)=x 1x 12−1−x 2x 22−1=(x 2−x 1)(1+x 1x 2)(x 12−1)(x 22−1),∵ 1>x 1>x 2>−1,∴ x 2−x 1>0,且x 12<1,x 22<1,x 1x 2<1,∴ f(x 1)−f(x 2)<0,即f(x 1)<f(x 2),故函数f(x)在区间(−1, 1)上是减函数.【答案】解:∵ P ={x|x 2+6x +9=0}={−3},又∵Q⊆P,当a=0,ax+1=0无解,故Q=⌀,满足条件,若Q≠⌀,则Q={−3},,即a=13故满足条件的实数a=0,或a=1.3【考点】集合的包含关系判断及应用【解析】由Q⊆P,可分Q=⌀和Q≠⌀两种情况进行讨论,根据集合包含关系的判断和应用,分别求出满足条件的a值,并写成集合的形式即可得到答案【解答】解:∵P={x|x2+6x+9=0}={−3},又∵Q⊆P,当a=0,ax+1=0无解,故Q=⌀,满足条件,若Q≠⌀,则Q={−3},,即a=13.故满足条件的实数a=0,或a=13【答案】解:(1)由分段函数可知,函数f(x)简图为:(2)∵f(3)=4−32=4−9=−5,∴f(f(3))=f(−5)=1−2(−5)=1+10=11;(3)当−4≤x<0时,1<f(x)≤9,当x=0时,f(0)=2,当0<x<3时,−5<f(x)<4,综上:−5<f(x)≤9.【考点】分段函数的解析式求法及其图象的作法函数的值域及其求法函数的求值【解析】(1)根据分段函数的表达式,画出函数f(x)简图即可;(2)利用分段函数直接代入求f(f(3))的值;(3)当−4≤x<3时,求f(x)的值域即可.【解答】解:(1)由分段函数可知,函数f(x)简图为:(2)∵f(3)=4−32=4−9=−5,∴f(f(3))=f(−5)=1−2(−5)=1+10=11;(3)当−4≤x<0时,1<f(x)≤9,当x=0时,f(0)=2,当0<x<3时,−5<f(x)<4,综上:−5<f(x)≤9.【答案】[2, +∞),2,4【考点】函数单调性的判断与证明【解析】(1)直接通过观察图表得到结论;(2)利用函数单调性的定义,在(0, 2)内任取两个不同的值,规定大小后,对相应的函数值作差判符号.【解答】解:①由表格可知,函数f(x)在[2, +∞)上递增,当x=2时函数取得最小值4.故答案为[2, +∞);2;4.②证明:设x1,x2∈(0, 2),且x1<x2,则f(x1)−f(x2)=(x1+4x1)−(x2+4x2)=(x1−x2)+(4x1−4x2)=(x1−x2)(x1x2−4)x1x2∵x1,x2∈(0, 2),x1<x2,∴x1−x2<0,x1x2∈(0, 4)∴f(x1)−f(x2)>0,即f(x1)>f(x2)∴f(x)=x+4x在区间(0, 2)上递减.。
最新人教A版高一数学必修一单元测试题全册带答案解析

最新人教A版高一数学必修一单元测试题全册带答案解析章末综合测评(一)集合与函数的概念(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U={x|x∈N*,x<6},集合A={1,3},B={3,5},则∁U(A∪B)等于()A.{1,4}B.{1,5}C.{2,5}D.{2,4}【解析】由题意得A∪B={1,3}∪{3,5}={1,3,5}.又U={1,2,3,4,5},∴∁U(A∪B)={2,4}.【答案】 D2.下列各式:①1∈{0,1,2};②∅⊆{0,1,2};③{1}∈{0,1,2};④{0,1,2}={2,0,1},其中错误的个数是()A.1个B.2个C.3个D.4个【解析】①1∈{0,1,2},正确;②空集是任何集合的子集,正确;③因为{1}⊆{0,1,2},故不正确;④根据集合的无序性可知正确.故选A.【答案】A3.下列各图形中,是函数的图象的是()【解析】函数y=f(x)的图象与平行于y轴的直线最多只能有一个交点,故A,B,C均不正确,故选D.【答案】 D4.集合A={x|y=x-1},B={y|y=x2+2},则如图1阴影部分表示的集合为()图1A .{x |x ≥1}B .{x |x ≥2}C .{x |1≤x ≤2}D .{x |1≤x <2}【解析】 易得A =[1,+∞),B =[2,+∞),则题图中阴影部分表示的集合是∁A B =[1,2).故选D.【答案】 D5.已知函数f (2x +1)=3x +2,则f (1)的值等于( ) A .2 B .11 C .5D .-1【解析】 由2x +1=1得x =0,故f (1)=f (2×0+1)=3×0+2=2,故选A . 【答案】 A6.下列四个函数:①y =x +1;②y =x -1;③y =x 2-1; ④y =1x ,其中定义域与值域相同的是( ) A .①②③ B .①②④ C .②③D .②③④【解析】 ①y =x +1,定义域R ,值域R ;②y =x -1,定义域R ,值域R ;③y =x 2-1,定义域R ,值域[-1,+∞);④y =1x ,定义域(-∞,0)∪(0,+∞),值域(-∞,0)∪(0,+∞).∴①②④定义域与值域相同,故选B .【答案】 B7.若函数f (x )=⎩⎨⎧x +1,(x ≥0),f (x +2),(x<0),则f (-3)的值为( )A .5B .-1C .-7D .2【解析】 依题意,f (-3)=f (-3+2)=f (-1) =f (-1+2)=f (1)=1+1=2,故选D. 【答案】 D8.函数y =f (x )在R 上为增函数,且f (2m )>f (-m +9),则实数m 的取值范围是( ) A .(-∞,-3)B .(0,+∞)C .(3,+∞)D .(-∞,-3)∪(3,+∞)【解析】 因为函数y =f (x )在R 上为增函数,且f (2m )>f (-m +9),所以2m >-m +9,即m >3.【答案】 C9.定义在R 上的奇函数f (x ),当x >0时,f (x )=3,则奇函数f (x )的值域是( ) A .(-∞,-3] B .[-3,3] C .[-3,3]D .{-3,0,3}【解析】 ∵f (x )是定义在R 上的奇函数, ∴f (-x )=-f (x ),f (0)=0,设x <0,则-x >0,f (-x )=-f (x )=3, ∴f (x )=-3,∴f (x )=⎩⎨⎧3,x >0,0,x =0,-3,x <0,∴奇函数f (x )的值域是{-3,0,3}.【答案】 D10.已知f (x )=x 5-ax 3+bx +2且f (-5)=17,则f (5)的值为( ) A .-13 B .13 C .-19D .19【解析】 ∵g (x )=x 5-ax 3+bx 是奇函数,∴g (-x )=-g (x ).∵f (-5)=17=g (-5)+2,∴g (5)=-15,∴f (5)=g (5)+2=-15+2=-13. 【答案】 A11.已知a ,b 为两个不相等的实数,集合M ={a 2-4a ,-1},N ={b 2-4b +1,-2},映射f :x →x 表示把集合M 中的元素x 映射到集合N 中仍为x ,则a +b 等于( )A .1B .2C .3D .4【解析】 ∵集合M 中的元素-1不能映射到N 中为-2,∴⎩⎨⎧ a 2-4a =-2,b 2-4b +1=-1,即⎩⎨⎧a 2-4a +2=0,b 2-4b +2=0,∴a ,b 为方程x 2-4x +2=0的两根, ∴a +b =4. 【答案】 D12.定义在R 上的偶函数f (x )满足:对任意的x 1,x 2∈[0,+∞)(x 1≠x 2),有f (x 2)-f (x 1)x 2-x 1<0,则( )A .f (3)<f (-2)<f (1)B .f (1)<f (-2)<f (3)C .f (-2)<f (1)<f (3)D .f (3)<f (1)<f (-2)【解析】 任意的x 1,x 2∈[0,+∞)(x 1≠x 2),有f (x 2)-f (x 1)x 2-x 1<0,∴f (x )在[0,+∞)上单调递减.又f (x )是偶函数,故f (x )在(-∞,0]上单调递增.且满足n ∈N *时,f (-2)=f (2),3>2>1>0,由此知,此函数具有性质:自变量的绝对值越小,函数值越大,∴f (3)<f (-2)<f (1),故选A .【答案】 A二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.若A ={-2,2,3,4},B ={x |x =t 2,t ∈A },用列举法表示集合B 为________. 【解析】 由A ={-2,2,3,4},B ={x |x =t 2,t ∈A },得B ={4,9,16}. 【答案】 {4,9,16}14.若函数f (x )=(a -2)x 2+(a -1)x +3是偶函数,则f (x )的增区间是________. 【解析】 ∵函数f (x )=(a -2)x 2+(a -1)x +3是偶函数,∴a -1=0,∴f (x )=-x 2+3,其图象是开口方向朝下,以y 轴为对称轴的抛物线.故f (x )的增区间为(-∞,0].【答案】 (-∞,0]15.已知函数f (x )=⎩⎨⎧2x ,x>0,x +1,x ≤0,若f (a )+f (1)=0,则实数a 的值等于________.【解析】 ∵f (1)=2×1=2, 若a >0,则f (a )=2a ,由2a +2=0,得a =-1舍去, 若a ≤0,则f (a )=a +1,由a +1+2=0得a =-3,符合题意. ∴a =-3. 【答案】 -316.函数f (x )的定义域为A ,若x 1,x 2∈A 且f (x 1)=f (x 2)时总有x 1=x 2,则称f (x )为单函数,例如,函数f (x )=2x +1(x ∈R )是单函数.下列命题:①函数f (x )=x 2(x ∈R )是单函数; ②函数f (x )=xx -1是单函数; ③若f (x )为单函数,x 1,x 2∈A 且x 1≠x 2,则f (x 1)≠f (x 2); ④在定义域上具有单调性的函数一定是单函数. 其中的真命题是________.(写出所有真命题的序号)【解析】 ①函数f (x )=x 2(x ∈R )不是单函数,例如f (1)=f (-1),显然不会有1和-1相等,故为假命题;②函数f (x )=x x -1是单函数,因为若x 1x 1-1=x 2x 2-1,可推出x 1x 2-x 2=x 1x 2-x 1,即x 1=x 2,故为真命题;③若f (x )为单函数,x 1,x 2∈A 且x 1≠x 2,则f (x 1)≠f (x 2)为真,可用反证法证明:假设f (x 1)=f (x 2),则按定义应有x 1=x 2,与已知中的x 1≠x 2矛盾; ④在定义域上具有单调性的函数一定是单函数为真,因为单函数的实质是一对一的映射,而单调的函数也是一对一的映射,故为真.【答案】 ②③④三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)设全集U =R ,集合A ={x |-1≤x <3},B ={x |2x -4≥x -2}. (1)求∁U (A ∩B );(2)若集合C ={x |2x +a >0},满足B ∪C =C ,求实数a 的取值范围.【解】 (1)由集合B 中的不等式2x -4≥x -2,解得x ≥2,∴B ={x |x ≥2},又A ={x |-1≤x <3},∴A ∩B ={x |2≤x <3},又全集U =R ,∴∁U (A ∩B )={x |x <2或x ≥3}. (2)由集合C 中的不等式2x +a >0,解得x >-a2,∴C =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x >-a 2. ∵B ∪C =C ,∴B ⊆C ,∴-a2<2,解得a >-4.18.(本小题满分12分)设A ={x |2x 2+ax +2=0},B ={x |x 2+3x +2a =0},且A ∩B ={2}. (1)求a 的值及集合A ,B ;(2)设全集U =A ∪B ,求(∁U A )∪(∁U B );(3)写出(∁U A )∪(∁U B )的所有子集.【解】 (1)由交集的概念易得2是方程2x 2+ax +2=0和x 2+3x +2a =0的公共解,则a =-5,此时A =⎩⎨⎧⎭⎬⎫12,2,B ={-5,2}. (2)由并集的概念易得U =A ∪B =⎩⎨⎧⎭⎬⎫-5,12,2.由补集的概念易得∁U A ={-5},∁U B =⎩⎨⎧⎭⎬⎫12,所以(∁U A )∪(∁U B )=⎩⎨⎧⎭⎬⎫-5,12.(3)(∁U A )∪(∁U B )的所有子集即为集合⎩⎨⎧⎭⎬⎫-5,12的所有子集:∅,⎩⎨⎧⎭⎬⎫12,{-5},⎩⎨⎧⎭⎬⎫-5,12. 19.(本小题满分12分)已知f (x )是R 上的奇函数,当x >0时,解析式为f (x )=2x +3x +1. (1)求f (x )在R 上的解析式;(2)用定义证明f (x )在(0,+∞)上为减函数. 【解】 (1)设x <0,则-x >0,∴f (-x )=-2x +3-x +1.又∵f (x )是R 上的奇函数,∴f (-x )=-f (x )=-2x +3-x +1,∴f (x )=-2x +3x -1.又∵奇函数在0点有意义,∴f (0)=0,∴函数的解析式为f (x )=⎩⎪⎨⎪⎧-2x +3x -1,x <0,0,x =0,2x +3x +1,x >0.(2)证明:设∀x 1,x 2∈(0,+∞),且x 1<x 2,则f (x 1)-f (x 2)=2x 1+3x 1+1-2x 2+3x 2+1=(2x 1+3)(x 2+1)-(2x 2+3)(x 1+1)(x 1+1)(x 2+1)=-x 1+x 2(x 1+1)(x 2+1).∵x 1,x 2∈(0,+∞),x 1<x 2,∴x 1+1>0,x 2+1>0,x 2-x 1>0, ∴f (x 1)-f (x 2)>0,∴f (x 1)>f (x 2),∴函数f (x )在(0,+∞)上为减函数.20.(本小题满分12分)某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数:R (x )=⎩⎪⎨⎪⎧400x -12x 2,0≤x ≤400,80 000,x >400,其中x 是仪器的月产量.当月产量为何值时,公司所获得利润最大?最大利润是多少?【解】 由于月产量为x 台,则总成本为20 000+100x , 从而利润f (x )=R (x )=⎩⎪⎨⎪⎧300x -12x 2-20 000,0≤x ≤400,60 000-100x ,x >400,当0≤x ≤400时,f (x )=-12(x -300)2+25 000, 所以当x =300时,有最大值25 000; 当x >400时,f (x )=60 000-100x 是减函数, 所以f (x )=60 000-100×400<25 000. 所以当x =300时,有最大值25 000,即当月产量为300台时,公司所获利润最大,最大利润是25 000元.21.(本小题满分12分)已知f (x )在R 上是单调递减的一次函数,且f (f (x ))=4x -1. (1)求f (x );(2)求函数y =f (x )+x 2-x 在x ∈[-1,2]上的最大值与最小值.【解】 (1)由题意可设f (x )=ax +b ,(a <0),由于f (f (x ))=4x -1,则a 2x +ab +b =4x -1,故⎩⎨⎧a 2=4,ab +b =-1,解得a =-2,b =1.故f (x )=-2x +1. (2)由(1)知,函数y =f (x )+x 2-x =-2x +1+x 2-x =x 2-3x +1,故函数y =x 2-3x +1的图象开口向上,对称轴为x =32,则函数y =f (x )+x 2-x 在⎣⎢⎡⎦⎥⎤-1,32上为减函数,在⎣⎢⎡⎦⎥⎤32,2上为增函数.又由f ⎝ ⎛⎭⎪⎫32=-54,f (-1)=5,f (2)=-1,则函数y =f (x )+x 2-x 在x ∈[-1,2]上的最大值为5,最小值为-54. 22.(本小题满分12分)已知函数f (x )=x +b1+x 2为奇函数. (1)求b 的值;(2)证明:函数f (x )在区间(1,+∞)上是减函数; (3)解关于x 的不等式f (1+x 2)+f (-x 2+2x -4)>0.【解】 (1)∵函数f (x )=x +b1+x 2为定义在R 上的奇函数,∴f (0)=b =0.(2)由(1)可得f (x )=x1+x 2,下面证明函数f (x )在区间(1,+∞)上是减函数. 证明:设x 2>x 1>1,则有f (x 1)-f (x 2)=x 11+x 21-x 21+x 22=x 1+x 1x 22-x 2-x 2x 21(1+x 21)(1+x 22)=(x 1-x 2)(1-x 1x 2)(1+x 21)(1+x 22). 再根据x 2>x 1>1,可得1+x 21>0,1+x 22>0,x 1-x 2<0,1-x 1x 2<0,∴(x 1-x 2)(1-x 1x 2)(1+x 21)(1+x 22)>0, 即f (x 1)>f (x 2),∴函数f (x )在区间(1,+∞)上是减函数. (3)由不等式f (1+x 2)+f (-x 2+2x -4)>0, 可得f (1+x 2)>-f (-x 2+2x -4)=f (x 2-2x +4),再根据函数f (x )在区间(1,+∞)上是减函数,可得1+x 2<x 2-2x +4,且x >1, 求得1<x <32,故不等式的解集为(1,32).章末综合测评(二) 第二章 基本初等函数(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若f (x )=1log 0.5(2x +1),则函数f (x )的定义域为( )A.⎝ ⎛⎭⎪⎫-12,+∞ B .(0,+∞)C.⎝ ⎛⎭⎪⎫-12,0D.⎝ ⎛⎦⎥⎤-12,0 【解析】 要使函数有意义,只需⎩⎨⎧2x +1>0,log 0.5(2x +1)>0,即⎩⎪⎨⎪⎧x >-12,2x +1<1,解得⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-12<x <0.故选C.【答案】 C2.已知函数t =-144lg ⎝ ⎛⎭⎪⎫1-N 100的图象可表示打字任务的“学习曲线”,其中t(小时)表示达到打字水平N (字/分钟)所需的学习时间,N 表示打字速度(字/分),则按此曲线要达到90字/分钟的水平,所需的学习时间是( )A .144小时B .90小时C .60小时D .40小时【解析】 t =-144lg ⎝ ⎛⎭⎪⎫1-N 100=-144lg 110=144.【答案】 A3.下列函数中,在区间(0,1)上为增函数的是( ) A .y =2x 2-x +3 B .y =⎝ ⎛⎭⎪⎫13xC .y =x 23D .y =log 12x【解析】 ∵y =2x 2-x +3的对称轴x =14,∴在区间(0,1)上不是增函数,故A 错; 又y =⎝ ⎛⎭⎪⎫13x及y =log 12x 为减函数,故B ,D 错;y =x 23中,指数23>0,在[0,+∞)上单调递增,故C 正确.【答案】 C4.如图1为函数y =m +log n x 的图象,其中m ,n 为常数,则下列结论正确的是( )图1A .m <0,n >1B .m >0,n >1C .m >0,0<n <1D .m <0,0<n <1【解析】 当x =1时,y =m ,由图形易知m<0,又函数是减函数,所以0<n <1. 【答案】 D5.已知f (x )=a -x (a >0且a ≠1),且f (-2)>f (-3),则a 的取值范围是( ) A .a >0 B .a >1 C .a <1D .0<a <1【解析】 ∵f (-2)>f (-3),∴f (x )=a -x =⎝ ⎛⎭⎪⎫1a x 是增函数,∴1a >1,∴0<a <1,则a 的取值范围是0<a <1,故选D.【答案】 D6.(2015·山东高考)设a =0.60.6,b =0.61.5,c =1.50.6,则a ,b ,c 的大小关系是( ) A .a <b <c B .a <c<b C .b <a <cD .b <c<a【解析】 因为函数y =0.6x 是减函数,0<0.6<1.5,所以1>0.60.6>0.61.5,即b <a <1.因为函数y =x 0.6在(0,+∞)上是增函数,1<1.5,所以1.50.6>10.6=1,即c >1.综上,b <a <c .【答案】 C7.已知函数f (x )=lg (1-x )的值域为(-∞,1],则函数f (x )的定义域为( ) A .[-9,+∞) B .[0,+∞) C .(-9,1)D .[-9,1)【解析】 因为函数f (x )=lg (1-x )的值域为(-∞,1],所以lg (1-x )≤1,即0<1-x ≤10,解得-9≤x <1,所以函数f (x )的定义域为[-9,1).【答案】 D8.已知函数f (x )是奇函数,当x >0时,f (x )=a x(a >0且a ≠1),且f (log 124)=-3,则a的值为( )A.3 B .3 C .9D.32【解析】 ∵f (log 124)=f ⎝ ⎛⎭⎪⎫log 214=f (-2)=-f (2)=-a 2=-3,∴a 2=3,解得a =±3,又a >0,∴a = 3.【答案】 A9.已知f (x )=a x ,g(x )=log a x (a >0且a ≠1),若f (3)·g(3)<0,则f (x )与g(x )在同一坐标系里的图象是( )【解析】 ∵a >0且a ≠1,∴f (3)=a 3>0,又f (3)·g(3)<0,∴g(3)=log a 3<0,∴0<a <1,∴f (x )=a x 在R 上是减函数,g (x )=log a x 在(0,+∞)上是减函数,故选C.【答案】 C10.设偶函数f (x )=log a |x +b |在(0,+∞)上具有单调性,则f (b -2)与f (a +1)的大小关系为( )A .f (b -2)=f (a +1)B .f (b -2)>f (a +1)C .f (b -2)<f (a +1)D .不能确定【解析】 ∵函数f (x )是偶函数,∴b =0,此时f (x )=log a |x |.当a >1时,函数f (x )=log a |x |在(0,+∞)上是增函数,∴f (a +1)>f (2)=f (b -2);当0<a <1时,函数f (x )=log a |x |在(0,+∞)上是减函数,∴f (a +1)>f (2)=f (b -2).综上可知f (b -2)<f (a +1).【答案】 C11.已知函数f (x )=⎩⎪⎨⎪⎧(a -2)x ,x ≥2,⎝ ⎛⎭⎪⎫12x-1,x <2满足对任意的实数x 1≠x 2都有f (x 1)-f (x 2)x 1-x 2<0成立,则实数a 的取值范围为( )A .(-∞,2) B.⎝ ⎛⎦⎥⎤-∞,138 C .(-∞,2]D.⎣⎢⎡⎭⎪⎫138,2 【解析】 由题意知函数f (x )是R 上的减函数,于是有⎩⎪⎨⎪⎧a -2<0,(a -2)×2≤⎝ ⎛⎭⎪⎫122-1,由此解得a ≤138,即实数a 的取值范围是⎝ ⎛⎦⎥⎤-∞,138,选B .【答案】 B12.若函数y =log a (x 2-ax +1)有最小值,则a 的取值范围是( ) A .0<a <1 B .0<a <2,a ≠1 C .1<a <2D .a ≥2【解析】 令g (x )=x 2-ax +1(a >0,且a ≠1),①当a >1时,g (x )在R 上单调递增,∴Δ<0,∴1<a <2;②当0<a <1时,g (x )=x 2-ax +1没有最大值,从而函数y =log a (x 2-ax +1)没有最小值,不符合题意.综上所述:1<a <2.故选C.【答案】 C二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.已知lg 2=a ,lg 3=b ,则用a ,b 表示log 125的值为________. 【解析】 ∵lg 2=a ,lg 3=b ,∴log 125=lg 5lg 12=1-lg 22lg 2+lg 3=1-a 2a +b .【答案】1-a2a +b14.方程log 2(9x -1-5)=log 2(3x -1-2)+2的解为________.【解析】 依题意log 2(9x -1-5)=log 2(4·3x -1-8),所以9x -1-5=4·3x -1-8, 令3x -1=t (t >0),则t 2-4t +3=0,解得t =1或t =3,当t =1时,3x -1=1,所以x =1,而91-1-5<0,所以x =1不合题意,舍去; 当t =3时,3x -1=3,所以x =2,92-1-5=4>0,32-1-2=1>0,所以x =2满足条件. 所以x =2是原方程的解. 【答案】 215.已知当x >0时,函数f (x )=(2a -1)x ⎝ ⎛⎭⎪⎫a >0,且a ≠12的值总大于1,则函数y =a 2x -x 2的单调增区间是________.【解析】 由题意知:2a -1>1,解得a >1,设t =2x -x 2,则函数y =a t 为增函数,∵函数t =2x -x 2的增区间为(-∞,1),∴函数y =a 2x -x 2的单调增区间是(-∞,1).【答案】 (-∞,1)(或(-∞,1]) 16.给出下列结论:①4(-2)4=±2; ②y =x 2+1,x ∈[-1,2],y 的值域是[2,5]; ③幂函数图象一定不过第四象限;④函数f (x )=a x +1-2(a >0,且a ≠1)的图象过定点(-1,-1); ⑤若ln a <1成立,则a 的取值范围是(-∞,e ).其中正确的序号是________.【解析】 ①4(-2)4=2,因此不正确;②y =x 2+1,x ∈[-1,2],y 的值域是[1,5],因此不正确;③幂函数图象一定不过第四象限,正确;④当x =-1时,f (-1)=a 0-2=-1,∴函数f (x )=a x +1-2(a >0,a ≠1)的图象过定点(-1,-1),正确;⑤若l n a <1成立,则a 的取值范围是(0,e),因此不正确.综上所述:只有③④正确.【答案】 ③④三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)求值: (1)⎝ ⎛⎭⎪⎫21412-(-9.6)0-⎝ ⎛⎭⎪⎫338-23+(1.5)-2;(2)log 2512·log 45-log 133-log 24+5log 52. 【解】 (1)⎝ ⎛⎭⎪⎫21412-(-9.6)0-⎝ ⎛⎭⎪⎫338-23+(1.5)-2=⎝ ⎛⎭⎪⎫9412-1-⎝ ⎛⎭⎪⎫278-23+⎝ ⎛⎭⎪⎫32-2 =32-1-⎝ ⎛⎭⎪⎫32-2+⎝ ⎛⎭⎪⎫232=32-1-49+49=12.(2)log 2512·log 45-log 133-log 24+5log 52=-14+1-2+2=34.18.(本小题满分12分)已知函数f (x )=a 2x +2a x -1(a >1,且a 为常数)在区间[-1,1]上的最大值为14.(1)求f (x )的表达式;(2)求满足f (x )=7时,x 的值.【解】 (1)令t =a x >0.∵x ∈[-1,1],a >1,∴t ∈⎣⎢⎡⎦⎥⎤1a ,a ,f (x )=t 2+2t -1=(t +1)2-2,故当t =a 时,函数f (x )取得最大值为a 2+2a -1=14,解得a =3,∴f (x )=32x +2×3x -1. (2)由f (x )=7,可得32x +2×3x -1=7,即(3x +4)·(3x -2)=0,求得3x =2,∴x =log 32. 19.已知函数f (x )是定义在R 上的偶函数,当x ≥0时,f (x )=⎝ ⎛⎭⎪⎫12x .图2(1)画出函数f (x )的图象;(2)根据图象写出f (x )的单调区间,并写出函数的值域.【解】 (1)先作出当x ≥0时,f (x )=⎝ ⎛⎭⎪⎫12x 的图象,利用偶函数的图象关于y 轴对称,再作出f (x )在x ∈(-∞,0)时的图象.(2)函数f (x )的单调递增区间为(-∞,0),单调递减区间为[0,+∞),值域为(0,1]. 20.(本小题满分12分)已知函数f (x )=log a (x -1),g (x )=log a (3-x )(a >0且a ≠1). (1)求函数h (x )=f (x )-g (x )的定义域;(2)利用对数函数的单调性,讨论不等式f (x )≥g (x )中x 的取值范围. 【解】 (1)由⎩⎨⎧x -1>0,3-x >0,得1<x <3.∴函数h (x )的定义域为(1,3). (2)不等式f (x )≥g (x ),即为log a (x -1)≥log a (3-x ).(*)①当0<a <1时,不等式(*)等价于⎩⎨⎧1<x <3,x -1≤3-x ,解得1<x ≤2.②当a >1时,不等式(*)等价于⎩⎨⎧1<x <3,x -1≥3-x ,解得2≤x <3.综上,当0<a <1时,原不等式解集为(1,2]; 当a >1时,原不等式解集为[2,3).21.(本小题满分12分)若函数y =f (x )=a ·3x -1-a3x -1为奇函数.(1)求a 的值; (2)求函数的定义域; (3)求函数的值域.【解】 ∵函数y =f (x )=a ·3x -1-a 3x -1=a -13x -1,(1)由奇函数的定义,可得f (-x )+f (x )=0, 即2a -13x-1-13-x -1=0,∴a =-12. (2)∵y =-12-13x -1,∴3x -1≠0,即x ≠0.∴函数y =-12-13x -1的定义域为{x |x ≠0}.(3)∵x ≠0,∴3x -1>-1.∵3x -1≠0,∴0>3x -1>-1或3x -1>0. ∴-12-13x -1>12或-12-13x -1<-12.即函数的值域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪y >12或y <-12. 22.(本小题满分12分)已知函数f (x )=lg ⎝⎛⎭⎪⎫1-x 1+x . (1)求证:f (x )是奇函数; (2)求证:f (x )+f (y )=f ⎝⎛⎭⎪⎫x +y 1+xy ; (3)若f ⎝⎛⎭⎪⎫a +b 1+ab =1,f ⎝ ⎛⎭⎪⎫a -b 1-ab =2,求f (a ),f (b )的值. 【解】 (1)证明:由函数f (x )=lg ⎝ ⎛⎭⎪⎫1-x 1+x ,可得1-x 1+x >0,即x -11+x <0,解得-1<x <1,故函数的定义域为(-1,1),关于原点对称.再根据f (-x )=lg 1+x 1-x =-lg 1-x1+x =-f (x ),可得f (x )是奇函数.(2)证明:f (x )+f (y )=lg1-x 1+x +lg 1-y 1+y =lg (1-x )(1-y )(1+x )(1+y ), 而f ⎝ ⎛⎭⎪⎫x +y 1+xy =lg 1-x +y 1+xy 1+x +y 1+xy=lg 1+xy -x -y 1+xy +x +y =lg (1-x )(1-y )(1+x )(1+y ),∴f (x )+f (y )=f ⎝⎛⎭⎪⎫x +y 1+xy 成立. (3)若f ⎝⎛⎭⎪⎫a +b 1+ab =1,f ⎝ ⎛⎭⎪⎫a -b 1-ab =2, 则由(2)可得f (a )+f (b )=1,f (a )-f (b )=2, 解得f (a )=32,f (b )=-12.章末综合测评(三) -第三章 函数的应用(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知函数f (x )在区间[a ,b ]上单调,且f (a )·f (b )<0,则函数f (x )的图象与x 轴在区间[a ,b ]内( )A .至多有一个交点B .必有唯一一个交点C .至少有一个交点D .没有交点【解析】 ∵f (a )f (b )<0,∴f (x )在[a ,b ]内有零点, 又f (x )在区间[a ,b ]上单调,所以这样的点只有一个,故选B . 【答案】 B2.若方程f (x )-2=0在(-∞,0)内有解,则y =f (x )的图象是( )【解析】 要使方程f (x )-2=0在(-∞,0)内有解,只需y =f (x )与直线y =2在(-∞,0)上有交点,故D 正确.故选D.【答案】 D3.已知下列四个函数图象,其中能用“二分法”求出函数零点的是( )【解析】 由二分法的定义与原理知A 选项正确. 【答案】 A 4.函数f (x )=(x -1)ln (-x )x -3的零点个数为( )A .1个B .2个C .3个D .4个【解析】 ∵函数f (x )=(x -1)ln (-x )x -3的零点个数即为f (x )=0的根的个数,∴f (x )=(x -1)ln (-x )x -3=0,即(x -1)ln(-x )=0,∴x -1=0或ln(-x )=0,∴x =1或x =-1,∵⎩⎨⎧-x >0,x -3≠0,解得x <0,∵函数f (x )的定义域为{x |x <0},∴x =-1,即方程f (x )=0只有一个根,∴函数f (x )=(x -1)ln (-x )x -3的零点个数为1个.故选A .【答案】 A5.甲、乙两人在一次赛跑中,从同一地点出发,路程s 与时间t 的函数关系如图1所示,则下列说法正确的是 ( )图1A .甲比乙先出发B .乙比甲跑的路程多C .甲、乙两人的速度相同D .甲比乙先到达终点【解析】 由题图可知,甲到达终点用时短,故选D.【答案】 D6.拟定从甲地到乙地通话m 分钟的电话费由f (m )=1.06(0.50×[m ]+1)给出,其中m >0,[m ]是大于或等于m 的最小整数(例如[2.72]=3,[3.8]=4,[3.1]=4),则从甲地到乙地通话时间为5.5分钟的电话费为多少元.( )A .3.71B .3.97C .4.24D .4.77【解析】 由[m ]是大于或等于m 的最小整数,可得[5.5]=6,所以f (5.5)=1.06×(0.50×6+1)=1.06×4=4.24.故选C .【答案】 C7.函数f (x )=3x +12x -2的零点所在的一个区间是( ) A .(-2,-1) B .(-1,0) C .(0,1)D .(1,2)【解析】 由已知可知,函数f (x )=3x +12x -2单调递增且连续,∵f (-2)=-269<0,f (-1)=-136<0,f (0)=-1<0,f (1)=32>0,∴f (0)·f (1)<0,由函数的零点判定定理可知,函数f (x )=3x +12x -2的一个零点所在的区间是(0,1),故选C .【答案】 C8.函数f (x )=⎩⎨⎧x 2+2x -3,x ≤0,-2+ln x ,x >0,的零点个数为( )A .0B .1C .2D .3【解析】 当x ≤0时,令x 2+2x -3=0,得x =-3;当x >0时,令-2+ln x =0,得x =e 2,所以函数有两个零点.故选C .【答案】 C9.函数f (x )=|x |+k 有两个零点,则( ) A .k =0 B .k >0 C .0≤k <1D .k <0【解析】 在同一平面直角坐标系中画出y 1=|x |和y 2=-k 的图象,如图所示.若f (x )有两个零点,则必有-k >0,即k <0.【答案】 D10.已知f (x )=(x -a )(x -b )-2,并且α,β是函数f (x )的两个零点,则实数a ,b ,α,β的大小关系可能是( )A .a <α<b <βB .a <α<β<bC .α<a <b <βD .α<a <β<b【解析】 ∵α,β是函数f (x )的两个零点, ∴f (α)=f (β)=0.又f (a )=f (b )=-2<0,结合二次函数的图象(如图所示)可知a ,b 必在α,β之间.故选C .【答案】 C11.已知函数f (x )=⎝ ⎛⎭⎪⎫13x-log 2x ,若实数x 0是函数f (x )的零点,且0<x 1<x 0,则f (x 1)的值为( )A .恒为正值B .等于0C .恒为负值D .不大于0【解析】 ∵函数f (x )在(0,+∞)上为减函数,且f (x 0)=0,∴当x ∈(0,x 0)时,均有f (x )>0,而0<x 1<x 0,∴f (x 1)>0.【答案】 A12.某商店计划投入资金20万元经销甲或乙两种商品,已知经销甲商品与乙商品所获得的利润分别为P (万元)和Q (万元),且它们与投入资金x (万元)的关系是:P =x 4,Q =a 2x (a >0);若不管资金如何投放,经销这两种商品或其中的一种商品所获得的纯利润总不少于5万元,则a 的最小值应为( )A.5 B .5 C .±5D .- 5【解析】 设投放x 万元经销甲商品,则经销乙商品投放(20-x )万元,总利润y =P +Q =x 4+a 2·20-x ,令y ≥5,则x 4+a 2·20-x ≥5.∴a 20-x ≥10-x 2,即a ≥1220-x 对0≤x <20恒成立,而f (x )=1220-x 的最大值为5,且x =20时,a 20-x ≥10-x2也成立,∴a min = 5.【答案】 A二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.如果函数f (x )=x 2+mx +m +3的一个零点为0,则另一个零点是________. 【解析】 函数f (x )=x 2+mx +m +3的一个零点为0,则f (0)=0,∴m +3=0,∴m =-3,则f (x )=x 2-3x ,于是另一个零点是3.【答案】 314.用二分法求方程ln x -2+x =0在区间[1,2]上零点的近似值,先取区间中点c =32,则下一个含根的区间是________.【解析】 令f (x )=ln x -2+x ,则f (1)=ln 1-2+1<0, f (2)=ln 2-2+2=ln 2>0,f ⎝ ⎛⎭⎪⎫32=ln 32-2+32=ln 32-12=ln 32-ln e =ln 32e =ln 94e <ln 1=0,∴f ⎝ ⎛⎭⎪⎫32·f (2)<0,∴下一个含根的区间是⎝ ⎛⎭⎪⎫32,2. 【答案】 ⎝ ⎛⎭⎪⎫32,215.将进货单价为8元的商品按10元一个销售,每天可卖出100个.若每个涨价1元,则日销售量减少10个.为获得最大利润,则此商品日销售价应定为每个________元.【解析】 设每个涨价x 元,则实际销售价为10+x 元,销售的个数为100-10x , 则利润为y =(10+x )(100-10x )-8(100-10x )=-10(x -4)2+360(0≤x <10,x ∈N ).因此,当x =4,即售价定为每个14元时,利润最大.【答案】 1416.已知函数f (x )=log ax +x -b (a >0,且a ≠1).当2<a <3<b <4时,函数f (x )的零点x 0∈(n ,n +1),n ∈N *,则n =________.【解析】 ∵2<a <3<b <4,∴f (2)=log a 2+2-b <1+2-b =3-b <0,f (3)=log a 3+3-b >1+3-b =4-b >0. 即f (2)·f (3)<0,易知f (x )在(0,+∞)上单调递增.∴函数f (x )在(0,+∞)上存在唯一的零点x 0,且x 0∈(2,3),∴n=2.【答案】 2三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)设函数f(x)=e x-m-x,其中m∈R,当m>1时,判断函数f(x)在区间(0,m)内是否存在零点.【解】f(x)=e x-m-x,所以f(0)=e-m-0=e-m>0,f(m)=e0-m=1-m.又m>1,所以f(m)<0,所以f(0)·f(m)<0.又函数f(x)的图象在区间[0,m]上是一条连续曲线,故函数f(x)=e x-m-x(m>1)在区间(0,m)内存在零点.18.(本小题满分12分)定义在R上的偶函数y=f(x)在(-∞,0]上递增,函数f(x)的一个零点为-12,求满足f(log14x)≥0的x的取值集合.【解】∵-12是函数的一个零点,∴f⎝⎛⎭⎪⎫-12=0.∵y=f(x)是偶函数且在(-∞,0]上递增,∴当log 14x≤0,解得x≥1,当log14x≥-12,解得x≤2,所以1≤x≤2.由对称性可知,当log 14x>0时,12≤x<1.综上所述,x的取值范围是⎣⎢⎡⎦⎥⎤12,2.19.(本小题满分12分)燕子每年秋天都要从北方飞向南方过冬,研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数v=5log2Q10,单位是m/s,其中Q表示燕子的耗氧量.(1)求燕子静止时的耗氧量是多少个单位;(2)当一只燕子的耗氧量是80个单位时,它的飞行速度是多少?【解】(1)由题知,当燕子静止时,它的速度v=0,代入题给公式可得:0=5log2Q 10,解得Q=10.即燕子静止时的耗氧量是10个单位.(2)将耗氧量Q=80代入题给公式得:v=5log28010=5log28=15(m/s).即当一只燕子的耗氧量是80个单位时,它的飞行速度为15 m/s.20.(本小题满分12分)设f(x)=ax2+(b-8)x-a-ab的两个零点分别是-3,2.(1)求f (x );(2)当函数f (x )的定义域为[0,1]时,求其值域. 【解】 (1)因为f (x )的两个零点分别是-3,2, 所以⎩⎨⎧f (-3)=0,f (2)=0,即⎩⎨⎧9a -3(b -8)-a -ab =0,4a +2(b -8)-a -ab =0,解得a =-3,b =5,f (x )=-3x 2-3x +18.(2)由(1)知f (x )=-3x 2-3x +18的对称轴x =-12,函数开口向下,所以f (x )在[0,1]上为减函数,f (x )的最大值f (0)=18,最小值f (1)=12,所以值域为[12,18].21.(本小题满分12分)如图2,直角梯形OABC 位于直线x =t 右侧的图形的面积为f (t ).图2(1)试求函数f (t )的解析式; (2)画出函数y =f (t )的图象. 【解】 (1)当0≤t ≤2时,f (t )=S 梯形OABC -S △ODE =(3+5)×22-12t ·t =8-12t 2, 当2<t ≤5时,f (t )=S 矩形DEBC =DE ·DC =2(5-t )=10-2t , 所以f (t )=⎩⎪⎨⎪⎧8-12t 2,(0≤t ≤2),10-2t ,(2<t ≤5).(2)函数f (t )图象如图所示.22.(本小题满分12分)某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为2.10元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费y 元.已知甲、乙两用户该月用水量分别为5x,3x 吨.(1)求y 关于x 的函数;(2)如甲、乙两户该月共交水费40.8元,分别求出甲、乙两户该月的用水量和水费. 【解】 (1)当甲的用水量不超过4吨时,即5x ≤4,乙的用水量也不超过4吨, y =(5x +3x )×2.1=16.8x ;当甲的用水量超过4吨,乙的用水量不超过4吨时,即3x ≤4且5x >4, y =4×2.1+3x ×2.1+3×(5x -4)=21.3x -3.6. 当乙的用水量超过4吨时,即3x >4,y =8×2.1+3(8x -8)=24x -7.2,所以y =⎩⎪⎨⎪⎧16.8x ⎝ ⎛⎭⎪⎫0≤x ≤45,21.3x -3.6⎝ ⎛⎭⎪⎫45<x ≤43,24x -7.2⎝ ⎛⎭⎪⎫x >43.(2)由于y =f (x )在各段区间上均为单调递增函数, 当x ∈⎣⎢⎡⎦⎥⎤0,45时,y ≤f ⎝ ⎛⎭⎪⎫45<40.8;当x ∈⎝ ⎛⎦⎥⎤45,43时,y ≤f ⎝ ⎛⎭⎪⎫43<40.8; 当x ∈⎝ ⎛⎭⎪⎫43,+∞时,令24x -7.2=40.8,解得x =2,所以甲用户用水量为5x =10吨,付费S 1=4×2.1+6×3=26.40(元);乙用户用水量为3x =6吨,付费S 2=4×2.1+2×3=14.40(元).模块综合测评(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U ={0,1,2,3,4},集合A ={1,2,3},B ={2,4},则(∁U A )∪B =( ) A .{1,2,4} B .{2,3,4} C .{0,2,4}D .{0,2,3,4}【解析】 ∵全集U ={0,1,2,3,4},集合A ={1,2,3},∴∁U A ={0,4},又B ={2,4},则(∁U A )∪B ={0,2,4}.故选C .【答案】 C2.设f (x )=⎩⎨⎧2e x -1,x <2,log 3(2x-1),x ≥2,则f (f (2))=( ) A .0 B .1 C .2D .3【解析】 ∵f (2)=log 3(22-1)=1, ∴f (f (2))=f (1)=2e 1-1=2. 【答案】 C3.同时满足以下三个条件的函数是( )①图象过点(0,1);②在区间(0,+∞)上单调递减;③是偶函数. A .f (x )=-(x +1)2+2 B .f (x )=3|x | C .f (x )=⎝ ⎛⎭⎪⎫12|x |D .f (x )=x -2【解析】 A .f (x )=-(x +1)2+2关于x =-1对称,不是偶函数,不满足条件③. B .f (x )=3|x |在区间(0,+∞)上单调递增,不满足条件②. C .若f (x )=⎝ ⎛⎭⎪⎫12|x |,则三个条件都满足.D .若f (x )=x -2,则f (0)无意义,不满足条件①.故选C . 【答案】 C4.与函数y =-2x 3有相同图象的一个函数是( ) A .y =-x -2xB .y =x -2xC .y =-2x 3D .y =x2-2x【解析】 函数y =-2x 3的定义域为(-∞,0],故y =-2x 3=|x |-2x =-x -2x ,故选A .【答案】 A5.函数f (x )=2x -1+log 2x 的零点所在区间是( ) A.⎝ ⎛⎭⎪⎫18,14 B.⎝ ⎛⎭⎪⎫14,12 C .⎝ ⎛⎭⎪⎫12,1 D .(1,2)【解析】 ∵函数f (x )=2x -1+log 2x , ∴f ⎝ ⎛⎭⎪⎫12=-1,f (1)=1, ∴f ⎝ ⎛⎭⎪⎫12f (1)<0,故连续函数f (x )的零点所在区间是⎝ ⎛⎭⎪⎫12,1,故选C . 【答案】 C6.幂函数y =f (x )的图象经过点⎝ ⎛⎭⎪⎫-2,-18,则满足f (x )=27的x 的值是( )A.13 B .-13 C .3D .-3【解析】 设幂函数为y =x α,因为图象过点⎝ ⎛⎭⎪⎫-2,-18,所以有-18=(-2)α,解得α=-3,所以y =x -3,由f (x )=27,得x -3=27,即x =13. 【答案】 A7.函数f (x )=2x 21-x +lg (3x +1)的定义域为( )A.⎝ ⎛⎭⎪⎫-13,1B.⎝ ⎛⎭⎪⎫-13,13 C .⎝ ⎛⎭⎪⎫-13,+∞ D.⎝ ⎛⎭⎪⎫-∞,13 【解析】 要使函数有意义,只需⎩⎨⎧1-x >0,3x +1>0,解得-13<x <1,故函数f (x )=2x 21-x +lg(3x +1)的定义域为⎝ ⎛⎭⎪⎫-13,1.【答案】 A8.设a =0.50.5,b =0.30.5,c =log 0.30.2,则a ,b ,c 的大小关系是( ) A .c <a <b B .b <a <c C .c <b <aD .a <b <c【解析】 因为y =x 0.5在(0,+∞)上是增函数,且0.5>0.3,所以0.50.5>0.30.5,即a >b ,c =log 0.30.2>log 0.30.3=1,而1=0.50>0.50.5.所以b <a <c .故选B . 【答案】 B9.若函数f (x )=(k -1)ax -a -x (a >0,且a ≠1)在R 上既是奇函数,又是减函数,则g (x )=log a (x +k )的图象是( )【解析】 由f (x )=(k -1)ax -a -x (a >0,且a ≠1)在R 上既是奇函数,又是减函数,所以k =2,0<a <1,再由对数的图象可知A 正确.【答案】 A10.已知函数f (x )=1+x 21-x 2,则有( )A .f (x )是奇函数,且f ⎝ ⎛⎭⎪⎫1x =-f (x )B .f (x )是奇函数,且f ⎝ ⎛⎭⎪⎫1x =f (x )C .f (x )是偶函数,且f ⎝ ⎛⎭⎪⎫1x =-f (x )D .f (x )是偶函数,且f ⎝ ⎛⎭⎪⎫1x =f (x )【解析】 ∵f (-x )=f (x ), ∴f (x )是偶函数,排除A ,B .又f ⎝ ⎛⎭⎪⎫1x =1+⎝ ⎛⎭⎪⎫1x 21-⎝ ⎛⎭⎪⎫1x 2=1+x 2x 2-1=-f (x ),故选C .【答案】 C11.在y =2x ,y =log 2x ,y =x 2这三个函数中,当0<x 1<x 2<1时,使f ⎝⎛⎭⎪⎫x 1+x 22>f (x 1)+f (x 2)2恒成立的函数的个数是( )A .0个B .1个C .2个D .3个【解析】 在0<x 1<x 2<1时, y =2x使f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2恒成立,y =log 2x 使f ⎝ ⎛⎭⎪⎫x 1+x 22>f (x 1)+f (x 2)2恒成立,y =x 2使f ⎝ ⎛⎭⎪⎫x 1+x 22<f (x 1)+f (x 2)2恒成立.故选B .【答案】 B12.若f (x )是奇函数,且在(0,+∞)上是增函数,又f (-3)=0,则(x -1)f (x )<0的解是( ) A .(-3,0)∪(1,+∞) B .(-3,0)∪(0,3)C .(-∞,-3)∪(3,+∞)D .(-3,0)∪(1,3)【解析】 ∵f (x )是R 上的奇函数,且在(0,+∞)内是增函数,∴f (x )在(-∞,0)内也是增函数.又∵f (-3)=0,∴f (3)=0,∴当x ∈(-∞,-3)∪(0,3)时,f (x )<0;当x ∈(-3,0)∪(3,+∞)时,f (x )>0.∵(x -1)·f (x )<0,∴⎩⎨⎧ x -1<0,f (x )>0或⎩⎨⎧x -1>0,f (x )<0,解得-3<x <0或1<x <3,∴不等式的解集是(-3,0)∪(1,3),故选D.【答案】 D二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上) 13.当a >0且a ≠1时,函数f (x )=ax -2-3必过定点________.【解析】 因为a 0=1,故f (2)=a 0-3=-2,所以函数f (x )=ax -2-3必过定点(2,-2).【答案】(2,-2)14.设A∪{-1,1}={-1,1},则满足条件的集合A共有________个.【解析】∵A∪{-1,1}={-1,1},∴A⊆{-1,1},满足条件的集合A为:∅,{-1},{1},{-1,1},共4个.【答案】 415.设f(x)是R上的奇函数,且当x∈[0,+∞)时,f(x)=x(1+3x),则f(-1)=________.【解析】由题意知f(-1)=-f(1)=-1×(1+31)=-2.【答案】-216.下列命题:①偶函数的图象一定与y轴相交;②定义在R上的奇函数f(x)必满足f(0)=0;③f(x)=(2x+1)2-2(2x-1)既不是奇函数也不是偶函数;④A=R,B=R,f:x→y=1x+1,则f为A到B的映射;⑤f(x)=1x在(-∞,0)∪(0,+∞)上是减函数.其中真命题的序号是________.(把你认为正确的命题的序号都填上)【解析】①不正确,如y=lg|x|,其在原点处无定义,其图象不可能与y轴相交;②正确,∵f(-x)=-f(x),∴f(-0)=-f(0)=f(0),∴f(0)=0;③不正确,∵f(x)=(2x+1)2-2(2x-1)=4x2+3,且f(-x)=f(x),∴f(x)为偶函数;④不正确,当x=-1时,在B中没有元素与之对应;⑤不正确,只能说f(x)=1x在(-∞,0)及(0,+∞)上是减函数.【答案】②三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)计算下列各式的值:(1)1.5-13×⎝⎛⎭⎪⎫-760+80.25×42-;(2)12lg3249-43lg 8+lg 245+10lg 3.【解】 (1)原式=×=2.(2)原式=12(lg 25-lg 72)-+12lg (72×5)+10lg 3=52lg 2-lg 7-2lg 2+lg 7+12lg 5+3=12lg 2+12lg 5+3=12(lg 2+lg 5)+3=72.18.(本小题满分12分)已知集合A ={x |(a -1)x 2+3x -2=0},B ={x |x 2-3x +2=0}. (1)若A ≠∅,求实数a 的取值范围; (2)若A ∩B =A ,求实数a 的取值范围.【解】 (1)①当a =1时,A =⎩⎨⎧⎭⎬⎫23≠∅,合题意;②当a ≠1时,由Δ=9+8(a -1)≥0,得a ≥-18且a ≠1. 综上所述,a 的范围为a ≥-18. (2)由A ∩B =A ,得A ⊆B .①当A =∅时,a <-18,显然合题意;②当A ≠∅时,得到B 中方程的解1和2为A 的元素,即A ={1,2}, 把x =1代入A 中方程,得a =0. 综上所述,a的范围为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫a ⎪⎪⎪a <-18,或a =0. 19.(本小题满分12分)已知函数f (x )=1-2x . (1)若g (x )=f (x )-a 为奇函数,求a 的值;(2)试判断f (x )在(0,+∞)内的单调性,并用定义证明. 【解】 (1)由已知得g (x )=1-a -2x , ∵g (x )是奇函数,∴g (-x )=-g (x ),即1-a -2-x=-⎝ ⎛⎭⎪⎫1-a -2x ,解得a =1.(2)函数f (x )在(0,+∞)内是单调增函数. 证明如下:任取x 1,x 2∈(0,+∞),且x 1<x 2,则f (x 1)-f (x 2)=1-2x 1-⎝ ⎛⎭⎪⎫1-2x 2=2(x 1-x 2)x 1x 2.∵0<x 1<x 2,∴x 1-x 2<0,x 1x 2>0,从而2(x 1-x 2)x 1x 2<0,即f (x 1)<f (x 2).∴函数f (x )在(0,+∞)内是单调增函数.20.(本小题满分12分)已知函数f (x )=x 2-2mx +m 2+4m -2. (1)若函数f (x )在区间[0,1]上是单调递减函数,求实数m 的取值范围; (2)若函数f (x )在区间[0,1]上有最小值-3,求实数m 的值. 【解】 f (x )=(x -m )2+4m -2.(1)由f (x )在区间[0,1]上是单调递减函数得m ≥1.(2)当m ≤0时,f (x )min =f (0)=m 2+4m -2=-3,解得m =-2-3或m =-2+ 3. 当0<m <1时,f (x )min =f (m )=4m -2=-3, 解得m =-14(舍).当m ≥1时,f (x )min =f (1)=m 2+2m -1=-3,无解. 综上可知,实数m 的值是-2±3.21.(本小题满分12分)已知函数f (x )=log a (2x +1),g (x )=log a (1-2x )(a >0且a ≠1), (1)求函数F (x )=f (x )-g (x )的定义域;(2)判断F (x )=f (x )-g (x )的奇偶性,并说明理由; (3)确定x 为何值时,有f (x )-g (x )>0.【解】 (1)要使函数有意义,则有⎩⎨⎧2x +1>0,1-2x >0,解得-12<x <12.∴函数F (x )的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-12<x <12. (2)F (x )=f (x )-g (x )=log a (2x +1)-log a (1-2x ),F (-x )=f (-x )-g (-x )=log a (-2x +1)-log a (1+2x )=-F (x ). ∴F (x )为奇函数. (3)∵f (x )-g (x )>0,∴log a (2x +1)-log a (1-2x )>0, 即log a (2x +1)>log a (1-2x ).①当0<a <1时,有0<2x +1<1-2x , ∴-12<x <0.②当a >1时,有2x +1>1-2x >0,∴0<x <12.综上所述,当0<a <1时,有x ∈⎝ ⎛⎭⎪⎫-12,0,使得f (x )-g (x )>0; 当a >1时,有x ∈⎝ ⎛⎭⎪⎫0,12,使得f (x )-g (x )>0. 21.(本小题满分12分)甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲,乙两图:甲 乙图1甲调查表明:每个鱼池平均产量直线上升,从第1年1万条鳗鱼上升到第6年2万条. 乙调查表明:全县鱼池总个数直线下降,由第1年30个减少到第6年10个. 请你根据提供的信息说明:(1)第2年全县鱼池的个数及全县出产的鳗鱼总数;(2)到第6年这个县的鳗鱼养殖业的规模比第1年扩大了还是缩小了?说明理由;(3)哪一年的规模(即总产量)最大?说明理由.【解】 由题意可知,图甲图象经过(1,1)和(6,2)两点,从而求得其解析式为y 甲=0.2x +0.8,图乙图象经过(1,30)和(6,10)两点,从而求得其解析式为y 乙=-4x +34.(1)当x =2时,y 甲=0.2×2+0.8=1.2,y 乙=-4×2+34=26,y 甲×y 乙=1.2×26=31.2.所以第2年鱼池有26个,全县出产的鳗鱼总数为31.2万条.(2)第1年出产鳗鱼1×30=30(万条),第6年出产鳗鱼2×10=20(万条),可见第6年这个县的鳗鱼养殖业规划比第1年缩小了.(3)设第m 年的规模最大,总出产量为n ,那么n =y 甲y 乙=(0.2m +0.8)(-4m +34)=-0.8m 2+3.6m +27.2=-0.8(m 2-4.5m -34)=-0.8(m -2.25)2+31.25,因此,当m =2时,n 最大值为31.2.即当第2年时,鳗鱼养殖业的规模最大,最大产量为31.2万条.。
高一数学第一单元测试卷

高一数学第一单元测试卷一.选择题(每题4分,共40分)1.已知集合{}{}{}1,0,1,3,1,3,2,1,0,1,2-==--=B A U ,则()U C A B =( )A .{}0,1-B .{}1,1-C .{}1,0D .{}1,0,1-2.已知函数()()R b a bx ax x f ∈++=,33,若()52=f ,则()=-2f ( ) A .4B .3C .2D .13.已知函数()xbax x f +=2是定义在(][),31,b b -∞--+∞上的奇函数.若()32=f ,则ba +的值为( ) A .1B .2C .3D .44.函数3492-++-=x x x y 的图象关于( )A .x 轴对称B .y 轴对称C .原点对称D .直线0=-y x 对称5.函数()()()41222--=x x x x f 的图象可能是( )A .B .C .D .6.已知非空集合B A ,满足以下两个条件 (i ){}1,2,3,4,5,6,AB A B ϕ==; (ii )若A x ∈,则B x ∈+1.则有序集合对()B A ,的个数为( ) A .12B .13C .14D .157.函数()x x x f 122-+-=在区间(]4,0上的值域为( ) A .⎥⎦⎤⎢⎣⎡415,23 B .⎥⎦⎤⎝⎛∞-415,C .⎥⎦⎤⎢⎣⎡2,23D .(]2,∞-8.已知)(x f 是定义在R 上的奇函数,若()()()31,2=-=+f x f x f ,则()()20192018f f +的值为( ) A .3-B .0C .3D .69.已知定义域为R 的函数)(x f 满足()2+x f 是偶函数,且当()2,,21∞-∈x x 时,()()[]()01212>--x x x f x f 恒成立,如果212x x <<,且421>+x x ,则()()21x f x f -的值( ) A .恒小于0B .恒大于0C .可能为0D .可正可负10.设函数(){}3,2,3min 2+-=x x x x f ,其中{}z y x ,,m in 表示z y x ,,中的最小者,下列说法错误的是( )A .函数()x f 是偶函数B .若⎥⎦⎤⎢⎣⎡-∈22,22x 时,有()()x f x f ≥-2 C .若R x ∈时,有()[]()x f x f f 2≤ D .若[)+∞∈,1x 时,有()()x f x f ≤-2 二.填空题(每空3分,共18分)11.已知函数()()()⎩⎨⎧>≤+=02012x xx x x f ,则()[]=-2f f.12.函数()26x x x f -=的单调增区间为 . 13.已知函数()162ax ax x f +-=,若()x f 的定义域为R ,则实数a 的取值范围是 :若()x f 的值域为[)+∞,0,则实数a 的取值范围是 .14.已知是定义在区间()1,1-上的奇函数,当0<x 时,()()1-=x x x f ,已知m 满足不等式()()0112<-+-m f m f ,则实数m 的取值范围为 .15.已知函数()()0482≤++=a x ax x f ,对于给定负数a ,有一个最大正数()a l ,使在整个区间()[]a l ,0上,不等式()6≤x f 恒成立,则()a l 的最大值为.高一数学第一单元测试答卷纸一.选择题:(本大题共10小题,每小题4分,共40分。
高一数学第一章集合与函数概念单元测试 试题
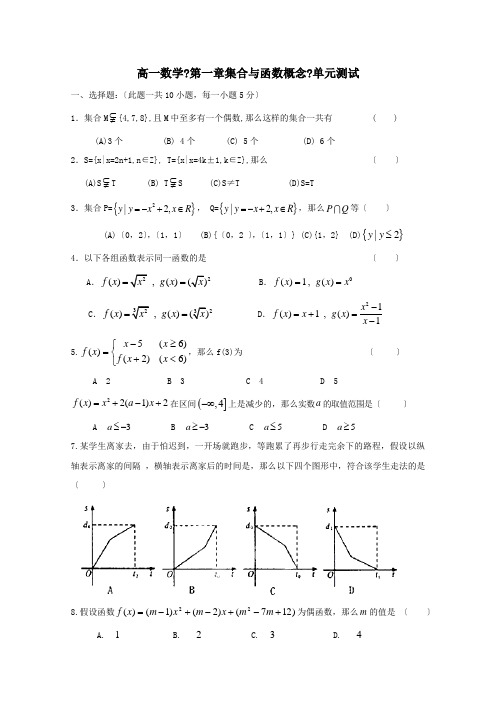
高一数学?第一章集合与函数概念?单元测试一、选择题:〔此题一共10小题,每一小题5分〕1.集合M ⊂≠{4,7,8},且M 中至多有一个偶数,那么这样的集合一共有 ( )(A)3个 (B) 4个 (C) 5个 (D) 6个2.S={x|x=2n+1,n ∈Z}, T={x|x=4k ±1,k ∈Z},那么 〔 〕(A)S ⊂≠T (B) T ⊂≠S (C)S ≠T (D)S=T3.集合P={}2|2,y y x x R =-+∈, Q={}|2,y y x x R =-+∈,那么P Q 等〔 〕(A)〔0,2〕,〔1,1〕 (B){〔0,2 〕,〔1,1〕} (C){1,2} (D){}|2y y ≤4.以下各组函数表示同一函数的是 〔 〕A .22(),()()f x x g x x == B .0()1,()f x g x x == C .3223(),()()f x x g x x == D .21()1,()1x f x x g x x -=+=- 5.⎩⎨⎧<+≥-=)6()2()6(5)(x x f x x x f ,那么f(3)为 〔 〕 A 2 B 3 C 4 D 52()2(1)2f x x a x =+-+在区间(],4-∞上是减少的,那么实数a 的取值范围是〔 〕A 3-≤aB 3-≥aC 5≤aD 5≥a7.某学生离家去,由于怕迟到,一开场就跑步,等跑累了再步行走完余下的路程,假设以纵轴表示离家的间隔 ,横轴表示离家后的时间是,那么以下四个图形中,符合该学生走法的是 〔 〕8.假设函数)127()2()1()(22+-+-+-=m m x m x m x f 为偶函数,那么m 的值是 〔 〕A. 1B. 2C. 3D. 49.下面四个结论:①偶函数的图象一定与y 轴相交;②奇函数f(x)假设在x=0处有定义,那么f(0)=0;③偶函数的图象关于y 轴对称;④既是奇函数又是偶函数的函数一定是()f x =0〔x ∈R 〕,其中正确命题的个数是〔 〕A 4B 3C 2D 110.定义域为R 的函数f (x )在区间(-∞,5)上单调递减,对任意实数t ,都有f (5+t )=f (5-t ),那么以下式子一定成立的是 〔 〕A .f (-1)<f (9)<f (13)B .f (13)<f (9)<f (-1)C .f (9)<f (-1)<f (13)D .f (13)<f (-1)<f (9)二、填空题(一共5小题,每一小题4分)11.假设函数x x x f 2)12(2-=+,那么)3(f12.函数]1,1[)20(32-<<++=在a ax x y 上的最大值是 ,最小值是 .13. 集合}023|{2=+-=x ax x A .假设A 中至多有一个元素,那么a 的取值范围是14.含有三个实数的集合既可表示成}1,,{ab a ,又可表示成}0,,{2b a a +,那么=+20042003b a .)(x f 在),0(),0()0,(+∞+∞⋃-∞上为奇函数,且在上为增函数,0)2(=-f ,那么不等式0)(<x xf 的解集为 .三、解答题(一共4小题,一共40分,解容许写出文字说明,证明过程或者演算步骤〕16.集合}33|{≤≤-=x x U ,}11|{<<-=x x M ,}20|{<<=x x N C U ,求集合N ,)(N C M U ⋂,N M ⋃.17. (1)集合}04{2=-=x x A ,集合}02{=-=ax x B ,假设A B ⊆,务实数a 的取值集合. (2)集合}71{<<=x x A ,集合}521{+<<+=a x a x B ,假设满足 }73{<<=x x B A ,务实数a 的值.18. 函数[]1(),3,5,2x f x x x -=∈+ ⑴ 判断函数()f x 的单调性,并证明;⑵ 求函数()f x 的最大值和最小值.19.底角是 45的等腰梯形ABCD ,底边BC 长为7cm ,腰长为22 cm ,当一条垂直于底边BC的直线l 〔垂足为F 〕从左到右挪动 〔与梯形ABCD 有两个公一共点〕时,直线l 把梯形分成两局部,设BF=x ,试写出左边局部的面积y 与x 的函数解析式.励志赠言经典语录精选句;挥动**,放飞梦想。
(2021年整理)高一数学《集合》单元测试题

高一数学《集合》单元测试题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高一数学《集合》单元测试题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高一数学《集合》单元测试题的全部内容。
高一数学《集合》单元测试题1。
下列表述中,不能形成集合的是( )A .全体正实数B .我校高一年级所有品学兼优的学生C .方程210x +=的实数解D .一切大于2的自然数2.已知全集{}1,2,3,4,5,6,7U =,{}2,4,5A =,则u C A =( )A 。
∅B 。
{}2,4,6 C. {}1,3,6,7 D. {}1,3,5,73.已知集合{}{}13,25A x x B x x A B =-≤<=<≤=,则( )A 。
{x|2<x 〈3}B 。
{x|-1≤x ≤5}C 。
{x | -1〈x 〈5}D 。
{x| -1〈x ≤5}4.图中阴影部分表示的集合是( )A. A ∩C U BB. C U A ∩BC. C U (A ∩B) D 。
C U (A ∪B ) 5.方程组23211x y x y -=⎧⎨+=⎩的解集是( )A. {}51,B. {}15,C. (){}51,D. (){}15,6.已知集合{}{}3,,6,A x x k k Z B x x k k Z ==∈==∈,则A 与B 之间的关系是( )A. A B ⊆B. A B ⊇C. B ∈A D 。
A=B7.已知全集U R =, 则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩(Venn )图是 ( )8.设集合{1,2}A =,则满足{1,2,3}A B ⋃=的集合B 的个数是( )A .1 B.3 C 。
高一数学必修测试题及答案

第一章三角函数单元检测试卷一、选择题:本答题共12小题;每小题5分;共60分..在每小题给出的四个选项中;只有一项是符合题目要求的..1.-300°化为弧度是 A.34π-B.35π- C .32π- D .65π- 2.为得到函数)32sin(π-=x y 的图象;只需将函数)62sin(π+=x y 的图像A .向左平移4π个单位长度 B .向右平移4π个单位长度 C .向左平移2π个单位长度 D .向右平移2π个单位长度3.函数sin(2)3y x π=+图像的对称轴方程可能是A .6x π=-B .12x π=-C .6x π=D .12x π=4.若实数x 满足㏒x2=2+sin θ;则 =-++101x x A. 2x-9 B. 9-2x C.11 D. 9 5.点Ax;y 是300°角终边上异于原点的一点;则xy值为 A.3 B. - 3 C. 33 D. -336. 函数)32sin(π-=x y 的单调递增区间是 A .⎥⎦⎤⎢⎣⎡+-125,12ππππk k Z k ∈ B .⎥⎦⎤⎢⎣⎡+-1252,122ππππk k Z k ∈ C .⎥⎦⎤⎢⎣⎡+-65,6ππππk k Z k ∈ D .⎥⎦⎤⎢⎣⎡+-652,62ππππk k Z k ∈ 7.sin -310π的值等于 A .21 B .-21C .23D .-238.在△ABC 中;若)sin()sin(C B A C B A +-=-+;则△ABC 必是 A .等腰三角形B .直角三角形C .等腰或直角三角形D .等腰直角三角9.函数x x y sin sin -=的值域是A .0B .[]1,1-C .[]1,0D .[]0,2-10.函数x x y sin sin -=的值域是A .[]1,1-B .[]2,0C .[]2,2-D .[]0,2-11.函数x x y tan sin +=的奇偶性是A .奇函数B .偶函数C .既奇又偶函数D .非奇非偶函数 12.比较大小;正确的是 A .5sin 3sin )5sin(<<- B .5sin 3sin )5sin(>>-C .5sin )5sin(3sin <-<D . 5sin )5sin(3sin >->二、填空题每小题5分;共20分13.终边在坐标轴上的角的集合为_________.14. 已知扇形的周长等于它所在圆的周长的一半;则这个扇形的圆心角是________________.15.已知角α的终边经过点P-5;12;则sin α+2cos α的值为______.16.一个扇形的周长是6厘米;该扇形的中心角是1弧度;该扇形的面积是________________.三、解答题:本大题共6小题;共70分..解答应写出文字说明及演算步骤... 17.8分已知tan 3α=-;且α是第二象限的角;求αsin 和αcos ; 18.10分 已知3tan =α;计算ααααsin 3cos 5cos 2sin 4+- 的值 ..19.12分求函数)32tan(π+=x y 的定义域和单调区间. 20. 12分求函数y=-x 2cos +x cos 3+45的最大值及最小值;并写出x 取何值时 函数有最大值和最小值.. 15分21. 12分已知函数y=)sin(φω+x A A >0;ω >0;πφ〈的最小正周期为32π; 最小值为-2;图像过95π;0;求该函数的解析式.. 22.14分 设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x .Ⅰ求ϕ;Ⅱ求函数)(x f y =的单调增区间;Ⅲ画出函数)(x f y =在区间],0[π上的图像..第一章三角函数单元检测试卷参考答案一、选择题每小题5分;共60分1----6、BBDCBA 7----12、CCDCAB 二、填空题每小题5分;共20分 13.{α|}Z n n ∈=,2πα 14.rad )2(-π 15.13216. 2 三、解答题共70分17. 1sin ,cos 10αα==- 2tan 2α=18.解、∵3tan =α ∴0cos ≠α∴原式=ααααααcos 1)sin 3cos 5(cos 1)cos 2sin 4(⨯+⨯- =ααtan 352tan 4+- =335234⨯+-⨯ =75 19.解:函数自变量x 应满足 πππk x +≠+232 ;z k ∈;即ππk x 23+≠;z k ∈所以函数的定义域是 ⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,23ππ.. 由ππk +-2<32π+x <ππk +2;z k ∈;解得 ππk 235+-<x <ππk 23+;z k ∈所以 ;函数的单调递增区间是)23,235(ππππk k ++-;z k ∈..20.解:令t=cosx; 则]1,1[t -∈所以函数解析式可化为:453y 2++-=t t =2)23(2+--t 因为]1,1[-∈t ; 所以由二次函数的图像可知:当23=t 时;函数有最大值为2;此时Z k k x ∈++=k 611262,或ππππ 当t=-1时;函数有最小值为341-;此时Z k ∈+=k 2x ,ππ 21解:32π函数的最小正周期为 ; 3322===∴ωπωπ即T又2-函数的最小值为 ; 2=∴A 所以函数解析式可写为)3sin(2y ϕ+=x又因为函数图像过点95π;0; 所以有:0)953(sin 2=+⨯ϕπ解得35ππϕ-=k 323,ππϕπϕ-=∴≤或 所以;函数解析式为:)323sin(2y )33sin(2y ππ-=+=x x 或22.解:Ⅰ8x π=是函数)(x f y =的图象的对称轴 Ⅱ由Ⅰ知34πϕ=-;因此3sin(2)4y x π=-由题意得3222,242k x k k Z πππππ-≤-≤+∈所以函数3sin(2)4y x π=-的单调递增区间为Ⅲ由3sin(2)4y x π=-可知故函数)(xfy=在区间[]0,π上的图象是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学单元测试题(八)
一、选择题
1、 若指数函数y a x =+()1在()-∞+∞,上是减函数,那么( )
A 、 01<<a
B 、 -<<10a
C 、 a =-1
D 、 a <-1
2、已知310x
=,则这样的x ( )
A 、 存在且只有一个
B 、 存在且不只一个
C 、 存在且x <2
D 、 根本不存在
3、函数f x x ()=-23在区间()-∞,0上的单调性是( )
A 、 增函数
B 、 减函数
C 、 常数
D 、 有时是增函数有时是减函数
4、下列函数图象中,函数y a a a x =>≠()01且,与函数y a x =-()1的图象只能是( ) y y y y O x O x O x O x
A B C D
1111
5、函数f x x ()=-21,使f x ()≤0成立的x 的值的集合是( )
A 、 {}x x <0
B 、 {}x x <1
C 、 {}x x =0
D 、 {}
x x =1
6、函数f x g x x x ()()==+22,,使f x g x ()()=成立的x 的值的集合( ) A 、 是φ B 、 有且只有一个元素
C 、 有两个元素
D 、 有无数个元素
7、若函数(1)x y a b =+-(0a >且1a ≠)的图象不经过第二象限,则有
( ) A 、1a >且1b < B 、01a <<且1b ≤
C 、01a <<且0b >
D 、1a >且0b ≤
8、函数y=1
212+-x x 是( ) A 、奇函数 B 、偶函数 C 、既奇又偶函数 D 、非奇非偶函数
二、填空题
9、 函数y x =-322的定义域是_________。
10、 指数函数f x a x ()=的图象经过点()2116,
,则底数a 的值是_________。
11、 将函数f x x ()=2的图象向_________平移________个单位,就可以得到函数g x x ()=-22的图象。
12、 函数f x x ()()
=-121,使f x ()是增函数的x 的区间是_________ 三、解答题
13、已知关于x 的方程2a
22-x -7a 1-x +3=0有一个根是2, 求a 的值和方程其余的根
14、设a 是实数,)(122)(R x a x f x ∈+-
=试证明对于任意a,)(x f 为增函数
15、已知函数x x a b y 22++=(a 、b 是常数且a>0,a ≠1)在区间[-2
3,0]上有y max =3,
y min =2
5,试求a 和b 的值. 单元测试题(八)答案
一、选择题B ;2、A ;3、B ;4、C ;5、C ;6、C ;7、D ;8、A
二、填空题9、 (]-∞,5 10、
14
11、 右、2 12、 (]-∞,1 三、解答题13、解: 2a 2-7a+3=0, ⇒a=2
1或a=3. a=21时, 方程为: 8·(21)x 2-14·(2
1)x +3=0⇒x=2或x=1-log 23 a=2时, 方程为: 21·2x 2-27·2x +3=0⇒x=2或x=-1-log 32 14、证明:设21,x x ∈R,且21x x < 则)
12)(12()22(222122)
122()122()()(2121122121++-=-+=+--+-
=-x x x
x x x x x a a x f x f 由于指数函数 y=x 2在R 上是增函数,且21x x <,所以
2122x x <即2122x x -<0, 又由x 2>0得12x +1>0, 22x +1>0所以)()(21x f x f -<0即)()(21x f x f < 因为此结论与a 取值无关,所以对于a 取任意实数,)(x f 为增函数15、解:令u =x 2+2x =(x +1)2-1 x ∈[-23,0] ∴当x =-1时,u min =-1 当x =0时,u max =0
.233222223225310)2222531)10110⎪⎪⎩
⎪⎪⎨⎧==⎩⎨⎧==⎪⎪⎩
⎪⎪⎨⎧==⎪⎩⎪⎨⎧=+=+<<⎩⎨⎧==⎪⎩
⎪⎨⎧=+=+>--b a b a b a a b a b a b a a b a b a 或综上得解得时当解得时当。
