chapter08相量法电路原理
合集下载
电路邱关源版第08章
•
– 相量的模表示正弦量的有效值 – 相量的幅角表示正弦量的初相位 – 同理可得正弦电压与相量的关系 – 振幅相量
i(t) = 2I cos(ωt +φi ) ⇔ I = I ∠φi
u(t) = 2U cos(ωt +φu ) ⇔ U = U∠φu
i(t) = Im cos(ωt +φu ) ⇔ I m = Im∠φu u(t) = Um cos(ωt +φi ) ⇔ Um = Um∠φi
R
i
L
+
us
uC
- C
i = 2I cos(ωt +φi )
1 2I sin(ωt +φi ) = 2Us cos(ωt +φu ) ωC
8.3 相量法的基础
• 为什么要用相量表示正弦量？ 为什么要用相量表示正弦量？
两个正弦量的相加： 两个正弦量的相加： i1 = 2 I1 cos(ωt +ψ1) i2 = 2 I2 cos(ωt +ψ2 )
U= 1 2 Um 或 Um = 2U u(t) = Um cos(ωt +ψu ) = 2U cos(ωt +ψu )
• 注意： 注意：
– 工程上说的正弦电压、电流一般指有效值，如设备铭牌 工程上说的正弦电压、电流一般指有效值， 额定值、电网的电压等级等。但绝缘水平、 额定值、电网的电压等级等。但绝缘水平、耐压值指的 是最大值。因此， 是最大值。因此，在考虑电器设备的耐压水平时应按最 大值考虑。 大值考虑。(U=220V, Um=311V U=380V, Um=537V) – 测量中，电磁式交流电压、电流表读数均为有效值。 测量中，电磁式交流电压、电流表读数均为有效值。 – 区分电压、电流的瞬时值、最大值、有效值的符号。 区分电压、电流的瞬时值、最大值、有效值的符号。
– 相量的模表示正弦量的有效值 – 相量的幅角表示正弦量的初相位 – 同理可得正弦电压与相量的关系 – 振幅相量
i(t) = 2I cos(ωt +φi ) ⇔ I = I ∠φi
u(t) = 2U cos(ωt +φu ) ⇔ U = U∠φu
i(t) = Im cos(ωt +φu ) ⇔ I m = Im∠φu u(t) = Um cos(ωt +φi ) ⇔ Um = Um∠φi
R
i
L
+
us
uC
- C
i = 2I cos(ωt +φi )
1 2I sin(ωt +φi ) = 2Us cos(ωt +φu ) ωC
8.3 相量法的基础
• 为什么要用相量表示正弦量？ 为什么要用相量表示正弦量？
两个正弦量的相加： 两个正弦量的相加： i1 = 2 I1 cos(ωt +ψ1) i2 = 2 I2 cos(ωt +ψ2 )
U= 1 2 Um 或 Um = 2U u(t) = Um cos(ωt +ψu ) = 2U cos(ωt +ψu )
• 注意： 注意：
– 工程上说的正弦电压、电流一般指有效值，如设备铭牌 工程上说的正弦电压、电流一般指有效值， 额定值、电网的电压等级等。但绝缘水平、 额定值、电网的电压等级等。但绝缘水平、耐压值指的 是最大值。因此， 是最大值。因此，在考虑电器设备的耐压水平时应按最 大值考虑。 大值考虑。(U=220V, Um=311V U=380V, Um=537V) – 测量中，电磁式交流电压、电流表读数均为有效值。 测量中，电磁式交流电压、电流表读数均为有效值。 – 区分电压、电流的瞬时值、最大值、有效值的符号。 区分电压、电流的瞬时值、最大值、有效值的符号。
电路原理(邱关源)习题答案第八章 相量法
第八章 相量法求解电路的正弦稳态响应，在数学上是求非齐次微分方程的特解。
引用相量法使求解微分方程特解的运算变为复数的代数运运算，从儿大大简化了正弦稳态响应的数学运算。
所谓相量法，就是电压、电流用相量表示，RLC 元件用阻抗或导纳表示，画出电路的相量模型，利用KCL,KVL 和欧姆定律的相量形式列写出未知电压、电流相量的代数方程加以求解，因此，应用相量法应熟练掌握：（1）正弦信号的相量表示；（2）KCL,KVL 的相量表示；（3）RLC 元件伏安关系式的相量形式；（4）复数的运算。
这就是用相量分析电路的理论根据。
8－1 将下列复数化为极坐标形式：（1）551j F --=；（2）342j F +-=；（3）40203j F +=；（4）104j F =；（5）35-=F ；（6）20.978.26j F +=。
解：（1）a j F =--=551θ∠25)5()5(22=-+-=a13555arctan -=--=θ(因1F 在第三象限)故1F 的极坐标形式为 135251-∠=F（2） 13.1435)43arctan(3)4(34222∠=-∠+-=+-=j F （2F 在第二象限）（3） 43.6372.44)2040arctan(40204020223∠=∠+=+=j F（4） 9010104∠==j F（5） 180335∠=-=F（6） 19.7361.9)78.220.9arctan(20.978.220.978.2226∠=∠+=+=j F注：一个复数可以用代数型表示，也可以用极坐标型或指数型表示，即θθj ae a ja a F =∠=+=21,它们相互转换的关系为：2221a a a += 12arctan a a =θ和 θcos 1a a = θsin 2a a =需要指出的，在转换过程中要注意F 在复平面上所在的象限，它关系到θ的取值及实部1a 和虚部2a 的正负。
8－2 将下列复数化为代数形式：（1） 73101-∠=F ；（2） 6.112152∠=F ；（3） 1522.13∠=F ；（4） 90104-∠=F ；（5） 18051-∠=F ；（6） 135101-∠=F 。
电路原理 第八章_相量法
复数 复数
—
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法(续）
—
已知正弦量 220√ 2 cos ( ω t－35° ) 有效值相量 最大值相量 220/ －35° — 220√ 2 /－35°
已知 相量 10/45° and 正弦量的角频率ω 相应的正弦量 — 10 √ 2 cos( ωt + 45° )
0 ωt1
ωt2
ωt
φ
图8-5 用旋转矢量表示的正弦量
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法 F = ⎪F⎪e j(ω t + ϕ )
ejθ = cosθ + jsinθ
设：有一复数
欧拉公式
F = ⎪F⎪ej(ωt + ϕ ) = ⎪F⎪cos(ωt + ϕ) + j⎪F⎪sin(ωt +ϕ) Re [F] = ⎪F⎪cos(ωt + ϕ ) Im [F] = ⎪F⎪sin(ωt + ϕ )
返回
第8章
三、旋转因子
/ϕ 旋转因子: e jϕ = 1 — A = ⎪A⎪ejα Aejϕ = ⎪A⎪ejαejϕ = ⎪A⎪ej(α+ϕ ) ejπ/2 = j1 e－jπ/2 = − j1
+j
Aejϕ
ϕ α
0
A
+1
e－jπ = − 1
孙惠英 shy@
上页
下页
返回
第8章
ϕ 12 = ϕ 1－ ϕ 2 —— u1 超前于 u2 的相角 ϕ 21 = ϕ 2－ ϕ 1 —— u2 超前于 u1 的相角
第八章 相量法(Phasor method
k =1
由相量的线性特性，有
& Re[ 2e jω t ∑ I k ] = 0
k =1
28
& Re[ 2e jω t ∑ I k ] = 0
k =1
n
上式成立的条件为
∑ I&
k =1
n
k
=0
——KCL的相量形式
表明：在正弦稳态电路中，流入（或流出）结点的各支 路电流相量的代数和为零。 同理可得KVL的相量形式：
对应的相量为 5∠−60° 2)
− 8 2 cos(ω t − 45°) = 8 2 cos(ω t − 45° + 180°) = 8 2 cos(ω t + 135°)
对应的相量为 8∠135°
18
3)
− 6 2 sin(ω t − 60°) = 6 2 sin(ω t − 60° + 180 °) = 6 2 sin(ω t + 120 °) = 6 2 cos(ω t + 120 ° − 90°) = 6 2 cos(ω t + 30°)
10
3）复数的三角形式 由图可见 a1= |A| cosθ a2= |A|sinθ A= |A|（cos θ +jsin θ ） 4）复数的指数形式 根据欧拉公式 e jθ
a2
Im |A|
θ
o a1 Re
= cos θ + j sin θ jθ A = Ae 复数的三角形式变为指数形式，即
A = A ∠θ
i1 = 100 i 2 = 10
2 cos( 6280 t − 60 o ) A 2 cos( 6280 t + 30 o ) A
s
20
由相量的线性特性，有
& Re[ 2e jω t ∑ I k ] = 0
k =1
28
& Re[ 2e jω t ∑ I k ] = 0
k =1
n
上式成立的条件为
∑ I&
k =1
n
k
=0
——KCL的相量形式
表明：在正弦稳态电路中，流入（或流出）结点的各支 路电流相量的代数和为零。 同理可得KVL的相量形式：
对应的相量为 5∠−60° 2)
− 8 2 cos(ω t − 45°) = 8 2 cos(ω t − 45° + 180°) = 8 2 cos(ω t + 135°)
对应的相量为 8∠135°
18
3)
− 6 2 sin(ω t − 60°) = 6 2 sin(ω t − 60° + 180 °) = 6 2 sin(ω t + 120 °) = 6 2 cos(ω t + 120 ° − 90°) = 6 2 cos(ω t + 30°)
10
3）复数的三角形式 由图可见 a1= |A| cosθ a2= |A|sinθ A= |A|（cos θ +jsin θ ） 4）复数的指数形式 根据欧拉公式 e jθ
a2
Im |A|
θ
o a1 Re
= cos θ + j sin θ jθ A = Ae 复数的三角形式变为指数形式，即
A = A ∠θ
i1 = 100 i 2 = 10
2 cos( 6280 t − 60 o ) A 2 cos( 6280 t + 30 o ) A
s
20
电路分析课件第八章相量法
KVL：任意时刻，任一回路，U=0
三、受控源的相量形式
i1
I1
R
正弦电流
i 1 电路时：
R
1I1
本章小结：
所谓相量法，就是电压、电流用相量表示， RLC元件用阻抗、感抗、容抗表示，画出电路的相 量模型，利用KCL、KVL和欧姆定律的相量形式写 出未知电压、电流相量的代数方程加以求解，因此， 应用相量法应熟练掌握:
∴ i =46.2 2cos(314t–27º)A j I1
+1 I
相量图
I2
注意：
在分析正弦交流电路时字母的写法：
i — 瞬时值 I — 有效值 Im — 最大值 I — 有效值相量 Im— 最大值相量
三、不同频率的正弦量不能用相量法运算。
相量只含有正弦量的有效值(最大值)和初相 位的信息，不包含频率的信息，即：在运用相量 法分析正弦量时，默认为同频率。
将 I (或 U)定义为电流i (或电压u) 的相量，它含有 正弦量的振幅和相位的信息。
注意：
有一个正弦量便可以得到一个相量； 有一个相量也可以写出对应的正弦
量。两者是一一对应的关系，决不
是相等的关系。
u=220 2 cos(314t+45º)V
U=220 45ºV u U
I=50 –30ºA 一一对应 i =50 2 cos(ωt–30º)A i I
U 相量形式电路图
相量关系既反映了u、i 的有效 值关系又反映了相位的关系。
I U 相量图
2、电感
iL
u
若：i = 2 Icos(ωt+ψi )
则：u=L
di dt
=–
2 IωLsin(ωt+ψi )
电路原理课件 第8章 相量法
三. 相位差 ：
两个同频率正弦量相位角之差。
i(t) 0
Im um
设 u(t)=Umcos(w t+ u)
2
i(t)=Imcos(w t+ i)
0
wt
则 相位差j : j = (w t+ u)- (w t+ i)
u- i
同频率正弦量的相位差等于它们的初相之差。 不同频率的两个正弦量之间的相位差不再是一个常数，而是 随时间变动。
j u与i正交; j u与i反相;
2
§8 - 3相量法的基础
1. 正弦量的相量表示
复函数 F F ej(wt)
没有物理意义
F cos(wt ) j F sin(wt Ψ )
若对F取实部：
Re[F] F cos(ωt Ψ ) 是一个正弦量，有物理意义。
对于任意一个正弦时间函数都可以找到唯一的与其对应的 复指数函数：
F e j
4、极坐标形式：
F F ej
=|F|
二 复数运算
(1)加减运算——代数形式
+j F2
若 F1=a1+jb1
F2=a2+jb2 O
则 F1±F2= (a1±a2) +j (b1±b2)
F= F1 +F1
F1 +1
+j
O - F2
F2 F1
F= F1 - F2 +1
(2) 乘除运算——指数形式或极坐标形式
⑶∫i2dt。
解： ⑴设 i i1 i2 2I cos(wt i ), 其相量为 I=I/Ψi
I I1 I2 10/600A+22/-1500A=（5+j8.66）A+（-19.05-j11）A
第八章向量法
Im——正弦量的振幅，且有：
imax = I m
ω——正弦量的角频率。
d ω = (ωt + ψ i ) dt
ϕi——正弦量在t=0时刻的相位，称为正弦量 的初相位（角），简称初相，即
(ωt + ω i ) t =0 = ψ i
正弦量的三要素是正弦量之间进行比较和区分的依据。
注意
正弦量乘以常数，正弦量的微分、积 分，同频正弦量的代数和等运算，其结果 仍为一个同频率的正弦量。 这是正弦量的一个重要性质。
由
1 + cos[2(ωt + ψ i )] cos (ωt + ψ i ) = 2
2
可得
I = I m / 2 = 0.707 I m
正弦量i可改写成：
i = 2 I cos(ωt + ϕ i )
四、相位差
相位差用来描述两个同频率正弦量之间的相位关系。 若
i1 = u2 = 2 I 1 cos( ω t + ψ i1 ) 2U 2 cos( ω t + ψ u 2 )
表示di/dt的相量为 高阶导数 d i / dt
n n
& jωI = ωI∠ψ i + π / 2
& ( jω ) n I ，其相量为
3、正弦量的积分
∫ idt =
∫ Re[
2 I&e jω t ]dt
= Re[ ∫ ( 2 I&e jω t ) dt ] = Re[ = 2 I 2( 1 ) e jω t ] jω
所以
uad = 15 2 cos(1000t )V
第八章 相量法
内容提要
本章介绍的相量法是线性电路正弦 稳态分析的一种简便而又有效的方法。 主要内容有：复数，正弦量，相量法的 基础，电路定律的相量形式。
第八章相量法
i i
i
i
i
如 i 26 2 cos(t 60) A 26e j 60 A 2660 A I 对应的有效值相量为：
Im 26 2e j 60 A 26 260 A 其最大值相量为：
U 同理若有： 220e j 30V 则有; u 220 2 cos(t 30)V 2.相量图 相量是一个复数，它在复平面上的图形称为相量图。 若用旋转相量表示为，2Ie j e jt 其中复常数 2Ie j 2I i 称为旋转相量的复振幅， e jt 是一个随时间变化而以角速度不断逆时针旋转 的因子，两者的乘积即表示复振幅在复平面上不断 逆时针旋转，故称之为旋转相量，这就是复指数 函数的几何意义。
dt 2
③正弦量的积分
i 2I cos(t i ) 则 idt Re [ 2 Ie jt ]dt Re [ 2 Ie jt dt ] 如
jt I I Re [ 2 ( )e ] 2 cos(t i ) j 2
即正弦量的积分为同频率正弦量，其相量等于原 j 相量 I 除以 . I I 表示为： ( i ) idt
F F1 F2 F1 F2 [cos( 1 2 ) j sin(1 2 )]
F1 a1 jb1 (a1 jb1 )(a2 jb2 ) a1a2 b1b2 a2 b1 a1b2 j 2 2 2 2 F2 a2 jb2 (a2 jb2 )(a2 jb2 ) a2 b2 a2 b2
1
i1 I1m cos(t i 1 ) A 和 i2 I 2 m cos(t i 2 ) A 则 i1 与 i 2 如 的相位差 12 (t i1 ) (t i 2 ) i1 i 2 （初相之差）
i
i
i
如 i 26 2 cos(t 60) A 26e j 60 A 2660 A I 对应的有效值相量为：
Im 26 2e j 60 A 26 260 A 其最大值相量为：
U 同理若有： 220e j 30V 则有; u 220 2 cos(t 30)V 2.相量图 相量是一个复数，它在复平面上的图形称为相量图。 若用旋转相量表示为，2Ie j e jt 其中复常数 2Ie j 2I i 称为旋转相量的复振幅， e jt 是一个随时间变化而以角速度不断逆时针旋转 的因子，两者的乘积即表示复振幅在复平面上不断 逆时针旋转，故称之为旋转相量，这就是复指数 函数的几何意义。
dt 2
③正弦量的积分
i 2I cos(t i ) 则 idt Re [ 2 Ie jt ]dt Re [ 2 Ie jt dt ] 如
jt I I Re [ 2 ( )e ] 2 cos(t i ) j 2
即正弦量的积分为同频率正弦量，其相量等于原 j 相量 I 除以 . I I 表示为： ( i ) idt
F F1 F2 F1 F2 [cos( 1 2 ) j sin(1 2 )]
F1 a1 jb1 (a1 jb1 )(a2 jb2 ) a1a2 b1b2 a2 b1 a1b2 j 2 2 2 2 F2 a2 jb2 (a2 jb2 )(a2 jb2 ) a2 b2 a2 b2
1
i1 I1m cos(t i 1 ) A 和 i2 I 2 m cos(t i 2 ) A 则 i1 与 i 2 如 的相位差 12 (t i1 ) (t i 2 ) i1 i 2 （初相之差）
第8章 相量法
T
0
i (t ) Rdt I RT
2 2
1 T 2 I 0 i (t )dt T
(1)式中代入
(1)式
i(t ) I m cos( t i ) 得
Im I 2
i(t ) I m cos( t i )
2.角频率（周期T、频率f）：表示变化快慢 Angular frequency(period, frequency) 定义：相角(t+i)随时间变化的速度（rad/s）
The Phasor
相量法即用复数为工具来表示正弦量。 正弦量 相量(复数)
变换的思想
相量是一个包含正弦量“幅值”和“相 位”信息的复数。
一、复习复数：
1.复数的表示形式 (1)代数形式 b 0
+j
F
r
θ
a +1
F a jb
(2)三角形式 (3)指数形式 (4)极坐标形式
F r
a b
u(t ) 2U cos( t u )
X Y 53.1
xy 3 X Y
4
2.复数的代数运算 相加(减):使用代数形式
(a jb) (a1 a2 ) j (b1 b2 )
相乘（除）:使用指数形式
F F1F2 r1r2e
j (1 2 )
F1 r1 j (12 ) F e F2 r2
二．正弦信号的相量表示
根据欧拉公式:
e
jx
cos x j sin x
j (t )
对于同频 正弦量而 言相同
u 2U cos ( t ) Re[ 2Ue
时域 一 一 对 应
] Re[ 2Ue j e jt ]
第8章 相量法
12.47 j 0.569 12.48 2.61
(17 j 9) (4 j 6) 220 35 ? 20 2 ： j5 例
19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04
180.2 j126.2 6.72870.16
我国国家标准规定的电力网额定电压有 10KV、35 kV、110 kV、220 kV、330 kV、500 kV，目前大力研究750KV,1000KV，已经有线路 试运行。 市区一般输电电压为 10 kV 左右（江苏在 试点 20KV）电压等级，通常需要设臵降压变电 所， 经配电变压器将电压降为 380/ 220 V， 再引出若干条供电线到各用电点的配电箱上， 配电箱将电能分配给各用电设备。
第8章
相量法
本章重点
8.1 8.2 8.3 8.4 复数 正弦量 相量法的基础
电路定律的相量形式
目的：交流电路的分析基础!
日常生活，交流电应用广泛!
回顾：直流电路中学习了哪些定理与方法？
i1
20
5
i2
u 1
140V
6
u 2
i3
u3
90V
三个基本工具：欧姆定理，(a) KCL,
几种不同值时的旋转因子：
Im
jI
0
I cos j sin j 2 2
Re
jI
j 2 , e cos( ) j sin( )j 2 2 2
I
, e j cos( ) j sin( ) 1
交流情况下电容如何处理？
i +
(17 j 9) (4 j 6) 220 35 ? 20 2 ： j5 例
19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04
180.2 j126.2 6.72870.16
我国国家标准规定的电力网额定电压有 10KV、35 kV、110 kV、220 kV、330 kV、500 kV，目前大力研究750KV,1000KV，已经有线路 试运行。 市区一般输电电压为 10 kV 左右（江苏在 试点 20KV）电压等级，通常需要设臵降压变电 所， 经配电变压器将电压降为 380/ 220 V， 再引出若干条供电线到各用电点的配电箱上， 配电箱将电能分配给各用电设备。
第8章
相量法
本章重点
8.1 8.2 8.3 8.4 复数 正弦量 相量法的基础
电路定律的相量形式
目的：交流电路的分析基础!
日常生活，交流电应用广泛!
回顾：直流电路中学习了哪些定理与方法？
i1
20
5
i2
u 1
140V
6
u 2
i3
u3
90V
三个基本工具：欧姆定理，(a) KCL,
几种不同值时的旋转因子：
Im
jI
0
I cos j sin j 2 2
Re
jI
j 2 , e cos( ) j sin( )j 2 2 2
I
, e j cos( ) j sin( ) 1
交流情况下电容如何处理？
i +
电路分析第08章.相量法
w1 w2
不能比较相位差
(4) i1(t ) 5 cos(100 t 300 ) i2 (t ) 3 cos(100 t + 300 )
i2 (t ) 3 cos(100t 1500 )
j 300 (1500 ) 1200
两个正弦量进行相位比较时应满足同频率、同函数、同符 号，且在主值范围比较。
则:
A1 A2
A1 e jq1
A2 e jq2
A1
A e j(q1 +q2 ) 2
A1 A2 q1 + q 2 乘法：模相乘，幅角相加。
A1 A2
| A1 | θ 1 | A2 | θ 2
| A1 | e jθ1 | A2 | e jθ 2
| A1 | e j( θ 1θ 2 ) | A2 |
反映正弦量变化幅度的大小。
(2) 角频率(angular frequency)ω
相位变化的速度， 反映正弦量变化快慢。
w
d dt
2
f
2
T
单位： rad/s ，弧度 / 秒
i
T
(3) 初相位(initial phse angle)qi
反映正弦量的计时起点时 的相角，常用角度表示。
qi
Im O
| A1 | | A2 |
θ1 θ2
除法：模相除，幅角相减。
返回 上页 下页
(3) 旋转因子：
复数 ejq =cosq +jsinq =1∠q
Im
A• ejq
q A
0
Re
A• ejq 相当于A逆时针旋转一个角度q ，而模不变。故
第08章相量法
？ 则：U＝10V U 10e j15V？ -j15º 已知： I 10050 A
？ 则： i＝100cos(t＋50º)A
100 2
（3-24）
§8.3 相量法的基础
无物理意义
一、正弦量为何可以用相量表示？
某复函数： A(t ) 2Iej(t)
为正弦量 有物理意义
（3-16）
+j
b
r
A
+1
a
欧拉公式
cos＋jsin ＝ej
A＝a＋jb …………………………代数式
＝r(cos＋j sin) …………三角函数式
＝rej …… …………………………指数式
＝r∠ …………………………极坐标形式
（3-17）
设a、b为正实数
A＝a＋jb ＝r∠
0<< 90º
2.KVL相量式
——任一瞬间任一回路上: u(t)＝0
若该回路上的电压均为同频率正 弦量,则用相量表示时仍满足KVL,即:
KVL相量形式 U 0
I
如右图,设uR,uL,uC均为同频率正弦量：
U R U L U C U 0
+R
U U R U L U C
相量——表示正弦电压、电流的复数
（3-15）
一、复数的基本形式
设复平面上某复数A ：
+j
b
r
A
+1
a
r a2 b2
arctan b
a a＝rcos
b＝ rsin
其中:r—复数的模; —辐角; a—实部; b —虚部
A＝a＋jb ＝rcos＋jrsin ＝r(cos＋j sin)
？ 则： i＝100cos(t＋50º)A
100 2
（3-24）
§8.3 相量法的基础
无物理意义
一、正弦量为何可以用相量表示？
某复函数： A(t ) 2Iej(t)
为正弦量 有物理意义
（3-16）
+j
b
r
A
+1
a
欧拉公式
cos＋jsin ＝ej
A＝a＋jb …………………………代数式
＝r(cos＋j sin) …………三角函数式
＝rej …… …………………………指数式
＝r∠ …………………………极坐标形式
（3-17）
设a、b为正实数
A＝a＋jb ＝r∠
0<< 90º
2.KVL相量式
——任一瞬间任一回路上: u(t)＝0
若该回路上的电压均为同频率正 弦量,则用相量表示时仍满足KVL,即:
KVL相量形式 U 0
I
如右图,设uR,uL,uC均为同频率正弦量：
U R U L U C U 0
+R
U U R U L U C
相量——表示正弦电压、电流的复数
（3-15）
一、复数的基本形式
设复平面上某复数A ：
+j
b
r
A
+1
a
r a2 b2
arctan b
a a＝rcos
b＝ rsin
其中:r—复数的模; —辐角; a—实部; b —虚部
A＝a＋jb ＝rcos＋jrsin ＝r(cos＋j sin)
高等教育出版社第六版《电路》第8章_相量法讲解
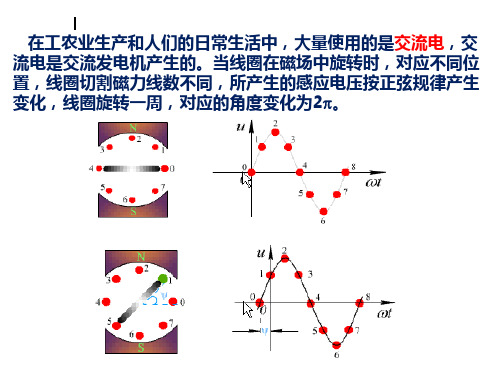
定义：随时间按正弦规律变化的电压和电流，称为正弦量。 i
&#， i(t) Im cos(t i )
注意：方向是随时间在周期性的变化，所以更要标定参考方向。 5
1、变化的快慢： ①频率f：每秒变化的次数。单位：Hz ②周期T：变化一次所需的时间。单位：s ③角频率ω：每秒变化的弧度数。单位：rad/s
一般地 i 2I cos(t i )A
可用相量表示为： I I e ji I iA
9
二、相量和正弦量的比较：
①联系： 实数范围的正弦时间函数和复数范围的复指数常数一一对应。
欧拉公式：e j cos jsin，
i 2I cos(t i ) Re[ Re[ 2 I eji ejt ] Re[
F
其中 F ： 模、§幅8值-1 复数： 幅角
b
四者之间有： a F cos b F sin
F a2 b2
arctan b
a
a
请注意：上式与教材P202倒数第二行的差别。
为正确判定θ所在的象限，我们将a、b的正负号分别
保留在分母分子中，而不用小括号。
例：
F
4
j4，
arctan
4 4
45
(第四象限)。
意
②正弦量的一个重要性质：
正弦量乘以常数，正弦量的微分、积分，同频 正弦量的代数和等，结果均为同频正弦量。
8
§8 - 3 相量法的基础(****)
§8 - 3 相量法的基础
一、相量定义：
表示正弦量的复常数称为相量。 例如：
正弦量 i 220 2 cos(314t 30 )A
可用相量I 220 ej30 A表示。
例 u(t) Um sin(t u )
第08章 相量法
F1 F2
F1
F1 F2
F2
+1
O
F2
3、乘法 用极坐标形式比较方便 设
F1 | F1 | 1
F2 | F2 | 2
F F2 F 1 F2 2 1 1
F F2 / 1 2 1
4、除法
F1 F2
| F1 | 1
| F2 | 2
(a1 a2 ) j(b1 b2 )
几何意义 +j
F1 F2
F1
F2
O
+1
2、减法 用代数形式进行， 设
F1 a1 j b1
F2 a2 j b2
F1 F2 (a1 j b1 ) (a2 j b2 )
几何意义
+j
(a1 a2 ) j(b1 b2 )
二、正弦量的三要素
i + 瞬时值表达式： i(t ) u -
I m cos(t i )
1、振幅Im 2、角频率ω
i(t ) I m cos(t i )
i
Im 2π π 2π ωt
正弦量在整个振荡过程中达到的最大值
反映正弦量变化的快慢 ω =d(ωt+ )/dt 单位时间内变化的角度, 单位:rad/s ωT=2π,ω=2πf , f=1/T 频率f :每秒钟完成循环的次数， 单位为赫兹（Hz） 周期T :完成一个循环变化所需 的时间,单位为秒（s）
接下来…… i(t)=Imcos( t + )
(a) 角频率 ( )
所有电压电流均以相 同角频率ω变化!!
(b) 幅值 (Im)
(c) 初相角( )
用什么可以同时表示幅 值和相位？
F1
F1 F2
F2
+1
O
F2
3、乘法 用极坐标形式比较方便 设
F1 | F1 | 1
F2 | F2 | 2
F F2 F 1 F2 2 1 1
F F2 / 1 2 1
4、除法
F1 F2
| F1 | 1
| F2 | 2
(a1 a2 ) j(b1 b2 )
几何意义 +j
F1 F2
F1
F2
O
+1
2、减法 用代数形式进行， 设
F1 a1 j b1
F2 a2 j b2
F1 F2 (a1 j b1 ) (a2 j b2 )
几何意义
+j
(a1 a2 ) j(b1 b2 )
二、正弦量的三要素
i + 瞬时值表达式： i(t ) u -
I m cos(t i )
1、振幅Im 2、角频率ω
i(t ) I m cos(t i )
i
Im 2π π 2π ωt
正弦量在整个振荡过程中达到的最大值
反映正弦量变化的快慢 ω =d(ωt+ )/dt 单位时间内变化的角度, 单位:rad/s ωT=2π,ω=2πf , f=1/T 频率f :每秒钟完成循环的次数， 单位为赫兹（Hz） 周期T :完成一个循环变化所需 的时间,单位为秒（s）
接下来…… i(t)=Imcos( t + )
(a) 角频率 ( )
所有电压电流均以相 同角频率ω变化!!
(b) 幅值 (Im)
(c) 初相角( )
用什么可以同时表示幅 值和相位？
chapter相量法电路原理实用
XC
w 0(直流), XC , 隔直作用;
w , XC 0, 旁路作用;
w (3) 由于容抗的存在使电流领先电压。
第23页/共36页
8. 4 电路定律的相量形式和电路的相量模型
一. 基尔霍夫定律的相量形式
i(t) 0 u(t) 0
I 0 U 0
二. 电路元件的相量关系
u Ri
R
相量形式：
I Iy
U R RIy I
相量关系
+
U R R I
U R
-
有效值关系：UR = RI
相位关系：u , i 同相
I
R
U
相量图
相量模型
第19页/共36页
二 . 电感
i(t)
+
u (t)
L
-
时域模型
时域
频域
i(t) 2I sinwt u(t ) L di(t )
dt
2wL I cos wt 2wL I sin(wt 90o )
|Z| X
j
R 阻抗三角形
第29页/共36页
具体分析一下 R-L-C 串联电路 Z=R+j(w L-1/w C)=|Z|∠j
w L > 1/w C ，X>0， j >0，电压领先电流，电路呈感性； w L<1/w C ，X<0， j <0，电压落后电流，电路呈容性； w L=1/w C ，X=0， j =0，电压与电流同相，电路呈电阻性。
2
•
U
2
e
jw
t
)
u(t) u1(t) u2(t) Im(
2
•
U
1
e
《电路原理》第8章 相量法
i 2 Icos(w t Ψ ) F (t ) 2 Ie
返 回
j( w t Ψ )
上 页
下 页
F(t) 还可以写成
复常数
F (t )
2 Ie e
jy
jwt
e jwt 2I
F(t) 包含了三要素：I、 、w， 正弦量对 复常数包含了两个要素：I , 。 应的相量
i(t ) 2I cos(w t Ψ ) I IΨ
180.2 j126.2 2.238 j6.329
182.5 j132.5 225.536
返 回
上 页
下 页
③旋转因子 复数
ej =cos +jsin =1∠
Im F• ej
F• ej
旋转因子 0
F Re
由复数的乘除运算得任意复数F乘或除复数ej ， 相当于 F 逆时针或顺时针旋转一个角度θ，而模不 变，故把 ej称为旋转因子。
Im
F1+F2
F2
F1 o 图解法 Re o
F1 Re
-F2 F1-F2
返 回 上 页 下 页
②乘除运算 —— 采用极坐标式 若 则:
F1=|F1| 1 ，F2=|F2| 2
F1 F2 F1 e F2 e
j1
j 2
F1 F2 e
jθ1
j(1 2 )
F1 F2 1 2
第8章
相量法
本章重点
8.1 8.2 8.3 8.4 复数 正弦量 相量法的基础
电路定律的相量形式
首页
重点：
1. 正弦量的表示、相位差 2. 正弦量的相量表示 3. 电路定律的相量形式
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
yy A 1A 2A 1A 212
3. 旋转因子
复数 ejy = cos y + jsin பைடு நூலகம் = 1∠y
Aejy
A逆时针旋转一个角度y ，模不变
j
e2 cosjsinj
ej( 2)c 2 o 2 s) 2 (js i 2 n) (j
j I
Im
I
Im A (t)[ ] 2Isiw n t (y)
wy i2 I sit n) ( A ( t)2 I e jw t ( y )
A(t)还可以写成
A(t) 2Iejyejwt 2 I ejwt
复常数
称
I Iy
为正弦量 i(t) 对应的相量。
i(t)2Isiw n t (y) II y
旋转相量在纵轴上的投影就是正弦函数
请看演示
三. 相量图
ωy y i(t)2 I sitn i() I I i
wy y u (t)2 U sitn u ( ) U U u
U
I
yu yi
四. 相量运算
(1) 同频率正弦量相加减
u1(t) 2U1s iw nt (y1)Im2(U 1ejwt)
(2) 角频率(angular frequency) w
(3) 初相位(initial phase angle) y
i i(t)=Imsin(w t+y)
Im
wt
y
波形图
ii
000 0 0
t
yy y =0y =/2 y =-/2
一般 |y |
二、同频率正弦量的相位差 (phase difference)。
u2(t) 2U2s iw nt (y2)Im2(U 2ejwt)
u (t)u 1(t)u 2(t)Im 2U (1ejwt)Im 2U (2ejwt)
Im2(U 1ejwt2U 2ejwt)Im2((U 1U 2)ejwt)
得：
U U1U2
U
这实际上是一种变换思想，由时域变换到频域
T0
wy wy T s2 ( it n ) d t T 1 c2 ( o t s ) d t 1 tT 1 T
0
0
2
20 2
I
T1Im 2 T2
Im 2
0.70I7m
Im 2I
注意:只适用正弦量
wy wy i( t) I m sitn ) ( 2 I sitn ) (
e j( ) co )s js ( i n ) (1
0
Re
+j , –j , -1 都可以看成旋转因子。
I
jI
二. 正弦量的相量表示
复函数
A(t) 2Iej(wty)
2 I co w t s y( ) j2 I siw tn y ()
若对A(t)取虚部：
U1 630o V
u2(t)4 2sin3(1t460o)V
U2 460o V
U U 1 U 2 6 3 0 4 6 0 5.19 j6 32j3.464
7.196j6.46 49.6 74.1 9oV
8. 2正弦量的相量表示
两个正弦量
i1
i2
w
w
Im1
Im2
y1
y2
一、复数及运算
1. 复数A表示形式： Im b
A
0
a Re
Aa jb
i1+ i2 i 3
w
Im3
y3
Im
b
A
|A|
y
0
a Re
AAejy|A| y
2. 复数运算 (1)加减运算——直角坐标 (2) 乘除运算——极坐标
A1±A2=(a1±a2)+j(b1±b2)
设 u(t)=Umsin(w t+y u), i(t)=Imsin(w t+y i) 相位差 j = (w t+y u)- (w t+y i)= y u-y i j >0， u 领先(超前)i ，或i 落后(滞后) u
j <0， i 领先(超前) u，或u 落后(滞后) i
u, i u i
0
wt
yu yi
相量的模表示正弦量的有效值 正弦量的相量表示: 相量的幅角表示正弦量的初相位
u (t)2U siw n ty () U U y
例1. 已知 i 14.41s in3(1t430o)A u311.11si4nt6(30o)V
试用相量表示 i, u 。
解：
I
10030o
A
U 220 60o V
i1 i2 = i3
时域
I1 I2 I3 频域
时域：在变量是时间函数条件下研究网络，以时间为自 变量分析电路。
频域：在变量经过适当变换的条件下研究网络，以频率为 自变量分析电路。
向量法：将正弦时间函数 “变换” 为相量后再进行分析, 属于频域分析。
例 u1(t)6 2sin3(1t430) V
例2.
已知 I5 015 oA,f 50H . z
试写出电流的瞬时值表达式。
解： i502si3 n1 (t 41o5 )A
相量的几何意义
I I y i(t)2 Isiw n t y ()
y I I A (t)2I ejw t
A(t)是旋转相量
相量 旋转因子
def
I
1 Ti2(t)dt
T0
有效值也称方均根值 (root-meen-square， 简记为 rms。)
电压有效值
def
U
1
T u2(t)dt
T0
2. 正弦电流、电压的有效值
设 i(t)=Imsin(w t + y )
I T 10TIm 2si2n(wty)dt
def
I
1 Ti2(t)dt
第8章 相量法
重点：
相位差 正弦量的相量表示 复阻抗复导纳 相量图 用相量法分析正弦稳态电路 正弦交流电路中的功率分析
8. 1 正弦量的基本概念
一. 正弦量的三要素： i + u_
i(t)=Imsin(w t +y )
(1) 幅值 (amplitude) (振幅、 最大值) Im
j
特殊相位关系：
j = 0， 同相：
u, i
u
i
0
wt
j = ( 180o ) ，反相：
u, i
i
u
0
wt
u, i u i
0
j = 90°
u 领先 i 90°
wt
或 i 落后 u 90°
规定： | j | (180°)
三. 有效值(effective value)
1. 定义
3. 旋转因子
复数 ejy = cos y + jsin பைடு நூலகம் = 1∠y
Aejy
A逆时针旋转一个角度y ，模不变
j
e2 cosjsinj
ej( 2)c 2 o 2 s) 2 (js i 2 n) (j
j I
Im
I
Im A (t)[ ] 2Isiw n t (y)
wy i2 I sit n) ( A ( t)2 I e jw t ( y )
A(t)还可以写成
A(t) 2Iejyejwt 2 I ejwt
复常数
称
I Iy
为正弦量 i(t) 对应的相量。
i(t)2Isiw n t (y) II y
旋转相量在纵轴上的投影就是正弦函数
请看演示
三. 相量图
ωy y i(t)2 I sitn i() I I i
wy y u (t)2 U sitn u ( ) U U u
U
I
yu yi
四. 相量运算
(1) 同频率正弦量相加减
u1(t) 2U1s iw nt (y1)Im2(U 1ejwt)
(2) 角频率(angular frequency) w
(3) 初相位(initial phase angle) y
i i(t)=Imsin(w t+y)
Im
wt
y
波形图
ii
000 0 0
t
yy y =0y =/2 y =-/2
一般 |y |
二、同频率正弦量的相位差 (phase difference)。
u2(t) 2U2s iw nt (y2)Im2(U 2ejwt)
u (t)u 1(t)u 2(t)Im 2U (1ejwt)Im 2U (2ejwt)
Im2(U 1ejwt2U 2ejwt)Im2((U 1U 2)ejwt)
得：
U U1U2
U
这实际上是一种变换思想，由时域变换到频域
T0
wy wy T s2 ( it n ) d t T 1 c2 ( o t s ) d t 1 tT 1 T
0
0
2
20 2
I
T1Im 2 T2
Im 2
0.70I7m
Im 2I
注意:只适用正弦量
wy wy i( t) I m sitn ) ( 2 I sitn ) (
e j( ) co )s js ( i n ) (1
0
Re
+j , –j , -1 都可以看成旋转因子。
I
jI
二. 正弦量的相量表示
复函数
A(t) 2Iej(wty)
2 I co w t s y( ) j2 I siw tn y ()
若对A(t)取虚部：
U1 630o V
u2(t)4 2sin3(1t460o)V
U2 460o V
U U 1 U 2 6 3 0 4 6 0 5.19 j6 32j3.464
7.196j6.46 49.6 74.1 9oV
8. 2正弦量的相量表示
两个正弦量
i1
i2
w
w
Im1
Im2
y1
y2
一、复数及运算
1. 复数A表示形式： Im b
A
0
a Re
Aa jb
i1+ i2 i 3
w
Im3
y3
Im
b
A
|A|
y
0
a Re
AAejy|A| y
2. 复数运算 (1)加减运算——直角坐标 (2) 乘除运算——极坐标
A1±A2=(a1±a2)+j(b1±b2)
设 u(t)=Umsin(w t+y u), i(t)=Imsin(w t+y i) 相位差 j = (w t+y u)- (w t+y i)= y u-y i j >0， u 领先(超前)i ，或i 落后(滞后) u
j <0， i 领先(超前) u，或u 落后(滞后) i
u, i u i
0
wt
yu yi
相量的模表示正弦量的有效值 正弦量的相量表示: 相量的幅角表示正弦量的初相位
u (t)2U siw n ty () U U y
例1. 已知 i 14.41s in3(1t430o)A u311.11si4nt6(30o)V
试用相量表示 i, u 。
解：
I
10030o
A
U 220 60o V
i1 i2 = i3
时域
I1 I2 I3 频域
时域：在变量是时间函数条件下研究网络，以时间为自 变量分析电路。
频域：在变量经过适当变换的条件下研究网络，以频率为 自变量分析电路。
向量法：将正弦时间函数 “变换” 为相量后再进行分析, 属于频域分析。
例 u1(t)6 2sin3(1t430) V
例2.
已知 I5 015 oA,f 50H . z
试写出电流的瞬时值表达式。
解： i502si3 n1 (t 41o5 )A
相量的几何意义
I I y i(t)2 Isiw n t y ()
y I I A (t)2I ejw t
A(t)是旋转相量
相量 旋转因子
def
I
1 Ti2(t)dt
T0
有效值也称方均根值 (root-meen-square， 简记为 rms。)
电压有效值
def
U
1
T u2(t)dt
T0
2. 正弦电流、电压的有效值
设 i(t)=Imsin(w t + y )
I T 10TIm 2si2n(wty)dt
def
I
1 Ti2(t)dt
第8章 相量法
重点：
相位差 正弦量的相量表示 复阻抗复导纳 相量图 用相量法分析正弦稳态电路 正弦交流电路中的功率分析
8. 1 正弦量的基本概念
一. 正弦量的三要素： i + u_
i(t)=Imsin(w t +y )
(1) 幅值 (amplitude) (振幅、 最大值) Im
j
特殊相位关系：
j = 0， 同相：
u, i
u
i
0
wt
j = ( 180o ) ，反相：
u, i
i
u
0
wt
u, i u i
0
j = 90°
u 领先 i 90°
wt
或 i 落后 u 90°
规定： | j | (180°)
三. 有效值(effective value)
1. 定义