截面的静矩和形心位置及惯性矩的计算参考文档
材料力学第六章 截面的几何性质惯性矩
IP
2dA
A
(y2
A
z2 )dA
IZ
Iy.
返回 下一张 上一张 小结
第三节 惯性矩和惯性积的 y1dA (y a)2 dA A
y2dA 2a ydA a2 dA
I z1 z a2 A; y1 y b2 A;
2dA
A
(y2
A
z2 )dA
IZ
Iy.
Izy
z y dA;
A
五、平行移轴公式:
I z1 z a2 A; y1 y b2 A;
I z1y1 I zy abA;
返回 下一张 上一张 小结
六、主惯性轴和主惯性矩: 主惯性轴(主轴)—使 I zoyo 0 的这对正交坐标轴; 主惯性矩(主惯矩)—截面对主惯性轴的惯性矩; 形心主惯性轴(形心主轴)—通过形心的主惯性轴; 形心主惯性矩(形心主惯矩)—截面对形心主轴的惯性矩。
I z1y1 I zy abA;
注意: y、z轴必须是形心轴。
二、转轴公式:
Iz1
A y12dA
( y cos z sin)2 dA;
A
I z1
Iz
Iy 2
Iz
Iy 2
cos 2
I zy
sin 2;
I y1
Iz
2
Iy
Iz
2
Iy
cos 2
I zy
sin 2;
I z1y1
Iz
Iy 2
三、惯性积:
定义:平面图形内, 微面积dA与其两个坐 标z、y的乘积zydA在整个图形内的积分称为 该图形对z、y轴的惯性积。
Izy
z y dA;
A
特点: ①惯性积是截面对某两个正交
惯性矩、静矩,形心坐标公式
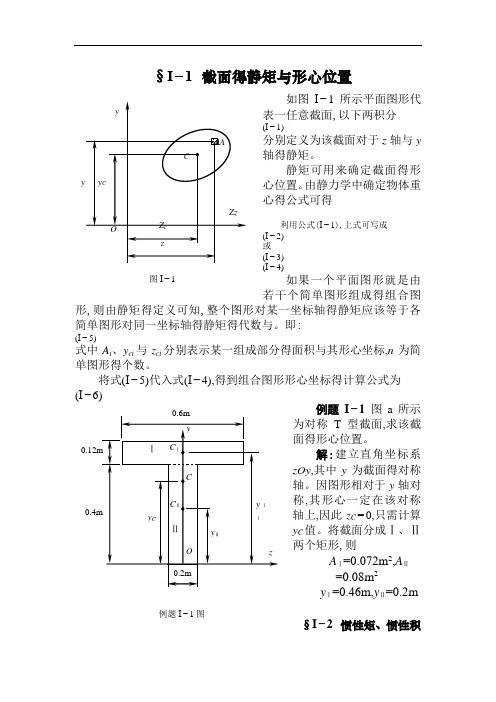
§I−1 截面得静矩与形心位置如图I −1所示平面图形代表一任意截面,以下两积分(I −1)分别定义为该截面对于z 轴与y 轴得静矩。
静矩可用来确定截面得形心位置。
由静力学中确定物体重心得公式可得利用公式(I −1),上式可写成 (I −2) 或 (I −3) (I −4)如果一个平面图形就是由若干个简单图形组成得组合图形,则由静矩得定义可知,整个图形对某一坐标轴得静矩应该等于各简单图形对同一坐标轴得静矩得代数与。
即:(I −5)式中A i 、y ci 与z ci 分别表示某一组成部分得面积与其形心坐标,n 为简单图形得个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标得计算公式为 (I −6)例题I −1 图a 所示为对称T 型截面,求该截面得形心位置。
解:建立直角坐标系zOy ,其中y 为截面得对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则 A Ⅰ=0.072m 2,A Ⅱ=0.08m 2y Ⅰ=0.46m,y Ⅱ=0.2m§I −2 惯性矩、惯性积例题I −1图图I −1与极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
现在图形内取微面积d A ,d A 得形心在坐标系zOy 中得坐标为y 与z ,到坐标原点得距离为ρ。
现定义y 2d A 与z 2d A 为微面积d A 对z 轴与y 轴得惯性矩,ρ2d A 为微面积d A 对坐标原点得极惯性矩,而以下三个积分(I −7)分别定义为该截面对于z 轴与y 轴得惯性矩以及对坐标原点得极惯性矩。
由图(I −2)可见,,所以有(I −8) 即任意截面对一点得极惯性矩,等于截面对以该点为原点得两任意正交坐标轴得惯性矩之与。
另外,微面积d A 与它到两轴距离得乘积zy d A 称为微面积d A 对y 、z 轴得惯性积,而积分(I −9)定义为该截面对于y 、z 轴得惯性积。
惯性矩地计算方法及常用截面惯性矩计算公式

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:(一).截面静矩和形心1•静矩的定义式如图1所示任意有限平面图形,取其单元如面积dA,定义它对任意轴的一次矩为它对该轴的静矩,即dS y xdAdSx ydA整个图形对y、z轴的静矩分别为S y xdAyASx 人 ydA2.形心与静矩关系(1-1 )设平面图形形心C的坐标为y c,z c-S x 一S y /、y , x (I-2 )A A推论1如果y轴通过形心(即x0),则静矩S y 0 ;同理,如果X轴通过形心(即y o),则静矩sx o;反之也成立。
推论2如果x、y轴均为图形的对称轴,则其交点即为图形形心;如果y轴为图形对称轴,贝昭形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为 A,A2,A3 A n的简单图形组成,且一直各族图形的形心坐标分别为丘,只;乂2*2;x3,y3 ,贝U图形对y轴和x轴的静矩分别为截面图形的形心坐标为nA i Xi 1 nA ii 14•静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2) 静矩有的单位为m 3。
(3) 静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定 为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式(1-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(1-2 )求图形的形心坐标。
组 合图形的形心位置,通常是先由式(I-3 )求出图形对某一坐标系的静 矩,然后由式(1-4 )求出其形心坐标。
(二)•惯性矩 惯性积 惯性半径1.惯性矩定义 设任意形状的截面图形的面积为 A (图I-3 ),则图形对0点的极 惯性矩定义为 I p2dA (1-5)KAn nS yS yiARi 1 i 1nnS xSxiA i Vi 1 i 1(1-3 )A i y i(1-4 )图形对y轴和x轴的光性矩分别定义为I y A x2dA , I x A y2dA (1-6)惯性矩的特征(1)界面图形的极惯性矩是对某一极点定义的;轴惯性矩是对某一坐标轴定义的。
材料力学 截面的几何性质

1、矩形截面 h
Iz
y2dA
A
2 h
y 2bdy
h
2
dy y
b y 3 2 1 bh3 3 h 12
2
同理
Iy
z2dA 1
A
12
hb3
b h z
y
26
2、实心圆截面
y
已知
IP
A2dA
D 4 32
D
z
则 I P A2 d A A y 2 d A A z 2 d I A z I y
A
Iz Iy
此式说明了极惯性矩与轴惯性矩之间的关系。
z
y
o
A dA
z
y
惯性积
定义
Iyz
yzdA
A
z y
A dA
为图形对y、z轴的惯性积 。
z
o
y
惯性积的数值可正,可负,也可为零。惯性积的量纲是[长 度]4 ,常用单位为m4和mm4。
定理:若有一个轴是图形的对称轴,则图形对这对轴 的惯性积必然为零。
4.3 形心主惯性轴和形心主惯性矩
若主惯性轴通过形心,则该轴称为形心主惯性轴(principal centroidal axis)。
图形对形心主惯性轴的惯性矩称为形心主惯性矩。 由于图形对于对称轴的惯性积等于零,而对称轴又过形心,所以,图形 的对称轴就是形心主惯性轴。
形心主惯性轴的特点可归纳为以下几点: ⑴形心主惯性轴是通过形心,由角定向的一对互 相垂直的坐标轴。
32
32
圆环形对y(或z)轴的惯性矩为
IyIz1 2Ip6 D4414
由于y轴为对称轴,故
Iyz 0
z
y
d D
截面的静矩和形心位及惯性矩的计算
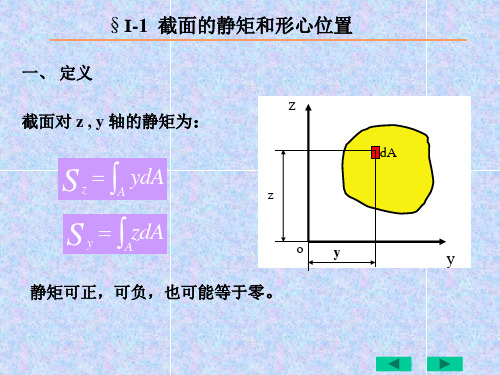
y
dA
x
x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
20 140
zc
20
1
yc
ZC
2
y
100
I1yC
1 12
20 1403
20 140
(8046.7)2
I
2 yC
1 12
100
203
100
20
(46.7)2
zc
120 103 152 120 10
1 12
703
10
(25)2
70
10
100.4 104 mm 4
Iy 278.4 104 mm4
70 20 10
120
y
80
c
x
10
y
I xy 0 15 20 120 10 0 (25) (35) 70 10
x2
10
70 2
45mm
y2 5mm
y 10
1 x1
y1
惯性矩的计算方法及常用截面惯性矩计算公式

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形,取其单元如面积dA ,定义它对任意轴的一次矩为它对该轴的静矩,即ydAdSx xdA dS y ==整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS (I-1)2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0AS y x=, A S x y = (I-2)推论1 如果y 轴通过形心(即0=x ),则静矩0=y S ;同理,如果x 轴通过形心(即0=y ),则静矩0=Sx ;反之也成立。
推论2 如果x 、y 轴均为图形的对称轴,则其交点即为图形形心;如果y 轴为图形对称轴,则图形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成,且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ;;,则图形对y 轴和x 轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii n i yi y y A S S x A S 1111S (I-3)截面图形的形心坐标为∑∑===ni ini ii AxA x 11 , ∑∑===ni ini ii AyA y 11 (I-4)4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2) 静矩有的单位为3m 。
(3) 静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式(I-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(I-2)求图形的形心坐标。
组合图形的形心位置,通常是先由式(I-3)求出图形对某一坐标系的静矩,然后由式(I-4)求出其形心坐标。
截面的静矩和形心位置及惯性矩的计算

x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Iy , A
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
I xy cos 2α
主惯性轴 —— 总可以找到一个特定的角 0 , 使截面对新坐标 轴 x0 , y0 的惯性积等于 0 , 则称 x0 , y0 为主惯轴。
主惯性矩——截面对主惯性轴的惯性矩。
形心主惯性轴 ——当一对主惯性轴的交点与截面的形心 重合时,则称为形心主惯性轴。
x
80
§ І -2 极惯性矩 惯性矩 惯性积
定义:
z dA
z
截面对 o 点的极惯性矩为
y
Ip Aρ2dA
y 0
截面对 y ,z 轴的惯性矩分别为
Iy A z2dA Iz A y2dA
因为 ρ2 y2 z2
I p Aρ2 dA
所以 Ip = Ix + Iy
y
y
dA
ix
Ix A
例 2 _ 1 求矩形截面对其对称轴 x , y 轴的惯性矩。
解:
dA = b dy
Ix
A y2dA
h
2h
by2dy
2
bh3 12
Ix A y2dA
截面的几何性质
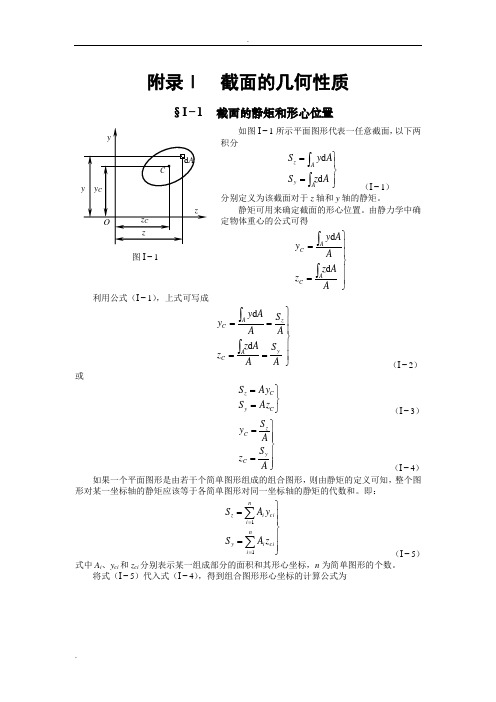
附录Ⅰ 截面的几何性质§I −1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面,以下两积分⎪⎭⎪⎬⎫==⎰⎰A z S A y S A y Az d d (I −1) 分别定义为该截面对于z 轴和y 轴的静矩。
静矩可用来确定截面的形心位置。
由静力学中确定物体重心的公式可得⎪⎪⎭⎪⎪⎬⎫==⎰⎰A A z z A A y y AC ACd d利用公式(I −1),上式可写成⎪⎪⎭⎪⎪⎬⎫====⎰⎰A S A A z z A S A Ay y y AC z AC d d (I −2) 或⎭⎬⎫==C y C z Az S Ay S (I −3)⎪⎪⎭⎪⎪⎬⎫==A S z A S y y C z C (I −4)如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。
即:⎪⎪⎭⎪⎪⎬⎫==∑∑==ni ci i y ni ci i z z A S y A S 11(I −5)式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。
将式(I −5)代入式(I −4),得到组合图形形心坐标的计算公式为图I −1⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫==∑∑∑∑====n i i ni ci i c ni i ni ci i c A z A z A y A y 1111(I −6) 例题I −1 图a 所示为对称T 型截面,求该截面的形心位置。
解:建立直角坐标系zOy ,其中y 为截面的对称轴。
因图形相对于y 轴对称,其形心一定在该对称轴上,因此z C =0,只需计算y C 值。
将截面分成Ⅰ、Ⅱ两个矩形,则A Ⅰ=0.072m 2,A Ⅱ=0.08m 2 y Ⅰ=0.46m ,y Ⅱ=0.2m m323.008.0072.02.008.046.0072.0III IIII I I 11=+⨯+⨯=++==∑∑==A A y A y A AyA y ni ini cii c§I −2 惯性矩、惯性积和极惯性矩如图I −2所示平面图形代表一任意截面,在图形平面内建立直角坐标系zOy 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则平行移轴公式为
y
yc
I x I xc a2 A
Iy Iyc b2 A
I xy I xcyc abA
a
C(a,b)
xc
ob
x
16
二、组合截面的惯性矩 惯性积
Ixi , Iyi , Ixyi —— 第 i个简单截面对 x ,y 轴的惯性矩、
§І-1 截面的静矩和形心位置
一、 定义
z
截面对 z , y 轴的静矩为:
dA
S z A ydA
z
S y AzdA
oy
y
静矩可正,可负,也可能等于零。
1
截面的形心 C 的坐标
公式为:
y A ydA S z
A
A
z
z
z
dA
c
z AzdA S y
o
y
y
A
A
y
Sz Ay
S y Az
若截面对某一轴的静矩等于零,则该轴必过形心。
22
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
I xy cos 2α
主惯性轴 —— 总可以找到一个特定的角 0 , 使截面对新坐标 轴 x0 , y0 的惯性积等于 0 , 则称 x0 , y0 为主惯轴。
主惯性矩——截面对主惯性轴的惯性矩。
23
形心主惯性轴 ——当一对主惯性轴的交点与截面的形心 重合时,则称为形心主惯性轴。
2h 2
b y2d y
bh3 12
Ix A y2dA
y
Iy
h b3 12
dy
h
y
C
x
b
13
例 2 - 2 求圆形截面对其对称轴的惯性矩 。
解:因为截面对其圆心 O 的
极惯性矩为 y
Iρ
π d4 32
Ix Iy Iρ
x
Ix Iy
所以
Ix
Iy
π d4 64
14
§ І -3 惯性矩和惯性积的平行移轴公式 组合截面的惯性矩和惯性积
y 0
9
截面对 y ,z 轴的惯性矩分别为
Iy A z2dA Iz A y2dA
因为 ρ2 y2 z2
I p Aρ2 dA
所以 Ip = Ix + Iy
y
y
dA
x
x 0
10
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
一、 平行移轴公式
y x , y ——任意一对坐标轴
C —— 截面形心
a
(a , b ) _____ 形心 c 在 xoy 坐标系下的
坐标。
o
xc , yc ——过截面的形心 c 且与 x , y 轴平 行的坐 标轴(形心轴)
yc
C(a,b)
xc
b
x
15
Ix , Iy , Ixy _____ 截面对 x , y 轴的惯性矩和惯性积。
20 140
zc
20
1
yc
2
y
100
18
A1 20 140 A2 100 20
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
20 140
zc
20
1
yc
ZC
2
y
100
19
I1yC
1 12
20
1403
20
140
(80
46.7)2
I
2 yC
1 12
y y1
逆時针转取为 + 号,
x1
顺時针转取为 – 号
o
x
21
I x1
Ix
Iy 2
Ix
2
Iy
cos 2α
I xy
sin 2α
I y1
Ix
Iy 2
Ix
2
Iy
cos 2α
I xy
sin 2α
I x1 y1
Ix
2
Iy
sin 2α
I xy
cos 2αy Leabharlann 1ox1x
上式称为转轴公式 显然
I x1 I y1 I x I y
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
11
截面对 x , y 轴的惯性半俓为
iy
Iy , A
ix
Ix A
12
例 2 _ 1 求矩形截面对其对称轴 x , y 轴的惯性矩。
解:
dA = b dy
Ix
A
y2d A
h
x
A1 x1 A 2 x2 A1 A2
37500 1900
20mm
y
A1 y1 A1
A2 y2 A2
75500 1900
40mm
y 10
1 x1
C(y, x)
y1
2 y2
10
o x2
x
80
8
§ І -2 极惯性矩 惯性矩 惯性积
定义:
z dA
z
截面对 o 点的极惯性矩为
y
Ip Aρ2dA
i1
y A1 y1 A2 y2 A1 A2
x1 1
y1
o x2
80
y2
2 10 x
6
矩形 1
A1 10 120 1200mm2
x1 5mm
y1 60mm
矩形 2
A2 10 70 700mm2
x2
10
70 2
45m
m
y2 5mm
y 10
1 x1
y1
o
2 y2
10
x2
x
80
7
所以
100
203
100
20
(46.7)2
zc
20
IyC
I1yC
I
2 yC
12.12 106
m4
1
yc
ZC
2
20 140
y
100
20
§ І -4 惯性矩和惯性积的转轴公式 截面的主惯性轴和主惯性矩
一、 转轴公式
xoy 为过截面上的任 – 点建立的坐标系 x1oy1 为 xoy 转过 角后形成的新坐标系
4
计算组合截面形心坐标的公式如下:
n
Ai
y i
y
i 1 n
Ai
i 1
n
Ai zi
z
i 1 n
Ai
i 1
5
例 1-1 试确定图示截面心 C 的位置。
解:将截面分为 1,2 两个矩形。
y 10
取 x 轴和 y 轴分别与截面 的底边和左边缘重合
n
x
Ai xi
i1 n
Ai
A1 x1 A1
A2 x2 A2
形心主惯性矩—— 截面对形心主惯性轴的惯性矩。
24
主惯性轴的位置:设 为主惯性轴与原坐标轴 之间的夹角,
则有 由此
I I x I y 2 sin 2 0 xy cos 2 0 0
tg 20
2Ixy
惯性积。
组合截面的惯性矩,惯性积
n
I x I xi i1
n
I y I yi i1
n
I xy I xyi i 1
17
例 3 -1 求梯形截面对其形心轴 yc 的惯性矩。
解:将截面分成两个矩形截面。
截面的形心必在对称轴 zc 上。 取过矩形 2 的形心且平行 于底边的轴作为参考轴, 记作 y 轴 。
截面对形心轴的静矩等于零。 2
二 、 组合截面 由几个简单图形组成的截面称为组合截面
截面各组成部分对于某一轴的静矩之代数和,就等于该截 面对于同一轴的静矩。
3
组合截面静矩的计算公式为
n
S
z
Ai
y i
i1
n
S y Ai zi i1
其中: Ai —— 第 i 个简单截面面积
(
y, i
z
i
)
——
第 i个简单截面的形心坐标
